1 Introduction

The standard theory of gravitational field known as general relativity (GR) was introduced by Albert Einstein in 1915. GR as gravitational field theory has been successfully tested in both weak and strong field regimes [1,2,3,4]. However, GR meets several fundamental problems which cannot be resolved within the basic principles of the theory. One of the above-mentioned problems is the existence of the singularity at the origin of most general relativistic solutions. On the other hand, the current resolutions of experiments and observations leave open the window for the development of alternative/modified theories of gravity, which can be further used to resolve the fundamental open issues of gravitational interaction.

One of the possible ways of extension of GR is to consider the low energy limit of string theory, where one may introduce the dilaton scalar field. This field will be included in the action as an additional supplement term to the Einstein–Hilbert action and has the form of the axion, gauge fields, and another non-trivial coupling of dilaton to fields. Particularly, some aspects of such combination like the causal structures and thermodynamic properties of black hole (BH) solution with dilaton have been investigated in Refs. [5,6,7,8,9,10,11,12,13]. Further, one may extend the black hole solution using the cosmological constant. The models with the presence of negative cosmological constants are prominent candidates for gravity theories defined in higher dimensions. Detailed analysis of these models and corresponding solutions can be found in Refs. [14,15,16,17,18,19]. One may also consider the heterotic string theory, where the scalar dilaton field is coupled to the electromagnetic field tensor [6]. Here, we plan to study the properties of the black hole solution within the Einstein–Maxwell-scalar (EMS) field theory using the dynamics of test particles.

The tests of the field theories based on the observations of compact objects allow us to get the constraints on the field parameters. Particularly, the modified and alternative theories of gravity and corresponding solutions describing the compact objects have been successfully tested using X-ray data from astrophysical objects by the Authors of Refs. [20,21,22]. One may also develop the tests of the general relativity and other models of gravitational interaction based on the test particle motion [23, 24].

One of the interesting features of the dynamics of test particles appears with the analysis of circular/bound orbits around compact objects. Particularly, circular orbits of test particles may lead to the phenomenon observed as quasi-periodic oscillations (QPOs) in astrophysics. QPOs are objects observed in the X-ray band from microquasars representing BH surrounded by matter flowing and a companion star. QPO has been first detected by analyzing the power spectra of the flux from X-ray binary pulsars [25]. After that pioneering discovery, a big number of works have been dedicated to studying of QPOs and corresponding models. Among a big number of models proposed to describe the behavior of the origin and nature of QPOs those models based on particle motion are the most promising. According to these models, the innermost stable circular orbits of test particles determine the frequencies of the QPOs. Thus, the investigations of QPOs using models based on circular orbits of test particles may lead to the test of gravity theories in the strong field regime. Particularly, the current high resolution of the observations of QPOs frequencies allows us to test the models of gravity and corresponding solutions and get the constraints on field parameters. Depending on the value of the frequencies, one may distinguish two types of QPOs: low frequency (up to 30 Hz, LF QPOs) and high frequency (up to 500 Hz, HF QPOs). A big number of works are devoted to studying the models where QPOs are considered as a result of the collective motion of particles in the accretion disk of different type [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. These models can be further used to develop a new test of EMS theory, and here we plan to explore this possibility.

Here we plan to study the spacetime properties as well as neutral particle dynamics around BH within EMS gravity. The paper has organized as follows: Sect. 2 is devoted to studying the spacetime properties of curvature scalars. Then in Sect. 3 we investigate the massive test particle motion around the compact object. We discuss the fundamental frequencies and their application to QPOs in Sect. 4. In Sect. 5 we study the quasi-periodic oscillations of circular orbits of the particles around BH in EMS gravity. Using the observation data on QPO objects, we obtained constraints on parameters of EMS gravity in Sect. 6. We conclude and summarize the obtained results of the paper in Sect. 7. Our study in this paper uses a space-like signature (−, +, +, +) for the spacetime and geometrized unit of the system where \(G = c = 1\). Latin (Greek) indices run from 1 (0) to 3.

2 Black holes in Einstein–Maxwell-scalar theory

We start with a brief review of BH solutions in EMS theory described by the action [5, 6, 43]

$$\begin{aligned} S=\int d^4x\sqrt{-g}\Big [R-2\nabla _{\alpha }\phi \nabla ^{\alpha }\phi -K(\phi ) F_{\alpha \beta }F^{\alpha \beta } \Big ], \end{aligned}$$

where \(\nabla _{\alpha }\) is the covariant derivative, g is the determinant of the metric tensor \(g_{\mu \nu }\), R is the Ricci scalar of the curvature, \(\phi \) is the massless scalar field, \(F_{\alpha \beta }\) is the electromagnetic field tensor, \(K(\phi )\) is the coupling function between the dilaton and the electromagnetic fields.

The exact analytical solutions for spacetime around the static black hole in general form have been found in Ref. [43] in the following form,

$$\begin{aligned} ds^2=-U(r)dt^2+\frac{dr^2}{U(r)}+f(r)\left( d\theta ^2+\sin ^2\theta d\varphi ^2\right) , \end{aligned}$$
(1)

where U(r) and f(r) are radial functions. In Ref. [43] Authors have used the following special forms for the function \(K(\phi )\)

$$\begin{aligned} K(\phi )=\frac{2e^{2\phi }}{\beta e^{4\phi }+\beta -2\gamma }, \end{aligned}$$
(2)

and obtained the solution in the form

$$\begin{aligned}{} & {} f(r)=r^2\left( 1+\frac{\gamma Q^2}{Mr}\right) , \nonumber \\{} & {} U(r)=1-\frac{2M}{r}+\frac{\beta Q^2}{f(r)}. \end{aligned}$$
(3)

It is worth noting that it has been assumed that the vector and the dilaton fields depend on the radial coordinate only as [43]

$$\begin{aligned}{} & {} A_t(r)=\frac{Q}{r}\left[ \gamma -\frac{\beta }{2}\left( 1+\frac{r^2}{f(r)}\right) \right] , \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \phi (r)=-\frac{1}{2}\ln \left( \frac{f(r)}{r^2}\right) . \end{aligned}$$
(5)

The spacetime metric (1) with the metric functions (3) turns to Schwarzschild solution when \(\beta =0\) and/or \(Q=0\), also it covers the Reissner–Nordström (RN) one when \(\gamma =0\) and \(\beta =1\).

Fig. 1
figure 1

The radius of the event horizon as a function of \(\gamma \) parameter for the different values of \(\beta \)

Full size image

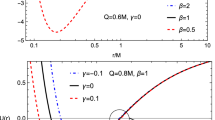
Now, we will analyze the event horizon structure of the spacetime (1) defined by the metric functions (3) using the condition \(U(r)=0\). In Fig. 1 the dependence of event horizons’ from the BH charge at zero (top left panel), positive (top right panel), and negative (bottom panel) values of parameter \(\gamma \) for the different values of the parameter \(\beta \) have been shown. One can easily see that the extreme value of the charge Q corresponding to the merging of the outer and inner (Cauchy) horizons decreases with the increase of the parameter \(\beta \). When \(\gamma =0\) (see top left panel of Fig. 1) when \(\beta =1\) i.e. in the RN limit the extreme charge equals to \(Q_{\textrm{extr}}=M\) where the outer and Cauchy horizons match at \(r=M\), and the minimum value of outer horizon, corresponding to the extreme value of the BH charge, weakly depend on \(\beta \). On the other hand, the positive (negative) values of \(\beta \) cause the increase (decrease) of the minimum value of the outer horizon.

One may set the following simple conditions

$$\begin{aligned} U(r)=U'(r)=0, \end{aligned}$$
(6)

with the aim of detailed analyses of the minimum radius of the outer horizon and extreme values of BH charge. In Fig. 2 we have presented the dependence of extreme values of the BH charge and minimum values of the event outer horizon from the parameter \(\gamma \) in the top left and right panels, respectively, for the fixed values of \(\beta =1/4\) and \(\beta =2\). We have also shown the relationships between the minimum values of the event outer horizon and the extremely charged EMS BH in the bottom panel of Fig. 2 for the different values of the parameter \(\beta \). The shaded areas in the top panels correspond to the set of values of the parameter \(\gamma \) and the BH charge representing BH described by the solution (1). Our numerical analysis shows that there is an extreme value for the parameter \(\gamma \) for all possible values of the parameter \(\beta \). Moreover, the extreme value of the BH charge and the corresponding value of the outer horizon, decrease with the increase of \(\beta \). However, in the case when \(\gamma =0\) minimum value of the event horizon take \(r=M\) for all values of \(\beta \), while extreme charge decrease with the increase of \(\beta \).

Fig. 2
figure 2

Critical values of the BH charge as a function of the parameter \(\gamma \) for the different values of \(\beta \)

Full size image

3 The motion of test particles around BH in EMS theory

The equation of motion of test particles with the rest mass m around a BH can be found using the Lagrangian of from

$$\begin{aligned} L_{\textrm{p}}=\frac{1}{2}m g_{\mu \nu } {\dot{x}}^{\mu } {\dot{x}}^{\nu }. \end{aligned}$$
(7)

The constants of motion read,

$$\begin{aligned} g_{tt}{\dot{t}}=-{{\mathcal {E}}}, \quad g_{\phi \phi }{\dot{\phi }} = {{\mathcal {L}}}, \end{aligned}$$
(8)

where \({{\mathcal {E}}}\) and \({{\mathcal {L}}}\) are the specific energy and angular momentum of the particle, respectively. Equations of motion for a test particle are governed by the normalization condition

$$\begin{aligned} g_{\mu \nu }u^{\mu }u^{\nu }=\epsilon \end{aligned}$$
(9)

where \(\epsilon \) takes the values 0 and \(-1\) for massless and massive particles, respectively.

For test neutral particles with non-zero rest mass, the equation of motion can be governed by time-like geodesics of spacetime. Using the condition (9) together with the Eq. (8) one can easily obtain the equation of motion in the following form [44,45,46]

$$\begin{aligned} {\dot{r}}^2= & {} {{\mathcal {E}}}^2+g_{tt}\left( 1+\frac{{\mathcal {K}}}{r^2}\right) , \end{aligned}$$
(10)
$$\begin{aligned} {\dot{\theta }}^2= & {} \frac{1}{g_{\theta \theta }^2}\Big ({{\mathcal {K}}}- \frac{{{\mathcal {L}}}^2}{\sin ^2\theta }\Big ), \end{aligned}$$
(11)
$$\begin{aligned} {\dot{\phi }}= & {} \frac{{{\mathcal {L}}}}{g_{\phi \phi }}, \end{aligned}$$
(12)
$$\begin{aligned} {\dot{t}}= & {} -\frac{{{\mathcal {E}}}}{g_{tt}}, \end{aligned}$$
(13)

where \({{\mathcal {K}}}\) is the Carter constant corresponding to the total angular momentum of the particle.

Restricting the motion of the particle to a constant plane with \(\theta ={\textrm{const}}\), and \({\dot{\theta }}=0\), and the Carter constant reads as \({{\mathcal {K}}}={{\mathcal {L}}}^2/\sin ^2\theta \). Consequently, one can easily obtain the equation of the radial motion in the standard form

$$\begin{aligned} {\dot{r}}^2={{\mathcal {E}}}^2-V_{\textrm{eff}}, \end{aligned}$$
(14)

where the effective potential of the motion of test particles has the following form

$$\begin{aligned} V_{\textrm{eff}} = U(r) \left( 1 + \frac{{{\mathcal {L}}}^2}{f(r)\sin ^2\theta }\right) . \end{aligned}$$
(15)
Fig. 3
figure 3

Profiles of the effective potential for the radial motion of test particles around charged BHs in EMS gravity for various values of the EMS parameters \(\beta \) and \(\gamma \). In all cases \(Q=M\) except Schw BH

Full size image

The radial dependence of the effective potential for the radial motion of test particles in the spacetime around charged EMS BHs is shown in Fig. 3 for the different values of the parameters of EMS theory \(\beta \) and \(\gamma \). In this figure, we fix the BH charge and angular momentum of the particles as \(Q=M\) and \({{\mathcal {L}}}=4.5M\), respectively, and consider the equatorial plane where \(\theta =\pi /2\). One can see from Fig. 3 that the maximum value of the effective potential decreases with the increase of \(\gamma \) at \(\beta =1\) case. While the increase of \(\beta \) causes the increase of the maximum in the effective potential. This leads to the fact that with the increase of \(\beta \) the radius of circular orbits where the effective potential takes maximum shifts towards the BH.

Now we consider the circular motion of test particles at the equatorial plane \((\theta =\pi /2).\) Circular orbits of the particles can be determined by the following conditions:

$$\begin{aligned} V_{\textrm{eff}}={{\mathcal {E}}}, \quad V_{\textrm{eff}}'=0, \quad V_{\textrm{eff}}'' \ge 0. \end{aligned}$$
(16)

Using the conditions (16) one may easily obtain the expressions for specific angular momentum and energy of the particle corresponding to the circular obits around the charged BHs in EMS gravity in the following form

$$\begin{aligned} {{\mathcal {L}}}^2= & {} \frac{r \left( M r+\gamma Q^2\right) }{{{\mathcal {P}}}(r)}\nonumber \\{} & {} \times {\left[ 2 M^2 r^2-2 M Q^2 r (\beta -2 \gamma )+\gamma Q^4 (2 \gamma -\beta )\right] },\nonumber \\ \end{aligned}$$
(17)
$$\begin{aligned} {{\mathcal {E}}}^2= & {} \frac{2 M r+\gamma Q^2 }{r \left( M r+\gamma Q^2\right) {{\mathcal {P}}}(r) } \nonumber \\{} & {} \times \Big [\gamma Q^2 r-2 M^2 r+M \left( Q^2 (\beta -2 \gamma )+r^2\right) \Big ]^2, \end{aligned}$$
(18)

where

$$\begin{aligned} {{\mathcal {P}}}(r)= & {} 2 M^2 r \left( r^2-3 M r+2 \beta Q^2\right) \\{} & {} +\gamma ^2 Q^4 (r-4 M)+\gamma M Q^2 \left( 3 r^2-10 M r+2 \beta Q^2\right) . \end{aligned}$$
Fig. 4
figure 4

The radial dependence of specific energy (left panel) and angular momentum (right panel) of test particles around EMS BHs for different values of the parameters \(\beta \) and \(\gamma \)

Full size image

The radial dependence of specific energy and specific angular momentum of the test particles at circular orbits around charged BHs in EMS theory are shown in Fig. 4. Here, we have fixed the BH charge as \(Q/M=1/2\). From Fig. 4 one can see that the presence of the BH charge decreases the minimum value of both energy and angular momentum. However, the minimum energy and angular momentum increase with the increase of \(\beta \). On the other hand, the increase of the parameter \(\gamma \) causes an increase in the minimum values of energy and angular momentum.

Figure 5 shows allowed values of the energy and angular momentum for bounded orbits around EMS BHs for the different values of the parameters \(\beta \) and \(\gamma \) and for the fixed value of the BH charge \(Q=M\). One may see from the figure that the particle energy may lie between its maximum and minimum \(({{\mathcal {E}}}_{\textrm{min}} \le {{\mathcal {E}}} \le {{\mathcal {E}}}_{\textrm{max}})\) for a fixed value of the angular momentum at \({{\mathcal {L}}}>{{\mathcal {L}}}_{\textrm{cr}}\), while at \({{\mathcal {L}}}={{\mathcal {L}}}_{\textrm{cr}}\) the maximum and minimum energies equals to each other and takes its critic value which is shown as black dots. The critical values of both energy and angular momentum decrease with the increase of \(\beta \) for the fixed values of \(\gamma \) parameters, while it increases with respect to the increase of \(\gamma \) for fixed \(\beta \).

3.1 Innermost stable circular orbits

The radius of innermost stable circular orbits (ISCO) of test particles can be defined using an additional condition \(V''_{\textrm{eff}} \ge 0\). Using this condition and Eqs. (17) and (18) one may obtain the equation for ISCOs of the form

$$\begin{aligned}{} & {} -12 M^5 r^5+2 M^4 r^4 \left( 3 Q^2 (3 \beta -8 \gamma )+r^2\right) \nonumber \\{} & {} \quad +2 M^3 Q^2 r^3 \left( Q^2 \left( -4 \beta ^2+26 \beta \gamma -38 \gamma ^2\right) +3 \gamma r^2\right) \nonumber \\{} & {} \quad +6 \gamma M^2 Q^4 r^2 \left( \gamma r^2-Q^2 (2 \beta -5 \gamma ) (\beta -2 \gamma )\right) \nonumber \\{} & {} \quad +2 \gamma ^2 M Q^6 r \left( \gamma r^2-3 Q^2 (\beta -2 \gamma )^2\right) \nonumber \\{} & {} \quad +\gamma ^3 Q^{10} \left( -(\beta -2 \gamma )^2\right) =0. \end{aligned}$$
(19)
Fig. 5
figure 5

The dependence of specific angular momentum of the test particles around the BH from its energy at circular orbits. Here the BH charge is taken as \(Q=M\)

Full size image

One may get an analytical solution corresponding to the case when \(\gamma =0\) as

$$\begin{aligned} r_{(\gamma =0)}=2M+\frac{M}{{\textrm{A}}}\left( 4 M^2-3 \beta Q^2\right) +\frac{{\textrm{A}}}{M}, \end{aligned}$$
(20)

where

$$\begin{aligned} {\textrm{A}}= & {} \Big [8 M^6-9 \beta M^4 Q^2+2 \beta ^2 M^2 Q^4+\\{} & {} +\sqrt{\beta ^2 M^4 Q^4 \left( 5 M^4-9 \beta M^2 Q^2+4 \beta ^2 Q^4\right) }\Big ]^{1/3}. \end{aligned}$$
Fig. 6
figure 6

Dependence of ISCO radius from the BH charge for different values of EMS parameters \(\beta \) and \(\gamma \)

Full size image

We have obtained the numerical solution of Eq. (19) for the case of when \(\gamma \ne 0\). The dependence of the BH charge on corresponding values of ISCO radius is shown in Fig. 6 for different values of the EMS parameters \(\beta \) and \(\gamma \). One can easily see from this dependence that at \(Q=0\) i.e. Schwarzschild limit the ISCO radius equals to 6M and the increase of the BH charge forces to decrease the ISCO radius, and it decreases rapidly with increasing \(\beta \). While the presence of the parameter \(\gamma \) causes the increase of the radius for the fixed values of Q \((Q<Q_{\textrm{extr}}).\)

Fig. 7
figure 7

Dependence of energy and angular momentum of test particles at ISCOs around EMS BHs from the ISCO radius \(({{\mathcal {E}}}_{\textrm{ISCO}}\) and \({{\mathcal {L}}}_{\textrm{ISCO}})\) for different values of parameters \(\beta \) and \(\gamma \) at the range of the BH charge from 0 to corresponding \(Q_{\textrm{extr}}\)

Full size image

In Fig. 7 we have shown relationships between energy (right panel) and angular momentum (left panel) of test particles at ISCO around EMS charged BHs for the different values of EMS parameters \(\beta \) and \(\gamma \). One can see from the figure that the increase of \(\gamma \) causes the increase of both energy and angular momentum corresponding to ISCOs, while \(\beta \) affects oppositely.

Fig. 8
figure 8

Relationships between \({{\mathcal {E}}}_{\textrm{ISCO}}\) and \({{\mathcal {L}}}_{\textrm{ISCO}}\) for different values of parameters \(\beta \) and \(\gamma \) at the range of the BH charge from 0 to corresponding \(Q_{\textrm{extr}}\)

Full size image

Relationships between energy and angular momentum of test particles at ISCO around charged BHs in EMS gravity, shown in Fig. 8 for the various values of \(\beta \) and \(\gamma \). Similar effects can be observed as it is seen in Fig. 7.

3.2 Energy efficiency

The energy of test particles along Keplerian orbits in the accretion disk around BHs takes its minimum value. According to the thin accretion disk mode, the energy depends on the properties of the spacetime circular geodesics [47]. The energy efficiency of the spacetime around BHs indicates the maximum extracted energy of the radiation of infalling particles into the BH, and it can be calculated as the difference of their rest energy and orbital energy at corresponding ISCOs \(({{\mathcal {E}}}_{\textrm{ISCO}})\) using the following expression

$$\begin{aligned} \eta =1-{{\mathcal {E}}}_{\textrm{ISCO}}, \end{aligned}$$
(21)

where \({{\mathcal {E}}}_{\textrm{ISCO}}\) characterizes the ratio of the binding energy.

Fig. 9
figure 9

The energy efficiency as a function of the BH charge Q for different values of EMS parameters \(\beta \) and \(\gamma \)

Full size image

The dependence of efficiency of energy release from EMS BHs from the BH charge Q is shown in Fig. 9 for various values of the EMS parameters \(\beta \) and \(\gamma \). Here, we have compared the results obtained in EMS gravity with the results for the RN BH case. One can see from the figure that the efficiency increases as the BH charge increases, up to about 16%.

4 Fundamental frequencies

In this section, we study the fundamental frequencies of test particles orbiting the charged BH in EMS gravity. Particularly, we analyze the frequency of Keplerian orbits and frequencies of oscillations of the particles along radial and vertical directions with respect to the circular orbits.

4.1 Keplerian frequency

The angular velocity \(\varOmega _K={\dot{\phi }}/{\dot{t}}\) of test particles in circular orbits or so-called Keplerian orbits around static BHs is defined as

$$\begin{aligned} \varOmega _K=\frac{d\phi }{dt}=-\frac{g_{tt}{{\mathcal {L}}}}{g_{\phi \phi }{{\mathcal {E}}}}. \end{aligned}$$
(22)

After mathematical calculations, the Keplerian frequency in spacetime (1) with metric functions (3) takes the following form,

$$\begin{aligned} \varOmega _K^2=\frac{2 M}{r^2 \left( 2r+\gamma Q^2\right) }- \frac{\beta Q^2}{r^2 \left( r+\gamma Q^2\right) ^2}. \end{aligned}$$

In order to estimate the value of the fundamental frequencies one may express them in the unit of Hz multiplying the frequencies by the factor \({c^3}/(2 \pi GM)\). Here, we use the values of the speed of light at vacuum as \(c=3\cdot 10^8~\hbox {m}/\hbox {s}\) as well as the gravitational constant as \(G=6.67\cdot 10^{-11}~\hbox {m}^3/(\hbox {kg}^2\cdot \hbox {s})\).

Fig. 10
figure 10

Keplerian frequency of test particles around charges BHs in EMS gravity as a function of the radial coordinate for various values of the EMS parameters \(\beta \) and \(\gamma \) and BH charge is taken as \(Q=M\) except Schw BH

Full size image

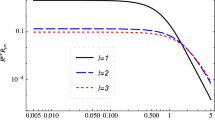
The radial profiles of the Keplerian frequencies of test particles around charges EMS BHs are presented in Fig. 10 for different values \(\beta \) and \(\gamma \) parameters and fixed value of \(Q/M=1\). One can see from the figure that the Keplerian frequency decreases with the increase of the parameter \(\gamma \) when \(\beta =1\). It is observed from the comparison of blue-dashed and red large-dashed lines that an increase of the parameter \(\beta \) causes an increase in the frequency.

4.2 Harmonic oscillations

The small perturbation of radial \((r\rightarrow r_0+\delta r)\) and vertical \((\theta \rightarrow \theta _0+\delta \theta )\) coordinates of the test particle, in their stable circular orbits at the equatorial plane around the BH, cause to oscillate the particles along these axes.

One can find the equation of the oscillations by expanding the effective potential in terms of the coordinates, r and \(\theta \), and using the condition for the extremes of the effective potential \(V_{\textrm{eff}}(r_0, \theta _0)=0\) and \(\partial _{r(\theta )}V_{\textrm{eff}}=0\) as

$$\begin{aligned} \frac{d^2\delta r}{dt^2}+\varOmega _r^2 \delta r=0, \quad \frac{d^2\delta \theta }{dt^2}+\varOmega _\theta ^2 \delta \theta =0, \end{aligned}$$
(23)

where

$$\begin{aligned}{} & {} \varOmega _r^2=-\frac{1}{2g_{rr}(u^t)^2}\partial _r^2V_{\textrm{eff}}(r,\theta ) \Big |_{\theta =\pi /2}, \end{aligned}$$
(24)
$$\begin{aligned}{} & {} \varOmega _\theta ^2=-\frac{1}{2g_{\theta \theta }(u^t)^2} \partial _\theta ^2V_{\textrm{eff}}(r,\theta )\Big |_{\theta =\pi /2}, \end{aligned}$$
(25)

are the square of radial and vertical angular frequencies of the particles around the BH measured by a distant observer, respectively. After small algebraic calculations, one easily gets expressions for the radial and vertical frequencies as,

$$\begin{aligned} \varOmega _r= & {} \frac{\Big \{ 2 f(r) f'(r) U'(r)+U(r) \left[ f(r) f''(r)-2 f'(r)^2\right] \Big \}}{f(r) \left[ f(r) U'(r)-U(r) f'(r)\right] } \nonumber \\{} & {} \times U'(r) -\frac{f(r) U(r) f'(r) U''(r)}{f(r) \left[ f(r) U'(r)-U(r) f'(r)\right] } \nonumber \\ \varOmega _\theta= & {} \varOmega _K=\varOmega _\phi , \end{aligned}$$
(26)

where \(\varOmega _\phi \) is the angular velocity of the particle measured by an observer at infinity. Using the Eq. (26) and the metric function (3) one can easily find the corresponding fundamental frequencies.

Fig. 11
figure 11

Radial profile of frequency of radial oscillations of test particles around the BH in EB gravity. In all cases \(Q=M\) except Schw BH

Full size image
Fig. 12
figure 12

Possible values of the frequencies of upper and lower peaks of QPOs from charged BHs in EMS gravity in the RP model

Full size image
Fig. 13
figure 13

Radius of QPOs orbits with the frequencies 3:2 and 5:4 and ISCO as a function of the BH charge for various values of \(\gamma \) and \(\beta \) in the frame of the RP model

Full size image

Figure 11 shows frequencies of the radial oscillations of test particles around charged BH in EMS theory for various values of EMS parameters \(\beta \) and \(\gamma \) for the fixed value of the BH charge as \(Q/M=1\). One can see from the figure that the frequency increases in the presence of the BH charge. Moreover, for the cases, when \(\beta =1/2\) and \(\gamma \ne 1\) the maximum in the radial frequencies increases, while at \(\beta >1\) and \(\gamma \ne 1\) the frequency increases sufficiently. The increase of both \(\gamma \) and \(\beta \) parameters causes a shift in the position of orbits, where the frequency of radial oscillations reaches its maximum, towards the central BH.

5 QPOs around BHs in EMS theory

In this section, we focus our attention on studies of twin peak QPOs around charged BHs in EMS gravity in the frame of relativistic precession (RP) model [48]. The upper and lower frequencies of the QPOs using combinations of the frequencies of the radial, vertical and orbital oscillations of the test particles along the stable circular orbits around the BH as \(\nu _U=\nu _\phi \) and \(\nu _L=\nu _\phi -\nu _r\), respectively.

In Fig. 12 we plot relationships between the upper and lower frequencies of twin-peak QPOs from charged BHs in EMS gravity in the RP model. Here, we fix the BH mass as \(M=15M_\odot \) and the charge as \(Q=M\). It is observed from this figure that the QPO frequencies grow in the presence of the BH charge when \(\beta =1\), while in cases of \(\beta <1\) the QPO can be observed near the LF QPOs. Similarly, the increase of \(\gamma \) also causes decreasing frequencies at \(\beta =1\). However, in \(\beta >1\) cases the frequencies take value near kHz QPOs. We have shown black dots where the black solid line and other colored lines cross, in zoom on the top of the figure zoomed. It does mean that at a fixed value of the BH charge and EMS parameters, the upper and lower frequencies can be the same as it is in the pure Schwarzschild case, but the QPO may occur at different distances from the central BH. However, the colored lines do not cross each other, implying there are no degeneracy values in the EMS parameters.

Fig. 14
figure 14

Locations of the QPOs detected microquasars GRS 1905+105, GRO J 1655-40, H 1745+322 and XTE 1550-564 in \(\nu _U-\nu _L\) space

Full size image
Fig. 15
figure 15

Relationships between BH charge and the parameter \(\gamma \) of the spacetime around the BHs in the microquasars GRS 1905+105, GRO J 1655-40, H 1745+322 and XTE 1550-564 for fixed values of \(\beta \)

Full size image

Figure 13 demonstrates the dependencies of the radius of QPO orbits with the frequency ratio 3:2 and 5:4 for various values of the EMS parameters. It is observed from the figure that the QPO orbits located out of ISCO and QPOs with a ratio near 1 shine at the orbits close to ISCOs. It is known that ISCO radius is one of the most critical properties of BHs to be measured. It is still a problematic issue in observations of stellar mass and intermittent BHs to solve. From this point of view, the studies may play a role in being a solution to this issue. It implies that one may calculate the ISCO radius using frequency data from twin peak QPOs with a frequency ratio less than 5:4. Moreover, the QPO radius comes closer to the ISCO at higher values of the BH charge. On the other hand, it is possible to get constraints and relations between the EMS parameters and BH charge using the results of studies of QPO orbits.

6 Constraints on EMS gravity parameters using QPO frequencies

Here we try to get constraints on the EMS parameters \(\beta \) and \(\gamma \) and the BH charge around EMS BHs using data from QPOs in the following microquasars:

  • GRS 1915-105 is observed in upper and lower frequencies as \(168\pm 5\) and \(113\pm 3\), respectively, with the central black hole, mass \(12.4^{+2.0}_{-1.8} M_\odot \) [49]

  • GRO J1655-40, powered by central black hole with mass \((5.4\pm 0.4)M_\odot \), observed in the high frequencies \(441\pm 2\) and \(298\pm 4\) and low frequency \(17.3\pm 0.1\) Hzs [50, 51].

  • XTE J1550-564, the mass of the black hole at the center of the microquasar is \((9.1\pm 0.61)M_\odot \) and it is detected in \(276\pm 3\) and \(184\pm 5\) Hzs [35, 52],

  • H1743+322 microquasar has been found in the frequency band of electromagnetic spectrum \(242\pm 3\) and \(166\pm 5\) Hzs, the mass of the central black hole lies in the range of between 8 and 14.07 solar mass [50, 53].

Fig. 16
figure 16

The same figure with Fig. 15 but for the different range of \(\gamma \), the figure from the top left corner accounts for from 0 to 0.1, while the others from 0.1 to 0.15

Full size image

Figure 14 shows coordinates of observed QPOs in the microquasars GRS 1905+105, GRO J 1655-40, H 1745+322, and XTE 1550-564 in the space of their upper and lower frequencies. One can see from the diagram that the selected QPOs are located close to the QPO line with a ratio of 3:2. On the other hand, the BHs’ masses are not also too much different from each other. Our expectation is that their charge and the EMS parameters for these microquasars must take values that are close to each other.

Since there are two independent parameters in EMS theory including the BH charge, it is not possible to get exact values for the parameters using the above-mentioned observational data from the objects. However, one may get relationships between the BH charge and the parameter \(\gamma \) by keeping the parameter \(\beta \) as a constant with the allowed values.

Now, we try to get the relationships on the EMS parameter \(\gamma \) and the BH charge Q for the fixed values of the parameter \(\beta \) solving the following equations, in the frame of RP model [40, 54, 55],

$$\begin{aligned} \nu _{\textrm{U}}(r;\beta ,\gamma ,Q)=\nu _{\textrm{U}}^{ob}, \qquad \nu _{\textrm{L}}(r;\beta ,\gamma ,Q)=\nu _{\textrm{L}}^{ob}, \end{aligned}$$
(27)

where \(\nu _{\textrm{U}}^{ob}\) and \(\nu _{\textrm{L}}^{ob}\) are observational values of the upper and lower frequencies of the QPOs. In order to get relationships between the possible values of the EMS parameters for the above-mentioned objects, we use their observational parameters. Below, we provide the relationships for the above-mentioned objects.

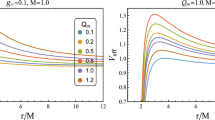
In Fig. 15 we provide dependence of charge of central BHs in the microquasars GRS 1905+105, GRO J 1655-40, H 1745+322, and XTE 1550-564 from the EMS parameter \(\gamma \) for the fixed values of \(\beta \). One can see from the figure that the BH charge increases linearly with the increase of the \(\gamma \) parameter and the increase of \(\beta \) causes to decrease in the charge. It is seen that the dependencies for each value of \(\beta \) are close to each other because the frequency ratios of the QPO objects are close to 3:2.

In order to show a clear picture of the difference in the relationships, we provide the sectional view of the dependence in the range \(\gamma \in (0.1 - 0.15)\) in Fig. 16, while, in order to see the charge of the RN BHs, we plot the top left panel from \(\gamma =0\) to 0.1. One can see from the panel that the charge of the BHs in the microquasars take the values between \(\sim \) 1.2 \(M_\odot \)–1.215\(M_\odot \), and the BH charges increase with the increase of the parameters \(\gamma \) and \(\beta \). Moreover, it is observed that the difference between the lines, corresponding to BH charge profiles, increases with the increase of \(\beta \).

7 Conclusion

In the present work, we have studied profiles of event horizon radius with respect to the variation of the EMS gravity parameters and the BH charge. It is found that when \(\gamma \rightarrow -\infty \) the extreme value of the BH charge tends to zero and the spacetime (3) turns to the pure Schwarzschild one. It has been shown that the \(\gamma \) parameter has an upper value that depends on the parameter \(\beta \) (see Fig. 2). Relationships between extreme charge, maximum in the values of \(\gamma \) and \(\beta \) parameters have obtained as \(\gamma _{\mathrm{}} \sim \beta \) and \(Q_{\textrm{extr}} \sim \beta ^{-\frac{1}{2}}\).

We have also investigated the dynamics of test particles in the spacetime of charged BHs in EMS theory. Analytic expressions for the specific angular momentum and energy of test particles at circular orbits are found, and the effects of the parameters \(\beta \) and \(\gamma \) on them are discussed. It has been shown that an increase of the BH charge causes decreasing the minimum of both energy and angular momentum, however, the presence of \(\gamma \) and \(\beta \) parameters increases.

We have analyzed EMS field effects on ISCO radius, energy, and angular momentum of particles at ISCOs, as well as the energy efficiency. It has been obtained that ISCO radius (energy efficiency) rapidly decreases (increases) with the increase of the BH charge Q with compare to RN BH case (and reaches up to about 16%).

Moreover, we have explored fundamental frequencies, such as Keplerian and radial frequencies of oscillations of particles orbiting the EMS BHs. As an astrophysical application of the studies, we have developed the RP model for twin peak QPOs.

It is well known that one of the problematic issues in observations of stellar mass and intermittent BHs is ISCO radius measurements, being an essential property of BHs. From this point of view, the study plays an important role in solving the problem. We have shown that ISCO radius can be measured by using frequency data from twin peak QPOs with a frequency ratio less than 5:4 with high accuracy. Moreover, the QPO radius comes closer to the ISCO at higher values of the BH charge. The frequency ratio becomes 1 when it is generated at ISCO.

Finally, we have got constraints on the BH charge and EMS parameters for observed QPOs in the microquasars GRS 1905+105, GRO J 1655-40, H 1745+322, and XTE 1550-564 which have frequency ratios close to each other and 3:2 with the stellar mass central BH.