1 Introduction

The gauge/gravity duality has been widely recognized as a fundamental feature of quantum gravity, and extensive research has been carried out in this field over the past two decades, leading to many important findings [1]. Holographic QCD offers a novel approach to study and compute the properties of various physical phenomena in QCD. Studying heavy quarkonium is beneficial for understanding the properties of quark–gluon plasma(\(\textrm{QGP}\)), as well as validate our understanding of the interactions between hadrons and fundamental particles [2, 3]. In holographic QCD, we can study the interaction between quarks and antiquarks by placing a pair of them inside a bulk. Then, we can utilize the tools of string theory to calculate the interaction between the two quarks and their corresponding potential energy.

The string breaking phenomenon is a result of the nonperturbative effects of QCD. Up to now, lattice QCD has been effectively utilized to investigate this phenomenon, albeit limited to meson modes at zero temperature and zero chemical potential [4]. As is widely acknowledged, the environment in which tetraquark are situated can often be complex. Therefore, introducing high-temperature factors into the model to study the behavior of four quark potentials at elevated temperatures can aid in better understanding the behavior of tetraquark under extreme conditions. In previous studies, it has been discovered that under sufficiently high temperatures, thermal excitations produce a plasma of quarks and gluons [5]. Subsequently, they discussed the potential at finite temperatures [5,6,7]. The deformed \(\mathrm{AdS_{5}}\) model [8,9,10] and Einstein–Maxwell-Dilaton model are employed to compute the quark–antiquark potential [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28] in these researches.

Recently, at the Large Hadron Collider, the LHCb collaboration observed a hadron state that contains four quarks [29, 30]. This tetraquark contains two charm quarks, a \({\bar{u}}\) and a \({\bar{d}}\) quark, with a mass of about 3875 \(\mathrm{MeV/c^{2}}\). This finding has renewed interest in studying the tetraquark theory. It is worth noting that lattice gauge theory is still a fundamental tool for studying non-perturbative phenomena in QCD, but research results on the potential of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) are limited [31,32,33,34,35,36].

The tetraquark model used in this paper was proposed by Andreev [37]. This model assumes that the heavy quarks are significantly heavier than the typical energy scale of the system, allowing us to treat them as static. The interaction potential between the quarks is determined by their relative separation. The main reason for studying this model is that its results on both quark–antiquark and tetraquark potentials are consistent with lattice calculations and QCD phenomenology [4, 38]. At zero temperature, the timelike Wilson loop is realized by a U-shaped macroscopic string for any interquark separation. At finite temperature, we have seen that the string configuration is either a pair of straight strings or U-shaped [5]. Our technique for extracting the potential of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) is similar to the one used in lattice QCD. We extract the potential from the expectation value of the \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) Wilson loop, \({{\textrm{W}}_{{\textrm{QQ}}{\bar{{\textrm{q}}}}{\bar{{\textrm{q}}}}}} (R, T)\). The \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) Wilson loop consists of heavy quark paths and light quark propagators. The separation distance between heavy quark pairs and the potential energy relationship of the model were calculated and analyzed at finite temperature [39,40,41,42,43,44,45,46,47]. Subsequently, three decay modes of tetraquark were studied to determine the most probable decay mode that occurs at high temperatures and to compare it with the decay of three quarks.

Section 2 provides a brief review of the theoretical foundation of the model and establishes a framework for studying \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) at finite temperature. Section 3 involves numerical solutions for the energy and separation distance between heavy quarks for these configurations at different temperatures. This is followed by a discussion of the results in Sect. 4. In this section, we will also discuss the melting of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) strings at finite temperatures by analyzing potential energy trends. Later in Sect. 5, the three types of decay modes in the \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) model will be discussed and compared with the decay modes in the QQq model. Finally, Sect. 6 presents the summary and conclusion of this paper.

2 Preliminaries

In this paper, we extend the study of the potential for doubly-heavy tetraquarks from zero temperature [37] to finite temperatures. To begin our discussion on the potential of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) at finite temperatures, let us first review the specific holographic model utilized in this paper. Following [37, 48, 49], the background metric at finite temperatures is given by:

$$\begin{aligned} d {\textbf{s}}^2&=\textrm{e}^{s r^2} \frac{R^2}{r^2}\left( f(r) d t^2+d \vec {x}^2+f^{-1}(r) d r^2\right) \nonumber \\&\quad +\textrm{e}^{-s r^2} g_{a b}^{(5)} d \omega ^a d \omega ^b, \end{aligned}$$
(1)

such model is a deformation of the Euclidean \({{\textrm{AdS}}_{5}}\) space of radius R, with a deformation parameter s [50]. In the five-dimensional compact space (sphere) characterized by the blackening factor f with coordinates \(\omega ^a\) and f(r), the Nambu–Goto action of a string is expressed as

$$\begin{aligned} S_{NG}=\frac{1}{2 \pi \alpha ^{\prime }} \int _0^1 d \sigma \int _0^T d \tau \sqrt{\gamma }, \end{aligned}$$
(2)

here, \(\gamma \) represents an induced metric on the string world-sheet with a Euclidean signature, while \(\alpha ^{'}\) is a parameter associated with the string. For the \({{\textrm{AdS}}_{5}}\) space, we assume that the blackening factor f takes the form \(f(r)=1-\left( \frac{r}{r_h}\right) ^4\), where \(f(0)=1\) at the boundary and \(f\left( r_h\right) =0\) at the horizon. The Hawking temperature, which is consistent with the temperature of the dual gauge theory, can be defined as \(T=\frac{1}{4 \pi }\left| \partial _r f\right| _{r=r_h}\).

Then, we consider baryon vertices which are string junctions [51]. According to the AdS/CFT correspondence, they are represented by a five-brane wrapped around the internal space X at the point where three strings intersect and appear to be joined together in five dimensions [52, 53]. Correspondingly, the antibaryon vertex is represented by an antibrane in the AdS/CFT correspondence. At leading order \(\alpha ^{'}\), the brane’s action is \(S_{\text{ vert } }={\mathcal {T}}_5 \int d^6 \xi \sqrt{\gamma ^{(6)}}\), where \( {\mathcal {T}}_5 \) represents the brane tension and \(\xi ^i\) denotes the world-volume coordinates. If we choose static specifications \(\xi ^0=t\) and \(\xi ^a=\theta _{a}\), where \(\theta _{a}\) represents the coordinates on X, then the resulting action is as follows

$$\begin{aligned} S_{\textrm{vert}}=\tau _v \int d t \frac{\textrm{e}^{-2 s r^2}}{r} \sqrt{f(r)}. \end{aligned}$$
(3)

Here, \({\mathcal {T}}_v\) is a dimensionless parameter defined by \({\mathcal {T}}_v ={\mathcal {T}}_5Rvol({{\textrm{X}}})\), where \(vol({{\textrm{X}}})\) represents the volume of X, and it serves as a free parameter. Additionally, we have the same action for both baryon and antibaryon vertices \(S_{{\bar{v}}}\) = \(S_{v}\) at finite temperature.

Finally, we consider the light quark located at the end of the string, a scalar field that is coupled to the boundary of the worldsheet via the open string tachyon \(S_{q} =\int \textrm{d} \tau e {{\textrm{T}}}\) [54]. Here, the integral is over a world-sheet boundary parameterized by \(\tau \),and e is a boundary metric. Assuming a constant background given by \({{\textrm{T}}(x,r)={\textrm{T}}_{0}}\) and worldsheets with boundaries along lines in the t direction. Thus, the action can be written as

$$\begin{aligned} S_{\textrm{q}}=\textrm{m} \int d t \frac{\textrm{e}^{\frac{s}{2} r^2}}{r} \sqrt{f(r)}. \end{aligned}$$
(4)

Here, \({{\textrm{m}}}= R {{\textrm{T}}_{0}}\) represents the mass of a point particle at rest, with \({{\textrm{T}}_{0}}\) as its mass. Therefore, the given action describes the behavior of a point particle with mass \({{\textrm{T}}_{0}}\) at rest. It should be noted that the same action also describes the behavior of light antiquarks located at string endpoints, and hence \(S_{{{\bar{q}}}}\) = \(S_{ q}\). In this model, the interaction of quarks is described by the string tension, which is consistent with Ref. [3].

The model parameters are selected as follows: \(g=\frac{R^{2} }{2\pi \alpha ^{'} }\), \(\textrm{k}=\frac{\tau _v}{3\mathrm {~g}}\) and \(n=\frac{m}{g}\). All our parameters are consistent with Refs. [4, 37, 48, 49] based on the lattice QCD. The value of s is fixed from the slope of the Regge trajectory of \(\rho (n)\) mesons in the soft wall model with the geometry Eq. (1). This gives \(s = 0.45 {{\textrm{GeV}}^2}\). Then, fitting the value of the string tension \(\sigma \) to its value in [39] gives \(g = 0.176\). According to the gauge/string duality g is related to the ’t Hooft coupling. Next, the parameter m is adjusted to reproduce the lattice result for the \({{\bar{{\textrm{Q}}}}Q}\) string breaking distance \(L_c^{(m)}\). With \(L_c^{(m)}=1.22 \textrm{fm}\) [39], it gives \(m=0.538\). The parameter n is expressed in terms of the parameters of as \(\textrm{n}=\frac{\textrm{m}}{\textrm{g}}\) [4]. For fixed the value of k, one should keep in mind two things. First, the value of k can be adjusted to fit the lattice data for the three-quark potential, as is done in [38] for pure SU(3) gauge theory. Unfortunately, at the moment, there are no lattice data available for QCD with two light quarks. Second, the range of allowed values for k is limited to \(-\frac{\textrm{e}^3}{15} \) to \(-\frac{1}{4} \textrm{e}^{\frac{1}{4}}\). We take \(k=-\frac{1}{4} \textrm{e}^{\frac{1}{4}}\) simply because it yields an exact solution to Eq. (20). Finally, the parameters of this article are as follows: \(s=0.45\) \({{{\textrm{GeV}}^2}}\), \(g= 0.176\), \(n = 3.057\), \(k =-\frac{1}{4} E^{\frac{1}{4}}\), and \(c=0.623\) \({{\textrm{GeV}}}\) in this model from Ref. [37] at zero temperature. No other extra parameters are introduced in this article.

3 The connected string configuration of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\)

3.1 Small L

Fig. 1
figure 1

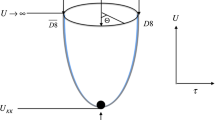
A static string configuration at small heavy-quark separation distance. The heavy quarks Q are located on the boundary, whereas the light antiquarks \({\bar{q}}\), baryon vertex \({{\textrm{V}}}\), and antibaryon vertex \({{\bar{{\textrm{V}}}}}\) are situated in the bulk of the five-dimensional space at \(r_{{\bar{q}}}\), \(r_v\) and \(r_{{\bar{v}}}\), respectively. \(r_h\) represents the position of the black-hole horizon, while \(r_w\) indicates the position of a dynamic wall in the confined phase

Full size image

The configuration of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) is illustrated in Fig. 1. The total action for this system is given by the sum of the Nambu–Goto actions, as well as the actions associated with the vertices and antiquarks.

$$\begin{aligned} S=\sum _{i=1}^5 S_{\textrm{NG}}^{(i)}+2 S_{\textrm{v}}+2 S_{{{\bar{{\textrm{q}}}}}}. \end{aligned}$$
(5)

We choose the static gauge \(\xi ^1=t\) and \(\xi ^2=r\) for the Nambu–Goto actions, the boundary conditions for x(r) become

$$\begin{aligned}&x^{(1)}(0)=-\frac{1}{2} \ell , \quad x^{(2)}(0)=\frac{1}{2} \ell , \quad x^{(1,2,3)}\left( r_v\right) =x^{(3,4,5)}\nonumber \\&\left( r_{{\bar{v}}}\right) =x^{(4,5)}\left( r_{{\bar{q}}}\right) =0. \end{aligned}$$
(6)

Considering the boundary conditions, we get the total action

$$\begin{aligned} \begin{aligned} S&=g T\left( 2 \int _0^{r_v} \frac{e^{s r^2}}{r^2} \sqrt{1+f(r)\left( \partial _r x\right) ^2} \mathrm {~d} r+\int _{r_v}^{r_{{\bar{v}}}} \frac{e^{s r^2}}{r^2} \mathrm {~d} r \right. \\&\quad \left. +2 \int _{r_{{\bar{v}}}}^{r_{{\bar{q}}}} \frac{e^{s r^2}}{r^2} \mathrm {~d} r+3 k \frac{e^{-2 s r_{{\bar{v}}}^2}}{r_{{\bar{v}}}} \sqrt{f\left( r_{{\bar{v}}}\right) }\right. \\&\quad \left. +3 k \frac{e^{-2 s r_v^2}}{r_v} \sqrt{f\left( r_v\right) }+2 n \frac{e^{\frac{1}{2} r_{{\bar{q}}}^2}}{r_{{\bar{q}}}} \sqrt{f\left( r_{{\bar{q}}}\right) }\right) . \end{aligned} \end{aligned}$$
(7)

Here \( \partial _{r} x=\frac{\partial x }{\partial r}\), \(T=\int _{0}^{T} \textrm{d}t \) and the straight strings are located at \(x=0\). For string (1) and (2), which correspond to the first term in (7), we can derive the equation of motion (EoM) for x(r) using the Euler–Lagrange equation. Thus, it is found that

$$\begin{aligned} {\mathcal {I}}=\frac{w(r) f(r) \partial _r x}{\sqrt{1+f(r)\left( \partial _r x\right) ^2}}, \quad w(r)=\frac{\textrm{e}^{\textrm{s} r^2}}{r^2}. \end{aligned}$$
(8)

\({\mathcal {I}}\) is a constant. We have \(\partial _{r}x=\cot \alpha \) when \(r=r_{v}\), and \({\mathcal {I}}\) can be expressed as

$$\begin{aligned} {\mathcal {I}}=\frac{w(r_{v}) f(r_{v}) \partial _r x}{\sqrt{1+f(r)\left( \partial _r x\right) ^2}}, \quad w(r)=\frac{\textrm{e}^{\textrm{s} r^2}}{r^2}. \end{aligned}$$
(9)

Then \(\partial _r x\) can be obtained:

$$\begin{aligned}&\partial _r x \nonumber \\&=\sqrt{\frac{\omega \left( r_v\right) ^2 f\left( r_v\right) ^2}{\left( f\left( r_\nu \right) +\tan ^2 \alpha \right) \omega (r)^2 f(r)^2-f(r) w\left( r_v\right) ^2 f\left( r_v\right) ^2}}. \end{aligned}$$
(10)

Using Eq. (10), we can obtain an expression for the separation distance L,

$$\begin{aligned} L=2 \int _0^{r_v} \frac{d x}{d r} d r. \end{aligned}$$
(11)

Next, we calculate the potential energy of doubly-heavy tetraquark. The energy of string (1) can be got from the first item in the Eq. (7),

$$\begin{aligned} E_1=\dfrac{S}{T}={\textbf{g}}\int _0^{r_s}\dfrac{\textrm{e}^{sr^2}}{r^2}dr\sqrt{1+f(r)\left( \partial _r x\right) ^2}. \end{aligned}$$
(12)

This expression is not well-defined, because the integral diverges at \(r = 0\). So we should subtract the divergent term

$$\begin{aligned} E_1&=\dfrac{S}{T}={\textbf{g}}\int _{0}^{r_{v}}\left( \dfrac{1}{r^{2}}\textrm{e}^{\textbf{sr}^{2}} \sqrt{1+f(r)\left( \partial _{r}x\right) ^{2}}-\dfrac{1}{r^{2}}\right) dr\nonumber \\&\quad -\dfrac{{\textbf{g}}}{r_{v}}+c, \end{aligned}$$
(13)

here c is a normalization constant. We can fix the constant by fitting the lattice results. For the heavy quarkonium, we can take 2c to fit the potential of heavy quarkonium with lattice. The choice of the normalization constant c for the energy of a single baryon configuration is equal to 3c. [55] String (2) is calculated in the same way as string (1), and thus \(E_{1}=E_{2}\). String (3) is described by the second term in Eq. (7), and represents a straight string stretched between the baryon vertex and antibaryon vertex. The energy can be calculated as

$$\begin{aligned} E_3=\frac{S}{T}=\textrm{g} \int _{r_v}^{r_{{\bar{v}}}} \frac{\textrm{e}^{s r^2}}{r^2} d r. \end{aligned}$$
(14)

String (4) and string (5) are both described by the third term in Eq. (7), and represent straight strings.

$$\begin{aligned} E_{4}=E_{5} =\dfrac{S}{T}=\int _{r_{{\bar{v}} } }^{r_{{\bar{q}}} }\frac{e^{sr^{2} } }{r^{2} } \textrm{d}r. \end{aligned}$$
(15)

Then, we can get the energy of \(QQ{\bar{q}}{\bar{q}}\) for this configuration.

$$\begin{aligned} \begin{aligned} E_{Q Q {\bar{q}} {\bar{q}}}&= g\left( 2 \int _0^{r_v}\left( \frac{e^{s r^2}}{r^2} \sqrt{1+f(r)\left( \partial _r x\right) ^2}-\frac{1}{r^2}\right) \textrm{d} r\right. \\&\quad \left. -\frac{2}{r_v}+\int _{r_v}^{r_{{\bar{v}}}} \frac{e^{s r^2}}{r^2} \mathrm {~d} r+2 \int _{r_{{\bar{v}}}}^{r_{{\bar{q}}}} \frac{e^{s r^2}}{r^2} \mathrm {~d} r\right. \\&\quad \left. +3 k \frac{e^{-2 s r_v^2}}{r_v} \sqrt{f\left( r_v\right) }+3 k \frac{e^{-2 s r_{{\bar{v}}}^2}}{r_{{\bar{v}}}} \sqrt{f\left( r_{{\bar{v}}}\right) }\right. \\&\quad \left. +2 n \frac{e^{\frac{1}{2} s r_{{\bar{q}}}^2}}{r_{{\bar{q}}}} \sqrt{f(r {\bar{q}})}\right) +2 c . \end{aligned} \end{aligned}$$
(16)

It can be observed from Eq. (16) that energy is a function of \(r_v\), \(\alpha \), and \(r_h\). To obtain the energy of this configuration, we will solve the position of the light antiquark. One crucial condition for equilibrium is that the net forces exerted on the vertices and antiquarks must cancel out. According to the model, the force (shown in Fig. 1) balance equation in the r direction at \(r_{{\bar{q}}}\) is given by:

$$\begin{aligned} 2f_{{\bar{q}}}+e_{4}^{'}+e_{5}^{'}=0. \end{aligned}$$
(17)

Here \(e_i\) is the string tension [56]. By varying the action with respect to \(r_{{\bar{q}}}\), we get the force \(f_{{\bar{q}}}{=}\Bigg (0,-{\textbf{g}}n\partial _{r_{{\bar{q}}}}(\frac{\textrm{e}^{\frac{1}{2}\text {s} \textrm{r}_{{\bar{q}}}^2}}{r_{{\bar{q}}}}\sqrt{f(r_{{\bar{q}}})})\Bigg )\), \(e_{4}^{'}{=}e_{5}^{'}{=}{{\textbf {g}}}w\left( r_{{\bar{q}}}\right) \left( 0,-1\right) \) on the antiquark. Hence, the Eq. (17) becomes

$$\begin{aligned}&-2nsr_{{\bar{q}}}^{2}(f^\frac{3}{2}(r_{{\bar{q}}}))+2n(f^\frac{3}{2}(r_{{\bar{q}}}))-nr_{{\bar{q}}}f' (r_{{\bar{q}}})\nonumber \\&-2f(r_{{\bar{q}}})e^\frac{sr_{{\bar{q}}}^2}{2}=0. \end{aligned}$$
(18)

\(r_{{\bar{q}}}\) (the position of the light antiquark) is only a function of \(r_h\). This equation gives us the position \(r_{{\bar{q}}}\) at a fixed temperature. Then, at \(r_{{\bar{v}}}\), the force balance equation is

$$\begin{aligned} f_{{\bar{v}}}+e_3^{\prime }+e_4+e_5=0. \end{aligned}$$
(19)

Here \(f_{{\bar{v}}}\) is the force on the antibaryon vertex, and each force is determined by

$$\begin{aligned} \begin{aligned} f_{{\bar{v}}}&=\left( 0,-3 \mathrm {~g} k \partial _{r_{{\bar{v}}}}\left( \frac{\textrm{e}^{-2 s r_{{\bar{v}}}^2}}{r_{{\bar{v}}}} \sqrt{f\left( r_{{\bar{v}}}\right) }\right) \right) ,\\ e_3^{\prime }&=g w\left( r_{{\bar{v}}}\right) (0,-1), \\ e_4&=e_5=g w\left( r_{{\bar{v}}}\right) (0,1) . \end{aligned} \end{aligned}$$

Then, the force balance equation changes

$$\begin{aligned}&\left( 4 s r_{{\bar{v}}}^2+1\right) k \sqrt{f\left( r_{{\bar{v}}}\right) } e^{-3 s r_{{\bar{v}}}^2} \nonumber \\&-\frac{1}{2} k r e^{-3 s r_{{\bar{v}}}^2} f^{\prime }\left( r_{{\bar{v}}}\right) +\frac{1}{3} \sqrt{f\left( r_{{\bar{v}}}\right) }=0. \end{aligned}$$
(20)

At fixed temperature, \(r_{{\bar{v}}}\) can be determined via the above equation. At \(r_{v}\), the force balance equation is

$$\begin{aligned} f_{v} +e_{1}+e_{2}+e_{3} =0, \end{aligned}$$
(21)

here the force on the baryon vertex is \(f_v=\left( 0,-3{\textbf{g}}k\partial _{r_{v}}(\frac{\textrm{e}^{-2\,s r_{v}^{2}}}{r_{v}}\sqrt{f(r_{v})})\right) \), and the string tensions at the \({r_{v}}\) are \(e_{3}=\text {g}w\left( r_v\right) \left( 0,1\right) \), \(e_{1}={\textbf{g}}w\big (r_{v}\big )\big (-\frac{f(r_{v})}{\sqrt{t a n^{2}\alpha +f(r_{v})}}, -\frac{1}{\sqrt{f(r_{v})c o t^{2}\alpha +1}}\big )\), \({e_{2}}={\textbf{g}}w\left( r_{v}\right) \Bigg (\frac{f(r_{v})}{\sqrt{t a n^{2}\alpha +f(r_{v})}},-\frac{1}{\sqrt{f(r_{v})c o t^{2}\alpha +1}}\Bigg )\). \(\alpha \) is the angle shown in Fig. 1. Putting these forces into Eq. (21), the force balance equation becomes

$$\begin{aligned}&(4sr_{v}^2+1)k\sqrt{f(r_{v})} e^{-3sr_{v}^2}-\frac{1}{2}kre^{-3sr_{v}^2}f' (r_{v})\nonumber \\&\quad +\frac{1}{3}\sqrt{f(r_{v})}(1-\frac{2}{\sqrt{f\left( r_v\right) \cot ^2 \alpha +1}})=0. \end{aligned}$$
(22)

By taking the variation of the action with respect to \(r_{v}\), we can deduce the relationship between \(r_{v}\) and \(\alpha \).

3.2 Slightly larger L

The second configuration is shown in Fig. 2, and we consider the second configuration as one in which a string (3) contracts to a single point. The total action is now expressed by

Fig. 2
figure 2

A static configuration is formed by a slightly larger separation distance of a heavy-quark pair. The baryon vertex and the antibaryon vertex are in the same position. The force acting on the point is indicated by the black arrow

Full size image
$$\begin{aligned} S=\sum _{i=1, i \ne 3}^5 S_{\textrm{NG}}^{(i)}+2 S_{\textrm{v}}+2 S_{{{\bar{{\textrm{q}}}}}}. \end{aligned}$$
(23)

We choose the same static gauge as before and the boundary conditions are

$$\begin{aligned}&x^{(1)}(0)=-\frac{1}{2} \ell , \quad x^{(2)}(0)=\frac{1}{2} \ell ,\nonumber \\&\quad x^{(i)}\left( r_v\right) =x^{(4,5)}\left( r_{{\bar{q}}}\right) =0. \end{aligned}$$
(24)

The separation distance of the slightly larger L is still determined by Eq. (11), which is the same as that used for the small L. Compared to the first configuration, the string (3) in the second configuration contracts to a point. Therefore, we need to consider other string tensions that satisfy Eqs. (13)–(15). Then, the energy of the slightly larger L can be expressed as

$$\begin{aligned} \begin{aligned} E_{Q Q {\bar{q}} {\bar{q}}}&= g\left( 2 \int _0^{r_v}\left( \frac{e^{s r^2}}{r^2} \sqrt{1+f(r)\left( \partial _r x\right) ^2}-\frac{1}{r^2}\right) \textrm{d} r\right. \\&\quad \left. -\frac{2}{r_v}+2 \int _{r_v}^{r_{{\bar{q}}}} \frac{e^{s r^2}}{r^2} \textrm{d} r+3 k \frac{e^{-2 s r_v^2}}{r_v} \sqrt{f\left( r_v\right) }\right. \\&\quad \left. +3 k \frac{e^{-2 s r_{{\bar{v}}}^2}}{r_{{\bar{v}}}} \sqrt{f\left( r_{{\bar{v}}}\right) }+2 n \frac{e^{\frac{1}{2} s r_{{\bar{q}}}^2}}{r_{{\bar{q}}}} \sqrt{f(r {\bar{q}})}\right) +2 c . \end{aligned} \end{aligned}$$
(25)

As before, we will now proceed with solving the force balance equation. The location of \(r_{{\bar{q}}}\) can be determined using Eq. (18). Then, the force balance equation at the point \(r = r_v=r_{{\bar{v}}}\) is

$$\begin{aligned} f_{v}+f_{{\bar{v}}}+e_{1}+e_{2}+e_{4}+e_{5} =0. \end{aligned}$$
(26)

Each force is determined by

$$\begin{aligned} \begin{aligned} f_v&=f_{{\bar{v}}}=\left( 0,-3 g k\partial _{r_{v}}(\frac{\textrm{e}^{-2s r_{v}^{2}}}{r_{v}}\sqrt{f(r_{v})})\right) ,\\ e_{1}&=g w_{(r_{v})}\left( -\frac{f(r_{v})}{\sqrt{t a n^{2}\alpha +f(r_{v})}},-\frac{1}{\sqrt{f(r_{v})c o t^{2}\alpha +1}}\right) , \\ e_{2}&={g w_{(r_{v})}\left( \frac{f(r_{v})}{\sqrt{t a n^{2}\alpha +f(r_{v})}},-\frac{1}{\sqrt{f(r_{v})c o t^{2}\alpha +1}}\right) }, \\ e_{4}&=e_{5}=\text {g}w\left( r_v\right) \left( 0,1\right) . \end{aligned} \end{aligned}$$

Then, the Eq. (26) becomes

$$\begin{aligned}&(24sr_{v}^2f(r_{v})+6f(r_{v})-3rf'(r_{v}))ke^{-3sr_{v}^2}\nonumber \\&\quad -\frac{2}{\sqrt{f\left( r_v\right) \cot ^2 \alpha +1}}+2\sqrt{f(r_v)}=0. \end{aligned}$$
(27)

3.3 Intermediate L

Fig. 3
figure 3

Static configuration at an intermediate separation distance of a heavy-quark pair. The baryon vertex, antiquark and the antibaryon vertex are in the same position. The force acting on the point is indicated by the black arrow

Full size image

The third configuration, as shown in Fig. 3, is characterized by the compression of points \(r_{{\bar{q}}}\), \(r_{{\bar{v}}}\) and \(r_v\) into a single location. The configuration of the total action is given by

$$\begin{aligned} S=\sum _{i=1}^2 S_{\textrm{NG}}^{(i)}+2 S_{\textrm{v}}+2 S_{{{\bar{{\textrm{q}}}}}}. \end{aligned}$$
(28)

Choosing the static gauge in the Nambu–Goto actions as before, then the boundary conditions can be obtained

$$\begin{aligned} x^{(1)}(0)=-\frac{1}{2} \ell , \quad x^{(2)}(0)=\frac{1}{2} \ell , \quad x^{(i)}\left( r_v\right) =0. \end{aligned}$$
(29)

Equation (11) gives us the separation distance in this configuration. To calculate the energies, we only need to consider the range from \(r=0\) to \(r=r_v\), as specified by Eq. (13). Naturally, the energy of the configuration is

$$\begin{aligned} \begin{aligned} E_{Q Q {\bar{q}} {\bar{q}}}&= g\left( 2 \int _0^{r_v}\left( \frac{e^{s r^2}}{r^2} \sqrt{1+f(r)\left( \partial _r x\right) ^2}-\frac{1}{r^2}\right) \textrm{d} r\right. \\&\quad \left. -\frac{2}{r_v}+6 k \frac{e^{-2 s r_{{\bar{v}}}{ }^2}}{r_{{\bar{v}}}} \sqrt{f\left( r_{{\bar{v}})}\right. }\right. \\&\quad \left. +2 n \frac{e^{\frac{1}{2} s r_{{\bar{q}}}^2}}{r_{{\bar{q}}}} \sqrt{f(r {\bar{q}})}\right) +2 c . \end{aligned} \end{aligned}$$
(30)

The force balance equation at the point \(r=r_v= r_{{\bar{v}}}= r_{{\bar{q}}}\) is

$$\begin{aligned} \begin{aligned} f_{v}+f_{{\bar{v}}}+2f_{{\bar{q}}}+e_{1}+e_{2} =0. \end{aligned} \end{aligned}$$
(31)

Each force is determined by

$$\begin{aligned} \begin{aligned} f_v&=f_{{\bar{v}}}=\left( 0,-3 g k\partial _{r_{v}}(\frac{\textrm{e}^{-2s r_{v}^{2}}}{r_{v}}\sqrt{f(r_{v})})\right) , \\ e_{1}&=g w_{(r_{v})}\left( -\frac{f(r_{v})}{\sqrt{t a n^{2}\alpha +f(r_{v})}},-\frac{1}{\sqrt{f(r_{v})c o t^{2}\alpha +1}}\right) ,\\ e_{2}&={g w_{(r_{v})}\left( \frac{f(r_{v})}{\sqrt{t a n^{2}\alpha +f(r_{v})}},-\frac{1}{\sqrt{f(r_{v})c o t^{2}\alpha +1}}\right) }, \\ {f}_{{\bar{q}}}&=\left( 0,-{\textbf{g}}n\partial _{r_{{\bar{q}}}} (\frac{\textrm{e}^{\frac{1}{2}\text {s}\textrm{r}_{{\bar{q}}}^2}}{r_{{\bar{q}}}}\sqrt{f(r_{{\bar{q}}})})\right) . \end{aligned} \end{aligned}$$

Here \(r_{{\bar{q}}}=r_{{\bar{v}}}=r_{v}\), then, the Eq. (31) becomes

$$\begin{aligned}&ke^{-2sr_{v}}(24sr_{v}^2f(r_{v})+6f(r_{v})-3r_{v}f' (r_{v}))\nonumber \\&\quad +ne^{\frac{1}{2}sr_{v}^2}(2f(r_{v}) -2sr_{v}^2f(r_{v})\nonumber \\&\quad -r_{v}f'(r_{v}))-\frac{2\sqrt{f(r)} e^{sr_{v}^2}}{\sqrt{f\left( r_v\right) \cot ^2 \alpha +1}}=0. \end{aligned}$$
(32)

3.4 Large L

Fig. 4
figure 4

Static configuration at a large separation distance of a heavy-quark pair. There are two turning points at strings (1) and (2) and they are symmetric about the Y-axis. The force acting on the point is indicated by the black arrow

Full size image

Figure 4 illustrates the fourth configuration. The total action for this configuration, denoted as intermediate L, is given by Eq. (28). We choose another static gauge \(\xi ^1=t\) and \(\xi ^2=x\) in the Nambu–Goto actions and the boundary conditions are

$$\begin{aligned} \begin{aligned} r^{(1)}(-L/2)=r^{(2)}(L/2)=0,\quad r^{(i)}(0)=r_v. \end{aligned} \end{aligned}$$
(33)

Then, the total action becomes

$$\begin{aligned} S=&gT\Big (\int _{- L/2}^{0}\frac{e^{sr^{2}}}{r^{2}}\sqrt{f(r)+(\partial _{r}x)^2\textrm{d}x}\nonumber \\ {}&+\int _{0}^{L/2}\frac{e^{sr^{2}} }{r^{2}}\sqrt{f(r)+(\partial _{r}x)^2\textrm{d}x}\nonumber \\ {}&+6k\frac{e^{- 2sr_{v}^{2}}}{r_{v}}\sqrt{f(r_{v})}+2n\frac{e^{-\frac{1}{2} sr_{\bar{q} }^{2}}}{r_{\bar{q}}}\sqrt{f(r_{\bar{q}})}\Big ). \end{aligned}$$
(34)

The action for string (1) is given by the first term in Eq. (34). The subsequent step is to compute the first integral.

$$\begin{aligned} \begin{aligned} \mathcal {I=}\dfrac{w(r)f(r)}{\sqrt{f(r)+\left( \partial _x r\right) ^2}}. \end{aligned} \end{aligned}$$
(35)

\({\mathcal {I}}\) is a constant. At the \(r_0\) and \(r_v\) points, we can obtain, respectively

$$\begin{aligned} \begin{aligned} \dfrac{w(r)f(r)}{\sqrt{f(r)+\left( \partial _x r\right) ^2}}=w(r_0)\sqrt{f(r_0)}. \end{aligned} \end{aligned}$$
(36)
$$\begin{aligned} \begin{aligned} \frac{w(r_v)f(r_v)}{\sqrt{f(r_v)+tan\alpha ^2}}=w(r_0)\sqrt{f(r_0)}. \end{aligned} \end{aligned}$$
(37)

Here \(\partial _x r\) can be obtained from Eqs. (36), (37)

$$\begin{aligned} \begin{aligned} \partial _x r=\sqrt{\frac{w(r)^2f(r)^2f(r_0)-f(r)w(r_0)^2f(r_0)^2}{w(r_0)^2f(r_0)^2}}. \end{aligned} \end{aligned}$$
(38)

The large L configuration has a turning point at \(r_{0}\), so the distance between heavy quarks is calculated in two parts. Then, the separation distance can be expressed as

$$\begin{aligned} \begin{aligned} L=2(L_1+L_2)=2\left( \int _0^{r_0}\dfrac{1}{r'}dr+\int _{r_v}^{r_0}\dfrac{1}{r'}dr\right) . \end{aligned} \end{aligned}$$
(39)

Here \(r'\) denotes \(\partial _x r\). By substituting Eq. (38) into Eq. (39), the separation distance can be obtained. The energy of string (1) was calculated in two parts, which is similar to the separation distance. Therefore, the energy of string (1) is given by

$$\begin{aligned} \begin{aligned} E_1&=E_{R_1}+E_{R_2}={\textbf{g}}\int _0^{r_0}w(r)\sqrt{1+f(r)x'^2}dr\\&\quad +{\textbf{g}}\int _{r_{{\bar{q}}}}^{r_0}w(r)\sqrt{1+f(r)x'^2}dr. \end{aligned} \end{aligned}$$
(40)

Same as the case of small L, we also need to subtract the divergent term here. Thus, Eq. (40) can be expressed as

$$\begin{aligned} E_1&={\textbf{g}}\int _0^{r_0}\left( w(r)\sqrt{1+f(r)x'^2}-\dfrac{1}{r^2}\right) dr\nonumber \\&\quad +{\textbf{g}}\int _{r_v}^{r_0}w(r)\sqrt{1+f(r)x'^2}dr-\dfrac{1}{r_0}+2c. \end{aligned}$$
(41)

String (2) is calculated in the same way as string (1). Therefore, the total energy of the configuration is

$$\begin{aligned} E_{Q Q \bar{q} \bar{q}}=&\textrm{2g} \int _0^{r_0}(w(r) \sqrt{1+f(r) x^{\prime 2}}-\frac{1}{r^2}) d r\nonumber \\&+2 \mathrm {~g} \int _{r_v}^{r_0} w(r) \sqrt{1+f(r) x^{\prime 2}} d r-\frac{2g}{r_0}\nonumber \\&+6 k g \frac{e^{-2 s r_{\bar{v}}}}{r_{\bar{v}}} \sqrt{f(r_{\bar{v}})}+2 n g \frac{e^{\frac{1}{2} s r_{\bar{q}}^2}}{r_{\bar{q}}} \sqrt{f(r_{\bar{q}})}+2 c . \end{aligned}$$
(42)

The force balance equation is the same as that for intermediate L, and the expressions of force are also the same as intermediate L. Equation (37) represents the functional relationship between \(r_{v}\) and \(\alpha \) when the temperature is fixed. We can first solve Eqs. (32) and (37), and then substitute the numerical values into Eqs. (39) and (42) to obtain the solutions for L and \(E_{QQ{\bar{q}}{\bar{q}}}\). For \(\alpha \), at small separate distance of heavy quarks, as \(r_v\) increases, the distance between the heavy quarks increases, and the curvature of the string between heavy quarks increases, causing \(\alpha \) to decrease. When the string reaches \(\alpha =0\) and \(r_v\) increases further, the string will become an M-shape, at which point \(\alpha \) becomes negative.

4 Numerical results and discussion

4.1 T = 0.08 GeV

Fig. 5
figure 5

\(r_0\) as a function of \(r_v\) in the larger L configuration, where the black line is \(r_0\) at \(T = 0\), while the blue line is \(r_0\) at \(T = 0.08\) \({\textrm{GeV}}\). \(r_w\) indicates the position of a dynamic wall

Full size image

At a low temperature of 0.08 \({{\textrm{GeV}}}\), the configurations of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) are confined. Below the black-hole horizon, there exists a dynamic wall that prevents the string from crossing. In this part, we investigate four configurations of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) at this temperature.

First, we will give a discussion about the dynamic wall at finite temperature. Different from the quark–antiquark pair, the configuration of QQqq shows a “M” shape at large separation distance. Thus, the maximum value of \(r_0\) at infinite separation distance gives the position of dynamic wall. By calculating the position of the dynamic wall, we obtain \(r_{w}=1.40\, {{\textrm{GeV}}^{-1}}\) at \(T = 0\) and \(r_{w}=1.45\,{{\textrm{GeV}}^{-1}}\) at \(T = 0.08\) \({{\textrm{GeV}}}\) as shown in Fig. 5. The increase of temperature leads to an increase of the position of dynamic wall in the r direction.

For small L, we use Eq. (18) to calculate the position of the antiquark. The result shows that at a temperature of 0.08 \({{\textrm{GeV}}}\), \(r_{{\bar{q}}}=1.13\) \({{\textrm{GeV}}^{-1}}\). Subsequently, the antibaryon vertex position can be calculated using Eq. (20), which yields \(r_{{\bar{v}}}=0.445\) \({{\textrm{GeV}}^{-1}}\). Within the range of \(0<r<r_{v}\), we can calculate \(\alpha \) using Eq. (22), as illustrated in Fig. 6. It can be observed that \(\alpha \) exhibits a decreasing trend as \(r_v\) increases. Then, the separation distance of a heavy-quark pair and its corresponding energy can then be obtained using Eqs. (11) and (16), respectively. These results are presented in Fig. 10 and Fig. 11.

Fig. 6
figure 6

\(\alpha \) as a function of \(r_v\) in the small L configuration. The unit for \(r_v\) is \({{\textrm{GeV}}^{-1}}\)

Full size image

When \(r_v\) increases to \(r_{{\bar{v}}}\), it reaches a critical value and transitions to the second configuration. In the second configuration, we can still determine the position of antiquark using Eq. (18). Subsequently, we use Eq. (27) to obtain \(\alpha \), as depicted in Fig. 7. \(\alpha \) exhibits an increasing trend as \(r_v\) increases, reaching its peak when \(r_v=r_{{\bar{v}}}\). Next, we can obtain the separation distance and energy of the second configuration using Eqs. (11) and (25), and it is observed that as \(r_v\) increases, L and E also exhibit an upward trend. When \(r_v\) reaches \(r_{{\bar{v}}}\), it attains its maximum value. Beyond this point, the configuration switches to the third configuration.

Fig. 7
figure 7

\(\alpha \) as a function of \(r_v\) in the slightly larger L configuration. The unit for \(r_v\) is \({{\textrm{GeV}}^{-1}}\)

Full size image

In the third configuration, \(r_{{\bar{v}}}\) overlaps with the \(r_{{\bar{q}}}\) point. Using Eq. (32), we can establish a functional relationship between \(r_v\) and \(\alpha \), as shown in Fig. 8. Clearly, \(\alpha \) exhibits a linear decrease with increasing \(r_v\) until it reaches 0. E and L can be obtained using Eqs. (11) and (30). In this configuration, E varies linearly with L. When \(r_v\) exceeds \(r_{{\bar{q}}}\), the configuration shifts into the fourth configuration.

Fig. 8
figure 8

\(\alpha \) as a function of \(r_v\) in the intermediate L configuration. The unit for \(r_v\) is \({{\textrm{GeV}}^{-1}}\)

Full size image

Then, in the configuration with large L, as \(r_v\) increases below the dynamic wall, strings (1) and (2) exhibit turning points. \(\alpha \) continues to decrease as \(r_v\) increases, as shown in Fig. 9. However, unlike before, \(\alpha \) becomes negative. As shown in Fig. 9, the maximum value of \(r_v\) is 1.40 \({{\textrm{GeV}}^{-1}}\), which corresponds to the position of the dynamic wall at \(r_w\approx r_0\approx 1.45\) \({{\textrm{GeV}}^{-1}}\). We can obtain E and L using Eqs. (39) and (42).

Fig. 9
figure 9

\(\alpha \) as a function of \(r_v\) in the large L configuration. The unit for \(r_v\) is \({{\textrm{GeV}}^{-1}}\)

Full size image
Fig. 10
figure 10

Separation distance L as a function of \(r_v\), where the black line represents the configuration with small L, blue represents slightly larger L, orange represents intermediate L, and red represents larger L. The unit of L is in \({{\textrm{fm}}}\) and that of \(r_v\) is in \({{\textrm{GeV}}^{-1}}\)

Full size image
Fig. 11
figure 11

Energy E as a function of separation distance L at \(T=0.08\) \({{\textrm{GeV}}}\). The black line represents the configuration with small L, blue line represents slightly larger L, orange line represents intermediate L, and red line represents larger L. The unit of E is in \({\textrm{GeV}}\) and that of \(r_v\) is in \({{\textrm{GeV}}^{-1}}\)

Full size image

At \(T=0.08\) \({\textrm{GeV}}\), the separation distance and energy plots for the tetraquark configuration are illustrated in Figs. 10 and 11, respectively. As can be observed from the figure, there is a smooth connection of L for each configuration. As \(r_v\) increases, L also approaches infinity. This implies that \(r_v\) cannot be infinite, and when the maximum value is exceeded, the configuration will decay into another state. We will discuss this further in the upcoming section. The energy increases as the separation distance increases. Notably, the energy is dominated by Coulomb potential at small separation distances and linear potential at large distances.

4.2 T = 0.115 GeV

At a temperature of \(T = 0.115\) \({\textrm{GeV}}\), the configurations of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) are deconfined. For a deconfined \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\), the melting of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) can happen at a certain separation distance. If the separation distance of heavy quark–antiquark pair is small enough, the \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) will not melt even at high temperature. When increasing the distance of heavy quark–antiquark pair, the color screening becomes important and the \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) will melt. In summary, the dynamic wall disappears and \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) will melt at a sufficiently far distance in this stage.

Firstly, similar to \(T=0.08\) \({\textrm{GeV}}\), we focus on the first configuration. The position of the antiquark can be determined using Eq. (18), which yields \(r_{{\bar{q}}}=1.1677\) \({{\textrm{GeV}}^{-1}}\) when \(T=0.115\) \({\textrm{GeV}}\). Next, we can calculate the position of the antibaryon vertex using Eq. (20), which yields \(r_{{\bar{v}}}=0.4626\) \({{\textrm{GeV}}^{-1}}\), and then use Eq. (22) to determine \(\alpha \). L and E can still be obtained from Eqs. (11) and (16), respectively. We can then proceed to investigate the second and third configurations using a similar approach as the \(T=0.08\) \({\textrm{GeV}}\) calculation. This will enable us to determine the separation distance and energy. As the value of \(r_v\) continues to increase, the value of L also exhibits a tendency to increase. However, as L approaches a maximum value, it will tend towards infinity, indicating that the quark is now free and large L configurations will no longer be possible as shown in Fig. 12 [57,58,59]. First, similar to \(T=0.08\) \({\textrm{GeV}}\), we focus on the first configuration. The position of the antiquark can be determined using Eq. (18), which yields \(r_{{\bar{q}}}=1.1677\) \({{\textrm{GeV}}^{-1}}\) when \(T=0.115\) \({\textrm{GeV}}\). Next, we can calculate the position of the antibaryon vertex using Eq. (20), which yields \(r_{{\bar{v}}}=0.4626\) \({{\textrm{GeV}}^{-1}}\), and then use Eq. (22) to determine \(\alpha \). L and E can still be obtained from Eqs. (11) and (16), respectively. Subsequently, we can investigate the second and third configurations at this temperature by adopting the same method as the \(T=0.08\) \({\textrm{GeV}}\) calculation, which allows us to determine the separation distance of heavy quarks and energy. As the value of \(r_v\) continues to increase, the value of L also exhibits a tendency to increase. However, as L approaches a maximum value (\(L_{max}=1.56{\textrm{fm}}\)), it will tend towards infinity, indicating that the quark is now free and large L configurations will no longer be possible [57,58,59]. The diagram of energy and separation distance is shown in Fig. 12.

Fig. 12
figure 12

Energy E as a function of separation distance L at \(T=0.115\) \({\textrm{GeV}}\). The black line represents the configuration with small L, blue line represents slightly larger L and orange line represents intermediate L. The unit of E is in \({\textrm{GeV}}\) and that of \(r_v\) is in \({{\textrm{GeV}}^{-1}}\)

Full size image
Fig. 13
figure 13

Energy E as a function of separation distance L at \(T=0.12\) \({\textrm{GeV}}\). The black line represents the configuration with small L and blue line represents slightly larger L. The unit of E is in \({\textrm{GeV}}\) and that of \(r_v\) is in \({{\textrm{GeV}}^{-1}}\)

Full size image

4.3 T = 0.12 GeV

To begin with, we can use Eq. (18) to determine the position of the antiquark, which is \(r_{{\bar{q}}}=1.1785\) \({{\textrm{GeV}}^{-1}}\) when \(T = 0.12\) \({\textrm{GeV}}\). Next, we can use Eq. (20) to calculate the position of the antibaryon vertex, which yields \(r_{{\bar{v}}}=0.46574\) \({{\textrm{GeV}}^{-1}}\). Following this, we can similarly obtain functional expressions for \(\alpha \), L, and E as \(r_v\) increased, which are illustrated in Fig. 13. As depicted in the figure, both L and E exhibit linear growth with respect to \(r_v\), and the energy function E shows a Cornell-like potential. At slightly larger L, Eqs. (11) and (25) are employed to calculate the separation distance and energy. However, at this temperature, as \(r_v\) keeps increasing, the configuration will eventually collapse, leading to the quark becoming a free state. Therefore, there exists a maximum value of L, beyond which L will tend towards infinity. Consequently, large values of L are not possible at this temperature.

Fig. 14
figure 14

Energy E as a function of separation distance L at \(T=0.15\) \({\textrm{GeV}}\). The black line represents the configuration with small L. The unit of E is in \({\textrm{GeV}}\) and that of \(r_v\) is in \({{\textrm{GeV}}^{-1}}\)

Full size image

4.4 T = 0.15 GeV

At this temperature, using the force balance equation, the position of the quark or antibaryon vertex is determined to be \(r_{{\bar{v}}}=0.4726\) \({{\textrm{GeV}}^{-1}}\). However, we have discovered that at this temperature there is no solution for the position of the antiquark, \(r_{{\bar{q}}}\). Therefore, we have computed the separation distance and energy for the first configuration, which are displayed in Fig. 14. As \(r_{{\bar{v}}}\) surpasses a certain value, the \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) configuration collapses, resulting in the quark becoming free.

Fig. 15
figure 15

The blue dash line is the energy at zero temperature, while the black line is the energy at \(T=0.11\) \({\textrm{GeV}}\)

Full size image

4.5 Short summary

Based on the calculation results of the \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) potential at the above mentioned four temperatures, it shows that both \(r_{{\bar{q}}}\) and \(r_{{\bar{v}}}\) become larger and gradually approach the position of the dynamic wall as the temperature increases. Furthermore, the melting of the \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) configuration happens at a small distance as the temperature increases. Comparing the two lines for \(T=0\) and \(T=0.11\) \({\textrm{GeV}}\) in Fig. 15, we observe that as temperature increases, the same separation distance L corresponds to a lower energy value. Besides, at small distances, \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) exhibits Coulombic behavior, whereas at large distances, the behavior is linear at finite temperature [60,61,62].

5 Decay modes

5.1 \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\)

Fig. 16
figure 16

Three disconnected configuration of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\)

Full size image

During the confinement phase, quarks are confined within hadrons. However, as the distance between heavy quarks increases, the strings connecting them eventually break [63]. In this context, we shall consider three decay modes for \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) configurations.

(43)

Figure 16 displays the configuration diagram for the three possible decay modes. We will proceed to analyze the energy of each disconnected configuration. \({{\textrm{Q}}{\bar{{\textrm{q}}}}}\) consists of a fundamental string and an antiquark, with the total action given by \(S_{Q{\bar{q}}}=S_{\textrm{NG}}+S_{\textrm{q}}\). \({\textrm{QQq}}\) comprises two strings, a vertex, and a light quark. The total action can be written as \(S_{QQq}=\sum _{i=1}^2S_{\text {NG}}^{(i)}+S_{\text {vert}}+S_{{{\bar{q}}}}\). On the other hand, \({{\textrm{Qq}}{\bar{{\textrm{q}}}}{\bar{{\textrm{q}}}}}\) consists of four strings, a vertex, a antibaryon vertex, a light quark and two antiquarks. The total action is \(S_{Qq{\bar{q}}{\bar{q}}}=\sum _{i=1}^4S_{\text {NG}}^{(i)}+S_{v}+S_{{\bar{v}}}+2S_{{{\bar{q}}}}+S_{q}\). Furthermore, \({\bar{q}}{\bar{q}}{\bar{q}}\) consists of a antibaryon vertex and three antiquarks, with the total action \(S_{{\bar{q}}{\bar{q}}{\bar{q}}}=S_{{\bar{v}}}+3S_{{{\bar{q}}}}\). We employ the same static gauge as before and obtain the total action for each configuration by specifying appropriate boundary conditions. The detailed calculation process of the energy of each configuration is given in Refs. [48, 49, 55, 56]. Subsequently, The action of each decay is then calculated.

$$\begin{aligned} \begin{aligned} S_{1}&=S_{Q{\bar{q}}}+S_{Q{\bar{q}}}\\ S_{2}&=S_{QQq}+S_{{\bar{q}}{\bar{q}}{\bar{q}}}\\ S_{3}&=S_{Qq{\bar{q}}{\bar{q}}}+S_{Q{\bar{q}}}. \end{aligned} \end{aligned}$$
(44)
Fig. 17
figure 17

a \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) and his three disconnected configuration energy at temperature \(T=0\) \({\textrm{GeV}}\). b \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) and his three disconneccted configuration energy at temperature \(T=0.08\) \({\textrm{GeV}}\). The black line is the energy of \(E_{QQ{\bar{q}}{\bar{q}}}\), the blue line is the energy of \(2E_{Q{\bar{q}}}\), the orange line is the energy of \(E_{QQq}+E_{{\bar{q}}{\bar{q}}{\bar{q}}}\), and the green line is the energy of \(E_{Qqq{\bar{q}}}+E_{Q{\bar{q}}}\)

Full size image

The results of the calculation are shown in Fig. 17. Here, we define the string-breaking distance as the intersection point of the two energies. As shown in Fig. 17b, we can see that when \(L_{QQ{\bar{q}}{\bar{q}}}=0.1870\) \({\textrm{fm}}\), \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) will decay into \({{\textrm{Q}}{\bar{{\textrm{q}}}}+{\textrm{Q}}{\bar{{\textrm{q}}}}}\), and when \(L_{QQ{\bar{q}}{\bar{q}}}=1.3036\) \({\textrm{fm}}\), \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) will decay into \({{\textrm{Qq}}{\bar{{\textrm{q}}}}{\bar{{\textrm{q}}}}+{\textrm{Q}}{\bar{{\textrm{q}}}}}\). However, at zero temperature (as shown in Fig. 17a), the former decay takes place at \(L_{QQ{\bar{q}}{\bar{q}}}=0.1874\) \({\textrm{fm}}\), while the latter occurs at \(L_{QQ{\bar{q}}{\bar{q}}}=1.3147\) \({\textrm{fm}}\). The first scenario is linked to the process of vertex annihilation, whereas the second pertains to the occurrence of string breaking through the production of light quark pairs. The \({{\textrm{QQ}}{\bar{{\textrm{q}}}}{\bar{{\textrm{q}}}}}\longrightarrow {{\textrm{Q}}{\bar{{\textrm{q}}}}+{\textrm{Q}}{\bar{{\textrm{q}}}}}\) is the most possible decay mode. The presence of small temperature will increase the string-breaking distance a little bit. There is always a energy difference for \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) and \({{\textrm{QQq}}+{\bar{{\textrm{q}}}}{\bar{{\textrm{q}}}}{\bar{{\textrm{q}}}}}\) as shown in Fig. 17. Thus, the decay mode \({{\textrm{QQ}}{\bar{{\textrm{q}}}}{\bar{{\textrm{q}}}}}\longrightarrow {{\textrm{QQq}}+{\bar{{\textrm{q}}}}{\bar{{\textrm{q}}}}{\bar{{\textrm{q}}}}}\) also will not happen.

5.2 The relation between \({\textrm{QQq}}\) and \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\)

In this part, we will discuss the difference between \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) and \({\textrm{QQq}}\) at a temperature of 0.08 \({\textrm{GeV}}\). The \({\textrm{QQq}}\) configuration has also garnered widespread attention. Similar to the \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) configuration, the decay process \({{\textrm{QQq}}\longrightarrow {\textrm{Qqq}}+{\textrm{Q}}{\bar{{\textrm{q}}}}}\) will occur in the \({\textrm{QQq}}\) configuration at high temperatures. As shown in Fig. 18, we calculated the two configurations separately as well as the energy after their decay. Then, \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) decays to \({{\textrm{Q}}{\bar{{\textrm{q}}}}}\) at \(E=2.3806\) \({\textrm{GeV}}\) \((L=0.1980\) \({\textrm{fm}})\), and \({\textrm{QQq}}\) decays to \({{\textrm{Qqq}}+{\textrm{Q}}{\bar{{\textrm{q}}}}}\) at \(E=3.0167\) \({\textrm{GeV}}\) \((L=1.2646\) \({\textrm{fm}})\). At lower energies and smaller separation distances, the \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) configuration will decay, while QQq is more stable. This difference may result from two distinct mechanisms: string breaking by light quarks for \({\textrm{QQq}}\) and string junction annihilation for \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\).

Fig. 18
figure 18

a The energy of the \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) and two \(\mathrm Q{\bar{q}}\). b The energy of the \({\textrm{QQq}}\) and \({{\textrm{Qqq}}}\)+\(\mathrm Q{\bar{q}}\)

Full size image

Here, we also consider another relation in [29, 37], which is \(E_{\mathrm {QQ {\overline{q}} \overline{ q }}}=E_{\textrm{QQq}}+E_{\textrm{Qqq}}-E_{\textrm{q} {\bar{Q}}}\). This relationship is derived from heavy quark–diquark symmetry, as illustrated in Fig. 19. Furthermore, similar to the case at zero temperature, we find that relationship occurs at a very small separation distance when \(T=0.08\) \({\textrm{GeV}}\). After \(L=0.2662\) \({\textrm{fm}}\), the potential energy of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) and \({{\textrm{QQq}}+{\textrm{Qqq}}-{\textrm{q}}{\bar{{\textrm{Q}}}}}\) continues to increase. So there’s a slight difference in energy, specifically, the energy of \({{\textrm{QQq}}+{\textrm{Qqq}}-{\textrm{q}}{\bar{{\textrm{Q}}}}}\) will be slightly higher than that of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\). In addition, we find that the energy difference between before and after equation will occur after \(L=0.2396\) \({\textrm{fm}}\) when it is at zero temperature, and after \(L=0.2662\) \({\textrm{fm}}\) when it is at \(T=0.08\) \({\textrm{GeV}}\). The increase in temperature will increase the critical distance for the appearance of energy difference.

Fig. 19
figure 19

a The energy of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) and \({{\textrm{QQq}}+{\textrm{Qqq}}-{\textrm{q}}{\bar{{\textrm{Q}}}}}\) at \(T=0\) \({\textrm{GeV}}\). b The energy of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) and \({{\textrm{QQq}}+{\textrm{Qqq}}-{\textrm{q}}{\bar{{\textrm{Q}}}}}\) at \(T=0.08\) \({\textrm{GeV}}\)

Full size image

6 Summary and conclusion

This paper focuses on the melting and breaking of strings in \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) at finite temperatures by using the five-dimensional effective string model, and compares it with QQq under same conditions. During the confinement phase, a dynamic wall which strings cannot penetrate forms below the black-hole horizon. As the temperature increases, the system enters the deconfinement phase. In this phase, the dynamic wall disappears, causing the \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) string to melt and the quarks to become free. We investigate the energy of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) at which string melting occurs at four different temperatures. Subsequently, the study of three decay modes of \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) configuration at high temperature is continued, and the temperature at which the different decay modes occur is calculated. Finally, we compare the decay model of the \({{\textrm{QQ}}}\bar{{\textrm{q}}}\bar{{\textrm{q}}}\) configuration at \(T=0.08\) \({\textrm{GeV}}\) with that of the QQq and conclude that the QQq configuration is more stable under the same conditions. Ultimately, we aim to provide additional insights for experiments through our study of the effective string model in the future work.