Minimally deformed anisotropic stars in dark matter halos under EGB-action

Abstract

In this paper, we introduce an anisotropic model using a dark matter (DM) density profile in Einstein–Gauss–Bonnet (EGB) gravity using a gravitational decoupling method introduced by Ovalle (Phys Rev D 95:104019, 2017), which has provided an innovative approach for obtaining solutions to the EGB field equations for the spherically symmetric structure of stellar bodies. The Tolman and Finch–Skea (TFS) solutions of two metric potentials, $g_{tt}$ and $g_{rr}$, have been used to construct the seed solution. Additionally, the presence of DM in DM halos distorts spacetime, causing perturbations in the $g_{rr}$ metric potential, where the quantity of DM is determined by the decoupling parameter $\beta$. The physical validity of the solution, along with stability and equilibrium analysis, has also been performed. Along with stability and equilibrium analysis, the solution’s physical validity has also been examined. Additionally, we have shown how both constants affect the physical characteristics of the solution. Using a $M{-}R$ diagram, it has been described how the DM component and the GB constant affect the maximum permissible masses and their corresponding radii for various compact objects. Our model predicts the masses beyond the $2~M_{\odot }$ and maximum radii $11.92^{+0.02}_{-0.01}$ and $12.83^{+0.01}_{-0.02}$ for larger value of $\alpha$ under density order $10^{15}~\text {g}/\text {cm}^3$ and $10^{14}~\text {g}/\text {cm}^3$, respectively, while the radii become $11.96^{+0.01}_{-0.01}$ and $12.81^{+0.01}_{-0.02}$ for larger value of $\beta$.

1 Introduction

Compact stars (CSs) are a family of stellar bodies such as white dwarfs (WDs), neutron stars (NSs), and quark stars (QSs), with very high density and matter extremely packed inside them. Their exact nature and the physics of the interior of CSs are still not completely known. Theorists have been investigating several different models to come up with a concrete theory of these objects. So far, these have been an enigma to all of us. Among many approaches, researchers have considered charge, anisotropy, and many other considerations in order to estimate the matter distribution of these objects. Also, alongside general relativity (GR), several modified gravities have also been used to model these objects. A particular approach has been very interesting, as some researchers have considered the existence of DM inside CSs. Before going into that, let us discuss some brief insights about DM.

In the present time, the dark contents of the universe are perhaps one of the most challenging aspects for scientists to understand. Despite its existence in the $\varLambda$-CDM model, the DM has not been detected anywhere. According to the $\varLambda$-CDM model, about 27% of the total mass of the Universe comes from DM [1, 2]. The analysis of spiral galaxies and their rotational curve first hinted at these enigmatic components [3,4,5]. Several efforts have been made to explain this since then, and among many approaches, Neutralino has been one of the main candidates as the key constituent in the search for the origin of DM. This Neutralino is a member of the lightest supersymmetric particle group [6,7,8]. Interestingly, CSs made of DM were proposed in a model [9], where the DM was represented as fermion gauge singlets in the standard model (SM) in a background made of dark energy (DE). This comes from the prediction of pseudo-complex GR. Several other works have been done to model CSs with DM. In the work of [10], the mass–radius ratio was analysed for varying DM profiles. In [11, 12], the polytropic equation of state (EoS) was used to model NSs, and it was studied how self-interacting and spin-polarised DM influence it. Furthermore, how the CSs made of condensed DM affect gravity was studied in [13, 14]. In [15], the potential of the existence of NS having a DM core was investigated.

The matter distribution of CSs is another interesting topic. It can be isotropic, anisotropic, or even contain charge. However, there are a very handful of exact interior solutions to Einstein’s field equations considering isotropic matter distribution. Whereas, there are many anisotropic solutions obtained by generalising the known isotropic solutions. Now, when the nuclear matter is packed in extremely dense conditions, it is less probable that the matter distribution may remain isotropic. This can be attributed to several facts, including energy dissipation due to the emission of low-mass or massless particles, exotic phase transitions, and an increase in viscosity. This was explained in a detailed manner in a paper by Herrera and Santos [16]. In fact, Ruderman [17] showed that when densities exceed the order of $10^{15}~\text {g}/\text {cm}^3$, then the pressure breaks into radial and tangential components with different magnitudes, resulting in pressure anisotropy. Several works have been done considering CSs with anisotropic matter distribution in various scenarios [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45].

In this current article, a specific kind of gravity theory named 5D EGB gravity has been used. Let us shed light on this 5D EGB gravity. Despite being one of the most ground-breaking and pioneering theories, Einstein’s GR theory failed to answer several questions later on. The most prominent of them is the accelerated expansion of the Universe and its dark components. Researchers have been trying to find suitable DM components, and some researchers are trying to formulate modified theories of gravity that explain all the observable phenomena that GR has failed to explain until now. One such theory is 5D EGB gravity. When the fields are quantized in curved spacetime, the higher curvature modifications need to be done in the Einstein–Hilbert action [46]. So, this motivated a recent interest in exploring the possibilities of higher-order gravity theories containing higher-order derivative curvature terms, and among them, the most recognised theory is Lovelock gravity. This was first incorporated by Lanczos [47] in 1938, and it was used again much later by Lovelock [48, 49] in the 1970s. One of the key features of the Lovelock gravity is that it is truncated after the second-order derivatives of the metric. Also, in this theory, the Bianchi identities are included, which makes sure that the energy is conserved, i.e., $\varDelta ^i T_{ij} = 0$. When the linearized theory is quantized, it is free of ghosts [50, 51]. So it can be said that the Lovelock theory is a generalisation of Einstein’s GR theory to contain higher curvature terms, and it provides an ideal way to test how higher curvature terms affect the gravitational effects. Now, it is worthwhile mentioning that the third term of the Lovelock Lagrangian is named the Gauss–Bonnet (GB) term, which is a second-order curvature term. Now, Einstein–Hilbert action containing the quadratic term, or the GB term, is famously called EGB gravity. In heterotic string theory, at low energy, the effective action is similar to this kind of action [52, 53]. In 4D, a scalar field can be included with the GB term, and its contribution is non-trivial [54]. In this way, some researchers included static and spherically symmetric black hole solutions [55, 56]. Several other works in EGB gravity have been done by the researchers in various scenarios, including CS solutions [57,58,59,60,61,62,63,64,65,66,67].

Our objective in the current work is to use gravitational decoupling via the MGD technique to investigate the feasibility of anisotropic stars within DM haloes under 5D EGB gravity. The analysis’s intriguing finding is that the self-gravitating system’s mass and stability are increased with the inclusion of a DM component through MGD. In this respect, studies on CS objects and a number of astrophysical phenomena conducted on the basis of both modified gravity theories and conventional GR are contained in the following Refs. [68,69,70,71,72,73,74,75,76,77,78,79,80,81,82] (The following references include a thorough explanation of many current applications, including black holes [83,84,85,86,87,88,89]).

The structure of the current paper is as follows: After a short introduction, we examine the foundations of the MGD-decoupling in Sect. 2 as it is applied to a static, spherically symmetric arrangement formed of an anisotropic star within the context of EGB gravity. The study of stellar anisotropic solutions produced by applying the well-known Finch–Skea spacetime and pseudo-isothermal density profiles using the MGD approach is covered in Sect. 3, which is divided into two subsections: Sect. 3.1. Seed solution via the Tolman–Finch–Skea (TFS) ansatz, and Sect. 3.2. Mimicking the density constraint to pseudo-isothermal density profiles, we match the anisotropic interior solution controlled by the anisotropic fluid to an external Boulware–Deser vacuum solution at a junction interface in Sect. 4. The physical characteristics of CSs, along with the stability and equilibrium conditions that resulted from gravitational decoupling using the MGD technique, are studied in Sects. 5 and 6. In Sect. 7, we discussed the analysis of physical parameters on the $r-\alpha$ planes and maximum mass constraints via the $M{-}R$ curve. The concluding remarks are in the last Sect. 8.

2 Revisit of basic field equations of EGB gravity in gravitational decoupling

We begin with the action of the 5-dimensional EGB gravity for the matter field as follows:

$$\begin{aligned} {\mathscr {I}}_{G}= & {} {\frac{1}{16 \pi }\int d^{5}x\sqrt{-g} \left[ {\mathscr {R}}-2\varLambda +\alpha {\mathscr {L}}_{\textrm{GB}} +{\mathscr {S}}_{\textrm{matter}}\right] }\nonumber \\{} & {} +\beta \,\int {\mathscr {S}}_{\theta }\sqrt{-g}~d^{5}x, \end{aligned}$$

(1)

where $\varLambda$ and ${\mathscr {R}}$ are the cosmological constant and the fifth-dimensional Ricci scalar, respectively. Since the Lagrangian of the matter field is ${\mathscr {S}}_{\textrm{matter}}$ and the Lagrangian of the additional field is ${\mathscr {S}}_{\theta }$. According to string theory, the coupling constant $\alpha$, which is associated with the inverse string tension, should have a positive value [90] and a dimension of $[\text {length}^2],$ but $\beta$ has no dimension. However, for the sake of generality, some scientists may have taken into account both scenarios as $\alpha >0$ and $\alpha <0$ (for a few other issues with positive and negative “$\alpha$,” see the following debates in [91, 92]). We only consider the situation of positive $\alpha$ in this study; for more current developments and references, see Refs. [93, 94]. Furthermore, the effect of cosmological constant $\varLambda$ on star stellar system is negligible because its observed value is $10^{-34}/\text {km}^{2}$. For the purposes of the study, we therefore assume it to be zero. The Ricci scalar, Ricci tensor, and Riemann curvatures are specifically combined to form the GB Lagrangian, which is given by

$$\begin{aligned} {\mathscr {L}}_{\textrm{GB}}={\mathscr {R}}^{ijkl} {\mathscr {R}}_{ijkl} -4 {\mathscr {R}}^{ij}{\mathscr {R}}_{ij}+ {\mathscr {R}}^2, \end{aligned}$$

(2)

where all indices run from 0 to 4. The variation of the action (1) relative to the coordinates $g^{ij}$ may be used to directly calculate the equation of motion as,

$$\begin{aligned} G_{ij}+\alpha H_{ij} = 8 \pi T^{\textrm{eff}}_{ij}, \quad \text{ where }\ T^{\textrm{eff}}_{ij}= {T}_{ij}+\beta \,T^\theta _{ij}, \end{aligned}$$

(3)

with

$$\begin{aligned} {T}_{ij}=-\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g} {\mathscr {S}}_m\right) }{\delta g^{ij}},\ \text {and}\ T^\theta _{ij}=\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}{\mathscr {S}}_{\theta }\right) }{\delta g^{ij}}.\nonumber \\ \end{aligned}$$

(4)

The symbol $H_{ij}$ serves as the part of the GB factor and $G_{ij}$ denotes the Einstein tensor having the corresponding equation

$$\begin{aligned} G_{ij}= & {} {\mathscr {R}}_{ij}-\frac{1}{2}{\mathscr {R}}~ g_{ij},\nonumber \\ H_{ij}= & {} 2\Big ( {\mathscr {R}} {\mathscr {R}}_{ij} -2{\mathscr {R}}_{ik} {{\mathscr {R}}}^k_j -2 {\mathscr {R}}_{ijkl}{{\mathscr {R}}}^{kl} - {\mathscr {R}}_{ikl\delta }{{\mathscr {R}}}^{kl\delta }_j\Big )\nonumber \\{} & {} -\frac{1}{2}~g_{ij}~{\mathscr {L}}_{\textrm{GB}}, \end{aligned}$$

(5)

where, accordingly, ${\mathscr {R}}$ is the Ricci scalar, ${\mathscr {R}}_{ijkl}$ is the Riemann tensor, and ${\mathscr {R}}_{ij}$ is the Ricci tensor. It should be emphasised that the gravitational dynamics in 4D spacetime are unaffected by the GB term.

For compact star modeling, we consider a static, spherically symmetric metric in a 5-dimensional spacetime as

$$\begin{aligned} ds^2_{5}= - e^{2\nu (r)} dt^2 + e^{2\lambda (r)}dr^2 + r^{2} d \varSigma ^2_3 , \end{aligned}$$

(6)

where r is a radial coordinate and $\nu (r)$ and $\lambda (r)$ are metric potentials. The line element of a three-dimensional hypersurface with constant scalar curvature k is denoted by the word $d \varSigma ^2_3$ in the metric above. Without losing generality, k can be adjusted to $k = 1, 0,$ or $-1,$ which, respectively, represent a sphere, plane, and hyperbola. Boulware and Deser [90] originally discovered a static black hole solution using spherically symmetric under EGB theory in 1985 by assuming $k = 1.$ After that, generalising black hole solutions with complex horizon topology were investigated using the cosmological constant [95]. These black holes in particular have an event horizon that can have a zero along with positive or negative constant curvature. They are also asymptotically anti-de Sitter black holes. See Ref. [96] for a similar solution that was discovered without the necessity for a cosmological constant component. In this article, we shall limit the range to $k=1$, which is the spherically symmetric solution.

Here, we make the assumption that the fluid inside the CS is anisotropic, as shown by the stress–energy tensor $T_{ij}$

$$\begin{aligned} {T}_{ij} = {\rho } u_{i}u_{j} +{P}_t (u_{i}u_{j}+g_{ij} -\chi _{i}\,\chi _{j})+ {P}_r \chi _{i}\,\chi _{j}, \end{aligned}$$

(7)

where, correspondingly, $\rho (r)$ indicates the energy density of matter and $P_r(r)$ and $P_t(r)$ indicate the radial and tangential pressures. Here, $u^{j}$ and $\chi ^i=\sqrt{1/g_{rr}}\,\delta ^i_1$ are called the 5-velocity contravariant and unit space-like vector in the direction of the radial coordinate, respectively. These vectors obey the relation: $\chi ^i\chi _i=-u_{j} u^{j}=1$. Hence, the effective stress–energy tensor ($T_{ij}$) is now defined as

$$\begin{aligned} T^{\textrm{eff}}_{ij} {=} (\rho ^{\textrm{eff}} {+} P^{\textrm{eff}}_t) \,u_{j} u_{j}{+} P^{\textrm{eff}}_t\, g_{ij}{+}(P^{\textrm{eff}}_r {-}P^{\textrm{eff}}_t)\chi _{i}\,\chi _{j},\nonumber \\ \end{aligned}$$

(8)

where $P^{\textrm{eff}}_r=P_r-\beta P^\theta _r$ and $P^{\textrm{eff}}_t=P_t-\beta P^\theta _t$ describe the radial and tangential pressures with $\rho ^{\textrm{eff}}_r=\rho +\beta \rho ^\theta$, which denotes the energy density for the matter tensor $T^{\textrm{eff}}_{ij}$. Additional anisotropic impact on $T^{\textrm{eff}}_{ij}$ is introduced by the existence of the $\theta$-term. It is well known that the covariant derivatives of the Einstein tensor $G_{ij}$ and Gauss–Bonnet tensor $H_{ij}$ is zero [97, 98], then the covariant derivative of the effective energy-momentum tensor given in Eq. (3) informs us that $T^{\textrm{eff}}_{ij}$ is also divergence-free i.e.

$$\begin{aligned} \nabla ^i\,T^{\textrm{eff}}_{ij}=0, \end{aligned}$$

(9)

which gives an equation

$$\begin{aligned} {\nu ^\prime }(\rho ^{\textrm{eff}}+P^{\textrm{eff}}_r)+(P^{\textrm{eff}}_r)^\prime +\frac{3}{r}(P^{\textrm{eff}}_r- P^{\textrm{eff}}_t)=0. \end{aligned}$$

(10)

The above equation is called a generalised hydrostatic equation in 5D-EGB gravity for the spacetime (6). Now, by utilising Eqs. (6) and (8) with the gravitational field equations (3), one may derive the non-vanishing components as follows:

$$\begin{aligned}{} & {} 8 \pi \rho ^{\textrm{eff}} =\frac{-3 \big ( 4 \alpha \lambda ^{\prime } + r e^{2 \lambda } - r e^{4 \lambda } - r^{2} e^{2 \lambda } \lambda ^{\prime } - 4 \alpha e^{2 \lambda } \lambda ^{\prime } \big )}{e^{4 \lambda } r^{3}} , \nonumber \\ \end{aligned}$$

(11)

$$\begin{aligned}{} & {} 8 \pi P^{\textrm{eff}}_r= \frac{3 \big (- r e^{4 \lambda } + \left( r^{2} \nu ^{\prime } + r + 4 \alpha \nu ^{\prime } \right) e^{2 \lambda } - 4 \alpha \nu ^{\prime } \big )}{e^{4 \lambda } r^{3}}, \end{aligned}$$

(12)

$$\begin{aligned}{} & {} 8 \pi P^{\textrm{eff}}_t = \frac{e^{-4 \lambda }}{ r^{2}} \big ( - 4 \alpha \nu ^{\prime \prime } -e^{4 \lambda } + 4 \alpha \nu ^{\prime } (3\lambda ^{\prime }- \nu ^{\prime } \big ) \nonumber \\{} & {} \quad + \frac{e^{-2 \lambda }}{ r^{2}} \big [ 1 + 2 r (\nu ^{\prime } - \lambda ^{\prime }) - r^{2} \nu ^{\prime } (\lambda ^{\prime }- \nu ^{\prime } \big ] \nonumber \\{} & {} \quad + \frac{e^{-2 \lambda }}{ r^{2}} \left[ (r^2+4 \alpha ) \nu ^{\prime \prime } - 4 \alpha \nu ^{\prime } (\lambda ^{\prime } - \nu ^{\prime } ) \right] . \end{aligned}$$

(13)

Here, the differentiation with regard to r is denoted by ‘$\prime$’. For an anisotropic fluid, the hydrostatic equilibrium condition is found by solving the equation Eq. (9) as,

$$\begin{aligned}{} & {} {\nu ^\prime }(\rho +P_r)+P^\prime _r +\frac{3}{r}(P_r-P_t) + \beta \,\Big [{\nu ^\prime }(\rho ^\theta -P^\theta _r) \nonumber \\{} & {} \quad -(P^\theta _r)^\prime -\frac{3}{r}(P^\theta _r-P^\theta _t)\Big ]=0. \end{aligned}$$

(14)

By using geometric deformation in the metric functions, it is possible to introduce the contribution of the source $\theta _{ij}$ in the system, which is given by

$$\begin{aligned}{} & {} \nu (r) \longrightarrow \xi (r)+\beta \, h(r), \end{aligned}$$

(15)

$$\begin{aligned}{} & {} \lambda (r)\longrightarrow -\frac{1}{2} \ln [\mu (r) +\beta \, f(r)], \end{aligned}$$

(16)

where the geometric deformations of the radial and temporal metric components, respectively, are h and f, respectively, and $\beta$ is an unrestricted parameter that “controls” the amount of deformation. The EGB solution is made to appear as a solution in the new gravitational sector via the MGD technique, as illustrated in the schematic figure in Fig. 1. Note that it can automatically restore in the domain of EGB when $\beta = 0$.

Here, we are interested in the MGD technique; therefore $f(r) \ne 0$ with $h(r) = 0$ must be set. Since MGD implies the deformation in the radial metric component only because the opposite (deformation only temporally and not radially) has no physical relevance, as it turns out to be a mere reparameterization. In this case, the radial deformation (16) introduces anisotropy into the system through the new source tensor $T^{\theta }_{ij}$.

The field equations (11)–(13) are divided into two sets by the transformation of (16). The system simplifies to being dependent on the gravitational potentials $\mu$ and $\nu$ when $\beta = 0$, so first we present the conventional EGB field equations that apply to the anisotropic situation as

$$\begin{aligned}{} & {} 8 \pi {\rho }=\frac{\big [12\alpha \mu ^{\prime 2} -12\alpha \mu ^{\prime } -3 r \mu ^\prime r-6r \mu + 6r\big ]}{2r^3} , \end{aligned}$$

(17)

$$\begin{aligned}{} & {} 8 \pi P_r=\frac{\big [ 12\alpha \mu ^{\prime 2} \nu ^\prime -12\alpha \mu ^{\prime } \nu ^\prime +3\,r \nu ^\prime \mu r+3\,r\mu -3\,r\big ]}{r^3} , \end{aligned}$$

(18)

$$\begin{aligned}{} & {} 8 \pi P_t=\frac{1}{2r^2}\big [(8\alpha \mu -8\alpha \mu ^2) (\nu ^{\prime 2}+\nu ^{\prime \prime })+4\alpha \mu ^\prime \nu ^\prime \nonumber \\{} & {} \quad -12\alpha \mu \mu ^\prime \nu ^\prime +2 \mu (\nu ^{\prime \prime } r^2+\nu ^{\prime 2} r^2+2 r \nu ^\prime +1)\nonumber \\{} & {} \quad +\mu ^\prime (\nu ^\prime r^2 +2 r) -2\big ]. \end{aligned}$$

(19)

Under the aforementioned supposition, the conservation equation (14) becomes

$$\begin{aligned} {\nu ^\prime }\,({\rho }+P_r)+P^\prime _r+\frac{3}{r}(P_r-P_t)=0. \end{aligned}$$

(20)

As a result, internal spacetime is represented as

$$\begin{aligned} ds^2_{5}= - e^{2\nu (r)} dt^2 + \frac{dr^2}{\mu (r)} + r^{2}d \varSigma ^2_3. \end{aligned}$$

(21)

The field equations for the second set of solutions, which includes the source $T^\theta _{ij}$, rely on the three unknown functions $\mu$, $\nu$, and f as

$$\begin{aligned}{} & {} 8 \pi \rho ^\theta = \frac{\big [ 12\alpha ( \beta f f^\prime + f^\prime (\mu -1)+f \mu ^\prime )-3\,r ( r f^\prime +2 f)\big ]}{2r^3} , \end{aligned}$$

(22)

$$\begin{aligned}{} & {} 8 \pi P^\theta _r = -\frac{3f \big [\nu ^\prime \, (-4\,\alpha \, f \beta -8\,\alpha \, \mu +4\,\alpha +r^2)+r\big ]}{r^3} , \end{aligned}$$

(23)

$$\begin{aligned}{} & {} 8 \pi P^\theta _t = -\frac{1}{2r^2}\,\big [-4\alpha \,\{2 [\beta f^2-2 (1-2\mu ) f] \nu ^{\prime \prime }\nonumber \\{} & {} \quad + (3 \mu +3 \beta f-1)\nu ^\prime f^\prime + (2\beta f \nu ^\prime + 2 \nu ^\prime (2 \mu -1) + 3 \mu ^\prime ) f \nu ^\prime \}\nonumber \\{} & {} \quad +2 r f^\prime \, + r^2 f^\prime \nu ^\prime +2( 1 + r^2 \nu ^{\prime 2} +r^2 \nu ^{\prime \prime }+2 \nu ^\prime r) f\big ]. \end{aligned}$$

(24)

The conservation equation $\nabla ^i\,T^\theta _{ij}=0$ explicitly read

$$\begin{aligned} -{\nu ^\prime }(\rho ^\theta -P^\theta _r)+(P^\theta _r)^\prime +\frac{3}{r}(P^\theta _r-P^\theta _t)=0. \end{aligned}$$

(25)

Therefore, we draw the conclusion that the MGD can successfully decouple the two sources $T_{ij}$ and $T^{\theta }_{ij}$. In the MGD condition, it is possible to observe a decoupling without an energy transfer between the sources [99].

3 Minimally deformed dark star in 5D EGB gravity

3.1 Seed solution via the Tolman-Finch–Skea (TFS) ansatz

Since we are dealing with two systems of equations that are highly non-linear differential equations in $\nu$ and $\mu$ given by Eqs. (17–19) and (22–24), respectively. It should be emphasised that the first system’s solution is necessary for the second system’s solution. Here, we are going to show how the minimum geometric deformation (MGD) technique in 5D EGB gravity may be used to construct a precise and physically viable solution.

The first apparent concern is what limitations we should put in place in order to close the seed system (17)–(19), yet there is no recognised solution to this problem. To set the scenario, we ought to keep the acceptable physics as much as required for a consistent stellar structure. In this direction, Delgaty and Lake [100] proposed a list of more than 130 isotropic solutions, in which only a small number of solutions that met the physical requirements could be categorised as physically relevant. Furthermore, recently a new methodology was proposed to generate some isotropic solutions using gravitational decoupling technique [101,102,103]. The isotropic Tolman IV [104], Durgapal [105], and Finch–Skea [107], Buchdahl [106] solutions are a few of the well-known models among them. These models were used by many researchers to build and analyse consistent astrophysical models for compact objects. In order to succeed in the aforementioned, let’s begin by taking into account a recently presented precise interior solution, known as the TFS metric ansatz,

$$\begin{aligned} \nu (r) {=} 2\ln [B (1+L\,r^2)]\quad \text {and}\,\mu (r) {=} 1/(1+N\,r^2),\nonumber \\ \end{aligned}$$

(26)

where B is a constant with no dimension and A and C are positive constants having a dimension of $[\text {Length}]^{-2}$. The metric potentials in the aforementioned form have been selected carefully to meet our requirements and allow us to observe the role of the decoupling function f(r). After that, the solutions of (17)–(19) are obtained by using metric potentials as,

$$\begin{aligned}&8\pi \,\rho =\frac{3 N (2 + 4 \alpha N + 3 N r^2 + N^2 r^4)}{(1 + N r^2)^3}, \end{aligned}$$

(27)

$$\begin{aligned}&8\pi \,P_r = \frac{3\big [N (1 + N r^2) + L (4 + 16 \alpha N + 3 N r^2 - N^2 r^4)\big ]}{(1 + L r^2) (1 + Nr^2)^2}, \end{aligned}$$

(28)

$$\begin{aligned}&8\pi \,P_t =\frac{P(r) + L^2 r^2 [S(r) + 16 \alpha N (5 + 2 N r^2)]}{(1 + L r^2)^2 (1 + N r^2)^3}, \end{aligned}$$

(29)

where $P(r) = 2 L (- N^3 r^6+ 7 N r^2+ 24 \alpha N+6 )-N (N^2 r^4 + 4 N r^2 +3 )$ and $S(r)=12 N^2 r^4- N^3 r^6+ 33 N r^2+20$.

Next, we want to use the DM density profile to find the decoupling function f(r). Therefore, we consider a mimic approach to solving the second system of equations (22)–(24), which is presented in the next section:

3.2 Mimicking the density constraint to the pseudo-isothermal density profile

To solve the $\theta$-sector, we introduce a pseudo-isothermal density profile,

$$\begin{aligned} \rho _{PI}=\frac{a}{1+b\,r^2}. \end{aligned}$$

(30)

For specific parameter values of a and b, research findings on DM halos and galaxies’ rotation curves may be found in Refs. [111, 112]. In our present investigation, however, we treated constants a and b as a free parameter. As we can see, the density profile $\rho _{PI}$ in any finite area is regular, singularity-free, and monotonously decreases with increasing radial coordinate r.

We discover the following differential equation by replicating $\rho ^\theta$ with $\rho _{PI}$, or by equating $\rho ^\theta$ and $\rho _{PI}$,

$$\begin{aligned}{} & {} 3 (1+b r^2) \big [4 \alpha \big (\mu ^\prime f+f^\prime (\beta f+\mu -1)\big )-r \left( r f^\prime +2 f\right) \big ] \nonumber \\{} & {} \quad -2 \alpha r^3 =0. \end{aligned}$$

(31)

After substituting $\mu$ form Eq. (26) in the above differential equation and solving it, we find the decoupler function f(r) as,

$$\begin{aligned} f(r)= \frac{1}{12} \Bigg [\frac{3 r^2 }{\alpha \beta }+\frac{12 N r^2}{ \beta (1+N r^2)}-\sqrt{\frac{3 f_1(r) \left( N r^2+1\right) ^{-2}}{\alpha \beta \left( br^2+1\right) }}\Bigg ], \end{aligned}$$

(32)

where,

$$\begin{aligned}{} & {} f_1(r)=\frac{1}{\alpha b^2 \beta }\Big [\left( br^2+1\right) \Big \{-8 \alpha a \beta \left( N r^2+1\right) ^2 \log \left( br^2+1\right) \\{} & {} \quad +b\big (48 \alpha ^2 b\left( N^2 r^4 \left( 1+F \beta ^2\right) +2 N F \beta ^2 r^2+F \beta ^2\right) +8 \alpha r^2\\{} & {} \quad {\times } \left( N r^2+1\right) \left( a \left( N \beta r^2+\beta \right) {+}3 bN r^2\right) {+}3 br^4 \left( N r^2{+}1\right) ^2\big )\Big \}\Big ], \end{aligned}$$

and F is the constant of integration. It is already well established that the decoupling function f(r) should vanish at the center to ensure the primary condition of the metric function $e^{2\lambda (0)}$ to be 1. Then f(0) leads to the integration constant $D=0$. After substituting $D=0$ in the above expression, we get the final form of f(r) as,

$$\begin{aligned} f(r)= \frac{1}{12} \Bigg [\frac{3 r^2 }{\alpha \beta }+\frac{12 N r^2}{ \beta (1+N r^2)}-\sqrt{\frac{3 f_2(r) \left( N r^2+1\right) ^{-2}}{\alpha \beta \left( br^2+1\right) }}\Bigg ],\nonumber \\ \end{aligned}$$

(33)

where,

$$\begin{aligned}{} & {} f_2(r){=}\frac{1}{\alpha b^2 \beta }\Big [\left( br^2{+}1\right) \Big \{-8 \alpha a \beta \left( N r^2{+}1\right) ^2 \log \left( br^2{+}1\right) \\{} & {} \quad +b\big (48 \alpha ^2 b N^2 r^4 +8 \alpha r^2 \left( N r^2+1\right) \big \{a \left( N \beta r^2+\beta \right) \\{} & {} \quad +3 bN r^2\big \} +3 br^4 \left( N r^2+1\right) ^2\big )\Big \}\Big ]. \end{aligned}$$

The expressions for all known functions $\nu$, $\mu$, and f(r) are now known, and from Eqs. (22)–(24) the expressions for $\theta$ components are derived as,

$$\begin{aligned} 8\pi \rho ^\theta= & {} \frac{a}{1+b r^2}, \end{aligned}$$

(34)

$$\begin{aligned} 8\pi P^\theta _r= & {} \frac{1}{12 \left( L r^2+1\right) \left( N r^2+1\right) ^2}\Big [-16 \alpha ^2 L \Big \{N^2 r^2 (a \beta ^2 r^4\nonumber \\{} & {} \times \left( 2 b r^2-3\right) +6 \beta (f_3(r)-3) r^2+36)+N \big [2 a \beta ^2 r^4 \nonumber \\{} & {} \times \left( 2 b r^2-3\right) +6 \beta (f_3(r)-6) r^2-36\big ]+a \beta ^2 r^2 \nonumber \\{} & {} \times \left( 2 b r^2-3\right) \Big \}+12 \alpha \big \{L \big (N^2 r^4 \left( 4 f_3(r)+3 \beta r^2-15\right) \nonumber \\{} & {} -2 \beta (f_3(r)-3) N r^4-2 (f_3(r)-3) \left( \beta r^2+2\right) \nonumber \\{} & {} -27 N r^2\big )-3 N \left( N r^2+1\right) \big \}+3 \left( 5 L r^2+1\right) \left( N r^2+1\right) \nonumber \\{} & {} \times \left( f_3(r) N r^2+f_3(r)-3\right) +1152 \alpha ^3 \beta L N^2 r^2\Big ], \end{aligned}$$

(35)

$$\begin{aligned} 8\pi P^\theta _t= & {} \frac{1}{36 f_3(r) \left( L r^2+1\right) ^2 \left( N r^2+1\right) ^4}\Big [-13824 L N^3 \beta r^2 \big (N r^2\nonumber \\{} & {} +3 L \left( N r^2+2\right) r^2+4\big ) \alpha ^4+f_5(r)-16 \left( N r^2+1\right) \nonumber \\{} & {} \times \left( -27 \left( N r^2+3\right) N^2+f_6(r)+f_7(r)\right) \alpha ^2+12 \nonumber \\{} & {} \times \left( N r^2+1\right) f_8(r)+27 \left( N r^2+1\right) ^4 (27 L^2 r^4+22 L r^2+3)\nonumber \\{} & {} -9 f_3(r) \left( N r^2+1\right) ^2 \big \{3 L^2 \left( 7 N r^2+9\right) r^4+N r^2\nonumber \\{} & {} +2 L \left( 7 N r^2+11\right) r^2+3\big \}\Big ]. \end{aligned}$$

(36)

We now go to the second method to determine the decoupling function f(r), as shown below:

4 Exterior space-time in EGB theory and junctions conditions

Specifying the boundary conditions for the desired solution is the last stage in system setup. In this instance, we compare the interior spacetime manifold ${\mathscr {M}}^{-}$ (26) to the outer Boulware–Deser space-time [90] manifold represented by,

$$\begin{aligned} ds^2_{5} = -F(r) dt^2 + \frac{dr^2}{F(r)} + r^{2}d \varSigma ^2_3, \end{aligned}$$

(37)

where the effective gravitational mass M is linked with

$$\begin{aligned} F(r) =\frac{r^2}{4 \alpha } \left( 1-\frac{\sqrt{r^4+16\,\alpha \, M}}{r^2}\right) +1. \end{aligned}$$

(38)

It is simple to verify that the following formula reduces to the 5D Schwarzschild solution in the limit $\alpha \rightarrow 0$. Additionally, in the current investigation, the following line element may be used to provide the interior star geometry under gravitational decoupling:

$$\begin{aligned} ds^2_{5} = -e^{2\nu (r)} dt^2 + \frac{dr^2}{\mu (r)+\beta f(r)} + r^{2}d \varSigma ^2_3, \end{aligned}$$

(39)

where $\mu (r)$ and $\nu (r)$ are the solutions for the seed spacetime supplied by Eq. (26), and the deformation function f(r) for the DM solution corresponding to the $\theta$-sector is given by Eq. (33). We will now examine the intersection of the outside and interior surfaces. The first fundamental form’s continuity at the boundary means that $g_{tt}^{-} = g_{tt}^{+}$ and $g_{rr}^{-} = g_{rr}^{+}$, where the symbols − and $+$ signify the inner and outside spacetime, respectively. This gives the following results:

$$\begin{aligned} e^{2\lambda ^{-}}|_{r=R}=e^{2\lambda ^{+}}|_{r=R} \quad \text{ and } \quad e^{2\nu ^{-}}|_{r=R}=e^{2\nu ^{+}}|_{r=R}, \end{aligned}$$

(40)

which gives

$$\begin{aligned}{} & {} e^{2\lambda (R)} = \frac{1}{\mu (R)+\beta f(R)} =\bigg [\frac{R^2}{4 \alpha }\bigg (1 - \sqrt{1 + \frac{16\, \alpha M}{R^4}}\bigg )+1\bigg ],\nonumber \\{} & {} \quad \text {and}\quad e^{2\nu (R)}=\bigg [\frac{R^2}{4\,\alpha } \bigg (1 - \sqrt{1 + \frac{16\, \alpha M}{R^4}}\bigg )+1\bigg ], \end{aligned}$$

(41)

where $\mu (R) = \big [1 + \frac{R^2}{4\,\alpha }\big (1 - \sqrt{1 + \frac{16\, \alpha \, M_{\textrm{EGB}}}{R^4}}\big )\big ]$ with $M_{\textrm{EGB}} = m_{\textrm{EGB}}(R)$ is the effective mass of the compact object for the metric (21). Then, using (41), we have

$$\begin{aligned} M = M_{\textrm{EGB}}+ \frac{\beta f(R) }{2} \left[ 2 \beta \alpha f(R)-\sqrt{16 \alpha M_{\textrm{EGB}}+R^4 }\right] .\nonumber \\ \end{aligned}$$

(42)

However, the second fundamental or extrinsic curvature must be continuous at the boundary, which provides the desired condition,

$$\begin{aligned} \big [(G_{ij}+\alpha \,H_{ij})\,r^j\big ]_{\varSigma }=0 . \end{aligned}$$

(43)

Here, $r_j$ denotes a unit radial vector in this case. Now, based on the aforementioned condition, one can estimate the Eq. (3) as

$$\begin{aligned} \big [T_{ij}\,r^j\big ]_{\varSigma }=0\quad \Longrightarrow \quad \big [P^{\textrm{eff}}_r\big ]_{r=R}=0, \end{aligned}$$

(44)

which gives

$$\begin{aligned} \big [{P}_r-\beta \,P^\theta _r\big ]_{r=R}=0, \end{aligned}$$

(45)

where $r=R$ defines the surface’s $\varSigma$. The size of the objects depends on condition (45).

We determine the constants L, B, and total mass M using the boundary conditions (41) and (45). We explore the limits of the constant parameters in depth in the Appendix for the sake of clarity.

$$\begin{aligned} L(R)= & {} \Big [3 \left( N R^2+1\right) \big (N \left( 12-12 \alpha \beta +\varPsi _1(R) \beta R^2\right) +(\varPsi _1(R)-3) \nonumber \\{} & {} \times \beta \big )\Big ] \Big [-1152 \alpha ^3 N^2 \beta ^2 R^2+16 \alpha ^2 \beta \big (N^2 R^2 \big \{a \beta ^2 R^4 \nonumber \\{} & {} \times (2 b R^2-3)+6 (\varPsi _1(R)-3) \beta R^2+36\big \} +N \big (2 a \beta ^2 R^4 \nonumber \\{} & {} \times \left( 2 b R^2-3\right) +6 (\varPsi _1(R)-6) \beta R^2-36\big )+a \beta ^2 R^2 \nonumber \\{} & {} \times \left( 2 b R^2-3\right) \big )-12 \alpha \big (N^2 \beta R^4 \left( 4 \varPsi _1(R)+3 \beta R^2-15\right) \nonumber \\{} & {} \quad -N \left( 2 (\varPsi _1(R)-3) \beta ^2 R^4+27 \beta R^2+48\right) -2 (\varPsi _1(R)-3) \nonumber \\{} & {} \times \beta \left( \beta R^2+2\right) \big )-3 \left( N R^2+1\right) \big (N R^2 \left( 5 \varPsi _1(R) \beta R^2+12\right) \nonumber \\{} & {} \quad +5 \varPsi _1(R) \beta R^2-15 \beta R^2-48\big )\Big ]^{-1} \end{aligned}$$

(46)

$$\begin{aligned} M(R)= & {} \frac{R^4}{{144 \left( N R^2+1\right) ^2}} \Big [-2 N \big (4 \alpha ^2 \beta ^2 \big \{a \beta R^2 \left( 2 b R^2-3\right) \nonumber \\{} & {} \quad +3 \varPsi _1(R)-18\big \} +3 \alpha \beta \big (\beta (\varPsi _1(R)-3) R^2-4 (\varPsi _1(R)-6)\big ) \nonumber \\{} & {} \quad -6 \beta \varPsi _1(R) R^2+9 \beta R^2-36\big )+2 \beta \big (2 \alpha ^2 a \beta ^2 \nonumber \\{} & {} \times \left( 3-2 b R^2\right) -3 \alpha \beta (\varPsi _1(R)-3)+3 (\varPsi _1(R)-3)\big ) \nonumber \\{} & {} \quad +N^2 \big (288 \alpha ^3 \beta ^2-4 \alpha ^2 \beta \big (a \beta ^2 R^4 \left( 2 b R^2-3\right) +6 \beta \nonumber \\{} & {} \times (\varPsi _1(R)-3) R^2+72\big )+3 \alpha \big \{3 \beta ^2 R^4+8 \beta (\varPsi _1(R)-3) \nonumber \\{} & {} \times R^2+48\big \}+6 R^2 \left( \beta \varPsi _1(R) R^2+12\right) \big )\Big ], \end{aligned}$$

(47)

$$\begin{aligned} B= & {} \frac{1}{(1+L r^2)}\Bigg [{\frac{1+\beta f(R) \left( N r^2+1\right) }{N r^2+1}}\Bigg ]^{1/4}, \end{aligned}$$

(48)

where we may calculate f(R) using Eq. (33) by substituting $r=R$.

5 Analyzing stellar physical parameters

5.1 Impact of the decoupling parameter (or DM component) on pressures, density and anisotropy

The thermodynamical observables of the confined matter, such as density, pressures, and anisotropy, play an important role in determining how stable the stellar structure is in resisting gravitational collapse. The gravitationally confined system collapses under its own gravity if, at the center, $r = 0$, the stellar density, $\rho ^{\textrm{eff}}(0)$, is greater than the critical density, $\rho ^{\textrm{eff}}(0)_{max}$. The central density, $\rho ^{\textrm{eff}}(0)$, for our stellar system is finite and reaches its maximum at the center, $r = 0$. It appears from Fig. 1 (top left) that stellar density decreases radially outward, with maxima appearing in the interval $\rho ^{\textrm{eff}}_c~\in ~[4.14478,~4.46698]\times ~10^{14}~[\text {g}.\text {cm}^{-3}]$ at the center, $r = 0$, where $\rho ^{\textrm{eff}}(0)= \rho ^{\textrm{eff}}_c$ and minima appearing in the interval $\rho ^{\textrm{eff}}_s~\in ~[3.46535,~3.64435] \times ~10^{14}~[\text {g}.\text {cm}^{-3}]$ at the surface, $r = R$, where $\rho ^{\textrm{eff}}(R)=\rho ^{\textrm{eff}}_s$ for all $\beta ~\in ~[0.0,~2.0]\times ~10^{-3}$. Interestingly, the decoupling parameter makes the stellar interior more dense i.e. DM allowing more dense objects.

Besides the finite central density, we note that the radial and tangential pressures are finite at the center $r = 0$, and decrease smoothly towards the stellar boundary $r = R$. As seen in Fig. 1 (top right) and (bottom left), both radial and tangential pressures stay positive, i.e., $P^{\textrm{eff}}_r > 0$ and $P^{\textrm{eff}}_t > 0$ inside the star, $r< R$, and decrease towards the stellar surface, $r = R$, where radial pressure disappears, i.e., $P^{\textrm{eff}}_r(R) = 0$. It is significant to observe that the maximum value of the central pressures ${P^{\textrm{eff}}_r(0)=P^{\textrm{eff}}_t(0)}$ increases from $0.719631 \times ~10^{34}$ to $1.63662\times ~10^{34}~[\text {dyne}.\text {cm}^{-2}]$ when the decoupling parameter increases from 0.0 to $2.0 \times ~10^{-3}$. Additionally, we found that the trend of tangential pressure exhibits opposite behavior when $r/R \ge 0.8$, i.e., its magnitude rises as $\beta$ rises. This may be owing to the non-linear surface turbulence because of the increasing DM contribution.

We also determined the associated anisotropy parameter, which means how tangential pressure and radial pressure are different from one another, to better probe the internal dynamics of our stellar system. We showed that the anisotropy vanishes at the center, $r = 0$, and grows consistently with r, as can be seen in Fig. 1 (bottom right). It’s interesting to mention here that when the decoupling parameter, $\beta$, grows, the surface turbulence reduces; this behavior corresponds to the nonlinearity induced by anisotropy in the early stages of turbulence in fluid dynamics.

5.2 Redshift

Zhou et al. [108] has explored how the upper limit of the spectral lines at high redshifts from the boundary of constant-density stars would change due to the inclusion of GB components in the context of EGB gravity. Contrary to popular belief, an upper limit for redshift cannot be calculated since it is not a constant in the GR complement but rather relies on the density value [108, 109]. The redshift may be calculated using the formula,

$$\begin{aligned} z=\sqrt{e^{-2\nu (r)}}-1. \end{aligned}$$

(49)

The redshift $z_s$ at the surface may also be estimated as [108],

$$\begin{aligned} z_{s}= \big [B\,(1+LR^2)\big ]^{-2}-1. \end{aligned}$$

(50)

Table 1 indicates that a large redshift is achieved in the presence of gravitational decoupling, as the surface redshift $Z_s$ rises with increasing the value of $\beta$. It is pointed out that the calculated values for $Z_s$ agree with the limit put forward by the GR situation [110].

Fig. 1

Variation of the density (top left), radial pressure (top right), tangential pressure (bottom left) and anisotropy (bottom right) of CSs along the radial coordinate r/R for different $\beta$ values with $N = 0.0012~\text {km}^{-2}$, $a= 0.3~\text {km}^{-2}$, $b= 0.008~\text {km}^{-2}$, $\alpha =30~ \text {km}^2$, and $R=10\,\text {km}$

Table 1 Numerical values of the physical parameters of the model

Fig. 2

Variation of the velocity of sounds $\text {v}^2_r$ and $\text {v}^2_t$ of CSs along the radial coordinate r/R for same parameters values used in this figure

6 Analyzing stellar stability parameters

6.1 Stellar cracking modes

The stellar core’s intense density causes the sound velocity to move into the ultra-relativistic region [111]. In this context, to assess the viability of the stellar model [112, 113], we can check the distribution of maximum sound velocity in the inner region. The upper bounds for radial sound velocity, $\text {v}^2_r(r)<1$, and tangential sound velocity, $\text {v}^2_t(r)<1$, are established using the causality limit. Their expressions, $\text {v}^2_r$, and $\text {v}^2_r$, can be defined as follows,

$$\begin{aligned}{} & {} \text {v}_r^2 = \frac{dP^{\textrm{eff}}_r}{d\rho ^{\textrm{eff}}}, \end{aligned}$$

(51)

$$\begin{aligned}{} & {} \text {v}_t^2 = \frac{dP^{\textrm{eff}}_t}{d\rho ^{\textrm{eff}}}. \end{aligned}$$

(52)

Figure 2 shows the radial profiles of $\text {v}^2_r$ and $\text {v}^2_t$. It has been indicated that both components remain causal throughout the inner zone. It’s also noteworthy to note that for all relevant intervals of $\beta$, with the exception of $\beta =0.0$, which remains constant, $\text {v}_r^2$ and $\text {v}_t^2$ grow monotonically from their lowest values at the center to their highest values at the surface. Figure 3 also shows the variation of the stability factor $\text {v}_r^2 - \text {v}_t^2$ of the CS along the radial coordinate r/R. Based on this graph, we can clearly see that $\text {v}_r^2 - \text {v}_t^2$ remains constant around the center but decreases slightly around the surface. This phenomenon can be explained by surface turbulence helped by anisotropy and a non-zero tangential pressure gradient at the stellar surface.

Fig. 3

Variation of the stability factor $\text {v}^2_r-\text {v}^2_t$ of CSs along the radial coordinate r/R for same parameters values used in Fig. 2

Fig. 4

Variation of the adiabatic index of CSs along the radial coordinate r/R for different $\beta$ values with $N = 0.0012~\text {km}^{-2}$, $a= 0.3~\text {km}^{-2}$, $b= 0.008~\text {km}^{-2}$, $\alpha =30~ \text {km}^2$, and $R=10\,\text {km}$

6.2 Adiabatic perturbations

When analyzing the dynamical stability of a stellar configuration, the adiabatic index $(\varGamma )$ plays a crucial role. A stable equilibrium of an isotropic fluid against gravitational collapse requires $\varGamma =4/3$. If non-vanishing anisotropy exists, the stability condition demands that $\varGamma > 4/3$ for all inherent points, $r < R$ in the gravitationally confined fluid. The sound velocity formula that was exploited to express the decoupled system’s adiabatic index $\varGamma$ for an anisotropic matter distribution is as follows,

$$\begin{aligned} \varGamma \equiv \left( 1+\frac{\rho ^{\textrm{eff}}}{P ^{\textrm{eff}}_r}\right) \left( \frac{dP ^{\textrm{eff}}_r}{d\rho ^{\textrm{eff}}}\right) _S, \end{aligned}$$

(53)

where entropy S is kept constant during the derivation. While $\left( \frac{dP ^{\textrm{eff}}_r}{d\rho ^{\textrm{eff}}}\right) _S$ is the sound velocity. It is clear that our stellar model is stable versus adiabatic perturbations for all points within the stellar model from the radial profile of $\varGamma$ shown in Fig. 4. Bear in mind that the decoupling parameter, $\beta$, favors a stiff EoS, as any increment in the decoupling parameter, $\beta$, maintains equilibrium at a higher value of $\varGamma$ for all inherent points, $r < R$. Moreover, $\varGamma$ is a measure for examining the stiffness of the star’s structure.

6.3 Dynamics balancing of interior forces in 5D EGB gravity

The ultimate fate of a CS depends on the stability of a gravitationally compact object under multiple stresses. In this concern, we are using the modified Tolman–Oppenheimer–Volkoff (TOV) equation, which incorporates the significant contribution of non-despairing anisotropy, to examine the dynamics and interplay of these stresses. The general equation incorporating all these stresses can be written as follows,

$$\begin{aligned} {\nu ^\prime }\,({\rho ^{\textrm{eff}}}+P^{\textrm{eff}}_r) +[P^\prime _r]^{\textrm{eff}}+\frac{3}{r}(P^{\textrm{eff}}_r -P^{\textrm{eff}}_t)=0. \end{aligned}$$

(54)

Here, the contributing terms can be classified as follows,

• $\text {Gravitational force}:~~ F_g= -{\nu ^\prime }\,({\rho ^{\textrm{eff}}}+P^{\textrm{eff}}_r)$,

• $\text {Hydrostatic force}:~~ F_h= -[P^\prime _r]^{\textrm{eff}}$,

• $\text {Anisotropic force}:~~ F_a=\frac{3}{r}(P^{\textrm{eff}}_t-P^{\textrm{eff}}_r)$.

According to Fig. 5, we discovered that our system is in dynamic equilibrium and stable against gravitational collapse because, for each causal branch of the decoupling parameter, $\beta ~\in ~[0.0,~2.0]\times ~10^{-3}$, the radial variation of the net force: $F_h~+~F_a~+~F_g = 0$ remains zero throughout the stellar interior, $r < R$.

Fig. 5

Variation of the different forces of CSs along the radial coordinate r/R for different $\beta$ values with $N = 0.0012~\text {km}^{-2}$, $a= 0.3~\text {km}^{-2}$, $b= 0.008~\text {km}^{-2}$, $\alpha =30~ \text {km}^2$, and $R=10\,\text {km}$

Fig. 6

Contour diagram for energy-density on $r-\alpha$-plane for parameter values $N = 0.0012~\text {km}^{-2}$, $a= 0.3~\text {km}^{-2}$, $b=0.008~\text {km}^{-2}$, and $\beta =0.001$

Fig. 7

Contour diagram for radial pressure on $r-\alpha$-plane for parameter values $N = 0.0012~\text {km}^{-2}$, $a=0.3~\text {km}^{-2}$, $b=0.008~\text {km}^{-2}$, and $\beta =0.001$

Fig. 8

Contour diagram for tangential pressure on $r-\alpha$-plane for parameter values $N = 0.0012~\text {km}^{-2}$, $a=0.3~\text {km}^{-2}$, $b=0.008~\text {km}^{-2}$, and $\beta =0.001$

Fig. 9

Contour diagram for anisotropy on $r-\alpha$-plane for parameter values $N = 0.0012~\text {km}^{-2}$, $a= 0.3~\text {km}^{-2}$, $b= 0.008~\text {km}^{-2}$, and $\beta =0.001$

7 Analyzing physical parameters on the $r-\alpha$ planes and maximum mass constraints via $M{-}R$ curves

7.1 Impact of GB constant $\alpha$ on energy density, radial and tangential pressures, and anisotropy variations

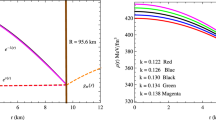
The contour diagram is employed in Figs. 6, 7, 8, and 9, to show the impact of GB on the energy, pressure components, and anisotropy that are distributed on the $r-\alpha$ plane. It clearly shows that for any fixed value of GB constant $\alpha$ in $[5.0, 50.0]~\times ~[\text {km}^2]$, density decreases systematically as we move towards the stellar surface, reaching its minimum value there. Moreover, the magnitude of the density increases with increasing parameter $\alpha$, reaching its maximum at the star’s core.

Having tested the distribution of energy density on the $r-\alpha$ plane via the contour diagram, we will now test the distribution of pressure components on the $r-\alpha$ plane via the same contour diagram. Both pressure components, $P^{\textrm{eff}}_r$ and $P^{\textrm{eff}}_t$, are systematically reduced with increasing radial distance r for a fixed value of $\alpha$ in $[5.0, 50.0]~\times ~[\text {km}^2]$, however, the magnitude of pressure components, $P^{\textrm{eff}}_r$ and $P^{\textrm{eff}}_t$, rises with rising $\alpha$. As expected from our analysis, the maximum pressure is indicated at the star’s core for any fixed value of $\alpha$.

Then, using the same contour diagram, we tested the anisotropy distribution on the $r-\alpha$ plane. We can clearly see that the anisotropy distribution on the $r-\alpha$ plane demonstrates that the anisotropy is increasing in this situation when $\alpha$ is increasing. But the impact of the GB constant $\alpha$ can be clearly seen close to the stellar surface.

Consequently, we can say that the constant GB constant $\alpha$ also plays an important role along with the decoupling parameter $\beta$ in constraining energy density, pressures, and anisotropy in DM halos using EGB action.

7.2 Maximum allowed mass via $M{-}R$ curves

To prove the usefulness of the present stellar model, we have analyzed the impact of $\alpha$ and $\beta$ on the maximum stable mass that can be contained within a given stellar radius, as shown by the $M{-}R$ curves in Figs. 10 and 11, for various levels of surface density. In this respect, we have considered two surface densities, e.g., $\rho ^{\textrm{eff}}_s\approx 10^{14}~\text {g}/\text {cm}^3$ and $\rho ^{\textrm{eff}}_s\approx 10^{15}~\text {g}/\text {cm}^3$, for our tests.

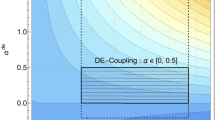
In Figs. 10 and 11, the $M{-}R$ relationship for stellar models has been plotted for different values of $\alpha$ (left panel) and $\beta$ (right panel) with surface densities $\approx 10^{14}~\text {and}~\approx 10^{15}~\text {g}/\text {cm}^3$. We noticed that the parameters $\alpha$ in $[5.0,~25.0]~\times ~[\text {km}^2]$ and $\beta$ in $[0.0,~2.0]~\times ~[10^{-3}]$ for surface density $\approx 10^{14}~ \text {g}/\text {cm}^3$ and $\alpha$ in $[10.0,~50.0] ~\times ~[\text {km}^2]$ and $\beta$ in $[0.0,~2.0]~\times ~[10^{-3}]$ for surface density $\approx 10^{15}~\text {g}/\text {cm}^3$ increases the equilibrium radius to enclose the star’s active gravitational mass with a slight change between the two cases from the resulting dataset represented by $M{-}R$ curves in both graphs. Interestingly, the stiffness of the EoS can be reduced by increasing the contribution of these two factors, $\alpha$ and $\beta$. The horizontal stripes in both graphics correspond to the mass constraints of GW 190814, PSR J0952-0607, PSR J0740+6620, and PSR J1614-2230.

Fig. 10

$M -R$ curve for different values of $\alpha$ (left panel) and $\beta$ (right panel) with surface density $\approx 10^{15}~\text {g}/\text {cm}^{3}$

Fig. 11

$M -R$ curve for different values of $\alpha$ (left panel) and $\beta$ (right panel) with surface density $\approx 10^{14}~\text {g}/\text {cm}^{3}$

On the other hand, the observations of the two-solar-mass binary millisecond pulsar PSR J1614-2230 by Demorest et al. [114] reveal that the masses lie within $1.97\pm 0.04~M_{\odot }$, ruling out almost all of the hyperon or boson condensate equations of state. In addition, the mass of the pulsar to be in the range $2.01\pm 0.04~M_{\odot }$ [115], has been confirmed by radio timing measurements of the pulsar PSR J0348+0432 and its white dwarf companion. In very recent surveys, masses of $2.08\pm 0.07~M_{\odot }$ and $2.35\pm 0.17~M_{\odot }$, respectively, have been reported for PSR J0740+6620 [116] and PSR J0952-0607 [117]. The equatorial radius and mass of PSR J0740+6620 are constrained to be $12.39^{+1.30}_{-0.98}$ km and $2.072^{+0.067}_{-0.066}~M_{\odot }$, respectively, by some recent studies [118, 119]. The maximum mass of gravitational wave event GW190814, as determined by recent measurements, has been estimated to be 2.5−2.67$~M_{\odot }$. The maximum compact object masses obtained for the research we are doing are 2.82$~M_{\odot }$ and 2.98$~M_{\odot }$ for $\alpha =25$ and $\beta =0.002$ with $\rho ^{\textrm{eff}}_s\approx 10^{15} g/cm^3$ as well as 3.17$~M_{\odot }$ and 3.02$~M_{\odot }$ for $\alpha =50$ and $\beta =0.002$ with $\rho ^{\textrm{eff}}_s\approx 10^{14}~\text {g}/\text {cm}^3$, respectively. These predicted values are in good agreement with recent observations of massive NSs. Furthermore, recent work by Rincón et al. [120, 121] has shown that the maximum mass profile via $M{-}R$ curve is attainable within the framework of the vanishing complexity factor, and this finding has been corroborated by them, who have shown that the resulting solutions display more compact objects than GR. In this regard, we have expanded our research in this direction to discover the maximum mass of the objects by using the $M{-}R$ profile in the EGB gravity theory under the DM component induced by the MGD formalism. These considerations and the preceding analysis lead us to the following conclusion: as $\beta$ and $\alpha$ decrease, we see more compact objects, while the mass of the objects increases when both constants increase.

Table 2 Prediction of radii for a few well-known CSs with a surface density $\approx 10^{15}~\text {g}/\text {cm}^3$

Table 3 Prediction of radii for a few well-known CSs with surface density $\approx 10^{14}~\text {g}/\text {cm}^3$

8 Concluding remarks

In this paper, the anisotropic stars within the DM haloes were tested under 5D EGB gravity. After discovering the solution, a thorough physical study was carried out along with the result, as discussed below. To start with, the thermodynamic parameters are discussed. It is observed that the energy density ($\rho ^{\textrm{eff}}$) has its maximum value at the center and decreases gradually towards the surface (Fig. 1 top left panel). Also, it is noticed that when $\beta =0$, i.e., without the introduction of DM via gravitational decoupling, the energy density is lowest and increases with $\beta$, which suggests that as gravitational decoupling becomes predominant, the energy density increases. The analysis of radial pressure $(P^{\textrm{eff}}_r)$ (Fig. 1 top right panel) and tangential pressure $(P^{\textrm{eff}}_t)$ (Fig. 1 bottom left panel) showed that they both have their maxima at the surface and the decreases in the radially outward direction. The pressure $P^{\textrm{eff}}_r$ at the boundary is decreasing and approaching zero, and the tangential pressure $(P^{\textrm{eff}}_t)$ remains positive as well as non-zero. It is also noticed that when $\beta =0$, i.e., in the absence of DM, the decreasing rate of tangential pressure is very low, which makes the curve look almost horizontal with $P_t^{\textrm{eff}} \approx 0.06\times 10^{-4}$. But when $\beta > 0$, then the curves behave properly. The curves for different values of $\beta$ intersect at the surface for radial pressure, as all the curves approach zero at the surface, while for tangential pressure, they intersect at $r/R \approx 0.8$ and at $P_t^{\textrm{eff}} \approx 0.06\times 10^{-4}$, which is exactly the value of $P_t^{\textrm{eff}}$ when $\beta =0$. Looking into the anisotropic factor $(\varDelta ^{\textrm{eff}}),$ it is observed that the anisotropy is zero at the center, while it increases as one moves in the radially outward direction and becomes maximum at the surface (Fig. 1 bottom right panel). It is noticed that anisotropy is at its maximum without gravitational decoupling, and as gravitational decoupling becomes predominant, anisotropy decreases. The decrease in anisotropy with $\beta$ can be attributed to the decrease in surface turbulence with the increase in $\beta$.

It is necessary to examine the causality requirement in order to determine any model’s feasibility, i.e., tangential or radial sound ($\text {v}_r$ or $\text {v}_t$) should never travel faster than light. Mathematically, this means that $0 \le \text {v}_r^2 \le 1$ and $0 \le \text {v}_t^2 \le 1$ (where the speed of light is scaled to unity). Looking into Fig. 2, it is seen that both the $0 \le \text {v}_r^2 \le 1$ and $0 \le \text {v}_t^2 \le 1$ conditions hold everywhere, which means that the causality condition is maintained everywhere within the model. However, it was observed that both velocity components have nearly zero value without gravitational decoupling, and they increase as gravitational decoupling gets predominant with the increase in $\beta$. Both $\text {v}_r^2$ and $\text {v}_t^2$ have minimum values and increases in radially outward direction, while the radial velocity is seen to be increasing more steeply than the tangential velocity.

The variation of the stability factor $\text {v}_r^2-\text {v}_t^2$ showed that it almost remains constant near the center and slightly decreases near the surface, which can be attributed to the anisotropy alongside the surface turbulence and non-zero value of tangential pressure near the surface (Fig. 3). It is also seen that the quantity $\text {v}_r^2-\text {v}_t^2$ decreases with $\beta$. The adiabatic index $(\varGamma )$ is one of the key aspects to look into while studying a CS model, especially when anisotropy is involved. From Fig. 4, it is noticed that $\varGamma$ has the lowest value at the center and then very slowly increases, and after a certain point at about $r/R \approx 0.7$, it starts to increase rapidly, then on up to the boundary. Also, it is seen that the presence of DM decreases the adiabatic index as $\beta$ is seen to decrease $\varGamma$. The effect of this $\beta$ is seen to have a maximum near the center and a minimum at the surface. Then, near the surface, i.e., at higher values of $\varGamma$, it maintains equilibrium despite the change in $\beta$. As $\varGamma$ is linked to the stiffness of the structure of the star, it can be said that $\beta$ supports a stiff EoS.

The study of hydrostatic balance based on different forces was done, and from Fig. 5 it is seen that for all circumstances, the attractive and negative gravitational force $(F_g)$ is balanced by the positive and repulsive hydrostatic force $(F_h)$ and anisotropic force $(F_a),$ and the hydrostatic balance is maintained. It is also noticed that the introduction of EGB gravity increases the attractive gravitational force, which is counterbalanced by $F_h$ and $F_a$. The increase in attractive gravitational force with the introduction of $\beta$ demonstrates that adding gravitational decoupling improves the model’s stability. The analysis of the surface redshift $(Z_s)$ indicated that because of the presence of gravitational decoupling and DM content, a large redshift is achieved as $Z_s$ increases with an increase in the $\beta$ Table 1. Also, the obtained values of $Z_s$ stay well within the limiting values in the GR scenario.

The impact of the GB constant $\alpha$ on the radial and tangential pressures has been studied, and it is represented by Figs. 6, 7, 8, 9 via the contour diagrams in $r {-} \alpha$ plane. It was noticed that all energy density and radial and tangential pressure decrease with r while $\alpha$ is fixed. For energy density, with a fixed r, it increases with $\alpha$. For radial and tangential pressure also, it is seen that for fixed r, both radial and tangential pressure increase with $\alpha$ near the center; however, for tangential pressure, it decreases with $\alpha$ near the boundary, and for radial pressure, it doesn’t change much with $\alpha$ near the surface. This flip of the $\alpha$ dependence of the tangential pressure occurs at about $r \approx 0.8$. While for anisotropy, it was recorded that it increases with r when $\alpha$ is fixed. When r is fixed, near the center, the $\alpha$ dependence on anisotropy is very less, but near the surface, anisotropy decreases with the increase in $\alpha$. The maximum anisotropy is achieved at the surface when $\alpha = 0$. For different choices of surface densities along with coupling constants $\alpha$ and $\alpha$, we have displayed the Mass–Radius relation in Figs. 10 and 11 to demonstrate the applicability of the current stellar models. In our investigation, two surface densities of order :$10^{14}~\text {g}/\text {cm}^3$ and $10^{15}~\text {g}/\text {cm}^3$, were taken into consideration to examine the impact of DM on star objects. The maximum masses for various $\alpha$ and $\beta$ can be observed from $M{-}R$ curves. On the other hand, this study is to use the observed masses of a small sample of stellar objects, including GW190814, PSR J0952-0607, PSR J0740+6620, and PSR J1614-2230, to make predictions about the stars’ radii. Tables 2 and 3 and Figs. 10 and 11 display the findings. The most plausible range for PSRJ1614-2230’s radius, in kilometers, is $8.3\le R \le 12$ [122]. Tables 2 and 3 show that as density decreases, objects become more compact, with the range of PSRJ1614-2230 radii being $11.87 \le R \le 11.96$ km for density on the order of $10^{14}~\text {g}/\text {cm}^3$ and $12.77 \le R \le 12.81$ km for density on the order of $10^{15}~\text {g}/\text {cm}^3$, respectively.

We conclude that the current method is a powerful tool for simulating compact objects under EGB gravity with DM.

Appendix

$$\begin{aligned} f_{3} (r)= & {} \sqrt{f_4(r)},\\ f_4(r)= & {} -\frac{4 \alpha \left[ N \left( a \beta r^2 \left( 2 b r^2-3\right) -18\right) +a \beta \left( 2 b r^2-3\right) \right] }{N r^2+1}\\{} & {} +9 +\frac{144 \alpha ^2 N^2}{\left( N r^2+1\right) ^2}, \\ f_5(r)= & {} 192 L N \Big [N^3 \big [a \beta ^2 \left( 13 b r^2-15\right) r^4+3 (2 f_3(r)-21) \beta r^2 \\{} & {} +3 L \left( a \beta ^2 \left( 7 b r^2-9\right) r^4+3 (2 f_3(r)-15) \beta r^2 +36\right) r^2\\{} & {} +36\big ] r^4+a \beta ^2 \left( 19 b r^2+9 L \left( 3 b r^2-4\right) r^2-24\right) r^2 \\{} & {} +3 N^2 \big \{3 a \beta ^2 \left( 5 b r^2-6\right) r^4+5 (2 f_3(r)-15) \beta r^2 \\{} & {} +L \left( a \beta ^2 \left( 23 b r^2-30\right) r^4+9 (2 f_3(r)-15) \beta r^2+48\right) r^2\\{} & {} +48\big \} r^2+3 N \big (a \beta ^2 \left( 17 b r^2-21\right) r^4+8 (f_3(r)-9) \beta r^2\\{} & {} +L \left( a \beta ^2 \left( 25 b r^2-33\right) r^4+12 (f_3(r)-9) \beta r^2-60\right) r^2\\{} & {} -36\big )\Big ] \alpha ^3,\\ f_6(r)= & {} 3 L^2 r^2 \Big [N^3 \big \{a f_3(r) \beta ^2 \left( 5 b r^2-6\right) r^4+3 \beta \big (4 a \left( 3 b r^2-4\right) \\{} & {} -9 (f_3(r)-3)\big ) r^2+9 (4 f_3(r)-49)\big \} r^4+3 N^2 \big [a \beta ^2 \\{} & {} \times \left( b (5 f_3(r)-7) r^2-6 f_3(r)+9\right) r^4+\beta [8 a \left( 2 b r^2-3\right) \\{} & {} -27 (f_3(r)-4)] r^2+16 f_3(r)-153\big ] r^2+a \beta [6 \beta r^2 \\{} & {} \times (6-f_3(r)) +b \left( (5 f_3(r)-27) \beta r^2-48\right) r^2+60] \\{} & {} +3 N \Big \{a \beta ^2 \left( b (5 f_3(r)-16) r^2-6 f_3(r)+21\right) r^4\\{} & {} -12 \beta \left( 2 f_3(r)+a \left( b r^2-1\right) -9\right) r^2-20 (f_3(r)-6)\Big \}\Big ],\\ f_7(r)= & {} L N^3 \Big [a f_3(r) \beta ^2 \left( 11 b r^2-12\right) r^4+3 \beta \big \{4 a \left( 5 b r^2-6\right) \\{} & {} -15 (f_3(r)-3)\big \} r^2+36 f_3(r)-702\Big ] r^4+3 N^2 \big \{a \beta ^2 \\{} & {} \times \left( b (11 f_3(r)-13) r^2-12 f_3(r)+15\right) r^4 +\beta \big \{16 a \\{} & {} \times \left( 2 b r^2-3\right) -45 (f_3(r)-4)\big \} r^2 +6 (8 f_3(r)-69)\big \} r^2 \\{} & {} +a \beta \big (b (11 f_3(r)-57) \beta r^4 -96 b r^2-12 (f_3(r)-6) \beta r^2\\{} & {} +108\big )+3 N \Big [a \beta ^2 \left( b (11 f_3(r)-32) r^2-12 f_3(r)+39\right) \\{} & {} \times r^4-4 \beta \left( 5 a b r^2-3 a+12 f_3(r)-54\right) r^2-36 (f_3(r)-6)\Big ], \\ f_8(r)= & {} \Big [-3 L^2 \Big \{\left( N r^2+1\right) \Big (N^2 \left( a \beta r^2 \left( 20 b r^2-27\right) -192\right) r^4\\{} & {} +\beta \left( 20 a b r^2-27 a+36\right) r^2+N \big (\beta r^2 \left( 40 a b r^2-54 a+27\right) \\{} & {} -186\big ) r^2+60\Big )-f_3(r) \Big (3 N^3 \left( 2 \beta r^2-7\right) r^6+6 N^2 (3 \beta r^2-10) r^4\\{} & {} +N \left( 21 \beta r^2-43\right) r^2+4 \left( 3 \beta r^2+5\right) \Big ) \Big \} r^2-\left( N r^2+1\right) \big (N^2 \\{} & {} \times \left( a \beta \left( 8 b r^2-9\right) r^2 +3 f_3(r)-36\right) r^2+a \beta \left( 8 b r^2-9\right) +N \\{} & {} \times \left( 2 a \beta \left( 8 b r^2-9\right) r^2+9 f_3(r)-54\right) \big )+L \Big \{3 f_3(r) \big (2 N^3 (2 \beta r^2\\{} & {} -7) r^6+4 N^2 \left( 3 \beta r^2-10\right) r^4+8 \beta r^2+N \left( 13 \beta r^2-38\right) r^2+12\big )\\{} & {} -\left( N r^2+1\right) \Big (\left( 52 a b \beta r^8-66 a \beta r^6-396 r^4\right) N^2+r^2 \big (\beta r^2 \big (4 a \\{} & {} \times \left( 26 b r^2-33\right) +45\big )-468\big ) N +2 \beta r^2 \left( 26 a b r^2-33 a+36\right) \\{} & {} +108\Big )\Big \}\Big ] \alpha . \\ \varPsi _1(r)= & {} \sqrt{\frac{144 \alpha ^2 N^2}{\left( N R^2+1\right) ^2}-\varPsi _2(R)+9}, \\ \varPsi _2(r)= & {} \frac{4 \alpha \left( N \left( a \beta R^2 \left( 2 b R^2-3\right) -18\right) +a \beta \left( 2 b R^2-3\right) \right) }{N R^2+1}. \end{aligned}$$