1 Introduction

The general relativity (GR) theory of Einstein proved incredibly effective in explaining the gravitational phenomena at both cosmological and astrophysical scales. Through the intrinsic gravitational systems, such as star and galaxy structures, which make up a sizable portion of our observable Universe, this theory of gravity achieves important achievements. The study of the evolution of these self-gravitating systems plays a crucial part in revealing the composition, evolution, and age of the universe, among other hidden characteristics. The process of gravitational collapse towards the demise of a celestial structure, which results in the production of compact star objects, is one of the key stages in the evolution of celestial structures. These end-points in the evolution of common celestial formations, or compact star objects, make for excellent research sites for the characteristics and make-up of high-density matter. Numerous compact stellar objects with high densities have recently been found [1], and they are frequently mistaken for pulsars, rotating stars with powerful magnetic fields.

In most galaxies, stars are dispersed in gas and dust clouds with non-uniformly distributed materials. All active stars eventually reach a point in their evolution when the radiation pressure from the internal nuclear fusions can no longer withstand the gravitational pull of space. The star experiences stellar death at this point when it collapses beneath the weight of itself [2]. This is the process that creates a compact star, also known as an extremely dense and compact stellar remnant, for the majority of stars. In other words, the evolution of common stars ends with compact stars, which also include white dwarfs, neutron stars, black holes, and quark stars. Compact star formation may potentially be influenced by the phase separations of the early universe after the Big Bang. Compact stars are distinguished from other stars by their extremely high density and the absence of nuclear processes inside of them. They are unable to support themselves against gravity because of this. The pressure of degraded gas acts as a resistance to gravity in white dwarfs and neutron stars. The star material is infinitely compressed in black holes, where the force of gravity entirely outweighs all other forces and results in infinite density [3]. A dense white dwarf is created when the core of a star similar to the Sun entirely collapses due to nuclear fuel exhaustion. However, an extremely dense neutron star or black hole is created when the inert iron cores of stars with masses equal to or greater than ten times that of the Sun collapse. Even though the universe is too young for any of the tiniest red dwarfs to have died, stellar models predict that they will gradually become brighter and hotter until they run out of hydrogen fuel, at which point they will eventually turn into low-mass white dwarfs.

In General Relativity (GR), it is common practice to assume that objects have properties of spherically symmetric and isotropic nature while tackling problems with compact stars. However, while ideal isotropy and homogeneity of astrophysical compact stellar objects may have solvable features, they are not always necessary to describe the general physical properties of stellar objects. Since inhomogeneity arises as a result of radial pressure \((p_{r})\) and tangential pressure \((p_{t}),\) the fluid pressure may therefore have two unique components that are responsible for giving an anisotropic factor \((\Delta =p_{t}-p_{r})\), and this may prevent the internal system of matter distribution from having an idealized isotropic scenario. Ruderman [4] originally raised this concept in his thorough examination of the structure and dynamics of pulsars. Later on, the problem was brought up in the writings of various scientists [5,6,7]. In the very high-density region of the core, different condensate states (such as pion condensates, meson condensates, etc.), superfluid 3A, a mixture of different types of fluids, rotational motion, the presence of a magnetic field, phase transition, relativistic particles in compact stars, etc. [8,9,10,11,12,13,14,15,16,17,18,19,20,21] are all thought to play a role in this anisotropy. However, there is another potential contributing cause to anisotropy in compact stars, namely the gravitational tidal effects. This is assumed to be the cause of the fluid distribution in the anisotropy of stars and consequent deformation [22,23,24,25,26,27,28,29,30]. We want to emphasize the anisotropic nature of compact stars in the current effort.

An estimated 27% of the universe’s mass-to-energy ratio is made up of dark matter, a hypothesized type of stuff. There are a lot of candidates from supersymmetric string theory and particle physics, such as axions and wimps, but as of now, there hasn’t been a direct scientific detection of dark matter. In spite of this, recent strong experimental evidence suggests that dark matter is present in a variety of astrophysical events, particularly in the development of galactic rotation curves [31], the dynamics of galaxy clusters [32], and to cosmological scales of anisotropies detected by PLANCK in the cosmic microwave background [33]. One of the biggest scientific puzzles of our day is dark matter. Given how little is known about its microphysical characteristics, there are countless possibilities for its identities. This is famously represented in the 90+ orders of the magnitude that dark matter masses may cover, from \(10^{8}M_{\circledcirc } \cong 10^{74}~\text {eV}\), the mass of DM in a compact galaxy, to \(10^{-24}\) eV, set by the greatest potential Compton wavelength, containable within a dwarf galaxy. DM can be characterized as a wave/field, a particle, a macroscopic entity, or a galactic substructure, including topological flaws and black holes, over this spectrum of masses. Exploiting physical systems with exceptional diversity in attributes is a viable tactic to deal with such amazing diversity in possibility.

Since its proposal by Bose [34], and generalization by Einstein [35, 36], the quantum statistics of integer spin particles (bosons) did represent a fundamental field of study in both theoretical and experimental physics. The most important characteristic of the bosonic systems is their phase transition to a condensed state. In such a state all the particles are in the same quantum ground state and this quantum bosonic system is called a Bose–Einstein Condensate (BEC). Physically, such a system is characterized by a sharp peak over a broader distribution in both coordinate and momentum space. In a BEC the particles are correlated with each other and there is an overlap of wavelengths. The Bose–Einstein condensation process is assumed to play a crucial role in the understanding of many fundamental processes in condensed matter physics. For example, superfluidity of low-temperature liquids, like \(^3He\), can be described by assuming a Bose–Einstein Condensation process [37]. Since Bose–Einstein condensation is a phenomenon that has been observed and thoroughly studied in Earthly systems, the possibility that it may also occur in bosonic systems existing at the astrophysical or cosmological scales cannot be rejected straightaway. So, it was speculated that dark matter, which is required to explain the dynamics of the neutral hydrogen clouds at large distances from the galaxy centers, and which is also supposed to be a cold bosonic gravitationally bounded system, could also exist in the form of a Bose–Einstein Condensate [38,39,40,41,42,43]. An organized study of the properties of Bose–Einstein Condensed galactic dark matter halos can be found in [44]. The astrophysical and cosmological implications of the existence of Bose–Einstein Condensed dark matter have been recently investigated thoroughly in literature [45,46,47,48,49,50,51,52,53,54,55]. Moreover, the possibility of the existence of some forms of BEC in neutron stars has been considered a long time ago [56]. Motivated by the above, we proceed to present a new model for anisotropic compact star confined to physical DM based on Bose–Einstein condensate DM density profile with a bag model type equation of state.

We have designed this article as follows: The Einstein field equations for a static and spherically symmetric matter sphere are mentioned in Sect. 2. The field equations are solved by considering the Bose–Einstein DM density profile and a linear EoS in Sect. 3. The matching analysis of our internal solution with the external Schwarzschild solution is set up in Sect. 4. We have analyzed our proposed model from the physical point of view in Sect. 5. Section 6 is dedicated to the analysis of the equilibrium and stability of the model and Sect. 7 deals with the moment of inertia of the system. Finally, the results and conclusion of this article are presented in Sect. 8.

2 Einstein’s field equations

In the standard i.e. Schwarzschild coordinate system \(x^a = (t, r, \theta , \phi )\), the line element to describe the interior of a spherically symmetric and static stellar matter distribution can be written as

$$\begin{aligned} ds^{2}=-e^{\nu (r)}dt^{2}+e^{\lambda (r)}dr^{2}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2} \right) , \end{aligned}$$
(1)

where \(e^{\nu (r)}\) and \(e^{\lambda (r)} \) are dimensionless functions, only depend on the radial coordinate r. Indeed, these two functions are called metric potential functions.

The field equations in the framework of Einstein’s gravity (Gravitational unit \(G = c = 1\)) can be written as

$$\begin{aligned} 8\pi {\mathcal {T}}_{\mu \nu } = {\mathcal {R}}_{\mu \nu }-{1\over 2}{\mathcal {R}}g_{\mu \nu }, \end{aligned}$$
(2)

where \({\mathcal {T}}_{\mu \nu }\) is the energy–momentum tensor for the underlying matter configuration, \({\mathcal {R}}_{\mu \nu }\) is the Ricci tensor, \({\mathcal {R}}\) is the Ricci scalar and \(g_{\mu \nu }\) is the metric tensor.

As we are willing to develop the model for anisotropic compact stars, so, we consider the energy–momentum tensor for anisotropic matter distribution as

$$\begin{aligned} {\mathcal {T}}_{\mu \nu }{} & {} = [\rho (r)+p_t(r)]U_\mu U_\nu -p_t(r) g_{\mu \nu }\nonumber \\{} & {} \quad +[p_r(r)-p_t(r)]\chi _\mu \chi _\nu . \end{aligned}$$
(3)

Here, \(\rho (r)\), \( p_r(r)\), and \( p_t(r)\) are the energy density, radial pressure, and transverse pressure of the compact stars, respectively. Also, \(\chi _\mu \) and \(U_\mu \) are called unit space-like vector and fluid-4 velocity satisfying the following conditions: (i) \(U^\mu U_\mu = -\chi ^\mu \chi _\mu = 1\) and (ii) \(U^\mu \chi _\mu =0\). On using the above conditions the components of the energy–momentum tensor (3) can be obtained as

$$\begin{aligned}{} & {} T_0^0=\rho (r),\quad T^1_1=-p_r(r),\quad T_2^2 = T_3^3=-p_t(r),\nonumber \\{} & {} \quad \text {and}\ T^i_j = 0,\quad \text {if}\ i \ne j. \end{aligned}$$
(4)

On imposing Eq. (4) in the field equations (2), the Einstein field equations for the metric (1) read as

$$\begin{aligned} 8\pi \rho (r)= & {} \frac{1-e^{-\lambda (r)}}{r^{2}}+\frac{e^{-\lambda (r)}\lambda '(r)}{r}, \end{aligned}$$
(5)
$$\begin{aligned} 8\pi p_{r}(r)= & {} \frac{e^{-\lambda (r)}-1}{r^{2}}+\frac{e^{-\lambda (r)}\nu '(r)}{r}, \end{aligned}$$
(6)
$$\begin{aligned} 8\pi p_t(r)= & {} e^{-\lambda (r)}\left[ \frac{\nu ''(r)}{2}+\frac{\nu '^{2}(r)}{4}-\frac{\nu '(r)\lambda '(r)}{4}\right. \nonumber \\{} & {} \quad \left. +\frac{\nu '(r)-\lambda '(r)}{2r} \right] . \end{aligned}$$
(7)

In the model of celestial massive compact stars, two very impotent parameters are (i) Anisotropic factor \(\Delta (r) = p_t(r) - p_r(r)\) and (ii) Equation of state parameters \(\omega _r(r) = p_r(r)/\rho (r)\) (Radial) and \(\omega _t(r) = p_t(r)/\rho (r)\) (Transverse). The anisotropic factor plays an impotent role in the equilibrium and stable positions of compact stars and for the physical nature of matter configurations \( 0<\omega _r(r),~\omega _t(r)<1\) [57]. Another impotent parameter \( \eta (r)= \frac{p_r(r)}{p_t(r)}\) helps to analyze the effects of the presence of anisotropy in equilibrium configurations.

The reason for the presence of anisotropic pressure in the matter distribution can be described in the following manner: The Newton stars are formed as the supper-dense core mostly composed of degenerate neutrons from the collapse of massive stars of masses more than 8 \(M_\odot \) after the exhaustion of core H-burning [58]. The magnetic flux of the main sequence star is conserved but its radius decreases during its entire post-main sequence stages, therefore, the magnetic field is confined within a region of a very small surface area that leads to a very high surface magnetic field \((10^{12}{-}10^{14} G).\) This huge amount of magnetic field may be responsible for generating anisotropic pressure within the celestial compact star [59]. The anisotropy pressure may also exist within the compact object with a solid stellar core or the presence of a type-IIIA superfluid [60], for different phase transitions [61], pion-condensation [62] and for slow rotation [63]. The matter configuration may be anisotropic when its density is of the order of \(10^{15}~\text {g}/\text {cm}^3\) [64]. In the year 1974, Bowers and Liang [65] studied the effect of anisotropy pressure in the framework of general relativity. It is found that the presence of anisotropic pressures in charged matter enhances the stability of the configuration under radial adiabatic perturbations as compared to isotropic matter [66, 67]. Recently, Pant et al. [68, 69] and Newton Singh et al. [70] discussed the analytical solutions with the anisotropic matter in isotropic coordinates and Newton Singh et al. [71] also studied the Tolman IV solution for charge anisotropic fluid configuration.

Now, the conservation equation for anisotropic matter distribution can be written as

$$\begin{aligned} p'(r)+\frac{v'(r)}{2}[\rho (r)+p_r(r)] = \frac{2}{r}[p_t(r) - p_r(r)]. \end{aligned}$$
(8)

Due to the presence of the anisotropy, there is a non-vanishing term \(2[p_t(r) - p_r(r)]/r\) in the above conservation equation (8), and this represents a force. The force will act in the outward direction if \(p_t(r) > p_r(r)\) and in the inward direction if \(p_t(r) < p_r(r)\) [72]. It is noted that the outward force for \(p_t(r) > p_r(r)\) helps to construct more massive compact objects with anisotropic fluid than with isotropic fluid.

3 The new model: solutions of field equations

The literature shows that due to the presence of high density in anisotropic compact stars researchers are continuously trying to investigate the exact nature of matter distribution. With this aim in mind, recently several researchers introduced some models for anisotropic compact stars with DM composition [73,74,75,76,77]. From these points of view, we consider the Bose–Einstein DM density profile [78] and a linear equation of state (EoS) to introduce a suitable new model for anisotropic compact stars formed by DM. The Bose–Einstein DM density profile [78] and the linear EoS can be written as

$$\begin{aligned} \rho (r)= & {} \frac{a}{kr}\sin (kr), \end{aligned}$$
(9)
$$\begin{aligned} p_r(r)= & {} \alpha \rho (r)-\beta , \end{aligned}$$
(10)

where \(a ~(\text {km}^{-1})\), k, \(\alpha \) and \(\beta ~(\text {km}^{-2})\) are non-zero positive constants. Chavanis and Harko [79] found that some celestial compact objects may contain a significant part of their matter in the form of a Bose–Einstein condensate. Pethik et al. [80] and Mosquera et al. [81] discussed the presence of Bose–Einstein Condensates in Neutron stars in the helium white dwarf stars, respectively. Moreover, Li et al. [82] investigated the matter distributions that may be formed from the Bose–Einstein condensation of dark matter. All these significant studies and the non-singular characteristic of the above density profile (9) inspired us to introduce this model.

The mass of a matter configuration depends on the energy density and it can be obtained as

$$\begin{aligned} m(r)=4\pi \int _0^r r'^2 \rho (r') dr'= \frac{4 \pi a}{k^3} [\sin (k r)-k r \cos (k r)].\nonumber \\ \end{aligned}$$
(11)

Also, the compactness parameter is defined in terms of the mass function as

$$\begin{aligned} u(r)=\frac{2m(r)}{r}=\frac{8 \pi a}{k^3 r} [\sin (k r)-k r \cos (k r)]. \end{aligned}$$
(12)

In a physically viable stellar compact stars model the compactness parameter u(r) needs to satisfy the Buchdahl Limit i.e. \(u(r) < 8/9\) [83].

Fig. 1
figure 1

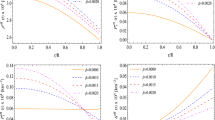
Variations of the metric potential functions (left) and energy density (right) against the radial coordinate r for the compact star Vela X-1 corresponding to the numerical values of constants given in Table 1

Full size image
Fig. 2
figure 2

Variations of the radial and transverse pressures (left) and anisotropic factor (right) against the radial coordinate r for the compact star Vela X-1 corresponding to the numerical values of constants given in Table 1

Full size image
Fig. 3
figure 3

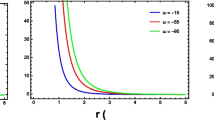
Radially symmetric profiles of the energy density (Green Centre), radial pressure (Magenta Centre) and transverse pressure (Yellow Centre) for the compact star Vela X-1 corresponding to the numerical values of constants given in Table 1

Full size image
Fig. 4
figure 4

Variations of the EoS parameters (left) and mass, compactness parameter (right) against the radial coordinate r for the compact star Vela X-1 corresponding to the numerical values of constants given in Table 1

Full size image

Now, the metric potential function \(e^{-\lambda (r)}\) can be defined in the framework of Schwarzschild coordinate system as

$$\begin{aligned} e^{-\lambda (r)} = 1-\frac{2m(r)}{r}= 1-\frac{8 \pi a}{k^3 r} [\sin (k r)-k r \cos (k r)].\nonumber \\ \end{aligned}$$
(13)

Imposing Eq. (9) in Eq. (10), we obtain the radial pressure as

$$\begin{aligned} p_r(r)= & {} \frac{a \alpha }{k r} \sin (k r)-\beta . \end{aligned}$$
(14)

On using Eqs. (13)–(14) in Eq. (6) we obtain the expression of \(\nu '(r)\) as

$$\begin{aligned} \nu '(r)= & {} \frac{k^2 \left[ 8 \pi a \alpha r \sin (k r)-8 \pi \beta k r^2+k\right] }{k^3 r-8 \pi a \sin (k r)+8 \pi a k r \cos (k r)}-\frac{1}{r}. \end{aligned}$$
(15)

The above equation of \(\nu '(r)\) does not provide the analytical expression for \(\nu (r)\) due to its complicated form. With this problem in mind, we have used the numerical technique to solve Eq. (15), and, then, provide a graphical demonstration for \(e^{\nu (r)}\) in Fig. 1 (Left). One can see from Fig. 1 (Left) that both the metric potential functions \(e^{\nu }\) and \(e^{-\lambda }\) are regular in nature with respect to the radial coordinate r, also, they meet at the surface of the compact star which ensures the matching of the boundary.

Now, we obtain the analytical expressions of transverse pressure and anisotropic as

$$\begin{aligned} p_t(r)= & {} \frac{1}{2 k r g_1}\left[ 2 \pi a^2 g_2+a \left( k r g_3-2 \pi a g_4+k^2 r^2 g_5\right) \right. \nonumber \\{} & {} \left. +2 \beta k^4 r^2 \left( 2 \pi \beta r^2-1\right) \right] , \end{aligned}$$
(16)
$$\begin{aligned} \Delta (r)= & {} \frac{1}{2 k r g_1}\big [2 \pi a^2 g_2+a \big (k r \left( g_6-2 \pi a (5 \alpha +1) \sin (2 k r)\right) \nonumber \\{} & {} -2 \pi a g_7 +k^2 r^2 g_8 \cos (k r)\big )+4 \pi \beta ^2 k^4 r^4\big ], \end{aligned}$$
(17)

where

$$\begin{aligned} g_1= & {} k^3 r-8 \pi a \sin (k r)+8 \pi a k r \cos (k r),\nonumber \\ g_2= & {} \alpha \left[ (\alpha +3) k^2 r^2-1\right] +1,\nonumber \\ g_3= & {} \sin (k r) \left( 12 \pi \beta +k^2 \left( \alpha -4 \pi (2 \alpha +1) \beta r^2\right) \right) \nonumber \\{} & {} -2 \pi a (\alpha +1) \sin (2 k r),\nonumber \\ g_4= & {} (\alpha -1) \left( \alpha k^2 r^2-1\right) \cos (2 k r),\nonumber \\ g_5= & {} \left( \alpha k^2-12 \pi \beta \right) \cos (k r),\nonumber \\ g_6= & {} -\sin (k r)\left( 4 \pi \beta +k^2 \left( \alpha +4 \pi (2 \alpha +1) \beta r^2\right) \right) \nonumber \\ g_7= & {} \cos (2 k r)\left( \alpha \left( (\alpha -1) k^2 r^2+3\right) +1\right) ,\nonumber \\ g_8= & {} 4 \pi \beta +\alpha k^2. \end{aligned}$$
(18)

The surface red-shift can be written in terms of the metric potential function \(e^{\lambda (r)}\) at the surface of the stellar configuration as

$$\begin{aligned} z_s \!= & {} \! e^\frac{\lambda (R)}{2}\!-\!1 \!= \!\left[ 1-\frac{8 \pi a}{k^3 R} \{\sin (k R)-k R \cos (k R)\}\right] ^{-\frac{1}{2}}\!-1.\nonumber \\ \end{aligned}$$
(19)

4 Matching of the internal and external solutions at the boundary

In a physical model, the interior solutions of the celestial matter configuration should be matched with the exterior Schwarzschild solutions at the surface \(r = R\) of this matter configuration. Interestingly, at the stage of the matching we can obtain the values of some model-dependent constants. The exterior Schwarzschild solution is given as

$$\begin{aligned} ds^{2} {=}{-}g_{tt}(r)dt^{2}+g_{rr}(r)dr^{2} +r^{2}\big (d\theta ^{2}{+}\sin ^{2}\theta d\phi ^{2} \big ),\nonumber \\ \end{aligned}$$
(20)

where \(g_{tt}(r) = g_{rr}^{-1}(r) = \left( 1-\frac{2M}{r}\right) \). Here, it is noted that the surface radius R needs to be greater than 2M to avoid any singularity.

Now, the matching of the internal solution with the external Schwarzschild solution at the boundary \(r = R\) of the matter configuration yields the following result

$$\begin{aligned} e^{-\lambda (R)} = 1-\frac{2M}{R}. \end{aligned}$$
(21)

Also, the vanishing value of the radial pressure at the boundary of the matter configuration implies

$$\begin{aligned} p_r(R) = 0. \end{aligned}$$
(22)

From the conditions (21)–(22), we obtain the expressions of a and \(\alpha \) in terms of k, the radius R and mass M of fluid sphere as

$$\begin{aligned} a= & {} k^3 M[4 \pi \big \{\sin (k R) - k R \cos (k R)\big \}]^{-1} , \end{aligned}$$
(23)
$$\begin{aligned} \alpha= & {} \frac{1}{a}\beta k R \csc (k R) , \end{aligned}$$
(24)

and we know that \(\beta =4B_g/3\). To design a realistic EoS, we chose the widely accepted value of \(B_g\) as \(75\, \text {MeV}/\text {fm}^3\), and k as per physical validity.

5 Physical analysis of the model

Here, we are going to reveal the physical acceptance of our model by analyzing different essential conditions.

5.1 Natures of physical parameters

For the sake of understanding, the exact behavior of the physical parameters, energy density, radial and transverse pressures, anisotropic factor, EoS parameters, mass, compactness parameter, and the parameter \(\eta (r)\) we demonstrate all these parameters graphically in Figs. 1 (Right), 2, 4 and 5 (Left) for the compact star Vela X-1 corresponding to \(k = \{0.122, 0.126, 0.130, 0.134, 0.138\}\). We obtained the following results

  1. (i)

    From Fig. 1 (Right), it is clear that the energy density is positive and maximum at the center of the compact star, moreover, it has a properly decreasing nature in the direction of the boundary of the compact star. Consequently, the reported energy density is physically acceptable.

  2. (ii)

    The pressures, radial and transverse are both positively finite and decreasing in nature (see Fig. 2 (left)), which ensure the physical acceptance of these pressures. It is further seen from Fig. 2 (left) that both the pressures are maximum at the center of the star with the same value, and, after the center, the transverse pressure is more than the radial pressure, and, therefore, this behavior of pressures generates the positive anisotropy within the star just after the center, clear from Fig. 2 (right). In Fig. 3, we have shown the radially symmetric profiles of energy density, radial pressure, and transverse pressure From that figure we can see that they all are maximum at the center of the star and decrease towards the surface.

  3. (iii)

    Here, the EoS parameters for our obtained solutions are within the region \(0< \omega _r(r), \omega _t{r} < 1\), Fig. 4 (left). Therefore, the reported solutions present the physical matter configuration.

  4. (iv)

    The exact behaviors of the mass function and compactness parameter are displayed in Fig. 4 (right). It is seen from Fig. 4 (right) that both the mass function and compactness parameter are positively increasing in nature against the radial coordinate r. Moreover, the values of the compactness parameter under the Buchdahl Limit.

  5. (v)

    The graphical demonstration of the parameter \(\eta (r) = \frac{p_r(r)}{p_t(r)}\) is shown in Fig. 5 (left), which clears that \(0 \le \eta (r) \le 1\) in \(0 ~\text {km} \le r \le 9.56~ \text {km}\), and, hence, the anisotropic factor \(\Delta (r) \ge 0\) within the fluid sphere, similar result as in Fig. 2 (right) i.e. anisotropic force acts in the outward direction.

Fig. 5
figure 5

Variations of the function \(\eta (r)\) (left) and energy conditions (right) against the radial coordinate r for the compact star Vela X-1 corresponding to the numerical values of constants given in Table 1

Full size image

5.2 Central density and pressures

It is mentioned earlier that the energy density, radial and transverse pressures should be positively finite for the physical acceptability of the solutions, and, therefore, the central values of energy density and pressures must be positively finite. Now, we obtain the central values of density and pressures for our solutions as

$$\begin{aligned} \rho _c= & {} a >0, \end{aligned}$$
(25)
$$\begin{aligned} p_{rc}= & {} p_{tc} = a\alpha -\beta > 0. \end{aligned}$$
(26)

It is well-known that any physical matter configuration satisfies the Zeldovich’s criterion [84]. The Zeldovich’s criterion [84] states that \(p_{rc}/ \rho _c \le 1\), which yields

$$\begin{aligned} \beta \ge {a(\alpha -1)}. \end{aligned}$$
(27)

Therefore, from Eqs. (26) and (27) one can easily get a boundary representing constraint on \(\beta \) as

$$\begin{aligned} {a(\alpha -1)} \le \beta < {a\alpha }. \end{aligned}$$
(28)

The above constraint on \(\beta \) gives the constraint on the bag constant \(B_g\) as

$$\begin{aligned} {\frac{3}{4}a(\alpha -1)} \le B_g < {\frac{3}{4}a\alpha }. \end{aligned}$$
(29)

5.3 Energy conditions

As all the physical parameters of this model have smooth and regular characteristics, now, it is needful to test the different energy conditions for our solutions, because, any gravitationally confined stellar physical matter configuration must satisfy all the energy conditions, namely (i) Null energy condition (NEC), (ii) Weak energy condition (WEC) and (iii) Strong energy condition (SEC). These energy conditions can be expressed as [85, 86]

$$\begin{aligned}{} & {} \text {NEC}_r : \rho (r)+p_r(r) \ge 0,~~ \text {NEC}_t : \rho (r)+p_t(r) \ge 0,\nonumber \\{} & {} \text {WEC}_r : \rho (r) \ge 0,~\rho (r)+p_r(r) \ge 0,\nonumber \\{} & {} \text {WEC}_t : \rho (r) \ge 0,~\rho (r)+p_t(r) \ge 0,\nonumber \\{} & {} \text {SEC} : \rho (r)+p_r(r)+2p_t(r) \ge 0. \end{aligned}$$
(30)

We test all these energy conditions by graphical demonstrations of the expressions that occurred in the L.H.S of all inequalities (30), provided in Fig. 5 (right). From Fig. 5 (right) and Fig. 1 (right), it is clear that the solutions satisfy all the energy conditions within the solutions representing matter configuration. Therefore, it can be concluded that our solution representing matter configuration is made of physical DM.

Fig. 6
figure 6

Variations of the three forces (left) and velocity of sound (right) against the radial coordinate r for the compact star Vela X-1 corresponding to the numerical values of constants given in Table 1

Full size image

Therefore, one can say that all the physical parameters of our reported solutions are physically well-behaved by satisfying all the essential conditions.

6 Equilibrium and stability analysis

Here, we are going to check the equilibrium and stability of our proposed model. We will analyze the equilibrium i.e. the dynamical balancing of interior forces with respect to the generalized Tolman–Oppenheimer–Volkoff (TOV) equation and stability with the help of (i) Velocity of sound, (ii) Adiabatic index, and (iii) Harrison–Zeldovich–Novikov’s Static condition.

6.1 Equilibrium: dynamical balancing of interior forces

The actual final fate of any stellar matter configuration depends on the dynamical balancing of interior forces, because, an anisotropic compact star stays in the equilibrium situation with the help of simultaneous action of three different forces, namely, (i) Gravitational force, (ii) Hydrostatic force, and (iii) Anisotropic force. Now, in order to analyze the interplay of these mentioned forces we consider the generalized TOV equation, which can be written as

$$\begin{aligned}{} & {} -\frac{1}{r}M_g(r)[\rho (r)+p_r(r)]e^{\{\nu (r)-\lambda (r)\}/ 2}\nonumber \\{} & {} \quad -\frac{dp_r(r)}{dr}+\frac{2}{r}[p_t(r)-p_r(r)]=0. \end{aligned}$$
(31)

Here, \(M_g(r) \) represents the gravitational mass of the stellar matter configuration. The Tolman–Whittaker formula for the expression of \(M_g(r) \) is given as

$$\begin{aligned} M_g(r)= & {} 4 \pi \int _0^r r^2 e^{[\nu (r)+\lambda (r)]/2}\big (T^t_t-T^r_r-T^\theta _\theta -T^\phi _\phi \big ) dr.\nonumber \\ \end{aligned}$$
(32)

On imposing the Einstein field equations (5)–(7) in the above Eq. (32), the expression for gravitational mass \(M_g(r) \) reads as

$$\begin{aligned} M_g(r)=\frac{1}{2}re^{[\lambda (r)-\nu (r)]/2}~\nu '(r). \end{aligned}$$
(33)

With this expression of \(M_g(r)\) the TOV equation Eq. (31) reduces as

$$\begin{aligned}{} & {} {-}\frac{\nu '(r)}{2}[\rho (r){+}p_r(r)]{-}\frac{dp_r(r)}{dr}{+}\frac{2}{r}[p_t(r)-p_r(r)]{=}0, \nonumber \\ \end{aligned}$$
(34)
$$\begin{aligned}{} & {} \text {i.e.}\ F_g(r)+F_h(r)+F_a(r)=0, \end{aligned}$$
(35)

where

$$\begin{aligned} \text {Gravitation force }: F_g(r)= & {} -\frac{\nu '(r)}{2}[\rho (r)+p_r(r)],\nonumber \\ \text {Hydrostatics force }: F_h(r)= & {} -\frac{dp_r(r)}{dr},\nonumber \\ \text {Anisotropic force}: F_a(r)= & {} {2\Delta (r) \over r}. \end{aligned}$$
(36)

For our solutions, the closed forms of these three forces are obtained as:

$$\begin{aligned} F_g(r)= & {} -\frac{1}{kr^2 g_1}\big [4 \pi h_1 (h_2 +a k r \cos (k r)+\beta k^3 r^3)\big ], \end{aligned}$$
(37)
$$\begin{aligned} F_h(r)= & {} \frac{a \alpha }{k r^2} [\sin (k r)-k r \cos (k r)] , \end{aligned}$$
(38)
$$\begin{aligned} F_a(r)= & {} \frac{1}{kr^2 g_1}\left[ 2 \pi a^2 h_3+a \left\{ k r \left( \sin (k r) \right. \right. \right. \nonumber \\{} & {} \times \left. \left( -\left( 4 \pi \beta +k^2 \left( \alpha +4 \pi (2 \alpha +1) \beta r^2\right) \right) \right) \right. \nonumber \\{} & {} \left. -2 \pi a (5 \alpha +1) \sin (2 k r)\right) \nonumber \\{} & {} -2 \pi a \left( \alpha \left( (\alpha -1) k^2 r^2+3\right) +1\right) \cos (2 k r)\nonumber \\{} & {} \left. \left. +k^2 r^2 \left( 4 \pi \beta +\alpha k^2\right) \cos (k r)\right\} +4 \pi \beta ^2 k^4 r^4\right] .\nonumber \\ \end{aligned}$$
(39)

where

$$\begin{aligned} h_1= & {} \beta k r-a (\alpha +1) \sin (k r),\nonumber \\ h_2= & {} -a \sin (k r)\left( \alpha k^2 r^2+1\right) , ~\text {and} \nonumber \\ h_3= & {} \alpha \left\{ (\alpha +3) k^2 r^2+3\right\} +1. \end{aligned}$$
(40)

We have highlighted the interplay of these three different forces graphically in Fig. 6 (left). It is clear from the Fig. 6 (left) that the net force \(F_g(r)+F_h(r)+F_a(r)\) remains zero throughout \(r \le R\) for each of the value of the parameter \(k\in \{0.122, 0.126, 0.130, 0.134, 0.138\}.\) Consequently, our model star Vela x-1 is in the equilibrium situation under the simultaneous action of three forces.

Fig. 7
figure 7

Variations of the stability factor (left) and adiabatic index (right) against the radial coordinate r for the compact star Vela X-1 corresponding to the numerical values of constants given in Table 1

Full size image

6.2 Stability analysis

The potentially stable position is also necessary for stellar physical matter distributions, and, it can be analyzed with the help of Velocity of sound, Adiabatic index, and Harrison–Zeldovich–Novikov’s static stability condition.

6.2.1 Velocity of sound

According to the GTR, the velocity of light c is the maximum velocity that ever exists. So, whenever sound is moving through a physical stellar matter sphere, its radial and transverse velocities, \(v_r(r)\) and \(v_t(r)<c\), this condition is known as the Causality condition. Otherwise, matter distribution will be nonphysical. Mathematically, the radial velocity \(v_{r}(r)\) and transverse velocity \(v_{t}(r)\) of sound can be expressed as

$$\begin{aligned} v_{r}(r) = \sqrt{{dp_r(r) \over d\rho (r)}}=\alpha ,\quad v_{t}(r) = \sqrt{{dp_t(r) \over d\rho (r)}}. \end{aligned}$$
(41)

Therefore, as per the causality condition \(0 \le v_r(r) < 1\) and \(0 \le v_t(r) < 1\) for physical matter sphere. For our model compact star Vela X-1, our solutions obey the causality condition, clear from Fig. 6 (right). Therefore, again, we have the result in favor of physical matter configuration.

In the year 1922, Herrera [87] introduced the Cracking method under the radial perturbations to test the stability of the anisotropic matter spheres. Later, the Cracking method taking in mind, Abreu et al. [88] analyzed the stability of the anisotropic fluid spheres with the help of the stability factor \({\mathcal {N}}(r) = [\{v_t(r)\}^2 - \{v_r(r)\}^2]\). According to Abreu et al. [88]

$$\begin{aligned} | {\mathcal {N}}(r) |\le 1 \implies {\left\{ \begin{array}{ll} -1 \le {\mathcal {N}}(r) \le 0: ~\text {Stable},\\ ~~0 < {\mathcal {N}}(r) \le 1:~ \text {Unstable}. \end{array}\right. } \end{aligned}$$
(42)

The stability factor \({\mathcal {N}}(r)\) is demonstrated graphically in Fig. 7 (left). One can see from Fig. 7 (left) that for our solutions \(-1< {\mathcal {N}}(r) < 0\) within \(r \le R\) corresponding to \(k\in \{0.122, 0.126, 0.130, 0.134, 0.138\},\) and, hence, the solutions represent the potentially stable mass distribution. It is interesting to note that the decreasing values of the parameter k yield the more negative values of \({\mathcal {N}}(r)\) i.e. the matter configuration is more stable for lower values of k.

6.2.2 Adiabatic index

The adiabatic index has a crucial role in the stable equilibrium against gravitational collapse. The isotropic matter configuration is in stable equilibrium if the adiabatic index \(\Gamma _r(r) = 4/3\). However, in the presence of anisotropy i.e. for anisotropic matter configuration the stability condition requires \(\Gamma _r(r) > 4/3\) within \(r < R\) [89,90,91,92]. The adiabatic index \(\Gamma _r(r)\) can be written in terms of energy density, radial pressure, and radial velocity of sound as

$$\begin{aligned} \Gamma _r(r)= \left( 1+\frac{\rho (r)}{p_r(r)}\right) \{v_r(r)\}^2. \end{aligned}$$
(43)

The exact behaviour \(\Gamma _r(r)\) is depicted in Fig. 7 (right). It is evident from Fig. 7 (right) that \(\Gamma _r(r) > 4/3\) for our proposed solution. Therefore, our model compact star is stable under the adiabatic index. Here, we can notice that as similar to the stability factor the lower values of \(k \in [0.122, 0.138]\) favor the more stable gravitationally confined matter configurations.

Fig. 8
figure 8

Variations of the mass M against the surface radius R (left) and Moment of Inertia I against the mass M (right) for the compact star Vela X-1 corresponding to the numerical values of constant given in Table 1

Full size image
Table 1 Numerical values of constants, central density, central pressure, surface density, surface gravitational redshift, and surface compactness parameter for the compact star Vela X-1 (M = 1.77\(M_{\odot }\), R = 9.56 km) with \(B_g = 75\, \text {MeV}/\text {fm}^3\)
Full size table

6.2.3 Harrison–Zeldovich–Novikov’s static stability condition

It is well-known that any static gravitationally confined matter sphere remains stable against its own gravitational pull mainly with the help of a central energy density profile. In this connection, Harrison et al. [93] and Zeldovich–Novikov [84] proposed the condition for static stability as \(\partial M(\rho _c)/\partial \rho _c > 0\) i.e. the mass of matter sphere will be increasing against the central density. Otherwise, unstable matter distribution.

The mass and surface radius in terms of \(\rho _c\) are obtained as

$$\begin{aligned} M(\rho _c)= & {} \frac{4R\rho _c}{k^3}\left[ \sin (kR)-kR\cos (kR)\right] . \end{aligned}$$
(44)

Therefore,

$$\begin{aligned} \frac{\partial M(\rho _c)}{\partial \rho _c}= \frac{4R}{k^3}\left[ \sin (kR)-kR\cos (kR)\right] . \end{aligned}$$
(45)

One can easily check that for \(R = 9.56~\text {km}\) and \(k\in \{0.122, 0.126, 0.130, 0.134, 0.138\},\) \(\sin (kR)-kR\cos (kR) > 0\) i.e. \(\partial M(\rho _c)/\partial \rho _c > 0\) and hence \(M(\rho _c)\) is increasing against the central density \(\rho _c\). Consequently, the reported stellar configuration is stable against the static stability condition.

7 Moment of inertia

According to the result of Lattimer and Prakash [94], the moment of inertia for a uniformly rotating star can be written as

$$\begin{aligned} I = {8\pi \over 3} \int _0^R r^4 (\rho (r)+p_r(r)) e^{(\lambda (r)-\nu (r))/2} ~{\bar{\omega } \over \Omega }~dr \end{aligned}$$
(46)

where \(\Omega \) is the angular velocity of the star and \(\bar{\omega }\) is the rotational drag that satisfy the Hartle’s equation [95] as

$$\begin{aligned} {d \over dr} \left( r^4 j ~{d\bar{\omega } \over dr} \right) =-4r^3\bar{\omega }~ {dj \over dr} . \end{aligned}$$
(47)

where \(j=e^{-(\lambda (r)+\nu (r))/2}\) with \(j(R)=1\). Bejger and Haensel [96] proposed the approximate solution for the moment of inertia I up to the maximum mass \(M_{max}\) as

$$\begin{aligned} I = {2 \over 5} \Big (1+x\Big ) {MR^2}, \end{aligned}$$
(48)

where parameter \(x = (M/R)\cdot \text {km}/M_\odot \).

For our reported solutions, the exact behavior of the moment of inertia I against the mass is shown in Fig. 8, (right), which indicates that as the mass increases the moment of inertia increases till up to the certain value of mass and then decreases. The red dots and the blue dots in the \(I-M\) profile represent the \(I_{max}\) and \(M_{max}\), and, it is evident that the mass is not maximum at \(I_{max}\). In fact, the mass is lower by a few amounts from \(M_{max}\) at \(I_{max}\), it occurs to the EoSs because of phase transition to an exotic state without any strong high-density softening [97]. It is noted that \(I_{max}\) and \(M_{max}\) increase for decreasing values of \(k\in \{0.122, 0.126, 0.130, 0.134, 0.138\}.\) This \(I-M\) graph helps to estimate the maximum moment of inertia for the particular choice of stellar matter configuration.

8 Results and conclusion

In this article, a new model of anisotropic stellar compact stars confined by physical DM is proposed based on the Bose–Einstein DM density profile and bag model type linear EoS. To clarify the physical acceptability of our model we have analyzed the solutions in the context of the well-known compact star Vela X-1 associated with the constant values \(k \in [0.122, 0.138]\), and \(B_g = 75~\text {MeV}/\text {fm}^3\) i.e. \(\beta = 100~\text {MeV}/\text {fm}^3\). The Vela X-1 is a high-mass X-ray binary matter source that is made by a neutron star in a close orbit around the 23.5 \(M_\odot \) B0.5 Ib supergiant donor star HD 77581. The rocket-borne experiment [98] first noticed that matter source and later observations [99] found that the source was extremely variable. The comprehensive study for Vela X-1 is done in Ref. [100]. Indeed, the mass of the neutron star in Vela X-1 was first calculated by Rawls et al. [101] as \(1.77 \pm 0.08~ M_\odot \) and Gangopadhyay et al. [102] estimated the radius of the neutron star in Vela X-1 as \(9.56 \pm 0.08~\text {km}\). It is worth mentioning that in the present study, we have matched our interior solutions with the exterior Schwarzschild metric that determined the values of involved parameters a and \(\alpha \) given in Table 1, where k is a free parameter. We have also shown the graphical analysis of the physical parameters, \(\rho (r)\), \(p_(r)\), \(p_t(r)\), \(\Delta (r)\) and investigated the stability of the model by exploring the energy conditions, equation of state, generalized TOV equation, causality condition, and adiabatic index. The proposed model has the following key features.

1. Metric potentials: The metric potential functions \(e^{\nu (r)}\) and \(e^{-\lambda (r)}\) are non-singular in nature for \(r \le R\). The metric potential function \(e^{\nu (r)}\) is increasing in nature whereas \(e^{-\lambda (r)}\) is decreasing in nature inside the compact star with \(e^{-\lambda (0)} = 1.\) Moreover, \(e^{\nu (r)}\) and \(e^{-\lambda (r)}\) together meet with the \(g_{tt}\) metric component of the external Schwarzschild solution at \(r = R = 9.56\), the surface of the compact star Vela X-1 (see Fig. 1 (left)), and hence, our internal solutions have properly matched with the external solution. Therefore, all these results ensure that these two metric potentials are suitable for constructing the non-singular compact stars model.

2. Energy density and pressures: In our model, the energy density \(\rho (r)\), radial pressure \(p_r(r)\), and transverse pressure \(p_t(r)\) all are positively finite, decreasing in behavior within the matter configuration (see Fig. 1 (right) and Fig. 2 (left) ). Moreover, \(\rho (0) = \{420, 423.9, 428, 432.4, 436.9\}~\text {MeV}/\text {fm}^3\) and \(\rho (R) =\{330.9, 328.5, 326, 323.4, 432.4\}~\text {MeV}/\text {fm}^3\) for \(k = \{0.122, 0.126, 0.130, 0.134, 0.138\}.\) Also, \(p_r(0) = p_t(0)\) = maximum values of the pressure = {26.87, 29.18, 31.28, 33.68, 36.22} \(\text {MeV}/\text {fm}^3\) for \(k = \{0.122, 0.126, 0.130, 0.134, 0.138\},\) and \(p_r(r) < p_t(r)\) for \(0 < r \le R\) with \(p_r(R) = 0\) and \(p_t(R) = \{23.6, 21.40, 19.07, 16.64, 14.10\}~\text {MeV}/\text {fm}^3\) for \(k = \{0.122, 0.126, 0.130, 0.134, 0.138\}.\) The result \(p_r(r) < p_t(r)\) for \(0 < r \le R\) is in favor of constructing a more compact matter configuration. It is interesting to note that the numerical values of central and surface densities both are of order \(10^{14}~\text {g}/\text {cm}^3\) and central pressure is of order \(10^{34}~\text {g}/\text {cm}^2\) for the model star Vela X-1 (See Table-1), which well-fitted to the observational data. Furthermore, we have displayed the radially symmetric profiles of energy density, radial pressure, and transverse pressure for Vela X-1 corresponding to \(k = \{0.122, 0.126, 0.130, 0.134, 0.138\}\) in Fig. 3 as follows the Refs. [103,104,105], which shows that they all are maximum at the center of the star and decrease towards the surface.

3. Anisotropy and EoS parameters: As we have seen that \(p_r(r) < p_t(r)\) within \(0 < r \le R\), which yield the positive anisotropic factor \(\Delta (r)\) for \(0 < r \le R\), also clear from Fig. 2 (right). Due to the positive anisotropy the anisotropic force \(2\Delta (r)/r\) acts in an outward direction within the star i.e. in this situation, a star can endure the gravitational pull a long time, and hence, the star becomes more compact. For our solutions, the EoS parameters \(\omega _r(r), \omega _t(r) \in [0, 1]\) (see Fig. 4 (left)), as a result, the solutions represent physical matter configuration.

4. Mass and compactness parameter and surface redshift: For the model compact star Vela X-1, the mass function and compactness parameter both are finitely positive as well as increasing in nature (Fig. 4 (right)). Furthermore, the compactness parameter for our solutions is under the Buchdahl Limit \(u(R) < 8/9\) [106] (see Fig. 4 (right) and Table 1). We have also calculated the numerical values of the surface redshift z(R) and found that they are under the proper range [107], given in Table 1.

5. Energy conditions: Any compact star confined by physical matter satisfies the NEC, WEC, and SEC, these results are found for our solutions, clear from Figs. 1 (left) and 5 (right). Therefore, the solution supporting matter distribution is physical in behavior.

6. Equilibrium: The anisotropic celestial compact star stays in an equilibrium state under the action of three forces: gravitational, hydrostatic, and anisotropic by satisfying the generalized TOV equation. Our proposed solutions have satisfied the TOV equation for the compact star Vela X-1 (see Fig. 6 (left)), here, the hydrostatic and anisotropic forces together defend the gravitational pull. Consequently, the solutions representing the matter sphere is in an equilibrium state.

7. Stability: The solutions are again in favor of representing physical matter distribution by obeying the causality conditions (see Fig. 6 (right)). Besides, for our solutions, it has been seen that the stability factor \({\mathcal {N}}(r) \) within the range \(-1< {\mathcal {N}}(r) < 0\) (see Fig. 7 (left)), the adiabatic index \(\Gamma _r(r)>\) \(\frac{4}{3}\) (see Fig. 7 (right)) inside the model star along with increasing mass profile against the central density. All These impotent results ensure that the solutions are holding static stable matter sphere.

8. \(M-R\) and \(I-M\) relations: The solutions generating maximum masses M with respect to the surface radius R are demonstrated in Fig. 8 (left) corresponding to \(k\in \{0.122, 0.126, 0.130, 0.134, 0.138\},\) showing that the maximum mass increases with decreasing values of \(k\in \{0.122, 0.126, 0.130, 0.134, 0.138\}.\) It is interesting to note that all these maximum masses under the Rhoades–Ruffini limit \(3.2 M_{\odot }\) [108]. For increasing values of mass M the moment of inertia I increases till up to the certain value of M and then decreases (see Fig. 8 (right)), and also, the mass is not maximum at \(I_{max}\) lower by few amount from \(M_{max}\). In this study, we have obtained that \(M_{max} = 2.821~ M_\odot ,~ 2.513 ~M_\odot , ~2.263~M_\odot , ~2.052~M_\odot , ~1.865~M_\odot \) and \(I_{max} = 244.7 ~\text {km}^{-2},~ 202.5~\text {km}^{-2},~ 171.2~\text {km}^{-2}, ~149~\text {km}^{-2},~ 124~\text {km}^{-2}\) corresponding to \(k = 0.122,\) 0.126, 0.130, 0.134, 0.138, respectively.

Finally, as a concluding remark, we can say that all the analysis and obtained outcomes ensure that our proposed model is physically well-behaved and ready to present the stable celestial compact star confined by physical DM, which is in an equilibrium state. So, in the future, the scientific research community would be interested in extending the present analysis for other compact stars in the Einstein gravity as well in the different modified theories of gravity.