Physical viability of exponential entropy on charged AdS black hole through thermodynamic geometries

Abstract

A detailed discussion on phase transition, stability and microscopic structure of a charged black hole in anti-de Sitter (AdS) by using exponential entropy is presented. For this black hole, the thermodynamic characteristics such as the Hawking temperature, specific heat and the $P-v$ curve will be developed and investigated with the variation of black hole horizon radius and monopole parameter. We also study the scalar curvatures of this black hole by using several thermodynamic geometry formulations, such as the Ruppeiner, Weinhold, HPEM, Quevedo in view of exponential entropy. Moreover, we extract the HPEM and Quevedo formulations of the charged AdS black hole which may provide more data on the phase-transition than the Weinhold and Ruppeiner techniques.

1 Introduction

Thermodynamic geometry is a field of study that explores the geometric structure of thermodynamic systems. It is a mathematical framework that connects the curvature of the state space of a thermodynamic system to its physical characteristics such as heat capacity, entropy and other thermodynamic parameters. The study of thermodynamic geometry has been shown to be beneficial in understanding the behavior of many complex systems, including black holes (BHs), condensation systems and biological systems. The basic idea behind thermodynamic geometry is that the operation of a thermodynamic system is inextricably connected to the geometry of its state space. The curvature of the state space, in particular, can reveal information about the system’s stability, phase transitions and other thermodynamic features. Researchers may gain insight into the behavior of the system while developing new ways for evaluating and foreseeing its behavior through investigating the geometry of the state space.

Thermodynamic geometry has its roots in the study of the thermodynamic properties of BHs, where it was discovered that the curvature of the BHs event horizon is connected to its thermodynamic properties. Since that time, the field has grown to embrace a wide range of systems, including biological, quantum and condensed matter systems. The subject of thermodynamic geometry has attracted considerable attention and interest from scholars in several domains in recent years. It has shown to be a useful tool for understanding complex systems and has various applications in new discoveries in science and technology and advances.

When Bekenstein discovered that the entropy of a thermodynamic system is quite similar to the region of a BHs event horizon, he stumbled upon the concept of a connectivity between BH and thermodynamic systems [1]. This led to the development of the concept of a connectivity between BH and thermodynamic systems with exponential entropy [2]. The study of BH thermodynamics, which postulates that BH follow laws comparable to those of classical thermodynamics, forms the basis of this link and serves as its foundation. Hawking offers a defence for this position by suggesting that BH are capable of emitting radiation [3]. There are two distinct varieties of BHs: the positive specific heat (bigger ones) represent a stable in their immediate surroundings, while the negative specific heat (smaller ones) leads to unstable in their immediate surroundings. When BH reach the temperature at which the transition takes place, they go through a phase shift into radiation that is referred to as the Hawking-Page phase-transition [4]. This significance of AdS BH may be attributed to the fact that they are the only form of BH that does not violate the laws of thermodynamics.

During the cooling period of the early universe, monopoles evolved along with other imperfections such as cosmic strings and domain walls [5, 6]. A global monopole (O(3) symmetry into U(1)) charge was found as a result of the observation that phase transitions in the cosmos are followed by the spontaneous breakdown [7]. In this particular instance, the Schwarzschild BH solution was changed to the static BH solution, which included a global monopole. The monopole BH solution has been the focus of debate in a number of articles published in participant scientific journals [8,9,10,11,12,13]. It has been shown that the existence of the worldwide monopole term in the BH solution perform a important role in the situation that is being discussed in this article.

For the time being, a variety of strategies for adding differential geometric concepts into BH thermodynamics have been suggested [14,15,16]. One such example is provided by Ruppeiner’s metric [17], which can be shown to have a compatibly equivalent relationship to Weinhold’s metric [18]. As a result of this investigation, it was found that Ruppeiner’s and Weinhold’s metrics are not stable using Legendre transformations [19, 20]. This apparent both in the dimensional space and the metric systems. After that, Quevedo [21] made an attempt to combine the geometry of the phase space along with the space of equilibrium states into a single coherent whole. Using the Hendi Panahiyan Eslam Momennia (HPEM) metric, which being discussed [22,23,24], it is possible to design a geometrical phase space based on data obtained from thermodynamic experiments. Our objective is to comprehend the phase transition of considered BH that contains a worldwide monopole through geometrical thermodynamics.

In the first step of this investigation, we look into an AdS BH solution that is global monopole. We provide an explanation of the Hawking temperature T, the specific heat $C_{\!p}$ and the electric potential $\varphi$ of the BH. The relationship between temperature and the horizon radius $r_+$ is investigated for a variety of charge, radius and monopole parameters. As $r_+$ continues to increase, the temperature eventually reaches its peak and then begins to drop. After a certain point, the rate of increase in temperature is proportional to $r_+$. In addition, we investigate monopole parameters, AdS radius and heat capacity for a wide range of charges. A physical limit zero point exists for heat capacity when it comes to specific parameter values. The heat capacity has two points of divergence both of which show the critical points of an AdS BH. We graphed the $P-v$ of a charged AdS BH based on the values of the parameters that are supplied. Under a key temperature, energy scale deformation arises. In contrast to critical pressure, volume and critical temperature increases as the amount of available energy increases.

Concerning to examine the phase-transition, we go more geometric frame of the Ruppeiner, Weinhold, HPEM and Quevedo formalisms. This allows us to see how these models describe the phase-transition. We study the general quantities of thermodynamic geometry for considered BH. Weinhold and Ruppeiner formalisms in order to justified the phase transition for BH in metric affine gravity. Further, based on the Hessian matrix of BH mass, we introduce thermodynamic geometric methods and provide its scalar curvatures (Weinhold and Ruppeiner). These two locations, which correspond to the two points in Quevedo metric (curvature scalar), are referred to as the zero point and the divergence point of heat capacity (case-I). Even if two of them merely coincide with transition roots of heat capacity and the curvature scalar of the Quevedo (case-II) metric has two points that are completely unique to themselves. The Ricci scalar divergence points coincide with the zero point and transition critical points of heat capacity in the HPEM metric. These are the two most crucial points of heat capacity. Therefore, the sites of divergence between the Quevedo (case-I) and HPEM Ricci scalars match with the heat capacity (phase-transitions).

The following is a step-by-step presentation of the paper in its entirety. Section 2 recapitulates charged AdS BH with exponential entropy. We can explore the thermodynamics of a charged AdS BH using exponential entropy in Sect. 3. Thermodynamic variables, such as mass, pressure, temperature, $P-v$ diagrams and heat capacity are analyzed graphically. Section 4 presents the geometrothermodynamics of the system using a number of different formalisms. The conclusion can be found in Sect. 5.

2 General formalism of charged AdS black hole

We will investigate the metric parameters of a charged AdS BH with a global monopole in this section. We analyze a charged AdS BH via Lagrangian density with a global monopole, which equals [7]

$$\begin{aligned} {L}=\mathcal {R}-\frac{\gamma }{4}(\Phi ^a \Phi ^{* a}-\nu _0^2)^2+\frac{1}{2}\partial _{\mu }\Phi ^{a} \partial ^\mu \Phi ^{* a} -2\Lambda , \end{aligned}$$

(2.1)

where $\mathcal {R},~\Lambda ,~\gamma ,~\nu _0$ and $\Phi$ represent the Ricci-scalar, cosmological constant, simple constant, energy of symmetry and triplet of the scalar field respectively. The modified Lagrangian density [25] for a charged particle with an electromagnetic field is given by:

$$\begin{aligned} \mathcal {L} = \frac{1}{2} \left( \partial _{\mu }\Phi \partial ^{\mu }\Phi - m^2\Phi ^2 \right) - \frac{1}{4} F_{\mu \nu } F^{\mu \nu } - e A_{\mu } J^{\mu }, \end{aligned}$$

where $\Phi$ is the scalar field representing the particle, $m$ is the mass of the particle, $e$ is the charge of the particle, $J^{\mu }$ is the four-current density vector that describes the charge and current distribution of the particle. The term $\frac{1}{2} \left( \partial _{\mu }\Phi \partial ^{\mu }\Phi - m^2\Phi ^2 \right)$ represents the kinetic and mass energy of the charged particle and the term $\frac{1}{4} F_{\mu \nu } F^{\mu \nu }$ corresponds to the energy density of the electromagnetic field. The Lagrangian density of a system can be modified to include the electromagnetic interaction with an electric charge Q by introducing the electromagnetic field tensor $F^{\mu \nu }$ and the electromagnetic covariant four-potential $A^{\mu }$. The electromagnetic field tensor $F^{\mu \nu }$ is defined as

$$\begin{aligned}F^{\mu \nu } = \partial ^{\mu }A^{\nu } - \partial ^{\nu }A^{\mu },\end{aligned}$$

where $\partial ^{\mu }$ denotes the partial derivative with respect to the spacetime coordinate $x^{\mu }$ (where $\mu , \nu$ are indices running from 0 to 3). The electromagnetic covariant four-potential $A^{\mu }$ is a four-vector that combines the electric potential $\varphi$ and the magnetic vector potential $A$ into a unified framework. In natural units (where $c = 1$), it is expressed as

$$\begin{aligned} A^{\mu } = (\varphi , \textbf{A}), \end{aligned}$$

where $\varphi$ is the electric potential and $\textbf{A}$ is the magnetic vector potential. The term $e A_{\mu } J^{\mu }$ describes the interaction between the particle and the electromagnetic field, where $A_{\mu }$ is the four-potential as defined above. The equations of motion derived from this Lagrangian will describe how the scalar field $\Phi$ and the electromagnetic field $A_{\mu }$ interact and evolve over spacetime, accounting for the presence of the electric charge $\bar{\mathcal {Q}}$ through the electromagnetic field tensor and four-potential. The following expression determines the arrangement of the scalar field triplet is provided by [26]

$$\begin{aligned} \Phi ^a=\nu _0 h(\bar{r}) \frac{\tilde{x}^a}{\bar{r}}, \end{aligned}$$

(2.2)

when $\tilde{x}^a \tilde{x}^a=\bar{r}^2$ is concerned. The formula [7] describes how to get a static spherical-symmetric metric with a global monopole.

$$\begin{aligned} d s^2=-\bar{f}(\bar{r}) d \bar{t}^2+\bar{f}(\bar{r})^{-1} d \bar{r}^2+\bar{r}^2(d \theta ^2+\sin ^2 \theta d \varphi ^2).\nonumber \\ \end{aligned}$$

(2.3)

You may find the field equation in the scenario of $\Phi ^{a}$ scalar field in the metric (2.3) by doing the following

$$\begin{aligned} \bar{f} h^{\prime \prime }+\bar{f}^{\prime } h^{\prime }+2 \bar{f} \frac{h^{\prime }}{ \bar{r}}-2 \frac{h}{\bar{r}^2}-\gamma \nu _0^2 h(h^2-1)=0. \end{aligned}$$

(2.4)

This gives a solution for charged AdS BH follows as [27]

$$\begin{aligned} \bar{f}(\bar{r})=1-8\pi \nu _0^2+\frac{\mathcal {\bar{\mathcal {Q}}}^2}{{\bar{r}}^2}-\frac{2\mathcal {\bar{M} }}{\bar{r}}+\frac{\bar{r}^2}{l^2}, \end{aligned}$$

(2.5)

where l is the radius of the AdS spacetime, which is connected to the cosmological constant as $l^2=-\frac{3}{\Lambda }$ and $\mathcal {\bar{M}}$ and $\mathcal {\bar{\mathcal {Q}}}$ are, respectively, the mass and electric charge of the BH. The thermodynamical quantities of BHs display an unusual dependency on the internal global monopole as a result of this metric and they completely meet the first law of thermodynamics together with Smarr relation [27]. This is due to the fact that this metric is used. The following content will make use of coordinate transformations [7, 28, 29]

$$\begin{aligned} \bar{t}=(1-8 \pi \nu _0^2)^{-\frac{1}{2}} t, \quad \bar{r}=(1-8 \pi \nu _0^2)^{\frac{1}{2}} {r}, \end{aligned}$$

(2.6)

The physical dependence of the BH variables on global monopole through parameter $1-\nu _0^2$ introduces interesting and convincing implications from both physical and geometric perspective. In this context, when $\nu _0^2$ approaches the value of 1, a attractive limit is reached. At this critical point, the BH space-time exhibits a significant angle insufficiency in a specific region, indicating the emergence of unique and non-trivial geometric features. This angle lack is an interesting result of the global monopole’s influence on the BH space-time structure. Moreover, significant research in [7, 28] highlights that the ADM mass and electric charge of the BH are directly related to the internal global monopole through the factor $1-\nu _0^2$. This finding establishes a deep link between the BH thermodynamic quantities and the existence of the global monopole. In addition to this, with the aid of recently introduced parameters

$$\begin{aligned}{} & {} \mathcal {M}=(1-8 \pi \nu _0^2)^{-\frac{3}{2}} \mathcal {\bar{M}}, \quad \mathcal {Q}=(1-8 \pi \nu _0^2)^{-1} \mathcal {\bar{\mathcal {Q}}}, \nonumber \\{} & {} \quad \nu ^2=8 \pi \nu _0^2, \end{aligned}$$

(2.7)

In order to start, the line segment has been identified as (2.3)

$$\begin{aligned} d s^2= & {} -f({r}) d t^2+(f({r}))^{-1} d {r}^2+(1-\nu _0^2) {r}^2\nonumber \\{} & {} \quad (d \theta ^2+\sin ^2 \theta d \varphi ^2), \end{aligned}$$

(2.8)

where

$$\begin{aligned} f({r})=1-\frac{2 \mathcal {M}}{{r}}+\frac{{r}^2}{l^2}+\frac{\mathcal {Q}^2}{{r}^2}. \end{aligned}$$

(2.9)

This spacetime displays a substantial angle deficiency in this region. Additionally, it provides the ADM mass and the electric charge $Q=(1-\nu _0^2) \mathcal {Q}$ along with $M =(1-\nu _0^2)\mathcal {M}$. The findings presented here lead us to the conclusion that the thermodynamical quantities of BH are dependent on the internal global monopole [7, 28, 29]. As a result, the thermodynamical properties of the BH system become fundamentally linked to the underlying topological defect, providing a novel and exciting way for investigating the interaction between BH physics and global monopole. The limit $\nu _0^2=1$ emerges as a particularly interesting scenario, waving further exploration to deepen our understanding of BH dynamics and the profound implications of topological defects in space-time.

3 Thermodynamics

To get the mass paramete r, we calculate the function $f({r_{+}})$ near the event horizon, indicated as ${r}={r_{+}}$. The modified entropy expression is given as [30]

$$\begin{aligned} S = \pi (1 - \nu _0^2)r_{+}^2 + e^{-\pi (1-\nu _0^2)r_{+}^2}. \end{aligned}$$

The first term, $\pi (1 - \nu _0^2)r_{+}^2$, represents the standard Bekenstein–Hawking entropy, which is proportional to the area of the BH horizon. The second term, $e^{-\pi (1-\nu _0^2)r_{+}^2}$, is the additional exponential term introduced in the entropy expression. The origin of the exponential term likely arises from the coupling of the BH with the global monopole. The presence of the global monopole and its nontrivial vacuum configuration may modify the BH thermodynamic properties, leading to this additional term in the entropy expression. The physical content of the exponential term is related to the effects of the global monopole on the BH horizon area and, consequently, its entropy. This non-standard factor may have implications for the BH thermodynamics, stability and quantum properties. The origin and physical implications of this modification is crucial for understanding the behavior of black holes in the presence of global monopoles and the implications for BH thermodynamics and quantum gravity. The mass of BH can be written as

$$\begin{aligned} M (S,Q,l){=}{-}\frac{\pi l^2 (\sqrt{2} (\nu _0 ^2-1) \sqrt{S{-}1}{-}\pi Q^2){-}2 S{+}2}{2^{5/4} \pi ^{3/2} l^2 \sqrt{1{-}\nu _0 ^2}(S{-}1)^{1/4}}.\nonumber \\ \end{aligned}$$

(3.1)

Fig. 1

Changes in mass M measured in terms of radial distance from the horizon $r_{+}$ with fixed values of $\nu _0$

Fig. 2

Changes in mass M measured in terms of radial distance from the horizon $r_{+}$ with fixed values of Q

For a charged AdS BH that has a global monopole, the first law of thermodynamics may be written as [28, 29]

$$\begin{aligned} d M =T d S+PdV+\varphi d Q, \end{aligned}$$

(3.2)

where $T=\frac{\partial M }{\partial S}$ represents the Hawking temperature, ${C_p}=T \frac{\partial S}{\partial T}$ is the heat capacity and $\varphi =\frac{\partial M }{\partial Q}$ describes the electric potential. These can be obtained as

$$\begin{aligned} T= & {} \frac{6S-\pi l^2(\pi Q^2+\sqrt{2} (\nu _0 ^2-1) \sqrt{S})}{2^{\frac{13}{4}} \pi ^{3/2} l^2S^{5/4} \sqrt{1-\nu _0 ^2} },\end{aligned}$$

(3.3)

$$\begin{aligned} {C_p}= & {} \frac{4 S (\pi l^2 (\pi \sqrt{2} Q^2 +2 (\nu _0 ^2-1) \sqrt{S})-6 \sqrt{2} S)}{\pi l^2 (-5 \pi \sqrt{2} Q^2-6 (\nu _0 ^2-1) \sqrt{S})+6 \sqrt{2} S},\end{aligned}$$

(3.4)

$$\begin{aligned} \varphi= & {} \frac{\sqrt{\pi } Q}{2^{1/4} S^{1/4} \sqrt{1-\nu _0 ^2}}. \end{aligned}$$

(3.5)

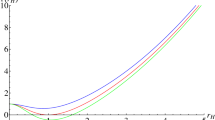
Here, the horizon radius associated to $\nu _0$ [28, 29]. Using vanishing derivatives at the critical point may provide critical parameters $T_c,~v_c\quad \text {and}~P_c.$ The behavior of thermodynamic parameters M, P, T and $C_p$ and are analyzed and the results are plotted against the horizon radius $r_+$. The behavior of the mass, temperature and heat capacity of a charged AdS BH is studied for taking fixed values of the BH charge Q, AdS radius l and energy of symmetry $\nu _0$. The results are presented in Figs. 1, 2, 3, 4, 5, 6, 7 and 8 respectively. The mass of the BH is shown in Figs. 1 and 2, which represent the minimum point at $r_+ = r_m$ for fixed values of $Q = 0.5$, $l= 4.2$ and $\nu _0 =0.5$ respectively. We show that, the parameters Q,  l and $\nu _0$ increases, the location of the minimum point changes and provide stable solution.

Figures 3 and 4 show the behavior of the temperature, which is negative for $r_+ < r_m$, reaches zero at $r_+ = r_m$ and becomes positive for $r_+ > r_m$, after that it increases and reaches to the maximum point. As we increase the principles of Q, $\nu _0$ and l, the highest value of the temperature gets to be smaller. The heat capacity of the BH is analyzed in Figs. 5, 6 and 7, where it is observed that the root of the heat capacity, corresponding to $T = 0$, marks the physical limitation point separating the regions for non-physical and physical BH. For $l = 5.263$, $Q = 0.5$ and $\nu _0 = 0.5$, the heat capacity meet at zero point at $r_1 =r_+= 0.451$, which relates to the point known as physical limitation. It also has divergence point at $r_+ = r_2 = 1.834$, corresponding to the phase transition critical points of the BH system and positive for $r_+ > r_3$, indicating a stable phase. The heat capacity remains negative for $r_+ < r_1$, indicating an unstable system in Fig. 7. Here $r_1$, $r_2$ and $r_3$ are the trajectories represented the divergence points. The location of the phase transition critical points changes as the values of l, Q and $\nu _0$ increase. In summary, the behavior of the mass, temperature and heat capacity of a charged AdS BH is investigated for specific values of l, Q and $\nu _0$ and the results indicate changes in the location and values of the physical parameters.

Fig. 3

Changes in temperature T measured in terms of radial distance from the horizon $r_{+}$ with fixed values $\nu _0$

Fig. 4

Changes in temperature T measured in terms of radial distance from the horizon $r_{+}$ with fixed values Q

Fig. 5

Heat capacity $C_p$ measured in terms of radial distance from the horizon $r_{+}$ with fixed values $\nu _0$

Fig. 6

Heat capacity $C_p$ measured in terms of radial distance from the horizon $r_{+}$ with fixed values Q

Fig. 7

Heat capacity $C_p$ measured in terms of radial distance from the horizon $r_{+}$ with fixed values l

In addition, a thermodynamic pressure may be considered a representation of the cosmological constant in terms of the expanded dimensional space [28, 29].

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }=\frac{3}{8\pi l^2}. \end{aligned}$$

(3.6)

And the fact that its conjugate amount is related to the thermodynamic volume $V=\frac{\partial M }{\partial P}$ as [28, 29]

$$\begin{aligned} V= & {} \frac{4\times 2^{3/4} (S-1)^{3/4}}{3 \sqrt{\pi -\pi \nu _0 ^2}},\nonumber \\= & {} \frac{4\times 2^{3/4} (-\pi (\nu _0 ^2-1) r_+^2+e^{\pi (\nu _0 ^2-1) r_+^2}-1)^{3/4}}{3 \sqrt{\pi } \sqrt{1 - \nu _0 ^2}}. \end{aligned}$$

(3.7)

Additionally, the EoS may be obtained by rearranging equations (3.3) and (3.6) in the form [28, 29]. This will get the results as

$$\begin{aligned} P= & {} \Bigg (2^{3/4} \pi Q^2-2 \root 4 \of {2} \sqrt{e^{\pi (\nu _0 ^2-1) r_+^2}-\pi (\nu _0 ^2-1) r_+^2}\nonumber \\{} & {} +2 \root 4 \of {2} \nu _0 ^2 \sqrt{e^{\pi (\nu _0 ^2-1) r_+^2}-\pi (\nu _0 ^2-1) r_+^2} +16 \sqrt{\pi -\pi \nu _0 ^2} T\nonumber \\{} & {} \times (e^{\pi (\nu _0 ^2-1) r_+^2}-\pi (\nu _0 ^2-1) r_+^2)^{5/4}\Bigg ) \Big / \Bigg (16\times 2^{3/4} (e^{\pi (\nu _0 ^2-1) r_+^2} \nonumber \\\end{aligned}$$

(3.8)

$$\begin{aligned}{} & {} -\pi (\nu _0 ^2-1) r_+^2)\Bigg ),\nonumber \\ P= & {} \frac{2^{3/4} \pi Q^2-2^{5/4} \sqrt{\gamma } + 2^{5/4} \nu _0 ^2 \sqrt{\gamma } +16\sqrt{\pi } (\sqrt{1 - \nu _0 ^2}) T (\gamma )^{5/4}}{16\times 2^{3/4} (\gamma )}.\nonumber \\ \end{aligned}$$

(3.9)

where, $\gamma =e^{\frac{\pi (\nu _0 ^2-1) v^2}{4 l^4}}-\frac{\pi (\nu _0 ^2-1) v^2}{4 l^4}.$

Fig. 8

The $P - v$ diagram for fixed $Q=1$, $l=5.256$ and different values of $\nu _0$ will show the dependence of the thermodynamic behavior on the dimensionless parameter $\nu _0$ and the occurrence of a critical point with a swallowtail shape

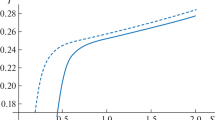
The $P - v$ diagram is a plot of the pressure P versus the specific volume v of a thermodynamic system. When considering a charged AdS BH in extended phase space, the diagram also includes the BH charge Q and the cosmological constant term related to the AdS spacetime. For a charged AdS BH with charge $Q=1$ and a fixed AdS radius determined by the value of the AdS length scale $l=5.256$, the $P -v$ diagram will depend on the value of the dimensionless parameter $\nu _0$. The specific shape of the Fig. 8 will vary for different values of $\nu _0$, but in general, it will show a critical point (first-order phase transition) occurs, corresponding to the point where the BH undergoes a small/large BH phase transition.

4 Thermal geometries

In this section, we analyze the shape of Ruppeiner, Weinhold, HPEM and Quevedo theoretic and analyze phase-transition of a charged AdS BH. Weinhold shape is given in mass representation as [31]

$$\begin{aligned} g_{jk} ^{W}=\partial _{j}\partial _{k} M (S,Q,l). \end{aligned}$$

(4.1)

A charged AdS BH has line element

$$\begin{aligned} d s_W^2= & {} M _{S S} d S^2+ M _{l l} d l^2+ M _{Q Q} d Q^2+2 M _{S l} d S d l \nonumber \\{} & {} +2 M _{S Q} d S d Q+2 M _{l Q} d l d Q. \end{aligned}$$

(4.2)

One can write the matrix form as

$$\begin{aligned} g^W=\left[ \begin{array}{ccc} M _{S S} &{} M _{S l} &{} M _{S Q} \\ M _{l S} &{} M _{l l} &{} 0 \\ M _{Q S} &{} 0 &{} M _{Q Q} \end{array}\right] . \end{aligned}$$

(4.3)

So, utilizing the above matrix, the Weinhold curvature scalar $(R^W)$ can be expressed as

$$\begin{aligned} R^W= & {} -\frac{1}{(\pi \Lambda -4 \pi ^2 l^2 Q^2-36 S+36)^3}\nonumber \\{} & {} \times \Bigg ({2}^{13/4} \pi ^{3/2} \sqrt{1-\nu _0 ^2} l^2 (S-1)^{1/4} (5 \pi \Lambda ^2\nonumber \\{} & {} +144 \pi \Lambda +40 \pi ^4 l^4 Q^4-20 \pi ^3 \Lambda l^2 Q^2\nonumber \\{} & {} +576 \pi ^2 l^2 Q^2 S-576 \pi ^2 l^2 Q^2\nonumber \\{} & {} +1944 S^2-144 \pi \Lambda S-3888 S+1944)\Bigg ), \end{aligned}$$

(4.4)

where,

$$\begin{aligned} \Lambda =\sqrt{2} l^2 (5 \sqrt{2} \pi Q^2+6 \nu _0 ^2 \sqrt{S-1}-6 \sqrt{S-1}). \end{aligned}$$

The Ruppeiner metric is the second kind of formalism that we take into consideration in this discussion. The Ruppeiner metric is presented in the thermodynamic system as [17, 32, 33]

$$\begin{aligned} d s_{R} ^2=\frac{1}{T} d s_{W} ^2, \end{aligned}$$

(4.5)

and the matrix that is pertinent to this discussion is denoted by

$$\begin{aligned} g^{R}=\frac{2^{\frac{13}{4}} \pi ^{3/2} l^2S^{5/4} \sqrt{1-\nu _0 ^2} }{6S-\pi l^2(\pi Q^2+\sqrt{2} (\nu _0 ^2-1) \sqrt{S})}\\ \left[ \begin{array}{ccc} M _{S S} &{} M _{S l} &{} M _{S Q} \\ M _{l S} &{} M _{l l} &{} 0 \\ M _{Q S} &{} 0 &{} M _{Q Q} \end{array}\right] . \end{aligned}$$

Since this is the case, the curvature scalar of the Ruppeiner representation may be computed by

$$\begin{aligned} R^{Rup}= & {} \Bigg (\pi ^6 (\nu _0^2-1) l^8 Q^4 S (S (20 S^2-2 S-81)\nonumber \\{} & {} +57)-54 \pi ^2 (\nu _0^2-1) l^4\nonumber \\{} & {} \times (S-1)^2 S^2 (S (23 S+21)-37)\nonumber \\{} & {} -\frac{1}{4} \pi ^4 (\nu _0^2-1) l^6 S (l^2 S^2-12 Q^2\nonumber \\{} & {} \times (S-1) (S (S (19 S-51)-169)+171))\nonumber \\{} & {} +\frac{1}{16}\sqrt{S}(46656\times S^{13/2}\nonumber \\{} & {} \times (3 S-19)-648 \pi ^2 l^4 (24 (\nu _0^2-1)^2 S^{13/2}\nonumber \\{} & {} +55 \pi ^2 Q^4)\Bigg ). \end{aligned}$$

(4.6)

In order to analyze thermodynamic phase transition, the resultant Ricci scalar of Weinhold together with Ruppeiner metrics is displayed along horizon radius $r_{+}$ see Figs. 9 and 10. In Sect. 3, the Figs. 5, 6 and 7 demonstrate interesting properties of the heat capacity for a positive-charged AdS BH. It has a true validity point at $r_+=0.425$, demonstrating the presence of a physically relevant condition. Furthermore, a separating point appears at $r_+=0.95$, providing support for the crucial points related with phase transitions in the BH [24]. These points were already mentioned in Sect. 3. Furthermore, as shown in Figs. 9 and 10, both the Weinhold and Ruppeiner metrics reveal a single isolated point at $r_+=0.425$. Notably, this point only corresponds to the root of the heat capacity at 0.

Fig. 9

Changes in the Weinhold together with Ruppeiner curvature scalar (magenta line) and the green line (heat capacity) as a function of $r_+$ for the parameters $Q=0.5$, $l=5.263$ and $\nu _0=0.5$

Fig. 10

Changes in the curvature scalar of the Ruppeiner and Weinhold metrics (Magenta line) and the green line (heat capacity) as a function of $r_+$ for the parameters $Q=0.5$, $\nu _0=1$ and $l=5.263$

Now, in order to explore the thermodynamic features of a charged AdS BH that has a global monopole, we will utilize the Quevedo and HPEM metrics. The generic type of the metric is provided by [21], which pertains to the Quevedo concept.

$$\begin{aligned} g=\Bigg (E^c \frac{\partial \Phi }{\partial E^c}\Bigg )\Bigg (\eta _{a b} \delta ^{b c} \frac{\partial ^2 \Phi }{\partial E^c \partial E^d} d E^a d E^d\Bigg ), \end{aligned}$$

(4.7)

where,

$$\begin{aligned} \frac{\partial \Phi }{\partial E^c}=\delta _{c b} I^b. \end{aligned}$$

(4.8)

In this context, whereas $\Phi ,~I^b$ and $E^a$ denote the thermodynamic potential, intense and extended variables respectively. In addition, the generalized HPEM metric that has n extended variables may be expressed as [14, 22,23,24]

$$\begin{aligned} d s_{H P E M}^2{} & {} =\frac{S M _S}{\Bigg (\prod _{i=2}^n \frac{\partial ^2 M }{\partial \chi _i^2}\Bigg )^3}\nonumber \\{} & {} \quad \times \Bigg (- M _{S S} d S^2+\sum _{i=2}^n\Bigg (\frac{\partial ^2 M }{\partial \chi _i^2}\Bigg ) d \chi _i^2\Bigg ), \end{aligned}$$

(4.9)

where are extensive parameters, $\chi _i(\chi _i \ne S), M _S=\frac{\partial M }{\partial S}$ and $M _{S S}=\frac{\partial ^2 M }{\partial S^2}$ respectively. It is possible to summarize the Quevedo and HPEM measurements by writing them as [14, 22,23,24]

$$\begin{aligned} d s^2= & {} (- M _{S S} d S^2+ M _{l l} d l^2+ M _{Q Q} d Q^2) \\ {}{} & {} \frac{S M _S}{(\frac{\partial ^2 M }{\partial l^2} \frac{\partial ^2 M }{\partial Q^2})^3} \Rightarrow \text{ HPEM },\\ d s^2= & {} (S M _S+l M _l+Q M _Q)(- M _{S S} d S^2+ M _{l l} d l^2\nonumber \\{} & {} \quad + M _{Q Q} d Q^2) \Rightarrow \text{ Quevedo } \text{ Case } \text{ I },\\ d s^2= & {} S M _S(- M _{S S} d S^2+ M _{l l} d l^2\nonumber \\{} & {} \quad + M _{Q Q} d Q^2) \Rightarrow \text{ Quevedo } \text{ Case } \text{ II }. \\ \end{aligned}$$

Furthermore, the Ricci scalars used in these measures have the following as their denominator [14, 23, 24]

$$\begin{aligned}{} & {} {\text {denom}}(R)\nonumber \\ {}{} & {} = {\left\{ \begin{array}{ll}2 M _{S S}^2 S^3 M _S^3 &{} \text{ HPEM }\\ 2 (S M _S+l M _l+Q M _Q)^3 M _{S S}^2 M _{l l}^2 M _{Q Q}^2 &{} \text{ Quevedo } \text{ Case } \text{ I } \\ 2 S^3 M _{S S}^2 M _{l l}^2 M _{Q Q}^2 M _S^3 &{} \text{ Quevedo } \text{ Case } \text{ II. } \\ \end{array}\right. }\nonumber \\ \end{aligned}$$

(4.10)

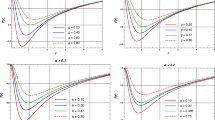
Solved equations are shown against horizon radius $r_+$ (see Fig. 11).

Fig. 11

Variation in the curvature scalar of Quevedo and HPEM metrics (shown by the blue line) as well as variation in heat capacity (represented by the red line), measured in terms of $r_+$ for $Q=0.5$, $l=5.263$ and $\nu _0=0.5$

The analysis of the curvature scalar of the Weinhold, Ruppeiner, Quevedo case-I, Quevedo case-II and HPEM metrics is a key tool for gaining insight into the thermodynamic behavior of BH systems in Fig. 11. Specifically, the singular points of the curvature scalar correspond to the physical limitation point and the transition critical points of the heat capacity. Importantly, the HPEM and Quevedo (case-I) metrics show singular points for both types of phase transitions, indicating that they provide more detailed information than the Weinhold and Ruppeiner metrics. These results underscore the importance of selecting the appropriate metric when studying the thermodynamic properties of BHs.

5 Conclusion

We have constructed the metric for a charged AdS BH and used geometrical thermodynamics with exponential entropy to describe the phase-transition of a charged AdS BH with exponential entropy. The Hawking temperature T, electric potential $\phi$ and specific heat $C_p$ of the system have all been clarified because of our efforts. We investigated the behavior of temperature along the horizon radius $r_+$ for a range of charge, monopole parameter and AdS radius values. The Hawking temperature first rises as the size of the event horizon increases until it reaches a maximum. Following that, the temperature starts to fall. However, after the event horizon radius $r_+$ exceeds a particular value, the Hawking temperature begins to rise again as the horizon radius expands further.

For a variety of charges, AdS radii and monopole parameters, we also presented a heat capacity against horizon radius graph. Surprisingly, we investigated that there is a single zero point for these characteristics that describes a physical restriction point in heat capacity. Furthermore, two divergence points in the heat capacity describe the key points of the phase transition of a charged AdS BH with monopole parameter. We have also mapped out the pressure-volume relation for the charged AdS BH for these values of the parameters. We have studied that the critical behaviour below the critical temperature that shifts with increasing energy scale. Only critical volume grows as the energy scale (monopole parameter) is scaled up, but critical temperature and critical pressure remain constant.

The phase transition of a charged AdS BH using exponential entropy has been investigated and we have obtained the geometric framework of the Ruppeiner, Weinhold, HPEM and Quevedo formalisms. The Ruppeiner and Weinhold (curvature scalars) metrics has been calculated as a first step in this direction. The scalar curvature vs horizon radius figure is presented in Figs. 9 and 10. According to these graphs, the zero-point of the heat capacity is the sole location where the curvature scalar of the Ruppeiner and Weinhold metrics converges.

Thermodynamic features of a super charged AdS BH are also explored by employing the Quevedo as well as HPEM formalisms. We observed two unique points in the curvature scalar during the investigation of the Quevedo metric (case-I). The first corresponds to the physical limitation point, where the curvature scalar becomes zero and the second corresponds to the transition critical points, when the curvature scalar diverges. unexpectedly these two places correspond exactly to the zero point of the heat capacity (including the a specific physical limitation) and the divergence point of the heat capacity (indicating a key transition). In the Quevedo (case-II) metric, there are regions where the heat capacity diverges, but none of these points overlap with the zero point of the heat capacity, as shown in Fig. 11. We found that the two types of heat capacity phase transitions coincide with the places where the Ricci scalar diverges for HPEM and Quevedo (case-I) metrics. Based on these analyzes, it appears that the HPEM and Quevedo approaches provide greater insight into the phase transition of the charged AdS BH using exponential entropy with monopole parameter than the Weinhold and Ruppeiner cases.