1 Introduction

In 1915, Albert Einstein formulated the general theory of relativity (GTR) which intrinsically linked matter to the curvature of spacetime via a system of highly nonlinear partial differential equations. This intellectual leap of viewing gravity as a consequence of the curvature of spacetime in the presence of matter rather than an action of a long-range force between material bodies has been immensely successful in accounting for many gravitationally-related phenomena. From Edwin Hubble’s observations of redshifts of starlight from distant galaxies pointing to a nonstatic universe through to the photographing of black hole shadows and detection of gravitational waves, GTR has continued to reward us richly. The exponential rise in technology in the form of satellites, detectors, telescopes and groundbreaking computer codes and simulations, GTR has been pushed beyond its domain of beautiful mathematical excursions into the realm of physical observations. Refined models of the evolution of the Universe together with current observations point to the existence (almost 95 %) of the dark sector viz., (dark matter and dark energy) in our cosmos. The study of the dark sector in the light of galaxy rotation curves and the late-time acceleration of the Universe has gathered momentum amongst astrophysicists and cosmologists [1,2,3,4,5,6,7,8,9]. While classical GTR has solidified its presence in both theoretical and observational foundations of gravity, it has become necessary to modify it in order to account for more fine-tuned observations in relativistic cosmology and astrophysics.

In recent years, a plethora of alternative modified theories of gravity that might be intended to assess the dynamical features of the evolving cosmos has been suggested. These modifications to GTR attempt to make the action a function of the spacetime curvature scalar \(\mathscr {R}\), \(f(\mathscr {R})\) [10,11,12], or other curvature invariants [13], by merging the Ricci scalar with a scalar field [14], by incorporating a vector field contribution [15] or by employing gravity attributes in higher dimensional spacetimes [16]. Amongst \(f(\mathscr {R})\) theories, there are theories that have proven to be successful in accounting for observational phenomena and improved theoretical considerations of the evolving Cosmos [17,18,19,20].

One can avoid the curvature established by the Levi-Civita connection and employ the Weitzenböck connection, which has torsion rather than curvature. This has the characteristic that the torsion is generated mainly through the products of the tetrad’s first derivatives, with no second derivatives occurring in the torsion tensor. In 1928, Albert Einstein [21,22,23] originally conceived of this approach referred to as “teleparallelism”. It is similar to standard GTR, with the exception of “boundary terms”, which involve entire derivatives in the action. The theory is effectively expressed by measuring external (spacetime) translation and underpinning the Weitzenböck spacetime, which is defined by the curvature tensor vanishing and by the metricity requirement. The group of universal coordinate transformations that underpins GTR is strongly related to translations. The theory has many desirable features which are appealing on both the geometrical and physical fronts [24,25,26,27,28,29,30,31,32,33].

The generic \(f(\mathscr {T})\)-theory is an amendment of the teleparallel equivalent of general relativity (TEGR), involving a Lagrangian linear in the torsion scalar \(\mathscr {T}\). The tetrad or vierbein field (vielbein in p dimensions) is the major dynamical variable in this framework. It is an orthonormal basis field in the tangent space. The torsion scalar \(\mathscr {T}\) is used to represent curvature in TEGR, and the tetrad field is used to represent the dynamical field rather than the metric field. The field equations are generated from a Lagrangian containing the torsion scalar \(\mathscr {T}\). It is worth noting that Einstein himself investigated a gravity theory with torsion, in his endeavor to construct a unifying theory of gravity and electromagnetism [34]. GTR and TEGR have the same dynamics, despite the fact that their geometric structures are different. This indicates that any GTR solution is also a TEGR solution. The gravitational Lagrangian in the so-called \(f(\mathscr {T})\)-theories is an analytic function of the torsion scalar \(\mathscr {T}\), hence they generalize TEGR exactly like the \(f(\mathscr {R})\) theories do for GTR. These theories of gravity are interesting since they are not analogous to GTR [35], and hence, they can be considered possible contenders for resolving the cosmic acceleration problem [36,37,38,39,40,41]. Several aspects in relation to \(f(\mathscr {T})\)-gravity were studied, including exact solutions and stellar models [42,43,44,45,46]. The spherically symmetric solutions in the context of \(f(\mathscr {T})\)-gravity theory are particularly essential since they may be employed to restrict these theories with observations of planetary movements in the Solar System by characterizing the gravitational field of point-like sources.

Recently, the concept of complexity in self-gravitating objects has received considerable interest from researchers. The notion of complexity is not new and there have been many earnest endeavors undertaken to identify a suitable criterion for measuring the degree of complexity in various scientific fields [47,48,49,50,51,52,53,54,55,56]. The majority of the definitions provided so far are associated with the principles of information and disequilibrium. However, the investigation of all of these factors indicates that the definition of complexity is not limited by the notions of information and entropy, but also contains some other intrinsic properties of the system under investigation. In reference [64] the authors introduce a definition of complexity for self-gravitating configurations drawing on the findings of López-Ruiz and co-workers [53,54,55,56]. The probability distribution, which shows up in the definitions of information and entropy, is modified by the energy density of the fluids. However, there are some major disadvantages to this definition, since it only includes the role of energy density, while other physical components such as pressure (an)isotropy which are anticipated to play a vital role in the structural properties of a system are entirely ignored. The role of pressure anisotropy in self-gravitating stellar configurations was thoroughly investigated by Herrera and co-workers [57,58,59,60,61,62,63].

A completely new definition of complexity for spherically symmetric and static self-gravitating sources has been proposed by Herrera [65]. It was shown that the condition for zero complexity bifurcates into two scenarios: (1) the stellar fluid has homogeneous density and isotropic pressure and (2) the pressure anisotropy cancels out the contributions from density inhomogeneity. Hererra demonstrated that the complexity factor is linked to the orthogonal splitting of the Riemann tensor. The notion of complexity was further extended to static systems experiencing a dissipative gravitational collapse in the sense of a radial heat flux [66]. It was further shown that the shear-free condition for radiating fluids is unstable and evolves into a shear-like regime mimicked by the presence of pressure anisotropy, density inhomogeneity and dissipation. The vanishing of the complexity factor in axially symmetric static fluids was also by Herrera [67].

In the past decade, the study of anisotropic compact objects has moved to the forefront of theoretical astrophysics, especially in the view of observational data arising from the study of pulsars, neutron stars and strange stars. The inclusion of pressure anisotropy accounted for higher surface redshifts, more refined mass-to-radius ratios and the fine-tuning of the state equation of the stellar fluid. A popular framework which helps construct anisotropic solutions is the so-called gravitational decoupling method [70,71,72,73,74,75], particularly through the minimal geometric deformation (MGD) technique. Casadio and coworkers [76] extended MGD in the context of the Randall–Sundrum braneworld to acquire an altered Schwarzschild geometry. The generation of isotropic solutions from anisotropic seed solutions together with the requirement of vanishing complexity has proved fruitful in the study of spherically symmetric, static fluid spheres [77,78,79,80,81,82,83,84,85].

Using the MGD technique, Maurya et al. [86], explored novel classes of solutions characterized by vanishing complexity in static spherically symmetric self-gravitating systems. This approach was extended by Maurya et al. [87,88,89] to study bounded hyperspheres in 5D Einstein–Gauss–Bonnet gravity. For more insight into the role played by vanishing complexity within the MGD framework, the reader is referred to the work contained in [90,91,92,93,94,95,96,97,98,99]. The MGD approach and its extension were successfully applied to study the energy exchange between the seed source and the decoupled fluid source [101,102,103,104].

In this paper, we are interested in implementing gravitational decoupling via the MGD scheme as the generating mechanism of anisotropic solutions. It should be emphasized that the decoupling via the MGD approach can be adopted for controlling many physical properties of static spherical self-gravitating systems. In this context, we are the first to successfully analyze the change in

complexity and isotropization of self-gravitating compact stars through gravitational decoupling in \(f(\mathscr {T})\)-gravity with a diagonal tetrad.

The paper is organized as follows. In Sect. 2, we present the field equations for \(f(\mathscr {T})\)-gravity with an extra source. Then in Sects. 3 and 4, we discuss the method of embedding class one along with the system of field equations via MGD approach and Herrera’s structure scalars with complexity formula under gravitational decoupling in \(f(\mathscr {T})\)-gravity, respectively. Section 5 introduces new classes of stellar solutions based on the Karori–Barua ansatz, including minimally deformed anisotropic solutions with vanishing complexity factors in Sect. 5.1 and isotropic solutions via gravitational decoupling in Sect. 5.2. The physical properties of the solutions are carefully analyzed in Sect. 6. We conclude our work by discussing our findings in Sect. 8.

2 Field equations for \(f(\mathscr {T})\)-gravity with extra source

The starting point is a manifold’s line element given by,

$$\begin{aligned} ds^{2}=g_{ij }dx^{i}dx^{j }=\eta _{kl}\theta _{i}^{k}\theta _{j }^{l}dx^{i}dx^{j } \end{aligned}$$
(1)

with

$$\begin{aligned} dx^{i}=e_{k}^{i}\theta ^{k},~\theta ^{k}=e_{i}^{k}dx^{i}~\text {and}~\eta _{kl}=diag[1,-1,-1,-1]. \end{aligned}$$

Here \(e_{k}^{i}e_{l}^{j }=\delta _{i}^{j }\) or \(e_{k}^{i}e_{l}^{j }=\delta _{k}^{l}\), the indices k, l correspond to the tetrad field \(\theta ^{k}_{i}\), and i, j are connected to the space-time coordinates, while the metric determinant has the root, \(e=\sqrt{-g}=det[e^{k}_{i}]\). When the Riemann tensor vanishes and torsion is non-zero, then the Weitzenböck anti-symmetric connections are stated as

$$\begin{aligned} \Gamma _{ij }^{l}= & {} e^{l}_{k}\partial _{j }e^{k}_{i}=-e^{i}_{k}\partial _{j }e^{l}_{k}. \end{aligned}$$
(2)

While the torsion and con-torsion tensors is given by,

$$\begin{aligned} \mathscr {T}_{ij }^{l}= & {} \Gamma _{ij }^{l} - \Gamma _{j i}^{l}=e^{l}_{k}\left( \partial _{i}e^{k}_{j }-\partial _{j }e^{k}_{i}\right) , \end{aligned}$$
(3)
$$\begin{aligned} K^{ij }_{l}= & {} -\frac{1}{2}\left( \mathscr {T}^{ij }_{l}-\mathscr {T}^{j i}_{l}-\mathscr {T}^{ij }_{l}\right) . \end{aligned}$$
(4)

The aforementioned two tensors, Eqs. (3) and (4), are combined to form a new tensor,

$$\begin{aligned} S^{ij }_{l}= & {} \frac{1}{2}\left( \delta ^{i}_{l}\mathscr {T}^{n j}_{n}+K^{ij}_{l}-\mathscr {T}^{n i}_{n} \delta ^{j }_{l}\right) . \end{aligned}$$
(5)

Now, we can express the torsion scalar as,

$$\begin{aligned} \mathscr {T}= & {} \mathscr {T}_{ij }^{l} S^{ij }_{l}. \end{aligned}$$
(6)

Similar to the modified gravitational action in f(R) theory, we can obtain action for modified gravity \(f(\mathscr {T})\) by replacing R with \(\mathscr {T}\) with inclusion of extra Lagrangian () for new source, as follows,

$$\begin{aligned} S=\int dx^{4} e\Big [ \frac{1}{16\pi } f(\mathscr {T})+\mathscr {L}_{Matter}+\mathscr {L}_{\theta }\Big ], \end{aligned}$$
(7)

where \(G = c = 1\) is the natural (geometrized) units, f is the function of trace \(\mathscr {T}\) and \(\mathscr {L}_{Matter}\) represents the Lagrangian density. The following set of equations of motion are obtained by varying Eq. (7) with regard to the tetrad field,

$$\begin{aligned}{} & {} e_{n}^{l}S_{l}^{ij }\partial _{n}\mathscr {T}f_{\mathscr {T}\mathscr {T}}+e^{-1}\left( ee_{n}^{l}S_{l}^{ij }\right) f_{\mathscr {T}}+e_{n}^{i}\mathscr {T}_{i k}^{l}S_{l}^{j k}f_{\mathscr {T}} - \frac{1}{4}e_{n}^{j }f \nonumber \\ {}{} & {} \quad =-4\pi e_{n}^{l}\big [T_{l }^{j}\big ]^{\text {eff}}.~~ \end{aligned}$$
(8)

Here, \(\big [T_{i}^j\big ]^{\text {eff}}=T^j_i+\theta ^i_j\). The tensor \(T^i_j\) denotes an energy-momentum tensor for Lagrangian density \(\mathscr {L}_{matter}\) while \(\theta ^i_j\) is for \(\mathscr {L}_{\theta }\). However, the derivatives of the function f are represented by the following notations: \(f_{\mathscr {T}}=\frac{\partial f}{\partial \mathscr {T}}\), \(f_{\mathscr {T}\mathscr {T}}=\frac{\partial ^{2} f}{\partial \mathscr {T}^2}\). For an anisotropic fluid distribution, the effective energy-momentum tensor is defined as,

$$\begin{aligned} \big [T_{i}^{j }\big ]^{\text {eff}}=(\rho ^{\text {eff}}+p^{\text {eff}}_{t})u_{i}u^{j }-p^{\text {eff}}_{t}\delta _{i}^{j }+(p^{\text {eff}}_{r}-p^{\text {eff}}_{t})v_{i}v^{j },\nonumber \\ \end{aligned}$$
(9)

where, the four-speed and radial four vectors are denoted by \(u_{j }=e^{l}\delta _{j }^{0}\) and \(v_{j }=e^{j }\delta _{j }^{1}\), respectively, whilst \(\rho ^{\text {eff}}\) is the effective energy density and \(p^{\text {eff}}_{r}\), \(p^{\text {eff}}_{t}\) denote effective pressures in radial and tangential directions.

Now, the equation of motions in \(f(\mathscr {T})\)-gravity can be rewritten in the following form using the covariant derivative formalism,

$$\begin{aligned} G_{ij }f_{\mathscr {T}}+S_{j i}^{l}\nabla _{l}\mathscr {T}f_{\mathscr {T}\mathscr {T}}+\frac{\mathscr {T}}{2}\left( \frac{f}{\mathscr {T}}-f_{\mathscr {T}}\!\right) g_{ij }\!=\frac{1}{16\pi }T_{ij }^{\text {eff}}, \nonumber \\ \end{aligned}$$
(10)

where, the Einstein tensor is represented by \(G_{ij }\). In this sense, Eq. (8) can be reformulated in the context of GR and f(R) field equations as,

$$\begin{aligned} G_{ij }=\frac{1}{16\pi f_{\mathscr {T}}}\left( T_{ij }^{\text {eff}}+\mathscr {T}_{ij }^{[\mathscr {T}]}\right) ,~~ \end{aligned}$$
(11)

where \(\mathscr {T}_{ij }^{[\mathscr {T}]}\) is a tensor that incorporates corrections from the torsion scalar given by,

$$\begin{aligned} \mathscr {T}_{ij }^{^{[\mathscr {T}]}}=\frac{-1}{64\pi }\left( 4S_{j i}^{l}\nabla _{l}f_{\mathscr {T}\mathscr {T}}\!+\!\left( Rf_{\mathscr {T}}-S_{j i}^{l}\nabla _{l}f_{\mathscr {T}\mathscr {T}}+\mathscr {T}\right) g_{ij }\right) , \nonumber \\ \end{aligned}$$
(12)

It is obvious that Eq. (10) leads to GR equations for a linear \(f(\mathscr {T})\), i.e., \(f(\mathscr {T})=\mathscr {T}\).

Let us now focus on the interior of the spherically symmetric static fluids distribution, whose metric is intended to be defined by the following line element,

$$\begin{aligned} ds^2= & {} -e^{\nu }dt^{2}+e^{\lambda }dr^{2}+r^{2} d \theta ^{2}+r^{2}\sin ^{2} \theta ~d \phi ^{2}.~~~~~~ \end{aligned}$$
(13)

The two unknown metric potentials that rely solely on the radial coordinate, r, are denoted by the symbols j and \(\lambda \). Further, we define the energy-momentum tensor for an anisotropic self-gravitating system in (3+1)-dimensions as,

$$\begin{aligned}{} & {} \big [T_{i}^{j}\big ]^{\text {eff}}=diag \left( -\rho ^{\text {eff}}, ~p^{\text {eff}}_{r},~p^{\text {eff}}_{t},~p^{\text {eff}}_{t} \right) , \end{aligned}$$
(14)

with

$$\begin{aligned}{} & {} \big [T_{i}^{j}\big ]^{\text {eff}}=0, \ \ if\ i \ne j, \end{aligned}$$
(15)

The pressure anisotropy is characterized by the formula \(\Delta ^{\text {eff}}=p^{\text {eff}}_{r}-p^{\text {eff}}_{t}\), and its value is determined by the metric potentials \(\nu \) and \(\lambda \). For the metric in Eq. (9), the tetrad matrix is provided by,

$$\begin{aligned} \Big [e^{n}_{i}\Big ]=diag\Big [e^{\nu /2 },e^{\lambda /2},r,r\sin \theta \Big ] \end{aligned}$$
(16)

with its determinant given as,

$$\begin{aligned} e=det\Big [e^{n}_{i}\Big ]=e^{(\nu +\lambda )/2}\,r^2\sin \theta . \end{aligned}$$
(17)

In terms of radial coordinate, r, the expression for torsion scalar along with its derivative is described by,

$$\begin{aligned}{} & {} \mathscr {T}(r)=\frac{2 e^{-\lambda }}{r} \Bigg [\nu '+\frac{1}{r}\Bigg ], \end{aligned}$$
(18)
$$\begin{aligned}{} & {} \mathscr {T}'(r)=\frac{e^{-\lambda }}{r} \Bigg [\nu ''-\frac{1}{r^2}-\left( \nu '+\frac{1}{r}\right) \left( \lambda '+\frac{1}{r}\right) \Bigg ].~ \end{aligned}$$
(19)

where, the derivative with regard to the radial coordinates is denoted by the prime \(()'\).

Now, by replacing the aforementioned tetrad field (16) and plugging the torsion scalar along with its derivative in Eq. (8), the equation of motions for an anisotropic fluid may be found explicitly in \(f(\mathscr {T})\)-gravity as,

$$\begin{aligned} 8\pi \rho ^{\text {eff}}= & {} f_\mathscr {T} \Big [\frac{1}{r^2}+\frac{1}{r}e^{-\lambda } \left( \lambda '+\nu '\right) -\mathscr {T}(r)\Big ]+\frac{f}{2},~~~ \end{aligned}$$
(20)
$$\begin{aligned} 8\pi p^{\text {eff}}_r= & {} f_\mathscr {T} \Big [-\frac{1}{r^2}+\mathscr {T}(r)\Big ]-\frac{f}{2}, \end{aligned}$$
(21)
$$\begin{aligned} 8\pi p^{\text {eff}}_t= & {} f_\mathscr {T} \Big [e^{-\lambda } \left( \left( \frac{\nu '}{4}+\frac{1}{2 r}\right) \left( \nu '-\lambda '\right) +\frac{\nu ''}{2}\right) +\frac{\mathscr {T}(r)}{2}\Big ]-\frac{f}{2}. \nonumber \\ \end{aligned}$$
(22)

The aforementioned field equations clearly lead to the corresponding field equations in GR for \(f(\mathscr {T}) = \mathscr {T}\), as shown by Eqs. (20)–(22). In the case of \(f(\mathscr {T})\)-gravity, an extra non-diagonal quantity is obtained as follows,

$$\begin{aligned} \frac{cot\theta }{2r^2} \mathscr {T}' f_{\mathscr {T}\mathscr {T}}=0,~ \end{aligned}$$
(23)

which differs from the case of GR. We get the following scenarios with respect to Eq. (23), (a) \(\mathscr {T}=0\) and (b) \(f_{\mathscr {T}\mathscr {T}}=0\), in the second scenario, we derive a linear functional form of \(f(\mathscr {T})\) as follows:

$$\begin{aligned} f(\mathscr {T})=\alpha \mathscr {T} + \gamma ,~ \end{aligned}$$
(24)

where, \(\alpha \) and \(\gamma \) are integration constants. The above linear functional has been effectively applied in other \(f(\mathscr {T})\)-gravity scenarios. Now our aim is to solve the \(f(\mathscr {T})\)-gravity field equations (20)–(22) under the functional form (24). In this regard, we intended to apply the famous methodology, called gravitational decoupling via the minimal geometric deformation (MGD) approach together with conditions on the complexity of a self-gravitating system, in order to find the solution under a different aspect.

3 Method of embedding class one

In 1925, Eisenhart [105] showed that if a symmetric tensor \(h_{\mu \nu }\) satisfies the following Gauss–Codazzi equations

  • Gauss’s equation:

    $$\begin{aligned} \mathscr {R}_{\mu \nu \alpha \beta }=-\epsilon \left( h_{\mu \beta }h_{\nu \alpha }-h_{\mu \alpha }h_{\nu \beta }\right) , \end{aligned}$$
    (25)

    with \(\epsilon =\pm 1\) is taken according to the normal to the manifold is time-like \((-1)\) or space-like \((+1)\).

  • Codazzi’s equation

    $$\begin{aligned} \nabla _{\alpha }h_{\mu \nu }-\nabla _{\nu }h_{\mu \alpha }=0. \end{aligned}$$
    (26)

Then an embedding Class one manifold can be described via a \((n+1)\) dimensional manifold \(V^{n+1}\), if \((n+1)\) dimensional manifold \(V^{n+1}\) is embedded into a \((n + 2)\) dimensional pseudo-Euclidean manifold \(E^{n+2} \). Here the Riemann curvature tensor is represented by \(\mathscr {R}_{\mu \nu \alpha \beta }\), and the coefficients of the 2nd order differential form are indicated by \(h_{\mu \nu }\). The necessary and sufficient condition was initially developed by Karmarkar [106] in the form of Riemann tensor components form as,

$$\begin{aligned} \mathscr {R}_{t\theta t\theta }\mathscr {R}_{r\phi r\phi }=\mathscr {R}_{trtr}\mathscr {R}_{\theta \phi \theta \phi }+\mathscr {R}_{r\theta t \theta }\mathscr {R}_{r\phi t\phi }, \end{aligned}$$
(27)

where

$$\begin{aligned}{} & {} \mathscr {R}_{rtrt}=-e^{\nu }\left( \frac{\nu ^{\prime \prime }}{2}-\frac{\lambda ^{\prime }\nu ^{\prime }}{4}+\frac{\nu ^{\prime 2}}{4}\right) ; ~~ \mathscr {R}_{r \theta r\theta }=-\frac{r}{2}\lambda ^{\prime }; \nonumber \\{} & {} \mathscr {R}_{\theta \phi \theta \phi }=-\frac{r^{2}\sin ^{2}\theta }{e^{\lambda }}\left( e^{\lambda }-1\right) ; ~~\mathscr {R}_{r\phi \phi t}=0, \nonumber \\{} & {} \mathscr {R}_{\phi t \phi t}=-\frac{r}{2}\nu ^{\prime }e^{\nu -\lambda }\sin ^{2}\theta ;~~ \mathscr {R}_{r\theta \theta t}=0.\nonumber \end{aligned}$$

This condition is a necessary and sufficient constraint for portraying a space-time (13) as being of Class one. At this stage, by incorporating the Riemann constituents in the condition (27), we obtain the following formula

$$\begin{aligned} 2\frac{\nu ^{\prime \prime }}{\nu ^{\prime }}+\nu ^{\prime }=\frac{\lambda ^{\prime }e^{\lambda }}{e^{\lambda }-1}, \end{aligned}$$
(28)

with \(e^{\lambda }\ne 1\). It should be noted that the solution of the differential equation stated in (28) requires that the spacetime (13) is of Class one. Actually, the integration of the previous formula (28) leads to the following relationship between the metric potentials,

$$\begin{aligned} e^{\nu }=\left[ A+B\int {\sqrt{e^{\lambda }-1}\,dr} \right] ^{2}, \end{aligned}$$
(29)

where A and B are the integration constants. It should be noted that the method described herein has been widely employed in the domain of compact stellar systems depicting realistic stellar objects. The next section is devoted to the MGD approach and corresponding solution in \(f(\mathscr {T})\)-gravity in the different scenario:

4 System of field equations via MGD and Herrera’s structure scalars with complexity formula under gravitational decoupling in \(f(\mathscr {T})\)-gravity

4.1 System of field equations via MGD

In this section, we will discuss the systems of field equations in \(f(\mathscr {T})\)-gravity under MGD methodology. Let us use the gravitational decoupling through the transformation over the metric potentials \(e^{\lambda (r)}\) and \(e^{\nu (r)}\),

$$\begin{aligned}{} & {} e^{-\lambda (r)} \longrightarrow \mu (r)+\beta \,f(r), \end{aligned}$$
(30)
$$\begin{aligned}{} & {} \nu (r) \longrightarrow \xi (r)+\beta \,g(r), \end{aligned}$$
(31)

where f(r) and g(r) are known as geometric deformation functions or decoupling functions corresponding to temporal and radial spacetime components, respectively. This deformation could be fixed via the constant \(\beta \). As usual, the standard or pure \(f(\mathscr {T})\)-gravity theory can be easily derived when \(\beta =0\). Since we are using here the MGD approach which allows us to fix \( h(r) = 0\) and \(f(r)\ne 0\), which implies that the transformation is applied along the metric function \(e^{-\lambda (r)}\) and the other metric function \(\nu (r)\) is unchanged. This MGD technique separates the decoupled system (22)–(24) into two subsystems such as: (i) first system exactly similar to \(f(\mathscr {T})\) for energy-momentum tensor \(T_{ij}\), (ii) other system corresponding to the extra source \(\theta _{ij}\). Let us suppose, the energy-momentum tensor \({T}_{ij}\) describes an anisotropic matter distribution,

$$\begin{aligned} T_{ij}=\rho u_{i}\,u_{j} +p_t u_{i}\,u_{j}+p_t\,g_{ij}-\left( p_t-p_r\right) v_{i}\,v_{j}, \end{aligned}$$
(32)

where, energy density (\(\rho \)), radial pressure (\(p_{r}\)), and tangential pressure (\(p_{t}\)) are connected to the seed matter distribution or seed solution. Let us define the new variable to denote the \(\ theta\) components,

$$\begin{aligned} \rho ^{\theta } = \beta \theta ^0_0,~~p_r^{\theta }=-\beta \theta ^1_1,~~p_t^{\theta } =-\beta \theta ^2_2,~~\Pi _{\theta }=p_r^{\theta }-p_t^{\theta }, \nonumber \\ \end{aligned}$$
(33)

Then, the effective pressures and effective density can be determined as,

$$\begin{aligned} p^{\text {eff}}_t=p_t+p_t^{\theta },~~p^{\text {eff}}_r=p_r+p_r^{\theta },~~\text {and}~~\rho ^{\text {eff}}=\rho +\rho ^{\theta }.~~~~ \nonumber \\ \end{aligned}$$
(34)

and we define,

$$\begin{aligned} \Pi ^{\text {eff}}=p_r^{\text {eff}}-p_r^{\text {eff}}=\Pi _s+\Pi _{\theta },~~~\text {where}, \Pi _s=p_r-p_t. \nonumber \\ \end{aligned}$$
(35)

Using the transformations (30) and (31) in to the system (22)–(24), we arrive the following set of equations of motions as:

i. Standard equation of motion corresponding to \(f(\mathscr {T}\) )-gravity (when \(\beta =0\)):

$$\begin{aligned}{} & {} 8\pi \rho =\alpha \,\Big ( \frac{1-\mu }{r^2}-\frac{\mu ^{\prime } }{r}\Big )-\frac{\gamma }{2}, \end{aligned}$$
(36)
$$\begin{aligned}{} & {} 8\pi p_r=\alpha \,\Big (-\frac{1-\mu }{r^2}+\frac{ \mu \xi ^{\prime } }{r}\Big )+\frac{\gamma }{2}, \end{aligned}$$
(37)
$$\begin{aligned}{} & {} 8\pi p_t= \alpha \,\Big (\frac{\xi ^{\prime } \mu ^{\prime } }{4}+\frac{\mu \xi ^{\prime \prime } }{2}+\frac{\xi ^{\prime 2} \mu }{4} +\frac{\mu ^{\prime } }{2 r} +\frac{\xi ^{\prime } \mu }{2 r}\Big )+\frac{\gamma }{2}, \nonumber \\ \end{aligned}$$
(38)

and respective conservation equation is,

$$\begin{aligned} -\frac{\xi ^\prime }{2}(\rho +p_r)-\frac{dp_r}{dr}+\frac{2}{r}( p_{t}-p_r)=0,~~ \end{aligned}$$
(39)

Moreover, the solution of the equations of motion (36)–(38) can be described by spacetime,

$$\begin{aligned} ds^2=\frac{dr^2}{\mu (r)}-e^{\xi (r)}dt^2+r^2(d\theta ^2+\text {sin}^2\theta \,d\phi ^2), \end{aligned}$$
(40)

ii. After turning on \(\beta \), the equations of motion for \(\theta \)-sector are:

$$\begin{aligned}{} & {} 8\pi \rho ^{\theta }=- \alpha \,\Big (\frac{f }{r^2}+\frac{f^\prime }{r}\Big ), \end{aligned}$$
(41)
$$\begin{aligned}{} & {} 8\pi p_r^{\theta }=-\alpha \, \Big (\frac{f }{r^2}+\frac{\xi ^{\prime } f }{r}\Big ), \end{aligned}$$
(42)
$$\begin{aligned}{} & {} 8\pi p_t^{\theta }=- \alpha \,\Big (\frac{1}{4} f^\prime \xi ^{\prime } +\frac{1}{2} \xi ^{\prime \prime } f +\frac{1}{4} \xi ^{\prime 2} f +\frac{f^\prime }{2 r}+\frac{\xi ^{\prime } f}{2 r}\Big ), \nonumber \\ \end{aligned}$$
(43)

and the linear combination of above Eqs. (41)–(43) gives,

$$\begin{aligned}{} & {} \frac{dp_r^{\theta }}{dr}=-\frac{\xi ^{\prime }}{2}\big (\rho ^{\theta }+p_r^{\theta }\big ) +\frac{2(p_t^{\theta }-p_r^{\theta })}{r}, ~~~ \end{aligned}$$
(44)

Moreover, the respective mass function for both systems can be obtained by formula,

$$\begin{aligned}{} & {} m_{\mathscr {T}}=\frac{1}{2} \int ^r_0 \rho (x)\, x^2 dx~\text {and}~m_{\theta }= \frac{1}{2}\,\int _0^r \rho ^{\theta } (x)\, x^2 dx, ~~~ \nonumber \\ \end{aligned}$$
(45)

where \(m_{\mathscr {T}}(r)\) and \(m_{\theta }8(r)\) represents the mass functions for the sources \(T_{\epsilon \varepsilon }\) and \(\theta _{\epsilon \varepsilon }\), respectively. Then mass of the effective system can be written as,

$$\begin{aligned} m(r)=m_{\mathscr {T}}+m_{\theta }=m_{\mathscr {T}}-\frac{\beta \,r}{2} f(r), \end{aligned}$$
(46)

In the \(f(\mathscr {T})\)-gravity theory with linear functional form, the most appropriate exterior spacetime can be given by exterior Schwarzschild de-Sitter solution,

$$\begin{aligned} ds^2= & {} -\bigg (1-\frac{2{\mathscr {M}}}{r}-{\Lambda \over 3}~r^2\bigg ) dt^2+ \frac{dr^2}{\bigg (1-\frac{2{\mathscr {M}}}{r}-{\Lambda \over 3}~r^2\bigg )} \nonumber \\{} & {} - r^2 (d\theta ^2 + \sin ^2\theta d\phi ^2).~~ \end{aligned}$$
(47)

where, M is a total mass of the object at boundary \(r=r_{_\Sigma }\) such that \(M=m(r_{_\Sigma })/\alpha \) and \(\Lambda =\alpha /2\gamma \). Moreover, the first and second fundamental forms leads the following result,

$$\begin{aligned} \bigg (1-\frac{2{\mathscr {M}}}{r}-{\Lambda \over 3}~r^2\bigg )= & {} e^{\nu _{_\Sigma }},~~~ \end{aligned}$$
(48)
$$\begin{aligned} \bigg (1-\frac{2{\mathscr {M}}}{r}-{\Lambda \over 3}~r^2\bigg )= & {} e^{-\lambda _{_\Sigma }},~~~ \end{aligned}$$
(49)
$$\begin{aligned} p^{\text {eff}}_r(r_{_\Sigma })= & {} 0.~~~ \end{aligned}$$
(50)

which are the most suitable boundary conditions for the joining of both spacetimes at surface \(r=r_{{_\Sigma }}\).

As per Herrera’s definition [65], the gravitationally decoupled mass function m(r) can be described in the form of homogeneous energy density and change caused by density inhomogeneity as,

$$\begin{aligned} m(r)=\frac{4\pi }{3}r^3\, \rho ^{\text {eff}} -\frac{4\pi }{3}\,\int ^r_0 x^3\, \big [\rho ^{\text {eff}}\big ]^{\prime } dx. \end{aligned}$$
(51)

Then, in view of relations (34) and (51), we have

$$\begin{aligned} m(r)= & {} \underbrace{\frac{4\pi }{3} r^3\,\rho -\frac{4\pi }{3}\,\int ^r_0 x^3\, \rho ^{\prime } dx}_{m_{\mathscr {T}}} \nonumber \\{} & {} + \underbrace{\frac{4\pi }{3}r^3\, \rho ^{\theta } - \frac{4\pi }{3}\,\int ^r_0 x^3\, \left[ \rho ^{\theta }\right] ^{\prime } dx}_{m_{\theta }}. \end{aligned}$$
(52)

4.2 Herrera’s structure scalars with complexity formula under gravitational decoupling

In 2018, Herrera [65] proposed a definition for the complexity factor in a self-gravitating system, which has been derived from the orthogonal splitting of the Riemann tensor, in terms of structure scalars. However, Herrera and his collaborators [100] have determined these structure scalars first time in 2009. During this investigation, they obtained a complete structure of the equations in the forms of five scalar quantities that describe the growth of self-gravitating anisotropic dissipative fluids in the context of the spherically symmetric spacetime determined by the orthogonal splitting of the Riemann tensor in the GR context. It is mentioned that these five scalar quantities are connected to essential properties of the fluid distribution such as local pressure anisotropy, energy density, dissipative flux, active gravitational mass, and energy density inhomogeneity, which are given as,

$$\begin{aligned} X_T= & {} 8\pi \,\rho ^{\text {eff}}= X^s_T + X^{\theta }_T, \end{aligned}$$
(53)
$$\begin{aligned} X_{TF}= & {} \frac{4\pi }{r^3}\,\int ^r_0 x^3\, \big [\rho ^{\text {eff}}\big ]^{\prime } dx = X^s_{TF}+X^{\theta }_{TF}, \end{aligned}$$
(54)
$$\begin{aligned} Y_T= & {} 4\pi (\rho ^{\text {eff}}+3p_r^{\text {eff}}-2\Pi )=Y^s_T + \,Y^{\theta }_T, \end{aligned}$$
(55)
$$\begin{aligned} Y_{TF}= & {} 8\pi \Pi - \frac{4\pi }{r^3}\,\int ^r_0 x^3\, \big [\rho ^{\text {eff}}\big ]^{\prime } dx =Y^s_{TF}+ Y^{\theta }_{TF}, ~~~ \end{aligned}$$
(56)

     with,

$$\begin{aligned}{} & {} X^s_T=8\pi \rho ,~~~ X^{\theta }_T=8\pi \rho ^{\theta },~~ X^s_{TF}=\frac{4\pi }{r^3}\,\int ^r_0 x^3\, \rho ^{\prime } dx, \end{aligned}$$
(57)
$$\begin{aligned}{} & {} X^{\theta }_{TF}=\frac{4\pi }{r^3}\,\int ^r_0 x^3\, [\rho ^{\theta }]^{\prime } dx,~~ Y^s_T = 4\pi (\rho +3p_r-2\Pi _s),~~~~ \end{aligned}$$
(58)
$$\begin{aligned}{} & {} Y^{\theta }_T= 4\pi \big [\rho ^{\theta }+3p_r^{\theta }-2\Pi _{\theta }\big ], \end{aligned}$$
(59)
$$\begin{aligned}{} & {} Y^s_{TF}=8\pi \Pi _s- \frac{4\pi }{r^3}\,\int ^r_0 x^3\, \rho ^{\prime } dx, \end{aligned}$$
(60)
$$\begin{aligned}{} & {} Y^{\theta }_{TF} = 8\pi \Pi _{\theta } - \frac{4\pi }{r^3}\,\int ^r_0 x^3\, [\rho ^{\theta }]^{\prime } dx. \end{aligned}$$
(61)

The above symbols \(Y_{TF}\), \(X_{TF}\), \(Y_{T}\) and \(X_T\) denote the complexity factor, density inhomogeneity, strong energy condition, and homogeneous energy density distribution of spherically symmetric matter distributions, respectively. Furthermore, all desired solutions of field equations of static spherically symmetric matter distribution can be written in terms of the above structure scalars.

5 Gravitationally decoupled solution in \(f(\mathscr {T})\)-gravity

5.1 Minimally deformed anisotropic solution with vanishing complexity factor

In this section, we will solve standard equation of motions (20)–(24) in \(f(\mathscr {T})\)-gravity using the well-known Krori–Barua [108] spacetime geometry

$$\begin{aligned} \mu (r)= & {} e^{-Ar^2}~~~\text {and}~~~ \xi = Br^2 +C, \end{aligned}$$
(62)

where, A and B are constant with dimension \(length^{-2}\) while C is a dimensional less constant. This spacetime geometry has been successfully used in modeling the self-gravitating stellar models in GR and modified gravity [109,110,111,112]. Recently Maurya et al. [80, 81] also applied the Krori–Barua ansatz to obtain gravitationally decoupled solutions using vanishing complexity factor condition in the context of a pure GR scenario. Utilizing of the Eq. (62) in to system of equations of motion (36)–(38), we find \(p_r(r)\), \(p_t(r)\), and \(\rho (r)\),

$$\begin{aligned}{} & {} 8\pi \rho (r)=\frac{\alpha e^{-A r^2} \big (2 A r^2+e^{A r^2}-1\big )}{r^2}-\frac{\gamma }{2}, \end{aligned}$$
(63)
$$\begin{aligned}{} & {} 8\pi p_r(r)= \frac{\alpha \, \big [e^{-A r^2} \big (2 B r^2+1\big )-1\big ]}{r^2}+\frac{\gamma }{2},\end{aligned}$$
(64)
$$\begin{aligned}{} & {} 8\pi p_t(r)=-\alpha \,e^{-A r^2} \left[ A B r^2+A-B \left( B r^2+2\right) \right] +\frac{\gamma }{2}.~~~~\nonumber \\ \end{aligned}$$
(65)

Now we focus on the second system associated with the \(\theta \)-sector depending on the deformation function f(r). There are many ways to discover the solution of the second system, but here we are interested to use the vanishing of complexity factor condition (\(Y_{TF}=0\)) for the effective system \(T^{\text {eff}}_{ij}\) by taking of non-vanishing complexity factor (\({Y}^{s}_{TF}\ne 0\)) for the system \({T}_{ij}\) to determine the solution of the system. In this situation, we must have,

$$\begin{aligned} Y_{TF}= 8\pi \Pi ^{\text {eff}} - \frac{4\pi }{r^3}\,\int ^r_0 x^3\, [\epsilon ^{\text {eff}}]^{\prime } dx =Y^s_{TF}+ Y^{\theta }_{TF} =0,~~~ \nonumber \\ \end{aligned}$$
(66)

with \(\beta =1\)Footnote 1. Here, \(Y^s_{TF}\) and \(Y^{\theta }_{TF}\) denote the complexity factors associated with the seed system and \(\theta \) system, respectively. Now using of the Eqs. (33)–(39) with Eq. (66), we find a ordinary differential equation (ODE) in f(r) of the form,

$$\begin{aligned}{} & {} r\,f^{\prime }\, [\alpha (\xi ^{\prime } r+2)+2]+f \,\big [\alpha \left( 2 \xi ^{\prime \,\prime } r^2+\xi ^{\prime \,2}\, r^2-2 \xi ^{\prime } r-4\right) \nonumber \\{} & {} \quad -4\big ]+4 r^2 \,Y^s_{TF}=0, \end{aligned}$$
(67)

As we noticed from Eq. (60), the complexity factor \(Y^s_{TF}\) totally depends on seed pressures (\(p_r\) and \(p_t\)) and seed energy density (\(\rho \)). We determine the expression for \(Y^s_{TF}\) as,

$$\begin{aligned} Y^s_{TF}=\alpha \,(A - B) B\,r^2\, e^{-A r^2}, \end{aligned}$$
(68)

Now plugging of \(Y^s_{TF}\) along with metric function \(\xi (r)\) and \(\mu (r)\) in Eq. (67), we find the expression for f(r) as,

$$\begin{aligned} f(r)= & {} r^2 e^{-B r^2} \Big [F (B r^2+2)+\frac{(A-B) e^{\frac{2 A}{B}-2}}{B} \Big ((A-B) (B r^2+2) \nonumber \\{} & {} \times \psi (r)+B e^{\frac{(B-A) (B r^2+2)}{B}}\Big )\Big ],~~~~~ \end{aligned}$$
(69)

where, \(\psi (r)=ExpIntegralEi\left[ \frac{(B-A) \left( B r^2+2\right) }{B}\right] \). Then the expressions for \(\theta \)-components can be given as,

Fig. 1
figure 1

Top panels: The trend of energy density (\(\rho ^{\text {eff}}\times 10^4\)) and radial pressure (\(p^{\text {eff}}_r\times 10^4\)) against the radial parameter r for different values of \(\beta \). Bottom panels: The trend of tangential pressure \((p^{\text {eff}}_t\times 10^4)\) and anisotropy \((\Delta ^{\text {eff}} \times 10^4)\) against radial parameter r are shown in above figures. We use the following numerical values, \(A = 0.0078~\text {km}^{-2}\) and \(B = 0.0093~\text {km}^{-2}\), \(\alpha =1.2~\text {km}^{-2}\), and \(\beta = 10^{-46}\), to plot above figures for solution 5.1

Full size image
Fig. 2
figure 2

Left panel: The behavior of complexity factor (\(Y_{TF}\times 10^4\)) against r with different \(\beta \) is shown, and Right panel: shows the trend of density inhomogeneity \(X_{TF}\times 10^4\) against r for different \(\beta \) for solution 5.1 with same numerical values as used in Fig. 1

Full size image
Fig. 3
figure 3

The left panel and right panel show the trend of scalars \(Y_T\times 10^4\) and \(X_T\times 10^4\) versus r for solution 5.1 that describe the strong energy condition and homogeneous energy density distribution. We use the same data set of values as used in Fig. 1

Full size image
$$\begin{aligned} 8\pi \rho ^{\theta }= & {} -\frac{\alpha \, e^{-B r^2}}{B} \Bigg [-2 e^{-A r^2-2} \Big [e^2 B \Big (B^2 \left( F\, r^4 e^{A r^2}-r^2 e^{B r^2}\right) \nonumber \\{} & {} +A e^{B r^2} \left( B r^2-1\right) -2 F\, e^{A r^2}+B e^{B r^2}\Big )+\psi (r) (A-B)^2 \nonumber \\{} & {} \times \left( B^2 r^4-2\right) e^{A \left( \frac{2}{B}+r^2\right) }\Big ]+(A-B) e^{\frac{2 A}{B}-2} \Big (\psi (r) (A-B) \nonumber \\{} & {} \times \left( B r^2+2\right) +B e^{\frac{(B-A) \left( B r^2+2\right) }{B}}\Big )+B F\, \left( B r^2+2\right) \Bigg ], \end{aligned}$$
(70)
$$\begin{aligned} 8\pi p_r^{\theta }= & {} \alpha e^{-B r^2} \left( 2 B r^2+1\right) \Bigg [\frac{1}{B}\Big \{(A-B) e^{\frac{2 A}{B}-2} \Big (\psi (r)\, (A-B) \nonumber \\{} & {} \times \left( B r^2+2\right) +B e^{\frac{(B-A) \left( B r^2+2\right) }{B}}\Big )\Big \}+F \left( B r^2+2\right) \Bigg ], \end{aligned}$$
(71)
$$\begin{aligned} 8\pi p_t^{\theta }= & {} -\frac{\alpha \, e^{-B r^2}}{4} \Bigg [\frac{1}{B}\Big [2 e^{-A r^2-2} \left( 2 B r^2+2\right) \Big \{e^2 B \Big (B^2 \big (F\, r^4 \nonumber \\{} & {} \times e^{A r^2}-r^2 e^{B r^2}\big )+A e^{B r^2} \left( B r^2-1\right) -2 F\, e^{A r^2}+B e^{B r^2}\Big )\nonumber \\{} & {} +\psi (r) (A-B)^2 \left( B^2 r^4-2\right) e^{A \left( \frac{2}{B}+r^2\right) }\Big \}\Big ]-4 r^2 \left( B r^2+2\right) \nonumber \\{} & {} \times \Big ((A-B) e^{\frac{2 A}{B}-2}\, \Big \{\psi (r) (A-B) \, \left( B r^2+2\right) \nonumber \\{} & {} +B e^{\frac{(B-A) \left( B r^2+2\right) }{B}}\Big \}\Big )+B F \left( B r^2+2\right) \Bigg ]. \end{aligned}$$
(72)

Using the boundary conditions (48)–(50), we find the constant F, \(\mathscr {M}\), and C for solution (5.1) as

$$\begin{aligned} F= & {} \frac{e^{-A R^2}}{2} \Big [-\frac{2\,\psi (r)\, (A-B)^2 e^{A \left( \frac{2}{B}+R^2\right) -2}}{B}\nonumber \\ {}{} & {} +\frac{e^{B R^2} \big (F_1(R)-2 \alpha e^{A R^2}+\beta R^2 e^{A R^2}\big )}{\alpha \beta R^2 \left( B R^2+2\right) \left( 2 B R^2+1\right) }\Big ],~~~~ \end{aligned}$$
(73)
$$\begin{aligned} \mathscr {M}= & {} \frac{R}{2} \big [1-e^{-A r^2}-\beta \,f(R)\big ], \end{aligned}$$
(74)
$$\begin{aligned} C= & {} \ln \big [e^{-A R^2}+\beta \,f(R)\big ]-B R^2. \end{aligned}$$
(75)

where, \(F_1(R)=2 \alpha \,(1+2 B R^2)\,(1-A \beta R^2+B \beta R^2)\), while f(R) can be obtained from Eq. (69) by replacing \(r=R\).

Moreover, the expression for the complexity factor \((Y_{TF})\) and density inhomogeneity (\(X_{TF}\)) for the effective system can be given as,

$$\begin{aligned} Y_{TF}= & {} \Big [\alpha B (1-\beta ) r^2 (A-B) e^{-A r^2}\Big ], \end{aligned}$$
(76)
$$\begin{aligned} X_{TF}= & {} \frac{\alpha e^{-B r^2-2}}{e^{A r^2}r^2} \Big [\beta r^4 (A-B)^2 \left( B r^2+1\right) e^{A \left( \frac{2}{B}+r^2\right) }\nonumber \\{} & {} \times \psi (r)-e^2 \Big (e^{B r^2} \big (-A \left( B \beta r^4+r^2\right) +B^2 \beta r^4\nonumber \\{} & {} -1\big ]-B \beta \beta r^4 e^{A r^2} \left( B r^2+1\right) +e^{r^2 (A+B)}\Big )\Big ]. \end{aligned}$$
(77)

We can note from Eq. (76) that complexity factor \(Y_{TF}\) vanishes at \(\beta =1\).

Fig. 4
figure 4

The variation of Mass (M/\({M_{\odot }}\)) versus complexity factor \(Y_{TF}\) for solution 5.1

Full size image

5.2 Isotropic solution for Krori–Barua model via gravitational decoupling

In this section, we will use Casadio et al. [113] novel approach for obtaining the gravitationally decoupled isotropic solution for the effective energy-momentum tensor \(T^{\text {eff}}_{ij}\) corresponding to the anisotropic system (20)–(24). Since the effective system is a combination of two sub-systems for energy-momentum tensor \(T_{ij}\) and \(\theta _{ij}\). In this regard, Casadio et al. [113] proposed that it is possible to transform an anisotropic system (36)–(39) given by \(T_{ij}\) with \(\Pi _s \ne 0\) into an isotropic system (7)–(11) provided by \(T^{\text {eff}}_{ij}\) with \(\Pi ^{\text {eff}}=0\) through the source \(\theta _{ij}\). It is obvious that this transformation can be controlled by fixing of the decoupling parameter \(\beta =0\) and \(\beta =1\) that describe anisotropic system (36)–(39) and isotropic system (20)–(24), respectively. In this case, the isotropization is done by fixing \(\beta =1\), for which \(\Pi ^{\text {eff}}=0\) leads,

$$\begin{aligned} \Pi _s=-\,\Pi _{\theta }~~\Longrightarrow ~~ \Pi _s=-(p_r^{\theta }-p_t^{\theta }). \end{aligned}$$
(78)

Now we get a non-linear ODE by using of Eqs. (33)–(43) into Eq. (41) as

$$\begin{aligned}{} & {} \alpha \big [f \beta \left( -2 \xi ^{\prime \prime } r^2-\xi ^{\prime 2} r^2+2 \xi ^{\prime } r+4\right) +\mu \big (2 \xi ^{\prime \prime } r^2+\xi ^{\prime 2} r^2 \nonumber \\ {}{} & {} \quad -2 \xi ^{\prime } r-4\big )-f^{\prime } \xi ^{\prime } \beta r^2-2 f^{\prime } \beta r+\mu ^{\prime } \xi ^{\prime } r^2+2 \mu ^{\prime } r+4\big ]=0, \nonumber \\ \end{aligned}$$
(79)

We note that the Eq. (79) depends on \(\xi (r)\), \(\mu (r)\), and f(r). Using the Krori–Barua solution: \(\xi =Br^2+C\) and \(\mu =e^{-Ar^2}\) from Eq. (62) into Eq. (79), we find the deformation function f(r) of the form,

$$\begin{aligned} f(r)=e^{-A r^2}+B r^2 e^{-B r^2-1} \Psi (r)+F r^2 e^{-B r^2}-1,~~~ \end{aligned}$$
(80)
Fig. 5
figure 5

Top panels: The trend of energy density (\(\rho ^{\text {eff}}\times 10^4\)) and radial pressure (\(p^{\text {eff}}_r\times 10^4\)) against the radial parameter r for different values of \(\beta \). Bottom panels: The trend of tangential pressure \((p^{\text {eff}}_t\times 10^4)\) and anisotropy \((\Delta ^{\text {eff}} \times 10^4)\) against radial parameter r are shown in above figures. We use the following numerical values, \(A = 0.0078~\text {km}^{-2}\) and \(B = 0.0093~\text {km}^{-2}\), \(\alpha =1.2~\text {km}^{-2}\), and \(\beta = 10^{-46}\), to plot above figures for isotropic solution 5.2

Full size image
Fig. 6
figure 6

Left panel and Right panel show the behavior of complexity factor (\(Y_{TF}\times 10^4\)) and density inhomogeneity \(X_{TF}\times 10^4\) versus r, respectively for different \(\beta \) for isotropic solution 5.2. We set same numerical values as used in Fig. 5

Full size image

where, \(\Psi (r)=ExpIntegralEi\left( B r^2+1\right) \) and F is a constant of integration. Then the effective energy density and effective pressures are,

$$\begin{aligned} 8\pi \rho ^{\text {eff}}(r)= & {} \alpha \beta \Big (2 A e^{-A r^2}-\frac{e^{-A r^2}}{r^2}-\frac{2 B^2 r^2}{B r^2+1}+2 B F r^2 e^{-B r^2} \nonumber \\{} & {} -3 F e^{-B r^2}+B \Psi (r) e^{-B r^2-1} \left( 2 B r^2-3\right) +\frac{1}{r^2}\Big )\nonumber \\{} & {} +\frac{\alpha e^{-A r^2} \left( 2 A r^2+e^{A r^2}-1\right) }{r^2}-\frac{\beta }{2}, \end{aligned}$$
(81)
$$\begin{aligned} 8\pi p_r^{\text {eff}}(r)= & {} \frac{1}{2} e^{-B r^2} \Big [-\frac{2 \alpha (\beta -1) \left( 2 B r^2+1\right) e^{-\left( r^2 (A-B)\right) }}{r^2}\nonumber \\ {}{} & {} -2 \alpha F \beta \left( 2 B r^2+1\right) -\frac{2 \alpha B \beta \Psi (r) \left( 2 B r^2+1\right) }{e}\nonumber \\ {}{} & {} +\frac{e^{B r^2} \left( 2 \alpha \left( 2 B \beta r^2+\beta -1\right) +\beta r^2\right) }{r^2}\Big ], \end{aligned}$$
(82)
$$\begin{aligned} 8\pi p_t^{\text {eff}}(r)= & {} \frac{1}{2} e^{-A r^2-B r^2-1} \Big [e \Big (-4 \alpha B \big (-\beta e^{r^2 (A+B)}+F \beta r^2 e^{A r^2}\nonumber \\{} & {} +(\beta -1) e^{B r^2}\big )+2 \alpha A (\beta -1) e^{B r^2} \left( B r^2+1\right) +\beta e^{r^2 (A+B)}\nonumber \\{} & {} -2 \alpha F \beta e^{A r^2}-2 \alpha B^2 (\beta -1) r^2 e^{B r^2}\Big )-2 \alpha B \beta e^{A r^2}\nonumber \\{} & {} \times \left( 2 B r^2+1\right) \Psi (r)\Big ]. \end{aligned}$$
(83)

and corresponding complexity factor \((Y_{TF})\) and density inhomogeneity (\(X_{TF}\)) are given,

$$\begin{aligned} Y_{TF}= & {} \frac{\alpha }{r^2}\Big [\Big (e^{-A r^2} \big (\beta \left( -A r^2 \, (B r^2+2)+B^2 r^4-2\right) \nonumber \\{} & {} + B r^4 (A-B)\big )-B^2\, \beta \, \Psi (r) r^4 e^{-B r^2-1} \nonumber \\{} & {} +\frac{\beta \left( B^2 r^4+2 B r^2+2\right) }{(1+B r^2)}-B\,F \beta r^4 e^{-B r^2}\Big )\Big ], \end{aligned}$$
(84)
$$\begin{aligned} X_{TF}= & {} \frac{\alpha }{r^2} \Big [(\beta +1) e^{-A r^2} \left( A r^2+1\right) +B^2 \beta \Psi (r) r^4 e^{-B r^2-1}\nonumber \\{} & {} +B F \beta r^4 e^{-B r^2}-B \beta r^2-\frac{\beta }{B r^2+1}-1\Big ], \end{aligned}$$
(85)

Using the boundary conditions (48)–(50), we find the constant F, \(\mathscr {M}\), and C for solution (5.2) as

$$\begin{aligned} F= & {} -\frac{(\beta -1)}{\beta R^2 e^{R^2 (A-B)}}-\frac{B ExpIntegralEi\left( B R^2+1\right) }{e} \nonumber \\{} & {} +\frac{e^{B R^2} \left( 2 \alpha \left( 2 B \beta R^2+\beta -1\right) +\beta R^2\right) }{2 \alpha \beta R^2 \left( 2 B R^2+1\right) }, \end{aligned}$$
(86)
$$\begin{aligned} \mathscr {M}= & {} \frac{R}{2} \big [1-e^{-A r^2}-\beta \,f(R)\big ], \end{aligned}$$
(87)
$$\begin{aligned} C= & {} \ln \big [e^{-A R^2}+\beta \,f(R)\big ]-B R^2 \end{aligned}$$
(88)

where, f(R) can be obtained by using Eq. (80).

6 Physical analysis

We will now carefully analyze the physical appropriateness of the new classes of stellar solutions based on the Krori–Barua model, including minimally deformed anisotropic solutions with vanishing complexity factors and isotropic solutions via gravitational decoupling which have been explored in the preceding Sects. 5.1 and 5.2 respectively. To test if they’re physically realizable, we’ll look at the trends in the graphical plots:

6.1 Solution 5.1

The minimally deformed anisotropic solution with vanishing complexity factor for the structural properties, namely the matter variables, \(\rho ^{\text {eff}}\), \(p^{\text {eff}}_r\), \(p^{\text {eff}}_t\), \(\Delta ^{\text {eff}}\) and the four scalars \(X_{TF}\), \(Y_{TF}\), \(X_{T}\), \(Y_{T}\), as well as the mass-complexity factor relationship \(M-Y_{TF}\) of the self-gravitating compact stars through gravitational decoupling in \(f(\mathscr {T})\)-gravity with a diagonal tetrad is presented in Figs. 1,2, 3 and 4 by taking into account all the permitted values of the decoupling constant \(\beta \), which lies in the range \( 0.0\le \beta \le 2.5\). Within the star, the energy density (Top, left panel), radial (Top, right panel)/tangential (Bottom, left panel) pressure components are positive, having higher values at the core and thereafter dropping monotonically to reach the lowest value at the surface, as shown in Fig. 1. It’s worth noting that when \(r\simeq 7.5\) and \(r\simeq 8\), the density and tangential pressure switch their tendencies, respectively, for all allowable values of the decoupling constant \(\beta \). Meanwhile, at some finite radius, \(r = R\), the radial pressure vanishes, defining the astronomical structure’s bounds for the whole band of \(\beta \) across each inner point of the astronomical structure. When \(\beta \) goes from 0.0 to 2.5, the anisotropy (bottom, right panel) is non-negative with a decreasing magnitude on the astronomical structure, causing a rise in stress at each inner point of the astronomical configuration, including the vanishing complexity factor. A non-negative anisotropy, \(\Delta \ge 0\), indicates that the force caused by the presence of pressure anisotropy is repulsive, assisting in the stabilization of the stellar structure in opposition to the gravitational attraction generated internally. In this regard, the anisotropy factor increases with increasing radius, which successfully stabilizes the stellar surface layers over the core’s central region. The implications from gravitational decoupling via the vanishing of the complexity factor also appear to reduce the anisotropy factor.

Next, by varying the decoupling constant \(\beta \) from 0.0 to 2.5, the profile of the four scalars, namely, the complexity factor, density inhomogeneity, homogeneous energy density distribution, and strong energy condition for the minimally deformed anisotropic solution, is investigated and shown in Figs. 2 and 3. There are some extremely interesting observations to be made here about these scalars. It is clear that the complexity factor \(Y_{TF}\) is negative in pure \(f(\mathscr {T})\)-gravity, however when gravitational decoupling is included and the decoupling constant \(\beta \) is varied from 1 to 2.5, the complexity becomes positive. Meanwhile, the complexity vanishes at \(\beta =1\) and its tendencies increase with its magnitude towards the boundary. However, as expected, Fig. 2 (top, right panel) shows the behavior of density inhomogeneity as a function of the radial coordinate, r. By growing the decoupling constant \(\beta \) from 0.0 to 2.5, we notice that the scalar \(X_{TF}\) is negative and a monotonically decreasing function with a slight increasing magnitude. In contrast, to Fig. 3, we present diagrams relating to the strong energy condition and homogeneous energy density distribution with respect to the radial coordinate r. As can be seen, both quantities viz., \(Y_T\) and \(X_T\) are regular at the center of the stellar structure and drops off monotonically towards the stellar surface. Moreover, we observe that when the decoupling constant \(\beta \) increases from 0.0 to 2.5, the strong energy condition and homogeneous energy density distribution switch their trends at some finite radius, \(r = r_*\) i.e., when \(r\simeq 8.5\) and \(r\simeq 8\), respectively.

Fig. 7
figure 7

The behavior of scalars \(Y_T\times 10^4\)-left panel and \(X_T\times 10^4\)-right panel describe the strong energy condition and homogeneous energy density distribution versus r for isotropic solution 5.2. We set same numerical values as used in Fig. 5

Full size image
Fig. 8
figure 8

The variation of Mass (\(M/M_{\odot }\)) versus complexity factor \(Y_{TF}\) for solution 5.2

Full size image

Next, we study the effect of the decoupling constant \(\beta \) in Fig. 4, where the \(M-Y_{TF}\) relationship is reported for different values of the constant \(\beta \). We can see how both the mass and the complexity factor change as the value of \(\beta \) increases. So this result strongly implies that the \(\beta \) constant is extremely important in determining the maximum mass of a self-gravitating compact star via gravitational decoupling in \(f(\mathscr {T})\)-gravity with a diagonal tetrad. It should be noted here that the mass grows monotonically with the growth of small values of the complexity factor, with linear trends for all permitted values of \(\beta \). We also note that the maximum mass of a self-gravitating compact star via gravitational decoupling in \(f(\mathscr {T})\)-gravity with a diagonal tetrad can be reduced than that in pure \(f(\mathscr {T})\)-gravity under a small effect of complexity factor.

6.2 Solution 5.2

The isotropic solution via gravitational decoupling for the structural characteristics of the self-gravitating compact stellar configurations in \(f(\mathscr {T})\)-gravity with a diagonal tetrad can be seen in Figs. 5, 6, 7 and 8, illustrating matter content with 4 scalars and the mass-complexity factor relationship namely, \(\rho ^{\text {eff}}\), \(p^{\text {eff}}_r\), \(p^{\text {eff}}_t\), \(\Delta ^{\text {eff}}\), \(X_{TF}\), \(Y_{TF}\), \(X_{T}\), \(Y_{T}\) and \(M-Y_{TF}\), depending on the radial coordinate r, for different values of the decoupling constant \(\beta \), where \(\beta \) \(\in [0.0,~1.0]\). Figure 5 interprets that the energy density (Top, left panel), as well as the radial (Top, right panel)/tangential (Bottom, left panel) pressure components, are positive and maximum at the center and become minimum at the larger values of the radial coordinate r within the star, while their trends switch around \(r\simeq 7.5\) for the energy density, \(r\simeq 5.5\) for the radial pressure and \(r\simeq 5.5\) for the tangential pressure by considering all allowable values of the decoupling constant \(\beta \). Whereas the anisotropy increases with increasing radius throughout the region for all allowed values of \(\beta \) i.e., \(\beta \in [0,~1[\), and enhances as \(\beta \) decreases, confirming that the extra source generates stronger anisotropy in the system, but when the decoupling constant \(\beta \) equals one i.e., \(\beta =1\), the anisotropy vanishes throughout the stellar region, as shown in Fig. 5 (bottom, right panel). In this regard, we have started with the anisotropic solution for the seed system and we use gravitational decoupling to find the isotropic solution in \(f(\mathscr {T})\)-gravity. We also revealed an interesting physical characteristic, which is that the gravitational decoupling approach is not only useful for extending the solution from the isotropic domain to the anisotropic domain or anisotropic domain to the anisotropic domain, but it is also useful for finding the isotropic solution from anisotropic domain. In Figs. 6 and 7 the profile of the four scalars, viz., \(Y_{TF}\), \(X_{TF}\), \(Y_{T}\) and \(X_{T}\) for the isotropic solution via gravitational decoupling are represented, by choosing different values of the decoupling constant \(\beta \) from 0.0 to 1. We can see that these scalars behave similarly to the previous solution 5.1, with a slight change around their magnitude and the location of the switch trends at some finite radius, \(r = r_*\) relating to the homogeneous energy density distribution and strong energy condition.

Fig. 9
figure 9

The variation of Mass (\(M/M_{\odot }\)) versus Radius (R) for solution 5.1, left panel for \(\rho _s\simeq 6 \times 10^{14} gm/cm^{3}\) and right panel for \(\rho _s\simeq 8 \times 10^{14} gm/cm^{3}\)

Full size image
Fig. 10
figure 10

The variation of Mass (\(M/M_{\odot }\)) versus Radius (R) for solution 5.2, left panel for \(\rho _s\simeq 6 \times 10^{14} gm/cm^{3}\) and right panel for \(\rho _s\simeq 8 \times 10^{14} gm/cm^{3}\)

Full size image

Our next step will be to describe our findings coming from \(M-Y_{TF}\) relationship, which is represented in Fig. 8, for various values of the decoupling parameter \(\beta \). We notice that the mass grows monotonically with the growth of small values of the complexity factor and has a linear trend for different values of the parameter \(\beta \). We can also see how both the mass and the complexity factor change as \(\beta \) goes from 0 to 1. It is worth noting here that, with a small effect of complexity factor, the maximum mass of a self-gravitating compact star via gravitational decoupling in \(f(\mathscr {T})\)-gravity with a diagonal tetrad can be reduced than that in pure \(f(\mathscr {T})\)-gravity.

Table 1 Numerical values of the predicted radii of different stars for Solution 5.1 with surface density \(\rho _s\simeq 6 \times 10^{14} gm/cm^{3}\), \(A = 0.0078, B = 0.0093, \alpha = 1.2\)
Full size table
Table 2 Numerical values of the predicted radii of different stars for Solution 5.1 with surface density \(\rho _s\simeq 8 \times 10^{14} gm/cm^{3}\), \(A = 0.0078, B = 0.0093, \alpha = 1.2\)
Full size table
Table 3 Numerical values of the predicted radii of different stars for Solution 5.2 with surface density \(\rho _s\simeq 6 \times 10^{14} gm/cm^{3}\), \(A = 0.0078, B = 0.0093, \alpha = 1.2\)
Full size table
Table 4 Numerical values of the predicted radii of different stars for Solution 5.2 with surface density \(\rho _s\simeq 8 \times 10^{14} gm/cm^{3}\), \(A = 0.0078, B = 0.0093, \alpha = 1.2\)
Full size table

7 Predicted radii for different compact objects via \(M{-}R\) curves

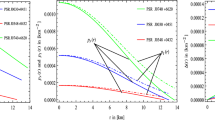
In this part, we concentrate on figuring out the radii of seven stellar object candidates via \(M{-}R\) curves, whose masses range from \(1.04\pm 0.09\) \({M_\odot }\) to \(2.50-2.67\) \({M_\odot }\). Therefore, in light of the seven stellar object candidates that were chosen for this work, Figs. 9 and 10 show the profile of the maximum mass \(M/M_{\odot }\) versus radius R for both solutions 5.1 and 5.2, having \(\rho _s\simeq 6 \times 10^{14} gm/cm^{3}\)-(left panel) and \(\rho _s\simeq 8 \times 10^{14} gm/cm^{3}\)-(right panel) for different values of the parameter \(\beta \). In this context, the availability of low and high-mass stellar objects is predicted by both solutions 5.1 and 5.2 for the two cases taken into consideration, as illustrated in Figs. 9 and 10 along with Tables 1, 2, 3, and 4. The occurrence of a higher-mass stellar object with a smaller radius i.e, more compact is predicted by our solutions 5.1 and 5.2 when \(\beta \) increases from 0.10 to 0.30. On the other hand, we observe from Tables 1, 2, 3 and 4 for solutions 5.1 and 5.2 that when density increases then radii decrease and obtained more compact objects.

Furthermore, our model successfully predicted the masses and radii of all neutron stars, as well as the massive stellar object with a mass in the range of 2.5 to 2.67 \({M_\odot }\) which is a secondary component of the GW190814 event in both solutions with the four cases for all selected values of \(\beta \). Also, our generated \(M{-}R\) curves match empirical findings for all known compact stars, including LMC X-4 [114], GW170817-2 [115], PSRJ 0037-4715 [116], X 1822-371 [117], PSR J 1614-2230 [118], PSR J 0952-0607 [119] and GW190814 [120].

Based on the above analysis, we, therefore, come to the conclusion that the gravitational decoupling constant \(\beta \) and surface density is playing an important role in the description of higher mass and more compact objects.

8 Conclusions

In this paper, we are the first to investigate how gravitational decoupling in \(f(\mathscr {T})\)-gravity changes the complexity and isotropization of self-gravitating compact stars using a diagonal tetrad. We start by implementing gravitational decoupling via MGD strategy as the generating mechanism of anisotropic solutions, which was inspired by recent applications of gravitational decoupling via MGD scheme as a ground-breaking instrument. It should be noted that the decoupling via the MGD approach can be utilized to control many physical attributes of static spherical self-gravitating systems. Further, we consider the Krori–Barua model, which includes minimally deformed anisotropic solutions with vanishing complexity factor and isotropic solutions via gravitational decoupling to explore the physical appropriateness of the new classes of stellar solutions describing meaningful static and spherically symmetric self-gravitating compact stars. We presented two new stellar solutions by exploiting the minimally deformed anisotropic solution with vanishing complexity factor and the isotropic solution via gravitational decoupling. These solutions were tested for their regularity, causality and instability by studying the associated thermodynamical observables, \(\rho ^{\text {eff}}\), \(p^{\text {eff}}_r\), \(p^{\text {eff}}_t\), \(\Delta ^{\text {eff}}\) and the four scalars \(X_{TF}\), \(Y_{TF}\), \(X_{T}\), \(Y_{T}\), as well as the mass-complexity factor relationship \(M-Y_{TF}\) of the self-gravitating compact stars in the context of \(f(\mathscr {T})\)-gravity with a diagonal tetrad by varying the decoupling constant \(\beta \) between 0 and 2.5. We observe that the thermodynamic observables fall monotonically to their lowest values at the stellar surface, from higher values at the center, while the radial pressure vanishes at the boundary. It’s worth noting that these quantities behave similarly within the star for both solutions, with a slight change around their magnitude and the location of the switch trends at some finite radius, \(r=r_*\), depending on different values of the decoupling constant \(\beta \) for each case. This clearly shows that the star’s center is very compact and that our current stellar model is viable for the area surrounding the star’s center. Nevertheless, the anisotropy parameter always remains positive at any interior point of the stellar configuration. On the one hand, we have demonstrated that for the minimally deformed anisotropic solution, the magnitude of the anisotropy parameter is sensitive to the decoupling constant and its connection to the vanishing of the complexity factor. In addition, the anisotropy parameter increases with increasing radius, successfully stabilizing the surface layers over the core’s central areas for all allowed values of \(\beta \in [0,~2.5[\). On the other hand, we have shown that for the isotropic solution via gravitational decoupling, the anisotropy increases with increasing radius throughout the region for \(\beta \in [0,~1[\), and improves as \(\beta \) decreases, proving that the extra source generates stronger anisotropy in the system, but when \(\beta =1\), the anisotropy vanishes throughout the stellar region. Our investigation also revealed that the gravitational decoupling approach is useful not only for extending the solution from the isotropic to the anisotropic domain or vice versa but also for generating new isotropic solutions from anisotropic solutions.

Furthermore, we have made a few notable observations about the four scalars derived from both solutions. We clearly observed that these scalars exhibit the same behavior with a slight variation in their magnitude, the range of the decoupling constant \(\beta \), and the placement of the switch trends at some finite radius, \(r=r_*\) corresponding to the homogeneous energy density distribution and strong energy condition. It is worth noting that the complexity factor is negative in pure \(f(\mathscr {T})\)-gravity, but becomes positive when gravitational decoupling is considered.

We then analysed the effect of the decoupling constant \(\beta \) on the \(M-Y_{TF}\) diagram. As the value of \(\beta \) increased, we observed how both the mass and the complexity factor changed. Consequently, this result strongly suggests that the \(\beta \) parameter is crucial in determining the maximum mass of a self-gravitating compact star via gravitational decoupling in \(f(\mathscr {T})\)-gravity with a diagonal tetrad. It should be noted that the mass increased monotonically with small increments of the complexity factor, displaying linear trends for different values of \(\beta \). We also note that with a small effect of complexity factor, the maximum mass of a self-gravitating compact star via gravitational decoupling in \(f(\mathscr {T})\) gravity with a diagonal tetrad can be lower than its counterpart in pure \(f(\mathscr {T})\) gravity.

A perfect agreement was revealed for a few compact stars, including LMC X-4, GW170817-2, PSRJ 0037-4715, X 1822-371, PSR J 1614-2230, PSR J 0952-0607 and GW190614 after we generated the \(M{-}R\) curves using our solutions. Hence, by varying the gravitational decoupling constant \(\beta \) as a free parameter, we were able to estimate the corresponding masses and their related radii from the \(M{-}R\) curves. In addition, we also shown the impact of the surface density on the mass-radius relation. In this regard, one may confirm that our solutions predicted the radii in good accordance with the empirical evidence by looking at the \(M{-}R\) curves.

Finally, it should be noted that by implementing gravitational decoupling via the MGD approach as the generating mechanism of anisotropic solutions, many physical properties of static spherical self-gravitating systems can be controlled. Through gravitational decoupling in \(f(\mathscr {T})\)-gravity with a diagonal tetrad, we successfully analyzed the change in complexity and isotropization of self-gravitating compact stars.