1 Introduction

The general theory of relativity, formulated by Albert Einstein, has some limitations in both theoretical and observational domains. However, it remains a very effective framework for elucidating a wide range of cosmological and astrophysical phenomena. In the field of general relativity, singularities are often encountered, and the absence of a self-consistent theory of quantum gravity is a common challenge. Furthermore, the general theory of relativity lacks the ability to adequately explain the dynamics of galaxies, extra-galactic systems, and the cosmos as a whole without taking into account the existence of the “dark” components of the matter-energy composition of the Universe, namely dark matter and dark energy.

Instead of modifying the Einstein field equations by introducing an unexplained matter-energy component, an alternative approach is to seek solutions from a geometric perspective. This allows for the inclusion of the missing matter-energy required to describe various phenomena in the observed Universe, such as galactic and cosmic dynamics, including the late-time acceleration of the Universe. Over time, a number of alternative or modified theories of gravity have been offered by various researchers [1,2,3,4]. In each of these theories, the Einstein field equations have been modified by altering the source side. Simultaneously, the geometrical component has been modified by including a generalised functional form of the argument as the gravitational Lagrangian in the appropriate action. Among the several hypotheses under consideration, a select handful stand out as particularly noteworthy. The literature discusses various modified gravity theories, including f(R) gravity [5,6,7,8], f(T) gravity [9,10,11], \(f(R,{\mathcal {T}})\) gravity [12,13,14,15], f(G) gravity [16, 17] and f(R, G) gravity [18]. In these theories, the symbols R, T, \({\mathcal {T}}\), and G represent the Ricci scalar, torsion scalar, trace of the energy–momentum tensor, and Gauss–Bonnet scalar, respectively. Like the generalization of the general theory of relativity to f(R) gravity, one can choose either the torsion T or the nonmetricity Q as the geometric basis which provides two different but equivalent descriptions of gravity and those are known as “teleparallel equivalent of general relativity” (TEGR) [19,20,21] and “symmetric teleparallel general relativity” (STGR) [22,23,24,25] respectively. In STGR instead of the curvature and the torsion, the nonmetricity describes the gravity where one can always choose the coincident gauge, under the teleparallelism constraint, which does restrict the affine connection to disappear as well as make the metric tensor the only basic variable. In analogy to f(R) gravity, STGR can be generalized to f(Q) gravity [25, 26] where the gravitational Lagrangian in the corresponding action can be taken as the function of nonmetricity Q. In the present study we are employing f(Q) gravity theory because of the fact that it has (i) a long historical background which was proposed in the year 1928 by Einstein [27] in connection to his GR and known as “Teleparallelism” or “teleparallel gravity”, and (ii) received attention to the scientists [28, 29] in the cosmological [30,31,32,33,34] as well as astrophysical [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54, 64,65,66] field of research. In [37, 38, 45,46,47,48,49,50,51,52] authors explored the wormhole geometries in f(Q) gravity under different physical scenarios. Mandal et al. [35] have studied the energy conditions in f(Q) gravity whereas Wang et al. [44] have found static and spherically symmetric solutions under the framework of f(Q) gravity. Flathmann and Hohmann [36] have analyzed the post-Newtonian approximation of a generalization of the symmetric teleparallel gravity, i.e., in f(Q) gravity with the help of the parameterized post-Newtonian (PPN) formalism. In Refs. [40,41,42,43, 53, 54] authors discussed different stellar models under the realm of f(Q) gravity considering different physically plausible possibilities. In a dark energy stellar model [55] using linear form of f(Q), the maximum mass of the dark energy star is found to be within the mass gap range (2.5–5 \(M_{\odot }\)) which eventually implies a possible candidate for the secondary component of the GW190814 event. Some other works [56, 57] with similar astrophysical implications, proposed the existence of dark energy stars, respectively, for quadratic form of f(Q) and under the Krori–Barua (KB) metric matched with the exterior Reissner–Nordström space-time in the presence of modified Chaplygin gas EOS fused within the Einstein–Maxwell field equations. Anisotropic compact stars with quintessence dark energy can be represented by a new family of solution [58, 59] in f(Q) gravity. In addition, the compact star model with anisotropy as well as quintessence is developed with physical validity in f(T) gravity [60]. With embedding Class 1 technique, a well behaved set of solutions [61,62,63] to the field equations in f(R, T) gravity is found exploring physical features of compact stars. Furthermore, Nashed and his collaborators have performed several study on compact objects in different gravity theories [67,68,69,70]. Various black hole configurations have been studied under the framework of f(Q) gravity in Refs. [39, 64,65,66].

This research investigates the anisotropic stellar configuration using the mimic constraint on the mass function suggested by Contreras and Stuchlik [71] in the context of f(Q) gravity theory. The analysis is conducted within the framework of the vanishing complexity formalism, as defined by Herrera [72, 73]. The analysis of the complexity of a system may be facilitated by considering a multitude of elements. The core principle pertains to the quantification of entropy and the information content inherent in the structure of a given system. There exist multiple definitions of complexity in the existing body of literature. However, our focus lies exclusively on the complexity of a self-gravitating system, which was initially introduced by the authors in the references [74,75,76,77,78,79]. This concept builds upon the research conducted by Lopez–Ruiz and his colleagues [80, 81].

Herrera [72, 73] has proposed a novel framework for assessing complexity in self-gravitating systems. In this framework, the complexity factor, which serves as the metric for quantifying complexity, emerges in the orthogonal decomposition of the Riemann tensor within the spacetime continuum under consideration. In the scenario of a static distribution of fluid, one may simplify the system by considering it as a homogeneous fluid with uniform energy density. In this configuration, it is straightforward to give a complexity factor of zero. The aforementioned concept bears resemblance to the Tolman mass concept introduced by Tolman in 1930 [82]. It can be understood as the gravitational mass that is actively involved in the system. In the case of an arbitrary distribution, this mass can be expressed as the sum of its value for the zero complexity case, along with two additional terms that depend on the inhomogeneity of energy density and the anisotropy of pressure. A single scalar function, called the complexity factor, may characterise the last two terms, which becomes zero when the fluid distribution exhibits both homogeneity in energy density and isotropy in pressure. However, these terms may also become zero when the components involving density inhomogeneity and anisotropic pressure counteract each other. Hence, the phenomenon of diminishing complexity may be seen in many systems, as elucidated in the work of Lopez [80]. In their research, Herrera et al. [83] utilised the axially symmetric geometry to evaluate the impact of complexity on various geometries. They identified three primary sources that contribute to complexity. In a separate study [84], the authors investigated the concept of complexity, specifically in relation to dissipation and non-dissipation. They examined the emergence of spherically symmetric non-static geometry using the quasi-homology concept to establish a relationship between the areal radius and the velocity of the areal radius.

Contreras and Fuenmayor [85] have investigated the stability of self-gravitating celestial bodies via the examination of gravitational cracking, using a similar methodology. In their earlier study, Herrera et al. [73] not only examined the influence of additional structural scalars derived from the orthogonal division of intrinsic curvature, but also extended the notion of complexity factor to hyperbolically symmetric geometry. In this connection, new developed gravitational decoupling via MGD and extended MGD techniques [86, 87] are very effective methodology to develop new solutions [88,89,90,91,92,93,94,95]. In this context, it is possible to examine the recent research publications [71, 96,97,98,99,100,101,102,103,104] that have undertaken an analysis of the complexity associated with static and spherically symmetric stellar structures within the framework of gravitational decoupling.

The unique feature of the present paper is that the isotropic fluid component corresponds to Vlasenko–Pronin space-time [105] to which CGD added by a new source. It is to be noted from the literature survey that Maurya and Gupta [106] have presented charged analogue of the Vlasenko–Pronin superdense star [105] in general relativity. Later on, Singh and Pant [107] have also studied the charged anisotropic Vlasenko–Pronin solutions [105] related to superdense stars with constant stability factor. Interestingly, the maximum mass and radius contained in the neutral physical system are 2.1434 \(M_{\odot }\) and 16.7300 km, respectively. on a recent study conducted by Maurya et al. [108], an anisotropic dark star model was developed. This model was formed by the Vlasenko–Pronin space-time induced anisotropy on a background of complexity-free domain. Additionally, the study investigated the influence of dark matter on gravitational wave echoes. So the present study in that sense related to varieties of physical aspects, starting from neutral to charged superdense star [109,110,111]. Esmakhanova et al. [113] developed a relation between the solution od Einstein equation, Ramanujan and Chazy equations, while cosmological model with fermionic field and with f-essence was discussed by Momeni [112].

Under the above mentioned physical background we have investigated various physical attributes and effect of f(Q) gravity along with the decoupling parameter on anisotropic stellar structure constructed by mass constraint approach. The study is organized as follows: In the next section we discuss the corresponding field equations of f(Q) gravity considering a linear form in nonmetricity Q for the function f(Q) and we define the corresponding complexity factor \(Y^Q_{TF}\) in f(Q) gravity. In Sect. 3 we provide the solutions to the corresponding field equations using complete geometric deformation method in complexity free scenario. The required matching conditions at the boundary are expressed in Sect. 4. This is followed by the physical analysis of complexity free anisotropic solution in f(Q) gravity in Sect. 5. Furthermore, in Sect. 6, we discuss different constraints on maximum mass and radii studying mass-radius relationships based on observational data for observed compact objects. Finally, concluding remarks are presented in Sect. 7.

2 Revisit of the decoupled field equations in f(Q) gravity

The revised action for f(Q) gravity is obtained by including an additional Lagrangian term, denoted as \(L_\theta \), which is coupled to the new source \(\theta _{\epsilon \nu }\) via a decoupling constant \(\alpha \) as:

$$\begin{aligned} {\mathcal {S}}={\int \frac{1}{2}\,f(Q)\sqrt{-g}\,d^4x+\int {\mathcal {L}}_m\,\sqrt{-g}\,d^4x}+\alpha { \int {\mathcal {L}}_\theta \,\sqrt{-g}\,d^4x}.\nonumber \\ \end{aligned}$$
(1)

In the context of the f(Q) gravity hypothesis, the Lagrangian density \({\mathcal {L}}_m\) represents the matter fields and is associated with the energy–momentum tensor \({T}_{\epsilon \nu }\). The nonmetricity scalar Q plays a crucial role in governing the gravitational interaction. The inclusion of the additional contribution in the f(Q) gravity matter field correction has the potential to enhance our comprehension of the system’s physical characteristics beyond the scope of the f(Q) gravity theory. The sources \(T_{\epsilon \nu }\) and \(T^\theta _{\epsilon \nu }\) are defined as

$$\begin{aligned} {T}_{\epsilon \nu }= & {} -\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}\,{\mathcal {L}}_m\right) }{\delta g^{\epsilon \nu }}, \end{aligned}$$
(2)
$$\begin{aligned} T^\theta _{\epsilon \,\nu }= & {} -\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}\,{\mathcal {L}}_\theta \right) }{\delta g^{\epsilon \nu }}. \end{aligned}$$
(3)

In addition to this, the combined action for both sources is denoted by the decoupling constant \(\alpha \) as \(T^{\text {tot}}_{\epsilon \nu }=\big (T_{\epsilon \nu }+\alpha \,T^\theta _{\epsilon \nu }\big )\).

The expression for the nonmetricity tensor \(Q_{\lambda \epsilon \nu }\) in relation to the affine connection is provided as follows

$$\begin{aligned} Q_{\lambda \epsilon \nu }=\bigtriangledown _{\lambda } g_{\epsilon \nu }=\partial _\lambda g_{\epsilon \nu }-\Gamma ^\delta _{\,\,\,\lambda \epsilon }g_{\delta \nu }-\Gamma ^\delta _{\,\,\,\lambda \nu }g_{\epsilon \delta }, \end{aligned}$$
(4)

The symbol \(\Gamma ^\delta _{\,\,\,\epsilon \nu }\) is often referred to as the affine connection, which takes on the following structure

$$\begin{aligned} \Gamma ^\delta _{\,\,\,\epsilon \nu }=L^\delta _{\,\,\,\epsilon \nu }+K^\delta _{\,\,\,\epsilon \nu }+\lbrace ^\delta _{\,\,\,\epsilon \nu } \rbrace . \end{aligned}$$
(5)

The symbols \(L^\delta _{\,\,\,\epsilon \nu }\), \(K^\delta _{\,\,\,\epsilon \nu }\), and \(\lbrace ^\delta _{\,\,\,\epsilon \nu } \rbrace \) represent the disformation, contortion tensors, and Levi–Civita connection, respectively. These tensors may be mathematically represented as:

$$\begin{aligned} \lbrace ^\delta _{\,\,\,\epsilon \nu } \rbrace= & {} \frac{1}{2}g^{\delta \sigma }\left( \partial _\epsilon g_{\sigma \nu }+\partial _\nu g_{\sigma \epsilon }-\partial _\sigma g_{\epsilon \nu }\right) ,\nonumber \\ L^\delta _{\,\,\,\epsilon \nu }= & {} \frac{1}{2}Q^\delta _{\,\,\,\epsilon \nu }-Q_{(\epsilon \,\,\,\,\,\,\nu )}^{\,\,\,\,\,\,\delta },\nonumber \\ K^\delta _{\,\,\,\epsilon \nu }= & {} \frac{1}{2} T^\delta _{\,\,\,\epsilon \nu }+T_{(\epsilon \,\,\,\,\,\,\nu )}^{\,\,\,\,\,\,\delta }. \end{aligned}$$
(6)

The symbol \(T^\delta _{\,\,\,\epsilon \nu }\) represents the torsion tensor, which characterises the antisymmetric component of the affine connection as: \(T^\delta _{\,\,\,\epsilon \nu }=2\Gamma ^\lambda _{\,\,\,[\epsilon \nu ]}\). Furthermore, the nonmetricity tensor associated with the superpotential may be expressed as:

$$\begin{aligned} P^\alpha _{\,\,\,\,\epsilon \nu }=\frac{1}{4}\left[ -Q^\alpha _{\,\,\,\,\epsilon \nu }+2 Q_{(\epsilon \,\nu )}^\alpha +Q^\alpha g_{\epsilon \nu }-{\tilde{Q}}^\alpha g_{\epsilon \nu }-\delta ^\alpha _{(\epsilon }Q_{\nu )}\right] ,\nonumber \\ \end{aligned}$$
(7)

where

$$\begin{aligned} Q_{\alpha }\equiv Q_{\alpha \,\,\,\epsilon }^{\,\,\epsilon },\; {\tilde{Q}}_\alpha =Q^\epsilon _{\,\,\,\,\alpha \epsilon }, \end{aligned}$$
(8)

are two independent traces that aid in the establishment of the nonmetricity scalar term as

$$\begin{aligned} Q=-Q_{\alpha \epsilon \nu }\,P^{\alpha \epsilon \nu }. \end{aligned}$$
(9)

By taking the variation of the action (1) with respect to the metric tensor \(g^{\epsilon \nu }\), the system of governing field equations in f(Q)-gravity may be derived as

$$\begin{aligned}{} & {} \frac{2}{\sqrt{-g}}\bigtriangledown _\gamma \left( \sqrt{-g}\,f_Q\,P^\gamma _{\,\,\,\,\epsilon \nu }\right) +\frac{1}{2}g_{\epsilon \nu }f +f_Q\big (P_{\epsilon \gamma i}\,Q_\nu ^{\,\,\,\gamma i}\nonumber \\{} & {} \quad -2\,Q_{\gamma i \epsilon }\,P^{\gamma i}_{\,\,\,\nu }\big ) =- T^{\text {tot}}_{\epsilon \nu },~~ \end{aligned}$$
(10)

where \(f_Q=\frac{d f}{d Q}\) and \(T^{\text {tot}}_{\epsilon \nu }=T_{\epsilon \nu }+T^{\theta }_{\epsilon \nu }\).

By using Eq. (1), it becomes feasible to deduce an additional restriction on the connection as

$$\begin{aligned} \bigtriangledown _\epsilon \bigtriangledown _\nu \left( \sqrt{-g}\,f_Q\,P^\gamma _{\,\,\,\,\epsilon \nu }\right) =0. \end{aligned}$$
(11)

The restrictions of torsionlessness and curvaturelessness result in the affine connection being rendered as such

$$\begin{aligned} \Gamma ^\lambda _{\,\,\,\epsilon \nu }=\left( \frac{\partial x^\lambda }{\partial \xi ^\beta }\right) \partial _\epsilon \partial _\nu \xi ^\beta . \end{aligned}$$
(12)

Moreover, it is possible to choose a certain coordinate system, known as the coincident gauge, in order to do this: \(\Gamma ^\lambda _{\,\,\,\epsilon \nu }=0\). Then, the nonmetricity Eq. (4) reduces to

$$\begin{aligned} Q_{\lambda \epsilon \nu }=\partial _\lambda g_{\epsilon \nu }. \end{aligned}$$
(13)

The computation is simplified since the metric function is the only significant variable. However, with the exception of conventional General Relativity (GR) as discussed in the work of Koivisto [114], it can be shown that the action no longer maintains invariance with respect to diffeomorphism. In order to address this issue, it is possible to use the covariant formulation of f(Q) gravity. The covariant formulation may be used by first determining the affine connection in without the presence of gravity [115]. This is necessary since the affine connection described in Eq. (12) is only inertial.

The primary objective of this research is to investigate the properties of compact stars within the framework of f(Q) gravity theory, specifically in relation to gravitational decoupling. In order to facilitate our analysis, we make the assumption of the following line element as

$$\begin{aligned} ds^2=-e^{\Phi (r)}dt^2+e^{\mu (r)}dr^2+r^2d\theta ^2+r^2\text {sin}^2\theta \,d\phi ^2. \end{aligned}$$
(14)

The metric potentials \(\Phi (r)\) and \(\mu (r)\) are denoted as unknown functions that are dependent on the radial coordinate r. The determination of the expression for the nonmetricity scalar Q in the context of the spherically symmetric line element (14) is as follows:

$$\begin{aligned} Q=-\frac{2 e^{-\mu (r)} \left( 1+r \Phi ^\prime (r)\right) }{r^2}. \end{aligned}$$
(15)

In addition, it is worth noting that the stellar model in f(Q) gravity is characterised by the presence of ideal matter distributions inside its internal structure. Subsequently, the expression \(T_{\epsilon \nu }\) may be represented as:

$$\begin{aligned} T_{\epsilon \,\nu }=\left( \rho +p\right) u_{\epsilon }\,u_{\nu }+p\,g_{\epsilon \,\nu }. \end{aligned}$$
(16)

In the context of pure f(Q) gravity theory, the symbols \(\rho \) and p represent the energy density and fluid pressure, respectively. The fluid four-velocity vector is represented by the symbol \(u^{\nu }\), where \(u^{0} u_{0}=-1\). In this context, the components for \(T^\theta _{\epsilon \nu }\) are denoted as:

$$\begin{aligned} {[}T^\theta ]^0_0=-\rho ^{\theta },\quad [T^\theta ]^1_1=p^{\theta }_r, \quad [T^\theta ]^2_2=[T^\theta ]^3_3=p^{\theta }_t. \end{aligned}$$
(17)

It is important to note that we have made the assumption that \(\theta ^1_1\) is not equal to \(\theta ^2_2\). Subsequently, the introduction of the new source will induce anisotropy within the f(Q) gravity system. To derive the field equations corresponding to Eq. (10), we introduce the components of the total energy–momentum tensor (\(T^{\text {tot}}_{\epsilon \nu }\)) as

$$\begin{aligned} \rho ^{\text {tot}}= \rho +\alpha \,\rho ^{\theta },\quad P^{\text {tot}}_r=p+\alpha \,p^{\theta }_r,\quad P^{\text {tot}}_t=p+\alpha \,p^{\theta }_t. \nonumber \\ \end{aligned}$$
(18)

Consequently, in f(Q) gravity the independent components of the equation of motion (10) can be written as follows:

$$\begin{aligned} \rho ^{\text {tot}}= & {} -\frac{f(Q)}{2}+f_{Q}\Big [Q+\frac{1}{r^2}+\frac{1}{r\,e^{\mu }}(\mu ^\prime )+\Phi ^\prime \Big ], \end{aligned}$$
(19)
$$\begin{aligned} P^{\text {tot}}_r= & {} \frac{f(Q)}{2}-Q f_{Q}-\frac{f_{Q}}{r^2}, \end{aligned}$$
(20)
$$\begin{aligned} P^{\text {tot}}_t= & {} \frac{f(Q)}{2}-f_{Q}\Big [\frac{Q}{2}-\frac{1}{e^{\mu }} \Big \{\frac{\Phi ^{\prime \prime }}{2}+\Big (\frac{\Phi ^\prime }{4}-\frac{1}{2r}\Big ) \nonumber \\ {}{} & {} \hspace{0.5cm}\times (\mu ^\prime -\Phi ^\prime )\Big \}\Big ], \end{aligned}$$
(21)
$$\begin{aligned} 0= & {} \frac{Q^\prime \,\text {cot}\theta }{2}\,f_{QQ}, \end{aligned}$$
(22)

where \(f_{Q}(Q)\) is defined as \(f_{Q}(Q)=\frac{\partial f(Q)}{\partial Q}\). The total anisotropy is therefore expressed as

$$\begin{aligned} \Delta ^{\text {tot}}= & {} p^{\text {tot}}_t-p^{\text {tot}}_r= \Delta _{\theta },~~ \text {where},~\Delta _\theta = \alpha \,(p^{\theta }_t-p^{\theta }_r). \end{aligned}$$
(23)

It has been seen that the signature of decoupling constant \(\alpha \) affects the behavior of anisotropy in the system. At first, the functional form of f(Q) must be defined to express the explicit form of the equations of motion (19)–(21). In this context, Wang et al. [116] have shown that the exact Schwarzschild (anti-) de Sitter solution can be produced as the exterior solution of field equations satisfying the essential condition \(f_{QQ}=0\). So, the condition \(f_{QQ} =0\) is further required to obtain the functional form of f(Q) which is necessary to find the solution of self-gravitating compact star models and hence \( f_{QQ}=0\) yields

$$\begin{aligned} f(Q)= & {} \beta _2+\beta _1\,Q. \end{aligned}$$
(24)

The variables \(\beta _1\) and \(\beta _2\) represent constants in the given context. On substitution of Eqs. (15) and (24), the Eqs. (19)–(21) can be expressed as

$$\begin{aligned} \rho ^{\text {tot}}= & {} \frac{1}{2\,r^2} \Big [\frac{2}{e^{\mu }} \, \beta _1 \left( r\, \mu ^\prime -1\right) +2\, \beta _1-\beta _2\,r^2 \Big ], \end{aligned}$$
(25)
$$\begin{aligned} P^{\text {tot}}_r= & {} \frac{1}{2\,r^2} \Big [r^2\, \beta _2-2\, \beta _1+2\, e^{-\mu } \,\beta _1 \left( 1+r\, \Phi ^\prime \right) \Big ], \end{aligned}$$
(26)
$$\begin{aligned} P^{\text {tot}}_{t}= & {} \frac{1}{4\,r e^{\mu }} \Big [-(r\,\beta _1\,\Phi ^\prime +2\beta _1)\, \left( \mu ^\prime -\Phi ^\prime \right) +2\, r\, \Phi ^{\prime \prime }\,\beta _1 \nonumber \\ {}{} & {} +2\,\beta _2\, r\, e^{\mu }\Big ]. \end{aligned}$$
(27)

Based on the functional form of f(Q) as described in Eq. (24), a corresponding conservation equation may be derived in the context of f(Q) gravity [116, 117]

$$\begin{aligned} -\frac{\Phi ^\prime }{2}(\rho ^{\text {tot}}+P^{\text {tot}}_r)-(P^{\text {tot}}_r)^{\prime }+\frac{2}{r}( P^{\text {tot}}_{t}-P^{\text {tot}}_r)=0. \end{aligned}$$
(28)

It is to be noted that Eq. (28) is comparable to the Tolman–Oppenheimer–Volkoff (TOV) equation [118, 119] in classical general relativity. Let us now concentrate on the method to obtain the solution of field equations (25)–(27) beyond the f(Q) gravity theory. It is worth mentioning some important brief reviews of widely adopted techniques which are useful to get solution of the field equations in general relativity and modified gravity theory. In this connection, Newton et al. [120] have described some relations which are related to three straightforward techniques mainly and the metric potentials. The relations are as follows:

  1. 1.

    Ivanov [121] proposed a relation which is related to conformally flat geometry [122, 123] given by

    $$\begin{aligned} e^{\Phi (r)}={\hat{A}}_1^2 r^2\, \cosh ^2 \Bigg (\int \sqrt{\frac{e^{\mu (r)}}{r^2}}\,dr +{\hat{B}}_1\Bigg ), \end{aligned}$$
    (29)

    where the constants are \({\hat{A}}_1\) and \({\hat{B}}_1\).

  2. 2.

    The second relation [124,125,126,127] subject to a conformal killing vector is given as

    $$\begin{aligned} e^{\Phi (r)}={\hat{A}}_2^2r^2\, \exp \Bigg (-\frac{2k}{{\hat{B}}_2}\sqrt{\frac{e^{\mu (r)}}{r^2}}\, dr\Bigg )^2, \end{aligned}$$
    (30)

    where integration constants are \({\hat{A}}_2\) and \({\hat{B}}_2\).

  3. 3.

    Another relation popularly known as the Karmarkar condition [128] given by

    $$\begin{aligned} e^{\Phi (r)}=\Bigg ({\hat{A}}_3+{\hat{B}}_3 \int \sqrt{e^{\mu (r)}-1}\,dr\bigg )^2, \end{aligned}$$
    (31)

    where constants of integration are \({\hat{A}}_3\) and \({\hat{B}}_3\).

To solve the current system of equations in the f(Q) gravity regime, with reference to the above relations, we now build a new bridge equation based on the vanishing complexity factor condition that connects metric functions. To establish the relation, we first use Herrera’s concept of the complexity factor for a compact object [72] to calculate the complexity factor (\(Y^Q_{TF}\)) in the f(Q) gravity factor for the system (25)–(27) as

$$\begin{aligned} Y^Q_{TF}= & {} 8\pi (P^{\text {tot}}_r-P^{\text {tot}}_t)-\frac{4\pi }{2r^3} \int ^r_0 x^3 (\rho ^{\text {tot}})^{\prime } (x) dx. \end{aligned}$$
(32)

Substituting \(\rho ^{\text {tot}}\), \(P^{\text {tot}}_r\) and \(P^{\text {tot}}_t\) in the above equation, we get \(Y^Q_{TF}\) as

$$\begin{aligned} Y^Q_{TF}= & {} \frac{\beta _1\, \big [ \big \{2-r (\Phi ^\prime -\mu ^\prime ) \big \} \Phi ^\prime -2 r \Phi ^{\prime \prime } \big ]}{4\, r\,e^{\mu } }. \end{aligned}$$
(33)

Then employing the vanishing condition, i.e., \(Y^Q_{TF}=0\) and integrating we got the required relation between the metric potentials \(\Phi \) and \(\mu \) as

$$\begin{aligned} e^{\Phi (r)}=\Bigg (A_1\,\int r\, e^{\mu (r)/2} dr +B_1 \Bigg )^2, \end{aligned}$$
(34)

where \(A_1\) and \(B_1\) are denoted as the constants of integration.

It is worth noting that the requirement for the absence of the complexity factor in f(Q) gravity theory, as expressed in Eq. (34), is equivalent to the condition found in Einstein’s general relativity, as discussed by Contreras and Stuchlik [71]. In the preliminary phase, our primary aim is to get a precise analytical solution of the field Eqs. (25)–(27) that describe a compact stellar object within the framework of the f(Q) gravity theory. In the subsequent section, the full geometric deformation (CGD) method, a well recognised technique for achieving gravitational decoupling, will be used for the aforementioned objective.

Fig. 1
figure 1

This diagram shows the procedure for generating gravitational decoupling anisotropic solution in f(Q) gravity via zero complexity factor

Full size image

3 Anisotropic complexity free solution in f(Q) gravity using gravitational decoupling

The present section commences with the implementation of a comprehensive geometric deformation (CGD) technique that employs a specific transformation along the gravitational potentials as:

$$\begin{aligned} \Phi (r)\longrightarrow & {} H(r)+\alpha \, \eta (r), \end{aligned}$$
(35)
$$\begin{aligned} e^{-\mu (r)}\longrightarrow & {} W(r)+\alpha \, \Psi (r), \end{aligned}$$
(36)

where \(\eta (r)\) and \(\Psi (r)\) are the geometric deformation functions along the temporal and radial metric components, respectively. The CGD method allows us to specify \( \eta (r) \ne 0\) and \(\Psi (r)\ne 0\). This is demonstrated in the diagram (Fig. 1), where a solution beyond the f(Q) gravity theory is obtained from the new sector due to CGD. Additionally, the decoupled system (25)–(27) in f(Q)-gravity is split into two subsystems on the application of the CGD technique. The first subsystem is for \(T_{\epsilon \,\nu }\), and the other subsystem is governed by the extra source \(\theta _{\epsilon \,\nu }\). The system of field equations for the two subsystems follows as:

3.1 A set of field equations for pure f(Q) gravity

$$\begin{aligned} \rho= & {} \frac{2\beta _1-2\beta _1 W-2r\,W^{\prime } \beta _1-\beta _2 r^2 }{2r^2}, \end{aligned}$$
(37)
$$\begin{aligned} p= & {} \frac{2\beta _1 W-2\beta _1 +2 r\,H^{\prime } W \beta _1+\beta _2\,r^2}{2r^2}, \end{aligned}$$
(38)
$$\begin{aligned} p= & {} \frac{\beta _1 H^{\prime }\,W^{\prime } +\beta _1 W H^{\prime 2} + 2 \beta _1 W H^{\prime \prime } }{4} \nonumber \\{} & {} +\frac{\beta _1\, W\,H^{\prime }+\beta _1\,W^{\prime } +\beta _2\, r }{2 r}, \end{aligned}$$
(39)

and following the TOV equation (28) we get

$$\begin{aligned} -\frac{H^\prime }{2}(\rho +p)-\frac{dp}{dr}=0, \end{aligned}$$
(40)

which is an equivalent TOV equation for the subsystem (37)–(39).

This has a solution which can be obtained by the following spacetime

$$\begin{aligned} ds^2=-e^{H(r)}dt^2+\frac{dr^2}{W(r)}+r^2d\theta ^2+r^2\text {sin}^2\theta \,d\phi ^2. \end{aligned}$$
(41)

3.2 System of field equations for new source \(\theta _{\epsilon \nu }\)

$$\begin{aligned} \rho ^{\theta }= & {} -\frac{\beta _1 \Psi ^\prime }{r}- \frac{\beta _1 \Psi }{r^2}, \end{aligned}$$
(42)
$$\begin{aligned} p^{\theta }_r= & {} \frac{\beta _1\,\Psi \,\Phi ^{\prime } }{r}+\frac{\beta _1\,\Psi }{r^2}+\frac{\beta _1\,\eta ^{\prime }\,W}{r}, \end{aligned}$$
(43)
$$\begin{aligned} p^{\theta }_t= & {} \beta _1 \Big ( \frac{1}{2} \Psi \,\Phi ^{\prime \prime } +\frac{\Psi ^\prime }{2 r}+\frac{\Phi ^{\prime } \Psi }{2 r}+\frac{1}{4} \Phi ^{\prime } \, \Psi ^\prime +\frac{1}{4} \Psi \Phi ^{\prime 2} \Big )\nonumber \\{} & {} +\beta _1\Big [\frac{W}{4}\,\big (\beta _1\,\eta ^{{\prime }\,2}+2\,\eta ^{\prime \prime }+\frac{2\,\eta ^{\prime }}{r}+2\,\eta ^{\prime }\,H^{\prime }\big )+\frac{\eta ^{\prime }\,W^{\prime }}{4}\Big ].\nonumber \\ \end{aligned}$$
(44)

The following conservation equation is provided by the system of Eqs. (42)–(44):

$$\begin{aligned} -\frac{H^\prime }{2}(\rho ^{\theta }+p^{\theta }_r)+\frac{2}{r}( p^{\theta }_{t}-p^{\theta }_r)-(p^{\theta }_r)^{\prime }= \frac{\eta ^\prime }{2}(\rho ^{\theta }+p^{\theta }_r),\nonumber \\ \end{aligned}$$
(45)

which demonstrates that the energy is transferred between the sources.

Both systems of equations are needed to be solved under the condition (34). In order to solve the Eq. (34) we need to find metric potential \(\mu \). Hence, we must have known forms of W(r) and \(\Psi (r)\). The first isotropic system of field equations needs to be solved first, since the solution to the second system depends on the solution to the first system. To serve the purpose, we get the isotropy condition in the context of f(Q) gravity by subtracting Eqs. (38) and (39)

$$\begin{aligned} W (2 H'' r^2+H^{\prime 2} r^2-4-2 H' r)+ [4+r\,W' (2+ r\,H' )]=0.\nonumber \\ \end{aligned}$$
(46)

Interestingly, in the above result (46), the isotropic condition in f(Q) gravity is comparable to the isotropic condition in standard general relativity. This has a simple implication that there exists an isotropic solution in f(Q) gravity for any known isotropic solution in general relativity. Therefore, we have chosen a well-known perfect fluid solution corresponding to Vlasenko–Pronin space-time geometry [105] to ensure the integrability of the Eq. (34). The Vlasenko–Pronin space-time geometry given as

$$\begin{aligned} ds^2= & {} - \Big \{A \cos \big [\log \sqrt{1-Cr^2} \big ]+B \sin \big [\log \sqrt{1-Cr^2} \big ] \Big \}^2 dt^2 \nonumber \\{} & {} +(1-Cr^2)^{-2}dr^2+r^2(d\theta ^2+\text {sin}^2\theta \,d\phi ^2), \end{aligned}$$
(47)
$$\begin{aligned} \rho (r)= & {} -\frac{\beta _2}{2}-5 \beta _1 C^2 r^2+6 \beta _1 C, \end{aligned}$$
(48)
$$\begin{aligned} p(r)= & {} \frac{1}{2 \left( A \cos \big [\log \sqrt{1-Cr^2} \big ]+B \sin \big [\log \sqrt{1-Cr^2} \big ] \right) }\nonumber \\{} & {} \times \Big \{\sin \big [\log \sqrt{1-Cr^2} \big ] \times \Big (B \left( \beta _2+2 \beta _1 C^2 r^2-4 \beta _1 C\right) \nonumber \\{} & {} -4 A \beta _1 C \left( C r^2-1\right) \Big )+\cos \big [\log \sqrt{1-Cr^2} \big ]\nonumber \\{} & {} \times \Big (A \big (\beta _2 +2 \beta _1 C^2 r^2-4 \beta _1 C\big )+4 B \beta _1 C \left( C r^2-1\right) \Big )\Big \}^{-1}. \nonumber \\ \end{aligned}$$
(49)

For both systems, the mass function for the distribution of matter may be found using the formula

$$\begin{aligned} m_{Q}=\frac{1}{2} \int ^r_0 \rho (x)\, x^2 dx~\text {and}~m_{\theta }= \frac{1}{2}\,\int _0^r \rho ^\theta (x)\, x^2 dx. \end{aligned}$$
(50)

The symbols \(m_Q\) and \(m_{\theta }\) represent the mass function for the first and second systems, respectively. However, subsequently the effective mass should be determined as

$$\begin{aligned} m(r) = m_{Q}(r) + \alpha ~ m_{\theta } (r). \end{aligned}$$
(51)

The next step involves determining the deformation function \(\Psi (r)\) in order to integrate condition (37). In order to achieve this objective, we use the utilisation of mimicking of mass constraints in order to determine the deformation function \(\Psi (r)\).

3.3 Mimicking of mass constraints (\(m_{Q}=m_\theta \))

The mimic constraint is used to compute the deformation function in accordance with the mass function suggested by Contreras and Stuchlik [71]. The mass restrictions technique yields the below outcomes

$$\begin{aligned} r\beta _1 \Psi ' +\beta _1 \Psi +r^2 \left( \beta _1 C \left( 6-5 C r^2\right) -\frac{\beta _2}{2}\right) =0. \end{aligned}$$
(52)

Upon performing the integration of the aforementioned differential equation, the resulting solution for the function \(\Psi (r)\) is obtained as

$$\begin{aligned} \Psi (r)=\frac{r^2 \left( \beta _2+6 \beta _1 C \left( C r^2-2\right) \right) }{6 \beta _1}+\frac{F}{r}. \end{aligned}$$
(53)

The symbol F represents the arbitrary constant of integration, which is assumed to be zero for the whole of the analysis to prevent singularity in the centre. Regarding this matter, the revised expression for the metric function \(e^{\mu }\) is

$$\begin{aligned} e^{-\mu (r)}=\frac{\alpha r^2 \left( \beta _2+6 \beta _1 C \left( C r^2-2\right) \right) +6 \beta _1 \left( 1-C r^2\right) ^2}{6 \beta _1}.\nonumber \\ \end{aligned}$$
(54)

By substituting the deformed metric function \(\mu (r)\) from Eq. (54) into the condition of vanishing complexity factor (37), we get the generalised version of the metric function \(\Phi \) as

$$\begin{aligned} e^{\frac{\Phi (r)}{2}}= & {} - \frac{A_1}{4 C\sqrt{\alpha +1}}\Bigg \{2 \tanh ^{-1}\nonumber \\ {}{} & {} \left( \frac{2 \sqrt{\alpha +1} \beta _1 C \left( \sqrt{6 \beta _1} \Phi _1(r)-6 r^2 \sqrt{(\alpha +1) C^2}\right) }{12 (\alpha +1) \beta _1 C-\alpha \beta _2}\right) \nonumber \\{} & {} +\log \Big [\alpha ^2 \beta _2^2-288 (\alpha +1)^2 \beta _1^2 C^4 r^4 +288 (\alpha +1)^2 \beta _1^2 C^3 r^2\nonumber \\ {}{} & {} +24 (\alpha +1) \beta _1 C^2 \Big (6 \alpha \beta _1+2 \sqrt{6 \beta _1} r^2 \nonumber \\{} & {} \times \sqrt{(\alpha +1) C^2} \Phi _1(r)-\alpha \beta _2 r^2\Big ){-}24 \alpha (\alpha +1) \beta _1 \beta _2 C\Big ]\Bigg \}{+}B_1, \nonumber \\ \end{aligned}$$
(55)

where

$$\begin{aligned} \Phi _1(r)=\sqrt{\beta _1 \left( 6 (\alpha +1) C^2 r^4-12 (\alpha +1) C r^2+6\right) +\alpha \beta _2 r^2}. \end{aligned}$$

As a result, the deformation function \(\eta (r)\) may be expressed in terms of Eq. (38) as \(\eta (r)=\frac{1}{\alpha } \big [\Phi (r)-H(r) \big ]\). This equation provides the formulation of \(\eta (r)\) in the following form:

$$\begin{aligned} \eta (r)= & {} \frac{1}{\alpha }\Bigg [2 \ln \Bigg (- \frac{A_1}{4 C\sqrt{\alpha +1}}\Bigg \{2 \tanh ^{-1}\nonumber \\ {}{} & {} \left( \frac{2 \sqrt{\alpha +1} \beta _1 C \left( \sqrt{6 \beta _1} \Phi _1(r)-6 r^2 \sqrt{(\alpha +1) C^2}\right) }{12 (\alpha +1) \beta _1 C-\alpha \beta _2}\right) \nonumber \\{} & {} +\log \Big [\alpha ^2 \beta _2^2-288 (\alpha +1)^2 \beta _1^2 C^4 r^4 \nonumber \\ {}{} & {} +288 (\alpha +1)^2 \beta _1^2 C^3 r^2+24 (\alpha +1) \beta _1 C^2 \Big (6 \alpha \beta _1\nonumber \\{} & {} +2 \sqrt{6 \beta _1} r^2 \sqrt{(\alpha +1) C^2} \Phi _1(r)-\alpha \beta _2 r^2\Big )\nonumber \\ {}{} & {} -24 \alpha (\alpha +1) \beta _1 \beta _2 C\Big ]\Bigg \}+B_1\Bigg )\nonumber \\{} & {} -2 \log \Bigg \{A \cos \big [\log \sqrt{1-Cr^2} \big ] +B \sin \big [\log \sqrt{1-Cr^2} \big ]\Bigg \}\Bigg ].\nonumber \\ \end{aligned}$$
(56)

4 Matching condition in f(Q) gravity

It is noteworthy that the most appropriate exterior solution in the f(Q) gravity theory assuming the linear functional form of f(Q) (24) is the Schwarzschild (Anti-) de Sitter solution. The exterior Schwarzschild (Anti-) de Sitter geometry is expressed by

$$\begin{aligned} ds^2_+= & {} -\bigg (1-\frac{2M}{r}-{\Lambda \over 3}~r^2\bigg )\,dt^2+\frac{dr^2}{\bigg (1-\frac{2M}{r}-{\Lambda \over 3}~r^2\bigg )} \nonumber \\{} & {} +r^2 \Big (d\theta ^2 +\sin ^2\theta \,d\phi ^2 \Big ). \end{aligned}$$
(57)

In the given context, M represents the aggregate mass, whereas \(\Lambda \) signifies the cosmological constant.

The unknown constants of the solution may be determined by ensuring that the internal spacetime matches the outside Schwarzschild (Anti-) de Sitter spacetime at the boundary, denoted as \(r=R\), when the pressure becomes zero. The matching procedure is performed using Darmois-Israel boundary conditions [129, 130] in order to get the appropriate boundary conditions known as the first and second basic forms. The mathematical representations of the requirements are provided as

$$\begin{aligned} \bigg (1-\frac{2M}{r}-{\Lambda \over 3}~r^2\bigg )= & {} e^{\nu (R)}, \end{aligned}$$
(58)
$$\begin{aligned} \bigg (1-\frac{2M}{r}-{\Lambda \over 3}~r^2\bigg )= & {} e^{-\lambda (R)}, \end{aligned}$$
(59)
$$\begin{aligned} P_r(R)= & {} 0. \end{aligned}$$
(60)

The cosmological constant \(\Lambda \) is related to the constants \(\beta _1\) and \(\beta _2\) as in the form \(\beta _2= 2\Lambda \beta _1\). In the present stellar model, nonzero smaller values of \(\Lambda \) and \(\beta _2\) are taken into consideration for the rest of the study. Formulas for arbitrary constants are derived by using the boundary conditions (58)–(60).

5 Physical analysis and impact of decoupling constants on f(Q) gravity solution

In this section, we will investigate the physical properties of stellar systems and their ability to maintain equilibrium in f(Q) gravity under zero complexity background.

5.1 Effect of the decoupling parameter (\(\alpha \)) and f(Q) gravity parameter (\(\beta _1\)) on the density, pressure and anisotropy

It has been presented in Fig. 2. the graphical representations of the physical behavior of energy density (\(\rho ^{tot}\)), radial pressure (\(P_r^{\text {tot}}\)), tangential pressure (\(P_t^{\text {tot}}\)), and anisotropy (\(\Delta ^{\text {tot}}\)) in a stellar system with respect to radial distance for different values of \(\alpha \). The quantities \(\{\rho ^{\text {tot}}, P_r^{\text {tot}}, P_t^{\text {tot}}\}\) are positive and finite throughout the region, and they are maximum at the center. They decrease with radial distance, and the radial pressure vanishes at the surface (\(r=R\)).

The positive anisotropy, i.e., (\(P_t^{\text {tot}}>P_r^{\text {tot}}\)) demonstrated in Fig. 2 (bottom right panel) is an increasing function with respect to radial distance. This is significant because positive anisotropy maintains hydrostatic equilibrium, which enhances the stability of the stellar system. Table 1 provides numerical values for the central density, surface density, and central radial pressure. It is evident from an examination of Fig. 2 that increasing values of \(\alpha \) increase the values of \(\{\rho ^{\text {tot}}, P_r^{\text {tot}}, P_t^{\text {tot}}, \Delta ^{\text {tot}}\}\). Therefore, the impact of the new source \(T^\theta _{\epsilon \nu }\) is to generate more dense stellar objects.

Fig. 2
figure 2

The variation of total energy density \(\rho ^{\text {tot}}\), total radial pressure \(P_r^{\text {tot}}\), total tangential pressure \(P_t^{\text {tot}}\), and total anisotropy \(\Delta ^{\text {tot}}\) versus radial coordinate r for \(\beta _1 = 1.2~\text {km}^{-2}\), \(C = 0.0023\), \(\Lambda = 0.00085\), \(\beta _2 = 0.00203~\text {km}^{-2}\)

Full size image
Fig. 3
figure 3

The variation of energy density (top-left), radial pressure (top-right), tangential pressure (bottom-left) and anisotropy (bottom-right) versus radial coordinate r for different \(\beta _1\) with fixed \(\alpha = -0.06\), \(C = 0.0023\), \(\beta _2 = 0.00203~\text {km}^{-2}\)

Full size image

Now, we would like to study the impact of increasing values of \(\beta _1\) on the physical quantities \(\{\rho ^{\text {tot}}, P_r^{\text {tot}}, P_t^{\text {tot}}, \Delta ^{\text {tot}}\}\) as shown in Fig. 3. It can be seen that energy density is increasing in nature throughout the region of the anisotropic star with respect to the increasing values of \(\beta _1\). This indicates that the presence of the new source \(T^\theta _{ij}\) in f(Q) gravity produces stellar objects of higher densities. The radial pressure and tangential pressure have the same behavior as of energy density with respect to increasing values of \(\beta _1\). Figure 3 reveals that the anisotropy is convergent near the central region of the star and differs near the surface for increasing values of \(\beta _1\). So, with the effect of \(\beta _1\) anisotropy of the star behaves as a monotonically increasing function throughout the star.

Table 1 The numerical values pertaining to the physical parameters of the model
Full size table

5.2 Stability analysis via adiabatic index

We must now examine the stability of the anisotropic star configuration by studying the adiabatic index (\(\Gamma \)), which is defined by

$$\begin{aligned} \Gamma = \frac{\rho ^{\text {tot}}+P_r^{\text {tot}}}{P_r^{\text {tot}}}\frac{dP_r^{\text {tot}}}{d\rho ^{\text {tot}}}. \end{aligned}$$
(61)

In the Newtonian limit, the stability condition for an isotropic fluid is that the adiabatic index \(\Gamma \) must be greater than 4/3 [131, 132]. However, for an anisotropic stellar model the stability condition may be changed [133, 134] given as

$$\begin{aligned} \Gamma > \frac{4}{3}\left( 1 + \frac{\Delta ^{\text {tot}}}{r|(P_{r0}^{\text {tot}})|^{\prime }}+\frac{1}{4}\frac{\kappa \rho _0^{\text {tot}} P_{r0}^{\text {tot}}r}{|(P_{r0}^{\text {tot}})|^{\prime }} \right) . \end{aligned}$$
(62)

The symbol “prime” denotes the derivative with respect to the variable r and \(P_{r0}^{\text {tot}}\) is radial pressure at center. The anisotropic corrections and relativistic corrections are represented by the second and third term in Eq. (62). In an anisotropic star model, the role of positive anisotropy factor (\(\Delta ^{\text {tot}}\)) [131] is very significant in increasing the limit for \(\Gamma \) in the stability condition.

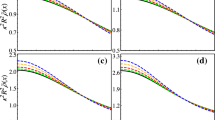
We have shown the variation of \(\Gamma \) with respect to radial distance for different values of \(\alpha \) in Fig. 4 (left panel). The central values of \(\Gamma \) for different \(\alpha \) have been listed in Table 1. It follows that \(\Gamma \), denoted as \(\Gamma _0\), is greater than 5 at center. Again, it shows an increasing nature with respect to radial distance for different values of \(\alpha \) and converges near the surface of the star. This is in confirmation with stable hydrostatic equilibrium as the anisotropic star model satisfies the stability condition given by Eq. (62). For fixed \(\alpha \) the nature of \(\Gamma \) remains independent of the values of \(\beta _1\) as it can be seen from Fig. 4 (right panel). So, the presence of new source in the background f(Q) has the effect on \(\Gamma \) and hence, is responsible for anisotropy as well as stability of the present stellar model.

Fig. 4
figure 4

Left panel: the variation of adiabatic index \(\Gamma \) versus radial coordinate r for different \(\alpha \) with fixed \(\beta _1 = 1.2~\text {km}^{-2}\), \(C = 0.0023\), \(\Lambda = 0.00085\), \(\beta _2 = 0.00203~\text {km}^{-2}\). Right panel: the variation of adiabatic index \(\Gamma \) versus radial coordinate r for different \(\beta \) with fixed \(\alpha =-0.06\), \(C = 0.0023\), \(\Lambda = 0.00085\), \(\beta _2 = 0.00203~\text {km}^{-2}\)

Full size image
Fig. 5
figure 5

The total mass variation and total mass gradient variation against the central density for \(\beta _1=1.2\), \(C = 0.0023\),\(\Lambda = 0.00085\), \(\beta _2 = 0.00203~\text {km}^{-2}\)

Full size image

5.3 Stability analysis via Harrison–Zel’dovich–Novikov criterion

A technique to find the constraints for stability of a stellar object under radial perturbations was developed by Chandrasekhar [135] which later simplified for polytropic equation of state \(P_r=K\epsilon ^{\Gamma }\) by Harrison et al. [136] and Zel’dovich–Novikov [137]. It turns out that the stellar configuration is stable under a small radial oscillation when the characteristic frequency is positive (\(\sigma ^2>0\)) only if we consider \(\Gamma >4/3\). Another interesting inference can be obtained from the mass-central density relation given by \(M(\rho _0) \propto \rho _0^{3(\Gamma - 4/3)/2}\) is that \(dM/d\rho _0 >0\), i.e., M has an increasing nature with respect to \(\rho _0\) only if \(\Gamma >4/3\). This is known as Harrison–Zel’dovich–Novikov criterion or the static stability criterion.

The static stability criterion can be analyzed with the help of following expressions for the physical quantities such as mass, central density and \(dM/d\rho ^{\text {tot}}_0\) given as

$$\begin{aligned} \hspace{-0.1cm}\rho ^{\text {tot}}_0= & {} 6 (\alpha +1) \beta _1 C-\frac{\alpha \beta _2}{2}, \end{aligned}$$
(63)
$$\begin{aligned} M= & {} \frac{1}{288 (\alpha +1) \beta _1^2} \Big [R^3 \Big (48 (\alpha +1) \beta _1 \rho ^{\text {tot}}_0-4 [\rho ^{\text {tot}}_0]^2 R^2 \nonumber \\{} & {} -4 \alpha \beta _2 \rho ^{\text {tot}}_0 R^2-\alpha ^2\beta ^2_2 R^2 \Big )\Big ], \end{aligned}$$
(64)
$$\begin{aligned} \frac{dM}{d\rho ^{\text {tot}}_0}= & {} \frac{12 (\alpha +1) \beta _1 R^3-2 \rho ^{\text {tot}}_0 R^5-\alpha \beta _2 R^5}{72 (\alpha +1) \beta _1^2}. \end{aligned}$$
(65)

Figure 5 shows that mass rises as the central density increases. The right panel of Fig. 5 demonstrates a clear positive and linear relationship between the gradient of the mass and the centre density. Hence, the present anisotropic star is stable under Harrison–Zel’dovich–Novikov criterion.

5.4 Energy exchange

In the completely deformed solution, the seed system and new generic system can be decoupled successfully only when there is an energy exchange between both sources [87]. This notion may be comprehended by the following elucidations: Given that the Einstein tensor \(G^{\{H,W\}}_{\epsilon \nu }\) associated with the line element (41) satisfies its corresponding Bianchi identity, it follows that the energy–momentum tensor \(T_{\epsilon \nu }\) is conserved within this particular spacetime geometry, as indicated by Eq. (40). This conservation can be explicitly expressed as

$$\begin{aligned} \bigtriangledown ^{\{H,W\}}_\epsilon \, T^{\epsilon }_ {\nu }=0. \end{aligned}$$
(66)

The symbol \(\bigtriangledown ^{\{H,W\}}\) denotes that the divergence mentioned above is computed with respect to the metric (44). It is observed that the expression

$$\begin{aligned} \bigtriangledown _\epsilon \, T^{\epsilon }_{ \nu } = \bigtriangledown ^{\{H,W\}}_\epsilon \, T^{\epsilon }_{\nu }-\frac{\alpha \,\eta '}{2} (T^0_0-T^1_1) \delta ^1_\nu , \end{aligned}$$
(67)

represents the calculation of the divergence on the left-hand side with respect to the deformed spacetime described by Eq. (14).

In the end, by taking into account the conditions (40), (44) and (66), the conservation equation Eq. (28) yields the following expression:

$$\begin{aligned} \bigtriangledown _\epsilon \, T^{\epsilon }_{ \nu } =-\frac{\alpha \, \eta '}{2} (T^0_0-T^1_1) \delta ^1_\nu . \end{aligned}$$
(68)

Additionally, we have

$$\begin{aligned} \bigtriangledown _\epsilon \, [T^\theta ]^{\epsilon }_{ \nu }= \frac{\alpha \, \eta '}{2} (T^0_0-T^1_1) \delta ^1_\nu . \end{aligned}$$
(69)

Subsequently, Ovalle et al. [138] and Contreras and Stuchlik [139] initiated a discussion on the crucial phenomena pertaining to the energy exchange between the sources denoted as \(T_{\epsilon \nu }\) and \(T^{\theta }_{\epsilon \nu }\). The energy transfer between the sources was represented as \( \Delta E\) and calculated using the equation

$$\begin{aligned} \Delta E=\frac{\eta ^\prime }{2} \big (p + \rho \big ). \end{aligned}$$
(70)

Given that p and \(\rho \) are positive, we may deduce from Eq. (70) that if \(\eta ^\prime >0\), it implies that \(\Delta E>0\). Consequently, Eq. (69) leads to the conclusion that \(\bigtriangledown _\epsilon \, [T^\theta ]^{\epsilon }_{ \nu }>0\). In the present scenario, the newly introduced source \({T^\theta }_{\epsilon \nu }\) is transferring energy to the surrounding environment, but the converse is seen when \(\eta ^\prime <0\).

The explicit expression for \(\Delta E\) is determined as

$$\begin{aligned} \Delta E(r)= & {} \frac{2}{\alpha } \Bigg [-A_1 \Bigg \{\Big [-1152 (\alpha +1)^2 \beta _1^2 C^4 r^3+576 (\alpha +1)^2 \beta _1^2 C^3 r+24 (\alpha +1) \beta _1 C^2 \Big (4 \sqrt{6} \sqrt{\beta _1} r \nonumber \\ {}{} & {} \times \sqrt{(\alpha +1) C^2} \sqrt{6 \beta _1 \left( (\alpha +1) C^2 r^4-2 (\alpha +1) C r^2+1\right) +\alpha \beta _2 r^2}+\Delta E_2(r)-2 \alpha \beta _2 r\Big )\Big ]\Big / \nonumber \\ {}{} & {} \times \Big [\alpha ^2 \beta _2^2-288 (\alpha +1)^2 \beta _1^2 C^4 r^4 +288 (\alpha +1)^2 \beta _1^2 C^3 r^2+24 (\alpha +1) \beta _1 C^2 \big (6 \alpha \beta _1+2 \sqrt{6} \nonumber \\ {}{} & {} \times \sqrt{6 \beta _1 \left( (\alpha +1) C^2 r^4-2 (\alpha +1) C r^2+1\right) +\alpha \beta _2 r^2} \sqrt{\beta _1} r^2 \sqrt{(\alpha +1) C^2}-\alpha \beta _2 r^2\big )-24 \alpha \nonumber \\ {}{} & {} \times (\alpha +1) \beta _1 \beta _2 C\Big ]+\Delta E_1(r)\Bigg \}\Bigg /\Bigg \{4 \sqrt{\alpha +1} C \Bigg (B_1-\frac{1}{4 \sqrt{\alpha +1} C}\Big [A_1 \Big (\log \Big \{\alpha ^2 \beta _2^2-288 \nonumber \\ {}{} & {} \times (\alpha +1)^2 \beta _1^2 C^4 r^4+288 (\alpha +1)^2 \beta _1^2 C^3 r^2+24 (\alpha +1) \beta _1 C^2 \big [6 \alpha \beta _1+2 \sqrt{6} \sqrt{\beta _1} r^2 \sqrt{(\alpha +1) C^2} \nonumber \\ {}{} & {} \times \sqrt{6 \beta _1 \left( (\alpha +1) C^2 r^4-2 (\alpha +1) C r^2+1\right) +\alpha \beta _2 r^2}-\alpha \beta _2 r^2\big ]-24 \alpha (\alpha +1) \beta _1 \beta _2 C\Big \} \nonumber \\ {}{} & {} +2 \tanh ^{-1}(\Delta E_3(r))\Big )\Big ]\Bigg )\Bigg \}-\Delta E_4(r)\Bigg ] \times \Delta E_5(r), \end{aligned}$$
(71)

where the expressions for \(\Delta E_1\), \(\Delta E_2\), \(\Delta E_3\), \(\Delta E_4\), and \(\Delta E_5\) are given in the Appendix.

Fig. 6
figure 6

Energy exchange between the fluid distributions with different values of \(\beta _1 = 0.8~\text {km}^{-2}\) (left panel) and \(\beta _1 = 1.2~\text {km}^{-2}\) (right panel) for fixed values of \(C = 0.0023\), \(\Lambda = 0.00085\), \(\beta _2 = 0.00203~\text {km}^{-2}\), \(A=-4\) and \(B=1\)

Full size image
Fig. 7
figure 7

Left panel: mass-radius curves w.r.t. different values of \(\alpha \) for \(\beta _1 = 1.2~\text {km}^{-2}\), \(C = 0.0023\), \(\rho _s = 7 \times 10^{14} g.cm^{-3}\), \(\Lambda = 0.00085\), \(\beta _2 = 0.00203~\text {km}^{-2}\). Right panel: mass-radius curves w.r.t. different values of \(\beta _1\) for \(\alpha =-0.10\), \(C = 0.0023\), \(\rho _s = 7 \times 10^{14} g.cm^{-3}\), \(\Lambda = 0.00085\), \(\beta _2 = 0.00203~\text {km}^{-2}\)

Full size image

The distribution of energy transfer (\(\Delta E\)) between the relativistic fluids is depicted in Fig. 6. The radial coordinate is plotted on the x-axis, while \(\Delta E\) for different values of \(\alpha \) are represented on the y-axis. The constant values \(A/B=-4\), \(C=0.0023~\text {km}^{-2}\), \(\beta _1=0.8~\text {km}^{-2}\), and \(\beta _2=0.00203\) are fixed for the Fig. 6. Similarly, for the right panel of Fig. 6, the constant values are \(A/B=-4\), \(C=0.0023~\text {km}^{-2}\), \(\beta _1=1.2~\text {km}^{-2}\), and \(\beta _2=0.00203\). The negative value of \(\Delta E\) may be detected from both panels Fig. 6. This observation indicates that the newly introduced source, denoted as \(T^\theta _{\epsilon \nu }\), consistently extracts energy from either the ideal fluid matter distribution or the surrounding environment. It was also observed that there is an increase in energy transfer when the values of \(\alpha \) and \(\beta _1\) grow.

Table 2 The numerical values pertaining to the expected radii of certain observable stars with \(\beta _1 = 1.2~\text {km}^{-2}\), \(C = 0.0023\), \(\rho _s = 7 \times 10^{14} g.cm^{-3}\), \(\Lambda = 0.00085\), \(\beta _2 = 0.00203~\text {km}^{-2}\)
Full size table
Table 3 The numerical values pertaining to the expected radii of certain observable stars with \(\alpha = -0.10\), \(C = 0.0023\), \(\rho _s = 7 \times 10^{14}\) g cm\(^{-3}\), \(\Lambda = 0.00085\), \(\beta _2 = 0.00203~\text {km}^{-2}\)
Full size table

6 The determination of the maximum mass and radii of observable compact objects via the use of M-R curves.

The mass–radius curves have been shown in Fig. 7 for fixed surface density (\(\rho _s = 7 \times 10^{14}~g.cm^{-3}\)) and different values of decoupling constant \(\alpha \) and model parameter \(\beta _1\) where positive values of \(\alpha \) have been dismissed for violating the Buchdahl limit. The M–R curves ensure that the present stellar model under f(Q) gravity is physically valid.

Based on the M-R curves we have calculated radii for observed masses of five different stellar objects such as SMC X-1 [140], 2 S 0921-630 [141], PSR J0437-4715 [142], Vela X-1 [140], PSR J1748-2021B [143]. From Tables 1 and 2 it can be seen that predicted radii of the stellar objects have larger values for increasing values of \(\alpha \) and \(\beta _1\). So, the present investigation indicates that increasing strength of f(Q) gravity with contribution of new source effectively reduce the compactness of a stellar object. In a research work [145], a model based on thermal X-ray emission constrained radii of a millisecond pulsar (assumed to have mass 1.4 \(M_{\odot }\)) to be 6.8–13.8 km with \(90\%\) confidence. In comparison, our model predicts radius of 7.74–10.63 km (see Table 2) for observed mass 1.44 \(M_{\odot }\) of 2 S 0921-630 where \(0.6<\beta _1<1.4\) and \(\alpha = -0.1\). It is to be noted that observed upper limit of radii can be achieved for \(\beta _1 >1.4\) for fixed value of \(\alpha \). Another X-ray analysis of PSR J0437-4715 by XMM-Newton [146] restricts the radii to be \(R>11.1\) km with \(3\sigma \) confidence. Now, this observed result is in well agreement with our model for case \(\beta _1=1.4~\text {km}^{-2}\) and \(\alpha = -0.1\) for PSR J0437-4715 (see Table 2).

We have explored some important results related to the maximum mass from the mass-radius curves (Table 3). For fixed \(\beta _1\) and increasing negative values of \(\alpha \), i.e., increasing contribution of the new source, we see from Fig. 7 (left panel) that the value of maximum mass increases significantly (energy exchange may be the possible physical reason) and reaches its highest value \(3.27~M_{\odot }\) for \(\alpha =0\), i.e., for pure f(Q) gravity. Again Fig. 7 (right panel) indicates that for a fixed \(\alpha \) the maximum mass of the stellar objects is directly proportional to the values of \(\beta _1\), i.e., the strength of nonmetricity scalar Q in f(Q) gravity. It reaches \(2.90~M_{\odot }\) for \(\beta _1=1.4~\text {km}^{-2}\) and \(\alpha = -0.1\) which matches the upper limit of \(M_{max} < 2.9 ~ M_{\odot }\) [147] satisfying causality and EOS of the low nuclear matter densities. Interestingly, the results \(2.90~M_{\odot }\) and \(3.27~M_{\odot }\) almost in agreement with the observed mass of the new pulsar PSR J1748-2021B in the globular cluster NGC 6440 [143, 144] which is expected to be a double neutron star considering purely relativistic effects. Its median pulsar, suspected to be a supermassive neutron star, have the observed mass \(2.74 ~M_{\odot }\), with upper limits \(2.95~ M_{\odot }\) with 1 \(\sigma \) uncertainty and \(3.15 ~M_{\odot }\) with 2 \(\sigma \) uncertainty. Another important study [148] constraints the range of maximum mass of neutron stars to be \(2.0 ~ M_{\odot }< M_{max} < 2.6 ~M_{\odot }\) which lies within the range of maximum masses as observed from the M-R curves obtained in our model.

7 Discussion and conclusion

In the recent work, we investigated anisotropic stars using a gravitational decoupling by means of complete geometric deformation approach in framework of symmetric teleparallel f(Q) gravity theory. The notion of complexity factor proposed by Herrera [72] has been used to derive a bridge equation between the metric functions related to the complete system. However, the deformation function \(\Psi (r)\) is determined by new technique given by Contreras [71], known as a mimicking of mass constraints. In this approach, the mass function of new source is equalised with mass profile of Vlasenko–Pronin space-time and determined the function \(\Psi (r)\). After finding the deformation function \(\Psi (r)\), the deformed temporal metric function is determined by bridge equation which is generated by null-complexity factor. In this way, we obtained a complete deformed space-time geometry in f(Q) gravity theory in the context of GD.

Subsequently, we have initially acquired the fundamental physical characteristics, such as density, pressure, and anisotropy, of the spherically symmetrical celestial object for different decoupling parameter \(\alpha \) and f(Q)-parameter \(\beta _1\), as shown in Figs. 2 and 3. The presented data provides evidence that the variables \(\rho ^{\text {tot}}\), \(P^{\text {tot}}_r\), and \(P^{\text {tot}}_t\) meet the fundamental criteria for a physically plausible stellar model. These criteria include: (i) maintaining positive and finite values within the specified region, (ii) attaining a maximum value at the central point and subsequently decreasing as a function of radial distance r, and (iii) satisfying the condition for the radial pressure to vanish at the surface, specifically when \(r=R\). In contrast, Fig. 3 (bottom right panel) demonstrates the presence of anisotropic property positivity, denoted as \(P^{\text {tot}}_t>P^{\text {tot}}_r\), which displays a rising trend as a function of radial distance r. This observation confirms the stability of the stellar system by ensuring the maintenance of hydrostatic equilibrium.

Many additional aspects of the physical characteristics have been covered in detail with the appropriate figures. However, we would like to highlight the major significance of the parameter \(\alpha \) and \(\beta _1\) in relation to Figs. 2 and 3, and it is noteworthy to note that the energy density changes to greater values across all regions for each increase of \(\alpha \) and \(\beta _1\). Observe additionally that, for all negative values of \(\alpha \) and positive values \(\beta _1\), the radial pressure is growing in the middle area, converging at the surface, and disappearing at 14 km. It can be shown in Table 1, the energy density of the model is maximum in absence of decoupling parameter \(\alpha \) which is \(\rho (0)=8.89271 \times 10^{14}~ g\,cm^{-3}\) and \(\rho (R)=5.55202 \times 10^{14}~ g\,cm^{-3}\), while for positive values of \(\beta _1\), the energy density is constrained to be no more than \(\rho (0) > 5.5 \times 10^{14}~ g\,cm^{-3}\) and \(\rho (R)> 3.5 \times 10^{14} ~g\,cm^{-3}\).

By using the adiabatic index and the Harrison–Zel’dovich–Novikov criteria, we have verified its relevance to stability analysis. It is worth mentioning that the stability requirement for an anisotropic stellar model, \(\Gamma > \frac{4}{3}\), is stated for an isotropic fluid in the Newtonian limit [131, 132]. Additionally, Hillebrandt [131] mentioned that a positive anisotropy factor (\(\Delta \)) play an essential role in raising the limit for \(\Gamma \) in the stability requirement for an anisotropic star model. We can see from Fig. 4 along with the Tables 1 and 2 that \(\Gamma >5\) is present at the center and that it is an increasing function with respect to the radial distance for various values of \(\alpha \) and \(\beta _1\). This characteristic demonstrates that our complexity-free anisotropic star model satisfies the stability criterion. However, the total mass (M) fluctuation with respect to the center density (\(\rho (0)\)) must be growing for a stable configuration of an anisotropic stellar object, as stated by the Harrison–Zel’dovich–Novikov criteria. Figure 5 shows that this condition is met, indicating that the current model of a complexity-free anisotropic star is in a stable state. Additionally, \(\alpha \) may be shown to play a part here, with a more pronounced impact at higher central densities.

In addition, we have examined the energy transfer across fluid distributions within the context of extended gravitational decoupling. The study has shown the presence of energy exchange variations over the star’s whole area can be seen in Fig. 6. The negative values are observed which imply that the new source is taking energy from its surrounding environment. The energy exchange \(\Delta E\) for various values of the coupling constant \(\beta _1\) and \(\alpha \) are calculated with with fixed values of \(C = 0.0023\), \(\Lambda = 0.00085\), \(\beta _2 = 0.00203\), \(A=-4\) and \(B=1\) as: \(|\Delta E|_{max} \approx 0.045~\text {km}^{-3}\) and \(|\Delta E|_{max} \approx 0.155~\text {km}^{-3}\) for \(\alpha =-0.02\) and \(\alpha =-0.06\), respectively with \(\beta _1=0.8~\text {km}^{-2} \) and \(|\Delta E|_{max} \approx 0.060~\text {km}^{-3}\) and \(|\Delta E|_{max} \approx 0.037~\text {km}^{-3}\) for \(\alpha =-0.02\) and \(\alpha =-0.06\), respectively with fixed \(\beta _1=1.2~\text {km}^{-2}\).

Moreover, the estimation of the maximum mass and radii of the discovered compact objects has been conducted using the \(M-R\) curves, as seen in Fig. 7, with varying values of \(\alpha \) and \(\beta _1\) along with fixed surface density \(\rho _s=7 \times 10^{14} ~g\,cm^{-3}\). The observation of Table 2 and Fig. 7 reveals that the current models predict the maximum mass and radii when \(\alpha =0\) i.e. in pure f(Q) gravity theory, while when \(\beta _1\) increases the object PSR J1748-2021B [143] of mass \(2.74\pm 0.21\) (which is beyond the 2\(M_{\odot }\)) is observed when \(\beta \ge 0.8\) and \(\alpha \le -0.15\). This implies that the mass and radii can be constrained through the decoupling parameter \(\alpha \) and f(Q) gravity parameter \(\beta _1\).