1 Introduction

Obtaining the exact solution for spherically symmetric perfect fluid solutions in general relativity and later on in modified gravity has been rigorously studied since the pioneering work by Schwarzschild. Schwarzschild obtained the first exterior solution [2] and interior solution [3] in 1916 considering that a uniform-density sphere corresponds to a fluid sphere. In the field of theoretical astrophysics, the quest for exact solutions of Einstein field equations for geometrically significant spacetime that satisfies physical constraints is momentous, as they enable the distribution of matter in the stellar interior to be modeled in terms of simple algebraic relations. However, the extreme nonlinearity of Einstein’s field equations makes it difficult to obtain exact solutions representing compact objects. Furthermore, a realistic solution must satisfy certain conditions for physical acceptability. Recently, the modeling of relativistic stars has progressed from the regime of toy models to much more sophisticated, realistic stellar structures.

Initially, it was assumed that the nature of spherically symmetric matter is similar to that of a perfect fluid, where radial pressure coincides with tangential pressure. But in 1922, Jeans’ [4] groundbreaking work changed this concept, suggesting that anisotropic pressure needs to be considered due to the extreme and unusual conditions reigning throughout the interior of compact objects. Later, Lemaître [5] examined the first anisotropic model entirely dependent on tangential pressure and constant density. In 1972, Ruderman [6] theoretically observed that, predominantly because of its high-density (\(>10^{15}\) g/cm\(^{3}\)) interior, the radial pressure may not be equal to the tangential pressure in massive stellar objects. Several studies have suggested various factors for the generation of anisotropy inside stellar objects, such as a very high magnetic field [7,8,9,10,11,12,13,14], pion condensation [15], phase transitions [16], relativistic nuclear interaction [17], crystallization of the core [18], and superfluid core [19,20,21]. Bowers and Liang [22] were the first to consider the anisotropic pressure on the equilibrium configuration of relativistic compact star-like neutron stars. The Bowers–Liang model is primarily based on the following assumptions: (i) the anisotropy should vanish quadratically at the origin, (ii) the anisotropy should depend nonlinearly on radial pressure, and (iii) the anisotropy is gravitationally induced [23]. Their study also claimed that anisotropy might have non-negligible effects on the surface redshift and equilibrium mass [24]. Since then, exact solutions of Einstein’s field equations (EFEs) considering anisotropic pressures have been studied extensively in several observations [25, 26]. Effects of anisotropy on macroscopic properties of a stellar structure, namely its mass, radius, moment of inertia, tidal deformability, and non-radial oscillation, can be found in [27,28,29,30,31,32,33,34,35,36,37,38].

Generally, with the increasing magnitude of the anisotropic parameter, the magnitudes of macroscopic properties are also observed to increase, and vice versa. Several authors have investigated anisotropic models; one of the remarkable works is by Lake [39], who obtained general algorithms for generating static anisotropic solutions. A complete review on anisotropic fluid spheres can be found in the work of Herrera and Santos [40]. Introducing charge into matter distribution, relativistic charged anisotropic super-dense star models were investigated by Maurya and Gupta [41]. Maurya et al. also studied the anisotropic analog of the Durgapal and Fuloria [42] perfect fluid solution [43]. Pandya et al. [44] observed a compact stellar model using the Finch–Skea metric and found it to be compatible with known data. Bhar and collaborators investigated an anisotropic solution in Tolman spacetime [45] and in \(2+ 1\) dimensions in Finch–Skea spacetime [46]. Some of the recent work on anisotropic compact stars and cosmological modeling can be found in  [47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63].

However, at this juncture we would specifically like to mention the seminal work by Herrera [64], where the result somehow supersedes all previous arguments to justify the presence of pressure anisotropy, and forces us to consider pressure anisotropy whenever relativistic fluids are involved. Indeed, as shown in [64], physical processes of the kind expected in stellar evolution will always tend to produce pressure anisotropy, even if the system is initially assumed to be isotropic. The important point to stress here is that any equilibrium configuration is the final stage of a dynamic regime, and there is no reason to think that the acquired anisotropy (no matter how small) during this dynamic process would disappear in the final equilibrium state; therefore, the resulting configuration, even if it initially had isotropic pressure, should in principle exhibit pressure anisotropy. In other words, we do not know of any real physical process expected in a collapse scenario which could “isotropize” the pressure anisotropy appearing during the evolution of a star. Accordingly, the presence of pressure anisotropy in compact objects is not an exception, but rather a rule.

In this paper, we study a compact stellar object with anisotropy inside the matter composition. A particular form of anisotropy is assumed to obtain an exact solution to Einstein field equations that represents the compact stellar structure. The remainder of the paper is organized as follows: Section 2 offers a brief discussion on Einstein field equations. The novel solution describing the anisotropic configuration is given in Sect. 3. Matching conditions at the boundary to obtain the model constants are discussed in Sect. 4. The physical analysis and stability analysis for the obtained model are described in Sects. 5 and 6, respectively. The compatibility of our model with other known compact objects is illustrated in Sect. 7. Finally, Sect. 8 presents concluding remarks on our obtained model.

2 Einstein field equations

The line element describing the spacetime of the interior of a spherically symmetric star with zero angular momentum in Schwarzschild coordinates \(x^0 = t\), \(x^1=r\), \(x^2 = \theta \), \(x^3 = \phi \) can be written as

$$\begin{aligned} \textrm{d}s_{-}^2 = -A_{0}^2(r)\textrm{d}t^2 + B_{0}^2(r)\textrm{d}r^2 + r^2(\textrm{d}\theta ^2 + \sin ^2\theta \textrm{d}\phi ^2), \end{aligned}$$
(1)

where \(A_{0}(r)\) and \(B_{0}(r)\) are the gravitational potentials, and these metric functions are functions of radial coordinate r only. For the matter distribution of the stellar interior to be anisotropic in nature, the energy-momentum tensor is described by that of a perfect fluid, considered in the form

$$\begin{aligned} T_{\alpha \beta } = (\rho + p_t)u_{\alpha } {u_\beta } - p_{t} g_{\alpha \beta } + (p_r - p_t)\chi _{\alpha } \chi _{\beta }, \end{aligned}$$
(2)

where \(\rho \) represents the energy density, \(p_r\) and \(p_t\) denote fluid pressure along the radial and transverse directions, respectively, \(u^\alpha \) is the 4-velocity of the fluid, and \(\chi ^\alpha \) is a unit space-like 4-vector along the radial direction. Since we considered the configuration of our system to be in a co-moving coordinate system, we have the following relations for the 4-vectors:

$$\begin{aligned} u^\alpha u_\alpha = 1;~ \chi ^\alpha \chi _\alpha =-1;~ u^\alpha \chi _\alpha =0. \end{aligned}$$
(3)

The spherically symmetric line element Eq. (1) then provides the Einstein field equations governing the evolution of the system as follows (we set \(G = c = 1\)):

$$\begin{aligned} 8\pi \rho= & {} \left[ \frac{1}{r^2}-\frac{1}{r^2 B_0^2}+\frac{2B_0'}{r B_0^3}\right] , \end{aligned}$$
(4)
$$\begin{aligned} 8\pi p_r= & {} \left[ -\frac{1}{r^2}+\frac{1}{B_0^2 r^2}+\frac{2A_0'}{r A_0B_0^2}\right] , \end{aligned}$$
(5)
$$\begin{aligned} 8\pi p_t= & {} \left[ \frac{A_0''}{A_0B_0^2} + \frac{A_0'}{rA_0B_0^2} - \frac{B_0'}{r B_0^3} - \frac{A_0'B_0'}{A_0 B_0^3}\right] , \end{aligned}$$
(6)

where “prime” in Eqs. (4)–(6) denotes differentiation with respect to radial coordinate r. Now, using Eqs. (5) and (6), we define the anisotropic parameter of the stellar system as [65]

$$\begin{aligned} \Delta (r)= & {} 8\pi (p_t-p_r) \nonumber \\= & {} \left[ \frac{A_0''}{A_0B_0^2} - \frac{A_0'}{r A_0B_0^2} - \frac{B_0'}{r B_0^3} - \frac{A_0'B_0'}{A_0B_0^3}- \frac{1}{r^2B_0^2} + \frac{1}{r^2}\right] . \nonumber \\ \end{aligned}$$
(7)

Anisotropy \(\Delta (r)\) is assumed to vanish at the interior of a stellar configuration, i.e. \(p_r(r) = p_t(r)\). The anisotropic force which is defined as \(2 \Delta /r\) will be repulsive or attractive in nature depending upon whether \(p_t>p_r\) or \(p_t<p_r\). For the matter distribution we have considered, repulsive force \(p_t > p_r\) supports the construction of compact objects other than isotropic fluid spheres [66]. Additionally, the mass contained within a radius r of the sphere is defined as

$$\begin{aligned} m(r)= 4\pi \int _0^r\omega ^2 \rho (\omega )\textrm{d}\omega . \end{aligned}$$
(8)

3 New analytical solution for the model

The system of field equations Eqs. (4)–(6) consists of three equations and five unknowns (\(\rho ,~ p_r,~ p_t,~ A_0,~ B_0\)), so to find exact solutions, any two of them can be freely chosen. We are motivated to investigate the metric potential in this form considering it as a \(g_{rr}\) metric, and given by

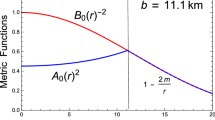
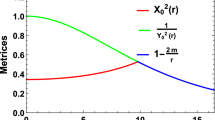
$$\begin{aligned} B_0^2 (r) = \frac{1-2 a C r^2}{1 + a C r^2}, \end{aligned}$$
(9)

where a is positive and C is assumed to be negative. Clearly, the metric is finite, continuous, and well defined within the stellar structure. This metric potential was used earlier by [67] to model a compact stellar object in isotropic pressure conditions. Interestingly, we are using the same potential for an anisotropic stellar structure in this paper. \(B_0^2 (r =0)=1\) depicts the finite nature and the non-singularity of the metric potential at the center of the stellar configuration. Also, \(\left( B_0^2(r)\right) '_{r = 0}= 0\) represents the regularity of metric potentials at the center. With this choice of \(B_0(r)\), Eq. (7) then reduces to

$$\begin{aligned}{} & {} \Delta (r) = \frac{r \left[ a C r \left( -r \left( 2 a C r^2+1\right) A_0''(r)+2 \left( a C r^2+2\right) A_0'(r)+6 a C r A_0(r)\right) +A_0''(r)\right] -A_0'(r)}{r A_0(r) \left( 1-2 a C r^2\right) ^2}. \end{aligned}$$
(10)

On rearranging Eq. (10), we get

$$\begin{aligned}{} & {} \frac{A_0''(r)}{A_0(r)}+\frac{\left[ 2 a C r^2(2+ a C r^2)-1 \right] A_0'(r)}{\left[ r - a C r^3 (1 + 2 a C r^2)\right] A_0(r)}\nonumber \\{} & {} \quad =\frac{r \Delta (r) (1 -2 a C r^2)^2 - 6 a^2 C^2 r^3}{\left[ r - a C r^3 (1 + 2 a C r^2)\right] }. \end{aligned}$$
(11)

Now, Eq. (11) can be solved for \(A_0(r)\) if \(\Delta (r)\) is specified in a particular form. The anisotropy factor needs to be taken in such a way that regularity at the center is satisfied and thefactor becomes a monotonically increasing function of radial coordinate \(`r'\) [66]. The increasing trend of anisotropy generally yields a well-behaved solution. We are considering anisotropy in polynomial form such that regularity and a monotonically increasing condition are satisfied, and at the same time Eq. (11) can be easily integrable.

Thus, we impose the second condition by assuming that the component \(g_{tt}\) has no contribution to the anisotropy parameter, so

$$\begin{aligned} \Delta (r)=\frac{ 6 a^2 C^2 r^2}{ \left( 1-2 a C r^2\right) ^2}. \end{aligned}$$
(12)

The above choice for anisotropy is physically reasonable, as at the center (\(r=0\)), anisotropy vanishes as expected. Also, \(\frac{\textrm{d}\Delta (r)}{\textrm{d}r}\) is positive throughout the stellar structure, as r is positive, which makes \(\Delta (r)\) a monotonically increasing function.

Now this choice of anisotropy provides a solution to Eq. (11) in closed form. Substituting Eq. (12) in Eq. (11), we obtain

$$\begin{aligned} \frac{A_0''(r)}{A_0(r)}+\frac{\left[ 2 a C r^2(2+ a C r^2)-1 \right] A_0'(r)}{\left[ r - a C r^3 (1 + 2 a C r^2)\right] A_0(r)}=0. \end{aligned}$$
(13)

We obtain a simple solution of Eq. (13) in the form

$$\begin{aligned}{} & {} A_0(r)\nonumber \\{} & {} \quad = \frac{D_1 \!\left( \!2 \sqrt{a C r^2\!+\!1} \sqrt{1\!-\!2 a C r^2}\!+\!3 \sqrt{2} \sin ^{-1}\!\left( \!\sqrt{\frac{2}{3}} \sqrt{a C r^2\!+\!1}\right) \!\!\right) }{4 a C}\!+\!D_2,\nonumber \\ \end{aligned}$$
(14)

where \(D_1\) and \(D_2\) are integration constants which will be obtained from the boundary conditions. With the choices of the metric potentials, the matter density, radial pressure, transverse pressure, and mass function are now obtained as

$$\begin{aligned} 8\pi \rho= & {} \frac{3 a C\left( 2 a C r^2-3\right) }{\left( 1-2 a C r^2\right) ^2}, \end{aligned}$$
(15)
$$\begin{aligned} 8\pi p_r= & {} -\frac{a C }{\left( 1-2 a C r^2\right) ^{3/2} \sqrt{a C r^2+1} \left( 2 D_1 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2}+3 \sqrt{2} D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) +4 a C D_2 \right) } \nonumber \\{} & {} \times \Bigg [ 14 D_1 \left( a C r^2 + 1\right) \left( 2 a C r^2-1\right) -9 D_1 \sqrt{2-4 a C r^2} \sqrt{a C r^2+1} \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) \nonumber \\{} & {} - 12 a C D_2 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2} \Bigg ], \end{aligned}$$
(16)
$$\begin{aligned} 8\pi p_t= & {} \frac{a C}{\left( 1-2 a C r^2\right) ^{5/2} \sqrt{a C r^2+1} \left( 2 D_1 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2}+3 \sqrt{2} D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) +4 a C D_2\right) } \nonumber \\{} & {} \times \Bigg [ 2 D_1 \left( a C r^2+1\right) \left( 2 a C r^2-1\right) \left( 8 a C r^2-7\right) +9 D_1 \sqrt{a C r^2+1} \sqrt{2-4 a C r^2} \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) \nonumber \\{} & {} + 12 a C D_2 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2} \Bigg ], \end{aligned}$$
(17)
$$\begin{aligned} m(r)= & {} \frac{(3 a C r^3)}{(-2 + 4 a C r^2)}. \end{aligned}$$
(18)

4 Junction condition for the obtained solution

In general relativity, the Jebsen–Birkhoff theorem states that the Schwarzschild solution is the unique spherically symmetric solution of the vacuum Einstein field equations. In that case, a spherically symmetric gravitational field in empty space outside a spherical star must be static and asymptotically flat. Therefore, the exterior spacetime for a non-radiating star can be described by the Schwarzschild metric, and given as

$$\begin{aligned} \textrm{d}s^2= & {} -\Big (1-\frac{2m}{r}\Big )\textrm{d}t^2+\Big (1-\frac{2m}{r}\Big )^{-1}\textrm{d}r^2\nonumber \\{} & {} + r^2(\textrm{d}\theta ^2+\sin ^2\theta \textrm{d}\phi ^2), \end{aligned}$$
(19)

where \(r>2m\), m is the stellar mass. Theoretically, the boundary conditions help to obtain the numerical values for the model parameters. Now, the junction conditions are essentially the continuity of the first and second fundamental forms (the intrinsic metric and extrinsic curvature) across the non-null boundary surface in the spacetime [68, 69].

Continuity of the first fundamental form at the boundary allows the matching of the interior solution to the vacuum exterior Schwarzschild solution at the boundary, provided the mass remains the same as above [70]. This continuity of the metric across the boundary leads to

$$\begin{aligned} A_0^2(b)=\Big (1-\frac{2m}{b}\Big )~~~~\text{ and }~~~~B_0^2(b)=\Big (1-\frac{2m}{b}\Big )^{-1}. \end{aligned}$$
(20)

Moreover, the continuity of the second fundamental form at the boundary indicates that the radial pressure drops to zero at a finite value of r, known as the radius of the star, and so from the condition \(p_r(r=b)=0\), one can easily find the radius of the star. Thus, from both the aforementioned boundary conditions for the spacetime and curvature, the model constants are determined in terms of the mass and radius of the star as

$$\begin{aligned} a C= & {} \frac{2 m}{b^2 (4 m-3 b)},\nonumber \\ D_1= & {} \frac{m \sqrt{\frac{b-2 m}{3 b-4 m}} \sqrt{1-\frac{2 m}{b}}}{b^2 \sqrt{\frac{b}{3 b-4 m}} (b-2 m)} \nonumber \\ D_2= & {} \frac{\sqrt{1-\frac{2 m}{b}} \left( 14 b \sqrt{b-2 m}-3 m \sqrt{8-\frac{6 b}{m}} \sqrt{3 b-4 m} \sqrt{-\frac{b}{m}} \sin ^{-1}\left( \frac{\sqrt{b-2 m}}{\sqrt{\frac{3 b}{2}-2 m}}\right) \right) }{8 b \sqrt{b-2 m}}. \end{aligned}$$
(21)

5 Analysis of the physical features of the model

5.1 Regularity of the metric

For our model, the gravitational potentials satisfy \(A^2_0(0)=\left( \frac{D_1 \left( 2 +3 \sqrt{2} \sin ^{-1}\left( \sqrt{\frac{2}{3}}\right) \right) }{4 a C}+D_2\right) ^2=constant\), \(B^2_0(0)=1\), i.e. finite at the center (\(r=0\)). Also, we have \((A^2_0(r))'_{r=0}=(B^2_0(r))'_{r=0}=0\), indicating the regularity of the metric at the center and the well-behaved nature throughout the stellar interior.

A physically acceptable model should comply with the regularity of matter variables along with that of the metric potentials at both the center and stellar interior. The density \(\rho \), radial pressure \(p_r\), and tangential pressure \(p_t\) should be positive inside the star, and \(\rho (0)\), \(p_r(0)\), and \(p_t(0)\) should be finite at the center. It is evident from Figs. 2 and 3 that our model satisfies the regularity of matter variables. It shows that the density decreases from its maximum value at the center towards its boundary. Moreover, the central density seems to be increased for the higher value of the model parameter a.

Fig. 1
figure 1

Metric potentials \(A_0^2(r)\) and \(B_0^2(r)\)

Full size image
Fig. 2
figure 2

Density profile

Full size image

The radial and tangential pressures also radially decrease outward to its boundary from its maximum value at the center. The radial pressure drops to zero at the boundary, but the tangential pressure remains nonzero at the boundary. The central density, central radial pressure, and central tangential pressure in this case are given as

$$\begin{aligned} \rho (0)= & {} -9 a C,\\ p_r(0)= & {} p_t(0) = \frac{a C \left[ 14 D_1 + 9 \sqrt{2} D_1 sin^{-1} \sqrt{\frac{2}{3}} + 12 a C D_2 \right] }{2 D_1 + 3 \sqrt{2} D_1 sin^{-1} \sqrt{\frac{2}{3}}+ 4 a C D_2}. \end{aligned}$$

Since aC is a negative quantity, the central density is always positive.

The key feature of the model is the similarity of \(p_r(0)\) and \(p_t(0)\), i.e. the absence of anisotropy at the center. However, the anisotropy increases within the configuration, as shown in Fig. 4, indicating that the direction of anisotropic force is outward. Theoretically, it proves the existence of a repulsive force which interpolates more compact objects using anisotropic force than using isotropic force [71].

Using the Zeldovich condition for the density and pressure of a stable configuration, we have \(\frac{p_r}{\rho }\le 1\) at the center, i.e. \(\frac{D_1}{D_2}\le \frac{-a C}{1.44066}\).

Fig. 3
figure 3

Radial pressure and transverse pressure

Full size image

5.2 Gradient

Any model is considered to be a viable model of an anisotropic compact star if the energy density \(\rho \) and pressures \((p_r,~p_t)\) are greatest at the center and decrease monotonically towards the surface of the star, i.e. \(\left( \frac{\textrm{d}\rho }{\textrm{d}r}\right) _{r=0}=0=\left( \frac{\textrm{d}p}{\textrm{d}r} \right) _{r=0}\) and \(\left( \frac{d^2\rho }{\textrm{d}r^2}\right) _{r=0}<0\), \(\left( \frac{d^2 p}{\textrm{d}r^2}\right) _{r=0}<0\) such that the gradients are negative within \(0~<r~<~b\), b being the star’s radius. Here, the gradient of energy density, radial pressure, and tangential pressure are respectively obtained as

$$\begin{aligned} \frac{\textrm{d}\rho }{\textrm{d}r}= & {} \frac{12 a^2 C^2 r \left( 5-2 a C r^2\right) }{\left( 2 a C r^2-1\right) ^3} \nonumber \\ \frac{\textrm{d}p_r}{\textrm{d}r}= & {} - \frac{8 a^2 C^2 r}{\left( 1-2 a C r^2\right) ^{5/2} \sqrt{a C r^2+1} \left( 2 D_1 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2}+3 \sqrt{2} D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) +4 a C D_2\right) ^2} \nonumber \\{} & {} \times \Bigg [48 a^3 C^3 D_1 D_2 r^4+4 a^2 C^2 \left( 7 D_1^2 r^4 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2}-6 D_2^2 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1}+12 D_1 D_2 r^2\right) \nonumber \\{} & {} - 8 D_1^2 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1} +2 a C D_1\left( D_1 r^2 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1}-18 D_2\right) \nonumber \\{} & {} + 9 D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) \Bigg (\sqrt{2} D_1 \left( 2 a C r^2-1\right) \left( 2 a C r^2+3\right) \nonumber \\{} & {} - 3 D_1 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1} \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) -4 a C D_2 \sqrt{a C r^2+1} \sqrt{2-4 a C r^2}\Bigg )\Bigg ] \nonumber \\ \frac{\textrm{d}p_t}{\textrm{d}r}= & {} \frac{8 a^2 C^2 r}{\left( 1-2 a C r^2\right) ^{7/2} \sqrt{a C r^2+1} \left( 2 D_1 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2}+3 \sqrt{2} D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) +4 a C D_2\right) ^2} \nonumber \\{} & {} \times \Bigg [ 2 \Bigg (8 a^3 C^3 D_1 r^4 \left( 2 D_1 r^2 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1}-3 D_2\right) -24 a^2 C^2 \Big (D_1^2 r^4 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2} \nonumber \\{} & {} - D_2^2 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1} +2 D_1 D_2 r^2\Big )+7 D_1^2 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2} \nonumber \\{} & {} - 6 a C D_1 \left( D_1 r^2 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1}-5 D_2\right) \nonumber \\{} & {} +9 D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) \Big (\sqrt{2} (-D_1) \left( 2 a C r^2-1\right) \left( 2 a C r^2+5\right) \nonumber \\{} & {} +6 D_1 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2} \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) +8 a C D_2 \sqrt{a C r^2+1} \sqrt{2-4 a C r^2}\Bigg ]. \end{aligned}$$
(22)
Fig. 4
figure 4

Variation of anisotropy \(\Delta \)

Full size image
Fig. 5
figure 5

Gradient of pressures and density

Full size image

The gradients of density, radial pressure, and tangential pressure are negative inside the stellar body, as shown graphically in Fig. 5. For our model, gradients of density and radial pressure are shown to be negative throughout the structure. However, the gradient of transverse pressure is positive up to 7.45 km and then eventually becomes negative.

5.3 Energy condition

A physically stable stellar composition must satisfy some energy conditions throughout the interior. Since the equation of state in any stellar interior is still an unexplored arena, the energy conditions of Einstein gravity (classical general relativity) are designed to decode as much information as possible from classical general relativity without the administration of a particular equation of state for the stress-energy [72]. Even if the information on the constituents that portray this material substance inside the compact structure is known, it could be extremely intricate to precisely depict the state of the stress-energy tensor [73]. Basically, the general relativity framework allows one to describe energy conditions as the local inequalities that process a relation between energy density \(\rho \) and pressures \((p_r,~p_t)\) with certain constraints. Though there are various ways to calculate energy conditions, the focus mainly revolves around the null energy condition (NEC), weak energy condition (WEC), strong energy condition (SEC), and dominant energy condition (DEC), defined as

$$\begin{aligned} \text {NEC}_r&:&\rho (r) + p_r(r)\ge 0,~~ NEC_t: \rho (r) + p_t(r)\ge 0,\nonumber \\ \text {WEC}_r&:&\rho (r)\ge 0,~~ \rho (r) + p_r(r)\ge 0,\nonumber \\ \text {WEC}_t&:&\rho (r)\ge 0,~~ \rho (r) + p_t(r)\ge 0,\nonumber \\ \text {DEC}_r&:&\rho (r) - |p_r(r)|\ge 0,~~ DEC_t: \rho (r) - |p_t(r)|\ge 0,\nonumber \\ \text {SEC}&:&\rho (r) + p_r(r) + 2p_t(r)\ge 0. \end{aligned}$$
(23)

All these energy conditions are satisfied simultaneously by the solutions presented herein, as shown graphically in Fig. 6. However, positive density and pressures lead to a positive SEC, so we have graphically examined the trace energy condition (TEC:  \(\rho - p_r - 2 p_t \ge 0\)), and it is found to be satisfied.

Now, to obtain the bounds on the model parameters, let us check the nature of the SEC at the center, such as

$$\begin{aligned}{} & {} 0 \le SEC|_{r =0} \nonumber \\{} & {} \quad \implies 0 \le \frac{2 a C \left( 12 a C D_2+14 D_1+9 \sqrt{2} D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}}\right) \right) }{4 a C D_2+2 D_1+3 \sqrt{2} D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}}\right) }\nonumber \\ {}{} & {} \qquad -\frac{a C \left( -12 a C D_2-14 D_1-9 \sqrt{2} D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}}\right) \right) }{4 a C D_2+2 D_1+3 \sqrt{2} D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}}\right) }-9 a C \nonumber \\{} & {} \quad \implies \frac{- a C}{1.54982} \le \frac{D_1}{D_2}. \end{aligned}$$
(24)
Fig. 6
figure 6

Different energy conditions plotted against radial coordinate r

Full size image

6 Stability analysis

6.1 Stability under three forces

The stability of any star in static equilibrium is checked under three forces, namely gravitational force, hydrostatic force, and anisotropic force. This equation, suggested by Tolman, Oppenheimer, and Volkoff, is known as the TOV equation [74, 75], and it states that the resultant forces must be zero throughout the star,

$$\begin{aligned} F_g+F_h+F_a=0. \end{aligned}$$
(25)

The TOV equation defines the internal structure of a spherically symmetric compact stellar body, and it is expressed in the presence of anisotropy as

$$\begin{aligned} -\frac{M_G}{r}(\rho +p_r)\frac{A_0(r)}{B_0(r)}-\frac{\textrm{d}p_r}{\textrm{d}r}+\frac{2}{r}(p_t-p_r)=0, \end{aligned}$$
(26)

where \(M_G(r)\) is the effective gravitational mass and can be derived with the help of the Tolman–Whittaker mass formula given as

$$\begin{aligned} M_G(r) = \frac{rB_0(r)A'_0(r)}{A_0(r)^2}. \end{aligned}$$
(27)

Using the expression of \(M_G(r)\) in Eq. (27), we obtain the expression as

$$\begin{aligned} -\frac{A'_0(r)}{A_0(r)}(\rho +p_r)-\frac{\textrm{d}p_r}{\textrm{d}r}+\frac{2}{r}(p_t-p_r)=0. \end{aligned}$$
(28)

Thus, equivalently, gravitational force, hydrostatic force, and anisotropic force can be represented respectively as

$$\begin{aligned} F_g= & {} -\frac{A'_0(r)}{A_0(r)}(\rho +p_r), \end{aligned}$$
(29)
$$\begin{aligned} F_h= & {} -\frac{\textrm{d}p_r}{\textrm{d}r}, \end{aligned}$$
(30)
$$\begin{aligned} F_a= & {} \frac{2}{r}(p_t-p_r). \end{aligned}$$
(31)

Figure 7 depicts the nature of these three forces.

6.2 Herrera cracking method

Another approach for investigating potentially unstable anisotropic configurations is by checking the overturning or the cracking of the model. The general idea is that at both sides of the cracking point, the fluid elements are accelerated with respect to each other. The cracking method is necessary to describe the behavior of a fluid distribution just after its departure from equilibrium [76].

This concept of cracking refers to the tendency of the configuration only to split (or to compress) at a particular point within the distribution but not to collapse or to expand. For self-gravitating compact objects, the concept of cracking for anisotropic matter distribution was first studied by Herrera [77]. This condition is used to determine the stability of a configuration of anisotropic fluid. The Herrera condition suggests that for any stellar model to be physically acceptable, both sound speeds (radial and transverse) need to satisfy causality conditions, i.e. \(v_{r}^2 \le 1\) and \( v_{t}^2 \le 1\) (taking \(c = 1\) and \(v = \frac{\textrm{d}p}{\textrm{d}\rho }\)).

Now, the radial and transverse velocity of sound for the model are given as

$$\begin{aligned} \frac{\textrm{d}p_r}{\textrm{d}\rho }= & {} \frac{-2 \left( 2 a C r^2-1\right) ^3}{3 \left( 1-2 a C r^2\right) ^{5/2} \left( 5-2 a C r^2\right) \sqrt{a C r^2+1} \left( 2 D_1 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2}+3 \sqrt{2} D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) +4 a C D_2\right) ^2} \nonumber \\{} & {} \times \Bigg [ 48 a^3 C^3 D_1 D_2 r^4+4 a^2 C^2 \left( 7 D_1^2 r^4 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2}-6 D_2^2 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1}+12 D_1 D_2 r^2\right) \nonumber \\{} & {} - 8 D_1^2 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1}+2 a C D_1 \left( D_1 r^2 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1}-18 D_2\right) \nonumber \\{} & {} + 9 D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) \Big (\sqrt{2} D_1 \left( 2 a C r^2-1\right) \left( 2 a C r^2+3\right) -3 D_1 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1} \nonumber \\{} & {} \times \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) -4 a C D_2 \sqrt{a C r^2+1} \sqrt{2-4 a C r^2}\Big )\Bigg ], \nonumber \\ \frac{\textrm{d}p_t}{\textrm{d}\rho }= & {} \frac{2 \left( 2 a C r^2-1\right) ^3}{3 \left( 1-2 a C r^2\right) ^{5/2} \left( 5-2 a C r^2\right) \sqrt{a C r^2+1} \left( 2 D_1 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2}+3 \sqrt{2} D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) +4 a C D_2\right) ^2} \nonumber \\{} & {} \times \Bigg [ 16 a^3 C^3 D_1 r^4 \left( 2 D_1 r^2 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1}-3 D_2\right) -48 a^2 C^2 \Big (D_1^2 r^4 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2} \nonumber \\{} & {} - D_2^2 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1}+2 D_1 D_2 r^2\Big )+14 D_1^2 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2}\nonumber \\{} & {} -12 a C D_1 \Big (D_1 r^2 \sqrt{1-2 a C r^2} \sqrt{a C r^2+1} - 5 D_2 \Big )+9 D_1 \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) \Bigg ( 8 a C D_2 \sqrt{a C r^2+1} \sqrt{2-4 a C r^2}\nonumber \\{} & {} -\sqrt{2} D_1 \left( 2 a C r^2-1\right) \left( 2 a C r^2+5\right) + 6 D_1 \sqrt{a C r^2+1} \sqrt{1-2 a C r^2} \sin ^{-1}\left( \sqrt{\frac{2}{3}} \sqrt{a C r^2+1}\right) \Bigg )\Bigg ]. \end{aligned}$$
(32)

The causality condition for our model is shown in Fig. 8. Additionally, Abreu et al. [76] reintroduced a range for Herrera’s cracking concept to determine the potentially stable (or unstable) anisotropic compact object. According to their study, a potentially stable model should follow the inequality \(-1 \le v_{t}^2 - v_{r}^2 \le 0\) provided there is no sign change of \(v_{t}^2 - v_{r}^2\) within the stellar radius. The inequality \(-1 \le v_{t}^2 - v_{r}^2 \le 0\) also holds for our model, as shown in Fig. 9.

Fig. 7
figure 7

Static equilibrium under three different forces

Full size image

Furthermore, the Herrera cracking concept at the center of the structure leads to the following inequality:

$$\begin{aligned} 24 a^2 C^2 D_2^2 \ge 50.2413 D_1^2 + 73.1517 a C D_1 D_2 \end{aligned}$$
(33)
Fig. 8
figure 8

Variation of sound velocities with the radial coordinate r

Full size image

6.3 Adiabatic index

Let us now test one of the important (in)stability criteria for any stable structure, the adiabatic index. For fixed energy density, the nature of the equation of state can be described by the adiabatic index. Thus, the stability of both relativistic and non-relativistic compact stars depends on the adiabatic index. Now, for a relativistic anisotropic structure, the adiabatic index \(\Gamma \) is described as the ratio of two specific heats and is defined as [78]

$$\begin{aligned} \Gamma = \frac{\rho +p}{p}\frac{\textrm{d}p}{\textrm{d}\rho }, \end{aligned}$$
(34)

where \(\frac{\textrm{d}p}{\textrm{d}\rho }\) is the velocity of sound in units of the velocity of light. Bondi [79] suggested that for the Newtonian sphere, the stability condition is \(\Gamma > {4 \over 3}\), and for neutral equilibrium, the stability condition becomes \(\Gamma = {4 \over 3}\). Later, Heintzmann and Hillebrandth [80] proposed that for an anisotropic sphere to be in equilibrium, the adiabatic index \(\Gamma \) must be \(>\frac{4}{3}\). Subsequently, some corrections were made by Chan et al. [78] for the case of a relativistic fluid, and it is expressed as

$$\begin{aligned} \Gamma < \frac{4}{3} \left[ \frac{4}{3} \frac{p_{t0} - p_{r0}}{r |p'_{r0}|} + \frac{8 \pi }{3} \frac{r \rho _0 p_{r0}}{|p'_{r0}|} \right] _{max} \end{aligned}$$
(35)

where \(\rho _0\), \(p_{r0}\), and \(p_{t0}\) are the initial density, the radial pressure, and the tangential pressure, respectively, in unperturbed equilibrium. Here, the first term on the right-hand side of Eq. (35) corresponds to anisotropy, and the second term represents the relativistic corrections to the Newtonian perfect fluid. Surprisingly, this correction term can also cause instability inside the configuration, as pointed out by Chandrasekhar [81]. Thus, a strict condition was imposed on the adiabatic indices to prevent such instability, and this is known as the critical value of the adiabatic index. The critical value depends on the amplitude of the Lagrangian displacement from the equilibrium and on the compactness factor (\(u(r) \equiv \frac{m(r)}{r}\)). Finally, taking a specific form of this amplitude, the stability condition reduces to \(\Gamma \ge \Gamma _{crit}\), where \(\Gamma _{crit} = \frac{4}{3} + \frac{19 u}{21}\).

Fig. 9
figure 9

Difference in sound speeds belonging to the region \((-1,0)\) with radial coordinate r

Full size image
Fig. 10
figure 10

Variation of adiabatic index with radial coordinate r for the pulsar 4U1820-30

Full size image

The growth of instability might be slowed due the effect of positive anisotropy, which eventually leads to gravitational collapse in the radial direction [82]. Therefore, the focus revolves mainly around the adiabatic index in the radial direction, and Fig. 10 shows that values of \(\Gamma _r\) are greater than \({4 \over 3}\) throughout the stellar configuration.

Fig. 11
figure 11

Variation of mass function and the compactness with radial coordinate r is increasing in nature

Full size image

6.4 Compactness and surface redshifts

An important feature for the stability of any stellar model is its mass and radius. Mathematically, to be a stable compact structure, the mass–radius ratio or the dimensionless compactness \([u(r)=m(r)/r]\) of the model should be \(<0.44\) [83], as proposed by Buchdahl. Although this Buchdahl limit was suggested for a spherically symmetric isotropic fluid sphere, several later research works [84,85,86] indicated that the same could be applied for an anisotropic sphere as well.

Additionally, the gravitational interior redshift is given as

$$\begin{aligned} z=\left( 1-\frac{2M}{r} \right) ^{-1/2}-1. \end{aligned}$$
(36)
Fig. 12
figure 12

Variation of compactness with radial coordinate r is increasing in nature

Full size image
Fig. 13
figure 13

Variation of gravitational redshift with radial coordinate r is increasing in nature

Full size image

From Eq. (36) it is evident that the interior redshift increases with the increase of \({M \over r}\). Since the compactness of a star satisfies the Buchdahl condition, there should exist an upper bound for gravitational redshifts; it cannot be arbitrarily large for any self-gravitating compact object. The surface redshifts \(z_b\) should be less than universal bounds when different energy conditions hold [87]. For an isotropic structure, \(z~<~2\) for a stable configuration [88]. In the anisotropic case, when the DEC holds, the upper limit is 5.211, and when the SEC holds, it is 3.842 [89]. A profile of the variation for the gravitational redshift is plotted in Fig. 13.

7 Applicability of the model

In this section, we delve into the realistic applicability of our model. We begin by obtaining the masses of some known compact objects and check their compatibility with our known data. Table 1 illustrates the mass values obtained for different compact objects using their radii. It also includes their respective compactness and surface redshifts, whose values are found to be within the stable boundary.

Table 1 Mass and radius of some known compact objects
Full size table

After checking the compatibility of the masses and radii of some of the known pulsars, we now check some of the physical properties of the model compatible with these pulsars. Table 2 describes some basic physical attributes, namely density, sound speeds, trace energy condition (TEC: \(\rho - p_r - 2p_t\)), and radial adiabatic index at both the center and the surface. In Table 2, \(|_0\) and \(|_b\) denote the value of these properties at the center and at the surface, respectively.

Table 2 Physical attributes of the model
Full size table

8 Discussion

In this work, we have studied a model for a spherically symmetric anisotropic fluid sphere by assuming a specific metric potential \(B_0^2(r)\). By imposing a specific form of anisotropy, we have obtained the exact solution for the field equation. Smooth matching of the interior solution with the exterior Schwarzschild allows us to obtain the mathematical expressions for the model constants. For graphical investigation, we have chosen the pulsar 4U1658-52 with its current estimated data (mass \(=1.57 ~M\odot \) and radius \(=9.8 \pm 0.8\) km [1]). Additionally, we have considered \(a = 1\), and eventually we obtain the value of the model constants as \(C= - 0.0023948; D_1= 0.0024604; D_2 = 2.141284\). The obtained solutions were then studied both analytically and graphically, and the details are given as follows:

  • The metric potentials and the matter variables are found to be well behaved and well defined for the model. We study the metrics and the physical matter variables \(\rho ,~p_r,~p_t\) graphically in Figs. 1, 2, and 3. Also, the anisotropy for the model increases throughout the structure, as shown in Fig. 4, which forms a base for our model to be a stable configuration. Moreover, the radial derivative of matter variables vanish at the center, and although the gradients for density and radial pressure are negative towards the boundary, the gradient for transverse pressure is seen to be positive up to 7.45 km and then becomes negative for the rest of the configuration (see Fig. 5).

  • To check the stability for the stellar interior, several different energy conditions are studied for our model graphically in Fig. 6, and each energy condition is satisfied inside the stellar structure. Since for positive density and pressure the SEC(\(\rho + p_r + 2 p_t\)) is bound to be \(\ge 0\), to check the stability, we explore the profile of the TEC (\(\rho - p_r - 2 p_t\)) graphically, and it is found to be fulfilled for our model. Additionally, the TEC for various known compact stars (both low mass and high mass) holds perfectly, as seen in tabular form in Table 2.

  • The effects of different forces on the model with regard to stability are shown graphically in Fig. 7, and it can be seen that the dominant gravitational force is balanced by the combined effect of hydrostatic and anisotropic forces.

  • To check the potentially (un)stable region for any anisotropic model, the cracking method is undoubtedly an important condition for the stability. The variation of both the radial and transverse sound speeds are studied graphically in Fig. 8. One interesting feature of our model is the negative form of transverse sound speed. However, the model is shown to be in a potentially stable region \((-1,0)\) as seen in Fig. 9, as suggested by Abreu et al. [76].

  • Our model also supports the stability under the adiabatic index. As positive anisotropy may be one of the causes of radial instability of any compact model, which eventually leads to gravitational collapse, we have checked the radial adiabatic index, and it is seen to be greater than both \(\frac{4}{3}\) and the critical value of the adiabatic index throughout the structure (see Fig. 10). Additionally, the radial adiabatic indices for several known compact objects are studied extensively in Table 2.

  • For the mass function and the compactness factor, both are increasing functions of r and they attain maximum value at the surface, as can be seen in Figs. 11 and 12. We have estimated the radii of some known compact objects and calculated their compactness in Table 1. Additionally, the gravitational redshift against the radius of the star is depicted in Fig. 13. It can be observed that the redshift vanishes at the center, attaining its maximum at the surface. In addition, the compactness values for the known compact stars are presented in Table 2 and are within the limit predicted by Buchdahl (\(< \frac{8}{9}\)). Similarly, the surface redshifts for several different stellar objects are seen to follow the upper bound ( \(<~2\)) in Table 2.

Hence, a novel model can be described by the aforementioned metric potentials, as several physical features and stability criteria required for a physically viable anisotropic compact configuration are satisfied by our model. However, this study was conducted considering \(a =1\), and similar or further observation can be conducted for another value of a.