1 Introduction

Since the first realization that supermassive black holes with mass of the order of \(\hbox {M} = 10^{6}\)–\(10^{10}\,\hbox {M}_{\odot }\) are present in centers of massive galaxies [1] and that they are eligible for powering the Active Galactic Nuclei (AGN) [2], serious investigations have been carried out to understand nature of these objects and their potential contribution to the evolution of galaxies. In addition to having prospects for astrophysics of galaxies, supermassive black holes are new laboratories for testing gravitational physics and spacetime metric. What is the structure of spacetime near these black holes? Can we constrain alternative theories of gravity through black hole observables? The scale of spacetime curvature presented by these objects is in between the very weak field regime of the solar system and very strong field regimes of binary pulsars and merging black holes observed by LIGO. This is an opportunity to test gravity in a new regime.

The Galactic Center supermassive black hole (henceforth GC black hole), Sgr A* has been extensively studied since more than two decades for understanding its gravitational environment by monitoring proper motion of bright stars. Astronomers in Europe (Max Planck Institute of Extraterrestrial Physics, MPE) using the NTT and VLT and astronomers in USA (UCLA) using the Keck telescope have performed near infrared imaging and spectroscopy of about 10,000 stars in the nuclear star cluster near the GC black hole. Orbits of nearly 40 stars have been determined by VLT [3] and Keck [4] through precision astrometry. The highly eccentric orbit (e~0.88) of the star S-2 (in MPE nomenclature)/ S0-2 (in UCLA nomenclature) has been used to determine the mass and distance of the GC black hole as \(M\approx 4\times {10}^{6}\,\hbox {M}_{\odot }\) and \(D\approx 8\, \textrm{kpc}\) [5, 6]. The pericenter passage of S-2 near the GC black hole has been observed in 2002 and 2018 during its 16 year orbital period. The pericenter distance, \(\hbox {r}_{p}=\) 120au of S-2 has given enough opportunity to astronomers to test Einstein’s GR in a relatively stronger gravitational field (\(\hbox {GM}/\hbox {c}^{2}\,\hbox {r}_{p}\)~\(10^{\, -\, 4}\) which is 100 time stronger than that we encounter at the neighbourhood of the Sun). The first post-Newtonian effects such as gravitational redshift of light from S-2 and Schwarzschild precession of its orbit have already been detected by using the GRAVITY beam combiner instrument in VLT [6, 7]. Tests of foundational aspects of GR such as Local Position Invariance (LPI), have also been performed near the GC black hole [8]. The gravitational field of the GC black hole is also realized as a potential laboratory to test viable alternatives to GR. Effect of massive graviton, Yukawa like gravity, f(R) gravity and higher dimensions of space on pericenter shift of compact stellar orbits near the GC black hole have been extensively studied [9,10,11,12,13].

Understanding gravity near black holes is facilitated by a remarkable general relativistic prediction known as the no-hair theorem. It asserts that the only vacuum solution of Einstein’s equations which is stationary, axisymmetric, asymptotically flat, free from pathologies and which contains a horizon is the Kerr metric [14,15,16,17,18,19] It is widely accepted that all astrophysical black holes are described by the Kerr metric. The metric is governed by only two parameters - mass and spin of the black hole. The GC black hole is a novel laboratory to test the black hole metric through orbital dynamics of the stars. A crucial step to test whether the black hole is described by the Kerr metric is to measure spin of the black hole through its effect on pericenter shift of the stars and gravitational redshift of light. Zhang et al. [20] extensively studied testability of the Kerr metric through spin induced effects on orbits of few short period stars near the GC black hole. They reported the astronomical facilities required to measure the black hole spin and concluded that the GRAVITY interferometer on VLT, the upcoming Thirty Meter Telescope (TMT) and the European Extremely Large Telescope will carry sufficient potential to probe compact orbits required for testing the black hole metric.

There are additional black hole metrics which are motivated by higher dimensional gravitational theories beyond GR. One example is the Reissner–Nordstrom (RN) metric including a tidal charge. A tidal charge can be thought of as a projection of gravitational degree of freedom from higher dimension to the 4 dimension where gravitational collapse occurs. Dadhich et al. [21] proposed that RN metric with tidal charge naturally appears in gravitational collapse of Randall–Sundrum 5 dimensional braneworld gravity. Astrophysical consequence of gravitational lensing near GC black hole in presence of RN metric with tidal charge has been discussed in earlier papers [22,23,24]. Zakharov [24] reported constraint on the RN metric through estimation of the tidal charge based on astrometric capabilities of the VLT, Keck and the upcoming TMT to measure pericenter shift of bright stars near the GC black hole. There are other distortions of the Schwarzschild metric such as the one caused by weak field limit of f(R) gravity [25] leading to Yukawa type potential. Testability of these metrics through upcoming astrometric facilities has been discussed in [12, 26].

Discovery of the horizon scale imaging along with the shadows of the M87* black hole and the GC black hole (Sgr A*), reported by the Event Horizon Telescope (EHT) [27, 28] has given new gravitational environments to test spacetime metric. A black hole shadow which is formed by gravitational light bending and photon capture near the event horizon, leading to a central brightness depression, is predominantly a metric phenomenon. However, there are alternative sources causing brightness depression. Radiative properties of plasma material encircling the black hole can produce flux diminutions. These are not yet strongly tested [29]. Moreover, Proca stars and boson stars are also found to mimic a brightness depression surrounded by photon rings [30].

The shape and size of the shadow are dependent largely on the spacetime metric near the black hole. However, plasma emission processes occurring near the event horizon get convolved with the uncertainties reported in the measurements of the angular diameter of the black hole shadow. Gravitational physics (spacetime metric) and emission physics lead to degeneracy in interpreting the shadow measurements [31]. The bright ring of light surrounding the shadow can be used to test spacetime physics if and only if the diameter of peak brightness is close enough to the critical impact parameter of photons below which they plunge into the black hole (\({3}\sqrt{{3}}\) m for Schwarzschild black hole, where \(m=GM/c^{2}\) – half of the gravitational radius). The alpha-calibration (\(\varvec{\alpha }= \frac{{d}_{{pb}}}{{d}_{{sh}}},\, d_{pb}\) and \(d_{sh}\) being diameter of the peak brightness and the shadow respectively) is often used to correlate the location of the bright emission ring with respect to theory dependent location of the critical impact parameter [32]. In this work we are concerned only with the metric effects on the shadow and refrain ourselves from taking into account the emission physics.

Constraints on tidal charge of the RN metric were derived from the black hole shadow of the M87* supermassive black hole observed by EHT during April 2017 [33]. Constraints on the Schwarzschild-de Sitter (SdS) and Kerr-de Sitter (KdS) metric which describe non-spinning and spinning black holes in de Sitter background space respectively, were also derived from the M87* shadow [34]. A novel way to test gravity through black hole shadow is to consider parametric deviation from the Kerr metric and constrain the parameters of the metric through observed shape and size of the black hole shadow. This method has been recently employed by the EHT Collaboration [27] to put constraint on several alternative spacetime metrics.

In this work we resort to several spacetime metrics, both within and outside general relativity and try to extract allowed ranges of the parameters of the metrics through measured angular diameter of the GC black hole (Sgr A*) shadow. The paper is organized as follows. In Sect. 2 we present necessary mathematical relations and the recent EHT measurement. In Sect. 3 parameter extraction from different spacetime metrics through Sgr A* shadow size is presented. Section 4 presents results and discussion. Section 5 concludes.

2 The shadow of Sgr A*

When observed from infinity, a Schwarzschild (non-spinning) black hole has a photon capture radius of \(3\sqrt{3} m\) [27]. This scale is larger than the size of event horizon, \(R_{g}=2m\). Photons emitted by some emission region outside the horizon, having impact parameter \(b<3\sqrt{3} m\) plunge into the black hole. On the other hand photons with \(b=3\sqrt{3} m\) constitute unstable circular orbits – the photon ring and photons with \(b>3\sqrt{3} m\) escape to infinity. Thus there occurs a central brightness depression whose size is \(3\sqrt{3} \hbox {m}\) and is known as the black hole shadow. For rotating (Kerr) black hole the shadow size is only slightly sensitive to spin of the black hole (change is < 4%, see for example, [35]).

For the spacetime metric,

$$\begin{aligned} {ds}^{2}=g_{tt}\left( r,\, P_{i} \right) c^{2}{dt}^{2}+\sum \limits _{i,j=1,2,3} {g_{ij}(r,P_{i}){dx}^{i}{dx}^{j}}, \end{aligned}$$
(1)

where \(P_{i}\) are the parameters appearing in the theory predicting the metric, the shadow radius is given by [27],

$$\begin{aligned} r_{sh}=\frac{r_{ph}(P_{i})}{\sqrt{g_{tt}\left( r_{ph},P_{i}\, \right) } \, }\,, \end{aligned}$$
(2)

where, \(r_{ph}\) denotes the photon sphere which is given by solution of the implicit equation,

$$\begin{aligned} r_{ph}(P_{i})=2g_{tt}(r_{ph}P_{i})\left( \left( \frac{dg_{tt}(r,P_{i})}{dr} \right) _{r_{ph}} \right) ^{-1}, \end{aligned}$$
(3)

which is parameterized by \(P_{i}\). Therefore, by solving the implicit equation (3) for the photon sphere and then substituting it in Eq. (2), one can extract the parameters of the metric, \(P_{i}\) from measured angular diameter of the black hole shadow, \(d_{sh}=2r_{sh}(P_{i})/D\), where D is the distance to the GC black hole for which we need prior information.

The EHT, is composed of eight very large baseline interferometric (VLBI) telescopes which are sensitive to radio wavelength of 1.3 mm at six specific locations around the globe namely, Chile, Hawaii, Mexico, Spain, Arizona and Antarctica. The combination is dedicated to observe the light rays of the hot plasma coming from the Sgr A*. The eight components of EHT combine images by interferometric technique (known as VLBI technique) and achieve desired angular resolution. Upon generating synthetic images and analyzing them [27] came to a conclusion that the calibration ofthe synthetic images along with the EHT measurements of the photon ring diameter describe the angular diameter of the black hole shadow for the GC black hole to be \(d_{sh}=48.7\pm 7.0\,\upmu \textrm{as}\). Given \(\hbox {D}= 8\) kpc (prior), it corresponds to a linear scale of about 0.39 au (nearly \(\hbox {5R}_{g}\)). The dimensionless gravitational potential \(GM/c^{2}r\) is about 1000 times larger than the one encountered at pericenter of the S-2 star (\(\hbox {r}_{p} =120 \,\hbox {au}\)). Thus it is an opportunity to constrain gravity/spacetime metric in a previously uncharted region of the universe.

3 Constraints on parameters of spacetime metrics

3.1 Schwarzschild de-Sitter metric

Schwarzschild de-Sitter (SdS) solution is one of the oldest solutions describing a static, spherically symmetric, uncharged black hole which forms in a background space containing a positive cosmological constant. The metric is given by,

$$\begin{aligned} {ds}^{2}= & {} \left( 1-\frac{2GM}{c^{2}r}-\frac{\lambda r^{2}}{3} \right) c^{2}{dt}^{2}\nonumber \\{} & {} -\left( 1-\frac{2GM}{c^{2}r}-\frac{\lambda r^{2}}{3} \right) ^{-1} {dr}^{2}\nonumber \\{} & {} -r^{2}{d\theta }^{2}-r^{2}{sin}^{2}\theta {d\phi }^{2}. \end{aligned}$$
(4)

One interesting feature of the Schwarzschild de-Sitter black hole as clearly seen in Eq. (4), is that it possesses two horizons- one is the black hole horizon \(R_{g}=2GM/c^{2}\) and the other is the cosmological horizon \(r_{\lambda }=\sqrt{3/\lambda }\) (de-Sitter horizon). In the limit of very small \((\lambda \rightarrow 0)\), these two horizonsare infinitely separated. But for appreciable values of the \(\lambda \) term, the SdS spacetime has two horizons. Emission of Hawking radiation due to temperatures of the two horizons is discussed in [36]. SdS spacetimes in five dimensional general relativity have been studied in [37]. For this metric,

$$\begin{aligned} g_{tt}=\left( 1-\frac{2GM}{c^{2}r}-\frac{\lambda r^{2}}{3} \right) . \end{aligned}$$
(5)

Using Eq. (5) in Eq. (3) we calculate the photon radius of the SdS spacetime as

$$\begin{aligned} r_{ph}=3m, \end{aligned}$$
(6)

and by using Eq. (2) we get the shadow radius as,

$$\begin{aligned} r_{sh}=\frac{3m}{\sqrt{\frac{1}{3}-3\lambda m^{2}} }. \end{aligned}$$
(7)

Thus the shadow diameter of the Schwarzschild de-Sitter metric is given by,

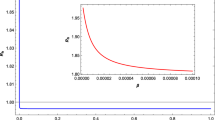
$$\begin{aligned} d_{sh}=\frac{6m}{\sqrt{\frac{1}{3}-3\lambda m^{2}} }. \end{aligned}$$
(8)

To put constraint on the cosmological constant, the metric parameter, we study the variation of the term with respect to shadow diameter within measured bounds [28]. The variation is shown in Fig. 1.

Fig. 1
figure 1

Constraining \(\lambda \) by using the observed shadow diameter of the GC black hole

Full size image

The allowed range of values of \(\lambda \) varies between 71.5687 and 71.57175 \(\textrm{au}^{-2}\). In normal unit the bound is

$$\begin{aligned} 3.19795\times {10}^{-25}\,\textrm{cm}^{-2}\le \lambda \le 3.19809\times {10}^{-25}\,\textrm{cm}^{-2}.\nonumber \\ \end{aligned}$$
(9)

An alternate way of applying an upper bound of the cosmological constant using the shadow of Sgr A* and the mass of the black hole is as follows. Equation (8) can be modified as

$$\begin{aligned} d_{sh}=\frac{6\sqrt{3} m}{\sqrt{1-9\lambda m^{2}} }. \end{aligned}$$
(10)

Clearly, the shadow diameter in Schwarzschild metric corresponds to \(\lambda =0\) which leads to \(d_{sh}\left( S \right) =6\sqrt{3} m\). Nowto produce the upper bound on the cosmological constant, we use the condition [34],

$$\begin{aligned} 1+\frac{E(d_{sh})}{d_{sh}}\ge \frac{d_{sh}(SdS)}{d_{sh}(S)}. \end{aligned}$$
(11)

Here \({E(d}_{sh})\) refers to the error in the measurement of the shadow diameter. Therefore, from the observed shadow diameter, \(\left( 48.7\pm 7.0 \right) \,\upmu \textrm{as}\), we obtain the following upper bound on the cosmological constant,

$$\begin{aligned} \lambda \le \frac{0.235}{9m^{2}}. \end{aligned}$$
(12)

We observe that black hole mass has potential role to play in putting constraint on the metric parameter, here the cosmological constant. We take two black hole masses as priors given by the Very Large Telescope (VLT)and the Keck and also consider one estimation of the black hole mass coming from the shadow size measurement for Sgr A*.

VLT: \({\textbf {M}} = (4.297 \pm 0.013) \times 10^{6}\,\textrm{M}_{\odot }\) [38]

Keck: \({\textbf {M}} = (3.951\pm 0.047) \times 10^{6}\,\textrm{M}_{\odot }\) [39]

EHT shadow: \({\textbf {M}} = (4.0^{1.1}_{-0.6})\, \times 10^{6}\,\textrm{M}_{\odot }\) [28]

We consider end-to-end masses in the errors to obtain the upper bounds on \(\lambda \). These bounds are as follows.

VLT mass: \(\lambda (+) = 6.468\times 10^{\, -\, 26\, }\hbox {cm}^{\, -\, 2\, }; \lambda (-) = 6.547\times 10^{\, -\, 26\, }\hbox {cm}^{\, -\, 2}\)

Keck mass: \(\lambda (+) \quad = 7.517\times 10^{\, -\, 26\, }\hbox {cm}^{\, -\, 2\, }; \lambda (-) = 7.884\times 10^{\, -\, 26\, }\hbox {cm}^{\, -\, 2}\)

EHT mass: \(\lambda (+) \quad = 4.6197\times 10^{\, -\, 26\, }\hbox {cm}^{\, -\, 2\, }; \lambda (-) = 1.0394\times 10^{\, -\, 25\, }\hbox {cm}^{\, -\, 2}\)

Therefore, a stringent bound, \({10}^{-25}\, \textrm{cm}^{-2}\) has been achieved through the SdS metric. In [34] another stringent bound on the cosmological constant, \({10}^{-32}\,\textrm{cm}^{-2}\) has been reported by using SdS metric for the M87* black hole shadow. Thus the bound on the cosmological constant derived from Sgr A * shadow is 7 orders of magnitude larger than the one realized for M87* black hole.

3.2 Reissner–Nordstrom metric

In modern tests of gravity a Reissner–Nordstrom (RN) metric refers to a black hole with tidal charge. According to [21], such a black hole appears in higher dimensional cosmology such as the Randall–Sundrum model. In this model gravitational effect of a 5 dimensional universe gets projected onto the 4 dimensional brane where matter is confined and collapses to form a black hole. This projection of gravitational effect from higher dimension to \(4\textrm{th}\) dimension appears as a charge in the metric known as the Reissner–Nordstrom (RN) metric. Zakharov [24] forecasted the constraints on tidal charge against the capabilities of GRAVITY interferometer in VLT, the Keck telescope and upcoming TMT in measuring pericenter shift of compact stellar orbits around the GC black hole, which gets affected by tidal charge. Constraints on tidal charge of the supermassive black hole M87* were reported in [33] on the basis of the shadow of the M87* black hole detected by the EHT Collaboration in 2017.

The Reissner–Nordstrom (RN) metric is given by:

$$\begin{aligned} {ds}^{2}= & {} \left( 1-\frac{2GM}{c^{2}r}+\frac{Q^{2}}{r^{2}} \right) c^{2}{dt}^{2}\nonumber \\{} & {} -\left( 1-\frac{2GM}{c^{2}r}+\frac{Q^{2}}{r^{2}} \right) ^{-1} {dr}^{2} \nonumber \\{} & {} -r^{2}{d\theta }^{2} -r^{2}{sin}^{2}\theta {d\phi }^{2}. \end{aligned}$$
(13)

Here,

$$\begin{aligned} g_{tt}=\left( 1-\frac{2GM}{c^{2}r}+\frac{Q^{2}}{r^{2}} \right) . \end{aligned}$$
(14)

We use Eq. (14) in (3) to obtain the photon radius of the RN metric as

$$\begin{aligned} r_{ph}=\frac{3m\pm m\sqrt{9m^{2}-8Q^{2}} }{2}. \end{aligned}$$
(15)

Now, using Eq. (2), we obtain the shadow radius as:

$$\begin{aligned} r_{sh}=\frac{{(3m\pm m\sqrt{9-8q} )}^{2}}{2\sqrt{{(3m\pm m\sqrt{9-8q} )}^{2}-4m\left( 3m\pm m\sqrt{9-8q} \right) +4qm^{2}} }.\nonumber \\ \end{aligned}$$
(16)

Here \(\hbox {q}= \hbox {Q}^{2}/\hbox {m}^{2}\).

Thus the shadow diameter of the RN metric is given as,

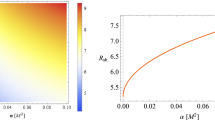
$$\begin{aligned} d_{sh}=\frac{{(3m\pm m\sqrt{9-8q} )}^{2}}{\sqrt{{(3m\pm m\sqrt{9-8q} )}^{2}-4m\left( 3m\pm m\sqrt{9-8q} \right) +4qm^{2}} }.\nonumber \\ \end{aligned}$$
(17)

We thus put constraint on q the tidal charge by studying the variation of q with the shadow diameter within measured bounds. The pattern of variation is shown in Fig. 2. The allowed values of q are found as,

$$\begin{aligned} -0.57934\le q\le 0.86525. \end{aligned}$$
(18)
Fig. 2
figure 2

Constraining q by using the observed shadow diameter of the GC black hole

Full size image

Constraints on tidal charge of the RN metric were derived from the shadow of the M87* supermassive black hole observed by EHT during April 2017 [33]. The range of q predicted in [33] for the M87* is \(-1.22\le q\le 0.814\).

Thus we have obtained a relatively stringent constraint on tidal charge q of Sgr A* relative to the one derived from M87* shadow.

3.3 Kerr metric

The Kerr metric is described as a stationary, axisymmetric and asymptotically flat exterior metric which is pathology free. The metric is governed by two parameters, its mass and spin. The Kerr metric is a rotating metric, thus not invariant under the transformation \(t\, \rightarrow -t\) [40]. Therefore, it is not static, but is stationary as the metric components are independent of time. However, perfectly stationary black holes and perfect vacuum conditions do not usually exist because for the presence of other objects or fields such as stars, accretion discs or dark matter, which can alter the nature of the Kerr black hole. But in this case, since we are testing the shadow, the conditions remain preserved as there in no perturbation close enough to the black hole shadow.

The Kerr (K) metric is described as:

$$\begin{aligned} {ds}^{2}= & {} \left( 1-\frac{2mr}{{\Sigma }} \right) c^{2}{dt}^{2}+\frac{4mra{sin}^{2}\theta }{{\Sigma }}cdtd\phi \nonumber \\{} & {} -\frac{{\Sigma }}{{\Delta }_{r}}dr^{2}-{\Sigma }d\theta ^{2}\nonumber \\{} & {} -\left( r^{2}+a^{2}+\frac{2ma^{2}r{sin}^{2}\theta }{{\Sigma }} \right) {sin}^{2}\theta {d\phi }^{2}, \end{aligned}$$
(19)

where, \(m=\frac{GM}{c^{2}}\), \({\Sigma }=r^{2}+a^{2}{cos}^{2}\theta \), \({\Delta }_{r}=r^{2}-2mr+a^{2}\) and \(a=J/Mc\) where a is the Kerr parameter.

The horizon of a Kerr black hole is expressed as:

$$\begin{aligned} r_{H}\left( \pm \right) =m\pm \sqrt{m^{2}-a^{2}}. \end{aligned}$$
(20)

From the above equation, we observe the existence of a horizon requires \(a\, \le m\) The limiting value of \(a \quad =\) m is called extreme Kerr black hole. If \(a > m\) then there is an occurrence of a naked singularity, which has not been observed till date.

Now,

$$\begin{aligned} g_{tt}=\left( 1-\frac{2mr}{{\Sigma }} \right) . \end{aligned}$$
(21)

We now use Eq. (21) in Eq. (3) to obtain the implicit equation of the photon radius. It is as follows:

$$\begin{aligned} r_{ph}^{4}- {3mr}_{ph}^{3}+{2r}_{ph}^{2}a^{2}{cos}^{2}\theta -{mr}_{ph}a^{2}cos2\theta +a^{4}{cos}^{4}\theta =0.\nonumber \\ \end{aligned}$$
(22)

Now since we obtained an implicit equation of the photon radius, we vary \(\chi \) from 0.1 to 0.99 [41] and calculate the photon radius, by substituting \(\hbox {m} = 0.04\,\hbox {au}\) for Sgr A*.

In terms of the spin parameter \(\chi \), Eq. (22) becomes

$$\begin{aligned}{} & {} r_{ph}^{4}-\, {3mr}_{ph}^{3}+{2r}_{ph}^{2}{(\chi m)}^{2}{cos}^{2}\theta \nonumber \\{} & {} \quad -{mr}_{ph}{(\chi m)}^{2}cos2\theta +{(\chi m)}^{4}{cos}^{4}\theta =0. \end{aligned}$$
(23)

The \(4\textrm{th}\) order polynomial equation is solved and only the real root is considered. The shadow diameter is then calculated numerically for specific values of \(\chi \) with inclination angles as (\(0^{\circ }\), \(5^{\circ }\), \(10^{\circ }\), \(15^{\circ }\), \(20^{\circ }\), \(30^{\circ }\), \(45^{\circ }\), \(60^{\circ }\), \(80^{\circ }\)). The variation is shown in Fig. 3.

Fig. 3
figure 3

Variation of shadow diameter with black hole spin for various inclination angles

Full size image

With higher values of black hole spin, the shadow diameter increases with increase in inclination angle. This sensitivity to inclination angle dies out for very low value of spin. For example, for spin near 0.1 derived from orbital orientation of S-stars [41], the shadow diameter is around 52 \(\upmu \) as for various inclination angles. It has also been observed that for all spin in the range \(\chi = 0.1{-}0.99\), the shadow size falls within the measured bounds. It is also found that for inclination of 0 degree it is difficult to reproduce the shadow size which satisfies the measured bounds.

3.4 Kerr de-Sitter metric

It is the generalization of the Schwarzschild de-Sitter solution and it describes a rotating black hole in de-Sitter space (\(\lambda > 0\)). In cosmology, the evidence of cosmic acceleration is established [42,43,44]. This is caused by some form of dark energy. The naïve candidate of dark energy is a positive cosmological constant which accounts for a large scale cosmic repulsion leading to runaway expansion of the universe. It is also generally accepted that astrophysical black holes are described by the Kerr solution. Thus a true spacetime description of black holes is the Kerr de-Sitter (KdS) solution – the Kerr black hole embedded in de-Sitter background. This solution was discovered by Carter in 1973 [45].

The metric is given by,

$$\begin{aligned} {ds}^{2}= & {} \frac{\left\{ \left( 1-\frac{\lambda r^{2}}{3} \right) \left( r^{2}+a^{2}-2mr \right) \right\} }{{\Sigma }L^{2}}\left( cdt-a{sin}^{2}\theta d\phi ^{2} \right) \nonumber \\{} & {} -\frac{{\Sigma }}{{\Delta }_{r}}{dr}^{2}-\frac{{\Sigma }}{{\Delta }_{\theta }}{d\theta }^{2}\nonumber \\{} & {} -\frac{{\Delta }_{\theta }{sin}^{2}\theta }{{\Sigma }L^{2}}{(acdt-\left( r^{2}+a^{2} \right) d\phi )}^{2}, \end{aligned}$$
(24)

where, \({\Sigma }=r^{2}+a^{2}{cos}^{2}\theta \)

$$\begin{aligned}{} & {} {\Delta }_{r}=\left( r^{2}-2mr+ a^{2} \right) \left( 1-\frac{\lambda r^{2}}{3} \right) \\{} & {} {\Delta }_{\theta }=\left( 1+\frac{\lambda a^{2}{cos}^{2}\theta }{3} \right) \\{} & {} L=\left( 1+\frac{\lambda a^{2}}{3} \right) \end{aligned}$$

Again following the same procedure as above, we use Eq. (24) in Eq. (3) and obtain the photon radius. In the case of Kerr de-Sitter metric, we have fixed the inclination angle at \(\theta \, =\pi /2\) (equatorial plane of the black hole is perpendicular to the line of sight). The implicit equation for the photon radius has been obtained as

$$\begin{aligned} 2\lambda mr_{ph}^{2}+2r_{ph}\left( 3-\lambda a^{2} \right) -18m=0. \end{aligned}$$
(25)

We now solve for the shadow radius numerically by varying values of \(\lambda \) from \(2.24\, \times \, {10}^{-30}\,\textrm{au}^{-2}\) to \(30\, \textrm{au}^{-2}\). The lower limit is justified as below. The cosmological constant is a satisfactory candidate of dark energy which causes accelerated expansion of the universe. The density parameter of dark energy is given by, \(\Omega _{\lambda } = 0.6889 \pm 0.0056\) [46] and the Hubble constant \(\hbox {H}_{0} = 67.4 \pm 0.5 \,\hbox {km}/\hbox {s}/\hbox {Mpc} = (2.1927664 \pm 0.0136) \times 10^{-18} \,\hbox {s}^{-1}\) [47].

Now, by definition, \(\lambda = 3(\hbox {H}_{0}/\hbox {c})^{2}\Omega _{\lambda } = 1.1056 \times 10^{-52} \,\hbox {m}^{-2} = 2.24\times 10^{-30}\,\hbox {au}^{-2}\). The upper bound \(30 \,\hbox {au}^{-2}\) (\(1.34 \times 10^{-25}\,\hbox {cm}^{-2}\)) has been chosen to match the bound obtained from the SdS case. We obtain the shadow diameter for the KdS metric numerically for two values of spin (\(\chi = 0.1, 0.5\)) and sketch the variation of shadow diameter with the cosmological constant to select its allowed range. Whereas the spin value 0.1 is given by measurements of orbital orientation of the S-stars [41] the value 0.5 has been recently realized by EHT measurements [28]. The bounds on the \(\lambda \) term are found as,

$$\begin{aligned}{} & {} 1.538\, \times \, {10}^{-40}\,\textrm{cm}^{-2}\le \lambda \le 1.239\, \times \, {10}^{-25}\,\textrm{cm}^{-2}\, (\chi =0.1),\nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned}{} & {} 1.655\, \times {10}^{-40}\, \textrm{cm}^{-2}\le \lambda \le 1.026\, \times \, {10}^{-25}\,\textrm{cm}^{-2}\, (\chi =0.5).\nonumber \\ \end{aligned}$$
(27)

3.5 Scalaron metric of f(R) gravity

Scalarons are scalar gravitational degrees of freedom in f(R) modified theories of gravity. f(R) gravity theories emerge from modified Einstein–Hilbert action,

$$\begin{aligned} A_{f\left( R \right) }=\frac{c^{4}}{16\pi G}\int d^{4}X\, \sqrt{|g|} f(R). \end{aligned}$$
(28)

Here f(R) represents a function of the Ricci scalar curvature. f(R) gravity has been extensively studied as viable alternatives to general relativity to explain primordial cosmic inflation [48,49,50], late cosmic acceleration and flat rotation curve of galaxies without invoking particle candidates of dark matter [47, 48, 51, 52]. Effect of f(R) gravity near the GC black hole has been studied earlier in the context of light bending [25], testability of modified gravity in a model independent way through upcoming Extremely Large Telescope facilities by considering pericenter shift of compact stellar orbits near the GC black hole as a probe [12, 24, 26, 53, 54]. Lalremruati and Kalita [13] reported breaking points of general relativity through f(R) gravity and higher dimensional gravity near the GC black hole. For f(R) gravity it was reported that at least near the orbit of the S-2 star there is no breaking point of general relativity brought by f(R) gravity. However, it was noted that the scalarons might be lurking deep inside the gravitational potential well of the black hole.

Kalita [25] derived the static spherically symmetric metric of f(R) scalaron gravity which appears as distortion of the Schwarzschild metric. The theory involves a scalar field \(\psi =f^{'}\left( R \right) =\frac{df\left( R \right) }{dR}\) with mass \(M_{\psi }=\sqrt{\left( \frac{1}{3} \right) \left( \frac{\psi _{o}}{\psi ^{'}_{o}}-R_{o} \right) } \) where, \(\psi _{o}\) and \({\psi '}_{o}\) are \({\mathrm {f'(R}}_{o})\) and \({\mathrm {f''(R}}_{o})\) respectively, evaluated at the background curvature \(\textrm{R}_{o}\). This is known as the scalaron field. Kalita [12, 26] studied deviation of the pericenter shift of stellar orbits near the GC black hole from general relativistic values with the help of scalarons with masses in the range \(M_{\psi } = {10}^{-22}{-} {10}^{-16} \,\hbox {eV}\). These are the massive gravitational degrees of freedom relative to graviton whose mass is bounded above by the observation of gravitational waves emitted by black hole binaries [55]. The upper bound \(10^{-16}\) eV corresponds to scalarons resulting from quantum gravitational corrections to vacuum fluctuations near the GC black hole [12]. In earlier studies of pericenter shift of compact stellar orbits near the GC black hole, scalarons with mass \({10}^{-22}\)–\({10}^{-16}\) eV were considered [12, 13, 26]. Development of scalar field quasi bound state through superradiance instability is well known [56]. These bound states can exist near spinning black holes. In [26] it was shown that scalarons of almost all masses in the above range are consistent with black hole spin in the range, \(\chi =0.1{-}0.9\). Scalar particles act as scalar hair for the black hole. In [57], effect of scalar hair with mass below \({10}^{-20}\) eV which can act as scalar dark matter has been studied in relation to the shadow of the M87* black hole. In [58], it was shown that scalar fields with mass \({10}^{-22}\) eV are eligible to explain \(M-\sigma \) relation for galaxies. In [59] it has been shown that scalar fields with masses \({10}^{-20}\)–\({10}^{-18}\) eV can be probed by orbital dynamics of the S-2 star neat the GC black hole. Here we consider scalarons with masses \({10}^{-22}\)–\({10}^{-16}\) eV and try to reproduce the observed shadow size of the GC black hole, thereby extracting the allowed ranges of the scalaron mass. The scalaron metric is expressed as,

$$\begin{aligned} {ds}^{2}= & {} \left( 1-\frac{2m}{\psi _{o}r}-\frac{2m}{3\psi _{o}r}e^{-M_{\psi }r} \right) c^{2}{dt}^{2}\nonumber \\{} & {} -\left( 1-\frac{2m}{\psi _{o}r}-\frac{2m}{3\psi _{o}r}e^{-M_{\psi }r} \right) ^{-1}{dr}^{2}\nonumber \\{} & {} -r^{2}{d\theta }^{2}-r^{2}{sin}^{2}\theta {d\phi }^{2}, \end{aligned}$$
(29)

where \(\frac{e^{-M_{\psi }r}}{r}\) is the Yukawa correction term. Here,

$$\begin{aligned} g_{tt}=\left( 1-\frac{2GM}{{c^{2}\psi }_{o}r}-\frac{2GM}{3{c^{2}\psi }_{o}r}e^{-M_{\psi }r} \right) . \end{aligned}$$
(30)

Since we are concerned with testing the metric at the shadow of Sgr A*, we fix a scale \(r_{o}=\frac{5GM}{c^{2}}\), the typical shadow radius of an astrophysical black hole. Thus we have,

$$\begin{aligned} g_{tt}=1-\frac{2GM}{c^{2}r_{o}}\left[ \frac{1}{\psi _{o}}+\frac{1}{{3\psi }_{o}}e^{-M_{\psi }r_{o}} \right] . \end{aligned}$$
(31)

We define an effective gravitational constant as:

$$\begin{aligned} G_{ff}=G\left[ \frac{1}{\psi _{o}}+\frac{1}{{3\psi }_{o}}e^{-M_{\psi }r_{o}} \right] . \end{aligned}$$
(32)

Now, we define a parameter, \(s=\left[ \frac{1}{\psi _{o}}+\frac{1}{3\psi _{o\, }}e^{-M_{\psi }r_{o\, }} \right] \). Therefore \(g_{tt}\) can be written as:

$$\begin{aligned} g_{tt}=1-\frac{2G_{eff}M}{c^{2}r_{o}}=1-\frac{2GMs}{c^{2}r}. \end{aligned}$$
(33)

Now we are in a position to calculate the photon radius and thus the shadow diameter. We use Eq. (33) in Eq. (3) and obtain the photon radius as \(r_{ph}=3\) ms and substituting this in Eq. (2) we obtain the shadow radius as \(r_{sh}=3\sqrt{3}\) ms. Clearly, in general relativity \(\hbox {f(R)} = \hbox {R}\) and \({\psi }_{o} = \psi = 1\). Also general relativity emerges as approximation of f(R) gravity with infinite scalaron mass limit, \(M_{\psi } \rightarrow \infty \). Therefore, from the above expression, \(\hbox {s} = 1\) in general relativity and \(r_{sh}=3\sqrt{3} m\), the standard result for a Schwarzschild metric.

We now fix the scalaron field \(\uppsi \) at 1 and vary \(M_{\psi }\) from \(1.2225\times {10}^{-5}\,\textrm{au}^{-1}\) (\({10}^{-22}\) eV) to 12.225 \(\textrm{au}^{-1}\) (\({10}^{-16}\) eV) and numerically obtain the shadow diameters for each scalaron mass.

From the above figures, we observe that the allowed range of \({M}_{\psi }\) falls in the range,

$$\begin{aligned} 6.658\, \times \, {10}^{-17\, }\textrm{eV}\, \le M_{\psi }\le {10}^{-16}\,\textrm{eV}. \end{aligned}$$
(34)

On the other hand, the allowed range of the parameters is found as:

$$\begin{aligned} 1\le s\le 1.06129. \end{aligned}$$
(35)

This result is consistent with the earlier reports [13] that some massive scalarons are deeply hidden very close to the black hole. As the value of s close to 1, there is no appreciable shift in the gravitational constant from the Newtonian one.

3.6 Extended parameterized post-Newtonian (EPPN) metric

In this section, we explore the correlation between black hole shadows, i.e., strong field regime with an extension of the PPN metric which is otherwise useful for weak field test. This extension is expressed as the \(g_{tt}\) component in powers of \(r^{-2}\) [60]

$$\begin{aligned} g_{tt}=1-\frac{2GM}{c^{2}r}+\frac{2\left( \beta -\gamma \right) }{c^{4}r^{2}}\left( GM \right) ^{2}-\frac{2\zeta \left( GM \right) ^{3}}{c^{6}r^{3}}. \end{aligned}$$
(36)

Here \(\beta \) and \(\gamma \) are the PPN parameters and we have added a third order PPN term \(\zeta \). We consider two cases, one where we set \(\left( \beta -\gamma \right) = 0\), which is allowed by various weak field tests within the solar system such as, light deflection which predicts the value of \(\upgamma = 1.000 \pm 0.002\) [61] and time delay, which predicts \(\upgamma = 1 + (2.1 \pm 2.3) \times \, {10}^{-5}\) [62]. The value of \(\upbeta \) can be predicted from precession of perihelion of Mercury (with known bounds on \(\upgamma \)). The bound is \(\upbeta = 1.000\pm 0.003\) [63].

The other case we consider is \(\left( \beta -\gamma \right) \ne 0\) with \(\upgamma = 1.18 \pm 0.34\) and \(\upbeta = 1.05 \pm 0.11\) as produced by observations of stellar orbits near Sgr A* [6].

For\(\, \beta -\gamma =0\), the second term in Eq. (36) vanishes and the implicit equation for the photon radius is found to be:

$$\begin{aligned} r_{ph}^{3}-{3mr}_{ph}^{2}-{5\zeta m}^{3}=0. \end{aligned}$$
(37)

In [34] \(\upzeta \) was constrained as \(4.47 \times \, {10}^{-26}\) on the basis of measured shadow of M87* black hole. We numerically solve the cubic equation by varying \(\upzeta \) from \({10}^{-30}\) to 1 and obtain the shadow diameter. We plot the shadow diameter vs \(\upzeta \) and constrain this parameter as (see Fig. 8):

$$\begin{aligned} -0.00376\le \zeta \le 0.75. \end{aligned}$$
(38)

We observe that the width of \(\upzeta \) is wide. Thus the present shadow measurement may not produce a very stringent constraint on the parameter \(\upzeta \).

In the second case, \(\beta -\gamma \ne 0\). We split both \(\upbeta \) and \(\upgamma \) into their positive and negative extrema and obtain two values for \(\beta -\gamma \), which are, \(-0.36\, \mathrm {[}{{(\upbeta -\upgamma )}}_{\mathrm {+}}]\) and 0.1 \(\mathrm {[}{{(\upbeta -\upgamma )}}_{\mathrm {-}}]\). For the second value we obtain imaginary roots of the cubic equation for the photon radius and hence, we drop this option. For \(\beta -\gamma =-0.36\), the implicit equation of the photon radius is as follows:

$$\begin{aligned} r_{ph}^{3}-{3mr}_{ph}^{2}-{1.44mr}_{ph}-{5\zeta m}^{3}=0. \end{aligned}$$
(39)

On numerically solving for the shadow diameter using the same range of values for \(\upzeta \) ( \({10}^{-30}\)–1), we observe that the values of the shadow diameter do not fall in the range as observed by the EHT. Thus we conclude that for non zero values of \(\upbeta -\upgamma \) we cannot reproduce the present shadow measurements.

4 Results and discussion

In this work we have used the angular size of the galactic center black hole shadow to estimate allowed ranges of the parameters appearing in various spacetime metrics of general relativity and alternative theories of gravity in the form of f(R) scalaron metric. The results of the metrics are discussed below.

Schwarzschild de-Sitter metric: The SdS metric was used to put bounds on the cosmological constant \(\uplambda \), which appears in the metric. The bounds are found in the range \((3.19795{-}3.19809) \times 10^{-25} \,\hbox {cm}^{-2}\), which can be observed in Fig. 1. We also considered prior masses provided by the two telescopes VLT and Keck to give bounds on the cosmological constant. For the VLT prior the bound is obtained as (\(6.468\times 10^{-26} \,\hbox {cm}^{-2} - 6.547\times 10^{-26}\,\hbox {cm}^{-2})\). On the other hand for Keck prior the bound is (\(7.517\times 10^{-26}\,\hbox {cm}^{-2}{-}7.884\times 10^{-26}\,\hbox {cm}^{-2}\) ) For the mass estimation of the EHT shadow measurements this bound is (\(4.6197\times 10^{-26}\,\hbox {cm}^{-2}{-}1.0394\times 10^{-25} \,\hbox {cm}^{-2})\). In an earlier work, by considering SdS metric, the bound on the cosmological constant was given on the basis of M87* black hole shadow [34]. This bound is \((1.542{-}2.214) \times 10^{-32}\,\hbox {cm}^{-2}\). In our case, the SdS metric has produced the bound on the cosmological constant as \((3.19795 - 3.19809) \times 10^{-25}\,\hbox {cm}^{-2}\). Therefore, the bounds for the shadow of Sgr A* are elevated with respect to those realized for M87* black hole. However, for KdS metric the bounds are much below (see below) the bounds of M87* black hole. Thus spin of a black hole improves the upper bound of the cosmological constant. Still these bounds are far above the cosmological bound, \(10^{-56}\,\hbox {cm}^{-2}\).

Reissner–Nordström metric: For the RN metric, we have obtained a relatively stringent constrain on tidal charge q of Sgr A* relative to the one derived from M87* shadow. It has been found from Fig. 2 that shadow size is highly sensitive to the value of tidal charge. The possibility of negative tidal charge has been pointed out earlier by [21] and [24]. It has been observed that shadow size becomes large for sufficiently large negative value of the tidal charge and becomes smaller than the minimum bound of the shadow size of Sgr A* for \(\hbox {q}>> 1\). The allowed range of q is found as [− 0.579, 0.865].

Kerr metric: From Fig. 3 we observe that for the Kerr metric, with higher values of black hole spin, the shadow diameter increases with increase in inclination angle. Up to spin around \(\upchi = 0.3\) the shadow diameter is not very sensitive to spin. The sensitivity to inclination angle dies out for very low value of spin. For example, for spin near 0.1 derived from orbital orientation of S-stars [41], the shadow diameter is around \(52 \upmu \) as for various inclination angles. It has also been observed that for all spin in the range \(\upchi = 0.1-0.99\), the shadow size falls within the measured bounds. It is noted that for inclination of 0 degree it is difficult to reproduce the shadow size which satisfies the measured bounds.

Kerr de-Sitter metric: For KdS metric, we put bounds on cosmological constant \(\uplambda \) for spin values of \(\upchi = 0.1\) and 0.5. The range is \(1.538 \times 10^{-40}\,\hbox {cm}^{-2}{-}1.239 \times 10^{-25}\, \hbox {cm}^{-2}\) for \(\upchi = 0.1\) and \(1.655 \times 10^{-40}\, \hbox {cm}^{-2}{-}1.026 \times 10^{-25} \,\hbox {cm}^{-2}\) for \(\upchi = 0.5\) (see Figs. 4 and 5). It has been found that the allowed range of the cosmological constant is stable against variation of the black hole spin. The allowed range of the \(\uplambda \) term is wider than the one obtained for the SdS case. However, the bounds are still larger than the cosmological bound.

Scalaron metric of f(R) gravity: From the scalaron metric we extract the bounds on scalaron mass \(\hbox {M}_{\uppsi }\) and the parameter s for \(\uppsi _{0}=1\). We observe that the bounds on \(\hbox {M}_{\psi }\) lie between 8.62403 to \(12.225 \,\hbox {au}^{-1}\) (\(6.658 \times 10^{-17}{-}10^{-16}\)) eV and that on s lies between 1 and 1.06129 (see Figs. 6 and 7). This result of scalaron mass is consistent with the earlier reports [12, 13] that some massive scalarons are deeply hidden very close to the black hole.

Fig. 4
figure 4

Constraining \(\lambda \) by using the observed shadow diameter for spin \(\chi = 0.1\) of the GC black hole

Full size image
Fig. 5
figure 5

Constraining \(\lambda \) by using the observed shadow diameter for spin \(\chi = 0.5\) of the GC black hole

Full size image

PPN metric: With the PPN metric, we test the third order parameter \(\upzeta \). We observe that the width of \(\upzeta \) is wide as shown in Fig. 8. Thus the present shadow measurement may not be producing a very robust bound, or a stringent constraint on the parameter \(\upzeta \). This is for the case of \(\upbeta -\upgamma = 0\). For \(\upbeta -\upgamma \quad \ne 0\), we observe that, the shadow diameter does not fall in the range as observed by the EHT. Thus we infer that for non zero values of \(\upbeta -\upgamma \) (Galactic Center constraints), we cannot reproduce the present shadow measurements.

We would like to emphasize that these bounds are not yet “clean” as the radiative processes operating in conjunction with the geometry of spacetime will affect these bounds. The present bounds are the best cases when one considers the metrical properties of spacetime alone.

Fig. 6
figure 6

Variation of shadow diameter of GC black hole with \(M_{\psi }\)

Full size image
Fig. 7
figure 7

Variation of shadow diameter of GC black hole with s parameter

Full size image
Fig. 8
figure 8

Constraining \(\zeta \) by using the observed shadow diameter of the GC black hole

Full size image

5 Conclusion

The parameters of black hole metrics within and outside GR are constrained on the basis of angular diameter of the GC (Sgr A*) black hole shadow. We conclude in the following lines. The shadow measurements indicate interesting aspects related to the cosmological constant, extra dimensions of space, the f(R) gravity scalarons and the PPN metric parameter \(\upzeta \).

From the effect of SdS and KdS metric on the shadow, we find that the bounds on cosmological constant are well above the cosmological bound (\(10^{\, -\, 56\, }\hbox {cm}^{\, -\, 2}\)). In SdS case the bounds are seven order magnitude larger than those realised for M87* shadow. The spin of the black hole improves the upper bound of the cosmological constant when compared with SdS case. At present we refrain ourselves from presenting a deep physical implication of a possible connection between black hole mass and spin with the cosmological constant, if there is any. But we wish to infer that cosmological constant of the dark energy phenomenon is not necessarily the same as the one we realise near black holes.

For RN metric we have been able to put narrow bounds on the tidal charge of the black hole relative to those realised for M87* shadow. It has been found that significant negative charge is ruled out. But the present shadow size measurements cannot rule out the existence of tidal charge and hence presence of extra dimensions of space advocated by the Randall-Sundrum model.

The range of scalaron mass derived from the Sgr A* shadow is quite narrow (\(10^{\, -\, 17\, }{-}10^{\, -\, 16}\) eV). This is a significant improvement of the earlier consideration of scalaron mass in the study of pericenter shift of compact stellar orbits near Sgr A*[12, 13]. The scalaron mass, \(10^{\, -\, 16}\) eV extracted in this work is consistent with the prediction of quantum gravitational origin of f(R) gravity near the black hole [12]. The estimation of the parameter s shows that there is no significant deviation of the gravitational constant from the Newtonian value.

From the PPN metric it has been found that it is not possible to constrain higher order correction in PPN metric for \(\upbeta \), \(\upgamma \) given by present measurements of stellar orbits near Sgr A*. However for solar system bounds (\(\upbeta - \upgamma = 0\)) there appears a wide range of the third order parameter \(\zeta \). Therefore, it has been realised that the GC black hole shadow carries sufficient potential to constrain GR metrics and alternatives.