Strange Quark Star (SQS) in Tolman IV potential with density dependent B-parameter and charge

Abstract

In this paper, the solutions of Einstein–Maxwell Field Equations for relativistic strange quark star in Tolman-IV potential considering MIT bag model EoS $p=\frac{1}{3}(\rho -4B)$ of interior matter in presence of charge in higher dimensions is presented, where B is bag parameter. Here we consider density dependent B as it has more practical application. We note some interesting results. It is observed that interior of a strange quark star may contain bulk stable quarks as a whole having energy per baryon $E_B<930.4$ MeV/fm$^3$ or stable quark matter core enclosed by a thin metastable quark matter layer enveloped by unstable quark matter. It is also found that interior composition depends on the value of space-time dimension (D) and net charge (Q). The model presented in this paper satisfies all the necessary stability and energy conditions for a viable stellar configuration. We also note the maximum mass of stable strange quark star is 1.773 $M_{\odot }$ for density dependent B and 1.684 $M_{\odot }$ for constant B.

1 Introduction

In last couple of decades compact objects have gained considerable interest among researchers in relativistic astrophysics. Compact objects may be categorized as White Dwarf (hence forth WD), Neutron Star (henceforth NS), Black Hole (hence forth BH). NS are fascinating astrophysical objects having high density near the core region ($\sim$ $2.7 \times 10^{14}$ g/cm$^3$ or more) and therefore are excellent test bed for the study of matter at extreme densities. It is not possible always to explain the observed masses and radii of many astrophysical compact objects at such extreme densities using available standard NS model till date. Both masses and radii of such objects are found to be less than that of NS but the compactification factor (defined as ratio of mass to radius) is higher. A new type of compact object called Strange Star (henceforth SS) has been hypothesized [1,2,3,4] for such class. These objects are grouped in the new family known as SS family. Within this family recent studies on compact astrophysical objects especially on strange quark stars find out importance after the hypothesis given by Bodmer [5] and Witten [6] that the ground state of matter at extreme conditions may be deconfined phase of quarks (u, d and s) and not $^{56}Fe$. The Quark-Gluon-Plasma (henceforth QGP) phase is important particularly at high temperature or low baryonic density. Such QGP phase may have been attained during the time of formation of the universe at early stage or in the experiments of heavy ion collision. Additionaly a deconfined phase of quarks may also results when baryonic matter is compressed to a high degree keeping the temperature low. Such situation may arise in the interior of compact objects. Consequently a compact star may be classified as ‘neutron star’ which is a gravitationally bound object primarily becomes a bare ‘strange quark star’ composed of 3-flavor quarks or a ‘hybrid star’ in which the quark core is supported by a crust made of hadronic matter. Due to the unavailability of exact neucleon-neucleon interaction potential, the EoS of compact stars is only model dependent. Hence predicted mass–radius of such objects varies widely [7]. Neutron star interior composition explorer (NICER), dedicated for the exploration of NS interior matter provides unprecedented sensitivity to the measurements of NS masses and radii [8].

Anisotropy in pressure inside a compact object may arise due to several reasons. One of the possible reason is the presence of type 3A superfluid in the solid core of compact objects [9]. Oweing to fermion, nucleons can not reside together in a given energy state due to Pauli exclusion principle. Again at very short range strong repulsive nucleon-nucleon interaction comes into play. All of these repulsive forces help to overcome gravitational collapse inside a neutron star. This scenario changes in low temperature limit when nucleons form cooper pairs [10] which are practically bosons. Thus at very low temperature nucleons behave collectively on a very large scale. Such nucleon condensates which is analogues to He-3 may flow without viscosity. Inside a neutron star the high pressure region increases effectively the critical temperature of cooper pair formation allows nuclear superfluidity to exist even at temperature of the order of billion degrees. Three different types of superfluid may exist [11] inside a neutron star core. Other possible causes of anisotropy in compact objects may include (i) phase transitions [12], (ii) pion condensation [13], (iii) slow rotation [14] etc.

It was Rosseland [15], who first predicted that a star may contain a copious amount of electrons and positive ions. Due to the enormously high kinetic energy, electrons have greater probability to escape from the star than that of positive ions. Consequently a star may contain significant amount of net positive charge. This process continues untill the internal electric field opposes electrons to escape further (please see Eddington [16] for a detail review on this problem). The Einstein Field Equations (henceforth EFE) in presence of electric field are very significant to study the properties of neutron stars, quark stars, gravastars, black holes etc in the context of relativistic astrophysics as electric field plays an important role in the gross properties of such compact objects. Sunzu et al. [17] obtained an exact solutions for the Einstein–Maxwell equations of quark star by considering equation of state (henceforth EoS) of linear form. They also obtained another classes of solution of the E–M equations for a different form of the metric potential among which the type of first class is regular in the interior of star having a constant potential whereas the second one has a variable potential and is singular at the centre [18]. According to Ivanov [19] a perfect fluid must have non vanishing net charge to avoid singularity. Bonnor [20] argued that charge plays a key role to give stability of a stellar structure against graviational collapse. The repulsive coulomb interaction can stop the fluid sphere from further collapsing to a point singularity. Stettner [21] showed that a uniform density star without charge is more unstable than that of a star carrying a net surface charge. Krasinski [22] showed that a net amount of charge is required to halt the collapse of matter of spherical distribution under inward pull of gravity towards a point singularity. By generalizing the Oppenheimer–Volkof equation, Bekenstein [23] analyzed the stability of charged fluid spheres qualitatively. A few number of authors also worked on this topic [24,25,26,27]. The physical behaviour and stability of charged dust stars were also discussed by some authors [28,29,30,31,32]. Extensive studies of Ivanov [19] and Sharma [33] revealed that presence of charge had affected advarsely the values of luminosity, surface redshift and maximum mass of a compact relativistic object. In this context, it is to be noted that various uncharged solutions were extended to charged regime previously by different authors such as Nduka [34] and Adler [35] who obtained charged version of the Kuchowicz [36] solutions; Singh and Yadav [37], Nduka [34] and Klein [38] modified the Wyman [39] solution; charged analogue of Schwarzschild’s interior solution was obtained by Gupta and Kumar [40], Gupta et al [41], Florides [42], Banerjee and Som [43] and Guilfoyle [44]. Charged analogue of Tolman [45] solutions was obtained by Cataldo and Mitskievic [46], Tikekar [47], Pant and Sah [48]. Charged anisotropic solutions of Einstein–Maxwell equation in presence of both linear and non linear EoS had been considered by Varela et al. [49].

In recent decades the inclusion of extra dimension in GTR to unify gravity with other fundamental forces in nature has been taken into consideration. In this context the credit for introducing higher dimension to unify gravity with electromagnetic interaction goes to both Kaluza [50] and Klein [51]. In cosmology the theory of higher dimension is important since it is known to us that the present universe is much larger than the early universe. It may be possible that in the evolutionary stage the present universe went through a higher dimensional space which gets reduced to four dimension subsequently in the sense that the extra dimensions become too minute to be detectable due to dynamical contraction as pointed out by Chodos and Detweiler [52]. A serious question arises now whether the concept of extra dimension is physically reachable or it is just a mathematical tool to build models in both cosmology and astrophysics. In this context Marciano [53] examined the time dependence of fundamental constants within the framework of Kaluza–Klein theory. He suggested that experimental detection of time variation in any of them might be a strong signature of the existance of multi dimensions. In connection with Kaluza–Klein cosmology Alvarez and Gavela [54] studied the dynamical compactification in a universe having multi dimensions and showed that an adiabatic contraction had led to a transfer of entropy to the four dimensional universe. Sahdev [55] obtained a homogeneous, anisotropic cosmological model in $1+d+D$ dimensions and showed that for an isentropic contraction of dimension of universe, the temperature T eventually dropped depending on the radius of the compact space. Later some astrophysical models were also genaralized in higher dimensions. Such as higher dimensional solution of spherically symmetric Schwarzschild and Reissner–Nordström black holes [56, 57], rotating Kerr black hole [58,59,60,61], black holes in compactified spacetime [62], no hair theorem [63], Hawking radiation [58], stability of Schwarzschild black hole against linearized perturbations of metrics [64] have been investigated. In the framework of higher dimension Paul [65] evaluated the upper bound of mass to radius ratio of uniform density star and the result showed that minimum mass to radius ratio is possible only when $D=4$. Cassisi et al. [66] discussed in detail the information about extra dimensions in the context of stellar evolution theory and hence the constraints therein.

Tolman [45] presented a wide varity of solutions of the EFE for a perfect fluid. In this article Tolman generated a total of 8 solutions by connecting the metric functions through a single equation and thereby imposing some restrictions on them. Out of the 8 solutions, Tolman-IV particularly assumes a simple form and admits a sphere of compressible fluid with nonzero central density and pressures. In the background of Tolman-IV potential Banerjee [67] obtained a regular and well behaved solution of the EFE within the framework of MIT bag model EoS which admits anisotropic matter distribution. Compact stellar model with Tolman IV potential in anisotropic regime has been obtained by Bhar et al. [68] which has been shown to be regular and stable. Das et al. [69] assumed a particular form of the $g_{rr}$ component of the metric which may be regarded as anisotropic extension of Tolman-IV potential. A vast amount of articles are available in which extensive study on strange quark star are performed [70,71,72,73,74,75]. Within relativistic approach several authors have studied properties of strange quark stars qualitatively making use of the MIT bag model EoS of the form $p=\frac{1}{3}(\rho -4B)$ [76,77,78,79,80], where B is vacuum energy density or bag constant. However, in the present article, we have adopted a different approach to obtain anisotropic extension of the isotropic Tolman IV solution for charged compact object in higher dimensions considering MIT Bag model EoS from which the isotropic and uncharged counterpart can readily be arrived by just switching off some parameters. In this article our basic aim is to construct stellar model for charged strange quark star admitting MIT bag model EoS in presence of extra dimensions ($D\ge 4$). In the MIT bag model the constituent quarks are assumed to be confined in a region of space of perturbative vaccum known as ‘bag’ by means of a net inward pressure B which is exerted by the surrounding non-perturbative vacuum. With rise in the baryon number density $n_B$, the distinction between these two vacua disappears and the bag parameter B which is the net inward pressure must vanish. Therefore it is more practical to consider B as a density dependent quantity [81]. In our approach we have considered that parameter B depends on the energy density or baryon number instead of constant B in MIT bag model.

In our analysis we have first determined the constraints on the charge ($\gamma$) and pressure ($\alpha$) anisotropy parameters for which central pressure of a star assumes positive value. Within these constraints of $\alpha$ and $\gamma$, we have studied the effects of dimensions (D), net charge (Q) and pressure anisotropy on the gross properties of stellar configuration such as maximum mass, surface redshift, stability window of bulk strange quark and we obtained some interesting results.

The paper is organized as follows: in Sect. 2 we have introduced the higher dimensional form of the Einstein–Maxwell field equations. Exact solutions of the field equations are obtained in Sect. 3 which corresponds to anisotropic and charged extension of isotropic Tolman IV solution. The physical plausibility of the solution and restrictions on model parameters are discussed in Sect. 4. The viability of the present model is also studied from the variation of different physical parameters. In Sect. 5 possible existence of strange quarks inside various compact objects is visualized with the help of MIT bag model EoS. A density dependence of the bag parameter B is employed here. In Sect. 6 stability of the present model is studied from different stability criteria. Finally we have concluded by mentioning some important aspects of our model in Sect. 7.

2 Einstein–Maxwell field equations and their solutions in higher dimensions

The space-time of interior configuration of a spherically symmetric and static line element in higher dimensions is described by

$$\begin{aligned} ds^2=-e^{2\nu (r)}dt^2+e^{2\lambda (r)}dr^2+r^2d{\varOmega _{n}}^2, \end{aligned}$$

(1)

where we consider $n=D-2$. D is known as the total number of space-time dimensions and the angular part of the metric element on the n-sphere is represented as $d{\varOmega _{n}}^2=d{\theta _{1}}^2+sin^2\theta _{1}d{\theta _{2}}^2+sin^2\theta _{1}sin^2\theta _{2}d{\theta _{3}}^2 +........+(sin^2\theta _{1}sin^2\theta _{2}........sin^2\theta _{n-1}) d{\theta _{n}}^2$. Consequently for $n=2$ we regain the metric in four dimension. In presence of electromagnetic field the corresponding energy momentum tensor of the interior matter of a compact object in higher dimensions is given by

$$\begin{aligned} T^{total}_{ij}= & {} \text{ diag } \bigg (-\rho -\frac{1}{2}E^2,p_{r}-\frac{1}{2}E^2,p_{t}\nonumber \\{} & {} +\frac{1}{2}E^2,\ldots ,p_{t}+\frac{1}{2}E^2\bigg ). \end{aligned}$$

(2)

In GR the EFE in the fundamental form is given by [82]:

$$\begin{aligned} \textbf{R}_{ij}-\frac{1}{2}g_{ij}{} \textbf{R}=8\pi G_{D}T^{total}_{ij}, \end{aligned}$$

(3)

where $\textbf{R}_{ij}$ and $\textbf{R}$ are called Ricci tensor and Ricci scalar respectively. $G_{D}=G V_{D-4}=G V_{n-2}$ represents the gravitational constant in D dimensions, G being the four dimensional Newtonian gravitational constant and $V_{D-4}$ is the volume of the extra dimensions given by $V_{n-2}=\frac{\pi ^{(n-2)/2}r^{(n-2)}}{\varGamma (\frac{n}{2})}$. Using Eqs. (1) and (2), the EFE system of equations given in Eq. (3) in presence of electric field give the following set of equations

$$\begin{aligned} \frac{ne^{-2\lambda }\lambda ^{\prime }}{r}+\frac{n(n-1)}{2r^2}(1-e^{-2\lambda })=8\pi G_{D}\rho + \frac{1}{2}E^2. \end{aligned}$$

(4)

$$\begin{aligned} \frac{ne^{-2\lambda }\nu ^{\prime }}{r}-\frac{n(n-1)}{2r^2}(1-e^{-2\lambda })=8\pi G_{D}p_{r} - \frac{1}{2}E^2. \end{aligned}$$

(5)

$$\begin{aligned} e^{-2\lambda }\left[ \nu ^{\prime \prime }+{\nu ^{\prime }}^2-\lambda ^{\prime }\nu ^{\prime }-\frac{(n-1)(\lambda ^{\prime }-\nu ^{\prime })}{r}\right] \end{aligned}$$

$$\begin{aligned} \;\;\; -\frac{(n-1)(n-2)}{2r^2}(1-e^{-2\lambda })=8\pi G_{D}p_{t} + \frac{1}{2}E^2. \end{aligned}$$

(6)

The charge density as measured by an observer within a radius ‘r’ is given by

$$\begin{aligned} \sigma (r)= \frac{1}{H}\frac{1}{r^n}e^{-\lambda }[r^nE(r)]^{\prime }, \end{aligned}$$

(7)

where $H=$ $\frac{(n+1)\pi ^{\frac{n+1}{2}}}{\varGamma \left( \frac{n+3}{2}\right) }$ [83]. Thus the net amount of charge resides within the radius ‘r’ can be obtained as

$$\begin{aligned} Q(r)=H\int ^{r}_{0}r'^n \sigma (r') e^{\lambda } dr' = r^n E(r). \end{aligned}$$

(8)

We now introduce the Durgapal–Bannerji [84] transformation

$$\begin{aligned} x=r^2,\quad Z(x)=e^{-2\lambda (r)},\quad y^2(x)=e^{2\nu (r)}, \end{aligned}$$

(9)

so that the Field equations in Eqs. (4)–(6) and the charge density in Eq. (7) in terms of the new variable ’x’ take the form

$$\begin{aligned} 8\pi G_{D} \rho +\frac{1}{2}E^2= & {} \frac{n(n-1)}{2x}\left( 1-Z\right) -n Z_x, \end{aligned}$$

(10)

$$\begin{aligned} 8\pi G_{D} p_r -\frac{1}{2}E^2= & {} 2nZ\frac{y_x}{y}-\frac{n(n-1)}{2x}\left( 1-Z\right) , \end{aligned}$$

(11)

$$\begin{aligned} 8\pi G_{D} p_t +\frac{1}{2}E^2= & {} Z\left[ 4x\frac{y_{xx}}{y}+2n\frac{y_x}{y}+2x\frac{y_x}{y}\frac{Z_x}{Z}+(n-1)\frac{Z_x}{Z}\right] \nonumber \\{} & {} -\frac{(n-1)(n-2)}{2x}\left( 1-Z\right) , \end{aligned}$$

(12)

$$\begin{aligned} \sigma (x)= & {} \frac{2}{H} \sqrt{\frac{Z}{x}}\left( \frac{n}{2}E+xE_x\right) , \end{aligned}$$

(13)

where $y_{xx}$, $y_x$, $Z_{xx}$, $Z_x$ and $E_x$ are the derivatives of these functions with respect to x. In presence of electro-magnetic field total mass of a star within radius ‘r’ can be determined using the following expression

$$\begin{aligned} m(r)=\frac{2\pi ^{\frac{n+1}{2}}}{\varGamma \left( \frac{n+1}{2}\right) }\int ^{r}_{0} r'^n \left[ \rho (r')+\frac{E^2(r')}{8\pi }\right] dr'. \end{aligned}$$

(14)

3 Generating exact solution

The exact solutions of the Einstein–Maxwell Field equations can be obtained using Eqs. (11) and (12). We subtract Eq. (11) from Eq. (12) and considering that $\varDelta =p_t-p_r$ is account for pressure anisotropy [85,86,87,88]. We finally obtain the following equation

$$\begin{aligned} Z_x+P_1(x)Z=P_2(x), \end{aligned}$$

(15)

where

$$\begin{aligned} P_1(x)=\frac{4x^2y_{xx}-(n-1)y}{2x^2y_x+(n-1)xy}. \end{aligned}$$

(16)

and

$$\begin{aligned} P_2(x)=\frac{\left[ (8\pi G_D\varDelta +E^2)x-(n-1)\right] y}{2x^2y_x+(n-1)xy}. \end{aligned}$$

(17)

Equation (15) is a first order linear differential equation having solution of the form

$$\begin{aligned} Z(x)= e^{-\int P_1(x) dx}\left[ \int P_2(x)e^{\int P_1(x) dx}dx+c\right] , \end{aligned}$$

(18)

where c is a constant. Variety of forms of the metric potental $e^{2\nu }$ may be chosen but it should be remembered that the choice should satisfy all the desirable features for a physically viable model. In this article we choose the Tolman-IV [45] type ansatz for the metric potential $e^{2\nu }$.

$$\begin{aligned} e^{2\nu }=y^2(x) =A^2(1+ax). \end{aligned}$$

(19)

This particular form of the metric ansatz is found to be nonsingular, continuous and well behaved throughout the interior of a stellar configuration and therefore physically acceptable for constructing stellar model. In order to integrate right hand side of Eq. (18), we have to choose the form of $\varDelta$ and $E^2$ suitably. Many authors [18, 89, 90] prefer a polynomial form of the pressure anisotropy $\varDelta$ which is regular and vanishes at the centre ($r=0$). In this work we choose $\varDelta$ following the work of Goswami et al. [91] as given below

$$\begin{aligned} \varDelta = \frac{(n-1)\alpha a^2x}{8\pi G_D (1+ax)^2}, \end{aligned}$$

(20)

which vanishes when $r=0$ and takes maximum value at surface. This particular form of $\varDelta$ extensively depends on dimension D. We also consider $E^2$ to be of the form

$$\begin{aligned} E^2 = \frac{\gamma a^2x}{(1+ax)^2}, \end{aligned}$$

(21)

this type of choice for $E^2$ has been utilized by Mafa Takisa and Maharaj [71] to find exact solution of the Einstein Field equation for a polytropic equation of state and also by Hansraj and Maharaj [92] to obtain charged solutions which contain uncharged form of the Finch–Skea solution. We now obtain the anisotropic and charged extension of the Tolman-IV solution in D ($=n+2$) dimensions as given by

$$\begin{aligned} Z(x) = \frac{(n-1)(1+ax)-[(n-1)\alpha +\gamma ]ax+cx(1+ax)}{n(1+ax)-1}. \nonumber \\ \end{aligned}$$

(22)

For $n=2$, $\alpha =\gamma =0$, Eq. (22) reduces to the isotropic, uncharged Tolman-IV [45] potential as given below

$$\begin{aligned} Z(x)=\frac{(1+ax)(1+cx)}{1+2ax}, \end{aligned}$$

(23)

In this model the expressions of various physical parameters relevant for a stellar configuration viz. energy density ($\rho$), radial pressure ($p_r$), transverse pressure ($p_t$) and charge density ($\sigma$) are given below:

$$\begin{aligned} \rho= & {} \frac{n(n-1)}{2}\left[ \frac{a-c(1+ax)+a\left\{ (n-1)\alpha +\gamma \right\} }{n(1+ax)-1}\right] \nonumber \\{} & {} +n\left[ \frac{n(1+ax)\left\{ a(n-1)+acx\right\} }{[n(1+ax)-1]^2} \right. \nonumber \\{} & {} \left. -\frac{a^2nx\left\{ (n-1)\alpha +\gamma \right\} }{[n(1+ax)-1]^2}\right] -n\left[ \frac{a(n-1)+c(1+2ax)}{n(1+ax)-1}\right. \nonumber \\{} & {} \left. -\frac{a\left\{ (n-1)\alpha +\gamma \right\} }{n(1+ax)-1}\right] -\frac{\gamma a^2x}{2(1+ax)^2}. \end{aligned}$$

(24)

$$\begin{aligned} p_r= & {} \frac{na}{1+ax}\left[ \frac{\left\{ (n-1)+cx\right\} (1+ax)}{n(1+ax)-1} \right. \nonumber \\{} & {} \times \left. \frac{-ax\left\{ (n-1)\alpha +\gamma \right\} }{n(1+ax)-1}\right] -\frac{n(n-1)}{2}\left[ \frac{a-c(1+ax)}{n(1+ax)-1}\right. \nonumber \\{} & {} \times \left. \frac{ax\left\{ (n-1)\alpha +\gamma \right\} }{n(1+ax)-1}\right] +\frac{\gamma a^2x}{2(1+ax)^2}. \end{aligned}$$

(25)

$$\begin{aligned} p_t= & {} p_r+\varDelta . \end{aligned}$$

(26)

$$\begin{aligned} \sigma= & {} \frac{1}{H}\sqrt{\frac{Z}{x}}\frac{\sqrt{\gamma x}a}{(1+ax)^2}\left[ (n+1)+ax(n-1)\right] . \end{aligned}$$

(27)

The arbitrary constants a and c have to be evaluated from matching conditions at the surface of the star given below:

• 1. The Reissner–Nördström [93, 94] metric in higher dimensions is given by

  $$\begin{aligned} ds^2= & {} -\left[ 1-\frac{K_n}{r^{n-1}}+\frac{q^2}{r^{2(n-1)}}\right] dt^2+\Bigg [1-\frac{K_n}{r^{n-1}} \nonumber \\{} & {} +\frac{q^2}{r^{2(n-1)}}\Bigg ]^{-1}dr^2+r^2d\varOmega _n^2, \end{aligned}$$

  (28)

  where $K_n$ is related to the mass of a star given by $K_n=\frac{16\pi G_D M}{nA_n}$ with $A_n=\frac{2\pi ^{\frac{n+1}{2}}}{\varGamma \left( \frac{n+1}{2}\right) }$. Matching of the internal metric with the external Reissner–Nördström metric at the boundary ($r=R_b$). Now at $r=R_b$ the continuity of metric function yields

  $$\begin{aligned}{} & {} e^{2\nu (r=R_b)}=e^{-2\lambda (r=R_b)}= \left[ 1-\frac{K_n}{R_b^{n-1}}+\frac{q^2}{R_b^{2(n-1)}}\right] \nonumber \\{} & {} \quad i.e. \frac{(n-1)(1+aR_b^2)-[(n-1)\alpha +\gamma ]aR_b^2}{n(1+aR_b^2)-1} \nonumber \\{} & {} \quad +\frac{cR_b^2(1+aR_b^2)}{n(1+aR_b^2)-1}=\left[ 1-\frac{K_n}{R_b^{n-1}}+\frac{q^2}{R_b^{2(n-1)}}\right] , \nonumber \\ \end{aligned}$$

  (29)

  and

  $$\begin{aligned} A^2(1+aR_b^2)=\left[ 1-\frac{K_n}{R_b^{n-1}}+\frac{q^2}{R_b^{2(n-1)}}\right] . \end{aligned}$$

  (30)

• 2. The radial pressure ($p_r$) which is a monotonically decreasing function of r should drops to zero at the surface $r=R_b$ i.e.

  $$\begin{aligned} p_r(r=R_b)=0, \end{aligned}$$

  (31)

  which on using Eqs. (25), (29) and (31) determines the constants a and c. Thus the complete determination of $\rho$, $p_r$, $p_t$ and charge density ($\sigma$) are now possible.

4 Physical analysis and bounds on the model parameters

In this section we discuss the physical viability of the model. We observe that at the centre of star the graviational potentials are $(e^{2\nu })_{r=0}=A^2$, $(e^{2\lambda })_{r=0}=1$ and their first derivatives $(e^{2\nu })_{r=0}^{\prime }=$ $(e^{2\lambda })_{r=0}^{\prime }=0$. Therefore the gravitational potentials and their derivatives are regular at the centre. The central density assumes the form

$$\begin{aligned} \rho _{0}=\frac{n(n+1)(a\left\{ 1+(n-1)\alpha +\gamma \right\} -c)}{2(n-1)}, \end{aligned}$$

(32)

which takes higher value in high dimensions. It follows that for $\rho _{0}>0$, the condition $a<0$ and $c>0$ is not possible. However for $a>0$ and $c>0$, we get a bound on their ratio given below

$$\begin{aligned} \frac{c}{a}<1+(n-1)\alpha +\gamma . \end{aligned}$$

(33)

Since for $a<0$ the electric field (E) and charge density ($\sigma$) become negative in view of Eqs. (21) and (27), the condition $a<0$, $c<0$ is prohibited which although may give positive value of $\rho _0$. Similarly the central pressure in this model is given by

$$\begin{aligned} (p_r)_{0}=\frac{n}{2}\left[ c-a\left\{ (n-1)\alpha +\gamma -1\right\} \right] , \end{aligned}$$

(34)

For $(p_r)_{0}>0$ the following cases are noted

$\bullet$ When $(n-1)\alpha +\gamma >1$ the combination $c<0$ and $a>0$ is not possible. However for $c>0$, $a>0$, the ratio of c and a follows the inequality

$$\begin{aligned} \frac{c}{a}>(n-1)\alpha +\gamma -1. \end{aligned}$$

(35)

$\bullet$ When $(n-1)\alpha +\gamma <1$, the combination $a>0$, $c>0$ is always allowed. However for $c<0$ and $a>0$ we get

$$\begin{aligned} \frac{c}{a}<1-(n-1)\alpha -\gamma . \end{aligned}$$

(36)

Equations (33), (35) and (36) indicate that dimension (D), pressure anisotropy parameter ($\alpha$) and charge anisotropy parameter ($\gamma$) have some effect on the construction of physically viable stellar model. The fulfilment of Zeldovich’s condition i.e. $(\frac{p_r}{\rho })_{0}\le 1$ leads to another restriction given below:

$$\begin{aligned} \frac{c}{a}\le \frac{1+n^2\alpha +n(\gamma -\alpha )}{n}. \end{aligned}$$

(37)

The square of radial sound velocity ($v_r^2$) is obtained as

$$\begin{aligned} v_r^2= & {} \left( \frac{\gamma a^2}{2(1+ax)^2}-\frac{\gamma a^3x}{(1+ax)^3}-\frac{na}{(1+ax)}f_1(x)\right. \nonumber \\{} & {} -\frac{n(n-1)}{2x}f_1(x)-\frac{na^2}{(1+ax)^2}f_2(x) \nonumber \\{} & {} \left. +\frac{n(n-1)}{2x^2}(1-f_2(x))\right) \nonumber \\{} & {} \Big /\left( \frac{\gamma a^3x}{(1+ax)^3}-\frac{\gamma a^2}{2(1+ax)^2} -nf_3(x)\right. \nonumber \\{} & {} \left. +\frac{n(n-1)}{2x}f_1(x) -\frac{n(n-1)}{2x^2}(1-f_2(x))\right) , \end{aligned}$$

(38)

where

$$\begin{aligned} f_1(x)= & {} \left[ \frac{an(n-1)(1+ax)}{[n(1+ax)-1]^2}+\frac{acnx(1+ax)}{[n(1+ax)-1]^2} \right. \nonumber \\{} & {} \left. -\frac{a(n-1)}{n(1+ax)-1}-\frac{acx}{n(1+ax)-1}-\frac{c(1+ax)}{n(1+ax)-1} \right. \nonumber \\{} & {} \left. -\frac{a^2nx\left\{ (n-1)\alpha +\gamma \right\} }{[n(1+ax)-1]^2}+\frac{a\left\{ (n-1)\alpha +\gamma \right\} }{n(1+ax)-1}\right] . \end{aligned}$$

(39)

$$\begin{aligned} f_2(x)= & {} \left[ \frac{(n-1)(1+ax)}{n(1+ax)-1}+\frac{cx(1+ax)}{n(1+ax)-1} \right. \nonumber \\{} & {} \left. -\frac{ax\left\{ (n-1)\alpha +\gamma \right\} }{n(1+ax)-1}\right] . \end{aligned}$$

(40)

$$\begin{aligned} f_3(x)= & {} \left[ \frac{2a^2n^2(n-1)(1+ax)}{[n(1+ax)-1]^3}+\frac{2a^2n^2cx(1+ax)}{[n(1+ax)-1]^3}\right. \nonumber \\{} & {} \left. -\frac{2a^2n(n-1)}{[n(1+ax)-1]^2}-\frac{2a^2cnx}{[n(1+ax)-1]^2} \right. \nonumber \\{} & {} \left. -\frac{2acn(1+ax)}{[n(1+ax)-1]^2}+\frac{2ac}{n(1+ax)-1} \right. \nonumber \\{} & {} \left. -\frac{2a^3n^2x\left\{ (n-1)\alpha +\gamma \right\} }{[n(1+ax)-1]^3}\right. \nonumber \\{} & {} \left. +\frac{2a^2n\left\{ (n-1)\alpha +\gamma \right\} }{[n(1+ax)-1]^2}\right] . \end{aligned}$$

(41)

Table 1 Tabulation of different compact objects and their observed mass, radius

Fig. 1

Plots of $\gamma$ against $\alpha$ corresponding to different central pressure for HER X-1 (blue line), EXO1745-248 (green line) and PSR J1614-2230 (red line). Here the regions below each line represent allowed combinations of $\alpha$ and $\gamma$ for which positive value of central pressure is obtained. The region above each of these lines represent forbidden region (negative central pressure). The plots are drawn for $D=4$ (top left), $D=5$ (top right), $D=6$ (bottom left) and $D=11$ (bottom right)

In case of higher dimensions the total mass of a charged star within radius ‘$R_b$’ is calculated in this model which is given by

$$\begin{aligned} M(R_b)= & {} A_n\frac{nR_b^{n+1}}{16\pi }\left[ \frac{\varGamma (\frac{n}{2})}{\pi ^{\frac{n-2}{2}}R_b^{(n-2)}}\frac{aC_1-c}{C_2} \right. \nonumber \\{} & {} \left. +\frac{2\gamma a}{n(n+1)}F(R_b^2) \right] , \end{aligned}$$

(42)

where $C_1=n \alpha - \alpha +\gamma +1-cR_b^2$ and $C_2=n(1+aR_b^2)-1$. $F(R_b^2)=_2F_{1}\left[ \frac{n+1}{2},1,\frac{n+3}{2},-aR_b^2\right] -$ $_2F_{1}\left[ \frac{n+1}{2},2,\frac{n+3}{2},-aR_b^2\right]$. Here $_2F_1[e,f,g,h]$ is known as Gauss hypergeometric function [95] having arguments e, f, g, h. The mass function in Eq. (42) vanishes as $R_b\rightarrow 0$ and is regular interior to a compact object. We now discuss the nature of variation of different physical parameters. We consider the compact objects HER X-1, PSR J1614-2230 and EXO1745-248 and their observed mass and radius are tabulated in Table  1.

Here $\alpha$ and $\gamma$ can not be chosen arbitrarily since beyond a certain limit the central pressure becomes negative which is not possible physically. We have plotted $\gamma$ with respect to $\alpha$ corresponding to different central pressure in Fig. 1. The allowed values of $\alpha$ and $\gamma$ are indicated by the region below the respective coloured lines for three different compact objects namely HER X-1, EXO1745-248 and PSR J1614-2230 in different dimensions. It is observed that the allowed range of $\alpha$ and $\gamma$ decreases as we increase the dimension D.

4.1 Trends of energy density and various pressures

In this section, we study the nature of variation of energy density ($\rho$), radial pressure ($p_r$), tangential pressure ($p_t$) and anisotropic pressure ($\varDelta$) for the compact objects as mentioned in Table 1. We scale these parameters in unit of ($8\pi G_D$) so that the rescaled energy density (${\tilde{\rho }}$), radial pressure ($\tilde{p_r}$), tangential pressure ($\tilde{p_t}$) and pressure anisotropy (${\tilde{\varDelta }}$) become

$$\begin{aligned} {\tilde{\rho }}=8\pi G_D \rho ,\quad \tilde{p_r}=8\pi G_D p_r, \nonumber \\ \tilde{p_t}=8\pi G_D p_t,\quad {\tilde{\varDelta }}=8\pi G_D \varDelta . \end{aligned}$$

(43)

The radial variation of ${\tilde{\rho }}$ for these compact objects are plotted in Fig. 2. It is clear that energy density (${\tilde{\rho }}$) picks up higher value in presence of higher dimension ($D>4$) for the compact objects chosen in the present analysis.

Fig. 2

Radial variation of energy density (${\tilde{\rho }}$) for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

Fig. 3

Radial variation of radial pressure ($\tilde{p_r}$) for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

Fig. 4

Radial variation of tangential pressure ($\tilde{p_t}$) for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

The plots of radial ($\tilde{p_r}$) and tangential ($\tilde{p_t}$) pressures are presented in Figs. 3 and 4 respectively. It is observed that $\tilde{p_r}$ picks up higher value in higher dimensions. The nature of variation of tangential pressure ($\tilde{p_t}$) is similar to that of ${\tilde{\rho }}$ and $\tilde{p_r}$ although it assumes a non zero value at the surface which can be seen from Fig. 4.

Fig. 5

Radial variation of anisotropic pressure (${\tilde{\varDelta }}$) for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

The variation of ${\tilde{\varDelta }}$ is shown in Fig. 5 where it is clearly observable that the regularity of the anisotropic pressure (${\tilde{\varDelta }}$) at the centre ($r=0$) is maintained at which both radial ($\tilde{p_r}$) and tangential ($\tilde{p_t}$) pressures become equal.

4.2 Causality condition

One of the criteria of a well behaved solution is that the sound speed should be causal throughout the interior of a compact object. For a star composed of anisotropic pressures two different sound velocities namely radial ($v_r^2$) and tangential ($v_t^2$) should satisfy the conditions $v_r^2 = (\frac{dp_r}{d\rho }) \le 1$ and $v_t^2 = (\frac{dp_t}{d\rho }) \le 1$. The two different sound velocities are plotted in Figs. 6 and 7 respectively. It is observed that causality condition is satisfied in this model. Apart from that it is also interesting to note that both of these sound velocities assume a monotonically decreasing nature.

Fig. 6

Radial variation of square of the radial sound velocity ($v_r^2$) for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

Fig. 7

Radial variation of square of the tangential sound velocity ($v_t^2$) for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

4.3 Behaviour of electric field and charge density

The variation of square of electric field ($E^2$) and charge density ($\sigma$) are plotted in Figs. 8 and 9 respectively. It is observed that electric field vanishes at the centre of the compact objects which is consistent with Eq. (21). It is also evident that $E^2$ takes maximum value at the surface which however decreases with increase in number of space time dimension (D). The variation of charge density ($\sigma$) follows an opposite nature of $E^2$ which takes maximum value at the centre and minimum at the surface. This type variation of $\sigma$ can also be found in the article of Varela et al. [49].

Fig. 8

Radial variation of square of the electric field ($E^2$) for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

Fig. 9

Radial variation of charge density ($\sigma$) for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

4.4 Energy conditions

For a charged anisotropic compact object the energy conditions namely (i) null energy condition (NEC), (ii) weak energy condition (WEC), (iii) dominant energy condition (DEC) and (iv) strong energy condition (SEC) should be satisfied [99, 100]. We have determined the mathematical expressions for different energy conditions using the approach discussed in [99] and are given below

$$\begin{aligned}{} & {} \mathbf{NEC:} {\tilde{\rho }} + \tilde{p_r} \ge 0,\nonumber \\{} & {} {\tilde{\rho }} + \tilde{p_t} + E^2 \ge 0. \end{aligned}$$

(44)

$$\begin{aligned}{} & {} \mathbf{WEC:} {\tilde{\rho }} + \frac{E^2}{2} \ge 0,\nonumber \\{} & {} {\tilde{\rho }} + \tilde{p_r} \ge 0,\nonumber \\{} & {} {\tilde{\rho }} + \tilde{p_t} + E^2 \ge 0. \end{aligned}$$

(45)

$$\begin{aligned}{} & {} \mathbf{DEC:} {\tilde{\rho }} + \frac{E^2}{2} \ge 0, \nonumber \\{} & {} {\tilde{\rho }} - \tilde{p_r} + E^2 \ge 0, \nonumber \\{} & {} {\tilde{\rho }} - \tilde{p_t} \ge 0. \end{aligned}$$

(46)

$$\begin{aligned}{} & {} \mathbf{SEC:} {\tilde{\rho }} + \tilde{p_r} \ge 0, \nonumber \\{} & {} {\tilde{\rho }} + \tilde{p_t} + E^2 \ge 0, \nonumber \\{} & {} (n-1){\tilde{\rho }} + \tilde{p_r} + n\tilde{p_t} + (n-1) E^2 \ge 0. \end{aligned}$$

(47)

The NEC, WEC, DEC and SEC are plotted in Figs. 10, 11, 12, 13, 14 and 15 respectively. It is evident that all of these energy conditions are satisfied for the compact objects used here for analysis.

Fig. 10

Radial variation of ${\tilde{\rho }} + \tilde{p_r}$ for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

Fig. 11

Radial variation of ${\tilde{\rho }} + \tilde{p_t} + E^2$ for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

Fig. 12

Radial variation of ${\tilde{\rho }} + \frac{E^2}{2}$ for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

Fig. 13

Radial variation of ${\tilde{\rho }} - \tilde{p_r} + E^2$ for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

Fig. 14

Radial variation of ${\tilde{\rho }} - \tilde{p_t}$ for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

Fig. 15

Radial variation of $(n-1){\tilde{\rho }} + \tilde{p_r} + n\tilde{p_t} + (n-1) E^2$ for different compact objects as indicated in the figure. Here plots with solid, dashed and dotted lines correspond to $D=4,5$ and 6 respectively. To obtain the plots we choose (i) $\alpha =0.4$, $\gamma =0.45$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.25$, $\gamma =0.2$ when $D=6$ for HER X-1, (ii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.25$ when $D=5$ and $\alpha =0.2$, $\gamma =0.15$ when $D=6$ for PSR J1614-2230, (iii) $\alpha =0.4$, $\gamma =0.5$ when $D=4$; $\alpha =0.3$, $\gamma =0.2$ when $D=5$ and $\alpha =0.2$, $\gamma =0.25$ when $D=6$ for EXO1745-248

5 Stability of strange quarks inside various compact objects in the framework of MIT bag model with density dependent B

In the MIT bag model the quarks are considered as a gas composed of degenerate fermi particles. In this model the dynamics of quark confinement is described in terms of the following equations [101]

$$\begin{aligned} p_r+B=\sum _{i=u,d,s,e^{-}} p_{i}, \end{aligned}$$

(48)

and

$$\begin{aligned} \rho =\sum _{i=u,d,s,e^{-}} \rho _{i} +B, \end{aligned}$$

(49)

where B is a constant also known as bag parameter. In the MIT bag model the quarks are assumed to be confined in a region of perturbative vaccum known as ‘bag’ by means of a net inward pressure B which is exerted by the surrounding non-perturbative vacuum. These two vacua may disappear with rise of baryon number density $n_B$ and the bag parameter B which is the net inward pressure must vanish. Consequently it is more practical to consider B as a density dependent quantity [81]. The baryon number density is given by

$$\begin{aligned} n_B = \frac{(n_u + n_d + n_s)}{3}, \end{aligned}$$

(50)

where $n_u$, $n_d$ and $n_s$ stand for number densities of up, down and strange quarks respectively. Using the charge neutrality condition $\frac{2}{3}n_u - \frac{1}{3}(n_d+n_s)=0$ and the expression for the energy density of quarks as given in the articles of Kettner et al. [102] and Kapusta [103], the energy density of quarks ($\rho _i$) may be obtained as a function of baryon number density ($n_B$) i.e. $\rho _i=\frac{g_i}{8\pi ^2}(\pi ^2 n_B)^{4/3}$. For density dependent $B (n_B)$, Eq. (49) implies that energy density of the system can be related to the baryon number density $n_B$ which in turn motivates us to write B as a function of the total energy density $\rho$ (i.e. $B(\rho )$). Following the work of Chattopadhyay and Paul [104], we assume a polynomial relation between $p_r$ and $\rho$ as

$$\begin{aligned} p_r=p_r(\rho )= \sum _{i=0}^{l} a_i \rho ^i, \end{aligned}$$

(51)

again if we consider the EoS of interior matter to be SQM obeying MIT bag model EoS

$$\begin{aligned} p_r=\frac{1}{3}(\rho -4B), \end{aligned}$$

(52)

then eliminating $p_r$ from Eqs. (51) and (52) we get density dependence of B as

$$\begin{aligned} B(\rho ) = \sum _{i=0}^{l} k_i \rho ^i, \end{aligned}$$

(53)

where the coefficients $k_i$ s are related to $a_i$ s through the relations $k_0=-\frac{3}{4}a_0$, $k_1=\frac{(1-3a_1)}{4}$, $k_j=-\frac{3}{4}a_j$, where j runs from 2 to l. We take the range of $i=0$ to 5 and the coefficients $k_i$ are tabulated in Tables 2, 3 and 4 for HER X-1, PSR J 1614-2230 and EXO1745-248 respectively. Effect of higher order polynomial ($i>5$) is negligible.

Table 2 Values of coefficients $k_i$ in different dimensions for HER X-1 taking $\alpha =0.1$ and $\gamma =0.2$

Table 3 Values of coefficients $k_i$ in different dimensions for PSR J 1614-2230 taking $\alpha =0.1$ and $\gamma =0.2$

Table 4 Values of coefficients $k_i$ in different dimensions for EXO1745-248 taking $\alpha =0.1$ and $\gamma =0.2$

It has already been stated that at the surface the radial pressure vanishes ($p_r=0$) from which Eq. (48) gives the energy per baryon of strange quark matter as follows [105]

$$\begin{aligned} E_B=2\sqrt{3}\left( \frac{3\pi ^2B}{4}\right) ^{\frac{1}{4}}. \end{aligned}$$

(54)

Quark matter consists of u, d and s quarks is stable relative to $^{56}Fe$ if the energy per baryon lies below 930.4 MeV. If however the energy per baryon exceeds the value 930.4 MeV but remains below the number 939 MeV (typical mass of nucleons), the 3-flavor quarks are said to be metastable [106]. Above this limit 3-flavor quarks are unstable.

Fig. 16

Variation of energy per baryon ($E_B$) with density ($\rho$) for HER X-1. Here the dashed line represents energy per baryon of $^{56}Fe$ which is 930.4 MeV and dot dashed line corresponds to the mass of nucleons (939 MeV)

Fig. 17

Variation of energy per baryon ($E_B$) with density ($\rho$) for PSR J 1614-2230. Here the dashed line represents energy per baryon of $^{56}Fe$ which is 930.4 MeV and dot dashed line corresponds to the mass of nucleons (939 MeV)

Fig. 18

Variation of energy per baryon ($E_B$) with density ($\rho$) for EXO1745-248. Here the dashed line represents energy per baryon of $^{56}Fe$ which is 930.4 MeV and dot dashed line corresponds to the mass of nucleons (939 MeV)

In Figs. 16, 17 and 18, we have plotted energy per baryon as a function of density. Following inferences can be drawn from these figures:

• (i) In case of HER X-1, bulk strange quark matter is absolutely stable throughout the star with respect to $^{56}Fe$ for $D=4$. For $D=5$ and 6 the stable region decreases and we get a 3 layered structure in which the core contains stable quark matter, a very thin layer of metastable quarks is formed above which quarks are found to be unstable as the energy per baryon exceeds the limit 939 MeV. However for $D\ge 7$ bulk strange quark matter is totally unstable resulting a pure hadron star. With inclusion of extra dimension the effective volume of phase space increases therefore the quarks can occupy the lowest possible energy states at $T=0$ K which results in a decrease of Fermi Energy of the system and can also be verified from the result obtained by Al-Jaber [107]. Therefore the value of bag parameter B must increase (see Fig. 19) to compensate for this decrement of fermi energy. It was shown by Tmurbagan et al. [108] that increased value of bag parameter may switch off hadron-quark phase transition and subsequently number of hyperons in the system increases. Which supports our results.

• (ii) For PSR J 1614-2230 and EXO1745-248 we get similar type of variation and it is noticeable that bulk Quark Star is possible upto $D=5$.

Fig. 19

Variation of bag parameter at the centre ($B(\rho _0)$) with dimensions (D) for different compact objects

Fig. 20

Cross sectional view of the star HER X-1 for different stability region of quarks. Here inner region marked with white colour represents stable quark relative to $^{56}Fe$ above which a thin layer of metastable quark exists which is shown in black colour and the outer layer in gray colour consists of unstable quarks. Figure in the top panel (a) is plotted without charge ($\gamma =0$) and in the bottom panel (b) we consider the effect of charge and take $\gamma =0.2$. The pressure anisotropy ($\alpha$) is set to 0.1

Fig. 21

Cross sectional view of the star PSR J1614-2230 for different stability region of quarks. Here inner region marked with white colour represents stable quark relative to $^{56}Fe$ above which a thin layer of metastable quark exists which is shown in black colour and the outer layer in gray colour consists of unstable quarks. Figure in the top panel (a) is plotted without charge ($\gamma =0$) and in the bottom panel (b) we consider the effect of charge and take $\gamma =0.2$. The pressure anisotropy ($\alpha$) is set to 0.1

Fig. 22

Cross sectional view of the star EXO1745-248 for different stability region of quarks. Here inner region marked with white colour represents stable quark relative to $^{56}Fe$ above which a thin layer of metastable quark exists which is shown in black colour and the outer layer in gray colour consists of unstable quarks. Figure in the top panel (a) is plotted without charge ($\gamma =0$) and in the bottom panel (b) we consider the effect of charge and take $\gamma =0.2$. The pressure anisotropy ($\alpha$) is set to 0.1

The cross sectional view of the compact objects are depicted in Figs. 20, 21 and 22. It is observed that the hadronic phase increases with inclusion of charge at the compensation of decrease in the number of stable quarks at the core of the star. In our model we have calculated radius of various compact objects by taking their observed masses using MIT bag model EoS considering the density dependence on B. The results are shown in Tables 5, 6 and 7. It is evident that in $D=4$ radius of a star increases with increase in amount of charge which is determined by the charge anisotropy parameter $\gamma$. This is physically acceptable since higher amount of charge increases coulomb repulsion therefore radius must increase. However reverse effect is noticed for $D>4$ which can be understood as follows: according to Cooperstock and La Cruz [109] in case of a charged sphere in equibrium the total mass and total charge should satisfy the condition $M^2>Q^2$. In Figs. 23, 24 and 25 we have combined the plots of $M^2$ and $Q^2$ against radial coordinate ’r’. It is worthwhile to note that with increase in number of space-time dimensions the difference between $M^2$ and $Q^2$ increases rapidly. Therefore for $D>4$ mass of a star has greater influence on equilibrium than charge. Therefore despite of increment of charge of the system the abrupt increment of mass results in decrement of the radius.

Table 5 Predicted radius of HER X-1 having mass $M=$ 0.85$M_\odot$. Here the bag parameter (B) is defined at the surface of the compact object where radial pressure vanishes. The pressure anisotropy parameter ($\alpha$) is taken as unity

Table 6 Predicted radius of PSR J1614-2230 having mass $M=$ 1.97$M_\odot$. Here the bag parameter (B) is defined at the surface of the compact object where radial pressure vanishes. The pressure anisotropy parameter ($\alpha$) is taken as unity

Table 7 Predicted radius of EXO1745-248 having mass $M=$ 1.4$M_\odot$. Here the bag parameter (B) is defined at the surface of the compact object where radial pressure vanishes. The pressure anisotropy parameter ($\alpha$) is taken as unity

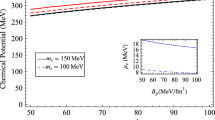
The mass–radius plot for compact objects with density dependent B and constant B is shown in Fig. 26. The figure indicates that a density dependence of the bag parameter (B) allows more mass and radius compared to a constant B value. The maximum mass corresponding to density dependent $B(\rho )=$ $82.11~MeV/fm^3$ at the surface is found to be 1.773 $M_{\odot }$ which however assumes the value 1.684 $M_{\odot }$ when a constant B of same value throughout the star is considered. Also the maximum radius in our model is about 10.03 km for density dependent B and is about 9.22 km when a constant value of B is considered. The corresponding compactness (u) are 0.261 and 0.269 respectively which are well below the Buchdahl bound $\frac{4}{9}$ [110].

Fig. 23

Radial variation of $M^2$ and $Q^2$ inside HER X-1. Here blue and black curves correspond to plots of $M^2$ and $Q^2$ respectively. Solid, dashed and dotted curves correspond to $D=4$, $D=5$ and $D=6$ respectively. To obtain these plots we have considered pressure isotropy condition and set $\gamma =0.4$

Fig. 24

Radial variation of $M^2$ and $Q^2$ inside PSR J1614-2230. Here blue and black curves correspond to plots of $M^2$ and $Q^2$ respectively. Solid, dashed and dotted curves correspond to $D=4$, $D=5$ and $D=6$ respectively. To obtain these plots we have considered pressure isotropy condition and set $\gamma =0.4$

Fig. 25

Radial variation of $M^2$ and $Q^2$ inside EXO1745-248. Here blue and black curves correspond to plots of $M^2$ and $Q^2$ respectively. Solid, dashed and dotted curves correspond to $D=4$, $D=5$ and $D=6$ respectively. To obtain these plots we have considered pressure isotropy condition and set $\gamma =0.4$

Fig. 26

Variation of mass (M) of compact objects with its radius ($R_b$) for $B_{surface}=82.11$ MeV/fm$^3$ defined at the surface where radial pressure vanishes. Here we consider two different cases (i) at first case we take B as constant and (ii) a density dependence of B is considered in accordance with Eq. (53) where the coefficients $k_i$ are $k_0=56.4636$, $k_1=0.02846$, $k_2=0.000217$, $k_3=-2.548\times 10^{-7}$, $k_4=1.892\times 10^{-10}$ and $k_5=-6.192\times 10^{-14}$. The maximum mass points are indicated with small filled circles

The surface redshift may be obtained from the relation

$$\begin{aligned} z_s = (1-2u)^{-1/2}-1. \end{aligned}$$

(55)

The maximum surface redshift obtained from our model are 0.446 when B is assumed to have density dependence and 0.471 when B is held fixed. The mass (M) vs central density ($\rho _0$) plot is shown in Fig. 27. According to Zeldovich and Novikov [111] for a stable stellar system, mass (M) of the star should increase with increase in central density ($\rho _0$) i.e. $\left( \frac{\partial {M}}{\partial {\rho _0}}\right) >0$. From Fig. 27 it is observed that central density corresponds to maximum mass are $2.428\times 10^{15}$ g/cm$^3$ and $2.699\times 10^{15}$ g/cm$^3$ for density dependent B and constant B respectively and above these values the Zeldovich-Novikov criteria is violated ($\left( \frac{\partial {M}}{\partial {\rho _0}}\right) <0$). Therefore these values for the central density may be regarded as the maximum central densities obtainable from our model for the chosen values of B.

Fig. 27

Variation of mass (M) of compact objects with central density ($\rho _0$) for $B_{surface}=82.11$ MeV/fm$^3$ defined at the surface where radial pressure vanishes. Here we consider two different cases (i) at first case we take B as constant and (ii) a density dependence of B is considered in accordance with Eq. (53) where the coefficients $k_i$ are $k_0=56.4636$, $k_1=0.02846$, $k_2=0.000217$, $k_3=-2.548\times 10^{-7}$, $k_4=1.892\times 10^{-10}$ and $k_5=-6.192\times 10^{-14}$. The maximum mass points are indicated with small filled circles

6 Stability conditions

The stability of the model analyzed here is studied from the following points of view:

• (i) Generalized TOV equation

• (ii) Herrera cracking condition and

• (iii) Variation of adiabatic index

6.1 Generalized TOV equation

The question how a charged fluid sphere remains in hydrostatic equilibrium in which the repulsive coulomb interaction is balanced by gravitational and other forces can be investigated by analyzing the TOV equation [45, 112]. Bekenstein [23] obtained an extended form of the TOV equation in case of charged compact object which later on followed by various authors [113,114,115,116]. Recently Das et al. [117] utilized the higher dimensional form of the TOV equation to study the equilibrium of a class of relativistic stellar model in EGB gravity.

$$\begin{aligned} -\frac{M_{G}(\rho +p_r)}{r^2}e^{\lambda -\nu }-\frac{dp_r}{dr}+\sigma Ee^{\lambda }+\frac{n}{r}(p_t-p_r)=0, \nonumber \\ \end{aligned}$$

(56)

here $M_G$ is reffered to as active gravitational mass within a radius r and can be obtained from Tolman-Whittaker formula as given below

$$\begin{aligned} M_G=r^2 e^{(\nu -\lambda )}\nu ^\prime . \end{aligned}$$

(57)

Equation (57) describes the equilibrium of a charged fluid sphere under the mutual influence of gravitational, hydrostatics, ani- sotropic and electric forces. Using Eq. (57) in Eq. (56) a modified form of the equation is obtained

$$\begin{aligned} -\nu ^\prime (\rho +p_r)-\frac{dp_r}{dr}+\sigma Ee^{\lambda }+\frac{n}{r}\varDelta =0, \end{aligned}$$

(58)

In the above equation the first term is known as gravitational force ($F_g$), second term is hydrostatic force ($F_h$), third term is electrostatic force ($F_e$) and the last term is called anisotropic force ($F_a$). Different forces are depicted in Figs. 28, 29 and 30. It is noticeable that gravitational force ($F_g$) assumes negative value though out the compact objects whereas hydrostatic ($F_h$), anisotropic ($F_a$) and electrostatic force ($F_e$) are positive. Here the force $F_g$ is balanced by combined actions of $F_h$, $F_a$ and $F_e$ and they summed up zero.

Fig. 28

Radial variation of different forces inside HER X-1. Here red, green, blue and black lines represent gravitational force ($F_g$), hydrostatic force ($F_h$), anisotropic force ($F_a$) and electrostatic force ($F_e$) respectively. Solid, dashed and dotdashed curves correspond to $D=4$, $D=5$ and $D=6$ respectively

Fig. 29

Radial variation of different forces inside PSR J1614-2230. Here red, green, blue and black lines represent gravitational force ($F_g$), hydrostatic force ($F_h$), anisotropic force ($F_a$) and electrostatic force ($F_e$) respectively. Solid, dashed and dotdashed curves correspond to $D=4$, $D=5$ and $D=6$ respectively

Fig. 30

Radial variation of different forces inside EXO1745-248. Here red, green, blue and black lines represent gravitational force ($F_g$), hydrostatic force ($F_h$), anisotropic force ($F_a$) and electrostatic force ($F_e$) respectively. Solid, dashed and dotdashed curves correspond to $D=4$, $D=5$ and $D=6$ respectively

6.2 Herrera cracking condition

In relativistic astrophysics it is an essential criteria that any anisotropic stellar model should be stable against fluctuations of its physical parameters. Herrera [118] in this context introduced a concept known as ‘cracking’ to verify whether an anisotropic matter distribution is stable or not. Based on Herrera’s concept, Abreu [119] on the other hand formulated a criteria which depicts that any stellar model will be stable if the radial ($v_{r}$) and tangential ($v_{t}$) sound velocities satisfy the condition

$$\begin{aligned} 0 \le |v_{t}^{2}-v_{r}^2| \le 1. \end{aligned}$$

(59)

Fig. 31

Radial variation of $|v_{t}^{2}-v_{r}^2|$ inside different compact objects as indicated in the figure. Here solid, dashed and dotdashed curves correspond to $D=4$, $D=5$ and $D=6$ respectively

It is evident from Fig. 31 that Abreu’s inequality is obeyed in our model.

6.3 Adiabatic index

For anisotropic star one may define the adiabatic index ($\varGamma$) through the following equation

$$\begin{aligned} \varGamma =\frac{\rho +p_{r}}{p_{r}}\frac{dp_{r}}{d\rho }=\frac{\rho +p_{r}}{p_{r}}v_{r}^{2} \end{aligned}$$

(60)

Heintzmann and Hillebrandt [120] gave a criteria according to which any stellar structure will be dynamically stable if $\varGamma > \frac{4}{3}$.

Fig. 32

Radial variation of adiabatic index ($\varGamma$) inside different compact objects as indicated in the figure. Here solid, dashed and dotdashed curves correspond to $D=4$, $D=5$ and $D=6$ respectively. The black horizontal line represents the value $\frac{4}{3}$

The radial variation of adiabatic index are shown in Fig. 32 for three different compact objects. It is obvious that for dimensions $D=4$, 5 and 6, the adiabatic index $\varGamma$ is greater than the limit 4/3 as given by Heintzmann and Hillebrandt.

7 Discussions

In this article we have tried to demonstrate a method to generate an exact solution of the Einstein equations for a class of anisotropic and charged compact object described by Tolman-IV metric potential in higher dimensional space-time. The metric function for the $g_{rr}$ component assumes a modified form of the Tolman-IV potential which is characterized by two constants a and c which are evaluated from matching conditions at the boundary of a star. The metric potentials and their derivatives are found to be regular at the centre. For the finite nature of energy density ($\rho$) and pressure ($p_r$) at the centre ($r=0$) of a star, the constants a and c are found to be constrained to certain limits. The condition that the central pressure ($p_r(0)$) should remain positive removes the arbitraryness of pressure anisotropy ($\alpha$) and charge anisotropy ($\gamma$). We have noted that a combinations of $\alpha$ and $\gamma$ are not allowed so that central pressure becomes negative. We restrict our analysis for allowed value of $\alpha$ and $\gamma$ indicated by respective coloured lines shown in Fig. 1 for three stars namely HER X-1, EXO1745-248 and PSR J1614-2230. Inclusion of extra dimension ($D>4$) reduces effectively the region in which combinations of $\alpha$ and $\gamma$ are allowed which is also observed from Fig. 1. The mass function given in Eq. (42) is regular, well behaved and vanishes as $r \rightarrow 0$. The behaviour of energy density ($\rho$), radial ($p_r$), tangential ($p_t$) and anisotropic ($\varDelta$) pressures are depicted in Figs. 2, 3, 4 and 5. It is evident from the figures that all these parameters are regular and continuous inside the compact objects. The central density ($\rho _0$) takes higher value in higher dimensions ($D>4$) thus higher dimension allows the formation of more compact structure compared to usual four dimension. Similar type of variations are also noted for $p_r$, $p_t$ and $\varDelta$. Both radial ($v_r^2$) and tangential ($v_t^2$) sound velocities are causal i.e. $0\le v_r^2\le 1$ and $0\le v_t^2\le 1$ in our model which may be seen from Figs. 6 and 7. It is also interesting to note that sound velocities are monotonically decreasing function of the radial distance ‘r’. The variation of $E^2$ is such that it always vanishes at the centre irrespective of dimension D and takes maximum value at the surface. The surface value of $E^2$ however increases with the increase of space-time dimension D. The charge density $\sigma$ shows an opposite type of variation taking maximum value at the centre then gradually falls to a minimum value at the surface. From the plots in Figs. 10, 11, 12, 13, 14 and 15 it is noticeable that the energy conditions for charged fluid sphere are obeyed for the chosen compact objects in our model. In the context of MIT Bag model EOS and density dependent B parameter [81], we study the stability of quark stars constitute with u, d and s quarks and try to explore the possibility of different compact stars to be a candidate of quark star family. Here we consider density dependent $B(\rho )$ for which energy density of the system can be related to the baryon number density. Subsequently the energy per baryon can be related to $B(\rho )$ through the relation $E_B=2\sqrt{3}\left( \frac{3\pi ^2B}{4}\right) ^{\frac{1}{4}}$ [105]. Depending on the value of $E_B$ we have three regions: (i) stable ($E_B<930.4$ MeV), (ii) metastable (930.4 MeV $<E_B<$ 939 MeV) and (iii) unstable ($E_B>939$ MeV). We consider a polynomial relation [104] between bag parameter B and energy density $\rho$ and find the energy per baryon ($E_B$) of the system. The variation of $E_B$ is studied as a function of $\rho$. The plots show that in case of HER X-1 when $D=4$ the interior of the star consists of stable strange quark matter having energy per baryon less than that of $^{56}Fe$ ($E_B<930.4$ MeV). For $D=5$ and 6 the stability window decreases and a thin metastable region is formed above which quarks are unstable. For $D>6$ the stable and metastable region disappears and the whole star is found to be composed of unstable quarks only. For PSR J 1614-2230 and EXO1745-248 a similar type of variation is observed and it is noticed that bulk strange quark is stable upto $D = 5$. This observation signifies that a three layered structure is possible for the compact objects in which the core consists of stable strange quarks, an intermediate layer of metastable quarks which holds the core and the outer region containing unstable quarks. From Figs. 20, 21 and 22 it is obvious that charge of the system has a major influence on the stability of 3-flavour quarks. With inclusion of charge, the unstable region increases at the cost of decrement of stability window. Thus we may conclude that hadronic phase increases with an increase of charge of a stellar system consisting of 3-flavour quarks. In this model we have predicted radius of compact objects HER X-1, PSR J1614-2230 and EXO1745-248 which are shown in tabular form in Tables 5 , 6 and 7. It is worthwhile to note that for $D=4$ a star has more radius for increased value of charge anisotropy ($\gamma$) which is physically relevant as for instance higher amount of charge increases coulomb repulsion which counterbalances the inward gravitational pull. However according to Cooperstock and La Cruz [109] a charged star should obey the condition $M^2>Q^2$ and the effect of mass on equilibrium over charge rapidly increases for $D>4$ (Figs. 23, 24, 25). Therefore in higher dimensions, gravity dominates over coulomb repulsion and the star shrinks to a lower radius. However this does not assert that the star will be ended up with collapse. To study the effects of dimensions on the stability window, we have plotted $E_B$ vs $\rho$ for different dimensions. Plots are shown in Figs. 16 , 17 and 18. It is noted that as space-time dimension increases, $E_B$ picks up higher values and beyond a specific dimension the value of energy per baryon $E_B > 939$ MeV implying unstable quark matter. Such configuration may be looked upon as pure hadronic star.

Table 8 Variation of $G_D\frac{M}{R_{b}^{D-3}}$ with space-time dimensions

We have also determined the maximum compactness in different space-time dimensions (D) and are tabulated in Table 8. The nature of variation is similar to that as obtained by Paul [65]. The mass–radius plot for compact objects is shown in Fig. 26 from which it is noted that the maximum mass of 1.773 $M_{\odot }$ is attainable with density dependent B parameter and is more relative to the value of mass 1.684 $M_{\odot }$ when a constant B is considered. We also note that the maximum radius is about 10.03 km for density dependent B whereas it reduces to the value 9.22 km when a constant value of B is assumed. The maximum surface redshifts are 0.446 and 0.471 for density dependent and constant B respectively. Both are well below the limit $z_s<5$ given by Böhmer and Harko [121] and also consistent with the upper limit $z_s<5.211$ predicted by Ivanov [19]. Following Zeldovich and Novikov [111] condition the maximum central densities are found to be $2.428\times 10^{15}$ g/cm$^3$ and $2.699\times 10^{15}$ g/cm$^3$ respectively for $B(\rho )$ and constant B. The stability of the system is studied with the help of (i) generalized TOV equation, (ii) Herrera cracking criteria and (iii) variation of adiabatic index. Equilibrium of the system in terms of generalized TOV equation demands that different forces i.e. $F_g$, $F_h$, $F_e$ and $F_a$ must be balanced as indicated in Figs. 28, 29 and 30. The fulfilment of Herrera cracking criteria and adiabatic index are shown graphically in Figs. 31 and 32 and it is obvious that all these conditions are well obeyed.