Stellar model with non-zero strange quark mass ($m_s\ne 0$) and Mak–Harko density profile admitting observational results

Abstract

This article describes the configuration of strange quark stars composed of three flavour quarks in hydrostatic equilibrium considering the energy density profile of Mak and Harko and non-zero strange quark mass ($m_s\ne {0}$). A suitable stellar model is proposed assuming equation of state of interior matter as modified MIT equation of state in bag model $p=\frac{1}{3}(\rho -4B_g)$, where $B_g$ is known as bag constant, to predict the viability of strange stars. The interior of such compact stars is mainly composed of quarks and electrons to establish charge neutrality condition. We have checked the various stability windows depending on the energy per baryon for different values of bag constant $B_g$ and mass of strange quark $m_s$. We have studied the effect of non-zero mass of the strange quark ($m_s$) on the physical properties of the strange star in the context of the modified MIT bag equation of state. We note that the maximum stellar mass decreases with increasing $m_s$. The model is suitable for predicting the radius, central density and other properties of compact stars having mass $\le 2.01M_{\odot }$, such as $4U~1820-30$, $PSR~J1614-2230$ etc, which are supposed to be strange stars. The radius of few recently observed compact stars are predicted in our model and they are found to be compatible with the value as predicted from observation. The model is found to be suitable in view of all the necessary criterion along with fulfilment of stability of the stellar configuration as well as stable in view of small radial perturbations.

1 Introduction

Compact objects are formed at the final stage of evaluation process of the main sequence star. Due to the presence of ultrahigh density, compact objects are of key importance in the present day for studying the properties of matter in such a high density regime. The Neutron star/Strange star is a type of gravitationally collapsed star, that is supported mainly by degenerate neutron/quark pressure. Although theoretical models have improved considerably in recent years, due to a lack of clear knowledge about particle interactions beyond nuclear density, many observed properties, such as the mass and radius, of many compact objects such as the $HER~X-1$, a known X-ray pulsar, millisecond pulsar $SAX~J1808.4-3658$, $4U~1820-30$ (X-ray burster), X-ray sources $PSR~0943+10$ and $4U~1728-34$ may not be predicted from available neutron star models in good aggreement. In the model of compact objects, it is well established that the maximum mass depends on many factors. One such factor is the obvious equation of state of the interior matter. According to Chandrashekhar [1, 2] the upper mass limit of White Dwarfs is 1.4 $M_{\odot }$, where $M_{\odot }$ is the solar mass. Very recently Das and Mukhopadhyay [3] proposed that the maximum mass of a White Dwarf could reach 2.58 $M_{\odot }$ assuming the existence of high value of magnetic fields in consequence of comparatively smaller number of occupied Landau layers. However, for neutron stars, there is no such specific definition of maximum mass. Hence, the maximum mass of this class is still a debatable issue among researchers. The maximum mass of a neutron star (henceforth NS) is dependent on the equation of state (henceforth EoS). Additionally, the EoS depends on the internal structure of the stellar configuration. Therefore, it is recommended to assume the internal composition properly of a compact object. Moreover, the observed properties of many compact objects, which are assumed to be NS, are not in good agreement with those predicted from standard neutron star model available to date. It is considered that the existence of strange quark matter (henceforth SQM) inside of such compact stars may be useful for predicting the observed physical features of such compact stars [4, 5]. Itoh [6] first pointed out that quark stars may exist in the hydrostatic equilibrium. These compact objects may be into the Strange Star (henceforth SS) family. In 1964, Gell-Mann [7] and George Zweig [8] independently proposed that hadrons are composed mainly of more fundamental particle quarks. Bodmer [9] argued that the strange matter composed of u, d and s quarks likely to be the absolute ground state of matter at the condition of zero temperature and pressure. Since the 3-flavour quark has less energy per baryon, it is more stable than the quark matter consistent with two flavour quarks (u and d). According to Witten [10] strange matter may be stable at zero external pressure and temperature, and this may constitute the true ground state of quantum chromodynamics (QCD). Dai et al. [11] predicted that after a explosion of supernova, the core of a comparatively massive star collapses and transforms into a star, which may be strange star, through a first or second order phase transition. The core of a neutron star is a favourable environment where ordinary matter may be converted into strange quark matter [12]. Alford [13] also proposed that inside the core environment of a neutron star, the presence of low temperature and suitable high density is sufficient to convert the hadronic matter into a deconfined quark matter.

It is important to consider the EoS of strange quark matter to study its properties. In the MIT bag model, the quark matter is assumed to be massless up (u), down (d) quarks, massive strange (s) quark and electrons ($e^{-}$). Such composition ensures that charge neutrality condition of quark matter. Such assembly of quarks is supposed to form degenerate Fermi gas exist only in a region of space called ’bag’ in MIT bag model, characterised by vacuum energy density $B_g$, which is also known as ’bag constant’. The term $B_g$ is the deference of perturbative and non perturbative vacuum energy. The MIT bag model may be useful for obtaining a relevant EoS for quark matter, assuming zero quark mass, and is given as follows [14]:

$$\begin{aligned} p=\frac{1}{3}(\rho -4B_g), \end{aligned}$$

(1)

where p is the pressure and $\rho$ is the energy density. Previously many authors [10, 15,16,17,18] have also studied such compact objects using the quark matter equation of state. In the articles [19,20,21,22,23,24,25] authors have studied strange quark star in $\beta$-equilibrium condition. Hybrid quark stars with quark matter in the core region have also been studied by several authors in the Refs. [26,27,28].

In the very early stage of study, researchers thought that there may be some anisotropy in pressure due to several reasons inside the star. These include the presence of superfluidity [29], the presence of a strong magnetic field [30] or slow rotational motion [31]. The work of Bowers and Liang [32] emphasises equation of state for local anisotropic relativistic fluid spheres and also indicates that anisotropy may have some non negligible effect on various parameters such as the maximum mass, stiffness of the equation of state (EoS), and radius. Ruderman [33] suggested that at very high density ($\approx 10^{15}$ g/cm$^{3}$), hadrons are crushed into quarks and that nuclear matter may have some anisotropic features. The term anisotropy in pressure means that the pressure in the radial ($p_r$) and transverse ($p_t$) directions are different at all points inside a star, except at the centre. It is the measure of difference between $p_t$ and $p_r$ and is defined as $\varDelta =p_t-p_r$. Dev and Gleiser [34,35,36] have shown that anisotropic stars are more stable than isotropic stars. Many authors [37,38,39,40,41,42,43,44] have investigated the effect of anisotropy on various physical properties of ultradense spherically symmetric fluid spheres. Many authors have considered different anisotropy profiles inside a star. In their paper, Mak and Harko [45] considered that the value of anisotropy is zero at the stellar centre and reaches a maximum inside the star and then becomes zero at the surface. Paul and Tikekar [46] considered that stellar structures are composed of two parts: an anisotropic core and an isotropic crust. Deb et al. [47] proposed an anisotropic stellar model for strange quark stars with the Mak and Harko [45] density profile assuming the EoS of quark matter as MIT EoS. In these articles [48, 49], the authors addressed the properties of strange stars using numerical integration of mass continuity and hydrostatic equilibrium and obtained numerical values for the maximum mass and radius of compact stars. However, we have considered the EoS of strange matter in presence of non-zero strange quark mass $(m_s)$.

The basic aim of this paper is to develop stellar model to study the effects of the strange quark mass $(m_s)$ on the gross properties of strange stars composed of three flavour quarks. We have considered the Mak and Harko [45] formalism as it is singularity free with functional form of the density possesses a monotonically decreasing nature along radially outward direction and satisfies all the required conditions for a stable configuration. Also, it simplifies the solution of Einstein field equations. Using the Mak and Harko density profile [45] and most general forms of the EoS of strange quark matter with $m_s\ne 0$, we have solved the Einstein Field Equations (henceforth EFE) to determine the $g_{rr}$ and $g_{tt}$ metric components. The solutions are subsequently used to solve the TOV equation to evaluate the possible maximum mass and radius of the strange star. We have noted some interesting results. With this model, it is possible to predict the radii of compact stars, which are assumed to be strange stars. For our analysis, we consider the range of bag constants ($B_g$) to be $57.55<B_g<95.11$ MeV/fm$^3$, for which strange matter is supposed to be stable relative to neutrons at zero external pressure. However, this range is modified in the presence of non-zero $m_s$. Different stability windows are explored depending on the values of $m_s$ and $B_g$.

The present paper is organised as follows: In Sect. 2, we studied the thermodynamical consequences of SQM and the constraints on the bag constant ($B_g$) for different stability windows of 3 flavour quark matter. In Sect. 3, we solved the EFE considering the Mak and Harko energy density profile inside the star. The metric potentials, general physical parameters and bounds on them are obtained in Sect. 4. In Sect. 5, we have discussed some physical applications of the present model by considering different known compact objects. The maximum mass and radius from our model is given in Sect. 6. We have also checked the various stability conditions in Sect. 7. Finally in Sect. 8, we present the conclusions of our model.

2 Thermodynamics inside the quark star

In the presence of high density and pressure inside a compact object, neutrons are assumed to be crushed into quarks, which remain in equilibrium and maintain charge neutrality throughout the interior of the star. These quarks constitute a single colour singlet baryon with baryon no A. Since quarks are fermions, the quark matter may be considered to be a Fermi gas of 3A quarks. The dynamics of quark confinement are approximated in the bag model [4, 15] using the following dynamical equation:

$$\begin{aligned} p= & {} \sum _{i=u,d,s,e^{-}}p_i-B_g \end{aligned}$$

(2)

$$\begin{aligned} \rho= & {} \sum _{i=u,d,s,e^{-}}\rho _i+B_g, \end{aligned}$$

(3)

where $p_i$ and $\rho _i$ are the pressure and energy density, respectively, of the ith type quarks. According to the work of [50], we also consider here that the interior of a star is composed mainly of up, down and strange quarks along with electrons ($e^{-}$). The existence of charm quarks is ruled out because charm stars are unstable against radial oscillations [4]. The charge neutrality condition of a strange star reads as follows:

$$\begin{aligned} \sum _{i=u,d,s,e^{-}} n_iq_i=0, \end{aligned}$$

(4)

where $q_i$ is termed as the charge and $n_i$ is known as the number density of the ith type particles. The expressions for the pressure ($p_i$), energy density ($\rho _i$) and number density ($n_i$) of quarks and leptons contained within the bag are obtained from the thermodynamic potential as:

$$\begin{aligned} d\varOmega _i=-S_idT-P_idV-N_id\mu _i. \end{aligned}$$

(5)

From Eq. (5), one can obtain the following expressions:

$$\begin{aligned} p_i= & {} \frac{g_iT}{2\pi ^2}\int _{0}^{\infty }dk_ik_i^2 ln\left[ 1+e^{-(E_i-\mu _i)/T}\right] ,\nonumber \\= & {} \frac{g_i}{6\pi ^2}\int _{m_i}^{\infty }\left( E_i^2-m_i^2\right) ^{3/2}f(E_i)dE_i, \end{aligned}$$

(6)

$$\begin{aligned} \rho _i= & {} \frac{g_i}{2\pi ^2}\int _{m_i}^{\infty }E_i^2\left( E_i^2-m_i^2\right) ^{1/2}f(E_i)dE_i, \end{aligned}$$

(7)

$$\begin{aligned} n_i= & {} \frac{g_i}{2\pi ^2}\int _{m_i}^{\infty }E_i\left( E_i^2-m_i^2\right) ^{1/2}f(E_i)dE_i, \end{aligned}$$

(8)

where $E_i^2=k^2+m_i^2$ and $m_i$ is the mass of the ith particle. The degeneracy factor for quarks is $g_i=6$ and that for lepton is 2. The function $f(E_i) =\frac{1}{1+e^{-(E_i-\mu _i)/T}}$ is known as the Fermi-Dirac distribution function. The necessary chemical equilibrium between the quark flavours and electrons are maintained, following the weak interactions given below:

$$\begin{aligned}{} & {} d\rightarrow u+e^{-}+\bar{\nu _{e^-}}, \end{aligned}$$

(9)

$$\begin{aligned}{} & {} \quad s\rightarrow u+e^{-}+\bar{\nu _{e^-}}, \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \quad s+u \longleftrightarrow d+u. \end{aligned}$$

(11)

The Eq. (11) contributes to the equilibrium conditions of different quark flavours. Again, the chemical potential of neutrinos can be equated to zero as they escape from the star. Therefore, to maintain equilibrium condition, we must have

$$\begin{aligned}{} & {} \mu _d=\mu _u+\mu _e, \end{aligned}$$

(12)

$$\begin{aligned}{} & {} \quad \mu _s=\mu _u+\mu _e, \end{aligned}$$

(13)

$$\begin{aligned}{} & {} \quad \mu _s=\mu _d\equiv \mu , \end{aligned}$$

(14)

where $\mu _{i}$ is the chemical potential of the ith particle ($i=u,d,s,e^{-}$). Since the chemical potentials given in Eqs. (12)–(14) are much greater than the temperature of the star, we can approximate the temperature of the star to approach zero ($T\rightarrow 0$). Although we are dealing with the situation with non-zero strange quark mass ($m_s\ne 0$), we first focused on the situation where the masses of quarks are assumed to be negligible or zero.

2.1 EoS of strange matter with zero quark mass ($m_s=0$)

If all the quarks are supposed to be massless, the expressions for $\rho _i$, $p_i$ and $n_i$ at an absolute zero temperature are approximated as

$$\begin{aligned} p_i= & {} \frac{g_i}{24\pi ^2}\mu ^4\eta _{i}^4, \end{aligned}$$

(15)

$$\begin{aligned} \rho _i= & {} \frac{g_i}{8\pi ^2}\mu ^4\eta _{i}^4, \end{aligned}$$

(16)

$$\begin{aligned} n_i= & {} \frac{g_i}{6\pi ^2}\mu ^3\eta ^3_{i}, \end{aligned}$$

(17)

where,

$$\begin{aligned} \eta _i= & {} 1-x, i=u \nonumber \\{} & {} \hspace{-0.4cm} =1,\;\;\;\;\;\;\;\;i=d,s \nonumber \\{} & {} \hspace{-0.4cm} =x,\;\;\;\;\;\;\;\;i=e^{-} \end{aligned}$$

(18)

with $x=\frac{\mu _e}{\mu }$, as presented in [4]. Then, using Eqs. (2), (3), (15) and (16), one can establish the relation between $\rho$ and $p_r$, as given in Eq. (1), also known as the equation of state (EoS) for strange quark matter (SQM) which has massless quarks in the MIT bag model.

2.2 EoS of strange matter with non-zero quark mass ($m_s\ne 0$)

In this case, as $T\rightarrow 0$, we have the following expressions from Eqs. (6)–(8):

$$\begin{aligned} p_i&{=}&\frac{g_i\mu ^4\eta _i^4}{24\pi ^2} \left[ \sqrt{1-z_i^2}\left( 1{-}\frac{5}{2}z_i^2\right) {+} \frac{3}{2}z_i^4ln\frac{1{+}\sqrt{1{-}z_i^2}}{z_i}\right] ,\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned} \rho _i&{=}&\frac{g_i\mu ^4\eta _i^4}{8\pi ^2}\left[ \sqrt{1-z_i^2} \left( 1-\frac{1}{2}z_i^2\right) {-} \frac{1}{2}z_i^4ln\frac{1{+}\sqrt{1-z_i^2}}{z_i}\right] ,\nonumber \\ \end{aligned}$$

(20)

$$\begin{aligned} n_i&{=}&\frac{g_i\mu ^3\eta _i^3}{8\pi ^2}\left[ 1{-}z_i^2\right] ^{\frac{3}{2}}, \end{aligned}$$

(21)

where $z_i$ is defined as: [4]

$$\begin{aligned} z_i=\frac{m_i}{\mu _i} \end{aligned}$$

(22)

The necessary condition for overall charge neutrality defined in Eq. (4) becomes:

$$\begin{aligned} 2\left( 1-\frac{\mu _{e^-}}{\mu }\right) ^3-\left( \frac{\mu _{e^-}}{\mu }\right) ^3-\left[ 1-\left( \frac{m_s}{\mu }\right) ^2\right] ^{\frac{3}{2}}-1=0\nonumber \\ \end{aligned}$$

(23)

Now, with the help of Eqs. (19–22), we obtain a general relation between the radial pressure and energy density in the presence of a strange quark mass as,

$$\begin{aligned} p_r=\frac{\rho -4B_1}{3} \end{aligned}$$

(24)

where $B_{1}=\frac{4B_g+\rho _s-3p_s}{4}$, $\rho _s=$ energy density and $p_s=$ pressure for the s quark. Since the radial pressure ($p_r$) vanishes at the surface of the star, we can evaluate the chemical potentials of different quarks and electrons corresponding to a constant bag ($B_g$) and strange quark mass ($m_s$). Again, at the boundary ($r=R$), as the radial pressure ($p_r$) is zero, from Eq. (24), we obtain $\rho _0=4B_1$, where $\rho _0$ is the surface density.

Fig. 1

Variation of the chemical potential of different quarks with $B_g$ at zero external pressure for two different $m_s$. Here, the red and black lines indicate chemical potential of s and u quarks, respectively. The solid and dashed lines indicate $m_s=~150$ MeV and 100 MeV, respectively. In the insight figure, the variations in the chemical potential for electrons is shown

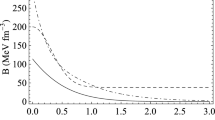
In Fig. 1, we show the variation in the chemical potential ($\mu$) against $B_g$ for zero external pressure. It is observed that as $\mu$ increases with $B_g$, $\mu _e$ decreases. Additionally, the difference in chemical potential between the quarks and electrons increases with increasing strange quark mass. Therefore, for a high strange quark mass, a small amount of electrons are required for charge neutrality of the system. Additionally, since the masses of electrons are small compared to the quark mass, the presence of electrons has a negligible effect on the average properties of the star. However, the presence of electrons is important for core-envelope structure formation [51, 52], which is beyond the scope of our present paper. We also checked the variation in energy per baryon ($E_B$) with bag value for different strange quark masses. For the 3 flavour quark matter structure to be stable relative to that of $Fe^{56}$, the energy per baryon should be lower than 930.4 MeV, which is the typical value of energy per baryon of $Fe^{56}$. Again, if the corresponding energy per baryon lies in the range 930.4 $<E_B<939$ MeV, there is a probability of metastable strange quark matter [53]. For any higher values of $E_B$ ($E_B>939$ MeV), the quark matter becomes unstable. Following Eq. (21), the expression for the baryon number density for the 3 flavour strange quark matter is $n_A=\frac{1}{3}\sum _{i=u,d,s}n_i$. We calculated the energy per baryon ($E_B$) for different masses of strange quark masses and plotted the same as a function of different bag values, as shown in Fig. 2. Since $E_B$ has a limiting value, relative to the stable, metastable state, we obtain an upper bound on the bag value depending on the strange quark mass ($m_s$). The restriction on bag constant is tabulated in Table 1.

Fig. 2

Variation of energy per baryon ($E_B$) for 3 flavour quarks with $B_g$ at zero external pressure

Table 1 Constraint on bag constant in MeV/fm$^3$ for different stability windows for different strange quark masses ($m_s$) at zero external pressure

Table 1 clearly shows that so far the stability quark matter is assumed, of $m_s$ has some effect on the value of $B_g$, for which the SQM is stable, metastable or unstable. If the value of $m_s$ increases, $B_g$ has a lower value in all three regions discussed in Table 1,

3 Field equations and their solution

The interior space-time of a static and spherically symmetric fluid sphere is defined by the line element of the type,

$$\begin{aligned} ds^2=-e^{\nu (r)}dt^2+e^{\lambda (r)}dr^2+r^2(d{\theta ^2}+\sin ^2{\theta }d{\phi ^2}), \end{aligned}$$

(25)

where $e^{\nu (r)}$ and $e^{\lambda (r)}$ are the unknown metric potentials and are functions of radial co-ordinate r only. The Einstein Field Equation, connecting matter and associated space-time geometry is given by:

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R=\frac{8{\pi }G}{c^4}T_{\mu \nu }, \end{aligned}$$

(26)

where $R_{\mu \nu }$ is termed as Ricci tensor, R is the Ricci scalar. G is the Newtonian gravitational constant. For fluid containing anisotropic pressure, the energy momentum tensor $T_{\mu \nu }$ is given as,

$$\begin{aligned} T_{\mu \nu }=\text{ diag }~(-\rho ,p_r,p_t,p_t), \end{aligned}$$

(27)

where $\rho$ is termed as energy density, $p_r$ and $p_t$ represent the radial and tangential parts of the pressure, respectively. Combining Eqs. (25), (26) and (27), we obtain the following three equations, (taking $8{\pi }G=1,c=1$):

$$\begin{aligned} \rho= & {} \frac{\lambda ^{\prime }e^{-\lambda }}{r}+\frac{1-e^{-\lambda }}{r^2}, \end{aligned}$$

(28)

$$\begin{aligned} p_r= & {} \frac{\nu ^{\prime }e^{_\lambda }}{r}-\frac{1-e^{-\lambda }}{r^2}, \end{aligned}$$

(29)

$$\begin{aligned} p_t= & {} e^{-\lambda }\left[ \frac{\nu ^{\prime \prime }}{2}+\frac{{\nu ^{\prime }}^2}{4}+\frac{\nu ^{\prime }-\lambda ^{\prime }}{2r}-\frac{\nu ^{\prime }\lambda ^{\prime }}{4}\right] , \end{aligned}$$

(30)

where “$\prime$” denotes differentiation with respect to r. We also consider here that $\varDelta =(p_t-p_r)$ as the measure of anisotropy in pressure following the references [54,55,56,57]. The mass function, i.e., the total mass of the star contained within a radius r is defined as,

$$\begin{aligned} m(r)=4\pi \int _{0}^{r}\rho (r)r^2dr \end{aligned}$$

(31)

Following the work of Mak and Harko [45], we consider that the matter density profile $\rho (r)$ within the star varies with the radial distance r following the expression given below:

$$\begin{aligned} \rho (r)=\rho _c\left[ 1-\left( 1-\frac{\rho _0}{\rho _c}\right) \frac{r^2}{R^2}\right] , \end{aligned}$$

(32)

where $\rho _c$ and $\rho _0$ are termed as central density and density at surface ($r=R$) respectively. Using Eqs. (31) and (32), we obtain the total mass of the star having radius R as,

$$\begin{aligned} M=\frac{R^3}{30}(12B_1+2\rho _c) \end{aligned}$$

(33)

4 Metric potentials and general model parameters

Solving Eqs. (28)–(30), with the help of Eqs. (24) and (32), we obtain the various physical parameters of the star as follows:

$$\begin{aligned} \lambda (r)= & {} -\ln \left[ 1-\frac{r^2\rho _c}{3}+\frac{r^4(\rho _c-4B_1)}{5R^2}\right] , \end{aligned}$$

(34)

$$\begin{aligned} \nu (r)= & {} \frac{c_1}{3}\left[ \tanh ^{-1}\frac{R(24B_1-\rho _c)}{c_2}\right. \nonumber \\{} & {} \left. -\tanh ^{-1}\frac{24B_1r^2+(5R^2-6r^2)\rho _c}{c_2R}\right] -\frac{2}{3}\ln \left[ 5R^2\right. \nonumber \\{} & {} \left. (r^2\rho _c-3)+3r^4(4B_1-\rho _c)\right] + c_3, \end{aligned}$$

(35)

$$\begin{aligned} p_r= & {} \frac{1}{3}(\rho _c-4B_1)\left[ 1-\frac{r^2}{R^2}\right] , \end{aligned}$$

(36)

$$\begin{aligned} p_t=\frac{c_4r^2+c_5r^4+c_6r^6-15R^4(\rho _c-1)}{3R^2\left[ 5R^2(r^2\rho _c-3)-3r^4(\rho _c-4B_1)\right] }, \end{aligned}$$

(37)

and the pressure anisotropy $\varDelta =p_t-p_r$ is given by

$$\begin{aligned} \varDelta = \frac{c_7r^4+c_8r^6+c_9r^2}{3R^2\left[ 5R^2(r^2\rho _c-3)-3r^4(\rho _c-4B_1)\right] }, \end{aligned}$$

(38)

where,

$$\begin{aligned} c_1= & {} \frac{12B_1R-R\rho _c}{\sqrt{R^2\rho _c^2-\frac{36\rho _c}{5}+\frac{144B_1}{5}}}, \end{aligned}$$

(39)

$$\begin{aligned} c_2= & {} \sqrt{720B_1+5\rho _c(5R^2\rho _c-36)}, \end{aligned}$$

(40)

$$\begin{aligned} c_3= & {} \ln \left[ 1-\frac{2R^2}{15}(\rho _c+6B_1)\right] \nonumber \\{} & {} +\frac{2}{3}\ln \left[ R^2\left\{ 2R^2(\rho _c+6B_1)-15\right\} \right] , \end{aligned}$$

(41)

$$\begin{aligned} c_4= & {} \left[ 30R^2\rho _c+10B_1R^4\rho _c-120B_1R^2\right. \nonumber \\{} & {} \left. -20B_1^2R^4-5R^4\rho _c^2\right] , \end{aligned}$$

(42)

$$\begin{aligned} c_5= & {} \left[ 64R^2B_1^2-36R^2B_1\rho _c+5R^2\rho _c^2\right] , \end{aligned}$$

(43)

$$\begin{aligned} c_6= & {} \left[ 16B_1\rho _c-32B_1^2-2\rho _c^2\right] , \end{aligned}$$

(44)

$$\begin{aligned} c_7= & {} \left[ 112B_1^2R^2-80R^2B_1\rho _c+13R^2\rho _c^2\right] , \end{aligned}$$

(45)

$$\begin{aligned} c_8= & {} \left[ 40B_1\rho _c-80B_1^2-5\rho _c^2\right] , \end{aligned}$$

(46)

$$\begin{aligned} c_9= & {} \left[ 30R^4\rho _cB_1-60R^2B_1-20R^4B_1^2 \right. \nonumber \\{} & {} \left. -10R^4\rho _c^2+15R^2\rho _c\right] . \end{aligned}$$

(47)

From Eq. (36), it is evident that $p_r=~0$ at $r=R$. However, the tangential pressure has a non-zero finite value at the surface, as evident from Eq. (37).

4.1 Boundary conditions

To construct a physically realistic stellar model the following conditions are satisfied in the interior of the star as well as at the boundary:

• 1. The interior solution should be matched at the stellar boundary with the exterior solution as established by Schwarzschild given below:

  $$\begin{aligned} ds^2= & {} -\left( 1-\frac{2M}{r}\right) dt^2+\left( 1-\frac{2M}{r}\right) ^{-1}dr^2 \nonumber \\{} & {} +r^2\left( d{\theta ^2}+\sin ^2{\theta }d{\phi ^2}\right) , \end{aligned}$$

  (48)

  where M represents the total mass of the star. Matching the interior and exterior solutions, we obtain $e^{\nu (r=R)}=e^{-\lambda (r=R)}=(1-\frac{2M}{R})$.

• 2. The metric potentials and physical parameters related to the stellar configuration should be well defined throughout the interior of the star as well as at the centre.

• 3. In the interior of a compact star the radial and tangential components of sound velocity should satisfy the necessary causality conditions, which indicates that the square of the radial velocity ($v_{r}^2$) and tangential velocity ($v_{t}^2$) of sound must lie in the range $0\le v_{r}^2 \le 1$, $0\le v_{t}^2 \le 1$ or equivalently $(\frac{dp_r}{d\rho })\le 1$ and $(\frac{dp_t}{d\rho })\le 1$, as $c=1$.

• 4. The radial pressure should vanish at the stellar surface, i.e., $p_r(R )=0$ [58].

• 5. The energy density ($\rho$), radial pressure ($p_r$) and transverse pressure ($p_t$) should be continuous, positive and monotonically decreasing function of r from the centre to the surface. Additionally the pressure to density ratio should follow the Zeldovich condition [59, 60] from the centre to the surface, i.e., $\frac{dp}{d\rho }<1$

5 Physical application

To describe the physical application of the model, we considered two known compact objects whose mass and radius are known from observations, namely: (1) $4U~1820-30$ with estimated mass and radius $1.46~M_\odot$ and $11.1\pm 1.8$km [61] and (2) $SMC~X-4$ with estimated mass and radius $1.29~M_\odot$ and $8.831\pm 0.09$ km [62]. Different physical parameters like metric potentials, energy density, radial pressure, transverse pressure and anisotropy are determined in the presence of non-zero value of $m_s$ to study the effect of $m_s$ on these parameters. In Fig. 3 the variations in metric potentials ($e^{\lambda (r)}$ and $e^{\nu (r)}$) are shown and it is evident that $m_s$ has some effect on the potentials. It is evident from Fig. 3 that throughout the star except for the surface, the value of $e^{\nu }$ decreases with increasing $m_s$ but at the surface $m_s$ has no effect on $e^{\nu }$. However, at the centre, $e^{-\lambda (r)}$ is independent of $m_s$ but away from the centre, $e^{-\lambda (r)}$ also decreases with increasing $m_s$. Thus, as metric potentials are related to the mass and properties of the star, it may be noted here that $m_s$ have some effect on the maximum mass, radius and other relevant properties. The variations in physical parameters such as the energy density, and pressure of the two compact objects as noted above, are shown in Figs. 4, 5, 6, 7, 8, 9, 10 and 11 and it is noted that $m_s$ has some effect on these parameters. Figure 12 shows the variation in the predicted radius for $4U~1820-30$ and $SMC~X-4$ with respect to $m_s$ for two different $B_g$. Figure 13 shows the variation in the radius of two stars with respect to $B_g$ for different values of $m_s$. For the estimation of the radius, we assumed that the pressure anisotropy becomes extreme at the surface [47]. This gives the following condition for the radius (R) in terms of the star central density $\rho _c$ and $B_1$,

$$\begin{aligned} \rho _c= & {} \frac{1}{4R^2+B_1R^4}\left[ 15+14B_1R^2-4B_{1}^2R^4\right. \nonumber \\{} & {} \left. -\sqrt{\left( 225-60B_1R^2-1076B_1^2R^4-400B_0^3R^6+400B_0^4R^8\right) }\right] . \qquad \end{aligned}$$

(49)

Fig. 3

Variation of metric potentials $e^{-\lambda }$ and $e^\nu$ with r for $4U~1820-30$ and $SMC~X-4$ taking different $m_s$ and $B_g=64$ MeV/fm$^3$. The black colour represents $m_s=~0$ MeV. The solid, dashed and dot-dashed lines indicate $m_s=~50,100$ and 150 MeV, respectively. The red and blue lines indicate plots of $e^{-\lambda }$ and $e^{\nu }$ for $4U~1820-30$ and $SMC~X-4$, respectively

Fig. 4

Variation of $\rho$ with radial distance r of $4U~1820-30$ for different values of $m_s$ for $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dot-dashed lines represent $m_s=50,100$ and 150 MeV respectively

Fig. 5

Variation of $\rho$ with r of $SMC~X-4$ for different values of $m_s$ for $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dot-dashed lines represent $m_s=50,100$ and 150 MeV respectively

Fig. 6

Variation of $p_r$ with respect to radial distance r of $4U~1820-30$ for different values of $m_s$ for $B_g=~64$ MeV/fm$^3$. Here, the solid, dashed and dot-dashed lines represent $m_s=50,100$ and 150 MeV respectively

Fig. 7

Variation of $p_r$ with r inside $SMC~X-4$ for different $m_s$ with $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dot-dashed lines represent $m_s=50,100$ and 150 MeV respectively

Fig. 8

Variation of $p_t$ with r of $4U~1820-30$ for different values of $m_s$ for $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dot-dashed lines represent $m_s=50,100$ and 150 MeV respectively

Fig. 9

Variation of $p_t$ with radial distance r of $SMC~X-4$ for different values of $m_s$ taking $B_g=64$ MeV/fm$^3$. Here solid, dashed and dot-dashed lines represent $m_s=50,100$ and 150 MeV respectively

Fig. 10

Variation of $\varDelta$ with r inside $4U~1820-30$ for different values of $m_s$ for $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dot-dashed lines represent $m_s=50,100$ and 150 MeV respectively

Fig. 11

Variation of $\varDelta$ with r inside $SMC~X-4$ for different $m_s$ for $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dot-dashed lines represent $m_s=50,100$ and 150 MeV respectively

Fig. 12

Variation of the predicted radius with $m_s$ for $B_g=57.55$ MeV/fm$^3$. Here, the solid and dashed lines indicate the variation for $4U~1820-30$ and $SMC~X-4$, respectively

Fig. 13

Variation of the radii of $4U~1820-30$ and $SMC~X-4$ with different $B_g$ for $m_s=50,100$ and 150 MeV, indicated by the solid, dashed and dot-dashed lines, respectively. The red, cyan and black colours represent stable, metastable and unstable regions, respectively

5.1 Energy condition

In general relativity, to evaluate a physically viable energy momentum tensor for fluid distribution, energy conditions are imposed. In general, such energy conditions are very helpful in determining the characteristic properties of fluid distribution without actually knowing the exact specifications of the interior structure of composed matter. Therefore, it may be possible to evaluate the physical behaviour of some of the extreme astrophysical phenomenons, like collapse of gravitating body or existence of space-time singularity, without adequate knowledge related to energy density of matter or its pressure. In principle, the analysis of energy conditions in astrophysical context is an algebraic problem [63], more precisely the eigenvalue problem related to the energy momentum tensor. Particularly, it may be told that general relativity cannot be taken into account if fluids violet the important energy conditions such as, SEC, WEC, NEC or DEC. The study of energy conditions of fluid in a 4-dimensional space-time leads to solutions of a 4 degree polynomial to get its roots, but it is complicated due to difficulty in finding the analytical solutions for eigenvalues. Even though it is difficult to obtain the general solutions for the roots, a physically realistic fluid distribution must follow the energy conditions known as the dominant, weak, null and strong energy conditions [63,64,65] simultaneously within the stellar configuration. For any fluid in 4 dimensions with pressure anisotropy, the above energy conditions should be satisfied. Mathematically these energy conditions can be expressed as follows [66, 67]:

• 1. Dominant Energy Condition (DEC: $\rho \ge 0,~\rho - p_{r}\ge 0,~\rho - p_{t}\ge 0$).

• 2. Weak Energy Condition (WEC: $\rho + p_{r}\ge 0,~\rho \ge 0, \rho + p_{t}\ge 0$).

• 3. Null Energy Condition (NEC: $\rho + p_{r}\ge 0,~\rho + p_{t} \ge 0$).

• 4. Strong Energy Condition (SEC: $\rho + p_{r}\ge 0,~\rho + p_{r} + 2p_{t}\ge 0$).

Moreover, the dominant energy condition indicates that the speed of sound energy within the stellar configuration should lie below the speed of light [68]. The variations in the different energy conditions for $4U~1820-30$ and $SMC~X-4$ are shown in Figs. 14, 15, 16, 17 and 18. These figures show that necessary energy conditions as discussed above are fully satisfied throughout the stellar interior and also at the surface of the stars in the presence of non-zero $m_s$.

Fig. 14

Variation of $(\rho +p_r)$ with respect to r of $4U~1820-30$ (red line) and $SMC~X-4$ (blue line) for different $m_s$ taking $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dotted lines represent $m_s=50,100$ and 150 MeV respectively

Fig. 15

Variation of $(\rho +p_t)$ with r of $4U~1820-30$ (red) and $SMC~X-4$ (blue) for different $m_s$ and $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dotted lines represent $m_s=50,100$ and 150 MeV respectively

Fig. 16

Variation of $(\rho +p_r+2p_t)$ with r of $4U~1820-30$ (red) and $SMC~X-4$ (blue) for different $m_s$ taking $B_g=64$ MeV/fm$^3$. The solid, dashed and dotted lines indicate $m_s=50,100$ and 150 MeV respectively

Fig. 17

Variation of $(\rho -p_r)$ with r of $4U~1820-30$ (red) and $SMC~X-4$ (blue) for different $m_s$, taking $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dotted lines represent $m_s=50,100$ and 150 MeV respectively

Fig. 18

Variation of $(\rho -p_t)$ with radial distance r of $4U~1820-30$ (red) and $SMC~X-4$ (blue) for different values of $m_s$ taking $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dotted lines represent $m_s=50,100$ and 150 MeV respectively

5.2 Causality condition

The validity of the causality conditions, i.e., the radial and transverse sound speed limits, within the interior of the star are shown in Figs. 19 and 20. From Figs. 19 and 20, it is clear that both sound speeds satisfy the causality limits, i.e., $0\le v_{r}^2\le 1$ and $0\le v_{t}^2\le 1$.

Fig. 19

Variation of $v_r^2$ and $v_t^2$ with r of $4U~1820-30$ for different $m_s$ taking $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dot-dashed line indicate the profile of $v_t^2$ from centre to the surface for $m_s=50,100$ and 150 MeV respectively. The solid red line indicates the variation in $v_r^2$

Fig. 20

Variation of $v_r^2$ and $v_t^2$ with r of $SMC~X-4$ for different of $m_s$ taking $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dot-dashed line indicates the profile of $v_t^2$ from centre to the surface for $m_s=50,100$ and 150 MeV respectively. The solid red line indicates the variation in $v_r^2$

Table 2 Maximum mass ($M_{max}(M_\odot )$), corresponding radius ($R_{max}$) and central density ($(\rho _c)_{max}$) for different strange quark masses ($m_s$)

6 Mass-radius relation, maximum mass and surface redshift

The total mass contained within a radius R of a star is given by Eq. (33) for the specific energy density profile as considered in Eq. (32). It is evident that the total mass depends on the radius (R), central density ($\rho _c$) and strange quark mass ($m_s$) through the constant $B_1$. For a static spherically symmetric perfect fluid, the mass M and radius R should satisfy the criterion that $\frac{M}{R}\le \frac{4}{9}$ known as the Buchdahl limit [69]. In Table 2, the maximum mass and corresponding radius are tabulated by solving the TOV equation. It is evident that with the increase of $m_s$ the maximum mass as well as maximum radius both decrease. However, central density ($\rho _c$) increases with increasing $m_s$. Table 4, shows that the mass to radius ratio ($u=\frac{M}{R}$) for compact objects slightly increases with increasing strange quark mass, although it lies within the above specified limit. The mass-radius variations for strange quark masses $m_s=~50,100$ and 150 MeV is shown in Fig. 21. We also studied the variations in mass and radius with respect to central density ($\rho _c$) for different strange quark masses and the variations are shown in Figs. 22 and 23 and it is evident that the Harrison–Zeldovich–Novikov static stability criterion [70, 71] is satisfied for the data set used in the model up to the maximum central density ($\rho _c$) which is tabulated in Table 2 for the parametric choices of $B_g$ and $m_s$. In Figs. 24 and 25, the variation of maximum mass with $B_g$ and $m_s$, respectively are shown. In Fig. 26, dependence of maximum radius of a compact star on $m_s$ is shown. From Figs. 24, 25, 26, it is evident that $m_s$ and $B_g$ have some effect on $M_{max}$ and $R_{max}$. From Table 2, it may be concluded that the radius of many compact stars, which are supposed to be SS, can be predicted using a suitable choice of $m_s$. In Table 3, central density ($\rho _c$), pressure anisotropy at the surface ($\varDelta (r=R)$) and central value of radial pressure ($p_{r0}$) of different compact objects for different values of $m_s$ have been tabulated. Table 3, shows that with increasing strange quark mass, the central density, central pressure and pressure anisotropy at the surface increase. From Table 3, it is also noted that the $2^{nd}$ derivative of $\varDelta$ at $r=R$ (surface) is minimal, indicating that anisotropy has the highest value at the surface in this model. Moreover, both the central density and pressure increase with the increase of $m_s$.

From a statistical point of view, the most important macroscopic variables of a quark star are, the total mass (M), the radius (R), the baryon number density ($n_i$) and the moment of inertia (I) for slow and rigid rotation. However, there is a directly observable parameter called “surface redshift” ($Z_s$), which accounts for the change in frequency of a photon that is travelling radially from the stellar surface to infinity. The expression for the surface redshift $Z_s$ is [72]

$$\begin{aligned} Z_s=\left( 1-\frac{2M}{R}\right) ^{-1/2}-1 \end{aligned}$$

(50)

In Table 4 we have evaluated surface redshift and it is noted that $Z_s$ increases with $m_s$.

Fig. 21

Variation of mass M with radial distance r for $B_g=64$ MeV/fm$^3$ and $m_s=50,100$ and 150 MeV, indicated by the solid, dashed and dot-dashed lines, respectively. The black dotted line corresponds to $B_g=57.55$ MeV/fm$^3$ and $m_s=50$ MeV. Straight lines parallel to radius axis indicate the mass of stars as tabulated in Table 5

Fig. 22

Variation of mass M with central density $\rho _c$ for different values of $m_s$ for $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dot-dashed line indicate $m_s=50,100$ and 150 MeV, respectively

Fig. 23

Variation of the radius R with central density $\rho _c$ for $B_g=~64$ MeV/fm$^3$ and $m_s=~50,100$ and 150 MeV, indicated by the solid, dashed and dot-dashed lines, respectively

Apart from the above analysis, we have estimated the radius of various compact objects having known mass, admitting MIT bag model EoS considering of non-zero strange quark mass (Eq. 24). In our model the observed radius for different strange stars can be predicted for different parametric combinations of $m_s$ and $B_g$ and the results are shown in Table 5.

Fig. 24

Variation of the maximum mass $M_{max}(M_\odot )$ with $B_g$ for different values of $m_s$. The solid, dashed and dot-dashed lines indicate $m_s=50,100$ and 150 MeV, respectively. Red, green and black represent stable, metastable and unstable regions, respectively

Fig. 25

Variation of the maximum mass ($M_{max}(M_\odot$)) with $m_s$ for different $B_g$. The solid and dashed lines indicate $B_g= 64$ MeV/fm$^3$ and 60 MeV/fm$^3$, respectively

Fig. 26

Variation of the maximum radius ($R_{max}$) with $m_s$ for different $B_g$. The solid and dashed lines indicate $B_g=~64$ MeV/fm$^3$ and 60 MeV/fm$^3$, respectively

The

6.1 Moment of Inertia (I)

To derive mass-moment of inertia ($M-I$) plot in this model we use an approximate expression of I of a star as predicted by Bejger and Haensel [75]. According to them [75], a static solution can be transformed into slowly rotating solution having the expression given below:

$$\begin{aligned} I=\frac{2}{5}\left( 1+\frac{(M/R).km}{M_\odot }\right) MR^2. \end{aligned}$$

(51)

Using Eq. (51), we have obtained the variation of mass with the moment of inertia (I) and the plot is shown in Fig. 27 for the EoS given in Eq. (24) with $B_g=64$ MeV/fm$^3$ and $m_s=50$ MeV. From Fig. 27 the value of moment of inertia are evaluated for several compact stars of known mass and are tabulated in Table 6.

7 Stability analysis

We perform the following stability analysis of our model to check its physical viability:

• 1. Tolman–Oppenheimer–Volkoff equation

• 2. Cracking condition as postulated by Herrera

• 3. Calculation of adiabatic index and

• 4. Variation of Lagrangian change in radial pressure with the frequency of normal modes of oscillation

Table 3 Central density ($\rho _c$), central pressure ($p_{r0}$) and pressure anisotropy at the surface ($\varDelta (R)$) and second derivative of $\varDelta$ at the surface ($\varDelta ^{\prime \prime }(R)$) for the compact objects for a parametric choice of $B_g=~64$ MeV/fm$^3$ and different $m_s$

Table 4 Table for mass to radius ratio ($u=\frac{M}{R}$) and surface redshift $Z_s$ of different physical stars for different $m_s$ and $B_g=~64$ MeV/fm$^3$

Table 5 Predicted radii of various strange stars from our model for parametric choices of $B_g$ and $m_s$

7.1 Tolman–Oppenheimer–Volkoff equation

The generalized TOV equation [76, 77] is represented as

$$\begin{aligned} -\frac{M_{G}(r)(\rho +p_{r})}{r^2}e^{(\lambda -\nu )/2}-\frac{dp_{r}}{dr}+\frac{2}{r}(p_{t}-p_{r})=0, \nonumber \\ \end{aligned}$$

(52)

where $\nu$ and $\lambda$ are defined earlier and can be obtained from Eqs. (34), (35) and $M_{G}(r)$ is termed as the effective gravitational mass encompasses within a spherical region of radius r and its expression is

$$\begin{aligned} M_{G}(r)=\frac{1}{2}r^{2}\nu ^{\prime }e^{(\nu -\lambda )/2}. \end{aligned}$$

(53)

Equation (53) can be obtained from the formula of Tolman–Whittaker and using the EFE. Substituting Eq. (53) into Eq. (52), the following equation can be derived:

$$\begin{aligned} -\frac{\nu ^{\prime }}{2}(\rho +p_{r})-\frac{dp_{r}}{dr}+\frac{2}{r}(p_{t}-p_{r})=0. \end{aligned}$$

(54)

Equation of Tolman–Oppenheimer–Volkoff given in Eq. (54), represents the fundamental condition of equilibrium inside a star under the joint action of three forces namely, force due to gravity ($F_{g}$), hydrostatic force denoted by $F_{h}$ and anisotropic force denoted by $F_{a}$, where $F_g=-\frac{\nu ^{\prime }}{2}(\rho +p_{r})$, $F_h=-\frac{dp_{r}}{dr}$ and $F_a=\frac{2\varDelta }{r}$. $\varDelta =p_t-p_r$ is the pressure anisotropy given by Eq. (38). It follows from Eq. (54) that the total force $F=F_g+F_h+F_a$ must be zero inside the star. In this paper, the units of $\rho$, $p_r$ and $p_t$ is MeV/fm$^3$. Although $\nu$ is unitless, derivative of $\nu$ with respect to r, i.e., $\nu ^{\prime }=\frac{d\nu }{dr}$ has the unit $km^{-1}$. Moreover, applying the transformation $1~km^{-2}=3\times 10^4$ MeV/fm$^3$ [78], one can express the units of $\rho$, $p_r$ and $p_t$ in $km^{-2}$. Therefore, the unit of $F_g$, $F_h$, and $F_a$ can be illustrated as $km^{-3}$. In Figs. 28 and 29, we plot the variations of these forces against the radial distance r for $4U~1820-30$ and $SMC~X-4$, respectively and it is evident that static equilibrium condition hold good inside the stellar configuration under the composite effect of the above mentioned three forces. We note that the total effect of the hydrostatic $(F_h)$ and anisotropic $(F_a)$ force balances the gravity force ($F_g$), to fulfill the condition that the sum of these forces equal to zero through out the compact stars with non-zero $m_s$. From Figs. 28 and 29, it is noted that the TOV equation holds good inside the stars considered here.

Fig. 27

Variation of mass (M) with the moment of inertia (I) for $m_s=50$ MeV and $B_g=64$ MeV/fm$^3$

Table 6 Approximate values of the moment of inertia of different compact objects for the parametric choices of $m_s$ and $B_g$ as given in Table 5

7.2 Herrera cracking condition

Compact objects whether isotropic or anisotropic in nature should be stable with respect to small fluctuations in its physical variables. Hererra [79] introduced the idea of cracking of self gravitating objects to determine whether an anisotropic fluid configuration is stable or unstable. On the basis of Herrera’s concept, Abreu [80] gave a criterion which states that a stellar model will be in stable equilibrium if the radial ($v_{r}^{2}$) and tangential ($v_{t}^{2}$) sound speeds obey the following condition:

$$\begin{aligned} 0 \le |v_{t}^{2}-v_{r}^2| \le 1 \end{aligned}$$

(55)

The nature of the plots shown in Figs. 28 and 29 satisfies the condition given in Eq. (55) and as a result we may conclude that the stellar structure remains stable in presence of non-zero strange quark mass ($m_s\ne 0$) also.

7.3 Adiabatic index

The adiabatic index $\varGamma$ for an isotropic star is defined as follows:

$$\begin{aligned} \varGamma =\frac{\rho +p_{r}}{p_{r}}\frac{dp_{r}}{d\rho }=\frac{\rho +p_{r}}{p_{r}}v_{r}^{2} \end{aligned}$$

(56)

For stable isotropic fluids, Heintzmann and Hillebrandt [81] noted that $\varGamma >\frac{4}{3}$ (Newtonian limit). However, according to Chan et al. [82], for a relativistic anisotropic fluid, $\varGamma$ has a new limit which given by $\varGamma >\varGamma ^{\prime }_{max}$, where,

$$\begin{aligned} \varGamma ^{\prime }_{max}=\frac{4}{3}-\left[ \frac{4}{3}\frac{p_r-p_t}{|p_r^{\prime }|r}\right] _{max} \end{aligned}$$

(57)

In Figs. 30 and 31 variation of adiabatic index with r are shown and it is evident that the requirement $\varGamma >\varGamma ^{\prime }_{max}$ hold good inside the stars $4U~1820-30$ and $SMC~X-4$.

7.4 Variation of Lagrangian change in radial pressure with frequency of normal modes of oscillation

The stability of the system can also be studied by the Lagrangian change in radial pressure at the stellar surface with respect to frequency ($\omega ^2$). To study such behaviour we perturbed the radial pressure and calculated the frequencies of the normal modes of vibration ($\omega _{0}^2$). Assuming the vibrations to be adiabatic, according to [83], the coupled equations governing the infinitesimal radial mode of oscillation are given below:

$$\begin{aligned} \frac{d\zeta }{dr}= & {} -\frac{1}{r}\left( 3\zeta +\frac{{\varDelta }p_r}{{\gamma }p_r}\right) +\frac{1}{2}\frac{d{\nu }}{dr}\zeta , \end{aligned}$$

(58)

$$\begin{aligned} \frac{d({\varDelta }p_r)}{dr}= & {} \zeta \left[ \frac{\omega ^2}{c^2}e^{(\lambda -\nu )}(\rho +p_r)r-4\frac{dp_r}{dr}\right. \nonumber \\{} & {} \left. -k(\rho +p_r)e^{\lambda }rp_r+\frac{r}{4}(\rho +p_r)\left( \frac{d\nu }{dr}\right) ^2\right] \nonumber \\{} & {} -{\varDelta }p_r\left[ \frac{1}{2}\frac{d\nu }{dr}+\frac{k}{2}(\rho +p_r)re^{\lambda }\right] , \end{aligned}$$

(59)

where $k=\frac{8{\pi }G}{c^4}=1$ and $\left| {\varDelta }p_r\right|$ represents the absolute value of the Lagrangian perturbation in radial pressure and the eigenfunction $\zeta (r)$ is given by $\zeta (r)=\frac{\xi (r)}{r}$, where $\xi (r)$ is the Lagrangian displacement. However, due to spherical symmetry the Lagrangian displacement must vanish at the centre, i.e., $\xi (0)=0$. According to [83], we adopt the approach in which the eigenfunction $\zeta$ is normalised, i.e., $\zeta (0)=1$. Furthermore, it is noted that Eq. (58) poses a singularity at $r=0$. Obviously, to solve Eqs. (58) and (59), one requires that the coefficient of $(\frac{1}{r})$ must vanish as $r\rightarrow 0$. This implies:

$$\begin{aligned} {\varDelta }p_r=-3{\gamma }{\zeta }p_r \end{aligned}$$

(60)

Additionally, at the stellar boundary the radial pressure must vanish. Therefore, the next boundary condition is that, the Lagrangian perturbation of the radial pressure must vanish at the boundary, i.e., as $r\rightarrow {R}$,

$$\begin{aligned} \left| {\varDelta }p_r(R)\right| =0 \end{aligned}$$

(61)

As observed from Fig. 32, since all $\omega _{0}^2$ are positive, our model is stable against small radial oscillations considering the effect of non-zero mass of the strange quark.

Fig. 28

Variation of different forces with r inside $4U~1820-30$ for $m_s=50,100$ and 150 MeV, indicated by the solid, dashed and dot-dashed lines, respectively and $B_g=64$ MeV/fm$^3$. Here, the red, blue and green lines indicate $F_g$, $F_h$ and $F_a$, respectively

Fig. 29

Variation of different forces with r inside $SMC~X-4$ for $m_s=50,100$ and 150 MeV, indicated by the solid, dashed and dot-dashed lines, respectively and $B_g=64$ MeV/fm$^3$. Here, the red, blue and green lines indicate $F_g$, $F_h$ and $F_a$, respectively

Fig. 30

Variation of $|v_t^2-v_r^2|$ with r inside $4U~1820-30$ for different values of $m_s$ for $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dot-dashed lines indicate $m_s=50,100$ and 150 MeV, respectively

Fig. 31

Variation of $|v_t^2-v_r^2|$ with r inside $SMC~X-4$ for different values of $m_s$ for $B_g=~64$ MeV/fm$^3$. Here, the solid, dashed and dot-dashed lines indicate $m_s=~50,100$ and 150 MeV, respectively

Fig. 32

Radial variation of the adiabatic index ($\varGamma$) inside $4U~1820-30$ for different values of $m_s$ with $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dotted lines indicate the variations in the adiabatic indices for $m_s=50,100$ and 150 MeV, respectively. The solid red and green lines indicate the values of $\varGamma =\frac{4}{3}$ and $\varGamma ^{\prime }_{max}$, respectively

Fig. 33

Radial variation of adiabatic index ($\varGamma$) inside $SMC~X-4$ for different $m_s$ with $B_g=64$ MeV/fm$^3$. Here, the solid, dashed and dotted lines indicate variations for $m_s=50,100$ and 150 MeV, respectively. The solid red and green lines indicate the values of $\varGamma =\frac{4}{3}$ and $\varGamma ^{\prime }_{max}$, respectively

Fig. 34

Plots of $\left| p_r(R)\right|$ with $\omega ^2$ for $m_s=100$ MeV. Here, the red and black lines indicate variations for $4U~1820-30$ and $SMC~X-4$, respectively for $B-g=64$ MeV/fm$^3$. The minima of each lines represent the correct value of frequencies of equilibrium modes of oscillation

Table 7 Nature of the SQM inside $4U~1820-30$ for a given mass $1.46~M_\odot$ and estimated radius 11.1 km [61] for different $m_s$ values

8 Discussion

In this paper, we studied the effect of non-zero strange quark mass ($m_s\ne 0$) on the physical parameters of the strange star configuration. With the inclusion of non-zero $m_s$, the MIT EoS is modified accordingly and is given in Eq. (24). We have used ensemble theory and various thermodynamic principles to derive Eq. (24). Considering the Mak and Harko density profile [47, 55] of the inside matter, which is composed of three flavour quarks (u, d and s), we solved the EFE to evaluate the $g_{rr}$ and $g_{tt}$ metric components and other physical parameters related to compact stars. The matter is assumed to be charge neutral in the presence of electrons. Figure 1 shows the variation in chemical potentials with $B_g$ for two different values of $m_s$. It is evident from Fig. 1 that the chemical potential of quark flavours increase with increasing $B_g$. However, for electrons, the chemical potential decreases with increasing $B_g$. From these variations it may be concluded that the effect of electrons on the average properties of the star is negligibly small. This is also established in the article [84]. Again from Fig. 1, we note that for any given $B_g$, $\mu _e$ decreases with decreasing $m_s$, and it is also noted that in the limit $m_s\rightarrow {0}$, $\mu _e\rightarrow {0}$, justifying the fact that almost no electrons are necessary for maintaining the charge neutrality condition when $m_s\rightarrow {0}$. Moreover, it is evident that with increasing strange quark mass, the chemical potential of strange and down quarks ($\mu _s=\mu _d=\mu$) slightly increases when $B_g$ is fixed, whereas the chemical potential of up quarks ($\mu _u$) remains almost constant for a specific value of $B_g$. The stability windows of quark matter are studied for different values of $m_s$ and $B_g$. The different stability windows are shown in Table 1. In Fig. 2, the energy per baryon is shown within the different stability windows. To observe the effect of the strange quark mass ($m_s$) on the gross properties of a star, we have shown graphically the metric components, energy density ($\rho$), radial pressure ($p_r$), tangential pressure ($p_t$) and anisotropy ($\varDelta$) in Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11 for the two different stars $4U~1820-30$ and $SMC~X-4$, respectively. The variations of different physical parameters are plotted for parametric values of $B_g$ and $m_s$ within the stable region, as shown in Table 1. It is noted from Fig. 3 that $m_s$ has some effect on metric components $g_{rr}$ and $g_{tt}$. $m_s$ has no effect on $e^{\nu }$ at the surface and on $e^{\lambda }$ at the centre. However, the values of metric potentials decrease with increasing of $m_s$, and it may be concluded that the maximum mass may have a lower value for higher values of $m_s$. From Figs. 4 and 5, we note that the energy density ($\rho$) increases with increasing $m_s$ in view of Eq. (32) as $\rho _c$ is a function of $m_s$ as given in Eq. (49). From Figs. 6, 7, 8, 9, 10, 11, we note that with the increasing $m_s$, both the radial and tangential pressure and anisotropy ($\varDelta$) increase throughout the star. Therefore, $p_r$, $p_t$ and $\varDelta$ pick up different values for non-zero $m_s$. In the present model, we also predicted the radii of two stars, $4U~1820-30$ and $SMC~X-4$, and the variation of predicted radius with $m_s$ and $B_g$ are shown in Figs. 12 and 13, respectively. It is evident that the radius of a star depends on $m_s$ and $B_g$. The greater the value of $m_s$ or $B_g$ is, the lower is the radius.

In estimating the radius of the stars, with known masses, we assume that the anisotropy is maximum at surface. Such assumption has been made as follows: in case of an isotropic star, the mutual balance between the forces arising due to gravity and radiation keep the star in a state of hydrostatic equilibrium. However, in the case of an anisotropic star, these two forces are not sufficient to maintain the equilibrium condition. In such a case, an extra force due to the anisotropy in pressure comes into play. The anisotropic force jointly with the forces of gravity and pressure gradient preserve the hydrostatic equilibrium condition. Now, both the gravity and pressure gradient forces are minimum at the surface. Therefore, the anisotropic force and hence the anisotropy in pressure must be maximum at the surface so that all the forces are summed up to zero. However, if by any chance the anisotropy becomes maximum at any intermediate point, the difference of the radial and cross-radial sound velocities will alter in sign. This will manifest as a ‘cracking’ of the fluid sphere. We have studied the validity of the energy conditions within the parameter space for the stable configuration of strange stars, and the results are shown in Figs. 14, 15, 16, 17, 18. The causality conditions are shown in Figs. 19 and 20 for the two compact stars considered here for different values of $m_s$. The energy conditions hold good for non-zero $m_s$ although higher values are assigned for higher $m_s$. Interestingly, it is evident that $v_r^2=\frac{1}{3}$ for all values of $m_s$ throughout the two stars considered here (Figs. 19 and 20) indicating that $\frac{dp_r}{d\rho }=\frac{1}{3}$, as expected for strange matter [85]. It is also noted from Figs. 19 and 20 that $v_t^2$ picks up different values in the presence of non-zero $m_s$. The TOV equation was solved to evaluate the maximum mass and corresponding radius using the modified MIT bag EoS in the presence of non-zero $m_s$ and is shown in Fig. 21. The maximum mass and corresponding radius and central density are tabulated in Table 2 for different values of $m_s$ and $B_g$. It is observed that both the maximum mass and radius decrease with increasing $m_s$ and $B_g$. Table 3 lists the central density, central radial pressure, anisotropy at the surface and second derivative of the anisotropy at the surface for the parametric choices of $B_g$ and $m_s$. The values of $\varDelta (R)$ and $\varDelta ^{\prime \prime }(R)$ at the surface indicate that the model is stable for the parametric choice of $m_s$ and $B_g$. The Surface redshift of few known strange stars are tabulated in Table 4 and it is noted that the maximum value of surface redshift lie within the range as given by Buchdhal [86]. From Table 4 we note that the surface redshift of the stars is within the range $0.17-0.41$, which is consistent with the restriction $Z_s\le {2}$ [86,87,88]. We have predicted the radii of few recently observed stars which are supposed to be strange stars and the predicted radii are tabulated in Table 5 for different choices of $m_s$ and $B_g$. It is noted that radii of a large number of strange stars containing stable SQM upto to mass value $\le ~2.01~M_{\odot }$ may be predicted in this model. However, it has been suggested that the quarks may form Cooper pairs [89]. In fact, pairing is unavoidable in a degenerate Fermi liquid if there is an attractive interaction parametrized by color superconductivity gap parameter. In that case maximum mass increases with increasing color superconductivity gap parameter for a given strange quark mass [24].

The Harrison–Zeldovich–Novikov stability condition requires that mass should increase with increasing central density, i.e., $\frac{dM}{d\rho _c}>0$ [70, 71]. Figure 22 shows the variation of the maximum mass with central density ($\rho _c$), and it is evident that the condition $\frac{dM}{d\rho _c}>0$ holds up to a local maxima. Beyond this point, $\frac{dM}{d\rho _c}<0$ shows instability in fluid configuration. This mass is known as the maximum mass. The Corresponding central density is the maximum central density. In Fig. 23, the maximum radius vs. central density variation is shown. It is noted from Fig. 24, that the maximum mass of the star is also a function of $B_g$, and the maximum mass decreases with increasing $B_g$. In Figs. 25 and 26, variations in $M_{max}$ and $R_{max}$ are shown for different values of $m_s$ for two arbitrary choices of $B_g=~60$ and 64 MeV/fm$^3$. Such types of variations are also reported by Li et al. [90]. As the maximum mass decreases with increasing $m_s$ for a fixed $B_g$, it may be concluded that for stable SQM, a lower value of $m_s$ is preferable because a higher $m_s$ corresponds to instability. The variation in the moment of inertia (I) is depicted in Fig. 27. With the help of this graph, we have predicted the values of I for the observed masses and predicted radius, and the values are listed in Table 6. The stability of the model is studied for the TOV equation, Herrera cracking condition and adiabatic index. From Figs. 28 and 29, it is evident that the TOV equation holds good inside the compact stars considered here. The cracking condition for both stars are also verified and are shown in Figs. 30 and 31. Another stability condition, the adiabatic index, has been checked for different values of $m_s$ and are shown in Figs. 32 and 33. From the plots, it is evident that our model is stable within the parameter space used here. In Fig. 34, we have studied the another stability condition by plotting the absolute value of the Lagrangian change in radial pressure at the surface of $4U~1820-30$ and $SMC~X-4$ against $\omega ^2$ for the parametric choice of $B_g$ and $m_s$. The minima of these plots correspond to the eigen frequencies of different modes. We note that the frequency spectrum is real ($\omega _n^2>0$) indicating the stable configuration.

In Table 7, we have tabulated the values of $B_g$ corresponding to a given $m_s$ value for which the observed radius of $4U~1820-30$ [61] can be predicted. From Table 7, it is evident that, a correlation exists between $m_s$ and $B_g$ in predicting the radius of a star. This can be explained as follows: as $m_s$ increases, the energy density of the ensemble of quarks increases. However, the gravitational energy density of the star remains unaltered. Therefore, to maintain the confinement condition of quarks, the value of bag constant ($B_g$) must decrease to compensate for this increase in the total energy density of the assembly of quarks. In Table 7, we have shown that SQM is stable inside $4U~1820-30$. However, if the SQM is unstable then quark matter will not be found inside $4U~1820-30$. The quarks may be converted into hadrons and in that case $4U~1820-30$ will be a stable neutron star. Same argument may also be valid for other strange quark stars too. Thus inclusion of strange quark mass into the theory may explain some observed features of strange stars within the parameter space used here.