Study of generalized Lemaître–Tolman–Bondi spacetime in Palatini f(R) gravity

Abstract

The objective of this paper is to investigate the continuation of Lemaître–Tolman–Bondi (LTB) space-time for dissipative dust configuration in the direction of Palatini f(R) theory. In this context, the generalized form of field and dynamical equations will be formulated. We explore the effects of kinematical variables and curvature invariant on our proposed fluid configuration. The significance of Palatini f(R) scalar variables computing through the orthogonal splitting of Riemann-tensor for dissipative dust spheres will be reported. Furthermore, two subcases of LTB space-time have been carried out to note down its symmetric aspects. It is revealed that extended LTB space-time has characteristics comparable to that of LTB and computed scalar variables in both situations have identical dependance on source profile even under the effects of Palatini technique.

1 Introduction

Indeed, high-quality findings obtained from the galactic cluster studies include mass, correlation concerns, and a plethora of variations with red-shift [1,2,3], Hubble preview of Type-Ia supernovae [4, 5], The galactic shearing [6, 7] determined via weak-lensing, cosmic-microwave-background anisotropies [8, 9], major structure optical measurements [10, 11] studies all point to spatial flatness in the cosmos, and sub-critical fluid composition enduring the cosmic accelerating expansion era. The key target of today’s cosmology is to combine all these kinds of data into a well-consistent configuration that provides a clear picture of the current observable cosmos. Even though it has some significant theoretical concerns that have motivated the researchers to look for other alternatives, which they regard as dark energy/quintessence. Mainly, the dark energy serves as a repulsive gravity. It contributes to the expanding mechanism and controls the entire energy content of the cosmos. Despite this, the rudimentary aspects and nature of dark energy are still unclear. Dark matter seems to be in a comparable scenario. Its grouping and allocation characteristics are fully grasped throughout all levels. However, in a rudimentary sense, its context is mysterious. Else ways, the inclusion of these dark source ingredients could well be interpreted as an indication of the inadequacy of general relativity (GR) at extra-galactic and large cosmic scales. In this scenario, modified gravity theories (MGTs) can be a captivating substitute in order to elucidate large-scales structures and cosmic speedy expansion. The MGTs are one of the attractive mathematical techniques that could be applied to analyze the dark side of the cosmos. By varying the geometric portion of the GR action, distinct dark energy frameworks have been suggested. In last few years, there have been proposed distinct MGTs likewise f(R), $f(\textit{T})$, f(G) , f(R, T), etc., where R identifies the curvature scalar, $\textit{T}$ is the torsion invariant, G symbolizes the Gauss–Bonnet correction, and T represents the stress-energy tensor (reviews on MGTs could be studied in [12,13,14,15,16,17]). Nojiri and Odintsov [18] investigated this approach to figure out the cosmic rapid-expansion together with the consequences of inflation.

The simplest way to generalize GR is the f(R) gravity [19,20,21,22] enables for geometrical degrees-of-freedom for dark energy substitute without need to introduce any new material ingredient. Olmo and Garcia [23] studied the formulation of a group of anisotropic static spheres under the context of f(R) theory and found the consequences of relating parameters representing the black hole structures whose central singularity is substituted by a definite wormhole. Cognola et al. [24] proposed the well-grounded formulations of f(R) dark energy configurations and categorized them into four-streams. Azadi et al. [25] found some vacuum consequences via Weyl-coordinates for cylindrical configuration within the insights of f(R) gravity. Durrer and Maartens [26] found that f(R) models might give valuable insights regarding the evolving cosmic configurations. Bamba et al. [27] analyzed the influence of dark energy via generalized cosmological configurations to study the acceleratory era of the cosmos. Cembranos et al. [28] studied the inflationary f(R) model by taking collapsing dust candidates under consideration. Reverberi [29] analyzed the curvature singularities through various aspects of f(R) models and concluded that these singularities emerge due to increase in mass/energy of the fluid configuration. Yousaf and Bhatti [30] examined the consequences of fluids candidates along with the f(R) corrections on the evolving cylindrical cosmic configuration. They found that some specific f(R) models try to attain super dense objects with considerably smaller radii. Owing to its simple reliability, f(R) theory has been attained considerable interest in characterizing dark matter and dark energy which is constructed by replacing the curvature invariant R by its generalized function. In this scenario, two distinct approaches could be adopted in order to get the generalised field equations. The first one is metric formalism, where the action function can be varied with regard to the metric, and second is the Palatini version, in which the metric and connections are considered to be independent. The key premise in such an approach is that matter-action is independent of connections; its disregard follows the metric-affine version which could recover the metric/Palatini f(R) theories within usual bounds. The field equations in metric-based theory are of order four. However, we come up with second-order field-equations in the Palatini f(R) scenario which are more easy to work with [31,32,33,34,35,36].

In Palatini f(R) scenario, Sotiriou [37] built an association of scalar-tensor theory to the f(R) gravity. He examined the connection between them and studied the consequences of their equivalency. He also showed how fluid configuration is associated with the independent connections within certain situations. Starobinsky [38] discovered a set of f(R)-models that result in a distinct and plausible cosmic formation. They showed that these configurations correspond to Minkowskian and de-Sitter line-elements in the vacuum scenario. Santos et al. [39] analyzed the energy constraints to scrutinize f(R) theories. They proposed the expansion evolution to determine the null and strong-energy constraints, and other ones via effective matter content. Bamba and Geng [40] studied the thermodynamical aspects of apparent-horizon in the Palatini f(R) version and found that the equilibrium perspective is suitable for understanding the entropy of the apparent-horizon. Olmo and Alepuz [41] investigated the Hamiltonian f(R) distribution by imposing the Palatini approach. They computed the constraint equation and determined that Cauchy-problem is well-suited for $\omega =-\frac{3}{2}$. Bhatti et al. [42] proposed isotropic spheres in order to analyse the stable zones of compact stars in a Palatini f(R, T) context. They constructed the stable regions as a result of physical conditions. Yousaf et al. [43] measured the complexity via structure scalar of the static spheres to examine the influence of physical parameters bearing the impact of Palatini f(R) corrections. To better interpret the physical meanings of the gravitating system, structure scalars are an effective approach. Herrera et al. [44] computed the set of stellar-equations that could express in the form of the scalar variables. They inferred that these scalars demonstrate the basic aspects of the gravitating fluid under concern. Yousaf [13] explored the consequences of strong-field gravitational interaction via scalar variables on the formulation of propagating source. They evaluated anisotropic dynamical source and determined the relating generalized scalars to check out the their effects on the systematic description of radiating stars. Bhatti et al. [45,46,47] computed the f(R) scalars for the physical manifestation of various gravitating bodies and formulated the stellar consequences via scalar functions to explore the physical aspects of matter configurations. They also developed static-solutions to entail the influence of f(R) version of scalars.

Bhatti and Tariq [48] studied expansion of dissipative star in the impact of charged-field under GR concerns. They attained the five scalars for the spherical system and showed that stellar-solutions could be well-expressed by means of such scalars in static scenarios. Herrera et al. [49] explained the Misner–Sharp approach for heat-fluxes and examined the thermodynamical consequences via heat conduction. Govender et al. [50] explored the influence of shearing motion on collapsing configurations under dissipative concerns and showed that shearing effects are the origins of increasing core temperature. They also studied the physical aspects of collapsing stars without considering shearing motion. Herrera et al. [51] inspected the characteristics of axial symmetric dissipative matter configuration, and determined the absence of gravitational-radiations in geodesic scenario. It is also deduced that in non-dissipative condition, the system proceeds to Friedmann–Robertson–Walker configuration provided the positivity of expansion factor. Reddy et al. [52] analyzed the consequences of dissipation on collapsing bodies and presented the dynamics of some particular cosmic models within the perturbative approach. They noticed that anisotropy of pressure affects the interior body’s temperature.

Inhomogeneous matter configuration has considerable consequences for comprehending the physical description of any cosmic system. Inhomogeneous space-times are regarded to be the exact-solutions of field equations and reveal details about the universe’s various eras. A revived interest in Lemaître–Tolman–Bondi (LTB) space-time has emerged in association with the current data from type-Ia supernovae that suggests that the universe’s expansion is accelerating. LTB space-time is considered to be the most common inhomogeneous spherical configuration that plays a key role in the investigation of cosmic configurations. It could be applied to analyze the formation of Cauchy and apparent-horizons. Sussman [53] proposed a numerical technique for the extension of LTB space-time and examined influence of pressure. He determined the basic conditions for the influence of collapsing procedure and particle formation. Herrera et al. [54] presented the generalization of LTB space-time by introducing tilted-congruence and explores the effects inhomogeneity of energy composition. Yousaf et al. [55, 56] performed the evolution of LTB geometry under the investigation of tilted-congruence with and without the influence of charged field in the perspective of MGTs. Fernandes et al. [57] checked the consequences of higher derivatives corrections on LTB space-time. They also analyzed the physical outcomes for Hubble constant and scale-factor for Proca structure and observed that magnetic effects disappear for such structures.

Herrera [58] considered the dissipative dust fluid to explored the consequences of dissipation in the configuration of energy density inhomogeneities. Herrera et al. [59] discussed the generalization of LTB spacetime with the help of structure scalars and symmetric properties. They considered the dissipative dust fluid to generalize the LTB spacetime for the dissipative case because LTB does agree with dissipative phenomena. They have mentioned that the state of pure dust, suggesting geodesic fluid in non-dissipative scenario while this condition remains not valid when we consider dissipative flux. Yousaf et al. [60] considered the imperfect fluid to examine the factors that create irregularities for a spherical star in f(R, T) theory. They studied particular cases of anisotropic, isotropic, and dust to analyze the irregularity factors in the dissipative and non-dissipative scenarios. They considered dissipative dust as a special case to analyze the effects of heat-fluxes as well as null-radiations. Herrera [61] studied the gravitational radiation and its properties by considering dissipative fluids as well as addressed some particular cases such as shear-free and perfect fluid to analyze their behavior. They found that dust fluid along with dissipation is the more consistent fluid distribution with gravitational radiation.

The Palatini version of f(R) gravity have its own significance since its inception. The theory has several fascinating properties, including the ability to predict the presence of a long range scalar-field, describing cosmic late-time acceleration. It is worth noting that Olmo [62] applied the scalar-tensor representation technique to work out the post-Newtonian limit of Palatini and metric versions of f(R) theory. They inferred that the f(R) Lagrangian must be linear in R in both formalisms but observations are quite opposite to the corrections that are obtained at low curvatures. This result demonstrated that the gravitational alteration at very low densities is irreversible. Olmo et al. [63] used Palatini approach to examine the formation of static spherically symmetric star, where Lagrangian is an undefined function of $f(R,R_{\mu \nu } R^{\mu \nu })$. They derived the TOV equations for such theories and indicated that under usual limits, they regain the f(R) and GR. They demonstrated that exterior vacuum findings are comparable with Schwarzschild de-Sitter ones, discussed the presumed changes of the interior solutions when matched with general relativity. Olmo and Garcia [64] utilized the tensor distributional technique to compute the matching conditions for Palatini f(R) gravity. They demonstrated that these conditions are required to construct the models of gravitational bodies with the matching of inner and outer regions at hyper-surface. They demonstrated their importance by taking into account the stellar surfaces within polytropic configurations and analyzed that the Palatini framework can safely model the white dwarfs and neutron stars. Olmo [21] studied the MGTs by using the Palatini context and discussed the cosmic speed-up problem in detail. The Cauchy problem and solar system tests have also been studied in this context. Amarzguioui et al. [65] studied the f(R) gravity using Palatini formalism for analyzing the expansion history of the cosmos by the choice of an arbitrary f(R) function. They explored the cosmological constraints of f(R) theory originated from cosmic-microwave-background observations and demonstrated that their results reveal that the choice of $\frac{1}{R}$ model is inconsistent with the data. Allemandi et al. [66] discussed the physical significance of conformal transformations by taking the Palatini technique in gravitational theories. They analyzed that the conformal transformations provide the physical signs which enable to differentiate the space-time and geodesic structures by taking into consideration the bi-metric structure within Palatini formalism. Meng and Wang [67] discussed the modified gravity with $R^2$ terms using the Palatini formalism. They indicated that the quantum effects of $R^2$ theory are different in metric and Palatini formalisms as well as demonstrated that $R^2$ term provides no information about the early time inflation in Palatini formalism.

The main idea of our work is to extend the LTB metric in the background of the Palatini f(R) theory to the dissipative case. We discussed a couple of aspects in this scenario. One is to explore some basic dynamical quantities, referred as the structure scalars, which have their own physical significance. The other is to discuss some symmetric aspects of the LTB metric and then generalize it under the influence of a specific generalized gravity, namely the Palatini f(R) approach, along with dissipative effects, because LTB geometry does not admit dissipation. Our manuscript is outlined as follows. Generalized field and dynamical laws together with Bianchi-identities and the Weyl propagation equations bearing the influence of Palatini f(R) corrections are presented in Sect. 2. The Palatini f(R) scalars will be computed in Sect. 3 using an orthogonal breakdown of the Riemann-tensor. Section 4 comprises a full demonstration of LTB space-time where the feasible findings of the evolving system with the graphical representation will be discussed. On the basis of symmetric characteristics and scalar variables, the continuation of LTB space-time would be attained in Sect. 5. In the last section, we conclude the findings of our work.

2 Palatini f(R) formalism

The action integral for f(R) gravity is expressed by

$$\begin{aligned} I_{f(R)}=\frac{1}{2\kappa } \int \sqrt{-g}[f(R)+S^{m}]d^{4}x, \end{aligned}$$

(1)

where $S^{m}$ is the matter action, g identifies the determinant of $g_{\beta \varrho }$ (metric tensor) and $\kappa$ represents the coupling constant. The curvature invariant R in (1) is constructed through the contraction of Ricci-tensor corresponding to connections by implying that R is the outcome of geometric connections. By varying (1) with regard to $g_{\beta \varrho }$ and connections $\Gamma ^{\mu }_{\beta \varrho }$, we get the following two equations

$$\begin{aligned} F(R)R_{\beta \varrho }-\frac{1}{2}g_{\beta \varrho }f(R)&=\kappa T_{\beta \varrho }, \end{aligned}$$

(2)

$$\begin{aligned} \nabla _{\mu }(g^{\beta \varrho }\sqrt{-g}F(R))&=0, \end{aligned}$$

(3)

where $T_{\beta \varrho }$ is the stress-energy having no dependence over independent connections and F(R) symbolizes the derivative of f by R. For the comparison between $T=g^{\beta \varrho } T_{\beta \varrho }$ and curvature scalar, we contract Eq. (2) with $g^{\beta \varrho }$ and get the trace-equation as below

$$\begin{aligned} 2f(R)-RF(R)=-\kappa T, \end{aligned}$$

(4)

showing that curvature scalar has clear dependence on trace of $T_{\beta \varrho }$. In the Palatini f(R) case, a single description of field equations of order two could obtain by computing the connections from Eq. (2) after that putting in Eq. (3), we get the following form

$$\begin{aligned} R_{\beta \varrho }-\frac{1}{2}g_{\beta \varrho }R&=\frac{\kappa }{F}T_{\beta \varrho } +\frac{1}{2}g_{\beta \varrho }\left( \frac{f}{F}-R\right) \nonumber \\&\quad +\frac{1}{F} (\nabla _{\beta }\nabla _{\varrho }-g_{\beta \varrho }\Box F)+\frac{3}{2F^2} \nonumber \\&\quad \times \left[ \frac{1}{2}g_{\beta \varrho }(\nabla F)^{2}-\nabla _{\beta }F \nabla _{\varrho }F\right] , \end{aligned}$$

(5)

here $\nabla _{\varrho }$, shows the covariant-derivative and $\Box \equiv g^{\beta \varrho }\nabla _{\beta } \nabla _{\varrho }$ is the box operator. The generalized field-equations in the term of the $G_{\beta \varrho }$ could be represented as

$$\begin{aligned} G_{\beta \varrho }=\frac{8\pi }{F} (T_{\beta \varrho }+T^{(D)}_{\beta \varrho }), \end{aligned}$$

(6)

here

$$\begin{aligned} T^{(D)}_{\beta \varrho }&=\frac{1}{\kappa } \left[ \nabla _{\beta }\nabla _{\varrho } F-g_{\beta \varrho } \Box F-\frac{F}{2} g_{\beta \varrho } R+\frac{f g_{\beta \varrho }}{2}\right. \nonumber \\&\quad \left. +\frac{3}{2F}\left( \frac{1}{2} g_{\beta \varrho }(\nabla F)^2-\nabla _{\beta }F\nabla _{\varrho }F\right) \right] , \end{aligned}$$

(7)

is the stress-energy tensor demonstrating the gravitational contribution via Palatini f(R) modifications. The metric version breaks down the quadratic-order aspects of GR, however, these could be reserved via Palatini approach. The generic line-element for the inner configuration of a spherical symmetric geodesic fluid can be given as

$$\begin{aligned} ds^2=B^2 dr^2+C^2d\theta ^2+C^2sin^2\theta d\phi ^2-dt^2, \end{aligned}$$

(8)

where $B=B(t, r)$ and $C=C(t, r)$. The geometric variable B have dimensionless while dimension of C is identical to that r. It is noteworthy that cold dark-matter is non collisional having the intense impact of rest-mass in which the pressure and heat-fluxes have ignorable consequences owing to their kinetic-nature. Henceforth, it would be important to analyze the stability/instability of such configuration together with the influence of certain kinetic factors, for instance, heat-fluxes in the perspective of a specific gravity theory namely; Palatini f(R) theory. For this purpose, the stress-energy tensor is chosen as in this scenario is given by

$$\begin{aligned} T_{\beta \varrho }=\mu V_{\beta } V_{\varrho }+\epsilon l_{\beta } l_{\varrho } +q_{\beta } V_{\varrho }+V_{\beta } q_{\varrho }, \end{aligned}$$

(9)

here, the fluid’s energy-density, null four-vector and four-velocity are represented by $\mu ,~l^{\varrho }$ and $V_{\varrho }$, respectively. The heat-flux is identified by $q_\varrho$ demonstrating the dissipative effects in term of diffusion-approximation. However, $\epsilon$ denotes radiation-density of the fluid configuration, providing the dissipative impact via streaming-out approximation. We have proposed the dissipative dust-fluid to describe the dissipative mechanism for distinct gravitating bodies. For a co-moving coordinates, we have

$$\begin{aligned} V^{\varrho }&=\delta ^{\varrho }_0, \quad q^{\varrho }=q B^{-1}\delta ^{\varrho }_1,\quad l^{\varrho }= \delta ^{\varrho }_0+B^{-1}\delta ^{\varrho }_1,\\ \chi ^{\varrho }&=B^{-1} \delta ^{\varrho }_1, \end{aligned}$$

accommodating the relations

$$\begin{aligned} V^{\varrho } V_{\varrho }&=-1, \quad V^{\varrho } q_{\varrho }=0, \quad l^{\varrho } V_{\varrho }=-1, \quad l^{\varrho } l_{\varrho }=0,\nonumber \\ \chi ^{\varrho } \chi _{\varrho }&=1, \quad \chi ^{\varrho } V_{\varrho }=0. \end{aligned}$$

(10)

The Palatini f(R) equations can acquire by utilizing the connections (affinities) represented to be $\Gamma ^{\alpha }_{\gamma \nu }=\{^{\alpha }_{\gamma \nu }\}+ \frac{1}{2F} \left[ (\delta ^{\alpha }_{\gamma } \partial _{\nu }+ \delta ^{\alpha }_{\nu } \partial _{\gamma })F -g_{\gamma \nu } g^{\alpha \sigma } \partial _{\sigma } F \right]$ as

$$\begin{aligned} 8\pi \hat{\mu }_{eff}&=\frac{\dot{C}}{C}\left( \frac{\dot{C}}{C}+2\frac{\dot{B}}{B}\right) -\frac{1}{B^2} \left[ 2\frac{C''}{C}+\left( \frac{C'}{C}\right) ^2\right. \nonumber \\&\quad \left. -\frac{B^2}{C^2} -2\frac{B' C'}{B C} \right] \end{aligned}$$

(11)

$$\begin{aligned} 8\pi \hat{q}_{eff}&=-\frac{2}{B}\left[ \frac{\dot{C'}}{C} -\frac{\dot{B}}{B}\left( \frac{C'}{C}\right) \right] , \end{aligned}$$

(12)

$$\begin{aligned} 8\pi \epsilon _{eff}&=-\left[ 2\frac{\ddot{C}}{C}+\left( \frac{\dot{C}}{C}\right) ^2\right] -\frac{1}{B^2}\left[ \left( \frac{B}{C}\right) ^2-\left( \frac{C'}{C}\right) ^2\right] , \end{aligned}$$

(13)

$$\begin{aligned} \xi _{22}&=-C^2\left[ \frac{\ddot{C}}{C}+\frac{\ddot{B}}{B}+\frac{\dot{B}}{B} \left( \frac{\dot{C}}{C}\right) \right] \nonumber \\&\quad -\left( \frac{C}{B}\right) ^2 \left[ \frac{B'}{B}\left( \frac{C'}{C}\right) -\frac{C''}{C}\right] . \end{aligned}$$

(14)

In our study, $\hat{\mu }_{eff}, ~\hat{q}_{eff}$ and $\epsilon _{eff}$ comprising the f(R) modifications together with usual constituents that are computed as

$$\begin{aligned} \hat{\mu }_{eff}&=\frac{1}{F} (\hat{\mu }+\xi _{00}), \quad \hat{q}_{eff}=\frac{1}{F}\left( \hat{q}+\frac{\xi _{01}}{B}\right) ,\nonumber \\ \epsilon _{eff}&=\frac{1}{F}\left( \epsilon +\frac{\xi _{11}}{B^2}\right) , \end{aligned}$$

(15)

here dot and prime represent the derivatives of related quantities by t and r, respectively. Moreover, $\hat{\mu }=\mu +\epsilon$ and $\hat{q}=q+\epsilon$, and $\xi _{00},~\xi _{01}, ~\xi _{11}$ and $\xi _{22}$ depicts the extra-curvature terms with the values given in the Appendix A. The expansion parameter $(\Theta )$, four-acceleration $(a_{\varrho })$, and shear-tensor $(\sigma _{\beta \varrho })$ could be expressed as

$$\begin{aligned} \Theta&= V^{\varrho };_{\varrho } \quad a_{\varrho }=V_{\varrho ;\alpha } V^{\alpha } \quad \sigma _{\beta \varrho }=V_{({\beta ;\varrho })}\nonumber \\&\quad -\frac{1}{3} \Theta h_{\beta \varrho }+a_{(\beta }V_{\varrho }). \end{aligned}$$

(16)

The projection tensor is given to be $(h_{\beta \varrho }=g_{\beta \varrho }+V_{\beta } V_{\varrho })$. Now, we would describe the non-vanishing components of the kinematical variables for our matter configuration within Palatini f(R) context as below

$$\begin{aligned} \Theta _{eff}&=2\left[ \frac{\dot{C}}{C}+\frac{\dot{B}}{2B}+\frac{\dot{F}}{F}\right] ,\quad a_{0}=\frac{1}{2}\left( \frac{\dot{F}}{F}\right) , \nonumber \\ a_{1}&=\frac{1}{2} \left( \frac{F'}{F}\right) , \end{aligned}$$

(17)

$$\begin{aligned} \sigma _{01}&=\frac{1}{4}\left( \frac{F'}{F}\right) , \quad \sigma _{11} =2\frac{B^2\sigma }{3}-\frac{B^2}{6}\left( \frac{\dot{F}}{F}\right) ,\nonumber \\ \sigma _{22}&=\frac{1}{sin^2 \theta }\sigma _{33}= -\frac{C^2}{3}\sigma -\left( \frac{C^2}{6}\right) \frac{\dot{F}}{F}, \end{aligned}$$

(18)

It is observed that fluid’s four-acceleration is entirely depends upon Palatini f(R) factors as noticed in Eq. (17). The shear-scalar $\sigma$ is computed in the following way

$$\begin{aligned} \sigma =-\left( \frac{\dot{C}}{C}-\frac{\dot{B}}{B} \right) , \end{aligned}$$

however, in Palatini f(R) scenario, its gets the form

$$\begin{aligned} \sigma _{eff}=\left[ \sigma ^2+\frac{1}{8}\left( \frac{\dot{F}^2}{F^2}\right) -\frac{3}{16B^2}\left( \frac{F'^2}{F^2}\right) \right] ^{\frac{1}{2}}. \end{aligned}$$

(19)

In order to quantify the matter in the interior of proposed gravitating source, Misner and Sharp [68] introduced expression for the mass-function that for our source under investigation read the form

$$\begin{aligned}&m=m(t, r)=\frac{(C^3)}{2} R_{23}^{~~23}= \left[ 1-\left( \frac{C'}{B}\right) ^2+\dot{C}^2\right] \frac{C}{2}, \end{aligned}$$

(20)

which may turn out as

$$\begin{aligned} E\equiv \frac{C'}{B}=\left[ U^2+1-\frac{2m(t,r)}{C}\right] ^{\frac{1}{2}}, \end{aligned}$$

(21)

here U is fluid’s collapsing velocity, that might be accounts for the variation of areal-radius C with its proper-time. For collapsing spheres it is considered to be negative. The collapsing fluid’s velocity, and could be defined as the variation of areal-radius C with proper-time that is $U=\dot{C}$. By applying afore said results, Eq. (12) could be expressed as

$$\begin{aligned} 4\pi \hat{q}_{eff}=-E \left[ -\frac{1}{3C'}(\Theta -\sigma )'+\frac{\sigma }{C}\right] . \end{aligned}$$

(22)

The variation of the mass-function by means of time and radial corrdinates read the form

$$\begin{aligned} \dot{m}&=-4\pi (U\epsilon _{eff}+\hat{q}_{eff} E) C^2, \end{aligned}$$

(23)

$$\begin{aligned} m'&=4\pi \left[ \hat{\mu }_{eff}+\hat{q}_{eff}\frac{U}{E}\right] C'C^2 , \end{aligned}$$

(24)

respectively. Integrating partially Eq. (24), we have

$$\begin{aligned} \frac{3}{C^3}m=4\pi \hat{\mu }_{eff}-\frac{4\pi }{C^3} \int _0^r C^3 \left[ \hat{\mu }_{eff}'-3\hat{q}_{eff}\frac{UC'}{EC}\right] dr. \end{aligned}$$

(25)

This outcome provides an association among fluid’s variables and relating mass-function under the influence of Palatini f(R) constituents.

2.1 Junction conditions in palatini f(R) context

The study of matching conditions has attracted a lot of interest in the field of relativistic astrophysics. Their implications are frequently discovered when studying the dynamical characteristics of fluid thin shells, cosmic phase-transitions, and collapsing star’s boundaries. These circumstances necessitate a thorough analysis of the star’s inside and outside configurations. Several paradigms of gravitating systems of observational and theoretical intrigue include the incorporation of two distinct regions of spacetime, matched at certain hyper-surfaces, detaching the inner from the outer region [69]. As in celestial bodies, such systems could effectively provide both geometries in which an internal one stuffed with a certain fluid composition detached from the outer vacuum solution [36, 70, 71]. On the other side, the two matter-crowded regions likewise in domains/brain walls [72] or thin shells [73,74,75]. In order for these designs to be well-stated mathematically, the gluing of the hyper-surface must meet a set of requirements, which in the background of GR are called Darmois–Israel junction (matching) conditions [76, 77]. The continuity of the first-fundamental form throughout the coinciding hyper-surface, as well as a variety of constraints linking the stress-energy tensor to the discontinuity in the extrinsic-curvature over said hyper-surface, are among these requirements. In the literature, the physical relevance of related configurations and the requirements for representing the particular stellar bodies have been widely presented [78,79,80,81]. The thermodynamical aspects and entropy of such thin-shells are investigated under various scenarios [82,83,84,85]. Various modified theories would have their own set of matching requirements, which are determined through their relative field equations, comprising extra degrees where the theories are grounded. Hence, the study of the matching conditions within the context of extended gravity theories is of great significance to frequently analyzing the phenomenology of stellar configurations. The deliberation of such modifications is enlightened in a multitude of ways to explore the regimes of the intense-field gravitational interaction within the field of astronomy and the challenges by the late and early-time cosmic configurations [86, 87]. These theories suggest new challenges involving higher degrees and significantly more dynamical aspects, necessitating the upgrade of the matching conditions. Olmo and Garcia [64] presented the junction-conditions for Palatini f(R) scenario to glue the exterior and interior geometries at hyper-surface. They showed that certain of these requirements depart from that of GR and counterparts metric f(R) ones. In our study, we would like to compute the matching conditions for the LTB spacetime in the context of Palatini f(R) formalism. Unlike its metric counterparts, the proposed formalism features a quadratic-order equations of motion bearing the novel gravitational circumstances owing to non-linear association produces by matter-fields having no influence on propagating degrees-of-freedom. The matching conditions within the context of Palatini f(R) gravity are expressed as [64]

$$\begin{aligned}&h_{\beta \varrho }=g_{\beta \varrho }-n_{\beta }n_{\varrho }, \end{aligned}$$

(26)

$$\begin{aligned}&[T]=0, \end{aligned}$$

(27)

$$\begin{aligned}&\tau =0, \end{aligned}$$

(28)

$$\begin{aligned}&[K^{\alpha }_{\alpha }]=-\frac{3}{2f_R}f_{RR}R_T|_{\Sigma }b \end{aligned}$$

(29)

$$\begin{aligned}&-[K_{\beta \varrho }]+\frac{1}{3}h_{\beta \varrho }[K^{\alpha }_{\alpha }] =\kappa ^2\frac{\tau _{\beta \varrho }}{f_{R_\Sigma }}, \end{aligned}$$

(30)

$$\begin{aligned}&\left( K^{+}_{\beta \varrho }+K^{-}_{\beta \varrho }\right) \tau ^{\beta \varrho } =2n^{\varrho }n^{\beta }[T_{\varrho \beta }]-\frac{3}{f_R}R^2_{T}F^2_{R}[b^2]. \end{aligned}$$

(31)

The continuity of first fundamental-form across hyper-surface is expressed in Eq. (26), however, the continuity of trace of fluid configuration, and the disappearing of its singular constituents across $\Sigma$ is represented by Eqs. (27) and (28). The condition presented in Eq. (30) is revealing the depart consequences (second fundamental form: discontinuity of the trace) from the Einstein’s gravity also in the metric f(R) scenarios. Since Palatini f(R) trace-equation is given by $\kappa ^2 T=Rf_R-2f\Longrightarrow R\equiv R(T)$ which is simple an algebraic relation associating matter and curvature of the corresponding system. The relation propose a radical variance in the characteristics of the framework regarded to the metric version, thereby a distributional study of the Palatini f(R) configuration must consider those factors. In order to match the exterior and interior geometries of our matter configurations, we consider the exterior metric of the form [62]

$$\begin{aligned} ds^{2+}&=-\bigg [1-\bigg (\frac{2M}{r}+\frac{r^2\tilde{R}}{12}\bigg ) \bigg ]d\nu ^2-2d\nu dr\nonumber \\&\quad +r^2d\theta ^2+r^2\sin ^2\theta d\phi ^2, \end{aligned}$$

(32)

here $\nu$ is the retarded-time, while $M(\nu )$ represents the entire mass of the configuration. To evaluate the matchings on the boundary surface $r =r_{\Omega }=$ constant. We are taking into account the null-fluid as well in the stellar configuration. The regions are assumed to be glued (matched) across a time like hyper-surface ($\Omega$) together with the usual representation of their respective boundaries as $\Omega ^-=\Omega ^+$. The several discontinuities in certain geometrical variables would be evaluated through Eqs. (30) and (31) for our case, depicting the influence of singular constituents of the source. Therefore, we get the following equations

$$\begin{aligned}&\frac{-1}{12r}\bigg \{\tilde{R}C^3+12C\bigg [ \dot{C}^2-\bigg (\frac{C'^2}{B^2}\bigg )+\frac{1}{C^2}\sin ^2\theta \bigg ]\bigg \}\nonumber \\&\qquad \bigg \{C\dot{C}-\bigg (C\bigg \{ \dot{C}^2-\frac{C'^2}{B^2}\bigg \}-\frac{\dot{F}}{2F}\bigg )\dot{\nu } \bigg \}\nonumber \\&=\frac{3\kappa ^2}{2F^2}(\dot{C}\dot{\mu })F_{R}, \end{aligned}$$

(33)

and

$$\begin{aligned}&\frac{1}{2C}\bigg \{\dot{C}^2-\frac{C'^2}{B^2}+1\bigg \} \bigg [\bigg \{\frac{C'^2}{B^2}-\dot{C} \bigg \}^{-2}\nonumber \\&\quad -\frac{C^2}{B^2}\frac{F'^2}{2F^2} \bigg (\frac{\dot{F}}{2F}\bigg )^{-2}\bigg ]-\frac{1}{36}\bigg [ C\dot{C}\nonumber \\&\quad -\bigg \{C\bigg (\dot{C}^2 -\frac{C'^2}{B^2}\bigg ) -\frac{\dot{F}}{2F}\bigg \}\bigg \{\frac{C'}{B} \bigg [\frac{C'^2}{B^2}-\dot{C} \bigg ]^{-1}\nonumber \\&\quad -\frac{C}{B}\frac{F'}{2F} \bigg (\frac{\dot{F}}{2F}\bigg )^{-1}\bigg \}\bigg ] \bigg \{\tilde{R}C^3+12C\bigg [\dot{C}^2-\frac{C'^2}{B^2} \bigg ] \nonumber \\&\quad +\frac{1}{C}\sin ^2\theta \bigg \}-\ddot{\nu }= \bigg (\frac{\kappa ^2}{F^2} \mu +\frac{\dot{F}}{F}(1-\dot{C})\bigg ) \bigg [\frac{C^{'2}}{B^2}\bigg \{ \frac{C^{'2}}{B^2}\nonumber \\&\quad -\dot{C}^2\bigg \}^{-2}-\frac{C^2}{B^2}\frac{F'^2}{2F^2} \bigg (\frac{\dot{F}}{2F}\bigg )^{-2}\bigg ] \nonumber \\&\quad +\frac{\dot{F}}{2F} \bigg \{\frac{C'}{B}\bigg (\frac{C^{'2}}{B^2}-\dot{C}^2\bigg )^{-1} -\frac{C}{B}\frac{F'}{2F} \bigg (\frac{\dot{F}}{F}\bigg )^{-1}\bigg \}, \end{aligned}$$

(34)

$$\begin{aligned}&\bigg \{-\frac{C'}{B}\bigg (\frac{C^{'2}}{B^2}-\dot{C}^2\bigg )^{-1} +\frac{C}{B}\frac{F'}{2F} \bigg (\frac{\dot{F}}{F}\bigg )^{-1}\bigg \}\nonumber \\&\qquad \times \bigg \{\left( -\frac{B^2}{3}+1\right) C\dot{C} -2\bigg [\frac{C^{'2}}{B^2}-\dot{C}^2\bigg ] \nonumber \\&\quad -\frac{\dot{F}}{F} \bigg \}\bigg [\tilde{R}C^3+12C\bigg \{\dot{C}^2-\frac{C'^2}{B^2} \bigg \}+\frac{1}{C}\sin ^2\theta \bigg ]-C\dot{C}=0, \end{aligned}$$

(35)

$$\begin{aligned}&\sin ^2\theta \bigg [ \bigg \{\frac{C'}{B}\bigg (\dot{C}^2-\frac{C^{'2}}{B^2}\bigg )^{-1} +\frac{C}{2B}\frac{F'}{F} \bigg (\frac{\dot{F}}{F}\bigg )^{-1}\bigg \}\nonumber \\&\qquad \times \bigg \{\frac{1}{3}(3-B^2)C\dot{C} -2\bigg [\frac{C^{'2}}{B^2}-\dot{C}^2\bigg ] \nonumber \\&\quad -\frac{\dot{F}}{F} \bigg \}\bigg \{\tilde{R}C^3+12C\bigg (\dot{C}^2-\frac{C'^2}{B^2} \bigg )+\frac{1}{C}\sin ^2\theta \bigg \}-C\dot{C}\bigg ]\nonumber \\&\qquad =0, \end{aligned}$$

(36)

respectively. The aforementioned consequences are persistent with tracelessness of singular section of the fluid under discussion. It is found that the outcomes (34)–(36) heavily deviate from the results in Einstein’s gravity where the singular segment of the $G_{\zeta \varrho }=\kappa \tau _{\zeta \varrho }$ does not set about the constrain (28). It is worthy to mention that Eq. (28) enforce a condition within the energy density and stresses on $\Sigma$ which usefully consider the source of reduction of the degree-of-freedom. It is revealed that trace of (30) displays $2[K^{\alpha }_{\alpha }]=\kappa ^2 \tau$ as shown in (21) of [64] under acceptable bounds. Therefore, the brane tension in the framework of GR is non disappearing generally. In contrast to it, the brane tension disappears on the grounds of Palatini f(R) approach, however, $[K^{\alpha }_{\alpha }]\ne 0$ as represented in Eqs. (34)–(36). The expressions for the first and second time-derivatives of the quantity $\nu$ are calculated as follows

$$\begin{aligned} \dot{\nu }&=\frac{C'}{B}\left[ \left( \frac{C'}{B}\right) ^2 -\dot{C}^2\right] ^{-1}-\frac{C}{2B}\frac{F'}{F} \left( \frac{\dot{F}}{F}\right) ^{-1}, \end{aligned}$$

(37)

$$\begin{aligned} \ddot{\nu }&=\frac{\frac{\dot{C}'}{B}- \frac{C'\dot{B}}{B^2}}{\bigg [\bigg (\frac{C'}{B}\bigg )^2-\dot{C}^2\bigg ]}- \frac{1}{[(\frac{C'}{B})^2-\dot{C}^2]} \bigg \{\frac{2C'^2}{B^2}\bigg (\frac{\dot{C}'}{B} -\frac{C'\dot{B}}{B^2}\bigg )\nonumber \\&\qquad -2\dot{C}C'\frac{\ddot{C}}{B}\bigg \} -\frac{1}{\frac{\dot{F}}{2F}}\bigg [\frac{C}{2B}\bigg ( \frac{\dot{C}}{C}-\frac{\dot{B}}{B} -\frac{\dot{F}}{F}\bigg )\frac{F'}{F} +\frac{C}{2B}\frac{\dot{F}}{2F}\bigg ] \nonumber \\&\quad -\frac{1}{\bigg (\frac{\dot{F}}{2F}\bigg )^2}\bigg [\frac{C}{B}\frac{F'}{2F} \bigg (\frac{\ddot{F}}{2F}+\frac{\dot{F}^2}{F^2}\bigg )\bigg ]. \end{aligned}$$

(38)

The sphere of our matter configuration is made up of entirely dust and dissipation by means of heat flow and bearing the influence of outgoing null-fluid. Thus, for our matter configuration, the computation of (31) for the matching of interior to the exterior geometry gets the following form

$$\begin{aligned}&\hat{q}_{eff}\overset{\Sigma }{=}\epsilon _{eff}-\frac{3\kappa ^2}{F}R^2_T F^2_R\bigg (\frac{\mu '}{\mu }\bigg )+\chi _0, \end{aligned}$$

(39)

here script $\overset{\Sigma }{=}$ identifies the measurements are computed across surface $\Sigma$. Alternatively, by using the Palatini f(R) field equations for our LTB source, the matchings of our geometrical configurations read

$$\begin{aligned}&m(t,r)\overset{\Sigma }{=}M+\frac{Rr^3}{24} \end{aligned}$$

(40)

$$\begin{aligned}&\hat{q}\overset{\Sigma }{=}\epsilon -\frac{\kappa R}{F}\left( \frac{f}{R}-F\right) -\frac{3\kappa ^2}{F}R^2_T F^2_{R}\bigg (\frac{\mu '}{\mu }\bigg )+\chi ^*_0, \end{aligned}$$

(41)

demonstrating the regimes of intense-field of gravitational interaction and these consequences could be recovered the GR ones under acceptable bounds just if $f_{RR}=0$. Equation (41) determines the energy content in cases when shells/branes are present. In our case, the matchings should be applied for the vacuum configuration provided the singular constituent of the stress-energy tensor disappear in (41) which is only possible if we regard the energy density of our source to be uniform. The quantity $\chi ^*_0=\chi _0+\xi _{11}-\xi _{01}$. The value of $\chi _0$ is revealing the intense gravitational interaction owing to high curvature regimes is computed as below

$$\begin{aligned} \chi _0&=\frac{F'}{BF}\bigg [\dot{C}^2-\frac{C'^2}{B^2} \bigg ]-\frac{C'}{B(\frac{\dot{F}}{F})^2}\bigg (\dot{C}^2 -\frac{C'^2}{B^2}\bigg )^{-2}\nonumber \\&\quad \times \bigg [\frac{C}{2B}\frac{F'}{F} \frac{\dot{F}}{2F}\bigg (\frac{\dot{C}}{C}-\frac{\dot{B}}{B} -\frac{\dot{F}}{2F}\bigg )+\frac{C}{2B}\frac{\dot{F}^2}{2F^2} \\&\quad -\frac{C}{2B}\frac{F'}{F}\bigg (\frac{\ddot{F}}{2F} +\frac{\dot{F}^2}{2F^2} \bigg )\bigg ]. \end{aligned}$$

It is shown that the findings that corresponds the extrinsic-curvature to the fluid configurations on gluing surface disagree from those ones computed in GR as well as in f(R) metric theories. Hence, one could match vacuum exteriors within Palatini f(R) context which is consistent to any stellar bodies. Additionally, the implications of such matchings outside stellar configurations (white-dwarfs, neutron-stars, among others) exist, e.g. braneworld or thin shell wormholes within Palatini f(R) context. Furthermore, we have the finding across $\Sigma$ as

$$\begin{aligned}&\epsilon _{eff}\overset{\Sigma }{=}\frac{L}{4\pi r^2}, \end{aligned}$$

(42)

where L represents the entire sphere’s luminosity computed on corresponding surface, having the form as

$$\begin{aligned}&L\overset{\Sigma }{=}L_{\infty }\bigg (1-\frac{2m}{r}+2\frac{dr}{d\nu } \bigg )^{-1} \end{aligned}$$

(43)

with entire luminosity computed by stationary observer at infinity

$$\begin{aligned}&L_{\infty }=\frac{dm}{d\nu }\overset{\Sigma }{=}-\bigg ( \frac{dm}{dt}\bigg (\frac{d\nu }{dt}\bigg )^{-1}\bigg ). \end{aligned}$$

(44)

Now, the boundary red shift would be given by

$$\begin{aligned}&\frac{d\nu }{dt}\overset{\Sigma }{=}z+1. \end{aligned}$$

(45)

The value of $\dot{\nu }$ is expressed earlier. Thus, the time formation of the compact body (black-hole) is

$$\begin{aligned}&\dot{\nu }^{-1}\overset{\Sigma }{=}E+U\overset{\Sigma }{=}0 \end{aligned}$$

(46)

From (43) and (37), it implies that

$$\begin{aligned}&L\overset{\Sigma }{=}\frac{L_{\infty }}{(E+U)^2}. \end{aligned}$$

(47)

However, by using $U=\dot{R}$ and (43) found to be

$$\begin{aligned}&\frac{dr}{d\nu }\overset{\Sigma }{=}U(E+U). \end{aligned}$$

(48)

Consequently, it is significant to highlight that under totally diffusion approximation that is entire luminosity of the system disappears even when the heat fluxes are non-vanishing within the spherical configuration. Therefore, in such scenario $\epsilon _{eff}=0$ and $\hat{q}_{eff}\ne 0$, thereby (41) follows that

$$\begin{aligned}&\hat{q}\overset{\Sigma }{=}\frac{\kappa R}{F}\left( \frac{f}{R}-F\right) -\frac{3\kappa ^2}{F}R^2_T F^2_{R}\bigg (\frac{\mu '}{\mu }\bigg )+\chi ^*_0, \end{aligned}$$

which could recover (32) of [59] within acceptable bounds. This outcome is the clear effect of the dust configuration (disappearing hydro-dynamic pressure) within Palatini f(R) context.

2.2 Matter variables and conformal scalar

The Weyl-tensor $C^{\rho }_{\beta \varrho \mu }$ could be written in the form of Riemann-tensor $R^{\rho }_{\beta \varrho \gamma },$ the curvature scalar R, and Ricci-tensor $R_{\beta \varrho }$ as

$$\begin{aligned} C^{\rho }_{\beta \varrho \gamma }&=R^{\rho }_{\beta \varrho \gamma } -\frac{1}{2}R^{\rho }_{\varrho }g_{\beta \gamma } +\frac{1}{2}R_{\beta \varrho }\delta ^{\rho }_{\gamma } -\frac{1}{2}R_{\beta \gamma } \delta ^{\rho }_{\varrho }\nonumber \\&\quad +\frac{1}{2}R^{\rho }_{\gamma } g_{\beta \varrho }+\frac{1}{6}R(\delta ^{\rho }_{\varrho } g_{\beta \gamma }-g_{\beta \varrho } \delta ^{\rho }_{\gamma }), \end{aligned}$$

(49)

that may be further split into its electric and magnetic sections. In the case of the spherical composition of the fluid configuration, the magnetic distribution of the Weyl-tensor disappears and it might only be represented in its electric constituents as

$$\begin{aligned} E_{\beta \varrho }=C_{\beta \gamma \varrho \alpha } V^{\gamma } V^{\alpha }. \end{aligned}$$

(50)

The electric components of the Weyl-tensor by projection-tensor and the unit four-vector get the form as below

$$\begin{aligned} E_{\beta \varrho }=\varepsilon \left( \chi _{\beta } \chi _{\varrho }-\frac{1}{3} h_{\beta \varrho }\right) . \end{aligned}$$

(51)

The scalar captures the consequences of the space-time curvature , having the mathematical expression given below

$$\begin{aligned} \varepsilon&=\frac{1}{2}\left[ \frac{\ddot{C}}{C}-\frac{\ddot{B}}{B} +\frac{\dot{C}}{C}\left( -\frac{\dot{C}}{C}+\frac{\dot{B}}{B}\right) \right] \nonumber \\&\quad +\frac{1}{B^2}\left[ -\frac{C''}{2C}+\left( \frac{B'}{B} +\frac{C'}{C}\right) \frac{C'}{2C}\right] -\frac{1}{2C^2}. \end{aligned}$$

(52)

Now, using Eqs. (11), (13), (14), (20) and (52), we have

$$\begin{aligned} -\varepsilon +4\pi (\hat{\mu }_{eff}-\epsilon _{eff})=\frac{3}{C^3}m-\frac{\xi _{22}}{C^2}, \end{aligned}$$

(53)

In the influence of extra curvature factors, the conformal scalar is dependent on the mass-function and the matter variables. The propagation equations of shear and expansion scalar that describe particles’ motion and their expansion, respectively, are written as

$$\begin{aligned} \frac{1}{3}\left( 3\dot{\Theta }_{eff}+\Theta _{eff}^2+2 \sigma _{eff}^2\right)&=-4\pi (\hat{\mu }_{eff}+\epsilon _{eff})\nonumber \\&\quad -\frac{\xi _{22}}{C^2}+D_{1}, \end{aligned}$$

(54)

$$\begin{aligned} \frac{1}{3}\left( 3\dot{\sigma }_{eff}+\sigma _{eff}^2 +2\Theta _{eff}\sigma _{eff}\right)&= T_{1}(4\pi \epsilon _{eff}+T_{2}-\varepsilon )+D_{2},\nonumber \\ \end{aligned}$$

(55)

along with $T_{1}=-2\left( \frac{\dot{C}}{C}-\frac{\dot{B}}{B}\right)$, $T_{2}=2\frac{\dot{B}}{B}\frac{\dot{C}}{C}-\frac{\dot{C}^2}{3C^2}-\frac{\dot{B}^2}{3B^2}$. The terms $D_{2}$ and $D_{1}$ emerge because of Palatini consequences of f(R) theory, which are listed in Appendix C. To discuss the dynamics of the fluid configuration, the dynamical equations utilizing matter-fields in the Palatini f(R) perspective as

$$\begin{aligned}&\dot{\hat{\mu }}_{eff}+\frac{\dot{B}}{B}(\hat{\mu }_{eff} +\epsilon _{eff})+2\frac{\dot{C}}{C} \hat{\mu }_{eff} +\frac{1}{B}\hat{q}'_{eff}\nonumber \\&\quad +2\frac{C'}{C B}\hat{q}_{eff} +\frac{5}{2}\hat{\mu }_{eff}\frac{\dot{F}}{F}+\frac{3}{B} \hat{q}_{eff}\frac{F'}{F}+\frac{\dot{F}}{2F} \epsilon _{eff}=0, \end{aligned}$$

(56)

$$\begin{aligned}&\dot{\hat{q}}_{eff}+2 \left( \frac{\dot{B}}{B} +\frac{\dot{C}}{C}\right) \hat{q}_{eff}+\frac{\epsilon '_{eff}}{B}+\frac{2C'}{BC} \epsilon _{eff} +\hat{q}_{eff}\left( \frac{3\dot{F}}{F}\right) \nonumber \\&\quad +\frac{5\epsilon _{eff}}{2B} \left( \frac{F'}{F}\right) +\frac{\hat{\mu }_{eff}}{2B}\left( \frac{F'}{F}\right) =0. \end{aligned}$$

(57)

The Bianchi-identities could be applied to acquire the propagation equation for the conformal tensor as

$$\begin{aligned}&\bigg [-4\pi (\hat{\mu }_{eff}-\epsilon _{eff}) +\varepsilon \bigg ]'+3(4\pi \epsilon _{eff}+\varepsilon )\frac{C'}{C}\nonumber \\&\quad =-12\pi \frac{B\dot{C}}{C} \hat{q}_{eff}+ \frac{\xi '_{22}}{2C^2}+\frac{\xi _{22}}{2C^2}\frac{C'}{C}. \end{aligned}$$

(58)

It demonstrates a connection between the matter variables and the conformal tensor within the influence of additional curvature constituents.

3 Palatini f(R) scalar variables

Bel [88] was the first to propose the splitting of the Riemann-tensor $R_{\beta \gamma \varrho \delta }$. It is worth noting that Herrera et al. [89] adopted the Bel’s technique, broke down the Riemann-tensor orthogonally to correlate the features of the matter configuration to that of structure scalars in the framework of GR. By orthogonal break down of the Riemann-tensor, they developed the electric $Y_{\beta \varrho }$ and magnetic $Z_{\beta \varrho }$, and the dual-part $X_{\beta \varrho }$ of the Riemann-tensor. The set of five scalars for spherical line-element is obtained by splitting the aforementioned tensors into trace-free and trace portions, and explained the physical consequences of each scalar. It is shown that the energy-density and pressure anisotropy of the are linked with the scalars $Y_{T}$ and $X_{T}$, respectively. It was explained that the scalar $Y_{T F}$ corresponds the pressure anisotropy together with the conformal scalar, on the other side, the energy irregularity is controlled by $X_{T F}$ in non-dissipative fluid. After that, many researchers [43, 44, 90, 91] utilized such scalars in order to better analyze the physical aspects of various cosmological configurations. Bhatti et al. [92, 93] calculated the scalar functions and discussed their role on the evolving gravitating objects using Palatini f(R) context in the presence of the electromagnetic field. They evaluated the kinematical factors to examine the fluid’s physical aspects as well as Bianchi identities and the Raychaudhuri equation. They broke the Riemann-tensor orthogonally to yield the scalar variables and associated them with the fluid’s aspects like energy-density and pressure stresses as well as explained that these Palatini scalar functions enable us to indicate the formation of the singularity in celestial objects. Now, we would like to define the tensors $Y_{\zeta \varrho }$ and $X_{\beta \varrho }$ for the evaluation of structure scalars in Palatini f(R) approach.

$$\begin{aligned} Y_{\beta \varrho }&=R_{\beta \lambda \varrho \delta } V^{\lambda } V^{\delta }, \quad X_{\beta \varrho }=~^{*}R^{*}_{\beta \lambda \varrho \delta } V^{\lambda } V^{\delta }\nonumber \\&=\frac{1}{2} \eta _{\beta \lambda }^{~~\epsilon \rho } R^{*}_{\epsilon \rho \varrho \delta } V^{\lambda } V^{\delta }, \end{aligned}$$

(59)

where $R^{*}_{\beta \varrho \lambda \delta }=\frac{1}{2} \eta _{\epsilon \lambda \rho \delta } R_{\beta \varrho }^{~~\epsilon \rho }$ and $~^{*}R^{*}_{\beta \lambda \varrho \delta }=\frac{1}{2} \eta _{\beta \lambda }^{~~\epsilon \alpha } R^{*}_{\epsilon \alpha \varrho \delta }$ denote the right and double-dual of the Riemann-tensor and $\eta _{\epsilon \rho \lambda \delta }$ is the Levi-Civita tensor. Following the usual approach of the orthogonal splitting for Riemann-tensor, $Y_{\beta \varrho }$ and $X_{\beta \varrho }$ including the fluid’s variables and some additional gravitational terms, and are presented in Appendix D. For our problem, the scalar quantities corresponding to trace-free and trace portions of the said tensors are found as

$$\begin{aligned} Y_{T}&=4\pi (\epsilon _{eff}+\hat{\mu }_{eff})+M^{(D)}_{1}, \end{aligned}$$

(60)

$$\begin{aligned} Y_{T F}&=-4\pi \epsilon _{eff}+\varepsilon +\frac{4\pi }{F} \xi _{11}+M^{(D)}_{2}, \end{aligned}$$

(61)

$$\begin{aligned} X_{T}&=8\pi \hat{\mu }_{eff}-\frac{8\pi }{F} \xi _{00}+M^{(D)}_{3}, \end{aligned}$$

(62)

$$\begin{aligned} X_{T F}&=-4\pi \epsilon _{eff}-\varepsilon +\frac{4\pi }{F}\chi _{11}+M^{(D)}_{4}, \end{aligned}$$

(63)

where

$$\begin{aligned} M^{(D)}_{2}=\frac{M^{(D)}_{\beta \varrho }}{\xi _{\beta } \i _{\varrho } -\frac{1}{3} h_{\beta \varrho }}; \quad M^{(D)}_{4} =\frac{N^{(D)}_{\beta \varrho }}{\xi _{\beta } \xi _{\varrho }-\frac{1}{3}h_{\beta \varrho }}. \end{aligned}$$

(64)

By making use of Eqs. (25), (53) and (61), we have

$$\begin{aligned} Y_{T F}&=-8\pi \epsilon _{eff}+4\pi \frac{1}{C^3} \int C^3\left[ \hat{\mu }'_{eff}-3\hat{q}_{eff}\frac{C'}{C}\frac{U}{E}\right] dr+\frac{\xi _{22}}{C^2}. \end{aligned}$$

(65)

The computed expressions for $M^{(D)}_{1},~M^{(D)}_{3},~M^{(D)}_{\beta \varrho }$ and $N^{(D)}_{\beta \varrho }$ are listed in the Appendix B. The scalar $Y_{TF}$ might be shown by energy irregularity,the null radiation, and the heat-fluxes, carrying intense gravitational terms. additionally, it has been described that $Y_{TF}$ govern the stable profile of the shear-free geodesic configuration. From Eqs. (60)–(63), the scalars variables may express via geometric variables as

$$\begin{aligned} Y_{T}&=-2\left( \frac{\ddot{C}}{C}+\frac{\ddot{B}}{2B}\right) -\frac{\xi _{22}}{C^2}+M^{(D)}_{1}, \end{aligned}$$

(66)

$$\begin{aligned} Y_{T F}&=-\left( \frac{\ddot{B}}{B}-\frac{\ddot{C}}{C}\right) -\frac{\xi _{22}}{C^2}+4\pi \frac{\xi _{11}}{F}+M^{(D)}_{2}, \end{aligned}$$

(67)

$$\begin{aligned} X_{T}&=\frac{1}{C^2}+2\left( \frac{\dot{B}}{B}+\frac{\dot{C}}{2C}\right) \frac{\dot{C}}{C}\nonumber \\&\quad -\frac{2}{B^2}\left[ \frac{C''}{C}+\frac{C'^2}{2C^2} -\frac{B'}{B}\left( \frac{C'}{C}\right) \right] \nonumber \\&\quad -\frac{8\pi }{F}\xi _{00}+M^{(D)}_{3}, \end{aligned}$$

(68)

$$\begin{aligned} X_{T F}&=-\frac{\dot{C}}{C}\left( -\frac{\dot{C}}{C}+\frac{\dot{B}}{B}\right) +\frac{1}{B^2}\left[ \frac{C''}{C}-\left( \frac{B'}{B}+\frac{C'}{C}\right) \frac{C'}{C}\right] \nonumber \\&\quad +\frac{1}{C^2} -\frac{\xi _{22}}{2C^2}+\frac{4\pi }{F} \xi _{11}+M^{(D)}_{4}. \end{aligned}$$

(69)

From above findings, one could retrieve these scalars within the context of GR [59] within the exclusion of higher curvature corrections. These scalar are directly connected in the description of dense stellar structures under f(R) gravity. To analyze the consequences of $\epsilon R^2$ in this scenario, the Raychaudhuri-equation could be applied as a potential approach. Alternatively, Eqs. (54), (55) and (58) may express as

$$\begin{aligned} \frac{1}{3}\left( 3\dot{\Theta }_{eff}+ \Theta ^2_{eff}+2 \sigma ^2_{eff}\right) =&-Y_{T}-\frac{\xi _{3}}{C^{2}}+M^{(D)}_{1}+D_{1}, \end{aligned}$$

(70)

deploying the expansion propagation of the source in association with the $Y_{T}$ structure scalar with the inclusion of additional curvature corrections owing to Palatini f(R) context. For the understanding of shearing motion of the fluid is linked with the equation given below

$$\begin{aligned}&\frac{1}{3}\bigg (3\dot{\sigma }_{eff}+\sigma ^2_{eff} +2\Theta _{eff}\sigma _{eff}\bigg )\nonumber \\&\quad =T_{1}\bigg [-Y_{T F}+\frac{4\pi }{F}\xi _{11}+M^{(D)}_{2}+T_{2}\bigg ]+D_{2}. \end{aligned}$$

(71)

Consequently, the shearing motion of compact stars is influenced by Palatini f(R) modifications. Moreover, the propagation equation indicates an association between fluid profile and the conformal tensor via scalar functions and higher curvature corrections is evaluated as

$$\begin{aligned} \bigg [X_{T F}+4\pi \hat{\mu }_{eff}\bigg ]'&=-3X_{T F}\left( \frac{C'}{C}\right) +4\pi \hat{q}_{eff}B(\Theta -\sigma )\nonumber \\&\quad -\frac{\xi '_{22}}{2C^2}+\frac{\xi _{22} C'}{2C^3}+ \left( 4\pi \frac{\xi _{11}}{F}+M_{4}^{(D)}\right) '\nonumber \\&\quad +3\left( 4\pi \frac{\xi _{11}}{F}+M_{4}^{(D)}\right) \frac{C'}{C}. \end{aligned}$$

(72)

In dissipation-free dust cloud scenario, Eq. (72) recovers

$$\begin{aligned} \bigg [X_{T F}+4\pi \hat{\mu }_{eff}\bigg ]'&=-3 X_{T F}\left( \frac{C'}{C}\right) -\frac{\xi '_{22}}{2C^2}+\frac{\xi _{22}}{2C^2}\left( \frac{C'}{C}\right) \nonumber \\&\quad +\left( 4\pi \frac{\xi _{11}}{F}+M_{4}^{(D)}\right) '\nonumber \\&\quad +3\left( 4\pi \frac{\xi _{11}}{F}+M_{4}^{(D)}\right) \frac{C'}{C}. \end{aligned}$$

(73)

Subsequently, $\hat{\mu }'_{eff}=0$ in the above finding implies

$$\begin{aligned} (X_{T F})'&=-3X_{T F}\left( \frac{C'}{C}\right) -\frac{\xi '_{22}}{2C^2} +\frac{\xi _{22}}{2C^2}\left( \frac{C'}{C}\right) \nonumber \\&\quad +\left( 4\pi \frac{\xi _{11}}{F}+M_{4}^{(D)}\right) ' +3\left( 4\pi \frac{\xi _{11}}{F}+M_{4}^{(D)}\right) \frac{C'}{C}, \end{aligned}$$

(74)

whose integration reads to

$$\begin{aligned} X_{T F}&=\frac{f(t)}{C^3}-\int \frac{1}{X_{T F}} \left[ \frac{\xi '_{22}}{2C^2}+\frac{\xi _{22} C'}{2C^3} +\left( \frac{4\pi }{F}\xi _{11}+M_{4}^{(D)}\right) '\right. \nonumber \\&\quad \left. +3\left( \frac{4\pi }{F}\xi _{11}+M_{4}^{(D)}\right) \frac{C'}{C}\right] dr. \end{aligned}$$

(75)

It is noticed from Eq. (75) that $X_{T F}$ manages the energy irregularity in the setting of zero dissipation and with the exclusion of $\epsilon _{eff}$ constituents. This is also true for a fluid that is isotropic in nature as discussed in [89]

4 LTB space-time

In present section, we would want to describe discuss the characteristics of LTB space-time for the dust fluid configuration without considering the effects of dissipation. We also find some LTB solutions for the corresponding propagation equation. In this direction, we propose a geodesic fluid that is dissipation-free in nature that is $(q_{eff}=0=\epsilon _{eff})$ for the generic feature of LTB configuration. In this regard, Eq. (12) after being integrated, reads the form

$$\begin{aligned} B(t, r)=\frac{1}{1+k(r)} \exp \left[ \int \frac{\frac{1}{2F}\left( \dot{F'}-\frac{5\dot{F}F'}{2F}\right) - \frac{\dot{C'}}{C}}{\left( \frac{F'}{2F}-\frac{C'}{C}\right) }dt\right] , \end{aligned}$$

(76)

here k is the integration constant, however, in metric version of f(R) theory the factor $\frac{5\dot{F}F'}{2F}$ is excluded since it arises because of connections. In the direction of GR, $F\longrightarrow 1$, $\dot{F},~F'\longrightarrow 0$ and aforesaid finding recovers

$$\begin{aligned} B(t,r)=\frac{1}{(1+k(r))^{\frac{1}{2}}}C'(t, r). \end{aligned}$$

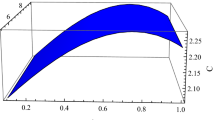
In case of Palatini f(R) approach, the evolution is observed on the comparison of Eq. (76) with Misner–Sharp mass given in Eq. (20). For the solution of propagation equation, we use $R+\alpha R^2$ (Starobinski) model and junction conditions. The equation is numerically solved and its solution is described through graphical representation which describe the impact of f(R) theory on different models of the universe and expressed in Figures 1,  2 and 3.

Fig. 1

Plots of C versus t and r for $\kappa =-0.5$ and $m=1.4$, indicating the open universe increasing exponentially with the passage of time

Fig. 2

Plots of C versus t and r for $\kappa =0$ and $m=1.4$, represents flat universe

Fig. 3

Plots of C versus t and r for $\kappa =0.5$ and $m=1.4$, indicating that f(R) terms effects the close universe instead of expanding to maximum size and then collapsing, it expands exponentially

Substituting the above expression into (8), the LTB model gets the expression

$$\begin{aligned} ds^2=-dt^2+\frac{C'^2}{\kappa (r)+1} dr^2+C^2 (d\theta ^2+sin^2\theta d\phi ^2). \end{aligned}$$

(77)

The metric (77) naturally associated to dust inhomogeneity, it is significant to express that fluid’s anisotropy is the leading cause that is compatible with LTB geometry. In dissipation free dust configuration, Bianchi identity then simplifies to subsequent form

$$\begin{aligned} \dot{\mu }_{eff}=2\mu _{eff}\left[ \frac{\dot{B}}{2B} +\frac{\dot{C}}{C}+\frac{5}{4}\left( \frac{\dot{F}}{F}\right) \right] . \end{aligned}$$

(78)

Taking integration of Eq. (78) follows

$$\begin{aligned} \mu _{eff}=\frac{3[1+\kappa (r)]^{\frac{1}{2}}h(r)}{(C^3)' F^{\frac{5}{2}}}, \end{aligned}$$

(79)

here h(r) is function of integration. Now, the scalars $Y_{T F},~Y_{T}, X_{T F},$ and $X_{T}$ for the space-time (77) yield

$$\begin{aligned} Y_{T}&=-\frac{\ddot{C'}}{C'}+\frac{\ddot{C}}{C}+M^{(D)}_{1}-\frac{\xi _{22}}{C^2}, \end{aligned}$$

(80)

$$\begin{aligned} Y_{T F}&=-2\left( -\frac{\ddot{C}}{C}+\frac{\ddot{C'}}{C'}\right) -\frac{\xi _{22}}{C^2}+M^{(D)}_{2}+4\pi \frac{\xi _{11}}{F} \end{aligned}$$

(81)

$$\begin{aligned} X_{T}&=\frac{2\dot{C} \dot{C'}}{C C'}+\frac{\dot{C}^2}{C^2} -\frac{\kappa }{C^2}-\frac{\kappa '}{C C'}-\frac{8\pi }{F} \xi _{00}+M^{(D)}_{3}, \end{aligned}$$

(82)

$$\begin{aligned} X_{T F}&=\frac{\dot{C}^2}{C^2}-\frac{\dot{C} \dot{C'}}{C C'}-\frac{\kappa }{C^2}+\frac{\kappa '}{2C' C}-\frac{\xi _{22}}{2C^2}\nonumber \\&\quad +\frac{4\pi }{F} \xi _{11}+M^{(D)}_{4}. \end{aligned}$$

(83)

It is shown from Eqs. (80) and (81) the scalars $Y_{TF}$ and $Y_{T}$ may not comprise the factor $\kappa$ in their descriptions.

5 Continuation of the LTB for dissipative scenario

We construct scalar functions for a generalized LTB configuration, called GLTB, by incorporating the heat flow in this portion. We make a comparison of the scalar variables related to both of the spacetimes to find the correspondence between them. We also address the symmetry-based continuation by considering streaming-out limit and diffusion scenarios. We provide the study of heat conduction to produce the temperature-profile for diffusion. It is shown in the previous section that the LTB geometry excluded the impact of heat fluxes. As a result, the extension of the LTB configuration has the major effect of generalizing it for the consequences of dissipation within the appearance of dark source factors. In a particular scenario, when there is no contribution of dissipation, GLTB recovers LTB space-time. To construct the space-times closer to the LTB, we regard the dust fluid in geodesic form. It is worth remembering that in the dissipation-free case, the total dust form shows the matter configuration to be geodesic. Consequently, GLTB gets a distinct formation in contrast to that of Palatini f(R) and GR contexts. Integrating Eq. (12), we have

$$\begin{aligned} B(t, r)=\frac{C'}{[K(t,r)+1]^{\frac{1}{2}}}, \end{aligned}$$

(84)

where $K(t,r)+1=\left[ C(r)+\int 4\pi \hat{q}_{eff}Rdt\right] ^2$ and $\hat{q}_{eff}$ is defined as $\hat{q}_{eff}=\frac{1}{F}\left( \hat{q}+\frac{\xi _{01}}{B}\right)$ while the value of $\xi _{01}$ in case of Palatini formalism is given by

$$\begin{aligned} \xi _{01}=&\frac{1}{\kappa } \left( \dot{F'}-\frac{5\dot{F}F'}{2F}-\frac{\dot{B}F'}{B}\right) . \end{aligned}$$

In case of GR, $F \longrightarrow 1$ and $\xi _{01} \longrightarrow 0$ and $\hat{q}_{eff}$ becomes $\hat{q}$. However, in case of metric f(R) formalism, the term $\frac{5\dot{F}}{2}\left( \frac{F'}{F}\right)$ in above expression is absent. Therefore, the generalized LTB metric in case of Palatini and metric formalism is given by

$$\begin{aligned} ds^2&=-dt^2+\frac{ (C')^2}{\left( C(r)+\int 4\pi \hat{q}_{eff} C dt\right) ^2} dr^2+C^2d\theta ^2\nonumber \\&+C^2sin^2\theta d\phi ^2. \end{aligned}$$

(85)

The form of $\hat{q}_{eff}$ is distinct for both formalism and in GR, $\hat{q}_{eff}$ reduces to $\hat{q}$. The generalized metric in Eq. (85) is obtained by substituting Eq. (84) in the general line element given in Eq. (8). The scalars $Y_{T F},~Y_{T},~X_{T F},$ and $X_{T}$ for the configuration (85) are

$$\begin{aligned} Y_{T}&=-2\left( \frac{\ddot{C}}{C}+\frac{\ddot{C'}}{2C'}\right) +\frac{\dot{K}}{K+1}\left( \frac{\dot{C'}}{C'} -\frac{3\dot{K}}{4(1+K)}\right) \nonumber \\&\quad +\frac{\ddot{K}}{2(K+1)} -\frac{\xi _{22}}{C^2}+M^{(D)}_{1}, \end{aligned}$$

(86)

$$\begin{aligned} Y_{T F}&=-\left( -\frac{\ddot{C}}{C}+\frac{\ddot{C'}}{C'}\right) +\frac{\dot{K}}{K+1}\left( \frac{\dot{C'}}{C'}-\frac{3\dot{K}}{4(K+1)}\right) \nonumber \\&\quad +\frac{\ddot{K}}{2(K+1)}-\frac{\xi _{22}}{C^2}+4\pi \frac{\xi _{11}}{F}+M^{(D)}_{2}, \end{aligned}$$

(87)

$$\begin{aligned} X_{T}&=2\left( \frac{\dot{C}\dot{C'}}{C C'}+\frac{\dot{C}^2}{2C^2}\right) -\frac{K'}{C C'}-\frac{K}{C^2}-\frac{\dot{C} \dot{K}}{C (1+K)}\nonumber \\&\quad -8\pi \frac{\xi _{00}}{F}+M^{(D)}_{3}, \end{aligned}$$

(88)

$$\begin{aligned} X_{T F}&=-\left( -\frac{\dot{C}^2}{C^2}+\frac{\dot{C} \dot{C'}}{C C'}\right) +\frac{K'}{2C C'}-\frac{K}{C^2}+\frac{\dot{K}\dot{C}}{2C(K+1)}\nonumber \\&\quad -\frac{\xi _{22}}{2C^2} +4\pi \frac{\xi _{11}}{F}+M^{(D)}_{4}. \end{aligned}$$

(89)

For further proceeding, we must impose certain constraints on particular solutions. The criteria for choosing such constraints would depend on the measures that require consequences that are closer to the LTB space-time. On these grounds, we examine the GLTB by relying on scalar variables in the proposed scenario. We would also discuss this continuation on the grounds of symmetric aspects. Firstly, we present the analysis of heat conduction in a complete diffusion event.

5.1 Generalization through scalar variables

It is observed from the analysis of scalar variables that the shear and expansion evolution is purely supervised by the scalars specifically $Y_{T}$ and $Y_{TF}$ in the setting of non-dissipative/dissipative geodesic fluid. The term differences for both the GLTB and LTB are noted to be the same. Now, we analyze scalar functions $Y_{TF}$ and $Y_{T}$ in such a manner that they provide the same form in both contexts, revealing that GLTB and LTB are maximally similar. Therefore, the comparison of Eqs. (81) and (87) follows

$$\begin{aligned} \frac{\ddot{K}}{2(K+1)}-\frac{\dot{K}}{K+1} \left[ \frac{3\dot{K}}{4(K+1)}-\frac{\dot{C'}}{C'}\right] =0. \end{aligned}$$

(90)

Integration of Eq. (90) provides

$$\begin{aligned} C_{1}(r)=\frac{C'\dot{K}^{\frac{1}{2}}}{(K+1)^{\frac{3}{4}}}, \end{aligned}$$

(91)

where $C_{1}(r)$ is the integration-function. Feeding Eq. (84) in (91), we get

$$\begin{aligned} C_{1}(r)=\frac{C'[8\pi \hat{q}_{eff} C]^{\frac{1}{2}}}{[1+\kappa (r)]^{\frac{1}{2}}+\int 4\pi \hat{q}_{eff}Cdt}. \end{aligned}$$

(92)

Integration of Eq. (91) gives

$$\begin{aligned} K+1=4\frac{1}{ \left[ C_{1}(r)^2 \int \frac{dt}{C'^2}+C_{2}(r)\right] ^2}, \end{aligned}$$

(93)

here $C_{2}(r)$ is also an arbitrary integration-function, the time variation of Eq. (93) provides

$$\begin{aligned} \dot{K}=-8\frac{C_{1}^2(r)}{C'^2 \left[ C_{2}(r)+C_{1}^2(r) \int \frac{dt}{(C'^2)}\right] ^3}. \end{aligned}$$

(94)

The comparison of Eqs. (84) and (94) delivers

$$\begin{aligned} 2\pi \hat{q}_{eff}=\frac{C_{1}^2(r)}{CC'^2 \left\{ C_{2}(r) +C_{1}^2(r) \int \frac{dt}{C'^2}\right\} ^2}. \end{aligned}$$

(95)

Furthermore, the comparison of Eqs. (92) and (95) provide the association between integration-functions $C_{2}(r)$ and C(r) as

$$\begin{aligned} C_{2}(r)=\frac{-2[-1+4\pi \hat{q}_{eff} C C'^2]}{C(r)+ 4\pi \int \hat{q}_{eff} C dt}. \end{aligned}$$

(96)

On the grounds of the considerations enforced on $Y_{TF}$ and $Y_{T}$, we may get the configuration of the GLTB. Given the time and radial dependence of R in Eq. (94), the GLTB heat-flow could be up to the two radial functions. The function $C_{1}(r)$ must meet the regularity requirement $C_{1}(0) = 0$, and if it does not, the LTB solution goes back to the prior configuration. The rest of the physical quantities are provided by the field-equations. To explain the procedure stated above, we would illustrate LTB’s parabolic sub-class. Consequently, we select

$$\begin{aligned} C(t,r)=-f(r) [t-T(r])^{\frac{2}{3}}, \end{aligned}$$

(97)

here T(r) and f(r) are the any LTB parabolic solution parameters. Using Eq. (97), we describe $\int \frac{dt}{(C')^2}$ in the form given below

$$\begin{aligned} I=\int \frac{dt}{C'^2}=\int \frac{[T(r)-t]^{\frac{2}{3}}dt}{[-f'(r)\{-T(r)+t\} +\frac{2f(r)}{3} T'(r)]^2}. \end{aligned}$$

(98)

Feeding $\tau ^3=T(r)-t$ in Eq. (98) and integration implies

$$\begin{aligned} I&=\int \frac{-3\tau ^4}{(a\tau ^{3}+b)^{2}}d\tau \nonumber \\ I&=\frac{\tau ^2}{\tau ^{3}a^{2}+ba}+\frac{1}{3\root 3 \of {ba^{5}}} \left[ 2\sqrt{3}\arctan \left( \frac{1-2\root 3 \of {\frac{a}{b}\tau }}{\sqrt{3}}\right) \right. \nonumber \\&\quad \left. -\ln \left( \frac{a\tau ^{3}+b}{(\root 3 \of {a}\tau +\root 3 \of {b})^{3}}\right) \right] , \end{aligned}$$

(99)

here $b=\frac{2f(r)}{3}T'(r)$ and $a=f'(r)$. Plugging Eq. (99) in (95) and using Eq. (97), we get

$$\begin{aligned} 2\pi \hat{q}_{eff}=\frac{C^{2}_{1}(r)f(r)^{-1}}{\left( C^{2}_{1}(r) \left[ \frac{\tau ^{2}}{a}+\frac{a\tau ^{3}+b}{3\root 3 \of {ba^{5}}} \left[ 2\sqrt{3}\arctan \left( \frac{1-2\root 3 \of {\frac{a}{b}\tau }}{\sqrt{3}}\right) -\ln \left( \frac{a\tau ^{3}+b}{(\root 3 \of {a}\tau +\root 3 \of {b})^{3}}\right) \right] \right] +C_{2}(r)(a\tau ^{3}+b)\right) ^{2}}. \end{aligned}$$

(100)

When variations on LTB are required, the quantity of dissipation is regulated by the f C1(r), which may be adjusted as smaller as needed. It is clear from the consequences that this GLTB recaptures the LTB in a dissipation-free configuration. The physical aspects of the GLTB provide acceptable results for a small value of $C_1(r)$related to the LTB.

5.2 Generalization via symmetric aspects

In this subsection, we present another approach for constructing GLTB space-time. This implies that the obtained GLTB has the same properties as the related LTB. The Lie-derivative of the fluid with vector-field $\psi$ is expressed as

$$\begin{aligned} {\L }_{\psi } T_{\beta \varrho }=0. \end{aligned}$$

(101)

The following equations are then acquired by utilizing the effective matter content together with the dissipative-flux in Eq. (116).

$$\begin{aligned}&\psi ^{0} \dot{\hat{\mu }}_{eff}+\psi ^{1} \hat{\mu }'_{eff} +2\hat{\mu }_{eff} \psi ^{0}_{,0}-2\hat{q}_{eff} B \psi ^{1}_{,0}=0, \end{aligned}$$

(102)

$$\begin{aligned}&-\psi ^{0} \dot{\hat{q}}_{eff}-\psi ^{1} \hat{q}'_{eff} +\hat{\mu }_{eff} \frac{\psi ^{0}_{,1}}{B}-\hat{q}_{eff}\left[ \psi ^{0}_{,0} +\psi ^{0}\frac{\dot{B}}{B}\right. \nonumber \\&\quad \left. +\psi ^{1}\frac{B'}{B}+\psi ^{1}_{,1}\right] +\epsilon _{eff} B \psi ^{1}_{,0}=0, \end{aligned}$$

(103)

$$\begin{aligned}&\psi ^0 \dot{\epsilon }_{eff}+\psi ^1 \epsilon '_{eff} -2\hat{q}_{eff} \frac{\psi ^0_{,1}}{B}+2\epsilon _{eff} \left[ \psi ^0 \frac{\dot{B}}{B}\right. \nonumber \\&\quad \left. +\psi ^1 \frac{B'}{B}+\psi ^1{,1} \right] =0. \end{aligned}$$

(104)

In the Palatini approach, we explore two strategies for extending the LTB based on symmetry. One is the diffusion-approximation $( q_{eff}\ne 0,~\epsilon _{eff}=0, ~~\hat{q}_{eff}=q_{eff})$ and the second is streaming-out limit $(\epsilon _{eff}\ne 0,~~q_{eff}=0,~\hat{q}_{eff}=\epsilon _{eff})$.

5.3 Diffusion approximation

In the scenario of diffusion, taking $(q_{eff}\ne 0, \epsilon _{eff}=0, \hat{q}_{eff}=q_{eff})$ applying Eqs. (12) and (84), we get the following expression

$$\begin{aligned} 8\pi q_{eff}=\frac{\dot{K}}{K+1}\frac{C'}{BC}, \end{aligned}$$

(105)

in this case, we get from Eq. (57)

$$\begin{aligned} q_{eff}=\frac{g(r)}{B^2 C^2 F^3}D_{3}, \end{aligned}$$

(106)

where $D_{3}=exp\left[ -\int \frac{F'\mu _{eff}}{2F B q_{eff}} dt\right]$, and g(r) regards arbitrarily defined function. Combining Eqs. (84), (105)–(106), the following result is obtained

$$\begin{aligned} 8\pi g(r)= C C'^2\frac{F^{3}}{D_{3}} \frac{\dot{K}}{[K+1]^{\frac{3}{2}}}. \end{aligned}$$

(107)

Additionally, Eq. (104) follows that $\psi ^0 =F(t)$ in LTB case, and by imposing this finding, Eqs. (102) and (103) read

$$\begin{aligned}&\dot{\mu }_{eff}F(t)+\psi ^1\mu '_{eff}+2\dot{F}(t)\mu _{eff}-2Bq_{eff}\psi ^1_{,0}=0, \end{aligned}$$

(108)

$$\begin{aligned}&\dot{q}_{eff}F(t)+\psi ^1 q'_{eff}+q_{eff}\left[ \dot{F}(t) +\frac{\dot{B}}{B}F(t)+\psi ^1\frac{B'}{B}+\psi ^1_{,1}\right] =0. \end{aligned}$$

(109)

Eq. (109) might be written as

$$\begin{aligned} \psi ^1\bigg [\ln (Bq_{eff}\psi ^1)\bigg ]'+F(t)\bigg [\ln (Bq_{eff}F(t))\bigg ]^{.} =0. \end{aligned}$$

(110)

Multiplying Eq. (110) by $Bq_{eff}$ implies

$$\begin{aligned} \bigg [Bq_{eff}\psi ^1)'+(q_{eff}BF\bigg ]^{.}=0, \end{aligned}$$

(111)

The partial solution of Eq. (111) may now be expressed as

$$\begin{aligned} Bq_{eff}\psi ^1 =-\dot{\zeta }(t,r), \end{aligned}$$

(112)

$$\begin{aligned} Bq_{eff}F(t)=\zeta '(t,r), \end{aligned}$$

(113)

using Eqs. (105) and (113) follow

$$\begin{aligned} \zeta '(t,r)=\frac{F(t)}{8\pi }\left( \frac{C'}{C}\right) \frac{\dot{K}}{K+1}. \end{aligned}$$

(114)

Manipulating Eqs. (84), (106), (113)–(114), it is inferred that

$$\begin{aligned} 8\pi g(r)=C C'^2\frac{F^{3}}{D_{3}} \frac{\dot{K}}{[1+K]^{\frac{3}{2}}}, \end{aligned}$$

(115)

that is completely identical to Eq. (107). Integrating Eq. (107) to obtain

$$\begin{aligned} \frac{1}{[1+K]^{\frac{1}{2}}}=4\pi g(r) \int \frac{-D_{3}}{C C'^2 F^3}dt+C'(r), \end{aligned}$$

(116)

here $C'(r)$ is the function of integration. In a specific scenario, utilizing the expression of C(t, r) presented in Eq. (97), it is obtained that

$$\begin{aligned} \frac{1}{(K+1)^{\frac{1}{2}}}&=-\frac{4\pi g(r)}{f'(r) f(r)[-f'(r)(-T(r)+t)+\frac{2}{3}f(r)T'(r)]F^3}\nonumber \\&\quad +C'(r)+4\pi g(r) \nonumber \\&\quad \times \int \frac{3\dot{F}F^2}{[-f'(r)(-T(r)+t)+\frac{2}{3}T'(r)f(r)]}. \end{aligned}$$

(117)

Feeding back Eq. (117) in (106) and applying Eq. (84), it is found that

$$\begin{aligned} q_{eff}&=\frac{g(r)}{f^{2}(r)F^{3}[T(r)-t]^{\frac{2}{3}}}\left[ -4\pi \frac{ g(r)}{f(r)f'(r)F^{3}} \right. \nonumber \\&\quad +\bigg (4\pi g(r)\int \frac{3\dot{F} F^2}{[f'(r)(T(r)-t)+\frac{2}{3}f(r) T'(r)]} \nonumber \\&\quad \left. +C'(r)\bigg ) \bigg (f'(r)(T(r)-t)+\frac{2}{3} f(r) T'(r)\bigg )\right] ^{-2}. \end{aligned}$$

(118)

As a result, GLTB contains four-function, one of which disappears because of r-coordinate invariance. Assuming that the LTB solution has the same r-dependence as $\psi ^1$, a few functions could be taken from the LTB seed model, and the rest could be computed using the equations.

5.4 Streaming-out approximation

In the setting of $\epsilon _{eff}\ne 0,~q_{eff}=0$, the Bianchi-identities brings down in the expression

$$\begin{aligned} \dot{\mu }_{eff}+2\mu _{eff}\left[ \frac{\dot{B}}{2B} +\frac{\dot{C}}{C}+\frac{5\dot{F}}{4F}-\frac{F'}{4BF}\right] =0. \end{aligned}$$

(119)

Integration of Eq. (119) yields

$$\begin{aligned} \mu _{eff}=\frac{1}{C^2BF^{\frac{5}{2}}}j(r)\exp \int \frac{F'dt}{2BF }. \end{aligned}$$

(120)

Using Eq. (84) in (120), we get

$$\begin{aligned} \mu _{eff}=\frac{3j(r)\bigg [\int 4\pi \epsilon _{eff}Cdt+(1 +\kappa (r))^{\frac{1}{2}}\bigg ]}{(C^{3})'F^{\frac{5}{2}}}\exp \int \frac{F' dt}{2BF}, \end{aligned}$$

(121)

where j(r) is constant of integration. Now, under the assumption $q_{eff}=0,~\epsilon _{eff}\ne 0$, Eqs. (102)–(104) take the following form

$$\begin{aligned}&\psi ^0(\mu _{eff}+\epsilon _{eff})^{.}+\psi ^1 (\mu _{eff} +\epsilon _{eff})'\nonumber \\&\quad +2(\mu _{eff}+\epsilon _{eff})\psi ^0_{,0}-2\epsilon _{eff}B\psi ^1_{,0}=0, \end{aligned}$$

(122)

$$\begin{aligned}&\psi ^0 \dot{\epsilon }_{eff}+\psi ^1 \epsilon '_{eff}-(\mu _{eff} +\epsilon _{eff})\frac{\psi ^0_{,1}}{B}+\epsilon _{eff} \left( \psi ^0_{,0}\right. \nonumber \\&\quad \left. +\psi ^0 \frac{\dot{B}}{B}+\psi ^1 \frac{B'}{B} +\psi ^1_{,1}\right) -\epsilon _{eff}B\psi ^1_{,0}=0, \end{aligned}$$

(123)

$$\begin{aligned}&\psi ^0 \dot{\epsilon }_{eff}+\psi ^1 \epsilon '_{eff} -2\epsilon _{eff} \frac{\psi ^0_{,1}}{B}+2\epsilon _{eff}\left( \psi ^0 \frac{\dot{B}}{B}\right. \nonumber \\&\quad \left. +\psi ^1 \frac{B'}{B}+\psi ^1_{,1}\right) =0. \end{aligned}$$

(124)

From Eqs. (122)–(124), we obtain

$$\begin{aligned} \psi ^0 \dot{\mu }_{eff}+\psi ^1 \mu '_{eff}+2\mu _{eff}\psi ^0_{,0}+2 \mu _{eff} \frac{\psi ^0_{,1}}{B}=0. \end{aligned}$$

(125)

After some manipulations, Eq. (125) gives

$$\begin{aligned} \psi ^1=-\frac{\mu _{eff}}{\mu '_{eff}} \left( 2\dot{F}(r,t)+F(r,t) \frac{\dot{\mu }_{eff}}{\mu _{eff}}+\frac{2 F'(r, t)}{B}\right) , \end{aligned}$$

(126)

where $\psi ^0=F(r,t)$. Suppose that $\psi ^0=F(t),$ in order to satisfy the obligation of maximal resemblance between LTB and GLTB. In that case, Eqs. (122)–(124) implies

$$\begin{aligned}&F(t)(\mu _{eff}+\epsilon _{eff})^{.}+\psi ^1 (\mu _{eff}+\epsilon _{eff})'\nonumber \\&\quad +2 (\mu _{eff}+\epsilon _{eff}) \dot{F}(t)-2\epsilon _{eff} B \psi ^1_{,0}=0, \end{aligned}$$

(127)

$$\begin{aligned}&F(t)\dot{\epsilon }_{eff}+\psi ^1 \epsilon '_{eff}+\epsilon _{eff} \left( \dot{F}(t)+F(t)\frac{\dot{B}}{B}+\psi ^1 \frac{B'}{B}\right. \nonumber \\&\quad \left. +\psi ^1_{,1} \right) -\epsilon _{eff} B \psi ^1_{,0}=0, \end{aligned}$$

(128)

$$\begin{aligned}&F(t) \dot{\epsilon }_{eff}+\psi ^1 \epsilon '_{eff}+2\epsilon _{eff} \left( F(t) \frac{\dot{B}}{B}+\psi ^1 \frac{B'}{B}+\psi ^1_{,1} \right) =0. \end{aligned}$$

(129)

Eq. (129) may turn into the following form

$$\begin{aligned} F(t)\left[ \ln (\epsilon _{eff} B^2 )\right] ^{.} + \psi ^1 \left[ \ln (\epsilon _{eff} (B \psi ^1)^2 ) \right] '=0, \end{aligned}$$

(130)

or it may be rewritten as

$$\begin{aligned} F(t)(B^2\epsilon _{eff})^{.}+\frac{1}{\psi ^1}[\epsilon _{eff} (B\psi ^1)^2]'=0. \end{aligned}$$

(131)

Also, in the presence of these conditions, Eq. (57) gets the following form

$$\begin{aligned}&\left[ \ln (\epsilon _{eff}(FBC)^2 ) \right] ^{.} +\frac{1}{B} \left[ \ln (\epsilon _{eff} C^2) \right] '+\frac{\dot{F}}{F}\nonumber \\&\quad +\frac{3 F'}{B} +\frac{F'}{2F B} \left( \frac{\mu _{eff}}{\epsilon _{eff}}\right) =0, \end{aligned}$$

(132)

or may be written as

$$\begin{aligned}&\left[ \epsilon _{eff} (FBC)^2 \right] ^{.}+B F^2(\epsilon _{eff} C^2)' +B^2 F \dot{F} C^2 \epsilon _{eff}\nonumber \\&\quad +\frac{F' B C^2 F}{2} \mu _{eff}+3B F^2 F' C^2 \epsilon _{eff}=0. \end{aligned}$$

(133)

It is now possible to acquire GLTB premised on the LTB (in the streaming-out approximation) in the impact of Palatini f(R) theory by adopting the following procedure. Suppose that LTB-solution gets the similar sort of r-dependence as $\psi ^{1}$. Obtain the value of $(\epsilon _{eff}B^{2})$ from Eq. (133) and then substitute in Eq. (131). Taking into account a definite LTB-model along with the given field $\psi$ and take $F(t)=1$, because it is arbitrary. Integrating Eq. (131) to get the effective radiation-density corresponding to r-coordinate.

6 Discussion

At large-scales, It is generally regarded that cold dark-matter is non collisional having the intense impact of rest-mass in which the pressure and heat-fluxes have ignorable consequences owing to their kinetic-nature. Henceforth, it would be important to analyze the stability/instability of such configuration together with the influence of certain kinetic factors, for instance, heat-fluxes in the perspective of a specific gravity theory namely; Palatini f(R) theory. It is well-accepted that the physical description of any cosmic system is significantly influenced by the inhomogeneous matter configuration. Inhomogeneous space times are exact solutions to field equations that disclose guidance about the universe’s several periods. According to recent data from type-Ia supernovae, indicating the universe’s expansion is accelerating, Henceforth, there has been a rising demand for LTB space-time. It is the most widely accepted non-homogeneous spherical configuration that is very important to the study of how the universe is set up. It is significant to note that in dissipation-free cases, the regime of entire dust implies geodesic fluid, however, this is not the case when considering dissipation. In current cosmology, the study of the continuation of LTB space-time with the help of structure scalars and symmetric properties is the significant goal.

In present manuscript, we have explored the consequences of Palatini f(R) correction on the continuation of the LTB space-time. The Palatini version of f(R) theory has several fascinating properties, including the ability to predict the presence of a long range scalar-field, describing cosmic late-time acceleration. Our primary concern is to investigate the relevance of Palatini f(R) curvature constituents, providing intense gravitational field interactions. To do so,

• Our investigation is commenced by considering the dust spheres. We have explored the relating field equations and kinematical factors in association to the matter configuration in Palatini f(R) context. In contrast to the GR outcomes, it has been seen that the kinematical factors also get modified via higher curvature correction due to the influence of connections within the Palatini context. As can be seen from Eq. (17), the occurrence of four-acceleration is entirely dependent on Palatini based modifications.

• In order to quantify the matter inside of the geometric configuration, we have explored the Misner–Sharp [68] expression for the relating mass-function. In the realm of relativistic astrophysics, the study of matching conditions has sparked a lot of interest. It is widely acknowledged that several paradigms of gravitating systems of observational and theoretical intrigue include the incorporation of two distinct regions of spacetime, matched at certain hyper-surfaces, detaching the inner from the outer region. To match the exterior Eq. (32) and interior region Eq. (8) of our matter configurations, we have constructed the set of Palatini f(R) matchings Eqs. (26)–(31), indicating the consequences of singular factors of the fluid under discussion Eqs. (34)–(36).

• It has been found that in contrast to GR, the brane tension disappears on the grounds of Palatini f(R) context, however, $[K^{\varrho }_{\varrho }]\ne 0$ as represented in Eqs. (34)–(36). As sphere of our matter configuration is composed up of entirely dust and dissipation by means of heat flow and bearing the influence of outgoing null-fluid. So, the computation for the matchings interior to the exterior geometry gets the form (40) and (41). These matchings have described the intense gravitational-field interactions, which could converted the GR ones within acceptable limits i.e., $F_{R}=0$ and Eq. (41) has the key role to determine the presence of shells/branes. From our study, the matchings would be applied for the vacuum configuration provided the singular constituent of the source disappears in (41) which is only feasible when the energy-density of our source is regarded to be uniform. In addition to such conditions, we have computed the entire luminosity across the surface of the sphere under discussion. Subsequently, we have highlighted that under totally diffusion-approximation, luminosity of the source disappears though the presence of heat-flux is accounted within the spheres. Henceforth, Eq. (41) could recover (32) of [59] within acceptable limits. Within the Palatini f(R) context, this finding described the clear consequences of the dust configuration.

• To evaluate the gravitational influence, a connection involving matter profile, Misner–Sharp mass, and conformal scalar together with the Palatini f(R) modifications has been established. Furthermore, we have constructed the Bianchi-identities, expansion evolution and propagation equations for the conformal scalar to analyze the dynamical aspects of the stellar system. Within the Palatini f(R) context, the tensors $Y_{\beta \varrho }$ and $X_{\beta \varrho }$ have been evaluated by the orthogonal break down strategy of the Riemann-tensor, and further distributed them in their trace-free and trace portions. It has concluded that $X_{T}$ manages the energy-density of the matter configuration and the some additional curvature factors illustrating the gravitational interaction at large-scales. However, the fluid’s anisotropy with the inclusion of Palatini f(R)-terms and the presence of mysterious form of matter and energy is revealed by $Y_{T}$. It is found that $Y_{TF}$ governs the fluid’s anisotropy in addition to the higher curvature constituents and the conformal scalar. To gain a better understanding of the physical meanings of the stellar configuration, we have formulated the propagation equations in the context of Palatini f(R) scalars.

• The LTB metric has formed by integrating the $G_{01}$ component of the Palatini f(R) field-equations. The various findings of the evolving configuration, depending upon the value of k in LTB space-time has established. We have formulated the Palatini f(R) scalars corresponding to the GLTB space-time and LTB space-time for dissipation and dissipation-free scenarios, respectively. We have examined the maximum similar aspects of both cases by comparing the related scalar functions. Furthermore, the continuation of the LTB on the grounds of symmetric aspects has been explored through two strategies, namely, streaming-out limit and diffusion approximation. The temperature profile of the source has attained via heat conduction in diffusion under Palatini f(R) context.

Appendices

Appendix A

The additional curvature constituents emerging in the Palatini f(R) field-equations for the system under discussion are computed as

$$\begin{aligned} \xi _{00}&=\frac{1}{16\pi } \left( \frac{-3\dot{F^2}}{F} +\frac{F'^2}{BF}+\frac{2F''}{B}-\frac{2\dot{B}\dot{F}}{B} -\frac{2F'B'}{B^3}\right. \nonumber \\&\quad \left. -\frac{4\dot{C}\dot{F}}{C}+\frac{4F'C'}{B^2C}+FR-f-\frac{3F'^2}{2B^2F}-\frac{9\dot{F}^2}{2F}\right) , \end{aligned}$$

(134)

$$\begin{aligned} \xi _{11}&=\frac{1}{16B^2\pi } \left( \frac{\dot{F}^2B^2}{F}+\frac{B^2}{2}\ddot{F}-\frac{3F'^2}{F}+\frac{4\dot{C}B^2\dot{F}}{C}\right. \nonumber \\&\quad \left. -\frac{2C'F'}{C}-B^2RF-fB^2 -\frac{3\dot{F}^2B^2}{2F}-\frac{3F'^2}{2F}\right) , \end{aligned}$$

(135)

$$\begin{aligned} \xi _{01}&=\frac{1}{16\pi }\left( 2\dot{F'}-2\frac{\dot{B}F'}{B} -5\frac{\dot{F}F'}{F}\right) , \end{aligned}$$

(136)

$$\begin{aligned} \xi _{22}&=\frac{1}{2F}\left( 2\dot{C}C\dot{F}+\frac{\dot{F}^2C^2}{F}-2\frac{C'CF'}{B^2}-\frac{F'^2C^2}{FB^2}+2 \ddot{F}C^2\right. \nonumber \\&\quad -2\frac{F''C^2}{B^2}+2\frac{\dot{B}C^2\dot{F}}{B}+\frac{B'C^2 F'}{B^3}-C^2FR \nonumber \\&\quad \left. -C^2f-\frac{3C^2\dot{F}^2}{2F}+\frac{3C^2F'^2}{2B^2F}\right) . \end{aligned}$$

(137)

Appendix B

The corrections for higher curvature effects caused by Palatini corrections in the scalar variables are listed as

$$\begin{aligned} M^{(D)}_{1}&=\frac{1}{F} \left( \ddot{F}+\frac{\dot{F}^2}{2 F} +\frac{F'^2}{4 F B^2}+\frac{\dot{C} \dot{F}}{C}-\frac{C' F'}{C B^2}-\frac{F''}{B^2}\right. \nonumber \\&\left. \quad +\frac{\dot{B} \dot{F}}{B}+\frac{B' F'}{B^3}+\frac{(f-F R)}{2}\right) , \end{aligned}$$

(138)

$$\begin{aligned} M^{(D)}_{\beta \varrho }&=-\frac{1}{2 F} \left[ (\nabla _{\beta } \nabla _{\varrho } F-g_{\beta \varrho } \Box F)-(\nabla _{\gamma } \nabla _{\delta } F\right. \nonumber \\&\quad \left. -g_{\gamma \delta } \Box F)g_{\beta \varrho } V^{\gamma } V^{\delta } \right] -\frac{3}{4F^2} \nabla _{\gamma } F \nabla _{\delta } F V^{\gamma } \nonumber \\&\quad \times V^{\delta } g_{\beta \varrho }+\frac{1}{F}\left[ \left( \frac{1}{F}\nabla _{\gamma } F \nabla _{\delta } F-\frac{2}{3}(\nabla _{\gamma } \nabla _{\delta } F\right. \right. \nonumber \\&\quad \left. \left. -g_{\gamma \delta } \Box F)\right) V^{\gamma } V^{\delta } h_{\beta \varrho }\right] -\frac{1}{2F} \Box F h_{\beta \varrho }, \end{aligned}$$

(139)

$$\begin{aligned} M^{(D)}_{3}&=\frac{1}{8F} \epsilon ^{\epsilon \alpha \varrho } \left[ -\epsilon _{\pi \alpha \varrho }\left( -\nabla ^{\pi } \nabla _{\epsilon } F+\frac{3}{2F} \nabla ^{\pi } F \nabla _{\epsilon } F\right) \right. \nonumber \\&\quad +\epsilon _{\pi \epsilon \varrho } \left( -\nabla ^{\pi } \nabla _{\alpha } F+\frac{3}{2F} \nabla ^{\pi } F \nabla _{\alpha } F\right) +\epsilon _{\alpha \theta \varrho } \nonumber \\&\quad \times \left( -\nabla ^{\theta } \nabla _{\epsilon }F+\frac{3}{2F} \nabla ^{\theta }F\nabla _{\epsilon }F\right) -\epsilon _{\epsilon \theta \varrho }\left( -\nabla ^{\theta } \nabla _{\alpha } F\right. \nonumber \\&\quad \left. \left. +\frac{3}{2F} \nabla ^{\theta } F \nabla _{\alpha } F\right) \right] +\frac{1}{F} h^{\varrho }_{\varrho }\left( \frac{-3}{4F}(\nabla F)^2\right. \nonumber \\&\quad \left. -\frac{(f-FR)}{2}+\Box F\right) +\frac{1}{F} \left( 2(R F -f)+3\Box F\right. \nonumber \\&\quad \left. -\frac{3}{F}(\nabla F)^2 -\frac{3}{2F}g^{\beta \varrho }\nabla _{\beta } \nabla _{\varrho }F \right) , \end{aligned}$$

(140)

$$\begin{aligned} N^{(D)}_{\beta \varrho }&=\frac{1}{16F} \epsilon ^{\epsilon \alpha \xi }\left( g_{\xi \beta }-\frac{1}{3} h_{\xi \beta }\right) \left[ \epsilon _{\pi \alpha \varrho }\left( 2\nabla ^{\pi } \nabla _{\epsilon } F\right. \right. \nonumber \\&\quad \left. -\frac{3}{F} \nabla ^{\pi } F \nabla _{\epsilon } F\right) -\epsilon _{\pi \epsilon \varrho }\left( 2\nabla ^{\pi } \nabla _{\alpha }F-\frac{3}{F} \right. \nonumber \\&\quad \left. \times \nabla ^{\pi } F \nabla _{\alpha } F\right) -\epsilon _{\alpha \theta \varrho }\left( 2\nabla ^{\theta } \nabla _{\epsilon }F-\frac{3}{F}\nabla ^{\theta } F \nabla _{\epsilon } F\right) \nonumber \\&\quad \left. +\epsilon _{\epsilon \theta \varrho }\left( 2\nabla ^{\theta } \nabla _{\alpha } F-\frac{3}{F} \nabla ^{\theta } F \nabla _{\alpha } F\right) \right] \nonumber \\&\quad -\frac{1}{2F}\left( g_{\beta \varrho }-\frac{1}{3} h_{\beta \varrho }\right) \left( \frac{3}{2F}(\nabla F)^2 +(f-R F)-2\Box F \right) . \end{aligned}$$

(141)

Appendix C

The corrections for higher curvature caused by Palatini corrections in the expansion and shearing evolution are provided as

$$\begin{aligned} D_{1}&=\frac{1}{2}\left( \frac{4\ddot{F}}{F} -\frac{7\dot{F}^2}{6F^2}\right) +\frac{1}{3}\left( \frac{4\dot{F}\dot{B}}{F B}+\frac{8\dot{C}\dot{F}}{FC}-\frac{F'^2}{24B^2F^2}\right) , \end{aligned}$$

(142)

$$\begin{aligned} D_{2}&=\frac{2}{3}\left[ -\left( -\frac{\dot{B}}{B} +\frac{\dot{C}}{C}\right) +\frac{\dot{F}^2}{8F^2} -\frac{3F'^2}{16F^{2}B^{2}}\right] ^{\frac{3}{2}}-\nonumber \\&\quad \times \frac{8\dot{F}}{3F}\left( -\frac{\dot{B}}{B} +\frac{\dot{C}}{C}\right) -\frac{8}{3}\left( -\frac{\dot{B}}{2B} -\frac{\dot{C}}{C}-\frac{\dot{F}}{F}\right) \nonumber \\&\quad \times \left( -\frac{3F'^2}{16F^2 B^2}+\frac{\dot{F}^2}{8F^2}\right) -\left( \frac{3F'^2}{16F^2 B^2}\right) ^{.} +\left( \frac{\dot{F}^2}{8F^2}\right) ^{.}. \end{aligned}$$

(143)

Appendix D

The tensors $Y_{\beta \varrho }$ and $Y_{\beta \varrho }$ for the evaluation of the Palatini scalar variables are determined as below

$$\begin{aligned} Y_{\beta \varrho }&=E_{\beta \varrho }+\frac{\kappa }{2F}(\hat{\mu } h_{\beta \varrho }-\epsilon \xi _{\beta } \xi _{\varrho })+\frac{\kappa }{3F}(-\hat{\mu }+\epsilon )h_{\beta \varrho }\nonumber \\&\quad -\frac{1}{2F}\left[ (\nabla _{\beta } \nabla _{\varrho } F-g_{\beta \varrho }\Box F)+(\nabla _{\gamma } \nabla _{\varrho } F \right. \nonumber \\&\quad -g_{\gamma \varrho }\Box F) V_{\beta } V^{\gamma } +(\nabla _{\beta }\nabla _{\delta }F-g_{\beta \delta } \Box F)V^{\delta }V_{\varrho }\nonumber \\&\quad \left. +(-\nabla _{\delta }\nabla _{\gamma }F +g_{\gamma \delta }\Box F) g_{\beta \varrho }V^{\delta } V^{\gamma }\right] +\frac{3}{4F^2} \nonumber \\&\quad \times \left[ \nabla _{\beta }F\nabla _{\varrho }F +\nabla _{\varrho } F \nabla _{\gamma }F V^{\gamma }V_{\beta }+\nabla _{\delta }F\nabla _{\beta } F V_{\varrho } V^{\delta }\right. \nonumber \\&\quad \left. -\nabla _{\delta } F \nabla _{\gamma } F g_{\beta \varrho }V^{\delta } V^{\gamma }\right] -\frac{1}{2F^2} \nonumber \\&\quad \times (g^{\beta \varrho }\nabla _{\varrho }F \nabla _{\beta } F -\Box F)h_{\beta \varrho }-\frac{1}{6}(F R-f)h_{\beta \varrho }\nonumber \\&\quad +\frac{1}{4} (\nabla F)^2 h_{\beta \varrho }, \end{aligned}$$

(144)

$$\begin{aligned} X_{\beta \varrho }&=-E_{\beta \varrho }+\frac{\kappa \epsilon }{2F}(\xi _{\beta } \xi _{\varrho }-h_{\beta \varrho })+\frac{\kappa }{3 F}(-\hat{\mu }+\epsilon )h_{\beta \varrho }\nonumber \\&\quad +\frac{1}{8} \epsilon ^{\epsilon \alpha }_{\beta }\left[ \epsilon _{\pi \alpha \varrho }\left( \nabla ^{\pi } \nabla _{\epsilon } F-\frac{3}{2F}\nabla ^{\pi } F \nabla _{\epsilon } F\right) \right. \nonumber \\&\quad -\epsilon _{\pi \epsilon \varrho }\left( \nabla ^{\pi } \nabla _{\alpha } F-\frac{3}{2F} \nabla ^{\pi } F \nabla _{\alpha } F\right) \nonumber \\&\quad -\epsilon _{\alpha \theta \varrho }\left( \nabla ^{\theta } \nabla _{\epsilon } F-\frac{3}{2F} \nabla ^{\theta } F \nabla _{\epsilon } F\right) +\epsilon _{\epsilon \theta \varrho } \nonumber \\&\quad \left. \times \left( \nabla ^{\theta } \nabla _{\alpha } F-\frac{3}{2F} \nabla ^{\theta } F \nabla _{\alpha } F\right) \right] -\frac{3}{2F^2} \nabla _{\beta } F \nabla _{\varrho } F\nonumber \\&\quad +\frac{g_{\beta \varrho }}{F}\left( \frac{1}{4 F}(\nabla F)^2+\frac{(f-R F)}{6}\right) \end{aligned}$$

(145)