1 Introduction

Structure of the universe can be described via cosmic expansion and density fluctuations among galaxies. A galaxy may contain millions of stars in it that are building blocks of the cosmos. Thus, being a component of galaxy, stars and their evolution has great importance in the consideration of stellar structure. Generally, stars are luminous compact objects, that tends to make use of internal nuclear fuel during various nuclear processes. Such nuclear phenomenon generates a large amount of energy that is the main cause of a star’s luminosity. Stability analysis of a gravitating system is of fundamental significance in the field of astronomy and astrophysics. A compact object is in stable state if outward drawn forces of the system are being balanced by the inward directed gravitational pull. Due to continuous consumption of energy in fusion process of the compact objects the inward directed gravitational force dominates the outward directed pressure stresses that leads to collapse of gravitating system. The gravitational collapse of compact objects may result in the formation of neutron stars, white dwarfs or black holes. It is the fundamental phenomenon to account evolution within galaxies and assemble supergiant structures, these stellar residues are extremely dense in nature [2].

Stellar evolution can be well described by considering small fluctuations in the gravitating system through some suitable perturbation approach. Perturbation theory includes mathematical methods to find an approximate solution to the problem. These techniques splits the problem into two parts, solvable and perturbed part. It plays vital role in approximating the solution to the problems that do not have a coupled exact solution. Accounting perturbation in physical parameters assist in the estimation of different evolutionary phases of a star defining stability/instability levels. Regge and Wheeler [3] described a metric perturbation in the mode of stability in a seminal paper on dynamics of relativistic objects. Density fluctuations, termed as local density perturbation (LDP) can also be catered to analyze range for stable or unstable regions, in which all physical parameters are considered to be density dependent.

General theory of relativity (GR) is the geometric theory of gravitation introduced by Albert Einstein [4]. According to GR, the objects warp spacetime around it, causing it to become curved. Consequently, gravitating bodies experience gravitational effects. This warping of spacetime explains how objects behave as they move through the space. Eventually, Einstein’s theory is strongly based on three basic postulates that must hold in relativistic analysis i.e., principle of relativity, equivalence principle, principle of general covariance. Theory of GR is best fit in weak gravitational fields but do not provide extensive description of strong field eras. Current image of universe suggests refinement in theoretical framework, that strongly necessitates alternative gravitational theories. Due to combined motivation from high energy physics, cosmology and astrophysics in recent years modified theories of gravity have received a lot of consideration.

The alternative theories have become a gauge in the explorations related to gravitational interaction, expected to contribute in exploring strong field eras such as approaching black hole singularities or at the Planck scales. The latest data sets from cosmic microwave background, supernovae type Ia and Planck data shows that 95% of energy budget of the universe consist of hidden matter constituting of dark matter and dark energy, leading to current accelerated cosmic expansion [5,6,7,8,9]. Till now, large number of extended theories have been introduced, these can be classified as scalar tensor gravities, extra spatial dimension and the theories with higher order curvature invariants. Inclusion of dark source terms having negative pressure on right side of field equations (FEs) is an approach to induce modification that cover quintessence, k-essence and perfect fluid models. Modifying left side of FEs is another approach to contribute modifications accompanying minimal or non minimal matter geometry coupling [10, 11].

Herein, we are considering f(R) gravity as extended theory of gravitation. Many researchers have worked on modification of the Einstein Hilbert (EH) action to include higher order curvature invariants [12,13,14,15]. This constitutes non-linear terms of curvature in a way that gravitational action of GR modifies to a general action, incorporating an arbitrary function of Ricci scalar (R) in it. The EH action in f(R) modifies to

$$\begin{aligned} S=\frac{1}{2\kappa }\int d^{4}x\sqrt{-g}f(R), \end{aligned}$$
(1)

where R is Ricci scalar, g stands for determinant of the metric \(g_{\mu \nu }\) and \(\kappa = \frac{8\pi G}{c^{4}}\) is coupling constant.

In the inner matter distribution of stars, anisotropic matter configuration implies that radial pressure \((p_{r})\) and tangential pressure \((p_{t})\) are not equal i.e., \((p_{r} \ne p_{t})\). Kasuar and Noureen [16] discussed about a gravitational collapse using \(f(R) = R+\alpha R^n\) model and electromagnetic field for stability/instability regions. A charged anisotropic fluid was assumed in [16] that dissipate energy through heat flow and showed that electromagnetic field, shear and phase transition, density irregularity on astrophysical objects can be integrated by locally anisotropic background. It was also shown that adiabatic index depend upon mass, radius and electromagnetic background of spherical objects. Dynamical equations become a gauge in evolution of self gravitating compact objects. Noureen et al. [17] presented dynamical instability of supersymmetric supergravity f(R) model that represents the more practical substitute of higher order curvature corrections. Significant attention has been paid to alternative gravitational theories to explore cosmological and astrophysical aspects of our universe. Many authors have worked on minimally and non-minimally coupled higher order curvature theories to incorporate exotic matter and study gravitational interaction with such generalizations [18,19,20,21,22].

The pioneer work on studying the instabilities was presented by Chandrasekhar [23] for spherically symmetric compact objects with the help of adiabatic index. Another way to check the instabilities occuring in compact objects was introduced by Herrera [24] named as cracking technique. Cracking originates in gravitating bodies from the evolution of radial forces, it occurs when perturbation in these forces changes the sign. In other words, cracking takes place when the inward directed forces in the inner part and outward directed forces of the configuration changes the sign from negative to positive values at some point, and overturning occurs when these forces changes sign from positive to negative values. Cracking plays significant role in refinement of stability regions of physically viable compact star models. The authors in [25] used Raychaudhuri equation to define departure from equilibrium state and discussed the constraints on occurrence of cracking. Herrera and Santos [26] worked on the causes of local anisotropy in a gravitating system and presented Jeans analysis of the system to identify occurrence of cracking. Prisco et al. [27] considered two families of homogeneous fluid distributions and concluded that the deviations in anisotropy may lead to the the appearance of cracking. Herrera and Varela [28] studied the effect of axially symmetric perturbations of matter variables in a perfect fluid matter distribution. Hernandez and Nunez [29] used nonlocal equation of state for anisotropic spherically symmetric distribution to obtain different physically acceptable solutions. To demonstrate the physical plausibility for different solutions which satisfied the nonlocal equation of state, the constraints imposed by energy, some spontaneous physical conditions and junction was studied. They [29] showed that fluids having nonlocal equation of state are anisotropic by satisfying Tolman Oppenheimer Volkov equation. It was also shown that starting from known density profiles, it is possible to obtain static anisotropic spherically symmetric matter configurations as well as for configuration in which tangential pressure disappear. Gonzalez et al. [30] extended the concept of cracking for isotropic general relativistic fluid spheres as well as described the behavior of anisotropic matter distributions just after its departure from equilibrium. The idea of cracking has been used in [30] with barotropic equations of state i.e., \( p=p(\rho )\) and \( p_t= p_t(\rho )\) concluding that both isotropic/anisotropic models could exhibit cracking or overturning. Azam and Mardan [31] analyzed the appearance of cracking using density perturbation in physical parameters. The same authors [32] studied about the existence of cracking in charged anisotropic cylindrical polytropes by considering generalized polytropic equation of state. Mak et al. [33] showed the presence of a cosmological constant upper limits for the mass-radius ratio, which are derived for arbitrary general relativistic matter distributions. Many researchers have explored the stability/instability levels of charged sphere using the mass-radius ratio. Bohmer and Harko [34] proved that for compact charged general relativistic objects there is a lower bound for the mass-radius ratio as in Buchdahl type inequality for charged objects which has been widely used for the proof of the existence of an upper bound to this ratio. Giuliani and Rothman [35] found an exact solution for the stability limit of relativistic charged spheres for the constant gravitational mass density and constant charge density. Andreasson [36] found an upper bound for given radius and charge on the critical stability radius for relativistic charged sphere

In modified gravitational theories, extension of cracking technique is not available for compact star models. For this purpose, we have developed the FEs for static spherically symmetric compact anisotropic star in context of f(R) gravity and making use of Krori Barua spacetime [37] coefficients for perturbation in equilibrium state. Up till now local density perturbation (LDP) is not available for stability/instability analysis. Here, we have worked on generalization of LDP Scheme to identify cracking of f(R) gravity model, in particular Starobinsky model [38, 40]. Considered f(R) model is interesting in a way that it indicates both the accelerated and decelerated regimes in expansion of the universe. Also, it caters the quadratic correction of Ricci scalar when it is inserted in FEs of gravitational part. In past Starobinsky model has been widely used in literature of cosmological and astrophysical context. In Starobinsky model [40] shows that this model can satisfy cosmological observational tests.

This paper is arranged as follows: in Sect. 2, we have developed the FEs for static spherically symmetric compact object for anisotropic source and making use of Krori Barua spacetime coefficients. In Sect. 3, we have used LDP on f(R) gravity model and presented physical analysis by using graphical representation of distribution force. Discussion of cracking or overturning for modified gravity is given in Sect. 4. In last section we have summarized our findings followed by appendix and list of references used in this work.

2 Development of field equations

The degree of freedom of constitutive equations can be reduced if a symmetry is present in the system that simplifies complications in the analysis. The gravitating sources are commonly analyzed with the consideration of spherical symmetry, observational data demonstrate that deformations in spherical symmetry are very rare and identical [41]. The deviations are not fundamental feature of gravitating sources, that is why mostly gravitating systems are discussed via spherical symmetry [42]. The line element for static spherically symmetric compact object is given by

$$\begin{aligned} ds^2 = -e^{\mu (r)}dt^{2}+e^{\nu (r)}dr^{2}+r^2d\theta ^2+r^2sin^{2}\theta d\phi ^2, \end{aligned}$$
(2)

where \(e^{\mu (r)}\) and \(e^{\nu (r)}\) represent the metric potentials/coefficients. The contribution of dark source constituent is induced by following tensor.

$$\begin{aligned} T^{(D)}_{\alpha \beta }=\frac{1}{\kappa }\left[ \frac{f-Rf_R}{2}g_{\alpha \beta } +\nabla _\alpha \nabla _\beta f_R-g_{\alpha \beta }\Box f_R\right] , \end{aligned}$$
(3)

The modified FEs incorporating dark source together with usual matter can be written as

$$\begin{aligned} G_{\alpha \beta }= & {} R_{{\alpha \beta }}-\frac{1}{2}R g_{\alpha \beta }=\frac{\kappa }{f_R}\left[ T^{(m)}_{\alpha \beta }+T^{(D)}_{\alpha \beta }\right] , \end{aligned}$$
(4)

where \(G_{\alpha \beta }\) represents the geometric part of FEs corresponding to metric (2), leads to following set of FEs.

$$\begin{aligned} G_{00}= & {} \frac{e^\mu }{f_R}\left[ -\frac{f-R f_R}{2}+\frac{1}{e^\nu }f''_R+\frac{2}{re^\nu }f'_R-\frac{\nu '}{2e^\nu }f'_R\right] \nonumber \\&+\frac{\kappa }{f_R}\rho e^{\mu }, \end{aligned}$$
(5)
$$\begin{aligned} G_{11}= & {} \frac{1}{f_R}\left[ \frac{f-R f_R}{2}e^\nu -\frac{2}{r}f'_R-\frac{\mu '}{2}f'_R\right] +\frac{\kappa }{f_R}P_re^{\nu }, \end{aligned}$$
(6)
$$\begin{aligned} G_{22}= & {} \frac{1}{f_R}\left[ \frac{f-R f_R}{2}r^2-\frac{r}{e^\nu }f'_R-\frac{r^2}{e^\nu }f''_R-\frac{r^2\mu '}{2e^\nu }f'_R\right. \nonumber \\&\left. +\frac{r^2\nu '}{2e^\nu }f'_R\right] +\frac{\kappa }{f_R}P_tr^2, \end{aligned}$$
(7)
$$\begin{aligned} G_{33}= & {} \frac{1}{f_R}\left[ \frac{f-R f_R}{2}r^2\sin ^{2}\theta -\frac{r\sin ^{2}\theta }{e^\nu }f'_R\right. \nonumber \\&\left. -\frac{r^2\sin ^{2}\theta }{e^\nu }f''_R-\frac{r^2\sin ^{2}\theta \mu '}{2e^\nu }f'_R+\frac{r^2\sin ^{2}\theta \nu '}{2e^\nu }f'_R\right] \nonumber \\&+\frac{\kappa }{f_R}P_tr^2\sin ^{2}\theta . \end{aligned}$$
(8)

Here prime (\(^{\prime }\)) denotes the differentiation with respect to ‘r’ and \(f_R= \frac{df}{dR}\), we assumed \(\kappa =1\). From the modified FEs (5)–(8), we obtain hydrostatic equilibrium equation for anisotropic fluid as follows:

$$\begin{aligned}&\frac{dp_r}{dr}=-\frac{\mu '}{2}\rho -\left( \frac{\mu '}{2}+\frac{2}{r}+\frac{f'_R R'}{f_R \rho '}\right) p_r+\frac{2}{r}p_t\nonumber \\&\quad +e^{-\nu }\left( -\frac{\mu '}{2}-\frac{2}{r}\right) f''_R \nonumber \\&\quad +e^{-\nu }\left( \frac{3\mu '\nu '}{4}+\frac{(\mu ')^2}{4}+\frac{3\nu '}{r}+\frac{2}{r^2}\right) f'_R\nonumber \\&\quad -\nu '(\frac{f-R f_R}{2})\nonumber \\&\quad +e^{\nu }f_R\left[ \frac{e^{-2\nu }}{f_R}\left\{ \left( \frac{2}{r} +\frac{\mu '}{2}\right) f'_R-\frac{f-R f_R}{2}e^{\nu }\right\} \right] _{,1}, \end{aligned}$$
(9)

leading to

$$\begin{aligned}&\Omega =-\frac{dP_r}{dr}-\frac{\mu '}{2}\rho -\left( \frac{\mu '}{2}+\frac{2}{r}+\frac{f'_R R'}{f_R \rho '}\right) p_r+\frac{2}{r}p_t\nonumber \\&\qquad +e^{-\nu }\left( -\frac{\mu '}{2}-\frac{2}{r}\right) f''_R \nonumber \\&\qquad +e^{-\nu }\left( \frac{3\mu '\nu '}{4}+\frac{(\mu ')^2}{4}+\frac{3\nu '}{r}+\frac{2}{r^2}\right) f'_R\nonumber \\&\qquad -\nu '\left( \frac{f-R f_R}{2}\right) \nonumber \\&\qquad +e^{\nu }f_R\left[ \frac{e^{-2\nu }}{f_R}\left\{ \left( \frac{2}{r} +\frac{\mu '}{2}\right) f'_R-\frac{f-R f_R}{2}e^{\nu }\right\} \right] _{,1}.\nonumber \\ \end{aligned}$$
(10)

Equation (10) describes the behavior of anisotropic inner fluid of compact star in equilibrium state, we shall use it for discussion of cracking by considering its perturbed form. Making use of Krori Barua spacetime coefficients [37] that is \(\nu = Ar^2\) and \(\mu = Br^2+C\) where A, B and C are constants in Eq. (10). We have

$$\begin{aligned}&\Omega =-\frac{dP_r}{dr}-Br\rho -\left( B r+\frac{2}{r}+\frac{f'_R R'}{f_R \rho '}\right) p_r\nonumber \\&\quad +\frac{2}{r}p_t+e^{-Ar^2} \left( -Br-\frac{2}{r}\right) f''_R\nonumber \\&\quad +\!\!\left( 3ABr^2e^{-Ar^2}\!+\!B^2r^2e^{-Ar^2} \!+\!\frac{2e^{-Ar^2}}{r^2}+6Ae^{-Ar^2}\right) \!f'_R\nonumber \\&\quad -\frac{f-R f_R}{2}(2Ar) +e^{Ar^2}f_R\nonumber \\&\quad \times \left[ \frac{e^{-2\nu }}{f_R}\left\{ \left( \frac{2}{r}+B r\right) f'_R-\frac{f-R f_R}{2}e^{Ar^2}\right\} \right] _{,1}, \end{aligned}$$
(11)

simplified form of above expression turns out to be.

$$\begin{aligned} \Omega= & {} -\frac{dP_r}{dr}-Br\rho -\left( B r+\frac{2}{r}+\frac{f'_R R'}{f_R \rho '}\right) p_r\nonumber \\&+\frac{2}{r}p_t+\left( -B r-\frac{2}{r}+\frac{2R'}{r\rho '}\right. \nonumber \\&\left. +\frac{Br R'}{\rho '}\right) f''_Re^{-Ar^2}+\left( -ABr^2e^{-Ar^2}\right. \nonumber \\&-2Ae^{-Ar^2}+Be^{-Ar^2}+B^2r^2e^{-Ar^2} \nonumber \\&\left. +\frac{R'f}{2\rho 'f_R}\right) f'_R-\frac{R'f'}{2\rho '}+\frac{R'f_R}{2\rho '}\nonumber \\&-\left( Br +\frac{2}{r}\right) \frac{(f'_R)^2 R'e^{-Ar^2}}{f_R\rho '}. \end{aligned}$$
(12)

This is the main equation that will help us to employe LDP and analyze instabilities in gravitating system.

3 Local density perturbation in f(R) gravity

The technique we explored is LDP, according to perturbation of density \(\rho \rightarrow \rho +\delta \rho \) in system with barotropic equations of state i.e.,\( p_r=p_r(\rho )\) and \( p_t= p_t(\rho )\) which perturbed the anisotropy of the system. We apply LDP i.e., \(\delta \rho \) on three stars Her X-1, SAX J1808.4-3658 and 4U 1820-30 in equilibrium state. Cracking takes place when the inward directed forces in the inner part and outward directed forces of the configuration changes the sign (\(\delta \Omega < 0\rightarrow \delta \Omega >0\)) and vice-versa. We apply the LDP to perturb all the physical variables as follow:

$$\begin{aligned}&p_r(\rho +\delta \rho )=p_r(\rho )+\frac{dP_r}{d\rho }\delta \rho , \end{aligned}$$
(13)
$$\begin{aligned}&\frac{dP_r}{dr}(\rho +\delta \rho )=\frac{dP_r}{dr}(\rho )\nonumber \\&\qquad +\left[ \frac{d}{dr}\left( \frac{dP_r}{d\rho }\right) +\frac{dP_r}{d\rho }\frac{d^2\rho }{dr^2}\frac{dr}{d\rho }\right] \delta \rho , \end{aligned}$$
(14)
$$\begin{aligned}&p_t(\rho +\delta \rho )=p_t(\rho )+\frac{dP_t}{d\rho }\delta \rho , \end{aligned}$$
(15)
$$\begin{aligned}&R(\rho +\delta \rho )=R(\rho )+\frac{R'}{\rho '}\delta \rho , \end{aligned}$$
(16)
$$\begin{aligned}&R'(\rho +\delta \rho )=R'(\rho )+\frac{R''}{\rho '}\delta \rho , \end{aligned}$$
(17)
$$\begin{aligned}&f_R(\rho +\delta \rho )=f_R(\rho )+f'_R\frac{R'}{\rho '}\delta \rho , \end{aligned}$$
(18)
$$\begin{aligned}&f'_R(\rho +\delta \rho )=f'_R(\rho )+f''_R\frac{R'}{\rho '}\delta \rho , \end{aligned}$$
(19)
$$\begin{aligned}&f''_R(\rho +\delta \rho )=f''_R(\rho )+f'''_R\frac{R'}{\rho '}\delta \rho , \end{aligned}$$
(20)
$$\begin{aligned}&f(\rho +\delta \rho )=f(\rho )+f'\frac{R'}{\rho '}\delta \rho , \end{aligned}$$
(21)
$$\begin{aligned}&f'(\rho +\delta \rho )=f'(\rho )+f''\frac{R'}{\rho '}\delta \rho , \end{aligned}$$
(22)
$$\begin{aligned}&\rho '(\rho +\delta \rho )=\rho '(\rho )+\frac{\rho ''}{\rho '}\delta \rho . \end{aligned}$$
(23)

The radial sound speed \(\nu ^2_r\) and tangential sound speed \(\nu ^2_t\) are defined as

$$\begin{aligned}&\nu ^2_r=\frac{dP_r}{d\rho }, \quad \nu ^2_t=\frac{dP_t}{d\rho }. \end{aligned}$$
(24)
Table 1 Calculated values of A, B, mass M \((M_{\bigodot })\), mass-radius ratio \(\frac{M}{R}\), radius R(km) for Her \(X-1\), SAX \(J1808.4-3658\), 4U \(1820-30\)
Full size table

The perturbed form of Eq. (12) can be expressed in following form.

$$\begin{aligned} \Omega = \Omega _o(\rho , \rho ', p_r, p'_r, p_t, f_R, f'_R, f''_R, R', f, f')+\delta \Omega ,\nonumber \\ \end{aligned}$$
(25)

where

$$\begin{aligned} \delta \Omega= & {} \frac{\partial \Omega }{\partial \rho }\delta \rho +\frac{\partial \Omega }{\partial \rho '}\delta \rho ' +\frac{\partial \Omega }{\partial p_r}\delta p_r+\frac{\partial \Omega }{\partial p'_r}\delta p'_r+\frac{\partial \Omega }{\partial p_t}\delta p_t\nonumber \\&+\frac{\partial \Omega }{\partial f_R}\delta f_R+\frac{\partial \Omega }{\partial f'_R}\delta f'_R +\frac{\partial \Omega }{\partial f''_R}\delta f''_R +\frac{\partial \Omega }{\partial R'}\delta R'\nonumber \\&+\frac{\partial \Omega }{\partial f}\delta f+\frac{\partial \Omega }{\partial f'}\delta f', \end{aligned}$$
(26)

that modifies to

$$\begin{aligned} \frac{\delta \Omega }{\delta \rho }= & {} \frac{\partial \Omega }{\partial \rho } +\frac{\partial \Omega }{\partial \rho '}(\rho ''(\rho ')^{-1})\nonumber \\&+\nu ^2_r\frac{\partial \Omega }{\partial p_r}+\frac{\partial \Omega }{\partial p'_r}\Bigg ((\nu _r^2)'+(\nu ^2_r \rho ''(\rho ')^{-1}\Bigg ) \nonumber \\&+\nu ^2_t\frac{\partial \Omega }{\partial p_t}+\Bigg (f'_R\frac{R'}{\rho '}\Bigg ) \frac{\partial \Omega }{\partial f_R}\nonumber \\&+\Bigg (f''_R\frac{R'}{\rho '}\Bigg )\frac{\partial \Omega }{\partial f'_R}+\Bigg (f'''_R\frac{R'}{\rho '}\Bigg ) \frac{\partial \Omega }{\partial f''_R}\nonumber \\&+\Bigg (\frac{R''}{\rho '}\Bigg ) \frac{\partial \Omega }{\partial R'}\nonumber \\&+\Bigg (f'\frac{R'}{\rho '}\Bigg )\frac{\partial \Omega }{\partial f}\nonumber \\&+\Bigg (f''\frac{R'}{\rho '}\Bigg )\frac{\partial \Omega }{\partial f'}, \end{aligned}$$
(27)

The values of other parameters used in above equation is given in Appendix as Eqs. (A1)–(A19). The partial derivatives appearing in above expression are given as

$$\begin{aligned}&\frac{\partial \Omega }{\partial \rho }=-B r, \quad \frac{\partial \Omega }{\partial p_r} = -\Bigg (Br+\frac{2}{r}+\frac{f'_R R'}{f_R \rho '}\Bigg ), \end{aligned}$$
(28)
$$\begin{aligned}&\frac{\partial \Omega }{\partial P'_r}= -1, \quad \frac{\partial \Omega }{\partial P_t}= \frac{2}{r}, \end{aligned}$$
(29)
$$\begin{aligned}&\frac{\partial \Omega }{\partial f}=\frac{R'f'_R}{2\rho 'f_R}, \quad \frac{\partial \Omega }{\partial f'}= -\frac{R'}{2\rho '}, \end{aligned}$$
(30)
$$\begin{aligned}&\frac{\partial \Omega }{\partial f_R}=-\frac{f'_R R'p_r}{(f_R)^2\rho '}-\frac{f'_R R'f}{2(f_R)^2\rho '}\nonumber \\&\qquad \qquad +\frac{R'}{2\rho '}+\Bigg (Br+\frac{2}{r}\Bigg )\frac{(f'_R)^2 R'e^{-Ar^2}}{(f_R)^2\rho '}, \end{aligned}$$
(31)
$$\begin{aligned}&\frac{\partial \Omega }{\partial f'_R}=-ABr^2e^{-Ar^2}-2Ae^{-Ar^2}\nonumber \\&\qquad \qquad +Be^{-Ar^2}+B^2r^2e^{-Ar^2}+\frac{R'p_r}{f_R\rho '} +\frac{R'f}{2\rho 'f_R} \nonumber \\&\qquad \qquad -2(Br+\frac{2}{r})\frac{f'_R R'e^{-Ar^2}}{f_R \rho '}, \end{aligned}$$
(32)
$$\begin{aligned}&\frac{\partial \Omega }{\partial f''_R} =e^{-Ar^2}\left( -B r-\frac{2}{r}+\frac{2R'}{r\rho '}+\frac{B r R'}{\rho '}\right) , \end{aligned}$$
(33)
$$\begin{aligned}&\frac{\partial \Omega }{\partial \rho '} =-\frac{R'f'_R p_r}{f_R(\rho ')^2}+\frac{f' R'}{2(\rho ')^2}\nonumber \\&\qquad \qquad -\frac{2R'f''_Re^{-Ar^2}}{(r\rho ')^2}\nonumber \\&\qquad \qquad -\frac{B r R'f''_Re^{-Ar^2}}{(\rho ')^2}-\frac{R'f f'_R}{2(\rho ')^2 f_R} \nonumber \\&\qquad \qquad -\frac{R'f_R}{2(\rho ')^2}+(Br+\frac{2}{r})\frac{(f'_R)^2 R'e^{-Ar^2}}{f_R(\rho ')^2}, \end{aligned}$$
(34)
$$\begin{aligned}&\frac{\partial \Omega }{\partial R'} = \frac{2}{r\rho '}f''_Re^{-Ar^2}+\frac{B r}{\rho '}f''_Re^{-Ar^2}+\frac{f}{2\rho 'f_R}f'_R\nonumber \\&\qquad \qquad +\frac{f_R}{2\rho '}-\frac{f'}{2\rho '}+\frac{f'_R p_r}{f_R \rho '}\nonumber \\&\qquad \qquad -(Br+\frac{2}{r})\frac{(f'_R)^2e^{-Ar^2}}{f_R\rho '}. \end{aligned}$$
(35)
Fig. 1
figure 1

Graphical representation of \(\frac{\delta \Omega }{\delta \rho } for \) Her X-1 \(A=0.0069062764281\) (km)\(^{-2}\), \(B=0.0042673646183\) (km)\(^{-2}\), \(R=7.7\) (km)

Full size image
Fig. 2
figure 2

Graphical representation of \(\frac{\delta \Omega }{\delta \rho } for SAX J1808.4-3658 A = .018231569740\) (km)\(^{-2}\), \(B = .014880115692\) (km)\(^{-2}\), \( R=7.07\) (km)

Full size image

4 Discussion of cracking and overturning

The f(R) theories can be used for various applications to cosmology and gravity such as local gravity constraints, dark energy, inflation, spherically symmetric solutions in weak and strong gravitational backgrounds and cosmological perturbations [10]. Felice et al. [55] discussed a number of ways to describe the difference between GR and various modified theories observationally and experimentally. The rapid development of observational cosmology shows that the universe has undergone two phases of cosmic acceleration. The first phase is called inflation which is believed to have occurred prior to the radiation domination [56,57,58]. In order to solve the flatness and horizon problems plagued in big-bang cosmology but also to explain the flat spectrum of temperature anisotropies observed in cosmic microwave background, the inflationary phase is of significant importance. The second accelerating phase has started after the matter domination. The late time acceleration is covered through dark energy which is aroused by unknown mysterious component [59].

The basic motivation to consider f(R) gravity is to search for an elementary theory of gravity that is capable to explain both dark energy and dark matter problems without referring to mysterious dark energy conception. In our manuscript, we consider the model with \(f(R)=R+\lambda R^2\) where \(\lambda >0\). This is the first model of inflation presented by Starobinsky in 1980 [38]. Soonafter construction of this model, Miji\(\acute{c}\) et al. [39] worked on \(R^2\) cosmology by taking different values of \(\lambda \) concluding that the potential \(\lambda \) has to be positive. Moreover, same authors remarked that its large values represent flat potential and inflation is derived by linear term R that leads to GR corrections. Recent interpretations of this model [43,44,45,46] shows that \(\lambda = \frac{1}{6M^2}\), M is a parameter with dimension of mass that is in fact the inflation mass given by Planck’s mass. So, \(\lambda = \frac{1}{6M^2}\) is one value among many possible choices to witness inflationary phase of the universe.

The fundamental equation for identification of disturbances or instabilities in considered model is Eq. (22), we have applied LDP on it to arrive at cracking points. For this purpose, the general framework of LDP through is tested on an already developed model presented by Zubair and Abbas [1]. The physically viable theoretical compact star model developed in [1] describes a class of theoretically stable stars namely \(Her X-1, SAXJ1808.4-3658\) and \(4U 1820-30\). Table 1 lists down mass, radius and values of constant parameters.

Graphical representation of distribution force for each star is given in following subsections.

4.1 Star 1: Her X-1

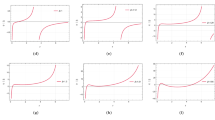
In (1972) Tananbaum et al. [50] observed Her X-1 with binary orbital period 1.7 d and pulse period 1.24 s. Li et al. [51] showed that X-ray pulsar Her X-1 is a strange star, and as model of a strange star is more logical with Her X-1 using parameters as binary orbital period and pulse period are 1.7 d and 1.24 s, pulsar mass M = 0.98 ± 0.12 \((M_{\bigodot })\), cyclotron line energy, companion mass, spin-up rate and X-ray luminosity. We have plotted \(\frac{\delta \Omega }{\delta \rho }\) from Eq. (27) for first star by taking different values of Starobinsky model parameter \(\lambda \) given in Fig. 1. The Fig. 1a, b, e shows some disturbances in the form of singularities near the center, while it remains stable while moving towards boundary. The Fig. 1c, d remains stable throughout the region.

4.2 Star 2: SAXJ1808.4-3658

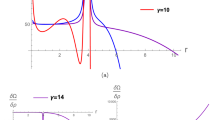
Millisecond X-ray pulsar the SAXJ1808.4-3658 was first discovered in (1996) by wide field camera on board BeppoSAX satellite [52]. Comparison of the mass to radius (M–R) relation of SAXJ1808.4-3658 with the theoretical M–R relation for neutron stars and strange stars reveals that it as a low mass X-ray binary as it emits almost all of its radiation in X-rays. Its orbital period is 2 h, the authors in [53] have concluded that the model of strange star is more logical with SAXJ1808.4-3658. The graph of \(\frac{\delta \Omega }{\delta \rho }\) for different values of \(\lambda \) is shown as Fig. 2. One can clearly see that in Fig. 2a, singularities are visible near the center, as we move towards boundary of the star the graph of distribution force remains stable. One cracking point occurs in Fig. 2b, c, d, g at different values of “r“ summarized in Table 2. Plot of distribution force for \(\lambda \in (0.85, 2]\) shows stable behavior given in Fig. 2e, f.

Table 2 Summary of singular and cracking points for \(\lambda \in (0, 2]\) and \(\lambda =\frac{1}{6M^2}\) in SAXJ1808.4-3658
Full size table

4.3 Star 3: 4U 1820-30

Another type of low mass X-ray binaries is 4U 1820-30. The authors in [54] analyzed the spectroscopic data on different thermonuclear explosion providing well constrained values for apparent emitting eras and the Eddington flux. They concluded that [54] both depend in a distinct way on the mass and radius of a neutron star. Using the distance measurements to the globular cluster NGC 6624 and the observed spectral parameters they have determine the mass of the neutron star in this binary to be \(M = 1.58 \pm 0.06 (M_{\bigodot })\) and its radius to be \(R = 9.11 \pm 0.40\) km. Finally, they have shown that only the smaller value of the two existing distance measurements to the globular cluster is logical with the spectroscopic data.

Plot of \(\frac{\delta \Omega }{\delta \rho }\) is given in Fig. 3 for third star 4U 1820-30. The graph give in Fig. 3a–f shows that compact object star exhibits cracking at different points for values of \(\lambda \in (0, 0.65]\). However, for \(\lambda \in (0.65, 02]\) and \(\lambda =\frac{1}{6M^2}\), star maintains stability.

Fig. 3
figure 3

Graphical representation of \(\frac{\delta \Omega }{\delta \rho }\) for 4U 1820-30 \(A = .010906441192\) (km)\(^{-2}\), \(B = .0098809523811\) (km)\(^{-2}\), \( R=10.0\) (km)

Full size image

5 Conclusion and discussion

The main objective of this work is to check the instabilities for compact objects in the framework of modified theory of f(R) gravity through cracking technique. For this purpose, we have developed mathematical expressions for distribution force by making use of local density perturbations on hydrostatic equilibrium equation. The f(R) model we have chosen for analysis is Starobinsky model that includes quadratic term of curvature invariant i.e., \(f(R)= R+\lambda R^2\), where \(\lambda \) takes positive value. It describes a cosmological inflationary model. The onset of modified field equations corresponding to anisotropic spherically symmetric matter configuration is constructed in Eqs. (5)–(8). The hydrostatic equilibrium equation or generalized TOV equation for static spacetime is developed by applying Bianchi identities on modified field equations given in Eq. (12).

Table 3 Summary of singular and cracking points for \(\lambda \in (0, 2]\) and \(\lambda =\frac{1}{6M^2}\) in 4U 1820-30
Full size table
Fig. 4
figure 4

Graphical representation of \(\frac{\delta \Omega }{\delta \rho }\) for \(\lambda =0\) i.e., GR case

Full size image

The effect of LDP in the framework of GR for anisotropic configuration is a useful tool to identify cracking in the system. However, up till now this technique is not available for modified theories to analyze static models. Models stable under LDP will be more suitable for discussion of astronomical objects. In order to check occurrence of cracking or overturning we have constructed density dependent perturbation pattern for f(R) gravity model presented in Eqs. (13)–(23) for f(R) gravity. Implementation of perturbation scheme to hydrostatic equilibrium equation leads to the perturbed equation that describe very small deviations in the system and explains distribution of forces acting on the gravitating system given by Eq. (22). It is worth mentioning here that Eq. (27) is the main equation that can identifies cracking points or instabilities occurring in the system. In order to check efficiency of our developed technique, we have applied our cracking model on an already developed physical viable model. In this paper the physical viability of developed technique is tested on the data of three different stars namely Her X-1, SAX J1808.4-3658, 4U 1820-30 presented in model of Zubair and Abbas [1].

Cracking describes the behavior of inner matter distribution just after its departure from equilibrium condition. It has been observed that when the system leaves its condition of equilibrium then cracking takes place for different values of Starobinsky model parameter \(\lambda \in (0, 2]\) and \(\lambda =\frac{1}{6M^2}\). Graphical representation of distribution force for different values of model parameter with discussion is given in previous section with summary of cracking points in Tables 2 and 3 for second and third star. No crack appears in the case of first star (Her X-1). Thus, this technique is very suitable in refinement of physically acceptable stable compact star models. As it identifies the possible cracks or singularities in the system.

Insertion of \(\lambda =0\) in considered modified gravity model and constitutive equations given in Appendix as Eqs. (A1)–(A19) and hydrostatic equilibrium Eq. (22) leads to the results in GR. The graphical representation of distribution force for \(\lambda =0\) is given in Fig. 4.

It is worth mentioning here that use of \(\lambda =0\) in our developed LDP frame work coincides with the frameworks of GR to arrive at cracking [24, 30, 60, 61]. Extension of this work to charged case is a well motivated generalization that is in process.