1 Introduction

In general relativity (GR), the gravitational collapse of massive stars at the final stage of their evolution can be regarded as the fundamental mechanism for the formation of astrophysical black holes. Therefore, they have been very attractive and intriguing objects due to their remarkable gravitational, thermodynamic and astronomical properties. The electromagnetic field remains an interesting aspect of astrophysical black holes. In GR, the gravitational collapse of massive objects can be decayed with \(t^{-1}\) [1, 2], thus suggesting that the black hole has no magnetic field of its own. However, external factors come into play for the presence of a magnetic field, namely the accretion discs surrounding rotating black holes [3] or neutron stars [1, 4, 5]. With this in view, it is believed that black holes are surrounded by a magnetic field in an astrophysical context. However, such a magnetic field can be referred to as a test field, namely \(B\ll B_{\mathrm{max}}\), which does not modify spacetime geometry (see e.g. [6,7,8,9,10,11,12] addressing the property of the test field analytically and numerically for given background spacetime). So far, the magnetic field has been measured to be of order \(\sim 10^{8}\) Gauss around stellar-mass black holes and \(\sim 10^{4}\) Gauss around supermassive black holes (see e.g. [13]). It was also estimated at the horizon (see e.g. [14, 15]). Subsequently it was found that the magnetic field can be between 200 and \(8.3 \times 10^{4}\)  Gauss at 1 Schwarzschild radius [16] and about \(B\sim 33.1 \pm 0.9~\mathrm {Gauss}\) in the corona as a consequence of observational analysis of the binary black hole system V404 Cygni  [17]. It was recently estimated to be of order \(B\sim (1{-}30)\) Gauss as a result of the analysis of imaged polarized emission around the supermassive black hole in M87 under the Event Horizon Telescope (EHT) Collaboration [18, 19]. However, those estimated values still remain candidates for the magnetic field around the astrophysical black holes.

It is well known that even small a magnetic field B can strongly affect the dynamics of a charged particle as a consequence of the large Lorentz force [see e.g. 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31]. Thus, the magnetic field could be increasingly important to consider as a background field to test the background geometry in the black hole vicinity. With this motivation, there is a family of solutions that suggests the involvement of the interaction between gravity and the axially symmetric magnetic field induced by external sources [32]. Another interesting solution that includes the additional gravity that stems the from magnetic field describes a static and spherically symmetric black hole with Melvin’s magnetic universe [33]. These kinds of solutions are so-called magnetized black holes. In this context the magnetized Reissner–Nordström black hole solution [34] and rotating and charged magnetized black hole solutions with some complicated asymptotic behaviours [35,36,37] have been considered as possible extensions of magnetized black holes. After that a new approach for the magnetized black hole solution was proposed by taking into account the global charge (see e.g. [38, 39]). Following [33, 34], there have been several investigations devoted to the study of the properties of the magnetized black hole [40,41,42,43].

Recent experiments and modern observations play a decisive role in testing the extreme geometric and remarkable gravitational properties of black holes in GR. However, along these lines one can also use astrophysical processes occurring in the environment surrounding astrophysical black holes, for example X-ray data produced by astrophysical compact objects [44,45,46] and the quasiperiodic oscillations (QPOs) with the X-ray power observed in microquasars related to the low-mass X-ray binary systems (e.g. a neutron star or a black hole binary system). The galactic microquasars are considered as a source of QPOs with the ratio 3/2 [47]. It is worth noting that QPOs characterized by either low frequency (LF) or high frequency (HF) are observed in the X-ray power spectra. The various kinds of HF QPO models were discussed in Refs. [48,49,50,51] addressing the epicyclic motion of hot spots and oscillatory models of accretion discs. It is believed that the these frequencies characterize the epicyclic motion with corresponding frequencies. The HF QPOs that will usually exist in binary systems relate to the twin peak HF QPOs that provide information on the matter moving around the compact objects. However, there exists no reasonable model that can explain the appearance of such HF QPOs [52]. For that reason, the epicyclic motion of charged particles around a black hole surrounded by a magnetic field has been proposed to explain such phenomena [53,54,55]. Also, twin peak HF QPOs that usually arise in pairs (i.e. upper \(\nu _U\) and lower \(\nu _L\) frequencies) have been observed in galactic microquasars. For these objects, HF QPOs can be observed at the fixed \(\nu _U/\nu _L=3/2\) ratio [51, 56]. The observed upper frequencies, \(\nu _U\), are very close to the orbital frequencies of test particles at the stable circular orbit located at the inner edge of the accretion disc around black holes. Thus, epicyclic motion of test particles with orbital, radial and latitudinal frequencies can be a useful tool in modelling and explaining the observed \(\nu _U/\nu _L=3/2\) HF QPOs in the low-mass X-ray binary systems. Following LF and HF QPOs that arise in various parts of the accretion disc, there have been several investigations/models addressing the QPOs [see e.g. 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68].

In the present paper we study the dynamics of test particles and epicyclic motion around the magnetized Ernst black hole. We further aim to constrain the magnetic field with the help of QPOs observed in three microquasars, namely GRO J1655-40, XTE J1550-564 and GRS 1915+105.

The paper is organized as follows: In Sect. 2 we briefly describe the black hole metric. We consider the particle dynamics in the environment surrounding the magnetized Ernst black hole in Sect. 3. In Sect. 4 we focus on epicyclic motion with the QPOs in the black hole vicinity, and we discuss constraints on the magnetic parameter of the magnetized Ernst black hole spacetime in Sect. 5. We present concluding remarks on the obtained results in Sect. 6.

Fig. 1
figure 1

Plot showing the configuration of magnetic field lines in the vicinity of a magnetized Ernst black hole. The grey-shaded area shows the black hole horizon. Note that left/right panels respectively refer to \(B=0.1/0.5\). (Note here that we consider \(B\rightarrow BM\) as a dimensionless quantity, having set \(G = c = 1\))

Full size image

Throughout the manuscript we use a system of units in which \(G=c=1\).

2 Magnetized Ernst black hole and its electromagnetic field

Here we briefly review the spacetime metric describing a magnetized Ernst black hole. It is given by

$$\begin{aligned} \mathrm{d}s^2 =\Lambda ^2\left( -F(r)\mathrm{d}t^2+\frac{\mathrm{d}r^2}{F(r)}+r^2\mathrm{d}\theta ^2\right) +\frac{r^2\sin ^2\theta }{\Lambda ^2}\mathrm{d}\phi ^2, \end{aligned}$$
(1)

where

$$\begin{aligned} F(r)=&1-\frac{2M}{r}, \end{aligned}$$
(2)
$$\begin{aligned} \Lambda (r,\theta ) =&1+B^2r^2\sin ^2\theta , \end{aligned}$$
(3)

with the magnetic field parameter B. Due to the presence of a strong magnetic field, the metric is not asymptotically flat, and it is also not spherically symmetric. It is worth noting that the event horizon is given by \(r_{h}=2M\), similar to what one obtains for the Schwarzschild black hole. The electromagnetic field around the magnetized Ernst black hole has the form

$$\begin{aligned} A_{\mu }\mathrm{d}x^{\mu }=\frac{B r^2 \sin ^2\theta }{2\Lambda }\mathrm{d}\phi . \end{aligned}$$
(4)

Since the magnetic field is assumed to be aligned axially, it breaks down the spherical symmetry of the spacetime as well. The underlying geometry of the spacetime is now axis-symmetric, as rotations along the \(\phi \) direction leave the metric and the electromagnetic field invariant. The orthonormal components of the magnetic field measured by zero-angular-momentum observers (ZAMO) with four-velocity components are given by the following expressions

$$\begin{aligned} B^{\hat{r}}= & {} -\frac{B}{\Lambda }\left( 1-\frac{B^2r^2\sin ^2\theta }{\Lambda } \right) \cos \theta , \end{aligned}$$
(5)
$$\begin{aligned} B^{\hat{\theta }}= & {} \frac{BF(r)^{1/2}}{\Lambda }\left( 1-\frac{B^2r^2\sin ^2\theta }{\Lambda } \right) \sin \theta . \end{aligned}$$
(6)

The magnetic field (5) and (6) depends on the parameter responsible for the external magnetic field, and under the condition that \(M/r\rightarrow 0\) and \(\Lambda \rightarrow 1\), we recover the solutions for the flat spacetime

$$\begin{aligned} B^{\hat{r}} =-B\cos \theta , ~~~ B^{\hat{\theta }}=B\sin \theta , \end{aligned}$$
(7)

which coincides with the homogeneous magnetic field in the Newtonian spacetime, as expected. The configuration of magnetic field lines in the vicinity of the magnetized black hole is depicted in Fig. 1.

Let us note that the magnetized Ernst metric is not spherically symmetric, but is actually axi-symmetric because it remains invariant under \(\phi =\phi +c\), which is also consistent with the orientation of the electromagnetic field. The fact that the spherical symmetry is broken leads to interesting phenomenological aspects such as a possibility to mimic the rotation to some extent. We note that one can check the topology of the Ernst solution at the horizon using the Gauss–Bonnet theorem. At a fixed moment in time t, the metric reduces to

$$\begin{aligned} \mathrm{d}s^2=\Lambda ^2\left( \frac{\mathrm{d}r^2}{F(r)}+r^2\mathrm{d}\theta ^2\right) +\frac{r^2\sin \theta ^2}{\Lambda ^2}\mathrm{d}\phi ^2, \end{aligned}$$
(8)

and using the Gaussian curvature with respect to \(g^{(2)}\) on \(\mathcal {M}\), the Gauss–Bonnet theorem states that

$$\begin{aligned} \iint _{\mathcal {M}} K dA=2 \pi \chi (\mathcal {M}). \end{aligned}$$
(9)

Note that dA is the surface line element of the two-dimensional surface and \(\chi (\mathcal {M})\) is the Euler characteristic number. It is sometimes convenient to express the above theorem in terms of the Ricci scalar, in particular for the two-dimensional surface at \(r=r_h\), and then using the Ricci scalar given by

$$\begin{aligned} \mathcal {R}=\frac{2}{r^2\Lambda ^2}, \end{aligned}$$
(10)

with \( \sqrt{g^{(2)}}=r^2\sin \theta \), evaluated at \(r=r_h\), yielding the following from

$$\begin{aligned} \frac{1}{4 \pi }\iint _{\mathcal {M}} \mathcal {R} \sqrt{-g^{(2)}} \,\mathrm{d}\theta \mathrm{d}\phi =\chi (\mathcal {M}). \end{aligned}$$
(11)

In general, the solution of the above integral is complicated due to \(\theta \) dependence. For small B we can expand in series and find in leading order terms \(\chi =2-8B^2 r_h^2/3\). This shows that the Euler characteristic number is smaller than 2 hence, in general, the topology of Ernst spacetime differs from a perfect sphere.

3 Charged particle dynamics around magnetized Ernst black hole

Now we focus on charged particle motion around the magnetized Ernst black hole. We assume that the test particle is endowed with the rest mass m and electric charge q. In general, the Hamilton–Jacobi equation of the system is then expressed as

$$\begin{aligned} H= & {} g^{\mu \nu }\left( \frac{\partial S}{\partial x^\mu }-qA_\mu \right) \left( \frac{\partial S}{\partial x^\nu }-qA_\nu \right) , \end{aligned}$$
(12)

where S is the action, \(x^{\mu }\) is the spacetime coordinates, and \(A_\mu \) denotes the vector potential components of the electromagnetic field. Note that the spacetime (1) and the vector potential components (4) are independent of coordinates (\(t, \phi \)), thus leading to two conserved quantities, namely specific energy E and angular momentum L. From the properties of the Hamiltonian, it is considered to be a constant \(H=k/2\) with relation to \(k/m^2=-1\) for a massive particle, with m being the mass of the particle. For photons, one has to set \(k=0\). Following the Hamilton–Jacobi equation, the action S can be written as follows:

$$\begin{aligned} S=-\frac{1}{2}k\lambda -Et+L\phi +S_r+S_\theta , \end{aligned}$$
(13)

where \(S_r\) and \(S_\theta \) are the radial and angular functions of r and \(\theta \). Note that \(\lambda =\tau /m\) represents the affine parameter with proper time \(\tau \). Inserting Eq. (13) into (12), the Hamilton equations reads

$$\begin{aligned}&k=&-\frac{F(r)^{-1}}{\Lambda ^2}E^2 + \frac{F(r)}{\Lambda ^2 } \left( \frac{\partial S_{r}}{\partial r}\right) ^2 +\frac{1}{\Lambda ^2 r^2}\left( \frac{\partial S_{\theta }}{\partial \theta }\right) ^2\nonumber \\&+ \frac{\Lambda ^2\left( L-qA_{\varphi }\right) ^2}{r^2\sin ^2\theta }. \end{aligned}$$
(14)

The Hamiltonian can be separated into dynamical and potential parts, i.e. \(H=H_{\text {dyn}}+H_{\text {pot}}\) with

$$\begin{aligned} H_{\text {dyn}}= & {} \frac{1}{2}\left[ \frac{1}{g_{rr}} \left( \frac{\partial S_{r}}{\partial r}\right) ^2 +\frac{1}{g_{\theta \theta }}\left( \frac{\partial S_{\theta }}{\partial \theta }\right) ^2\right] , \end{aligned}$$
(15)
$$\begin{aligned} H_{\text {pot}}= & {} \frac{1}{2}\left[ \frac{\mathcal {E}^2}{g_{tt}}+\frac{\left( \mathcal {L}-\frac{q}{m}A_{\varphi }\right) ^2}{g_{\phi \phi }}+1\right] . \end{aligned}$$
(16)

Here we note that we further use the potential part of the Hamiltonian, \(H_{\text {pot}}\), to define the epicyclic frequencies.

For further analysis we shall restrict motion for the charged test particle to the equatorial plane (i.e. \(\theta =\pi /2\)). Following Eq. (14), we obtain the radial equation of motion for charged particles in the following form

$$\begin{aligned} \dot{r}^2=\Big (\mathcal {E}-\mathcal {E}_-(r)\Big )\Big (\mathcal {E}-\mathcal {E}_+(r)\Big )\, , \end{aligned}$$
(17)

where \(\mathcal {E}_{+}(r)\) and \(\mathcal {E}_{-}(r)\) are the two roots of the equation \(\dot{r}=0\). As seen from Eq. (17), we have either \(\mathcal {E}>\mathcal {E}_{+}(r)\) or \(\mathcal {E}<\mathcal {E}_{-}(r)\), since \(\dot{r}^2\ge 0\). However, we shall restrict ourselves to the case \(\mathcal {E}_{+}(r)\) which is physically acceptable, and consequently we select \(\mathcal {E}_{+}(r)\) as an effective potential, i.e. \(V_\mathrm{eff}(r)=\mathcal {E}_{+}(r)\). Thus we have

$$\begin{aligned} V_\mathrm{eff}(r)= \left( 1-\frac{2M}{r}\right) ^{1/2}\left[ {\Lambda ^2} +\frac{\Lambda ^4}{r^2}\left( \mathcal {L}-\frac{q\,B\,r^2}{2m\Lambda }\right) ^2\right] ^{1/2}. \nonumber \\ \end{aligned}$$
(18)

Here, we denote parameters \(\mathcal {E}=E/m\) and \(\mathcal {L}=L/(M m)\). From Eq. (18), the effective potential can easily recover the one as in the Schwarzschild spacetime in case we eliminate all parameters except black hole mass M. As can be seen from Eq. (18), the vector potential is involved in the expression of the effective potential because the charged particle depends upon the magnetic field component.

Fig. 2
figure 2

Radial dependence of the effective potential for the radial motion of test particles around the magnetized Ernst black hole. Left panel: \(V_\mathrm{eff}\) is plotted for various combinations of B for the neutral particle case, i.e. \(q/m=0\). Middle/right panels: \(V_\mathrm{eff}\) is plotted for various combinations of charged particle parameters q/m for the fixed magnetic field parameter \(B=0.1\)

Full size image
Fig. 3
figure 3

Trajectories of the particle at the equatorial plane around the magnetized Ernst black hole for magnetic field parameter \(B=0\) (solid curve) and \(B=0.04\) (dashed curve) for various combinations of angular momentum \(\mathcal {L}=3\) (left panel), \(\mathcal {L}=4\) (middle panel) and \(\mathcal {L}=6\) (right panel) for all possible orbits. Note that the particle starts from \(r_{0}/M=10\) towards the black hole

Full size image

Let us then analyse the effective potential in order to understand more deeply the radial motion of test particles moving around the black hole. In Fig. 2, we show the radial dependence of \(V_\mathrm{eff}\) radial motion of neutral/charged particles. In Fig. 2, the left panel demonstrates the impact of the magnetic field parameter B on the profile of the effective potential for the neutral particle, while the middle and right panels demonstrate the impact of parameter q/m for the charged particle. As can be seen from the left panel of Fig. 2, the shape of the effective potential shifts upward as a consequence of an increase in the value of the magnetic field parameter B, thus strengthening the gravitational potential. Similarly, for negative values of the charged particle parameter q/m, the right panel illustrates the same behaviour as that for the left panel. However, the shape of the effective potential shifts downward with increasing positive values of q/m, thereby giving rise to a decrease in the strength of the gravitational potential, as seen in Fig. 2. Also note that as a consequence of the positive charged particle, stable circular orbits shift to the left to smaller r.

We also analyse the particle trajectories of test particles moving around the magnetized Ernst black hole. Here, we demonstrate the trajectory of particles at the equatorial plane. In Fig. 3, all plots show various behaviour of the particle trajectory around the magnetized Ernst black hole. It is increasingly important to understand more deeply the behaviour of possible orbits and trajectories of particles around the black hole. With this in view, we consider the terminating orbits (left panel), the bound orbits and the escape orbits for particles. As can be seen in Fig. 3, the middle panel shows the bound orbits that appear in the balance between the centrifugal force and the gravitational force that stem from the parameters B and M, whereas in the right panel no bound orbits appear, as the particle can escape from the pull of the black hole when the centrifugal force dominates over the gravitational one as a consequence of the absence of the magnetic field parameter \(B=0\). Thus, in this case the overall force becomes repulsive. It becomes however attractive once the magnetic field parameter is involved, and thus the particle orbits become more unstable, allowing the particles to fall into the black hole, as seen in Fig. 3.

Fig. 4
figure 4

Plot showing the radial dependence of the angular momentum as a function of r/M in the equatorial plane (i.e. \(\theta =\pi /2\)). Left panel: \(\mathcal {L}\) is plotted for various combinations of magnetic field parameter B for the neutral particle case, i.e. \(q/m=0\). Right panel: \(\mathcal {L}\) is plotted for various combinations of charged particle parameter q/m for the fixed \(B=0.025\)

Full size image

Let us then consider stable circular orbits around the magnetized Ernst black hole. For particles to be at circular orbits, one needs to solve the following equations simultaneously

$$\begin{aligned} V_\mathrm{eff}(r)=\mathcal {E}\quad \text{ and }\quad V_\mathrm{eff}^{\prime }(r)=0, \end{aligned}$$
(19)

where \(^{\prime }\) refers to a derivative with respect to r. For particles to be at the circular orbits, one needs to have the following angular momentum \(\mathcal {L}\)

$$\begin{aligned} \mathcal {L}_{\pm }= & {} \frac{\Lambda ^{-2} }{2 \big (r \Lambda F(r)'-2 F(r) \left( \Lambda -2 r \Lambda '\right) \big )}\nonumber \\&\times \Big [(q/m)\, B r^3 \Lambda \left( \Lambda F(r)'+3 F(r) \Lambda '\right) \nonumber \\&\pm \Big (r^3 \Lambda ^2 \left( F(r)^2 \left( -4 \left( (q/m)^2\,B^2 r^2-4\right) \Lambda \Lambda '\right. \right. \nonumber \\&+ \left. r \left( (q/m)^2\,B^2 r^2-32\right) \Lambda '^2+4 (q/m)^2\,B^2 r \Lambda ^2\right) \nonumber \\&+ \left. 8 F(r) \Lambda F(r)' \left( \Lambda -3 r \Lambda '\right) -4 r \Lambda ^2 F(r)'^2\right) \Big )^{1/2}\Big ].\nonumber \\ \end{aligned}$$
(20)

In Fig. 4 we show the radial dependence of the \(\mathcal {L}\) (note that by \(\mathcal {L}\) we would mean positive \(\mathcal {L}_{+}\)) of test particle circular orbits around the magnetized Ernst black hole for various combinations of magnetic field and charged particle parameters. We note that as a consequence of the presence of magnetic field parameter B, the circular orbits shift towards the left to smaller r, thus increasing the value of \(\mathcal {L}\) for particles on circular orbits with small radii (see Fig. 4, left panel). However, we show the dependence on \(\pm q/m\) of the angular momentum for charged particles in circular orbits (see Fig. 4, right panel). Also, it is clear from Fig. 4 that both \(-q/m\) and B have a similar effect, thereby reducing the radii of the circular orbits.

Fig. 5
figure 5

Plot showing the ISCO radius as a function of B in the case with both neutral and charged particles

Full size image

We shall now determine the ISCO for test particles orbiting the magnetized Ernst black hole. The radii of ISCO is defined by the second derivative of \(V_\mathrm{eff}\) as follows:

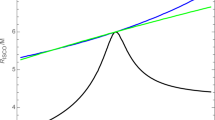
$$\begin{aligned} V_\mathrm{eff}^{\prime \prime }(r)=0. \end{aligned}$$
(21)

From the last equation, we determine the ISCO radius using Eq. (20). In Fig. 5, we show the dependence on magnetic field parameter B of \(r_{ISCO}\) for the test particles. As can be seen from Fig. 5, the ISCO radius decreases as a consequence of an increase in the value of B for all cases. However, one can observe that \(r_{ISCO}\) is slightly influenced by the presence of oppositely charged particles, \(\pm q/m\), while keeping the magnetic field parameter B fixed.

4 Epicyclic frequencies

We now consider the periodic motion of the test particle which orbits at stable circular orbits. For that, all orbits that the particle can move on should occur with \(r\ge r_{isco}\) determined by the minimum of \(V_\mathrm{eff}(r)\). Given the small perturbation \(r = r_0 + \delta r\) and \(\theta =\pi /2+\delta \theta \), the particle starts to oscillate around the circular orbit with \(r_0\) with so-called radial and latitudinal frequencies that respectively refer to the epicyclic motion. Thus, for the given small perturbation \(\delta r\) and \(\delta \theta \), one can write the equations for a linear harmonic oscillation as

$$\begin{aligned} \delta \ddot{ r}+\bar{\omega }_r^2 \delta r = 0, \ \ \ \delta \ddot{ \theta }+\bar{\omega }_\theta ^2 \delta \theta = 0, \end{aligned}$$
(22)

with the radial \(\bar{\omega }_r\) and the latitudinal \(\bar{\omega }_\theta \) frequencies for epicyclic oscillations. Note that the dot in the above equation denotes the derivative with respect to the proper time. These frequencies are measured by a local observer and defined by the following equations [55, 69]

$$\begin{aligned} \bar{\omega }_r^2= & {} \frac{1}{g_{rr}}\frac{\partial ^2 H_{\text {pot}}}{\partial r^2}, \end{aligned}$$
(23)
$$\begin{aligned} \bar{\omega }_\theta ^2= & {} \frac{1}{g_{\theta \theta }}\frac{\partial ^2 H_{\text {pot}}}{\partial \theta ^2}, \end{aligned}$$
(24)
$$\begin{aligned} \bar{\omega }_\phi= & {} \frac{1}{g_{\phi \phi }}\Big (\mathcal {L}-\frac{q}{m} A_\phi \Big ). \end{aligned}$$
(25)

Before representing the above epicyclic frequencies \(\omega _{r,\theta }\), we now consider the periodic motion for both neutral and charged particles. For that we write the normalization condition, \(u^{\alpha }u_{\alpha }=-1\), for particles as

$$\begin{aligned} g_{tt}(u^{t})^2+g_{rr}(u^{r})^2+g_{\theta \theta }(u^{\theta })^2+g_{\phi \phi }(u^{\phi })^2=-1, \end{aligned}$$
(26)

For the periodic motion for the rest particle that orbits a black hole with the fundamental frequencies, namely Keplerian and Larmor frequencies, one needs to focus on the stable circular orbits for which \(u^{\alpha }= (u^{t}, 0, 0,u^{\phi })\). With this in view, we have the following equations

$$\begin{aligned} u^{t}= & {} \frac{1}{\sqrt{-g_{tt}-\omega ^2g_{\phi \phi }}}, \end{aligned}$$
(27)
$$\begin{aligned} \mathcal {E}= & {} -\frac{g_{tt}}{\sqrt{-g_{tt}-\omega ^2g_{\phi \phi }}}, \end{aligned}$$
(28)
$$\begin{aligned} \mathcal {L}= & {} \frac{g_{\phi \phi }\omega }{\sqrt{-g_{tt}-\omega ^2g_{\phi \phi }}}+\frac{q}{m}A_{\phi }\, , \end{aligned}$$
(29)

where we have defined \(\omega = \frac{\mathrm{d}\phi }{\mathrm{d}t}\). We then obtain the general expression for the orbital frequency \(\omega \), referred to as the Keplerian frequency, using the non-geodesic equation for charged particles

$$\begin{aligned} g_{tt,r}+\omega ^2g_{\phi \phi ,r}= & {} -\frac{2q}{m}\big ({A_{t,r}}+\omega A_{\phi ,r}\big )\nonumber \\&\times \left( -g_{tt}-\omega ^2g_{\phi \phi }\right) ^{1/2}. \end{aligned}$$
(30)

For the Keplerian frequency, \(\omega _k\), the above equation is solved to give

$$\begin{aligned} \omega ^2_{k}= & {} \Bigg [{\omega _{0}^2}-2{g_{tt}}\left( \frac{qA_{\phi ,r}}{mg_{\phi \phi ,r}}\right) ^2\pm \frac{2qA_{\phi ,r}}{mg_{\phi \phi ,r}} \nonumber \\&\times \left\{ -\omega _{0}^2g_{tt} -\omega _{0}^4g_{\phi \phi }+\left( \frac{qA_{\phi ,r}\,g_{tt}}{mg_{\phi \phi ,r}}\right) ^2 \right\} ^{1/2}\Bigg ]\nonumber \\&\times \left[ 1+4g_{\phi \phi }\left( \frac{qA_{\phi ,r}}{mg_{\phi \phi ,r}}\right) ^2\right] ^{-1}. \end{aligned}$$
(31)

This clearly shows that as a consequence of \(q=0\), the above equation becomes simple and is given by \(\omega _{0}^2={-g_{tt,r}/g_{\phi \phi ,r}}\), which refers to the Keplerian frequency for a neutral particle orbiting the magnetized black hole. Note that for \(q\ne 0\), Eq. (31) turns out to be a very long and complicated expression for explicit display. We therefore further resort to numerical evolution for \(\omega _k\). However, in the case of neutral particle \(q=0\), Eq. (31) has the form

$$\begin{aligned} \omega _{k}=\sqrt{\frac{\left( 1+B^2 r^2\right) ^4 \left( M+2 B^2 r^3-3 M B^2 r^2\right) }{r^3 \left( 1-B^2 r^2\right) }}. \end{aligned}$$
(32)

Using Eqs. (27–29) and (31), one can define epicyclic frequencies \(\omega _{r}\) and \(\omega _{\theta }\) as follows

$$\begin{aligned} \bar{\omega }_{r}^2= & {} \left[ -\frac{g_{tt,r}^2}{g_{tt}g_{rr}}+\frac{g_{tt,rr}}{g_{rr}}-\frac{\omega _{k}^2}{g_{rr}}\left( \frac{g_{\phi \phi ,r}^2}{g_{\phi \phi }}-\frac{g_{\phi \phi ,rr}}{2}\right) \right. \nonumber \\&+ \frac{q}{m}\frac{\omega _{k}}{g_{rr}}\left( A_{\phi ,rr}-2A_{\phi ,r}\frac{g_{\phi \phi ,r}}{g_{\phi \phi }}\right) \left( -g_{tt}-\omega _{k}^{2}g_{\phi \phi }\right) ^{1/2}\nonumber \\&+\left. \left( \frac{q}{m}\right) ^2\frac{A_{\phi ,r}^2}{g_{rr}}\left( \omega _{k}^2+\frac{g_{tt}}{g_{\phi \phi }}\right) \right] \left( \frac{1}{g_{tt}+\omega _{k}^{2}g_{\phi \phi }}\right) \, \end{aligned}$$
(33)
$$\begin{aligned} \bar{\omega }_{\theta }^2= & {} \left[ -\frac{g_{tt,\theta }^2}{g_{tt}g_{\theta \theta }}+\frac{g_{tt,\theta \theta }}{g_{\theta \theta }}-\frac{\omega _{k}^2}{g_{\theta \theta }}\left( \frac{g_{\phi \phi ,\theta }^2}{g_{\phi \phi }}-\frac{g_{\phi \phi ,\theta \theta }}{2}\right) \right. \nonumber \\&+ \frac{q}{m}\frac{\omega _{k}}{g_{\theta \theta }}\left( A_{\phi ,\theta \theta }-2A_{\phi ,\theta }\frac{g_{\phi \phi ,\theta }}{g_{\phi \phi }}\right) \left( -g_{tt}-\omega _{k}^{2}g_{\phi \phi }\right) ^{1/2}\nonumber \\&+\left. \left( \frac{q}{m}\right) ^2\frac{A_{\phi ,\theta }^2}{g_{\theta \theta }}\left( \omega _{k}^2+\frac{g_{tt}}{g_{\phi \phi }}\right) \right] \left( \frac{1}{g_{tt}+\omega _{k}^{2}g_{\phi \phi }}\right) . \end{aligned}$$
(34)

From the above equations, the epicyclic frequencies turn out to be a complicated expression for explicit display. Thus we carry out further numerical analysis to represent them explicitly.

Since the above-mentioned frequencies, \(\bar{\omega }_{i}\), respectively refer to the locally measured frequencies, one needs to measure these frequencies at infinity for distant observers. Let us then define \(\nu \) as a frequency measured by a distant observer located at infinity. It is worth noting that the frequencies measured by local and distant observers are related by the following transformation [55, 69]

$$\begin{aligned} \bar{\omega }\rightarrow \frac{\bar{\omega }}{-g^{tt}\mathcal {E}}, \end{aligned}$$
(35)

which stems from the redshift factor for the transformation from the proper time \(\tau \) to the time measured at infinity t. Thus, frequencies \(\bar{\omega }\) and \(\nu _{\phi }\) are related by the following relation to G and c

$$\begin{aligned} \nu =\frac{1}{2\pi }\frac{c^3}{GM}\frac{\bar{\omega }}{(-g^{tt})\mathcal {E}}\, . \end{aligned}$$
(36)

The above frequency can then be measured by real observers at infinity and can be directly used to analyse the observation data.

Fig. 6
figure 6

Plot showing the epicyclic frequencies as a function of r/M in the case with a neutral particle. Radial, latitudinal and orbital frequencies are plotted for various combinations of magnetic field parameter B. Note that solid lines refer to the epicyclic frequencies for the Schwarzschild black hole

Full size image
Fig. 7
figure 7

Plots showing the epicyclic frequencies as a function of r/M in the case with a charged particle. Radial, latitudinal and orbital frequencies are plotted for various combinations of charge parameter \(\pm q/m\) while keeping the magnetic parameter \(B=0.005\) fixed

Full size image

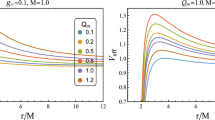
In Fig. 6 we show the epicyclic frequencies as a function of r/M for a neutral particle moving around the magnetized Ernst black hole for various combinations of magnetic field parameter B. As can be seen from Fig. 6, the radial frequency increases and its oscillation shifts left to larger \(\nu \) as a consequence of an increase in the value of the magnetic field parameter B. However, for the latitudinal frequency it remains almost unchanged, while for the orbital frequency the magnetic field parameter causes an increase in the frequency value at larger distances as compared with the one around the Schwarzschild black hole (see Fig. 6, solid lines). Similarly, in Fig. 7 we present the radial dependence of the epicyclic frequencies of charged particles around the magnetized Ernst black hole for fixed B. From Fig. 7, the impact of parameter q/m gives rise to an increase in the value of all frequencies. That is, the radial frequency increases significantly while the latitudinal and orbital frequencies increase slightly at larger distances when increasing the value of parameter q/m. However, the opposite behaviour is the case for the parameter \(-q/m\), thus resulting in decreasing values for all epicyclic frequencies as \(-q/m\) increases (see Fig. 7, right panel). Note that the orbital frequency decreases slightly as a consequence of the presence of parameter \(-q/m\).

5 Constraints on the magnetic field

In this final section we are interested in putting observational constraints on the parameters of the four-dimensional magnetized black hole using our theoretical results and the experimental data for three microquasars. In particular, the appearance of two peaks at 300 Hz and 450 Hz in the X-ray power density spectra of galactic microquasars has stimulated many theoretical works to explain the value of the 3/2-ratio [70]. Although there is no well-accepted explanation yet, the occurrence of \(\nu _U/\nu _L=3/2\) with lower \(\nu _L\) Hz QPO and of the upper \(\nu _U\) Hz QPO has been reported for the microquasars GRO J1655-40, XTE J1550-564 and GRS 1915+105. Below we give the corresponding frequencies of the three microquasars [70]

$$\begin{aligned} \text {GRO J1655-40 : } \nu _U=450\pm 3 \text { Hz},\;\nu _L=300\pm 5 \text { Hz}, \nonumber \\ \end{aligned}$$
(37)
$$\begin{aligned} \text {XTE J1550-564 : } \nu _U=276\pm 3 \text { Hz},\;\nu _L=184\pm 5 \text { Hz}, \nonumber \\ \end{aligned}$$
(38)
$$\begin{aligned} \text {GRS 1915+105 : } \nu _U=168\pm 3 \text { Hz},\;\nu _L=113\pm 5 \text { Hz},\nonumber \\ \end{aligned}$$
(39)

One possible explanation of the twin values of the QPOs is linked to the so-called phenomenon of resonance. The main idea is that near the vicinity of the ISCO, the infalling particles can perform both radial and vertical oscillations, and the two oscillations generally couple non-linearly, yielding the observed quasiperiodic power spectra [71, 72]. Note that the frequency ratio \(\nu _U/\nu _L\) describes the resonance phenomena for HF QPOs. Thus there exist specific models representing different types of resonance. In the present work, we shall assume that the resonance observed in the three microquasars (37), (38) and (39) is described by the parametric resonance that is given by

$$\begin{aligned} \nu _U = \nu _r \quad \text{ and }\quad \nu _L =\nu _{\theta }. \end{aligned}$$
(40)

To constrain the model, we assume a three-parameter model for the QPO frequency, and perform a Monte Carlo simulation with a \(\chi \)-square analysis

$$\begin{aligned} \chi ^{2}(M,B,r)=\frac{(\nu _{r}-\nu _{1\mathrm {U}})^{2} }{\sigma ^2_{1\mathrm {U}}} +\frac{(\nu _{\theta }-\nu _{1\mathrm {L}})^{2} }{\sigma _{1\mathrm {L}}}. \end{aligned}$$

To further simplify the problem, we set the charge of the particle to zero. In what follows, we present our results for the constraints on the black hole mass and magnetic field.

  • Microquasar GRO J1655-40

Within 1\(\sigma \) we obtain for the black hole mass \(M/M _\odot =5.86^{+0.06}_{-0.08}\) and \(r/M=6.03^{+0.05}_{-0.02}\). For the magnetic field we obtain \(B\sim 2.93 \times 10^{-30}\, m^{-1}\). Since B in geometric units has a dimension of inverse of length \([L^{-1}]\) for the particular case, we find for the magnetic field \(B\sim 3.61 \times 10^{-7}\) Gauss. The parametric plot between the magnetic field and the black hole mass is presented in Fig. 8.

  • Microquasar XTE J1550-564:

Here we find within 1\(\sigma \) a black hole mass \(M/M _\odot =9.42^{+0.19}_{-0.35}\) along with the radii \(r/M=6.08^{+0.15}_{-0.06}\). For the magnetic field we obtain \(B\sim 4.76 \times 10^{-30}\, m^{-1}\), which can be written as \(B\sim 5.87 \times 10^{-7}\) Gauss. The parametric plot between the magnetic field and the black hole mass is presented in Fig. 9.

Fig. 8
figure 8

Plot showing the magnetic field B and black hole mass between \(68\%\) and \(95\%\) CL

Full size image
Fig. 9
figure 9

Plot showing the parametric plot of magnetic field B and black hole mass between \(68\%\) and \(95\%\) CL

Full size image
Fig. 10
figure 10

Plot showing the parametric plot of magnetic field B and black hole mass between \(68\%\) and \(95\%\) CL

Full size image

  • Microquasar GRS 1915+105

In this final case, we find within 1\(\sigma \) a black hole mass \(M/M _\odot =14.10^{+0.68}_{-1.35}\) along with \(r/M=6.45^{+0.43}_{-0.20}\). On the other hand, for the magnetic field we obtain \(B\sim 7.79 \times 10^{-30}\, m^{-1}\), or alternatively written in Gauss, \(B\sim 9.61 \times 10^{-7}\) Gauss. The parametric plot for this case can be found in Fig. 10.

6 Conclusions

The recent astrophysical data suggest that accretion discs play a key role in creating the QPOs around supermassive black holes and are the primary source for obtaining information about gravity and the nature of the geometry in the strong field regime as well as the existing fields surrounding such black holes [73]. The existing fields also play an important role in altering a particle’s geodesics, thus strongly influencing observable properties (the shadow, the ISCO, the QPOs, etc.). With this in view, the magnetic field is increasingly important in the dynamics of charged particles in the very close vicinity of black holes. Thus, it is worth studying the effect of magnetic fields on the particles moving in the discs around astrophysical black holes. In this paper we consider an interesting solution describing a static and spherically symmetric black hole that includes the additional gravity due to a non-linear coupling of the Schwarzschild black hole with Melvin’s magnetic universe [33]. For these reasons the study of the properties of such a solution is valuable.

In the present paper we have studied the dynamics of charged particles around the magnetized black hole known as the Ernst black hole. We have found that the radius of the ISCO for both neutral and charged test particles is strongly affected by the magnetic field, thus shrinking its values. The ISCO radius rapidly decreases for the charged test particles. This happens because the magnetic field reflects the combined effects of gravitational and Lorentz forces on the charged particles. Also we have shown that the epicyclic frequencies of particles moving around the black hole are significantly increased as a consequence of the effect of the magnetic field.

In the first part of this work, we presented the generic form of the epicyclic frequencies and selected three microquasars with known astrophysical QPO data to constrain the magnetic field. In all three cases, we found that the magnetic field is of the order of magnitude \(B\sim 10^{-7}\) Gauss. It is interesting to note that here we have identified the upper frequency with \(\nu _r\) and the lower frequency with \(\nu _{\theta }\) to explain the QPOs. Generally, when the rotation is introduced, scientists in most cases in this resonance model identify the upper frequency with \(\nu _{\theta }\) and lower frequency with \(\nu _r\). This suggests that the Ernst metric due to the magnetic field effect which has a backreaction effect on the spacetime can mimic the rotation of the black hole to some extent. This is explained from the fact that when the backreaction effect is considered, the spherical symmetry is broken and this leads to very interesting results which can be important from a phenomenological point of view. Finally, we note that a more realistic estimation of the value of the magnetic parameter should include the particle charge. In that case, one must specify the particle; for example, it could be an electron, proton or ionized atom having specific q/m. Introducing a quantity \(c^4/(GM q/m)\), for electrons we obtain a typical factor of \(10^2\), which may suggest an increase in the magnetic field to the magnitude \(B\sim 10^{-5}\) Gauss, which is consistent with the result found in [74, 75].

Interestingly, it turns out that the magnetized Reissner–Nordström black hole solution causes axially symmetric spacetime that is regarded as an analogue of the rotating Ernst spacetime as a consequence of the presence of magnetic field parameter B, thereby mimicking the black hole rotation parameter a/M [42]. With this in mind, one could therefore consider the possible extensions of recent analysis to the case of axially symmetric magnetized black hole spacetime to constrain its parameters, which we intend to investigate next in a separate work.