1 Introduction

The spacetime geometry of Reissner–Nordström black holes (RN BH) is an asymptotically flat, static solution of the Einstein–Maxwell equations, describing a non-rotational, charged spherical BHs and/or naked singularities [1]. These spacetimes define gravitational source comprise both magnetic, and electric charges. For the first time, these spacetimes were introduced by Plebanski and Demianski [2], a while later revisited by Griffiths and Podolský in Ref. [3]. Theoretically, they outline stars or BHs and can additionally be described by acceleration, angular momentum, the NUT charge, and a cosmological constant. The authors of Ref. [4] established a higher dimensional concept of the RN BH. Besides, Turimov et al. [5] investigated test particle dynamics and curvature structure near BHs in the Einstein–Maxwell-scalar (EMS) theory.

The existence of magnetic fields has an extremely solid impact on charged matter and on the process of accretion. It is well known that BHs have an accretion disk inaugurated due to a conducting plasma and its dynamics can originate uniform magnetic field. In the scenario of Keplerian accretion disks [6], the role of local magnetic fields is much essential to the accretion’s viscosity mechanism because of the magnetorotational instability [7]. The electromagnetic field of a BH could possess an inner origin, hence charged particle motion becomes entirely regular in the background of Kerr–Newman BH [8]. Eatough et al. [9] found that the existence of strong magnetic fields near supermassive BH in the Galaxy center encounters no connection with the accretion disk. Kološ et al. [10] deduced that BHs can be immersed in external magnetic fields comprising complicated nature near horizons. BHs on the equatorial plane of a magnetar can be immersed in a homogeneous magnetic field if the magnetar is situated at an enough far distance [11, 12].

Particle dynamics around BHs are of ample interest and can be used to investigate BH’s physical properties, previously explored by numerous researchers [13,14,15,16,17,18,19,20]. The analytical, as well as numerical solution of geodesics equation, can be obtained. They can dispatch important information and reveal the prolific formation of background geometry. Hagihara [21] initiated the analytical solution of geodesics. Grunau and Kagramanova [1] by considering the RN spacetime studied analytical solutions of magnetically and electrically charged test particles. Chandrasekhar [22] was among the pioneers who investigate the geodesics in the spacetime of Schwarzschild, RN, and Kerr BHs. The circular geodesics can also be used to understand and explore BH’s quasinormal modes [23]. One can easily integrate and separate the electrically charged particle motion [24], which has been widely explored by many researchers [25,26,27,28,29]. Particles collision in ergoregion and the motion of particles are respectively investigated in the braneworld Kerr and Kerr–Newman–Kasuya BHs [20, 30, 31]. Recently, by studying the RN spacetime, it is found that both the external magnetic field and electric charge mimic BH’s magnetic charge [32].

The study of the dynamics of test magnetized particle motion around compact gravitational objects is one of the most important specific issues in relativistic astrophysics to testing gravity theories in both strong and weak limits. This might also be useful to discover novel techniques for understanding gravitational and electromagnetic interactions in the strong and weak field regimes. For the first time, motion of magnetized particles around Schwarzschild and rotating Kerr BHs immersed in external asymptotically uniform external magnetic fields have been investigated by de Felice and Sorge in Refs. [33, 34]. In past years, several studies investigated the characteristics of electromagnetic fields and their impact on the magnetized particles’ dynamics in various gravity theories [35,36,37,38,39,40]. Recently, Bokhari et al. investigated the influence of test magnetized particles on deformed electrically and magnetically charged RN BH [41]. Additionally, Refs. [42, 43] have been studied the effect of modified gravity (MOG) and \(\gamma \)-spacetime on the magnetized particle dynamics.

In this work, we use signature \((-,+,+,+)\) for the space-time and geometrized unit system \(G_\mathrm{N}= c = 1\). The Latin indices run from 1 to, 3 and the Greek ones from 0 to 3. In Sect. 2, we will revisit BH’s spacetime geometry. In Sect. 3, our main focus will be to investigate magnetized particle motion in EMS theory. Section 4, will explore some astrophysical applications of the said BH. Section 5, is devoted to the explorations of the center of mass energy in collisions of magnetized and electrically charged particles around the magnetically and electrically charged BHs. Finally, in Sect. 6, we discuss all the obtained results and findings with concluding remarks.

2 Static BHs in Einstein–Maxwell-scalar theory

The spacetime around an electrically charged BH in EMS gravity having total mass M and electric charge Q describes by the following metric using spherical coordinates [44]:

$$\begin{aligned} ds^2=-U(r)dt^2+\frac{dr^2}{U(r)}+f(r)\left( d\theta ^2+\sin ^2\theta d\varphi ^2\right) , \end{aligned}$$
(1)

where the radial metric function is

$$\begin{aligned} U(r)=1-\frac{2M}{r}-\frac{\lambda }{3}f(r)+\frac{\beta Q^2}{f(r)}, \end{aligned}$$
(2)

with

$$\begin{aligned} f(r)=r^2\left( 1+\frac{\gamma Q^2}{Mr}\right) . \end{aligned}$$
(3)

Here the dimensionless parameters \(\beta \) and \(\gamma \) come from the EMS theory. Moreover, the \(\lambda \) parameter corresponds to the cosmological constant (\(\lambda >0\) for de Sitter and \(\lambda <0\) for anti-de Sitter spacetime). The metric (2) turns to Schwarzschild BH for, \(\lambda =\beta =0\) and it reflects RN BH spacetime when \(\lambda =\gamma =0\) and \(\beta =1\). In this work, we will consider the case \(\lambda =0\).

Non-zero component of the electromagnetic four potentials is

$$\begin{aligned} A_t = \frac{Q}{r}\left[ \gamma -\frac{\beta }{2}\left( 1+\frac{rQ}{f(r)}\right) \right] . \end{aligned}$$
(4)
Fig. 1
figure 1

Graphical behaviour of the event horizon radius is a function of the parameter \(\gamma \) for the different values of the parameter \(\beta \)

Full size image

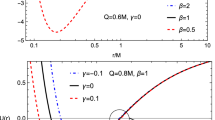
In Fig. 1, we demonstrate the dependence of radius of event horizons from the BH charge at zero (top left panel), positive (top right panel) and negative (bottom panel) values of parameter \(\gamma \) for the different values of the parameter \(\beta \). It is seen that the critical value of the charge Q increases with an increase of the parameter \(\beta \). when \(\gamma =0\) the minimum of outer horizon corresponding the critical value of the BH charge, while positive (negative) values of \(\beta \) cause to increase (decrease) of the minimum value of the outer horizon.

Next, we briefly describe the analyses of the minimum radius of the outer horizon. We can find extreme values of the BH charge and outer horizon using the following simple conditions:

$$\begin{aligned} U(r)=U'(r)=0. \end{aligned}$$
(5)

Due to the complicated form of Eq. (5), below, we provide an analysis of the solution graphically.

Fig. 2
figure 2

The minimum radius of the outer horizon as a function of the critical BH charge \(Q_\mathrm{cr}\), at the corresponding upper values of the parameter \(\gamma \) for different values of the parameter \(\beta \)

Full size image

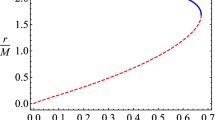
In Fig. 2, we present the dependence of minimum values of the outer horizon from critical values of the BH charge corresponding to the maximum values of \(\gamma \) for the different values of the parameter \(\beta \). It is seen from the figure that the minimum radius of the outer horizon has a linearly decreasing function of the critical BH charge, and its decreasing rate is proportional to the parameter \(\beta \).

Fig. 3
figure 3

Critic values of BH charge and minimal radius of the event horizon, as a function of the parameter \(\gamma \) for different values of the parameter \(\beta \)

Full size image

In Fig. 3, we show minimum values of the event outer horizon of the extremely charged EMS BH (left panel) and the extreme charge of the BH (right panel) as a function of the parameter \(\gamma \) for different values of the parameter \(\beta \). Our numerical analysis shows that for all possible values of parameter \(\beta \) the limits of the event horizon radius

$$\begin{aligned} \lim _{\gamma \rightarrow \infty } \left\{ (r_h)_\mathrm{min}, Q_{\mathrm{extr}}\right\} =\{2M,0\}, \end{aligned}$$
(6)

and,

$$\begin{aligned} \lim _{\gamma \rightarrow \gamma _{\mathrm{max}}} \left\{ (r_h)_\mathrm{min}, Q_{\mathrm{extr}}\right\} =\{0,Q_{\mathrm{extr}}\}. \end{aligned}$$
(7)

The upper value of \(\gamma _{\mathrm{max}}\) (\(Q_{\mathrm{extr}}\)) increases (decreases) as the \(\beta \) parameter increases (decreases). Below, we will show them in table form. From Table 1, one can clearly understand the relation between \(Q_{\mathrm{extr}}\), \(\gamma _{\mathrm{max}}\) and \(\beta \). Analytically, it can be expressed as

$$\begin{aligned} \gamma _{\mathrm{max}}=\frac{\beta }{2}, \quad Q_{\mathrm{extr}}=\frac{2}{\sqrt{\beta }} . \end{aligned}$$
(8)
Table 1 The extreme BH charge and maximum value of \(\gamma \) for different values of the parameter \(\beta \)
Full size table

3 Magnetic fields around in Einstein–Maxwell-scalar theory

In fact, the EMS BH spacetime is a Ricci flat out of the inner horizon [5] and on the other hand, the BH charge does not generate magnetic fields in the spacetime around the static BH with respect to a proper observer. Thus, no electromagnetic forces act on the magnetized particles by electrostatic field around the BH in EMS theory and the effect of electric charge of the BH can only be geometrically in the spacetime. In other words, in the above considerations, i.e. when an electrically charged EMS BH is immersed in an external asymptotically uniform magnetic field and one may use the Wald method [45]. Consequently, we have the electromagnetic four-potential corresponding to the magnetic field around BH in the following form

$$\begin{aligned} A_{\phi }= & {} \frac{1}{2}B_0f(r)\sin ^2\theta , \end{aligned}$$
(9)

where \(B_0\) is the asymptotic value of the external uniform magnetic field measured by the proper observer. One may easily calculate the non-zero components of the electromagnetic tensor using the definition \(F_{\mu \nu }=A_{\nu ,\mu }-A_{\mu ,\nu }\) in the form

$$\begin{aligned} F_{r \phi }= & {} B_0\left[ r+\frac{\gamma Q^2}{2 M}\right] \sin ^2\theta , \end{aligned}$$
(10)
$$\begin{aligned} F_{\theta \phi }= & {} B_0f(r)\sin \theta \cos \theta , \end{aligned}$$
(11)
$$\begin{aligned} F_{rt}= & {} \frac{Q}{r^2} \left\{ \frac{\beta }{2} \left[ 1+\frac{2Q}{rf(r)}\left( 1-\frac{Q^2r}{Mf(r)}\right) \right] -\gamma \right\} . \end{aligned}$$
(12)

Non-zero components of the external magnetic fields around an electrically charged BH in EMS theory, measured in the frame of reference where the proper observer is located, are expressed as

$$\begin{aligned} B^{\alpha } = \frac{1}{2} \eta ^{\alpha \beta \sigma \mu } F_{\beta \sigma } w_{\mu }, \end{aligned}$$
(13)

where the four-velocity of the proper observer is denoted by \(w_{\mu }\). Furthermore, \(\eta _{\alpha \beta \sigma \gamma }\) represents the pseudo-tensorial form of the Levi-Civita symbol \(\epsilon _{\alpha \beta \sigma \gamma }\) with the following mathematical expressions,

$$\begin{aligned} \eta _{\alpha \beta \sigma \gamma } = \sqrt{-g}\epsilon _{\alpha \beta \sigma \gamma }, \quad \eta ^{\alpha \beta \sigma \gamma } = -\frac{1}{\sqrt{-g}}\epsilon ^{\alpha \beta \sigma \gamma }. \end{aligned}$$
(14)

Here g is for spacetime metric (1) with \(g=-f(r)^2\sin ^2\theta \). The Levi-Civita symbol is \(\epsilon _{0123}=1\) with even permutations, and for odd permutations, it is \(-1\).

$$\begin{aligned} B^{\hat{r}}=B_0 \cos \theta , \ B^{\hat{\theta }}=\sqrt{\frac{U(r)}{f(r)}}B_0\left( r+\frac{\gamma Q^2}{2 M}\right) \sin \theta . \end{aligned}$$
(15)
Fig. 4
figure 4

Magnetic field lines around an EMS BH for different values of the parameter \(\gamma \). Here we fixed BH charge at \(Q/M=0.8\) and take \(\beta =1\)

Full size image

The features of external magnetic field lines around EMS BHs are presented in Fig. 4 for different values of the parameter \(\gamma \) at \(Q=0.8\). It is seen that when \(\gamma =0\) the magnetic field is uniform and for negative and positive values of \(\gamma \) the field is parabolic and hyperbolic like, respectively.

Fig. 5
figure 5

Orthonormal angular component of the magnetic field around EMS BHs for different values of the parameters \(\gamma \) and \(\beta \). Here we fixed the BH charge as \(Q/M=0.8\)

Full size image

In Fig. 5 we demonstrate the radial dependence of normalized values of the angular component of an external magnetic field around the EMS BH to its asymptotic values, for different values of parameters \(\gamma \) and \(\beta \). It is observed from the figure that the angular component shows decreasing behaviour with respect to increasing the \(\gamma \) parameter. A similar pattern can also be seen for the case of the \(\beta \) parameter as well.

3.1 Equation of motion for magnetized particles

In this subsection, we consider the motion of magnetized particles with mass m, around the electrically charged EMS BH immersed in an external asymptotically uniform magnetic field. The equation for the motion of magnetized particles describes by the following Hamilton–Jacobi equation (see [33, 46,47,48,49])

$$\begin{aligned} g^{\mu \nu }\frac{\partial {{\mathcal {S}}}}{\partial x^{\mu }} \frac{\partial {{\mathcal {S}}}}{\partial x^{\nu }}=-\Bigg (m-\frac{1}{2} D^{\mu \nu }F_{\mu \nu }\Bigg )^2, \end{aligned}$$
(16)

where \({{\mathcal {S}}}\) is an action for the magnetized particle, and \(D^{\mu \nu }F_{\mu \nu }\) is the product of polarization (\(D^{\mu \nu }\)) and electromagnetic field tensors reflecting the interaction between the external and proper magnetic field of magnetized particles with dipole moment. The polarization tensor correspond to the magnetic dipole moment of the magnetized particles, and it describes by the following relation [33]:

$$\begin{aligned} D^{\alpha \beta }=\eta ^{\alpha \beta \sigma \nu }u_{\sigma }\mu _{\nu } , \qquad D^{\alpha \beta }u_{\beta }=0, \end{aligned}$$
(17)

where \(\mu ^{\nu }\) and \(u^{\nu }\) are the four-vector of magnetic dipole moment and four-velocity of magnetized particles by the fiducial comoving observer. The electromagnetic field tensor can be decomposed through \(F_{\alpha \beta }\) by electric \(E_{\alpha }\) and magnetic \(B^{\alpha }\) field components as

$$\begin{aligned} F_{\alpha \beta }=u_{[\alpha }E_{\beta ]}-\eta _{\alpha \beta \sigma \gamma }u^{\sigma }B^{\gamma }. \end{aligned}$$
(18)

One can find the product of polarization and electromagnetic tensors taking into account the condition given in Eq. (17) as

$$\begin{aligned} D^{\mu \nu }F_{\mu \nu }=2\mu ^{\hat{\nu }}B_{\hat{\nu }}=\mu B_0 \mathcal {B}(r). \end{aligned}$$
(19)

Here \(\mu ^2=\mu _{\hat{i}}\mu ^{\hat{i}}\) is the norm of the dipole magnetic moment of magnetized particles and

$$\begin{aligned} \mathcal {B}(r)=\sqrt{\frac{U(r)}{f(r)}}\left( r+\frac{\gamma Q^2}{2 M}\right) . \end{aligned}$$
(20)

To investigate the equatorial motion of dipolar magnetized particles in circular orbits around an electrically charged BH in Einstein–Maxwell-scalar theory, we use the following action for the motion of magnetized particles in the equatorial plane around the BH which describes in the form

$$\begin{aligned} {{\mathcal {S}}}=-Et+L\phi +{{\mathcal {S}}}_r, \end{aligned}$$
(21)

that allow variables separation of the Hamilton–Jacobi equation. The equation for radial motion of magnetized particles can be found as

$$\begin{aligned} \dot{r}^2={{\mathcal {E}}}^2-V_\mathrm{eff}(r;{{\mathcal {L}}}), \end{aligned}$$
(22)

where the effective potential for the radial motion of magnetized particles has the following form:

$$\begin{aligned} V_\mathrm{eff}(r; b )=U(r)\left( \left[ 1-b {{\mathcal {B}}}(r)\right] ^2+\frac{{{\mathcal {L}}}^2}{f(r)}\right) . \end{aligned}$$
(23)

In the above equation, \({{\mathcal {L}}}=L/m\) is the specific angular momentum of magnetized particles and \(b = \mu B_0/m\) is the magnetic interaction parameter responsible for the interaction between the dipole moment of magnetized particles and the external magnetic field. On the other hand, the effective potential is also a function of the parameters \(Q,\beta ,\gamma ,\) and \(\lambda \).

In real astrophysical cases, when exploring the dynamics of a neutron star with the magnetic dipole moment \(\mu =(1/2)B_\mathrm{NS}R_\mathrm{NS}^3\), is treated as a magnetized particle, orbiting around an SMBH at the center of a galaxy to be as EMS BH. In the presence of the external magnetic fields around the EMS SMBH, the magnetic coupling parameter b can be expressed in the following form, including the parameters of the neutron star and the external magnetic field value around the SMBH,

$$\begin{aligned} b =\frac{B_\mathrm{NS}R_\mathrm{NS}^3B_\mathrm{ext}}{m_\mathrm{NS}}\simeq & {} \frac{\pi }{10^3}\left( \frac{B_\mathrm{NS}}{10^{12}\mathrm G}\right) \left( \frac{B_\mathrm{ext}}{10\mathrm G}\right) \nonumber \\&\times \left( \frac{R_\mathrm{NS}}{10^6\mathrm cm}\right) ^3\left( \frac{m_\mathrm{NS}}{1.4 M_{\odot }}\right) ^{-1} . \end{aligned}$$
(24)
Fig. 6
figure 6

Radial dependence of effective potential for the radial motion of magnetized particles around electrically charged BHs in EMS theory immersed in an external magnetic field at various values of the parameters \(\gamma , \beta \) and b

Full size image

We show radial dependence of the effective potential of radial motion of test magnetized and neutral particles around electrically charged EMS BH in Fig. 6 by varying \(\gamma , \beta \), and b parameters. It is assumed that the BH is immersed in an external asymptotically uniform magnetic field and the BH charge is \(Q/M=1.2\) and angular momentum is taken as \({{\mathcal {L}}}^2/M^2=19\). It can be observed that in the absence of the external magnetic field and/or magnetic moment of the particle, the maximum in the effective potential increase as the parameter \(\beta \) increase, while the orbits where the effective potential takes the maximum shifts towards the central BH, meanwhile, positive values of \(\gamma \) cause a decrease in the maximum. it is also seen that at the distances about \(\sim 10M\) from the BH, the effects of EMS parameters weakens, being almost the same as it is around the Schwarzschild BH. However, the magnetic interaction forces to decrease the effective potential everywhere.

The stability of circular orbits of test particles around axially symmetric BHs can be described using the following general condition:

$$\begin{aligned} \partial _r V_\mathrm{eff}(r;{{\mathcal {L}}})=0. \end{aligned}$$
(25)

The possible values of the angular momentum of the magnetized corresponding to stable circular orbits around the BHs can be found using the solution of Eq. (25) and we get,

$$\begin{aligned} {{\mathcal {L}}}^2= & {} \frac{f(r)^2 \left[ 1-b \mathcal {B}(r)\right] }{f(r) U'(r)-U(r) f'(r)}\nonumber \\&\times \left\{ 2 b U(r) \mathcal {B}'(r)-[1-b \mathcal {B}(r)] U'(r)\right\} . \end{aligned}$$
(26)

Immediately, one may obtain the energy of the particles at the orbits by omitting Eq. (26) into Eq. (23) as (Fig. 7),

$$\begin{aligned} {{\mathcal {E}}}^2= & {} \frac{U(r)^2 [1-b \mathcal {B}(r)] }{f(r) U'(r)-U(r) f'(r)}\nonumber \\&\times \left\{ 2 b f(r) \mathcal {B}'(r)-[1-b \mathcal {B}(r)] f'(r)\right\} . \end{aligned}$$
(27)
Fig. 7
figure 7

Radial profiles of specific energy (left panel) and angular momentum (right panel) correspond to circular orbits of test neutral and magnetized particles around EMS BHs for the different values of parameters \(\beta , \gamma \) and \(\beta \). In both plots, we chose the BH charge as \(Q/M=1.2\)

Full size image

Figure 7 demonstrates radial dependence of specific angular momentum and energy of test magnetized particles along circular stable orbits around charged EMS BHs. It is seen from this figure by the comparisons of grey, black-dotted and blue dot-dashed lines which correspond to test neutral particles, the existence of BH charge and increase of the parameter \(\beta \) cause decrease in the minimal values of both energy and angular momentum, while the non-zero and positive values of the parameter \(\gamma \) force to increase it. However, at larger distances from the BH, the EMS parameters and BH charge effects on the energy and angular momentum almost vanish. Moreover, in the presence of magnetic dipole moment of particles and/or the external magnetic field, i.e. the magnetic interaction, the values of the energy and angular momentum sufficiently decrease even as far from the central objects.

In order to find the radius of innermost stable circular orbits’ (ISCOs) of magnetized particles around electrically charged EMS BHs in the presence of the external magnetic field can be found using the general condition \(\partial _{rr}V_\mathrm{eff} (r;{{\mathcal {L}}})\). Here, we use Eq. (26) as the particle’s angular momentum \({{\mathcal {L}}}\). After some algebraic calculations, one can immediately obtain the following large equation that can help to find the ISCO radius:

$$\begin{aligned}&2 U(r) \left[ 1-b \mathcal {B}(r)\right] f'(r)^2 \Big [2 b U(r) \mathcal {B}'(r)+\left[ 1-b \mathcal {B}(r)\right] \nonumber \\&\quad \times U'(r)\Big ]+f(r)\Big (2 b U(r)^2 \Big \{(b \mathcal {B}(r)-1) \mathcal {B}'(r) f''(r)\nonumber \\&\quad +f'(r) \Big \{ \mathcal {B}''(r)-b \Big [ \mathcal {B}(r) \mathcal {B}''(r)+ \mathcal {B}'(r)^2\Big ]\Big \}\Big )\nonumber \\&\quad +2 \left[ 1-b \mathcal {B}(r)\right] ^2 f'(r) U'(r)^2+U(r) \left[ 1-b \mathcal {B}(r)\right] ^2 \nonumber \\&\quad \times \left[ f''(r) U'(r)-f'(r) U''(r)\right] \Big \}+2 b f(r)^2 \nonumber \\&\quad \times \Big \{2 (b \mathcal {B}(r)-1) \mathcal {B}'(r) U'(r)^2 +U(r) \Big [\left[ 1-b \mathcal {B}(r)\right] \mathcal {B}'(r) \nonumber \\&\quad \times U''(r)+U'(r) \left( \left[ 1-b \mathcal {B}(r)\right] \mathcal {B}''(r)+b \mathcal {B}'(r)^2\right) \Big ]\Big \} \ge 0.\nonumber \\ \end{aligned}$$
(28)

In fact, it is seen from Eq. (28) that to have an analytical solution of Eq. (28) with respect to radial coordinate is quite hard, even impossible, due to its complicated form. For this reason, to see the effects of EMS parameters and BH charge on the ISCO radius of test magnetized particles, we have included a graphical analysis below.

Fig. 8
figure 8

ISCO radius of magnetized particles around EMS BHs as a function of electric charge of the BH for different values of parameters \(\beta , \gamma \) and b

Full size image

In Fig. 8, we illustrate how the ISCO radius of magnetized and test particles in the spacetime around electrically charged BH in EMS gravity varies with the BH charge for different EMS theory parameters. The figure shows that when the parameter \(\gamma \) increases, the minimum of ISCO decreases due to the decrease of the extreme charge of the BH, but the existence of an external magnetic field causes the ISCO radius to rise.

4 Magnetized particles motion around magnetically charged BHs in Einstein–Maxwell-scalar theory

The electromagnetic four-potential of the electromagnetic field around magnetically charged BHs describes as

$$\begin{aligned} A_{\phi }= & {} Q_{m}\cos \theta . \end{aligned}$$
(29)

Using the potential in Eq. (29) one may immediately obtain the non-zero component of the electromagnetic field tensor as

$$\begin{aligned} F_{\theta \phi }=-Q_m \sin \theta . \end{aligned}$$
(30)

The orthonormal radial component of the magnetic field is generated by the magnetic charge of the BH

$$\begin{aligned} B^{\hat{r}}=\frac{Q_m}{f(r)}. \end{aligned}$$
(31)

Equation (31) implies that the radial component of the magnetic field around magnetically charged BHs is not affected by the spacetime curvature, and it looks its standard Newtonian expression.

In dynamics of the magnetized particle around magnetically charged BH in EMS. We generally assume (a) the direction of the magnetic dipole moment of the particle must be always parallel to the equatorial plane and the proper magnetic field of the EMS BH, (b) magnetic dipole components have to be in the following form: \(\mu ^{i}=(\mu ^{r},0,0)\). We note that other configurations can not provide stable equilibrium in the motion of magnetized particles. The fact is that, in equilibrium energetic states, the energy of the magnetic interactions take its minimum and magnetic field lines and the dipole moment directions become the same. Moreover, (c) using the second part of the condition (17) one may study the motion of magnetized particles in the proper observer frame of references. Choosing this frame of reference helps to avoid the problem of finding the observer’s velocity due to the relative motion. Finally, (d) we assume the magnetic moment to be constant. Consequently, we rewrite the interaction taking into account Eqs. (19) and (30) in the following form

$$\begin{aligned} {{\mathcal {D}}}^{\alpha \beta }F_{\alpha \beta } = \mu ^{\hat{r}} B_{\hat{r}}. \end{aligned}$$
(32)

Since the axial symmetric configuration of the proper magnetic field of the BH in EMS theory does not break the spacetime symmetries, therefore, one can still consider the particle’s energy \(p_t = -E\) and angular momentum \(p_{\phi }= l\) are conserved quantities. The radial motion of a magnetized particle around a magnetically charged EMS BH at the equatorial plane, where \(\theta =\pi /2\), with \(p_{\theta }=0\), using (19), (16) and the action (21) takes the following form

$$\begin{aligned} \dot{r}^2={{\mathcal {E}}}^2-V_\mathrm{eff}(r;l,\tilde{{{\mathcal {B}}}}), \end{aligned}$$
(33)

where the effective potential has the form

$$\begin{aligned} V_\mathrm{eff}(r;l,\tilde{{{\mathcal {B}}}})=U(r)\left[ \left( 1-\frac{\tilde{\mathcal {B}}}{f(r)} \right) ^2+\frac{{{\mathcal {L}}}^2}{f(r)}\right] . \end{aligned}$$
(34)

In the above Eq. (34), \(\tilde{{{\mathcal {B}}}} =\mu Q_m/m\) is a parameter corresponding to magnetic interaction between magnetic fields of the magnetic dipole and magnetically charged BH. Additionally, we denote the parameter \({{\mathcal {B}}}=\mu /(m M)\) characterizing magnetic dipole moment and mass of the magnetized particle and mass of the central BH. One can easily see that the parameter \({\mathcal {B}}\) is positive, and it is for the system of a neutron star orbiting around an SMBH, treating neutron stars as magnetized particles have the form,

$$\begin{aligned} {{\mathcal {B}}}= & {} \frac{B_\mathrm{NS}R_\mathrm{NS}^3}{2m_\mathrm{NS}M_\mathrm{SMBH}}\nonumber \\\simeq & {} 0.18 \left( \frac{B_\mathrm{NS}}{10^{12}\mathrm G}\right) \left( \frac{R_\mathrm{NS}}{10^6 \mathrm cm}\right) ^3\left( \frac{m_\mathrm{NS}}{M_{\odot }}\right) ^{-1}\left( \frac{M_\mathrm{SMBH}}{10^6M_{\odot }}\right) ^{-1}.\nonumber \\ \end{aligned}$$
(35)

Here, we evaluate the approximate value of the parameter \({{\mathcal {B}}}\), using data from real astrophysical observations of the system of magnetar called SGR (PSR) J1745–2900 (\(\mu \simeq 1.6\times 10^{32} \mathrm G\cdot cm^3\) and \(m \approx 1.4 M_{\odot }\)) orbiting SMBH Sgr A* (\(M \simeq 3.8 \times 10^6M_{\odot }\)) [50] is \( {{\mathcal {B}}}\approx 10.2\) .

The circular stable orbits of particles around a central object are defined by the following conditions:

$$\begin{aligned} V_\mathrm{eff}'=0, V_\mathrm{eff}'' \ge 0. \end{aligned}$$
(36)

Specific angular momentum and energy of the magnetized particle along the circular orbits can be expressed by the following expressions,

$$\begin{aligned} {{\mathcal {L}}}^2= & {} \frac{f(r)-\tilde{{{\mathcal {B}}}}}{f(r) \left( U'(r) f(r)-f'(r) U(r)\right) } \nonumber \\&\times \left[ 2 \tilde{{{\mathcal {B}}}} U(r)f'(r)-f(r) \left( f(r)-\tilde{{{\mathcal {B}}}}\right) U'(r)\right] , \end{aligned}$$
(37)
$$\begin{aligned} {{\mathcal {E}}}^2= & {} \frac{\left( f^2(r)-\tilde{{{\mathcal {B}}}}^2\right) U(r)f'(r)}{f^2(r) \left( U'(r) f(r)-f'(r) U(r)\right) }. \end{aligned}$$
(38)
Fig. 9
figure 9

Radial dependence of specific angular momentum (at left) and energy (at right) correspond to the circular orbits of the magnetized particles around magnetically charged BHs in EMS theory for different values of the parameters \(\beta , \gamma \) and \({{\mathcal {B}}}\)

Full size image

Figure 9 demonstrates radial dependence of specific angular momentum and energy of magnetized particles at their circular stable orbits around magnetically charged EMS BH. In this figure, we show the relationship for the different values of the parameter \(\beta =1/4\), 1/2. We also compare the ISCO radius of neutral and magnetized particles with \({{\mathcal {B}}}=5\) and 10. It is obtained that as the value of \(\beta \) grows, the minimum of both energy and angular momentum are decreased. While in the presence of \(\gamma \), the minimum and radius of the orbit increases where the minimums take place. However, in the presence of magnetic interaction, the orbital energy (angular momentum) of the magnetized particles sufficiently decrease (increase).

One can easily obtain the equation of ISCO taking into account the conditions (36) for the effective potential (34) in the following form

$$\begin{aligned} 0\le & {} 2 f(r)^2 f'(r) U'(r)^2 \left[ f(r)^2-\tilde{\mathcal {B}}^2\right] -2 \tilde{\mathcal {B}}^2 U(r)^2 f'(r)^3 \nonumber \\&+f(r) U(r) \Bigg \{f(r) f'(r) U''(r) \left[ \tilde{\mathcal {B}}^2-f(r)^2\right] +U'(r)\nonumber \\&\times \Big [f(r) f''(r) \left( f(r)^2-\tilde{\mathcal {B}}^2\right) +f'(r)^2 \left( 4 \tilde{\mathcal {B}}^2-2 f(r)^2\right) \Big ]\Bigg \}.\nonumber \\ \end{aligned}$$
(39)

It is impossible to solve Eq. (39) analytically with respect to the radial coordinate, therefore, we analyse the ISCO graphically.

Fig. 10
figure 10

ISCO radii as a function of the magnetic charge of the EMS BH for the different values of parameters \(\beta , \gamma \) and \(\beta \)

Full size image

Figure 10 depicts the relationship between the ISCO radius of magnetized particles around an EMS BH and the magnetic charge of the BH for various EMS and magnetic interaction parameters. The figure clearly shows that the ISCO radius lowers as the magnetic charge of the BH increases and that raising the parameters \(\beta \) and \({{\mathcal {B}}}\) causes a rise in the decreasing rate in the ISCO profiles. The positive values of the parameter, on the other hand, reduce the rate.

5 Magnetized particles collisions around magnetically and electrically charged BHs in Einstein–Maxwell-scalar theory

The mechanisms of energy extraction from rotating BHs are still one of the major issues in relativistic astrophysics. R. Penrose has first been introduced an energy extraction model from rotating Kerr BHs [51]. The model suggests that a particle comes to the region called the ergosphere, and decays by two particles. According to the scenario, one of these particles falls into the BH with negative energy and the other one goes away from the BH with an energy higher than the initial one. When the ergoregion vanishes, the energy released from the BH doesn’t happen by the above discussed mechanism. This process in the presence of an external magnetic field called the magnetic Penrose process (MPP) has been introduced by Wagh et al. [52] and later developed by N.Dadhich et al. [53]. Recently, Tursunov et al. [54] have first shown the role of an electric field of charged BHs in the Penrose process. Another scenario for the energy release process is studied by Banados–Silk–West explained by collisions of particles near the BH horizon. In this work, we will explore the collisions of particles around magnetically electrically charged BHs in EMS theory and study the behaviour of the center of mass energy. The energy of two colliding particles has the form

$$\begin{aligned} {{{\mathcal {E}}}}_{cm}^{2}=\frac{E_{cm}^{2}}{4m^{2}c^{4}}=1-g_{\alpha \beta }u_{1}^{\alpha } u_{2}^{\beta }. \end{aligned}$$
(40)

Where \(u_{i}^{\alpha }\) (\(i=1,2\)) is the four velocities of the particles relative to distance observer. We consider the collision occurs in the background of equatorial plane, where \(\theta =\pi /2\) and \(\dot{\theta }=0\) (\(p_\theta =0\)).

5.1 Collisions of magnetized particles

In this subsection, we investigate the magnetized particle’s collision in a magnetically charged BH environment. In the equatorial plane, the components of the four-velocity are expressed in the form

$$\begin{aligned} \dot{t}= & {} \frac{{{\mathcal {E}}}}{U(r)}, \end{aligned}$$
(41)
$$\begin{aligned} \dot{\phi }= & {} \frac{{{\mathcal {L}}}}{f(r)}, \end{aligned}$$
(42)
$$\begin{aligned} \dot{r}^{2}= & {} {{\mathcal {E}}}^2-U(r)\left[ \left( 1-{{\mathcal {B}}}\frac{M Q_m}{f(r)} \right) ^2+\frac{{{\mathcal {L}}}^2}{f(r)}\right] . \end{aligned}$$
(43)

Using the above equations the expression for the center of mass energy takes the following form

$$\begin{aligned} {{{\mathcal {E}}}}_{cm}^2= & {} 1-\frac{{{\mathcal {L}}}_1 {{\mathcal {L}}}_2}{f(r)}+\frac{{{\mathcal {E}}}_1 {{\mathcal {E}}}_2}{U(r)}-\frac{1}{U(r)} \nonumber \\&\times \sqrt{{{\mathcal {E}}}_1^2-U(r)\left[ \left( 1-{{\mathcal {B}}}_1 \frac{M Q_m}{f(r)}\right) ^2+\frac{{{\mathcal {L}}}_1^2}{f(r)}\right] } \nonumber \\&\times \sqrt{{{\mathcal {E}}}_2^2-U(r)\left[ \left( 1-{{\mathcal {B}}}_2 \frac{M Q_m}{f(r)}\right) ^2+\frac{{{\mathcal {L}}}_2^2}{f(r)}\right] }. \end{aligned}$$
(44)
Fig. 11
figure 11

Dependence of center of mass energy of two magnetized particles collision for different values of \(\beta \) and critical charge Q

Full size image

The radial dependence of the center of mass energy in the case of two colliding particles having the same positive dipole moment is shown in Fig. 11. Here we check the behaviour of the energy at \(\beta =0.25, 1, 1.5\) for different values of the parameter \(\gamma \), and near the corresponding critical values of the BH charge, \(Q_{cr}\). While plotting this figure, we chose \({{\mathcal {L}}}_1=-{{\mathcal {L}}}_2=2M\), and the same initial energies \({{\mathcal {E}}}_1={{\mathcal {E}}}_2=1\) and the magnetar PSRJ175-2900 orbiting \(SgrA^*\) is treated as a magnetized particle with \({{\mathcal {B}}}=10.2\) in all cases. It is observed from the figures that by increasing the value of \(\beta \), the peak value of the energy decreases. However, it increases by increasing the value of the parameter \(\gamma \).

5.2 Collisions of magnetized and electrically charged particle

In this case, we consider collisions of charged and magnetized particles. The four-velocity of the charged particle is obtained by using the following Lagrangian, as

$$\begin{aligned} L = \frac{1}{2} m g_{\mu \nu } u^\mu u^\nu + e u^\mu A_\mu , \end{aligned}$$
(45)

where e is the particle charge. Then the expressions of the energy and angular momentum are,

$$\begin{aligned} {{\mathcal {E}}} = mg_{tt}\dot{t},\quad {{\mathcal {L}}} = mg_{\phi \phi }\dot{\phi }+ e A_\phi , \end{aligned}$$
(46)

Consequently, expressions of the four-velocity for the charged particles in the equatorial plane take the following form

$$\begin{aligned} \dot{t}= & {} \frac{{{\mathcal {E}}}}{U(r)}, \end{aligned}$$
(47)
$$\begin{aligned} \dot{\phi }= & {} \frac{{{\mathcal {L}}}-{\mathcal {Q}}}{f(r)}, \end{aligned}$$
(48)
$$\begin{aligned} \dot{r}^{2}= & {} {{\mathcal {E}}}^2-U(r)\left[ 1+\frac{{{\mathcal {L}}}}{f(r)}({{\mathcal {L}}}-{\mathcal {Q}})\right] , \end{aligned}$$
(49)

where (\({{\mathcal {Q}}}=e Q_m/m\) stands for the interaction between the BH and particle charges. Thus, the expression of the collision energy takes the form,

$$\begin{aligned} {{{\mathcal {E}}}}_{cm}^2= & {} 1- \frac{{{\mathcal {L}}}_1-{\mathcal {Q}}}{f(r)}{{\mathcal {L}}}_2 + \frac{{{\mathcal {E}}}_1 {{\mathcal {E}}}_2}{U(r)} -\frac{1}{U(r)}\nonumber \\&\times \sqrt{{{\mathcal {E}}}_1^2-U(r)\left[ 1+\frac{{{\mathcal {L}}}_1}{f(r)}({{\mathcal {L}}}_1-{\mathcal {Q}})\right] }\nonumber \\&\times \sqrt{{{\mathcal {E}}}_2^2-U(r)\left[ \left( 1-{{\mathcal {B}}} \frac{M Q_m}{f(r)}\right) ^2+\frac{{{\mathcal {L}}}_2^2}{f(r)}\right] }. \end{aligned}$$
(50)
Fig. 12
figure 12

Dependence of center of mass energy of magnetized and charged particle collision with respect to \(\beta \) at the corresponding values of \(\gamma \) and critical charge

Full size image

Figure 12 shows the behaviour of center of mass energy in magnetized and positively charged particles’ collision around the charged BH in EMS theory. Similar to the previous case, these graphs are plotted for different values of parameter \(\beta \) and \(\gamma \) at a critical value of the BH charge. It can be easily seen from the figure that the energy shows decreasing behaviour upon increasing the value of parameter \(\gamma \). However, the energy possesses a slight increment in case of the increasing value of parameter \(\beta \). The result can be explained by the characteristic of the electromagnetic interaction between the BH with magnetic charge and the particles with an electrical charge being different.

5.3 Collision of magnetized and neutral particles

Finally, we explore the center of mass energy in the collision of the magnetized and neutral particle around magnetically charged RN BH in EMS theory. The equations of motion for neutral particles in the vicinity of a BH may be found in the following form:

$$\begin{aligned} \dot{t}= & {} \frac{{{\mathcal {E}}}}{U(r)}, \end{aligned}$$
(51)
$$\begin{aligned} \dot{\phi }= & {} \frac{{\mathcal {L}}}{f(r)}, \end{aligned}$$
(52)
$$\begin{aligned} \dot{r}^{2}= & {} {{\mathcal {E}}}^2-U(r)\left[ 1+\frac{{{\mathcal {L}}}^2}{f(r)}\right] . \end{aligned}$$
(53)

Similarly, using the above equations, the expression for the center of mass energy in case of magnetized and neutral particle collision can be obtained as

$$\begin{aligned} {{{\mathcal {E}}}}_{cm}^2= & {} 1- \frac{{{\mathcal {L}}}_1{{\mathcal {L}}}_2}{f(r)} + \frac{{{\mathcal {E}}}_1 {{\mathcal {E}}}_2}{U(r)} -\frac{1}{U(r)}\nonumber \\&\times \sqrt{{{\mathcal {E}}}_1^2-U(r)\left[ 1+\frac{{{\mathcal {L}}}_1^2}{f(r)}\right] }\nonumber \\&\times \sqrt{{{\mathcal {E}}}_2^2-U(r)\left[ \left( 1-{{\mathcal {B}}} \frac{M Q_m}{f(r)}\right) ^2+\frac{{{\mathcal {L}}}_2^2}{f(r)}\right] }. \end{aligned}$$
(54)
Fig. 13
figure 13

Dependence of center of mass energy of the magnetized and neutral particle collision with respect to \(\beta \), at the corresponding values of \(\gamma \) and critical charge

Full size image

In Fig. 13, we present the dependence of the center of mass energy of magnetized and neutral particle collision around EMS charged BHs with respect to \(\beta \) and \(\gamma \) at \(Q=Q_{cr}\) for \({{\mathcal {B}}}=10.2\) and \({{\mathcal {L}}}_1=-{{\mathcal {L}}}_2=2M\). From the figures, one can clearly observe the growth of the energy after increasing the values of parameter \(\beta \). The graphical representation of the collision of magnetized and neutral particles also shows that the center of mass energy decreases by increasing the parameter \(\gamma \).

5.4 Collisions of magnetized particles near electrically charged EMS BHs

Now we consider collisions of two magnetized particles, their collisions with electrically charged and neutral particles in the close environment of an electrically charged EMS BHs. WE assume that the BH is immersed in external asymptotically uniform magnetic fields in the proper frame of reference, and we consider the external magnetic field is a test field.

5.4.1 Two magnetized particles

Using the Hamilton–Jacobi equation one can obtain the four components of velocity as

$$\begin{aligned} \dot{t}= & {} \frac{{{\mathcal {E}}}}{U(r)}, \end{aligned}$$
(55)
$$\begin{aligned} \dot{\phi }= & {} \frac{{{\mathcal {L}}}}{f(r)}, \end{aligned}$$
(56)
$$\begin{aligned} \dot{r}^{2}= & {} {{\mathcal {E}}}^2-U(r)\left( \left[ 1-b B(r)\right] ^2+\frac{{{\mathcal {L}}}^2}{f(r)} \right) . \end{aligned}$$
(57)

Therefore, we have

$$\begin{aligned} {{{\mathcal {E}}}}_{cm}^2= & {} 1- \frac{{{\mathcal {L}}}_1 {{\mathcal {L}}}_2}{f(r)} + \frac{{{\mathcal {E}}}_1 {{\mathcal {E}}}_2}{U(r)} -\frac{1}{U(r)}\nonumber \\&\times \sqrt{{{\mathcal {E}}}_1^2-U(r)\left[ 1-b_1 B(r)+\frac{{{\mathcal {L}}}_1^2}{f(r)} \right] } \nonumber \\&\times \sqrt{{{\mathcal {E}}}_2^2-U(r)\left[ 1-b_2 B(r)+\frac{{{\mathcal {L}}}_2^2}{f(r)} \right] }. \end{aligned}$$
(58)
Fig. 14
figure 14

Dependence of center of mass energy of two magnetized particles with respect to \(\beta \) for different values of the magnetic parameter b, at the corresponding values of \(\gamma \) and critical charge

Full size image
Fig. 15
figure 15

Dependence of center of mass energy of the magnetized and charged particles with respect to the BH charge Q, for different values of the magnetic parameter b

Full size image
Fig. 16
figure 16

Dependence of center of mass energy of magnetized and neutral particles for the different values of the EMS parameters \(\gamma \) and \(\beta \)

Full size image

A graphical representation of the dependence of center of mass energy of two magnetized particles collision with respect to \(\gamma \) and \(\beta \) is shown in Fig. 14. Here, the graphs are plotted corresponding to the same direction of magnetic dipole moment. Here, we observe that the center of mass energy increases upon the increasing values of parameter \(\beta \). Similar behaviour of center of mass energy can be observed in the case of parameter \(\gamma \).

5.4.2 Magnetized and charged particle

Here, we study collisions of magnetized and electrically charged particles around electrically charged BH in EMS theory immersed in an external asymptotically uniform magnetic field. The four-velocity of a charged particle, with the charge e and mass m, can be described by the following form of Lagrangian for charged particles in the electromagnetic field:

$$\begin{aligned} L = \frac{1}{2} m g_{\mu \nu } u^\mu u^\nu + e u^\mu A_\mu . \end{aligned}$$
(59)

We find the four-velocity of the particle using the well-known Euler-Lagrange equation, in the following form:

$$\begin{aligned} \dot{t}= & {} \frac{{{\mathcal {E}}}}{U(r)}, \end{aligned}$$
(60)
$$\begin{aligned} \dot{\phi }= & {} \frac{{{\mathcal {L}}}}{f(r)}-\omega _B, \end{aligned}$$
(61)
$$\begin{aligned} \dot{r}^{2}= & {} \left( {{\mathcal {E}}}-\frac{e Q}{m r}\right) ^2-U(r)\left[ 1+\left( \frac{{{\mathcal {L}}}}{f(r)}-\omega _B r\right) ^2 \right] . \end{aligned}$$
(62)

Immediately, after small algebraic calculations, the expression for the center of mass energy finds as,

$$\begin{aligned} {{{\mathcal {E}}}}_{cm}^2= & {} 1- \left( \frac{{{\mathcal {L}}}_1}{f(r)}-\omega _B\right) {{\mathcal {L}}}_2 + \frac{{{\mathcal {E}}}_1 {{\mathcal {E}}}_2}{U(r)} -\frac{1}{U(r)}\nonumber \\&\times \sqrt{\left( {{\mathcal {E}}}_1-\frac{e Q}{m r}\right) ^2-U(r)\left[ 1+\left( \frac{{{\mathcal {L}}}_1}{f(r)}-\omega _B r\right) ^2 \right] }\nonumber \\&\times \sqrt{{{\mathcal {E}}}_2^2-U(r)\left( \left[ 1-b B(r)\right] ^2+\frac{{{\mathcal {L}}}_2^2}{f(r)} \right) }. \end{aligned}$$
(63)

Figure 15 presents the radial dependence of the center of mass energy in collisions of a magnetized and electrically charged particle with respect to parameter \(\gamma \). We have plotted graphs for three different cases of \(\beta \) and positive values of magnetic coupling and magnetic interaction parameter are taken as \(|\omega _B|=0.1\) as well as \(b=0.1\), respectively. It is seen from the result in this figure that the energy increases by increasing the value of parameter \(\beta \). However, the center of mass energy shows decrements upon increment in the value of the parameter \(\gamma \).

5.4.3 Magnetized and neutral particles

Finally, we investigate head-on collisions of particles with and without magnetic dipole moment near the EMS BH. In this case, the expression of the center of mass energy takes as,

$$\begin{aligned} {{\mathcal {E}}}_{cm}^2= & {} 1- \frac{{{\mathcal {L}}}_1{{\mathcal {L}}}_2}{f(r)} + \frac{{{\mathcal {E}}}_1 {{\mathcal {E}}}_2}{U(r)} -\frac{1}{U(r)}\nonumber \\&\times \sqrt{{{\mathcal {E}}}_1^2-U(r )\left( \left[ 1-b B(r)\right] ^2+\frac{{{\mathcal {L}}}_1^2}{f(r)} \right) } \nonumber \\&\times \sqrt{{{\mathcal {E}}}_2^2-U(r)\left[ 1+\frac{{{\mathcal {L}}}_2^2}{f(r)} \right] }. \end{aligned}$$
(64)

Graphical illustrations of the center of mass energy of collisions of neutral and magnetized particles are shown in Fig. 16 for the different values of the parameters \(\gamma \) and \(\beta \). It is also seen from the figure that the positive values of \(\gamma \) cause to increase the energy.

6 Conclusion

In the present paper, we have studied magnetized particles dynamics and collisions of the particles with electrically charged particles around both magnetically and electrically charged BHs in EMS theory, and the following main results are obtained:

  • maximum value of the \(\gamma \) parameter and extreme values of the BH charge are numerically found for different values of the \(\beta \) parameter.

  • studies on the magnetic field around the BH have shown that negative values of the parameter \(\gamma \) increase the angular component of the magnetic field measured by a distant observer.

  • it is obtained from the studies of the radial motion of magnetized particles around electrically charged particles EMS BHs immersed in an external asymptotically uniform magnetic field that the magnetic interaction cause to decrease the maximum value of the effective potential and minimum values of the energy and angular momentum of the magnetized particles corresponding to circular stable orbits;

  • the behaviour of ISCO radius on the BH charge has shown that as the parameter \(\beta \) increase the radius decreases more rapidly;

  • studying circular magnetized particles’ motion around magnetically charged EMS BHs, we assumed the magnetic must keep the direction of magnetic dipole moment radially along proper magnetic field lines of the BH. It is shown that the ISCO radius of the particle decreases faster as compared to the radius of test neutral particles. Moreover, the decreasing rate also increases at the higher values of the EMS parameters \(\beta \) and \(\gamma \);

  • we study the effects of EMS parameters in the center of mass energy of collisions of magnetized particles and charged particles around electrically and magnetically charged BHs, and show that positive (negative) values of the parameter \(\gamma \) increases (decreases) the energy in the collisions of magnetized particles with magnetized and electrically charged particles. However, it is vice-versa in the case of the collisions of charged and magnetized particles.