1 Introduction

Theories of gravity are fundamental in understanding the origins and development of our universe. They play a crucial role in investigating the conduct of celestial phenomena such as galaxies and stars, as well as the physics of dense gravitational objects such as neutron stars and black holes (BHs).

Recently, several independent tests and observations have shown that dark energy and dark matter dominate the Universe [1, 2]. Currently, there is no complete theoretical foundation to describe the behavior of such types of matter. The general theory of relativity (GR) presents fundamental problems, including singularities in certain solutions and inconsistencies with quantum field theory (QFT). Spacetime singularities challenge the fundamental principles of physics due to their infinite curvature. It is widely accepted in the scientific community that the singularity of a BH is a point of infinite density. The presence of singularities raises questions about the theory’s accuracy in extreme situations and calls for a more thorough explanation. The QFT accurately describes quantum particles, electromagnetic and strong nuclear forces, but not gravity. The unification of GR with QFT, known as quantum gravity, poses significant challenges. Integrating the discrete nature of quantum particles with GR’s spacetime framework poses conceptual and mathematical barriers in constructing a unified theory. To solve these concerns, GR has been modified, and alternative gravity theories have been introduced. The scalar–tensor–vector gravity (STVG) hypothesis developed by Moffat [3] is one of several efforts to improve and broaden Einstein’s theory of gravity. It may be seen as an alternative to GR in the current universe in the absence of dark matter. This theory uses scalar and massive vector fields to develop a unifying gravity theory called the MOG theory. Moffat [4] formulated the non-spinning and spinning BHs, respectively known as the Schwarzschild-MOG and Kerr-MOG BHs.

Magnetic fields around BHs affect the accretion and charged matter dynamics. The acceleration of a BH’s conducting plasma accretion disk may create a continuous magnetic field. Recent findings suggest that the correlation between the presence of an accretion disk and the proximity of a robust magnetic field to a supermassive BH in the galactic core is not supported [5]. The latest discovery by the Event Horizon Telescope team reveals that the net azimuthal linear polarization structure could be attributed to well-structured poloidal magnetic fields in the emission region [6]. Their finding also provides insights into the accretion disk, accretion rate, and magnetic field structures surrounding a supermassive BH in the M87 galaxy. Hence, BHs can experience the impact of an external magnetic field, resulting in the formation of an intricate configuration near the BH horizon.

However, as the distance from the BH increases, the magnetic field configuration changes to a simple and consistent structure [7]. In a study conducted by Kovar et al. [8], it was found that a BH can potentially coexist with a uniform magnetic field when positioned on the equatorial plane of a magnetar, provided that the magnetar is situated at a considerable distance. The investigation of both charged and chargeless particle dynamics has been the subject of multiple scholarly articles [9,10,11,12,13,14,15,16,17]. In a study by Konoplya [18], an analysis of the motion of particles surrounding a magnetized BH was performed. The findings revealed that the tidal charge significantly influences the mobility of both massive and massless particles. Studying the motion of charged particles around Kerr BH in split monopole magnetic fields, Khan and Chen [19] explored the location of stable circular orbits and observed that a positive magnetic field enhances the stability of the effective potential.

Collisions of particles near the horizon of a rotating and charged BH are an important and exciting phenomenon that may result in high-energy releases. As of now, several physical methods have been proposed for extracting energy from a BH. Roger Penrose [20] was one of the first to describe a simple process for collecting energy from BHs. Such processes related to the Penrose process have been examined by Piran et al. [21, 22]. Collisions, according to Banados, Silk, and West (BSW) [23], may produce an enormous amount of center-of-mass energy particles in the case of fast-revolving BHs. In an ideal setup, this kind of energy might exceed Planckian energy; hence, BHs could be identified as ultrahigh-energy colliders. Over the last few years, a significant amount of emphasis has been placed on investigating this issue [24,25,26,27,28,29,30,31,32,33,34,35,36,37]. Even when the spin or charge of the particles is taken into consideration, collisions near the revolving BH horizon produce arbitrarily large center-of-mass energy [38, 39]. This property is absent in the case of non-spinning BHs as long as collisions between particles sink into the BH from a large axial distance [40].

The goal of this research work is to explore the spinning BH magnetosphere in modified gravity with magnetic dipole moment near magnetized Kerr BH. In Sect. 2, we review the spacetime metric of Kerr-MOG BH. For the magnetization purpose, we consider an external asymptotically uniform magnetic field around our model. Section 3 of our article is devoted to the investigation of magnetized particle dynamics in the Kerr-MOG BH. In Sect. 4, by incorporating an external magnetic field, we study the collisions of the magnetized particles near Kerr-MOG BH. Lastly, in Sect. 5, we summarize our findings with concluding remarks. In this paper, use the geometric unit system and take \(G_N=c=1\).

2 Rotating Kerr-MOG BHs in external magnetic fields

In this section, we briefly review magnetic fields surrounded by Kerr-MOG BHs, which can be described in Boyer–Linquist coordinates as [4]

$$\begin{aligned} ds^{2}=g_{tt}dt^{2}+g_{rr}dr^{2}+g_{\theta \theta }d\theta ^{2}+g_{\phi \phi }d\phi ^{2}+2g_{t\phi }dtd\phi , \end{aligned}$$
(1)

where the metric components \(g_{\alpha \beta }\) are functions of the radial and angular coordinate, r and \(\theta \) in the following form

$$\begin{aligned} g_{tt}= & {} -\frac{\varDelta _{m}-a^{2}\sin ^{2}\theta }{\varSigma }, \,\ g_{rr}=\frac{\varSigma }{\varDelta _{m}}, \,\ g_{\theta \theta }=\varSigma , \\ g_{\phi \phi }= & {} \frac{\sin ^{2}\theta }{\varSigma }\left[ \left( r^{2}+a^{2}\right) ^{2}-\varDelta _{m}\,a^{2}\sin ^{2}\theta \right] , \\ g_{t\phi }= & {} \frac{a\sin ^{2}\theta }{\varSigma }\left[ \varDelta _{m}-\left( r^{2}+a^{2}\right) \right] . \end{aligned}$$

where

$$\begin{aligned} \varDelta _{m}= & {} r^{2}-2GMr+a^{2}+\alpha G_{N}GM^{2}, \\ \varSigma= & {} r^2+a^2\cos ^2{\theta }. \end{aligned}$$

Here, \(G=G_{N}\left( 1+\alpha \right) \) is the enhanced gravitational constant, M is the mass of the BH, and \(G_{N}\) is the gravitational Newtonian constant. The dimensionless parameter \(\alpha \) determines the gravitational field strength. For \(\alpha =0\) and \(a=0\), the Kerr-MOG BH reduces to the Kerr and Schwarzschild-MOG BH, respectively.

The BH horizon can be found using \(\varDelta _m(r)=0\), as \(r_\pm =(1+\alpha )M\pm \sqrt{(1+\alpha )M^2-a^2}\). One may see that the maximum of the BH spin must be \(a/M<\sqrt{(1+\alpha )}M\) and the corresponding minimum event horizon is \(r^h_{min}/M=1+\alpha \).

We suppose that the Kerr-MOG BH is chargeless and immersed in an external asymptotically uniform magnetic field, with asymptotic values B. One can find the electromagnetic four-vector potentials by setting timelike \(\xi _{(t)}^\alpha \) and spacelike \(\xi _{(\phi )}^\alpha \) axial Killing vectors, as obtained in Ref. [41]

$$\begin{aligned} A^\alpha= & {} aB\left[ 1-(1+\alpha )\alpha \frac{M^2}{2r^2}\sin ^2{\theta }\right] \xi _{(t)}^\alpha \nonumber \\{} & {} +\frac{B}{2}\left[ 1-(1+\alpha )\alpha \frac{M^2}{r^2}\right] \xi _{(\phi )}^\alpha . \end{aligned}$$
(2)

So, we have only two nonvanishing covariant components of the four-vector potential \(A_\alpha =g_{\alpha \beta }A^\beta \).

If we consider the induced charge relatively small, then using Eq. (2), we can write the electromagnetic tensor in the form,

$$\begin{aligned} F_{r\phi }=-B r\sin ^2{\theta }. \end{aligned}$$

Thus, as a consequence, we can find magnetic fields using the following expression:

$$\begin{aligned} B^\alpha =\frac{1}{2}\eta ^{\alpha \beta \sigma \gamma } F_{\sigma \gamma }u_\alpha , \end{aligned}$$
(3)

where, \(u_{\alpha }\) is the four-velocity of the proper observer, \(\eta _{\alpha \beta \sigma \gamma }\), is the pseudo-tensorial form of the Levi-Civita symbol, \(\eta ^{\alpha \beta \sigma \gamma }=-\frac{1}{\sqrt{-g}}\epsilon ^{\alpha \beta \sigma \gamma }\), where the Levi-Civita symbol \(\epsilon _{\alpha \beta \sigma \gamma }=1\) for even permutations and for odd ones, \(-1\) while the determinant of the metric is \(g=\left( g_{tt}g_{\phi \phi }-g^2_{t\phi } \right) g_{rr}g_{\theta \theta }\). The four-velocity satisfies the normalization condition \(u_\alpha u^\alpha =-1\). For ZAMO, \(u_t\ne 0\), we can write \(u_t=\frac{1}{\sqrt{-g^{tt}}}\). In addition, we have \(u^\alpha =g^{\alpha \beta }u_\beta \), and finally, we can find the corresponding four-velocities in the form

$$\begin{aligned} u^\alpha =\sqrt{-g^{tt}}\left( 1,0,0,-g^{t\phi }/g^{tt}\right) . \end{aligned}$$
(4)

The orthonormal \(\theta \) components of the magnetic field measured by ZAMO can be expressed using the electromagnetic field tensor in the following form:

$$\begin{aligned} B^{\hat{\theta }}=\frac{B r}{\sqrt{g_{rr}g_{\phi \phi }}}\sin ^2{\theta }. \end{aligned}$$

3 The motion of particles with magnetic dipole moment near Kerr-MOG black holes in magnetized fields

The Hamilton–Jacobi equation that takes into account both interactions between the magnetized particles with scalar and magnetic fields has the form

$$\begin{aligned} g^{\mu \nu }\left( \frac{\partial S}{\partial x^\mu }-q\varPhi _\mu \right) \left( \frac{\partial S}{\partial x^\nu }-q\varPhi _\nu \right) =-m^2\left( 1-\frac{\mathcal{U}}{2m}\right) ^2, \end{aligned}$$
(5)

where \(q=\sqrt{\alpha }m\) is gravitational test particle charge, and \(q\varPhi _\mu \) is the term that defines MOG interaction between the particles and the scalar field. The product \(\mathcal{U}=D^{\mu \nu }F_{\mu \nu }\) corresponds to the magnetic interaction and is scalar. \(D^{\mu \nu }\) and \(F_{\mu \nu }\) are the polarization electromagnetic field tensors. The interaction term has been calculated in Refs. [42,43,44,45,46,47,48,49,50,51,52,53] as \(\mathcal{U}=\mu _{\hat{\alpha }}B^{\hat{\alpha }}\). In our further analyses, we consider the magnetic dipole of the particles to be perpendicular to the equatorial plane (so it has components \(\mu ^{\hat{\alpha }}=(0,0,\mu ,0)\)) and restricted the particle’s motion in that plane. On the other hand, there is an additional interaction with the particles and the scalar field,

$$\begin{aligned} \varPhi _\mu =\frac{\sqrt{\alpha } Mr}{\varSigma }\left( -1,0,0,a \sin ^2{\theta }\right) . \end{aligned}$$
(6)

The Lagrangian of the magnetized particles near rotating Kerr BHs in MOG has a form including electromagnetic and MOG interactions,

$$\begin{aligned} \mathcal{L}=\frac{1}{2}\left( m+\mathcal{U} \right) g_{\mu \nu } u^\mu u^\nu -\frac{1}{2}\kappa \mathcal{U} +q \varPhi _\mu u^\mu , \end{aligned}$$
(7)

where \(\kappa =1\) [9]. One may easily find integrals of motion of magnetized particles (\(p_\phi =L=mu^\phi \) and \(p_t=-E=mu^t\) denoting the total angular momentum and total energy of the particle, respectively) using the above Lagrangian in the following form,

$$\begin{aligned} -\mathcal{E}= & {} (1+\beta F(r))\left[ g_{tt}\dot{t}+g_{t\phi }\dot{\phi }\right] +\frac{q}{m}\varPhi _t, \end{aligned}$$
(8)
$$\begin{aligned} l= & {} (1+\beta F(r))\left[ g_{\phi \phi }\dot{\phi }+g_{t\phi }\dot{t} \right] +\frac{q}{m}\varPhi _\phi , \end{aligned}$$
(9)

where \(\mathcal{E}=E/m\) and \(l=L/m\) are the specific energy and angular momentum, while \(\beta =\mu B/m\) is the magnetic interaction parameter and the radial function can be expressed as \(F(r)=r\sin ^2{\theta }/\sqrt{g_{rr}g_{\phi \phi }}\). On solving the above Eqs. (8) and (9), we obtain

$$\begin{aligned} {\dot{t}}= & {} \frac{g_{\phi \phi } (\mathcal{E}+\frac{q}{m} {\varPhi _t}) + g_{t\phi }({l}-\frac{q}{m}\varPhi _\phi ) }{\left( g_{t\phi }^2- g_{tt} g_{\phi \phi }\right) \left( 1+ \beta F(r)\right) }, \end{aligned}$$
(10)
$$\begin{aligned} {\dot{\phi }}= & {} -\frac{g_{t\phi } (\mathcal{E}+\frac{q}{m} \varPhi _t)+ g_{tt} ({{l}}-\frac{q}{m} {\varPhi _\phi })}{\left( g_{t\phi }^2- g_{tt} g_{\phi \phi }\right) \left( 1+ \beta F(r)\right) }. \end{aligned}$$
(11)
Fig. 1
figure 1

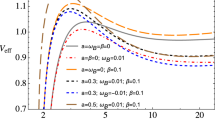
Radial dependence of the effective potential for the selected values of BH spin a, coupling parameter \(\beta \), and MOG parameter \(\alpha \). For simplicity, we choose \(M=1\). In the upper row, the effective potential profiles are shown without taking into account the MOG interaction. In the bottom row, the profiles are presented with the MOG interaction term

Full size image

The Hamilton–Jacobi action for the motion of magnetized particles in the equatorial plane (\(\theta =\pi /2\)) can be separated as follows

$$\begin{aligned} S=-Et+L\phi +S_r(r). \end{aligned}$$
(12)

Using the Hamilton–Jacobi equation (5), we can easily obtain the equation of radial motion of the magnetized particles:

$$\begin{aligned} g_{rr} \dot{r}^2= & {} -\Bigg [g^{tt}\left( \mathcal {E}+\frac{q\varPhi _t}{m}\right) ^2+g^{\phi \phi }\left( l-\frac{q\varPhi _{\phi }}{m}\right) ^2 \nonumber \\{} & {} - 2g^{t\phi }\left( \mathcal {E}+\frac{q\varPhi _t}{m}\right) \left( l-\frac{q\varPhi _\phi }{m}\right) +\Big ( 1-\beta F(r)\Big )^2\Bigg ] \nonumber \\= & {} \left[ \mathcal{{E}}-V^+_\textrm{eff}(r)\right] \left[ \mathcal{{E}}-V^-_\textrm{eff}(r)\right] . \end{aligned}$$
(13)

After some calculations, we get the following,

$$\begin{aligned} V_\textrm{eff}^\pm= & {} \frac{\alpha M}{r}+\frac{g_{t\phi }}{g_{\phi \phi }}\left( l-\frac{\alpha Ma}{r}\right) \nonumber \\{} & {} \pm \sqrt{\left[ \frac{g_{t\phi }^2}{g_{\phi \phi }}-g_{tt}\right] \left[ \Big (1-\beta F(r) \Big )^2+g^{\phi \phi }\left( l-\frac{aM\alpha }{r}\right) ^2\right] }.\nonumber \\ \end{aligned}$$
(14)

We have plotted the radial dependence of the effective potential at various discrete values of the space-time parameters \(a, \beta \) and l in Fig. 1. From our graphical illustration, we interestingly observe that in comparison with the Schwarzschild and Kerr BHs, the Kerr-MOG BH have the highest and minimum unstable circular orbits at \(\alpha >0\), near BH in the absence of an external magnetic field (for details, see the upper left panel of Fig. 1). On the other hand, in the magnetized case, the Schwarzschild BH has minimum unstable circular orbits near BH (for details, see the upper right and bottom left panels of Fig. 1). Surprisingly, the interaction of gravitational field strength \(\alpha \) and magnetic field contributes to the stability of circular orbits. One can also observe that due to the interaction of the MOG interaction, in the \(\beta =0\) case, the effective potential in the bottom row behaves just as shown in the top one, with an increase to the maximum of the effective potential and the orbits where the effective potential takes maximum shifts towards the BH. In the case of \(\beta \ne 0\), the magnetic interaction also enhances its maximum values. In the sense that in both cases, the Schwarzschild BH has the minimum unstable orbits. While the Schwarzschild BH has more stable orbits in comparison with Kerr and Kerr-MOG BHs.

Fig. 2
figure 2

The dependence of the unstable circular radii from MOG parameter \(\alpha \). Here, we consider the MOG interaction. For simplicity, we choose \(G_N=1, M=1\)

Full size image

We provide graphical analyzes of unstable orbits of neural and magnetized test particles (with angular momentum \(l^2=20\)) for different values of \(\beta \) and \(\alpha \) in Fig. 2. It is observed that the outer and inner unstable orbits of neutral test particles coincide at a critical value of \(\alpha \) and the critic value increases with the increase of the Kerr-MOG BH spin a. The outer and inner unstable orbits increase with an increase in the values of \(\alpha \). It is also seen that the increasing rate of outer unstable orbits of magnetized particles with \(\beta =0.3\) is higher than the inner one’s rate. Also, the radius of both inner and outer unstable orbits slightly decreases with increasing the value of \(\beta \).

Fig. 3
figure 3

Graphical illustration of the ISCO radius along \(\alpha \) “with MOG” and “without MOG”, where “with MOG” means that the interaction with MOG is taken into consideration and “without MOG” means that it is not considered

Full size image

The stability of circular orbits can be located with the help of effective potential minima. In short, \(V_\textrm{eff}''(r)<0\), results in unstable circular orbits, while all circular stable orbits satisfy the condition of \(\partial _{rr}V_\textrm{eff}(r_\textrm{ISCO})>0\). On the contrary, ISCO satisfies the condition \(V_\textrm{eff}''(r_\textrm{ISCO})=0\). To understand the influence of the MOG intersection and magnetic field, we have numerically plotted the behavior of the ISCO radius in Fig. 3. We observe that the BH spin diminishes the ISCO radius, whereas the MOG interaction contributes to the ISCO in both rotating and non-rotating cases. Moreover, one can observe the strong influence of the magnetic field interaction parameter \(\beta \) on the ISCO radius in the presence of MOG interactions, as \(\beta \) contributes considerably to the ISCO radius.

Fig. 4
figure 4

Graphical illustration of the ISCO angular momentum along \(\alpha \) “with MOG” and “without MOG”, where “with MOG” means that the interaction with MOG is taken into consideration and “without MOG” means that it is not considered

Full size image

Figure 4 demonstrates the behavior of magnetized particles’ angular momentum in their ISCOs under the influence of BH spin and magnetic-field interactions. Our finding reveals that both MOG interactions and the magnetic field reduce the angular momentum at their ISCO. In other words, the Schwarzschild and Kerr magnetized BHs have greater angular momentum compared to the Schwarzschild-MOG and Kerr-MOG magnetized BHs, respectively. Whereas, the Schwarzschild magnetized BH has the greatest and Kerr-MOG magnetized BH has the smallest angular momentum at their respective ISCOs.

4 Magnetized particles’ collisions near the Kerr-MOG BH immersed in magnetic field

The study of collisional processes near BHs remains a significant and intriguing topic within the realm of general relativity. Energy extraction from a BH is a key aspect of these collisions, and various approaches can be employed to understand the mechanisms involved, especially in the context of spinning-charged BHs.

Exploring the total energy extracted through different methods occurring in the vicinity of BHs could potentially provide insights into why the luminosity of active galactic nuclei (AGN) reaches magnitudes on the order of \(10^{45}\mathrm{erg/sec}\), possibly driven by supermassive BHs.

Penrose [20], who introduced a simple process in which a particle entering the ergosphere of a spinning BH splits into a pair of particles: one collides with the BH, while the other escapes to infinity with more energy than the original particle. This technique has been further explored in recent studies found in the literature, with notable contributions discussed in references such as [54,55,56,57].

Banados-Silk-West (BSW) [58, 59] delved into the exploration of particle collisions near BH horizons as a means of extracting energy, an approach further investigated in subsequent works [37, 47, 49, 59,60,61,62,63,64,65,66,67,68,69,70,71]. It has been observed that the efficiency of energy extraction from the central BH is notably higher in head-on collision scenarios.

In this section, we investigate the particle acceleration near the BH of two colliding particles in the presence of an external magnetic field. Also, we consider collision in two cases, taking MOG interaction into account, and do not take this effect.

Following Ref. [37, 58], we also use the general expression for the center-of-mass energy \(E_\textrm{cm}\) of colliding particles

$$\begin{aligned} \left\{ \frac{1}{\sqrt{-g_{tt}}} \ E_\textrm{cm}, 0, 0, 0\right\} = m_{1}u_{1}^{\mu }+m_{2}u_{2}^{\nu }, \end{aligned}$$
(15)

with \(u_{(1)}^{\mu }\) and \(u_{(2)}^{\nu }\) are the four-velocities and \(m_{1,2}\) are rest masses of the colliding particles. we obtain the expression for \(E_\textrm{cm}\) as

$$\begin{aligned} \frac{E^2_{cm}}{m_1m_2}=\frac{m_1^2+m_2^2}{m_1m_2}-2g_{\mu \nu } u^{\mu }_1u^{\nu }_2. \end{aligned}$$
(16)

For simplicity, we consider the masses of colliding particles to be equal, i.e., \(m_1=m_2=m\). In doing so, we study the high-energy collisions of particles. As we are interested in the collision energy of the two magnetized particles, Eq. (16) can be expressed as:

$$\begin{aligned} \mathcal {E}_{cm}^2= & {} 1-\big (g_{tt}\dot{t}_1\dot{t}_2+g_{\phi \phi }\dot{\phi }_1 \dot{\phi }_2+g_{t\phi }\left( \dot{t}_1\dot{\phi }_2+\dot{t}_2\dot{\phi }_1\right) \nonumber \\{} & {} +g_{rr}\dot{r}_1\dot{r}_2\big ), \end{aligned}$$
(17)

where \(\dot{t}\), \(\dot{\phi }\) and \(\dot{r}\) are given in Eqs. (10), (11) and (13), respectively.

4.1 Critical angular momentum

It is well known that the energy of the non-extremal BH collision is finite [72]. However, in any way, we have to find the limiting values of the angular momentum for the falling particles. This can be obtained by solving \(V_{eff}=0, \partial _rV_{eff}=0\) simultaneously.

Table 1 The limiting values of the angular momentum for different non-extremal cases of a Kerr-MOG (\(a=0.7\)) BH for magnetized particles. Here, we do not consider the effect of MOG interaction
Full size table
Table 2 The limiting values of the angular momentum for different non-extremal cases of a Kerr-MOG (\(a=0.7\)) BH for magnetized particles. Here, we consider the effect of MOG interaction
Full size table

In Tables 1 and 2, we have shown the allowed range of angular momentum for magnetized particles, considering and not considering the MOG interaction, respectively. We should say that during this calculation we used an approximation to obtain values of the angular momentum.

4.2 Collision of two magnetized particles

Consider the two magnetized particles with rest masses \(m_1\) and \(m_2\) moving in the equatorial plane of the Kerr-MOG BH. These particles come from infinity with the energies \(\mathcal{E}_1=\mathcal{E}_2=1\), towards the BH and collide in the vicinity of the event horizon. One may easily make graphical analyses of \(\mathcal{E}_{cm}\) using Eq. (17).

Fig. 5
figure 5

Graphical illustration of the center-of-mass energy resulting from the collision of magnetized particles with equivalent starting energies \(\mathcal {E}_1=\mathcal {E}_2=1\), without considering MOG effect (top row) and taking into account the effects of MOG (bottom row)

Full size image

In Fig. 5, we illustrate the radial distribution of the center-of-mass energy of magnetized particles for various values of the MOG parameter \(\alpha \) and BH spin parameter a. The top row represents the scenario without considering the MOG impact, while the bottom one includes the MOG effect. We observed from our graphical results that the magnetic-field interaction considerably influences the center-of-mass energy. One can note that the magnetic field diminishes while the MOG parameter \(\alpha \) contributes to the center-of-mass energy. Moreover, we also observed that, compared to the absence of the MOG effect, in the case of the MOG effect, one can obtain much more center-of-mass energy.

4.3 Collision of two magnetized and neutral particles.

Then, one can find the expression for the center-of-mass energy of the collision of neutral and magnetized particles using Eq. (17).

Fig. 6
figure 6

Graphical illustration of the center-of-mass energy resulting from the collision of magnetized and neutral particles with identical initial energy \(\mathcal {E}_1=\mathcal {E}_2=1\), without considering the MOG effect (top row) and taking into account the MOG interaction (bottom row)

Full size image

In Fig. 6, we have graphically illustrated how the center-of-mass energy depends on the radius without considering the MOG interaction (in the top row) and with considering the MOG interaction (see the bottom row), respectively. Just like the previous case, our graphical analysis revealed a significant impact of the magnetic field on the center-of-mass energy. We observed that in the case of neutral particle collision, more center-of-mass could be released as compared to the collision of magnetized particles (for details, see the two panels at the bottom). As a result, the parameters \(\beta _1=\beta _2 >0\), as well as \(\alpha <0\), decrease, while the positive interactions of \(\alpha \), on the other hand, contribute to the center of mass energy. The MOG effect is found to have a significant impact on the energy release rate and results in a substantial increase in the center-of-mass energy.

5 Conclusion

Since the general relativistic magnetohydrodynamic simulations demonstrate that the genuine magnetic field around the BHs may have a very complex nature [73,74,75]. Thus, in our present study, we used asymptotic uniform magnetic fields as the primary model for the massive-scale BH magnetosphere having an axial nature.

In this study, we have investigated the dynamics of test particles possessing a magnetic dipole moment as they orbit around rotating Kerr-MOG BHs embedded in external asymptotically uniform magnetic fields within the framework of STVG theory, a form of MOG theory.

We have derived the effective potential governing the circular orbits of these magnetized particles, considering the combined influence of both magnetic and STVG interactions. Our examination has focused on analyzing the characteristics of the ISCOs for these magnetized particles. Our findings indicate that the STVG interaction is crucial, and the magnetic interaction amplifies its impact on both the ISCO radius and the angular momentum at ISCO. Additionally, we have explored collisional scenarios involving magnetized particles, identifying the maximum and minimum values for angular momentum that allow particles to collide near the BH horizon. Finally, we have conducted an analysis of the center-of-mass energy for colliding magnetized particles in the vicinity of the BH horizon. Some key aspects of our results are:

  • The magnetic field interaction considerably influences the center-of-mass energy and diminishes it while the MOG parameter \(\alpha \) contributes to the center-of-mass energy.

  • In comparison with the absence of the MOG effect, in the presence of the MOG effect, one can obtain much more center-of-mass energy.

  • We found that in the case of neutral particle collision, BH releases more center-of-mass as compared to the collision of magnetized particles (for details, see Fig. 6).

  • Negative values of the gravitational field strength \(\alpha <0\) decrease, whereas its positive interactions \(\alpha \), contribute to the center-of-mass energy.

  • The MOG effect is found to have a significant impact on the energy release rate and results in a substantial increase in the center-of-mass energy.