1 Introduction

Although general relativity is an important theory that is in agreement with a variety of observational tests [1, 2], however this theory has some important challenges [3,4,5,6]. Study of the viable alternative gravity theories, known as modified theories of gravity, is one of the best candidates for the possible explanation of its problems. Among the various modified theories of gravity, the ST theories pioneered by Brans and Dicke [7, 8], have provided fascinating results [9,10,11]. In the low energy limit of string theory, the Einstein–Hilbert action is recovered which is coupled with a scalar field called the dilaton [12]. Existence of the BHs, as the fascinating prediction of general relativity, is an interesting area of research in both of the ST and Ed theories. Recently, charged dilatonic BHs coupled to nonlinear electrodynamics in lower and higher dimensions have received more attention. Charged Ed BH solutions in the presence of one or two Liouville-type potential have also been constructed with linear and nonlinear electrodynamics [13,14,15,16,17,18]. In addition, study of charged ST BHs with linear and nonlinear theories of electrodynamics has provided many interesting results [19,20,21,22]. It is well-known that the of ST theory which is written in the Jordan frame (JF) is strongly coupled to an scalar field. Thus the related field equations cannot be solved easily. The JF action can be translated to the EF by use of a CT. In the EF, where the scalar and gravitational fields are decoupled, solving the equations of motion is not very difficult. Then by use of the inverse CTs one can find the solution of JF equations from their EF counterparts [23, 24].

One of the main failures of the standard linear Maxwell theory is that, for a point charge, it leads to infinite self-energy at the charge position. Born and Infeld introduced a model of nonlinear electrodynamics to overcome this problem by imposing a maximum strength of the electromagnetic field [25,26,27,28]. The BI-like models of nonlinear electrodynamics, known as the logarithmic and exponential electromagnetic theories, have the same consequences as BI electrodynamics [29,30,31]. Moreover, Maxwell’s electromagnetic theory, which predicts existence of the massless photons as the mediator of electromagnetic interactions, violates conformal symmetry in the spacetimes with dimension non-equal to four. Power-Maxwell nonlinear electrodynamics is an interesting theory which preserves conformal symmetry in the spcetimes with arbitrary dimensions [32,33,34,35]. Stability of the charged BH solutions in the presence of the linear and nonlinear electrodynamics have been studied extensively [36,37,38,39,40]. Many studies have been published on the charged BH and black brane solutions with nonlinear electrodynamics coupled to general relativity [41,42,43,44,45,46]. In addition, cosmological models, including nonlinear electromagnetic fields, have been studied by many authors [47,48,49,50,51,52,53]. In the resent papers [54, 55], we have studied three-dimensional ST BHs in the presence of Maxwell and power-Maxwell theories of electrodynamics, respectively. Also, thermodynamics and especially thermal stability and phase transition properties of the Ed and ST BHs have been investigated. The aim of this work is to extend these studies to the case of nonlinearly charged ST BHs by considering BI electrodynamics.

Throughout this article, the metric signature is considered as \((-,\;+,\;+)\). Also, in terms of the connection coefficints, the Riemann tensor is defined as follows

$$\begin{aligned} \mathcal{{{R}}}^\kappa _{\;\;\lambda \mu \nu }=\partial _\mu \Gamma ^\kappa _{\lambda \nu }+ \Gamma ^\kappa _{\mu \alpha } \Gamma ^\alpha _{\lambda \nu }-\partial _\nu \Gamma ^\kappa _{\lambda \mu }-\Gamma ^\kappa _{\nu \alpha } \Gamma ^\alpha _{\lambda \mu }, \end{aligned}$$
(1.1)

and the Ricci tensor and Ricci scalar are obtained as \(\mathcal{{{R}}}_{\mu \nu }=\mathcal{{{R}}}^\alpha _{\;\;\mu \alpha \nu }\) and \(\mathcal{{{R}}}=g^{\mu \nu }\mathcal{{{R}}}_{\mu \nu }\), respectively [56].

The structure of this paper is as follows: in Sect. 2, The action of three-dimensional Ed theory is obtained from that of ST, by applying CTs, and the new scalar-coupled BI is introduced. The Ed field equations are solved in Sect. 3, by use of a circularly symmetric geometry. As the result, two novel classes of EdBI BHs are obtained. All the solutions recover the corresponding values when the BI parameter is chosen very large. In Sect. 4, thermodynamic quantities of EdBI BHs are calculated and it is shown that they satisfy the standard form of the first law. In Sect. 5 Thermal stability or phase transition of Ed BHs are studied by use of the BHs’ specific heat (SH). In Sect. 6, the JF exact solutions are obtained by applying the inverse CT on the EF solutions. As the result, two classes of ST BH solutions are obtained which, by fixing the parameters, can produce one-horizon, two-horizon and naked singularity STBI BHs. It is shown that thermodynamic quantities are identical in the Jordan and Einstein frames. Also, STBI BHs have the same thermal stability and phase transition properties as EdBI BHs. We summarize and discuss the results in Sec. 7.

2 The fundamental equations

We prefer to introduce the ST modified gravity theory with the following action, which is written in the JF [22, 54, 55], thus we have

$$\begin{aligned} I^{(ST)}= & {} -\frac{1}{16\pi }\int \sqrt{-{\bar{g}}}\left[ A_1({{\bar{\phi }}})\bar{\mathcal{{{R}}}}+A_2({{\bar{\phi }}}){\bar{g}}^{\mu \nu }{\bar{\nabla }}_\mu {{\bar{\phi }}}{\bar{\nabla }}^\nu {{\bar{\phi }}}\right. \nonumber \\&\left. -2A_3({{\bar{\phi }}})+{{{\mathcal {L}}}}(\bar{{{{\mathcal {F}}}}})\right] d^3x. \end{aligned}$$
(2.1)

As it is customary, we have used a bar sign over for introducing the quantities in the JF. Therefore, \(\bar{\mathcal{{{R}}}}\) denotes the Ricci scalar of the spacetime with the metric tensor \({\bar{g}}_{\mu \nu }\), which has been multiplied by the arbitrary function \(A_1({{\bar{\phi }}})\) in which \({{\bar{\phi }}}\) is a scalar field. The functions \(A_2({{\bar{\phi }}})\) and \(A_3({{\bar{\phi }}})\) are also other ones to be determined. Evidently, the covariant derivative is taken with respect to the JF metric \({\bar{g}}_{\mu \nu }\). Here, \(\bar{{{{\mathcal {F}}}}}={\bar{F}}^{\alpha \beta }{\bar{F}}_{\alpha \beta }\) denotes the JF Maxwell invariant and \({{{\mathcal {L}}}}(\bar{{{{\mathcal {F}}}}})\) is the electromagnetic Lagrangian in this frame. In the present work, we are interested in the BI electromagnetic theory which is introduced as [27, 57, 58]

$$\begin{aligned} {{{\mathcal {L}}}}(\bar{{{{\mathcal {F}}}}})=4a^2\left( 1-\sqrt{1+\frac{\bar{{{{\mathcal {F}}}}}}{2a^2}}\;\right) .\end{aligned}$$
(2.2)

It is a model of nonlinear electrodynamics, and a is the BI/ or nonlinearity parameter. The function \({{{\mathcal {L}}}}(\bar{{{{\mathcal {F}}}}})\) can be expanded in powers of \(\bar{{{{\mathcal {F}}}}}\), as follows

$$\begin{aligned} {{{\mathcal {L}}}}(\bar{{{{\mathcal {F}}}}})=-\bar{{{{\mathcal {F}}}}}+\frac{\bar{{{{\mathcal {F}}}}}^2}{8a^2}-\frac{\bar{{{{\mathcal {F}}}}}^3}{32a^4}+ \cdots \end{aligned}$$
(2.3)

from which, one can conclude that the BI electromagnetic theory reduces to that of Maxwell if a is chosen very large or the electromagnetic fields are very weak.

The JF field equations can be obtained from Eq. (2.1) by applying the variational principle. Since the gravitational and scalar fields are strongly coupled to each other, they cannot be solved simply. To overcome this problem, making use of a CT, one can obtain the corresponding quantity in the Einstein frame (EF) known as the Ed action [54, 55]. To do so, we consider the following CT [20,21,22]

$$\begin{aligned} {\bar{g}}_{\mu \nu }\rightarrow {\bar{g}}_{\mu \nu }=(\Omega ({{\bar{\phi }}}))^2g_{\mu \nu }, \end{aligned}$$
(2.4)

by which the components of JF metric are related to those of EF denoted by \(g_{\mu \nu }\). It must be noted that the transformation identified by Eq. (2.4), with \(\Omega ({{\bar{\phi }}})\) as a well-behavior function, is not a coordinate transformation such as \(x^\mu \rightarrow x'^\mu \), it transforms the metric structure and may shrink or stretch the manifold. From such a transformation the Ricci scalar transforms according to the following relation [59]

$$\begin{aligned} \bar{\mathcal{{{R}}}} \rightarrow \bar{\mathcal{{{R}}}}= & {} (\Omega ({{\bar{\phi }}}))^{-2}\mathcal{{{R}}}-4(\Omega ({{\bar{\phi }}}))^{-3}\partial _\mu \partial ^\mu \Omega ({{\bar{\phi }}})\nonumber \\&+2(\Omega ({{\bar{\phi }}}))^{-4}\Box \Omega ({{\bar{\phi }}}). \end{aligned}$$
(2.5)

The electromagnetic field transforms as \({\bar{F}}_{\mu \nu } \rightarrow F_{\mu \nu }\) and \({\bar{F}}^{\rho \lambda }\rightarrow {\bar{F}}^{\rho \lambda }={\bar{g}}^{\rho \mu }{\bar{g}}^{\lambda \nu }{\bar{F}}_{\mu \nu }=(\Omega ({{\bar{\phi }}}))^{-4}F^{\rho \lambda }\). Thus the Maxwell invariant transforms as

$$\begin{aligned} \bar{{{{\mathcal {F}}}}}\rightarrow \bar{{{{\mathcal {F}}}}}=(\Omega ({{\bar{\phi }}}))^{-4} {{{\mathcal {F}}}}, \end{aligned}$$
(2.6)

where, \({{{\mathcal {F}}}}=F_{\mu \nu }F^{\mu \nu }\) is the EF Maxwell invariant with \(F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu \) and \(A_\mu \) is the electromagnetic potential.

We need to have another scalar field, which we label by \(\phi \) in the EF, which will be correspond to the JF scalar field \({{\bar{\phi }}}\). Also, we assume that they are related to each other through the relation [19]

$$\begin{aligned} \left( \frac{d \ln \Omega ({{\bar{\phi }}})}{d {{\bar{\phi }}}}\right) ^2+\frac{A_2({{\bar{\phi }}})}{2\Omega ({{\bar{\phi }}})}=\left( \frac{d \phi }{d {{\bar{\phi }}}} \right) ^2. \end{aligned}$$
(2.7)

The function \(\Omega ({{\bar{\phi }}})\) must to be considered positive valued. This fact guaranties the positivity of energy carried by the scalar field, and noting Eq. (2.7), one obtained [19]

$$\begin{aligned} 2 \left( \frac{d \Omega ({{\bar{\phi }}})}{d {{\bar{\phi }}} }\right) ^2+\Omega ({{\bar{\phi }}})A_2({{\bar{\phi }}})\ge 0. \end{aligned}$$
(2.8)

By substituting Eqs. (2.4), (2.5) and (2.6) into Eq. (2.1), and making use of the following definitions

$$\begin{aligned}&\Omega ({{\bar{\phi }}})=A_1^{-1}({{\bar{\phi }}}), \;\;\;\text{ and }\;\;\;A_2({{\bar{\phi }}})=-2 A_1({{\bar{\phi }}}),\nonumber \\&\text{ and }\;\;\;V(\phi )=2A_3({{\bar{\phi }}})A_1^{-3}({{\bar{\phi }}}), \end{aligned}$$
(2.9)

and for the electromagnetic Lagrangian, we have

$$\begin{aligned}&{{{\mathcal {L}}}}(\bar{{{{\mathcal {F}}}}})\rightarrow L({{{\mathcal {F}}}}, \phi )=\Omega ^{3}({{\bar{\phi }}}){{{\mathcal {L}}}}\left( \Omega ^{-4}({{\bar{\phi }}}){{{\mathcal {F}}}}\right) ,\nonumber \\&\text{ with }\;\;\;{{\bar{\phi }}}={{\bar{\phi }}}(\phi ),\end{aligned}$$
(2.10)

we can transform the JF action (II.1) to its corresponding value in the EF. Thus, for the Ed gravity in a three-dimensional spacetime, we have

$$\begin{aligned} I^{(Ed)}= & {} -\frac{1}{16\pi }\int \sqrt{-g}\left[ {{{\mathcal {R}}}}-2g^{\mu \nu }\nabla _\mu \phi \nabla _\nu \phi \right. \nonumber \\&\left. -V(\phi )+L({{{\mathcal {F}}}}, \phi )\right] d^3x.\end{aligned}$$
(2.11)

Note that, \({{{\mathcal {R}}}}=g^{\mu \nu }{{{\mathcal {R}}}}_{\mu \nu }\), and the EF covariant derivative \(\nabla \) is defined with respect to \(g_{\mu \nu }\). The function \(V(\phi )\) is the scalar potential, and \(L({{{\mathcal {F}}}}, \phi )\) is the scalar-coupled BI electrodynamics. Its explicit form is

$$\begin{aligned} L({{{\mathcal {F}}}}, \phi )=4a^2e^{6\alpha \phi }\left( 1-\sqrt{1+X}\;\right) ,\;\;\;\;\;X=\frac{{{{\mathcal {F}}}}}{2a^2}e^{-8\alpha \phi },\nonumber \\\end{aligned}$$
(2.12)

and the parameter \(\alpha \), is named as the scalar-electromagnetic coupling constant. Note that the function \(\Omega ({{\bar{\phi }}}(\phi ))\) has been chosen as \(\Omega (\phi )=e^{2\alpha \phi }\). By expanding the Lagrangian (II.12) we have

$$\begin{aligned} L({{{\mathcal {F}}}}, \phi )=-{{{\mathcal {F}}}}e^{-2\alpha \phi }+\frac{{{{\mathcal {F}}}}^2e^{-10\alpha \phi }}{8a^2}-\frac{{{{\mathcal {F}}}}^3e^{-18\alpha \phi }}{32a^4}+ \cdots \nonumber \\ \end{aligned}$$
(2.13)

When the limit \(a\rightarrow \infty \) (or \({{{\mathcal {F}}}}\rightarrow 0\)) is taken, it reduces as \(L({{{\mathcal {F}}}}, \phi )=-{{{\mathcal {F}}}}e^{-2\alpha \phi }\), which is nothing but the Lagrangian of Maxwell’s electrodynamics in the Ed gravity theory [54].

Now, the EF exact solutions can be obtained easily. This will be done in the next section by use of the action (2.11).

3 Exact solutions in the EF

By applying variational principal to the action (2.11), the EF field equations can be obtained. The vector electromagnetic field satisfies the equation

$$\begin{aligned} \nabla _\mu \left[ \partial _{_{{{{\mathcal {F}}}}}} L({{{\mathcal {F}}}}, \phi )F^{\mu \nu }\right] =0, \end{aligned}$$
(3.1)

the tensorial gravitational field equation is

$$\begin{aligned} {{{\mathcal {R}}}}_{\mu \nu }= & {} V(\phi )g_{\mu \nu }+2\partial _\mu \phi \partial _\nu \phi -g_{\mu \nu }L({{{\mathcal {F}}}}, \phi )\nonumber \\&+2\partial _{_{{{{\mathcal {F}}}}}}L({{{\mathcal {F}}}}, \phi )\left( {{{\mathcal {F}}}}g_{\mu \nu }-F_{\mu \sigma }F_{\nu }^{\;\sigma }\right) , \end{aligned}$$
(3.2)

and the scalar field \(\phi =\phi (r)\) and scalar potential \(V(\phi )\) satisfy the following differential equation

$$\begin{aligned} 4g^{\mu \nu }\nabla _\mu \nabla _\nu \phi =\frac{d V(\phi )}{d\phi }-\partial _{\phi } L({{{\mathcal {F}}}}, \phi ). \end{aligned}$$
(3.3)

We are interested in obtaining the solution of above field equations in a circularly symmetric geometry with the following line element

$$\begin{aligned} ds^2= & {} g_{\mu \nu }dx^{\mu }dx^{\nu }=-W(r)dt^2\nonumber \\&+\frac{1}{W(r)}dr^2+r^2R^2(r)d\theta ^2.\end{aligned}$$
(3.4)

Here, W(r) and R(r) are two unknown functions of r which must be calculated. W(r) is known as metric function and R(r) is a dimensionless quantity indicating the effect of dilaton field on the spacetime geometry. It must reduce to unity as the dilaton field disappears.

Making use of Eqs. (3.1) and (3.4), and noting the fact that \( {{{\mathcal {F}}}}=-2F_{tr}^2\), the only nonzero component of the Faraday tensor can be determined. That is

$$\begin{aligned} F_{tr}=\frac{qe^{2\alpha \phi }}{rR(r)\sqrt{1+\xi }},\;\;\;\;\;\;\;\text{ with }\;\;\;\;\;\;\; \xi =\frac{q^2e^{-4\alpha \phi }}{a^2r^2R^2(r)}. \end{aligned}$$
(3.5)

Various components of gravitational field equations (III.2), with the help of (III.4), take the following explicit forms

$$\begin{aligned} C_{tt}\equiv & {} W''(r)+\left[ \frac{1}{r}+\frac{R'(r)}{R(r)}\right] W'(r)+2V(\phi )\nonumber \\&-4a^2e^{6\alpha \phi }\left( 2-\frac{2+\xi }{\sqrt{1+\xi }} \right) =0, \end{aligned}$$
(3.6)
$$\begin{aligned} C_{rr}\equiv & {} C_{tt}+2\left[ \frac{R''(r)}{R(r)}+\frac{2R'(r)}{rR(r)}+2\phi '^2(r)\right] W(r)=0, \end{aligned}$$
(3.7)
$$\begin{aligned} C_{\theta \theta }\equiv & {} \left[ \frac{1}{r}+\frac{R'(r)}{R(r)}\right] W'(r)+\left[ \frac{R''(r)}{R(r)}\right. \nonumber \\&\left. +\frac{2R'(r)}{rR(r)}\right] W(r)+V(\phi )-4a^2e^{6\alpha \phi }\left( 1-\sqrt{1+\xi }\right) =0.\nonumber \\ \end{aligned}$$
(3.8)

They are the tt, rr and \(\theta \theta \) components of the gravitational field equations. Now, by use of Eqs. (3.3), (3.5), (3.6), (3.7) and (3.8), after some calculations, one can show that

$$\begin{aligned} \left[ \frac{1}{r}+\frac{R'(r)}{R(r)}\right] \left( C_{tt}-2C_{\theta \theta }\right) =\frac{dC_{\theta \theta }}{dr}.\end{aligned}$$
(3.9)

This mean that Eqs. (3.6) and (3.8) are not independent. Thus the number of independent equations is one less than those of unknown quantities, and they are not sufficient for obtaining the full solutions. This problem can be solve by introducing an ansatz. As it was done by Chan and Mann [60, 61], we consider a power-law function for R(r). In terms of a constant of dimensionality \(r_0\), one can write

$$\begin{aligned} R(r)=\left( \frac{r}{r_0}\right) ^\nu . \end{aligned}$$
(3.10)

Note that similar solution has been used previously for finding exact BH solutions in various spacetime dimensions. See for example [55, 60, 61].

The scalar field \(\phi (r)\) can be determined by use of Eqs. (3.7) and (3.10). After solving the related differential equation, we have

$$\begin{aligned} \phi (r)=\gamma \ln \left( \frac{b}{r}\right) ,\quad \text{ with }\quad \gamma =\sqrt{-\nu (\nu +1)/2}, \end{aligned}$$
(3.11)

which is acceptable if b is positive and \(\nu \) is restricted to the range \(-1< \nu \le 0\).

Note that Eq. (3.5), in the limiting case \( a \rightarrow \infty \), reduces to

$$\begin{aligned} F_{tr}=\frac{qe^{2\alpha \phi }}{rR(r)},\end{aligned}$$
(3.12)

which, by redefinition of the integration constant q as \(q r_0^\nu b^{2\alpha \gamma } \rightarrow q\), recovers the corresponding quantity in the Einstein–Maxwell-dilaton (EMd) gravity theory [54]. Now, the zeroth component of \(A_\mu \) can be obtained as (Appendix-A)

$$\begin{aligned} A_t(r)= & {} \frac{q}{2\alpha \gamma + \nu } \left( \frac{b}{r} \right) ^{2\alpha \gamma } \left( \frac{r_0}{r} \right) ^{\nu }{} _2F_1 \left[ \frac{1}{2}, \frac{2\alpha \gamma + \nu }{4 \gamma \lambda }, 1 + \frac{2\alpha \gamma +\nu }{4 \gamma \lambda }, -\xi \right] . \end{aligned}$$
(3.13)

Here, we have used the definition \(\lambda =-\alpha +\frac{1}{2\beta },\;\text{ with }\; \beta =\frac{\gamma }{\nu +1}\). By expanding the Hypergeometric function \(\;_2F_1\), we have

$$\begin{aligned} A_t(r)=\frac{q}{2\alpha \gamma +\nu } \left( \frac{b}{r}\right) ^{2\alpha \gamma }\left( \frac{r_0}{r}\right) ^{\nu } +{{{\mathcal {O}}}}\left( \frac{1}{a^2}\right) ,\end{aligned}$$
(3.14)

which is compatible withe result of [54] when a is chosen very large.

By use of these quantities in Eqs. (3.3) and (3.8), after some manipulations, one can show that the remaining unknown functions W(r) and \(V(\phi )\) satisfy the following differential equations

$$\begin{aligned}&W'(r)+\frac{\nu }{r}W(r)-\frac{r}{\nu +1}\left[ 4a^2\left( 1-\sqrt{1+\xi } \right) e^{6\alpha \phi }- V(\phi )\right] =0, \end{aligned}$$
(3.15)
$$\begin{aligned}&\frac{d V(\phi )}{d\phi } - 4\beta V(\phi ) + 8a^2 \left[ (2\beta - 3\alpha ) \left( 1 - \frac{1}{\sqrt{1 + \xi }}\!\right) - \frac{2\xi (\beta - \alpha )}{\sqrt{1 + \xi }} \right] e^{6\alpha \phi }=0. \end{aligned}$$
(3.16)

By solving the differential equation (III.16), and fixing the integration constant, we obtain

$$\begin{aligned} V(\Phi ) = 2 \Lambda e^{4 \beta \Phi }+4 a^2\left[ 1 - \sqrt{1 + \xi } +\frac{ \sqrt{1 + \xi } - H}{ 4 \beta ( \alpha - \beta ) + 1 }\right] e^{6 \alpha \Phi },\nonumber \\\end{aligned}$$
(3.17)

where, H is a hypergeometric function with the following explicit form

$$\begin{aligned} H = \;_2F_1\left[ \frac{1}{2},\;\frac{3 \alpha - 2 \beta }{ 2\lambda },\; 1+\frac{3 \alpha - 2 \beta }{2 \lambda },\; -\xi \right] .\end{aligned}$$
(3.18)

By expanding the last terms of Eq. (3.17) in powers of \(\xi \) and taking the limit \( a \rightarrow \infty \), and redefining the constant q, one can show that

$$\begin{aligned} V(\phi )=2\Lambda e^{2\beta \phi }+\frac{2q^2\beta (2\beta -\alpha )}{b^2(\alpha \beta -2\beta ^2+1)}\left( \frac{r_0}{b} \right) ^{2\nu } e^{2(3\alpha +2\lambda )\phi },\nonumber \\\end{aligned}$$
(3.19)

which is just the same as that obtained in Ref. [54]. After returning (III.17) into (III.15), we obtain the solution as metric function W(r). That is

$$\begin{aligned} W(r) = \left\{ \begin{array}{ll} -m r^{-\nu } -\frac{2 \Lambda r^2}{(1 + \nu ) (2 + 3 \nu )} \left( \frac{b}{r}\right) ^{4 \beta \gamma }+\frac{4 a^2 r^2 \eta (r)}{1 + 3 \nu + 4 \alpha \gamma }\left( \frac{b}{r}\right) ^{6 \alpha \gamma }, \;\;\;\; \nu \ne -\frac{2}{3},\\ -m r^{\frac{2}{3}} -6 \Lambda b^2 \ln \left( \frac{r}{\ell }\right) +\frac{18 a^2 r^2 \zeta (r)}{(4 \alpha -3)^2}\left( \frac{b}{r}\right) ^{2 \alpha }, \;\;\;\;\nu =-\frac{2}{3}. \end{array} \right. \end{aligned}$$
(3.20)

Here, m is an integration constant, and

$$\begin{aligned} \eta (r)= & {} \frac{\sqrt{1+\xi }}{4 \alpha \gamma -1}+\frac{2 \gamma \lambda H_1}{(6 \alpha \gamma -2 - \nu ) (4 \alpha \gamma - 1)}+\frac{3 \alpha - 2 \beta }{2 \lambda (2 + 3 \nu )}\left( \Gamma \left[ \frac{3 \alpha - 2 \beta }{2 \lambda }\right] H_2-\Gamma \left[ \frac{6\alpha \gamma -\nu +2}{4\gamma \lambda }\right] H_3 \right) , \end{aligned}$$
(3.21)
$$\begin{aligned} \zeta (r)= & {} 2\sqrt{1+\xi _0}-\frac{1-2\alpha }{2-3\alpha }H_4+\frac{3-4 \alpha }{1-2 \alpha }\Gamma \left[ \frac{2-3 \alpha }{2 \alpha -1}\right] \times \Gamma \left[ \frac{1- \alpha }{2 \alpha -1}\right] H_5, \end{aligned}$$
(3.22)
$$\begin{aligned} H_1= & {} \;_2F_1\left[ \frac{1}{2},\;\frac{6\alpha \gamma -\nu -2}{4\gamma \lambda },\;1+\frac{6\alpha \gamma -\nu -2}{4\gamma \lambda },\;-\xi \right] , \end{aligned}$$
(3.23)
$$\begin{aligned} H_2= & {} \;_2{\tilde{F}}_1\left[ \frac{1}{2},\;\frac{3\alpha -2 \beta }{2\lambda },\;1+\frac{3\alpha -2 \beta }{2\lambda },\;-\xi \right] ,\end{aligned}$$
(3.24)
$$\begin{aligned} H_3= & {} \;_2{\tilde{F}}_1\left[ \frac{1}{2},\;\frac{6\alpha \gamma -\nu -2}{4\gamma \lambda },\;1+\frac{6\alpha \gamma -\nu -2}{4\gamma \lambda },\;-\xi \right] , \end{aligned}$$
(3.25)
$$\begin{aligned} H_4= & {} \;_2F_1\left[ \frac{1}{2},\;\frac{2-3\alpha }{2\alpha -1},\;1+\frac{2-3\alpha }{2\alpha -1},\;-\xi _0 \right] ,\end{aligned}$$
(3.26)
$$\begin{aligned} H_5= & {} \;_3{\tilde{F}}_2\left[ \frac{1}{2},\;\frac{2-3\alpha }{2\alpha -1},\;\frac{2-3\alpha }{2\alpha -1},\;\frac{1-\alpha }{2\alpha -1},\;\frac{1-\alpha }{2\alpha -1},\;-\xi _0\right] ,\end{aligned}$$
(3.27)

with

$$\begin{aligned}&\xi _0=\frac{q^2}{a^2b^2}\left( \frac{b}{r_0}\right) ^{\frac{4}{3}}\left( \frac{b}{r}\right) ^{\frac{2}{3}(1-2\alpha )},\nonumber \\&\xi =\frac{q^2}{a^2b^2}\left( \frac{r_0}{b}\right) ^{2\nu }\left( \frac{b}{r}\right) ^{2\gamma \left( \frac{1}{\beta }-2\alpha \right) }.\end{aligned}$$
(3.28)

Note that the Mathematica-7 software has been used for solving the differential equations, and we have used the notations \(_2{\widetilde{F}}_1[a,\;b,\;c,\;z]\) and \(_3{\widetilde{F}}_2[a,\;b,\;c,\;d,\;e,\;z]\) for representing the HypergeometricPFQRegularized functions. They take the following general form

$$\begin{aligned}&_p{\widetilde{F}}_q[a_1,\;a_2,...,\;a_p,\;b_1,\;b_2,...,\;b_q,\;z]\nonumber \\&\quad \equiv HypergeometricPFQRegularized\nonumber \\&\qquad [a_1,\;a_2,\;...,a_p,\;b_1,\;b_2,...,\;b_q,\;z], \end{aligned}$$
(3.29)

which is related to the Hypergeometric function \(_pF_q[a_1,\;a_2,...,a_p,\;b_1,\;b_2,...b_q,\;z]\) via

$$\begin{aligned}&_p{\widetilde{F}}_q[a_1,\;a_2,...,a_p,\;b_1,\;b_2,...,\;b_q,\;z]\nonumber \\&\quad =\frac{_p F_q [a_1\;,a_2\;,...,a_p\;,b_1\;,b_2\;,...,\;b_q,\;z]}{\Gamma (b_1)\Gamma (b_2)...\Gamma (b_q)}. \end{aligned}$$
(3.30)

By expanding the terms in powers of \(\xi \) (or \(\xi _0\)), we obtain

$$\begin{aligned} W(r)=\left\{ \begin{array}{ll} -\frac{m}{r^\nu }-\frac{2\Lambda r^{2}}{(\nu +1)(2+3\nu )}\left( \frac{b}{r}\right) ^{2\beta \gamma } +\frac{2q^{2}r^2}{\delta b^{2\delta }(2\alpha \gamma +\nu )}\left( \frac{b}{r}\right) ^{2\delta }\\ +{{{\mathcal {O}}}}\left( \frac{1}{a^2}\right) ,\;\; \delta =2\alpha \gamma +\nu +1, \;\;\;\nu \ne -\frac{2}{3},\\ \\ -m\;r^{\frac{2}{3}}-6\Lambda b^2\left( \frac{r}{b}\right) ^{\frac{2}{3}} +\frac{9q^{2}r^2}{b^2(\alpha -1)^2}\left( \frac{b}{r_0}\right) ^{\frac{4}{3}}\left( \frac{b}{r}\right) ^{\frac{2}{3}(\alpha +1)}\\ +{{{\mathcal {O}}}}\left( \frac{1}{a^2}\right) , \;\;\;\;\;\nu =-\frac{2}{3}, \end{array} \right. \end{aligned}$$
(3.31)

which are just the same as obtained in [54] when the limit \( a \rightarrow \infty \) is taken.

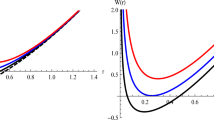
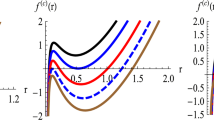
Now, we explore existence of the horizon radii, if any. They are the real roots of \(W(r=r_+)=0\), and cannot be determined analytically. Therefore, we use the plots of W(r) versus r as shown in Figs. 1 and 2. The figures show that, for the properly fixed parameters, two-horizon, one-horizon and naked singularity BHs can occur.

Fig. 1
figure 1

W(r) versus r for \(b=1,\;\alpha = 2.2,\; r_0 = 1,\; m = 10,\; \Lambda = -1,\; q = 1\). Left:\(\nu =-0.37\) and \(a=1.26\text{(black) },\;1.346\text{(blue) },\;1.44\text{(red) }\). Right: \(a=1.44\) and \( \nu =-0.362\text{(black) },\;-0.376\text{(blue) },\;-0.385\text{(red) }\)

Full size image
Fig. 2
figure 2

W(r) versus r for \(\nu =-\frac{2}{3},\;b=1,\;\ell =1,\; r_0 = 1,\; m =8,\; \Lambda = -1,\; q = 1\). Left:\(\alpha =2\) and \(a=1.06\text{(black) },\;1.13\text{(blue) },\;1.25\text{(red) }\). Right: \(a=1.4\) and \( \alpha =1.98\text{(black) },\;2.023\text{(blue) },\;2.08\text{(red) }\)

Full size image

It is well-known that one can interpret the solutions given in Eq. (3.20) as BHs, if two following conditions are fulfilled together. (i) The solutions are required to have at least one horizon radius, which has been confirmed regarding the plots of Figs. 1 and 2. (ii) The curvature scalars are needed to have at least one essential singularity. This requirement can be explored by analyzing the Ricci and Kretschmann scalars. As it can be seen by calculations, these scalars take the following forms

$$\begin{aligned}&{{{\mathcal {R}}}} = -W''-\frac{2(\nu +1)}{r}W'-\frac{2\nu (\nu +1)}{r^2}W, \end{aligned}$$
(3.32)
$$\begin{aligned}&{{{\mathcal {R}}}}^{\alpha \beta \rho \lambda }{{{\mathcal {R}}}}_{\alpha \beta \rho \lambda }=\left( W'' \right) ^2+2 \left( \nu + 1 \right) ^2 \left( \frac{W'}{r} \right) ^2 + 4\nu \left( \nu + 1 \right) ^2\frac{W W'}{r^3} + 4\nu ^2 \left( \nu + 1 \right) ^2 \left( \frac{W}{r^2} \right) ^2 . \end{aligned}$$
(3.33)

By substituting Eq. (3.20) and it’s first and second derivatives into Eqs. (3.32) and (3.33), after analyzing the final relations, we found that these curvature scalars diverge as the limit \(r\rightarrow 0^+\) is taken. It means that the spacetimes identified by the metric functions (3.20) include an essential singularity at the point \(r=0\). Therefore, noting existence of both, the horizon for the metric functions and the essential singularity for the spacetime, our solutions are really BHs. Thermodynamics of the new Ed BHs are studied in the next section.

4 Thermodynamics of EdBI BHs

In this section, at first we calculate the thermodynamic quantities then, making use of them we explore validity of the first law of BH thermodynamics for both of new Ed BHs. The Hawking temperature on the BH horizon, which is defined in terms of the surface gravity \(\kappa \) as \(T=\frac{\kappa }{2\pi }\) with \(\kappa =\sqrt{-\frac{1}{2}(\nabla _\mu \chi _{_{\nu }})(\nabla ^\mu \chi ^\nu )}\) and \(\chi ^\mu =(-1,\;0,\;0)\), is obtained as [62, 63]

$$\begin{aligned} T=\frac{1}{4 \pi }\left( \frac{dW(r)}{dr}\right) _{r=r_{+}} = \left\{ \begin{array}{ll} - \frac{r_+}{2\pi (\nu +1)} \left[ \Lambda \left( \frac{b}{r_{+}}\right) ^{4\beta \gamma } +\frac{2a^{2}\left( \sqrt{1+\xi _+} -H_+ \right) }{4\alpha \beta -4\beta ^2+1}\left( \frac{b}{r_{+}}\right) ^{6\alpha \gamma }\right] , \nu \ne -\frac{2}{3}\\ \\ -\frac{3}{2\pi }\left[ \Lambda b\left( \frac{b}{r_{+}}\right) ^{\frac{1}{3}} +\frac{2a^{2}r}{4\alpha -3}\left( \frac{b}{r_+}\right) ^{2\alpha }\left( \sqrt{1+\xi _{0+}}-H_{0+}\right) \right] , \nu =-\frac{2}{3}. \end{array} \right. \end{aligned}$$
(4.1)

we have used the following notations

$$\begin{aligned}&H_+ = \;_2F_1\left[ \frac{1}{2},\;\frac{3 \alpha - 2 \beta }{ 2\lambda },\; 1+\frac{3 \alpha - 2 \beta }{2 \lambda },\; -\xi _+\right] \nonumber \\&\text{ with }\;\;\; \xi _+=\frac{q^2}{a^2b^2}\left( \frac{r_0}{b}\right) ^{2\nu }\left( \frac{b}{r_+}\right) ^{2\gamma \left( \frac{1}{\beta }-2\alpha \right) }. \end{aligned}$$
(4.2)
$$\begin{aligned}&H_0 = \;_2F_1\left[ \frac{1}{2},\;\frac{3 \alpha - 2}{1- 2\alpha },\; 1+\frac{3 \alpha - 2}{1-2 \alpha },\; -\xi _{0+}\right] ,\nonumber \\&\text{ with }\;\;\; \xi _{0+}=\frac{q^2}{a^2b^2}\left( \frac{b}{r_0}\right) ^{\frac{4}{3}}\left( \frac{b}{r_+}\right) ^{\frac{2}{3}(1-2\alpha )}.\end{aligned}$$
(4.3)

The mass parameter m is absent in Eq. (4.1). This is due to the fact that it has been eliminated by use of the condition \(W(r_{+})=0\). A notable point is that the extreme BHs (i.e. the BHs with zero temperature) can exist provided that the BHs charge (i.e. \(q=q_{ext}\)) and horizon radius (i.e. \(r_{+}=r_{ext}\)) are chosen such that the equation \(T(r_{ext}, q_{ext})=0\) is satisfied. To find the vanishing point of the BH temperature labeled by \(r_+=r_{ext}\), we use the plots. The plots of T versus \(r_{+}\) are shown in Figs. 3 and 4 (blue curves). The left panel of Fig. 3 show that, for the BHs with \(\nu =-\frac{2}{3}\), temperature may be positive every where. There is no vanishing point for temperature and extreme BHs does not exist. Noting right panel of Fig. 3, one can conclude that the BH temperature vanishes at \(r_+=r_{ext}\), the BHs with horizon radius equal to \(r_{ext}\) are known as extreme BHs. The physically reasonable BHs, with positive temperature, occur for \(r_+>r_{ext}\), and those with horizon radii smaller than \(r_{ext}\) have negative temperature. The BHs with negative temperature cannot be physically reasonable. We call them as the unphysical BHs. Also, the plots of T versus \(r_+\), for BHs with \(\nu \ne -\frac{2}{3}\), have been shown in Fig. 4. The plots show that extreme BHs can exist with horizon radius equal to \(r_{ext}\). The physical BHs occur with horizon radii greater than \(r_{ext}\), and unphysical BHs exist with horizon radii smaller than \(r_{ext}\).

The BH entropy is proportional to the BH surface area. Thus, as a pure geometrical quantity, it can be calculated as

$$\begin{aligned} S=\frac{2\pi r_{+}R(r_{+})}{4}=\frac{\pi r^{\nu +1}_{+}}{2r^\nu _0}.\end{aligned}$$
(4.4)

Where, \(r_+\) is the BH horizon radius, and is the real root of \(W(r_+)=0\). Also, in the absence of dilaton field (i.e. \(\nu =0\)) Eq. (4.4) reduces to its corresponding value in the Einstein gravity theory [33].

The electric potential on the horizon of the charged BHs, as a thermodynamic quantity, can be calculated by use of the following relation [64, 65]

$$\begin{aligned} U(r_+)=A_\mu \chi ^\mu |_{\text{ reference }}-A_\mu \chi ^\mu |_{r=r_{+}},\end{aligned}$$
(4.5)

which gives the electric potential relative to a reference point. Noting Eq. (3.13) the electric potential can be written as [32, 66]

$$\begin{aligned} U(r_+)= & {} \frac{cq}{2\alpha \gamma +\nu } \left( \frac{b}{r_+}\right) ^{2\alpha \gamma }\left( \frac{r_0}{r_+}\right) ^{\nu } \;_2F_1\left[ \frac{1}{2},\; \frac{2\alpha \gamma +\nu }{4 \gamma \lambda },\;1\right. \nonumber \\&\left. +\frac{2\alpha \gamma +\nu }{4 \gamma \lambda },\;-\xi _+\right] .\end{aligned}$$
(4.6)

that we have assumed that the electric potential vanishes at the reference point located at infinity. This is possible for all values of \(\nu \) in its allowed range, provided that the other constants are chosen properly. Also, c is a constant coefficient which will be fixed later.

Regarding the Gauss’s electric law, total charge Q of the BHs can be calculated as a conserved quantity. That is [67, 68]

$$\begin{aligned} Q=\frac{1}{4\pi }\int \sqrt{-g}L_{{{\mathcal {F}}}}({{{\mathcal {F}}}}, \phi )F_{tr} d\Omega .\end{aligned}$$
(4.7)

Now, by use of Eqs. (2.12), (III.5) and (IV.7) one can show that

$$\begin{aligned} Q=\frac{q}{2},\end{aligned}$$
(4.8)

which is just the electric charge of BTZ BHs.

Now, we proceed to calculate the BH mass by use of the Brown-York mass proposal. Thus, we need the line element to be rewritten in the following form [60, 61, 69, 70]

$$\begin{aligned} ds^2=-F^2(\rho )dt^2+\frac{d\rho ^2}{G^2(\rho )}+\rho ^2d\theta ^2.\end{aligned}$$
(4.9)

Since the matter field does not contain derivatives of metric, the quasilocal mass \({{{\mathcal {M}}}}\) must be calculated based on the following relation

$$\begin{aligned} {{{\mathcal {M}}}}=2F(\rho )[G_0(\rho )-G(\rho )].\end{aligned}$$
(4.10)

The \(G_0(\rho )\) is determined by imposing the zero mass condition on the \(G(\rho )\). By introducing the new variable \(\rho =rR(r)\), we have

$$\begin{aligned} dr^2=\frac{d\rho ^2}{(1+\nu )^2R^2},\end{aligned}$$
(4.11)

and comparing with the line element (3.4), in terms of the metric function W(r), we have

$$\begin{aligned} F^2(\rho )=W\left( r(\rho )\right) ,\end{aligned}$$
(4.12)

and

$$\begin{aligned} G^2(\rho )=(1+\nu )^2\left( R(\rho )\right) ^2W\left( r(\rho )\right) .\end{aligned}$$
(4.13)

By substituting \(F(\rho )\) and \(G(\rho )\) into Eq. (4.10), after taking the limit \(\rho \rightarrow \infty \) the BH mass M can be calculated. That is

$$\begin{aligned} M=\frac{\nu +1}{8r_{_0}^{\nu }}m,\end{aligned}$$
(4.14)

which is the same as that obtained in [54], and reduces to that of the BTZ BHs if we set \(\nu =0\).

Now, by use of the condition \(W(r_+)=0\) one can obtain the mass parameter m, and after substituting it into Eq. (4.14) we obtain

$$\begin{aligned}&M(r_+,q)=\left\{ \begin{array}{ll} \frac{-1}{2} \left( \frac{r_+}{r_0} \right) ^{\nu +1} \left[ \frac{ \Lambda r_0^2}{2 (2 + 3 \nu )} \left( \frac{b}{r_+}\right) ^{4 \beta \gamma }-\frac{ a^2 r_0^2(\nu +1) \eta (r_+)}{1 + 3 \nu + 4 \alpha \gamma }\left( \frac{b}{r_+}\right) ^{6 \alpha \gamma }\right] ,\;\;\;\;\;\;\;\nu \ne -\frac{2}{3},\\ \\ -\frac{ \Lambda b^2}{4}\left( \frac{r_0}{b} \right) ^{\frac{2}{3}} \ln \left( \frac{r_+}{\ell }\right) +\frac{3 a^2 r^2_+ \zeta (r_+)}{4(4 \alpha -3)^2}\left( \frac{r_0}{r_+} \right) ^{\frac{2}{3}}\left( \frac{b}{r_+}\right) ^{2 \alpha }, \;\;\;\;\nu =-\frac{2}{3}, \end{array} \right. \end{aligned}$$
(4.15)

which can be regarded as a Smarr-type mass formula, and regarding Eqs. (4.4) and (4.8) it can be considered as a function of S and Q. Making use of Eq. (4.15) and noting Eq. (4.1) one can show that

$$\begin{aligned} \left( \frac{\partial M}{\partial S}\right) _Q=T, \;\; \text{ for }\;\;\;\;\nu =-\frac{2}{3} \;\;\;\; \text{ and }\;\;\;\nu \ne -\frac{2}{3}. \end{aligned}$$
(4.16)

Also, by fixing the constant c introduced in Eq. (4.6) to \(c=(4\alpha \beta -4\beta ^2+1)^{-1}\) [32, 71], we have

$$\begin{aligned} \left( \frac{\partial M}{\partial Q}\right) _S=U, \;\;\text{ for }\;\;\;\;\nu =-\frac{2}{3} \;\;\;\;\; \text{ and }\;\;\;\nu \ne -\frac{2}{3}. \end{aligned}$$
(4.17)

Thus, by considering T and U as intensive quantities conjugate to extensive parameters S and Q, one can conclude that the first law of BH thermodynamics in the form of

$$\begin{aligned} d M(S,Q)= T dS+U dQ,\end{aligned}$$
(4.18)

is valid for both of our novel EdBI BHs.

5 SH and BH stability

Thermal stability of a BH can be analyzed by use of the canonical ensemble method and noting the signature of SH. In this method, a BH with positive SH is locally stable. The unstable BHs, those with negative SH, experience phase transition to be stable. The points at which SH vanishes are known as the first-order phase transition points. The divergent points of SH are the positions of second-order phase transition [72,73,74]. Therefore, we must to calculate SH of our new dilatonic BHs. The SH of a BH, as a thermodynamic system, can is defined through the following relation

$$\begin{aligned} {{{\mathcal {H}}}}_Q =T\left( \frac{\partial S}{\partial T}\right) _Q. \end{aligned}$$
(5.1)

By combining Eqs. (4.16) and (5.1), we can write

$$\begin{aligned} {{{\mathcal {H}}}}_Q =\frac{T}{M_{SS}},\;\;\;\;\text{ and }\;\;\;\;\; M_{SS}=\left( \frac{\partial T}{\partial S}\right) _Q. \end{aligned}$$
(5.2)

Note that the subscript Q emphasizes that in working derivative with respect to S, Q must be considered as a constant. In the following subsections, after calculating the SH, with constant BH charge, we will analyze thermal stability of BHs separately.

5.1 The case of \(\nu =-\frac{2}{3}\)

As it is shown in Eq. (5.2), the numerator of SH is just the BH temperature which has been presented in Eq. (4.1). The denominator can be find by use of Eqs. (4.1) and (4.4). That is

$$\begin{aligned} M_{SS}=\frac{3}{\pi ^2}\left( \frac{r_{+}}{r_0}\right) ^{\frac{2}{3}}\left\{ \Lambda \left( \frac{b}{r_{+}}\right) ^{\frac{4}{3}} -\frac{2a^{2}(1-2\alpha )}{4\alpha -3}\left( \frac{b}{r_{+}}\right) ^{2\alpha }\times \left[ 3\left( \sqrt{1+\xi _{0+}}-H_{0+}\right) -\left( \frac{\xi _{0+}}{\sqrt{1+\xi _{0+}}}+2\xi _0H_{0+}' \right) \right] \right\} , \end{aligned}$$
(5.3)

where

$$\begin{aligned} H'_{0+}= & {} -\frac{\partial H_{0+}}{\partial \xi _{0+}}=\frac{3\alpha -2}{2(\alpha -1)}\;\nonumber \\&\times _2F_1 \left[ \frac{3}{2},\;\frac{\alpha -1}{1-2\alpha },\;\frac{-\alpha }{1-2\alpha },\;-\xi _{0+} \right] . \end{aligned}$$
(5.4)
$$\begin{aligned} H_0= & {} H_4=\;_2F_1\left[ \frac{1}{2},\;\frac{2-3\alpha }{2\alpha -1},\;1+\frac{2-3\alpha }{2\alpha -1},\;-\xi _0 \right] .\nonumber \\ \end{aligned}$$
(5.5)

The divergent and vanishing points of SH cannot be obtained by analytic calculation. Thus, to find the points of first- and second-order phase transition points, we use the plots. The left panel of Fig. 3 show that, for the BHs with positive-valued temperature, there is only one point of second-order phase transition located at \(r_+=r_1\). There is no point of first-order phase transition, and BHs with \(r_+<r_1\) are locally stable. Noting the right panel of Fig. 3, one can conclude that the BHs with the horizon radii equal to \(r_{ext}\) and \(r_+=r_2\) undergo first- and second-order phase transition, respectively. The BHs with horizon radii in the range \(r_{ext}<r_{+}<r_2\) are locally stable.

5.2 The case of \(\nu \ne -\frac{2}{3}\)

Just like the previous case, after some algebraic calculations, the denominator of SH can be written in the following form

$$\begin{aligned} M_{SS}= & {} -\frac{1}{\pi ^2(\nu +1)^2}\left( \frac{r_0}{r_+}\right) ^{\nu }\left\{ \frac{2a^2(\nu +1)}{4\alpha \beta -4\beta ^2+1}\times \left( \frac{b}{r_{+}}\right) ^{6\alpha \gamma }\Bigg [(1-6\alpha \gamma )\left( \sqrt{1+\xi _+}-H_+ \right) \right. \nonumber \\&\quad \left. -2\gamma \lambda \left( \frac{\xi _+}{\sqrt{1+\xi _+}}+2\xi _+H'_+ \right) \Bigg ]+\Lambda (1+2\nu )\left( \frac{b}{r_{+}}\right) ^{4\beta \gamma } \right\} , \end{aligned}$$
(5.6)

in which

$$\begin{aligned} H'_+ = -\frac{\partial H_+}{\partial \xi _+}=\frac{3\alpha -2\beta }{2(3\alpha -2\beta +2\lambda )}\;_2F_1\left[ \frac{3}{2},\;\frac{3\alpha -2\beta +2\lambda }{2\lambda },\;\frac{3\alpha -2\beta +4\lambda }{2\lambda },\;-\xi _+ \right] . \end{aligned}$$
(5.7)

The plots of T and \({{{\mathcal {H}}}}_Q\) versus \(r_+\) have been shown in Fig. 4, for finding the phase transition points. According the left panel there is only one point of first-order phase transition located at \(r_{+}=r_{ext}\), no second-order phase transition takes place and the BHs with horizon radii greater than \(r_{ext}\) are locally stable. As the right panel shows the first- and second-order phase transitions occur for the BHs with \(r_{+}=r_{ext}\) and \(r_{+}=r_{2}\), respectively. The BHs with the horizon radii in the range \(r_{ext}<r_{+}<r_{2}\), with positive SH and temperature, are locally stable.

Fig. 3
figure 3

T(blue) and \({{{\mathcal {H}}}}_Q\)(black) versus \(r_+\) for \(\nu =-\frac{2}{3},\;b=1,\;\ell =1,\; r_0 = 1,\; m =8,\; \Lambda = -1,\; q = 1\). Left:\(\alpha =2\) and \(a=1.06\text{(black) },\;1.13\text{(blue) },\;1.25\text{(red) }\). Right: \(a=1.4\) and \( \alpha =1.98\text{(black) },\;2.023\text{(blue) },\;2.08\text{(red) }\)

Full size image
Fig. 4
figure 4

T(blue) and \({{{\mathcal {H}}}}_Q\)(black) versus \(r_+\) for \(\nu \ne -\frac{2}{3},\;b=1,\;\ell =1,\; r_0 = 1,\; m =8,\; \Lambda = -1,\; q = 1\). Left:\(\alpha =2\) and \(a=1.06\text{(black) },\;1.13\text{(blue) },\;1.25\text{(red) }\). Right: \(a=1.4\) and \( \alpha =1.98\text{(black) },\;2.023\text{(blue) },\;2.08\text{(red) }\)

Full size image

6 BHs in the STBI theory

In the previous sections, we have provided exact BH solutions and related thermodynamic properties in EdBI gravity theory. Now, we are in the situation to extend these studies to the case of STBI theory. This can be done by use of the inverse CT on the solutions of EdBI gravity. At fist, we calculate elements of the STBI metric \({\bar{g}}_{\mu \nu }\). Making use of Eq. (2.4) we have \({\bar{g}}_{\mu \nu }=\left( \frac{b}{r}\right) ^{4\alpha \gamma }g_{\mu \nu }\) for the following ST line element

$$\begin{aligned} d{\bar{s}}^2\!=\!{\bar{g}}_{\mu \nu }dx^\mu dx^\nu \!=\!-A(r)dt^2+\frac{1}{B(r)}dr^2+r^2C^2(r)d\theta ^2.\nonumber \\ \end{aligned}$$
(6.1)

As the result, we can write

$$\begin{aligned} \left. \begin{array}{ll} A(r)=\left( \frac{b}{r}\right) ^{4\alpha \gamma }W(r),\\ \\ B(r)=\left( \frac{b}{r}\right) ^{-4\alpha \gamma }W(r),\\ \\ C(r)=\left( \frac{b}{r}\right) ^{2\alpha \gamma }R(r). \end{array} \right. \end{aligned}$$
(6.2)

Note that R(r) and W(r), as the exact solutions of EdBI theory, have presented in Eqs. (3.10) and (3.20), respectively. We have plotted B(r) versus r, for the cases of \(\nu =-\frac{2}{3}\) and \(\nu \ne -\frac{2}{3}\) in Figs. 5 and 6, respectively. It is clear that, the two-horizon, extreme and naked singularity ST BHs can occur.

Also, having \(\Omega \) and combining Eqs. (2.7) and (2.9), after some calculations, we have

$$\begin{aligned} {{\bar{\phi }}}(\phi )=\sqrt{1-\left( 2\alpha \right) ^{-2}}\;e^{2\alpha \phi },\;\;\;\;\;\;\;\;\;\alpha >\frac{1}{2}.\end{aligned}$$
(6.3)

It gives the JF scalar function \({{\bar{\phi }}}\) in terms its corresponding quantity in the EF labeled by \(\phi \), presented in Eq. (3.11). Now, one can calculate the arbitrary functions \(A_1\), \(A_2\) and \(A_3\), appeared in the JF action (II.1). Noting Eq. (2.9), we have

$$\begin{aligned} \left. \begin{array}{ll} A_1(\phi )=e^{-2\alpha \phi },\\ \\ A_2(\phi )=-2e^{-2\alpha \phi },\\ \\ A_3(\phi )=\frac{1}{2}V(\phi )e^{-6\alpha \phi }. \end{array} \right. \end{aligned}$$
(6.4)
Fig. 5
figure 5

B(r) versus r for \(b=1,\;\alpha = 2.2,\; r_0 = 1,\; m = 10,\; \Lambda = -1,\; q = 1\). Left:\(\nu =-0.37\) and \(a=1.315\text{(black) },\;1.347\text{(blue) },\;1.38\text{(red) }\). Right: \(a=1.44\) and \( \nu =-0.373\text{(black) },\;-0.3758\text{(blue) },\;-0.379\text{(red) }\)

Full size image
Fig. 6
figure 6

B(r) versus r for \(\nu =-\frac{2}{3},\;b=1,\;\ell =1,\; r_0 = 1,\; m =8,\; \Lambda = -1,\; q = 1\). Left:\(\alpha =2\) and \(a=1.1\text{(black) },\;1.129\text{(blue) },\;1.17\text{(red) }\). Right: \(a=1.25\) and \( \alpha =2.005\text{(black) },\;2.0133\text{(blue) },\;2.02\text{(red) }\)

Full size image

Thermodynamic properties of the STBI BHs can be studied noting those of EdBI theory. The temperature on the horizon of STBI BHs \({\bar{T}}\) as follows

$$\begin{aligned} \left. \begin{array}{ll} {\bar{T}}=\frac{1}{4\pi }\left( \sqrt{\frac{B(r)}{A(r)}}\frac{d A(r)}{dr}\right) _{_{r=r_{+}}}\\ \\ =\frac{1}{4\pi }\left( \frac{b}{r_{+}}\right) ^{-4\alpha \gamma }\frac{d}{dr}\left[ \left( \frac{b}{r}\right) ^{4\alpha \gamma }W(r)\right] _{_{r=r_{+}}}\\ \\ =\frac{1}{4\pi }\frac{d W(r)}{dr}|_{_{r=r_{+}}}\\ \\ =T. \end{array} \right. \end{aligned}$$
(6.5)

An immediate consequence is that the horizon temperature of the STBI BHs is just equal to that of EdBI BHs. Also, other quantities such as charge, mass, entropy and electric potential are identical in both of the Einstein and Jordan frames. Through calculation of a Smarr-type mass formula for the STBI, we obtain

$$\begin{aligned} {\bar{U}}=\frac{\partial {\bar{M}}({\bar{S}},{\bar{Q}})}{\partial {\bar{Q}}}, \;\;\;\;\;\;\;\;\text{ and }\;\;\;\;\;\;\;\;{\bar{T}}=\frac{\partial {\bar{M}}({\bar{S}},{\bar{Q}})}{\partial {\bar{S}}},\end{aligned}$$
(6.6)

from which we can write

$$\begin{aligned} d{\bar{M}}({\bar{S}},{\bar{Q}})=\frac{\partial {\bar{M}}({\bar{S}},{\bar{Q}})}{\partial {\bar{S}}}d{\bar{S}}+\frac{\partial {\bar{M}}({\bar{S}},{\bar{Q}})}{\partial {\bar{Q}}}d{\bar{Q}},\end{aligned}$$
(6.7)

which confirms validity of the first law of BH thermodynamics for STBI BHs. It can be easily shown that the SH of STBI BHs is just equal to that of EBId BHs. Consequently, the STBI and EdBI BHs have the same stability properties as shown in Figs. 3 and 4.

7 Conclusions

Here, we studied thermodynamic properties of charged \((2+1)\)-dimensional ST BHs in the presence of BI nonlinear electrodynamics. Since the analytic solutions to the field equations of ST gravity theory, which are written in the JF, can not be obtained directly, we have translated the JF action to the EF by use of the CTs. The EF field equations, known as the Ed gravity theory, have been solved in a static and circularly symmetric geometry. The corresponding solutions in the ST gravity have been obtained by applying the inverse CTs. As the result, we introduced two novel classes of exact BH solutions in both of the Jordan and Einstein frames, which can produce the two-horizon, extreme and naked singularity BHs. It is notable that all the exact solutions of EdBI theory recover the corresponding values in the Ed-Maxwell gravity, when the nonlinearity parameter a is chosen very large. The thermodynamic quantities such as BH entropy, electric potential and temperature, as well as the BH charge and mass, as the conserved quantities, have been calculated under the influence of BI nonlinear electrodynamics. It has been shown that these thermodynamic and conserved quantities are identical in both of the Jordan and Einstein frames. Also, through a Smarr-type mass formula, it has been proved that the standard form of the first law of BH thermodynamics is valid for both of the ST and Ed BHs. Thermal stability or phase transition of the BHs have been explored, in both of the ST and Ed theories, by use of the canonical ensemble method. From the viewpoint of canonical ensemble method, and noting properties of the CTs, we found that both of the ST and Ed BHs have the same thermodynamic behaviors.

Geometrical thermodynamics and P-V criticality of the ST and Ed BHs will be studied in a forthcoming paper.