1 Introduction

Elusive signals of new particles involving boosted hadronic jets may arise in a variety of models, see for example Refs. [1,2,3,4,5]. Their detection at the Large Hadron Collider (LHC) is quite demanding and requires tools that distinguish between ‘signal’ jets originating from boosted massive particles, and ‘background’ jets from quarks and gluons produced by QCD interactions. Jet substructure tools [6,7,8,9,10] originally introduced for the discrimination of Standard Model (SM) heavy particles (top quarks and W/Z/H bosons) from QCD jets, are essential for this goal.

In order not to rely on specific assumptions about the nature of the new particles, a generic tagger is necessary to search for these elusive signals. This was indeed the motivation for the anti-QCD tagger in Ref. [11]. This tagger uses a relatively simple neural network (NN) architecture and is trained with QCD jets (background) and various types of multi-pronged signal jets. It is remarkable that, despite being a fully-supervised tool, the anti-QCD tagger is able to recognise as signal a wide variety of massive multi-pronged jets. The key aspect to achieve this, is the use of the so-called model-independent (MI) data in the training: massive jets with \(n= 2,3,4\) prongs (this number can of course be increased above \(n=4\)) but otherwise phase-space agnostic. As it was shown in Ref. [11], this setup provides sensitivity to six-pronged jets not used in the training. Mass unspecific supervised tagging (MUST) [12] extends this concept by including the jet mass (\(m_J\)) and transverse momentum (\(p_{TJ}\)) as training variables, so that the taggers are applicable across a quite wide range of \(m_{J}\) and \(p_{TJ}\). An alternative to MI data is explored in Ref. [13].

Generic taggers for multi-pronged jets can also be built by using representation learning, e.g. with an autoencoder [14,15,16,17,18]. Without the need of any signal assumption, but only using background (pseudo-)data, an unsupervised tagger can learn the background features in order to pinpoint outliers, i.e. signal jets that deviate from the known pattern. A great advantage of unsupervised learning is that the tool does not depend on our modeling of the signals and backgrounds, and can directly be trained on data. On the other hand, the performance is worse than with supervised learning, as shown for example in Ref. [19].

The application of supervised taggers to data raises concerns about their dependence on the modeling of parton showers and hadronisation, as well as other effects that are not described from first principles but phenomenologically. These issues were studied in Ref. [20] for a W boson tagger using jet images. For that specific setup, a variation of signal efficiency \(\varepsilon _\text {sig} = 0.4-0.56\) is found at fixed background rejection \(\varepsilon _\text {bkg}^{-1} = 10\) by using several Monte Carlo codes.Footnote 1 We note that the size of this variation is expected to depend on

  1. (a)

    the type of signal jet (mass and prongness);

  2. (b)

    the transverse momentum;

  3. (c)

    the specific method used to build the tagger: jet images versus jet substructure variables, NN architecture, etc.

In this respect, it is important to point out that Ref. [20] also finds a variation of the same size, \(\varepsilon _\text {sig} = 0.35-0.52\) for \(\varepsilon _\text {bkg}^{-1} = 10\), by using as discriminant the jet mass and subjettiness ratio \(\tau _{21}\) [7, 8] and pseudo-data generated by several Monte Carlo codes. Obviously, the variation in the latter case is not due to the design of the discriminant – in other words, whether it is trained using certain Monte Carlo code or another – which is the same in both cases. Rather, the difference arises from how pseudo-data is.

In this paper we address the modeling dependence for a generic tagger built upon MUST. We consider two Monte Carlo hadronisation schemes, using Pythia [21] and Herwig [22], and explore the differences when training taggers and applying them to pseudo-data obtained with each of these generators. We study 18 benchmarks with signal jets of different mass, transverse momentum and prongness. There are two meaningful comparisons to be made: (i) different tagger, same data; (ii) same tagger, different data. The conclusions, which we anticipate here, are:

  1. (i)

    For a given pseudo-data set, the dependence of the results on the generator used for the design (training) of the tagger is small, and insignificant in many cases.

  2. (ii)

    On the other hand, there is a significant dependence of the results on how pseudo-data is: the same tagger exhibits differences when applied to Pythia and Herwig simulation.

The first test suggests that, even if Monte Carlo does not perfectly model the showering and hadronisation, MUST-based taggers correctly learn prongness from simulation and will perform well on real data. The second test shows that tagging performance will mostly depend on how real data actually is, i.e. if the subjets within a multi-pronged jet are more or less resolved. (Notice that this is in agreement with the differences found in Ref. [20] when using the same discriminator \(\tau _{21}\) on different pseudo-data.) And of course, the latter statement not only applies to supervised taggers, but also to unsupervised ones: if real data is such that it is harder to distinguish the substructure of a multi-pronged jet from a QCD jet, this will be the case for any tool.

The remainder of this paper is structured as follows. In Sect. 2 we describe our setup for the Monte Carlo generation and training of the NNs. We compare the jet substructure observables obtained with either simulation scheme in Sect. 3. When possible, we compare our qualitative results obtained with subjettiness variables with the findings of Ref. [20] using jet images. We compare the tagging performances in Sect. 4. Finally, our results are discussed in Sect. 5.

2 Monte Carlo generation and design of the taggers

In Ref. [12] we developed a supervised generic jet tagger, dubbed as GenT, in order to discriminate between quark/gluon one-pronged jets and multi-pronged jets from boosted massive particles. Here we train taggers GenT \(^x\) with the same NN architecture, in the transverse momentum range \(p_{TJ}\in [200,2200]\) GeV and extending the mass range to \(m_J \in [10,500]\) GeV.

QCD jets are generated with MadGraph [23], in the inclusive process \(pp \rightarrow jj\). Event samples are generated in 100 GeV bins of \(p_T\), starting at [200, 300] GeV and up to \(p_T \ge 2.2\) TeV. Large event samples are required in order to have sufficient events at high \(m_J\): \(10^6\) events are generated in each bin of \(p_{TJ}\), and both jets are used in the analysis, amounting to a total of 42 million QCD jets, which are used in the training and validation of the NNs, as well as for tests.

The MI data used to train and validate the NNs are generated with Protos [24] in the process \(pp \rightarrow ZS\), with \(Z \rightarrow \nu \nu \) and S a scalar. We consider the six decay modes

$$\begin{aligned}&\text {4-pronged (4P):}&S \rightarrow u \bar{u} u \bar{u} \,,~ S \rightarrow b \bar{b} b \bar{b} \,, \nonumber \\&\text {3-pronged (3P):}&S \rightarrow F \,\nu \,; \quad F \rightarrow u d d,~ F \rightarrow u d b \,, \nonumber \\&\text {2-pronged (2P):}&S \rightarrow u \bar{u} \,,~ S \rightarrow b \bar{b} \,, \end{aligned}$$
(1)

to generate multi-pronged jets (F is a colour-singlet fermion). To remain as model-agnostic as possible, the S and F decays are implemented with a flat matrix element, so that the decay weight of the different kinematical configurations only corresponds to the four-, three- or two-body phase space. Signal jet samples are also generated in 100 GeV bins of \(p_T\). To cover different jet masses, the mass of S (and of F for 3-pronged decays) is randomly chosen event by event within the interval [10, 800] GeV, and setting an upper limit \(M_S \le p_T R/2\) to ensure that all decay products are contained in a jet of radius \(R=0.8\).

The signals used to evaluate the performance of the taggers are generated with MadGraph. The models of Refs. [4, 5] are implemented in Feynrules  [25] and interfaced to MadGraph using the universal Feynrules output [26]. We consider the production of a neutral gauge boson \(Z'\) with decay into SM particles as well as new scalars. We generically denote by A the new scalars decaying into a quark pair, and by S the new scalars decaying into an AA pair. (The actual scalar decays are \(Z' \rightarrow A_i A_j\), \(Z' \rightarrow S_i S_j\), with \(i\ne j\), but we omit subindices for simplicity and consider \(M_{A_i} = M_{A_j}\), \(M_{S_i} = M_{S_j}\)). The various processes considered are

  1. (1)

    \(Z' \rightarrow WW\), \(W \rightarrow q \bar{q}\).

  2. (2)

    \(Z' \rightarrow AA\), \(A \rightarrow b \bar{b}\).

  3. (3)

    \(Z' \rightarrow t \bar{t}\), \(t \rightarrow W b \rightarrow q \bar{q} b\).

  4. (4)

    \(Z' \rightarrow SS\), with \(S \rightarrow WW \rightarrow 4q\).

  5. (5)

    \(Z' \rightarrow SS\), with \(S \rightarrow AA \rightarrow 4b\).

All signal samples contain \(2 \times 10^{5}\) events except the \(t \bar{t}\) samples, which contain \(6 \times 10^{5}\) events.

The parton-level event samples are showered and hadronised either with Pythia 8.3 or with Herwig 7.2, with standard settings. The former uses dipole showers by default [27], while the latter uses angular-ordered showers [28]. In both cases, a fast detector simulation is performed with Delphes [29], using the CMS card. Jets are reconstructed with FastJet [30] applying the anti-\(k_T\) algorithm [31] with \(R=0.8\), and groomed with Recursive Soft Drop [32] with parameters \(N = 3\), \(\beta = 1\), \(z_\text {cut} = 0.05\). Jet substructure is characterised by a set of subjettiness variables proposed in [7, 33],

$$\begin{aligned} \left\{ \tau _1^{(1/2)}, \tau _1^{(1)}, \tau _1^{(2)}, \dots , \tau _{5}^{(1/2)}, \tau _{5}^{(1)}, \tau _{5}^{(2)}, \tau _{6}^{(1)}, \tau _{6}^{(2)} \right\} , \end{aligned}$$
(2)

computed for ungroomed jets.Footnote 2 These 17 subjettiness variables constitute the input to the NN together with the groomed jet mass and \(p_T\).

Two taggers are built exactly in the same way, but using either Pythia or Herwig showering and hadronisation. The training sets are obtained by dividing the \(m_J\) range in ten bins, all of 50 GeV except the first one [10, 50] GeV, and the \(p_T\) range in 100 GeV bins, starting at [200, 300] GeV and up to [2100, 2200] GeV. In the lower \(p_T\) samples the higher mass bins are dropped, considering the full \(m_J\) range only for the \(p_T\) bins above 1200 GeV. In each two-dimensional bin of \(m_{J}\) and \(p_{TJ}\) we select for the training set 3000 events from each of the six types of signal jets in (1), and 18,000 background events, in order to have a balanced sample. The proportion of quark and gluon jets in the background samples is \(p_T\)-dependent. The total size of the training sets is around 5.5 million events. The validation sets used to monitor the NN performance are similar to the training ones.

The NNs are implemented using Keras [34] with a TensorFlow backend [35]. For the training, a standardisation of the 19 inputs, based on the SM background distributions, is performed. The NNs contain two hidden layers of 2048 and 128 nodes, with Rectified Linear Unit (ReLU) activation for the hidden layers. For the output layer a sigmoid function is used, yielding the NN score, i.e. the signal probability, that can be used to discriminate signal jets from QCD jets. The NNs are optimised by minimising the binary cross-entropy loss function, using the Adam [36] algorithm, and a batch size of 64. The NNs obtained after the training with these large event sets are remarkably stable. We train five instances of each NN, with different initial random seeds and select the ones that give the largest area under the \((\varepsilon _\text {sig},\varepsilon _\text {bkg})\) curve (AUC) for the validation sets. The rest of NNs are used to estimate the stability of the results.

3 Substructure observables

With the default options for parton showering and hadronisation used here, Pythia and Herwig produce the two most differing results among five combinations studied in Ref. [20]. It is very difficult, if not impossible, to fully understand the results obtained next section from the behaviour observed in substructure observables: there are many non-trivial correlations among the inputs to the NNs. However, there a few qualitative aspects that can be learnt by the comparison of the subjettiness variables obtained after Pythia and Herwig simulation.

For the comparison we consider QCD and multi-pronged jets with \(p_{TJ}\in [1.4,1.6]\) TeV and two ranges for the jet masses: (a) \(m_{J}\in [60,100]\) GeV; (b) \(m_{J}\in [350,450]\) GeV. The multi-pronged jets are generated from the decay of a 3.3 TeV \(Z'\):

  • For \(m_{J}\in [60,100]\) GeV we use \(Z' \rightarrow WW\), \(W \rightarrow q \bar{q}\) (two-pronged, 2P) and \(Z' \rightarrow SS\), \(S \rightarrow AA \rightarrow 4b\) with \(M_S = 80\) GeV, \(M_A = 30\) GeV (four-pronged, 4P)

  • For \(m_{J}\in [350,450]\) GeV we use \(Z' \rightarrow AA\), \(A \rightarrow b \bar{b}\) with \(M_A = 400\) GeV (2P) and \(Z' \rightarrow SS\), \(S \rightarrow AA \rightarrow 4b\) with \(M_S = 400\) GeV, \(M_A = 80\) GeV (4P).

We present in Fig. 1 the normalised distributions of \(\tau _n^{(1)}\) with \(n=1,2,3,4\), for QCD and multi-pronged jets with \(m_{J}\in [60,100]\) GeV. The results for \(m_{J}\in [350,450]\) GeV are displayed in Fig. 2.

Fig. 1
figure 1

Normalised distributions of \(\tau _n^{(1)}\) with \(n=1,2,3,4\), for QCD and multi-pronged jets with \(m_{J}\in [60,100]\) GeV (see the text for details)

Full size image
Fig. 2
figure 2

Normalised distributions of \(\tau _n^{(1)}\) with \(n=1,2,3,4\), for QCD and multi-pronged jets with \(m_{J}\in [350,450]\) GeV (see the text for details)

Full size image
Fig. 3
figure 3

ROC curves 2P jets with \(m_{J}\sim 80\) GeV

Full size image
Fig. 4
figure 4

ROC curves for 4P jets with \(m_{J}\sim 80\) GeV

Full size image
Fig. 5
figure 5

ROC curves for 3P top jets

Full size image

The distributions for \(n=1\) (top rows) are quite the same when using Pythia (red) or Herwig (blue). For \(n = 2\) there is some difference, which increases with n for 2P and 4P jets. Furthermore, for 2P and 4P jets the level of (dis)agreement between Pythia and Herwig distributions is alike, with the exception of \(\tau _4^{(1)}\) for \(m_{J}\in [350,450]\) GeV. Because the discrimination between 2P jets and the QCD background is less sensitive to higher-order \(\tau _n^{(i)}\), one then expects that the differences in tagger performance found for 2P jets will be milder. This is confirmed by the results presented in the next section. In addition, we remark that the differences are more significant for lighter boosted particles, i.e. \(m_{J}\in [60,100]\) GeV.

We also observe that in all cases the Pythia and distributions for QCD jets are very similar. On the other hand, Herwig distributions for \(\tau _n^{(1)}\), \(n \ge 2\) are slightly shifted towards larger values for 2P and 4P jets. This fact indicates that in 2P and 4P jets the subjets are less resolved, and is in agreement with Ref. [20], which shows for W jets that Herwig with angular-ordered shower produces more radiation between the subjet cores, which are therefore less resolved. This pattern suggests that the discrepancy is mainly due to the hadronisation scheme, rather than parton showering. The results in Ref. [20] confirm this point: the differences that arise when using the same hadronisation scheme but different showering (e.g. Herwig with either angular-ordered or dipole shower; Pythia with either dipole or antenna showers) are quite small.

Fig. 6
figure 6

ROC curves for 4P jets with \(m_{J}\sim 200\) GeV

Full size image

4 Tagging performance

In this section we test the two taggers trained either with Pythia (P) or Herwig (H) on pseudo-data, generated with either of these Monte Carlo simulations. This allows to disentangle two important aspects that are independent:

  1. (a)

    the modeling dependence, that is, the different performance of the two taggers when applied to the same pseudo-data;

  2. (b)

    the dependence of the performance on pseudo-data itself, that is, applying the same tagger to different pseudo-data.

We consider the five signal processes mentioned in Sect. 2 with different masses, totaling 18 benchmarks:

  1. (1)

    \(Z' \rightarrow WW\), with \(M_{Z'} = 1.1\), 2.2, 3.3 TeV.

  2. (2)

    \(Z' \rightarrow AA\), with \((M_{Z'},M_A) =\) (1100, 80), (2200, 80), (3300, 80), (3300, 400) GeV.

  3. (3)

    \(Z' \rightarrow t \bar{t}\) with \(M_{Z'} =\) 2.2, 3.3 TeV.

  4. (4)

    \(Z' \rightarrow SS\), \(S \rightarrow WW\) with \((M_{Z'},M_S) =\) (2200, 200), (3300, 200), (3300, 400) GeV.

  5. (5)

    \(Z' \rightarrow SS\), \(S \rightarrow AA\) with \((M_{Z'},M_S,M_A) =\) (1100, 80, 30), (2200, 80, 30), (3300, 80, 30), (2200, 200, 80), (3300, 200, 80), (3300, 400, 80) GeV.

For the benchmarks with \(M_{Z'} = 1.1\), 2.2, 3.3 TeV we select jets with transverse momentum within the respective intervals \(p_{TJ}\in [0.4,0.6]\), [0.9, 1.1], [1.4, 1.6] TeV. For the benchmarks with jet mass \(m_{J}\sim 80\), 175, 200, 400 GeV we select jets with mass in the respective intervals \(m_{J}\in [60,100]\), [150, 200], [160, 240], [350, 450] GeV.

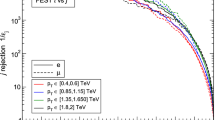
We first present in Fig. 3 the receiver operating characteristic (ROC) curves for light 2P jets: \(Z' \rightarrow WW\) and \(Z' \rightarrow AA\) with \(M_A = 80\) GeV, with \(M_{Z'} = 1.1\), 2.2 and 3.3 TeV. Figure 4 shows results for 4P jets of the same mass, using \(Z' \rightarrow SS\) with \(M_S = 80\) GeV, \(M_A = 30\) GeV, and the same \(Z'\) masses. The gray bands around the curves represent the variation of \((\varepsilon _\text {sig},\varepsilon _\text {bkg}^{-1})\) among the five trainings of the NN. Except at the upper left side, the bands are barely visible and their width is comparable to the thickness of the curves. Showing the variation of \((\varepsilon _\text {sig},\varepsilon _\text {bkg}^{-1})\) among trainings can be used to test whether the difference between P and H taggers is a statistical artifact. We also include horizontal lines at \(\varepsilon _\text {bkg}^{-1} = 20\), 100 to guide the eye to estimate the variation in \(\varepsilon _\text {sig}\) between the different curves.

The W and S benchmarks with \(m_{J}\sim 80\) GeV, \(p_{TJ}\sim 1\) TeV were already studied for the anti-QCD tagger [11] and the differences between P and H taggers were quite more pronounced than when using MUST. Overall, there are several important conclusions that can be drawn from Figs. 3 and 4:

  1. (i)

    The P and H pseudo-data have significant differences. This can be seen by comparing, e.g. the two red lines in the plots, which correspond to the same (P) tagger.

  2. (ii)

    However, the taggers very effectively learn to discriminate jets of different prongness, independently of the details of the parton shower and hadronisation. The P and H taggers have nearly the same performance on a given pseudo-data set, especially for W bosons. This can be verified by comparing solid and dashed lines of the same colour.

  3. (iii)

    Consequently, the ability to distinguish between multi-pronged and QCD jets depends rather on which pseudo-data is considered (in other words, how pseudo-data is), than on the simulation employed in the tagger training. Pictorially, the curves corresponding to different tagger, same pseudo-data are (much) closer than the curves corresponding to same tagger, different pseudo-data.

The differences between taggers increase with \(p_{TJ}\), corresponding to more collimated jets, in which case the higher-order \(\tau _n^{(i)}\) are expected to play a more important role in the discrimination. Also, one can notice that for 2P signals the P tagger is better on P and H pseudo-data, while the opposite behaviour is seen for 4P signals except (partially) for \(p_{TJ}\sim 500\) GeV. We believe this is a consequence of the NN training and the balance in the minimisation of the loss function for several multi-pronged jet MI data, which favours a better discrimination of 2P signals in the case of P training, and a better discrimination of 4P signals in the case of H training. The small spread between trainings (gray band) shows this is not a statistical effect.

Fig. 7
figure 7

ROC curves for jets with \(m_{J}\sim 400\) GeV

Full size image

Results for 3P top jets are presented in Fig. 5. With a larger ratio \(m_{J}/p_{TJ}\), the impact of higher-order \(\tau _n^{(i)}\) is smaller for the discrimination between signal jets and the background. Consequently, all the ROC curves are quite close for \(M_{Z'} = 2.2\) TeV (top panel), and slightly spread for \(M_{Z'} = 3.3\) TeV (bottom panel).

Detailed results for 4P jets of \(m_{J}\sim 200\) GeV, with four light quarks or four b quarks, are shown in Fig. 6. They confirm the claims (i-iii) above. Also as expected, the spread between curves is larger than for 3P jets of similar mass (compare with Fig. 5) because higher-order \(\tau _n^{(i)}\) are more important for the discrimination. For the same reason, the curves are closer for \(M_{Z'} = 2.2\) TeV than for \(M_{Z'} = 3.3\) TeV, the latter corresponding to more collimated jets.

Finally, we present results for heavier jets with \(m_{J}\sim 400\) GeV in Fig. 7. Again, the three conclusions (i-iii) above hold, as well as the other two features observed, namely (a) the differences are smaller for 2P than for 4P jets; (b) the curves are closer for larger \(m_{J}/p_{TJ}\). We note that the gray bands are wider in these benchmarks because of the smaller statistics of the samples, which is also seen by the wavy behaviour at low signal efficiencies.

5 Discussion

In this paper we have addressed the modeling dependence of jet taggers designed using the MUST method. There are two independent aspects to be considered here: modeling dependence (difference between taggers designed using Pythia or Herwig) and data dependence (difference when a given tagger is applied to either Pythia or Herwig pseudo-data). From our analysis of 18 benchmarks in Sect. 4, two salient conclusions can be drawn:

  1. (i)

    Pseudo-data generated with Pythia and Herwig have significant differences.

  2. (ii)

    MUST-based taggers very effectively learn to discriminate jets of different prongness, independently of the details of the parton shower and hadronisation.

Here, (i) is inferred from the comparison of same tagger, different pseudo-data, whereas (ii) results from comparing different taggers, and same pseudo-data. Within the several cases analysed, we find that for 2P jets the modeling dependence is insignificant, and completely negligible in some of the benchmarks. For 3P and 4P jets it is small or quite small.

The urging question is, of course, whether either Pythia or Herwig in their different tunes, or other Monte Carlo code for showering and hadronisation like Sherpa [37] describe sufficiently well the jet substructure in data, so that supervised generic taggers can be reliably used to search for new physics. Although this cannot be answered only with Monte Carlo studies, the conclusion (ii) above shows that MUST-designed taggers are quite robust and gives confidence in their application to real data. In this regard, possible improvements in the description of the substructure variables of boosted W jets (which can be measured in data) would also benefit the Monte Carlo description for four-pronged jets.

Because the MUST-based taggers effectively learn prongness when trained either with Pythia or with Herwig Monte Carlo simulation, one expects that their performance on real data will mostly depend on data itself, that is, whether the subjets within a multi-pronged jet are more or less resolved, so that they are easier or more difficult to distinguish from QCD jets. Of course, this data feature also affects unsupervised tools. Consequently, the price to pay by using supervised generic taggers (modeling dependence) may well not be so high, while one can benefit from their better discrimination power.