Rational non-linear electrodynamics of AdS black holes and extended phase space thermodynamics

Abstract

The critical behaviour of magnetically charged AdS black holes based on rational non-linear electrodynamics (RNED) in an extended phase space is investigated herein. The cosmological constant is considered as thermodynamic pressure, and the black hole mass is identified with the chemical enthalpy. An analogy with the van der Walls liquid–gas system is found, and the critical exponents coincide with those of the van der Waals system. The thermodynamics of RNED-AdS black holes and phase transitions are studied, and new thermodynamic quantities conjugated to the non-linear parameter of RNED and magnetic charge are defined. The consistency of the first law of black hole thermodynamics and the Smarr formula is demonstrated.

1 Introduction

Nowadays, black holes are treated as thermodynamic systems [1,2,3], with the area of a black hole being the entropy and its surface gravity identified with the temperature [4, 5]. This has advanced our understanding of the link between gravity and quantum physics. The consideration of anti-de Sitter (AdS) spacetime with a negative cosmological constant gave rise to the phase behaviour of black holes [6]. An important step was later made to consider a holographic picture where black holes are a system which is dual to conformal field theories [7,8,9]. The study of the holography has led to progress in solving problems in quantum chromodynamics [10] and condensed matter physics [11, 12]. It was recently proposed that the cosmological constant plays a role of pressure which is a conjugate to volume in black hole thermodynamics. This has allowed scientists to compare the phase transitions in black holes with those in liquid–gas thermodynamics [13,14,15,16]. Various aspects of Born–Infeld (BI) electrodynamics in AdS spacetime with a negative cosmological constant were studied in [17,18,19,20,21,22,23], and an analogy to van der Waals fluids in black hole physics was found. In this paper, we study the thermodynamics in the framework of rational non-linear electrodynamics (RNED) [24, 25] coupled to gravity with a negative cosmological constant. Previous studies [25] have considered the thermodynamics in asymptotically flat spacetime in the framework of Einstein’s theory of relativity without the cosmological constant. As a result, pressure was not introduced, the pressure–volume (P-V) term was absent in black hole thermodynamics, and there was no analogy with van der Vaals fluid. In addition, in [25], the local stability of black holes for the canonical ensemble (the charge is fixed) was investigated by calculating the specific heat. In the present paper, we study the global black hole stability by analysing the Gibbs free energy within the grand canonical ensemble in extended phase space. The RNED model possesses attractive properties such as the absence of singularity of charges at the origin and finite electrostatic energy. Similar features take place in Born–Infeld electrodynamics. In addition, RNED coupled to gravity describes the inflation of the universe [26] and provides the correct shadow of the M87* black hole [27]. Electrically charged black holes within RNED coupled to gravity without the cosmological constant were studied in [28]. Here, we investigate magnetically charged black holes in the framework of gravity with the cosmological constant.

The structure of the paper is as follows. In Sect. 2 we obtain the RNED-AdS metric function with the asymptotic as $r\rightarrow \infty$ and $r\rightarrow 0$. When the Schwarzschild mass is zero, the solution is non-singular, with the de Sitter core as $r\rightarrow 0$. The extended thermodynamic phase space including a negative cosmological constant as pressure with the conjugate volume and coupling $\beta$ of RNED is analysed in Sect. 3. We find the thermodynamic magnetic potential and the thermodynamic conjugate to the coupling. The generalized Smarr relation is obtained. The black hole thermodynamics is studied in Sect. 4. We obtain critical values of the specific volume, critical temperature and critical pressure. The Gibbs free energy is analysed in Sect. 4.1. The black hole mass is considered as a chemical enthalpy. We depict the pressure and the critical isotherms. In Sect. 4.2, the critical exponents are established. Section 5 is a summary.

We use units with $c=1$, $\hbar =1$ and $k_B=1$.

2 RNED-AdS solution

The action of Einstein-RNED theory in AdS spacetime is given by

$$\begin{aligned} I=\int \mathrm{d}^{4}x\sqrt{-g}\left( \frac{R-2\Lambda }{16\pi G_N}+{\mathcal {L}}({\mathcal {F}}) \right) , \end{aligned}$$

(1)

where the negative cosmological constant is $\Lambda =-3/l^2$, with l being the AdS radius. The RNED Lagrangian [24] in Gaussian units reads

$$\begin{aligned} {{{\mathcal {L}}}}({\mathcal {F}}) =-\frac{{{{\mathcal {F}}}}}{4\pi (1+2\beta {{{\mathcal {F}}}})}, \end{aligned}$$

(2)

with ${{{\mathcal {F}}}}=F^{\mu \nu }F_{\mu \nu }/4=(B^2-E^2)/2$, $F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu$. The maximum electric field in the origin is $E(0)=1/\sqrt{\beta }$ [24]. By varying action (1) with respect to $g_{\mu \nu }$ and $A_{\mu }$, one can obtain the equations of gravitational and electromagnetic fields as follows

$$\begin{aligned}&R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R+\Lambda g_{\mu \nu } =8\pi G_N T_{\mu \nu }, \end{aligned}$$

(3)

$$\begin{aligned}&\partial _{\mu }\left( \sqrt{-g}{\mathcal {L}}_{{\mathcal {F}}}F^{\mu \nu }\right) =0, \end{aligned}$$

(4)

where R is the Ricci scalar and $R_{\mu \nu }$ is the Ricci tensor. The energy–momentum symmetric tensor of electromagnetic fields can be found by the variation of ${\mathcal {L}}\left( {\mathcal {F}}\right)$ with respect to the metric tensor, and it is given by

$$\begin{aligned} T_{\mu \nu }=F_{\mu \rho }F_{\nu }^{~\rho }{\mathcal {L}}_{{\mathcal {F}}}+g_{\mu \nu }{\mathcal {L}}\left( {\mathcal {F}}\right) , \end{aligned}$$

(5)

and ${\mathcal {L}}_{{\mathcal {F}}}=\partial {\mathcal {L}}( {\mathcal {F}})/\partial {\mathcal {F}}$.

We consider the four-dimensional static spherical symmetric line element

$$\begin{aligned} \mathrm{d}s^{2}=-f(r)dt^{2}+\frac{1}{f(r)}\mathrm{d}r^{2}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}\right) . \end{aligned}$$

(6)

The spherical symmetry leads to the tensor $F_{\mu \nu }$ which involves only the radial electric field $F_{01}=-F_{10}$ and radial magnetic field $F_{23}=-F_{32}=q_\mathrm{m}\sin (\theta )$, where $q_\mathrm{m}$ is the magnetic charge. The energy–momentum tensor becomes diagonal with $T_{0}^{~0}=T_{r}^{~r}$ and $T_{\theta }^{~\theta }=T_{\phi }^{~\phi }$. The metric function, within general relativity, with spherical symmetry is given by

$$\begin{aligned} f(r)=1-\frac{2m(r)G_N}{r}, \end{aligned}$$

(7)

where the mass function is [29]

$$\begin{aligned} m(r)=m_0+4\pi \int _{0}^{r}\rho (r)r^{2}\mathrm{d}r, \end{aligned}$$

(8)

where $m_0$ is the integration constant corresponding to the Schwarzschild mass, and $\rho$ is the energy density, which also includes the term due to the cosmological constant. In the following, we consider only magnetic black holes because the electrically charged black holes (for models which have Maxwell’s weak-field limit) lead to singularities [29].

Now, we will study the static magnetic black holes. Taking into account that the electric charge $q_e=0$, ${\mathcal {F}}=q_\mathrm{m}^2/(2r^4)$ ($q_\mathrm{m}$ is a magnetic charge), we obtain from Eq. (5) the magnetic energy density plus the term corresponding to the negative cosmological constant

$$\begin{aligned} \rho =\frac{q_\mathrm{m}^2}{8\pi (r^4+\beta q_\mathrm{m}^2)}-\frac{3}{8\pi G_Nl^2}. \end{aligned}$$

(9)

With the help of Eqs. (8) and (9), one finds the mass function

$$\begin{aligned} m(r)= & {} m_0+\frac{q_\mathrm{m}^{3/2}}{8\sqrt{2}\beta ^{1/4}}\biggl [\ln \left( \frac{r^2-\sqrt{2q_\mathrm{m}}\beta ^{1/4}r+q_\mathrm{m}\sqrt{\beta }}{r^2 +\sqrt{2q_\mathrm{m}}\beta ^{1/4}r+q_\mathrm{m}\sqrt{\beta }}\right) \nonumber \\&+2\arctan \left( \frac{\sqrt{q_\mathrm{m}}\beta ^{1/4}+\sqrt{2}r}{\sqrt{q_\mathrm{m}}\beta ^{1/4}}\right) \nonumber \\&-2\arctan \left( \frac{\sqrt{q_\mathrm{m}}\beta ^{1/4}-\sqrt{2}r}{\sqrt{q_\mathrm{m}}\beta ^{1/4}}\right) \biggr ]-\frac{r^3}{2G_Nl^2}. \end{aligned}$$

(10)

The black hole magnetic mass is given by [25]

$$\begin{aligned} m_M= & {} 4\pi \int _0^\infty \frac{q_\mathrm{m}^2}{8\pi (r^4+\beta q_\mathrm{m}^2)}r^2\mathrm{d}r=\frac{\pi q_\mathrm{m}^{3/2}}{4\sqrt{2}\beta ^{1/4}}\nonumber \\\approx & {} 0.56\frac{q_\mathrm{m}^{3/2}}{\beta ^{1/4}}. \end{aligned}$$

(11)

Equation (11) shows that at the limit $\beta =0$ (Maxwell’s case), the magnetic energy becomes infinite. Making use of Eqs. (7) and (10), we obtain the metric function

$$\begin{aligned} f(r)=1-\frac{2m_0G_N}{r}-\frac{q_\mathrm{m}^{3/2}G_Ng(r)}{4\sqrt{2}\beta ^{1/4}r}+\frac{r^2}{l^2}, \end{aligned}$$

(12)

where

$$\begin{aligned} g(r)\equiv & {} \ln \left( \frac{r^2-\sqrt{2q_\mathrm{m}}\beta ^{1/4}r+q_\mathrm{m}\sqrt{\beta }}{r^2+\sqrt{2q_\mathrm{m}}\beta ^{1/4}r+q_\mathrm{m}\sqrt{\beta }}\right) \\&+2\arctan \left( \frac{\sqrt{q_\mathrm{m}}\beta ^{1/4}+\sqrt{2}r}{\sqrt{q_\mathrm{m}}\beta ^{1/4}}\right) \nonumber \\&-2\arctan \left( \frac{\sqrt{q_\mathrm{m}}\beta ^{1/4}-\sqrt{2}r}{\sqrt{q_\mathrm{m}}\beta ^{1/4}}\right) . \end{aligned}$$

In general relativity without the cosmological constant (neglecting $r^2/l^2$ in Eq. (12)), the metric function as $r\rightarrow \infty$ approaches [25]

$$\begin{aligned} f(r)= & {} 1-\frac{2(m_0+m_M)G_N}{r}\nonumber \\&+\frac{q_\mathrm{m}^2G_N}{r^2}+{\mathcal {O}}(r^{-5})~~~\text{ as }~r\rightarrow \infty . \end{aligned}$$

(13)

In this case, the correction to the Reissner–Nordström solution, according to Eq. (13), is in the order of ${\mathcal {O}}(r^{-5})$. The total mass (ADM mass) of the black hole $M\equiv m_0+m_M$ includes the Schwarzschild mass $m_0$ and the magnetic mass $m_M$. It is worth noting that if we put $m_0=0$, i.e the black hole mass is the magnetic mass, as $r\rightarrow 0$, from Eq. (12), we find the asymptotic with a de Sitter core

$$\begin{aligned} f(r)= & {} 1-\frac{G_Nr^2}{\beta }+\frac{r^2}{l^2}+\frac{G_Nr^6}{7\beta ^2q_\mathrm{m}^2}-\frac{G_Nr^{10}}{11\beta ^3q_\mathrm{m}^4}\nonumber \\&+{\mathcal {O}}(r^{12})~~~\text{ as }~r\rightarrow 0. \end{aligned}$$

(14)

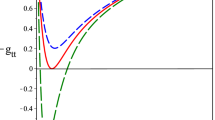
The solution (14) is regular because at $r= 0$, we have $f(0)= 1$. The plot of the metric function (12) is depicted in Fig. 1 at $m_0=0$, $G_N=1$, $l=10$ for different parameters $q_\mathrm{m}$ and $\beta$. Figure 1 shows that black holes can have two horizons, one extreme horizon or no horizons depending on model parameters.

Fig. 1

The plot of the function f(r) at $m_0=0$, $G_N=1$ and $l=10$

3 First law of black hole thermodynamics and the Smarr relation

If one considers that black holes are classical objects, then there is an analogy between black hole mechanics and thermodynamics. The role of temperature is played by the surface gravity, and the event horizon corresponds to entropy S. Despite the fact that classical black holes have zero temperature, Hawking proved that black holes emit radiation with a blackbody spectrum [5]. The first law of black hole thermodynamics reads $\delta M=T\delta S+\Omega \delta J+\Phi \delta Q$, with black hole mass M, charge Q and angular momentum J, where M, J, Q are the extensive, and T, $\Omega$, $\Phi$ are intensive thermodynamic variables. The disadvantage of the formulated first law of black hole thermodynamics was the absence of the pressure–volume term $P\delta V$. To improve the first law of black hole thermodynamics, the pressure was associated with a negative cosmological constant $\Lambda$, which gives a positive vacuum pressure in spacetime. Then, the generalized first law of black hole thermodynamics became $\delta M=T\delta S+ V\delta P+\Omega \delta J+\Phi \delta Q$, with $V=\partial M/\partial P$ at constant S, J, Q [30,31,32]. A comparison of the first law of black hole mechanics with ordinary thermodynamics requires us to interpret M as a chemical enthalpy [30], $M=U+PV$, where U is the internal energy.

To obtain the Smarr formula from the first law of black hole thermodynamics, we consider dimensions of physical quantities [33] (see also [30]). Let us consider the units with $G_N=1$. Then, from the dimensional analysis, we obtain $[M]=L$, $[S]=L^2$, $[P]=L^{-2}$, $[J]=L^2$, $[q_\mathrm{m}]=L$, $[\beta ]=L^2$. Considering $\beta$ as a thermodynamic variable and taking into consideration Euler’s theorem (see [15]) (the Euler scaling argument), we obtain the mass $M(S,P,J,q_\mathrm{m},\beta )$,

$$\begin{aligned} M=2S\frac{\partial M}{\partial S}-2P\frac{\partial M}{\partial P}+2J\frac{\partial M}{\partial J}+q_\mathrm{m}\frac{\partial M}{\partial q_\mathrm{m}}+2\beta \frac{\partial M}{\partial \beta },\nonumber \\ \end{aligned}$$

(15)

where $\partial M/\partial \beta \equiv {{{\mathcal {B}}}}$ is the thermodynamic conjugate to the coupling $\beta$, and the black hole volume V and pressure P are given by [34, 35]

$$\begin{aligned} V=\frac{4}{3}\pi r_+^3,~~~P=-\frac{\Lambda }{8\pi }=\frac{3}{8\pi l^2}. \end{aligned}$$

(16)

We consider the non-rotating stationary black hole so that $J=0$. From Eq. (12) and equation $f(r_+)=0$, where $r_+$ is the horizon radius, we find (at $G_N=1$)

$$\begin{aligned} M=\frac{r_+}{2}+\frac{r_+^3}{2l^2}+\frac{\pi q_\mathrm{m}^{3/2}}{4\sqrt{2}\beta ^{1/4}}-\frac{q_\mathrm{m}^{3/2}g(r_+)}{8\sqrt{2}\beta ^{1/4}}. \end{aligned}$$

(17)

Making use of Eq. (17), we obtain

$$\begin{aligned} \delta M&=\left( \frac{1}{2}+\frac{3r_+^2}{2l^2}-\frac{q_\mathrm{m}^{3/2}}{8\sqrt{2}\beta ^{1/4}}\frac{\delta g(r_+)}{\delta r_+}\right) \delta r_+ -\frac{r_+^3}{l^3}\delta l\nonumber \\&\quad +\left( \frac{q_\mathrm{m}^{3/2}g(r_+)}{32\sqrt{2}\beta ^{5/4}}-\frac{\pi q_\mathrm{m}^{3/2}}{16\sqrt{2}\beta ^{5/4}}-\frac{q_\mathrm{m}^{3/2}}{8\sqrt{2}\beta ^{1/4}}\frac{\delta g(r_+)}{\delta \beta }\right) \delta \beta \nonumber \\&\quad +\left( \frac{3\pi q_\mathrm{m}^{1/2}}{8\sqrt{2}\beta ^{1/4}}-\frac{3q_\mathrm{m}^{1/2}g(r_+)}{16\sqrt{2}\beta ^{1/4}}-\frac{q_\mathrm{m}^{3/2}}{8\sqrt{2}\beta ^{1/4}}\frac{\delta g(r_+)}{\delta q_\mathrm{m}}\right) \delta q_\mathrm{m}. \end{aligned}$$

(18)

The Hawking temperature is given by

$$\begin{aligned} T=\frac{f'(r)|_{r=r_+}}{4\pi }. \end{aligned}$$

(19)

From Eqs. (12) and (19) we obtain the Hawking temperature ($G_N=1$)

$$\begin{aligned} T=\frac{1}{4\pi }\biggl (\frac{1}{r_+}+\frac{3r_+}{l^2}-\frac{q_\mathrm{m}^2r_+}{r_+^4+\beta q_\mathrm{m}^2}\biggr ), \end{aligned}$$

(20)

where we have used the equation

$$\begin{aligned} \frac{\delta g(r_+)}{\delta r_+}=\frac{4\sqrt{2q_\mathrm{m}}\beta ^{1/4}r_+^2}{r^4+q_\mathrm{m}^2\beta }. \end{aligned}$$

(21)

Making use of Eqs. (17), (20) and (21), we obtain

$$\begin{aligned} \frac{\partial M(r_+)}{\partial r_+}=2\pi r_+T. \end{aligned}$$

(22)

Then we find the entropy in our case of the RNED-AdS black hole

$$\begin{aligned} S=\int \frac{d M(r_+)}{T}=\int \frac{1}{T}\frac{\partial M(r_+)}{\partial r_+}\mathrm{d}r_+=\pi r_+^2. \end{aligned}$$

(23)

Thus, the Bekenstein–Hawking entropy holds. Then, from relations

$$\begin{aligned} \frac{\delta g(r_+)}{\delta \beta }= & {} -\frac{\sqrt{2q_\mathrm{m}}r_+^3}{\beta ^{3/4}(r_+^4+\beta q_\mathrm{m}^2)} ,~~~\frac{\delta g(r_+)}{\delta q_\mathrm{m}}\\= & {} -\frac{2\sqrt{2}\beta ^{1/4}r_+^3}{q_\mathrm{m}^{1/2}(r_+^4+\beta q_\mathrm{m}^2)} \end{aligned}$$

and Eqs. (16), (18), (20) and (23), we obtain the first law of black hole thermodynamics

$$\begin{aligned} \delta M = T\delta S + V\delta P + \Phi _\mathrm{m} \delta q_\mathrm{m} + {{{\mathcal {B}}}}\delta \beta , \end{aligned}$$

(24)

where the thermodynamic magnetic potential $\Phi _\mathrm{m}$ and the thermodynamic conjugate to the coupling $\beta$ are given by

$$\begin{aligned} \Phi _\mathrm{m}= & {} \frac{q_\mathrm{m}r_+^3}{4(r_+^4+\beta q_\mathrm{m}^2)}+\frac{3\pi q_\mathrm{m}^{1/2}}{8\sqrt{2}\beta ^{1/4}}- \frac{3q_\mathrm{m}^{1/2}g(r_+)}{16\sqrt{2}\beta ^{1/4}},\nonumber \\ {{{\mathcal {B}}}}= & {} \frac{q_\mathrm{m}^{3/2}g(r_+)}{32\sqrt{2}\beta ^{5/4}}-\frac{\pi q_\mathrm{m}^{3/2}}{16\sqrt{2}\beta ^{5/4}}+ \frac{q_\mathrm{m}^2r_+^3}{8\beta (r_+^4+\beta q_\mathrm{m}^2)}. \end{aligned}$$

(25)

The ${{{\mathcal {B}}}}$ in the Born–Infeld AdS case was referred to as ‘Born–Infeld vacuum polarization’ [36]. The presence of ${{{\mathcal {B}}}}$ is needed for consistency of the Smarr formula. The plot of $\Phi _\mathrm{m}$ vs $r_+$ is depicted in Fig. 2. According to Fig. 2, when coupling $\beta$ increases, the magnetic potential decreases, and at $r_+\rightarrow \infty$ it vanishes, $\Phi _\mathrm{m}(\infty )=0$. At $r_+ = 0$, $\Phi _\mathrm{m}$ is the finite value. The plot of the function ${{{\mathcal {B}}}}$ vs $r_+$ is presented in Fig. 3. It is worth noting that at $r_+ = 0$, the vacuum polarization ${{{\mathcal {B}}}}$ is finite. Figure 3 shows that when coupling $\beta$ increases, the absolute value of vacuum polarization decreases, and at $r_+\rightarrow \infty$ it becomes zero, ${{{\mathcal {B}}}}(\infty )=0$.

Fig. 2

The plot of the function $\Phi _\mathrm{m}$ vs $r_+$ at $q_\mathrm{m}=1$. The solid curve is for $\beta =0.05$, the dashed curve corresponds to $\beta =0.1$, and the dashed/dotted curve corresponds to $\beta =0.5$

Fig. 3

The plot of vacuum polarization ${{{\mathcal {B}}}}$ vs $r_+$ at $q_\mathrm{m}=1$. The solid curve is for $\beta =0.05$, the dashed curve corresponds to $\beta =0.1$, and the dashed/dotted curve corresponds to $\beta =0.5$

Making use of Eqs. (16), (17), (23) and (25), one can verify that the generalized Smarr formula holds,

$$\begin{aligned} M=2ST-2PV+q_\mathrm{m}\Phi _\mathrm{m}+2\beta {{{\mathcal {B}}}}. \end{aligned}$$

(26)

Making use of the Bekenstein and Hawking arguments [4, 37], we conclude that the second law of thermodynamics for AdS black holes also holds. The study of Born–Infeld electrodynamics in AdS spacetime in the extended phase space was presented in [38,39,40,41].

Table 1 Critical values of the specific volume and temperature at $q_\mathrm{m}=1$

4 The black hole thermodynamics

Making use of Eq. (20), we obtain the equation of state (EoS) for the RNED-AdS black hole

$$\begin{aligned} P=\frac{T}{2r_+}-\frac{1}{8\pi r_+^2}+\frac{q_\mathrm{m}^2}{8\pi (r_+^4+\beta q_\mathrm{m}^2)}. \end{aligned}$$

(27)

At $\beta =0$, Eq. (27) becomes the EoS for a charged (by linear Maxwell electrodynamics) AdS black hole [42]. If one compares the EoS of a charged AdS black hole with the van der Waals equation, then the specific volume v should be identified with $2l_Pr_+$ [42]. With $l_P=\sqrt{G_N}=1$, the horizon diameter $2r_+$ plays the role of the specific volume of the corresponding fluid. Thus, Eq. (27) becomes

$$\begin{aligned} P=\frac{T}{v}-\frac{1}{2\pi v^2}+\frac{2q_\mathrm{m}^2}{\pi (v^4+16\beta q_\mathrm{m}^2)}. \end{aligned}$$

(28)

Equation (28) qualitatively mimics the behaviour of the van der Waals fluid. Critical points take place at the inflection in the $P-v$ diagram with

$$\begin{aligned} \frac{\partial P}{\partial v}= & {} -\frac{T}{v^2}+\frac{1}{\pi v^3}-\frac{8q_\mathrm{m}^2v^3}{\pi (v^4+16\beta q_\mathrm{m}^2)^2}=0,\nonumber \\ \frac{\partial ^2 P}{\partial v^2}= & {} \frac{2T}{v^3}-\frac{3}{\pi v^4}-\frac{8q_\mathrm{m}^2v^2(48\beta q_\mathrm{m}^2-5v^4)}{\pi (v^4+16\beta q_\mathrm{m}^2)^3}=0. \end{aligned}$$

(29)

From Eq. (29) we obtain the equation for the critical points as follows

$$\begin{aligned} 8q_\mathrm{m}^2v_\mathrm{c}^6(3v_\mathrm{c}^4-80\beta q_\mathrm{m}^2)-(v_\mathrm{c}^4+16\beta q_\mathrm{m}^2)^3=0. \end{aligned}$$

(30)

It is difficult to obtain an analytical solution to Eq. (30). Equation (30) can be represented as the cubic equation for the parameter $\beta$ with the solution

$$\begin{aligned} \beta \!=\!\frac{\sqrt{5}v_\mathrm{c}^3}{2\sqrt{6}q_\mathrm{m}}\sinh \left( \frac{1}{3}\sinh ^{-1}\left( \frac{3\sqrt{6}}{5\sqrt{5}q_\mathrm{m}}v_\mathrm{c}\right) \right) \!-\!\frac{v_\mathrm{c}^4}{16q_\mathrm{m}^2}, \end{aligned}$$

(31)

where $\sinh ^{-1}(x)$ is the inverse hyperbolic $\sinh$ function. Making use of Eq. (31), the function $v_\mathrm{c}$ vs $\beta$ with $q_\mathrm{m}=1$ is depicted in Fig. 4. In accordance with Fig. 4, at $\beta >1.41$ (approximately), there are no real solutions to Eq. (30). At $0<\beta <1.41$, for each $\beta$ there are two real solutions for $v_\mathrm{c}$. The expression for the critical temperature follows from Eq. (27)

$$\begin{aligned} T_\mathrm{c}=\frac{1}{\pi v_\mathrm{c}}-\frac{8q_\mathrm{m}^2v_\mathrm{c}^5}{\pi (v_\mathrm{c}^4+16\beta q_\mathrm{m}^2)^2}. \end{aligned}$$

(32)

Fig. 4

The plot of the function $v_\mathrm{c}$ vs $\beta$ at $q_\mathrm{m}=1$

Numerical solutions to Eq. (30) and the critical temperatures for different values of $\beta$ are presented in Table 1, showing two inflection points for each $\beta$. The plot of $T_\mathrm{c}$ vs $\beta$ is depicted in Fig. 5. In accordance with Fig. 5, at $0<\beta <0.42$ (approximately) there is one critical temperature (for each $\beta$), but for $0.42<\beta <1.41$, two critical temperatures. It is worth noting that Fig. 4 also shows that for each $\beta$, there are two real positive critical points $v_\mathrm{c}$, but for the interval $0<\beta <0.42$, only one $v_\mathrm{c}$ gives the physical positive critical temperature. At the point $v_\mathrm{c}$, we have a second-order phase transition. The $P-v$ diagrams are given in Figs. 6 and 7 for some values of T. According to Fig. 6, for $q_\mathrm{m}=\beta =1$, there are two critical values, $v_{\mathrm{c}1}\approx 2.94305$ ($T_{\mathrm{c}1}=0.0402936$) and $v_{\mathrm{c}2}\approx 4.45663$ ($T_{\mathrm{c}2}=0.0448542$). Thus, there are inflection points, and the EoS in our case is more complicated compared to the van der Waals gas EoS and similar to the Born–Infeld AdS case. Figure 7 shows the non-critical behaviour of $P-v$ diagrams for $T=1, 2, 3$ and 4. The critical pressure is given by

$$\begin{aligned} P_\mathrm{c}=\frac{1}{2\pi v_\mathrm{c}^2}+\frac{2q_\mathrm{m}^2(16\beta q_\mathrm{m}^2-3v_\mathrm{c}^4)}{\pi (v_\mathrm{c}^4+16\beta q_\mathrm{m}^2)^2}. \end{aligned}$$

(33)

The plot of $P_\mathrm{c}$ vs $\beta$ is presented in Fig. 8. According to Fig. 8, at $0<\beta <0.77$ (approximately), there is one critical pressure (for each $\beta$), but for $0.77<\beta <1.41$, two. Also, for each $\beta$, there are two real positive solutions to Eq. (30) for critical points $v_\mathrm{c}$, but for the interval $0<\beta <0.77$, only one $v_\mathrm{c}$ gives the physical positive critical pressure. Making use of Eqs. (32) and (33), one obtains the critical ratio

$$\begin{aligned} \rho _\mathrm{c}=\frac{P_\mathrm{c}v_\mathrm{c}}{T_\mathrm{c}}=\frac{(v_\mathrm{c}^4+16\beta q_\mathrm{m}^2)^2+4q_\mathrm{m}^2v_\mathrm{c}^2(16\beta q_\mathrm{m}^2-3v_\mathrm{c}^4)}{2[(v_\mathrm{c}^4+16\beta q_\mathrm{m}^2)^2-8q_\mathrm{m}^2v_\mathrm{c}^6]},\nonumber \\ \end{aligned}$$

(34)

where $\beta$ is given by Eq. (31). The plot of $\rho _\mathrm{c}$ vs $\beta$ at $q_\mathrm{m}=1$ is depicted in Fig. 9. At $\beta =0$, we obtain $\rho _\mathrm{c}=3/8$ as for a van der Waals fluid. In accordance with Fig. 9, the critical ratio in our model decreases with $\beta$.

Fig. 5

The plot of the critical temperature $T_\mathrm{c}$ vs $\beta$ at $q_\mathrm{m}=1$

Fig. 6

The plot of the function P vs v at $q_\mathrm{m}=\beta =1$. The critical isotherms correspond to $T_{\mathrm{c}1}=0.0402936$ and $T_{\mathrm{c}2}=0.0448542$

Fig. 7

The plot of the function P vs v at $q_\mathrm{m}=\beta =1$ for $T=1, 2, 3$ and 4

Fig. 8

The plot of the critical pressure $P_\mathrm{c}$ vs $\beta$ at $q_\mathrm{m}=1$

Fig. 9

The plot of the critical ratio $\rho _\mathrm{c}$ vs $\beta$

4.1 The Gibbs free energy

Let us consider the expression for the Gibbs free energy for a fixed charge, coupling $\beta$ and pressure

$$\begin{aligned} G = M - TS. \end{aligned}$$

(35)

Here, M is considered as a chemical enthalpy that is the total energy of a system with its internal energy U and the energy PV to displace the vacuum energy of its environment: $M =U+PV$. From Eqs. (16) and (35) (at $G_N=1$), we obtain

$$\begin{aligned} G=\frac{r_+}{2}+\frac{4\pi r_+^3P}{3}+\frac{\pi q_\mathrm{m}^{3/2}}{4\sqrt{2}\beta ^{1/4}}-\frac{q_\mathrm{m}^{3/2}g(r_+)}{8\sqrt{2}\beta ^{1/4}} -\pi Tr_+^2,\nonumber \\ \end{aligned}$$

(36)

where $r_+$ is a function of P and T (see Eq. (27)). The plot of G vs T is depicted in Fig. 10. The behaviour of G depends on pressure P and coupling $\beta$. As an example, we consider the case with $\beta =0.6$ where there is one physical critical point (see Table 1 and Figs. 5 and 8), and $v_\mathrm{c}\approx 4.6745$, $T_\mathrm{c}\approx 0.0441$ and $P_\mathrm{c}\approx 0.0035$. The behaviour of the Gibbs free energy is similar to the RN-AdS black hole with one critical point and the corresponding first-order phase transition between small and large black holes (in subplots 1 and 2). In this case, there is a point at which two black holes have equal free energy. One can see two branches of black holes with a cusp, and the Gibbs free energy shows “swallowtail” behaviour with a first-order phase transition between two branches for $P<P_\mathrm{c}$. Subplots 3 and 4 in Fig. 10 display a characteristic shape similar to the Hawking–Page behaviour for the Schwarzschild-AdS case, and there is no first-order phase transition in the system for $P>P_\mathrm{c}$.

Fig. 10

The plot of the Gibbs free energy G vs T with $q_\mathrm{m}=1$, $\beta =0.6$

4.2 Critical exponents

We expand the critical values in small parameter $\beta$ as

$$\begin{aligned} v_\mathrm{c}= & {} 2\sqrt{6}q_\mathrm{m}-\frac{7}{9\sqrt{6}}\frac{\beta }{q_\mathrm{m}}+{{{\mathcal {O}}}}(\beta ^2),~~~\nonumber \\ T_\mathrm{c}= & {} \frac{1}{3\sqrt{6}\pi q_\mathrm{m}}+\frac{1}{108\sqrt{6}\pi }\frac{\beta }{q_\mathrm{m}^3}+{{{\mathcal {O}}}}(\beta ^2),~~~\nonumber \\ P_\mathrm{c}= & {} \frac{1}{96\pi q_\mathrm{m}^2}+\frac{7}{10368\pi }\frac{\beta }{q_\mathrm{m}^4}+{{{\mathcal {O}}}}(\beta ^2). \end{aligned}$$

(37)

It is worth noting that the critical point (37) at $\beta =0$ is the same as in charged AdS black hole [36], but there are corrections due to coupling $\beta$. The critical ratio $\rho _\mathrm{c}$ vs $\beta$ is depicted in Fig. 9, and the analytical expression for small $\beta$ is given by

$$\begin{aligned} \rho _\mathrm{c}=\frac{3}{8}+\frac{1}{96}\frac{\beta }{q_\mathrm{m}^2}+{{{\mathcal {O}}}}(\beta ^2). \end{aligned}$$

(38)

The value $\rho _\mathrm{c}=3/8$ takes place for the van der Waals fluid. The critical exponents show the physical quantity behaviour in the vicinity of the critical points which do not depend on details of the system. The exponent $\alpha$ defines the behaviour of the specific heat at the constant volume

$$\begin{aligned} C_v=T\frac{\partial S}{\partial T}\propto |t|^{-\alpha }, \end{aligned}$$

(39)

where $t=(T-T_\mathrm{c})/T_\mathrm{c}$. Because the entropy $S=\pi r_+^2=(3V/(4\pi ))^{2/3}$ is constant, we have $C_v=0$, and therefore $\alpha =0$. Let us define the quantities [15]

$$\begin{aligned} p=\frac{P}{P_\mathrm{c}},~~\nu =\frac{v}{v_\mathrm{c}}=\root 3 \of {\omega +1},~~\tau =\frac{T}{T_\mathrm{c}}=t+1. \end{aligned}$$

(40)

Taking into account Eq. (28), we obtain

$$\begin{aligned} p=\frac{\tau }{\nu \rho _\mathrm{c}}-\frac{1}{2\pi \nu ^2P_\mathrm{c}v_\mathrm{c}^2}+\frac{2q_\mathrm{m}^2}{\pi P_\mathrm{c}(\nu ^4v_\mathrm{c}^4+16\beta q_\mathrm{m}^2)}, \end{aligned}$$

(41)

where $P_\mathrm{c}$ is given by Eq. (33). One can expand p in small parameters t and $\omega$ near the critical point

$$\begin{aligned} p=1+At-Bt\omega -C\omega ^3-Dt\omega ^2+{{{\mathcal {O}}}}(\omega ^4), \end{aligned}$$

(42)

where

$$\begin{aligned} A= & {} \frac{1}{\rho _\mathrm{c}},~~~~B=\frac{1}{3\rho _\mathrm{c}},~~~~D=-\frac{2}{9\rho _\mathrm{c}},\nonumber \\ C= & {} \frac{14}{81 \rho _\mathrm{c}}-\frac{20}{81\pi P_\mathrm{c}v_\mathrm{c}^2}\nonumber \\&-\frac{8q_\mathrm{m}^2v_\mathrm{c}^8[(16\beta q_\mathrm{m}^2)^2+224\beta q_\mathrm{m}^2v_\mathrm{c}^4-35v_\mathrm{c}^8]}{81\pi P_\mathrm{c}v_\mathrm{c}^4(v_\mathrm{c}^4+16\beta q_\mathrm{m}^2)^4}. \end{aligned}$$

(43)

We included in Eq. (42) the additional term $Dt\omega ^2$, compared to [15], which is in the same order as $\omega ^3$. The small $\beta$ expansion gives

$$\begin{aligned} C=\frac{4}{81}+{{{\mathcal {O}}}}(\beta ). \end{aligned}$$

It is worth noting that value 4/81 is realized in the RN-AdS case [15]. We will follow the same avenue as in [15] to obtain critical exponents. Making use of Eq. (40), we obtain

$$\begin{aligned} dP=-P_\mathrm{c}(Bt+2Dt\omega +3C\omega ^2)d\omega . \end{aligned}$$

(44)

By using Maxwell’s equal area law [36], one finds [15]

$$\begin{aligned}&\omega _\mathrm{l}(Bt+Dt\omega _\mathrm{l}+C\omega _\mathrm{l}^2)=\omega _\mathrm{s}(Bt+Dt\omega _\mathrm{s}+C\omega _\mathrm{s}^2), \end{aligned}$$

(45)

$$\begin{aligned}&\int _{\omega _\mathrm{l}}^{\omega _\mathrm{s}} \omega \mathrm{d}P=0, \end{aligned}$$

(46)

where $\omega _\mathrm{s}$ and $\omega _\mathrm{l}$ correspond to the small and large black holes, respectively. The solution to Eqs. (45) and (46) is given by

$$\begin{aligned} \omega _\mathrm{l}= & {} \frac{-Dt+\sqrt{D^2t^2-4BCt}}{2C},~~~\nonumber \\ \omega _\mathrm{s}= & {} \frac{-Dt-\sqrt{D^2t^2-4BCt}}{2C}. \end{aligned}$$

(47)

At $D=0$, Eq. (47) becomes the solution obtained in [36]. Equation (47) is satisfied in the leading order up to ${{{\mathcal {O}}}} (t^{5/2})$. We use the following definitions: the difference of the large and small black hole volume on the given isotherm $v_\mathrm{l}-v_\mathrm{s}$, isothermal compressibility $\kappa _\mathrm{T}$, $|P-P_\mathrm{c}|$ on the critical isotherm $T = T_\mathrm{c}$,

$$\begin{aligned}&\eta = v_\mathrm{l}-v_\mathrm{s}\propto |t|^\beta ,~~\kappa _\mathrm{T}=-\frac{1}{v}\frac{\partial v}{\partial P}|_\mathrm{T}\propto |t|^{-\gamma }, \nonumber \\&|P-P_\mathrm{c}| \propto |v-v_\mathrm{c}|^\delta . \end{aligned}$$

(48)

Following the procedure of [36], one obtains the same values of critical exponents as in the BI-AdS case

$$\begin{aligned} \beta =\frac{1}{2},~~~~\gamma =3,~~~~\delta =3. \end{aligned}$$

(49)

We have studied critical exponents in the vicinity of the critical point for a small non-linearity parameter $\beta$ and obtained the result as in the mean field theory. Thus, we have the same universality class as for the van der Waals fluid. When parameter $\beta$ is not small, we cannot expand the critical temperature and pressure in $\beta$. Therefore, equalities in Eq. (40) will not hold, and the non-linearity of electromagnetism will influence the the critical exponents.

5 Summary

We have studied the thermodynamic behaviour of RNED charged black holes in an extended thermodynamic phase space. In this approach, the cosmological constant is identified with a thermodynamic pressure, and the mass of the black hole is the chemical enthalpy. We show an analogy with the van der Walls liquid–gas system, with the specific volume in the van der Waals equation being the diameter of the event horizon (at $G_N=1$). The critical ratio $\rho _\mathrm{c} = P_\mathrm{c}v_\mathrm{c}/T_\mathrm{c}$ is equal to the van der Waals value of 3/8 plus corrections ${{{\mathcal {O}}}}(\beta )$ due to coupling $\beta$. The critical exponents coincide with those of the van der Waals system, similar to the BI-AdS case. The thermodynamics of the RNED-AdS model was investigated, showing the critical behaviour and phase transitions. The phase space includes the conjugate pair $({{{\mathcal {B}}}},\beta$). A thermodynamic quantity ${{{\mathcal {B}}}}$ conjugated to the non-linear parameter $\beta$ of RNED has been defined. We have demonstrated the consistency of the first law of black hole thermodynamics and the Smarr formula which depends on the quantities ${{{\mathcal {B}}}}$, $\Phi _\mathrm{m}$ introduced. The critical points and phase transitions also depend on the RNED parameter $\beta$. Therefore, black hole thermodynamics (and black hole physics) is modified in our model of RNED-AdS. The critical exponents were calculated, and are the same as in the BI-AdS case.