Possible molecular states of $D^{(*)}D^{(*)}$ and $B^{(*)}B^{(*)}$ within the Bethe–Salpeter framework

Abstract

Recently the LHCb collaboration reported a new exotic state $T^+_{cc}$ which possesses $cc\bar{u}\bar{d}$ flavor structure. Since its mass is very close to the threshold of $D^0D^{*+}$ (or $D^{*0}D^{+}$) and its width is very narrow, it is inclined to conjecture that $T^+_{cc}$ is a molecular state of $D^0D^{*+}$ (or $D^{*0}D^{+}$). In this paper we study the possible molecular structures of $D^{(*)}D^{(*)}$ and $B^{(*)}B^{(*)}$ within the Bethe–Salpeter (B–S) framework. We employ one boson exchange model to stand the interaction kernels in the B–S equations. With reasonable input parameters we find the isospin eigenstate $\frac{1}{\sqrt{2}}(D^0D^{*+}-D^{*0}D^{+})$ ($J^P=1^+$) constitutes a solution, which supports the ansatz of $T^+_{cc}$ being a molecular state of $D^0D^{*+}$ (or $D^{*0}D^{+}$). With the same parameters we also find that the isospin-1 state $\frac{1}{\sqrt{2}}(D^{*0}D^{*+}+D^{*0}D^{*+})$ ($J^P=0^+$) can exist. Moreover, we also study the systems of $B^{(*)}B^{(*)}$ and their counterparts exist as possible molecular states. Consistency of theoretical computations based on such states with the data of the future experiments may consolidate the molecular structure of the exotic state $T^+_{cc}$.

1 Introduction

Recently the LHCb Collaboration reported a new exotic state $T_{cc}^+$ in the $D^0D^0\pi ^+$ invariant mass spectrum. Apparently $T_{cc}^+$ possesses a $cc\bar{u} \bar{d}$ flavor component. The difference between its mass and the mass threshold of $D^0D^{*+}$ is $-273\pm 61\pm 5^{+11}_{-14}$ keV and its width is $410\pm 165\pm 43^{+18}_{-38}$ keV [1, 2]. The new state attracts great interest because it is the first double-charm tetraquark which was measured. Since 2003 many exotic states [3,4,5,6,7,8,9] such as X(3872), X(3940), Y(3940), $Z(4430)^{\pm }$, $Z_{cs}(4000)$, $Z_{cs}(4220)$, $Z_b$, $Z_b'$, $P_c(4312)$, $P_c(4440)$, $P_c(4457)$ have been measured. $T_{cc}^+$ have been observed in experiments and the achievements broaden our field of view about the flavor structure of exotic states.

It is difficult to attribute so many exotic states into a basket determined by the traditional hadronic picture where a meson contains a quark and anti-quark pair and a baryon is composed of three valence quarks. Instead, it is suggested that they should be multi-quark states which are predicted by the SU(3) quark model [10]. During these years it turns out to be a hot topic to discuss the structures of exotic states. Those new states are often proposed to be molecular states, compact tetraquarks, a mixing of both structures or dynamical effect [11, 12].

The mass of $T_{cc}^+$ is very close to the mass threshold of $D^0D^{*+}$ or ($D^+D^{*0}$) so naturally many authors suggested that $T_{cc}^+$ could be a loose $D^0D^{*+}$ ($D^+D^{*0}$) bound state [13,14,15,16,17,18]. Some authors also consider it as a tetraquark [19, 20]. Generally a compact tetraquark has a wide decay width whereas a molecular state has a relatively narrow one. Viewing the width of $T_{cc}^+$ we also tend to accept $T_{cc}^+$ as a $D^0D^{*+}$ ($D^+D^{*0}$) bound state. In this paper we study the possible bound state of $D^0D^+$, $D^0D^{*+}$ and $D^{*0}D^{*+}$ systems within the Bethe-Salpeter (B–S) framework where the relativistic corrections are automatically included.

In this work we will study the systems composed of two charmed or bottomed mesons and the scenario has not been explored in the B–S framework yet. In our early papers [21,22,23] we deduced the B–S equations for the systems containing one vector and one pseudoscalar, two pseudoscalars and two vectors respectively. Following the approach in [21,22,23] we investigate the systems with two charmed or bottomed constituents such as $T_{cc}^+$. Since the interaction kernels are not the same as given in [21,22,23] and the objects under investigation are new it needs to re-study the whole scenario.

If the interaction between two constituents is attractive and large enough a bound state could be formed. In this work we employ the one-boson-exchange model to calculate the interaction kernels where the effective vertices are taken from the heavy meson chiral perturbation theory [24,25,26,27,28,29]. The exchanged particles are some light mesons such as $\pi$, $\rho$ and $\omega$. We ignore the contribution from $\eta$ exchange because its mass is larger than $\pi$ and there exists an additional suppression factor $\frac{1}{\sqrt{3}}$ at the effective vertex (see Appendix A). In Ref. [24] the authors indicated that $\sigma$ exchange makes a secondary contribution, thus we also do not include it. With the effective interactions we derive the kernel and establish the corresponding B–S equation. The B–S equation is solved in momentum space so the kernel we obtain by calculating the corresponding Feynman diagrams can be used directly rather than converting it into a potential form in coordinate space.

With all the input parameters, these B–S equations are solved numerically. In some cases there no solution which satisfies the equation exists as long as the parameters are set within a reasonable range, it implies the proposed bound state should not emerge in the nature. On the contrary, a solution of the B–S equation with reasonable parameters implies that the corresponding bound state is formed. In that case, the obtained B–S wave function can be used to calculate the decay rate of the bound state.

After this introduction we deduce the B–S equations and the corresponding kernels for the two meson systems with different quantum numbers. Then in Sect. 3 we present our numerical results of the binding energies along with explicitly displaying all input parameters. Section 4 is devoted to a brief summary.

2 The Bethe–Salpeter formalism

Initially, people employed the B–S equation to explore the bound states of two fermions. Later this approach was extended to study the bound states made of one fermion and one boson [30,31,32]. In Refs. [33,34,35,36,37] the B–S equation was used to study the spectra of the meson-meson molecular states and then deal with their decays. The method was extended to explore some other systems in our early papers [21,22,23, 38].

In Ref. [34, 35] the B–S equation for a bound state made of two pseudoscalars was deduced. Later we deduced the B–S equations for a system composed of one pseudoscalar and one vector or two vectors which are one particle and one antiparticle [21,22,23].

In this work we are only concerned with the ground states where the orbital angular momentum between two constituent mesons is zero (i.e. $l=0$). For a system whose constituents are two pseudoscalars or one pseudoscalar and one vector, its $J^{P}$ is $0^+$ or $1^+$. For the molecular states which consist of two vector mesons their $J^{P}$ may be $0^+$, $1^+$ and $2^+$.

Obviously, these systems composed of two charmed (or bottomed) hadrons (off-shell ) should belong to the same representations of isospin. In this case, the total wave function for the combined systems of $D^0$ and $D^{+}$ ($D^{*0}$ and $D^{*+}$) must be symmetric under group $O(3)\times SU_I(2)\times SU_S(2)$, where $SU_I(2)$ and $SU_S(2)$ are isospin and spin groups respectively. For the $D^0D^{+}$ system its total spin is 0 so its isospin should be 1. Instead, for the $D^{*0}D^{*+}$ system its isospin is 0 as $J^{P}=1^+$, whereas it is 1 as $J^{P}=0^+$ or $J^{P}=2^+$. For the $D^{*+}D^0$ or $D^{*0}D^+$ systems two isospin states are possible: $\frac{1}{\sqrt{2}}(D^{*+}D^0+D^{*0}D^+)$ ($I=0$) and $\frac{1}{\sqrt{2}}(D^{*+}D^0-D^{*0}D^+)$ ($I=1$).

2.1 The B–S equation of $0^+$ which is composed of two pseudoscalars

The B–S wave function for the bound state $|S\rangle$ of two pseudoscalar mesons can be defined as following:

$$\begin{aligned} \langle 0 | \mathrm{T}\,\phi _1(x_1)\phi _2(x_2) | S \rangle = {\chi }_{{}_S}^{}(x_1,x_2), \end{aligned}$$

(1)

where $\phi _1(x_1)$ and $\phi _2(x_2)$ are the field operators of two mesons, respectively, the relative coordinate x and the center of mass coordinate X are

$$\begin{aligned} X=\eta _1 x_1 + \eta _2 x_2,\quad x = x_1 - x_2 , \end{aligned}$$

(2)

where $\eta _i = m_i/(m_1+m_2)$ and $m_i\, (i=1,2)$ is the mass of the ith constituent meson.

After some manipulations we obtain the B–S equation in the momentum space

$$\begin{aligned} {\chi }_{{}_S}^{}(p) = \Delta _1\int {d^4p'\over (2\pi )^4} { K_{S}}(p,p'){\chi }_{{}_S}^{}(p')\Delta _{2}, \end{aligned}$$

(3)

where $\Delta _i$ is the propagator of the ith meson and $\Delta _1=\frac{i}{p_1^2-m_1^2}$, $\Delta _2=\frac{i}{p_2^2-m_2^2}$.

The relative momenta and the total momentum of the bound state in the equations are defined as

$$\begin{aligned} p= & {} \eta _2p_1 - \eta _1p_2,\quad p' = \eta _2p'_1 - \eta _1p'_2, \nonumber \\ P= & {} p_1 + p_2 = p'_1 + p'_2 , \end{aligned}$$

(4)

where P denotes the total momentum of the bound state.

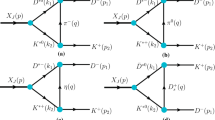
$D^0$ and $D^+$ can constitute two possible bound states: $\frac{1}{\sqrt{2}}(D^0D^++D^+D^0)$ with $I=1$ and $\frac{1}{\sqrt{2}}(D^0D^+-D^+D^0)$ with $I=0$. Since only $l=0$ is considered and the total spin wavefunction is symmetric the system of an isospin-scalar is forbidden and the isospin-1 state is reduced to $D^0D^+$. The exchanged mesons between the two pseudoscalars are vector mesons, obviously we only need to keep the lightest vector mesons $\rho$ and $\omega$ [34, 35], the Feynman diagrams corresponding these effective interactions are depicted in Fig. 1.

Fig. 1

A bound state composed of two pseudoscalars. In the Feynman diagram (a) $\omega$ exchange should also be included

With the Feynman diagrams depicted in Fig. 1 and the effective interactions shown in appendix A we obtain the interaction kernel

$$\begin{aligned}&K_{S}(p,p')=K_{S0}(p,p',m_\rho )+{ K_{S0}}(p.p',m_\omega ),\nonumber \\&{K_{S0}}(p,p',m_{ V}) = i C_{S0}\, g_{DDV}^2 \nonumber \\& \quad {(p_1+p_1')\cdot (p_2+p_2')-(p_1+p_1')\cdot q(p_2+p_2')\cdot q/m_{ V}^2 \over q^2-m_{ V}^2}\nonumber \\&\qquad F( q)^2, \end{aligned}$$

(5)

where $q=p_1-p_1'$. For exchanging $\rho$ the expression $K_{S0}(p, p',m_\rho )$ includes the contributions from figures Fig. 1 (a) and (b) but for exchanging $\omega$ it only includes the contribution from figure Fig. 1a. $C_{S0}=\frac{1}{2}$ for $\rho$ and $\omega$. Since the constituent meson is not a point particle, a form factor at each interaction vertex among hadrons must be introduced to reflect the finite-size effects of these hadrons. The form factor is assumed to be in the following form:

$$\begin{aligned} F({k}) = {\Lambda ^2 - M_{ V}^2 \over \Lambda ^2 -{k}^2}, \end{aligned}$$

(6)

where $\Lambda$ is a cutoff parameter.

Solving the Eq. (3) is rather difficult. In general one needs to use the so-called instantaneous approximation:$p_0'=p_0=0$ for ${K_{0}}(p,p')$ by which the B–S equation can be reduced to

$$\begin{aligned} {E^2-(E_1+E_2)^2\over (E_1+E_2)/E_1E_2} \mathcal {\psi }_{{}_S}^{}(\mathbf{p}) ={i\over 2}\int {d^3\mathbf {p}'\over (2\pi )^3}\, {\overline{} K_{S}}(\mathbf{p},\mathbf{p}')\mathcal {\psi }_{{}_S}^{}(\mathbf{p}'),\nonumber \\ \end{aligned}$$

(7)

where $E_i \equiv \sqrt{\mathbf{p}^2 + m_i^2}$, $E=P^0$, and the equal-time wave function is defined as $\psi _{_S}(\mathbf{p})= \int dp^0 \, \chi _{_S}(p) \,.$ For exchange of a light vector between the mesons, the kernel is

$$\begin{aligned} K_{S}(\mathbf{p},\mathbf{p}')=K_{S0}(\mathbf{p},\mathbf{p}',m_\rho )+K_{S0}(\mathbf{p},\mathbf{p}',m_\omega ), \end{aligned}$$

(8)

where the expressions of $K_{S0}(\mathbf {p},\mathbf {p}',m_V)$ can be found in Appendix B.

2.2 The B–S equation of $1^+$ which is composed of a pseudoscalar and a vector

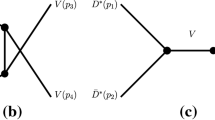
The B–S wave function for the bound state $|V\rangle$ composed of one pseudoscalar and one vector mesons is defined as following:

$$\begin{aligned} \langle 0 | \mathrm{T}\,\phi _1(x_1)\phi ^\mu _2(x_2) | V \rangle ={\chi }_{{}_V}^{}(x_1,x_2)\epsilon ^\mu , \end{aligned}$$

(9)

where $\epsilon$ is the polarization vector of the bound state, ${\chi }_{{}_V}$ is the B–S wave function, $\phi _1(x_1)$ and $\phi ^\mu _2(x_2)$ are respectively the field operators of the two mesons. The equation for the B–S wave function is

$$\begin{aligned} {\chi _{_V}}(p)\epsilon ^\mu = \Delta _1 \int {d^4p'\over (2\pi )^4} { K_{V\alpha \beta }}({ p},{ p}'){\chi _{_V}}(p')\epsilon ^\beta \Delta _{2\mu \alpha }. \end{aligned}$$

(10)

Here $\Delta _1=\frac{i}{p_1^2-m_1^2}$ and $\Delta _{2\mu \alpha }=\frac{i}{p_2^2-m_2^2}(\frac{p_{2\mu }p_{2\alpha }}{m_2^2}-g_{\mu \alpha })$ are the propagators of pseudoscalar and vector mesons. We multiply an $\epsilon ^*_\mu$ on both sides, sum over the polarizations and then deduce a new equation

$$\begin{aligned}&{\chi }_{{}_{V}}^{}(p)\nonumber \\&\quad = \frac{-1}{3(p_1^2-m_1^2)(p_2^2-m_2^2)}\int {d^4p'\over (2\pi )^4} { K_{V\alpha \beta }}(p,p'){\chi }_{{}_{V}}^{}(p')\nonumber \\&\qquad \times \left( \frac{p_{2}^\mu p_{2}^\alpha }{m_2^2} -g^{\mu \alpha }\right) \left( \frac{P_\mu P^\beta }{M^2}-g_\mu ^\beta \right) . \end{aligned}$$

(11)

Fig. 2

A bound state composed of a pseudoscalar and a vector by exchanging $\pi$

Fig. 3

A bound state composed of a pseudoscalar and a vector by exchanging $\rho$. In the two Feynman diagrams (a) and (c) exchange of $\omega$ also is also taken into account

With the Feynman diagrams depicted in Figs. 2 and 3 we eventually obtain

$$\begin{aligned}&K_{V\alpha \beta }(p,p')=K_{V1\alpha \beta }(p,p',m_\rho )+{ K_{V2\alpha \beta }}(p,p',m_\rho )\nonumber \\&\qquad +{ K_{V1\alpha \beta }}(p,p',m_\omega )\nonumber \\&\qquad +{K_{V2\alpha \beta }}(p,p',m_\omega )+{ K_{V3\alpha \beta }}(p,p',m_\pi ),\nonumber \\&{K_{V1\alpha \beta }}(p,p',m_{V}) =C_{V1}g_{_{DDV}}\Bigg \{g_{_{D^*D^*V}}\Bigg [g_{\alpha \beta }(p_2+p_2')\nonumber \\&\qquad \cdot (p_1+p_1')+g_{\alpha \beta }\frac{q\cdot (p_1+p_1')q\cdot ( p_2+p_2')}{m_{V}^2}\Bigg ] \nonumber \\&\qquad +2g'_{_{D^*D^*V}}\left[ q^\alpha (p_1+p_1')^\beta -q^\beta (p_1+p_1')^\alpha \right] \Bigg \}\nonumber \\&\qquad \frac{i}{q^2-m_{V}^2}F(q)^2\nonumber \\&{K_{V2\alpha \beta }}(p,p',m_{ V})= C_{V2}\varepsilon ^{\mu \nu \beta \tau }(q'_\nu g_{\lambda \mu }-q'_\mu g_{\lambda \nu })\nonumber \\&\qquad \times (p_2'-p_1)_\tau \varepsilon ^{\mu '\nu '\alpha \tau '}(q'_\mu g_{\lambda '\nu }-q'_\nu g_{\lambda '\mu })(p_2-p_1')_{\tau '}\nonumber \\&\qquad \times \frac{i}{q'^2-m_{V}^2}(-g^{\lambda \lambda '}+q'^\lambda q'^{\lambda '}/m^2_V)F(q')^2,\nonumber \\&K_{V3\alpha \beta }(p,p',m_P)=C_{V3}g_{_{DD^*P}}^2\frac{i}{q'^2-m_{P}^2}q'_\alpha q'_\beta F(q')^2,\nonumber \\ \end{aligned}$$

(12)

where $q'=p_1-p_2'$. The contributions from Fig. 2 are included in $K_{V3\alpha \beta }(p,p',m_\pi )$ and those from Fig. 3a, b are included in $K_{V1\alpha \beta }(p,p',m_V)$. When the bound state is an isospin-scalar $C_{V1}=-\frac{3}{2}$ and $C_{V2}=\frac{3}{2}$ for $\rho$, $C_{V1}=\frac{1}{2}$ and $C_{V2}=-\frac{1}{2}$ for $\omega$ and $C_{V3}=\frac{3}{2}$ for $\pi$. When the bound state is an isospin-vector $C_{V1}=\frac{1}{2}$ and $C_{V2}=\frac{1}{2}$ for $\rho$, $C_{V1}=\frac{1}{2}$ and $C_{V2}=\frac{1}{2}$ for $\omega$ and $C_{V3}=\frac{1}{2}$ for $\pi$.

Defining $K_{V}(p,p')={ K_{V\alpha \beta }}(q)(\frac{p_{2}^\mu p_{2}^\alpha }{m_2^2}-g^{\mu \alpha })(\frac{P_\mu P^\beta }{M^2}-g_\mu ^\beta )$ and setting $p_0=q_0=0$ we derive the BS equation which is similar to Eq. (7) but possesses a different kernel,

$$\begin{aligned} {E^2-(E_1+E_2)^2\over (E_1+E_2)/E_1E_2} \mathcal {\psi }_{{}_V}^{}(\mathbf{p}) ={i\over 2}\int {d^3\mathbf {p}'\over (2\pi )^3}\, {\overline{} K_{V}}(\mathbf{p},\mathbf{p}')\mathcal {\psi }_{{}_V}^{}(\mathbf{p}'),\nonumber \\ \end{aligned}$$

(13)

where

$$\begin{aligned} K_{V}(\mathbf {p},\mathbf {p}')= & {} K_{V1}(\mathbf {p},\mathbf {p}',m_\rho )+{ K_{V2}}(\mathbf {p},\mathbf {p}',m_\rho )\nonumber \\&\qquad +{ K_{V1}}(\mathbf {p},\mathbf {p}',m_\omega )\nonumber \\&\qquad +{K_{V2}}(\mathbf {p},\mathbf {p}',m_\omega )+{ K_{V3}}(\mathbf {p},\mathbf {p}',m_\pi ), \end{aligned}$$

(14)

where the expressions of $K_{V1}(\mathbf {p},\mathbf {p}',m_V)$, $K_{V2}(\mathbf {p},\mathbf {p}',m_V)$ and ${ K_{V3}}(\mathbf {p},\mathbf {p}',m_P)$ can be found in Appendix B.

Fig. 4

A bound state composed of two vectors. a $\pi$ is exchanged and in fact there totally are four diagrams like those in Fig. 3. b $\rho$ ($\omega$) is exchanged and there are four (two) diagrams like those in Fig. 3

2.3 The bound state ($0^+$) composed of two vector mesons

The quantum number $J^P$ of the bound state composed of two vectors can be $0^+$, $1^+$ and $2^+$. The corresponding B–S wave function $|{S'}\rangle$ is defined as following:

$$\begin{aligned} \langle 0 | \mathrm{T}\,\phi _{1}^\mu (x_1)\phi ^\nu _2(x_2) |{S'} \rangle = {\chi }_{{}_{{0}}}^{}(x_1,x_2)g^{\mu \nu }. \end{aligned}$$

(15)

The equation for the B–S wave function is derived as

$$\begin{aligned} \chi _{_{{}_{0}}}({ p})= & {} \frac{1}{4}\Delta _{1\mu \lambda }\int {d^4{p}'\over (2\pi )^4}\,K_0^{\alpha \alpha '\mu \mu '}({ p},{ p}')\nonumber \\&\qquad \chi _{_{{}_{0}}}^{}({ p}')\Delta _{2\mu '\lambda '}g_{\alpha \alpha '}g^{\lambda \lambda '}, \end{aligned}$$

(16)

where $\Delta _{j\mu \lambda }=\frac{i}{p_j^2-m_j^2}(\frac{p_{j\mu }p_{j\lambda }}{m_2^2}-g_{\mu \lambda })$.

With the Feynman diagrams depicted in Fig. 4 and the effective interaction we obtain pg

$$\begin{aligned}&K_{0}^{\alpha \alpha '\mu \mu '}(p,p')=K_{01}^{\alpha \alpha '\mu \mu '}(p,p',m_\rho )\nonumber \\&\quad +K_{02}^{\alpha \alpha '\mu \mu '}(p,p',m_\rho )\nonumber \\&\quad + K_{01}^{\alpha \alpha '\mu \mu '}(p,p',m_\omega )\nonumber \\&\quad +K_{02}^{\alpha \alpha '\mu \mu '}(p,p',m_\omega )+ K_{03}^{\alpha \alpha '\mu \mu '}(p,p',m_\pi )\nonumber \\&\quad +K_{04}^{\alpha \alpha '\mu \mu '}(p,p',m_\pi ),\nonumber \\&K_{01}^{\alpha \alpha '\mu \mu '}(p,p',m_V)=iC_{01}\frac{{q^\nu q^{\nu '}}/{{m_V}^2}-g^{\nu {\nu '}}}{q^2-m_{V}^2}\nonumber \\&\quad \times \Bigg [g_{_{D^*D^*V}}g^{\alpha \mu } (p_1+p_1')_\nu -2g_{_{D^*D^*V}}'({q}^{\alpha } g_{\mu \nu }-{q}^\mu g_{\alpha \nu })\Bigg ]\nonumber \\&\quad \times \Bigg [g_{_{D^*D^*V}}g^{\alpha '\mu '}(p_2+p_2')_{\nu '}\nonumber \\&\quad +2g_{_{D^*D^*V}}'({q}^{\alpha '} g_{\mu '\nu '}-{q}^{\mu '} g_{\alpha '\nu '})\Bigg ]F(q)^2,\nonumber \\&K_{02}^{\alpha \alpha '\mu \mu '}(p,p',m_V)=iC_{02}\frac{{q'^\nu q'^{\nu '}}/{{m_V}^2}-g^{\nu {\nu '}}}{q'^2-m_{V}^2}\nonumber \\&\quad \times \Bigg [g_{_{D^*D^*V}}g^{\alpha \mu } (p_1+p_2')_\nu -2g_{_{D^*D^*V}}'({q'}^{\alpha } g_{\mu \nu }-{q'}^\mu g_{\alpha \nu })\Bigg ]\nonumber \\&\quad \times \Bigg [g_{_{D^*D^*V}}g^{\alpha '\mu '} (p_2+p_1')_{\nu '}\nonumber \\&\quad +2g_{_{D^*D^*V}}'({q'}^{\alpha '} g_{\mu '\nu '}-{q'}^{\mu '}g_{\alpha '\nu '})\Bigg ]F(q')^2,\nonumber \\&K_{03}^{\alpha \alpha '\mu \mu '}(p,p',m_P)=C_{03}g_{_{D^*D^*P}}^2\varepsilon ^{\alpha \beta \mu \nu }\nonumber \\&\quad \times q_\nu (p_1+p_1')_\beta \varepsilon ^{\alpha '\beta '\mu '\nu '}q_{\nu '} (p_2+p_2')_{\beta '}\frac{-i}{q^2-M_\pi ^2}F(q)^2,\nonumber \\&K_{04}^{\alpha \alpha '\mu \mu '}(p,p',m_P)=C_{04}g_{_{D^*D^*P}}^2\varepsilon ^{\alpha \beta \mu \nu }\nonumber \\&\quad \times q'_\nu (p_1+p_2')_\beta \varepsilon ^{\alpha '\beta '\mu '\nu '}q'_{\nu '} (p_2+p_1')_{\beta '}\frac{-i}{q'^2-m_P^2}F(q')^2.\nonumber \\ \end{aligned}$$

(17)

The contributions from vector-exchanges are included in $K_{01}^{\alpha \alpha '\mu \mu '}(p,p',m_V)$ and $K_{02}^{\alpha \alpha '\mu \mu '}(p,p',m_V)$ and those for exchanging pseudoscalars are included in $K_{03}^{\alpha \alpha '\mu \mu '}(p,p',m_P)$ and $K_{04}^{\alpha \alpha '\mu \mu '}(p,p',m_P)$. When the bound state is an isospin-scalar $C_{01}=-\frac{3}{2}$ and $C_{02}=\frac{3}{2}$ for $\rho$, $C_{01}=\frac{1}{2}$ and $C_{02}=-\frac{1}{2}$ for $\omega$ and $C_{03}=-\frac{3}{2}$ and $C_{04}=\frac{3}{2}$ for $\pi$. When the bound state is an isospin-vector $C_{01}=\frac{1}{2}$ and $C_{02}=\frac{1}{2}$ for $\rho$, $C_{01}=\frac{1}{2}$ and $C_{02}=\frac{1}{2}$ for $\omega$ and $C_{03}=\frac{1}{2}$ and $C_{04}=\frac{1}{2}$ for $\pi$.

Defining $K_{0}(p,p')=\frac{1}{4}{ K_0^{\alpha \alpha '\mu \mu '}}({ p},{ p}')(\frac{p_{2\mu '} p_{2\lambda '}}{m_2^2}-g_{\mu '\lambda '})(\frac{{p_{1}}_\mu {p_{1}}_{\lambda }}{m_1^2}-g_{\mu \lambda })$ we derive the B–S equation which is similar to Eq. (7) but possesses a different kernel.

The B–S equation can be reduced to

$$\begin{aligned} {E^2-(E_1+E_2)^2\over (E_1+E_2)/E_1E_2} \mathcal {\psi }_{{}_0}^{}(\mathbf{p}) ={i\over 2}\int {d^3\mathbf {p}'\over (2\pi )^3}\, {\overline{} K_{{0}}}(\mathbf{p},\mathbf{p}')\mathcal {\psi }_{{}_0}^{}(\mathbf{p}'),\nonumber \\ \end{aligned}$$

(18)

where

$$\begin{aligned} K_{0}(\mathbf {p},\mathbf {p}')= & {} K_{01}(\mathbf {p},\mathbf {p}',m_\rho )+{ K_{02}}(\mathbf {p},\mathbf {p}',m_\rho )\nonumber \\&+{K_{01}}(\mathbf {p},\mathbf {p}',m_\omega )+{K_{02}}(\mathbf {p},\mathbf {p}',m_\omega )\nonumber \\&+{ K_{03}}(\mathbf {p},\mathbf {p}',m_\pi )+{K_{04}}(\mathbf {p},\mathbf {p}',m_\pi ), \end{aligned}$$

(19)

The expressions of $K_{01}(\mathbf {p},\mathbf {p}',m_V)$, $K_{02}(\mathbf {p},\mathbf {p}',m_V)$, ${ K_{03}}(\mathbf {p},\mathbf {p}',m_P)$ and ${ K_{04}}(\mathbf {p},\mathbf {p}',m_P)$ can be found in Appendix B.

2.4 The B–S equation of $1^+$ state which is composed of two vectors

The B–S wave function of $1^+$ state $|{V'}\rangle$ composed of two axial-vectors is defined as

$$\begin{aligned} \langle 0|T\phi _\alpha (x_1)\phi _{\alpha '}(x_2)|{V'}\rangle =\frac{\varepsilon _{\alpha \alpha '\tau \tau '}}{\sqrt{6}M}\chi _{_{{1}}}(x_1,x_2)\varepsilon ^\tau P^{\tau '}, \end{aligned}$$

(20)

where $\varepsilon$ is the polarization vector of $1^+$ state.

The corresponding B–S equation is

$$\begin{aligned}&\chi _{_{{1}}}(p) =\frac{1}{6M^2}\varepsilon ^{\lambda \lambda ' \omega \sigma }\varepsilon _\sigma P_\omega \Delta _{1\mu \lambda }\nonumber \\&\quad \times \int {d^4{p'}\over (2\pi )^4}\,K_1^{\alpha \alpha '\mu \mu '}(p, p') \varepsilon _{\alpha \alpha '\omega '\sigma '}\nonumber \\&\qquad \chi _{_{{1}}}(p')\varepsilon ^{\sigma '}P^{\omega '}\Delta _{2\mu '\lambda '}, \end{aligned}$$

(21)

where $K_1^{\alpha \alpha '\mu \mu '}(p,p')$ is the same as $K_0^{\alpha \alpha '\mu \mu '}(p,p')$ in Eq. (17).

Defining $K_{1}(p,p')=\frac{{ K_1^{\alpha \alpha '\mu \mu '}}({ p},{ p}')}{6\,M^2}\varepsilon ^{\lambda \lambda ' \omega \sigma }\varepsilon _\sigma P_\omega (\frac{p_{2\mu '} p_{2\lambda '}}{m_2^2}-g_{\mu '\lambda '})(\frac{{p_{1}}_\mu {p_{1}}_{\lambda }}{m_1^2}-g_{\mu \lambda })\varepsilon _{\alpha \alpha '\omega '\sigma '}\varepsilon ^{\sigma '}P^{\omega '}$ the B–S equation is reduced to

$$\begin{aligned} {E^2-(E_1+E_2)^2\over (E_1+E_2)/E_1E_2} \mathcal {\psi }_{{}_{1}}^{}(\mathbf{p}) ={i\over 2}\int {d^3\mathbf {p}'\over (2\pi )^3}\, {\overline{} K_{1}}(\mathbf{p},\mathbf{p}')\mathcal {\psi }_{{}_{1}}^{}(\mathbf{p}'),\nonumber \\ \end{aligned}$$

(22)

with

$$\begin{aligned} K_{1}(\mathbf {p},\mathbf {p}')= & {} K_{11}(\mathbf {p},\mathbf {p}',m_\rho )+{ K_{12}}(\mathbf {p},\mathbf {p}',m_\rho )\nonumber \\&+{ K_{11}}(\mathbf {p},\mathbf {p}',m_\omega ) +{K_{12}}(\mathbf {p},\mathbf {p}',m_\omega )\nonumber \\&+{K_{13}}(\mathbf {p},\mathbf {p}',m_\pi )+{K_{14}}(\mathbf {p},\mathbf {p}',m_\pi ). \end{aligned}$$

(23)

The expressions of $K_{11}(\mathbf {p},\mathbf {p}',m_V)$, $K_{12}(\mathbf {p},\mathbf {p}',m_V)$, ${ K_{13}}(\mathbf {p},\mathbf {p}',m_P)$ and ${ K_{14}}(\mathbf {p},\mathbf {p}',m_P)$ can be found in Appendix B.

2.5 The B–S equation of $2^+$ state $|T'\rangle$ which is composed of two vectors

The B–S wave-function of $2^+$ state composed of two axial-vectors is written as

$$\begin{aligned} \langle 0|T\phi ^\alpha (x_1)\phi ^{\alpha '}(x_2)|T'\rangle =\frac{1}{\sqrt{5}}\chi _{_{2}}(x_1,x_2)\varepsilon ^{\alpha \alpha '}, \end{aligned}$$

(24)

where $\varepsilon$ is the polarization vector of the $2^+$ state.

The B–S equation can be expressed as

$$\begin{aligned} \chi _{_{2}}(p)= & {} \frac{1}{5}\varepsilon ^{\lambda \lambda '}\Delta _{1\mu \lambda }\int {d^4{q}\over (2\pi )^4}\,K_2^{\alpha \alpha '\mu \mu '}(p,p') \varepsilon _{\alpha \alpha '}\nonumber \\&\qquad \chi _{_{2}}(q)\Delta _{2\mu '\lambda '}, \end{aligned}$$

(25)

where $K_2^{\alpha \alpha '\mu \mu '}(p,p')$ is the same as $K_0^{\alpha \alpha '\mu \mu '}(p,p')$ in Eq. (17).

Defining $K_{2}(p,p')= \frac{{ K_2^{\alpha \alpha '\mu \mu '}}({ p},{ p}')}{5}\varepsilon ^{\lambda \lambda ' }(\frac{p_{2\mu '} p_{2\lambda '}}{m_2^2}-g_{\mu '\lambda '})(\frac{{p_{1}}_\mu {p_{1}}_{\lambda }}{m_1^2}-g_{\mu \lambda })\varepsilon _{\alpha \alpha '}$ the B–S equation can be reduced to

$$\begin{aligned} {E^2-(E_1+E_2)^2\over (E_1+E_2)/E_1E_2} \mathcal {\psi }_{{}_{2}}^{}(\mathbf{p}) ={i\over 2}\int {d^3\mathbf {p}'\over (2\pi )^3}\, {\overline{} K_{2}}(\mathbf{p},\mathbf{p}')\mathcal {\psi }_{{}_{2}}^{}(\mathbf{p}'),\nonumber \\ \end{aligned}$$

(26)

where

$$\begin{aligned} K_{2}(\mathbf {p},\mathbf {p}')= & {} K_{21}(\mathbf {p},\mathbf {p}',m_\rho )+{ K_{22}}(\mathbf {p},\mathbf {p}',m_\rho )\nonumber \\&+{ K_{21}}(\mathbf {p},\mathbf {p}',m_\omega )+{ K_{22}}(\mathbf {p},\mathbf {p}',m_\omega )\nonumber \\&+{K_{23}}(\mathbf {p},\mathbf {p}',m_\pi )+{ K_{24}}(\mathbf {p},\mathbf {p}',m_\pi ). \end{aligned}$$

(27)

The expressions of $K_{21}(\mathbf {p},\mathbf {p}',m_V)$, $K_{22}(\mathbf {p},\mathbf {p}',m_V)$, ${ K_{23}}(\mathbf {p},\mathbf {p}',m_P)$ and ${ K_{24}}(\mathbf {p},\mathbf {p}',m_P)$ can be found in Appendix B.

3 Numerical results

Now let us solve the B–S Eqs. (7), (13), (18), (22) and (26). Since we are interested in the ground state of a bound state the function $\psi _{J}(\mathbf {p})$ (J represents S, V, 0, 1 or 2) only depends on the norm of the three-momentum and we may first integrate over the azimuthal angle of the functions in (7), (13), (18), (22) or (26)

$$\frac{i}{2}\int {d^3\mathbf {p}'\over (2\pi )^3}\, {\overline{} K_J}(\mathbf{p},\mathbf{p}'), $$

to obtain a potential form $U_J(|\mathbf {p}|,|\mathbf {p}'|)$, then the B–S equation turns into a one-dimension integral equation

$$\begin{aligned} \psi _J(\mathbf{|p|}) ={(E_1+E_2)/E_1E_2\over E^2-(E_1+E_2)^2 }\int {d \mathbf {|p}'|}\, {\overline{} U_J}(\mathbf{|p|},\mathbf{|p}'|)\psi _J(\mathbf{|p}'|).\nonumber \\ \end{aligned}$$

(28)

When the potential $U_{J}(\mathbf {p},\mathbf {p}')$ is attractive and strong enough the corresponding B–S equation has a solution(s) and we can obtain the mass of the possible bound state.

Generally the standard way of solving an integral equation is to discretize and perform algebraic operations. Concretely, we let $\mathbf |p|$ and $\mathbf |p'|$ take n ( n is sufficiently large) order discrete values $Q_1$, $Q_2,\ldots ,Q_n$ and the gap between two adjacent values be $\Delta Q$, then the integral equation is transformed into n coupled algebraic equations. $\psi _{{}_J}^{}(Q_1),\psi _{{}_J}^{}(Q_2),\ldots \psi _{{}_J}^{}(Q_n)$ ( the subscript J denotes S, V, 0, 1 or 2) constitute a column matrix and the coefficients would stand as an $n\times n$ matrix M, thus these algebraic equations can be regarded as a matrix equation with a unique eigenvalue 1. If one can obtain a value of E which satisfies the equation with reasonable input parameters and E is not far from $E_1+E_2$ the corresponding eigenvector should exist as a bound state.

In our calculation the values of the parameters $g_{_{DDV}}, g_{_{DD^*P}}, g_{_{DD^*V}}$, $g_{_{D^*D^*V}}$ and $g'_{_{D^*D^*V}}$ are presented in Appendix A. Supposing $T^+_{cc}$ is a $D^0D^{*+}$ bound state, by fitting its mass we fix $\Lambda =1.134$ GeV. In Ref. [39, 40] the authors suggested a relation: $\Lambda =m+\alpha \Lambda _{QCD}$ where m is the mass of the exchanged meson, $\alpha$ is a number of O(1) and $\Lambda _{QCD}=220$ MeV i.e. $\Lambda \sim 1$GeV for exchanging $\rho$ or $\omega$. The value of $\Lambda$ we obtained locates within the range.

The masses of the concerned constituent mesons $m_D$, $m_{D^*}$, $m_B$ and $m_{B^*}$ are directly taken from the databook [41].

3.1 The results of $D^{(*)}D^{(*)}$ system

Now let us try to calculate the eigenvalues of these systems of $D^0 D^+(J^P=0^+, I=1)$, $D^0 D^{*+}(J^P=1^+, I=1)$, $D^0 D^{*+}(J^P=1^+, I=0)$, $D^{*0} D^{*+}(J^P=0^+, I=1)$, $D^{*0} D^{*+}(J^P=1^+, I=0)$ and $D^{*0} D^{*+}(J^P=2^+, I=1)$ respectively. Apparently with the parameters $\Lambda$ and coupling constants, not all B–S equations are solvable. For $D^0D^{*+}$ system with $I=0$ the B–S equation has a solution. It implies that $D^0D^{*+}$ can form an isospin scalar bound state by exchanging light mesons. In Ref. [42] the authors also obtained the same results with similar approach. For the $D^0D^{*+}$ ($I=1$) or $D^0D^{+}$ ($I=1$) system, employing a larger $\Lambda$ and coupling constant we can obtain a solution. It may imply the effective interaction between the two constituents is weak. For the $D^{*0}D^{*+}$ system we can obtain an eigenvalue 18.51 MeV, the corresponding eigenstate is a bound state of $J=0$ and $I=1$. In Table 1 there are many places symbolized by $``*''$ or $``-''$ which means such bound states cannot exist due to the symmetry restriction or the B–S equation has no solution. However in Ref. [43] $D^{*}D^{*}$ system with $J=1$ and isospin $I=0$ was suggested to exist, which contradicts to our result. The reason is that the authors of Ref. [43] did not symmetrize and antisymmetrize the flavor wave functions of $D^*D^*$ for $I=0$ and $I=1$ states [44, 45]. Instead, we redo the calculation as the total symmetry of the wave-function including flavor, spin parts and orbital angular momentum is taken into account. For the $D^{*0}D^{*+}$ system the spin wave-function is symmetrized and/or antisymmetrized so that the flavor wave functions need to be correspondingly symmetrized and antisymmetrized when $l=0$. For $I=1$ and $I=0$ states of $D^{*0}D^{*+}$ the symmetric and antisymmetric flavor wave-functions were considered in Ref. [46].

3.2 The results of the $B^{(*)}B^{(*)}$ system

Considering the flavor SU(3) symmetry and heavy quark effective symmetry we generalize those relations as $g_{_{BBV}}=g_{_{DDV}}, g_{_{BB^*P}}=g_{_{DD^*P}}, g_{_{BB^*V}}= g_{_{DD^*V}}$, $g_{_{B^*B^*V}}=g_{_{D^*D^*V}}$ and $g'_{_{B^*B^*V}}=g'_{_{D^*D^*V}}$ which should be a not-bad approximation.

Table 1 The binding energy of the ground $DD^{(*)}$ system (in unit of MeV)

Table 2 The eigenvalues of the ground $BB^{(*)}$ system (in unit of MeV)

We use the same parameter $\Lambda$ fixed for the $DD^*$ systems to solve the B–S equation for the $B^{(*)}B^{(*)}$ systems. We find that two states which are the counterparts of $D^{(*)}D^{(*)}$ can exist. The binding energy of each state shown in Table 2 is apparently larger than that of the corresponding state of $D^{(*)}D^{(*)}$ since the mass of $B^{(*)}$ meson is larger than that of $D^{(*)}$ meson (Fig. 5).

Fig. 5

The unnormalized wave functions of the bound states

4 A brief summary

In this work we study whether two charmed (or bottomed) mesons can form a hadronic molecule. We employ the B–S framework to search for possible bound states of $D^{(*)}D^{(*)}$ [47] and $B^{(*)}B^{(*)}$. In Ref. [21, 22, 34, 35, 38] the B–S wave functions for the systems of one vector and one pseudoscalar, two pseudoscalar mesons and two vectors were studied. It is noted that all those works are dealing with bound states made of one particle and one-antiparticle, no matter they are pseudoscalar or vector bosons. In comparison, this work is concerning particle-particle bound states(charmed $D^{(*)}D^{(*)}$ or bottomed $B^{(*)}B^{(*)}$). Since the two constituents are accounted as identical, symmetrization of the total wavefunctions is necessarily required. In this work we deduce the interaction kernels for these systems and solve these B–S equations.

In order to obtain the interaction kernels for B–S equations we use the heavy meson chiral perturbation theory to calculate the corresponding Feynman diagrams where $\pi$, $\rho$ or $\omega$ are exchanged. All coupling constants are taken from relevant references. For making predictions we use the binding energy of $T_{cc}^+$ to fix the parameter $\Lambda$ under the hypothesis that $T_{cc}^+$ is a bound state of $D^0D^{*+}$ with $I=0$ and $J=1$. With the same parameters we confirm that $D^{*0}D^{*+}$ with $I=1$ and $J=0$ should exist. For the $D^{*0}D^{*+}$ system with $I=1$ and $J=2$, a larger $\Lambda$ or large coupling constants are needed to form bound states.

Considering the flavor SU(3) symmetry and heavy quark spin symmetry we employ the same parameters to calculate possible bound states of $B^{(*)}B^{(*)}$. Two states which are the counterparts of $D^{(*)}D^{(*)}$ can exist. The binding energy of each state is apparently larger than that of the corresponding state of $D^{(*)}D^{(*)}$ since $B^{(*)}$ meson is heavier than $D^{(*)}$ meson.

Since the parameters are fixed from data which span a relatively large range we cannot expect all the numerical results to be very accurate. The goal of this work is to study whether two charmed (or bottomed) mesons can form a molecular state. Our results, even if not accurate, have obvious qualitative significance. Definitely, further theoretical and experimental works are badly needed for gaining better understanding of these exotic hadrons.

Appendices

Appendix A: The effective interactions

The effective interactions can be found in[24,25,26]

$$\begin{aligned} \mathcal {L}_{_{DDV}}= & {} g_{_{DDV}}(D_{b}{\mathop {\partial }\limits ^{\leftrightarrow }}_{\beta } D^{\dag }_{a})( \mathcal {V}^\beta )_{ba}, \end{aligned}$$

(A1)

$$\begin{aligned} \mathcal {L}_{_{DD^*V}}= & {} ig_{_{DD^*V}}\varepsilon ^{\alpha \beta \mu \nu }({\partial }_{\alpha }\mathcal {V}_\beta -{\partial }_{\beta }\mathcal {V}_\alpha )_{ba}\nonumber \\&\times (\partial _\nu D_{b}D^{*\mu \dag }_{a}-\partial _\nu D^{*\mu \dag }_{b}D_{a}),\end{aligned}$$

(A2)

$$\begin{aligned} \mathcal {L}_{_{DD^*P}}= & {} g_{_{DD^*P}}D_{b}(\partial _\mu \mathcal {M})_{ba}D^{*\mu \dag }_{a}\nonumber \\&+g_{_{DD^*P}}D^{*\mu }_{b}(\partial _\mu \mathcal {M})_{ba}D^{\dag }_{a},\end{aligned}$$

(A3)

$$\begin{aligned} \mathcal {L}_{_{D^*D^*P}}= & {} g_{_{D^*D^*P}}(D^{*\mu }_{b}{\mathop {\partial }\limits ^{\leftrightarrow }}^{\beta } D^{*\alpha \dag }_{a})(\partial ^\nu \mathcal {M})_{ba}\varepsilon _{\nu \mu \alpha \beta },\end{aligned}$$

(A4)

$$\begin{aligned} \mathcal {L}_{_{D^*D^*V}}= & {} ig_{_{D^*D^*V}}(D^{*\nu }_{b}{\mathop {\partial }\limits ^{\leftrightarrow }}_{\mu } D^{*\dag }_{a\nu })(\mathcal {V})_{ba}^\mu \nonumber \\&+ig'_{_{D^*D^*V}}(D^{*\mu }_{b} D^{*\nu \dag }_{a}-D^{*\mu \dag }_{b} D^{*\nu }_{a})\nonumber \\&\quad ( \partial _\mu \mathcal {V}_\nu -\partial _\nu \mathcal {V}_\mu )_{ba} \end{aligned}$$

(A5)

where a and b represent the flavors of light quarks. In Refs. [24] $\mathcal {M}$ and $\mathcal {V}$ are $3\times 3$ hermitian and traceless matrix

$\left( \begin{array}{lll} \frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{6}} &{}\pi ^+ &{}K^+ \\ \pi ^- &{} -\frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{6}}&{}K^0\\ K^-&{} \bar{K^0} &{} -\sqrt{\frac{2}{3}}\eta \end{array}\right)$ and

$\left( \begin{array}{lll} \frac{\rho ^0}{\sqrt{2}}+\frac{\omega }{\sqrt{2}} &{}\rho ^+ &{}K^{*+} \\ \rho ^- &{} -\frac{\rho ^0}{\sqrt{2}}+\frac{\omega }{\sqrt{2}}&{}K^{*0}\\ K^{*-}&{} \bar{K^{*0}} &{} \phi \end{array}\right)$

respectively.

In the chiral and heavy quark limit, the above coupling constants are $g_{_{DDV}}=\frac{\beta g_V}{\sqrt{2}}, g_{_{DD^*V}}=\frac{\lambda g_V}{\sqrt{2}}, g_{_{D^*D^*P}}=\frac{g}{f_\pi },$ $g_{_{DD^*P}}=-\frac{2\,g}{f_{\pi }} \sqrt{M_{D}M_{D^*}}, g_{_{D^*D^*V}}=-\frac{\beta g_V}{\sqrt{2}},\,\, g'_{_{D^*D^*V}}=-\sqrt{2}\lambda g_V M_{D^*}$ with $f_\pi =132$ MeV [25], $g=0.64$ [26], $\kappa =g$, $\beta =0.9$, $g_V=5.9$ [48] and $\lambda =0.56$ GeV$^{-1}$ [49].

Appendix B: Kernel

$$\begin{aligned}&K_{S0}(\mathbf{p},\mathbf{p}',m_v) = i C_{S1}\,g_{_{DDV}}^2\nonumber \\&\quad {(\mathbf{p}+\mathbf{p}')^2 + 4\eta _1\eta _2 E^2 + (\mathbf{p}^2-\mathbf{p}'{}^2)^2/m_{ V}^2 \over (\mathbf{p}-\mathbf{p}')^2 + m_{ V}^2}F(\mathbf{q})^2. \end{aligned}$$

(B1)

$$\begin{aligned}&{K_{V1}}(\mathbf {p},\mathbf {p}',m_{ V}) =\frac{iC_{V1}g_{_{DDV}}F(\mathbf{q})^2}{-(\mathbf {p} - \mathbf {p}')^2-m_{V}^2}\nonumber \\&\quad \times \Bigg \{-g_{_{D^*D^*V}} \mathbf {p}^2 [4 \eta _1 \eta _2 M^2 + (\mathbf {p} + \mathbf {p}')^2]/m_2^2\nonumber \\&\quad -\,\,3 g_{_{D^*D^*V}} (\mathbf {p}^2 - \mathbf {p}'^2)^2/m_V^2\nonumber \\&\quad -\,\,g_{_{D^*D^*V}} \mathbf {p}^2(\mathbf {p}^2 - \mathbf {p}'^2)^2/(m_2^2 m_V^2)\nonumber \\&\quad +\,\,4 \eta _1 \eta _2 g'_{_{D^*D^*V}} M^2 (-\mathbf {p}^2 + \mathbf {p}\cdot \mathbf {p}')/m_2^2\Bigg \}\nonumber \\&{K_{V2}}(\mathbf {p},\mathbf {p}',m_{V}) = \frac{i C_{V2}g^2_{_{D^*DV}}F(\mathbf{q}')^2}{-(\mathbf {p}+\mathbf {p'})^2-m_{V}^2}\nonumber \\&\quad \times [-8 \eta _1\eta _2 M^2 (\mathbf {p}-\mathbf {p}')^2-4 \mathbf {p}^2 \mathbf {p}'^2 + 4 \mathbf {p}\cdot \mathbf {p}'^2]\nonumber \\&K_{V3}(\mathbf {p},\mathbf {p}',m_P) =\frac{i C_{V3}g_{_{DD^*P}}^2F(\mathbf{q}')^2}{-(\mathbf {p}+\mathbf {p'})^2-m_{P}^2}\nonumber \\&\quad \times \,\, [-(\mathbf {p} + \mathbf {q})^2-(\mathbf {p}^2 (\mathbf {p} + \mathbf {q})^2/m2^2)] \end{aligned}$$

(B2)

$$\begin{aligned}&K_{01}=\frac{iC_{01} g^2_{_{D^*D^*V}} F(\mathbf{q})^2}{4[-(\mathbf {p} - \mathbf {p}')^2-m_{V}^2]}\nonumber \\&\quad \times \,\, \{-16 \eta _1 \eta _2 M^2-4 (\mathbf{p}+\mathbf{p}')^2\nonumber \\&\quad -\,\,\frac{(\eta _1 \eta _2 M^2+\mathbf{p}^2)^2 (\mathbf{p}^2-\mathbf{p}'^2)^2}{(m_1^2 m_2^2 m_V^2)}\nonumber \\&\quad +\,\,(\eta _1^2 M^2-\mathbf{p}^2) (\mathbf{p}^2-\mathbf{p}'^2)^2/(m_1^2 m_V^2)\nonumber \\&\quad +\,\,(\eta _2^2 M^2-\mathbf{p}^2) (\mathbf{p}^2-\mathbf{p}'^2)^2/(m_2^2 m_V^2)\nonumber \\&\quad -\,\,4 (\mathbf{p}^2-\mathbf{p}'^2)^2/m_V^2 -(\eta _1 \eta _2 M^2+\mathbf{p}^2)^2 [4 \eta _1 \eta _2 M^2\nonumber \\&\quad +\,\,(\mathbf{p}+\mathbf{p}')^2]/(m_1^2 m_2^2)\nonumber \\&\quad +\,\,(\eta _1^2 M^2-\mathbf{p}^2) [4 \eta _1 \eta _2 M^2+(\mathbf{p}+\mathbf{p}')^2]/m_1^2\nonumber \\&\quad +\,\,(\eta _2^2 M^2-\mathbf{p}^2) [4 \eta _1 \eta _2 M^2+(\mathbf{p}+\mathbf{p}')^2]/m_2^2\}\nonumber \\&\quad +\,\,\frac{iC_{01}g_{_{D^*D^*V}}g'_{_{D^*D^*V}}F(\mathbf{q})^2}{-(\mathbf {p} - \mathbf {p}')^2-m_{V}^2} (\eta _1+\eta _2)^2 M^2 (\eta _1 \eta _2 M^2\nonumber \\&\quad +\,\,\mathbf{p}^2) (\mathbf{p}^2-\mathbf{p}\cdot \mathbf{p}') /(m_1^2 m_2^2)\nonumber \\&\quad +\,\,\frac{iC_{01}{g'}^2_{_{D^*D^*V}} F(\mathbf{q})^2}{4[-(\mathbf {p} - \mathbf {p}')^2-m_{V}^2]} \{[8 (\mathbf{p}^2\nonumber \\&\quad +\,\,\eta _1 \eta _2 M^2) (\mathbf{p}^2 \mathbf{p}'^2-\mathbf{p}\cdot \mathbf{p}'^2)\nonumber \\&\quad -\,\,4 (\eta _1^2 \eta _2^2 M^4+4 \eta _1 \eta _2 \mathbf{p}^2 M^2+3 \mathbf{p}^4) (\mathbf{p}-\mathbf{p}')^2]/(m_1^2 m_2^2)\nonumber \\&\quad -\,\,24 (\mathbf{p}-\mathbf{p}')^2+[4 (\eta _1^2 M^2-3 \mathbf{p}^2) (\mathbf{p}-\mathbf{p}')^2\nonumber \\&\quad +\,\,8 (\mathbf{p}^2 \mathbf{p}'^2-\mathbf{p}\cdot \mathbf{p}'^2)]/m_1^2\nonumber \\&\quad +\,\,[4 (\eta _2^2 M^2-3 \mathbf{p}^2) (\mathbf{p}-\mathbf{p}')^2+8 (\mathbf{p}^2 \mathbf{p}'^2-\mathbf{p}\cdot \mathbf{p}'^2)]/m_2^2\} \nonumber \\&K_{02}=\frac{iC_{02} g^2_{_{D^*D^*V}} F(\mathbf{q}')^2}{4[-(\mathbf {p} + \mathbf {p}')^2-m_{V}^2]}\{-16 \eta _1 \eta _2 M^2-4 (\mathbf{p}-\mathbf{p}')^2\nonumber \\&\quad -\,\,\frac{(\eta _1 \eta _2 M^2 +\mathbf{p}^2)^2 (\mathbf{p}^2-\mathbf{p}'^2)^2}{(m_1^2 m_2^2 m_V^2)}\nonumber \\&\quad +\,\,(\eta _1^2 M^2-\mathbf{p}^2) (\mathbf{p}^2-\mathbf{p}'^2)^2/(m_1^2 m_V^2)\nonumber \\&\quad +\,\,(\eta _2^2 M^2-\mathbf{p}^2) (\mathbf{p}^2-\mathbf{p}'^2)^2/(m_2^2 m_V^2) \nonumber \\&\quad -\,\,(4 (\mathbf{p}^2-\mathbf{p}'^2)^2)/m_V^2- (\eta _1 \eta _2 M^2+\mathbf{p}^2)^2 [4 \eta _1 \eta _2 M^2\nonumber \\&\quad +\,\,(\mathbf{p}-\mathbf{p}')^2]/(m_1^2 m_2^2)\nonumber \\&\quad +\,\,(\eta _1^2 M^2-\mathbf{p}^2) [4 \eta _1 \eta _2 M^2+(\mathbf{p}-\mathbf{p}')^2]/m_1^2\nonumber \\&\quad +\,\,(\eta _2^2 M^2-\mathbf{p}^2) [4 \eta _1 \eta _2 M^2+(\mathbf{p}-\mathbf{p}')^2]/m_2^2\} \nonumber \\&\quad +\,\,\frac{iC_{02} g_{_{D^*D^*V}}g'_{_{D^*D^*V}} F(\mathbf{q}')^2}{-(\mathbf {p} + \mathbf {p}')^2-m_{V}^2} (\eta _1+\eta _2)^2 M^2 (\eta _1 \eta _2 M^2\nonumber \\&\quad +\,\,\mathbf{p}^2) (\mathbf{p}^2+\mathbf{p}\cdot \mathbf{p}') /(m_1^2 m_2^2)\nonumber \\&\quad +\,\,\frac{iC_{02} {g'}^2_{_{D^*D^*V}} F(\mathbf{q}')^2}{4[-(\mathbf {p} + \mathbf {p}')^2-m_{V}^2]} \{[8 (\mathbf{p}^2\nonumber \\&\quad +\,\,\eta _1 \eta _2 M^2) (\mathbf{p}^2 \mathbf{p}'^2-\mathbf{p}\cdot \mathbf{p}'^2)\nonumber \\&\quad -\,\,4 (\eta _1^2 \eta _2^2 M^4+4 \eta _1 \eta _2 \mathbf{p}^2 M^2\nonumber \\&\quad +\,\,3 \mathbf{p}^4) (\mathbf{p}+\mathbf{p}')^2]/(m_1^2 m_2^2)\nonumber \\&\quad -\,\,24 (\mathbf{p}+\mathbf{p}')^2+[4 (\eta _1^2 M^2-3 \mathbf{p}^2) (\mathbf{p}+\mathbf{p}')^2\nonumber \\&\quad +\,\,8 (\mathbf{p}^2 \mathbf{p}'^2-\mathbf{p}\cdot \mathbf{p}'^2)]/m_1^2\nonumber \\&\quad +\,\,[4 (\eta _2^2 M^2-3 \mathbf{p}^2) (\mathbf{p}+\mathbf{p}')^2\nonumber \\&\quad +\,\,8 (\mathbf{p}^2 \mathbf{p}'^2-\mathbf{p}\cdot \mathbf{p}'^2)]/m_2^2\}\nonumber \\&K_{03}=2 \frac{iC_{03} g^2_{_{D^*D^*P}} F(\mathbf{q})^2}{(\mathbf {p} - \mathbf {p}')^2+m_{P}^2} [-\mathbf{p}\cdot \mathbf{p}'^2\nonumber \\&\quad +\,\,\eta _1 \eta _2 M^2 (\mathbf{p}-\mathbf{p}')^2+\mathbf{p}^2 \mathbf{p}'^2]\nonumber \\&K_{04}=2\frac{iC_{04} g^2_{_{D^*D^*P}} F(\mathbf{q}')^2}{(\mathbf {p} + \mathbf {p}')^2 +m_{P}^2}\nonumber \\&\quad [-\mathbf{p}\cdot \mathbf{p}'^2 + \eta _1 \eta _2 M^2 (\mathbf{p} + \mathbf{p}')^2+ \mathbf{p}^2 \mathbf{p}'^2 ] \end{aligned}$$

(B3)

$$\begin{aligned}&K_{11} =-\frac{iC_{11} g^2_{_{D^*D^*V}} F(\mathbf{q})^2}{-(\mathbf {p} - \mathbf {p}')^2-m_{V}^2}\{4 \eta _1 \eta _2 M^2 m_V^2\nonumber \\&\quad +\,\,[m_V^2+(\mathbf{p}-\mathbf{p}')^2] (\mathbf{p}+\mathbf{p}')^2\}\nonumber \\&\quad \times [(3 m_2^2+\mathbf{p}^2) m_1^2+m_2^2 \mathbf{p}^2] /(3 m_1^2 m_2^2 m_V^2)\nonumber \\&\quad +\,\,4\frac{iC_{11} g_{_{D^*D^*V}} g'_{_{D^*D^*V}} F(\mathbf{q})^2}{-(\mathbf {p} - \mathbf {p}')^2-m_{V}^2}\eta _1 \eta _2 M^2 (m_1^2+m_2^2) \nonumber \\&\quad \times (\mathbf{p}^2-\mathbf{p}\cdot \mathbf{p}') /(3 m_1^2 m_2^2) - \frac{iC_{11} {g'}^2_{_{D^*D^*V}} F(\mathbf{q})^2}{-(\mathbf {p} - \mathbf {p}')^2-m_{V}^2} \nonumber \\&\quad \times \, \{[4(2 m_2^2+\mathbf{p}^2) m_1^2+4m_2^2 \mathbf{p}^2] (\mathbf{p}-\mathbf{p}')^2\nonumber \\&\quad +\,\,2 (m_1^2+m_2^2) (\mathbf{p}\cdot \mathbf{p}'^2-\mathbf{p}^2 \mathbf{p}'^2)\}/(3 m_1^2 m_2^2) \nonumber \\&K_{12}=-\frac{iC_{12} g^2_{_{D^*D^*V}} F(\mathbf{q}')^2}{-(\mathbf {p} + \mathbf {p}')^2-m_{V}^2}[(3 m_2^2+\mathbf{p}^2) m_1^2\nonumber \\&\quad +\,\,m_2^2 \mathbf{p}^2] \{4 \eta _1 \eta _2 M^2 m_V^2\nonumber \\&\quad +\,\, [m_V^2+(\mathbf{p}+\mathbf{p}')^2](\mathbf{p}-\mathbf{p}')^2\}/(3 m_1^2 m_2^2 m_V^2)\nonumber \\&\quad +\,\,4\frac{iC_{12} g_{_{D^*D^*V}}g'_{_{D^*D^*V}} F(\mathbf{q}')^2}{-(\mathbf {p} + \mathbf {p}')^2-m_{V}^2} \eta _1 \eta _2 M^2 (m_1^2+m_2^2) (\mathbf{p}^2\nonumber \\&\quad +\,\mathbf{p}\cdot \mathbf{p}') /(3 m_1^2 m_2^2) \nonumber \\&\quad -\,\frac{iC_{12} {g'}^2_{_{D^*D^*V}} F(\mathbf{q}')^2}{-(\mathbf {p} + \mathbf {p}')^2-m_{V}^2} \{[4(2 m_2^2+\mathbf{p}^2) m_1^2\nonumber \\&\quad +\,4m_2^2 \mathbf{p}^2] (\mathbf{p}+\mathbf{p}')^2\nonumber \\&\quad +2 (m_1^2+m_2^2) (\mathbf{p}\cdot \mathbf{p}'^2-\mathbf{p}^2 \mathbf{p}'^2)\}/(3 m_1^2 m_2^2) \nonumber \\&K_{13}=\frac{4}{3}\frac{iC_{13} g^2_{_{D^*D^*P}} F(\mathbf{q})^2}{-(\mathbf {p} - \mathbf {p}')^2 -m_{P}^2}\eta _1 \eta _2 M^2 (\mathbf{p}-\mathbf{p}')^2\nonumber \\&K_{14}=\frac{4}{3}\frac{iC_{14} g^2_{_{D^*D^*P}} F(\mathbf{q}')^2}{-(\mathbf {p} + \mathbf {p}')^2 -m_{P}^2}\eta _1 \eta _2 M^2 (\mathbf{p}+\mathbf{p}')^2 \end{aligned}$$

(B4)

$$\begin{aligned}&K_{21} =- \frac{iC_{21} g^2_{_{D^*D^*V}} F(\mathbf{q})^2}{-(\mathbf {p} - \mathbf {p}')^2-m_{V}^2}g^2_{D^*D^*V} [5 m_2^2 \mathbf{p}^2 + 2 \mathbf{p}^4 \nonumber \\&\quad + \, 5 m_1^2 (3 m_2^2 + \mathbf{p}^2)] \{4 \eta _1 \eta _2 M^2 m_V^2 \nonumber \\&\quad +\, [m_V^2 + (\mathbf{p} - \mathbf{p}')^2] (\mathbf{p} + \mathbf{p}')^2\}/(15 m_1^2 m_2^2 m_V^2)\nonumber \\&\quad +\,4 \frac{iC_{21} g_{_{D^*D^*V}}{g'}_{_{D^*D^*V}} F(\mathbf{q})^2}{-(\mathbf {p} - \mathbf {p}')^2-m_{V}^2}\eta _1 \eta _2 M^2 \nonumber \\&\quad \times \, (5 m_1^2 + 5 m_2^2 + 4 \mathbf{p}^2) (\mathbf{p}^2 - \mathbf{p}\cdot \mathbf{p}')/( 15 m_1^2 m_2^2)\nonumber \\&\quad + \frac{iC_{21} {g'}^2_{_{D^*D^*V}} F(\mathbf{q})^2}{-(\mathbf {p} - \mathbf {p}')^2-m_{V}^2} \{ [20 m_1^2 (2 m_2^2 + \mathbf{p}^2) \nonumber \\&\quad + 4\mathbf{p}^2 (-2 \eta _1 \eta _2 M^2 + 5 m_2^2 + 2 \mathbf{p}^2)] (\mathbf{p} - \mathbf{p}')^2/( 15 m_1^2 m_2^2)\nonumber \\&\quad + 2 (-6 \eta _1 \eta _2 M^2 + 5 m_1^2 + 5 m_2^2 + 2 \mathbf{p}^2) (\mathbf{p}\cdot \mathbf{p}'^2\nonumber \\&\quad - \mathbf{p}^2 \mathbf{p}'^2)/(15 m_1^2 m_2^2)\}\nonumber \\&K_{22}=- \frac{iC_{22} g^2_{_{D^*D^*V}} F(\mathbf{q}')^2}{-(\mathbf {p} + \mathbf {p}')^2-m_{V}^2}[5 m_2^2 \mathbf{p}^2 + 2 \mathbf{p}^4 \nonumber \\&\quad + 5 m_1^2 (3 m_2^2 + \mathbf{p}^2)] \{4 \eta _1 \eta _2 M^2 m_V^2\nonumber \\&\quad + [m_V^2 + (\mathbf{p} + \mathbf{p}')^2](\mathbf{p} - \mathbf{p}')^2 \}/(15 m_1^2 m_2^2 m_V^2)\nonumber \\&\quad +4\frac{iC_{22} g_{_{D^*D^*V}}{g'}_{_{D^*D^*V}} F(\mathbf{q}')^2}{-(\mathbf {p} + \mathbf {p}')^2-m_{V}^2} \eta _1 \eta _2 M^2 \nonumber \\&\quad \times (5 m_1^2 + 5 m_2^2 + 4 \mathbf{p}^2) (\mathbf{p}^2 + \mathbf{p}\cdot \mathbf{p}')/( 15 m_1^2 m_2^2)\nonumber \\&\quad + \frac{iC_{22}{g'}^2_{_{D^*D^*V}} F(\mathbf{q}')^2}{-(\mathbf {p} + \mathbf {p}')^2-m_{V}^2} \nonumber \\&\quad \times \{ [20 m_1^2 (2 m_2^2 + \mathbf{p}^2) + 4\mathbf{p}^2 (-2 \eta _1 \eta _2 M^2 + 5 m_2^2 + 2 \mathbf{p}^2)] \nonumber \\&\quad \times (\mathbf{p} + \mathbf{p}')^2/( 15 m_1^2 m_2^2) \nonumber \\&\quad +\, 2 (-6 \eta _1 \eta _2 M^2 + 5 m_1^2 + 5 m_2^2 + 2 \mathbf{p}^2) \nonumber \\&\quad \times (\mathbf{p}\cdot \mathbf{p}'^2 - \mathbf{p}^2 \mathbf{p}'^2)/(15 m_1^2 m_2^2)\} \nonumber \\&K_{23}=-\frac{4}{3}\frac{iC_{23} g^2_{_{D^*D^*P}} F(\mathbf{q})^2}{-(\mathbf {p} - \mathbf {p}')^2-m_{P}^2} \eta _1 \eta _2 M^2 (\mathbf{p}-\mathbf{p}')^2 \nonumber \\&K_{24}=-\frac{4}{3}\frac{iC_{24} g^2_{_{D^*D^*P}} F(\mathbf{q}')^2}{-(\mathbf {p} + \mathbf {p}')^2-m_{P}^2} \eta _1 \eta _2 M^2 (\mathbf{p}+\mathbf{p}')^2 \end{aligned}$$

(B5)

where $\mathbf {q}= (\mathbf {p} - \mathbf {p}')$ and $\mathbf {q}= (\mathbf {p} + \mathbf {p}')$.