1 Introduction

Searching for the \(B_{c}\)(-like) states is one of the important targets of particle physics, which provides opportunities to understand the nonperturbative behavior of strong interaction. In theory, the traditional \(B_{c}\) meson spectra were predicted by quark models [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15], QCD sum rules [16, 17], effective field theories [18,19,20,21], lattice QCD [22,23,24], and continuum functional methods for QCD [25,26,27]. However, currently, there are only two \(B_{c}\) states, i.e., the \(B_{c}(6275)\) and \(B_{c}(6872)\) listed in the Particle Data Group (PDG) [28]. Excitingly, both the CMS [29] and LHCb [30] Collaborations found the excited \(B_{c}^{+}(2^{1}S_{0})\) and \(B_{c}^{*+}(2^{3}S_{1})\) states in the \(B_{c}^{+}\pi ^{+}\pi ^{-}\) invariant mass spectrum recently.

These observations in experiments lead us to further explore the \(B_{c}\)-like states in theory. Apart from the traditional mesons of \(b{\bar{c}}\) quarks picture, the exotic \(B_{c}\)-like states were studied widely for a long time in the past. For instance, in view of the compact tetraquark states, Ref. [31] studied the mass spectra of \(B_{c}\)-like states with \({\bar{b}}cq{\bar{q}}\), \({\bar{b}}cs{\bar{q}}\), \({\bar{b}}cq{\bar{s}}\), and \({\bar{b}}cs{\bar{s}}\) components based on the chromomagnetic interactions model. In Ref. [32], with the improved chromomagnetic interactions model, the mass spectra of \(b{\bar{c}}q{\bar{q}}\), \(b{\bar{c}}s{\bar{q}}\), and \(b{\bar{c}}s{\bar{s}}\) were predicted, particularly, the S-wave states with the quark content \(b{\bar{c}}s{\bar{s}}\) and different quantum numbers were found around the thresholds of \(B_{c}\phi \) and \({\bar{B}}_{s}^{(*)}{\bar{D}}_{s}^{(*)}\) channels. Another important picture for studying \(B_{c}\)-like states is the hadronic molecular state generated by meson-meson interaction. Early in 2009, based on the QCD sum rule, the \({\bar{B}}{\bar{D}}\), \({\bar{B}}^{*}{\bar{D}}\), \({\bar{B}}{\bar{D}}^{*}\) and \({\bar{B}}^{*}{\bar{D}}^{*}\) molecular states mass spectra were predicted in Ref. [33]. In 2012, the interactions of \(B_{(s)}^{(*)}D_{(s)}^{(*)}\) systems were investigated with the one-boson-exchange model [34], where it was found that the \({\bar{b}}cs{\bar{s}}\) bound states may be formed. Reference [35] evaluated the S-wave interactions of the pseudoscalar and vector mesons systems with the quark contents \({\bar{b}}cq{\bar{q}}\) and \({\bar{b}}{\bar{c}}qq\) using the chiral unitary approach. Recently, the \(bc{\bar{s}}{\bar{q}}\), \(b{\bar{c}}s{\bar{q}}\), and \(b{\bar{c}}{\bar{s}}q\) systems were investigated [36], where six \(bc{\bar{s}}{\bar{q}}\) bound states were predicted, while no \(b{\bar{c}}s{\bar{q}}\) or \(b{\bar{c}}{\bar{s}}q\) states were found. More discussions about the molecular states can be referred to the reviews of Refs. [37, 38].

With this background, we will utilize the chiral unitary approach to predict the mass spectra of hidden strange \(B_{c}\)-like states in the present work. The chiral unitary approach is successfully applicated in studying states generated by meson-meson and meson-baryon interactions, see, for instance, Refs. [39,40,41,42,43]. On the one hand, in this approach, one takes into account the Lagrangians constructed by the global chiral symmetry as well as the hidden gauge symmetry [44,45,46,47,48,49]. On the other hand, one can solve the Bethe-Salpeter equation of the on-shell approximation to deal with the nonperturbative physics restoring two-body unitarity in coupled channels [50,51,52,53,54]. In this paper, focusing on the \(b{\bar{c}}s{\bar{s}}\) sector, we will consider the hidden strange channels \({\bar{B}}_{s}{\bar{D}}_{s}\), \({\bar{B}}_{s}^{*}{\bar{D}}_{s}\), \({\bar{B}}_{s}{\bar{D}}_{s}^{*}\), and \({\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}\) as well as the \({\bar{B}}{\bar{D}}\), \({\bar{B}}^{*}{\bar{D}}\), \({\bar{B}}{\bar{D}}^{*}\), and \({\bar{B}}^{*}{\bar{D}}^{*}\) channels. The interactions of light-vector-meson exchange, four pseudoscalar contact terms, and four vector mesons contact terms will be considered in these systems. And we can see whether or not the hidden strange \(B_{c}\)-like molecular states exist by searching for the poles of the modulus square amplitudes in the complex energy plane, which correspond to the dynamically generated states.

This work is organized as follows. We will introduce the pseudoscalar-pseudoscalar, pseudoscalar-vector, and vector-vector mesons interactions formulas in Sect. 2. Next, the numerical results of scattering amplitudes and poles are shown in Sect. 3. In addition, more discussions on the results are presented in Sect. 4. Finally, we end this work with a brief summary in Sect. 5.

2 Formalism

2.1 Lagrangians

In the present work, we study the S-wave interactions in the \({\bar{B}}_{s}{\bar{D}}_{s}\), \({\bar{B}}_{s}^{*}{\bar{D}}_{s}\), \({\bar{B}}_{s}{\bar{D}}_{s}^{*}\), and \({\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}\) hidden strange channels as well as another four channels \({\bar{B}}{\bar{D}}\), \({\bar{B}}^{*}{\bar{D}}\), \({\bar{B}}{\bar{D}}^{*}\), and \({\bar{B}}^{*}{\bar{D}}^{*}\). The vertices VPP and VVV are needed to calculate the light-vector-meson exchange potentials. Moreover, the contact terms PPPP and VVVV are also needed. Here, V and P denote the vector and pseudoscalar mesons fields, respectively. The relevant local hidden gauge Lagrangians are constructed by adopting the hidden gauge symmetry and chiral symmetry, which are shown in the following [55,56,57]

$$\begin{aligned} {\mathcal {L}}_{V P P}= & {} -i g\left\langle \left[ P, \partial _\mu P\right] V^\mu \right\rangle , \end{aligned}$$
(1)
$$\begin{aligned} {\mathcal {L}}_{V V V}= & {} i g\left\langle \left( V^\mu \partial _\nu V_\mu -\partial _\nu V^\mu V_\mu \right) V^\nu \right\rangle , \end{aligned}$$
(2)
$$\begin{aligned} {\mathcal {L}}_{P P P P}= & {} -\frac{1}{24f_{\pi }^2}\left\langle \left[ P, \partial _\mu P\right] \left[ P, \partial ^\mu P\right] \right\rangle , \end{aligned}$$
(3)
$$\begin{aligned} {\mathcal {L}}_{V V V V}= & {} \frac{g^2}{2}\left\langle V_\mu V_\nu V^\mu V^\nu -V_\nu V_\mu V^\mu V^\nu \right\rangle . \end{aligned}$$
(4)

The coupling constant \(g=M_{V}/(2f_{\pi })\) with \(M_{V}\) the mass of the vector meson taken as 800 MeV [36, 58] and \(f_{\pi }=93\) MeV the decay constant of pion. The symbol \(\left\langle ...\right\rangle \) means the trace of the matrices. In this work, we consider the SU(5) flavor symmetry since we study the interactions between the charmed and bottomed mesons. The fields P and \(V^{\mu }\) in Eqs. (1)–(4) are written as

$$\begin{aligned} P= & {} \left( \begin{array}{ccccc} \frac{\eta }{\sqrt{3}}+\frac{\eta ^{\prime }}{\sqrt{6}}+\frac{\pi ^0}{\sqrt{2}} &{} \pi ^{+} &{} K^{+} &{} {\bar{D}}^0 &{} B^{+} \\ \pi ^{-} &{} \frac{\eta }{\sqrt{3}}+\frac{\eta ^{\prime }}{\sqrt{6}}-\frac{\pi ^0}{\sqrt{2}} &{} K^0 &{} D^{-} &{} B^0 \\ K^{-} &{} {\bar{K}}^0 &{} -\frac{\eta }{\sqrt{3}}+\sqrt{\frac{2}{3}}\eta ^{\prime } &{} D_s^{-} &{} B_s^0 \\ D^0 &{} D^{+} &{} D_s^{+} &{} \eta _c &{} B_c^{+} \\ B^{-} &{} {\bar{B}}^0 &{} {\bar{B}}_s^0 &{} B_c^{-} &{} \eta _b \end{array}\right) ,\nonumber \\ \end{aligned}$$
(5)
$$\begin{aligned} V^{\mu }= & {} \left( \begin{array}{ccccc} \frac{\omega +\rho ^0}{\sqrt{2}} &{} \rho ^{+} &{} K^{*+} &{} {\bar{D}}^{* 0} &{} B^{*+} \\ \rho ^{-} &{} \frac{\omega -\rho ^0}{\sqrt{2}} &{} K^{* 0} &{} D^{*-} &{} B^{* 0} \\ K^{*-} &{} {\bar{K}}^{* 0} &{} \phi &{} D_s^{*-} &{} B_s^{* 0} \\ D^{* 0} &{} D^{*+} &{} D_s^{*+} &{} J / \psi &{} B_c^{*+} \\ B^{*-} &{} {\bar{B}}^{* 0} &{} {\bar{B}}_s^{* 0} &{} B_c^{*-} &{} \Upsilon \end{array}\right) ^{\mu }, \end{aligned}$$
(6)

respectively.

In the following, we will use the above Lagrangians and fields to calculate the potentials of \({\bar{B}}^{(*)}{\bar{D}}^{(*)}\)/\({\bar{B}}_{s}^{(*)}{\bar{D}}_{s}^{(*)}\) systems with the isospin \(I=0\), where we take the isospin phase convention \(|B^{(*)-}\rangle =-| 1/2,-1/2\rangle \), \(|{\bar{B}}^{(*)0}\rangle =| 1/2,1/2\rangle \), \(|D^{(*)-}\rangle =| 1/2,-1/2\rangle \), \(|{\bar{D}}^{(*)0}\rangle =| 1/2,1/2\rangle \), \(|{\bar{B}}^{(*)0}_{s}\rangle =|0,0\rangle \), and \(|D^{(*)-}_{s}\rangle =|0,0\rangle \).

2.2 The \({\bar{B}}{\bar{D}}\)/\({\bar{B}}_{s}{\bar{D}}_{s}\) system

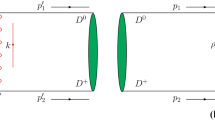
In this subsection, we consider the \({\bar{B}}{\bar{D}}\) and \({\bar{B}}_{s}{\bar{D}}_{s}\) coupled system. The elementary interactions can be obtained from the t-channel contributions, whose corresponding diagrams are shown in Fig. 1. Note that we neglect the heavy-vector-meson exchange processes, since they are too massive and the amplitudes are suppressed. Using the Lagrangians in Eq. (1), we obtain the effective potentials of the two pseudoscalar mesons by the light-vector-meson exchange as follows

Fig. 1
figure 1

The light-vector-meson exchange contribution for the two pseudoscalar mesons coupled system

Full size image
$$\begin{aligned} v^{ex}_{{\bar{B}}{\bar{D}}\rightarrow {\bar{B}}{\bar{D}}}&= \left( -\frac{3}{2m^{2}_{\rho }}-\frac{1}{2m^{2}_{\omega }}\right) g^2(k_{1}+k_{3})\cdot (k_{2}+k_{4}),\nonumber \\ v^{ex}_{{\bar{B}}{\bar{D}}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}}&= -\frac{\sqrt{2}}{m^{2}_{{\bar{K}}^{*}}+m^{2}_{{\bar{B}}_{s}}-m^{2}_{{\bar{B}}}}g^2(k_{1}+k_{3})\nonumber \\&\qquad \ \cdot (k_{2}+k_{4}), \nonumber \\ v^{ex}_{{\bar{B}}_{s}{\bar{D}}_{s}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}}&= -\frac{1}{m^{2}_{\phi }}g^2(k_{1}+k_{3})\cdot (k_{2}+k_{4}), \end{aligned}$$
(7)

where \(k_{1}\) and \(k_{2}\) are the four-momentums of the initial mesons, and \(k_{3}\) and \(k_{4}\) are the four-momentums of the final mesons. As done in Refs. [59, 60], in \(v_{{\bar{B}}{\bar{D}}\rightarrow {\bar{B}}{\bar{D}}}\) and \(v_{{\bar{B}}_{s}{\bar{D}}_{s}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}}\), we take

$$\begin{aligned} \begin{aligned} \frac{1}{q^2-m_V^2+i \epsilon } \approx -\frac{1}{m_V^2}, \end{aligned} \end{aligned}$$
(8)

where the transferred four-momentum q in the propagator is neglected. Since we only focus on the energy region near the threshold of \({\bar{B}}_{s}{\bar{D}}_{s}\) channel, the three-momentums of external particles can be ignored relative to their masses, one can safely take \(q=k_{1}-k_{3}\approx 0\) in the calculation. Even so, we will also discuss the results of preserving transferred four-momentum in Sect. 4. However, this reduction does not work well for \(v_{{\bar{B}}{\bar{D}}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}}\) due to the large mass difference between the initial and final mesons. And we adopt the following approximation [61]

$$\begin{aligned} \begin{aligned} q^2&=(p_{{\bar{B}}}-p_{{\bar{B}}_{s}})^2=p^2_{{\bar{B}}}+p^2_{{\bar{B}}_{s}}-2p_{{\bar{B}}}\cdot p_{{\bar{B}}_{s}}\\&=m^2_{{\bar{B}}}-m^2_{{\bar{B}}_{s}}. \end{aligned} \end{aligned}$$
(9)

In this way, we have

$$\begin{aligned} \begin{aligned} \frac{1}{q^2-m^{2}_{{\bar{K}}^{*}}+i \epsilon } \approx -\frac{1}{m^{2}_{{\bar{K}}^{*}}+m^{2}_{{\bar{B}}_{s}}-m^{2}_{{\bar{B}}}}. \end{aligned} \end{aligned}$$
(10)

Nevertheless, this correction is still a fairly rough approximation in the absence of experimental data. For more precise calculations are needed, the scheme in Ref. [62] is a good solution. Similar approximations are used in the pseudoscalar-vector and vector-vector systems as well. After performing the partial wave projection, one can obtain the S-wave potentials as functions of the rest frame energy.

Fig. 2
figure 2

The contact term connecting four pseudoscalar mesons

Full size image

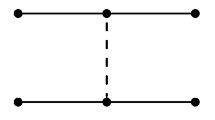
In addition, the interactions contributed by four pseudoscalar meson contact terms are shown in Fig. 2. The corresponding potentials are as follows

$$\begin{aligned} \begin{aligned}&v^{co}_{{\bar{B}}{\bar{D}}\rightarrow {\bar{B}}{\bar{D}}}\\&\quad =-\frac{1}{6f_{\pi }^{2}}\left( -k_1\cdot k_2-2k_1\cdot k_4+k_1\cdot k_3+k_2\cdot k_4\right. \\&\qquad \left. -2k_2\cdot k_3-k_3\cdot k_4\right) , \\&v^{co}_{{\bar{B}}{\bar{D}}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}}\\&\quad ={-}\frac{\sqrt{2}}{12f_{\pi }^{2}}\left( -k_1\cdot k_2-2k_1\cdot k_4{+}k_1\cdot k_3{+}k_2\cdot k_4{-}2k_2\right. \\&\qquad \left. \cdot k_3-k_3\cdot k_4\right) , \\&v^{co}_{{\bar{B}}_{s}{\bar{D}}_{s}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}}\\&\quad =-\frac{1}{12f_{\pi }^{2}}\left( -k_1\cdot k_2-2k_1\cdot k_4+k_1\right. \\&\qquad \ \left. \cdot k_3+k_2\cdot k_4-2k_2\cdot k_3-k_3\cdot k_4\right) . \end{aligned}\nonumber \\ \end{aligned}$$
(11)

2.3 The \({\bar{B}}^{*}{\bar{D}}\)/\({\bar{B}}{\bar{D}}^{*}\)/\({\bar{B}}_{s}^{*}{\bar{D}}_{s}\)/\({\bar{B}}_{s}{\bar{D}}_{s}^{*}\) system

In this subsection, we take into account the interactions between the pseudoscalar and vector mesons, where there exist four coupled channels, i.e., \({\bar{B}}^{*}{\bar{D}}\), \({\bar{B}}{\bar{D}}^{*}\), \({\bar{B}}_{s}^{*}{\bar{D}}_{s}\), and \({\bar{B}}_{s}{\bar{D}}_{s}^{*}\). The quantum number of this system is \(I(J^{P})=0(1^{+})\). The diagrams of the possible processes are shown in Fig. 3. Note that there is no vector meson exchange interaction between \({\bar{B}}^{*}{\bar{D}}\)/\({\bar{B}}_{s}^{*}{\bar{D}}_{s}\) and \({\bar{B}}{\bar{D}}^{*}\)/\({\bar{B}}_{s}{\bar{D}}_{s}^{*}\), because the vertex VVP is anomalous. Based on Eqs. (1) and (2), we get the effective potentials with \(I=0\)

$$\begin{aligned}{} & {} v_{{\bar{B}}^{*}{\bar{D}}\rightarrow {\bar{B}}^{*}{\bar{D}}}= \left( -\frac{3}{2m^{2}_{\rho }}-\frac{1}{2m^{2}_{\omega }}\right) \nonumber \\{} & {} \qquad \times g^2(k_{1}+k_{3})\cdot (k_{2}+k_{4})(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{3}^{\,\dagger }), \nonumber \\{} & {} v_{{\bar{B}}^{*}{\bar{D}}\rightarrow {\bar{B}}{\bar{D}}^{*}}=0, \nonumber \\{} & {} v_{{\bar{B}}^{*}{\bar{D}}\rightarrow {\bar{B}}_{s}^{*}{\bar{D}}_{s}}=-\frac{\sqrt{2}}{m^{2}_{{\bar{K}}^{*}}+m^{2}_{{\bar{B}}_{s}^{*}}-m^{2}_{{\bar{B}}^{*}}}\nonumber \\{} & {} \qquad \times g^2(k_{1} +k_{3})\cdot (k_{2}+k_{4})(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{3}^{\,\dagger }), \nonumber \\{} & {} v_{{\bar{B}}^{*}{\bar{D}}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}^{*}}=0, \nonumber \\{} & {} v_{{\bar{B}}{\bar{D}}^{*}\rightarrow {\bar{B}}{\bar{D}}^{*}}=\left( -\frac{3}{2m^{2}_{\rho }}-\frac{1}{2m^{2}_{\omega }}\right) \nonumber \\{} & {} \qquad \times g^2(k_{1}+k_{3})\cdot (k_{2}+k_{4})(\vec {\epsilon }_{2}\cdot \vec {\epsilon }_{4}^{\,\dagger }), \nonumber \\{} & {} v_{{\bar{B}}{\bar{D}}^{*}\rightarrow {\bar{B}}_{s}^{*}{\bar{D}}_{s}}=0, \nonumber \\{} & {} v_{{\bar{B}}{\bar{D}}^{*}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}^{*}}=-\frac{\sqrt{2}}{m^{2}_{{\bar{K}}^{*}}+m^{2}_{{\bar{B}}_{s}}-m^{2}_{{\bar{B}}}}\nonumber \\{} & {} \qquad \times g^2(k_{1}+k_{3})\cdot (k_{2} +k_{4})(\vec {\epsilon }_{2}\cdot \vec {\epsilon }_{4}^{\,\dagger }), \nonumber \\{} & {} v_{{\bar{B}}_{s}^{*}{\bar{D}}_{s}\rightarrow {\bar{B}}_{s}^{*}{\bar{D}}_{s}}\nonumber \\{} & {} \quad =-\frac{1}{m^{2}_{\phi }}g^2(k_{1}+k_{3})\cdot (k_{2}+k_{4})(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{3}^{\,\dagger }), \nonumber \\{} & {} v_{{\bar{B}}_{s}^{*}{\bar{D}}_{s}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}^{*}}=0, \nonumber \\{} & {} v_{{\bar{B}}_{s}{\bar{D}}_{s}^{*}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}^{*}}\nonumber \\{} & {} \quad =-\frac{1}{m^{2}_{\phi }}g^2(k_{1}+k_{3})\cdot (k_{2}+k_{4})(\vec {\epsilon }_{2}\cdot \vec {\epsilon }_{4}^{\,\dagger }). \end{aligned}$$
(12)

In the above equations, \(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{3}^{\,\dagger }\) and \(\vec {\epsilon }_{2}\cdot \vec {\epsilon }_{4}^{\,\dagger }\) are the products of the polarization vectors of the initial and final mesons. Since the three-momentums of the external mesons are small, we take \(\epsilon ^{0}=0\).

Fig. 3
figure 3

The light-vector-meson exchange contribution for the pseudoscalar and vector mesons coupled system

Full size image

2.4 The \({\bar{B}}^{*}{\bar{D}}^{*}\)/\({\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}\) system

There are also only two channels \({\bar{B}}^{*}{\bar{D}}^{*}\) and \({\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}\) for this system, whose quantum numbers could be \(I(J^{P})=0(0^{+})\), \(0(1^{+})\), and \(0(2^{+})\).

As shown in Fig. 4, the elementary interactions from the t-channel contributions are provided by the light-vector-meson exchange.

Fig. 4
figure 4

The light-vector-meson exchange contribution for the two vector mesons coupled system

Full size image

According to the Lagrangians in Eq. (2), we obtain the effective potentials with \(I=0\) as follows

$$\begin{aligned} \begin{aligned}&v^{ex}_{{\bar{B}}^{*}{\bar{D}}^{*}\rightarrow {\bar{B}}^{*}{\bar{D}}^{*}}\\&\quad =\left( -\frac{3}{2m^{2}_{\rho }}-\frac{1}{2m^{2}_{\omega }}\right) g^2(k_{1} +k_{3})\cdot (k_{2}+k_{4})(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{3}^{\,\dagger })\\&\quad \times (\vec {\epsilon }_{2}\cdot \vec {\epsilon }_{4}^{\,\dagger }), \\&v^{ex}_{{\bar{B}}^{*}{\bar{D}}^{*}\rightarrow {\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}}\\&\quad =-\frac{\sqrt{2}}{m^{2}_{{\bar{K}}^{*}}+m^{2}_{{\bar{B}}_{s}^{*}}-m^{2}_{{\bar{B}}^{*}}}g^2(k_{1} +k_{3})\cdot (k_{2}+k_{4})(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{3}^{\,\dagger })\\&\quad \times (\vec {\epsilon }_{2}\cdot \vec {\epsilon }_{4}^{\,\dagger }), \\&v^{ex}_{{\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}\rightarrow {\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}}\\ {}&\quad =-\frac{1}{m^{2}_{\phi }}g^2(k_{1}+k_{3})\cdot (k_{2}+k_{4})(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{3}^{\,\dagger }) (\vec {\epsilon }_{2}\cdot \vec {\epsilon }_{4}^{\,\dagger }). \end{aligned}\nonumber \\ \end{aligned}$$
(13)

Additionally, the interactions provided by the contact terms are shown in Fig. 5, and the corresponding potentials read

$$\begin{aligned} \begin{aligned} v^{co}_{{\bar{B}}^{*}{\bar{D}}^{*}\rightarrow {\bar{B}}^{*}{\bar{D}}^{*}}=&-2g^2\left[ -(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{2})(\vec {\epsilon }_{3}^{\,\dagger } \cdot \vec {\epsilon }_{4}^{\,\dagger })\right. \\&\quad \left. -(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{3}^{\,\dagger })(\vec {\epsilon }_{2} \cdot \vec {\epsilon }_{4}^{\,\dagger })\right. \\&\left. +2(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{4}^{\,\dagger })(\vec {\epsilon }_{2} \cdot \vec {\epsilon }_{3}^{\,\dagger })\right] , \\ v^{co}_{{\bar{B}}^{*}{\bar{D}}^{*}\rightarrow {\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}}=&-\sqrt{2}g^2\left[ -(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{2})(\vec {\epsilon }_{3}^{\,\dagger } \cdot \vec {\epsilon }_{4}^{\,\dagger })\right. \\&\left. -(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{3}^{\,\dagger })(\vec {\epsilon }_{2} \cdot \vec {\epsilon }_{4}^{\,\dagger })\right. \\&\left. +2(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{4}^{\,\dagger })(\vec {\epsilon }_{2} \cdot \vec {\epsilon }_{3}^{\,\dagger })\right] , \\ v^{co}_{{\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}\rightarrow {\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}}=&-g^2\left[ -(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{2})(\vec {\epsilon }_{3}^{\,\dagger } \cdot \vec {\epsilon }_{4}^{\,\dagger })\right. \\&\left. -(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{3}^{\,\dagger })(\vec {\epsilon }_{2} \cdot \vec {\epsilon }_{4}^{\,\dagger })\right. \\&\left. +2(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{4}^{\,\dagger })(\vec {\epsilon }_{2} \cdot \vec {\epsilon }_{3}^{\,\dagger })\right] . \end{aligned} \end{aligned}$$
(14)

With the following spin projection operators [59], one can obtain the potentials of spin \(J=0\), 1, and 2,

$$\begin{aligned} \begin{aligned} {\mathcal {P}}^{(0)}=&\, \frac{1}{3}(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{2}) (\vec {\epsilon }_{3}^{\,\dagger }\cdot \vec {\epsilon }_{4}^{\,\dagger }), \\ {\mathcal {P}}^{(1)}=&\, \frac{1}{2}\left[ (\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{3}^{\,\dagger }) (\vec {\epsilon }_{2}\cdot \vec {\epsilon }_{4}^{\,\dagger })-(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{4}^{\,\dagger }) (\vec {\epsilon }_{2}\cdot \vec {\epsilon }_{3}^{\,\dagger })\right] , \\ {\mathcal {P}}^{(2)}=&\, \frac{1}{2}\left[ (\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{3}^{\,\dagger }) (\vec {\epsilon }_{2}\cdot \vec {\epsilon }_{4}^{\,\dagger })+(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{4}^{\,\dagger }) (\vec {\epsilon }_{2}\cdot \vec {\epsilon }_{3}^{\,\dagger })\right] \\&-\frac{1}{3}(\vec {\epsilon }_{1}\cdot \vec {\epsilon }_{2}) (\vec {\epsilon }_{3}^{\,\dagger }\cdot \vec {\epsilon }_{4}^{\,\dagger }). \end{aligned} \end{aligned}$$
(15)

2.5 The Bethe–Salpeter equation

Once the effective potentials are obtained, we solve the Bethe–Salpeter equation with the on-shell approximation, which is shown below [39,40,41],

$$\begin{aligned} \begin{aligned} T = [1-vG]^{-1}v. \end{aligned} \end{aligned}$$
(16)

Here, v denotes the effective potential matrix. G is a diagonal matrix composed of the loop functions, for which the element with the dimensional regularization is [63]

$$\begin{aligned} G_{ii}(s)&= \,\frac{1}{16 \pi ^{2}}\left[ a_{ii}(\mu )+\log \left( \frac{m_{1}^{2}}{\mu ^{2}}\right) -x_{+}\text {log}\left( \frac{x_{+}-1}{x_{+}}\right) \right. \nonumber \\&\quad \left. -x_{-}\text {log}\left( \frac{x_{-}-1}{x_{-}}\right) \right] \end{aligned}$$
(17)

with

$$\begin{aligned} x_{\pm }= & {} \frac{s+m_{2}^{2}-m_{1}^{2}}{2s}\nonumber \\{} & {} \quad \pm \frac{1}{2s}\sqrt{(s+m_{2}^{2}-m_{1}^{2})^{2}-4s(m_{2}^{2}-i0^{+})}, \end{aligned}$$
(18)

where \(m_{1}\) and \(m_{2}\) are the masses of the mesons in the loop, \(\sqrt{s}\) is the energy of the system, \(\mu \) is the regularization scale and \(a_{ii}(\mu )\) is the subtraction constant. This formula is valid in the whole complex s plane.

Fig. 5
figure 5

The contact term connecting four vector mesons

Full size image
Table I The masses (in MeV) of pseudoscalar and vector mesons and the thresholds (in MeV) of relevant channels
Full size table

Since the dynamically generated states will be searched on the complex Riemann sheets, we need to extrapolate the loop function \(G_{ii}(s)\) to the second Riemann sheet, i.e.,

$$\begin{aligned} G_{ii}^{(I I)}(s)= & {} G_{ii}(s)-2 i {\text {Im}} G_{ii}(s)\nonumber \\= & {} G_{ii}(s)+\frac{i}{4\pi } \frac{q_{cmi}(s)}{\sqrt{s}}, \end{aligned}$$
(19)

where \(q_{cmi}(s)\) is the three-momentum of the particle in the center-of-mass frame,

$$\begin{aligned} \begin{aligned} q_{cmi}(s)=\frac{\lambda ^{1 / 2}\left( s, m_{1}^{2}, m_{2}^{2}\right) }{2 \sqrt{s}} \end{aligned} \end{aligned}$$
(20)

with the usual Källen triangle function \(\lambda (a, b, c)=a^{2}+b^{2}+c^{2}-2(a b+a c+b c)\).

For the single channel approach, there are only two Riemann sheets for the complex energy plane. The poles on the real energy axis and below the threshold on the first Riemann sheet are bound states, while the poles on the real energy axis and below the threshold on the second Riemann sheet are called virtual states, and the poles off the real energy axis but above the threshold on the second Riemann sheet are resonances [38, 64]. For n coupled channels approach, there are n cuts and thus \(2^{n}\) Riemann sheets [65]. We use the sign of \(+\) to represent the first Riemann sheet, and the sign of − to represent the second Riemann sheet in each coupled channel. Let us take two coupled channels as an example, the unstable bound states appear as poles off the real energy axis on the unphysical Riemann sheet \((-+)\) which in the ordering of the channels with lower threshold energy. The inelastic virtual states appear as poles off the real energy axis on the unphysical Riemann sheet \((+-)\).Footnote 1 For more detailed discussions, see Ref. [64].

The scattering amplitudes close to the pole can be written as [67, 68]

$$\begin{aligned} \begin{aligned} T_{i j}(s)=\frac{g_{i} g_{j}}{s-s_{p}}, \end{aligned} \end{aligned}$$
(21)

where \(g_i\) and \(g_j\) are the couplings of the i-th and j-th channels, and \(s_{p}\) is the square of the energy corresponding to the pole on the complex energy plane.

3 Results

Firstly, we determine the values of the regularization scale \(\mu \) and the subtraction constant \(a_{ii}(\mu )\) in the loop functions. In the studies of the \({\bar{b}}cq{\bar{q}}\) and \(bc{\bar{s}}{\bar{q}}\) systems in Refs. [35, 36], another regularization scheme of the three-momentum cutoff approach is applied to solve the singular integral, where the free parameter of the cutoff \(q_{max}\) is taken from 400 to 600 MeV. Due to the absence of the experimental data, following Refs. [44, 69, 70], we take \(\mu =q_{max}\), and match the real values of loop function from the two renormalization schemes at the threshold to determine the subtraction constant \(a_{ii}(\mu )\). This ensures that the two methods can get similar results near the threshold and avoids the influence of singularity above the threshold of loop function with the three-momentum cutoff approach.

Fig. 6
figure 6

The modulus square of \({\bar{B}}_{s}{\bar{D}}_{s}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}\) amplitude

Full size image

In Table 1, we show the masses of the particles and the thresholds of the different channels needed in the calculations. At first we use \(\mu =400\) MeV to perform numerical analyses. For the \({\bar{B}}{\bar{D}}\) and \({\bar{B}}_{s}{\bar{D}}_{s}\) coupled channels with the total spin \(J=0\), we show the result of modulus square of \(T_{{\bar{B}}_{s}{\bar{D}}_{s}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}}\) amplitude in Fig. 6, where two extremely narrow peaks locate near the thresholds. The first peak is about 10 MeV below the \({\bar{B}}_{s}{\bar{D}}_{s}\) threshold and has a very small width, see Table 2. This state mainly couples to \({\bar{B}}_{s}{\bar{D}}_{s}\) and below the threshold indicating that it is a inelastic virtual state of \({\bar{B}}_{s}{\bar{D}}_{s}\), since the pole of this state locates on the Riemann sheet \((+-)\) where the signs of − and \(+\) represent the corresponding channel is open or closed. In this case, the modulus square of amplitudes exhibit the cusp effect near threshold in all \({\bar{B}}_{s}^{(*)}{\bar{D}}_{s}^{(*)}\) systems, see Figs. 7 and 8. The second one near the \({\bar{B}}{\bar{D}}\) threshold is the bound state of \({\bar{B}}{\bar{D}}\), which has been analyzed in details in Ref. [35].

We also show the scattering lengths of S-wave in the last column of Tables 2, 3, 4, 5. Following Ref. [35], they are calculated by

$$\begin{aligned} \begin{aligned} a=-\frac{1}{8 \pi M_{\textrm{th}}} T\left( M^2_{\textrm{th}}\right) , \end{aligned} \end{aligned}$$
(22)

where \(M_{\textrm{th}}\) is the energy of the corresponding threshold, and T is the scattering amplitude in Eq. (16).

In Fig. 7 and Table 3, the results of the pseudoscalar-vector system of spin \(J=1\) are given. The two states located at \(7382.82-0.25i\) MeV and \(7478.57-0.18i\) MeV on the complex plane couple mostly to the \({\bar{B}}_{s}^{*}{\bar{D}}_{s}\) and \({\bar{B}}_{s}{\bar{D}}_{s}^{*}\) channels, respectively. And the couplings are \(|g_i|=9.96\) GeV and \(|g_i|=8.79\) GeV. This indicates that the first and second states are composed mainly of \({\bar{B}}_{s}^{*}{\bar{D}}_{s}\) and \({\bar{B}}_{s}{\bar{D}}_{s}^{*}\), respectively.

For the systems formed by the two vector mesons, we get three states \(7526.96-0.17i\) MeV, \(7526.83-0.18i\) MeV, and \(7527.24-0.14i\) MeV on the complex Riemann sheet with the spin \(J=0\), 1, and 2, respectively. And they all couple mostly to \({\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}\) channel. The results are shown in Fig. 8 and Table 4. As discussed in previous section, these poles are not on the physical sheet, i.e., \((+-)\), the most relevant channel \({\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}\) is open, while below the corresponding channel threshold, indicating that they are inelastic virtual states. Besides, it is worth mentioning that the differences among the three poles come from the contributions of the contact terms, since the meson exchange processes have the same contributions.

Next, we take the regularization scale \(\mu =600\) MeV. Then we find the corresponding poles on the different Riemann sheets, which are listed in Table 5. Except for the first state generated by the two pseudoscalar mesons system is the inelastic virtual state, the other ones are the unstable bound states, since the most relevant channel of the first state is open, while the most relevant channels of the other states are closed. Nevertheless, they have similar masses and widths with the inelastic virtual states in the case of \(\mu =400\) MeV. For the results in different parameters, we prefer that these systems can form the inelastic virtual states rather than unstable bound states based on the following reason. With the chiral unitary approach, the experimental data of the heavy flavor state \(T_{cc}(3875)\) can be well reconstructed by taking \(q_{max}=415\) MeV in Ref. [71], while one needs \(q_{max}=600\) MeV in the study of the low lying scalar mesons [72,73,74,75].

Fig. 7
figure 7

The modulus square of \({\bar{B}}_{s}^{*}{\bar{D}}_{s}\rightarrow {\bar{B}}_{s}^{*}{\bar{D}}_{s}\) and \({\bar{B}}_{s}{\bar{D}}_{s}^{*}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}^{*}\) amplitudes

Full size image
Fig. 8
figure 8

The modulus square of \({\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}\rightarrow {\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}\) amplitudes. a The total spin \(J=0\). b The total spin \(J=1\). c The total spin \(J=2\)

Full size image
Table II The pole position (in MeV), couplings \(g_i\) (in GeV) to every channel, and the scattering length a (in fm) in the two pseudoscalar mesons system. We use a minus sign of − and a plus sign of \(+\) to represent the corresponding channel is open or not in the parentheses after the pole position, and highlight the largest coupling of each pole in bold font
Full size table

4 Discussions

In this section, we discuss the results of preserving the transferred four-momentum in the t-channel amplitudes. Here, we want to investigate the impact of using Eq. (8) approximation, so we only retain the transferred four-momentum in Eq. (8), while not in the numerator of the propagators nor in the polarization vectors. The S-wave potentials in the two pseudoscalar mesons system are shown in Fig. 9, where the partial wave projection has been done. It is obvious that there are “unphysical” left-hand cuts in the potentials with the on-shell factorization, as shown by the red solid and blue dashed lines in Fig. 9. For diagonal elements \(V_{{\bar{B}}{\bar{D}}\rightarrow {\bar{B}}{\bar{D}}}\) and \(V_{{\bar{B}}_{s}{\bar{D}}_{s}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}}\), the left-hand cuts appear below their thresholds, respectively, while the ones of off-diagonal element \(V_{{\bar{B}}{\bar{D}}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}}\) appear at or very close to the two thresholds. In this case, the scattering amplitudes in the coupled channels are affected by the left-hand cuts, which makes it impossible for us to obtain the physical results. It should be emphasized that this problem can be solved by the solution in Ref. [62]. We will not do more accurate calculations here due to a lack of experimental data. Similar situations occur in the systems of pseudoscalar and vector mesons, and also two vector mesons.

Table III The poles positions (in MeV), couplings \(g_i\) (in GeV) to every channel, and the scattering lengths a (in fm) in the pseudoscalar and vector mesons system
Full size table
Table IV The poles positions (in MeV), couplings \(g_i\) (in GeV) to every channel, and the scattering lengths a (in fm) in the two vector mesons system
Full size table
Table V The poles positions (in MeV), couplings \(g_i\) (in GeV) to every channel, and the scattering lengths a (in fm) in the case of \(\mu =600\) MeV
Full size table

In view of the present situation, we provide the results of single channel approach in Fig. 10, where \(\mu =400\) MeV is shown in Fig. 10a and \(\mu =600\) MeV is shown in Fig. 10b. The first structures in the curves are caused by the left-hand cut, and their positions are consistent with that in Fig. 9c. The second ones are dynamically generated through the interaction of two pseudoscalar mesons. Accordingly, we find that the poles are located on the second Riemann sheet below the \({\bar{B}}_{s}{\bar{D}}_{s}\) threshold for both cases of \(\mu =400\) MeV and \(\mu =600\) MeV, which are written in Table 6. Note that this state is a virtual state and has zero width in the single channel approach, but the positions of the poles are consistent with the results in Tables 2 and 5, respectively. The poles of other systems are also shown in Table 6.

5 Conclusions

We make a study of the \(B_{c}\)-like hadronic molecular states with the quark content \(b{\bar{c}}s{\bar{s}}\) in this work. Three kinds of systems composed of the pseudoscalar-pseudoscalar, pseudoscalar-vector, and vector-vector mesons are calculated. The S-wave interactions are evaluated from the local hidden gauge Lagrangians which are extended to SU(5) case, and the total scattering amplitudes are obtained by solving the Bethe–Salpeter equation.

Fig. 9
figure 9

The potentials of S-wave in the two pseudoscalar mesons system. The solid (red) and dashed (blue) curves are the real and imaginary parts of the potentials which retain the transferred momentum, respectively, while the dot-dashed (black) curves are the potentials which neglect the transferred momentum. The dotted (black) lines correspond to the \({\bar{B}}{\bar{D}}\) (first) and \({\bar{B}}_{s}{\bar{D}}_{s}\) (second) thresholds

Full size image
Fig. 10
figure 10

The modulus square of \({\bar{B}}_{s}{\bar{D}}_{s}\rightarrow {\bar{B}}_{s}{\bar{D}}_{s}\) amplitude in the cases of a \(\mu =400\) MeV and b \(\mu =600\) MeV when retain the transferred momentum in the potentials

Full size image

In the case of \({\bar{B}}{\bar{D}}\) and \({\bar{B}}_{s}{\bar{D}}_{s}\) coupled system, we get a state with the quantum number \(I(J^{P})=0(0^{+})\) near the \({\bar{B}}_{s}{\bar{D}}_{s}\) threshold, which mainly couples to \({\bar{B}}_{s}{\bar{D}}_{s}\) channel. In the case of \({\bar{B}}^{*}{\bar{D}}\)/\({\bar{B}}{\bar{D}}^{*}\)/\({\bar{B}}_{s}^{*}{\bar{D}}_{s}\)/\({\bar{B}}_{s}{\bar{D}}_{s}^{*}\) system, two states mainly composed of \({\bar{B}}_{s}^{*}{\bar{D}}_{s}\) and \({\bar{B}}_{s}{\bar{D}}_{s}^{*}\) are obtained, whose quantum numbers are \(I(J^{P})=0(1^{+})\). For \({\bar{B}}^{*}{\bar{D}}^{*}\)/\({\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}\) system, three states with \(I(J^{P})=0(0^{+})\), \(0(1^{+})\), and \(0(2^{+})\) are found, which all mainly couple to the \({\bar{B}}_{s}^{*}{\bar{D}}_{s}^{*}\) channel. The slight differences of the masses and widths of these three states come from the contact terms contributions. Note that all the states above are of small widths and their masses are slightly below the corresponding thresholds. Under different parameter conditions in the pseudoscalar-vector and vector-vector systems, the masses and widths of the found states are similar, except for one case (\(\mu =400\) MeV) where they are the inelastic virtual states and another case (\(\mu =600\) MeV) where they are the unstable bound states. In addition, we also present the results of preserving the transferred four-momentum in the single channel approach, and the poles positions are consistent with the ones from above approximation. We expect the experiments can search for these predicted hadronic molecules in the future.

Table VI The poles positions (in MeV) in the cases of \(\mu =400\) MeV and \(\mu =600\) MeV in the single channel approach
Full size table