1 Introduction

The Kaluza–Klein (KK) theory is one of the oldest theories of the last century which proposed the extension of general relativity in higher dimensions and incorporated extra fields such as electromagnetism. In the past few decades, the KK theory has been extended into a more general class of string theories, however, the KK theory is still relevant as a low energy effective version of string theory [1,2,3,4,5,6]. The simplest KK theory is obtained using general relativity in five dimensions and then performing dimensional reduction to four dimensions. This extended framework contains both gravity and electromagnetism. Although the original five-dimensional theory is not a realistic theory of nature, it has been interpreted in a quantum mechanical framework as well as string theory. KK theory has also been attracted to non-commutative differential geometry, which may be viewed as a KK theory in which the extra fifth dimension is taken to be a discrete set of points rather than a continuum [7]. However, stationary and spherically symmetric black holes (BHs) were derived in [8]. Rotating BH solutions in four and five dimensions were found by Larsen [9]. These BHs typically have four free parameters: mass, spin, and electric and magnetic charges. Also, six- and higher-dimensional versions of KK BHs have been constructed [10]. In this paper, we study a four-dimensional rotating KK BH.

From thermodynamic considerations, we know that under certain conditions, a thermodynamic system can experience a phase transition. Davies found that a discontinuity of the heat capacity represents the second-order phase transition in BHs about 40 years ago [11,12,13] while the analysis of phase structure was done by Hut [14]. This approach is in the framework of the canonical ensemble. Note that at the extremal limit, heat capacity vanishes because of zero temperature. This is called a type 1 phase transition since the sign of heat capacity is changed, hence the BH with negative heat capacity is unstable, and therefore, the system is undergoing a phase transition.

When the background spacetime of a BH undergoes dynamical perturbations, the resultant behavior involves some sort of oscillations in spacetime geometry called quasinormal modes (QNMs). The QNMs are independent of initial perturbed configuration and they are the intrinsic fingerprint of the BH response to the external perturbations. The QNMs usually have an imaginary part giving the damping time of perturbations, while a real part represents the actual oscillations. Investigating vibrations in the background geometry of BHs is one of the most important and exciting topics in the context of compact star physics. These oscillations describe the evolution of fields on the background spacetime [15, 16]. The QNM spectrum reflects the properties of the spacetime, and we can probe the properties of the background by studying these vibrations. Therefore, the perturbed BH encodes its intrinsic properties, such as mass, charge and angular momentum in the QNM spectrum. The QNMs of supermassive BHs undergoing gravitational perturbations can be observed by future space-based gravitational wave detectors [17], and investigation of BH oscillations have attracted much attention recently after the detection of the gravitational waves produced by compact binary mergers [18].

Scalar fields have been widely studied in the area of cosmology as inflatons [19], and also considered as candidates for dark energy [20] and dark matter [21]. They can play a role in constructing a consistent theory of quantum gravity [22, 23] and modifying the background geometry of BHs in the strong-field regime [24, 25]. Scalar fields can produce clouds through instabilities around BHs [26, 27]. In different models with non-minimal interaction of scalar fields with the spacetime metric, we expect gravitational waves to be supplemented with a scalar mode. In these models, the gravitational waves of the spacetime geometry will be a linear combination of gravitational waves in the underlying gravitational theory and the scalar field solutions [28]. The final QNMs are included components oscillating with a combination of the background metric and scalar field that could potentially be observed. Therefore, the fingerprint of scalar fields on gravitational waves could be detected by employing future gravitational wave detectors. However, the interactions of scalar and tensor waves generally depend on the scalar propagation speed such that the interactions are negligible whether the scalar waves are luminal or quasi-luminal [29].

On the other hand, a minimally coupled scalar field describes the QNMs in the area of scalar–tensor theories, and observing quasi-resonance modes and anomalous decay rate of QN modes motivates one to investigate these models as well. Besides, more recently it has been shown that if the primary supermassive BHs in the extreme mass ratio inspirals do not carry a significant scalar charge, the non-minimal coupling factor vanishes, which the Laser Interferometer Space Antenna (LISA) will still be able to detect and further measure scalar charge [30].

The test scalar fields minimally coupled to the background metric were investigated for a Schwarzschild BH [31,32,33], Reissner–Nordström BH [34,35,36], magnetized Schwarzschild BH [37], Kerr geometry [38], BHs in Einstein–Weyl gravity [39], conformal Weyl BH solutions [40, 41] and three-dimensional BHs [42]. In this paper, we focus on perturbations of minimal coupled massive scalar fields in the background of four-dimensional static KK BHs to investigate the effects of the free parameters p and q on the scalar QNM spectrum. Moreover, we shall explore the quasi-resonance modes and anomalous decay rate of QN modes for our BH case study.

The layout of the paper is as follows. The next section is devoted to introducing the field equations and corresponding rotating KK black holes in four dimensions. Thermodynamic quantities such as entropy, temperature, and electric and magnetic potential, as well as the examination of the first law of BH thermodynamics, are studied in Sect. 2.1. The thermal stability of the BH in the canonical ensemble is investigated in Sect. 3. Then, in Sect. 4, dynamical perturbations are considered and QNMs are extracted. We finish the paper with a summary and closing remarks.

2 Field equations, solutions and thermodynamics

The solution of five-dimensional rotating KK BHs with electric charge (Q) and magnetic charge (P) in the presence of Maxwell electrodynamics is obtained within the framework of four-dimensional Einstein–Maxwell-dilaton gravity [4]. The complete action is described as

$$\begin{aligned} {\mathcal {S}}=-\int \left( \frac{{\mathcal {R}}}{\kappa ^{2}}+\frac{2}{3\kappa ^{2}\varphi ^{2}}\partial _{\mu }\varphi \partial ^{\mu }\varphi +\frac{1}{4} \varphi ^{2}F^{2}\right) \varphi \sqrt{-g}{\mathrm{d}}^{4}x, \end{aligned}$$
(1)

where \({\mathcal {R}}\) represents the Ricci scalar and \(\kappa ^{2}=16 \pi G\). Also, the dilaton field is represented by \(\varphi \) and \(F^{2}=F_{\mu \nu }F^{\mu \nu }\), where \(F_{\mu \nu }\) is the Maxwell field tensor. Field equations could be found by variation of the action (1) with respect to the metric, Maxwell and dilaton fields, respectively, resulting in

$$\begin{aligned} G_{\mu \nu }= & {} \frac{\kappa ^{2}\varphi ^{2}}{2}T_{\mu \nu }^{EM}-\frac{1}{ \varphi }\left( \partial _{\mu }\partial _{\nu }-g_{\mu \nu }\square \right) \varphi , \end{aligned}$$
(2)
$$\begin{aligned} T_{\mu \nu }^{EM}= & {} F_{\mu \rho }F_{\nu }^{\rho }-\frac{1}{4}g_{\mu \nu }F^{2}, \end{aligned}$$
(3)
$$\begin{aligned} \partial ^{\mu }F_{\mu \nu }= & {} -3\frac{\partial ^{\mu }\varphi }{\varphi } F_{\mu \nu }, \end{aligned}$$
(4)
$$\begin{aligned} \square \varphi= & {} \frac{\kappa ^{2}\varphi ^{3}}{3}F_{\mu \nu }F^{\mu \nu }. \end{aligned}$$
(5)

By using a solution-generating technique, Larsen obtained the following five-dimensional solution [9]

$$\begin{aligned} {\mathrm{d}}s_{5}^{2}= & {} \frac{H_{2}}{H_{1}}({\mathrm{d}}y+{\mathbf {A}})^{2}-\frac{H_{3}}{H_{2}}({\mathrm{d}}t+ {\mathbf {B}})^{2} \nonumber \\&+H_{1}\left( \frac{{\mathrm{d}}r^{2}}{\Delta }+{\mathrm{d}}\theta ^{2}+\frac{\Delta }{H_{3}}\sin ^{2}\theta {\mathrm{d}}\phi ^{2}\right) . \end{aligned}$$
(6)

The extra coordinate y is assumed to be periodic with period \(2\pi R_{KK}\), where \(R_{KK}\) is its radius. Also, \(\partial /\partial y\) is considered a Killing component so that the five-dimensional metric components can be functions of \( \{t,r,\theta ,\phi \}\) only [3]. Here we use the following definitions

$$\begin{aligned} H_{1}= & {} r^{2}+a^{2}\cos ^{2}\theta +r(p-2m) \nonumber \\&+\frac{p}{p+q}\frac{(p-2m)(q-2m)}{ 2}\nonumber \\&-\frac{p}{2m(p+q)}\sqrt{(q^{2}-4m^{2})(p^{2}-4m^{2})}a\cos \theta , \end{aligned}$$
(7)
$$\begin{aligned} H_{2}= & {} r^{2}+a^{2}\cos ^{2}\theta +r(q-2m)\nonumber \\&+\frac{q}{p+q}\frac{(p-2m)(q-2m)}{ 2} \nonumber \\&-\frac{q}{2m(p+q)}\sqrt{(q^{2}-4m^{2})(p^{2}-4m^{2})}a\cos \theta , \end{aligned}$$
(8)
$$\begin{aligned} H_{3}= & {} r^{2}+a^{2}\cos ^{2}\theta -2mr,\quad \Delta =r^{2}+a^{2}-2mr, \end{aligned}$$
(9)
$$\begin{aligned} {\mathbf {A}}= & {} -\left[ 2Q\left( r+\frac{p-2m}{2}\right) {+}\sqrt{\frac{ q^{3}(p^{2}-4m^{2})}{4m^{2}(p+q)}}a\cos \theta \right] \nonumber \\&\times \frac{{\mathrm{d}}t}{H_{2}}{-} \left[ 2P(H_{2}{+}a^{2}\sin ^{2}\theta )\cos \theta {+}\sqrt{\frac{p(q^{2}-4m^{2}) }{4m^{2}(p+q)^{3}}}\right. \nonumber \\&\times \left[ (p+q)(pr-m(p-2m))+q(p^{2} \right. \nonumber \\&\left. \left. -4m^{2})\right] a\sin ^{2}\theta \right] \frac{{\mathrm{d}}\phi }{H_{2}}, \end{aligned}$$
(10)
$$\begin{aligned} {\mathbf {B}}= & {} \sqrt{pq}\frac{(pq{+}4m^{2})r{-}m(p-2m)(q-2m)}{2m(p+q)H_{3}}a\sin ^{2}\theta {\mathrm{d}}\phi .\nonumber \\ \end{aligned}$$
(11)

The four free parameters m, p, q and a are related to the physical parameters through

$$\begin{aligned}&\text {Mass:}\quad M=\frac{p+q}{4}, \end{aligned}$$
(12)
$$\begin{aligned}&\text {magnetic charge:}\quad P^{2}=\frac{p(p^{2}-4m^{2}) }{4(p+q)}, \end{aligned}$$
(13)
$$\begin{aligned}&\text {electric charge:}\quad Q^{2}=\frac{q(q^{2}-4m^{2})}{ 4(p+q)}, \end{aligned}$$
(14)
$$\begin{aligned}&\text {angular momentum:}\quad J=\frac{\sqrt{pq}(pq+4m^{2})}{4m(p+q)}a. \end{aligned}$$
(15)

It is notable that two charges q and p are not independent parameters. They can change angular momentum and the mass of the BH. Also, the definition of charges forces us to select p and q larger than 2m. Furthermore, zero electric or magnetic charge causes the angular momentum J to vanish. In addition, it is clear that two horizons can be obtained by solving \(\Delta =0\), so \(r_\pm =m\pm \sqrt{m^2-a^2}\) which are impressed by mass (M) and both charges (P, Q) based on their definitions in Eqs. (12)–(15).

Setting \(a=m\) yields Kerr like extremal limit which named “fast rotation” by \(J > QP\). In addition if \(a\rightarrow 0\) and \(m\rightarrow 0\) but the ratio \(a/m<1\) we get the next extremal limit for our solution which gets \(J<PQ\) or “slow rotation” [5].

The corresponding four-dimensional BH metric after dimensional reduction is the following [9]

$$\begin{aligned} {\mathrm{d}}s_4^2= & {} -\frac{H_3}{\sqrt{H_1H_2}}({\mathrm{d}}t+{\mathbf {B}})^2+ \sqrt{H_1H_2}\left( \frac{ {\mathrm{d}}r^2}{\Delta } +{\mathrm{d}}\theta ^2 \right. \nonumber \\&\left. +\frac{\Delta }{H_3}\sin ^2\theta {\mathrm{d}}\phi ^2\right) . \end{aligned}$$
(16)

It is interesting to introduce the dimensionless form of the solution. In this regard, we use the following dimensionless parameters [43]

$$\begin{aligned}&p\equiv b\,m\quad q\equiv c\,m \nonumber \\&\epsilon ^{2}=\frac{Q^{2}}{M^{2}}\quad \mu ^{2}=\frac{P^{2}}{ M^{2}} \\&\alpha =\frac{a}{M}\quad x=\frac{r}{M}\nonumber \end{aligned}$$
(17)

so the free independent parameters are \(x,M,\alpha ,b,c\) and the metric functions transform as

$$\begin{aligned} \frac{H_{1}}{M^{2}}= & {} \frac{8(b-2)(c-2)b}{(b+c)^{3}}+\frac{4(b-2)}{b+c} x+x^{2} \nonumber \\&-\frac{2b\sqrt{(b^{2}-4)(c^{2}-4)}\alpha \cos \theta }{(b+c)^{2}} +\alpha ^{2}\cos ^{2}\theta , \nonumber \\ \frac{H_{2}}{M^{2}}= & {} \frac{8(b-2)(c-2)c}{(b+c)^{3}}+\frac{4(c-2)}{b+c} x+x^{2} \nonumber \\&-\frac{2c\sqrt{(b^{2}-4)(c^{2}-4)}\alpha \cos \theta }{(b+c)^{2}} +\alpha ^{2}\cos ^{2}\theta , \nonumber \\ \frac{H_{3}}{M^{2}}= & {} x^{2}+\alpha ^{2}\cos ^{2}\theta -\frac{8x}{b+c}, ~~\frac{\Delta }{M^{2}}{=}x^{2}+\alpha ^{2}{-}\frac{8x}{b+c}, \nonumber \\ \frac{H_{4}}{M^{3}}= & {} \frac{2\sqrt{bc}\Big [(bc{+}4)(b{+}c)x-4(b{-}2)(c{-}2)\Big ] \alpha \sin ^{2}\theta }{(b+c)^{3}}, \nonumber \\ m= & {} \frac{4M}{b+c},\quad \epsilon ^{2}=\frac{4c(c^{2}-4)}{(b+c)^{3}} ,\nonumber \\ \mu ^{2}= & {} \frac{4b(b^{2}-4)}{(b+c)^{3}},\quad J=\frac{\sqrt{bc}(bc+4) }{(b+c)^{2}}M^{2}\alpha . \end{aligned}$$
(18)

One of the advantages of this notation is a simple understanding of the physical properties of the solution. Indeed, the physical properties of this spacetime can be more clearly explained in terms of b, c and \(\alpha \) parameters, and further comparisons with the Kerr–Newman BH can be made possible. We should also note that some of the observational constraints on free parameters and physical properties of the mentioned KK BH solution (such as analysis of the gyroscope precession frequency [43], X-ray reflection spectroscopy [44], and shadow, quasinormal modes and quasi-periodic oscillations [45]) have been studied before.

2.1 Thermodynamics

Now, we turn to consider thermodynamics of the four-dimensional KK BH. We start with the calculation of horizon area (\({\mathcal {A}}\)) using its definition [9]

$$\begin{aligned} {\mathcal {A}}= & {} \int _{0}^{\pi }{\mathrm{d}}\theta \int _{0}^{2\pi }\sqrt{g_{_{\theta \theta }}g_{_{\phi \phi }}}_{\big |_{r=r_{+}}} \\ {\mathrm{d}}\phi= & {} -\frac{\pi \sqrt{bc}}{{\left( b{+}c\right) ^{2}}}\,{\ }\left[ {{2{+}\frac{\left( bc+4\right) }{\left( b+c\right) }\sqrt{1-\left( \frac{\left( b+c\right) {\alpha }}{2}\right) ^{2}} }}\right] M^{2}. \end{aligned}$$

In [46], the author proved that the entropy of the KK BH obeys the area formula which is given as [9]

$$\begin{aligned} S= & {} \frac{{\mathcal {A}}}{4\pi }=\frac{\pi {M}^{2}\sqrt{bc}}{2\left( b+c\right) } \left[ \frac{{x_{+}^{6}}-{\alpha }^{6}}{\left( {x_{+}^{2}}+{\alpha } ^{2}\right) x_{+}^{2}}-\frac{2\left( {x_{+}^{2}}+{\alpha }^{2}\right) }{x_{+} } \right. \nonumber \\&\left. +{\alpha }^{2}+\frac{4\,bc}{\left( b+c\right) ^{2}} \right] . \end{aligned}$$
(19)

Here \(x_{+}\) denotes the event horizon. If \(x_+\) is large, then

$$\begin{aligned} S\Big |_{x_{+}\rightarrow \infty }= & {} \frac{\pi {M}^{2}\sqrt{bc}}{\left( b+c\right) }\left[ \frac{{x}_{+}^{2}}{2}-x_{+}+{\frac{2\,bc}{\left( b+c\right) ^{2}}}-{\frac{{\alpha }^{2}}{x_{+}}}\right] \nonumber \\&+O\left( \frac{1}{ x_{+}^{2}}\right) , \end{aligned}$$
(20)

which confirms an expected result \(S \propto r^2_{+}\) for large values of \( r_{+}\), since this BH behaves similarly to four-dimensional static BH solutions.

The rotational velocity of the BH horizon (\(\Omega =-g_{_{\phi t}}/g_{_{\phi \phi }}\)) reads

$$\begin{aligned} \Omega =\frac{\left( b+c\right) ^{2}\alpha }{2M\,\sqrt{bc}}\left[ 2+\frac{ \left( bc+4\right) }{\left( b+c\right) }\sqrt{1-\left( \frac{\left( b+c\right) {\alpha }}{2}\right) ^{2}}\right] ^{-1}. \end{aligned}$$
(21)

It is worthy to recall that \(\Delta =0\) whenever we want to calculate \( \Omega \). One of the most important thermodynamic parameters in BH physics is temperature. It is shown that [46] temperature can be calculated using the Euclidean method or surface gravity method. However, in our paper, we shall use the later one. The common Hawking temperature is related to surface gravity of BHs (\(T=\kappa /2\pi \)). In our case, we encounter a stationary and axisymmetric solution, and corresponding to the Killing vector field is \(\chi =\partial /\partial t+\Omega \,\partial /\partial \phi \) the surface gravity reads

$$\begin{aligned} \kappa =\sqrt{-\frac{1}{2}(\partial _{\mu }\chi _{\nu })(\partial ^{\mu }\chi ^{\nu })}. \end{aligned}$$
(22)

It is easy to show that the Hawking temperature is given by

$$\begin{aligned} T= & {} \frac{\kappa }{4\pi }=\frac{x_{+}\left( {x_{+}^{4}}-{\alpha }^{4}\right) \left( b+c\right) }{2M\pi \sqrt{bc}}\left[ \left( {\alpha }^{2} +{\frac{4bc}{ \left( b+c\right) ^{2}}}\right) \right. \nonumber \\&\left. \times {x_{+}^{2}}\left( {x_{+}^{2}}-{\alpha } ^{2}\right) +{x_{+}^{6}}-{\alpha }^{6}+2\,x_{+}\left( {x_{+}^{2}}+{\alpha } ^{2}\right) ^{2}\right] ^{-1},\nonumber \\ \end{aligned}$$
(23)

which vanishes for \(r_{+}=0\) or \(r_{+}=a\). We should note that the vanishing temperature after the origin may be related to the horizon of the extremal BH.

Fig. 1
figure 1

Behavior of temperature with respect to entropy for \(q = 8\) (left) and \(p=8\) (right)

Full size image

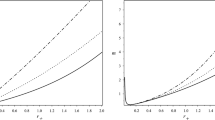
According to Fig. 1 one finds the minimum of the entropy related with the vanishing T and it is consistent with the third law of thermodynamics.

Fig. 2
figure 2

Behavior of temperature with respect to \(r_+\)

Full size image

From Fig. 2, it is clear that the position of the root and local maximum of T can change based on the metric parameters. For instance, one finds that by increasing the spin parameter a, temperature vanishes for larger \(x_+\). It is worth noting that changing the magnetic (electric) parameter does not alter the position of the root.

In addition, the expansion of temperature for a large radius is observed as

$$\begin{aligned} T\Big |_{x_{+}\rightarrow \infty }=\frac{\left( b+c\right) }{M\pi \sqrt{bc}} \left( \frac{1}{2x_{+}}-\frac{1}{x_{+}^{2}}\right) +O\left( \frac{1}{ x_{+}^{3}}\right) . \end{aligned}$$
(24)

Interestingly enough, from (20) and (24) one can find that, for \(x_{+}\rightarrow \infty \), the temperature vanishes but the entropy diverges! This may suggest the existence of an infinite radius for KK BHs [46].

The first law of BH thermodynamics can be verified as [9]

$$\begin{aligned} {\mathrm{d}}M=T{\mathrm{d}}S+U{\mathrm{d}}Q+\Phi {\mathrm{d}}P+\Omega {\mathrm{d}}J, \end{aligned}$$
(25)

in which U and \(\Phi \) are electric and magnetic potential, respectively, given by

$$\begin{aligned} U=\left( \frac{\partial M}{\partial Q}\right) _{S,P,J}, \quad \text {and} \quad \Phi =\left( \frac{\partial M}{\partial P}\right) _{S,Q,J}. \end{aligned}$$
(26)

After some manipulations, one can find the following explicit form of U and \(\Phi \)

$$\begin{aligned} U= & {} \pi TM\,\sqrt{{\frac{\left( {c}^{2}-4\right) b}{\left( b+c\right) ^{3}}}} \left( b+{\frac{4}{\sqrt{4-{\alpha }^{2}\left( b+c\right) ^{2}}}}\right) , \end{aligned}$$
(27)
$$\begin{aligned} \Phi= & {} \pi TM\,\sqrt{{\frac{\left( {b}^{2}-4\right) c}{\left( b+c\right) ^{3}}}}\left( c+{\frac{4}{\sqrt{4-{\alpha }^{2}\left( b+c\right) ^{2}}}} \right) . \end{aligned}$$
(28)

It is notable that for \(p=2m\) (\(q=2m\)) which is equal to \(b=2\) (\(c=2\)), the magnetic (electric) potential vanishes. Also, both potentials vanish when \( x_{_{+}}\rightarrow \infty \) since

$$\begin{aligned} \Phi \Big |_{x_{_{+}}\rightarrow \infty }= & {} \sqrt{{\frac{{b}^{2}-4}{\left( b+c\right) b}}}\left( c+{\frac{4}{\sqrt{-{\alpha }^{2}\left( b+c\right) ^{2}+4}}}\right) \nonumber \\&\times \left( \frac{1}{2x_{_{+}}}-\frac{1}{x_{_{+}}^{2}}\right) +O\left( \frac{1}{x_{_{+}}^{3}}\right) \nonumber \\ U\Big |_{x_{_{+}}\rightarrow \infty }= & {} \sqrt{{\frac{{c}^{2}-4}{\left( b+c\right) c}}}\left( b+{\frac{4}{\sqrt{-{\alpha }^{2}\left( b+c\right) ^{2}+4}}}\right) \nonumber \\&\times \left( \frac{1}{2x_{_{+}}}-\frac{1}{x_{_{+}}^{2}}\right) +O\left( \frac{1}{x_{_{+}}^{3}}\right) , \end{aligned}$$
(29)

which is expected for localized charged objects.

3 Thermal stability via canonical ensemble approach

We are in a position to study thermal stability and phase transition of solutions. By looking at the behavior of the heat capacity in the presence of positive temperature, we predict criteria for thermally stable BHs. This approach is known as stability in the canonical ensemble. When a system is unstable, phase transitions usually take place. In other words, unstable systems go under a phase transition to acquire stability. Discontinuity of heat capacity marks the second-order phase transition in BHs [11, 12].

The heat capacity for fixed values of extensive quantities obeys

$$\begin{aligned} C_{P,Q,J}=T\frac{\partial S}{\partial T}\Big |_{P,QJ}. \end{aligned}$$
(30)

In our case, entropy is not an explicit function of temperature. Instead, they have common variables. Therefore, we use the chain rule of derivatives to compute \(C_{P,Q,J}\). It is notable that P,  Q and J are constants, simultaneously, so we consider \({\mathrm{d}}Q={\mathrm{d}}J={\mathrm{d}}P=0\) to compute the heat capacity. For the sake of complexity, we use some figures to analyze the treatment of the heat capacity. It is important to note that we use different scales for temperature to make it comparable with the heat capacity. In order to find the critical point of heat capacity, we should use the first and second derivative of temperature with respect to \(r_{+}\). Firstly, we solve the first derivative of temperature (\(\frac{\partial T}{\partial x_{+}}=0\)) to obtain the critical angular momentum. Then, by substitution in the second derivative \((\frac{\partial ^{2}T}{\partial x_{+}^{2}}=0),\) we may obtain the critical horizon. These two functions are complicated, and it is not a trivial task to solve them analytically. The practical solution is to use the numerical method.

In Table 1, the critical values of spin parameter are presented. It is clear that by increasing p (q) when q (p) is constant, the value of critical a increases. It is notable that replacing p with q does not change the critical value of the rotation parameter.

Table 1 Critical values of rotation parameter a
Full size table
Fig. 3
figure 3

Behavior of \(C_{_{P,Q,J}}\) (green curve) and \(10^{5}T\) (red curve) with respect to \(r_+\)

Full size image

Regarding Eq. (30), one may find positive heat capacity for negative T and \(\frac{\partial S}{\partial T}\Big |_{P,QJ}<0\) which is not physical stability. In order to remove such an ambiguity, we plot both temperature and heat capacity in Fig. 3. By adjusting the electric and magnetic charge parameters, we can find the critical rotation parameter \(a_{\mathrm{crit}}\). Numerical calculations show that increasing the magnetic (electric) charge makes the critical rotation parameters larger. By exchanging the value of two parameters, no change in \(a_{\mathrm{crit}}\) is observed.

Figure 3 shows two divergences and one zero value in the heat capacity function in the presence of positive temperature, and their positions change by increasing the magnetic (electric) parameter. As we mentioned before, the only acceptable \(C_x\) (x means P, Q, J) is positive, so the stable BH is only allowed to have limited radii. Based on the figures, the heat capacity is negative after the final divergence. Accordingly, large BHs are not thermodynamically stable.

Another interesting note is related to the position of two divergences relative to each other. Increasing the metric parameters makes them farther apart. However, it does not have much effect on the allowable values of the radius. The final point is that, as the divergences occur between positive and negative values of \(C_x\), the plots do not predict first- or second-order phase transitions, but the Davis phase transition is possible.

Finally, we plot heat capacity when the magnetic charge parameter is fixed, but the curves do not contain additional information.

4 Quasinormal modes

4.1 Setup

Here, we consider a massive scalar perturbation in the background geometry of four-dimensional static KK BHs and obtain the QN frequencies by employing the WKB approximation [47,48,49,50]. The line element of four-dimensional KK BHs (16) for the static case \( a=0\) reduces to

$$\begin{aligned} {\mathrm{d}}s_{4}^{2}=-f(r){\mathrm{d}}t^{2}+\frac{{\mathrm{d}}r^{2}}{f(r)}+g(r)\left( {\mathrm{d}}\theta ^{2}+\sin \theta {\mathrm{d}}\phi ^{2}\right) , \end{aligned}$$
(31)

with \(f(r)=H_{3}/g(r)\) and \(g(r)=\sqrt{H_{1}H_{2}}\). The equation of motion for a minimally coupled massive scalar field \(\Psi \) is given by the following Klein–Gordon equation

$$\begin{aligned} \square \Psi -\mu ^{2}\Psi =0, \end{aligned}$$
(32)

in which \(\mu \) is the mass of the scalar field \(\Psi \) and \(\square =\nabla _{\nu }\nabla ^{\nu }\). It is notable that we cannot obtain a second-order Schrödinger-like wave equation for the radial part of perturbations by expanding the scalar field versus either spherical or spheroidal harmonics. In order to find a Schrödinger-like master equation, hence being able to use the WKB approximation, we first define \(R= \sqrt{g(r)}\) and rewrite the metric (31) in the following form

$$\begin{aligned} {\mathrm{d}}s_{4}^{2}=-f(R){\mathrm{d}}t^{2}+\frac{{\mathrm{d}}R^{2}}{f(R)h^{2}(R)}+R^{2}\left( {\mathrm{d}}\theta ^{2}+\sin \theta {\mathrm{d}}\phi ^{2}\right) , \end{aligned}$$
(33)

where f(R) and h(R) can be obtained by converting r versus R through \(R=\sqrt{g(r)}\). However, we should note that, to calculate r(R), the equation \(R-\sqrt{g(r)}=0\) has four independent solutions. Here, we choose the solution which maps the event horizon \(r_{+}\) of (31) to a positive definite event horizon \(R_{+}\) for (33).

Now, by expanding the scalar field eigenfunction \(\Psi \) in the form

$$\begin{aligned} \Psi \left( t,R,\theta ,\varphi \right) =\sum _{l,m}\frac{1}{R}\psi _{l}\left( R\right) Y_{l,m}\left( \theta ,\varphi \right) e^{-i\omega t}, \end{aligned}$$
(34)

in which \(Y_{l,m}\left( \theta ,\varphi \right) \) denotes the spherical harmonics on \(S^{2}\), we can find that the equation of motion (32) reduces to a wavelike equation for the radial part \(\psi _{l}\left( R\right) \) as follows

$$\begin{aligned} \left[ \partial _{R_{*}}^{2}+\omega ^{2}-V_{l}\left( R\right) \right] \psi _{l}\left( R_{*}\right) =0. \end{aligned}$$
(35)

In this equation, \(R_{*}\) is the tortoise coordinate

$$\begin{aligned} R_{*}=\int \frac{{\mathrm{d}}R}{f(R)h(R)}, \end{aligned}$$
(36)

and the effective potential \(V_{l}\left( R\right) \) is given by

$$\begin{aligned} V_{l}\left( R\right) =f\left( R\right) \left[ \mu ^{2}+\frac{l\left( l+1\right) }{R^{2}}+\frac{h\left( R\right) }{R}\partial _{R}\left[ f(R)h(R) \right] \right] , \end{aligned}$$
(37)

where l is the multipole number.

By imposing some proper boundary conditions on the master wave equation (35), we can find a discrete set of eigenvalues \(\omega \). The quasinormal boundary conditions imply that the wave at the event horizon is purely incoming and the modes are purely outgoing at spacial infinity.

$$\begin{aligned} \begin{array}{c} \psi _{l}\left( R\right) \sim e^{-i\omega R_{*}}\quad \hbox {as}\ R_{*}\rightarrow -\infty \ (r\rightarrow r_{+}) \\ \psi _{l}\left( R\right) \sim e^{i\omega R_{*}}\quad \hbox {as}\ R_{*}\rightarrow \infty \ (r\rightarrow \infty ) \end{array} , \end{aligned}$$
(38)

We should consider these boundary conditions to obtain the QNMs spectrum.

Fig. 4
figure 4

Profiles of the effective potential versus the radial coordinate. The potential forms a barrier and vanishes at both infinities

Full size image

4.2 WKB approximation

In this paper, we use the WKB approximation to calculate the QN modes. This approximation is based on matching WKB expansion of the modes \(\psi _{l}\left( r_{*}\right) \) at the event horizon and spatial infinity with the Taylor expansion of the effective potential (37) near the peak of the potential barrier through two turning points at \(\omega ^{2}-V_{l}\left( R\right) =0\). Thus, we can use the WKB approximation to calculate the QN frequencies for potentials that form a potential barrier and take constant and/or zero values at the event horizon and spatial infinity. The WKB approximation was first applied to the problem of scattering around black holes [47], and subsequently extended to the third order [48], sixth order [49] and 13th order [50]. The 13th order of the WKB approximation is given by the following formula

$$\begin{aligned} \omega ^{2}= & {} V_{0}+\sum _{j=1}^{6}\Omega _{2j}-i\sqrt{-2V_{0}^{\prime \prime }} \left( n+\frac{1}{2}\right) \nonumber \\&\times \left( 1+\sum _{j=1}^{6}\Omega _{2j+1}\right) ;\quad n=0,1,2,\ldots , \end{aligned}$$
(39)

where \(V_{0}\) is the maximum value of the effective potential, \(\Omega _{j}\)’s are the WKB correction terms of the jth order, and n is the overtone number. It is worth mentioning that the WKB formula does not give reliable frequencies for \(n\ge l\), whereas it leads to quite accurate values for \(n<l\) and exact values in the eikonal limit \(l\rightarrow \infty \). We use this formula up to the 13th order to calculate the QN frequencies of perturbations.

However, at the first step, we should note that the relation r(R) is generally quite complicated and leads to a cumbersome form for the effective potential. Thus, obtaining the QN frequencies even by using the third-order WKB formula is time-consuming. But, fortunately, for an equal value of p and q (\(p=Q=q\)), we receive a quite simple relation as \(r(R)=m+R-Q/2\) and the effective potential takes a more simple form as follows

$$\begin{aligned} V_{l}\left( R\right) =f(R)\left( \mu ^{2}+\frac{l\left( l+1\right) }{R^{2}}+ \frac{f^{\prime }(R)}{R}\right) , \end{aligned}$$
(40)

with

$$\begin{aligned} f(R)=-\frac{m^{2}}{R^{2}}+\frac{\left( Q-2R\right) ^{2}}{4R^{2}}. \end{aligned}$$
(41)

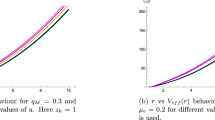
We shall use this potential to calculate the QNMs. Figure 4 shows the behavior of this effective potential (40) versus radial coordinate for different values of charge Q and the multipole number l. The potential forms a barrier and vanishes at the event horizon and spatial infinity, thus we can use the WKB formula to calculate the QN frequencies.

As we have mentioned before, the WKB formula usually gives the best accuracy for \(l>n\) and it provides an accurate and economic way to compute the QN frequencies [49, 51]. In this regard, we compare two sequential orders of the formula (39) to estimate the error of the WKB approximation. However, since each WKB correction term affects either the real or imaginary part of the squared frequencies, we should use the following quantity [51]

$$\begin{aligned} \Delta _{k}=\frac{\left| \omega _{k+1}-\omega _{k-1}\right| }{2}, \end{aligned}$$
(42)

to obtain the error estimation of \(\omega _{k}\) that is calculated with the WKB formula of the order k, and \(\Delta _{k}\) gives the WKB order in which the error is minimal. Therefore, we can use the error estimation (42) to find the WKB order which gives the most accurate approximation for the QN modes.

Table 2 The fundamental modes calculated by the WKB formula of different orders for \(m=1\), \(\mu =0\), \(n=0\), \(l=1\) and \(Q=0.1\) left (\(Q=0.2\) right). The minimal error estimation is given in bold form
Full size table

In Table 2, we show the QN frequencies and the error estimation of the WKB formula for the fundamental QN modes. From this table, we see that the best order of the WKB formula for calculating the QN frequency for \(Q=0.1\) is the seventh order, whereas the QN frequency for \(Q=0.2\) has the best accuracy with the help of the fifth order. Thus, the minimum error of the WKB formula depends on the charge value Q. The oscillations increase and the modes live longer as the charge Q decreases.

4.3 Anomalous decay rate of QN modes

One of the motivations for considering the test massive fields comes from the fact that, depending on the mass of the scalar field, the QNMs either grow or decay with an increasing multipole number l. This novel behavior was first uncovered for Schwarzschild BH [33], and then confirmed for the Reissner–Nordström BH [36], Schwarzschild-dS spacetime and BH solutions in conformal Weyl gravity [52]. This anomalous behavior is due to the presence of a sub-leading \(\mu ^{2}\)-term in the eikonal expression of \(\omega _{i}\) [33]. In this scenario, there is a critical scalar mass \({\tilde{\mu }}\) such that \(\omega _{i}\) increases (decreases) with an increase in l for \(\mu >{\tilde{\mu }}\) (\(\mu < {\tilde{\mu }}\)). For low-l values, the critical mass \({\tilde{\mu }}\) decreases when l increases, but there is a fixed critical mass for large-l values.

Fig. 5
figure 5

The imaginary part of the fundamental overtone versus \(\mu \) calculated by using the sixth-order WKB formula for \(m=1\). The vertical black line indicates the critical mass \(\tilde{\mu }\) where the curves cross each other for large-l values

Full size image
Fig. 6
figure 6

The effective potential for \(m=1\) and \(Q=0.1\). The potential takes a constant value at the spacial infinity and the dotted horizontal lines show these asymptotic values

Full size image

Here, we numerically investigate the possibility of this anomalous behavior for our BH case study with the line element (33). Note that since we are going to calculate the fundamental QN frequencies for large-l values, the WKB approximation will lead to accurate results. Thus, we have used the sixth-order WKB formula to plot the Fig. 5. This figure shows the imaginary part of the QN modes \(\omega _{i}\) as a function of \(\mu \) for different values of l and Q. From both panels, we find that the curves cross over at a special mass \({\tilde{\mu }}\), and thus the QNM spectrum of KK BHs in asymptotically flat spacetime contains this anomaly. It is worth noting that the charge parameter Q affects the critical mass and \({\tilde{\mu }}\) increases with a decrease in Q.

4.4 Quasi-resonance modes

In addition to the anomalous decay rate of QNMs related to massive test fields, observing arbitrarily long life (purely real) modes is also one of the interesting motivations for studying massive scalar fields [34]. These kinds of modes with vanishing imaginary parts are called quasi-resonance modes. The oscillations do not decay in the quasi-resonances and the situation is similar to the standing waves on a string. The quasi-resonance modes were investigated for Schwarzschild BH [31, 32], Reissner–Nordström BH [35], magnetized Schwarzschild BH [37], Kerr geometry [38], BHs in Einstein–Weyl gravity [39] and wormholes [53]. However, it is not possible to find these modes for asymptotically dS spacetimes [52, 54]. The quasi-resonance modes can be found for special values of the field mass whenever the effective potential is non-zero at the event horizon or spatial infinity (see Fig. 6 for the profile of the effective potential (40) of our BH case study). In this scenario, the QNMs disappear, and this happens just for lower overtones.

We recall that the WKB approximation provides quite a simple, powerful and accurate tool for studying the dynamical properties of BHs, such as the scattering problems and QN modes for low overtones and high multipole numbers. However, this method cannot be used for the calculation of quasi-resonance modes in general and it just allows one to calculate large-l QN frequencies of massive test fields close to the quasi-resonance regime [51]. The reason is that the effective potential does not have a local maximum for large values of the field mass, thus the WKB expansion cannot be performed. However, as long as the asymptotic value of the effective potential is lower than its peak, \(\mu ^{2}<V_{0}\) (like the green and red curves in Fig. 6), the ordinary WKB formula (39) is accurate enough for \(l\ge 1\); hence the error is negligible [51].

In order to calculate the quasi-resonances by employing the WKB approximation, we use an approach based on averaging of Padé approximations [50] which is developed for quasi-resonances of the Schwarzschild BH [51] which can considerably improve the accuracy of the quasi-resonance modes for \(\mu ^{2}>V_{0}\) when the maximum of the potential still exists (see the blue curves in Fig. 6). The fundamental QN modes calculated by averaging results obtained by Padé approximations of various orders and related standard deviation (SD) formula are shown in Tables 3 and 4 for \(l=1,2\) in order. As we observe from these tables, the minimal SD changes based on the scalar mass so that the higher orders lead to minimal SD for low-\(\mu \) values and the lower orders lead to minimal SD for high-\(\mu \) values, unlike the Schwarzschild case in which the SD formula of averaging Padé approximates of 13th order is minimal for all values of field mass (see table XI of Ref. [51]).

Table 3 The fundamental modes calculated by averaging of Padé approximations for \(m=1\), \(Q=0.1\) and \(l=1\). The minimal standard deviation formula is given in bold
Full size table
Table 4 The fundamental modes calculated by averaging of Padé approximations for \(m=1\), \(Q=0.1\) and \(l=2\). The minimal standard deviation formula is given in bold
Full size table

Figure 7 shows the behavior of QN frequencies with increasing \( \mu \) ranges from zero to 1.27 (2.1) for \(l=1\) (\(l=2\)). The red curves show the QNMs of the Reissner–Nordström BH and have been plotted for comparison. As \(\mu \) increases, the real part of frequencies also increases, whereas the imaginary part tends to zero; hence QNMs disappear and the quasi-resonances dominate.

Fig. 7
figure 7

The QN modes for \(m=1\) and \(Q=0.1\). The red curves show the QNMs of Reissner–Nordström BH for \(q_{RN}=0.1\). The imaginary part tends to zero as the field mass increases; hence QNMs disappear and the quasi-resonances dominate

Full size image

5 Closing remark

In conclusion, we investigated the critical behavior of a rotating KK BH solution in the presence of Maxwell electrodynamics. Firstly, the conserved and thermodynamic quantities were introduced. The first law is established and limited behavior of thermodynamic quantities was considered. The interesting point was the non-vanishing values of entropy in the presence of a large radius while the temperature was zero in this condition. Electric and magnetic potential are constant when \(x_+\rightarrow \infty \).

In order to study the critical behavior of the solution, we considered the treatment of heat capacity. It is a famous approach, as the stability in the canonical ensemble indicates that stable BHs have positive heat capacity. In order to specify thermodynamically stable conditions of the solution, we used the numerical method.

Based on the plots, we observed that the BH solution should have a small event horizon radius, since large event horizon radii caused negative heat capacity even though the temperature was positive. To understand the impact of the charges on the heat capacity, we plotted three figures and increased the value of the magnetic parameter when the electric charge parameter was fixed. Two divergences were observed such that the sign of heat capacity was changed by them, and therefore, we could not call them first-order phase transitions. These may be interpreted as Davis phase transitions.

In addition, we considered a massive scalar perturbation minimally coupled to the background geometry of four-dimensional static KK BHs. First, we converted the KK background to a spherically symmetric line element to obtain a second-order radial master wave equation, and then calculated the QN modes by employing the WKB approximation of various orders. From the error estimation of the WKB formula, we found that the minimum error of this approximation depends on the charge value Q such that the best order of the WKB formula for \(Q=0.1\) was the seventh order, whereas the QN frequency had the best accuracy with the help of the fifth order for \(Q=0.2\). The oscillations increased and the modes lived longer as the charge Q decreased.

Moreover, the anomalous decay rate of the quasinormal mode spectrum was investigated by using the sixth-order WKB formula, and we observed that the curves crossed over at a special critical mass \({\tilde{\mu }}\). Thus, the KK BHs in asymptotically flat spacetime had the anomalous decay rate in its QNM spectrum. We also found that the charge parameter Q affects the critical mass and \({\tilde{\mu }}\) increases with a decrease in Q.

Moreover, the quasi-resonance modes of our BH case study were investigated by employing the averaging of Padé approximations. It was shown that, unlike the Schwarzschild case, in which the SD formula of averaging Padé approximates of 13th order is minimal for all values of the field mass, the minimal SD changed based on the scalar mass for the KK BHs so that the higher orders led to minimal SD for low-\(\mu \) values and the lower orders led to minimal SD for high-\(\mu \) values.