Polarization control in spin-transparent hadron colliders by weak-field navigators involving lattice enhancement effect

Abstract

Hadron polarization control schemes for Spin Transparent (ST) synchrotrons are analyzed. The spin dynamics and beam polarization in such synchrotrons are controlled by spin navigators (SN) which are special small insertions of weak magnetic fields. An SN stabilizes the beam polarization and allows for setting any desirable spin orientation at an interaction point in the operational regime, including a frequent spin flip. We present a general approach to design of SNs. We distinguish different types of SNs, namely, those not causing closed orbit perturbation as well as those producing local and global orbit distortions. In the second case, the concept of the spin response function in an ST synchrotron is applied and expanded to reveal the effect of the SN strength enhancement by magnetic lattice of the synchrotron. We provide conceptual schemes for SN designs using longitudinal and transverse magnetic fields allowing for polarization control at low as well as high energies. We also develop the ST concept for ultra-high energies. This development may enable and stimulate interest in polarized beam experiments in possible polarized collider projects such as Large Hadron Collider (LHC), Future Circular Collider (FCC) and Super Proton Proton Collider (SPPC).

1 Introduction

Origin of the spin of a nucleon is one of the fundamental questions of modern nuclear physics [1]. The intrinsic spins and orbital momenta of quarks, anti-quarks, and gluons each contribute to the characteristic spins of observed particles. However, the mechanism of how such a complex system results in the total spin is not yet understood. Precision measurements with highly-polarized electron, proton, and light nuclear ion beams are required to attain deeper understanding of the spin structure [2,3,4]. The electron beam provides a precision probe through electromagnetic interaction. Highly-polarized nucleon beams with adjustable polarization orientations are required to study the correlations of sea quark and gluon distributions with the nucleon’s spin. High values of polarization reduce the uncertainties in measurements of these correlations [5].

Polarized beam experiments in colliders pose new demands on polarization control. Besides preserving the polarization during acceleration to the experimental energy, maintaining it for periods of time of over ten hours, and stabilizing longitudinal or transverse polarization at the interaction point using spin rotators, there is an additional requirement of manipulating the polarization direction during the experiment [6]. The importance of spin-flipping systems particularly stands out. They provide multiple spin reversals while the beam is stored in the collider thus allowing for a substantial reduction of the experiment’s systematic errors and achievement of a new level of measurement precision.

The Spin Transparency (ST) mode in colliders allows for efficient control of the polarization direction of any kind of particles including deuterons [7]. It offers a new methodology for polarized beam experiments. The ST concept is based on the use of a ring structure where the magnetic elements return an arbitrarily-directed spin to its original orientation after a single particle turn around the collider, i.e. the structure is transparent to the spin. Examples of such structures include a figure-8 collider [8], a racetrack collider with two Siberian snakes [9, 10], as well as a racetrack without snakes at certain energies corresponding to integer spin resonances [11].

In the ST mode, the particles are technically in the region of a spin resonance (ST resonance) where the spin motion is highly sensitive to small perturbations in magnetic fields. This allows for flexible control of the polarization direction by weak-field SNs. For stability of the spin dynamics, the spin effect of the navigator fields must significantly exceed that due to imperfections and misalignments of the collider elements as well as the effect due to the orbital beam emittances.

Let us emphasize the different roles of the weak navigator and strong structural magnetic fields. The former “guide” the stable polarization direction $\mathbf {n_{\mathrm{nav}}}$ in the collider: a spin initially directed along $\mathbf {n_{\mathrm{nav}}}$ steadily repeats its orientation every particle turn while spins directed transversely to $\mathbf {n_{\mathrm{nav}}}$ are not stable and precess about $\mathbf {n_{\mathrm{nav}}}$ by a small angle every particle turn $2\pi \nu _{\mathrm{nav}}$. The precession angle defines the spin tune $\nu _{\mathrm{nav}}$ (the navigator tune) induced by the SN. The structural magnetic fields determine the polarization kinematics along the orbit returning the spin to its initial orientation after every particle turn [12].

In this paper, we for the first time present application of the spin response function formalism earlier obtained for the ST mode [13] to develop a general method for design of a SN. The method is based on a new concept of a “partial navigator field”, which is induced by inserting weak additional longitudinal and transverse magnetic fields into the synchrotron lattice. We introduce a coefficient describing the enhancement of the navigator strength by the ring optics. We describe an interference mechanism enhancing the navigator strength and thus allowing for polarization control by such low magnetic fields that they practically do not perturb the orbital beam parameters. We also give examples of SN schemes for polarization control in different ranges of collider energies starting with low and ending with ultra-high energies.

2 Spin navigator field: stationary case

In the ST concept, magnetic fields of the structural elements are chosen so that their net effect on the spin is completely compensated over one particle turn along the design orbit. In such structures, any spin direction repeats itself on each particle turn at any location on the design orbit. This means that the resulting spin transformation over one particle turn is represented by the identity matrix. Therefore, the spin tune is zero and the spin motion is degenerate. Thus, in an ST synchrotron, one can define a periodic spin reference frame

$$\begin{aligned} \mathbf {s}_\alpha (z)=\mathbf {s}_\alpha (z+L), \quad \alpha =1,2,3, \end{aligned}$$

(1)

where L is the length of the design orbit and z is the longitudinal coordinate of the accelerator reference frame. The unit vectors $\mathbf {s}_\alpha (z)$ are determined by actual motion of three orthogonal spins along the design orbit. The dynamics of an arbitrary spin along the design orbit can be represented as a superposition of the spin unit vectors:

$$\begin{aligned} \mathbf {S}(z)=S_1\,\mathbf {s}_1(z)+S_2\,\mathbf {s}_2(z)+S_3\,\mathbf {s}_3(z)=\sum \limits _{\alpha =1}^3 S_\alpha \,\mathbf {s}_\alpha (z). \end{aligned}$$

(2)

In the accelerator frame, the z dependence of $\mathbf {S}(z)$ is only related to the dependence of the spin unit vectors on the longitudinal coordinate. In the spin frame, the $\mathbf {S}$ vector is fixed and has constant components $(S_1,S_2,S_3)$.

In a ST structure, the spin dynamics is highly sensitive to introduction of additional weak fields, which allow for removal of the aforementioned spin degeneracy. The ST mode offers a unique capability of flexible control of the polarization direction at any orbital location using SNs composed of inserted magnetic elements with low field integrals. SNs allow for adjusting any required spin direction $\mathbf {n_{\mathrm{nav}}}(z)$ at any orbital location as well as for setting the spin tune $\nu _{\mathrm{nav}}\ll 1$. The navigator spin field is the angular spin rotation velocity as a 3-vector, of a particle moving along the closed orbit [7]

$$\begin{aligned} \varvec{\omega }_{\mathrm{nav}}(z)=\nu _{\mathrm{nav}}\,\mathbf {n_{\mathrm{nav}}}(z). \end{aligned}$$

(3)

It describes the spin precession at a given orbital location with a coordinate z. The spin rotates by an angle $2\pi \nu _{\mathrm{nav}}$ about the $\mathbf {n_{\mathrm{nav}}}(z)$ direction in one particle turn.

The spin navigator field $\varvec{\omega }_{\mathrm{nav}}$ takes the simplest form in the spin frame where its components $\omega _{\mathrm{nav},\alpha }$ are independent of the longitudinal coordinate z [13]

$$\begin{aligned} \varvec{\omega }_{\mathrm{nav}}(z)= \sum \limits _{\alpha =1}^3 \omega _{\mathrm{nav},\alpha }\,\mathbf {s}_\alpha (z)\,, \qquad \omega _{\mathrm{nav},\alpha }=(\varvec{\omega }_{\mathrm{nav}}\cdot \mathbf {s}_\alpha )\,. \end{aligned}$$

(4)

The magnitude of the navigator field $|\varvec{\omega }_{\mathrm{nav}}(z)|$ is independent of z and determines the spin tune induced by the navigator

$$\begin{aligned} \nu _{\mathrm{nav}}=|\varvec{\omega }_{\mathrm{nav}}(z)|=\text{ const }. \end{aligned}$$

(5)

As in the case with the dynamics of an arbitrary spin along the design orbit Eq. (2), the $\varvec{\omega }_{\mathrm{nav}}(z)$ vector in the spin system is fixed. In the accelerator frame, the z dependence of $\varvec{\omega }_{\mathrm{nav}}(z)$ is only related to the dependence of the spin unit vectors $\mathbf {s}_\alpha (z)$ on the longitudinal coordinate. The unit vector directed along the SN field

$$\begin{aligned} \mathbf {n_{\mathrm{nav}}}(z)=\frac{\varvec{\omega }_{\mathrm{nav}}(z)}{|\varvec{\omega }_{\mathrm{nav}}(z)|}. \end{aligned}$$

(6)

specifies the stable polarization direction induced by the SN.

The contribution of inserted weak magnetic fields $b_x(z)$, $b_y(z)$, $b_z(z)$ to the constant navigator field components $\omega _{\mathrm{nav},i}$ is determined by the three periodic spin response functions $\mathbf {F}_x(z)$, $\mathbf {F}_y(z)$, $\mathbf {F}_z(z)$ [13, 14]

$$\begin{aligned} \omega _{\mathrm{nav},\alpha }=\frac{1}{2\pi }\int \limits _0^L \frac{b_x F_{x,\alpha }+b_y F_{y,\alpha }+b_z F_{z,\alpha }}{B\rho }\,dz. \end{aligned}$$

(7)

where $B\rho$ is the magnetic rigidity and $F_{x,\alpha }=(\mathbf {F}_x\cdot \mathbf {s}_\alpha$), $F_{y,\alpha }=(\mathbf {F}_y\cdot \mathbf {s}_\alpha$), $F_{z,\alpha }=(\mathbf {F}_z\cdot \mathbf {s}_\alpha$) are the components of the response functions along the spin unit vectors.

The spin response functions are determined solely by the structural elements of the synchrotron. We consider an approximation where the magnetic fields of an SN are sufficiently small so that they have practically no effect on the orbital beam parameters.

The transverse $\mathbf {F}_\perp$ (radial $\mathbf {F}_x$ or vertical $\mathbf {F}_y$) and longitudinal $\mathbf {F}_z$ spin response functions have different physical origins. Longitudinal fields do not perturb the closed orbit and function $\mathbf {F}_z$ is determined only by its direct effect on the spin. A local region of longitudinal field $b_{z}$ of length $L_z$ situated at a point $z=z_c$ induces the following spin tune $\nu _{\mathrm{nav}}$ and the stable polarization direction $\mathbf {n_{\mathrm{nav}}}(z)$:

$$\begin{aligned} \nu _{\mathrm{nav}}= & {} \frac{|\mathbf {F}_z|}{2\pi }\frac{|b_z L_z|}{B\rho }=\frac{|\varphi _z|}{2\pi }, \qquad |\mathbf {F}_z|=1+G \,, \nonumber \\ \mathbf {n_{\mathrm{nav}}}(z)= & {} \sum \limits _{\alpha =1}^3 \frac{F_{z,\alpha }(z_c)}{|\mathbf {F}_z|}\,\mathbf {s}_\alpha (z)= \sum \limits _{\alpha =1}^3 \bigl (\mathbf {e}_z\cdot \mathbf {s}_\alpha (z_c)\bigr )\, \mathbf {s}_\alpha (z). \end{aligned}$$

(8)

where $\varphi _z$ is the spin rotation angle in the region of the longitudinal field. The magnitude of the function $|\mathbf {F}_z|$ does not depend on the energy.

At the location of the solenoid, $\mathbf {n_{\mathrm{nav}}}(z_c )=\mathbf {e}_z$, i.e., the navigator “points the way” that the stable polarization is longitudinal at this point. At other orbital locations, the spin vector is rotated by the structural magnetic elements of the synchrotron returning to the longitudinal direction after a full particle turn.

Transverse fields cause distortion of the closed orbit and function $\mathbf {F}_{\perp }$ is determined not only by the direct effect of this field on the spin but also by the spin effect of the fields along the perturbed orbit. Transverse field $b_{\perp }$ locally introduced in a region of length $L_\perp$ at a point $z=z_c$ sets the following spin tune $\nu _{\mathrm{nav}}$ and the stable polarization direction $\mathbf {n_{\mathrm{nav}}} (z)$:

$$\begin{aligned} \nu _{\mathrm{nav}}= & {} \frac{|\mathbf {F}_\perp (z_c)|}{2\pi }\frac{|b_{\perp }\,L_\perp |}{B\rho }=\frac{|\varphi _{\perp }|}{2\pi } k_\perp (z_c) \, \nonumber \\ \mathbf {n}_{\mathrm{nav}}(z)= & {} \sum \limits _{\alpha =1}^3 \frac{F_{\perp ,\alpha }(z_c)}{|\mathbf {F}_\perp (z_c)|}\,\mathbf {s}_\alpha (z)\,. \end{aligned}$$

(9)

where $\varphi _\perp =\gamma G \alpha _\perp$ is the spin rotation angle, $\alpha _\perp$ is the orbital bending angle in the region of the transverse field. We introduce an enhancement coefficient $k_\perp$ of the spin tune over the direct effect of the transverse field on the spin

$$\begin{aligned} k_\perp (z) =\frac{|\mathbf {F}_\perp (z)|}{\gamma G}\,. \end{aligned}$$

(10)

The function magnitude $|\mathbf {F}_\perp |$ is proportional to the energy. The enhancement coefficient $k_\perp$ characterizes the net spin effect of all elements in the ring. Depending on synchrotron’s lattice and energy, magnetic fields along the distorted orbit can strengthen the “direct” effect of the introduced transverse field as well as weaken it. In contrast to a region with longitudinal field, the direction $\mathbf {n}_{\mathrm{nav}} (z_c )$ does not in general coincide with the direction of the transverse field $\mathbf {b}_{\perp }$ at the point of its insertion.

Let us calculate the contribution of $M_{\mathrm{el}}$ additional weak magnetic elements to the navigator field. Small magnetic fields $b_i$ introduced at locations with coordinates $z_i$ induce partial navigator fields $\varvec{\omega }_i=\nu _i\,\mathbf {n}_i$. Under the linear approximation in $b_i$, one can apply the superposition principle to $\varvec{\omega }_i$ to find the resulting spin navigator field

$$\begin{aligned} \varvec{\omega }_{\mathrm{nav}}(z)=\sum \limits _{i=1}^{M_{\mathrm{el}}} \varvec{\omega }_i(z)=\sum \limits _{i=1}^{M_{\mathrm{el}}} \nu _i\,\mathbf {n}_i(z). \end{aligned}$$

(11)

For stability of the spin dynamics, the spin effect of an SN must significantly exceed that of imperfections and misalignments of the synchrotron’s magnetic elements as well as the impact of betatron and synchrotron oscillations. This means that the spin tune induced by an SN must significantly exceed the ST-resonance strength $\omega$ [7]

$$\begin{aligned} \nu _{\mathrm{nav}}\gg \omega \,. \end{aligned}$$

(12)

When operating at an integer spin resonances in a conventional racetrack synchrotron with the spin tune proportional to the energy, there are additional constraints on the navigator tune related to the synchrotron energy modulation [11].

One can distinguish two types of spin navigators:

• SN not perturbing the closed orbit;

• SN causing closed orbit distortion.

Closed orbit distortion can be localized to the region of placement of SN magnetic fields or distributed around the entire ring.

Examples of SN of these types are provided below.

3 SN not perturbing the closed orbit

SN schemes with no distortion of the closed orbit are based on the use of solenoids [15,16,17,18,19]. The lattice enhancement coefficient for the fields of the navigator solenoids is a unit, since the closed orbit after their insertion still coincides with the design one. For maintaining the navigator tune, the required field integrals of the solenoids grow proportionally to the beam momentum. A solenoid field integral of 10 T$\cdot$m allows for setting a navigator spin tune of 0.013 for protons and 0.004 for deuterons at the beam momentum of 100 GeV/c. Such a field integral is sufficient to control proton and deuteron polarizations in a figure-8 collider in the momentum range of up to 100 GeV/c where the ST resonance strength does not exceed $10^{-2}$ for protons and $10^{-5}$ for deuterons [7].

3.1 SN scheme with two solenoids

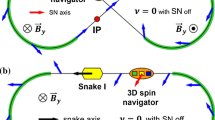
Figure 1 shows a scheme for polarization control using two weak solenoids. It was first proposed for control of the deuteron polarization in a figure-8 collider [16].

Fig. 1

SN based on two solenoids

In this scheme, the two solenoids are separated by arc dipoles rotating the spin about the vertical axis by an angle $\varphi _y=\gamma G \alpha _{\mathrm{orb}}$. The scheme with two solenoids allows for setting any angle $\Psi$ between the polarization and velocity directions in the collider’s plane. An exception is the case when $\varphi _y = k\pi$ and the navigator solenoids stabilize only the longitudinal polarization. A diagram of the partial fields constituting the total SN field is shown in Fig. 2.

Fig. 2

Diagram of the partial fields of an SN with two solenoids

SN schemes with two solenoids were also proposed for manipulation of the proton spin directions in the NICA [18] and RHIC [11] colliders.

3.2 SN scheme with fixed orbit bump and solenoids

The concept of spin control in the collider’s plane using an SN with two solenoids separated by a section with arc dipoles can be further developed for the case of 3D spin control. It involves use of radial fields to create a fixed-size local orbit bump in one of the straight sections of a collider. Figure 3 illustrates an SN scheme with a vertical orbit bump allowing for setting of the vertical spin component at its location and for inducing a spin tune of

$$\begin{aligned} \nu _{\mathrm{nav}}=\frac{\varphi _z}{2\pi } \sin \varphi _x\,, \end{aligned}$$

(13)

where $\varphi _z$ and $\varphi _x=\gamma G \alpha _{\mathrm{bump}}$ are the spin rotation angles by a solenoid and a dipole, respectively, and $\alpha _{\mathrm{bump}}$ is the angle of the orbital bump. The bump is kept constant by adjusting the dipole fields proportionally to the beam momentum.

Fig. 3

SN with a vertical orbit bump for control of the vertical spin component

Switching the radial-field dipoles in the scheme of Fig. 3 to vertical-field ones converts it into an SN with a horizontal bump for control of the radial polarization component. SNs with fixed orbit bumps were used in a figure-8 collider project to design a universal 3D SN allowing for control of the proton and deuteron polarizations in the momentum range of up to 100 GeV/c [19].

4 SN with a local perturbation of the design orbit

Use of SNs based on solenoids is limited by growth of the required longitudinal field integrals with increase in the beam momentum. At sufficiently high energies, it is more appropriate to design SNs using transverse fields. Their integral required to rotate the spin by a given angle does not grow with energy.

4.1 SN with two helical magnets

The net spin rotation axis of a helical magnet with a small field integral is practically longitudinal. This allows for replacement of solenoids with helical magnets in SN designs for high energies.

Let us give an example of a scheme analogous to an SN with two solenoids where the solenoids are replaced by helical magnets [20]. The closed orbit offset in the region with a helical magnet is compensated by a pair of dipoles with opposite field directions placed on both sides of the helical magnet. Figure 4 depicts deviation of the closed orbit in the area of the helical magnet insert.

Fig. 4

Deflection of the closed orbit in the region with a helical magnet at $p=20$ GeV/c. The blue x and green y lines are the radial and vertical components of the closed orbit, respectively, and the red $\rho$ line is the absolute distance to the design orbit

Such an SN provides a spin tune of 0.01 at the beam momentum of 20 GeV/c. The calculation used the following insertion parameters:

$$\begin{aligned} L_y= & {} 0.5\, \mathrm{m}\,, \quad L_{\mathrm{hlx}}=1.5\, \mathrm{m}\,,\quad L_{\mathrm{tot}}=3.1\,\mathrm{m}\,, \nonumber \\ B_y= & {} 0.3\, \mathrm{T}\,, \quad B_{\mathrm{hlx}}=1.0\, \mathrm{T}\,. \end{aligned}$$

(14)

The transverse closed orbit deflection in this example does not exceed 2 mm.

Note that maintaining the navigator tune at $\nu _{\mathrm{nav}}=0.01$ in the scheme with helical magnets requires a transverse field integral of 1.8 T$\cdot$m per magnet independent of the beam energy. Meanwhile, the scheme with solenoids would requires 1.8 T$\cdot$m per solenoid at the beam momentum of 24 GeV/c and 22 T$\cdot$m at 300 GeV/c.

4.2 SN with radial dipoles

In the SN scheme with a helical magnet, the navigator tune is proportional to the square of the field integral $\nu _{\mathrm{nav}} \propto (B L_{hlx})^2$. The transverse field integral can be reduced by using weak radial fields. The navigator tune is then proportional to the first power of the field integral $\nu _{\mathrm{nav}} \propto B_x L$.

Figure 5 shows an SN scheme using weak radial-field dipoles placed around two vertical-field arc dipoles. Such an SN induces radial partial SN field at its center $z=z_c$ of

$$\begin{aligned} \varvec{\omega }_{\mathrm{nav}}(z_c)=\nu _{\mathrm{nav}} \,\mathbf {e}_x\,, \qquad \nu _{\mathrm{nav}}=\frac{2\varphi _x}{\pi } \sin ^2 \frac{\varphi _y}{2}\,, \end{aligned}$$

(15)

where $\varphi _x$ the angle of small spin rotation by a radial dipole, $\varphi _y=\gamma G \alpha _y$ is the spin rotation angle of an arc dipole and $\alpha _y$ is the fixed orbital bending angle of an arc dipole.

Fig. 5

SN scheme based on radial-field dipoles

Figure 6 shows the energy dependence of the field integral of one of the radial-field dipole when stabilizing a navigator tune of $\nu _{\mathrm{nav}}=0.01$ in the momentum range from 100 to 275 GeV/c. This calculation used the following navigator parameters:

$$\begin{aligned} L_x=0.4\, \mathrm{m}\,, \quad L_y=1.3\, \mathrm{m}\,, \quad \alpha _y=8.7\, \mathrm{mrad}\,. \end{aligned}$$

(16)

Fig. 6

Dependence of the field integral of a radial-field dipole on the beam momentum when stabilizing $\nu _{\mathrm{nav}}=0.01$

The maximum deflection of the vertical bump created by the radial-field dipoles is less than 1 mm at the beam momentum of 100 GeV/c. The total field integral of the radial-field dipoles does not exceed 0.2 T$\cdot$m, which is an order of magnitude lower than in the scheme with a helical magnet. The beam polarization can be controlled in the collider’s plane using two such “partial” SNs separated by arc dipole as in the SN scheme with two solenoids.

5 SN globally perturbing the closed orbit

There is an additional opportunity of reducing the transverse field integral of an SN when manipulating the beam polarization in the ST mode. It is implemented by distributing the closed orbit distortion around the entire ring of a synchrotron. The gain in this case comes from the additional spin effect of the fields on the perturbed closed orbit produced by all magnetic elements of the synchrotron ring. As noted in Sect. 2, the contribution to the navigator tune of a local region with transverse field is determined by the spin coefficient $k_\perp$, which describes the enhancement of the direct spin effect by the synchrotron lattice

$$\begin{aligned} k_\perp =\frac{2\pi \nu _{\mathrm{nav}}}{\varphi _\perp } \end{aligned}$$

(17)

where $\varphi _\perp$ is the spin rotation angle in the region with the inserted transverse field. The coefficient $k_\perp$ is determined by the synchrotron lattice and depends on both the location of the additional dipole insertion and the energy.

Let us give an example of calculating the partial field of an SN for protons when inserting an additional navigator dipole in the NICA collider [21]. The spin transparency mode is implemented in the NICA collider using two identical solenoidal snakes inserted in its opposite straights. Calculation of the radial and vertical proton response functions was given in an earlier publication [13].

In colliders with uncoupled vertical and radial betatron oscillations (e.g. [8]), the vertical response function vanishes $\mathbf {F}_y (z)=0$ and the radial response function has zero vertical component $F_{x,2} (z)=0$. This allows for use of only radial dipoles to control the spin in the collider’s plane (2D-SN). The existence of strong betatron oscillation coupling in the NICA collider allows for efficient use of both radial- and vertical-field dipoles to implement a 3D-SN.

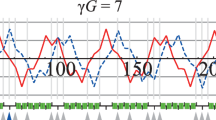
Figure 7 shows the dependence of the navigator tune enhancement coefficients $k_x$ (blue) and $k_y$ (red) on the longitudinal coordinate z of the NICA collider for protons at $\gamma G=6.5$. The graphs of $k_x$ and $k_y$ show that there are locations in the collider where dipoles have practically no effect on the spin ($k_{x,y}\approx 0$). To the contrary, in the final beam focusing regions near the interaction points, the spin dynamics is particularly sensitive to insertion of additional dipoles ($k_{x,y}\approx 20$). The maximum enhancement coefficients in the arcs are $k_{x,y}\approx 10$, which allows for using a transverse field integral of $B_{x,y} L_{x,y}\sim 0.01$ T$\cdot$m to provide a navigator tune of 0.01.

Fig. 7

Navigator tune enhancement coefficients $k_x$ and $k_y$ as a function of the longitudinal coordinate in the NICA collider for protons at $\gamma G=6.5$. The black and green rectangles indicate quadrupoles and arc dipoles, respectively. The origin of the coordinate frame corresponds to an interaction point

Figure 8 shows the navigator tune enhancement coefficients $k_x$ and $k_y$ versus the beam momentum in the NICA collider when a radial-(blue) or vertical-(red) field dipole is placed in the middle of an arc. The dependence of the $k_x$ and $k_y$ coefficients on the beam momentum exhibits areas of constructive interference where the spin effects of individual elements add up coherently. At the points of interference maxima, $k_{x,y}\approx 70$, which allows for reducing the transverse field integral down to $B_{x,y} L_{x,y}\sim 0.0013$ T$\cdot$m for $\nu _{\mathrm{nav}}=0.01$. Thus, for the NICA collider, navigator dipoles with field integrals of 1-10 mT$\cdot$m are sufficient to provide efficient control of the proton polarization in 3D in the presence of field and alignment errors of the lattice magnetic elements as discussed in Sect. 7.

Fig. 8

Navigator tune enhancement coefficients $k_x$ and $k_y$ versus the beam momentum in the NICA collider for protons

6 SN-based spin flipper

SNs based on weak longitudinal and transverse fields allow implementation of stable spin-flipping systems where the spins are reversed over a large number of turns [22]. The SN sets the required polarization direction and spin tune as functions of its introduced magnetic fields:

$$\begin{aligned} \mathbf {n}_{\mathrm{nav}}= & {} \mathbf {n}_{\mathrm{nav}}(\mathbf {b}_1, \mathbf {b}_2, \ldots , \mathbf {b}_i, \ldots , \mathbf {b}_{M_{\mathrm{el}}} )\,, \nonumber \\ \nu _{\mathrm{nav}}= & {} \nu _{\mathrm{nav}}(\mathbf {b}_1, \mathbf {b}_2, \ldots , \mathbf {b}_i, \ldots , \mathbf {b}_{M_{\mathrm{el}}} )\,. \end{aligned}$$

(18)

Both the polarization direction and the spin tune can be adjusted by adiabatically changing the magnetic fields of the SN. SN prevents resonant beam depolarization by stabilizing the spin tune $\nu _{\mathrm{nav}}=\mathrm{const}$ during adiabatic adjustment of the polarization direction. The condition of adiabatic rearrangement of the spin motion in this case is given by [11]

$$\begin{aligned} \left| \left( \frac{d \mathbf {b}_i}{dt}\cdot \frac{\partial }{\partial \mathbf {b}_i}\right) \,\mathbf {n}_{\mathrm{nav}} \right| \ll \frac{2\pi \nu _{\mathrm{nav}}}{T}, \quad i=1,2,\ldots ,M_{\mathrm{el}}\,,\nonumber \\ \end{aligned}$$

(19)

where T is the particle revolution period in the synchrotron.

The condition of adiabatic adjustment of the polarization can be rewritten in terms of the polarization reversal time $\tau$ as

$$\begin{aligned} \tau \gg \frac{T}{\nu _{\mathrm{nav}}}\,. \end{aligned}$$

(20)

For example, typical times of polarization reversal in NICA are of the order of 1 ms for protons ($\nu _{\mathrm{nav}}=10^{-2}$) and 10 ms for deuterons ($\nu _{\mathrm{nav}}=10^{-3}$).

7 Compensation of the coherent part of the ST resonance strength

The ST resonance field $\varvec{\omega }$ consists of two parts of different physical origins. The first one, the coherent part of the ST resonance field $\varvec{\omega }_{\mathrm{coh}}$, is related to construction imperfections and misalignments of the lattice magnetic elements. They result in additional periodic perturbing fields along the design orbit causing coherent effects on the orbit and particle spins. The second part, the incoherent part of the ST resonance field $\varvec{\omega }_{\mathrm{emit}}$, has to do with betatron and synchrotron particle oscillations and is proportional to the orbital beam emittances. In practice, the coherent part of the ST resonance strength $\omega _{\mathrm{coh}}$ significantly exceeds the strength of the incoherent part $\omega _{\mathrm{emit}}$ [7].

The field $\varvec{\omega }_{\mathrm{coh}}$ does not lead to depolarization of the beam but only coherently rotates the spins about an a priori unknown direction $\varvec{\omega }_{\mathrm{coh}}$ by an angle $2\pi \omega _{\mathrm{coh}}$. In principle, the field $\varvec{\omega }_{\mathrm{coh}}$ can be measured experimentally and compensated by an additional SN by inducing a field

$$\begin{aligned} \varvec{\omega }_{\mathrm{comp}}=-\varvec{\omega }_{\mathrm{coh}}\,. \end{aligned}$$

(21)

The coherent field $\varvec{\omega }_{\mathrm{coh}}$ can be measured, for example, by “monitoring” the polarization at different settings of the navigator field. In a real collider, the polarization is stable along the direction $\mathbf {n}$ of the total field resulting from addition of the fields generated by the spin navigator $\varvec{\omega }_{\mathrm{nav}}$ and lattice imperfections $\varvec{\omega }_{\mathrm{coh}}$:

$$\begin{aligned} \mathbf {n}=\frac{\varvec{\omega }_{\mathrm{nav}}+\varvec{\omega }_{\mathrm{coh}}}{|\varvec{\omega }_{\mathrm{nav}}+\varvec{\omega }_{\mathrm{coh}}|}\,. \end{aligned}$$

(22)

By measuring and analyzing the polarization behavior as a function of the navigator field direction $\mathbf {n}_{\mathrm{nav}}$ and strength $\nu _{\mathrm{nav}}$, one can extract the information about the field $\varvec{\omega }_{\mathrm{coh}}$.

The compensation accuracy determines the requirements on the navigator tune for polarization control. For stable manipulation of the polarization, it is sufficient to use the control navigator to induce a spin tune with an appropriately large margin

$$\begin{aligned} \nu _{\mathrm{nav}} \sim \omega _{\mathrm{coh}}\,. \end{aligned}$$

(23)

The ST resonance strength can theoretically be compensated down to its incoherent part. The constraint on the navigator tune can then be relaxed to

$$\begin{aligned} \nu _{\mathrm{nav}} \gg \omega _{\mathrm{emit}}\,. \end{aligned}$$

(24)

8 ST mode at ultra-high energies

It may appear that the area of applicability of the ST concept does not include high energies. Indeed, on one hand, the compensation condition requires that the navigator tune must be of the order of the ST resonance strength:

$$\begin{aligned} \nu _{\mathrm{nav}} \sim \omega \end{aligned}$$

(25)

and $\omega$ grows proportionally to the energy:

$$\begin{aligned} \omega \propto \gamma \end{aligned}$$

(26)

along with the response functions.

On the other hand, the navigator tune must remain small

$$\begin{aligned} \nu _{\mathrm{nav}} \ll 1\,, \end{aligned}$$

(27)

so that perturbation of the orbital beam parameters by the navigator magnetic fields is negligible. The principle of superposition of partial SN fields is applicable in this case. It becomes unrealistic to meet the condition of $\nu _{\mathrm{nav}}$ being small at sufficiently high energies.

However, the ST mode concept can be used in case of ultra-high energies as well. For example, one can design a lattice with a large number of super-periods $N_p$, each satisfying the spin transparency condition, i.e. any spin direction repeats at each super-period. Figure 9 shows a schematic of a possible “spin” super-period where spin transparency is provided by insertion of two identical snakes into its lattice. The arc dipoles in the illustrated super-period bend the orbit by an angle $2\alpha _y=2\pi /N_p$ rad.

Fig. 9

Schematic of an ST super-period with a pair of identical snakes

In such a synchrotron, one can provide coherent control of the spins using identical SNs in each super-period. All SNs induce the same spin tunes $\nu _i$ and set the same stable polarization direction $\mathbf {n}_i (z)$. The stable polarization direction $\mathbf {n}_{\mathrm{nav}} (z)$ has the property of super-periodicity:

$$\begin{aligned} \mathbf {n}_{\mathrm{nav}} (z)=\mathbf {n}_i (z)=\mathbf {n}_{\mathrm{nav}} (z+L/N_p)\,, \end{aligned}$$

(28)

and the total navigator tune $\nu _{\mathrm{nav}}$ is proportional to the number of super-periods:

$$\begin{aligned} \nu _{\mathrm{nav}}=N_p \nu _i\,. \end{aligned}$$

(29)

At the same time, the partial navigator tune in the region of a single super-period must be small:

$$\begin{aligned} \nu _i\sim \omega /N_p \ll 1\,. \end{aligned}$$

(30)

The total spin tune can be of the order of a unit or even significantly greater. Thus, the required number of snake pairs is determined by the condition:

$$\begin{aligned} N_p \gg \omega \,. \end{aligned}$$

(31)

Let us consider the possibility of operating with polarized protons in a collider in the ST mode at an energy of the order of 10 TeV. For our estimates, we assume that the ST resonance strength is 0.01 at an energy of about 100 GeV, which is a typical value found earlier [7]. The resonance strength at 10 TeV is then of the order of a unit and about ten pairs of snakes are sufficient to provide stable manipulation of the proton polarization. It is most appropriate to compensate the coherent part in each super-period using navigators with local orbit perturbation discussed in Sect. 3. They do not perturb the closed orbit in the rest of the super-periods. The polarization can be controlled using navigators with perturbation of the entire closed orbit described in Sect. 5. They take advantage of the interference mechanism to enhance the navigator field and practically do not disturb the closed orbit. The provided estimate demonstrates the possibility of using the ST mode at ultra-high energies.

9 Conclusions

We use the spin response function formalism to develop a general approach to the design of SNs, which allow for efficient control of the spin tune and manipulation of the hadron polarization direction in ST colliders. SNs based on weak longitudinal and transverse fields expand the toolkit of polarization control techniques when performing high-precision experiments at low and medium energies as well as at high ones. The presented SN schemes can be used for polarization control in the ST modes of the EIC and NICA colliders, as well as of the COSY synchrotron.

Expansion of the ST-mode concept to ultra-high energies in lattices with a large number of super-periods opens opportunities for possible polarized proton experiments at Large Hadron Collider (LHC) [23], Future Circular Collider (FCC) [24] and Super Proton Proton Collider (SPPC) [25].