1 Introduction

The Spin-Transparent (ST) technique has been proposed as an efficient, high flexibility method to control the beam polarization, from acceleration to long term maintenance and spin manipulation in real time of an experimental run of a collider [1,2,3,4,5]. Attractiveness of the ST method is that it allows for control of the polarization using small insertions of weak magnetic fields (stationary or quasi-static), which can be operated and varied as needed even in real time of an experimental run.

The ST mode in colliders allows one to [1]:

  • Control of the polarization by weak magnetic fields not affecting the orbital dynamics,

  • Accelerate the beam without polarization loss,

  • Maintain stable polarization during an experiment,

  • Set any required polarization direction at any orbital location in a collider,

  • Change the polarization direction during an experiment,

  • Monitor the polarization on-line during an experiment,

  • Do frequent coherent spin flips of the beam to reduce experiment’s systematic errors,

  • Carry out ultra-high precision experiments.

Thus, the ST mode allows one to significantly expand the capabilities of polarized beam experiments at the EIC in the US [6], NICA in Russia [5], EicC in China [7], and other future facilities.

The polarization dynamics in a ST synchrotron is based on the following basic elements.

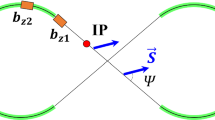
The degenerate spin dynamics design. Design spin motion along the design orbit of a ST synchrotron is degenerate, i.e., any spin direction at any orbit points repeats itself every particle turn. The most natural example of a ST synchrotron is a synchrotron shaped as a plane figure 8 where the spin rotation about the vertical field in the first arc is compensated by an opposite rotation in the second arc [3, 8] (Fig. 1a). Other example is a racetrack with two identical Siberian Snakes installed in two opposite straights [4, 5] (Fig. 1b). In both examples, the spin tune \(\nu \) is independent of energy and equals zero.

Fig. 1
figure 1

ST synchrotrons: a a figure-8 ring and b a racetrack with two identical snakes. The blue arrows illustrate the spin dynamics along the design orbit for longitudinal polarization at the interaction point (IP)

Full size image

Spin navigators. At a first glance, such a situation is not constructive since particles are in the \(\nu =0\) resonance. In this case spin dynamics is highly sensitive to any small perturbative fields associated with lattice errors, focusing fields and other. These fields determine an effective spin field of the ST resonance \(\mathbf {\omega }\): the particle spins precess about an uncontrolled direction \(\mathbf {\omega }/\omega \) with a tune \(\omega \) equal to the ST resonance strength, i.e., the spin makes a full turn in \(1/\omega \) particle turns.

On the other hand, the indicated resonance sensitivity actually makes it possible to realize a firm spin control and preservation by inserting spin navigators (SN) – small coherent spin rotators [9, 10]. The SN effect on a group of spins is characterized by the axis \(\mathbf {n}_N\) and angle \(2\pi \nu _N\) of the spin precession about the axis in one particle turn. The only general requirement on an SN to provide the polarization stability is that the induced spin tune must significantly exceed the ST resonance strength:

$$\begin{aligned} \nu _N\gg \omega . \end{aligned}$$
(1)

Thank to the smallness of their fields, SNs can be widely varied in both \(\mathbf {n}_N\) and \(\nu _N\), thus providing an effective and flexible polarization control and preservation in all stages of a polarized beam operation, from acceleration to maintenance and manipulation in a storage ring.

Spin response function. An important aspect of a polarized beam synchrotron design and practice is correct accounting for effect of various sources of small perturbative resonance or quasi-resonance fields. A particular source type can be localized or distributed randomly or regularly over the design orbit. Examples of elementary sources: field and alignment errors of magnetic lattice elements, betatron and synchrotron oscillations, SN fields, non-linearities of the magnetic lattice, non-linear fields of the colliding beams, etc.

Each elementary field effects particle spin and trajectory simultaneously; with further particle propagation through magnetic lattice, the latter does effect spin in certain correlation with the direct kick from the perturbative element. After a large number of particle revolutions the resulting effect to spin is represented by integral over elementary kicks in product with a factor called the spin response function, kind of a spin’s Green function of the lattice.

The spin response factor of the synchrotron lattice was first analyzed and accounted in [12]. The term “spin response function” has been introduced in [13]. The formalism was later generalized for other synchrotrons including those with snakes and strong betatron coupling [14, 15]. The response function was widely applied. For example, it was used to calculate the resonance strengths and evaluate the beam–beam effects for colliding electron-positron beams [13], to minimize depolarization rate and increase stored polarization lifetimes [16], to calculate the ion resonance strengths [17], to explain the experimental data on the rf-resonance strengths [18, 19], to analyze the design parameters of a spin flipper [20].

The response function was used in the above studies to analyze rings where the design lattice defines a unique (distinct) stable spin direction (n-axis) [11]. Below we call such a mode of spin motion a “Distinct Spin” (DS) mode. In this mode, the spin tune is not an integer. The response functions for DS synchrotrons are defined using a distinct n-axis and allow for calculation of the spin field components transverse to the n-axis only. Extension of the response function formalism to the ST case is the subject of this paper.

2 Spin dynamics in the ST mode

2.1 Orbital motion in the accelerator reference frame

The particle orbital motion is described using a design orbit specified by a 3D vector \(\mathbf {r}_0(z)\) in the Cartesian lab frame where z is the path length along the design orbit. The longitudinal unit vector \(\mathbf {e}_z(z)=d\mathbf {r}_0/dz\) is directed along the tangential vector and is a continuous function of the length z. In the general case, the design orbit itself can deviate from the plane and have crossing points. The binormal \(\mathbf {K}(z)\) of such a design orbit defined as a vector perpendicular to the local orbital plane is given by:

$$\begin{aligned} \mathbf {K}(z)=\mathbf {e}_z \times \frac{d\mathbf {e}_z}{dz} \equiv \mathbf {e}_z \times \mathbf {e}_z^{\,\prime } , \end{aligned}$$
(2)

which has no longitudinal component: \(\mathbf {K}\cdot \mathbf {e}_z=0\). For a design orbit, the longitudinal unit vector is a periodic function and satisfies the equation

$$\begin{aligned} \frac{d\mathbf {e}_z}{dz} = \mathbf {K}(z) \times \mathbf {e}_z, \qquad \mathbf {e}_z(z)=\mathbf {e}_z(z+L) , \end{aligned}$$
(3)

where L is the design orbit length.

The unit vectors transverse to \(\mathbf {e}_z\) can be selected arbitrarily. For a design orbit consisting of only straights and arcs, one can define the transverse unit vectors from the solutions of the same equation that the longitudinal unit vector satisfies [21]:

$$\begin{aligned} \frac{d\mathbf {e}_x}{dz} = \mathbf {K}(z) \times \mathbf {e}_x, \quad \frac{d\mathbf {e}_y}{dz} = \mathbf {K}(z) \times \mathbf {e}_y , \end{aligned}$$
(4)

which are continuous and periodic as the longitudinal unit vector \(\mathbf {e}_z\). The particle’s position vector \(\mathbf {r}\) near the design orbit can be written as:

$$\begin{aligned} \mathbf {r}(x,y,z)=\mathbf {r}_0(z)+x\,\mathbf {e}_x(z)+y\,\mathbf {e}_y(z) , \end{aligned}$$
(5)

where x and y are particle’s transverse coordinates.

The introduced accelerator reference frame allows one to consider not only flat design orbits with only vertical component of vector \(\mathbf {K}\) \((K_x = 0)\) but non-planar orbits \((K_x \ne 0)\) as well. This is important for designing ST colliders whose orbits may come out of plane, for example, in snakes and in sections where the two beams are brought into collision.

Linearized equations for the transverse deviations x and y can be obtained from the Hamiltonian \({\mathcal {H}}(x,P_x,y,P_y,z)\)

$$\begin{aligned} {\mathcal {H}}= & {} \varDelta H_x y - \varDelta H_y x - \frac{x^2}{2}\frac{\partial (g H_y)}{\partial x}+\frac{y^2}{2}\frac{\partial (g H_x)}{\partial y} \nonumber \\&+\frac{xy}{2} \left( \frac{\partial (g H_x)}{\partial x}-\frac{\partial (g H_y)}{\partial y}\right) \nonumber \\&+\frac{1}{2}\left( P_x - \frac{H_z}{2}y\right) ^{\!\!2}+ \frac{1}{2}\left( P_y + \frac{H_z}{2}x\right) ^{\!\!2} \end{aligned}$$
(6)

whose canonically conjugate variables are the generalized coordinates \(\mathbf {u}=(x,y)\) and momentum \(\mathbf {P}=(P_x, P_y)\), while the coordinate z plays the role of time, \(g=1+K_x y-K_y x\), \(\mathbf {H}=(H_x,H_y)\) and \(H_z\) are the normalized transverse and longitudinal magnetic fields in units of the magnetic rigidity. The fields and its derivatives are taken on the design orbit while changes in the normalized field \(\varDelta \mathbf {H}=(\varDelta H_x, \varDelta H_y)\)

$$\begin{aligned} \varDelta H_x=H_x-K_x , \quad \varDelta H_y = H_y - K_y \end{aligned}$$
(7)

account for the fields on the design orbit related to momentum deviation and imperfections in construction and alignment of the magnetic elements.

The equations of motion in the canonical form are

$$\begin{aligned} \frac{d\mathbf {u}}{dz}= & {} \frac{\partial {\mathcal {H}}}{\partial \mathbf {P}}= \mathbf {P}+\frac{H_z}{2}\,\mathbf {e}_z\times \mathbf {u}, \nonumber \\ \frac{d\mathbf {P}}{dz}= & {} -\frac{\partial {\mathcal {H}}}{\partial \mathbf {u}}= \left[ \left( \mathbf {u}\cdot \frac{\partial }{\partial \mathbf {u}}\right) \mathbf {H}-\frac{1}{2}\left( \frac{\partial }{\partial \mathbf {u}}\cdot \mathbf {H}\right) \mathbf {u}\right] \times \mathbf {e}_z \nonumber \\&+\frac{H_z}{2}\left( \mathbf {e}_z\times \mathbf {P} -\frac{H_z}{2}\mathbf {u}\right) +\varDelta \mathbf {H}\times \mathbf {e}_z\,. \end{aligned}$$
(8)

2.2 Thomas-BMT equation in the accelerator reference frame

The spin motion is described by the Thomas-BMT equation [22, 23]. After switching from the time t to the coordinate z similarly to how it is done when describing the transvers coordinates of the orbital motion, the Thomas-BMT equation in the accelerator reference frame takes the form:

$$\begin{aligned} \frac{d\mathbf {S}}{dz} = \mathbf {W} \times \mathbf {S}, \quad \mathbf {W}=\mathbf {W}_0+\mathbf {w} . \end{aligned}$$
(9)

Here \(\mathbf {W}\) is a spin angular rate. When moving on the design orbit, the spin angular rate is

$$\begin{aligned} \mathbf {W}_0 = \gamma G \mathbf {K} + (1+G) H_z \mathbf {e}_z , \mathbf {W}_0(z) = \mathbf {W}_0(z+L) . \end{aligned}$$
(10)

When deviating from the design orbit, the spin perturbation \(\mathbf {w}=\mathbf {W}-\mathbf {W}_0\) in the linear approximation becomes:

$$\begin{aligned} \mathbf {w}= & {} (1+\gamma G)\, \mathbf {e}_z \times \frac{d^2\mathbf {u}}{dz^2}+(1+G)H_z\frac{d\mathbf {u}}{dz} \nonumber \\&+\mathbf {e}_z \left( (1+G) \frac{d}{dz} (\mathbf {K}\mathbf {u})-(1+\gamma G)\mathbf {K}\frac{d\mathbf {u}}{dz} \right) . \end{aligned}$$
(11)

Here we assume that design dipoles and solenoids are installed in different places: \(H_z(z) \cdot \mathbf {K}(z) =0\).

2.3 Spin perturbations in the ST mode

In addition to the “accelerator reference frame” connected to the design orbit and allowing one to describe small orbital deviations from it, we introduce a “spin reference frame” connected to the spin dynamics when the particles travel on the design orbit. The spin motion looks simplest in the spin frame: the particle spins remain fixed (the spin components along the spin unit vectors are constant) on the design orbit in case of a perfect ring and experience small deviations from the design spin motion in the presence of sufficiently small perturbing fields. According to the linear approximation for the spin, here and below we assume that the spin deviation due to these perturbing fields remains small \(|\varDelta \mathbf {S}(z)|\ll 1\) everywhere in the ring during one turn of a particle. The fields can be considered small if the following sufficient conditions are satisfied \(|\gamma G(d \mathbf {u}/dz)|\ll 1\) and \(|\gamma G(\varDelta \gamma /\gamma )|\ll 1\). However, at very high energies, when special measures are taken to prevent depolarization such as Siberian snakes, these conditions are modified to significantly weaker ones.

In the ST mode, one can introduce three periodic spin unit vectors \({\mathbf {s}_{i}}(z)={\mathbf {s}_{i}}(z+L)\) on the design orbit, which satisfy the Thomas-BMT equation:

$$\begin{aligned} \frac{d{\mathbf {s}_{i}}}{dz}=\mathbf {W}_0 \times {\mathbf {s}_{i}} . \end{aligned}$$
(12)

The choice of the reference frame origin and initial orientations of the spin unit vectors is arbitrary. One can make this selection from the point of view of experimental convenience. For example, one can select the detector (injection point, polarimeter, interaction point, etc.) as the frame origin and align the spin unit vectors at that location with the accelerator ones. Even though the spin unit vectors are different from the accelerator ones at any other point of the design orbit, at the detector, the polarization components in the accelerator frame are the same as in the spin frame.

In the spin reference frame, the equation for the spin vector \(\mathbf {S}=\sum S_i {\mathbf {s}_{i}}\) is determined by the \(w_i\) perturbation components along the spin unit vectors: \(\mathbf {w} = \sum w_i {\mathbf {s}_{i}}\). The spin equation in the spin reference frame becomes:

$$\begin{aligned} \frac{d\mathbf {S}}{dz} = \mathbf {w} \times \mathbf {S} . \end{aligned}$$
(13)

In the linear approximation, we get the following expressions for the spin perturbation components in the spin reference frame

$$\begin{aligned} w_i = \,\mathbf {w}\, {\mathbf {s}_{i}} = w_{i,\mathrm{dir}} + w_{i,\mathrm{orb}} , \end{aligned}$$
(14)

where

$$\begin{aligned} w_{i,\mathrm{dir}}= & {} \left( \frac{\varDelta \gamma }{\gamma } \gamma G \mathbf {K} + (1+G)\varDelta H_z\mathbf {e}_z \right) {\mathbf {s}_{i}} , \end{aligned}$$
(15)
$$\begin{aligned} w_{i,\mathrm{orb}}= & {} \,\gamma G \left( \frac{d {\mathbf {s}_{i}}}{dz} \times \frac{d\mathbf {u}}{dz} \right) \mathbf {e}_z - \left( \mathbf {K} \frac{d\mathbf {u}}{dz} \right) \Bigl ({\mathbf {s}_{i}}\,\mathbf {e}_z \Bigr ) \nonumber \\&- (1+G) (\mathbf {K}\mathbf {u}) \left( \frac{d {\mathbf {s}_{i}}}{dz} \,\mathbf {e}_z\right) + \frac{d\varPhi }{dz} \end{aligned}$$
(16)

with the full-derivative terms separated out:

$$\begin{aligned} \varPhi = \,(1 + \gamma G) (\mathbf {e}_z \times \mathbf {\tau } \cdot {\mathbf {s}_{i}}) + (1+G) (\mathbf {K}\mathbf {u}) (\mathbf {e}_z {\mathbf {s}_{i}}). \end{aligned}$$
(17)

Parameter \(\varDelta \gamma /\gamma \) is the relative deviation of energy from its design value and \(\varDelta H_z\) is the deviation of the normalized longitudinal field.

We separate Eq. (14) into two terms giving different contributions to the spin perturbation components. The first term \(w_{i,\mathrm{dir}}\) is due to a “direct effect on the spin”, which gives a contribution to the spin perturbation even when moving along the design orbit. The second term \(w_{i,\mathrm{orb}}\) consists of expressions proportional to transverse deviations from the design orbit \(\mathbf {u}\) and their derivatives \(d\mathbf {u}/dz\) and describe the spin effect of perturbing fields through the perturbed orbit.

In the linear approximation in the variables \(\mathbf {u}\) and \(\mathbf {P}\), the spin perturbation components describing the orbital spin effect in the spin reference frame take the form

$$\begin{aligned} w_{i,\mathrm{orb}} \,=\, \frac{\partial w_i}{\partial \mathbf {u}} \mathbf {u} + \frac{\partial w_i}{\partial \mathbf {P}} \mathbf {P}, \end{aligned}$$
(18)

where the respective contributions of the generalized momenta and coordinates equal

$$\begin{aligned} \frac{\partial w_i}{\partial \mathbf {P}}= & {} \gamma G \left( \mathbf {e}_z\times \frac{d {\mathbf {s}_{i}}}{dz}\right) - \mathbf {K}\left( \mathbf {e}_z {\mathbf {s}_{i}} \right) , \nonumber \\ \frac{\partial w_i}{\partial \mathbf {u}}= & {} \gamma G \frac{H_z}{2}\frac{d {\mathbf {s}_{i}}}{dz}- (1+G)\mathbf {K}\left( \mathbf {e}_z\cdot \frac{d {\mathbf {s}_{i}}}{dz}\right) . \end{aligned}$$
(19)

Combining the canonically conjugate variables \(\mathbf {u}\) and \(\mathbf {P}\) into a single 4-dimensional state vector V with components \(V^T=(x, \, {P_x}, \, y, {P_y})\), the spin perturbation components can be expressed as

$$\begin{aligned} w_{i,\mathrm{orb}} = \frac{\partial w_i}{\partial V_\alpha }V_\alpha . \end{aligned}$$
(20)

Note that the components \(\partial w_i/\partial V_\alpha \) do not depend on the orbital motion and are determined by the design values of the vector \(\mathbf {K}\) and the longitudinal field \(H_z\) as well as by the spin unit vectors. Thus, the components \(\partial w_i/\partial V_\alpha \) are periodic functions with a period \(z=L\).

2.4 Spin field of the ST resonance

In the linear approximation of the method of 1st order averaging, the spin field components \(\omega _i\) are determined by the average values \(w_i\) in the spin reference frame:

$$\begin{aligned} \omega _i = \frac{L}{2\pi }\langle \mathbf {w}{\mathbf {s}_{i}}\rangle = \frac{L}{2\pi }\langle w_i\rangle = const. \end{aligned}$$
(21)

The spin field becomes azimuthally dependent through the z dependence of the spin basis vectors when written in the accelerator frame

$$\begin{aligned} \mathbf {\omega }(z)=\sum \omega _i {\mathbf {s}_{i}}(z). \end{aligned}$$
(22)

After averaging, the last term of \(w_{i,\mathrm{orb}}\) in Eq. (16) separated out into a full derivative does not contribute to the spin field. A full derivative can be separated out from \(w_{i,\mathrm{orb}}\) in different ways thus giving different equivalent forms of the spin field \(\mathbf {\omega }\), which can be used depending on their convenience for further analysis and quantitative computation of \(\mathbf {\omega }\).

In the ST mode, the spin at an orbital location z precesses about the direction \(\mathbf {n}=\mathbf {\omega }/|\mathbf {\omega }|\) with a small tune \(\nu =|\mathbf {\omega }|\) where the three components of the spin field are given by the following expressions:

$$\begin{aligned} \omega _i = \omega _{i,\mathrm{dir}} + \omega _{i,\mathrm{orb}}. \end{aligned}$$
(23)

In the expression for the spin field (23), as in the expression for the spin perturbation (14), we distinguish two terms \(\omega _{i,\mathrm{dir}}\) and \(\omega _{i,\mathrm{orb}}\) giving contributions due to the “direct spin effect” and the spin effect through the perturbed orbit. Particles deviating from the design orbit execute betatron oscillations as well as forced oscillations caused by perturbing fields along the deviating orbit. Since the spin unit vectors and the vector \(\mathbf {K}\) are periodic functions of z, betatron oscillations after averaging do not contribute to the spin field \(\omega _{i,\mathrm{orb}}\). A nonzero contribution to the spin field comes only from periodic perturbations whose spectrum contains harmonics of the particle circulation frequency. One can identify two main types of perturbations contributing to the spin field in the ST mode: the first one is the spin effect of the momentum spread and the second type is the spin effect caused by construction and alignment errors of the lattice elements (lattice imperfections).

3 Response function in the ST mode

3.1 Longitudinal and transverse spin response functions

In the ST mode, the spin response functions allow one to calculate the ST resonance strength and the spin navigator field. In the spin reference frame, the contribution of periodic perturbing fields \(\varDelta H_x\), \(\varDelta H_y\), and \(\varDelta H_z\) to the spin field components \(\omega _i\) is described by three vector spin response functions \(\mathbf {F}_x=(F_{x1},F_{x2},F_{x3})\), \(\mathbf {F}_y=(F_{y1},F_{y2},F_{y3})\) and \(\mathbf {F}_z=(F_{z1},F_{z2},F_{z3})\)

$$\begin{aligned} \omega _i = \frac{1}{2\pi } \int \limits _0^L \left( \varDelta H_x {F_{xi}}+ \varDelta H_y {F_{yi}}+ \varDelta H_z {F_{zi}}\right) \,dz , \end{aligned}$$
(24)

where \(\mathbf {F}_x\), \(\mathbf {F}_y\) and \(\mathbf {F}_z\) are the radial, vertical, and longitudinal response functions, respectively, determined by the ring design lattice. In other words, in our approximation, the perturbing fields do not modify the response functions.

It is important to emphasize that the effects of the longitudinal and transverse perturbing fields on the spin have different characters.

The longitudinal fields \(\varDelta H_z\) contribute to the spin field \(\omega _{i,\mathrm{dir}}\), but do not perturb the closed orbit. Comparing the expressions for \(w_{i,\mathrm{dir}}\) in Eq. (15) and \(\omega _i\) in Eq. (24), we get the following result for the components of the longitudinal response function

$$\begin{aligned} {F_{zi}}= (1+G) \mathbf {e}_z {\mathbf {s}_{i}}(z) . \end{aligned}$$
(25)

The transverse fields \(\varDelta H_x\) and \(\varDelta H_y\) perturb the orbit causing the closed orbit to deviate from the design orbit and contribute to the spin field \(\omega _{i,\mathrm{orb}}\) through the perturbed orbit. The forced particle oscillations \({\widetilde{V}}\) caused by transverse fields can be calculated using:

$$\begin{aligned} {\widetilde{V}} = \mathrm{Im} \left( f_1 \!\!\int \limits _{-\infty }^z \!(f_1^{*T}\varDelta {\hat{H}}) dz + f_2 \!\!\int \limits _{-\infty }^z \!(f_2^{*T}\varDelta {\hat{H}}) dz \right) , \end{aligned}$$
(26)

where \(\varDelta {\hat{H}}\) is the transverse perturbation of the magnetic field written in a 4-dimensional form with the components \(\varDelta {\hat{H}}^T = (-\varDelta H_y, \, 0, \, \varDelta H_x, \, 0)\) and \(f_1\) and \(f_2\) are the Floquet functions having the following periodicity properties

$$\begin{aligned} f_1(z+L) = e^{i2\pi \nu _1} f_1(z), \quad f_2(z+L) = e^{i2\pi \nu _2} f_2(z) , \end{aligned}$$
(27)

where \(\nu _1\) and \(\nu _2\) are the tunes of the two independent betatron oscillation modes.

Using the periodicity properties of the Floquet functions, the integrals from “\(-\infty \)” to “z” can be reduced to integration over a single turn

$$\begin{aligned} \int \limits _{-\infty }^z (f_i^{*T}\varDelta {\hat{H}}) dz= & {} \frac{1}{e^{-2\pi i\nu _i} -1} \int \limits _0^L (f_i^{*T}\varDelta {\hat{H}}) dz \nonumber \\&+ \int \limits _0^z (f_i^{*T}\varDelta {\hat{H}}) dz. \end{aligned}$$
(28)

Substituting the forced motion \({\widetilde{V}}\) into the expression for the spin perturbation \(w_{i,\mathrm{orb}}\) (16) and taking the field perturbation out of the integral by integration by parts, we get the following expressions for the radial and vertical response function components

$$\begin{aligned} {F_{xi}}= & {} \mathrm{Im} \left( \!f_{1,3}^* \int \limits _{-\infty }^z\frac{\partial w_i}{\partial V_\alpha } f_{1,\alpha } dz + f_{2,3}^* \int \limits _{-\infty }^z \frac{\partial w_i}{\partial V_\alpha } f_{2,\alpha } dz \!\right) \!,\nonumber \\ \end{aligned}$$
(29)
$$\begin{aligned} {F_{yi}}= & {} -\mathrm{Im} \left( \!f_{1,1}^* \int \limits _{-\infty }^z \frac{\partial w_i}{\partial V_\alpha } f_{1,\alpha } dz + f_{2,1}^* \int \limits _{-\infty }^z \frac{\partial w_i}{\partial V_\alpha } f_{2,\alpha } dz \!\right) \!,\nonumber \\ \end{aligned}$$
(30)

where \(f_{i,\alpha }\) denotes the \(\alpha ^{\mathrm{th}}\) component of the 4-dimensional Floquet function \(f_i\).

3.2 Response function in a ST synchrotron without betatron coupling

In the absence of betatron oscillation coupling, the two lower components of the vector \(f_{1}\) and the two upper components of the vector \(f_{2}\) become zero: \(f_{1,3}=f_{1,4}=0\), \(f_{2,1}=f_{2,2}=0\). The Floquet function components can be expressed in terms of \(\beta \)-functions in the following way

$$\begin{aligned} f_{1,1}= & {} \sqrt{\beta _x} \exp \left( i \int \limits _{0}^z \frac{dz}{\beta _x} \right) =f_x, \quad f_{1,2}=\frac{df_x}{dz}\equiv f_x^{\prime }, \nonumber \\ f_{2,3}= & {} \sqrt{\beta _y} \exp \left( i \int \limits _{0}^z \frac{dz}{\beta _y} \right) =f_y, \quad f_{2,4}=f_y^{\prime }. \end{aligned}$$
(31)

In that case, the equations for the response functions get simplified

$$\begin{aligned} {F_{xi}}= & {} \mathrm{Im} \Biggl (f_y^* \int \limits _{-\infty }^z K_y \Bigl [ (\gamma ^2 G^2-1)f_y^\prime \,(\mathbf {e}_z\,{\mathbf {s}_{i}}) \Bigr .\Biggr . \nonumber \\&\Biggl .\Bigl . +\gamma G (1+G) K_y f_y (\mathbf {e}_x\, {\mathbf {s}_{i}}) \Bigr ] dz \Biggr ), \end{aligned}$$
(32)
$$\begin{aligned} {F_{yi}}= & {} \mathrm{Im} \Biggl (f_x^* \int \limits _{-\infty }^z K_x \Bigl [ (\gamma ^2 G^2-1)f_x^\prime \,(\mathbf {e}_z\,{\mathbf {s}_{i}}) \Bigr .\Biggr . \nonumber \\&\Biggl .\Bigl . +\gamma G (1+G) K_x f_x (\mathbf {e}_y\,{\mathbf {s}_{i}}) \Bigr ] dz \Biggr ). \end{aligned}$$
(33)

Integration in the response functions reduces to integration over dipoles. In the derivation of Eqs. (32) and (33), we used the conditions of the absence of betatron coupling: \(H_z(z)=0\) and \(K_x(z)\cdot K_y(z) =0\).

In the ultra-relativistic limit, we get

$$\begin{aligned} {F_{xi}}= & {} \gamma ^2 G^2\, \mathrm{Im} \Biggl (f_y^* \int \limits _{-\infty }^z K_y f_y^\prime (\mathbf {e}_z {\mathbf {s}_{i}}) dz \Biggr ), \end{aligned}$$
(34)
$$\begin{aligned} {F_{yi}}= & {} \gamma ^2 G^2 \,\mathrm{Im} \Biggl (f_x^* \int \limits _{-\infty }^z K_x f_x^\prime (\mathbf {e}_z {\mathbf {s}_{i}}) dz \Biggr ). \end{aligned}$$
(35)

3.3 A conventional synchrotron in the ST mode at an integer spin resonance

In a conventional synchrotron consisting of straight sections and arcs (\(K_x = 0\), \(K_y \ne 0\)), the stable polarization direction is vertical and the spin tune is proportional to the beam energy. Conventional synchrotrons operate in the DS mode everywhere except for narrow energy bands in the regions of integer spin resonances \(\nu =\gamma G=k\), i.e. when the combined effect of the arcs on the spin results in an integer number of rotations about the vertical axis. In these regions, a conventional synchrotron operates in the ST mode at integer spin resonances.

Let us choose that, at the reference origin, \({\mathbf {s}_{1}}(0) =\mathbf {e}_x \) is oriented along the radial direction, \({\mathbf {s}_{2}}(0) =\mathbf {e}_y \) is vertical, and \({\mathbf {s}_{3}}(0) =\mathbf {e}_z \) is along the particle velocity. For such a choice, the spin unit vector \({\mathbf {s}_{2}}\) is constant along the whole design orbit. As the particle moves along its path, the other two unit vectors \({\mathbf {s}_{1}}\) and \({\mathbf {s}_{3}}\) rotate about the vertical field in the arcs staying in the ring’s plane.

The dynamics of the spin unit vectors is determined by the angle \(\varPsi \) accumulated by the spin as it rotates about the vertical direction in the arcs in the accelerator reference frame:

$$\begin{aligned} \varPsi (z)=\gamma G \int \limits _0^z K_y\, dz. \end{aligned}$$
(36)

The spin unit vectors as functions of the z coordinate are given by

$$\begin{aligned} {\mathbf {s}_{2}}(z) = \mathbf {e}_y, \quad {\mathbf {s}_{1}}(z) + i \,{\mathbf {s}_{3}}(z) = (\mathbf {e}_x + i \,\mathbf {e}_z) e^{i \varPsi (z)}. \end{aligned}$$
(37)

Since the particle is in an integer spin resonance, after a full turn, the final spin rotation angle in the ring’s plane is \(\varPsi (L)=2\pi k\) and the spin unit vectors become again aligned with their initial directions.

Equations (32) and (33) show that, of all of the response function components, the only non-zero ones are \(F_{x1}\) and \(F_{x3}\), which lie in the orbital plane. Only the radial perturbations of magnetic field contribute to the ST resonance spin field \(\mathbf {\omega }\) through the orbital effect on the spin. Thus, in the same-direction guiding magnetic field, the spin field \(\mathbf {\omega }\) has only two components transverse to the vertical unit vector \(\mathbf {e}_y\), which coincides with the n-axis of the DS synchrotron. In this case, the spin field \(\mathbf {\omega }\) can be calculated using the response function formalism for DS synchrotrons, which gives the \(\mathbf {\omega }\) components transverse to the n-axis. The response functions F of the DS formalism are related to the components of the radial response function of the ST formalism as

$$\begin{aligned} F= F_{x1}+i F_{x3} \end{aligned}$$
(38)

where

$$\begin{aligned} F= & {} \frac{1}{2} \Biggl (\! f_y^* \!\!\int \limits _{-\infty }^z\! \Bigl (\! (\gamma ^2 G^2+G)K_y f_y^\prime +(1+G) K_y^\prime f_y \!\Bigr ) e^{i\varPsi } dz \Biggr . \nonumber \\&\Biggl . - f_y\!\! \int \limits _{-\infty }^z \! \Bigl (\! (\gamma ^2 G^2+G)K_y f_y^{\prime *} +(1+G) K_y^\prime f_y^* \!\Bigr ) e^{i\varPsi } dz \Biggr ). \nonumber \\ \end{aligned}$$
(39)

This form of the spin response function is used in [17,18,19].

In conventional synchrotrons in the ST mode at integer resonances, spin navigators can be realized using weak radial or longitudinal fields for polarization control in the collider’s plane. Detuning the energy from the resonance by a value of \(\varepsilon =\varDelta \gamma G\) is equivalent to turning on a vertical navigator of the strength \(\nu _N=\varepsilon \), which moves the polarization out of the collider’s plane. It is not possible to compensate the effect of such a vertical navigator at a fixed energy using small navigator fields.

The obtained results also apply to the case of a flat figure-8 ring, where the vector \(\mathbf {K}\) is vertical and changes sign when going from one arc into the other. Equation (37) for the spin unit vectors remain the same but are periodic at any energy. The spin field \(\mathbf {\omega }\) due to lattice imperfections lie in the synchrotron’s plane. However, due to the energy independence of the spin tune \(\nu =0\), one can now arrange weak-field spin navigators for polarization control in the synchrotron’s plane at any energy. A navigator for control of the vertical polarization component must use radial fields. Reference [3] provides an example of such a navigator with a design based on weak solenoids in a vertical orbit bump.

4 Applications of response function in ST synchrotrons

4.1 Statistical calculation of the ST resonance strength

The ST resonance strength \(\omega \) is determined by the magnitude of the ST resonance spin field \(\mathbf {\omega }\), which consists of two parts: a coherent part arising due to additional transverse and longitudinal fields on the closed orbit deviating from the design orbit and an incoherent part associated with the particles’ betatron and synchrotron oscillations (beam emittances) [2, 24]

$$\begin{aligned} \mathbf {\omega } = \mathbf {\omega }_{\mathrm{coh}}+\mathbf {\omega }_{\mathrm{emitt}}, \qquad \omega _{\mathrm{coh}} \gg \omega _{\mathrm{emitt}}. \end{aligned}$$
(40)

The coherent part of the resonance strength is determined by the linear approximation in the spin perturbations and can be calculated using the response functions. The incoherent part in this approximation vanishes after averaging over the betatron and synchrotron oscillations. The incoherent part is determined by higher-order approximations in the spin perturbations and depends on the orbital beam emittances. In practice, the coherent part \(\omega _{\mathrm{coh}}\) significantly exceeds the incoherent one \(\omega _{\mathrm{emitt}}\).

The \(\omega _{\mathrm{coh}}\) part resulting from the lattice’s imperfections can be calculated using a statistical model. It allows one to account for random perturbations \(\varDelta H_x\), \(\varDelta H_y\), and \(\varDelta H_z\) of the design fields of the magnetic elements. The rms value of the coherent part of the resonance strength \(\omega _{\mathrm{coh}}\) is calculated in the following way

$$\begin{aligned} \omega _{\mathrm{coh}}^2= & {} \frac{1}{4 \pi ^2 } \sum _{\mathrm{elem}} \Biggl ( \sigma _{xx} |\mathbf {F}_{x}|^2 + \sigma _{yy} |\mathbf {F}_{y}|^2 + \sigma _{zz} |\mathbf {F}_{z}|^2 \nonumber \Biggr .\\&\Biggl . +2\sigma _{xy} \mathbf {F}_{x}\mathbf {F}_{y} + 2\sigma _{xz} \mathbf {F}_{x}\mathbf {F}_{z}+2\sigma _{yz} \mathbf {F}_{y}\mathbf {F}_{z} \Biggr ) L_{\mathrm{el}}^2 , \end{aligned}$$
(41)

where \(L_{\mathrm{el}}\) is the length of the perturbing element and

$$\begin{aligned} \sigma _{xx}= & {} {\overline{\varDelta H_x^2}}, \quad \sigma _{yy} ={\overline{\varDelta H_y^2}}, \quad \sigma _{zz} ={\overline{\varDelta H_z^2}}, \\ \sigma _{xy}= & {} {\overline{\varDelta H_x \varDelta H_y}}, \quad \sigma _{xz} ={\overline{\varDelta H_x \varDelta H_z}}, \quad \sigma _{yz} ={\overline{\varDelta H_y \varDelta H_z}}. \nonumber \end{aligned}$$
(42)

are the correlation coefficients of the random field perturbations of the magnetic elements. The bar denotes averaging over the field and alignment errors of the lattice elements.

4.2 Spin navigators in the ST mode

Use of spin navigators with weak magnetic field integrals is sufficient to stabilize the desired polarization direction at the detector. The spin navigator field \(\mathbf {\omega }_{\mathrm{nav}}\) induced by insertion of small transverse \(h_x\), \(h_y\) and longitudinal \(h_z\) magnetic fields can be calculated in the spin reference frame using the response functions:

$$\begin{aligned} \omega _{\mathrm{nav}, i}=\frac{1}{2 \pi } \int \limits _0^L\Bigl (h_x {F_{xi}}+h_y {F_{yi}}+h_z {F_{zi}}\Bigr ) dz. \end{aligned}$$
(43)

In the spin frame, all three field components \(\mathbf {\omega }_{\mathrm{nav}}\) are constant. In the accelerator frame, change of the field components \(\mathbf {\omega }_{\mathrm{nav}}\) is related to evolution of the spin unit vectors

$$\begin{aligned} \mathbf {\omega }_{\mathrm{nav}}(z)=\sum \omega _{\mathrm{nav}, i} \,{\mathbf {s}_{i}}(z). \end{aligned}$$
(44)

In a perfect lattice, the spin precesses about the navigator field \(\mathbf {\omega }_{\mathrm{nav}}(z)\) with a tune \(\nu _N=|\mathbf {\omega }_{\mathrm{nav}}|\) independent of z. In the presence of small perturbations (\(\omega \ll \nu _N\)), the polarization is stable along the navigator field and repeats every particle turn.

We emphasized above the different characters of the spin effects of the longitudinal and transverse magnetic fields. Solenoids do not change the closed orbit. The longitudinal response function components contain no terms proportional to the energy and account for the direct effect of the solenoids on the spin.

Use of weak transverse fields leads to closed orbit excursion especially at low energies. The transverse response function components contain terms proportional to the energy and account for the effect on the spin through the distorted orbit. At high energies, the spin rotation angles in transverse-field elements significantly exceed the orbital rotation angles. One can arrange a coherent enhancement of the spin effect of transverse fields distributed along the design orbit. This can be done practically without perturbing the beam’s orbital characteristics. Thus, use of solenoids is suitable for polarization control at low and medium energies. At high energies, it is preferable to use transverse fields for polarization control.

Spin navigators can be used not only to stabilize the polarization but to empirically compensate the ST resonance strength as well. A real synchrotron with lattice imperfections then becomes equivalent to an ideal one that has no alignment and setup errors of its magnetic elements. After such a compensation, the resonance strength is determined only by the beam emittances that allows one to realize a stable spin-flipping system to reduce the systematic errors in polarized beam experiments.

Compensation of imperfection resonance strengths was earlier done using a system of small variable dipoles at the ZGS, Argonne, USA [25] and AGS, BNL, USA [26]. It may be of interest to study the possibility of efficient systematic use of SNs together with the spin response function approach for compensation of the ST resonance strength relying on polarization measurement information. This may also allow one to extend the energy range where the ST technique can be used for spin manipulation.

4.3 Suppression of the depolarizing effect caused by beam–beam interaction

The spin response method can be applied to suppress the depolarizing effect of the beam–beam interaction [27]. This can be done by designing the ring optics with a small value of the spin response function in the interaction region. Note that the spin response function can be made small or even zero not only at the interaction point but in the whole interaction straight. Such a porblem is similar to designing a lattice with a dispersion-free region around the interaction point necessary to ensure the highest luminosity of the colliding beams. One must keep in mind that the degree of such a suppression is limited by the nonlinear betatron tune spread caused by the beam–beam interaction. A detailed analysis of this limitation can be the subject of further studies.

4.4 Effect of the energy spread on the spin dynamics in the ST mode

It is particularly important to account for the effect of the energy spread on the spin motion when going to high energies. At medium energies, \(\gamma G \sim 1\) and the polarization lifetime is comparable to the beam lifetime. In contrast to the orbital perturbation, the spin perturbation contains terms proportional to the energy, which, with increase in energy, can lead to a significant reduction of the polarization lifetime.

Effect of the energy spread on the spin dynamics can be determined using the spin response functions. Momentum deviation creates the following perturbations in the normalized magnetic field

$$\begin{aligned} \varDelta H_x = - \frac{\varDelta p}{p} K_x, \quad \!\!\! \varDelta H_y = - \frac{\varDelta p}{p} K_y, \quad \!\!\! \varDelta H_z = - \frac{\varDelta p}{p} H_z,\nonumber \\ \end{aligned}$$
(45)

which give the following contribution to the spin field

$$\begin{aligned} \omega _{\mathrm{disp}, i}= & {} \frac{\varDelta \gamma }{\gamma } \frac{1}{2\pi } \int \limits _{0}^{L} \gamma G (\mathbf {K} {\mathbf {s}_{i}}) dz \nonumber \\&- \frac{\varDelta p}{p} \frac{1}{2\pi } \int \limits _{0}^{L} \Bigl ( K_x {F_{xi}}+ K_y {F_{yi}}+ H_z {F_{zi}}\Bigr ) dz. \end{aligned}$$
(46)

The first term above accounts for the explicit dependence of the spin angular rate \(\mathbf {W_0}\) on the energy while the second one gives the contribution to the spin field through the response functions.

When the condition

$$\begin{aligned} \omega _{\mathrm{disp}, i}=0 \end{aligned}$$
(47)

is satisfied, it means that the spin transparency is achieved not only at the design energy but to 1st order at any energy within the energy spread. Such a type of ST synchrotrons with “zero spin dispersion” is of interest for high-precision experiments with polarized beams.

Let us consider the effect of the energy spread on the spin dynamics for three configurations of the ST mode: a conventional synchrotron at an integer spin resonance point, a figure-8 ring, and a racetrack ring with two identical snakes.

4.4.1 A conventional synchrotron at an integer spin resonance

Considering that the spin unit vectors in a conventional synchrotron have the form of Eq. (37), let us calculate the spin field due to the explicit dependence of the spin angular rate on the energy:

$$\begin{aligned} \frac{\gamma G}{2 \pi } \int \limits _0^L K_y dz = \gamma G \gg 1. \end{aligned}$$
(48)

Thus, in conventional rings, when setting the ST mode at integer spin resonance points, the energy spread has a strong effect on the spin dynamics especially in the high energy region.

4.4.2 A figure-8 synchrotron

For a figure-8 synchrotron, calculation of the direct effect of the energy spread on the spin motion gives:

$$\begin{aligned} \frac{\gamma G}{2 \pi } \int \limits _0^L K_y dz = 0. \end{aligned}$$
(49)

The effect of the energy spread on the spin through the response functions is also zero, since the vertical response function components \({F_{yi}}=0\) and there are no radial and longitudinal design fields. Thus, in figure-8 rings, there is no effect in the 1st order of the energy spread on the spin dynamics. Due to the ring topology and the absence of betatron coupling, a figure-8 synchrotron has zero spin dispersion.

4.4.3 A racetrack with two identical snakes

Dynamics of the spin unit vectors in a ring with two identical snakes is more complicated and is determined not only by the spin’s angle accumulated in the arcs but also the directions of the snake axes \(\mathbf {m}\), about which the spin rotates by \(180^{\circ }\). Let the axes of both snakes make an angle \(\alpha \) with the radial direction in the ring’s plane \((m_x+im_z=e^{i\alpha })\).

As before, we choose the reference frame origin at the detector located in one of the experimental straights and direct the spin unit vectors along the accelerator unit vectors at that point. The unit vector \({\mathbf {s}_{2}}(z)\) then remains vertical in the arcs changing its sign \(\zeta =\pm 1\) when passing through a snake from one arc into the other \({\mathbf {s}_{2}}= \zeta \mathbf {e}_y\). The other two unit vectors \({\mathbf {s}_{1}}\) and \({\mathbf {s}_{3}}\) lie in the ring’s plane rotating about the vertical axis in the arcs:

$$\begin{aligned} {\mathbf {s}_{1}}+i\,{\mathbf {s}_{3}}=e^{i\,\varPsi } \left\{ \begin{array}{ll} \mathbf {e}_x+i\,\mathbf {e}_z, &{} \quad \text{ in } \text{ the } 1^{\mathrm{st}} \text{ arc } \\ e^{2i\,\alpha }(\mathbf {e}_x-i\,\mathbf {e}_z), &{} \quad \text{ in } \text{ the } 2^{\mathrm{nd}} \text{ arc } \end{array} \right. \,, \end{aligned}$$
(50)

where

$$\begin{aligned} \varPsi (z)=\gamma G \int \limits _0^z K_y \zeta dz, \qquad \varPsi (z)=\varPsi (z+L) \end{aligned}$$
(51)

is the periodic spin phase accumulated by the particle in the arc (\(\zeta =0\) outside of the arcs). The above formulas show that the integrand in the phase \(\varPsi \) changes sign at each pass through a snake. As a result, the phase \(\varPsi \) becomes periodic instead of growing monotonically and the effect of the first arc on the spin is “compensated” by the second arc. After a full turn, the phase value \(\varPsi (L)=0\). The spin dynamics in a ring with two snakes becomes equivalent to the spin dynamics in a figure-8 ring.

The dynamics of the spin unit vectors inside the snakes depends on the particular designs of the snakes. However, the formulas for the spin unit vectors in the arcs are universal and allow one to calculate the contribution of the arcs to the spin field due to the energy spread:

$$\begin{aligned} \omega _{\mathrm{disp}, i} = -\frac{\varDelta p}{p} \frac{1}{2\pi } \int \limits _{\mathrm{arcs}} K_y {F_{yi}}\,dz\,. \end{aligned}$$
(52)

The contribution of the arcs to the spin field \(\omega _{\mathrm{disp},i}\) is related to the vertical response function.

To eliminate the influence of the energy spread on the spin, the snakes’ design and the ring optics must satisfy the following condition:

$$\begin{aligned} \int \limits _{\mathrm{snakes}} \Bigl ( K_x {F_{xi}}+ K_y {F_{yi}}+H_z {F_{zi}}-v^2 \gamma G (\mathbf {K}{\mathbf {s}_{i}} ) \Bigr ) dz&\nonumber \\ + \int \limits _{\mathrm{arcs}} K_y {F_{yi}}\,dz= & {} 0. \nonumber \\ \end{aligned}$$
(53)

If the condition of Eq. (53) is satisfied, a racetrack will also have zero spin dispersion as a figure-8 ring.

5 Numerical example

Let us provide a calculation of the response functions in a ST synchrotron with strong betatron oscillation coupling using an example of the NICA collider at JINR (Dubna, Russia) where the ST mode is implemented using two solenoidal snakes [5]. Figure 2 shows the dependence of the response functions components \(F_{xi}\), \(F_{yi}\) and \(F_{zi}\) in the spin reference frame on the z coordinate for protons at \(\gamma G=6.5\). The origin of the reference frame is selected at the interaction point of the spin detector. The response function components corresponding to the radial, vertical and longitudinal directions in the detector are drawn in blue, green, and red colors, respectively [28, 29].

Fig. 2
figure 2

Radial \(\mathbf {F}_{x}\), vertical \(\mathbf {F}_{y}\), and longitudinal \(\mathbf {F}_{z}\) response functions for protons at \(\gamma G=6.5\) in the NICA collider

Full size image

Our calculation shows that the response function \(\mathbf {F}_z\) describing the direct effect of the longitudinal field perturbations on the spin is about an order of magnitude lower than the response functions \(\mathbf {F}_x\) and \(\mathbf {F}_y\) describing the effect of the transverse field perturbations on the spin through the distorted closed orbit.

In the NICA collider, in contrast to a figure-8 collider, the spin is influenced by not only the radial but also the vertical magnetic field perturbations contributing to all three components of the spin field. The response functions indicate the places in the collider lattice where the effect of the introduced transverse fields on the spin can be enhanced manifold. Such information is necessary for the design of efficient 3D navigators by placing transverse fields at the points of maxima of the response functions and adding their spin effects coherently.

The presented structure of the NICA collider has not been optimized for polarized protons. However, the response function approach can already be applied to it to develop an efficient polarization control scheme that requires only small field integrals in the ST mode. For example, setting the spin tune of \(\nu =0.01\) necessary to stabilize the proton polarization requires a longitudinal field integral of

$$\begin{aligned} (BL)_\parallel \approx \frac{2\pi \nu }{F_z} B\rho \approx 0.4 \text{ T }\cdot \text{ m }, \end{aligned}$$
(54)

where \(F_z\sim 3\) and \(B\rho \sim 20\) T\(\cdot \)m. When considering only the direct spin effect of a transverse field, its integral needed to produce a spin rotation by an angle \(2\pi \nu \) at \(\gamma G\sim 10\) is

$$\begin{aligned} (BL)_\perp \approx \frac{2\pi \nu }{\gamma G} B\rho \approx 0.12 \text{ T }\cdot \text{ m }. \end{aligned}$$
(55)

When a spin navigator dipole is placed at the maximum of the transverse response function (\(F_\perp \sim 100\)), the required field integral becomes

$$\begin{aligned} (BL)_\perp \approx \frac{2\pi \nu }{F_\perp } B\rho \approx 0.01 \text{ T }\cdot \text{ m }, \end{aligned}$$
(56)

i.e. the collider’s optical structure amplifies the spin effect of the navigator dipole by about a factor of 10.

6 Conclusions

In conclusion, we briefly state our main results. We developed a spin response function formalism for spin-transparent synchrotrons. The response functions are determined by the design lattice of a ST synchrotron and can be applied to complete the following tasks:

  • Calculate the spin field of the ST resonance caused by field and alignment errors of the lattice magnetic elements.

  • Design the 3D spin navigators using insertions of small fields for manipulation of the polarization direction during an experiment.

  • Compensate for chromatic spin tune spread caused by particular design elements of a ST synchrotron.

  • Suppress the depolarizing resonant effect of non-linear fields of the colliding beams.

Thus, the response functions are a valuable tool for calculation of the optics parameters of ST synchrotrons necessary for performing high-precision experiments with high-luminosity polarized beams.