Spin Matching

Abstract

When spin rotating devices are used in an electron accelerator ring the stochastic depolarization caused by synchrotron radiation becomes an issue. Special design of the ring optics is required in order to minimize harmful effect of stochastic depolarization. Ring optics adjustments which help to minimize the depolarization are called spin matching. In this lecture the formalism for deriving spin matching conditions is presented. Then, spin matching conditions are derived for examples of a spin rotator based on solenoidal magnets and a spin rotator based on vertical and horizontal bending magnets.

This manuscript has been authored by Brookhaven Science Associates, LLC under Contract No. DE-SC0012704 with the U.S. Department of Energy. The United States Government and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes.

7.1 Introduction

Consider designing two spin rotators, one for a proton ring, another for an electron ring. Let’s assume that the energies of proton and electron rings are similar, say 5 GeV. At this energy we decide to use a spin rotator design based on interleaved solenoidal and bending magnets since it does not create excessive beam orbit excursions. During the design work in both electron and proton cases we have found spin rotation angles of all rotator magnets required to transform the vertical polarization at the rotator entrance into the longitudinal one at the rotator exit point. Therefore requirements on the field strengths of the solenoidal and dipole magnets become known. At this point the design for proton rotator is well defined. But the electron rotator requires some more work: the spin matching is needed to minimize the effect of stochastic depolarization (spin diffusion).

7.2 Electron Polarization Parameters

Synchrotron radiation determines the polarization evolution through Sokolov-Ternov spin-flip emission and spin diffusion caused by quantum emission of SR photons. Both processes combined define the equilibrium polarization P_eq and polarization relaxation time τ, according to

$$\displaystyle \begin{aligned} P(t) = (P_0 - P_{eq})\; \mathrm{e}^{-t/\tau} + P_{eq} {} \end{aligned} $$

(7.1)

where P₀ is the initial polarization (at t = 0). Consideration of polarizing and depolarizing effects caused by synchrotron radiation was done in [1] where following expressions for P_eq and τ were obtained:

$$\displaystyle \begin{aligned} \begin{array}{rcl} P_{eq} & =&\displaystyle -\frac{8}{5 \sqrt{3}} \frac{\alpha_{-}}{\alpha_{+}} {} \end{array} \end{aligned} $$

(7.2)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \tau^{-1} & =&\displaystyle \frac{5 \sqrt{3}}{8} \frac{\hbar\; r_0}{m} \; \gamma^5 \; \alpha_{+} {} \end{array} \end{aligned} $$

(7.3)

where

$$\displaystyle \begin{aligned} \begin{array}{rcl} \alpha_{-} & =&\displaystyle \big\langle\frac{\hat{\mathbf{b}}}{\rho^3}(\hat{\mathbf{n}} - \mathbf{d}) \big\rangle {} \end{array} \end{aligned} $$

(7.4)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \alpha_{+} & =&\displaystyle \big\langle\frac{1}{\rho^3} \big[ 1- \frac{2}{9} (\hat{\mathbf{n}} \hat{\mathbf{v}})^2 + \frac{11}{18} |\mathbf{d}|{}^2 \big] \big\rangle {} \end{array} \end{aligned} $$

(7.5)

and following notation is used:

• m is electron mass

• r₀ is electron classic radius

• ρ is a bending radius of horizontal and vertical bending magnets

• unit vector $\hat {\mathbf {b}}$ in direction of magnetic field

• unit vector $\hat {\mathbf {v}}$ along the electron velocity,

• unit vector $\hat {\mathbf {n}}$ describes so-called invariant spin field, composed of spin solutions in the orbital phase space which are periodical with the ring azimuth and with phases of orbital motion

Averaging in formulas (7.4), (7.5) is done over accelerator ring circumference and over the orbital motion phase space. But away from spin resonances one can use $\hat {\mathbf {n}}_{\mathbf {0}}$ instead of $\hat {\mathbf {n}}$ and skip averaging over the phase space to get sufficiently accurate evaluation of the polarization characteristics. Minus sign in formula (7.2) shows that the build-up of the electron polarization over time happens in the direction opposite to the magnetic field.

Depolarization caused by spin diffusion is defined by a derivative of invariant spin field over δ =  ΔE∕E:

$$\displaystyle \begin{aligned} \mathbf{d} = \left(\frac{\partial \hat{\mathbf{n}}}{\partial \delta}\right)_{x,x',y,y'} \end{aligned} $$

(7.6)

This derivative must be taken at constant values of x, x′, y, y′, and in terms of complex betatron amplitudes can be rewritten as:

$$\displaystyle \begin{aligned} \mathbf{d} = \left(\frac{\partial \hat{\mathbf{n}}}{\partial \delta}\right)_{A_x,A_y} + \left(\frac{\partial \hat{\mathbf{n}}}{\partial A_x}\right)_{\delta,A_y}\cdot\left(\frac{\partial {A_x}}{\partial \delta}\right) + \left(\frac{\partial \hat{\mathbf{n}}}{\partial A_y}\right)_{\delta,A_x}\cdot\left(\frac{\partial {A_y}}{\partial \delta}\right) +c.c. {} \end{aligned} $$

(7.7)

First term in the equation above come from direct electron energy change when the photon is emitted, which happens in all bends. Second term contribute in the horizontal bends where there is non-zero horizontal dispersion. And third term is due to radiation in places with non-zero vertical dispersion that can appear due to errors or betatron coupling or in spin rotators with vertical bends.

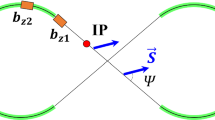
In order to minimize depolarization one needs to minimize the amplitude of the vector d in elements where the synchrotron radiation happens, that is in bending magnets. Let’s consider an ideal circular accelerator (Fig. 7.1). Such ideal accelerator ring does not contain any spin rotators or snakes, thus, there is no horizontal dipole or longitudinal fields on the design beam orbit. Also there is no betatron coupling and no misalignment and magnet errors. The spin invariant field $\hat {\mathbf {n}}$ in this ideal accelerator ring is only coupled with the vertical betatron motion of particle. Indeed, the stable spin direction $\hat {\mathbf {n}}$ remains vertical for any particles having A_y = 0 even if they have some energy offset or performing horizontal betatron oscillations. Thus, $\left (\frac {\partial \hat {\mathbf {n}}}{\partial \delta }\right ) = 0$ and $\left (\frac {\partial \mathbf {n}}{\partial A_x}\right ) = 0$ on the beam orbit. The vertical betatron oscillations lead to the deviation of $\hat {\mathbf {n}}$ from vertical due to horizontal field of the quadrupole magnets experienced by particles with non-zero A_y. Thus the derivative of the invariant field over the vertical betatron amplitude A_y, $\left (\frac {\partial \hat {\mathbf {n}}}{\partial A_y}\right )$, is non-zero. But, since the ideal ring has no betatron coupling and no vertical dispersion, the $\left (\frac {\partial {A_y}}{\partial \delta }\right )$ is equal to 0 everywhere, including bending magnets. Which means that the vertical betatron motion is not affected by the synchrotron radiation in this case. Since all terms contributing to the vector d in formula (7.7) are equal to zero, the vector d is also zero all around ring in the ideal accelerator ring.

Fig. 7.1

The ideal accelerators has stable spin direction vertical everywhere

As soon as one adds a spin rotator or a Snake into the accelerator ring the vector d is excited. Then a question arises on how to design the ring optics to minimize the vector d and, hence, minimize the stochastic depolarization. We will go through a technique of deriving the spin matching conditions on the optics in next sections.

Magnet misalignments and rolls can also excite d and enhance the stochastic depolarization. For the errors we can not really design spin matching, unless these errors are very localized. The standard way would be to establish tolerances on misalignments and rolls during accelerator design stage in order to achieve acceptable depolarization level. This studies are done by using spin simulation codes.

7.3 Spin Matching Formalism

For calculation in this lecture the transverse orbital motion will be described by using its presentation through components of betatron motion eigen-vectors f_I,f_II and horizontal and vertical dispersion functions D_x, D_y:

$$\displaystyle \begin{aligned} \begin{array}{rcl} x & =&\displaystyle f_{Ix} A_x + f^*_{Ix} A^*_x + f_{IIx} A_y + f^*_{IIx} A^*_y + D_x \delta \\ y & =&\displaystyle f_{Iy} A_x + f^*_{Iy} A^*_x + f_{IIy} A_y + f^*_{IIy} A^*_y + D_y \delta \end{array} \end{aligned} $$

(7.8)

where A_x and A_y are complex amplitudes of horizontal and vertical betatron motion, δ = dp∕p presents a particle momentum offset.

Without betatron coupling the transverse motion expressions are simplified to:

$$\displaystyle \begin{aligned} \begin{array}{rcl} x & =&\displaystyle f_{Ix} A_x + f^*_{Ix} A^*_x + D_x \delta \\ y & =&\displaystyle f_{IIy} A_y + f^*_{IIy} A^*_y + D_y \delta \end{array} \end{aligned} $$

(7.9)

where

$$\displaystyle \begin{aligned} \begin{array}{rcl} f_{Ix} = f_x & =&\displaystyle \sqrt{\beta_x} e^{i\Psi_x} \end{array} \end{aligned} $$

(7.10)

$$\displaystyle \begin{aligned} \begin{array}{rcl} f_{IIy} = f_y & =&\displaystyle \sqrt{\beta_y} e^{i\Psi_y} \end{array} \end{aligned} $$

(7.11)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \Psi_{x,y} & =&\displaystyle \int_0^s \frac{1}{\beta_{x,y}} ds \end{array} \end{aligned} $$

(7.12)

Let’s consider an accelerator ring which can include, besides the vertical guiding fields of horizontal bending magnets, also solenoidal and vertical field in locations where spin rotating devices are used. The spin motion on the design beam orbit can be resolved and the periodical spin solution $\hat {\mathbf {n}}_{\mathbf {0}}$ can be found all along the ring circumference. One can also define two spin solutions on the design orbit orthogonal to the vector $\hat {\mathbf {n}}_{\mathbf {0}}$ and to each other, the vectors $\hat {\mathbf {l}}_{\mathbf {0}}$ and $\hat {\mathbf {m}}_{\mathbf {0}}$. The vector set $(\hat {\mathbf {l}}_{\mathbf {0}}, \hat {\mathbf {m}}_{\mathbf {0}},\hat {\mathbf {n}}_{\mathbf {0}})$ form right-handed orthonormal triad, which is convenient for considering spin motion perturbations. To simplify mathematical description one can combine vectors $\hat {\mathbf {l}}_{\mathbf {0}}$ and $\hat {\mathbf {m}}_{\mathbf {0}}$ into the complex vector $\hat {\mathbf {k}}_{\mathbf {0}} = \hat {\mathbf {l}}_{\mathbf {0}}-i \hat {\mathbf {m}}_{\mathbf {0}}$. Together with $\hat {\mathbf {n}}_{\mathbf {0}}$, the vectors $\hat {\mathbf {k}}_{\mathbf {0}}$ and $\hat {\mathbf {k}}_{\mathbf {0}}^*$ are the eigenvectors of the one-turn spin transformation. One turn transformation of $\hat {\mathbf {k}}_{\mathbf {0}}$ at any accelerator azimuth s is written as:

$$\displaystyle \begin{aligned} \hat{\mathbf{k}}_{\mathbf{0}} (s+C) = \mathrm{e}^{i 2\pi u_{sp}} \hat{\mathbf{k}}_{\mathbf{0}} (s) \end{aligned} $$

(7.13)

Arbitrary spin can be presented by a complex variable α:

$$\displaystyle \begin{aligned} \mathbf{S} = \sqrt{1-|\alpha|{}^2} \hat{\mathbf{n}}_{\mathbf{0}} + \mathrm{Re} (i \alpha \hat{\mathbf{k}}_{\mathbf{0}}^*) \end{aligned} $$

(7.14)

Far from spin resonances the spin deviation from the $\hat {{\mathbf {n}}_0}$ due to momentum deviation or betatron motion is expected to be small, therefore |α|≪ 1. In the first order the spin deviation α is described by the following equation:

$$\displaystyle \begin{aligned} \frac{d\alpha}{d s} = - i \mathbf{w} \cdot \hat{\mathbf{k}}_{\mathbf{0}}. {} \end{aligned} $$

(7.15)

The components of perturbation spin precession vector w can be derived from the BMT equation:

$$\displaystyle \begin{aligned} \begin{array}{rcl} w_x & =&\displaystyle (1+u_0) y'' +(u_0+\frac{a}{\gamma})K_x \delta + (1+a)K_s x' \\ w_s & =&\displaystyle (1+a)(K^{\prime}_x x+ K^{\prime}_y y - K_s \delta ) - (u_0 - a) (K_x x'+K_y y' ) {} \\ w_y & =&\displaystyle -(1+u_0) x'' +(u_0 + \frac{a}{\gamma}) K_y \delta + (1+a) K_s y' \end{array} \end{aligned} $$

(7.16)

where the magnet anomaly a = 0.00116 for electrons, ν₀ = γa and the fields of bending and solenoidal magnets are presented by the normalized fields K_x,y,s = B_x,s,y∕(Bρ).

One can find a solution α_inv of the Eq. (7.15) which is periodical not only with ring azimuth, but also with betatron motion phases. This solution corresponds to the invariant spin field $\hat {\mathbf {n}}$, and thus defines also the derivatives o f the invariant spin field over δ, A_x and A_y which is of interest when calculating the vector d (7.7).

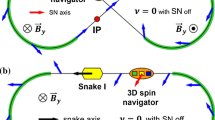
Now let’s consider an accelerator ring with spin rotators (Fig. 7.2). Usually, two spin rotators are installed around the collision point in order transform the polarization direction from vertical to longitudinal, and then back to vertical. We call the spin rotator system to be spin matched if the spin invariant field (α_inv) dependence on horizontal betatron amplitude A_x and energy deviation δ is cancelled outside the rotator system. The following integral over the whole spin rotator system must be made 0 (or at least minimized) for terms proportional to A_x and δ:

$$\displaystyle \begin{aligned} \int_{s_{in}}^{s_{out}} [w_x {\hat{k}}_{0x} + w_s {\hat{k}}_{0s}+w_y {\hat{k}}_{oy}] ds {} \end{aligned} $$

(7.17)

Fig. 7.2

The ring with spin rotator insertion has the stable spin direction non-vertical inside the insertion

We will demonstrate how the spin matching conditions are derived using two examples of spin rotators systems:

• 1. Combination of solenoidal and horizontal bends, as in the spin rotator for EIC,

• 2. Combination of horizontal and vertical bends, as in the spin rotator for HERA.

7.4 Spin Matching for Solenoidal Spin Rotators

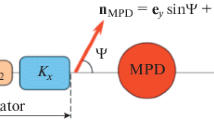
The EIC spin rotator [2] includes solenoidal magnets (spin rotation angle φ_j) and horizontal bends (spin rotation angle ψ_j), as shown in Fig. 7.3.

Fig. 7.3

The EIC spin rotator utilizes a sequence of solenoidal magnets and horizontal bends in order to create longitudinal stable spin direction in the experimental detector

From spin matrix analysis of this rotator system one can derive conditions for achieving the longitudinal polarization at the experimental point:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \tan \varphi_1 & =&\displaystyle \pm \frac{\cos \psi_2}{\sqrt{-\cos (\psi_1 + \psi_2 ) \cos (\psi_1 - \psi_2 ) }} \end{array} \end{aligned} $$

(7.18)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \cos \varphi_2 & =&\displaystyle \cot \psi_1 \cot \psi_2 \end{array} \end{aligned} $$

(7.19)

From here the required solenoidal fields on all energy range can be found.

For spin-matching of this rotator system the spin-orbital integral (Eq. (7.17)) needs to be evaluated and made equal 0 if possible. For evaluating this integral one can assume following reasonable optics conditions which are accommodated by the rotator optics design:

• 1. betatron coupling is fully compensated individually for each solenoidal insertion,

• 2. the vertical dispersion function D_y does not leak into the horizontal bends.

When evaluating the integral the integration by parts can be used to get a simpler form of spin matching condition:

$$\displaystyle \begin{aligned} \begin{array}{rcl} y'' k_{0x} & =&\displaystyle (y' {\hat{k}}_{0x})' -y' {\hat{k}}^{\prime}_{0x} \\ x'' k_{0y} & =&\displaystyle (x' {\hat{k}}_{0y})' -x' {\hat{k}}^{\prime}_{0y} \end{array} \end{aligned} $$

(7.20)

Applying this one can find that the spin-orbit integral needs to be taken only over bending and solenoidal magnets:

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \int_{s_b}^{s_e} \{ -(1+u_0) y' (K_s {\hat{k}}_{0y} - u_0 K_y {\hat{k}}_{0s}) + K_s x' {\hat{k}}_{0x} + ( K^{\prime}_y y - K_s \delta - u_0 K_y y') {\hat{k}}_{0s} - \\ & -(1+u_0) x' K_s {\hat{k}}_{0x} + (u_0 K_y \delta+ K_s y') {\hat{k}}_{0y} \} ds = \\ & \int_{sol} \{ -u_0 K_s (x' {\hat{k}}_{0x} + y' {\hat{k}}_{0y}) - K_s \delta {\hat{k}}_{0s} \} ds + \\ & + \int_{bends} \{ u_0^2 K_y y' {\hat{k}}_{0s} + K^{\prime}_y y {\hat{k}}_{0s} + u_0 K_y \delta {\hat{k}}_{0y} \} ds = 0 \end{array} \end{aligned} $$

(7.21)

Thus the integration has two terms. One includes integration over solenoids and another over horizontal bending magnets.

Selecting terms proportional to A_x, $A^*_x$ and δ one comes to the following form of the spin matching conditions. The solenoids are assumed divided in two halves with compensation quadrupoles between:

$$\displaystyle \begin{aligned} \sum_{i=1}^{4} H(f_I)_i = 0 \end{aligned} $$

(7.22)

where H(f_I)_i is:

$$\displaystyle \begin{aligned} \begin{array}{rcl} & H(f_I) = \frac{\phi_i}{2} [ \left ( (f^{\prime}_{Ix} +\frac{K_s}{2} f_{Iy}) {\hat{k}}_{0x} + (f^{\prime}_{Iy} -\frac{K_s}{2} f_{Ix} ) {\hat{k}}_{0y} \right )_{entr} + \\ & \left ( (f^{\prime}_{Ix} +\frac{K_s}{2} f_{Iy}) {\hat{k}}_{0x} + (f^{\prime}_{Iy} -\frac{K_s}{2} f_{Ix} ) {\hat{k}}_{0y} \right )_{exit} ] {} \end{array} \end{aligned} $$

(7.23)

where the entrance and the exit denote points just before the first solenoid of the solenoidal insertion and right after the second solenoid.

A condition for the terms proportional to $A_I^*$ is derived the same way to get:

$$\displaystyle \begin{aligned} \sum_{i=1}^{4} H(f^*_I)_i = 0 \end{aligned} $$

(7.24)

Next the terms in the integral proportional to δ should be considered. The integration in solenoid of the term with $(D^{\prime }_x {\hat {k}}_{0x} + D^{\prime }_y {\hat {k}}_{0y})$ is done the same way as for horizontal betatron motion. Other terms are trivially integrated. As result one gets the following spin-matching condition related electron energy deviation:

$$\displaystyle \begin{aligned} -u_0 \sum_{i=1}^{4} H(\mathcal{D})_i - \sum_{i=1}^{4} (\phi_i ({\hat{k}}_{0s})_i) + \sum_{j=1}^{4} (\psi_j ({\hat{k}}_{0y})_j ) = 0 \end{aligned} $$

(7.25)

Note that each of three conditions is complex. Thus, in fact there are total of six conditions that needs to be satisfied by proper rotator layout and optics.

Spin matching conditions related with betatron motion can be satisfied for each individual solenoidal insertion, using two solenoid halves and (at least) 6 quadrupoles between them (Fig. 7.4). In this case one can find a solution which nullifies H(f_I)_i and $H(f^*_I)_i$ for each individual solenoid insertion. This solution can be presented in optics matrix form: The configuration of solenoidal and bending magnets in the EIC spin rotator has been chosen to satisfy the spin-matching condition for off-momentum motion at 18 GeV energy. For operation at lower energies it is not fully satisfied.

(7.26)

where

$$\displaystyle \begin{aligned} K_s = \frac{B_s}{B\rho}\, ; \,\,\,\,\,\,\, \phi = (1+a) K_s\end{aligned} $$

(7.27)

Fig. 7.4

The EIC rotator solenoidal insertion uses quadrupoles between two solenoid halves to compensate for the betatron coupling and satisfy the spin matching condition

Figures 7.5 and 7.6 demonstrate how the absolute value of the vector d looks like without and with spin matching. In first case, shown in Fig. 7.5, large oscillation of d-function propagates all over the ring circumference. After spin matching realized (Fig. 7.6) the vector d is only present in the area between rotators. Thus, no stochastic depolarization comes from the machine arcs. The depolarization is limited only to the area between rotators where non-zero d vector still exists. Spin matched optics considerably reduces depolarization, making the spin resonances narrower. An example demonstrating improvement from spin matching for the EIC is shown in Fig. 7.7.

Fig. 7.5

The vector d along the EIC electron storage ring azimuth before the spin matching done

Fig. 7.6

The vector d along the EIC electron storage ring azimuth after the spin matching done

Fig. 7.7

The effect of spin matching on the depolarization time in the EIC electron storage ring

7.5 Spin Matching for Dipole Rotators

Let’s now consider the Steffen-Buon rotator based on dipole magnets [3] described in the lecture on spin rotators and shown in Fig. 7.8. A variant of this rotator scheme was used the electron ring of electron-proton collider HERA .

Fig. 7.8

The schematics of HERA rotator based on a sequence of horizontal and vertical bending magnets

According to our recipe for calculations of spin matching conditions one needs to know the spin eigenvectors. For instance in the interval between rotators the eigenvectors are found to be:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{\mathbf{n}}_{\mathbf{0}} & =&\displaystyle (-\sin (\gamma a K_y), \cos (\gamma a K_y), 0); \\ \hat{\mathbf{k}}_{\mathbf{0}} & =&\displaystyle (\cos (\gamma a K_y), \sin (\gamma a K_y), i); \end{array} \end{aligned} $$

(7.28)

where $K_y = \int ^{0}_{s} K_y ds$.

Using (7.16) the precession vector components can be written as:

$$\displaystyle \begin{aligned} \begin{array}{rcl} w_x & =&\displaystyle u_0 y''+ u_0 K_x \delta \\ w_s & =&\displaystyle 0 \\ w_y & =&\displaystyle -u_0x''+ u_0 K_y \delta \end{array} \end{aligned} $$

(7.29)

where only terms dominant at large energy are left for brevity.

Spin matching conditions can be separated into horizontal and vertical betatron contributions, proportional to A_x and A_y correspondingly, and longitudinal contribution, proportional to δ. From term proportional to A_x one gets the following condition:

$$\displaystyle \begin{aligned} \int_{-s_r}^{s_r}u_0 f^{\prime\prime}_x {\hat{k}}_{0y}ds = \int_{-s_r}^{s_r}-u_0 g_x(s) {\hat{k}}_{0y} \sqrt{\beta_x} \exp(i \Psi_x)ds = 0 \end{aligned} $$

(7.30)

And from term proportional to $A^*_x$ :

$$\displaystyle \begin{aligned} \int_{-s_r}^{s_r}u_0 {f^*}^{\prime\prime}_x {\hat{k}}_{0y} ds = \int_{-s_r}^{s_r}-u_0 g_x(s) {\hat{k}}_{0y} \sqrt{\beta_x} \exp(-i \Psi_x)ds \end{aligned} $$

(7.31)

Condition derived from term proportional to δ is:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{-s_r}^{s_r}[u_0(D^{\prime\prime}_y {\hat{k}}_{0x}-D^{\prime\prime}_x {\hat{k}}_{0y})+u_0(K_x {\hat{k}}_{0x} + K_y {\hat{k}}_{0y})]ds = \\ = \int_{-s_r}^{s_r}[u_0 (g_x(s)D_x {\hat{k}}_{0y}-g_y(s)D_y {\hat{k}}_{0x}] ds \end{array} \end{aligned} $$

(7.32)

At the derivation of the condition above the well-known equation for the orbital motion functions f_x, D_x and D_y were used:

$$\displaystyle \begin{aligned} \begin{array}{rcl} f_{x,y}^{\prime\prime}+ g_{x,y}(s)f_{x,y} = 0 \\ D_{x}^{\prime\prime} + g_{x}(s)D_x = K_y. \\ D_{y}^{\prime\prime} + g_{y}(s)D_{y} = -K_x \end{array} \end{aligned} $$

(7.33)

In spin rotators which include vertical bends the synchrotron radiation happening in the vertical bends couples with vertical betatron amplitude. Thus, in this case an additional spin matching needs to be realized: minimizing the spin-orbital integral terms proportional to A_y and $A^*_y$ . Since any quadrupole in the ring arc contributes to the spin coupling with the vertical orbital motion the integration has to be done over the whole ring circumference. Thus, following integrals have to be minimized to suppress depolarization effect coming from the synchrotron radiation in the rotator:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{-s_r}^{s_r}u_0 f^{\prime\prime}_y {\hat{k}}_{0x}ds & =&\displaystyle \int_{-s_r}^{s_r}-u_0 g_y(s) {\hat{k}}_{0x} \sqrt{\beta_y} \exp(i \Psi_y)ds \\ \int_{-s_r}^{s_r}u_0 {f^*_y}'' {\hat{k}}_{0x}ds & =&\displaystyle \int_{-s_r}^{s_r}-u_0 g_y(s) {\hat{k}}_{0x} \sqrt{\beta_y} \exp(-i \Psi_y)ds \end{array} \end{aligned} $$

(7.34)

These integrals should be considered for both rotators on left and right sides from the experimental point.

7.6 Calculating Vector d in Computer Programs

A popular algorithm for calculating the vector d in a spin program is SLIM. Originated in the first-order SLIM code [4], it presently can be found in several other accelerator codes (for instance, BMAD [5]).

In the SLIM algorithm the 8-D spin-orbital vector consisting of 6 orbit variables (x, p_x, y, p_y, τ, δ) and 2 spin variables (α, β) is used to represent motion of a particle and its spin. The spin-orbital vector transport is described by extending standard 6-D matrices M_6×6 for orbital transport to 8-D case:

(7.35)

Vector d is calculated using components v and w of one-turn 8-D transformation eigenvectors q_j:

(7.36)

Another algorithm, ASPIRRIN [6], calculates vector d unified in one set with other spin-orbital functions, called response functions, using standard transport matrices of the orbital motion and special vectors for dipole and solenoidal magnets.

Calculations using SLIM and ASPIRRIN is done in first-order of orbital and spin dynamics. On the basis of this first-order vector d the equilibrium polarization as well as polarization relaxation time is calculated in both codes.

When designing the spin rotators the first-order calculations are important to realize the spin matching and confirm that it works as intended. But then further spin studies has to be done using a spin tracking code and including different kind of machine errors. These spin tracking studies will reveal also higher-order spin resonances, not seen by the first-order codes, giving more complete evaluation of the equilibrium polarization and the polarization relaxation time.

7.7 Summary

In order to minimize stochastic depolarization spin rotators in electron rings require satisfying special lattice conditions, called spin matching. Main idea of spin matching is to minimize or totally nullify the absolute value of vector $\mathbf {d} = \partial \hat {\mathbf {n}} / \partial \delta$ in the accelerator arcs where synchrotron radiation happens. Analytically spin matching conditions can be derived using spin-orbit integrals. In spin programs the SLIM algorithm is often used for evaluating the d-vector.