1 Introduction

Polytropes, in the context of general relativity have great importance in study of different changes in characteristics and physical models of a astronomical objects. These characteristics and physical models can easily be described by the polytropic equation of state (PEoS). Polytropes are the solution of Lane-Emden equation (LEe), which is a pair of non linear differential equations so these are always attracted by many researchers in astrophysics and mathematics. Lane [1] used polytropes to give some basic results associated to the modeling of cosmological structures. Chandrasekhar [2] used the idea of polytropes to estimate the maximum mass limit for a stable white dwarf star in Newtonian physics. Tooper [3] made use of PEoS to analysis the solution of basic field equations in the context of general theory of relativity for spherical compressible fluid under gravitational equilibrium. He [4] also found the numerical solutions of hydrostatic equilibrium equation in general relativity using spherical compressible fluid which governed by the relation of pressure-energy density. Kaplan and Lupanov [5] studied the relativistic effects in the theory of the structure of polytropic sphere and they obtained an analytical relation between central density and spherical mass in weak relativity. Managhan and Roxburgh [6] investigated the structure of rotating polytropes for different values of polytropic index. For this purpose they used method of approximation for the matching of two solutions at an interface. Kaufmann [7] used PEoS under static spherical symmetry to obtain a single integro-differential equation and its solution depended on different values of polytropic index n. Occhionero [8] evaluated the impact of rotation on the structure of polytropes for \(n\geqslant 2\), which were in equilibrium to the second order with suitable parameter. Kovetz [9] reviewed the theory of slowly rotating polytropes of Chandrasekhar [2] and removed some inconsistencies in it.

Horedt [10] discussed the instability of weakly distorted polytropic sphere for polytropic index \(n>3\). He also observed that slowly rotating cylinder and polytropic rings did not show any instability under the external pressure. Sharma [11] tabulated the values of radius of static polytropic sphere for polytropic index \(n=0, 1, 3\) and values of other physical parameters for \(n=0,1\) by using the pade (2, 2) approximation. Singh and Singh [12] carried out a study of rotationally distorted and tidally polytropes by using the method of [6]. Horedt [13] analyzed the properties like mass acceleration gravitational potential and mean density of \(N-\) dimensional radially symmetric polytropes with the help of gamma function. He also discussed the mass−radius relation in case cylindrical and spherical symmetry. Pandey [14] calculated various parameters to study the spherical static structure by using PEoS. For a certain region of sun interior, Hendry [15] developed three polytropic models.

Herrera and Barreto [17] evaluated the relativistic polytropes by using the two different definitions of relativistic polytropes giving same Newtonian limit for self gravitating sphere. They [20] also gave a general structure for the modeling of polytropes in the context of general relativity and derived the LEe. Herrera et al. [23] used the PEoS to analyze the spherically symmetric fluid which is distributed conformally flat and constructed models of highly compact star for anisotropic polytropes in mass density case. Herrera et al. [24] examined the effects of different variations in energy density and pressure anisotropy under cracking technique for spherical non static compact objects satisfying the PEoS.

The generalized polytropic equation of state (GPEoS) is used to discuss the generalized polytrops (GPs) for the study of gravitating objects. This equation consists of two parts: (i) polytropic part \(P_{r}= K\mu ^{\gamma }_{o}=K\mu _{o}^{1+\frac{1}{n}}\) and (ii) linear part \(P_{r}=\alpha _{1}\mu _{o}\). Combination of these two parts define the GPEoS [25] as

$$\begin{aligned} P_{r}= K\mu ^{\gamma }_{o}+\alpha _{1}\mu _{o}=K\mu _{o}^{1+\frac{1}{n}}+\alpha _{1}\mu _{o} , \end{aligned}$$
(1)

where \(P_{r}\), K, \( \gamma \), \(\alpha _{1}\) and n are called principal stress, polytropic constant , polytropic exponent, linear coefficient constant and polytropic index respectively. Change of \(\mu _{o}\) by \(\mu \) gives

$$\begin{aligned} P_{r}= K\mu ^{1+\frac{1}{n}}+\alpha _{1}\mu . \end{aligned}$$
(2)

Azam et al. [25, 26] carried out spherical and cylindrical symmetric fluid distribution to study the charged polytropes with relativistic GPEoS. Mardan et al. [27, 28] used spherical symmetric GPs to investigate some gravitating objects. They found exact solutions of field equations by taking different values of polytropic index n and analyzed some mathematical models which were found physically viable and well behaved. Mardan et al. [29, 30] established new classes of polytropic models using spherical symmetry and analyzed the mass and radius of different astronomical objects.

Different equations of state are playing an important role to describe the two very fundamental aspect of universe, dark energy and dark matter. Babichev et al. [35] used a form of linear equation of state, called generalized linear equation of state with perfect fluid distribution to describe the different scenarios for dark energy. Mukhopadhyay et al. [18] discussed the real nature of dark energy through the parameter of PEoS specially in non-dust situation. Chavanis [19, 21, 22] used GPEoS in his series of papers to study dark energy and dark matter. He considered dark fluid with GPEoS in which its linear and polytropic part describes the dark energy and dark matter respectively and used different values of parameters of GPEoS to explain the early and late universe.

Herrera [31] used orthogonal splitting of Riemann tensor into structure scalars for a self gravitating system to present a new concept of complexity factor (CF). Abbas and Nazar [32,33,34,35] carried out this concept of vanishing CF for self gravitating object in the context of modify gravity f(R) and expressed the physical behavior of f(R) model for some compact objects in spherically static, dynamical and axially symmetry . Sharif and Iqra [36, 37] implemented the CF on cylindrical system and discussed the electromagnetic effect on this system. Khan  et al. [38, 39] used the idea of CF to study the GPs and charged GPs for spherical self gravitating fluid.

The layout of this paper will be follow Sect. 2 will contain the detail of basic field equations using cylindrical static symmetry and Tolman–Opphenheimar–Volkoff (TOV) equation. In this section, we will also use the the Weyl tensor to discuss the mass function for gravitating object. Section 3 will be devoted for the study of structure scalars, which are obtained through orthogonal splitting of Riemann tensor and then CF will be defined. In Sect. 4 a discussion will be carried out about GPs and physical conditions. We will give a graphical solution of cylindrical GPs with CF in Sect. 5. In the last Sect. 6 we will summarize our study.

2 Basic equations and mass function

Let us consider a static cylindrical symmetric line element, as

$$\begin{aligned} ds^2=-A^{2}dt^{2}+B^{2}dr^{2}+C^{2} d\theta ^{2}+a^{2} C^{2}d z^{2}, \end{aligned}$$
(3)

where \(A=A(r)\), \(B=B(r)\), \(C=C(r)\), a is an arbitrary constant and coordinates are: \(x^{0}=t\), \(x^{1}=r\), \(x^{2}=\theta \), \(x^{3}=z\). The stress-energy tensor is defined as

$$\begin{aligned} T_{\mu \nu }=(P_{r}-P_{\perp })s_{\mu }s_{\nu }+ (P_{\perp }+\mu )u_{\mu }u_{\nu }-P_{\perp }g_{\mu \nu }, \end{aligned}$$
(4)

here \( P_{\perp }\) is an other principal stress, four vector and four velocity respectively are defined as \(s_{\mu }=(0,\frac{1}{B},0,0)\) and \(u_{\mu }=(\frac{1}{A},0,0,0)\), with properties:

$$\begin{aligned} s^{\mu }u_{\mu }=0,\quad s^{\mu }s_{\mu }=1,\quad u^{\mu }u_{\mu }=-1. \end{aligned}$$

It will be more convenient if we take stress−energy tensor as

$$\begin{aligned} T^{\lambda }_{\gamma }=\mu u^{\lambda }u_{\gamma }+Ph^{\lambda }_{\gamma }+ \Delta ^{\lambda }_{\gamma }, \end{aligned}$$
(5)

with

$$\begin{aligned} \Delta ^{\lambda }_{\gamma }= & {} \Delta (s^{\lambda }s_{\gamma }+\frac{1}{3}h^{\lambda }_{\gamma }); \; 3 P=2P_{\perp }+P_{r}\nonumber \\ \Delta= & {} -(P_{\perp }-P_{r});\quad h^{\lambda }_{\gamma }=\delta ^{\lambda }_{\gamma }-u^{\lambda }u_{\gamma }. \end{aligned}$$
(6)

Basic equations are

$$\begin{aligned}&8\pi \mu =\frac{2C^{**}}{B^{2}C}-\frac{2B^{*}C^{*}}{B^{3}C}+\frac{C^{*2}}{B^{2}C^{2}}, \end{aligned}$$
(7)
$$\begin{aligned}&-8\pi P_{r}=\frac{C^{*2}}{B^{2}C^{2}}+\frac{2 A^{*} C^{*}}{A B^{2}C}, \end{aligned}$$
(8)
$$\begin{aligned}&-8\pi P_{\perp }{=}\frac{A^{*}C^{*}}{AB^{2}C}{+}\frac{C^{**}}{B^{2}C} {-}\frac{{B^{*}C^{*}}}{B^{3}C}+\frac{A^{**}}{A B^{2}}-\frac{A^{*} B^{*}}{A B^{3}}, \end{aligned}$$
(9)

where ‘\(*\)’ indicates the derivative w. r. t. ‘r’. The corresponding exterior geometry is considered as [40].

$$\begin{aligned} ds^{2}=\frac{2M}{R}d\nu ^{2}-2dRd\nu +R^{2}(d\theta ^{2}+a^{2})dz^{2}, \end{aligned}$$
(10)

where M represents the total mass in the exterior. On the hyper surface \(\Sigma \), the necessary and sufficient conditions for smooth matching of two metrics (3) and (10) are given in [40] as \(C(r)=r\) \(\Rightarrow \) \(C^{*}(r)=1\) and \(C^{**}(r)=0\), then Eqs. (7–9) become,

$$\begin{aligned} \mu= & {} \frac{1}{8\pi }\left[ -\frac{2B^{*}}{B^{3}r}+\frac{1}{B^{2}r^{2}}\right] , \end{aligned}$$
(11)
$$\begin{aligned} P_{r}= & {} -\frac{1}{8\pi }\left[ \frac{1}{B^{2}r^{2}}+\frac{2 A^{*}}{A B^{2}r}\right] , \end{aligned}$$
(12)
$$\begin{aligned} P_{\perp }= & {} -\frac{1}{8\pi }\left[ \frac{A^{**}}{A B^{2}}-\frac{A^{*} B^{*}}{A B^{3}}+\frac{A^{*}}{AB^{2}r}-\frac{{B^{*}}}{B^{3}r}\right] . \end{aligned}$$
(13)

Solving Eqs. (11–13) simultaneously we obtain generalized TOV equation as

$$\begin{aligned} P^{*}_{r}=-\frac{A^{*}}{A}(\mu +P_{r})+\frac{2(P_{\bot }-P_{r})}{r}. \end{aligned}$$
(14)

Thorne [41] defined C-energy in the form of mass function as

$$\begin{aligned} \mathbf{E} =\frac{1}{8}\left( 1-\frac{1}{l}\nabla _{\rho }r\nabla ^{\rho }r\right) , \end{aligned}$$
(15)

it yields

$$\begin{aligned} m(r)\cong \mathbf{E} =l\mathbf{E} =-\frac{ra}{2B^2}\left( 1-\frac{B^2}{4}\right) , \end{aligned}$$
(16)

using Eqs. (11) and (16)

$$\begin{aligned} m(r)=\frac{ar}{8}-4\pi \int ^{r}_{0}\overline{r}^{2}\mu d\overline{r}. \end{aligned}$$
(17)

From Eqs. (11–13) and (16), we have

$$\begin{aligned} m= & {} \frac{ra}{8}+8\pi (\mu -P_{r}+P_{\bot })-\frac{1}{B^{2}}\left( \frac{ra}{2}+\frac{1}{r_{2}}\right) \nonumber \\&+\frac{1}{AB^{2}}\left[ A^{* *} -\frac{A^{*}B^{*}}{B}-\frac{A^{*}}{r}\frac{A}{r^{2}}+\frac{A B^{*}}{r B}\right] . \end{aligned}$$
(18)

Now with the help of Weyl tensor, we can simplify above expression. For cylindrical symmetric fluid distribution Wely tensor has electric and magnetic components. For the purpose of simplification, we take electric component as

$$\begin{aligned} E_{\alpha \beta }=C_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }, \end{aligned}$$
(19)

where

$$\begin{aligned} C_{\mu \nu \kappa \lambda }=(g_{\mu \nu \alpha \beta }g_{\kappa \lambda \gamma \delta }-\eta _{\mu \nu \alpha \beta }\eta _{\kappa \lambda \gamma \delta })u^{\alpha }u^{\gamma }E^{\beta \delta }, \end{aligned}$$
(20)

with \(g_{\mu \nu \alpha \beta }=g_{\mu \alpha }g_{\nu \alpha }\) and \(\eta _{\mu \nu \alpha \beta }\). Note that

$$\begin{aligned} E_{\alpha \beta }=E\left( s_{\alpha }s_{\beta }+\frac{1}{3}h_{\alpha \beta }\right) , \end{aligned}$$
(21)

and

$$\begin{aligned} E=A^{**}-\frac{A^{*}B^{*}}{B}-\frac{A^{*}}{r}-\frac{A}{r^{2}}+\frac{A B^{*}}{r B}, \end{aligned}$$
(22)

satisfying the following properties:

$$\begin{aligned} E_{11}=\frac{1}{3A}E,\; E_{22}=-\frac{r^{2}}{6AB^{2}}E,\; E_{33}=\frac{a^{2}{r^{2}}}{6AB^{2}}E. \end{aligned}$$
(23)

From Eqs. (18) and (22) we have

$$\begin{aligned} m=\frac{ra}{8}+8\pi (\mu -P_{r}+P_{\bot })-\frac{1}{B^{2}}\left( \frac{ra}{2}+\frac{1}{r^{2}}\right) +\frac{E}{AB^{2}}.\nonumber \\ \end{aligned}$$
(24)

Using Eqs. (17) in (24)

$$\begin{aligned} E= & {} \frac{4}{3}\pi a A B^{2}\int ^{r}_{0}\overline{r}^{3}\mu ^{*} d \overline{r}-\frac{4}{3}\pi a A B^{2}r^{3}\mu +A\left( \frac{ra}{2}+\frac{1}{r^{2}}\right) \nonumber \\&-8\pi A B^{2}\mu +8 \pi A B^{2}(P_{r}-P_{\bot }). \end{aligned}$$
(25)

Then Eq. (24) will be

$$\begin{aligned} m=\frac{ra}{8}+ \frac{4}{3}\pi a\int ^{r}_{0}\overline{r}^{3}\mu ^{*} d \overline{r}-\frac{4}{3}\pi a r^{3}\mu . \end{aligned}$$
(26)

Using Eq. (16) in (12)

$$\begin{aligned} \frac{A^{*}}{A}=-\frac{16a\pi r^{2}P_{r}}{ra-8\pi m}-\frac{1}{2r}. \end{aligned}$$
(27)

Put Eq. (27) in (12), the TOV equation becomes

$$\begin{aligned} P^{*}_{r}=\left( \frac{16a\pi r^{2}P_{r}}{ra-8\pi m}+\frac{1}{2r}\right) (\mu +P_{r})+\frac{2(P_{\bot }-P_{r})}{r}. \end{aligned}$$
(28)

3 Structure scalars and vanishing complexity factor

CF is defined [31] through structure scalars, which are obtained from orthogonal splitting of curvature tensor [43]. This splitting of curvature tensor give the following tensors [44, 45].

$$\begin{aligned} Y_{\alpha \beta }= & {} R_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }, \end{aligned}$$
(29)
$$\begin{aligned} X_{\alpha \beta }= & {} ^{\bullet }R^{\bullet }_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta } =\frac{1}{2}\eta _{\alpha \gamma }^{\epsilon \mu }R^{\bullet }_{\epsilon \mu \beta \delta }u^{\gamma }u^{\delta }, \end{aligned}$$
(30)

where \(\bullet \) denote the dual tensor i.e. \(R^{\bullet }_{\alpha \beta \gamma \delta }=\frac{1}{2}\eta _{\epsilon \mu \gamma \delta }\; R_{\alpha \beta }^{\epsilon \mu }\). While the trace free parts \((Y_{TF},X_{TF})\) and trace part \((Y_{T},X_{T})\) of these tensors are related as [44, 45]. and so the tensors in Eqs. (29) and (30) can be represented as

$$\begin{aligned} Y_{\alpha \beta }= & {} Y_{TF}\left( \frac{1}{3}h_{\alpha \beta }+s_{\alpha }s_{\beta }\right) +\frac{1}{3}Y_{T}h_{\alpha \beta }, \end{aligned}$$
(31)
$$\begin{aligned} X_{\alpha \beta }= & {} X_{TF}\left( \frac{1}{3}h_{\alpha \beta }+s_{\alpha }s_{\beta }\right) +\frac{1}{3}X_{T}h_{\alpha \beta }. \end{aligned}$$
(32)

After using the field equations, we have

$$\begin{aligned} X_{T}= & {} 8\pi \mu , \end{aligned}$$
(33)
$$\begin{aligned} X_{TF}= & {} 4\pi \Delta _{\alpha \beta } -E. \end{aligned}$$
(34)

Using Eq. (25) in (34)

$$\begin{aligned} X_{TF}= & {} 4\pi \Delta (1-2 A B^{2})-\frac{4}{3}\pi a A B^{2}\int ^{r}_{0}\overline{r}^{3}\mu ^{*} d \overline{r}\nonumber \\&+\frac{4}{3}\pi a A B^{2}r^{3}\mu \nonumber \\&-A\left( \frac{r a}{2}+\frac{1}{r^{2}}\right) +8\pi A B^{2}\mu , \end{aligned}$$
(35)
$$\begin{aligned} Y_{T}= & {} 4\pi (\mu +3P_{r}-2\Delta ), \end{aligned}$$
(36)
$$\begin{aligned} Y_{TF}= & {} 4\pi \Delta +E, \end{aligned}$$
(37)

or using Eq. (25) in (37)

$$\begin{aligned} Y_{TF}= & {} 4\pi \Delta (1+2 A B^{2})+\frac{4}{3}\pi a A B^{2}\int ^{r}_{0}\overline{r}^{3}\mu ^{*} d \overline{r}\nonumber \\&-\frac{4}{3}\pi a A B^{2}r^{3}\mu \nonumber \\&+A\left( \frac{ra}{2}+\frac{1}{r^{2}}\right) -8\pi A B^{2}\mu . \end{aligned}$$
(38)

From Eqs. (35) and (38)

$$\begin{aligned} 8\pi \Delta =X_{TF}+Y_{TF}. \end{aligned}$$
(39)

In order to discuss stellar structure the basic field Eqs. (11–13) form a system of three ordinary differential equations (DEs) for static cylindrical symmetry in five variables \((A, B,\mu ,P_{\perp },P_{r})\). So we implement condition \(Y_{TF}=0\) which gives the vanishing CF Eq. (38), as [36]

$$\begin{aligned} \Delta= & {} \frac{-1}{4\pi (1+2AB^{2})}\left[ \frac{4}{3}\pi a A B^{2}\int ^{r}_{0}\overline{r}^{3}\mu ^{*} d \overline{r}\right. \nonumber \\&\left. -\frac{4}{3}\pi a A B^{2}r^{3}\mu +A\left( \frac{ra}{2}+\frac{1}{r^{2}}\right) -8\pi A B^{2}\mu \right] . \end{aligned}$$
(40)

but we may still required one more condition to explain the stellar structure for this purpose we will use GPEoS.

4 Generalized cylindrical polytropes

Since GPEoS are widely used \([20-26,31,32]\) to discuss the different characteristics of inner structure of self gravitating objects. So we use it for cylindrical static symmetry anisotropic fluid as

4.1 Case 1

$$\begin{aligned} P_{r}=K\mu _{o}^{1+\frac{1}{n}}+\alpha _{1}\mu _{o}, \end{aligned}$$
(41)

energy density \(\mu \) connected with the mass density \(\mu _{o}\) [23] as

$$\begin{aligned} \mu =\mu _{o}+nP_{r}. \end{aligned}$$
(42)

following assumptions are to be considered

$$\begin{aligned}&r=\frac{\xi }{N}, \quad \alpha =\frac{P_{rc}}{\mu _{c}} ,\quad N^{2}=\frac{4\pi \mu _{c}}{(1+n)\alpha }. \end{aligned}$$
(43)
$$\begin{aligned}&\psi _{o}=\frac{\mu _{o}}{\mu _{oc}},\quad v(\xi )=\frac{m(r)N^{3}}{4\pi \mu _{c}}. \end{aligned}$$
(44)

Then TOV Eq. (15) becomes

$$\begin{aligned}&\xi N^{-4}\alpha ^{-2}\big [-16 \pi {\psi _o}^{2 n} \xi ^3 a {P_{rc}}^2 ({\alpha _1}\nonumber \\&\quad + ( \alpha {\alpha _1} n -{\alpha _1}+\alpha ){\psi _o}-\alpha {\alpha _1} n)\nonumber \\&\quad \times ((1+n) {\psi _o} (\alpha -{\alpha _1}+\alpha {\alpha _1} n)\nonumber \\&\quad +(1-\alpha n) ({\alpha _1}+{\alpha _1} n+1))-2 (\alpha N^2 \xi \nonumber \\&\quad -32 \pi {P_{rc}} v) (2 \alpha \Delta -\xi {P_{rc}} {\psi _o}^{n-1} {\psi _o}' \nonumber \\&\quad \times ((1+n) (\alpha -{\alpha _1}+\alpha {\alpha _1} n){\psi _o}\nonumber \\&\quad -{\alpha _1} n (\alpha n-1)))\big ]=0. \end{aligned}$$
(45)

where prime indicates the derivative w. r. t. \(\xi \). Using Eqs. (43, 44) in (17) we have

$$\begin{aligned} \dfrac{dv}{d\xi }= & {} \frac{a}{8(n+1)\alpha }-a\xi ^{2}\psi _{o}^{n} \big [(1-n\alpha )(1+n\alpha _{1})\nonumber \\&+n(\alpha -\alpha _{1}+n\alpha \alpha _{1})\big ]. \end{aligned}$$
(46)

At boundary surface \(\xi =\xi _{n}\) such that \(\psi _{o}(\xi _{n})=0\) and we have boundary conditions as

$$\begin{aligned} \psi _{o}(\xi =0)=1 \quad and \quad v(\xi =0)=0. \end{aligned}$$
(47)

Equations (45, 46) constitute the LEe for this case

$$\begin{aligned}&\frac{1}{\alpha ^3 N^4}\Bigg [2 \Bigg (-\frac{2}{n+1}\big [ (2 \alpha \Delta -\xi {P_{rc}} {\psi _{ o}}^{n-1} {\psi _{ o}}' ((n+1) {\psi _{ o}}\beta \nonumber \\&\quad +{\alpha _{ 1}} n (1-\alpha n)))\nonumber \\&\quad \times (\xi (\alpha ^2 N^2 (n+1)-2 \pi a {P_{rc}})+16 \pi \alpha (n+1) {P_{rc}} \nonumber \\&\quad \times (a \xi ^3 {\psi _{ o}}^n (n {\psi _{ o}} \beta +(1-\alpha n)\nonumber \\&\quad \times ({\alpha _{ 1}} n+1))-v))\big ]-8 \pi a \alpha (n+1) \xi ^4 {P_{rc}}^2 \beta {\psi _{ o}}^{2 n} {\psi _{ o}}' \nonumber \\&\quad \times ({\alpha _{1}}+{\psi _{ o}} \beta -\alpha {\alpha _{ 1}} n)\nonumber \\&\quad +8 \pi a \alpha n \xi ^4 {P_{rc}}^2 {\psi _{ o}}^{2 n-1} {\psi _{ o}}' ({\alpha _{ 1}}+{\psi _{ o}} \beta \nonumber \\&\quad +\alpha {\alpha _{ 1}} (-n)) ((\alpha n-1) \beta _{1}-(n+1)\nonumber \\&\quad \times {\psi _{ o}} \beta )-8 \pi a \alpha \xi ^3 {P_{rc}}^2 {\psi _{ o}}^{2 n-1} \nonumber \\&\quad \times ((n+1) {\psi _{ o}} \beta -(\alpha n-1) \beta _{1}) (\xi {\psi _{ o}}' ((n+1) {\psi _{ o}} \beta \nonumber \\&\quad +{\alpha _{ 1}} n(1-\alpha n))+4 {\psi _{ o}} ({\alpha _{ 1}}+{\psi _{ o}} \beta +\alpha {\alpha _{ 1}} (-n)))\nonumber \\&\quad +\alpha \xi {P_{rc}} {\psi _{ o}}^{n-2} (\alpha N^2 \xi \nonumber \\&\quad -32 \pi {P_{rc}} v)(-{\alpha _{ 1}} (n-1) n \xi (\alpha n-1) {\psi _{ o}}'^2\nonumber \\&\quad +(n+1) {\psi _{ o}}^2 \beta (\xi {\psi _{ o}}''+{\psi _{o}}')\nonumber \\&\quad +n {\psi _{ o}} ({\alpha _{ 1}} \xi (1-\alpha n) {\psi _{ o}}''+{\psi _{ o}}' \nonumber \\&\quad \times ({\alpha _{ 1}}+(n+1) \xi \beta {\psi _{ o}}'+\alpha {\alpha _{ 1}} (-n))))\Bigg )\Bigg ], \end{aligned}$$
(48)

where \(\beta =(\alpha -{\alpha _{ 1}}+\alpha {\alpha _{ 1}} n)\) and \(\beta _{1}=({\alpha _{ 1}}+{\alpha _{ 1}} n+1)\)

4.2 Case 2

Now we consider [25]

$$\begin{aligned} P_{r}=K\mu ^{1+\frac{1}{n}}+\alpha _{1}\mu , \end{aligned}$$
(49)

in this case energy density \(\mu \) and mass desity \(\mu _{o}\) are expressed as [46]

$$\begin{aligned} \mu (K\mu _{o}^{1/n}-1)^{n}=(-1)^{n}\mu _{o}. \end{aligned}$$
(50)

By taking \(\psi ^{n}=\frac{\mu }{\mu }_{o}\) TOV equation becomes

$$\begin{aligned}&\frac{\xi }{\alpha ^2 N^4}\big [-16 \pi a \xi ^3 {P_{rc}}^2 \psi ^{2 n} ((\alpha -{\alpha _{ 1}}) \psi +{\alpha _{ 1}})\nonumber \\&\quad \times ((\alpha -{\alpha _{ 1}}) \psi +{\alpha _{ 1}}+1)\nonumber \\&\quad -2(\alpha N^2 \xi -32 \pi {P_{rc}} v)(2 \alpha \Delta -\xi {P_{rc}} \psi ^{n-1} \psi '(\xi )\nonumber \\&\quad \times ((n+1) (\alpha -{\alpha _{1}}) +{\alpha _{ 1}} n)\big ]=0. \end{aligned}$$
(51)

and from Eq. (17) we have

$$\begin{aligned} \dfrac{dv}{d\xi }=\frac{a}{8(n+1)\alpha }-a\xi ^{2}\psi ^{n}. \end{aligned}$$
(52)

Equations (51, 52) together give the generalized LEe

$$\begin{aligned}&\frac{2}{\alpha {^3} N^{4}}\Bigg [\frac{-1}{n+1}\big [2 (2 \pi a \xi {P_{rc}} (8 \alpha (n+1) \xi {^2} \psi {^n-1})\nonumber \\&\quad +\alpha ^2 N^2 (n+1) \xi \nonumber \\&\quad -16 \pi \alpha (n+1){P_{rc}} v) (2 \alpha \Delta +\xi {P_{rc}} \psi ^{n-1} \psi ' \nonumber \\&\quad \times ((1+n) ({\alpha _{1}}-\alpha ) \psi \nonumber \\&\quad -{\alpha _{1}} n))\big ]-8 \pi a \alpha \xi ^4 {P_{rc}}^2 (\alpha -{\alpha _{1}})\psi ^{2 n} \psi ' \nonumber \\&\quad \times ((\alpha -{\alpha _{1}}) \psi +{\alpha _{1}})\nonumber \\&\quad -8 \pi a \alpha n \xi ^4 {P_{rc}}^2 \psi ^{2 n-1} \psi ' ((\alpha -{\alpha _{1}}) \psi \nonumber \\&\quad +{\alpha _{1}}) ((\alpha -{\alpha _{1}}) \psi +{\alpha _{1}}+1)\nonumber \\&\quad -8 \pi a \alpha \xi ^3 {P_{rc}}^2 \psi ^{2 n-1} ((\alpha -{\alpha _{1}}) \psi \nonumber \\&\quad +{\alpha _{1}}+1) (4 \psi ((\alpha -{\alpha _{1}}) \psi +{\alpha _{1}})\nonumber \\&\quad +\xi \psi ' ((n+1) (\alpha -{\alpha _{1}}) \psi +{\alpha _{1}} n))\nonumber \\&\quad +\alpha \xi {P_{rc}} \psi ^{n-2} (\alpha N^2 \xi \nonumber \\&\quad -32 \pi {P_{rc}} v) ((n+1) (\alpha -{\alpha _{1}}) \psi ^2 (\xi \psi ''+\psi ')\nonumber \\&\quad +n \psi ({\alpha _{1}} \xi \psi ''+\psi ' ({\alpha _{1}}\nonumber \\&\quad +(1+n) \xi \psi ' (\alpha -{\alpha _{1}})))-{\alpha _{1}} \nonumber \\&\quad \times (1-n) n \xi \psi '^2)\Bigg ]=0. \end{aligned}$$
(53)

Both cases have to satisfy the physical conditions

$$\begin{aligned} \mu >0,\quad \frac{P_{r}}{\mu }\le 1, \quad \frac{P_{\perp }}{\mu }\le 1. \end{aligned}$$
(54)

Conditions (54) takes the form for case 1 as

$$\begin{aligned}&(1-n\alpha )+(1+n\alpha _{1})+n(\alpha -\alpha _{1}+n\alpha \alpha _{1})\psi _{o}>0,\nonumber \\&\frac{\alpha _{1}}{\psi _{o}}+(\alpha _{1}+\alpha \psi _{o})\le (1-n\alpha )+(1+n\alpha _{1})\nonumber \\&\quad +(\alpha n \alpha _{1}-\alpha _{1}+\alpha )n\psi _{o},\nonumber \\&\frac{v}{\xi ^{3}\psi _{o}^{n}}-\frac{a}{8\alpha (n+1)\xi ^{2} \alpha _{o}^{n}}\le (1-a^{2})\nonumber \\&\quad \times {[}n(1-n\psi _{o})(\alpha -\alpha _{1}n\alpha \alpha _{1})-1]\nonumber \\&\quad +a[\alpha _{1}(1-n\alpha )+n\alpha ^{2}\psi _{o}]. \end{aligned}$$
(55)

and in Case 2 these conditions (54) becomes as

$$\begin{aligned}&\mu >0,\; \alpha _{1}(1-\psi )+\alpha \psi \le 1,\;\nonumber \\&\quad \frac{v}{a\xi ^{3}\psi ^{-n}}{-}\frac{1}{8\alpha (n{+}1)\xi ^{2}\psi ^{-n}}\le \alpha _{1}(1{-}n\alpha )(\psi -1)\nonumber \\&\qquad {-}(1+\alpha \psi -a). \end{aligned}$$
(56)

5 Vanishing complexity factor with generalized cylindrical polytropes

As we already have discussed CF as a single scalar and now it is merged with cylindrical GPEoS so that we are able to develop a consistent system of DEs for both cases.

5.1 Case No. 1

In this case Eqs. (43, 44) are used with \(Y_{TF}=0\), as

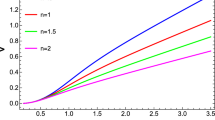
$$\begin{aligned}&4 \pi (\Delta '+2 B^2 (\Delta A'+A \Delta ')+4 A B \Delta B')\nonumber \\&\qquad -\frac{1}{24 \alpha ^2 N^3 \xi ^3}\Bigg [\alpha \xi A' (\xi ^2 B^2 (32 \pi {P_{rc}}\nonumber \\&\qquad \times ((6 N^3-a \xi ^3) {\psi _{o}}^n (n (\alpha -{\alpha _{1}}) {\psi _{o}}\nonumber \\&\qquad +\alpha (-n)+{\alpha _{1}} n+1)-3 v)+a \alpha \xi (3 N^2\nonumber \\&\qquad +32 \pi \xi ^2))-12 \alpha N^2 (a \xi ^3+2 N^3))+A \Bigg (12 \alpha ^2 N^2 (4 N^3-a \xi ^3)\nonumber \\&\qquad +\xi ^3 B \Bigg (2 \alpha B'(32 \pi {P_{rc}} ((6 N^3-a \xi ^3) {\psi _{o}}^n\nonumber \\&\qquad \times (n (\alpha -{\alpha _{1}}) {\psi _{o}}+\alpha (-n)+{\alpha _{1}} n+1) -3 v)+a \alpha \xi \nonumber \\&\qquad \times (3 N^2+32 \pi \xi ^2))+B \Bigg (32 \pi \alpha n {P_{rc}} {\psi _{o}}^{n-1} ((6 N^3-a \xi ^3) {P_{rc}\psi _{o}}' \nonumber \\&\qquad \times ((n+1) (\alpha -{\alpha _{1}}) {\psi _{o}}\nonumber \\&\qquad +\alpha (-n)+{\alpha _{1}} n+1)+3 a \alpha {\alpha _{1}} n \xi ^2 ({\psi _{o}}-1) {\psi _{o}})\nonumber \\&\qquad +3 a \Bigg (32 \pi \alpha ^2 \xi ^2+\alpha ^2 N^2 -\frac{4 \pi {P_{rc}}}{n+1}\Bigg )\Bigg )\Bigg )\Bigg )\Bigg ]=0. \end{aligned}$$
(57)

Now Eqs. (45, 46, 57) form a system of ordinary DEs having three variables v, \(\psi _{o}\) and \(\Delta \). This system of ordinary DEs is solved numerically and its solution is described graphically. Figures 1, 2 and 3 depicted the behavior of v, \(\psi _{o}\) and \(\Delta \) for \(\alpha _{1}=.5\), \(\alpha =.5\), \(A=.5\), \(B=.5\) and \(a=5\).

Fig. 1
figure 1

Graphs between \(\xi \) and v

Full size image
Fig. 2
figure 2

Graphs between \(\xi \) and \(\psi _{o}\)

Full size image
Fig. 3
figure 3

Graphs between \(\xi \) and \(\Delta \)

Full size image

5.2 Case No. 2

CF for case 2 will be read the as

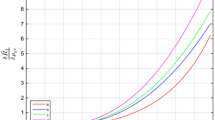
$$\begin{aligned}&4 \pi (\Delta '+2 B^2(\Delta A'+A \Delta ')+4 A B \Delta B')\nonumber \\&\quad -\frac{1}{24 N^3 \xi ^5}\Bigg [\Big (2 A B\Big (B\Big (\frac{1}{\alpha ^2 (n+1)}\nonumber \\&\quad \times \big [\pi (a+1) \xi ^3 {P_{rc}}\big ]+6 N^5\Big )-3 N^5 \xi B'\Big )\nonumber \\&\quad +N^5(4-3 \xi B^2 A')\Big )+\frac{1}{\alpha ^2}\Bigg [\xi ^2\Bigg (\alpha \xi A'\nonumber \\&\quad \times (\xi ^2 B^2 (a \alpha \xi (3 N^2+32 \pi \xi ^2)-32 \pi {P_{rc}}\nonumber \\&\quad \times ((a \xi ^3-6 N^3) \psi ^n+3 v))-12 \alpha N^2(a \xi ^3\nonumber \\&\quad +2 N^3))+A\Bigg (12 \alpha ^2 N^2(4 N^3-a \xi ^3)\nonumber \\&\quad +\xi ^2 B\Bigg (2 \alpha \xi B'(a \alpha \xi (3 N^2+32 \pi \xi ^2)\nonumber \\&\quad -32 \pi {P_{rc}}((a \xi ^3-6 N^3) \psi ^n+3 v))\nonumber \\&\quad +B\Bigg (4 \alpha (-8 \pi n \xi {P_{rc}}(a \xi ^3-6 N^3) \psi ^{n-1} \psi '(\xi ))\nonumber \\&\quad +3 a \xi \Bigg (32 \pi \alpha ^2 \xi ^2+\alpha ^2 N^2\nonumber \\&\quad -\frac{4 \pi {P_{rc}}}{n+1}\Bigg )\Bigg )\Bigg )\Bigg )\Bigg )\Bigg ]\Bigg ]=0. \end{aligned}$$
(58)

Equations (51, 52, 58) constitute a system of ordinary DEs containing three variables \(\Delta \), v and \(\psi \). This system of ordinary DEs is numerically solved and its solution is explained through graphs in Figs. 4, 5 and 6 for \(\alpha _{1}=.5\), \(\alpha =.5\), \(A=.5\), \(B=.5\) and \(a=5\).

Fig. 4
figure 4

Graphs between \(\xi \) and v

Full size image
Fig. 5
figure 5

Graphs between \(\xi \) and \(\psi \)

Full size image
Fig. 6
figure 6

Graphs between \(\xi \) and \(\Delta \)

Full size image

6 Summary

We have used the CF to provide a general framework for the development of modify form of LEes for both cases of GPEoS. For this purpose static anisotropic fluid distribution with cylindrical symmetry is used for stellar structure. Basic field equations and TOV equation is established. The C-energy is applied to develop a expression for mass function. Curvature and Weyl tensors are brought into play to calculate the structure scalars. These structure scalars are used to define vanishing CF. We applied assumptions Eqs. (43, 44) to establish the LEes for static cylindrical fluid distribution for two cases \(\mathbf (1) \) mass density \((\mu _{o})\) and \(\mathbf (2) \) energy density \((\mu )\) to study the physical characteristics of GPs. The physical conditions have also been studied for these two cases under same the assumptions. These two set of LEes led us to the two system of three ordinary DEs with CF. These system of DEs numerically solved and discussed as

For case 1 the solutions of system of three DEs (45, 46, 57) are shown in the Figs. 1, 2 and 3. These solutions reveal the response of variables v, \(\psi _{o}\) and \(\Delta \) corresponding to different values of parameters. The curves of Fig. 1 indicates that v has zero value at center and uniformly increases in straight line.It can also be observed from Fig. 1 that for small value of polytropic index n v has maximum value (curve a) but when values of n increases value of v decreases at boundary (curve b, c, d). In Fig. 2 curves show the pattern of \(\psi _{o}\) which has maximum value at center and gradually deceases towards the boundary and becomes zero in case of curve (a) and (b). While curves (c) and (d) show that value of \(\psi _{o}\) is considerable high. In Fig. 3 anisotropic factor \(\Delta \) has zero value near center of compact star and gradually increases but with the increase of polytropic index n value of \(\Delta \) decreases at boundary surface

For case 2 the Figs. 4, 5 and 6 display the pattern of v, \(\psi \) and \(\Delta \). It can be seen from the curves of Fig. 4 that value of v is minimum at the boundary and gradually increases towards center with the increase of polytropic index n. The values of \(\psi \) and \(\Delta \) in Figs. 5, 6 behave in same manner both variables have zero values at center and maximum values at boundary of surface.