1 Introduction

The theory of polytropes is very important in the study of stellar structure of compact objects. Many researchers have been attracted to the study of polytropes due to the availability of a very simple equation of state (EoS) and resulting Lane–Emden equation, which helped us in the interpretation of various phenomena related to compact objects. Chandrasekhar [1] established the theory of polytropes, arising from the laws of thermodynamics. Tooper [2, 3] developed the basic framework of polytropes under the assumption of a quasi-static equilibrium. Kovetz [4] revolutionized the theory of polytropes by refining the work of [1]. Abramowicz [5] extended the concept of polytropes to higher dimensions for the development of the Lane–Emden equation.

The discussion of charge has always been an area of concern for scientist and researchers in astrophysics. Bekenstein [6] discussed gravitational collapse through the development of a hydrostatic equilibrium equation (HEe). Bonnor [7, 8] showed that the existence of charge on compact object affects the gravitational collapse, possibly delaying it. Bondi [9] studied the contraction of compact stars in the presence of electromagnetism. Koppar et al. [10] discussed a charge generalization in compact stars with static charged fluid distribution. Ray et al. [11] presented the properties of a higher density charge and evaluated the maximum amount of charge which a star can hold. Herrera [12] discussed the charged compact stars through structure scalars. Takisa et al. [13] studied the polytropic models of compact stars.

The role of anisotropy is very important in the theory of relativistic objects. Cosenza et al. [14] developed a novel approach for mathematical models of anisotropic fluid distribution. Herrera and Santos [15] derived the Newtonian and relativistic anisotropic general model. Herrera and Barreto [16] used effective variables to describe the anisotropic polytropic model. Herrera et al. [17] studied the governing equation for the description of anisotropic stresses in compact objects. Herrera and Barreto [18, 19] used the Tolman mass to study the stability of anisotropic compact star models. Herrera [20] developed a pattern to reduce the physical variable by means of the conformal flatness condition.

Stability analysis is critically important in the mathematical modeling of compact objects. Bondi [21] introduced HEe for the stability of uncharged compact object. Herrera [22] introduced the technique of cracking (overturning) to discuss the behavior of inner fluid distribution of compact stars just after equilibrium state has been disturbed. Gonzalez et al. [23, 24] extended the concept of cracking by introducing a local density perturbation (LDP) scheme. Azam et al. [25,26,27,28,29] applied LDP to check the stability of different compact star mathematical models. Sharif [30] developed a general frame work for anisotropic cylindrical polytropes. Azam et al. [31, 32] initially presented the theory of generalized polytropic equation of state (GPEoS) for spherically and cylindrical symmetry in the frame work of general relativity. Herrera et al. [33] tested the stability of polytropes by perturbing model parameters. Azam and Mardan [34] extended the technique of Herrera et al. [33] for charged polytropes.

The plan of this work is as follows. In Sect. 2, we provide some basic conventions and equations. Sections 3 and 4 are devoted to the discussion of cracking through LDP and parametric perturbation, respectively. In the last section we conclude our result.

2 Einstein–Maxwell Field Equations

We consider a static cylindrically symmetric space time [32],

$$\begin{aligned} \mathrm{d}s^2=-A^{2}\mathrm{d}t^{2}+B^{2}\mathrm{d}r^{2}+C^2 \mathrm{d}\theta ^{2}+{\mathrm{d} z^2}, \end{aligned}$$
(1)

where \(t\in (-\infty ,\infty )\), \(r\in [0,\infty )\), \(\theta \in [0,2\pi ]\) and \(z\in (-\infty ,\infty )\) are the conditions on the cylindrical coordinates. The energy-momentum tensor for a charged anisotropic fluid distribution is

$$\begin{aligned} \nonumber T_{i j}= & {} (P_r+\rho ) V_{i} V_{j} -(P_r-P_z)S_{i}S_{j}\\&-\,(P_r-P_\theta )K_{i}K_{j}+P_r g_{ij}\nonumber \\&+\,\frac{1}{4\pi }\left( F_i^\gamma F_{j \gamma }- \frac{1}{4}F^{\gamma \beta } F_{\gamma \beta }g_{ij} \right) , \end{aligned}$$
(2)

where \(P_r,~P_\theta ,~P_z\) and \(\rho \) represent pressures in the \(r,~\theta ,~z \) directions and energy density of fluid inside cylindrical geometry [32]. We consider the exterior metric for the cylindrical symmetric geometry with retarded time coordinate \(\nu \) defined as

$$\begin{aligned} \mathrm{d}s^2=-\left( -\frac{2M}{R}+\frac{Q^2}{R^2}\right) \mathrm{d}\nu ^2-2\mathrm{d}\nu \mathrm{d}R+R^2(\mathrm{d}\theta ^2+\beta ^2\mathrm{d}z^2), \end{aligned}$$
(3)

where \(\beta \) and M represent an arbitrary constant and the total mass for object under consideration. For the continuity and matching of two space times, junction conditions on the boundary \(\Sigma \) yield [35, 36]

$$\begin{aligned} m(r)-M\overset{\Sigma }{=}\frac{l}{8},~~\Leftrightarrow ~~Q^2\overset{\Sigma }{=}\frac{q l^2}{8},~~l\overset{\Sigma }{=}4C,~~P_r\overset{\Sigma }{=}0. \end{aligned}$$
(4)

If \(C=r\) is selected as Schwarzschild coordinate, then the Einstein–Maxwell field equations take the form

$$\begin{aligned}&\frac{B^\prime }{r B^3}=8\pi \rho - q^2, \end{aligned}$$
(5)
$$\begin{aligned}&\frac{A^\prime }{A B^2 r}=8\pi P_r +q^2, \end{aligned}$$
(6)
$$\begin{aligned}&\frac{A^{\prime \prime }}{A B^2}-\frac{A^\prime B^\prime }{A B^3} =8\pi P_\theta -q^2, \end{aligned}$$
(7)
$$\begin{aligned}&\frac{A^{\prime \prime }}{A B^2}-\frac{A^\prime B^\prime }{A B^3} -\frac{B^\prime }{B^3 r}-\frac{A^\prime }{A B^2 r} =8\pi P_z -q^2. \end{aligned}$$
(8)

Solving Eqs. (5)–(8) simultaneously lead to HEe

$$\begin{aligned} \frac{\mathrm{d} P_r}{\mathrm{d}r}+\frac{A^\prime }{A}\big (\rho +P_r\big )+\frac{\Delta }{r} +\frac{q q^\prime r - q^2}{4\pi ^2 r^3} +\frac{2 q^2}{\pi r^3}=0, \end{aligned}$$
(9)

where we have used \(\Delta =P_r-P_\theta \).

The C-energy defined by Thorne [37], in the form of a mass function, is given by

$$\begin{aligned} \widetilde{E} =\frac{1}{8}[1-l^{-2}\nabla ^a\widetilde{r}\nabla _a\widetilde{r}], \end{aligned}$$

with

$$\begin{aligned} \mu ^2=\xi _{(1)a}\xi ^a_{(1)},\quad l^2=\xi _{(2)a}\xi ^a_{(2)},\quad \widetilde{r}=\mu l, \end{aligned}$$

here \(\widetilde{r},\mu ,l\) represents areal radius, circumference radius, specific length, respectively, and for the static case the C-energy can be written as

$$\begin{aligned} m(r)=\widetilde{E}^\prime =\frac{1}{8}\left[ 1-\frac{1}{B^2}\right] +qr. \end{aligned}$$
(10)

Differentiating Eq. (10) and using Eq. (6), we obtain

$$\begin{aligned} \frac{A^\prime }{A}=\frac{8\pi r P_r+q^2}{r-8mr+4 q^2}. \end{aligned}$$
(11)

The HEe (9) with the above equation takes the form

$$\begin{aligned} \frac{\mathrm{d} P_r}{\mathrm{d}r}+\frac{8\pi r P_r+q^2}{r-8mr+4 q^2} \big (\rho +P_r\big )+\frac{\Delta }{r} +\frac{q q^\prime r - q^2}{4\pi ^2 r^3} +\frac{2 q^2}{\pi r^3}=0. \end{aligned}$$
(12)

The theory of polytropes is based on HEe and EoS of the compact object under consideration. In Sects. 3 and 4, we will discuss the stability of charged relativistic cylindrical polytropes with GPEoS.

3 Effect of local density perturbation on cracking

In this section, we apply LDP [23, 24] on charged conformally flat polytropes in equilibrium state. In the LDP scheme, it is assumed that all the physical parameters involved in the model and their derivatives are functions of the density. Here, we will discuss two different kinds of polytropes available in the literature.

3.1 Case 1

We consider the GPEoS [31, 32]

$$\begin{aligned} P_r=\alpha _1\rho _o+K\rho _o^{\gamma }=\alpha _1\rho _o+K\rho _o^{1+\frac{1}{n}}, \end{aligned}$$
(13)

where the mass density \(\rho _o\) is defined with the total energy density \(\rho \) as [31, 32]

$$\begin{aligned} \rho =\rho _{o}+n P_r. \end{aligned}$$
(14)

Now we make the following assumptions:

$$\begin{aligned}&\alpha =\frac{P_{rc}}{\rho _{gc}},\quad r=\frac{\xi }{X}, \quad \rho _{o}=\rho _{gc}\theta ^n,\nonumber \\&m(r)=\frac{2\pi \rho _{gc} v({\xi })}{X^2},\quad X^2= \frac{16\pi P_{rc}}{\alpha }, \end{aligned}$$
(15)

where \(P_{rc}\) is the pressure, \(\rho _{gc}\) is the mass density calculated at the center, \(\xi \), \(\theta \) and v are dimensionless variables. Using assumptions (15) with EoS (13), the HEe (12) becomes

$$\begin{aligned} \nonumber R_1= & {} \left( \frac{1-v({\xi })+32\pi ^{1/2} \sqrt{\frac{P_{rc}}{\alpha }}\frac{q^2}{ \xi }}{1+(n+1)(\alpha _1+\alpha \theta )}\right) \frac{\mathrm{d} \theta }{\mathrm{d} \xi }\nonumber \\&+\, \left( \frac{2P_{rc}\alpha (\alpha _1+\alpha \theta ) \theta ^n+\frac{4 q^2 P_{rc}}{\alpha \xi }}{n\alpha _1 \theta ^{-n}+(n+1)\alpha \theta }\right) \frac{\alpha \xi }{4P_{rc}}\nonumber \\&+\, \frac{\left( \Delta +\frac{4 P_{rc}}{\alpha \xi } (\xi q \frac{\mathrm{d} q}{\mathrm{d} \xi }-q^2)+\frac{32 q^2 P_{rc} }{\alpha \xi }\right) \left( 1-v({\xi })+32\pi ^{1/2}\sqrt{ \frac{P_{rc}}{\alpha }}\frac{q^2}{ \xi }\right) }{(1+(n+1)(\alpha _1+\alpha \theta )) (n\alpha _1 \theta ^{-n}+(n+1)\alpha )}\nonumber \\&\times \frac{\theta ^{-n}}{\xi P_{rc}}. \end{aligned}$$
(16)

Now taking the derivative of Eq. (10) with respect to r and taking assumption (15) into account, we have

$$\begin{aligned} \frac{\mathrm{d}v(\xi )}{\mathrm{d}\xi }=\xi \theta ^n (1+n\alpha _1+n\alpha \theta ) +\frac{(4-\pi )\alpha \xi E}{2 P_{rc}}+ \frac{\alpha \xi ^2}{ P_{rc}}\frac{\mathrm{d} E}{\mathrm{d}\xi }.\nonumber \\ \end{aligned}$$
(17)

We use the conformal flatness condition to find the expression of the anisotropy factor \(\Delta \). For this purpose, the Weyl scalar is defined in terms of the Kretchman scalar, Ricci tensor and Ricci scalar by [32]

$$\begin{aligned} C^2=\mathcal {R}+\frac{R^2}{3}-2R^{\mu \nu }R_{\mu \nu }. \end{aligned}$$
(18)

For our line element, the above equation become

$$\begin{aligned} \nonumber C^2= & {} \frac{4}{3 r^2 A^2 B^6} \Big [\Big (A^2-r A A' +r^2 A'^2\Big ) B'^2\nonumber \\&+\,B^2 \Big (A'^2-r A' A''+r^2 A''^2\Big )\nonumber \\&+\,B B' \Big (r A' \Big (A'-2 r A''\Big )+A \Big (A'+r A''\Big )\Big )\Big ]. \end{aligned}$$
(19)

The anisotropy factor from the above equation with the field equations (5)–(8) and (11) under conformally flatness i.e., \(C^2=0\), takes the form

$$\begin{aligned} \nonumber \Delta= & {} -\pi E^2+ \frac{1}{8 \pi }\left( \phantom {\left. \left. -\, \frac{\Big (8 \pi P_r+4 \pi ^2 r E^2\Big ) \Big (16 \pi ^2 E^2-8 m'+32 \pi ^2 r E E'\Big )}{\Big (1-8 m+16 \pi ^2 r E^2\Big )^2}\right) ^2\right) }8 \pi P_r+4 \pi ^2 E^2+ \Big (8 \pi P_r+4 \pi ^2 E^2\Big )^2\right. \nonumber \\&\left. +\,\Big (8 \pi P_r+4 \pi ^2 E^2\Big ) \Big (-4 \pi ^2 E^2+8 \pi \rho \Big )\right. \nonumber \\&\left. +\,\Big (-4 \pi ^2 E^2+8 \pi \rho \Big )^2+\,\Big (-1-8 \pi P_r-8 \pi ^2 E^2+8 \pi \rho \Big )\right. \nonumber \\&\left. \times \,\left[ \frac{\Big (8 \pi P_r+4 \pi ^2 r E^2\Big )^2}{\Big (1-8 m+16 \pi ^2 r E^2\Big )^2}\right. \right. \nonumber \\&\left. \left. -\,\frac{r \Big (8 \pi P_r+4 \pi ^2 r E^2\Big ) \Big (-4 \pi ^2 E^2+8 \pi \rho \Big )}{1-8 m+16 \pi ^2 r E^2}\right. \right. \nonumber \\&\left. \left. +\, \frac{4 \pi ^2 E^2+8 \pi P_r'+8 \pi ^2 r E E'}{1-8 m+16 \pi ^2 r E^2}\right. \right. \nonumber \\&\left. \left. -\,\frac{\Big (8 \pi P_r+4 \pi ^2 r E^2\Big ) \Big (16 \pi ^2 E^2-8 m'+ 32 \pi ^2 r E E'\Big )}{\Big (1-8 m+16 \pi ^2 r E^2\Big )^2}\right] \right. \nonumber \\&\left. +\, \left( \frac{\Big (8 \pi P_r+4 \pi ^2 r E^2\Big )^2}{\Big (1-8 m+16 \pi ^2 r E^2\Big )^2}\right. \right. \nonumber \\&\left. \left. -\,\frac{r \Big (8 \pi P_r+4 \pi ^2 r E^2\Big ) \Big (-4 \pi ^2 E^2+8 \pi \rho \Big )}{1-8 m+ 16 \pi ^2 r E^2}\right. \right. \nonumber \\&\left. \left. +\, \frac{4 \pi ^2 E^2+8 \pi P_r'+8 \pi ^2 r E E'}{1-8 m+16 \pi ^2 r E^2}\right. \right. \nonumber \\&\left. \left. -\, \frac{\Big (8 \pi P_r+4 \pi ^2 r E^2\Big ) \Big (16 \pi ^2 E^2-8 m'+32 \pi ^2 r E E'\Big )}{\Big (1-8 m+16 \pi ^2 r E^2\Big )^2}\right) ^2\right) .\nonumber \\ \end{aligned}$$
(20)

where \(E=\frac{q}{2\pi r}\) and \(\prime \) represents the derivative w.r.t. r.

Next, we apply LDP to perturb all the physical variables in Eq. (16); thus we can write [38]

$$\begin{aligned} \theta (\rho _{gc}+\delta \rho _{gc})= & {} \theta (\rho _{gc}) +\frac{\mathrm{d} \theta }{\mathrm{d}\rho _{gc}}\delta \rho _{gc}\nonumber \\= & {} \theta (\rho _{gc})+ \frac{\frac{\mathrm{d} \theta }{\mathrm{d}\xi }}{\frac{\mathrm{d} \rho _{gc}}{\mathrm{d}\xi }}\delta \rho _{gc},\end{aligned}$$
(21)
$$\begin{aligned} \frac{\mathrm{d} \theta }{\mathrm{d} \xi }(\rho _{gc}+ \delta \rho _{gc})= & {} \frac{\mathrm{d} \theta }{\mathrm{d} \xi }(\rho _{gc}) +\frac{\frac{d^2 \theta }{\mathrm{d} \xi ^2}}{\frac{ \mathrm{d} \rho _{gc}}{\mathrm{d}\xi }} \delta \rho _{gc},\end{aligned}$$
(22)
$$\begin{aligned} v(\rho _{gc}+\delta \rho _{gc})= & {} v(\rho _{gc})+ \frac{\frac{d v}{\mathrm{d} \xi }}{\frac{\mathrm{d} \rho _{gc}}{\mathrm{d}\xi }} \delta \rho _{gc}, \end{aligned}$$
(23)
$$\begin{aligned} P_{rc}(\rho _{gc}+\delta \rho _{gc})= & {} P_{rc}(\rho _{gc})+ \frac{\frac{d P_{rc}}{\mathrm{d} \xi }}{\frac{\mathrm{d} \rho _{gc}}{\mathrm{d}\xi }} \delta \rho _{gc},\end{aligned}$$
(24)
$$\begin{aligned} q(\rho _{gc}+\delta \rho _{gc})= & {} q(\rho _{gc})+ \frac{\frac{d q}{\mathrm{d} \xi }}{\frac{\mathrm{d} \rho _{gc}}{\mathrm{d}\xi }} \delta \rho _{gc},\end{aligned}$$
(25)
$$\begin{aligned} \frac{d q }{\mathrm{d} \xi }(\rho _{gc}+ \delta \rho _{gc})= & {} \frac{d q }{\mathrm{d} \xi }(\rho _{gc}) + \frac{\frac{d^2 q }{\mathrm{d} \xi ^2}}{ \frac{\mathrm{d} \rho _{gc}}{\mathrm{d}\xi }} \delta \rho _{gc}. \end{aligned}$$
(26)

The perturbed form of Eq. (16) yields

$$\begin{aligned} R_1=R_1 \left( \theta ,\frac{\mathrm{d} \theta }{\mathrm{d} \xi }, v, P_{rc}, q, \frac{d q }{\mathrm{d} \xi }, \rho _{gc}\right) +\delta R_1, \end{aligned}$$
(27)
Fig. 1
figure 1

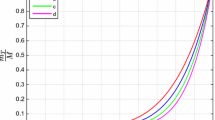
Case 1: Perturbation through LDP. \(\frac{\delta R_1}{\delta \rho _{gc}}\) as a function of \(\xi \) for \(n=1,~\alpha =8 \times 10^{-11},~\alpha _1=0.2\), Red curve  \(\rho _{gc}=10^{7}\), \(q=0.2\) \(M_\odot \), blue curve  \(\rho _{gc}=10^{7}\), \(q=0.4\) \(M_\odot \), green curve  \(\rho _{gc}=10^{11}\), \(q=0.2\) \(M_\odot \), magenta curve  \(\rho _{gc}=10^{11}\), \(q=0.4\) \(M_\odot \)

Full size image

where

$$\begin{aligned} \nonumber \delta R_1= & {} \left( \frac{\mathrm{d} \rho _{gc}}{\mathrm{d} \xi }\right) ^{-1} \left\{ \frac{\partial R_1}{\partial \rho _{gc}}\delta \rho _{gc} + \frac{\partial R_1}{\partial \theta } \frac{\mathrm{d}\theta }{\mathrm{d} \xi } + \frac{\partial R_1}{\partial \frac{\mathrm{d} \theta }{\mathrm{d} \xi }} \frac{\mathrm{d}^2\theta }{\mathrm{d} \xi ^2} \right. \\&\left. + \,\frac{\partial R_1}{\partial v}\frac{\mathrm{d} v}{\mathrm{d} \xi } +\, \frac{\partial R_1}{\partial P_{rc}}\frac{\mathrm{d} P_{rc}}{\mathrm{d} \xi } + \frac{\partial R_1}{\partial q} \frac{\mathrm{d} q}{\mathrm{d} \xi } + \frac{\partial R_1}{\partial \frac{d q }{\mathrm{d} \xi }} \frac{\mathrm{d}^2 q }{\mathrm{d} \xi ^2} \right\} \delta \rho _{gc}.\nonumber \\ \end{aligned}$$
(28)

We will plot the force distribution \(\frac{\delta R_1}{\delta \rho _{gc}}\) against the dimensionless radius \(\xi \) to observe the possible occurrence of cracking. Figures 1 and 2 represent the cracking of cylindrical polytropes of case 1 through LDP.

3.2 Case 2

Here, we consider the GPEoS [31, 32]

$$\begin{aligned} P_r=\alpha _1\rho +K\rho ^{1+\frac{1}{n}}, \end{aligned}$$
(29)

where the mass density \(\rho _o\) is replaced by total energy density \(\rho \) in Eq. (14) and they are related to each other as [31, 32]

$$\begin{aligned} \rho =\frac{\rho _o}{\big (1-K \rho _o^{\frac{1}{n}}\big )^n}. \end{aligned}$$
(30)

We make the following assumptions:

$$\begin{aligned}&\alpha =\frac{P_{rc}}{\rho _{c}},\quad r=\frac{\xi }{X},\quad \rho =\rho _{c}\theta ^n,\nonumber \\&m(r)=\frac{2\pi \rho _{c}v({\xi })}{X^2},\quad X^2=\frac{16\pi P_{rc}}{\alpha }. \end{aligned}$$
(31)
Fig. 2
figure 2

Cracking has been observed for \(10^{7}< \rho _{gc} < 10^{11}\)

Full size image

Following the same procedure as in case 1, we obtain

$$\begin{aligned} \nonumber R_2= & {} \left( \frac{1-v({\xi })+4\pi ^{3/2}\sqrt{\frac{\alpha }{ P_{rc}}}E^2 \xi }{1+\alpha _1+\alpha \theta }\right) \frac{\mathrm{d} \theta }{\mathrm{d} \xi }\\&+\, \left( \frac{2P_{rc}\alpha (\alpha _1+\alpha \theta )\theta ^n+\pi E^2}{n\alpha _1 \theta ^{-n}+(n+1)\alpha \theta }\right) \frac{\alpha \xi }{4P_{rc}}\nonumber \\&+\, \frac{\left( \Delta +\pi \xi E \frac{\mathrm{d} E}{\mathrm{d} \xi }+8 \pi E^2\right) \left( 1-v({\xi })+4\pi ^{3/2} \sqrt{\frac{\alpha }{ P_{rc}}}E^2 \xi \right) }{(1+\alpha _1+\alpha \theta ) (n\alpha _1 \theta ^{-n}+(n+1)\alpha \theta )}\nonumber \\&\times \frac{\theta ^n}{\alpha \xi P_{rc}}=0 \end{aligned}$$
(32)

and

$$\begin{aligned} \frac{\mathrm{d}v(\xi )}{\mathrm{d}\xi }=\xi \theta ^n+\frac{(4-\pi )\alpha \xi E}{2 P_{rc}}+\frac{\alpha \xi ^2}{P_{rc}}\frac{\mathrm{d} E}{\mathrm{d}\xi }. \end{aligned}$$
(33)

We will plot the force distribution \(\frac{\delta R_2}{\delta \rho _{gc}}\) against the dimensionless radius \(\xi \) to observe possible occurrence of cracking. Figures 3 and 4 represents the cracking of relativistic cylindrical anisotropic polytropes for case 2 against LDP.

4 Effect of parametric perturbation on cracking

In this section, we will study the stability of charged cylindrical polytropes by perturbing the polytropic index, charge and anisotropy factor. For this purpose, we assume that our distribution satisfies the following relation:

$$\begin{aligned} \Delta =D(\rho +P_r) r^n f(P_r, r,q), \end{aligned}$$
(34)

where D is a parameter which measures the anisotropy, the function f and n needed to be specified for developing any specific model. Using the above equation in Eq. (12), we obtain

$$\begin{aligned}&\frac{\mathrm{d} P_r}{\mathrm{d}r}+\frac{8\pi r P_r+q^2}{r-8mr+4 q^2} \big (\rho +P_r\big )\nonumber \\&\quad +\,D(\rho +P_r) f(P_r, r,q) r^{n-1}+\frac{q q^\prime r - q^2}{4\pi ^2 r^3} +\frac{2 q^2}{\pi r^3}=0.\nonumber \\ \end{aligned}$$
(35)

Further, we assume that

$$\begin{aligned} f(P_r, r,q)r^{n-1}=\frac{A^\prime }{A}, \end{aligned}$$
(36)

the sole purpose of this assumption is to simplify the calculations. Consequently, Eq. (35) reads

$$\begin{aligned}&\frac{\mathrm{d} P_r}{\mathrm{d}r}+h \left( \frac{8\pi r P_r+q^2}{r-8mr+4 q^2}\right) \big (\rho +P_r\big ) \nonumber \\&\quad +\,\frac{q q^\prime r - q^2}{4\pi ^2 r^3} +\frac{2 q^2}{\pi r^3}=0, \end{aligned}$$
(37)

with \(h=1+D\). Now we shall briefly review the main results for each case.

Fig. 3
figure 3

Case 2: Perturbation through LDP. \(\frac{\delta R_2}{\delta \rho _{gc}}\) as a function of \(\xi \) for \(n=1,~\alpha =8 \times 10^{-11},~\alpha _1=0.2\), red curve  \(\rho _{gc}=10^{6.6}\), \(q=0.4\) \(M_\odot \), blue curve  \(\rho _{gc}=10^{6.6}\), \(q=0.64\) \(M_\odot \), green curve  \(\rho _{gc}=10^{11.8}\), \(q=0.4\) \(M_\odot \), magenta curve  \(\rho _{gc}=10^{11.8}\), \(q=0.64\) \(M_\odot \)

Full size image

4.1 Case 1

Let the perturbation be carried out through polytropic model parameters,

$$\begin{aligned}&n\longrightarrow \tilde{n}+\delta n, \quad q\longrightarrow \tilde{q}+\delta q, \quad h\longrightarrow \tilde{h}+\delta h, \end{aligned}$$
(38)

assuming that the radial pressure remains the same after perturbation, then from Eq. (13) we can write

$$\begin{aligned} \tilde{P_r}=P_r=\alpha _1 \rho _{gc}\theta ^n + K \rho _{gc}^{1+\frac{1}{n}}\theta ^{1+n}. \end{aligned}$$
(39)

Thus, Eq. (14) becomes

$$\begin{aligned} \tilde{\rho }=\rho _{gc}\theta ^{1+\tilde{n}}+\tilde{n}P_r. \end{aligned}$$
(40)

The perturbed form of Eq. (37) is

$$\begin{aligned} \tilde{R_3}= & {} \frac{\mathrm{d} P_r}{\mathrm{d}r}+\tilde{h} \left( \frac{8\pi r P_r+\tilde{q}^2}{r-8\tilde{m}r+4 \tilde{q}^2}\right) \big (\tilde{\rho } +P_r\big ) \nonumber \\&+\,\frac{\tilde{q} \tilde{q}^\prime r - \tilde{q}^2}{4\pi ^2 r^3} +\frac{2 \tilde{q}^2}{\pi r^3}=0. \end{aligned}$$
(41)

Substituting Eqs. (15), (39) and (40) in the above equation, we get

$$\begin{aligned} \nonumber \tilde{R_3}= & {} (n \alpha _1 \theta ^{n-1}+(n+1) \alpha \theta ^{n})\frac{\mathrm{d} \theta }{\mathrm{d} \xi }+ \frac{4 \tilde{q}}{\pi \xi ^2} \frac{\mathrm{d} \tilde{q}}{\mathrm{d} \xi }\nonumber \\&-\,\frac{4 (\tilde{q})^2}{\pi \xi ^3} +32\frac{\tilde{q^2} }{\xi ^3}+ \tilde{h} (\theta ^{\tilde{n}}\nonumber \\&+(2\tilde{n}+1) (\alpha _1 \theta ^{n}+\alpha \theta ^{n+1}))\nonumber \\&\times \left( \frac{2\sqrt{\frac{\pi P_{rc}}{\alpha }} (\alpha _1 \theta ^{n}+\alpha \theta ^{n+1})+ \frac{(\tilde{q})^2}{\xi }}{1-\tilde{v} +16 \sqrt{\frac{\pi P_{rc}}{\alpha }} \frac{(\tilde{q})^2}{\xi }}\right) , \end{aligned}$$
(42)

which yield up to first order

$$\begin{aligned} \delta \tilde{R_3}=\tilde{R_3}\Big (\xi ,1+\delta n, h+\delta h, v+\delta v, q +\delta q\Big ), \end{aligned}$$
(43)

where

$$\begin{aligned} \nonumber \delta {R_3}= & {} \left( \frac{\partial {\tilde{R_3}}}{\partial \tilde{n}}\right) \mathrel {\mathop {\Big |_{\tilde{n}=n,~\tilde{v}=v}}_ {\tilde{\mathrm{h}}=\mathrm{h},~\tilde{\mathrm{q}}=\mathrm{q}}} \delta n + \left( \frac{\partial {\tilde{R_3}}}{\partial \tilde{v}}\right) \mathrel {\mathop {\Big |_{\tilde{n}=n,~\tilde{v}=v}}_ {\tilde{\mathrm{h}}=\mathrm{h},~\tilde{\mathrm{q}}=\mathrm{q}}} \delta v\\&+\, \left( \frac{\partial {\tilde{R_3}}}{\partial \tilde{h}}\right) \mathrel {\mathop {\Big |_{\tilde{n}=n,~\tilde{v}=v}}_{\tilde{\mathrm{h}}=\mathrm{h}, ~\tilde{\mathrm{q}}=\mathrm{q}}} \delta h+ \left( \frac{\partial {\tilde{R_3}}}{\partial \tilde{q}}\right) \mathrel {\mathop {\Big |_{\tilde{n}=n,~\tilde{v}=v}}_ {\tilde{\mathrm{h}}=\mathrm{h},~\tilde{\mathrm{q}}=\mathrm{q}}} \delta q.\nonumber \\ \end{aligned}$$
(44)

Now, we calculate all the derivatives involved in the above equation as

$$\begin{aligned}&\frac{\partial \tilde{R_3}}{\partial \tilde{n}}\nonumber \\&\quad =\frac{h (\theta ^n \text {log}[\theta ]+2 (\alpha \theta ^{1+n}+\theta ^n \alpha _1)) \left( \frac{q^2}{\xi } + \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi }},\nonumber \\ \end{aligned}$$
(45)
$$\begin{aligned}&\frac{\partial \tilde{R_3}}{\partial \tilde{v}}\nonumber \\&\quad =\frac{h (\theta ^n+(1+2 n) (\alpha \theta ^{1+n}+\theta ^n \alpha _1)) \left( \frac{q^2}{\xi } +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{\left( 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} \frac{q^2}{\xi }\right) ^2},\nonumber \\ \end{aligned}$$
(46)
$$\begin{aligned}&\frac{\partial \tilde{R_3}}{\partial \tilde{h}}\nonumber \\&\quad =\frac{(\theta ^n+(1+2 n)(\alpha \theta ^{1+n}+\theta ^n \alpha _1)) \left( \frac{q^2}{\xi } +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}(\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi } },\nonumber \\ \end{aligned}$$
(47)
$$\begin{aligned} \nonumber \frac{\partial \tilde{R_3}}{\partial \tilde{q}}= & {} \frac{2 h q (\theta ^n+(1+2n)(\alpha \theta ^{1+n} +\theta ^{n}\alpha _1))}{\xi \left( 1-v+16 \sqrt{ \frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{xi}\right) }\nonumber \\&-\,\frac{8 q}{\pi \xi ^3}+\frac{4\frac{\mathrm{d} q}{\mathrm{d} \xi }}{\pi \xi ^2}+\frac{4 q \frac{\mathrm{d}^2 q}{\mathrm{d} \xi ^2}}{\pi \xi ^2} +\frac{64 q}{\xi ^3} \nonumber \\&-\left( 32 h q \sqrt{\frac{\pi P_{rc}}{\alpha }} (\theta ^n +(1+2n)(\alpha \theta ^{n+1}+\theta ^n \alpha _1)\right) \nonumber \\&\times \,\left( \frac{q^2}{\xi } +2 \sqrt{\frac{\pi P_{rc}}{\alpha } } (\alpha \theta ^{n+1}+\theta ^{n} \alpha )\right) \nonumber \\&\times \left( \xi \left( {1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi } }\right) ^2\right) ^{-1}. \end{aligned}$$
(48)

Also, from Eq. (17), we have

$$\begin{aligned} \tilde{v}= & {} \int _0^{\xi } \left[ \phantom {\left. +\,(2-\pi )\sqrt{\frac{\alpha }{\pi P_{rc}}}q +2\bar{\xi }\sqrt{\frac{\alpha }{\pi P_{rc}}} \frac{\mathrm{d} q}{\mathrm{d} \xi }\right] }\bar{\xi } \big \{\theta ^{\tilde{n}}+\tilde{n} (\alpha _1\theta ^{n}+\alpha \theta ^{n+1})\big \}\right. \nonumber \\&\left. +\,(2-\pi )\sqrt{\frac{\alpha }{\pi P_{rc}}}q +2\bar{\xi }\sqrt{\frac{\alpha }{\pi P_{rc}}} \frac{\mathrm{d} q}{\mathrm{d} \xi }\right] \mathrm{d} \bar{\xi } \end{aligned}$$
(49)

and

$$\begin{aligned} \delta v=F_1 \delta n,\quad \delta q=\frac{F_1}{F_2}\delta n\quad \delta h=-\Gamma \delta n, \end{aligned}$$
(50)

where

$$\begin{aligned}&F_1=\int _0^{\xi } \bar{\xi }\big \{\theta ^{\tilde{n}}log \theta + (\alpha _1\theta ^{n}+\alpha \theta ^{n+1})\big \} \mathrm{d} \bar{\xi }, \end{aligned}$$
(51)
$$\begin{aligned}&F_2 = \int _0^{\xi } \sqrt{\frac{\alpha }{\pi P_{rc}}} \left[ (2-\pi )+\frac{2\bar{\xi }}{\frac{\mathrm{d} q}{\mathrm{d} \bar{\xi }}}\frac{\mathrm{d}^2 q}{\mathrm{d} \bar{\xi }^2}\right] \mathrm{d} \bar{\xi } \end{aligned}$$
(52)

and

$$\begin{aligned} \Gamma =\left( \frac{F_1\frac{\partial {\tilde{R}}}{\partial \tilde{v}} +F_2\frac{\partial {\tilde{R}}}{\partial {\tilde{q}}} +\frac{\partial {\tilde{R}}}{\partial \tilde{n}} }{\frac{\partial {\tilde{R}}}{\partial \tilde{h}}}\right) \mathrel {\mathop {\Big |_{\tilde{n}=n,~\tilde{v}=v}} _{\tilde{\mathrm{h}}=\mathrm{h},~\tilde{\mathrm{q}}=\mathrm{q}}}. \end{aligned}$$
(53)
Fig. 4
figure 4

Cracking has been observed for \(10^{6.6}< \rho _{gc} < 10^{11.8}\)

Full size image

Consequently, Eq. (44) becomes

$$\begin{aligned} \nonumber \delta R_3= & {} \delta n \left[ \frac{h (\theta ^n \text {log}[\theta ]+2 (\alpha \theta ^{1+n}+\theta ^n \alpha _1)) \left( \frac{q^2}{\xi } + \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{ 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi } } \right. \nonumber \\&\left. +\,\frac{h F_1 (\theta ^n+(1+2 n) (\alpha \theta ^{1+n}+\theta ^n \alpha _1)) \left( \frac{q^2}{\xi } +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{\left( 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi } \right) ^2} \right. \nonumber \\&\left. -\,\Gamma \left( \frac{(\theta ^n+(1+2 n)(\alpha \theta ^{1+n}+\theta ^n \alpha _1)) \left( \frac{q^2}{\xi } +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}(\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi } } \right) \right. \nonumber \\&\left. +\,\frac{F_1}{F_2}\left( \frac{2 h q (\theta ^n+(1+2n) (\alpha \theta ^{1+n} +\theta ^{n}\alpha _1))}{\xi \left( 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} \frac{q^2}{\xi }\right) }-\frac{8 q}{\pi \xi ^3}+\frac{4 \frac{\mathrm{d} q}{\mathrm{d} \xi }}{\pi \xi ^2}+\frac{4 q \frac{\mathrm{d}^2 q}{\mathrm{d} \xi ^2}}{\pi \xi ^2} \right. \right. \nonumber \\&\left. \left. +\,\frac{64 q}{\xi ^3} -\left( 32 h q \sqrt{\frac{\pi P_{rc}}{\alpha }} (\theta ^n +(1+2n)(\alpha \theta ^{n+1}+\theta ^n \alpha _1) ) \right. \right. \right. \nonumber \\&\times \,\left. \phantom {\left[ \frac{h (\theta ^n \text {log}[\theta ]+2 (\alpha \theta ^{1+n}+\theta ^n \alpha _1)) \left( \frac{q^2}{\xi } + \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{ 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi } } \right. }\left. \phantom {\left. +\frac{F_1}{F_2}\left( \frac{2 h q (\theta ^n+(1+2n) (\alpha \theta ^{1+n} +\theta ^{n}\alpha _1))}{\xi \left( 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} \frac{q^2}{\xi }\right) }-\frac{8 q}{\pi \xi ^3}+\frac{4 \frac{\mathrm{d} q}{\mathrm{d} \xi }}{\pi \xi ^2}+\frac{4 q \frac{\mathrm{d}^2 q}{\mathrm{d} \xi ^2}}{\pi \xi ^2} \right. \right. }\left. \left( \frac{q^2}{\xi }+2 \sqrt{\frac{\pi P_{rc}}{\alpha } } (\alpha \theta ^{n+1}+\theta ^{n} \alpha )\right) \right) \times \, \left( \xi \left( {1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi } }\right) ^2\right) ^{-1} \right) \right] . \end{aligned}$$
(54)

It would be more convenient to use the variable x defined by

$$\begin{aligned} \xi = \bar{A}x,\quad \bar{A}=A r_\Sigma =\xi _\Sigma . \end{aligned}$$
(55)

Thus Eq. (54) reads

$$\begin{aligned} \nonumber \delta R_3= & {} \delta n \left[ \frac{h (\theta ^n \text {log}[\theta ]+2 (\alpha \theta ^{1+n}+\theta ^n \alpha _1))\left( \frac{q^2}{x \bar{A}} + \sqrt{\frac{ \pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{x \bar{A}} }\right. \nonumber \\&\,\left. +\frac{h F_1 (\theta ^n+(1+2 n) (\alpha \theta ^{1+n}+\theta ^n \alpha _1)) \left( \frac{q^2}{x \bar{A}} +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{\left( 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{x \bar{A}}\right) ^2}\right. \nonumber \\&\,\left. -\Gamma \left( \frac{(\theta ^n+(1+2 n)(\alpha \theta ^{1+n}+\theta ^n \alpha _1)) \left( \frac{q^2}{x \bar{A}} +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}(\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} \frac{q^2}{x \bar{A}} } \right) \right. \nonumber \\&\,\left. + \frac{F_1}{F_2}\left( \frac{2 h q (\theta ^n+(1+2n) (\alpha \theta ^{1+n} +\theta ^{n}\alpha _1))}{x \bar{A} \left( 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} \frac{q^2}{x \bar{A}}\right) }-\frac{8 q}{\pi (x \bar{A})^3} +\frac{4\frac{\mathrm{d} q}{\mathrm{d} x }}{\pi x^2 \bar{A}^3}+ \frac{4 q \frac{\mathrm{d}^2 q}{\mathrm{d} x^2}}{\pi x^2 \bar{A}^4}\right. \right. \nonumber \\&\,\left. \left. +\frac{64 q}{(x \bar{A})^3} -\left( 32 h q \sqrt{\frac{\pi P_{rc}}{\alpha }} (\theta ^n +(1+2n)(\alpha \theta ^{n+1}+\theta ^n \alpha _1) ) \right. \right. \right. \nonumber \\&\, \left. \phantom {\left[ \frac{h (\theta ^n \text {log}[\theta ]+2 (\alpha \theta ^{1+n}+\theta ^n \alpha _1))\left( \frac{q^2}{x \bar{A}} + \sqrt{\frac{ \pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{x \bar{A}} }\right. }\left. \phantom {\left. + \frac{F_1}{F_2}\left( \frac{2 h q (\theta ^n+(1+2n) (\alpha \theta ^{1+n} +\theta ^{n}\alpha _1))}{x \bar{A} \left( 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} \frac{q^2}{x \bar{A}}\right) }-\frac{8 q}{\pi (x \bar{A})^3} +\frac{4\frac{\mathrm{d} q}{\mathrm{d} x }}{\pi x^2 \bar{A}^3}+ \frac{4 q \frac{\mathrm{d}^2 q}{\mathrm{d} x^2}}{\pi x^2 \bar{A}^4}\right. \right. }\left. \left( \frac{q^2}{x \bar{A}} +2 \sqrt{\frac{\pi P_{rc}}{\alpha } } (\alpha \theta ^{n+1} +\theta ^{n} \alpha )\right) \right) \left( x \bar{A} \left( {1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{x \bar{A}} }\right) ^2\right) ^{-1} \right) \right] . \end{aligned}$$
(56)

We will use the above equation to plot the force distribution function \(\frac{\delta R_3}{\delta n}\) against x to observe cracking (overturning) of polytropes. Figures 5,6 and 7 represent the cracking of relativistic anisotropic cylindrical polytropes corresponding to case 1.

Fig. 5
figure 5

Case 1: Perturbation through n, h, q. \(\frac{\delta R_3}{\delta n}\) as a function of x for \(n=1,~\alpha =0.2 ,~\alpha _1=0.8,~h=0.5\), red curve  \(q=0.2 \; M_\odot \), blue curve  \(q=0.4\; M_\odot \), green curve  \(q=0.6\; M_\odot \), magenta curve  \(q=0.64\; M_\odot \)

Full size image
Fig. 6
figure 6

Case 1: Perturbation through n, h, q. \(\frac{\delta R_3}{\delta n}\) as a function of x for \(n=1,~\alpha =0.4,~\alpha _1=0.9,~h=0.5\), red curve  \(q=0.2\) \(M_\odot \), blue curve  \(q=0.4\) \(M_\odot \), green curve  \(q=0.6\) \(M_\odot \), magenta curve  \(q=0.64\) \(M_\odot \)

Full size image

4.2 Case 2

Now, we apply parametric perturbations to the polytropes of the second kind and in this case Eq. (41) transforms as

$$\begin{aligned} \nonumber \tilde{R_4}= & {} (n \alpha _1 \theta ^{n-1}+(n+1) \alpha \theta ^{n})\frac{\mathrm{d} \theta }{\mathrm{d} \xi }+ \frac{4 \tilde{q}}{\pi \xi ^2} \frac{\mathrm{d} \tilde{q}}{\mathrm{d} \xi }\\&-\,\frac{4 (\tilde{q})^2}{\pi \xi ^3} +32\frac{\tilde{q^2} }{\xi ^3}+ \tilde{h}(\theta ^{\tilde{n}}\nonumber \\&\,+ (\alpha _1 \theta ^{n}+\alpha \theta ^{n+1}))\left( \frac{2\sqrt{\frac{\pi P_{rc}}{\alpha }} (\alpha _1 \theta ^{n}+\alpha \theta ^{n+1})+\frac{(\tilde{q})^2}{\xi }}{1-\tilde{v} +16 \sqrt{\frac{\pi P_{rc}}{\alpha }} \frac{(\tilde{q})^2}{\xi }}\right) .\nonumber \\ \end{aligned}$$
(57)
Fig. 7
figure 7

Case 1: Perturbation through n, h, q. \(\frac{\delta R_3}{\delta n}\) as a function of x for \(n=1,~\alpha =2 \times 10 ^{-10},~\alpha _1=0.2,~h=0.5\), red curve  \(q=100\), blue curve  \(q=5000,\) green curve  \(q=0.4\) \(M_\odot \), magenta curve  \(q=0.64\) \(M_\odot \)

Full size image

Repeating here a similar procedure to case 1, we obtain

$$\begin{aligned} \nonumber \delta R_4= & {} \delta n \left[ \frac{h \theta ^n \text {log}[\theta ]\left( \frac{q^2}{\xi } +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{ 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi } }\right. \nonumber \\&\,\left. +\frac{h F_3 (\theta ^n+ \alpha \theta ^{1+n}+\theta ^n \alpha _1) \left( \frac{q^2}{\xi } +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+ \theta ^n \alpha _1)\right) }{\left( 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi } \right) ^2}\right. \nonumber \\&\,\left. -\Gamma \left( \frac{(\theta ^n+\alpha \theta ^{1+n}+\theta ^n \alpha _1) \left( \frac{q^2}{\xi } +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}(\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} \frac{q^2}{\xi } } \right) \right. \nonumber \\&\,\left. + \frac{F_3}{F_2}\left( \frac{2 h q (\theta ^n+\alpha \theta ^{1+n} + \theta ^{n}\alpha _1)}{\xi \left( 1-v+16 \sqrt{\frac{ \pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi }\right) } -\frac{8 q}{\pi \xi ^3}+\frac{4\frac{\mathrm{d} q}{\mathrm{d} \xi }}{\pi \xi ^2}+\frac{4 q \frac{\mathrm{d}^2 q}{\mathrm{d} \xi ^2}}{\pi \xi ^2}\right. \right. \nonumber \\&\,\left. \left. +\frac{64 q}{\xi ^3} -\left( 32 h q \sqrt{\frac{\pi P_{rc}}{\alpha }} (\theta ^n +\alpha \theta ^{n+1}+\theta ^n \alpha _1 )\right. \right. \right. \nonumber \\&\times \,\left. \left( \frac{q^2}{\xi } +2 \sqrt{\frac{\pi P_{rc}}{\alpha } }(\alpha \theta ^{n+1}+\theta ^{n} \alpha )\right) \right) \nonumber \\&\,\left. \phantom {\left[ \frac{h \theta ^n \text {log}[\theta ]\left( \frac{q^2}{\xi } +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{ 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi } }\right. }\left. \phantom {\left. + \frac{F_3}{F_2}\left( \frac{2 h q (\theta ^n+\alpha \theta ^{1+n} + \theta ^{n}\alpha _1)}{\xi \left( 1-v+16 \sqrt{\frac{ \pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi }\right) } -\frac{8 q}{\pi \xi ^3}+\frac{4\frac{\mathrm{d} q}{\mathrm{d} \xi }}{\pi \xi ^2}+\frac{4 q \frac{\mathrm{d}^2 q}{\mathrm{d} \xi ^2}}{\pi \xi ^2}\right. \right. }\times \left( \xi \left( {1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{\xi } }\right) ^2\right) ^{-1} \right) \right] , \end{aligned}$$
(58)

where

$$\begin{aligned} F_3=\int _0^{\xi } \bar{\xi } \theta ^{\tilde{n}} \mathrm{log}\,\theta \, \mathrm{d} \bar{\xi }. \end{aligned}$$

Thus the above equation can be written as

$$\begin{aligned} \nonumber \delta R_4= & {} \delta n \left[ \frac{h \theta ^n \text {log}[\theta ]\left( \frac{q^2}{x\bar{A}} +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} \frac{q^2}{x \bar{A}} } \right. \nonumber \\&\left. +\, \frac{h F_3 (\theta ^n+ \alpha \theta ^{1+n} +\theta ^n \alpha _1) \left( \frac{q^2}{x\bar{A}} +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{\left( 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{x\bar{A}} \right) ^2}\right. \nonumber \\&\left. -\, \Gamma \,\left( \frac{(\theta ^n+\alpha \theta ^{1+n}+\theta ^n \alpha _1) \left( \frac{q^2}{x\bar{A}} +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}(\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} \frac{q^2}{x \bar{A}} } \right) \right. \nonumber \\&\left. +\, \frac{F_3}{F_2}\left( \phantom {\left. \left. \left. (\alpha \theta ^{n+1}+\theta ^{n} \alpha ))\right) \times \left( x\bar{A} \left( {1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{x \bar{A}} }\right) ^2 \right) ^{-1} \right) \right] } \frac{2 h q (\theta ^n+\alpha \theta ^{1+n} +\theta ^{n}\alpha _1)}{x\bar{A} \left( 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{x \bar{A}}\right) }-\frac{8 q}{\pi (x \bar{A})^3}\right. \right. \nonumber \\&+\, \frac{4\frac{\mathrm{d} q}{\mathrm{d} x}}{\pi x^2 \bar{A}^3} +\frac{4 q \frac{\mathrm{d}^2 q}{\mathrm{d} x^2}}{\pi x^2 \bar{A}^4}+\frac{64 q}{(x \bar{A})^3} \nonumber \\&\left. \left. -\,\left( 32 h q \sqrt{\frac{\pi P_{rc}}{\alpha }} (\theta ^n +\alpha \theta ^{n+1}+\theta ^n \alpha _1 )\right. \right. \right. \nonumber \\&\times \,\left. \left( \frac{q^2}{x\bar{A}} +2 \sqrt{\frac{\pi P_{rc}}{\alpha } }(\alpha \theta ^{n+1}+\theta ^{n} \alpha )\right) \right) \nonumber \\&\left. \phantom {\left[ \frac{h \theta ^n \text {log}[\theta ]\left( \frac{q^2}{x\bar{A}} +2 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} (\alpha \theta ^{1+n}+\theta ^n \alpha _1)\right) }{1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }} \frac{q^2}{x \bar{A}} } \right. }\left. \phantom {\left( \phantom {\left. \left. \left. (\alpha \theta ^{n+1}+\theta ^{n} \alpha ))\right) \times \, \left( x\bar{A} \left( {1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{x \bar{A}} }\right) ^2 \right) ^{-1} \right) \right] } \frac{2 h q (\theta ^n+\alpha \theta ^{1+n} +\theta ^{n}\alpha _1)}{x\bar{A} \left( 1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{x \bar{A}}\right) }-\frac{8 q}{\pi (x \bar{A})^3}+ \frac{4\frac{\mathrm{d} q}{\mathrm{d} x}}{\pi x^2 \bar{A}^3} +\frac{4 q \frac{\mathrm{d}^2 q}{\mathrm{d} x^2}}{\pi x^2 \bar{A}^4}+\frac{64 q}{(x \bar{A})^3} \right. }\times \left( x\bar{A} \left( {1-v+16 \sqrt{\frac{\pi P_{\text {rc}}}{\alpha }}\frac{q^2}{x \bar{A}} }\right) ^2 \right) ^{-1} \right) \right] . \end{aligned}$$
(59)

We will use the above equation to plot the force distribution function \(\frac{\delta R_4}{\delta n}\) against x to observe cracking (overturning) of polytropes. Figures 8 and 9 represent the cracking for case 2.

Fig. 8
figure 8

Case 2: Perturbation through n, h, q. \(\frac{\delta R_4}{\delta n}\) as a function of x for \(n=1,~\alpha =2 \times 10 ^{-10},~\alpha _1=0.4,~h=0.5\), red curve  \(q=0.2\) \(M_\odot \), blue curve  \(q=0.4\) \(M_\odot \), green curve  \(q=0.6\) \(M_\odot \), magenta curve  \(q=0.64\) \(M_\odot \)

Full size image
Fig. 9
figure 9

Case 2: Perturbation through n, h, q. \(\frac{\delta R_4}{\delta n}\) as a function of x for \(n=1,~\alpha =0.2,~\alpha _1=0.4,~h=0.5\), red curve  \(q=0.2\) \(M_\odot \), blue curve  \(q=0.4\) \(M_\odot \), green curve  \(q=0.6\) \(M_\odot \), magenta curve  \(q=0.64\) \(M_\odot \)

Full size image

4.3 Conclusion and discussion

We studied the appearance of cracking in charged anisotropic cylindrical polytropes through the LDP technique and by perturbing the parameters involved in the model. In the scenario of LDP, we perturb all the physical parameters of HEe and plot these results corresponding to a different choice of the mass density. We summarize the results of cases 1 and 2 as follows.

Figures 1 and 2 described the main consequences of LDP analysis carried out for polytropes of the first kind under the conformal flatness condition. Figure 1 depicts that the system remains stable (no overturning) for values of central density \(10^{7}\le \rho _{gc}\) and \(\rho _{gc}\ge 10^{11}\) for various values of parameters. It is noted that the system remains stable even for very large hypothetical values of charge, while there exists overturning as the value of the central density lies between \(10^{7}<\rho _{gc}<10^{11}\) even for a very small amount of charge as shown in Fig. 2. Thus, it is found that the gradually increasing amount of charge will stabilize the system and radial forces balance each other. Hence, under LDP it is concluded that cracking appears for a low amount of charge, whereas the system gets stabilized for sufficiently high values of the charge. A similar analysis has been performed for polytropes of the second kind under the conformal flatness condition, and Figs. 3 and 4 show that the system remains stable for \(10^{6.6}\le \rho _{gc}\) and \(\rho _{gc}\ge 10^{11.8}\), and cracking appears for \(10^{6.6}<\rho _{gc}<10^{11.8}\) with various values of parameters.

We also discuss the cracking of polytropes by perturbing parameters like n,  h,  and q. We have plotted Eqs. (56) and (59), corresponding to different values of the charges. The results are shown in Figs. 5, 6, 7, 8 and 9 corresponding to \(\frac{\delta R_3}{\delta n}\) (Figs. 5, 6, 7) and \(\frac{\delta R_4}{\delta n}\) (Figs. 8, 9) against the radius of the star for polytropes of type I and II, respectively. For polytropes of the first kind, we observe overturning near the center and cracking appears corresponding to a large value of \(\alpha \) and different model parameters as shown in Fig. 5. Figure 6 represents overturning for anisotropic charged cylindrical polytropes for an increasing value of \(\alpha \), and cracking shifts towards the boundary. On the other hand, for small values of \(\alpha \), we have a stable configuration as shown in Fig. 7. Thus, we conclude that cracking (overturning) does not appear for small values of \(\alpha \) even for very high or low values of the charge parameters.

Figures 8 and 9 describe the results for polytropes of the second kind. We have found strong cracking near the center and middle of the star and overturning as we move towards the boundary for a small value of \(\alpha \) and different values of the parameters (Fig. 8). But for a large value of \(\alpha \), there exists overturning near the center and then strong cracking as shown in Fig. 9. It is worthwhile to mentioned here that there is no stable configuration for polytropes of the second kind either for small or large values of \(\alpha \) and charge.

From the above discussion, we conclude that charged polytropes of both kinds developed under GPEoS show stable behavior, when LDP is applied to a certain range of the density. However, when a parametric perturbation is applied to both kind of polytropes, we get a stable as well as an overturning configuration for the first kind of polytropes while there exists cracking for cylindrical polytropes of the second kind. Hence, polytropes of the first kind can be preferred for any mathematical modeling or any future development when cylindrical symmetry is taken into account.