1 Introduction

Polytropic equation of state (PEoS) has great significance in the study of stellar structure and played a unique roll in astrophysics. Many researchers and mathematicians have applied PEoS in the context of general relativity to investigate different astronomical objects. Lane [1] studied some basic outcomes which were incorporated to the modeling of stellar structure by using polytropes. Chandrasekhar [2] obtained the density and mass limit of white dwarf by using the idea of thermodynamics in Newtonian polytropes. In the context of general relativity, Tooper [3, 4] used Lane–Emden equation (LEe) to study the different models of very large radiating star and with the help of PEoS he discussed compressible fluid sphere through the solution of field equation. Managhan and Roxburgh [5] used approximation technique for matching two solutions at interface to investigate the structure of turning polytropes. Occhionero [6] studied the second order approximation for internal core of polytropic structures was more suitable than first order approximation with appropriate parameters for polytropic index \(n\geqslant 2\). Horedt [7, 8] investigated the unstable distorted sphere with polytropic index \(n>3\) and analyzed the finiteness of mass and radius for one dimension (Slabe), for two dimension (Cylinder) and for three dimension (Sphere) with the help of gamma function. By using the method defined in [5], Singh and Singh [9] developed some models for the structure of turning, tidally and distorted relativistic polytropes. For static spherically symmetric structure, Pandey et al. [10] used relativistic PEoS to study the all possible variations of various parameters. Hendry [11] showed that certain region of sun’s interior exhibited the polytropic power-law and developed some polytropic models which were easily computable. Herrera and Barreto [12] presented a method to evaluate the relativistic polytropes for the static dissipative fluid sphere. They [13] also laid out general structure to model some static spherical relativistic stars by using PEoS and brought out Tolman mass to explain some features of these models. The PEoS was used [14, 15] to discuss the spherical static fluid in case of mass and energy density under conformally flat condition and cracking technique. Some physical models and numerical results were also discussed about spherical compact stars.

Astronomical objects can be studied more deeply by using the generalized polytropic equation of state (GPEoS) which is defined as,

$$\begin{aligned} P_{r}=\alpha _{1}\mu _{o} + K\mu ^{\gamma }_{o}=\alpha _{1}\mu _{o}+K\mu _{o}^{1+\frac{1}{n}}, \end{aligned}$$
(1)

where \(\alpha _{1}\), \(P_{r}\), \( \gamma \), n and K are constant of proportionality, radial pressure, polytropic exponent, polytropic index and polytropic constant respectively. First and second terms in R.H.S. of Eq. (1) discuss dark energy and dark matter of universe respectively.

If \(\mu _{o}\) is changed by \(\mu \) then Eq. (1) takes the form

$$\begin{aligned} P_{r}=\alpha _{1}\mu + K\mu ^{1+\frac{1}{n}}. \end{aligned}$$
(2)

With the help of GPEoS, Azam et al. [16, 17] discussed the effect of charge on generalized polytropes (GPs) by taking into account the spherical and cylindrical inner fluid distribution. Mardan et al. [18, 19] carried out spherical symmetry to study the gravitational effects of massive compact objects (COs) through the GPs. They also used GPEoS to analyze some mathematical models of COs with radiation factor for different values of polytropic index n and found that these models were physically feasible and well behaved. By using GPEoS and spherical symmetry, Mardan et al. [20, 21] developed new classes of mathematical models and investigated the radius-mass of compact stars.

Electric charge plays an important role in the stability of stars under the strong gravitational field. Bonnor [22] used general relativity to investigate the electromagnetic effect on the static spherically symmetric mass distribution. He estimated the input of electric energy to the gravitation mass with the help of certain models. Bondi [23] gave a rigorous and useful method in Minkowski coordinates to examine the contraction of radiating CO under a relation of density and pressure for high gravitational potential. Wilson [24] computed the self-energy contribution to the total gravitational mass by obtaining the exact solution of field equation for charged spherically static fluid distribution. In [25] Bekenstein made a formalism to split the mass of charged black hole into two parts, irreducible part and charged reducible part in spherical symmetry. Takisa and Maharaj [26] used charged spherical anisotropic fluid distribution to find the exact solution of Einstein-Maxwell field equations. They also discussed some graphical results of different quantities with help of polytropic equation of state (PEoS).

Karmarkar [27] embedded n dimension Riemannian space in to higher dimension \(n+p\), called class p dimension. When \(n=4\) and \(p=1\), this is called class I Karmarkar condition. Maurya et al. [28] used Karmarkar condition for static spherically symmetric metric with charge to study some stellar models. Singh and Pant [29, 30] obtained some exact solution for anisotropic fluid distribution using Karmarkar class I condition and discussed some well behaved models for different neutron stars. Ramos et al. [31] developed class I interior solution using PEoS for spherically symmetric interior space time. They obtained a compatible LEs with Karmarkar condition under isothermal and non isothermal regimes.

Herrera [32] gave a new idea for the complexity factor (CF) by taking into consideration the orthogonal splitting of curvature tensor into scalars, called structure scalars for a spherical symmetric object. Abbas and Nazar [33] brought about this idea of CF in the context of f(R) theory for anisotropic self gravitating fluid distribution. They observed the effects of f(R) term on CF and also obtained exact solution of modify field equation. Sharif and Butt [34, 35] studied the static cylindrical system with CF in general relativity and also discussed the impacts of charge on this system. Khan et al. [36, 37] applied the idea of CF with GPEoS by using spherical anisotropic fluid distribution to develop two system of DEs and analyzed the GPs and charged GPs. They [38] also studied the same idea for static cylindrical GPs with CF.

The outline of this work will be as. In Sect. 2 Einstein Maxwell field equations and Tolman–Oppenheimer–Volkoff (TOV) equation will be developed for spherically static symmetry. In Sect. 3 Weyl tensor will be taken into consideration for the development of mass function for self gravitating source under the influence of charge. Section 4 will be devoted for the study of CF which is defined by structure scalars derived from orthogonal splitting of curvature tensor. In Sect. 5, a discussion will be carried out about relativistic GPs for two cases (i) mass density and (ii) energy density. We will establish the charged class I GPs using Karmarkar condition in Sect. 6 and physical conditions about different cases will also be derived. A graphical solution will be given for the charged class I GPs with CF complemented by Karmarkar condition in Sect. 7. In Sect. 8 we will conclude our work.

2 Einstein Maxwell field equations

Let us consider a metric for an anisotropic fluid distribution which is spherically symmetric and static, as

$$\begin{aligned} ds^2=e^{\nu }dt^{2}-e^{\uplambda }dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(3)

where \(\nu =\nu (r)\) and \(\uplambda =\uplambda (r)\). Einstein field equation \( G^{\mu }_{\nu }=-8\pi T^{\mu }_{\nu } \) must be satisfied by Eq. (3). Coordinates are numbered as: \(x^{0}=t, x^{1}=r, x^{2}=\theta , x^{3}=\phi \). The matter content for anisotropic fluid distribution is defined by the energy–momentum tensor

$$\begin{aligned} T_{\mu \nu }=(\mu +P_{\perp })u_{\mu }u_{\nu }-P_{\perp }g_{\mu \nu }+(P_{r}-P_{\perp })s_{\mu }s_{\nu }, \end{aligned}$$
(4)

where \( P_{\perp }\) is the tangential pressure.

$$\begin{aligned} u^{\mu }=(e^{\frac{-\nu }{2}},0,0,0), \end{aligned}$$
(5)

is the four velocity and four vector \(s_{\mu }\) of the fluid distribution is given by

$$\begin{aligned} s^{\mu }=(0,e^{\frac{-\uplambda }{2}},0,0), \end{aligned}$$
(6)

with \(s^{\mu }u_{\mu }=0,\quad s^{\mu }s_{\mu }=-1\).

The electromagnetic tensor is defined by

$$\begin{aligned} \Gamma ^{i}_{j}=\frac{1}{4\pi }\left( -F^{i}_{\mu }F^{\mu }_{j}+\frac{1}{4}F^{\mu \nu }F_{\mu \nu }g^{i}_{j}\right) , \end{aligned}$$

where \(F_{ij}\) is the Maxwell field tensor defined by \(F_{ij}=\varphi _{j,i}-\varphi _{i,j}\) and \(\varphi _{j}\) is four potential given by \(\varphi _{i}=\varphi \delta ^{0}_{i}.\)

The Maxwell field equations in term of four-vector are

$$\begin{aligned} F^{ij}_{;j}=\phi _{o}J^{i}, \quad F_{[ij;k]}=0, \end{aligned}$$

where \(\phi _{o}\) is the magnetic permeability and \(J^{i}\) is the four current defined by \(J^{i}=\sigma u^{i}\), where \(\sigma \) is the charge density. The Maxwell field equation for metric (3), given as

$$\begin{aligned} \varphi ^{''}+\left( \frac{2}{r}-\frac{\nu ^{'}}{2}-\frac{\uplambda ^{'}}{2}\right) \varphi ^{'}=4\pi \sigma e^{\frac{\nu +\uplambda }{2}}. \end{aligned}$$

Above equation implies that

$$\begin{aligned} \varphi ^{'}=\frac{q(r)e^{\frac{\nu +\uplambda }{2}}}{r}, \end{aligned}$$

where \(q(r)=4\pi \int _{0}^{r}\sigma e^{\frac{\uplambda }{2}}{\overline{r}} d{\overline{r}}\) denote the total charge inside the sphere.

The basic field equations are

$$\begin{aligned} 8\pi \mu= & {} -e^{-\uplambda }\left( \frac{1}{r^{2}}+\frac{\uplambda '}{r}\right) -\frac{1}{r^{2}}+\frac{q^{2}}{r^{4}}, \end{aligned}$$
(7)
$$\begin{aligned} 8\pi P_{r}= & {} e^{-\uplambda }\left( \frac{1}{r^{2}}-\frac{\nu '}{r}\right) -\frac{1}{r^{2}}+\frac{q^{2}}{r^{4}}, \end{aligned}$$
(8)
$$\begin{aligned} 8\pi P_{\perp }= & {} \frac{e^{-\uplambda }}{4}\left( 2\nu ''+\nu '^{2}-\uplambda '\nu '+2\frac{\nu '-\uplambda '}{r}\right) -\frac{q^{2}}{r^{4}}, \end{aligned}$$
(9)

where primes shows the derivative with respect to ‘r’. At the exterior of the fluid distribution, we take Schwarzschild space time, as

$$\begin{aligned} ds^{2}= & {} \left( 1-\frac{2M}{r}dt^{2}\right) -\left( 1-\frac{2M}{r}\right) ^{-1}dr^{2}\nonumber \\&-r(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$
(10)

We require the continuity of the first and second fundamental form (Darmois condition) for the smooth matching of two metrics Eqs. (3) and (10) on the boundary \(r=r_{\Sigma }=\) constant. This matching gives following results

$$\begin{aligned} 1-\frac{2M}{r_{\Sigma }}= & {} e^{\nu _{\Sigma }}, \end{aligned}$$
(11)
$$\begin{aligned} 1-\frac{2M}{r_{\Sigma }}= & {} e^{-\uplambda _{\Sigma }}, \end{aligned}$$
(12)
$$\begin{aligned} P_{\Sigma }= & {} 0. \end{aligned}$$
(13)

Using Eqs. (7)–(9) the hydrostatic equilibrium equation, called generalized TOV equation, can be read as

$$\begin{aligned} P^{'}_{r}= \frac{2[(P_{\bot }-P_{r})+\frac{qq'}{8\pi r^{3}}]}{r}-\frac{\nu ^{'}}{2}(\mu +P_{r}), \end{aligned}$$
(14)

but

$$\begin{aligned} \nu '=2\frac{r m+4\pi P_{r}r^{4}-q^{2}}{r(r^{2}-2 r m+q^{2})}, \end{aligned}$$
(15)

then

$$\begin{aligned} P'_{r}= & {} \frac{2[(P_{\bot }-P_{r})+\frac{qq'}{8\pi r^{3}}]}{r}\nonumber \\&-\frac{r m+4\pi P_{r}r^{4}-q^{2}}{r(r^{2}-2 r m+q^{2})}(\mu +P_{r}), \end{aligned}$$
(16)

here the mass function m is given by

$$\begin{aligned} \frac{2m}{r}-\frac{q^{2}}{r^{2}}=1-e^{-\uplambda }, \end{aligned}$$
(17)

otherwise

$$\begin{aligned} m=4\pi \int ^{r}_{0}{\overline{r}}^{2}\mu d{\overline{r}}+\int ^{r}_{0}\frac{qq'}{{\overline{r}}}d{\overline{r}}. \end{aligned}$$
(18)

Energy–momentum tensor can be put down as

$$\begin{aligned} T_{\nu }^{\mu }= \Delta _{\nu }^{\mu }+\mu u^{\mu }u_{\nu }-Ph_{\nu }^{\mu }, \end{aligned}$$
(19)

with

$$\begin{aligned} \Delta _{\nu }^{\mu }= & {} \Delta (s^{\mu }s_{\nu }+\frac{1}{3}h_{\nu }^{\mu });\quad P = \frac{P_{r}+2P_{\perp }}{3}. \nonumber \\ \Delta= & {} P_{r}-P_{\perp };\quad h_{\nu }^{\mu }=\delta _{\nu }^{\mu }-u^{\mu }u_{\nu }. \end{aligned}$$
(20)

3 The Weyl tensor and mass function

Riemann tensor \(R^{\rho }_{\alpha \beta \mu }\), can be demonstrated through Weyl tensor \(C^{\rho }_{\alpha \beta \mu }\), Ricci scalar R and Ricci tensor \(R_{\alpha }^{\beta }\), as

$$\begin{aligned} R^{\rho }_{\alpha \beta \mu }=&C^{\rho }_{\alpha \beta \mu }+\frac{1}{2}R^{\rho }_{\beta g\alpha \mu }-\frac{1}{2}R_{\alpha \beta }\delta _{\mu }^{\rho }+\frac{1}{2}R_{\alpha \mu }\delta _{\beta }^{\rho }\nonumber \\&-\frac{1}{2}R_{\mu }^{\mu } g_{\alpha \beta }-\frac{1}{6}R(\delta _{\beta }^{\rho } g_{\alpha \mu }-g_{\alpha \beta }\delta _{\mu }^{\rho }). \end{aligned}$$
(21)

The electric part \((E_{\alpha \beta }=C_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta })\) of the Weyl tensor can be write as

$$\begin{aligned} C_{\mu \nu \kappa \uplambda }=(g_{\mu \nu \alpha \beta }g_{\kappa \uplambda \gamma \delta }-\eta _{\mu \nu \alpha \beta }\eta _{\kappa \uplambda \gamma \delta })u^{\alpha }u^{\gamma }E^{\beta \delta }, \end{aligned}$$
(22)

with \(g_{\mu \nu \alpha \beta }=g_{\mu \alpha }g_{\nu \alpha }\) and \(\eta _{\mu \nu \alpha \beta } \) denoting the Levi-Civita tensor while, in spherical symmetric case its magnetic part dissipates. Note that \(E_{\alpha \beta }\) can also be expressed as

$$\begin{aligned} E_{\alpha \beta }=E\left( s_{\alpha }s_{\beta }+\frac{1}{3}h_{\alpha \beta }\right) , \end{aligned}$$
(23)

with

$$\begin{aligned} E=-\frac{e^{-\uplambda }}{4}\Big [\nu ''+\frac{\nu ^{'2}-\uplambda '\nu '}{2}-\frac{\nu '-\uplambda '}{r}+\frac{2(1-e^{\uplambda })}{r^{2}}\Big ], \end{aligned}$$
(24)

satisfying

$$\begin{aligned} E_{\alpha }^{\alpha }=0,\quad E_{\alpha \gamma }=E_{(\alpha \gamma )},\quad E_{\alpha \gamma }u^{\gamma }=0. \end{aligned}$$
(25)

Using Eqs. (7)–(9), (17), (21) and (23) we have

$$\begin{aligned} m=\frac{8\pi q^{2}}{3r}+\frac{r^{3}E}{3}+\frac{4\pi }{3}r^{3}(P_{\perp }-P_{r}+\mu ), \end{aligned}$$
(26)

and

$$\begin{aligned} \frac{E}{4\pi }= & {} -\frac{1}{r^{3}}\int _{0}^{r}{\overline{r}}^{3}\mu 'd{\overline{r}}+(P_{r}-P_\perp )-\frac{2q^{2}}{r^{4}}\nonumber \\&+\frac{3}{4\pi r^{3}}\int _{0}^{r}\frac{qq'}{{\overline{r}}}d{\overline{r}} . \end{aligned}$$
(27)

Using Eqs. (27) and (26) we have

$$\begin{aligned} m(r)=\frac{4\pi }{3}r^{3}\mu -\frac{4\pi }{3}\int _{0}^{r}{\overline{r}}^{3}\mu 'd{\overline{r}}+\int _{0}^{r}\frac{qq'}{{\overline{r}}}d{\overline{r}}. \end{aligned}$$
(28)

4 Orthogonal splitting of Riemann tensor and vanishing complexity factor

Now we discuss structure scalars which are obtained by orthogonal splitting of curvature tensor [39]. These scalars helps us to define CF [32] and the following tensors are the result of this splitting [40, 41].

$$\begin{aligned} Y_{\alpha \beta }= & {} R_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }, \end{aligned}$$
(29)
$$\begin{aligned} Z_{\alpha \beta }= & {} ^{*}R_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }=\frac{1}{2}\eta _{\alpha \gamma \epsilon \mu }R^{\epsilon \mu }_{\beta \delta }u^{\gamma }u^{\delta }, \end{aligned}$$
(30)
$$\begin{aligned} X_{\alpha \beta }= & {} ^{*}R^{*}_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }=\frac{1}{2}\eta _{\alpha \gamma }^{\epsilon \mu }R^{*}_{\epsilon \mu \beta \delta }u^{\gamma }u^{\delta }, \end{aligned}$$
(31)

where \(*\) represents the dual tensor i.e. \(R^{*}_{\alpha \beta \gamma \delta }=\frac{1}{2}\eta _{\epsilon \mu \gamma \delta }\; R_{\alpha \beta }^{\epsilon \mu }\). Using the field equations, Eq. (21) may be expressed as

$$\begin{aligned} R_{\beta \delta }^{\alpha \gamma }=C^{\alpha \gamma }_{\beta \delta }+28\pi T_{[\beta ^{\delta }\delta ]}^{[\alpha \gamma ]}+8\pi T\left( \dfrac{1}{3}\delta ^{\alpha \gamma }_{[\beta ^{\delta }\delta ]}-\delta _{[\beta ^{\delta }\delta ]}^{[\alpha \gamma ]}\right) , \end{aligned}$$
(32)

we split the Riemann tensor by using Eq. (18) into Eq. (32)

$$\begin{aligned} R_{\beta \delta }^{\alpha \gamma }=R_{(I)\beta \delta }^{\alpha \gamma }+\beta _{(II)\beta \delta }^{\alpha \gamma }+R_{(III)\beta \delta }^{\alpha \gamma }, \end{aligned}$$
(33)

where

$$\begin{aligned} R_{(I)\beta \delta }^{\alpha \gamma }= & {} 16\pi \mu u^{[\alpha \gamma ]}u_{[\beta ^{\delta }\delta ]}-28\pi Ph^{[\alpha \gamma ]}_{[\beta ^{\delta }\delta ]}\nonumber \\&+8(\mu -3P)(\dfrac{1}{3}\delta ^{[\alpha \gamma ]}_{[\beta ^{\delta }\delta ]})-\delta ^{[\alpha \gamma ]_{[\beta ^{\delta }\delta ]}}, \end{aligned}$$
(34)
$$\begin{aligned} R_{(II)\beta \delta }^{\alpha \gamma }= & {} 16\pi \Delta ^{[\alpha \gamma ]}_{[\beta ^{\delta }\delta ]}, \end{aligned}$$
(35)
$$\begin{aligned} R_{(III)\beta \delta }^{\alpha \gamma }= & {} 4u^{[\alpha \gamma ]}u_{[\beta ^{E}\delta ]}-\epsilon ^{\alpha \gamma }_{\mu }\epsilon _{\beta \delta \nu }E^{\mu \nu }=0, \end{aligned}$$
(36)

with

$$\begin{aligned} \epsilon _{\alpha \gamma \beta }=u^{\mu }\eta _{\mu \alpha \gamma \beta },\quad \epsilon _{\alpha \gamma \beta }u^{\beta }=0. \end{aligned}$$
(37)

We can find the explicit expressions for the three tensors \(Y_{\alpha \beta },\;Z_{\alpha \beta }\) and \(X_{\alpha \beta }\) in term of the physical variables by using the above results, as

$$\begin{aligned} Y_{\alpha \beta }= & {} \frac{4\pi }{3}(\mu +3P)h_{\alpha \beta }+4\pi \Delta _{\alpha \beta }+E_{\alpha \beta }, \end{aligned}$$
(38)
$$\begin{aligned} Z_{\alpha \beta }= & {} 0, \end{aligned}$$
(39)

and

$$\begin{aligned} X_{\alpha \beta }=\frac{8\pi }{3}\mu h_{\alpha \beta }+4\pi \Delta _{\alpha \beta }-E_{\alpha \beta }. \end{aligned}$$
(40)

The structure scalars can be derived from these tensors [39]. The scalars functions \(X_{T},\; X_{TF},\; Y_{T},\; Y_{TF}, \) are defined by using tensor \(X_{\alpha \beta }\) and \( Y_{\alpha \beta }\), as

$$\begin{aligned} X_{T}= & {} 8\pi \mu +\frac{q^{2}}{r^{4}}, \end{aligned}$$
(41)
$$\begin{aligned} X_{TF}= & {} 4\pi \Delta _{\alpha \beta } -E +\frac{q^{2}}{r^{4}}, \end{aligned}$$
(42)
$$\begin{aligned} X_{TF}= & {} \frac{4\pi }{r^3} \int _{0}^{r}\overline{r^3}\mu 'd{\overline{r}}+(8\pi -\frac{1}{2})+\frac{q^{2}}{r^{4}}, \end{aligned}$$
(43)
$$\begin{aligned} Y_{T}= & {} 4\pi (3P_{r}+\mu +-2\Delta )+\frac{q^{2}}{r^{4}}, \end{aligned}$$
(44)
$$\begin{aligned} Y_{TF}= & {} E+\frac{q^{2}}{r^{4}}+4\pi \Delta , \end{aligned}$$
(45)

using Eq. (27)

$$\begin{aligned} Y_{TF}=8\pi \Delta -\frac{4\pi }{r^3}\int _{0}^{r}{\overline{r}}^3\mu 'd{\overline{r}}+\left( \frac{5}{2}-8\pi \right) \frac{q^{2}}{r^{4}}. \end{aligned}$$
(46)

From Eqs. (43) and (46)

$$\begin{aligned} 8\pi \Delta +\frac{2q^{2}}{r^{4}} =X_{TF}+Y_{TF}. \end{aligned}$$
(47)

Complexity of a system depends on many elements like viscosity, heat dissipation, charge, pressure anisotropy and density inhomogeneity. Any system, in general without these elements except isotropic pressure and energy density is to be considered simplest system with vanishing complexity. But for fluid distribution, inhomogenous density and anisotropic pressure are responsible for complexity in system. Since Eq. (46), which define structure scalar \(Y_{TF}\) contains these elements, so the term complexity factor is associated with structure scalar \(Y_{TF}\). Therefore, when we apply condition \(Y_{TF}=0\) on (46), it gives

$$\begin{aligned} \Delta =\frac{1}{2r^3}\int _{0}^{r}{\overline{r}}^3\mu 'd{\overline{r}} +\left( 1-\frac{5}{16\pi }\right) \frac{q^{2}}{r^{4}}. \end{aligned}$$
(48)

5 Relativistic generalized charged polytropes

Now we discuss two cases, mass density and energy density of GPEoS for anisotropic fluid [16], with non-isothermal and isothermal regimes.

5.1 Non-isothermal regime

5.1.1 Case 1

In this case GPEoS is studied with mass density as

$$\begin{aligned} P_{r}=\alpha _{1}\mu _{o} + K\mu ^{\gamma }_{o}=\alpha _{1}\mu _{o}+K\mu _{o}^{1+\frac{1}{n}}, \end{aligned}$$
(49)

for non-isothermal regime we take \(\gamma \ne 1\) and mass density \(\mu _{o}\) connected with total energy density \(\mu \) [14] as

$$\begin{aligned} \mu =\mu _{o}+nP_{r}. \end{aligned}$$
(50)

Let us now introduce the following assumption

$$\begin{aligned} \alpha= & {} \frac{P_{rc}}{\mu _{c}},\quad r=\frac{\xi }{A},\quad A^{2}=\frac{4\pi \mu _{c}}{\alpha (n+1)}. \end{aligned}$$
(51)
$$\begin{aligned} \psi _{o}= & {} \frac{\mu _{o}}{\mu _{oc}},\quad v(\xi )=\frac{m(r)A^{3}}{4\pi \mu _{c}}. \end{aligned}$$
(52)

Then charged TOV Eq. (16) reads as

$$\begin{aligned}&-\frac{A^4 q q'}{4 \pi \xi ^4}+\frac{1}{\alpha \xi (\alpha A^4 q^2+\xi (\alpha A^2 \xi -8 \pi {P_{rc}} v))}\nonumber \\&\quad \times \Big [A {P_{rc}} {\psi _{o}}^n ((n+1) {\psi _{o}} (\alpha \nonumber \\&\quad -{\alpha _{1}}+\alpha {\alpha _{1}} n)-(\alpha n-1) ({\alpha _{1}}+{\alpha _{1}} n+1)) \nonumber \\&\quad \times (4 \pi \xi {P_{rc}} (\xi ^3 {\psi _{o}}^n ({\alpha _{1}}+{\psi _{o}} (\alpha \nonumber \\&\quad -{\alpha _{1}}+\alpha {\alpha _{1}} n)+\alpha {\alpha _{1}} (-n))+v)-\alpha A^4 q^2)\Big ]\nonumber \\&\quad -\frac{2 A \Delta }{\xi }+\frac{1}{\alpha }\Big [A {P_{rc}} {\psi _{o}}^{n-1}{\psi _{o}}' ((n+1) {\psi _{o}} (\alpha -{\alpha _{1}} \nonumber \\&\quad +\alpha {\alpha _{1}} n)+{\alpha _{1}} n (1-\alpha n))\Big ]=0, \end{aligned}$$
(53)

where prime indicates the differentiation with respect to \(\xi \). From the definition of mass function Eqs. (17) and (7), we have

$$\begin{aligned} m'=4\pi r^{2}\mu +\frac{qq'}{r}, \end{aligned}$$
(54)

or using Eqs. (51) and (52),

$$\begin{aligned} \dfrac{dv}{d\xi }= & {} \frac{\alpha A^4 q q'}{4 \pi \xi {P_{rc}}}+\xi ^2 {\psi _{o}}^n (n {\psi _{o}} (\alpha -{\alpha _{1}}+\alpha {\alpha _{1}} n)\nonumber \\&-(\alpha n-1) ({\alpha _{1}} n+1)). \end{aligned}$$
(55)

The boundary of surface of sphere is defined by \(\xi =\xi _{n}\) such that \(\psi _{o}(\xi _{o})=0\) and following boundary conditions are applied

$$\begin{aligned} {\psi _{o}}({\xi }={0})=1 \quad and \quad v({\xi }={0})={0}. \end{aligned}$$
(56)

Equations (53) and (55) to gather give the generalized charged LEe equation for GPEoS in this case

$$\begin{aligned}&\frac{1}{\alpha }\Big [4 (n-1) {P_{rc}} (n (1-n \alpha ) {\alpha _{1}}+(n+1) (n {\alpha _{1}} \alpha +\alpha \nonumber \\&\quad -{\alpha _{1}}) {\psi _{o}}) {\psi _{o}}'^2 {\psi _{o}}^{n-2}\Big ]+\frac{1}{\alpha }\Big [4 (n+1) {P_{rc}} (n {\alpha _{1}} \alpha +\alpha \nonumber \\&\quad -{\alpha _{1}}) {\psi _{o}}'^2 {\psi _{o}}^{n-1}\Big ]+\frac{1}{\alpha }\Big [4 {P_{rc}} (n (1-n \alpha ) {\alpha _{1}}+(n \nonumber \\&\quad +1) \beta _{1} {\psi _{o}}) {\psi _{o}}'' {\psi _{o}}^{n-1}\Big ]+\frac{1}{\beta ^2}\Big [8 {P_{rc}} {\psi _{o}}^n ((n+1) \beta _{1} {\psi _{o}} \nonumber \\&\quad -(n \alpha -1) (n {\alpha _{1}}+{\alpha _{1}}+1)) (4 \pi {P_{rc}} \xi (\xi ^3 (-n \alpha {\alpha _{1}}+{\alpha _{1}} \nonumber \\&\quad +(n {\alpha _{1}} \alpha +\alpha -{\alpha _{1}}) {\psi _{o}}) {\psi _{o}}^n+v) \nonumber \\&\quad -A^4 \alpha q^2) (4 \pi {P_{rc}} (\xi ^3 (n \beta _{1} {\psi _{o}}-(n \alpha \nonumber \\&\quad -1) (n {\alpha _{1}}+1)) {\psi _{o}}^n+v)-A^2 \alpha \xi )\Big ]+\frac{4 A^3 q q'}{\pi \xi ^5}+\frac{1}{\beta }\Big [4 (n \nonumber \\&\quad +1) {P_{rc}} \beta _{1} {\psi _{o}}^n (4 \pi {P_{rc}} \xi (\xi ^3 (-n \alpha {\alpha _{1}}+{\alpha _{1}}+\beta _{1} {\psi _{o}}) {\psi _{o}}^n \nonumber \\&\quad +v)-A^4 \alpha q^2) {\psi _{o}}'\Big ]+\frac{1}{\beta }\Big [4 n {P_{rc}} {\psi _{o}}^{n-1} ((n+1) \beta _{1} {\psi _{o}}\nonumber \\&\quad -(n \alpha -1) (n {\alpha _{1}}+{\alpha _{1}}+1)) (4 \pi {P_{rc}} \xi (\xi ^3 (-n \alpha {\alpha _{1}}+{\alpha _{1}}\nonumber \\&\quad +(n {\alpha _{1}} \alpha +\alpha -{\alpha _{1}}) {\psi _{o}}) {\psi _{o}}^n+v)-A^4 \alpha q^2) {\psi _{o}}'\Big ]\nonumber \\&\quad +\frac{1}{\beta }\Big [4 {P_{rc}} {\psi _{o}}^{n-1} ((n+1) \beta _{1} {\psi _{o}}-(n \alpha -1) (n {\alpha _{1}}+{\alpha _{1}}\nonumber \\&\quad +1)) (4 \pi {P_{rc}} \xi ^3 ({\psi _{o}} ((n+4) \beta _{1} {\psi _{o}}-(n \alpha -1) ((n+4) {\alpha _{1}}+1))\nonumber \\&\quad +\xi (n (1-n \alpha ) {\alpha _{1}}+(n+1) \beta _{1} {\psi _{o}}) {\psi _{o}}') {\psi _{o}}^n+4 \pi {P_{rc}} v {\psi _{o}}\nonumber \\&\quad -A^4 \alpha q q' {\psi _{o}})\Big ]+\frac{8 \Delta }{\xi ^2}-\frac{A^3 q'^2}{\pi \xi ^4}-\frac{A^3 q q''}{\pi \xi ^4}\nonumber \\&\quad -\frac{1}{\xi \;\beta }\Big [4 {P_{rc}} {\psi _{o}}^n ((n\nonumber \\&\quad +1) \beta _{1} {\psi _{o}}-(n \alpha -1) (n {\alpha _{1}}+{\alpha _{1}}+1)) (4 \pi {P_{rc}} \xi (\xi ^3 (-n \alpha {\alpha _{1}}\nonumber \\&\quad +{\alpha _{1}}+\beta _{1} {\psi _{o}}) {\psi _{o}}^n+v)-A^4 \alpha q^2)\Big ], \end{aligned}$$
(57)

where \(\alpha \xi (\alpha q^2 A^4+\xi (A^2 \alpha \xi -8 \pi {P_{rc}} v))=\beta \) and \((n {\alpha _{1}} \alpha +\alpha -{\alpha _{1}})=\beta _{1}.\)

5.1.2 Case 2

GPEoS with energy density case can be consider [16] as

$$\begin{aligned} P_{r}=\alpha _{1}\mu +K\mu ^{1+\frac{1}{n}}, \end{aligned}$$
(58)

mass density \(\mu _{o}\) is replaced by total energy density \(\mu \) in Eq. (50), by the relation as [42]

$$\begin{aligned} \mu =\frac{\mu _{o}}{(1-K\mu _{o}^{1/n})^{n}}. \end{aligned}$$
(59)

taking

$$\begin{aligned} \psi ^{n}=\frac{\mu }{\mu }_{c}, \end{aligned}$$
(60)

charged TOV equation is obtained as

$$\begin{aligned}&-\frac{A^4 q q'}{4 \pi \xi ^4}+\frac{1}{\beta }\Big [A P_{rc} \psi ^n ((\alpha -\alpha _{1}) \psi +\alpha _{1}+1) (-\alpha A^4 q^2 \nonumber \\&\quad +4 \pi \xi ^4 P_{rc} \psi ^n ((\alpha -\alpha _{1}) \psi +\alpha _{1})+4 \pi \xi P_{rc} v)\Big ]-\frac{2 A \Delta }{\xi }\nonumber \\&\quad +\frac{1}{\alpha }\Big [A P_{rc} \psi ^{n-1} \psi ' ((n+1) (\alpha -\alpha _{1}) \psi +\alpha _{1} n)\Big ]=0,\nonumber \\ \end{aligned}$$
(61)

and from Eq. (54) we have

$$\begin{aligned} \frac{dv}{d\xi }=\xi ^{2}\psi ^{n}+\frac{\alpha A^4 q q'}{4 \pi \xi P_{rc}}. \end{aligned}$$
(62)

Equations (61) and (62) to gather give the generalized charged LEe

$$\begin{aligned}&-\frac{A^3 q q''}{\pi \xi ^4}+\frac{4 A^3 q q'}{\pi \xi ^5}-\frac{A^3 q'^2}{\pi \xi ^4}+\frac{1}{\beta }\Big [4 P_{rc} \psi ^{n-1} ((\alpha -\alpha {_1}) \psi \nonumber \\&\quad +\alpha {_1}+1) (-\alpha A^4 \psi q q'+4 \pi \xi ^3 P_{rc} \psi ^n (\psi (4 (\alpha -\alpha {_1}) \psi \nonumber \\&\quad +4 \alpha {_1}+1)+\xi \psi ' ((n+1) (\alpha -\alpha {_1}) \psi +\alpha {_1} n))+4 \pi P_{rc} \psi v)\Big ]\nonumber \\&\quad +\frac{1}{\beta }\Big [4 n P_{rc} \psi ^{n-1} \psi ' ((\alpha -\alpha {_1}) \psi +\alpha {_1}+1) (-\alpha A^4 q^2\nonumber \\&\quad +4 \pi \xi ^4 P_{rc} \psi ^n ((\alpha -\alpha {_1}) \psi +\alpha {_1})+4 \pi \xi P_{rc} v)\Big ]+\frac{1}{\beta }\Big [4 P_{rc} (\alpha \nonumber \\&\quad -\alpha {_1}) \psi ^n \psi ' (-\alpha A^4 q^2+4 \pi \xi ^4 P_{rc} \psi ^n \nonumber \\&\quad \times ((\alpha -\alpha {_1}) \psi +\alpha {_1})+4 \pi \xi P_{rc} v)\Big ]\nonumber \\&\quad +\frac{1}{\beta ^2}\Big [8 P_{rc} \psi ^n ((\alpha -\alpha {_1}) \psi +\alpha {_1}+1) (4 \pi P_{rc} (\xi ^3 \psi ^n+v)\nonumber \\&\quad -\alpha A^2 \xi ) (-\alpha A^4 q^2+4 \pi \xi ^4 P_{rc} \psi ^n ((\alpha -\alpha {_1}) \psi +\alpha {_1})\nonumber \\&\quad +4 \pi \xi P_{rc} v)\Big ]\nonumber \\&\quad -\frac{1}{\xi \beta }\Big [4 P_{rc} \psi ^n ((\alpha -\alpha {_1}) \psi +\alpha {_1}+1) \nonumber \\&\quad \times (-\alpha A^4 q^2+4 \pi \xi ^4 P_{rc} \psi ^n ((\alpha \nonumber \\&\quad -\alpha {_1}) \psi +\alpha {_1})+4 \pi \xi P_{rc} v)\Big ]+\frac{8 \Delta }{\xi ^2}\nonumber \\&\quad +\frac{1}{\alpha }\Big [4 P_{rc} \psi ^{n-1} \psi '' ((n+1) (\alpha \nonumber \\&\quad -\alpha {_1}) \psi +\alpha {_1} n)\Big ]+\frac{1}{\alpha }\Big [4 (n-1) P_{rc} \psi ^{n-2} \psi '^2 \nonumber \\&\quad \times ((n+1) (\alpha -\alpha {_1}) \psi +\alpha {_1} n)\Big ]\nonumber \\&\quad +\frac{1}{\alpha }\Big [4 (n+1) P_{rc} (\alpha -\alpha {_1}) \psi ^{n-1} \psi '^2\Big ]=0. \end{aligned}$$
(63)

5.2 Isothermal regime

In isothermal regime \((\gamma =1)\) we see that both cases, mass density \((\mu _{o})\) and energy density \((\mu )\) become same so here we discuss only energy density \((\mu )\). In this regime \(\psi \) is defined as

$$\begin{aligned} e^{-\psi }=\frac{\mu }{\mu _{c}}. \end{aligned}$$
(64)

Introducing dimensionless variables

$$\begin{aligned} \alpha =\frac{P_{rc}}{\mu _{c}},\quad r=\frac{\xi }{B},\quad B^{2}=\frac{4\pi \mu _{c}}{\alpha } \quad v(\xi )=\frac{m(r)B^{3}}{4\pi \mu _{c}}, \end{aligned}$$
(65)

so Eq. (54) becomes

$$\begin{aligned} \frac{dv}{d\xi }=e^{-\psi }\xi ^{2}+\frac{\alpha B^4 q q'}{4 \pi \xi P_{rc}}, \end{aligned}$$
(66)

and TOV equation will be read as

$$\begin{aligned}&-\frac{B^4 q q'}{4 \pi \xi ^4}+\frac{1}{\beta _{2}}\Big [(\alpha +1) B P_{rc} e^{-2 \psi } \nonumber \\&\quad \times (e^{\psi } (4 \pi \xi P_{rc} v-\alpha B^4 q^2)+4 \pi \alpha \xi ^4 P_{rc})\Big ] \nonumber \\&\quad -\frac{2 B \Delta }{\xi }-B P_{rc} e^{-\psi } \psi '=0 \end{aligned}$$
(67)

where \(\alpha \xi (\alpha B^4 q^2+\xi (\alpha B^2 \xi -8 \pi P_{rc} v))=\beta _{2}\). From Eqs. (66) and (67), we have second ordered generalized LEe

$$\begin{aligned}&-\frac{B^3 q q''}{\pi \xi ^4}+\frac{4 B^3 q q'}{\pi \xi ^5}-\frac{B^3 q'^2}{\pi \xi ^4}\nonumber \\&\quad -\frac{1}{\beta _{2}}\Big [4 (\alpha +1) P_{rc} e^{-2 \psi } (e^{\psi } (\alpha B^4 q (q'\nonumber \\&\quad +q \psi ')-4 \pi P_{rc} v (\xi \psi '+1))-4 \pi (4 \alpha +1) \xi ^3 P_{rc})\Big ]\nonumber \\&\quad -\frac{1}{\beta _{2}}\Big [8 (\alpha +1) P_{rc} e^{-2 \psi } \psi ' (e^{\psi } (4 \pi \xi P_{rc} v-\alpha B^4 q^2)\nonumber \\&\quad +4 \pi \alpha \xi ^4 P_{rc})\Big ]+\frac{1}{\beta _{2}^2}\Big [8 (\alpha +1) P_{rc} e^{-3 \psi } (e^{\psi } (4 \pi P_{rc} v\nonumber \\&\quad -\alpha B^2 \xi )+4 \pi \xi ^3 P_{rc}) (e^{\psi } (4 \pi \xi P_{rc} v-\alpha B^4 q^2)\nonumber \\&\quad +4 \pi \alpha \xi ^4 P_{rc})\Big ]\nonumber \\&\quad -\frac{1}{\xi \beta _{2}}\Big [4 (\alpha +1) P_{rc} e^{-2 \psi } (e^{\psi } (4 \pi \xi P_{rc} v-\alpha B^4 q^2)\nonumber \\&\quad +4 \pi \alpha \xi ^4 P_{rc})\Big ]\nonumber \\&\quad +\frac{8 \Delta }{\xi ^2}-4 P_{rc} e^{-\psi } \psi ''+4 P_{rc} e^{-\psi } \psi '^2=0. \end{aligned}$$
(68)

6 Class I generalized charged polytropes

During the study of cosmological objects it is often found useful to marge four dimension space time to higher dimension [27] and one of this merging is Karmarkar condition [28] for spherical symmetric fluid distribution, read as

$$\begin{aligned} R_{1010}R_{2323}=R_{1212}R_{0303}+R_{1202}R_{1303}, \end{aligned}$$
(69)

with \( R_{2323}\ne 0\), gives

$$\begin{aligned} 2\nu ''=\frac{e^{\uplambda }\uplambda '}{e^{\uplambda }-1}-\uplambda '^{2},\quad e^{\uplambda } \ne 1. \end{aligned}$$
(70)

6.1 Case 1

From Eqs. (49)–(52) and (70) we have

$$\begin{aligned} \Delta= & {} -\frac{1}{8 \pi r^3 (q^2-2 m r)}\Big [(-r^2 m'+3 m r-2 q^2+q r q') (m \nonumber \\&+4 \pi \alpha _{1} r^3 {\psi _{o}}^n (n {P_{rc}}-{\mu _{c}})-4 \pi r^3 {\psi _{o}}^{n+1} (-\alpha _{1} {\mu _{c}} \nonumber \\&+\alpha _{1} n {P_{rc}}+{P_{rc}}))\Big ], \end{aligned}$$
(71)

and the dimensionless form of Eq. (71) is

$$\begin{aligned}&\Delta =\frac{1}{2 \xi ^3 (8 \pi {\mu _{c}} \xi v-A^4 q^2)}\Big [{\mu _{c}} (v-\xi ^3 {\psi _{o}}^n ({\alpha _{1}}+{\psi _{o}} (\alpha -{\alpha _{1}} \nonumber \\&\quad +\alpha {\alpha _{1}} n)+\alpha {\alpha _{1}} (-n))) (A^3 (\xi q q'-A (2 q^2+\xi q q')) \nonumber \\&\quad -4 \pi {\mu _{c}} \xi ^4 {\psi _{o}}^n (n {\psi _{o}} (\alpha -{\alpha _{1}}+\alpha {\alpha _{1}} n)-(\alpha n-1) ({\alpha _{1}} n \nonumber \\&\quad +1))+12 \pi {\mu _{c}} \xi v)\Big ]. \end{aligned}$$
(72)

After using Eq. (72) with Eq. (53), we obtain class I generalized charged TOV equation

$$\begin{aligned}&-\frac{A^4 q q'}{4 \pi \xi ^4}+\frac{1}{\alpha \xi ^4 (\alpha A^4 q^2-8 \pi \xi P_{rc} v)}\nonumber \\&\quad \times \Big [A P_{rc} (\xi ^3 {\psi _{o}}^n ({\alpha _{1}}+{\psi _{o}} (\alpha -{\alpha _{1}}\nonumber \\&\quad +\alpha {\alpha _{1}} n)+\alpha {\alpha _{1}} (-n))-v) (\alpha A^3 (2 A q^2+A \xi q q'-\xi q q')\nonumber \\&\quad +4 \pi \xi ^4 P_{rc} {\psi _{o}}^n (n {\psi _{o}} (\alpha -{\alpha _{1}}+\alpha {\alpha _{1}} n)-(\alpha n-1) ({\alpha _{1}} n+1))\nonumber \\&\quad -12 \pi \xi P_{rc} v)\Big ]+\frac{1}{\beta }\Big [A P_{rc} {\psi _{o}}^n ((n+1) {\psi _{o}} \nonumber \\&\quad \times (\alpha -{\alpha _{1}}+\alpha {\alpha _{1}} n)-(\alpha n\nonumber \\&\quad -1) ({\alpha _{1}}+{\alpha _{1}} n+1)) (4 \pi \xi P_{rc} (\xi ^3 {\psi _{o}}^n \nonumber \\&\quad \times ({\alpha _{1}}+{\psi _{o}} (\alpha -{\alpha _{1}}+\alpha {\alpha _{1}} n)\nonumber \\&\quad +\alpha {\alpha _{1}} (-n))+v)-\alpha A^4 q^2)\Big ]\nonumber \\&\quad +\frac{1}{\alpha }\Big [A P_{rc} {\psi _{o}}^{n-1} {\psi _{o}}' ((n+1) {\psi _{o}} (\alpha -{\alpha _{1}}\nonumber \\&\quad +\alpha {\alpha _{1}} n)+{\alpha _{1}} n (1-\alpha n))\Big ]=0, \end{aligned}$$
(73)

so second ordered class I generalized charged LEe takes the form

$$\begin{aligned}&\frac{1}{\alpha }\Big [4 (n-1) P_{rc} (n (1-n \alpha ) \alpha _{1}+(n+1) \beta _{1} \psi _{o}) \psi _{o}'^2 \psi _{o}^{n-2}\Big ]\nonumber \\&\quad +\frac{1}{\alpha }\Big [4 (n+1) P_{rc} \beta _{1} \psi _{o}'^2 \psi _{o}^{n-1}\Big ]+\frac{1}{\alpha }\Big [4 P_{rc} (n (1-n \alpha ) \alpha _{1}\nonumber \\&\quad +(n+1) \beta _{1} \psi _{o}'' \psi _{o}^{n-1}\Big ]+\frac{1}{\alpha \xi (\alpha q^2 A^4+\xi (\beta _{3}))^2}\nonumber \\&\quad \times \Big [ 8 P_{rc} \psi _{o}^n ((n\nonumber \\&\quad +1) \beta _{1} \psi _{o}-(n \alpha -1) (n \alpha _{1}+\alpha _{1}+1)) (4 \pi P_{rc} \xi (\xi ^3 (-n \alpha \alpha _{1}\nonumber \\&\quad +\alpha _{1}+(\beta _{1}) \psi _{o}) \psi _{o}^n+v) -A^4 \alpha q^2) \nonumber \\&\quad \times (4 \pi P_{rc} (\xi ^3 (n (\beta _{1}) \psi _{o}-(n \alpha \nonumber \\&\quad -1) (n \alpha _{1}+1)) \psi _{o}^n+v)-A^2 \alpha \xi )\Big ]+\frac{4 A^3 q q'}{\pi \xi ^5}\nonumber \\&\quad -\frac{1}{\alpha \xi ^5 (\beta _{4})}\Big [16 P_{rc} (\xi ^3 \psi _{o}^n (-n \alpha \alpha _{1}+\alpha _{1}+\beta _{1}\psi _{o})-v) \nonumber \\&\quad \times (4 \pi P_{rc} \xi ^4\nonumber \\&\quad \times (n \beta _{1} \psi _{o}-(n \alpha -1) (n \alpha _{1}+1)) \psi _{o}^n-12 \pi P_{rc} \xi v\nonumber \\&\quad +A^3 \alpha (2 A q^2-\xi q' q+A \xi q q'))\Big ]+\frac{1}{\alpha \xi ^4 (\beta _{4})^2}\nonumber \\&\quad \times \Big [8 P_{rc} (v-\xi ^3 \psi _{o}^n (-n \alpha \alpha _{1}+\alpha _{1}\nonumber \\&\quad +\beta _{1} \psi _{o})) (4 \pi P_{rc} \xi ^3 (n (\beta _{1}) \psi _{o}-(n \alpha -1) \nonumber \\&\quad \times (n \alpha _{1} +1)) \psi _{o}^n+4 \pi P_{rc} v\nonumber \\&\quad +A^4 \alpha q q') (-4 \pi P_{rc} \xi ^4 (n (\beta _{1}) \psi _{o}-(n \alpha -1) (n \alpha _{1}+1)) \psi _{o}^n\nonumber \\&\quad +12 \pi P_{rc} \xi v+A^3 \alpha (q \xi q'-A (2 q^2+\xi q q')))\Big ]\nonumber \\&\quad +\frac{1}{\alpha \xi (\alpha q^2 A^4+\xi (\beta _{3}))}\Big [4 (n+1) P_{rc}\beta _{1} \psi _{o}^n \nonumber \\&\quad \times (4 \pi P_{rc} \xi (\xi ^3 (-n \alpha \alpha _{1}+\alpha _{1}\nonumber \\&\quad +\beta _{1} \psi _{o}) \psi _{o}^n+v)-A^4 \alpha q^2) \psi _{o}'\Big ]+\frac{1}{\alpha \xi (\alpha q^2 A^4+\xi (\beta _{3}))}\nonumber \\&\quad \times \Big [4 n P_{rc} \psi _{o}^{n-1}((n +1) \beta _{1} \psi _{o}-(n \alpha -1) (n \alpha _{1}+\alpha _{1}+1)) \nonumber \\&\quad \times (4 \pi P_{rc} \xi (\xi ^3 (-n \alpha \alpha _{1}\nonumber \\&\quad +\alpha _{1}+\beta _{1} \psi _{o}) \psi _{o}^n+v)-A^4 \alpha q^2) \psi _{o}'\Big ] \nonumber \\&\quad -\frac{1}{\pi \alpha \xi ^5 (A^4 q^2 \alpha -8 \pi P_{rc} \xi v ) \psi _{o}}\Big [(4 \pi P_{rc} \xi ^4 (n (\beta _{1}) \psi _{o}-(n \alpha \nonumber \\&\quad -1) (n \alpha _{1}+1)) \psi _{o}^n-12 \pi P_{rc} \xi v+A^3 \alpha (2 A q^2-\xi q' q\nonumber \\&\quad +A \xi q q')) (4 n \pi P_{rc} (n \alpha -1) \alpha _{1} \xi ^4 \psi _{o}' \psi _{o}^n-4 \pi P_{rc} \xi ^3 \nonumber \\&\quad \times ((n \alpha -1) ((n-3) \alpha _{1}\nonumber \\&\quad +1)+(n+1) (\beta _{1}) \xi \psi _{o}') \psi _{o}^{n+1}+4 (n-3) \pi P_{rc} (n \alpha _{1} \alpha +\alpha \nonumber \\&\quad -\alpha _{1}) \xi ^3 \psi _{o}^{n+2}+A^4 \alpha q q' \psi _{o})\Big ]\nonumber \\&\quad +\frac{1}{\alpha \xi (\alpha q^2 A^4+\xi (\beta _{3}))}\Big [4 P_{rc} \psi _{o}^{n-1} ((n+1) (n \alpha _{1} \alpha +\alpha \nonumber \\&\quad -\alpha _{1}) \psi _{o}-(n \alpha -1) (n \alpha _{1}+\alpha _{1}+1)) \nonumber \\&\quad \times (4 \pi P_{rc} \xi ^3 (\psi _{o} ((n+4) (n \alpha _{1} \alpha \nonumber \\&\quad +\alpha -\alpha _{1}) \psi _{o}-(n \alpha -1) ((n+4) \alpha _{1}+1))+\xi (n (1-n \alpha ) \alpha _{1}\nonumber \\&\quad +(n+1) (\beta _{1}) \psi _{o}) \psi _{o}') \psi _{o}^n+4 \pi P_{rc} v \psi _{o}-A^4 \alpha q q' \psi _{o})\Big ]\nonumber \\&\quad +\frac{1}{\alpha \xi ^4 (\beta _{4}) \psi _{o}}\Big [4 P_{rc} (\xi ^3 \psi _{o}^n (-n \alpha \alpha _{1}+\alpha _{1}+(n \alpha _{1} \alpha \nonumber \\&\quad +\alpha -\alpha _{1}) \psi _{o})-v) (4 \pi P_{rc} \xi ^3 (\psi _{o} (n (\beta _{1}) \psi _{o}-(n \alpha \nonumber \\&\quad -1) (n \alpha _{1}+1))+n \xi ((n+1) (\beta _{1}) \psi _{o}-(n \alpha \nonumber \\&\quad -1) (n \alpha _{1}+1)) \psi _{o}') \psi _{o}^n-12 \pi P_{rc} v \psi _{o}+A^3 \alpha (A \xi q'^2-q q' \nonumber \\&\quad +A q (\xi q''-2 q')) \psi _{o})\Big ]-\frac{A^3 q'^2}{\pi \xi ^4}-\frac{A^3 q q''}{\pi \xi ^4}\nonumber \\&\quad -\frac{1}{\alpha \xi ^2 (\alpha q^2 A^4+\xi (\beta _{3}))}\Big [4 P_{rc} \psi _{o}^n ((n+1) (n \alpha _{1} \alpha +\alpha \nonumber \\&\quad -\alpha _{1}) \psi _{o}-(n \alpha -1) (n \alpha _{1}+\alpha _{1}+1)) (4 \pi P_{rc} \xi (\xi ^3 (-n \alpha \alpha _{1}+\alpha _{1}\nonumber \\&\quad +(\beta _{1}) \psi _{o}) \psi _{o}^n+v)-A^4 \alpha q^2)\Big ]=0, \end{aligned}$$
(74)

where \(\beta _{3}=A^{2}\alpha \xi -8\pi P_{rc} v\) and \(\beta _{4}=A^{4} q\alpha - 8\pi P_{rc}\xi v\).

6.2 Case 2

Using Eqs. (58), (60) and Eq. (70)

$$\begin{aligned}&\Delta =\frac{1}{8 \pi r^3 (q^2-2 m r)}\Big [(-r^2 m'+3 m r-2 q^2+q r q') (m \nonumber \\&\qquad -4 \pi r^3 \psi ^{n+1} (P_{rc}-\alpha _{1} \mu _{c})-4 \pi \alpha _{1} \mu _{c} r^3 \psi ^n)\Big ], \end{aligned}$$
(75)

dimensionless form of Eq. (75) is

$$\begin{aligned}&\Delta =\frac{1}{2 \xi ^3 (8 \pi \mu _{c} \xi v-A^4 q^2)}\Big [\mu _{c} (\xi ^3 \psi ^n ((\alpha _{1}-\alpha ) \psi -\alpha _{1})+v) \nonumber \\&\qquad (A^3 ( -2 A q^2-A \xi q q'+\xi q q')-4 \pi \mu _{c} \xi ^4 \psi ^n+12 \pi \mu _{c} \xi v)\Big ]\nonumber \\ \end{aligned}$$
(76)

for energy density case, class I generalized charged TOV equation is

$$\begin{aligned} \nonumber&-\frac{A^4 q q'}{4 \pi \xi ^4}+\frac{1}{\alpha \xi \beta _{3}}\Big [4 \pi A P_{rc}^2 \psi ^n ((\alpha -\alpha _{1}) \psi +\alpha _{1}+1) (v \nonumber \\&\quad -\xi ^3 \psi ^n ((\alpha _{1}-\alpha ) \psi -\alpha _{1}))\Big ]-\frac{1}{\alpha \xi ^4\beta _{4}}\Big [A P_{rc} (\xi ^3 \psi ^n ((\alpha _{1}\nonumber \\&\quad -\alpha ) \psi -\alpha _{1})+v) (\alpha A^3 (2 A q^2+A \xi q q'-\xi q q')\nonumber \\&\quad +4 \pi \xi ^4 P_{rc} \psi ^n-12 \pi \xi P_{rc} v)\Big ]+\frac{1}{\alpha }\Big [A P_{rc} \psi ^{n-1} \psi ' ((n\nonumber \\&\quad +1) (\alpha -\alpha _{1}) \psi +\alpha _{1} n)\Big ]=0. \end{aligned}$$
(77)

Then by using the Eqs. (62) and (77), second ordered class I generalized charged LEe for this case is

$$\begin{aligned}&\frac{1}{\alpha }\Big [4 P_{rc} \psi ^{n-2} (\psi \psi '' ((n+1) (\alpha -\alpha _{1}) \psi +\alpha _{1} n)+n \psi '^2 ((n\nonumber \\&\quad +1) (\alpha -\alpha _{1}) \psi +\alpha _{1} (n-1)))\Big ]+\frac{1}{\alpha \xi (\beta _{3})}\Big [16 n \pi P_{rc}^2 (\alpha _{1}\nonumber \\&\quad +(\alpha -\alpha _{1}) \psi +1) (v-\xi ^3 \psi ^n ((\alpha _{1}-\alpha ) \psi -\alpha _{1})) \psi ' \psi ^{n-1}\Big ]\nonumber \\&\quad -\frac{1}{\alpha \xi ^2 (\beta _{3} )}\Big [16 \pi P_{rc}^2 (\alpha _{1}+(\alpha -\alpha _{1}) \psi +1) (v\nonumber \\&\quad -\xi ^3 \psi ^n ((\alpha _{1}-\alpha ) \psi -\alpha _{1})) \psi ^n\Big ]+\frac{1}{\alpha \xi (\beta _{3} )}\Big [16 \pi P_{rc}^2 (\alpha \nonumber \\&\quad -\alpha _{1}) (v-\xi ^3 \psi ^n ((\alpha _{1}-\alpha ) \psi -\alpha _{1})) \psi ' \psi ^n\Big ]\nonumber \\&\quad +\frac{1}{\alpha \xi ^2 (\beta _{3})^2}\Big [16 \pi P_{rc}^2 \psi ^n (\alpha _{1}\nonumber \\&\quad +(\alpha -\alpha _{1}) \psi +1) (v-\xi ^3 \psi ^n ((\alpha _{1}-\alpha ) \psi -\alpha _{1})) (8 \pi P_{rc} \xi ^3 \psi ^n\nonumber \\&\quad -A^2 \alpha \xi +2 A^4 \alpha q q')\Big ]+\frac{1}{\alpha \xi ^5 (\beta _{4})}\Big [16 P_{rc} (\xi ^3 ((\alpha _{1}\nonumber \\&\quad -\alpha ) \psi -\alpha _{1}) \psi ^n+v) (4 \pi P_{rc} \xi ^4 \psi ^n\nonumber \\&\quad -12 \pi P_{rc} \xi v+A^3 \alpha (2 A q^2-\xi q' q\nonumber \\&\quad +A \xi q q'))\Big ]+\frac{1}{\alpha \xi ^4 (\beta _{4})^2}\Big [8 P_{rc} (\xi ^3 ((\alpha _{1}-\alpha ) \psi -\alpha _{1}) \psi ^n\nonumber \\&\quad +v) (\alpha q q' A^4+4 \pi P_{rc} (\xi ^3 \psi ^n+v)) \nonumber \\&\quad \times (-4 \pi P_{rc} \xi ^4 \psi ^n+12 \pi P_{rc} \xi v+A^3 \alpha (\nonumber \\&\quad -2 A q^2+\xi q' q-A \xi q q'))\Big ]+\frac{1}{\alpha \xi ^2 (\beta _{3})}\Big [4 P_{rc} \psi ^{n-1} (\alpha _{1}+(\alpha \nonumber \\&\quad -\alpha _{1}) \psi +1) (4 \pi P_{rc} \xi ^3 (\psi (3 \alpha _{1}+3 (\alpha -\alpha _{1}) \psi +1)\nonumber \\&\quad +\xi (n \alpha _{1}+(n+1) (\alpha \nonumber \\&\quad -\alpha _{1}) \psi ) \psi ') \psi ^n+A^4 \alpha q q' \psi )\Big ]-\frac{1}{\pi \alpha \xi ^5 (\beta _{4}) \psi }\Big [(4 \pi P_{rc} \xi ^4 \psi ^n\nonumber \\&\quad -12 \pi P_{rc} \xi v+A^3 \alpha (2 A q^2-\xi q' q+A \xi q q')) \nonumber \\&\quad \times (4 \pi P_{rc} \xi ^3 (\psi (-3 \alpha _{1}\nonumber \\&\quad +3 (\alpha _{1}-\alpha ) \psi +1)+\xi ((n+1) (\alpha _{1}-\alpha ) \psi \nonumber \\&\quad -n \alpha _{1}) \psi ') \psi ^n+A^4 \alpha q q' \psi )\Big ]\nonumber \\&\quad +\frac{1}{\alpha \xi ^4 (\beta _{4} ) \psi }\Big [4 P_{rc} (-\xi ^3 ((\alpha _{1}-\alpha ) \psi -\alpha _{1}) \psi ^n-v) \nonumber \\&\quad \times (4 \pi P_{rc} \xi ^3 (\psi \nonumber \\&\quad +n \xi \psi ') \psi ^n+(A^3 \alpha (A \xi q'^2-q q'+A q (\xi q''-2 q'))\nonumber \\&\quad -12 \pi P_{rc} v) \psi )\Big ]\nonumber \\&\quad -\frac{1}{\pi \xi ^5}{A^3 (\xi q'^2+q (\xi q''-4 q'))}=0. \end{aligned}$$
(78)

Now we repeat the same procedure for isothermal regime \((\gamma =1)\) for which only energy density case is taken into consideration. For this purpose, we use Eqs. (58), (64) and Eq. (70), so obtain

$$\begin{aligned} \Delta= & {} \frac{-1}{8 \pi r^3 (q^2-2 m r)}\Big [e^{-\psi } (m e^{\psi }-4 \pi {P_{rc}} r^3) \nonumber \\&\times (-r^2 m'+3 m r-2 q^2+q r q')\Big ], \end{aligned}$$
(79)

dimensionless form of Eq. (79) is

$$\begin{aligned} \Delta= & {} \frac{1}{2 \xi ^3 (8 \pi \mu _{c} \xi v-B^4 q^2)}\Big [\mu _{c} e^{-\psi } (v e^{\psi }-\alpha \xi ^3) (-2 B^4 q^2 \nonumber \\&+B^3 \xi q q'-4 \pi \mu _{c} \xi ^2 v'+12 \pi \mu _{c} \xi v)\Big ], \end{aligned}$$
(80)

class I generalized charged TOV equation \((\gamma =1)\) is

$$\begin{aligned}&-\frac{B^4 q q'}{4 \pi \xi ^4}+\frac{1}{\alpha \xi (\alpha B^2 \xi -8 \pi P_{rc} v)}\nonumber \\&\quad \times \Big [4 \pi B P_{rc}^2 e^{-2 \psi } (\alpha +e^{2 \psi }) (\alpha \xi ^3+e^{\psi } v)\Big ] \nonumber \\&\quad +\frac{1}{\alpha \xi ^4 (\alpha B^4 q^2-8 \pi \xi P_{rc} v)}\nonumber \\&\quad \times \Big [B P_{rc} e^{-\psi } (\alpha \xi ^3-e^{\psi } v) (\alpha B^3 q ((B-1) \xi q' \nonumber \\&\quad +2 B q)+4 \pi \xi P_{rc} (\xi ^3 e^{\psi }-3 v))\Big ]-B P_{rc} e^{-\psi } \psi '=0,\nonumber \\ \end{aligned}$$
(81)

and second ordered class I generalized charged LEe is

$$\begin{aligned}&\frac{4 q q' B^3}{\pi \xi ^5}-\frac{q'^2 B^3}{\pi \xi ^4}-\frac{q q'' B^3}{\pi \xi ^4}+4 e^{-\psi } P_{rc} \psi '^2\nonumber \\&\quad +\frac{1}{\alpha \xi ^2 (B^2 \alpha \xi -8 \pi P_{rc} v)^2}\Big [16 e^{-2 \psi } \pi P_{rc}^2 (\alpha +e^{2 \psi }) (\alpha \xi ^3\nonumber \\&\quad +e^{\psi } v) (2 \alpha q q' B^4+8 e^{\psi } \pi P_{rc} \xi ^3-B^2 \alpha \xi )\Big ]\nonumber \\&\quad +\frac{1}{\alpha \xi (8 \pi P_{rc} v-B^2 \alpha \xi )}\Big [32 e^{-2 \psi } \pi P_{rc}^2 (\alpha +e^{2 \psi }) (\alpha \xi ^3\nonumber \\&\quad +e^{\psi } v) \psi '\Big ]+\frac{1}{\alpha \xi (B^2 \alpha \xi -8 \pi P_{rc} v)}\nonumber \\&\quad \times \Big [32 \pi P_{rc}^2 (\alpha \xi ^3+e^{\psi } v) \psi '\Big ]\nonumber \\&\quad +\frac{1}{\pi \alpha \xi ^5 (8 \pi P_{rc} \xi v-B^4 \alpha q^2)}\nonumber \\&\quad \times \Big [e^{-\psi } (\alpha q (2 B q+(B-1) \xi q') B^3\nonumber \\&\quad +4 \pi P_{rc} \xi (e^{\psi } \xi ^3-3 v)) (4 \pi P_{rc} (e^{2 \psi }-3 \alpha ) \xi ^3\nonumber \\&\quad +e^{\psi } (\alpha q q' B^4+4 \pi P_{rc} \xi v \psi '))\Big ]\nonumber \\&\quad +\frac{1}{\alpha \xi ^4 (8 \pi P_{rc} \xi v-B^4 \alpha q^2)}\Big [4 e^{-\psi } P_{rc} (e^{\psi } v\nonumber \\&\quad -\alpha \xi ^3) (\alpha ((B-1) \xi q'^2+q ((2 B-1) q'+(B-1) \xi q'')) B^3\nonumber \\&\quad -12 \pi P_{rc} v+4 e^{\psi } \pi P_{rc} \xi ^3 (\xi \psi '+1))\Big ]-4 e^{-\psi } P_{rc} \psi ''\nonumber \\&\quad +\frac{1}{\alpha \xi ^2 (8 \pi P_{rc} v-B^2 \alpha \xi )}\Big [16 e^{-2 \psi } \pi P_{rc}^2 (\alpha +e^{2 \psi }) (\alpha \xi ^3+e^{\psi } v)\Big ]\nonumber \\&\quad -\frac{1}{\alpha \xi ^2 (8 \pi P_{rc} v-B^2 \alpha \xi )}\Big [4 e^{-2 \psi } P_{rc} (\alpha +e^{2 \psi }) (4 \pi P_{rc} (3 \alpha \nonumber \\&\quad +e^{2 \psi }) \xi ^3+e^{\psi } (\alpha q q' B^4+4 \pi P_{rc} \xi v \psi '))\Big ]\nonumber \\&\quad -\frac{1}{\alpha \xi ^4 (B^4 \alpha q^2-8 \pi P_{rc} \xi v)}\Big [4 e^{-\psi } P_{rc} (\alpha \xi ^3-e^{\psi } v) (\alpha q (2 B q \nonumber \\&\quad +(B-1) \xi q') B^3+4 \pi P_{rc} \xi (e^{\psi } \xi ^3-3 v)) \psi '\Big ]\nonumber \\&\quad -\frac{1}{\alpha \xi ^5 (B^4 \alpha q^2-8 \pi P_{rc} \xi v)}\nonumber \\&\quad \times \Big [16 e^{-\psi } P_{rc} (\alpha \xi ^3-e^{\psi } v) (\alpha q (2 B q\nonumber \\&\quad +(B-1) \xi q') B^3+4 \pi P_{rc} \xi (e^{\psi } \xi ^3-3 v))\Big ]\nonumber \\&\quad -\frac{1}{\alpha \xi ^4 (B^4 \alpha q^2-8 \pi P_{rc} \xi v)^2}\Big [32 e^{-\psi } \pi P_{rc}^2 (e^{\psi } \xi ^3+v) (e^{\psi } v\nonumber \\&\quad -\alpha \xi ^3) (\alpha q (2 B q+(B-1) \xi q') B^3 \nonumber \\&\quad +4 \pi P_{rc} \xi (e^{\psi } \xi ^3-3 v))\Big ] =0. \end{aligned}$$
(82)

Following energy conditions must be satisfied

$$\begin{aligned} \mu +\frac{q^{2}}{8\pi r^{4}}>0,\quad \frac{P_{r}}{\mu }\le 1+\frac{q^{2}}{4\pi r^{4}}, \quad \frac{P_{\perp }}{\mu }\le 1. \end{aligned}$$
(83)

For case 1 \((\gamma \ne 1)\) conditions (83) takes the form

$$\begin{aligned}&\frac{A^{4}q}{8\pi \xi ^{4}} (q+2\xi q')+\mu _{o} \psi _{o}[(1-n \alpha )(1+n\alpha _{1})+n(\alpha \nonumber \\&\qquad -\alpha _{1}+n\alpha \alpha _{1})\psi _{o}]>0,\nonumber \\&A^4 q (\xi q'+q)+4 \pi \xi ^4 \psi _{o}^n (-\alpha _{1} \mu _{oc}+\psi _{o} (\alpha _{1} \mu _{oc}+\alpha _{1} \mu _{c} n (\alpha n\nonumber \\&\qquad -1)+\alpha \mu _{c} (n-1))+\mu _{c} (-(\alpha n-1)) (\alpha _{1} n+1))\ge 0,\nonumber \\&\frac{1}{2 \xi ^3 (8 \pi \mu _{c} \xi v-A^4 q^2)}\Big [\mu _{c} (v-\xi ^3 \psi _{o}^n (\alpha _{1}\nonumber \\&\qquad +\psi _{o} (\alpha -\alpha _{1}+\alpha \alpha _{1} n)\nonumber \\&\qquad +\alpha \alpha _{1} (-n))) (A^3 (\xi q q'-A (2 q^2+\xi q q'))\nonumber \\&\qquad -4 \pi \mu _{c} \xi ^4 \psi _{o}^n (n \psi _{o} (\alpha \nonumber \\&\qquad -\alpha _{1}+\alpha \alpha _{1} n)+(1-\alpha n) (\alpha _{1} n+1))+12 \pi \mu _{c} \xi v)\Big ]\nonumber \\&\quad \le \frac{A^4 q q'}{4 \pi \xi ^3}\nonumber \\&\qquad +\mu _{c} \psi _{o}^n (n \psi _{o} (\alpha -\alpha _{1}+\alpha \alpha _{1} n)+(1-\alpha n) (\alpha _{1} n+1))\nonumber \\&\qquad +\alpha _{1} \mu _{oc} (\psi _{o}-1) \psi _{o}^n, \end{aligned}$$
(84)

and for Case 2 \((\gamma \ne 1)\) these conditions (83) are

$$\begin{aligned}&\mu +\frac{A^{4} q_{2}}{8\pi \xi ^{4}}>0,\quad \alpha _{1}+\psi (\alpha -\alpha _{1})\le 1+\frac{A^{4} q_{2}}{4\pi \xi ^{4}\psi ^{n}},\nonumber \\&\frac{1}{2 \xi ^3 (8 \pi \mu _{c} \xi v-A^4 q^2)}\Big [\mu _{c} (\xi ^3 \psi ^n ((\alpha _{1}-\alpha ) \psi -\alpha _{1})+v) (A^3 q (-(A\nonumber \\&\quad -1) \xi q'-2 A q)-4 \pi \mu _{c} \xi (\xi ^3 \psi ^n-3 v))\Big ]\nonumber \\&\quad +\alpha \mu _{c} \psi ^{n+1}\le \frac{A^4 q q'}{4 \pi \xi ^3}\nonumber \\&\quad +\psi ^n (\alpha _{1} \mu _{oc} \psi -\alpha _{1} \mu _{oc}+\mu _{c}). \end{aligned}$$
(85)

Now for isothermal regime \((\gamma =1)\) energy conditions will be

$$\begin{aligned}&\mu _{c}e^{-\psi }+\frac{A^{4} q_{2}}{8\pi \xi ^{4}}>0,\quad \alpha \le 1,\quad \frac{1}{2} \mu {_c} e^{-2 \psi } (2 \alpha e^{\psi }\nonumber \\&\qquad +\frac{1}{\xi ^3 (8 \pi \mu {_c} \xi v-B^4 q^2)}\Big [(\alpha \xi ^3-e^{\psi } v) (e^{\psi } (B^3 q ((B\nonumber \\&\qquad -1) \xi q'+2 B q)-12 \pi \mu {_c} \xi v)+4 \pi \mu {_c} \xi ^4)\Big )\nonumber \\&\quad \le \frac{B^4 q q'}{4 \pi \xi ^3}+\mu {_c} e^{-\psi }. \end{aligned}$$
(86)

7 Class I relativistic generalized polytropes with vanishing complexity factor

7.1 Case no. 1

Class I GPEoS with the notation in Eqs. (51, 52) will be integrated with vanishing complexity factor \(Y_{TF}=0\), and read as

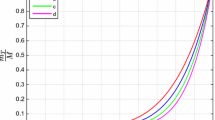
$$\begin{aligned}&(5-16 \pi ) A^4 \xi q q'+(8 \pi -1) A^4 q^2\nonumber \\&\quad +\frac{1}{8 \pi \mu _{c} \xi v-A^4 q^2}\Big [12 \pi \xi (\mu _{c} \xi ^3 \psi _{o}^n (\alpha _{1}\nonumber \\&\quad +\psi _{o} (\alpha -\alpha _{1}+\alpha \alpha _{1} n)+\alpha \alpha _{1} (-n))-\mu _{c} v) \nonumber \\&\quad \times (A^3 q ((A-1) \xi q'+2 A q)\nonumber \\&\quad +4 \pi \mu _{c} \xi (\xi ^3 \psi _{o}^n (n \psi _{o} (\alpha -\alpha _{1}+\alpha \alpha _{1} n)\nonumber \\&\quad +(1-\alpha n) (\alpha _{1} n+1))-3 v))\Big ]\nonumber \\&\quad +8 \pi \xi ^5 \Delta '-4 \pi \mu _{c} n \xi ^5 \psi _{o}^{n-1} \psi _{o}' ((n+1) \psi _{o} (\alpha -\alpha _{1}+\alpha \alpha _{1} n)\nonumber \\&\quad -(\alpha n-1) (\alpha _{1} n+1))=0. \end{aligned}$$
(87)

Equations (55, 73, 87) form a system of first order DEs. This system is solved numerically for fixed values of \(\alpha =.5\), \(\alpha _{1}=.5\) and \(q=.5\). Figures 1, 2 and 3 show the patterns of v, \(\psi _{o}\) and \(\Delta \) for different values of n.

Fig. 1
figure 1

Curves of \(v(\xi )\)

Full size image
Fig. 2
figure 2

Curves of \(\psi _{o}(\xi )\)

Full size image
Fig. 3
figure 3

Curves of \(\Delta (\xi )\)

Full size image

7.2 Case no. 2

In this case the complexity factor will be read as

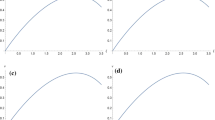
$$\begin{aligned}&(5-16 \pi ) A^4 \xi q q'+(8 \pi -1) A^4 q^2 \nonumber \\&\quad -\frac{1}{8 \pi \mu _{c} \xi v-A^4 q^2}\Big [12 \pi \mu _{c} \xi (\xi ^3 \psi ^n ((\alpha _{1} \nonumber \\&\quad -\alpha ) \psi -\alpha _{1})+v) (A^3 q ((A-1) \xi q'+2 A q)\nonumber \\&\quad +4 \pi \mu _{c} \xi (\xi ^3 \psi ^n-3 v))\Big ]\nonumber \\&\quad +8 \pi \xi ^5 \Delta '-4 \pi \mu _{c} n \xi ^5 \psi ^{n-1} \psi '=0. \end{aligned}$$
(88)

For \(\alpha _{1}=.5\), \(\alpha =.5\) and \(n=.5\). Figures 4, 5 and 6 show the behaviors of v, \(\psi \) and \(\Delta \) for fixed values of \(\alpha =.5\), \(\alpha _{1}=.5\), \(q=.125\) and different values of n. These behaviors are numerically obtained by solving the system of ordinary DEs (62, 77, 88).

Fig. 4
figure 4

Curves of \(v(\xi )\)

Full size image
Fig. 5
figure 5

Curves of \(\psi (\xi )\)

Full size image
Fig. 6
figure 6

Curves of \(\Delta (\xi )\)

Full size image

Now we set class I GPs \((\gamma =1)\) with vanishing complexity factor \(Y_{TF}=0\) will be consider as

$$\begin{aligned}&(5-16 \pi ) B^4 \xi q q'+(8 \pi -1) B^4 q^2 \nonumber \\&\quad +\frac{1}{8 \pi \mu _{c} \xi v-B^4 q^2}\Big [12 \pi \mu _{c} \xi e^{-2 \psi } (\alpha \xi ^3 \nonumber \\&\quad -e^{\psi } v) (e^{\psi } (B^3 q ((B-1) \xi q'+2 B q)-12 \pi \mu _{c} \xi v) \nonumber \\&\quad +4 \pi \mu _{c} \xi ^4)\Big ] \nonumber \\&\quad +8 \pi \xi ^5 \Delta ' +4 \pi \mu _{c} \xi ^5 e^{-\psi } \psi '=0. \end{aligned}$$
(89)

Equations (64, 81, 89) form a system of first order DEs with the same variables as discussed in case \({\textbf {2}}\; (\gamma \ne 1)\). This system also solved numerically for fixed value of \(\alpha \) and different values of charge. Its solution is depicted through graphs of Figs. 7, 8 and 9, describe the behavior of v, \(\psi \) and \(\Delta \).

Fig. 7
figure 7

Curves of \(v(\xi )\)

Full size image
Fig. 8
figure 8

Curves of \(\psi (\xi )\)

Full size image
Fig. 9
figure 9

Curves of \(\Delta (\xi )\)

Full size image

8 Conclusion

To study the different physical features and characteristics of self gravitating sources, the idea of GPEoS [16,17,18,19,20,21, 36,37,38], Karmarkar condition [27,28,29,30,31], complexity factor [32,33,34,35,36,37,38] and phenomena of charge [16, 17, 22,23,24,25,26, 35, 38] have been widely used in the recent past. In the present work these ideas regarding self gravitating sources have been integrated to discuss some properties \((v, \psi _{o},\psi ,\Delta )\) under non-isothermal and isothermal regimes. For this purpose a generalized framework is established to develop a modified form of class I charged LEe by using the spherical symmetry for static anisotropic fluid distribution. Basic field equations are implemented to set up class I TOV equation under electromagnetic effect. The Weyl tensor and mass function are developed, structure scalars are calculated with the help of curvature and tensor and CF is defined through these scalars. Class I charged GPs, with two cases: \({\textbf {(1)}}\) mass density, and \({\textbf {(2)}}\) energy density for spherically charged static fluid distribution brought into play to establish the class I charged LEe under both non-isothermal and isothermal regimes. Energy conditions for all the cases have also been established in the presence of charge. Then three pair of LEs (53, 73), (62, 77) and (66, 81) form three sets of ordinary DEs with vanishing CF. These sets of DEs are solved numerically and their solutions are discussed graphically below.

It is noticeable that behaviors of v, \(\psi _{o}\), \(\psi \) and \(\Delta \) functions Figs. 1, 2, 3, 4, 5 and 6, are not much effected by the charge. It is observed that the systems (55, 73, 87) and (62, 77, 88) remain stable only for very low fixed value of charge. It is made out that in Figs. 1 and 4 the value of mass v for case \({\textbf {(1)}}\) and case \({\textbf {(2)}}\) respectively in non isothermal regime behave in the same manner. Curves of these figures show that a self gravitating astronomical object is more dense in mass at boundary surface and becomes less dense with the increase of value of n at boundary.

Figures 2 and 5 tell us about the pattern of \(\psi _{o}\) and \(\psi \) for mass density case and energy density case respectively. These figures show that \(\psi _{o}\) and \(\psi \) have maximum value at center and gradually decreases with the increase of value of n toward the boundary of object.

The value of anisotropic factor \(\Delta \) shows entirely different pattern for case (1) and case (2) in Figs. 3 and 6 respectively. As we know the fact that radial and tangential pressure must be same at center for the stability of self gravitating object, so the Fig. 3 is exactly according to this fact but Fig. 6, in energy density case shows abnormality.

For isothermal regime \((\gamma =1)\), the solutions of set of DEs (64), (81), (89) illustrate the results of variables v, \(\psi \) and \(\Delta \) for fixed value of parameters and decreasing values of charge q, shown in Figs. 7, 8 and 9. Figure 7 shows that value of mass function v increases from center to the boundary as value of q increases. While variable \(\psi \) in Fig. 8 has maximum value at center then become constant going along radius and then decreasing at boundary surface of self gravitating source. The variable \(\Delta \) in Fig. 9 exhibit almost same behavior for different value of charge as shown by variable v in Fig. 7. It is worth mentioning that sets of DEs (53, 73, 87), (62, 77, 88) and (64, 81, 89) give numerical solution for constant and decreasing value of charge. If we change this configuration of charge all these set of DEs show singularity and system dose not remain stable. The main purpose of this work is to established the modified form of class I charged generalized LEe in connection with CF complemented by the Karmarkar condition as it gives solution of some system of DEs numerically in view of spherically symmetry to describe the internal structure of self gravitating object.