Abstract
Predictions for the Higgs masses are a distinctive feature of supersymmetric extensions of the Standard Model, where they play a crucial role in constraining the parameter space. The discovery of a Higgs boson and the remarkably precise measurement of its mass at the LHC have spurred new efforts aimed at improving the accuracy of the theoretical predictions for the Higgs masses in supersymmetric models. The “Precision SUSY Higgs Mass Calculation Initiative” (KUTS) was launched in 2014 to provide a forum for discussions between the different groups involved in these efforts. This report aims to present a comprehensive overview of the current status of Higgs-mass calculations in supersymmetric models, to document the many advances that were achieved in recent years and were discussed during the KUTS meetings, and to outline the prospects for future improvements in these calculations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The spectacular discovery of a scalar particle with mass around 125 GeV by the ATLAS and CMS collaborations [1,2,3] at CERN constitutes a milestone in the quest for understanding the physics of electroweak symmetry breaking (EWSB). While the properties of the observed particle are compatible with those predicted for the Higgs boson of the Standard Model (SM) within the present experimental and theoretical uncertainties [4], they are also in agreement with the predictions of many models of physics beyond the SM (BSM). For the latter, the requirement that the model under consideration include a state that can be identified with the observed particle can translate into important constraints on the model’s parameter space.
One of the prime candidates for BSM physics is supersymmetry (SUSY), which predicts scalar partners for all SM fermions, as well as fermionic partners for all bosons. A remarkable feature of SUSY extensions of the SM is the requirement of an extended Higgs sector, with additional neutral and charged bosons. In such models the couplings of the Higgs bosons to matter fermions and to gauge bosons can differ significantly from those of the SM Higgs. Moreover, in contrast to the case of the SM, the masses of the Higgs bosons are not free parameters, as SUSY requires all quartic scalar couplings to be related to the gauge and Yukawa couplings. For example, in the minimal SUSY extension of the SM, the MSSM, the tree-level mass of the lighter neutral CP-even scalar in the Higgs sector is bounded from above by the mass of the Z boson. However, radiative corrections involving loops of SM particles and their SUSY partners alter the tree-level predictions for the Higgs masses, introducing a dependence on all of the SUSY-particle masses and couplings. The most relevant corrections to the Higgs masses in the MSSM are those controlled by the top Yukawa coupling, which involve the top quark and its scalar partners, the stops. These corrections are enhanced by logarithms of the ratio between stop and top masses, and also show a significant dependence on the value of the left–right stop mixing parameter \(X_t\). In particular, a SM-like Higgs boson with mass around 125 GeV can be obtained in the MSSM with an average stop mass \(M_S\) of about 2 TeV when \(|X_t/M_S| \approx 2\), whereas for vanishing \(X_t\) the stops need to be heavier than 10 TeV.
Non-minimal SUSY extensions of the SM have also been considered: in the next-to-minimal extension, the NMSSM, the Higgs sector of the MSSM is augmented with a gauge-singlet complex scalar and its fermionic partner; the so-called “\(\mu \)-from-\(\nu \)” extension, or \(\mu \nu \)SSM, includes right-handed neutrinos and their scalar partners; models with Dirac gauginos include additional scalars and fermions in the adjoint representation of their gauge groups. Most of these models feature additional tree-level contributions to the quartic Higgs couplings, as well as additional contributions to the radiative corrections to the Higgs masses. As a consequence, the tree-level bound on the mass of the lightest neutral scalar is in general relaxed, and a SM-like Higgs boson of suitable mass can be obtained with smaller stop masses than in the case of the MSSM.
Since the first realization of the importance of the radiative corrections in the early 1990s, an impressive theoretical effort has been devoted to the precise calculation of the Higgs masses in SUSY extensions of the SM. This effort focused initially on the simplest realization of the MSSM, assuming the conservation of CP symmetry, R-parity and flavor, but it eventually grew to include the most general MSSM Lagrangian, as well as non-minimal SUSY extensions of the SM such as those mentioned above. The discovery of a Higgs boson in 2012 at CERN has given new impetus to the quest for high-precision predictions for the Higgs masses in SUSY models. First of all, the need for multi-TeV stop masses (namely, \(M_S\gtrsim 2\) TeV, at least in the MSSM) to ensure a Higgs mass of about 125 GeV implies that the logarithmically-enhanced corrections controlled by the top Yukawa coupling are particularly large. To obtain a reliable prediction for the mass of the SM-like Higgs boson, these corrections should be resummed to all orders in the perturbative expansion by means of an effective field theory (EFT) approach. More generally, for the available information on the Higgs mass to be most effectively exploited when constraining the parameter space of SUSY models, the uncertainty of the theory prediction should ideally be below the experimental precision of the measurement, which has already reached the per-mille level.
The uncertainty of the theory prediction for the Higgs masses in a given SUSY model should be estimated for each considered point of the SUSY parameter space. The uncertainty has a “parametric” component, arising from the experimental uncertainty of the SM input parameters, and a proper “theory” component, arising from unknown corrections that are of higher order with respect to the accuracy of the calculation. While the former can be straightforwardly estimated, and is currently dominated by the uncertainty of the top mass, the latter, which we are henceforth denoting as “theory uncertainty”, requires a fair amount of guesswork on the expected size of the uncomputed corrections. Rule-of-thumb estimates of about 3 GeV for the theory uncertainty of the prediction for the SM-like Higgs mass in the MSSM were provided in the early 2000s, based on the accuracy of the then-available calculations and on the expectation that the SUSY scale would be at most of the order of 1 TeV. While the progress in the Higgs-mass calculations in SUSY models should have naturally entailed an overall reduction of the theory uncertainty, further studies made it clear that the latter can still vary substantially, depending on the specific region of the SUSY parameter space that is being considered. Even in the most favorable scenarios, the theory uncertainty of the prediction for a SM-like Higgs mass in the MSSM remains at the percent level, i.e. one order of magnitude larger than the experimental precision of the measurement. For SUSY models beyond the MSSM only a few studies of the theory uncertainty of the Higgs-mass predictions have been performed so far. The presence of additional particles and interactions contributing to the radiative corrections generally increases the theory uncertainty in these models compared to the MSSM. For specific regions in the parameter space, however, the radiative corrections required to obtain a Higgs mass of 125 GeV, and thus the associated uncertainty, can be smaller than is typically the case in the MSSM.
In order to address this situation and bring the theory uncertainty of the Higgs-mass predictions in SUSY models closer to the experimental precision, the “Precision SUSY Higgs Mass Calculation Initiative” (KUTS)Footnote 1 was launched in 2014. The initiative aims to provide a forum for discussions between the different groups involved in the calculation of the Higgs masses in SUSY models. Since its inception, eleven KUTS meetings have taken place,Footnote 2 discussing the advances achieved over the years. These included: new fixed-order (FO) calculations of the Higgs masses in the MSSM and other SUSY models; new EFT calculations for the all-order resummation of large logarithmic effects; the improved combination of FO and EFT calculations; efforts to provide a reliable estimate of the theory accuracy as a function of the SUSY parameters; new or improved computer codes for a state-of-the-art numerical evaluation of SUSY Higgs boson masses.
The purpose of this report is two-fold. On the one hand, we aim to provide a comprehensive overview of the status of Higgs-mass calculations in SUSY models. On the other hand, we document the specific advances that were achieved in recent years and were discussed during the KUTS meetings, and we outline the prospects for future improvements in these calculations. The report is written as a non-technical review, in which the interested reader is guided to the literature where detailed accounts of the different topics can be found. In Sect. 2 we provide a general introductionFootnote 3 to high-precision predictions for the Higgs masses in SUSY models; in Sects. 3 to 5 we discuss in detail the recent advances in the FO, EFT and “hybrid” calculations, respectively; Sect. 6 concerns the estimation of the theory uncertainty; Sect. 7 provides an outlook. Finally, we include in the Appendix a survey of the existing public codes for Higgs-mass calculations in SUSY models.
2 Calculating the Higgs masses in SUSY extensions of the SM
2.1 Radiative corrections to the Higgs masses
The squared physical masses of a set of n scalar fields that mix with each other are the real parts of the solutions for \(p^2\) of the equation
where \(\Gamma _{ij}(p^2)\) denotes the \(n\times n\) inverse-propagator matrix, p being the external momentum flowing into the scalar self-energies. We can decompose \(\Gamma _{ij}(p^2)\) as
where \({\mathcal {M}}_{ij,\,0}^2\) denotes the tree-level mass matrix written in terms of renormalized parameters, and \(\Delta {\mathcal {M}}_{ij}^2(p^2)\) collectively denotes the radiative corrections to the mass matrix.
The entries of \({\mathcal {M}}_{ij,\,0}^2\) are in general combinations of mass parameters (\(m^2_{ij}\)) for the scalar fields and of products of trilinear (\(a_{ijk}\)) and quartic (\(\lambda _{ijkl}\)) scalar couplings with appropriate powers of the vacuum expectation values (vevs) of the scalar fields, \(v_i\). The minimum conditions of the scalar potential relate the mass parameters in the tree-level mass matrix to combinations of other mass parameters, couplings and vevs. In SUSY models, the quartic scalar couplings are not free parameters, but are related to combinations of the gauge couplings (via the D-term contributions to the scalar potential) and of the Yukawa couplings (via the F-term contributions). This leads to non-trivial relations among the scalar masses and the other parameters of the model. For example, in the MSSM – whose Higgs sector consists of two SU(2) doublets \(H_1\) and \(H_2\) with opposite hypercharge – one finds the well-known tree-level formula for the masses of the lighter and heavier CP-even Higgs bosons, denoted as h and H, respectively
where \(M_A\) is the mass of the CP-odd Higgs boson, \(M_Z\) is the mass of the Z boson, and \(\tan \beta \equiv v_2/v_1\) is the ratio of the vevs of the two doublets. This leads to the tree-level bound \(M_h<M_Z|\cos 2\beta |\), which is saturated for \(M_A\gg M_Z\).
At each order in the perturbative expansion, the radiative corrections \(\Delta {\mathcal {M}}_{ij}^2(p^2)\) in Eq. (2) include: momentum-dependent contributions of the scalar self-energies, \(\Sigma _{ij}(p^2)\); “tadpole” contributions, \(T_i\), arising if the minimum conditions of the potential have been used to simplify the tree-level matrix; contributions of the renormalization constants of the scalar fields, \(\delta Z_{ij}\); finally, counterterm contributions arising from the renormalization of the parameters that enter the lower-order parts of \(\Gamma _{ij}(p^2)\). In a pure FO approach, the radiative corrections to the scalar masses are obtained by evaluating \(\Delta {\mathcal {M}}_{ij}^2(p^2)\) as a power series in the various coupling constants up to a certain order in the perturbative expansion. For example, the numerically dominant one-loop corrections to the Higgs mass matrix in the MSSM, i.e. those involving top and stop loops and controlled only by the top Yukawa coupling \(y_t\), are proportional to \(y_t^4\,v^2/(16\pi ^2)\), where \(v^2\equiv v_1^2 + v_2^2 ~{\approx (174~\mathrm{GeV})^2}\). The dominant two-loop corrections are in turn proportional to \(y_t^6\,v^2/(16\pi ^2)^2\) and to \(y_t^4\,g_s^2\,v^2/(16\pi ^2)^2\), where \(g_s\) is the strong gauge coupling.Footnote 4 We also note that the calculation of each physical scalar mass \(M_i^2\) requires that Eq. (1) be solved at the complex pole \(p^2=M_i^2 - i\Gamma _i M_i\), which turns it into an implicit equation. This can be solved either order by order or via a numerical iterative solution. The latter approach leads to a mixing of orders in the perturbative expansion, which can have undesirable consequences such as, e.g., a violation of gauge invariance by terms that are of higher order with respect to the accuracy of the calculation.
The complexity of a calculation of radiative corrections increases with the number of loops and the number of scales (masses and external momenta) on which the corresponding loop integrals depend. At the one-loop level, a general solution in terms of analytic functions is always possible, and the most complicated functions entering one- and two-point diagrams such as tadpoles and self-energies are simple logarithms. Hence, fully analytic calculations of the one-loop corrections to the Higgs masses are by now available for most of the SUSY models considered in the literature. Beyond the one-loop level, fully analytic results are currently available only for special cases, and in general a numerical evaluation of the loop integrals is required. On the other hand, much simpler results for the two-loop and higher-order integrals can be obtained analytically by adopting certain approximations; most notably, when setting the external momentum in the self-energy to zero, the two-loop integrals can be expressed in terms of at most dilogarithms. In contrast, some three-loop integrals with vanishing external momentum but arbitrary masses still need to be evaluated numerically. In the presence of hierarchies between some of the masses, however, analytical results for the three-loop integrals can be obtained via asymptotic expansions. In order to obtain the most accurate predictions available for the Higgs masses it is standard practice to combine the full results for the one-loop corrections with approximate results for the higher-loop corrections.
In the limit of vanishing external momentum, tadpole and self-energy diagrams can be connected to the derivatives of the effective potential \(V_{\mathrm{eff}} = V_0 + \Delta V\), where \(V_0\) is the tree-level potential and \(\Delta V\) is the sum of one-particle-irreducible (1PI) vacuum diagrams, expressed in terms of field-dependent particle masses and couplings. In particular, one has
where the derivatives are evaluated at the minimum of \(V_{\mathrm{eff}}\). As it requires only the calculation of vacuum diagrams, followed by a straightforward application of the chain rule to obtain the derivatives of \(\Delta V\) with respect to the Higgs fields \(\phi _i\), the effective-potential approach typically allows for a simpler calculation of tadpoles and zero-momentum self-energies when compared to the direct calculation of Feynman diagrams with one or two external legs. The two approaches must of course give the same final result, as long as the same approximations and the same renormalization conditions are employed in each calculation.
Strictly speaking, the approximation of vanishing external momentum in the two-loop corrections to a particle’s mass is justified only if the tree-level mass of that particle can itself be considered vanishing. For the mass of the lighter CP-even Higgs boson of the MSSM, in view of the tree-level upper bound \(M_h<M_Z|\cos 2\beta |\), that approximation can be consistently adopted in the so-called “gaugeless limit”, in which the electroweak (EW) gauge couplings g and \(g^\prime \) are set to zero in the two-loop corrections (indeed, this also implies \(M_Z\rightarrow 0\)). In the gaugeless limit the two-loop corrections to the MSSM Higgs masses depend only on the Yukawa couplings and on \(g_s\,\); the numerically dominant corrections are indeed those of \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) and \({{{\mathcal {O}}}}(\alpha _t^2)\), while the corrections involving the bottom and tau Yukawa couplings become relevant only at large values of \(\tan \beta \). All complications of the non-Abelian \(SU(2)\times U(1)\) gauge group, such as, e.g., those related to gauge fixing and ghost fields, are absent in this limit, and the number of diagrams contributing to the Higgs-mass corrections is smaller than in the general case.
For the heavier CP-even scalar, as well as for the CP-odd and charged scalars, the approximation of vanishing tree-level mass is in general not justified. However, in most of the phenomenologically relevant MSSM scenarios the tree-level masses of the heavier Higgs bosons are large enough that the impact of the radiative corrections is much reduced with respect to the case of the lighter, SM-like Higgs boson. In these scenarios, a precise calculation of the masses of the heavier Higgs bosons is relevant only if their differences are studied. For example, in the MSSM with complex parameters a CP-violating mixing between the two heavy neutral states can lead to resonance-type effects that sensitively depend on the difference between their masses. In models beyond the MSSM, the approximation of vanishing external momentum in the two-loop corrections to the mass of the lighter Higgs boson can be consistently adopted only if all of the couplings contributing to its tree-level mass are in turn neglected. For example, as will be discussed in Sect. 3.2, in the NMSSM this approximation requires that the doublet-singlet superpotential coupling \(\lambda \) be set to zero along with the EW gauge couplings, in which case the two-loop corrections to the masses of the Higgs bosons residing in the two SU(2) doublets correspond to those computed in the MSSM.
To illustrate the relevance of the radiative corrections to the Higgs masses in SUSY models, we show in Fig. 1 the predictions for the mass of the lighter CP-even Higgs boson in a simplified MSSM scenario characterized by a degenerate mass parameter \(M_S\) for all SUSY particles as well as for the heavier Higgs doublet. We choose \(\tan \beta = 20\) so that the tree-level prediction for the lighter Higgs mass in Eq. (3) essentially saturates its upper bound, i.e. \(M_h^\mathrm{tree}\approx M_Z\). In the left plot of Fig. 1 we show the prediction for \(M_h\) as a function of \(M_S\) for two values of the ratio \(X_t/M_S\), where \(X_t\) is the left-right stop mixing parameter. In the right plot we set \(M_S=2\) TeV and show instead the prediction for \(M_h\) as a function of \(X_t/M_S\). The yellow band in each plot corresponds to \(M_h=125.10 \pm 0.14\) GeV, as results from a recent combination of Run-1 and partial Run-2 data from ATLAS and CMS [6]. It appears from the plots in Fig. 1 that, in this simplified MSSM scenario, a prediction for the Higgs mass compatible with the measured value can be obtained with stop masses of about 2 TeV when \(|X_t/M_S| \approx 2\), whereas the stop masses need to exceed 10 TeV when \(X_t=0\).
The predictions for \(M_h\) presented in Fig. 1 were obtained with the latest version (2.17.0) of the code FeynHiggs, and they account for most of the advances that will be reviewed in Sects. 3–5. However, the bulk of the dependence of \(M_h\) on \(M_S\) and \(X_t\) can be traced to the contributions of one-loop diagrams involving top and stops. In the limit \(M_S\gg M_t\), these so-called \({{{\mathcal {O}}}}(\alpha _t)\) contributions can be approximated as
The logarithmic increase of \(M_h\) as a function of \(M_S\) visible in the left plot of Fig. 1 follows from the first term within parentheses in Eq. (5), whereas the double-peaked dependence of \(M_h\) on \(X_t\) visible in the right plot follows from the second and third terms. We note that the one-loop correction in Eq. (5) is symmetric with respect to the sign of \(X_t\), and it is maximized when \(X_t/M_S=\pm \sqrt{6}\). The asymmetry between positive and negative \(X_t\) visible in the right plot of Fig. 1 is a two-loop effect, arising from terms linear in \(X_t\) in the one-loop correction to the top mass. Finally, we stress that the quartic dependence of the dominant one-loop correction on \(M_t\) means that the prediction for the Higgs mass is particularly sensitive to the measured value of the top mass, as well as to the choices made for the renormalization of \(M_t\) in the computation of the Higgs-mass corrections beyond one loop.
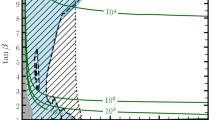
To further illustrate how the predictions for the SM-like Higgs mass can constrain the parameter space of the MSSM, we plot in Fig. 2 the lines in the (\(X_t/M_S,\,M_S\)) plane that, in our simplified scenario with degenerate SUSY masses, lead to the prediction \(M_h=125.1\) GeV. Note that neither theory nor experimental uncertainties are taken into account in this example. The lower (blue) line corresponds to \(\tan \beta =20\), while the upper (red) line corresponds to \(\tan \beta =5\). The overall shape of the blue and red lines in Fig. 2 follows from the dependence on \(X_t/M_S\) of the Higgs-mass correction in Eq. (5). In particular, the value of \(M_S\) required to obtain an acceptable prediction for \(M_h\) is minimal for \(|X_t/M_S| \approx 2\), and it has a local maximum for \(|X_t/M_S|\approx 0\) (for very large \(|X_t/M_S|\), on the other hand, the EW vacuum is unstable). Since for \(\tan \beta =20\) the tree-level prediction for the lighter Higgs mass in Eq. (3) is essentially maximized, the blue line implies a lower bound on \(M_S\) of about 2 TeV in this simplified scenario. On the other hand, the comparison between the blue and red lines shows that, for lower values of \(\tan \beta \), larger stop masses are required to obtain \(M_h\approx 125\) GeV, reflecting the \(\tan \beta \)-dependence of the tree-level prediction. It is also worth pointing out that, in more-complicated MSSM scenarios where, e.g., the gauginos are allowed to be lighter than the stops, an acceptable prediction for \(M_h\) can be obtained with somewhat smaller values for the stop masses than those found here. In summary, the requirement that the theory prediction for the SM-like Higgs mass agree with the measured value establishes non-trivial correlations between the SUSY parameters. However, even in the idealized situation of Fig. 2 where both experimental and theory uncertainties are neglected, direct measurements of some of the SUSY parameters will be necessary to obtain firm constraints on the remaining ones.
2.2 Input parameters and renormalization schemes
When the theoretical prediction for an observable (e.g., the physical mass of a particle) is computed beyond the leading order in perturbation theory, it becomes necessary to specify a renormalization scheme for the parameters entering the lower-order terms in the calculation. While the divergent parts of the counterterms are fixed by the requirement that all divergences cancel out of the predictions for physical observables up to the considered order in perturbation theory, the finite parts of the counterterms define the renormalization scheme. Which choice of renormalization condition is the most “sensible” for a given parameter may depend on a combination of factors, including practical convenience (e.g., some choices can significantly simplify the calculations), explicit gauge-independence, an improved convergence of the perturbative expansion, and whether or not that parameter can be connected to an already-measured physical quantity.
Technically the simplest renormalization scheme is “minimal subtraction” (MS), which only absorbs poles in \(\epsilon =(4-D)/2\) into the counterterms, where D is the number of space-time dimensions assumed for the dimensionally regularized theory. In fact, the MS scheme is a one-parameter class of schemes, distinguished by the renormalization scale Q on which the renormalized parameters depend. Incomparably more popular than the MS scheme itself is a variant, the \(\overline{\text {MS}}\) scheme, related to MS by the simple rescaling \(Q^2\rightarrow Q^2\,e^{\gamma _\text {E}}/(4\pi )\), where \(\gamma _\text {E}=0.57721\ldots \) is the Euler–Mascheroni constant. In SUSY theories, dimensional regularization (DREG) explicitly breaks the balance between bosonic and fermionic degrees of freedom within a superfield. Therefore, one usually works in a variant called dimensional reduction (DRED), where this balance is re-established by supplementing each D-dimensional vector field \(A^{\mu }(x)\) with a \(2\epsilon \)-dimensional “\(\epsilon \)-scalar” \(\tilde{A}(x)\), where x is the D-dimensional space-time variable. Applying the modified minimal subtraction to this theory results in the \(\overline{\text {DR}}\) renormalization scheme (we remark that, beyond one loop, the SUSY-preserving properties of this scheme have been explicitly proven only for limited classes of corrections). In the prediction for a physical quantity the scale dependence of the renormalized parameters cancels against an explicit logarithmic Q dependence in the radiative corrections, up to the considered order in the perturbative expansion. The residual scale dependence of the prediction is formally a higher-order effect, and it is therefore often exploited as a (partial) estimate of the theory uncertainty of the calculation.
Ideally, for a theory depending on a given number of free parameters, an equal number of physical observables would be chosen as input to determine those free parameters. In that case, predictions for further observables in terms of the input observables could be made within the theory. Such relations between physical observables are expected to be gauge-independent and free of ambiguities from, for instance, the recipe adopted for the treatment of tadpole contributions. This does not necessarily hold, however, for the relations between physical observables and parameters renormalized in minimal-subtraction schemes. It is also worth noting that, in these schemes, the contributions of arbitrarily heavy particles do not necessarily decouple from the predictions for low-energy observables. Particular care is therefore needed to avoid the occurrence of unphysical effects in calculations where some of the input parameters are defined directly in a minimal-subtraction scheme such as \(\overline{\text {MS}}\) or \(\overline{\text {DR}}\) rather than being connected to a physical observable.
In order to directly relate the parameters entering the Higgs-mass calculation to physical quantities, non-minimal renormalization definitions can be chosen, which lead to non-vanishing finite parts of the counterterms. Among the physical quantities that can be used to define the parameters of a given SUSY model, an obvious distinction can be made between those that have already been measured and those that are still unknown. The former include the gauge-boson masses, the third-generationFootnote 5 fermion masses, the Fermi constant \(G_F\) and the strong gauge coupling \(\alpha _s(M_Z)\) (the latter defined as a SM parameter in the \(\overline{\text {MS}}\) scheme). For example, the Z-boson mass entering the tree-level mass matrix for the MSSM Higgs masses can be naturally identified with the measured pole mass, in which case the corresponding counterterm involves the Z-boson self-energy. This kind of renormalization condition is usually denoted as “on-shell” (OS). Even if the alternative choice is made to renormalize the Z-boson mass in a minimal-subtraction scheme, the corresponding \(\overline{\text {MS}}\) or \(\overline{\text {DR}}\) parameter still needs to be computed starting from the measured pole mass at the required order in the perturbative expansion.
In contrast, for parameters such as the masses and couplings of the SUSY particles, the choice of renormalization conditions is a matter of convenience, depending also on the kind of analysis that is being performed on the model’s parameter space. When the parameters of the soft SUSY-breaking Lagrangian are obtained via renormalization-group (RG) evolution from a set of high-energy boundary conditions, as in, e.g., the gravity-mediation or gauge-mediation scenarios of SUSY breaking, they are naturally expressed in the \(\overline{\text {DR}}\) scheme. It might therefore be practical to perform the computation of the radiative corrections to the Higgs masses directly in that scheme, taking care to avoid the unphysical effects discussed above. If, on the other hand, the SUSY parameters are taken as input directly at the TeV scale, we may choose to express them in terms of yet-to-be-measured physical observables. While an OS definition for the masses of the SUSY particles can be formulated in an unambiguous way and connects the mass counterterms to the particles’ self-energies, for the parameters that determine their couplings multiple options are available. For example, particles that carry the same quantum numbers mix among each other, and their couplings involve the rotation matrix that diagonalizes their mass matrix. For \(2\times 2\) mixing, as in the case of the “left” and “right” sfermions \((\tilde{f}_L, \tilde{f}_R)\) that mix under EWSB, the rotation matrix can be parametrized by a single mixing angle (plus a phase, in the case of complex parameters). It is then possible to express the couplings of the corresponding mass eigenstates in terms of this angle, and impose a renormalization condition on the latter. A minimal-subtraction condition would be straightforward, but it is known to be gauge dependent. A proper OS definition, connecting the angle to a physical process (such as a decay) that depends on it at tree level, brings along a number of other disadvantages: the choice of a specific process may destroy the symmetries between the particles that mix, infra-red (IR) divergences may need to be dealt with, and seemingly reasonable values for the input parameters may in fact correspond to large couplings that undermine the convergence of the perturbative expansion. An alternative non-minimal – but process-independent – definition requires that, in the renormalization of any interaction vertex that involves external particles that mix, the counterterm of the mixing angle cancel out the antisymmetric part in ij of the field-renormalization constants \(\delta Z_{ij}\). This definition, which is also commonly denoted as “OS”, is often used for the renormalization of the sfermion mixing angles in Higgs-mass calculations, although it too becomes gauge dependent when EW corrections are taken into account.
A further complication of non-minimal schemes is that, even if the renormalization conditions are imposed on the masses and mixing angles of the SUSY particles, what is often taken as input in phenomenological studies are the underlying Lagrangian parameters. For example, in the case of the third-generation squarks these parameters include the soft SUSY-breaking masses \(M_{{\tilde{Q}}}\), \(M_{{\tilde{t}}_R}\) and \(M_{{\tilde{b}}_R}\), and the trilinear couplings \(A_t\) and \(A_b\). The OS definition of the soft SUSY-breaking parameters in the squark sector interprets them as the parameters entering tree-level mass matrices for stops and sbottoms that are diagonalized by the respective OS mixing angles (defined as described above) and have the pole squark masses as eigenvalues. However, the SU(2) relation \(M_{{\tilde{b}}_L}=M_{{\tilde{t}}_L}=M_{{\tilde{Q}}}\) only applies to bare or minimally-renormalized parameters. In this OS scheme, as a result of EWSB, the soft SUSY-breaking mass entering the LL element of the tree-level mass matrix for the sbottoms differs from its stop counterpart by a finite shift. One possible approach is to identify \(M_{{\tilde{t}}_L}\) with the renormalized doublet-mass parameter \(M_{{\tilde{Q}}}\), which is taken as input, and compute \(M_{{\tilde{b}}_L}\) up to the required order in the perturbative expansion by requiring that the bare doublet-mass parameter be the same for stops and sbottoms. Alternatively, one can consider a different OS scheme in which the relation \(M_{{\tilde{b}}_L}=M_{{\tilde{t}}_L}\) is imposed at the level of the renormalized soft SUSY-breaking parameters. In that case only three of the squark masses can be defined as pole masses, while the fourth is treated as a dependent parameter, and is extracted from the SU(2) relation that connects at tree level the masses and mixing angles of stops and sbottoms.
Even when OS renormalization conditions are chosen for most of the parameters entering a given calculation, it is quite common that some parameters are still defined via minimal subtraction. For example, in the calculation of the radiative corrections to the Higgs masses in the MSSM, both \(\tan \beta \) and the Higgs/higgsino mass parameter in the superpotential, \(\mu \), are usually renormalized in the \(\overline{\text {DR}}\) scheme. In addition, a \(\overline{\text {DR}}\) definition is commonly adopted for the field-renormalization constants. We remark that the latter drop out of the Higgs-mass calculation when Eq. (1) is solved order by order in the perturbative expansion, but they are nevertheless introduced to ensure that the individual elements of \(\Delta {\mathcal {M}}_{ij}^2(p^2)\) are free of UV divergences for all values of \(p^2\). Finally, the strong gauge coupling, whose definition becomes relevant in Higgs-mass calculations beyond two loops, is usually renormalized by minimal subtraction, irrespective of the choices made for the other parameters.
In general, Higgs-mass calculations that are performed at the same order in the perturbative expansion but employ different renormalization schemes (or scales) will give numerically different results. Since this difference is formally of higher order, it is often included in the estimate of the theory uncertainty of the prediction. We stress that a proper comparison between two calculations must also take into account the different definitions of the input parameters. In practice, the values of the renormalized parameters must be given as input in the scheme employed by one calculation, and then properly converted into the scheme employed by the other one. We postpone to Sect. 6 an extensive discussion of the available estimates for the theory uncertainty of the Higgs-mass calculation in SUSY models.
2.3 Scenarios with large mass hierarchies
As shown in Sect. 2.1, for values of \(M_A\) and \(\tan \beta \) large enough to saturate the tree-level bound, a SM-like Higgs boson with mass around 125 GeV can be obtained in the MSSM with an average stop mass \(M_S\) of about 2 TeV for \(|X_t/M_S|\approx 2\), whereas for vanishing \(X_t\) the average stop mass needs to be heavier than 10 TeV. Lower values of \(M_A\) and/or \(\tan \beta \) imply lower predictions for \(M_h\) at tree level, and thus require even larger stop masses to ensure that the mass of the SM-like Higgs boson is compatible with the observed value. In contrast, SUSY models beyond the MSSM – such as, e.g., the NMSSM – may allow for additional contributions to the tree-level prediction, alleviating the need for heavy SUSY particles.
In general, when the SUSY scale \(M_S\) is significantly larger than the EW scale (which we can identify, e.g., with the top-quark mass \(M_{t}\)), any fixed-order computation of the Higgs boson masses may become inadequate, because radiative corrections of order n in the loop expansion contain terms enhanced by as much as \(\ln ^n(M_S/M_{t})\). In the presence of a significant hierarchy between the scales, the computation of the Higgs masses needs to be reorganized in an EFT approach: the heavy particles are integrated out at the scale \(M_S\), where they only affect the matching conditions for the couplings of the EFT valid below \(M_S\); the appropriate renormalization group equations (RGEs) are then used to evolve these couplings between the SUSY scale and the EW scale, where the running couplings are related to physical observables such as the Higgs masses and the masses of fermions and gauge bosons. In this approach, the computation is free of large logarithmic terms both at the SUSY scale and at the EW scale, while the effect of those terms is accounted for to all orders in the loop expansion by the evolution of the couplings between the two scales. More precisely, large corrections can be resummed to the (next-to)\(^n\)-leading-logarithmic (N\(^n\)LL) order by means of n-loop calculations at the SUSY and EW scales combined with \((n+1)\)-loop RGEs.
In the simplest heavy-SUSY scenario, all of the superparticles as well as all of the BSM Higgs bosons are clustered around a single scale \(M_S\), so that the EFT valid below this scale is just the SM. In this case, the Higgs-mass calculation can rely in part on results already available within the SM: full three-loop plus partial higher-loop RGEs for all parameters of the SM Lagrangian, and full two-loop plus partial higher-loop relations between the \(\overline{\text {MS}}\)-renormalized parameters and appropriate sets of physical observables at the EW scale. These are combined with the matching conditions for the Lagrangian parameters at the SUSY scale: in particular, the calculation of the matching condition for the quartic Higgs coupling at one, two and three loops is required for the resummation of the large logarithmic corrections at NLL, NNLL and N\(^3\)LL, respectively.
Of particular interest from the phenomenological point of view are SUSY scenarios in which an extended Higgs sector is within the reach of the LHC. In the MSSM, direct searches for BSM Higgs bosons decaying to pairs of down-type fermions already constrain significant regions of the parameter space, favoring relatively low values of \(\tan \beta \). However, multi-TeV stop masses are required to obtain a prediction for \(M_h\) of about 125 GeV when \(\tan \beta \lesssim 10\), and an EFT approach is warranted. If all SUSY particles are heavy and all Higgs bosons are relatively light, the EFT valid below the matching scale is a two-Higgs-doublet model (2HDM), for which only the NLL resummation of large logarithms (i.e., one-loop matching conditions and two-loop RGEs) is currently available in full. More complicated hierarchical scenarios include the case in which the BSM-Higgs masses sit at an intermediate scale between the mass of the observed Higgs boson and the heavy SUSY masses, “Split SUSY” scenarios in which gauginos and higgsinos are significantly lighter than the sfermions, and, conversely, scenarios in which they are significantly heavier. In each of these scenarios an appropriate tower of EFTs needs to be constructed, which involves the computation of threshold corrections at each of the scales where some heavy particles are integrated out.
In the standard EFT approach to the Higgs-mass calculation, the high-energy SUSY theory is matched to a renormalizable low-energy theory (e.g., the SM or the 2HDM) in the unbroken phase of the EW symmetry, and the effect of non-zero vevs for the Higgs fields is taken into account only at the EW scale. The resulting prediction for the Higgs mass neglects terms suppressed by powers of \(v^2/M_S^2\,\) – where we denote by v the vev of a SM-like scalar – which can be mapped to the effect of non-renormalizable, higher-dimensional operators in the EFT, such as, e.g., dimension-six scalar interactions \(|\phi _i|^6\). These terms are clearly suppressed in the limit of large \(M_S\), where the resummation of logarithmic corrections provided by the EFT approach is numerically important. In contrast, the FO calculation of the Higgs masses is performed directly within the SUSY theory and in the broken phase of the EW symmetry. Such a calculation does not include the resummation of the large logarithms, but does account for all \(M_S\)-suppressed effects up to the considered perturbative order. In order to obtain accurate predictions for the Higgs masses in SUSY scenarios with intermediate values of \(M_S\), for which neither the \({{{\mathcal {O}}}}(v^2/M_S^2)\) effects nor the higher-order log-enhanced effects are obviously negligible, a number of “hybrid” approaches that combine existing FO and EFT calculations have been proposed in recent years. To avoid double counting, these hybrid approaches require a careful subtraction of the terms that are accounted for by both the FO and the EFT parts of the calculation. Indeed, a few successive adjustments – some of which stemmed from extensive discussions held during the KUTS meetings – were necessary to obtain predictions for the Higgs masses that, in the limit of very large \(M_S\), show the expected agreement with the pure EFT calculation.
In the following three sections we will describe in detail the recent advances of the Higgs-mass calculations in SUSY models in the FO, EFT and hybrid approach, respectively.
3 Fixed-order calculations
3.1 Higgs-mass calculations in the MSSM
The MSSM [7, 8] is one of the best-motivated extensions of the SM, and probably the most studied. The existence of a tree-level upper bound, \(M_h<M_Z\,|\cos 2\beta |\), on the mass of the lighter CP-even Higgs boson of the MSSM was recognized early in the 1980s [9]. One-loop radiative corrections to this bound were computed shortly thereafter [10], but the computation neglected the effects of the top Yukawa coupling, which at the time was expected to be sub-dominant with respect to the EW gauge couplings, resulting in an upper bound of at most 95 GeV. In 1989, two papers [11, 12] did consider the effect of large Yukawa couplings, but focused on the corrections to mass sum rules as opposed to individual masses. In 1991, as the searches for the top quark and for the stops implied that they all had to be heavier than the Z boson, three seminal papers [13,14,15] pointed out that the one-loop corrections controlled by the top Yukawa couplings had the potential to increase the upper bound on \(M_h\) well above \(M_Z\). The importance of these corrections for Higgs phenomenology at the LEP was swiftly recognized [16,17,18], and by the mid-1990s full one-loop calculations of the Higgs masses had become available [19,20,21,22,23,24] for a simplified (“vanilla”) version of the MSSM Lagrangian that does not include CP-violating phases, flavor mixing or R-parity violation. Between the late 1990s and the mid 2000s [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39], two-loop corrections to the masses of the neutralFootnote 6 Higgs bosons were also computed, under the approximations of vanishing external momenta in the self-energies and of vanishing EW gauge couplings (i.e., adopting the “gaugeless limit” described in Sect. 2.1). This combination of full one-loop and gaugeless, zero-momentum two-loop corrections to the Higgs masses was also implemented in widely-used codes for the determination of the MSSM mass spectrum, such as FeynHiggs [42,43,44], SOFTSUSY [45, 46], SuSpect [47] and SPheno [48, 49].Footnote 7
In the past two decades, a substantial effort has been devoted to the improvement of the fixed-order calculation of the Higgs masses in the MSSM, along three general directions:
-
Completing the two-loop calculation, including momentum dependence and corrections controlled by the EW gauge couplings;
-
Including the dominant three-loop corrections;
-
Extending the Higgs-mass calculation to the most general MSSM Lagrangian, including CP violation, R-parity violation and the effects of flavor mixing in the sfermion mass matrices.
In the following we summarize the developments along each of these directions, highlighting in separate paragraphs the calculations that were presented and discussed during the KUTS meetings.
3.1.1 Completing the two-loop calculation in the vanilla MSSM
A full calculation of the two-loop corrections to the neutral Higgs masses in the effective potential approach – i.e., including the effects of the EW gauge couplings but neglecting external-momentum effects – became available already in 2002 [50]. The two-loop self-energies of the scalar Higgs bosons, see Eq. (4), were obtained from a numerical differentiation of the two-loop effective potential of the MSSM, which had been computed in the \(\overline{\text {DR}}\) renormalization scheme and in the Landau gauge in Ref. [51]. It was found in Ref. [50] that the two-loop EW corrections to the Higgs masses suffer from singularities when the tree-level squared masses of the would-be Goldstone bosons entering the loops pass through zero, and it was argued that these singularities would be cured by the inclusion of the full momentum dependence in the two-loop self-energies.
Two years later, a calculation of the two-loop contributions involving the strong gauge coupling or the third-family Yukawa couplings to the self-energies of both neutral and charged Higgs bosons was presented in Ref. [52]. That calculation, based on the methods of Refs. [53, 54], went beyond the two-loop results implemented in the existing public codes in that it included external-momentum effects, as well as contributions involving the D-term-induced EW interactions between Higgs bosons and sfermions. Combined with the effective-potential results of Ref. [50], the results of Ref. [52] provided an almost-complete two-loop calculation of the Higgs masses in the MSSM – the only missing part being the external-momentum dependence of diagrams that vanish when the EW gauge couplings are turned off (namely, the part required to tame the above-mentioned singularities). However, no code for the calculation of the MSSM mass spectrum based on the results of Refs. [50, 52] was made available, and the way those results were organized did not lend itself to a straightforward implementation in the existing public codes. On the one hand, the \(\overline{\text {DR}}\) renormalization scheme adopted in Refs. [50, 52] for the parameters of the MSSM Lagrangian does not match the “mixed OS–\(\overline{\text {DR}}\)” scheme adopted in FeynHiggs, where some of the relevant parameters (e.g., the mass and mixing terms for the squarks) are renormalized on-shell [55,56,57]. On the other hand, the implementation of the results of Refs. [50, 52] in SOFTSUSY, SuSpect and SPheno, which also adopt the \(\overline{\text {DR}}\) scheme, is complicated by the different choice of gauge in these codes, and by the singularities in the two-loop, zero-momentum EW corrections. The latter restrict the applicability of the calculation to the range of renormalization scales where none of the tree-level Higgs masses is tachyonic, which may depend on the considered scenario and should be determined by the codes on a case-by-case basis.
Advances during KUTS In 2014, at the early stages of the KUTS initiative, the two-loop contributions to the Higgs self-energies that involve the strong gauge coupling and the top Yukawa coupling, i.e. those denoted as \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\), were computed again with full momentum dependence in Refs. [58, 59]. In particular, Ref. [58] relied on the sector-decomposition algorithm of Refs. [60, 61] for the numerical calculation of the two-loop integrals, and adopted the mixed OS–\(\overline{\text {DR}}\) renormalization scheme of FeynHiggs. Reference [59] relied instead on the methods of Refs. [53, 54] for the loop integrals, and obtained results both in the \(\overline{\text {DR}}\) scheme and in a mixed OS–\(\overline{\text {DR}}\) scheme. Reference [59] also computed the two-loop corrections that involve both the strong gauge coupling and the EW couplings, under the approximation that the only non-vanishing Yukawa coupling is the top one.Footnote 8 The \(\overline{\text {DR}}\) results of Ref. [59] were found to be in full agreement with those of the earlier Ref. [52]. On the other hand, a discrepancy between the OS–\(\overline{\text {DR}}\) results of Ref. [59] and those of Ref. [58] was traced to different renormalization prescriptions for the parameter \(\tan \beta \) and for the field-renormalization constants. The scheme dependence associated with the former is numerically small, while the latter enter the prediction for the Higgs mass only at higher orders, and their effect can be considered part of the theory uncertainty [62]. As to the numerical impact of the corrections, it was found that both the momentum-dependent part of the \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) corrections and the whole \({{{\mathcal {O}}}}(\alpha \alpha _s)\) corrections can shift the prediction for the Higgs mass by a few hundred MeV in representative scenarios with stop masses of about 1 TeV, but there can be significant cancellations between the two classes of corrections. Finally, in 2018, Ref. [63] computed all of the two-loop corrections to the Higgs mass that involve the strong gauge coupling, including also the mixed EW–QCD effects, with full dependence on the external momentum and allowing for complex parameters. In the limit of real parameters, the calculation of Ref. [63] improved on the one of Ref. [59] in that it included also the effects of Yukawa couplings other than the top.
3.1.2 Dominant three-loop corrections
Another obvious direction for the improvement of the fixed-order calculation of the Higgs masses in the MSSM is the inclusion of three-loop effects. The logarithmic terms in the three-loop corrections to the mass of the lighter, SM-like Higgs scalar can be identified in the EFT approach by solving perturbatively the appropriate system of boundary conditions and RGEs, without actually computing any three-loop diagrams (see Sect. 4 for further details). In the approximation where only the top Yukawa coupling and the strong gauge coupling are different from zero, the three-loop logarithmic terms were computed at LL in Ref. [64], at NLL in Ref. [65] and at NNLL in Ref. [66].
The first genuinely three-loop computation of the corrections to the lighter Higgs mass was presented in Refs. [67, 68]. It was restricted to the terms of \({{{\mathcal {O}}}}(\alpha _t\alpha ^2_s)\), i.e. those involving the highest power of the strong gauge coupling, which can be consistently computed in the limit of vanishing external momentum. Since some three-loop integrals cannot currently be solved analytically for arbitrary values of the masses, a number of possible hierarchies among the SUSY masses was considered, for which analytical results can be obtained via asymptotic expansions. The relevant parameters were renormalized in the \(\overline{\text {DR}}\) scheme, with the exception of the stop masses for which a modified scheme, denoted as \(\overline{\text {MDR}}\), was introduced in scenarios with a heavy gluino. Indeed, in the \(\overline{\text {DR}}\) scheme potentially large contributions proportional to powers of the gluino mass \(M_3\) affect the corrections to the Higgs mass already at two loops [33].Footnote 9 In the \(\overline{\text {MDR}}\) scheme of Refs. [67, 68] the corrections proportional to \(M_3^2\) are instead absorbed in the definition of the squared stop masses. It was found that the three-loop \({{{\mathcal {O}}}}(\alpha _t\alpha ^2_s)\) corrections to the Higgs mass are typically of the order of a few hundred MeV in scenarios with stop masses of about 1 TeV. These corrections were made available in the public code H3m [68], which relies on FeynHiggs for the one- and two-loop parts of the calculation. Since in FeynHiggs the parameters in the top/stop sector are renormalized in the OS scheme, an internal conversion of the relevant one- and two-loop corrections to the \(\overline{\text {DR}}\) (or \(\overline{\text {MDR}}\)) scheme is performed within H3m.
Advances during KUTS In 2014, Ref. [69] re-examined the two-loop determination of the \(\overline{\text {DR}}\)-renormalized top mass of the MSSM, which enters the corrections to the Higgs mass in the three-loop calculation of Refs. [67, 68]. It was shown that the renormalization-scale dependence of the Higgs-mass prediction of H3m can be improved by performing the conversion from the \(\overline{\text {MS}}\)-renormalized top mass of the SM (in turn extracted from the pole mass) to the \(\overline{\text {DR}}\)-renormalized top mass of the MSSM at a fixed scale of the order of the SUSY masses. In 2017, the three-loop corrections of Refs. [67, 68] were implemented in the stand-alone module Himalaya [70], which can be directly linked to codes that perform the two-loop calculation of the MSSM Higgs masses in the \(\overline{\text {DR}}\) scheme. In 2018, Ref. [71] studied the compatibility of DRED with SUSY at three loops, extending the earlier analyses of Refs. [72,73,74]. It was shown that, in the gaugeless limit, the Slavnov–Taylor relations expressing SUSY invariance are respected by DRED, and no SUSY-restoring counterterms are required. Finally, in 2019 the \({{{\mathcal {O}}}}(\alpha _t\alpha ^2_s)\) corrections to the lighter Higgs mass in the limit of vanishing external momentum were computed for arbitrary values of the SUSY masses in Refs. [75, 76]. The three-loop integrals that do not have analytical solutions were computed numerically with the methods of Ref. [77]. The effects of the \({{{\mathcal {O}}}}(\alpha _t\alpha ^2_s)\) corrections on the prediction for the Higgs mass were found to be in good agreement with those of the corresponding corrections implemented in H3m.
3.1.3 Beyond the vanilla MSSM
Going beyond the simplified MSSM Lagrangian considered in the previous sections, the direction that has received the most attention so far is the inclusion of the effects of complex parameters in the calculation of the Higgs boson masses and mixing. At tree level, CP symmetry is conserved in the MSSM Higgs sector. In the presence of complex parameters in the MSSM Lagrangian, however, radiative corrections induce a mixing among the CP-even bosons, h and H, and the CP-odd boson, A, such that beyond tree level they combine into three neutral mass eigenstates usually denoted as \(h_i\) (with \(i=1,2,3\)). Since the CP-odd boson mass \(M_A\) is no longer a well-defined quantity beyond tree level, it is convenient to express the tree-level mass matrix for the neutral Higgs bosons in terms of the charged-Higgs mass \(M_{H^\pm }\). The dominant one-loop corrections to the Higgs mass matrix in the presence of complex parameters, under various approximations, were computed between the late 1990s and the early 2000s in Refs. [78,79,80,81,82,83,84,85,86] (the calculations of Refs. [80, 82, 85] also included two-loop leading-logarithmic terms). Full calculations of the one-loop corrections became available in 2004 [87] and in 2006 [88], and the two-loop \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) corrections were computed in 2007 [89]. The results of Refs. [81, 82, 85, 87] were implemented in the public code CPsuperH [90,91,92], whereas the results of Refs. [88, 89] were implemented in FeynHiggs. For the two-loop corrections other than \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\), which were only known for real MSSM parameters at the time, the dependence on the relevant phases was approximated in FeynHiggs through an interpolation between the corrections obtained with positive and with negative values of the corresponding parameters.
Another direction of development for the Higgs-mass calculation beyond the vanilla MSSM was the inclusion of the effects of the mixing between different generations of sfermions. In the most general MSSM Lagrangian, the soft SUSY-breaking mass and trilinear-interaction terms for the sfermions are \(3\times 3\) matrices in flavor space. After EWSB, all sfermions with the same electric charge mix with each other, via \(6\times 6\) mass matrices for the up- and down-type squarks and the charged leptons, and a \(3\times 3\) mass matrix for the sneutrinos. A calculation of the one-loop corrections to the Higgs masses allowing for generic mixing between the second and third generations of squarks was first performed in 2004 [93] (for further studies of the effects of stop-scharm mixing see also Refs. [94, 95]). A version of the calculation of Ref. [93] extended to full three-generation mixing was implemented in FeynHiggs, and was later cross-checked (and amended) in Ref. [96]. It was found that corrections to the mass of the lighter Higgs boson of up to several GeV can arise in the presence of large mixing between the second and third generations in the soft SUSY-breaking trilinear couplings, although for down-type squarks the constraints from B physics must be taken into account. Finally, the effects of slepton-flavor mixing on the one-loop corrections to the Higgs masses were studied in Ref. [97], and found to be very small in the considered scenarios.
Advances during KUTS A fruitful line of activity in recent years has been the extension to the case of complex MSSM parameters of all two-loop corrections to the Higgs masses that were implemented in FeynHiggs beyond \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\). In 2014, the two-loop corrections of \({{{\mathcal {O}}}}(\alpha _t^2)\), i.e. those involving only the top Yukawa coupling, were computed in the limit of vanishing external momentum in Refs. [98,99,100]. In 2017, the calculation of the two-loop Yukawa-induced corrections was extended to \({{{\mathcal {O}}}}(\alpha _t^2,\alpha _t\alpha _b,\alpha _b^2)\) in Ref. [101], thus accounting for the terms controlled by the bottom Yukawa coupling, which are relevant for large \(\tan \beta \), but still in the limit of vanishing momentum. Finally, as mentioned in Sect. 3.1.1, a complete calculation of the two-loop corrections that involve the strong gauge coupling, including the full dependence on the external momentum, was presented in 2018 in Ref. [63]. All of these calculations adopted the mixed OS–\(\overline{\text {DR}}\) scheme of FeynHiggs, see Refs. [55,56,57], allowing for a seamless implementation in the code, and they collectively removed the need for approximations in the dependence of the two-loop corrections on the complex parameters. They also provided useful cross-checks of the earlier calculations of Refs. [34, 37, 59] for the case of real MSSM parameters.
Another independent line of activity in recent years stemmed from the inclusion of the two-loop corrections to the Higgs masses in SARAH [102,103,104,105,106,107], a package that automatically generates versions of the “spectrum generator” SPheno for generic, user-specified BSM models. The calculation of the Higgs masses employs the \(\overline{\text {DR}}\) renormalization scheme, and in the two-loop part it is restricted to the gaugeless limit and to the approximation of vanishing external momentum. It relies on the earlier results of Ref. [108] for the complete two-loop effective potential in a general renormalizable theory, which is adapted within SARAH to the specific BSM model under consideration. In the original 2014 paper describing the two-loop extension of SARAH, Ref. [109], the derivatives of the effective potential were determined numerically, but an analytic computation of the derivatives was provided soon thereafter in Ref. [110]. This new version of SARAH was quickly put to work in a variety of SUSY (as well as non-SUSY) extensions of the SM. For what concerns the vanilla MSSM, Ref. [110] provided a useful cross-check of the \(\overline{\text {DR}}\) formulas for the two-loop corrections to the Higgs masses implemented in the standard version of SPheno, namely those of Refs. [33,34,35,36,37,38]. Beyond the vanilla MSSM, in 2014 Ref. [111] studied the effects of R-parity violating couplings, showing that they can induce positive corrections to the lighter Higgs mass of up to a few GeV. In 2015, Ref. [112] studied the effects of flavor mixing in the soft SUSY-breaking terms, finding that a large stop-scharm-Higgs coupling can induce shifts of a few GeV in the two-loop corrections to the lighter Higgs mass. Finally, in 2016 Ref. [113] studied the dependence of the Higgs masses on CP-violating phases for the MSSM parameters. A direct comparison with the earlier results of Refs. [88, 89, 98,99,100] was, however, not feasible, due to the different (namely, mixed OS–\(\overline{\text {DR}}\)) renormalization scheme employed in that set of calculations.
3.2 Higgs-mass calculations in the NMSSM
In the NMSSM – for reviews, see Refs. [114, 115] – the Higgs sector is augmented with a gauge-singlet superfieldFootnote 10\(\hat{S}\). The simplest and most-studied version of the NMSSM involves a \(Z_3\) symmetry that forbids terms linear or quadratic in the Higgs superfields. The superpotential mass term for the MSSM Higgs doublets is replaced by a trilinear singlet-doublet interaction, plus a cubic interaction term for the singlet
and the corresponding term in the soft SUSY-breaking scalar potential is replaced as
In addition, the potential contains a mass term \(m_S^2\,|S|^2\) for the singlet. For appropriate values of the soft SUSY-breaking parameters the singlet takes a vev, \(v_s\equiv \langle S\rangle \), inducing effective \(\mu \) and \(B_\mu \) parameters for the doubletsFootnote 11:
This provides a solution to the so-called “\(\mu \) problem” of the MSSM, i.e. the question of why the superpotential mass parameter \(\mu \) should be at the same scale as the soft SUSY-breaking parameters.
In the absence of complex parameters in the NMSSM Lagrangian, the CP-even component of the singlet mixes with the CP-even components of the two doublets via a \(3\times 3\) mass matrix, while its CP-odd component mixes with the CP-odd boson A via a \(2\times 2\) mass matrix (after the combination of CP-odd components of the doublets that corresponds to the neutral would-be-Goldstone boson is rotated out). In turn, the fermionic component of the singlet superfield – the singlino – mixes with the neutral components of higgsinos and EW gauginos via a \(5\times 5\) mass matrix. Even in the CP-conserving case, the presence of mixing in the CP-odd sector makes it unpractical to express the tree-level mass matrix of the CP-even bosons in terms of a pseudoscalar mass, as is done in the MSSM. The matrix is usually expressed either directly in terms of \(A_\lambda \) or in terms of \(M_{H^\pm }\), which at tree level is given by:
where we define \(\tan \beta \equiv v_2/v_1\) and \(v^2 \equiv v_1^2+v_2^2\approx (174~\mathrm{GeV})^2\) as in the MSSM. Beyond tree level, \(A_\lambda \) is usually renormalized in the \(\overline{\text {DR}}\) scheme, whereas \(M_{H^\pm }\) is usually identified with the pole mass. For non-zero phases of the parameters in the Higgs sector, CP violation can arise in the NMSSM already at tree level. In this case all of the neutral Higgs bosons mix via a \(5\times 5\) mass matrix (again, after the neutral would-be-Goldstone boson is rotated out). As in the case of the MSSM, the radiative corrections can in turn induce CP violation in the Higgs sector in the presence of non-zero phases for the Higgs-sfermion trilinear couplings and for the gaugino and higgsino mass parameters.
In the NMSSM, the upper bound on the mass of the lightest CP-even boson \(h_1\) is weaker than the corresponding bound on h in the MSSM, thanks to an additional contribution to the quartic Higgs coupling controlled by the singlet-doublet superpotential coupling:
In principle, this allows for a smaller contribution from radiative corrections in order to reproduce the observed value of the SM-like Higgs mass. Note that the second contribution to the upper bound in Eq. (10) is significant only for small or moderate \(\tan \beta \), which in turn suppresses the first contribution. Large values of \(\lambda \) are thus required for \(M_{h_1}\) to be significantly larger than \(M_Z\) at tree-level. However, if \(\lambda \) is larger than about 0.7–0.8 at the weak scale it develops a Landau pole below the GUT scale, in which case the NMSSM can only be viewed as a low-energy effective theory to be embedded in a further-extended SUSY model. On the other hand, if \(\lambda \rightarrow 0\), with \(A_\lambda \) held fixed, the singlet and the singlino decouple from the Higgs and higgsino sectors, respectively. If in addition \(v_s\rightarrow \infty \), with both \(\lambda \,v_s\) and \(\kappa \,v_s\) held fixed, one recovers the so-called “MSSM limit” of the NMSSM. In this limit, the masses and couplings of the Higgs doublets are exactly the same as in the MSSM, with the effective \(\mu \) and \(B_\mu \) parameters given in Eq. (8).
The mechanism to dynamically generate a superpotential mass term for the Higgs doublets via the coupling to a singlet was proposed already in 1975 [116], and again by several groups in the early 1980s [117,118,119,120,121]. The first detailed studies of the Higgs sector of the NMSSM at tree level date to 1989 [122, 123]. However, in the course of the following two decades the radiative corrections to the Higgs masses were computed only at one loop, for vanishing external momentum and, with few exceptions, in the gaugeless limit. In the CP-conserving NMSSM, analytic formulas for the quark/squark contributions were obtained in the effective potential approach in Refs. [124,125,126,127,128,129]; the Higgs/higgsino contributions controlled by \(\lambda \) and \(\kappa \) were obtained in Ref. [128] from a numerical differentiation of the corresponding contributions to the one-loop effective potential; Ref. [130] computed the leading-logarithmic terms of the one-loop corrections induced by Higgs, chargino and neutralino loops, including also the effects of the EW gauge couplings. For the NMSSM with complex parameters, the one-loop corrections to the Higgs masses (including the EW effects) were computed in the effective potential approach in Refs. [131,132,133].
In 2009, a one-loop calculation of the corrections to the neutral Higgs masses in the NMSSM with real parameters was presented in Ref. [134], under the sole approximation of neglecting the Yukawa couplings of the first two generations. One year later that one-loop calculation was replicated (including also the tiny effects from the first-two-generation Yukawa couplings) and extended to the charged Higgs mass in Ref. [135], relying on an early version of SARAH [102,103,104]. Both calculations assumed that the tree-level mass matrices for the Higgs bosons are fully expressed in terms of \(\overline{\text {DR}}\)-renormalized parameters, and included the necessary one-loop formulas to extract the EW gauge couplings and the parameter v from a set of physical observables (e.g., Ref. [134] used \(M_Z\), \(M_W\) and the muon decay constant \(G_\mu \)). In 2011 the one-loop calculation of the Higgs-mass corrections was performed again in Ref. [136], where several renormalization schemes were considered: the pure \(\overline{\text {DR}}\) scheme, in which the earlier results of Refs. [134, 135] were reproduced; a mixed OS–\(\overline{\text {DR}}\) scheme in which the tree-level mass matrices are expressed in terms of the physical masses \(M_Z\), \(M_W\) and \(M_{H^\pm }\), the electric charge e in the Thomson limit, plus the \(\overline{\text {DR}}\) parameters \(\tan \beta \), \(v_s\), \(\lambda \), \(\kappa \) and \(A_\kappa \); a scheme, denoted as OS, in which \(\tan \beta \) is still \(\overline{\text {DR}}\), but \(v_s\), \(\lambda \), \(\kappa \) and \(A_\kappa \) are traded for combinations of the CP-odd Higgs masses and of the chargino and neutralino masses. In 2012 the one-loop calculation of the Higgs masses in the mixed OS–\(\overline{\text {DR}}\) scheme of Ref. [136] was extended to the NMSSM with complex parameters in Ref. [137]. Also, SARAH was used in Ref. [138] to extend the one-loop calculation of Ref. [135] to the most general version of the NMSSM, known as GNMSSM, in which there is no \(Z_3\) symmetry that forbids linear and quadratic terms in the superpotential and in the soft SUSY-breaking potential.
Beyond one loop, an effective-potential calculation of the \({{{\mathcal {O}}}}(\alpha _t \alpha _s, \alpha _b\alpha _s)\) correctionsFootnote 12 to the masses of the neutral Higgs bosons in the NMSSM with real parameters was also presented in Ref. [134]. The results of this calculation are restricted to the gaugeless and vanishing-momentum limits, and assume that all of the relevant parameters in the tree-level mass matrices and in the one-loop corrections are renormalized in the \(\overline{\text {DR}}\) scheme. Note that, in contrast to the case of the MSSM, in the NMSSM the parameter v enters the tree-level Higgs mass matrix even in the gaugeless limit, in combination with the coupling \(\lambda \), and it should therefore be extracted from physical observables at two loops. However, the effective-potential approach of Ref. [134] does not provide the necessary two-loop contributions to the gauge-boson self-energies. Moreover, as already mentioned in Sect. 2.1, a vanishing-momentum calculation of the lightest Higgs mass in which \(\lambda \) itself is not considered vanishing misses corrections that are of the same order in the couplings as those that are being computed, because the mass receives a tree-level contribution proportional to \(\lambda \), see Eq. (10). In summary, it can be argued that an effective-potential calculation such as the one of Ref. [134] fully captures the \({{{\mathcal {O}}}}(\alpha _t \alpha _s, \alpha _b\alpha _s)\) corrections to the mass of the lightest, SM-like Higgs boson only in the limit \(\lambda \rightarrow 0\), where they reduce to those already computed for the MSSM in Ref. [33].
The calculations described above were promptly implemented in public codes for the determination of the NMSSM mass spectrum. In particular, the full one-loop and \({{{\mathcal {O}}}}(\alpha _t \alpha _s, \alpha _b\alpha _s)\) two-loop corrections in the \(\overline{\text {DR}}\) scheme from Ref. [134] were implemented in NMSSMTools [139, 140] and in the NMSSM-specific version of SOFTSUSY [141]. These codes included also the MSSM results of Ref. [37] for the remaining two-loop corrections controlled by the third-family Yukawa couplings, in the gaugeless and vanishing-momentum limits. The inclusion of these additional corrections, applied only to the \(2\times 2\) sub-matrix that involves the Higgs doublets, allowed the codes to better reproduce the MSSM predictions for the Higgs masses in the “MSSM limit” of the NMSSM. The one-loop corrections in the \(\overline{\text {DR}}\) scheme from Ref. [135] were made available in the NMSSM-specific version of SPheno that is generated automatically by SARAH. These one-loop corrections, combined with the two-loop corrections of Ref. [134] and, for the MSSM limit, Ref. [37], were also implemented in FlexibleSUSY [142, 143], a package that relies on SARAH to generate C++ spectrum generators for generic, user-specified BSM models. Finally, the one-loop corrections of Refs. [136, 137] were implemented in NMSSMCALC [144], which computes masses and decay widths of the Higgs bosons in the NMSSM with either real or complex parameters. The code adopts a variant of the mixed OS–\(\overline{\text {DR}}\) scheme defined in Ref. [136], slightly modified to comply with the input format for complex parameters established in the “SUSY Les Houches Accord” (SLHA) [145, 146]. In addition, NMSSMCALC provides the option to use the \(\overline{\text {DR}}\) parameter \(A_\lambda \) instead of the pole mass \(M_{H^\pm }\) as input for the mixed OS–\(\overline{\text {DR}}\) scheme.
Advances during KUTS Broadly speaking, the recent developments in the Higgs-mass calculations for the NMSSM followed four directions which we will discuss separately below: the calculation of two-loop corrections tailored for inclusion in SARAH/SPheno and in NMSSMCALC, respectively; the development of an NMSSM-specific version of FeynHiggs; detailed comparisons between the predictions of the available codes.
In 2014, as soon as the automatic Higgs-mass calculation in SARAH was extended to two loops [109], the code was used to reproduce the \({{{\mathcal {O}}}}(\alpha _t \alpha _s, \alpha _b\alpha _s)\) corrections of Ref. [134]. Shortly thereafter, in Ref. [147], it was used to compute the remaining two-loop corrections to the full Higgs-mass matrices of the NMSSM with real parameters, in the \(\overline{\text {DR}}\) renormalization scheme and in the gaugeless and vanishing-momentum limits. Compared to the earlier practice of including the two-loop corrections beyond \({{{\mathcal {O}}}}(\alpha _t \alpha _s, \alpha _b\alpha _s)\) only in the MSSM limit, the calculation of Ref. [147] allowed for the inclusion of the two-loop corrections controlled by the NMSSM-specific superpotential couplings \(\lambda \) and \(\kappa \). In 2016, the calculation was extended to the NMSSM with complex parameters in Ref. [113]. It should be noted that the two-loop Higgs-mass calculations of Refs. [109, 113, 147] share the limitations described earlier for the calculation of Ref. [134]: the limit of vanishing momentum misses terms that are of the same order in the couplings as those included in the two-loop result, and the extraction of the \(\overline{\text {DR}}\)-renormalized parameter v from physical observables is performed only at one-loop order.
A peculiarity of the Higgs-mass calculation in the NMSSM is the fact that the singularities for vanishing tree-level masses of the would-be-Goldstone bosons, first described in Ref. [50] for the two-loop EW corrections in the MSSM, affect the two-loop corrections even in the gaugeless limit, due to the presence of Higgs self-couplings controlled by \(\lambda \). The origin of these singularities, known as “Goldstone Boson Catastrophe” (GBC), was discussed in Refs. [148,149,150,151] for the SM and in Ref. [152] for the MSSM. It was shown in these papers that the singularities can be removed from the effective potential and from its first derivatives by a resummation procedure that effectively absorbs them in the mass terms of the would-be-Goldstone bosons entering the one-loop corrections. However, this resummation does not fully address the singularities in the second derivatives of the effective potential, which enter the zero-momentum calculation of the Higgs masses. In 2016, the solution to the GBC was extended to a general renormalizable theory in Ref. [153]. It was shown that, at the two-loop order, the resummation procedure of Refs. [148,149,150,151,152] is equivalent to imposing an OS condition on the masses of the would-be-Goldstone bosons. Moreover, the momentum-dependent terms that are needed to compensate the singularities of the second derivatives of the potential in the gaugeless limit were obtained in Ref. [153] from an expansion in \(p^2\) of the full two-loop self-energies given earlier in Ref. [154]. In 2017, the implementation of these results in SARAH, described in Ref. [155], eventually allowed for a GBC-free calculation of the two-loop corrections to the Higgs masses in the gaugeless limit of the NMSSM.
In 2014, the two-loop \({{{\mathcal {O}}}}(\alpha _t \alpha _s)\) corrections to the Higgs masses in the NMSSM with complex parameters were computed in Ref. [156] and implemented in NMSSMCALC. The computation employed the mixed OS–\(\overline{\text {DR}}\) scheme defined in Refs. [136, 144] for the parameters in the Higgs sector, whereas the parameters in the top/stop sector were renormalized either in the \(\overline{\text {DR}}\) or in the OS scheme. The two-loop results of Ref. [156] were restricted to the limit of vanishing external momentum, but, in contrast to the effective-potential calculations of Refs. [109, 113, 134, 147], they did include the \({{{\mathcal {O}}}}(\alpha _t \alpha _s)\) contributions to the gauge-boson self-energies that are involved in the renormalization of v. It was shown that, in a representative scenario with stop masses around 1 TeV, these contributions shift the Higgs masses by less than 50 MeV. In 2019, the Higgs-mass calculation of NMSSMCALC was extended by the inclusion of the two-loop \({{{\mathcal {O}}}}(\alpha _t^2)\) corrections at vanishing external momentum and in the MSSM limit. These corrections were computed in Ref. [157] starting from a CP-violating NMSSM setup, where the parameters of the Higgs sector are renormalized in the mixed OS–\(\overline{\text {DR}}\) scheme of Refs. [136, 144] but the limits \(\lambda ,\kappa \rightarrow 0\) and \(v_s \rightarrow \infty \) (with \(\mu _{\mathrm{eff}} = \lambda \, v_s\) fixed) are taken. The effects of different choices (\(\overline{\text {DR}}\), OS or a mixture) for the renormalization of the parameters in the top/stop sector were also investigated. Finally, the issue of a residual gauge dependence affecting the Higgs-mass predictions at higher orders when the one-loop self-energies are computed at the mass pole was discussed in Refs. [158, 159].
A one-loop calculation of the Higgs masses in a renormalization scheme suitable for implementation in FeynHiggs was performed for the NMSSM with real parameters in 2016 [160]. It was extended to the NMSSM with complex parameters in 2017 [161], and to the GNMSSM with complex parameters in 2018 [162]. The mixed OS–\(\overline{\text {DR}}\) scheme employed for the Higgs sector in Refs. [160,161,162] differs from the one of Refs. [136, 144] in that the Lagrangian parameters \((g, g^\prime , v)\) are connected to the physical observables \((M_Z, M_W, G_\mu )\) instead of \((M_Z, M_W, e)\). In the GNMSSM calculation of Ref. [162] the additional \(Z_3\)-violating parameters are all renormalized in the \(\overline{\text {DR}}\) scheme. The dominant two-loop corrections, as well as a resummation of higher-order logarithmic effects which will be discussed in Sect. 5, were included in Refs. [160,161,162] only in the MSSM limit, exploiting the gaugeless, zero-momentum results implemented in FeynHiggs at the time (namely, those of Refs. [33,34,35, 37] in the real case, and Refs. [89, 98,99,100] in the complex case and in the GNMSSM). The effectiveness of this approximation for the two-loop corrections was assessed in Ref. [160] by considering the impact of the same approximation on the one-loop corrections from the top/stop sector. However, the extensions of FeynHiggs to the (G)NMSSM presented in Refs. [160,161,162] have not been made available to the public so far.
A significant effort was also devoted during KUTS to the comparison between the predictions of the available codes for Higgs-mass calculations in the NMSSM. In 2015, Ref. [163] compared the results of the \(\overline{\text {DR}}\) calculations implemented in FlexibleSUSY, NMSSMCALC, NMSSMTools, SOFTSUSY and SARAH/SPheno, in six representative points of the NMSSM parameter space. The bulk of the discrepancies between the predictions of the five codes could be traced back to differences in the determination of the running parameters (in particular, the top Yukawa coupling) entering the calculation of the radiative corrections. Once these differences were accounted for, the residual discrepancies were mainly due to different approximations adopted by the codes in the two-loop corrections. In points with large \(\lambda \), the results of SARAH/SPheno – which allow for a more-complete determination of the two-loop corrections controlled by that coupling – differed from those of the other codes by up to a few GeV. The predictions of NMSSMCALC were in general different from the others because, at the time, the code included two-loop corrections only at \({{{\mathcal {O}}}}(\alpha _t \alpha _s)\). Four years later, Ref. [157] showed how the inclusion in NMSSMCALC of the \({{{\mathcal {O}}}}(\alpha _t^2)\) corrections in the MSSM limit improves the agreement with the other \(\overline{\text {DR}}\) codes in all of the test points of Ref. [163].
Detailed comparisons between the mixed OS–\(\overline{\text {DR}}\) calculations implemented in NMSSMCALC and in FeynHiggs were presented in Refs. [160, 161, 164]. It was shown that the effect of the different choices of renormalization scheme for the EW parameters \((g, g^\prime , v)\) in the one-loop part of the calculation is numerically small. At \({{{\mathcal {O}}}}(\alpha _t \alpha _s)\), the two codes differ in that NMSSMCALC implements the full calculation of Ref. [156], whereas FeynHiggs includes these corrections only in the MSSM limit. The effect of this approximation on the Higgs masses is obviously more relevant at large \(\lambda \), in which case, however, the corrections involving top and stop loops might not even be the dominant ones. In the four test points considered in Ref. [164], all characterized by \(\lambda < 0.7\), the effect of taking the “MSSM limit” in the \({{{\mathcal {O}}}}(\alpha _t \alpha _s)\) corrections was found to be below 1 GeV. The bulk of the differences found in Refs. [160, 161, 164] between the predictions of the two codes at the two-loop level stemmed instead from the fact that FeynHiggs did include the \({{{\mathcal {O}}}}(\alpha _t^2)\) corrections in the MSSM limit, while those corrections were not implemented in NMSSMCALC until later, see Ref. [157].
3.3 Higgs-mass calculations in other SUSY models
Calculations of the radiative corrections to the Higgs boson masses, of varying degrees of accuracy, have also been performed for a plethora of non-minimal extensions of the (N)MSSM. In this section we summarize a number of calculations that were presented and discussed during the KUTS initiative. These include both automated calculations obtained with the SARAH package, and calculations performed directly within specific models.
Models with Dirac gauginos In this class of models, first proposed in the late 1970s [165], a Dirac mass for each gaugino is obtained via a superpotential term that couples the gauge-strength superfield, whose fermionic component is the gaugino, to an additional chiral superfield in the adjoint representation of the gauge group. In the minimal Dirac-gaugino extension of the MSSM, or MDGSSM [166], the superfield content of the MSSM is thus supplemented with a singlet, an SU(2) triplet and an SU(3) octet, and the superpotential and the soft SUSY-breaking Lagrangian are supplemented with all gauge-invariant terms that involve the adjoint (super)fields. In the scalar sector, the singlet and the neutral component of the triplet mix with the neutral components of the MSSM-like Higgs doublets, resulting in \(4\times 4\) mass matrices when CP is conserved. Another well-studied model, known as MRSSM [167], involves an R-symmetry that forbids Majorana mass terms for the gauginos, a \(\mu \) term in the superpotential, and MSSM-like trilinear interaction terms in the soft SUSY-breaking Lagrangian. Adjoint superfields for each gauge group are introduced as in the MDGSSM to allow for Dirac gaugino masses, and additional chiral superfield doublets \(\hat{R}_1\) and \(\hat{R}_2\), which couple to the MSSM-like Higgs doublets in the superpotential but do not obtain vevs, are introduced to allow for higgsino mass terms.
In models with such intricate Higgs sectors, the SARAH package proved useful to compute automatically the radiative corrections to the Higgs masses. Full one-loop results in the \(\overline{\text {DR}}\) scheme were obtained in Ref. [168] for the MDGSSM, in Ref. [169] for a variant of the MDGSSM with additional fields allowing the unification of gauge couplings, and in Ref. [170] for the MRSSM. For what concerns the two-loop corrections, in Dirac-gaugino models those of \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) differ from their MSSM counterparts because they contain a sum on two gluino mass eigenstates, as well as additional contributions from diagrams involving the scalar component of the octet superfield, the sgluon. In 2015, the \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) corrections were computed with SARAH – as usual, in the \(\overline{\text {DR}}\) scheme and in the gaugeless and vanishing-momentum limits – for the MDGSSM in Ref. [171] and for the MRSSM in Ref. [172]. In the latter it was found that, for multi-TeV values of the Dirac-gluino mass \(M_3\), the contribution of the two-loop diagrams involving sgluons can increase the prediction for the SM-like Higgs mass by more than 10 GeV. Subsequently, in 2016, Ref. [173] presented explicit analytic formulae for the \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) corrections in both the MDGSSM and the MRSSM, obtained with an effective-potential calculation. It was pointed out in Ref. [173] that, in the pure \(\overline{\text {DR}}\) scheme adopted by SARAH, the large two-loop corrections stem from non-decoupling effects – analogous to those already discussed in Sect. 3.1.2 – that are enhanced by \(M_3^2/M_{{\tilde{t}}_i}^2\,\), where \(M_{{\tilde{t}}_i}\) (with \(i=1,2\)) are the stop mass eigenstates. In contrast, the sgluon contributions are much more moderate if an OS scheme is adopted for the parameters in the stop sector. We stress that the two-loop results of Refs. [171,172,173] share the limitations of the analogous results obtained in the NMSSM: in the presence of non-vanishing Higgs self-couplings at tree-level, a zero-momentum calculation does not fully capture the two-loop corrections to the mass of the SM-like Higgs boson even if the gaugeless limit is assumed.
Other automated calculations The SARAH package allowed for full one-loop and partial (i.e., gaugeless and zero-momentum) two-loop calculations of the Higgs masses in a few other non-minimal extensions of the MSSM. In 2015, Ref. [174] considered a model in which the superfield content of the MSSM is supplemented with a pair of vector-like top superfields, identifying regions of the parameter space in which the two-loop corrections involving the additional particles can be as large as the MSSM-like corrections. Also in 2015, Ref. [175] studied a left-right model in which the Higgs sector contains two bi-doublets of \(SU(2)_L \times SU(2)_R\) and two doublets of \(SU(2)_R\), resulting in \(6\times 6\) mass matrices for the neutral scalars when CP is conserved. The authors found that, in this model, radiative corrections involving vector-like colored states can significantly lower the mass of the scalar that is mostly right-doublet, allowing for scenarios where a SM-like Higgs with mass around 125 GeV is accompanied by a light neutral scalar with mass of \({{{\mathcal {O}}}}(10)\) GeV.
In 2017, a SUSY model with an extended gauge group that originates from the exceptional group \(E_6\) was studied with FlexibleSUSY in Ref. [143]. This so-called E\(_6\)SSM features an NMSSM-like Higgs sector, plus a large set of exotic particles. The calculation of the Higgs masses in Ref. [143] included the full one-loop corrections generated by SARAH. To facilitate the comparison between NMSSM and E\(_6\)SSM, a subset of two-loop corrections that are in common between the two models was also included, relying on the results of Refs. [37, 134].
Models with right-handed neutrinos The so-called “MSSM see-saw model” [176] is an extension of the MSSM in which the neutrino masses are generated by a supersymmetric version of the standard see-saw mechanism. The superpotential includes a Yukawa interaction \(Y^\nu _{ij}\,\hat{H}_2 \hat{L}_i\,\hat{\nu }^c_j\) and a Majorana mass term \(\frac{1}{2} M_{ij} \hat{\nu }^c_i\hat{\nu }^c_j\) for the right-handed neutrino superfields, so that a suitable pattern of masses and mixing for the light neutrinos can be obtained with Yukawa couplings of \({{{\mathcal {O}}}}(1)\) and Majorana masses in the range of \(10^{13}\!-\!10^{15}\) GeV. In 2010 (pre-KUTS), Ref. [177] computed the one-loop corrections to the Higgs masses arising from a single generation of right-handed neutrinos and sneutrinos. These corrections turned out to be negligible if the parameter \(\tan \beta \) entering the tree-level Higgs mass matrix is renormalized in an OS scheme, but they can amount to several GeV if \(\tan \beta \) is defined in the \(\overline{\text {DR}}\) scheme (or in a variant thereof denoted in the paper as m\(\overline{\text {DR}}\)). In 2013, Ref. [178] pointed out that the strong sensitivity of the Higgs-mass predictions to the presence of additional SUSY multiplets at arbitrarily high scales should be considered an artifact of minimal-subtraction schemes such as \(\overline{\text {DR}}\), in which the decoupling of heavy particles is not manifest. The authors of Ref. [178] proposed additional “OS-like” definitions for \(\tan \beta \) that also lead to negligible contributions to the Higgs masses from the heavy supermultiplets, and discussed how these contributions match those that would be obtained in an EFT calculation where the heavy particles are integrated out at a scale comparable to their mass. Finally, in 2014 Ref. [179] extended the calculation of Ref. [177] to the case of three generations of right-handed neutrino superfields.
Another model for which radiative corrections to the Higgs masses were computed in recent years is the so-called “\(\mu \)-from-\(\nu \) Supersymmetric Standard Model”, or \(\mu \nu \)SSM [180], a variant of the NMSSM in which the role of the singlet superfield is played by three right-handed neutrino superfields \(\hat{\nu }^c_i\). The superpotential includes an additional Yukawa interaction \(Y^\nu _{ij}\,\hat{H}_2 \hat{L}_i\,\hat{\nu }^c_j\), but it does not include large Majorana mass terms for the right-handed neutrinos. Therefore, a suitable pattern of masses and mixing for the neutrinos is obtained through an “EW see-saw” mechanism in which the role of the large mass scale is played by the neutralino masses, and the new Yukawa couplings can be comparable in size to the electron Yukawa coupling. In this model the right-handed neutrino interactions that replace the singlet interactions of Eqs. (6) and (7) break both R-parity and lepton number conservation. Consequently, the Higgs doublets mix with the left- and right-handed sneutrinos, resulting in \(8\times 8\) mass matrices for the neutral scalars when CP is conserved.
In 2017, Ref. [181] presented a full one-loop calculation of the corrections to the Higgs masses in a simplified version of the \(\mu \nu \)SSM with only one right-handed neutrino, adopting a mixed OS-\(\overline{\text {DR}}\) renormalization scheme that, for the parameters that have a counterpart in the NMSSM, matches the one of Ref. [160]. The extension of this calculation to three generations of right-handed neutrinos was presented two years later in Ref. [182]. In both papers, the dominant two-loop corrections in the MSSM limit, as well as the resummation of higher-order logarithmic effects, were also included following Ref. [160]. In this way, a comparison between the \(\mu \nu \)SSM predictions of Refs. [181, 182] and the NMSSM predictions of Ref. [160] singles out the effects of the one-loop corrections controlled by the neutrino Yukawa couplings. It was found that, for values of the Yukawa couplings of \({{{\mathcal {O}}}}(10^{-7})\), which in this model correspond to sub-eV neutrino masses, the corresponding effects on the prediction for the mass of the SM-like Higgs are negligible. On the other hand, in the full \(\mu \nu \)SSM the presence of two additional singlets interacting with the Higgs doublets can lead to predictions for the scalar sector that differ substantially from those of the NMSSM. In 2020, the one-loop corrections computed in Refs. [181, 182] were made available in the public code munuSSM [183]. Through an automated link to FeynHiggs, the code includes in the Higgs-mass calculation also the dominant two-loop and higher-order corrections that are in common between the \(\mu \nu \)SSM and the MSSM.
A supersymmetric Goldstone-Higgs model In this model, the idea of an elementary pseudo-Goldstone boson that acquires mass through radiative corrections and plays the role of the observed Higgs boson, see Refs. [184, 185], is exploited in a supersymmetric setup to relate the SUSY-breaking scale with the radiatively-generated EW scale. In 2016, Ref. [186] obtained an approximate picture of the mass spectrum of the model, computing the leading contributions to the mass of the pseudo-Goldstone boson via the one-loop effective potential. For a more precise investigation of the viability of this model, and of its ability to reproduce the observed value of the Higgs mass, a calculation that goes beyond the one-loop effective-potential approximation would be desirable.
3.4 Prospects
As discussed earlier in this section, a full two-loop calculation of the corrections to the Higgs masses, including momentum dependence and all of the effects controlled by the EW gauge couplings, is not yet available in any SUSY extension of the SM. For what concerns the MSSM, even in the calculation of Refs. [50, 52], which did include an effective-potential calculation of the EW effects, the momentum dependence of the two-loop corrections was included only in the gaugeless limit. Beyond the MSSM, two-loop corrections to the Higgs masses have so far been computed only under the combined approximations of vanishing momentum and vanishing EW gauge couplings. However, in models that feature additional Higgs self-couplings at tree level, such as the NMSSM, a consistent calculation of the corrections to the lighter Higgs mass requires the inclusion of the momentum dependence even in the gaugeless limit. Closing these gaps, and obtaining results for each of the different renormalization schemes considered in the literature, will certainly be a priority in the near future.
As an alternative to performing individual calculations of the missing corrections in many different models, a sensible approach might consist in computing the full two-loop corrections only once for a general renormalizable theory, and then adapting the results to the field-and-interaction content of the specific model under consideration. This approach, pioneered already in the 2000s by Refs. [108, 154, 187], was at the origin of the MSSM-specific results of Refs. [50, 52]. It was also at the origin of the zero-momentum and gaugeless calculation of the two-loop corrections in generic BSM models implemented in SARAH, see Refs. [109, 110, 155]. However, a complete calculation of the two-loop corrections controlled by the EW gauge couplings remained elusive, because the momentum-dependent contributions from diagrams that involve more than one massive-gauge-boson propagator were not available until very recently. At last, in 2019 a complete two-loop calculation of tadpoles and self-energies for the scalars of a general renormalizable theory was presented in Ref. [188]. When adapted to specific SUSY models, the results of Ref. [188] will allow for complete two-loop calculations of the Higgs masses, starting from a set of \(\overline{\text {DR}}\)-renormalized Lagrangian parameters. However, the choice of the most convenient renormalization scheme depends on the kind of phenomenological analysis that is aimed for, as well as on the considered region of the model’s parameter space. It thus remains something to be determined on a case-by-case basis. Any change of renormalization scheme for the parameters that enter only the radiative corrections to the Higgs mass matrices – e.g., the parameters in the quark/squark sector – amounts to a product of one-loop effects, and should not, as such, present particular difficulties. In contrast, in order to connect the \(\overline{\text {DR}}\) parameters g, \(g^\prime \) and v entering the tree-level mass matrices to a set of physical observables – usually chosen among \(M_Z\), \(M_W\), \(G_\mu \) and e – it will still be necessary to obtain complete two-loop results for the gauge-boson self-energies, and possibly a two-loop (but zero-momentum) calculation of the muon-decay amplitude.
Beyond two loops, fixed-order calculations of the corrections to the Higgs masses in SUSY models exist only for the MSSM. In particular, the three-loop corrections to the lighter Higgs mass of \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\), i.e. those involving the top Yukawa coupling and the highest power of the strong gauge coupling, have already been computed by different groups in the vanishing-momentum limit, see Sect. 3.1.2. A first direction of improvement, still under the approximation of vanishing momentum and vanishing EW gauge couplings, would be the calculation of the three-loop corrections that involve lower powers of the strong gauge coupling, among which the most relevant are expected to be those of \({{{\mathcal {O}}}}(\alpha _t^2\alpha _s)\) and \({{{\mathcal {O}}}}(\alpha _t^3)\). Indeed, it was noticed already in Refs. [65, 66, 189] that, at least for what concerns the logarithmic terms, there can be significant cancellations between these contributions and the \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\) ones. As in the case of the two-loop corrections, going beyond the gaugeless limit in the MSSM, or extending the calculation to models with additional Higgs self-couplings, would require for consistency also the inclusion of external-momentum effects in the three-loop self-energies. This might be achieved via numerical methods, see e.g. Ref. [190]. However, at least for the MSSM, it still has to be determined whether the effort would be justified by the size of the resulting corrections.
To conclude this section we recall that, in SUSY models, both the measured value of the SM-like Higgs mass and the exclusion bounds from direct searches at the LHC are most easily accommodated by scenarios with multi-TeV SUSY masses. In such scenarios, any fixed-order calculation of the Higgs masses may become inadequate, because the uncomputed higher-order corrections involve higher powers of the logarithm of the ratio between the SUSY scale and the EW scale. In order to obtain an accurate prediction for the Higgs masses, such potentially large logarithmic corrections must be resummed to all perturbative orders in an EFT approach. The current status of this kind of calculations will be reviewed in the next section.
4 EFT calculations
4.1 Overview
As mentioned already in Sect. 2.3, a generic n-loop amplitude has a logarithmic dependence, up to the nth power, on the masses of the particles circulating in the loops. In the presence of hierarchies between the masses, terms enhanced by logarithms of large mass ratios can counteract the suppression arising from the loop factors, slowing down (or even endangering) the convergence of the perturbative expansion. It is then necessary to reorganize the calculation in an EFT approach: the heavy particles are integrated out of the theory at a renormalization scale comparable to their masses, leaving behind threshold corrections to the couplings of the light particles. These couplings are then evolved via appropriate RGEs to a scale of the order of the masses of the light particles, where physical observables (e.g., on-shell masses for the Higgs bosons) are computed including only the light particles in the loops. In this approach, the calculations at both the heavy- and light-particle mass scales are free of large logarithmic terms, while the effect of those terms is accounted for by the RG evolution. If a BSM theory involves multiple widely-split mass scales, a tower of EFTs must be built, computing threshold corrections at each of the scales where some heavy particles are integrated out.
In the simplest realization of the EFT approach for SUSY models, all of the superparticles and all of the BSM Higgs bosons are integrated out at a common scale \(M_S\), so that the EFT valid below this scale is just the SM. The calculation of the pole mass of the Higgs boson then requires the determination of the matching condition at the scale \(M_S\) for the quartic Higgs couplingFootnote 13\(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\), which we can decompose in a tree-level part and a loop correction as \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}= \lambda _{{\scriptscriptstyle \mathrm{SM}}}^\mathrm{tree} + \Delta \lambda \). The tree-level matching condition includes the original tree-level value of the coupling in the SUSY model, plus possible contributions from the decoupling of the heavy scalars that, in the limit of unbroken EW symmetry, have a non-vanishing trilinear coupling to two SM-like Higgs bosons. For example, in the MSSM there are no such couplings, and the tree-level matching condition is just
In contrast, in the NMSSM there is an additional contribution proportional to \(\lambda ^2\) in the original quartic coupling, plus a term arising from the decoupling of the singlet scalar:
In general, the correction \(\Delta \lambda \) contains contributions of three different kinds: (i) contributions of one-particle-irreducible (1PI) diagrams with four external Higgs fields, which involve only loop integrals with vanishing external momenta; (ii) contributions involving the renormalization constant of the Higgs field, which require a computation of the \({{{\mathcal {O}}}}(p^2)\) part of the Higgs-boson self-energy; (iii) contributions that arise from changes in the definition of the parameters entering the matching condition. Concerning the third kind, a first contribution arises from the fact that the SUSY model provides a prediction for the quartic Higgs coupling in the \(\overline{\text {DR}}\) scheme, whereas \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) is generally interpreted as an \(\overline{\text {MS}}\)-renormalized quantity. Moreover, the prediction is expressed in terms of the \(\overline{\text {DR}}\)-renormalized parameters of the SUSY model, some of which need to be connected to their \(\overline{\text {MS}}\)-renormalized counterparts in the SM. For example, the conversion of the EW gauge couplings in Eqs. (11) and (12) requires the computation of the \({{{\mathcal {O}}}}(p^2)\) part of the gauge-boson self-energies. Beyond one loop, \(\Delta \lambda \) contains also terms resulting from the product of lower-order contributions of different kinds. As in the case of the fixed-order calculation, the dominant contributions to \(\Delta \lambda \) are generally those involving the top Yukawa coupling and, beyond one loop, the strong gauge coupling.Footnote 14
Once the matching condition for \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) is determined at the SUSY scale \(M_S\) from a full set of SUSY parameters, the quartic coupling is evolved down to the EW scale. There \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) can be used to compute the pole Higgs mass, including only the contributions of SM particles in the radiative corrections. Alternatively, \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) can be extracted at the EW scale from the measured value of the Higgs mass, evolved up to the SUSY scale, and used there to constrain the SUSY parameters. In this case, one requires that the coupling obtained via RG evolution coincide with the prediction of the SUSY model. We recall that a N\(^n\)LL resummation of the logarithms of the ratio between the SUSY and EW scales requires n-loop calculations at each scale, combined with \((n+1)\)-loop RGEs. On the other hand, the standard procedure of matching the full SUSY model to a renormalizable EFT in the unbroken phase of the EW symmetry amounts to neglecting corrections suppressed by powers of \(v^2/M_S^2\), which can be mapped to the effect of non-renormalizable, higher-dimensional operators in the EFT Lagrangian.
The scenarios in which all of the BSM particles are integrated out at the same scale have the advantage that existing SM calculations can be exploited to extract the running parameters of the EFT Lagrangian from a set of physical observables at the EW scale and evolve them up to the SUSY scale. In particular, the full NNLL resummation of the large logarithmic corrections can rely on the results of Refs. [191,192,193] for the full two-loop relations between running SM parameters and physical observables at the EW scale, and on the results of Refs. [194,195,196,197,198,199,200] for the full three-loop RGEs of the SM. For a partial N\(^3\)LL resummation that involves only the highest powers of the strong gauge coupling, the three-loop relation between \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) and the pole Higgs mass of Refs. [201,202,203,204] and the four-loop RGE for \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) of Refs. [205, 206] can be exploited.
In scenarios with more-complicated mass hierarchies, the EFT valid below the SUSY scale may differ from the SM. For example, both Higgs doublets might be significantly lighter than the superparticles, in which case the considered SUSY model is matched at the scale \(M_S\) with a 2HDM, whose scalar potential reads
where \(\Phi _1\) and \(\Phi _2\) are SU(2) doublets with the same hypercharge, related to the Higgs doublets of the MSSM by \(\Phi _1= -i\sigma _2 H_1^*\) and \(\Phi _2 = H_2\). We work in a basis where both of the Higgs vevs are real and non-negative. While in the MSSM the tree-level interactions of the Higgs doublets with quarks and leptons are those of a “Type-II” 2HDM [207], i.e. \(H_1\) couples only to down-type fermions and \(H_2\) couples only to up-type fermions, couplings of the Higgs doublets to the “wrong” fermion species are generated at loop level when the SUSY particles are integrated out. As a result, the EFT valid below the SUSY scale is in fact a “Type-III” 2HDM, which includes all possible dimension-four Yukawa couplings that are allowed by gauge invariance. In the calculation of the Higgs masses, matching conditions are computed for all of the quartic Higgs couplings \(\lambda _i\) (with \(i=1\ldots 7\)), and the loop corrections \(\Delta \lambda _i\) include contributions from diagrams involving the SUSY particles. The couplings are then evolved either directly to the EW scale, where masses and mixing are computed at once for the extended Higgs sector, or to an intermediate scale \(M_A\) where the heavier Higgs doublet is integrated out, leaving again the SM as EFT. In this case the tree-level matching condition for the quartic Higgs coupling of the SM reads
The loop correction \(\Delta \lambda \) includes contributions that arise from diagrams involving the heavy doublet. The RG evolution of \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) then allows for the all-orders resummation of terms enhanced by \(\ln (M_A/M_t)\), where again we take the top mass as a proxy for the EW scale.
Other examples of non-trivial mass hierarchies are given by “Split SUSY” scenarios, in which the gauginos and the higgsinos are significantly lighter than the sfermions. In this case the EFT valid below the sfermion scale includes additional Higgs-higgsino-gaugino couplings, which differ from the corresponding gauge couplings due to the breaking of SUSY. These additional interactions contribute to both the RGE(s) for the quartic Higgs coupling(s) and the corrections to the Higgs mass(es) at the EW scale. Conversely, in scenarios where the gluino is significantly heavier than the squarks it might be convenient to decouple it from the full SUSY model at its own mass scale, in order to avoid the occurrence of two-loop corrections to the quartic Higgs couplings enhanced by gluino-squark mass ratios such as \(M_3^2/M_{\tilde{Q}}^2\) at the scale where the squarks are integrated out. Scenarios in which one of the stops is much lighter than the other sfermions have also been considered for their implications for EW baryogenesis.
4.2 Pre-KUTS developments
The EFT approach to the calculation of the Higgs mass in SUSY models dates back to the early 1990s [208,209,210]. Over the years, it has also been exploited to determine the coefficients of the logarithmic terms in the Higgs-mass corrections at fixed order, by solving perturbatively the appropriate systems of boundary conditions and RGEs. For example, in the case of the MSSM the logarithmic corrections have been determined at one [211], twoFootnote 15 [212,213,214], three [64, 65], and even four loops and beyond [66, 189]. However, as long as the focus was on “natural” scenarios with SUSY masses of a few hundred GeV, the omission of \({{{\mathcal {O}}}}(v^2/M_S^2)\) terms limited the accuracy of the EFT approach, and the effect of the resummation of logarithmic corrections was not expected to be important enough to justify abandoning the fixed-order calculations of the Higgs mass in favor of a complicated EFT set-up with higher-dimensional operators.Footnote 16
Starting from the mid 2000s, however, an interest in “unnatural” scenarios with SUSY masses far above the TeV scale brought the EFT approach to the calculation of the Higgs mass back into fashion. In particular, in 2004 Refs. [216, 217] pointed out that Split SUSY preserves some positive aspects of the MSSM (such as gauge-coupling unification and a candidate for Dark Matter) while getting rid of some negative ones (e.g., the flavor problem). Early phenomenological studies of scenarios with light gauginos and higgsinos involved a LL determination of the Higgs mass, i.e., one-loop RGEs and tree-level boundary conditions. A Split-SUSY scenario in which one of the stops is also light was studied at LL in Ref. [218]. Beyond LL, the one-loop contributions of gauginos and higgsinos to the radiative corrections to the Higgs mass at the EW scale were computed already in 2004 in Ref. [219], and reproduced a few years later in Ref. [220]. The former paper also included the two-loop RGE for the quartic Higgs coupling, obtained by adapting the results valid for a general renormalizable theory from Refs. [221,222,223,224], while the latter included partial one-loop results for the boundary conditions at the sfermion-mass scale. The remaining ingredients for a NLL determination of the Higgs mass in Split SUSY became available in 2011, when Ref. [225] computed the one-loop boundary conditions at the sfermion-mass scale for the Higgs-higgsino-gaugino couplings, and Ref. [226] computed the one-loop boundary condition for the quartic Higgs coupling (neglecting the effects of all Yukawa couplings except \(y_t\) ) as well as the two-loop RGEs for all of the parameters of the Split-SUSY Lagrangian.Footnote 17 Finally, in 2013 Ref. [229] obtained predictions for the Higgs mass in a variant of Split SUSY inspired by Dirac gaugino models, in which the Higgs-higgsino-gaugino couplings are suppressed. The paper also highlighted the importance of decoupling the gluino at a separate scale if its mass is in the multi-TeV range.
Abandoning naturalness as a criterion to fix the sfermion masses opens up the scenario in which all of the BSM particles are super-heavy, leaving the SM as an effective theory valid up to scales well above the reach of the LHC. First evoked humorously in 2005 in an April Fool’s prankFootnote 18 on “Supersplit Supersymmetry” [230], this “high-scale SUSY” scenario attracted renewed attention in 2009, when Ref. [231] pointed out that the hypothesis of a SUSY-breaking scale near the GUT scale singles out the relatively narrow range of 128–141 GeV for the mass of the SM-like Higgs boson. In 2011 the predictions for the Higgs mass in the high-scale SUSY scenario were further studied in Ref. [232], which employed two-loop RGEs but only a partial one-loop calculation of the boundary conditions, and in Ref. [226], which employed a full NLL calculation. In 2012, after the Higgs-boson discovery at the LHC, Ref. [233] updated the analysis of Ref. [226], including also the dominant two-loop corrections (in the gaugeless limit) to the relation between \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) and the Higgs mass at the EW scale.
The first phase of operations of the LHC also brought under the spotlight scenarios where at least some of the SUSY particles have masses of a few TeV. This was due to both the increasingly stringent bounds from direct searches of colored SUSY particles, and the fact that, at least in the MSSM, multi-TeV stop masses are needed to obtain a prediction for the SM-like Higgs mass of about 125 GeV. While this kind of hierarchy seems too mild to endanger the convergence of the perturbative expansion, it still implies that the uncertainty of a fixed-order calculation of the Higgs mass arising from the uncomputed two- and higher-loop corrections can be significantly larger than the experimental precision of its measurement. In 2013, two papers discussed the use of the EFT approach to improve the prediction for the SM-like Higgs mass in the MSSM with multi-TeV stop masses. Reference [189], whose main focus was the combination of fixed-order and EFT techniques that will be discussed in detail in Sect. 5, included a NLL resummation of the logarithmic corrections controlled by the top Yukawa coupling in the gaugeless limit. Reference [66] included additional NLL effects (e.g., terms involving both the top-Yukawa and EW-gauge couplings), plus a NNLL resummation of the top-induced corrections in the gaugeless limit. To obtain the latter, simplified formulas for the two-loop \({{{\mathcal {O}}}}(y_t^4 g_s^2)\) and \({{{\mathcal {O}}}}(y_t^6)\) contributions to \(\Delta \lambda \) were derived in the limit of degenerate masses of the stops, the gluino and the heavy Higgs doublet, adapting the results of the Higgs-mass calculation of Ref. [32]. Both analyses found that, in scenarios with stop masses above 1 TeV, the resummation of higher-order logarithmic corrections leads to predictions for the SM-like Higgs mass that could differ by as much as a few GeV from those of the available fixed-order calculations, which included the two-loop corrections in the gaugeless limit and only the \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\) corrections at three loops. By highlighting the impact of the resummation even in mildly hierarchical scenarios, Refs. [66, 189] made the case for a systematic improvement, at the NLL level and beyond, of the EFT calculation of the Higgs mass in SUSY models.
4.3 Advances during KUTS
4.3.1 Matching the MSSM directly to the SM
As mentioned earlier, in scenarios where all of the SUSY particles as well as the heavy Higgs bosons are clustered around the same high scale the calculation of the Higgs mass can rely on existing results for the RGEs of the parameters of the SM Lagrangian, and for the relations between running parameters and physical observables. What is left to compute in these scenarios is thus the matching condition at the SUSY scale for the quartic Higgs coupling of the SM. We stress that this requires also the calculation of the matching conditions for the other SM couplings, at a perturbative order that depends on how these couplings – or their MSSM counterparts – enter the matching condition for \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) (e.g., in a two-loop calculation, the matching conditions for the couplings entering at tree level must be computed at two loops, while those for the couplings entering only at one loop can be computed at one loop).
During the years of the KUTS initiative, a substantial effort was devoted to the calculation of \(\Delta \lambda \) in the heavy-SUSY scenario where the MSSM is matched directly to the SM. In 2014, Ref. [227] revised and corrected the one-loop calculation of \(\Delta \lambda \) of Ref. [226], and computed in addition the two-loop \({{{\mathcal {O}}}}(y_t^4 g_s^2)\) contribution for arbitrary values of all of the relevant MSSM parameters, thus generalizing the result of Ref. [66] which was valid in the limit of degenerate stop and gluino masses. It was found in Ref. [227] that the inclusion of the \({{{\mathcal {O}}}}(y_t^4 g_s^2)\) contribution to \(\Delta \lambda \) can increase the prediction for the Higgs mass by about 1 GeV in scenarios with \(|X_t|\approx 2\,M_S\), where \(M_tX_t\) is the off-diagonal entry in the stop mass matrix and \(M_S\) denotes an average stop mass. In 2015, Ref. [234] included in \(\Delta \lambda \) the subset of one-loop contributions controlled by the bottom and tau Yukawa couplings that are enhanced at large values of \(\tan \beta \). It also confirmed the result of Ref. [227] for the two-loop \({{{\mathcal {O}}}}(y_t^4 g_s^2)\) contribution, and corrected the result of Ref. [66] for the two-loop \({{{\mathcal {O}}}}(y_t^6)\) contribution in the limit of degenerate stop and heavy-Higgs masses. In 2017, Ref. [235] provided the full one-loop contributions to \(\Delta \lambda \) involving the bottom and tau Yukawa couplings, the full two-loop contributions of \({{{\mathcal {O}}}}(y_b^4 g_s^2)\), and the full two-loop contributions that involve only the third-family Yukawa couplings,Footnote 19 of which the dominant ones are those of \({{{\mathcal {O}}}}(y_t^6)\). It also discussed how, in order to avoid potentially large two-loop contributions enhanced by \(\tan \beta \), the one-loop contributions to \(\Delta \lambda \) should be expressed in terms of the bottom Yukawa coupling of the MSSM. Combined with the earlier one- and two-loop results of Ref. [227], the results of Ref. [235] allow for a complete NNLL resummation of the large logarithmic corrections to the Higgs mass in the gaugeless limit, for arbitrary (but real) values of all of the relevant MSSM parameters. A study of the numerical impact of the two-loop contributions to \(\Delta \lambda \) in scenarios where the stop masses are not degenerate showed that the use of simplified formulas with an average stop mass can lead to a rather poor approximation of the results obtained with the exact formulas.
A first step beyond the NNLL resummation was taken in 2018, when Ref. [236] provided the three-loop \({{{\mathcal {O}}}}(y_t^4 g_s^4)\) contribution to \(\Delta \lambda \). Combined with the four-loop \({{{\mathcal {O}}}}(y_t^4 g_s^6)\) contribution to the RGE for \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) and the three-loop \({{{\mathcal {O}}}}(y_t^4 g_s^4 v^2)\) contribution to the relation between \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) and the Higgs mass, the results of Ref. [236] allow for a N\(^3\)LL resummation of the logarithmic corrections that involve the top Yukawa coupling and the highest powers of the strong gauge coupling. The three-loop contribution to \(\Delta \lambda \) was extracted from the Higgs-mass calculation of Refs. [67, 68, 70], which relied on a set of expansions around various limiting cases for the SUSY masses. A study of the numerical impact of the newly-computed contribution revealed a strong dependence on the stop mixing term. For vanishing \(X_t\) the inclusion of the three-loop contribution shifts the Higgs mass by 20 MeV or less, but when the stop mixing term approaches the “maximal” value \(|X_t| = \sqrt{6}\,M_S\) the shift can reach up to 600 MeV. However, the latter figure should only be taken as an estimate of the possible size of the mass shift, because in the scenario with degenerate squark and gluino masses the three-loop calculation of Ref. [236] involves an expansion in the stop mixing parameter that becomes unreliable when \(|X_t| \gtrsim M_S\).
In 2019, Ref. [237] took a step beyond the gaugeless limit in the NNLL calculation of the Higgs mass, providing the two-loop contributions to \(\Delta \lambda \) that involve both the strong and the EW gauge couplings,Footnote 20 for generic values of all the relevant SUSY parameters. In contrast to the “gaugeless” two-loop contributions of Refs. [66, 227, 234, 235], where \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}(M_S)\) can be considered vanishing at tree level – see Eq. (11) – and all of the relevant two-loop diagrams can be computed at vanishing external momenta, the calculation of the mixed QCD–EW contributions requires also the \({{{\mathcal {O}}}}(p^2)\) parts of the two-loop self-energies of the Higgs boson (for the field-renormalization contributions) and of the gauge bosons (for the MSSM–SM conversion of the EW gauge couplings). A study of the effects of the mixed QCD–EW contributions to \(\Delta \lambda \) in scenarios with multi-TeV stop masses showed that they are largely sub-dominant with respect to the gaugeless two-loop contributions, and their inclusion can shift the prediction for the Higgs mass by \({{{\mathcal {O}}}}(100)\) MeV. Alternatively, it can shift the values of the stop masses required to obtain the observed value of the Higgs mass by \({{{\mathcal {O}}}}(100)\) GeV.
If the squark mass and mixing terms entering the one-loop contributions to \(\Delta \lambda \) are renormalized in the \(\overline{\text {DR}}\) scheme, the two-loop contributions controlled by the strong gauge coupling contain terms that, in the limit of large gluino mass, depend linearly or quadratically on the ratios of \(M_3\) over the various squark masses. Even for a mild hierarchy between the gluino and the squarks, which would normally not warrant a separate decoupling scale for the gluino, the dependence on mass ratios such as \(M_3^2/M_{\tilde{Q}}^2\) may result in rather large two-loop effects. To circumvent this problem in the \({{{\mathcal {O}}}}(y_t^4g_s^2)\) contribution to \(\Delta \lambda \), the authors of Ref. [234] had proposed to renormalize the stop mass and mixing terms in an OS scheme. However, it was subsequently pointed out in Ref. [238] that the definition of Ref. [234] for the stop mixing term leads to the occurrence of terms enhanced by \(\ln M_S/M_t\) in the \({{{\mathcal {O}}}}(y_t^6)\) contribution to \(\Delta \lambda \), spoiling the underlying assumptions of the EFT approach. As an alternative, the authors of Ref. [238] proposed to adopt for the stop parameters the \(\overline{\text {MDR}}\) scheme of Refs. [67, 68], see Sect. 3.1.2, which they extended with an appropriate definition for \(X_t\).
The calculations of the various contributions to \(\Delta \lambda \) discussed so far were restricted to the case of real parameters in the MSSM Lagrangian. In 2020, Ref. [239] extended the full one-loop contributions, as well as the two-loop contributions in the limit of vanishing EW-gauge and tau-Yukawa couplings, to the case of complex parameters. The predictions for \(M_h\) obtained with the full dependence of \(\Delta \lambda \) on the CP-violating phases were compared with predictions in which the phase dependence is approximated by an interpolation, observing deviations of up to 1 GeV in scenarios with more than one non-zero phase. Reference [239] also discussed the impact of including in the determination of the Yukawa couplings corrections that are formally of higher order with respect to the accuracy of the Higgs-mass calculation. In particular, the inclusion of one-loop EW corrections and two-loop \({{{\mathcal {O}}}}(\alpha _s^2)\) corrections – the latter adapted from Refs. [240,241,242] – in the relation between the bottom Yukawa coupling of the MSSM and its SM counterpart at the SUSY scale allows for an improved treatment of effects that are enhanced at large \(\tan \beta \). The inclusion of three-loop \({{{\mathcal {O}}}}(\alpha _s^3)\) corrections in the relation between the top Yukawa coupling of the SM and the top mass at the EW scale accounts for the bulk of the N\(^3\)LL effects that involve the highest powers of the strong gauge coupling. This was found in Ref. [239] to be a sufficient approximation of those effects, in view of the uncertainty of the expansion in the stop mixing parameter that was employed in Ref. [236] to obtain the three-loop \({{{\mathcal {O}}}}(y_t^4g_s^4)\) contributions to \(\Delta \lambda \).
4.3.2 Matching the MSSM to a 2HDM
Compared with the case in which the EFT valid at the EW scale is just the SM, the heavy-SUSY scenario in which both Higgs doublets are within reach of the LHC has an obvious appeal from the point of view of phenomenology. However, the calculation of the Higgs masses in this scenario cannot rely on the existing SM results, and the resummation of large logarithmic corrections has so far been performed only at the NLL order (i.e., involving one-loop corrections and two-loop RGEs).
For the MSSM with real parameters, the one-loop squark contributions to \(\Delta \lambda _i\) had already been obtained in the 1990s, see Ref. [211]. In 2015, Ref. [243] extended the results of Ref. [211] to the case of complex parameters, neglecting however some of the terms that involve the EW gauge couplings. In 2019, the missing terms for the squark contributions in the complex case were included in Ref. [244]. A full one-loop calculation of \(\Delta \lambda _i\), including also the higgsino-gaugino contributions and the contributions arising from the \(\overline{\text {DR}}\)–\(\overline{\text {MS}}\) translation of the quartic couplings, had become available in 2009, see Ref. [245], and in 2018 it was reproduced in Ref. [246]. The latter paper also pointed out that the parameter \(\tan \beta \) of the 2HDM differs from its MSSM counterpart by a loop-induced shift.
For what concerns the two-loop contributions to \(\Delta \lambda _i\), in 2015 Ref. [247] proposed a procedure to identify those of \({{{\mathcal {O}}}}(y_t^4g_s^2)\) from the \(\tan \beta \)-dependence of the various terms entering the corresponding contribution to the quartic coupling of the SM. Shortly thereafter, Ref. [243] extended that calculation to the case of complex parameters, and also resolved an ambiguity in the results for \(\Delta \lambda _3\), \(\Delta \lambda _4\) and \(\Delta \lambda _5\), for which the procedure of Ref. [247] determines only the sum. These results were, however, restricted to the case of degenerate soft SUSY-breaking masses for the stops. In 2020, Ref. [248] computed the \({{{\mathcal {O}}}}(y_t^4g_s^2)\) contributions to \(\Delta \lambda _i\) for arbitrary complex values of all of the relevant parameters, as well as the \({{{\mathcal {O}}}}(y_t^6)\) contributions in the limit of degenerate stop masses.
The two-loop RGEs for the 2HDM can be extracted from the formulas of Refs. [221,222,223,224] for a general renormalizable theory, which have been implemented in public codes such as SARAH [106] and PyR@TE [249,250,251,252]. In 2014, Ref. [253] used SARAH to obtain explicit results for the RGEs of the Type-II 2HDM. In 2015, these RGEs were revised and corrected in Ref. [247], where they entered the EFT calculation of the Higgs masses under the approximation of neglecting the RG evolution of the loop-induced “wrong” Yukawa couplings. In 2018, Ref. [246] used SARAH to obtain RGEs for the Type-III 2HDM, neglecting all Yukawa couplings except those of the two doublets to top quarks. However, later in 2018 Refs. [254, 255] found that the implementation in SARAH and PyR@TE of the general results of Refs. [221,222,223,224] was not appropriate for models, such as the 2HDM, that feature mixing in the scalar sector. Reference [255] provided the correct two-loop RGEs for the Type-III 2HDM, and Ref. [254] computed the three-loop contributions that involve only \(\lambda _i\) to the RGEs for the masses and quartic couplings of the Higgs doublets. Also in late 2018, the correct two-loop RGEs for the Type-III 2HDM were independently derived in Ref. [256] and made available in the public code 2HDME [257]. Meanwhile, the three-loop RGEs for the gauge and Yukawa couplings of the Type-III 2HDM had been presented in 2017 in Ref. [258].
After the quartic couplings are evolved down to the EW scale, they can be used in conjunction with \(\tan \beta \) and an input mass parameter – usually taken as either \(M_A\) or \(M_{H^\pm }\) – to compute masses and mixing angles in the Higgs sector.Footnote 21 In the approximation of neglecting the “wrong” Yukawa couplings, so that the relevant EFT is a type-II 2HDM, the one-loop contributions to the Higgs mass matrix from fermions and gauge bosons are the same as in the MSSM and can be found in the literature, see e.g. Refs. [19,20,21,22,23,24]. In contrast, the Higgs contributions must be computed in terms of the quartic Higgs couplings of the 2HDM. In 2015, Ref. [263] used SARAH to obtain the full one-loop corrections to the Higgs mass matrix for the type-II 2HDM. Two-loop corrections to the Higgs mass matrix at vanishing external momentum are also generated by SARAH in the gaugeless limit, which in the 2HDM includes also the contributions of the quartic Higgs couplings. These corrections were discussed in 2017 in Ref. [155], but they have not yet been applied to the case in which the 2HDM is treated as the EFT of the MSSM with heavy SUSY particles.
If there is a substantial gap between the masses of the heavy Higgs bosons and the EW scale, the radiative corrections to the Higgs mass matrix computed within the 2HDM contain logarithmic terms involving the ratio of the two scales, which might be large enough to require resummation. To this effect, the heavier Higgs doublet is integrated out at the scale \(Q=M_A\), leaving the SM as EFT. The tree-level matching condition for the quartic Higgs coupling \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) is given in Eq. (14), and the threshold correction \(\Delta \lambda \) from one-loop diagrams involving the heavier Higgs doublet was computed in Ref. [246]. The contribution to \(\Delta \lambda \) from two-loop diagrams involving the heavier Higgs doublet and top quarks was subsequently computed in Ref. [248]. After the RG evolution of the quartic coupling down to the EW scale, typically at \(Q=M_t\), the mass of the lighter Higgs boson can be computed including the known SM results for the radiative corrections.
References [244, 246, 247] also proposed a procedure that resums the corrections enhanced by \(\ln (M_A/M_t)\) while still retaining information on the corrections to the masses of the heavy Higgs bosons and on their mixing with the SM-like Higgs. While the proposals of the three papers differ in minor details, their central idea consists in computing the higher-order logarithmic contributions to \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) using the SM as EFT, and inserting them in the full Higgs mass matrix of the 2HDM, which is then diagonalized to determine masses and mixing at once. It was shown in Ref. [244] that this procedure provides a satisfactory interpolation between the pure-2HDM calculation, which is appropriate when both Higgs doublets are at the EW scale, and the two-step calculation where the heavier Higgs doublet is integrated out at an intermediate scale.
The availability of proper EFT calculations in the setup with heavy SUSY particles and a light 2HDM allowed for an assessment of the benchmark scenarios used by ATLAS and CMS to interpret their Higgs searches in the low-\(\tan \beta \) region of the MSSM, where ultra-heavy stops are required to obtain a prediction for the SM-like Higgs mass around 125 GeV. In the “low-tb-high” scenario proposed in Ref. [264], the Higgs masses had been computed with an early version of FeynHiggs that performed the resummation of logarithmic corrections by decoupling the SUSY particles and the heavy Higgs doublet at the same high scale. It was shown in Refs. [246, 247] that, at low values of \(\tan \beta \) and \(M_A\), this approximation can overestimate the prediction for the SM-like Higgs mass by as much as 8 GeV. In 2019, a new benchmark scenario for the low-\(\tan \beta \) region, based on the EFT calculation of Ref. [246], was eventually proposed in Ref. [265].
In some instances, rather than interpreting their Higgs searches in a specific MSSM scenario, ATLAS and CMS relied on a simplifying approach, the so-called “hMSSM” [266,267,268,269]. This approximation assumes that the Higgs sector is CP conserving, that all SUSY particles are too heavy to affect Higgs production and decays, that any non-decoupling SUSY corrections to the Higgs couplings are negligible, and that the radiative corrections to the elements other than (2, 2) in the mass matrix of the neutral CP-even components of \(H_1\) and \(H_2\) are also negligible, i.e. \(\Delta {\mathcal {M}}_{1j}^2 \approx 0\) for \(j=1,2\), see Eq. (2). In this case, the remaining radiative correction \(\Delta {\mathcal {M}}_{22}^2\) can be expressed in terms of the parameters that determine the tree-level mass matrix (i.e. \(\tan \beta \), \(M_Z\) and \(M_A\)) plus the smaller eigenvalue \(M_h\), which is treated as an input and identified with the mass of the observed Higgs boson. Consequently, the larger eigenvalue \(M_H\) and the angle \(\alpha \) that diagonalizes the mass matrix can in turn be expressed in terms of just those four input parameters, of which only \(\tan \beta \) and \(M_A\) are unknown. While the hMSSM approach does bring some benefits – namely, the limited number of input parameters, and the fact that the measured value of the Higgs mass is one of them – its predictions for the Higgs properties can be mapped only to regions of the MSSM parameter space in which the approximations of neglecting the \(\Delta {\mathcal {M}}_{1j}^2\) corrections and the SUSY corrections to the Higgs couplings are justified. Indeed, in Refs. [247, 265] the comparison between the EFT calculations and the hMSSM approach found regions of the MSSM parameter space where the predictions for \(\alpha \), which determines the couplings of the CP-even Higgs bosons, can differ by more than \(10\%\). Moreover, the EFT calculations show that, for low values of \(\tan \beta \) and \(M_A\), a prediction for the lighter Higgs mass of about 125 GeV may require stop masses as large as the GUT scale, putting into question the validity of the MSSM as the underlying high-energy theory.
4.3.3 Split-SUSY scenarios for the MSSM
In the original Split-SUSY scenario of Refs. [216, 217], where the heavy Higgs doublet is integrated out at the same scale as the sfermions, the one-loop threshold corrections and two-loop RGEs necessary to the NLL resummation of the large logarithmic corrections had become available by the beginning of the KUTS initiative, see Sect. 4.2. In 2018, Ref. [246] included in the threshold corrections to the Higgs-higgsino-gaugino couplings terms suppressed by \(X_t^2/M_S^2\) that had been neglectedFootnote 22 in Refs. [225, 227]. Going beyond NLL, the two-loop threshold corrections to \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) obtained in Refs. [227, 235, 237] can be trivially adapted to this scenario by taking the limits of vanishing gluino and higgsino masses (i.e., \(M_3\rightarrow 0\) and \(\mu \rightarrow 0\)). However, a full NNLL resummation of the logarithmic corrections in Split SUSY will require not only the remaining two-loop corrections controlled by the EW couplings, but also the three-loop part of the RGEs.
A Split-SUSY scenario that came under attention in the course of the KUTS initiative is the one in which both Higgs doublets are significantly lighter than the sfermions. In this case the EFT valid below the sfermion mass scale is a 2HDM augmented with the gauginos and the higgsinos. In 2014, one-loop RGEs for this EFT were presented in Ref. [270], and in 2015 Ref. [263] used SARAH to obtain the 2-loop RGEs. In 2018, Ref. [246] also used SARAH to include in the RGEs the effects of the “wrong” Yukawa couplings of the two Higgs doublets with SM fermions and with higgsinos and gauginos. These interactions, absent at tree level, are generated at one loop when the sfermions are integrated out of the MSSM, but in Split SUSY they are suppressed by ratios of the higgsino and gaugino masses over the sfermion masses. The EFT calculation of the Higgs masses in Ref. [246] employed independent decoupling scales for the heavy Higgs doublet, for the EW gauginos and the higgsinos, and for the gluino. One-loop threshold corrections to the effective couplings were computed at each of these scales, under the approximation of degenerate masses for the higgsinos and the EW gauginos. This allowed for a NLL resummation of the logarithmic corrections in all of the considered EFT towers.
It was shown in Refs. [247, 264] that, in the Split-SUSY scenario with a light 2HDM, an acceptable prediction for the lighter Higgs mass at low \(\tan \beta \) can be obtained for lower values of the stop masses than in the scenario with a light 2HDM where all SUSY particles are decoupled at the high scale. Finally, a benchmark scenario for Higgs searches in the MSSM setup where the sfermions are very heavy while both Higgs doublets, the higgsinos and the gauginos are at or below the TeV scale was proposed in Ref. [265], relying on the NLL EFT calculation of Ref. [246].
4.3.4 Beyond the MSSM
Compared with the case of the MSSM, the effort devoted so far to the EFT calculation of the Higgs masses in non-minimal SUSY extensions of the SM with hierarchical mass spectra has been relatively limited. In view of the number of different models that could in principle be studied, a sensible approach is the one already discussed in Sect. 3.4 for the FO calculations: compute all of the necessary corrections only once for a general theory, and then specialize the results to the model under consideration. As mentioned earlier, the two-loop RGEs for a general theory have been computed long ago in Refs. [221,222,223,224], and they are available in public codes such as SARAH and PyR@TE. The calculation of the physical Higgs mass(es) from the parameters of the EFT Lagrangian at the low scale can rely on the existing SM results or, if the relevant EFT is an extension of the SM, on the general Higgs-mass calculation implemented in SARAH. In addition, a NLL resummation of the large logarithmic corrections requires the calculation of one-loop matching conditions for the Higgs couplings between a general high-energy theory and a general renormalizable EFT from which the heavy states have been integrated out.
In 2018, the general one-loop matching conditions were computed independently in Refs. [271, 272], under the restriction that the high-energy theory does not contain heavy gauge bosons. In particular, Ref. [271] discussed different choices that can be made in the renormalization of the masses, couplings and mixing angles entering the tree-level part of the matching conditions, as well as several subtleties concerning the treatment of tadpoles, gauge dependence and infrared divergences. As an application of the general formulas, Ref. [271] reproduced the MSSM results of Ref. [227], and obtained novel results for the one-loop matching condition for the quartic Higgs coupling in the scenario where the high-energy theory is the MDGSSM and the EFT is the SM plus higgsinos. Reference [272] focused instead on the implementation of the general one-loop matching conditions in the package SARAH. In addition to reproducing the results of Ref. [227] for the MSSM scenario with one light Higgs doublet and those of Ref. [211] for the MSSM scenario with two light Higgs doublets, Ref. [272] provided a novel NLL calculation of the Higgs mass in the scenario where the high-energy theory is the NMSSM and the EFT is the SM. In 2019, a follow-up paper [273] employed SARAH to study the Split-SUSY scenario where the high-energy theory is the GNMSSM and the EFT is the SM plus higgsinos, gauginos, and all of the components of the singlet superfield.
Other EFT calculations of the Higgs masses performed in the years of the KUTS initiative focused on SUSY models with Dirac gauginos. In 2018, Ref. [274] studied the conditions for “Higgs alignment” – i.e., one of the Higgs bosons being SM-like independently of the masses of the others – in Dirac-gaugino models with an extended SUSY in the gauge sector. In the process, Ref. [274] provided a novel EFT calculation of the Higgs mass at the NLL level in the scenario where the high-energy theory is the MDGSSM and the EFT is a type-II 2HDM augmented with Dirac bino and wino. It also considered the scenario where the high-energy theory is the MRSSM and the EFT is just a type-II 2HDM. In both cases the two-loop RGEs were obtained with SARAH. The one-loop threshold corrections to the quartic Higgs couplings at the matching scale were computed directly, although in the MRSSM case only the contributions from loops involving the adjoint scalars were included.
In 2019, Ref. [275] computed the two-loop \({{{\mathcal {O}}}}(y_t^4g_s^2)\) corrections to the quartic coupling of the SM-like Higgs boson that arise when a Dirac gluino and its associated octet scalar (the sgluon) are integrated out of the theory at the respective mass scales. In a rare departure from the gaugeless limit at two loops, Ref. [275] also obtained the threshold corrections of \({{{\mathcal {O}}}}(y_t^4g^2)\) and \({{{\mathcal {O}}}}(g^6)\) that arise from diagrams involving a Dirac wino and its adjoint scalar, in the “Split Dirac SUSY” modelFootnote 23 of Ref. [276]. A numerical study showed that, in the scenarios with vanishing \(X_t\) considered in the paper, the shift induced by all of these two-loop corrections on the prediction for the Higgs mass is small, typically below 100 MeV. Indeed, by explicitly decoupling the gluino from the EFT one avoids the occurrence of corrections to the quartic Higgs coupling enhanced by \(M_3^2/M_{\tilde{Q}}^2\).
4.3.5 Public codes for the EFT calculation of the Higgs masses in SUSY models
In the course of the KUTS initiative, the EFT calculations of the Higgs masses discussed in the previous sections have been implemented in a number of public codes, which we list briefly here (detailed descriptions and complete lists of references can be found in the Appendix).
-
SusyHD, based on Ref. [234], provides a full NLL and “gaugeless” NNLL calculation of the Higgs mass in the MSSM scenario where all SUSY particles and the heavy Higgs doublet are integrated out at the same scale, as well as an NLL calculation in the original Split-SUSY scenario with only one light Higgs doublet.
-
MhEFT implements the calculation of Ref. [66] for the MSSM scenario with heavy SUSY particles and only one light Higgs doublet, and the calculation of Ref. [247] for the scenario with two light Higgs doublets. In both scenarios, the code also allows for light higgsinos and EW gauginos,Footnote 24 under the approximation that the effects of the light SUSY particles are included only in the one-loop RGEs, without distinguishing the effective Higgs-higgsino-gaugino couplings from the gauge couplings.
-
FeynHiggs provides, in addition to the “hybrid” calculation that will be described in Sect. 5, the option of a pure EFT calculation of the MSSM Higgs masses. For the heavy-SUSY scenario where the EFT is the SM, it implements a full NLL and “gaugeless” NNLL calculation, relying on the one- and two-loop threshold corrections with full dependence on the CP-violating phases from Ref. [239]. For the scenario where the EFT is a 2HDM, it implements the NLL calculation of Ref. [246], which covers eight different EFT towers depending on the relative position of the thresholds for the heavy Higgs doublet, the higgsinos and EW gauginos, and the gluino. The matching conditions for the quartic Higgs couplings of the 2HDM also include the two-loop \({{{\mathcal {O}}}}(y_t^4g_s^2)\) and \({{{\mathcal {O}}}}(y_t^6)\) contributions from Ref. [248].
-
FlexibleSUSY contains several modules for the EFT calculation of the MSSM Higgs masses. For the simplest heavy-SUSY scenario where the EFT valid below the matching scale is the SM, the module HSSUSY implements a full NLL and “gaugeless” NNLL calculation that relies on the one- and two-loop corrections from Refs. [227, 235], plus a partial N\(^3\)LL calculation that relies on the three-loop corrections from Ref. [236], provided by the code Himalaya. For the Split-SUSY scenario with only one light Higgs doublet, the module SplitMSSM implements one- and two-loop corrections from Refs. [226, 227]. When the EFT valid below the matching scale is a 2HDM, the code contains separate modules for the scenarios with SUSY particles all heavy, with light higgsinos, and with light higgsinos and gauginos. They allow for the inclusion of either the dominant one-loop corrections of Ref. [211] or the full corrections of Ref. [245], plus the two-loop \({{{\mathcal {O}}}}(y_t^4g_s^2)\) corrections in the approximation of Ref. [247]. Note that FlexibleSUSY includes also a module, named FlexibleEFTHiggs, that allows for the automated “hybrid” NLL calculation of the Higgs mass in any SUSY model matched directly to the SM. This will be described in Sect. 5.
-
SARAH allows for automated EFT calculations of the Higgs masses at the NLL level, relying on the general one-loop matching conditions of Refs. [271, 272]. The package comes with model files for several heavy-SUSY scenarios. In the case where the theory valid above the matching scale is the MSSM, these cover six different EFT towers depending on the relative position of the thresholds for the heavy Higgs doublet and for the SUSY fermions (in contrast to FeynHiggs, the gluino is always decoupled at the same scale as the EW gauginos). There are also model files for the NMSSM matched either directly to the SM, or to the SM plus higgsinos, gauginos, singlet and singlino. Finally, SARAH allows for automated “hybrid” Higgs-mass calculations similar to those in FlexibleEFTHiggs, but the accuracy of the resummation of the large logarithmic effects is only LL in this case.
While the EFT calculations implemented in the codes listed above differ from each other in several aspects – e.g., in the classes of threshold corrections that they include at the SUSY scale, and in the renormalization scheme adopted for some of the SUSY parameters – their predictions for the Higgs masses are generally in good agreement with each other in the appropriate limits. For the heavy-SUSY scenario where the high-energy theory is the MSSM and the EFT is the SM, a comparison between SusyHD and HSSUSY was presented in Ref. [277], a comparison between SusyHD and FeynHiggs was presented in Ref. [278], and a comparison between SusyHD and the relevant module of SARAH was presented in Ref. [272]. For the scenario where the high-energy theory is the MSSM and the EFT is a 2HDM, a comparison between MhEFT and the relevant module of FlexibleSUSY was presented in Ref. [143], a comparison between MhEFT and FeynHiggs was presented in Ref. [246], and a comparison between MhEFT and the relevant module of SARAH was presented in Ref. [272].
4.4 Prospects
As discussed earlier in this section, full EFT calculations of the Higgs masses at the NLL level – i.e., involving one-loop threshold corrections and two-loop RGEs – are already available for a variety of SUSY models and of mass hierarchies within these models. For any other model (or mass hierarchy, e.g. one light stop) that should come under attention in the future, the necessary ingredients for the NLL calculation of the Higgs masses can in principle be obtained “automatically” from general formulas, with the current limitation that the high-energy theory must not involve heavy gauge bosons. In contrast, calculations beyond NLL have so far been performed only for the simplest heavy-SUSY scenario where the MSSM is matched directly to the SM, and they are restricted to subsets of contributions: at NNLL they neglect most of the effects that involve the EW gauge couplings, while at N\(^3\)LL they account only for the effects that involve the top Yukawa coupling combined with the highest powers of the strong gauge coupling.
In heavy-SUSY scenarios where the high-energy theory is matched directly to the SM, a full NNLL calculation of the Higgs mass should be well within reach. Indeed, in these scenarios one can rely on the existing SM results for the three-loop RGEs and for the two-loop relations between Lagrangian parameters and physical masses at the EW scale, and all is left to compute is the full two-loop matching condition for the quartic Higgs coupling at the SUSY scale. In contrast to the case of the FO calculations described in Sect. 3, all of the relevant two-loop diagrams can be computed in the limit of unbroken EW symmetry and through an expansion in the external momentum, and should not present particular difficulties. The most economic approach could again be the one of computing the two-loop matching condition only once for a general high-energy theory, and then adapting the result to the particular SUSY model under consideration. However, some additional work will still be required, on a case-by-case basis, to establish the most convenient renormalization scheme for the Lagrangian parameters, also in order to avoid the occurrence of spuriously large corrections such as, e.g., those enhanced by powers of \(\tan \beta \) or by \(M_3^2/M_{\tilde{Q}}^2\).
In scenarios where the EFT valid below the SUSY scale is an extension of the SM, an NNLL calculation of the Higgs mass(es) requires the three-loop RGEs for the parameters of the EFT. Lacking those, the inclusion of two-loop matching conditions for the couplings of the EFT can be considered an improvement of the calculation only if the hierarchy between the SUSY and EW scales is not so large that the resummation of higher-order logarithmic effects is really mandatory. The computation of the two-loop matching conditions for the quartic Higgs coupling(s) should not involve additional conceptual difficulties with respect to the case in which the EFT is just the SM. However, if the EFT contains singlets or triplets of SU(2), there are also cubic interactions for which the computation of the two-loop matching conditions is required.
For what concerns the N\(^3\)LL calculation of the Higgs mass in the scenario where the MSSM is matched to the SM, a generalization of the three-loop \({{{\mathcal {O}}}}(y_t^4 g_s^4)\) matching condition for the quartic Higgs coupling of Ref. [236] to arbitrary values of \(X_t/M_S\) could be envisaged. In view of the modest impact of this presumably dominant correction, however, it is doubtful that the effort necessary to compute additional three-loop corrections and four-loop RGEs – in this scenario or even in more complicated ones – will be considered justified in the short term. We stress here that the smallness of the gain that results from going to higher perturbative orders in the calculation is in fact a desirable feature of the EFT approach, in which the dominant effects are accounted for by the evolution of the parameters between the SUSY scale and the EW scale. For example, the large cancellations that had been noticed between the \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\), \({{{\mathcal {O}}}}(\alpha _t^2\alpha _s)\) and \({{{\mathcal {O}}}}(\alpha _t^3)\) corrections in the FO calculation of the Higgs mass are already incorporated in the RGEs. Consequently, one can speculate that the omission of the three-loop \({{{\mathcal {O}}}}(y_t^6 g_s^2)\) and \({{{\mathcal {O}}}}(y_t^8)\) contributions to the matching condition in the EFT calculation has a far less dramatic impact than the omission of the corresponding terms in the FO calculation.
Another possible direction of improvement, aimed at increasing the accuracy of the EFT calculation of the Higgs masses in scenarios where the hierarchy between the SUSY scale and the EW scale is mild, could be the inclusion of terms suppressed by \(v^2/M_S^2\). As mentioned in Sect. 2.3, these terms can be mapped to the effect of dimension-six operators in the EFT Lagrangian, and they are neglected when the high-energy theory is matched to a renormalizable EFT in the unbroken phase of the EW symmetry. For example, in the EFT approach the one-loop corrections to the Higgs mass proportional to \(y_t^2\,M_t^4/M_S^2\) arise from the inclusion in the scalar potential of the term \(c_6\,|H|^6\), where \(c_6\) is a Wilson coefficient that scales like \(M_S^{-2}\), induced when the stops are integrated out of the high-energy theory. In general, multiple dimension-six operators contribute to the Higgs mass. In recent years, several papers [279,280,281,282,283] provided the one-loop contributions to the Wilson coefficients of the relevant dimension-six operators that arise when the squarks are integrated out of the MSSM, employing a technique known as “covariant derivative expansion” [284,285,286,287].Footnote 25 In addition, Ref. [235] presented a direct computation of the two-loop \({{{\mathcal {O}}}}(y_t^6 g_s^2)\) contribution to \(c_6\) in the MSSM, relying on the effective-potential approach. However, Ref. [235] also found that, for the values of the stop masses that lead to a Higgs-mass prediction in the vicinity of 125 GeV, the dominant one- and two-loop \({{{\mathcal {O}}}}(v^2/M_S^2)\) effects arising from dimension-six operators are already largely suppressed. Moreover, in the context of the Higgs-mass calculation, the usefulness of a full inclusion of the dimension-six operators in the EFT setup – with matching conditions computed at the SUSY scale, and subsequent RG evolution to the EW scale – can be questioned on general grounds, as the logarithmic enhancement of the higher-order corrections that are thus resummed is always trumped by their power-like suppression.
An alternative approach to the inclusion of the \({{{\mathcal {O}}}}(v^2/M_S^2)\) effects stems from the consideration that these effects are automatically accounted for in the FO calculation of the Higgs masses, which is usually performed in the broken phase of the EW theory and does not necessarily involve any expansion in \(v^2\). In order to cover the whole spectrum of scenarios – from those with a mild hierarchy between the SUSY and EW scales, where the \({{{\mathcal {O}}}}(v^2/M_S^2)\) effects can be relevant, to those with a strong hierarchy, where the resummation of large logarithmic effects is required – it is conceivable to combine a FO calculation of the former effects with an EFT calculation of the latter. Indeed, a number of such “hybrid” approaches to the Higgs-mass calculation in SUSY models have been proposed in the course of the KUTS initiative, as will be reviewed in the next section.
5 Hybrid calculations
5.1 Motivation
As discussed in the previous sections, EFT calculations of the Higgs masses account, to all orders in the perturbative expansion, for the logarithmic corrections that involve the ratio between different mass scales (e.g., the SUSY scale \(M_S\) and the EW scale v), and are therefore suited to scenarios with large hierarchies between scales. However, they neglect contributions to the Higgs masses suppressed by powers of the ratio of scales, e.g. \(v^2/M_S^2\), unless higher-dimensional operators are included in the EFT, at the price of a significant increase in the complexity of the calculation. In contrast, FO calculations of the Higgs masses do not necessarily involve any expansion in ratios of scales, hence they can be applied without loss of accuracy to scenarios with new physics near the EW scale. However, they are unsuited to scenarios with large hierarchies between scales, because the uncomputed higher-order corrections involve higher powers of the logarithm of their ratio.
A novel approach to the determination of the Higgs masses consists in combining the resummation of the logarithmic effects from the EFT calculations with the complete treatment of the contributions suppressed by powers of \(v^2/M_S^2\) from the FO calculations. The aim of this “hybrid” approach is to obtain a single calculation that can be applied to the whole spectrum of SUSY scenarios, from those with light SUSY particles to those with a large hierarchy between the SUSY and EW scales, covering also the intermediary region with SUSY masses of \(0.5{-}2\) TeV. Indeed, while the latter region is of particular interest in view of LHC phenomenology, it sits at the border of the domains of applicability of the FO and EFT calculations, where it is not immediately obvious which, if either, of the two approaches can be considered sufficiently accurate. It should be stressed that there is no unique way to realize such combination of the FO and EFT calculations, and that the proverbial Devil resides in the detail: the contributions to the Higgs masses that are included in both calculations must be subtracted to avoid double counting, and possible differences in the definition of the parameters entering the two calculations must be accounted for, all in a way that does not spoil the resummation of higher-order logarithmic effects.
Since late 2013, three distinct methods for combining the FO and EFT calculations in a hybrid approach have been proposed, and they have been thoroughly discussed during the KUTS meetings. In the following we summarize their main features.
5.2 The hybrid approach of FeynHiggs
A version of FeynHiggs combining a two-loop FO calculation of the MSSM Higgs masses with a resummation of higher-order logarithmic corrections was first presented in 2013 in Ref. [189]. The hybrid approach of FeynHiggs was subsequently refined in Refs. [239, 246, 278, 288,289,290,291], and in Ref. [292] it was used in the production of benchmark scenarios for MSSM Higgs searches at the LHC. The main idea consists in supplementing the FO corrections to the Higgs mass matrix, see Eq. (2), with higher-order logarithmic terms computed numerically in the EFT approach. In MSSM scenarios where the mass of the heavier Higgs doublet is comparable to the SUSY masses, this amounts to the replacement:
where \(\Delta {\mathcal {M}}_{hh}(p^2)\) is the FO correction to the hh element of the mass matrix, in the basis of tree-level mass eigenstates (h, H), which FeynHiggs computes in full at one loop and in the gaugeless limit at two loops; \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}(M_t)\) is a SM-like quartic Higgs coupling obtained in the EFT approach through a numerical solution of the appropriate RGEs, starting from boundary conditions at the SUSY scale; the subtraction term \(\left[ \Delta {\mathcal {M}}_{hh}(p^2)\right] _{\mathrm{d.c.}}\) is meant to avoid double counting, removing the contributions that are present in both the FO result and the EFT result. In the latest implementation of the hybrid approach of FeynHiggs, see Ref. [290], the subtraction term contains the tree-level Higgs mass plus the \({{{\mathcal {O}}}}(v^2)\) terms of an expansion of the SUSY contributions to \(\Delta {\mathcal {M}}_{hh}(p^2)\) in powers of \(v^2\) (i.e., the terms that do not vanish in the limit \(v^2/M_S^2 \rightarrow 0\)). If the one-loop stop contributions to \(\Delta {\mathcal {M}}_{hh}(p^2)\) are expressed in terms of OS-renormalized stop masses and mixing, the two-loop contributions of the corresponding counterterms are not included in the subtraction term (this will be further discussed below). Once the mass matrix has been improved with the inclusion of the higher-order logarithmic terms, the pole masses of the MSSM Higgs bosons are numerically determined from the zeroes of the inverse-propagator matrix as in the regular FO calculation, see Eq. (1).
In the original implementation of the hybrid approach in FeynHiggs, Ref. [189], the resummation of higher-order logarithmic effects was performed only in the scenario where the EFT valid below the SUSY scale is the SM, and it included only the LL and NLL contributions controlled by the top Yukawa coupling and the strong gauge coupling. In 2016, Ref. [288] extended the hybrid approach by including also the LL and NLL contributions controlled by the EW gauge couplings, as well as the NNLL contributions controlled by the top Yukawa coupling and the strong gauge coupling. Reference [288] also adapted the hybrid approach to split-SUSY scenarios in which the EW gauginos and the higgsinos, and possibly also the gluino, are integrated out at intermediate scales between the SUSY and EW scales. In 2017, Ref. [278] identified some spurious higher-order logarithmic contributions that are included in the hybrid result for the lighter Higgs mass when the poles of the inverse-propagator matrix, Eq. (1), are determined numerically. In principle, these spurious contributions would cancel out order by order in a complete FO calculation, and they can be removed by truncating the determination of the propagator poles at the perturbative order covered by the available FO calculation (in FeynHiggs, this means full one-loop and gaugeless two-loop). It was found in Ref. [278] that this modification can shift the prediction for the lighter Higgs mass by about 1.5 GeV when \(M_S\) is of \({{{\mathcal {O}}}}(10~\mathrm{TeV})\).
In 2018, Refs. [246, 289] extended the hybrid approach of FeynHiggs to MSSM scenarios in which both Higgs doublets are much lighter than the SUSY scale. In this case the EFT valid below the SUSY scale is a 2HDM, and the resummation of the logarithmic effects is performed at NLL, with independent decoupling scales for the gluino and for higgsinos and EW gauginos. It was pointed out in Ref. [289] that, in the presence of scalar mixing, the perturbative determination of the propagator poles proposed in Ref. [278] can lead to discontinuities in the Higgs-mass predictions near the crossing points where the masses of the scalars that mix with each other are degenerate.Footnote 26 Reference [289] proposed an alternative procedure in which the spurious logarithmic terms that would cancel out only in a complete FO calculation are removed from the Higgs self-energies via a redefinition of the Higgs fields, after which the poles of the propagator can be determined numerically.
In 2020, Ref. [239] extended the hybrid approach of FeynHiggs – in scenarios with only one light Higgs doublet – to include the full NLL and gaugeless NNLL resummation of the corrections controlled by the bottom Yukawa coupling, which were previously computed only at fixed (i.e., two-loop) order. To facilitate the combination with the EFT component of the calculation, the renormalization scheme for the bottom Yukawa coupling and for the soft SUSY-breaking term \(A_b\) in the FO component of the calculation was changed from the OS scheme of Refs. [35, 37] to the \(\overline{\text {DR}}\) scheme. It was found in Ref. [239] that, in scenarios where the SUSY contributions enhance the bottom Yukawa coupling, the differences in its treatment between the pure FO calculation and the hybrid calculation can lead to significant variations in the predictions for \(M_h\) at large \(\tan \beta \). Also in 2020, Ref. [291] extended the hybrid approach of FeynHiggs – in scenarios where both Higgs doublets are light – to the case of complex parameters in the MSSM Lagrangian, largely relying on Ref. [244] for the EFT component of the Higgs-mass calculation.
An open issue in the hybrid approach of FeynHiggs is the possible mismatch between the renormalization schemes employed in the FO and EFT calculations. In the original implementation, the FO calculation adopted an OS definition for the input parameters that determine the stop masses and mixing, whereas the EFT calculation required \(\overline{\text {DR}}\)-renormalized parameters. It was therefore necessary to either convert the input parameters from OS to \(\overline{\text {DR}}\) before passing them to the EFT calculation, or modify the EFT calculation in such a way that the boundary conditions at the SUSY scale are expressed in terms of OS parameters. However, with the usual OS definition of the stop-mixing parameter – in which \(M_t\,X_t\) is the off-diagonal element of a \(2\times 2\) matrix whose eigenvalues are the pole stop masses, and \(M_t\) is the pole top mass – the one-loop conversion of \(X_t\) between the OS and \(\overline{\text {DR}}\) schemes involves potentially large logarithmic terms:
where the ellipses denote additional, non-logarithmic terms of \({{{\mathcal {O}}}}(\alpha _s)\) or \({{{\mathcal {O}}}}(\alpha _t)\), as well as terms depending on other couplings. The alternative OS definition proposed in Ref. [234], in which the pole top mass in the off-diagonal element of the stop mass matrix is replaced by the running parameter \(m_t(M_S)\), removes some of the logarithmic terms in Eq. (16), but it does not affect the term proportional to \(X_t^2/M_S^2\). The latter stems from a threshold effect in the loop integrals, and is specific to the case of degenerate stop masses (see Ref. [293] for a detailed discussion). In the case of a strong hierarchy between the SUSY and EW scales, the presence of large logarithmic terms either in the conversion of the input parameters or in the boundary conditions at the SUSY scale spoils the resummation of the logarithmic corrections. To circumvent this problem, Ref. [278] modified the hybrid calculation of FeynHiggs, adding the option to use directly a \(\overline{\text {DR}}\) definition for the stop parameters entering the FO part of the calculation. In that case no conversion is needed, and the logarithmic corrections are fully resummed at the desired order (i.e. NLL or beyond, depending on the scenario). If however the input parameters in the stop sector are defined in the OS scheme, FeynHiggs includes only the logarithmic terms of Eq. (16) in their conversion to the \(\overline{\text {DR}}\) scheme. The presence of counterterm contributions in the FO part of the calculation – as mentioned above, those are not subtracted in \(\left[ \Delta {\mathcal {M}}_{hh}(p^2)\right] _{\mathrm{d.c.}}\) – ensures that the prediction for the Higgs mass is correct up to the two-loop order, but the resummation of the higher-order logarithmic corrections is incomplete. As will be discussed in Sect. 6, this is duly accounted for in the estimate of the theoretical uncertainty of the Higgs-mass prediction of FeynHiggs.
5.3 The hybrid approach of FlexibleEFTHiggs
An alternative method to combine the EFT resummation of large logarithmic corrections with the FO calculation of corrections suppressed by powers of \(v^2/M_S^2\) was proposed in 2016 in Ref. [277], and it was implemented in the FlexibleSUSY module FlexibleEFTHiggs. In 2017 a similar approach was implemented in SARAH [294]. The main idea of this approach consists in incorporating the corrections to the Higgs mass suppressed by powers of \(v^2/M_S^2\) into the boundary condition for the quartic Higgs coupling at the SUSY scale, \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}(M_S)\), then proceeding as in a regular EFT calculation (i.e., evolving \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) down to the EW scale and computing there the pole Higgs mass \(M_h\)). The boundary condition is determined by the requirement that the FO result for the pole Higgs mass computed at the SUSY scale be the same in the low-energy EFT (which is assumed to be the SM) and in the high-energy SUSY model. Decomposing the FO result for the Higgs mass computed in the SM as \((M_h^2)_{{\scriptscriptstyle \mathrm{SM}}} = 2\,\lambda _{{\scriptscriptstyle \mathrm{SM}}}(M_S)\,v^2(M_S) + (\Delta M_h^2)_{{\scriptscriptstyle \mathrm{SM}}}\), one obtains
where \((M_h^2)_{{\scriptscriptstyle \mathrm{HET}}}\) is the FO result for the Higgs mass computed in the high-energy theory (HET). Since the FO calculation does not involve any expansion in \(v^2/M_S^2\), the \(M_S\)-suppressed terms are included in \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}(M_S)\), and after the RG evolution of \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) they enter the result for \(M_h\) computed at the EW scale. We remark that, in this approach, the resummation of higher-order logarithmic effects is correct only for the terms that are not suppressed by powers of \(v^2/M_S^2\), because the RG evolution of the higher-dimensional operators that, in a pure EFT approach, would account for the \(M_S\)-suppressed terms differs from the RG evolution of the quartic coupling. On the other hand, the \(M_S\)-suppressed terms are fully included in the Higgs-mass prediction up to the loop order covered by the FO calculation.
An advantage of the hybrid approach of FlexibleEFTHiggs is that the matching procedure is largely independent of the considered high-energy theory, and is therefore well-suited to be implemented in “automated” codes such as FlexibleSUSY and SARAH, which can compute the Higgs masses in generic SUSY (and non-SUSY) extensions of the SM. Indeed, in Ref. [277] FlexibleEFTHiggs was employed to obtain predictions for the Higgs mass in several SUSY models beyond the MSSM, namely the NMSSM, the E\({_6}\)SSM and the MRSSM. On the other hand, the “pole matching” condition of Eq. (17) can only be applied to scenarios in which only one Higgs doublet is light, although it could in principle be extended to cases in which the EFT includes additional light particles that do not mix with the Higgs boson (e.g., to the original Split-SUSY scenario).
In the early implementations of FlexibleEFTHiggs, see Refs. [143, 277], the FO calculation of the Higgs mass entering the boundary condition in Eq. (17) contained only the one-loop corrections computed “automatically” by FlexibleSUSY, allowing for the NLL resummation of the higher-order logarithmic terms in a generic SUSY model matched to the SM. In early 2020, Ref. [295] improved the accuracy of the boundary condition for the MSSM case by including the two-loop corrections in the gaugeless limit, as well as the dominant three-loop corrections of Refs. [67, 68, 70] which are obtained from Himalaya. Combined with full three-loop and partial four-loop RGEs for the SM, this allows for the resummation of the NNLL corrections in the gaugeless limit, and also for the resummation of the N\(^3\)LL corrections that involve only the top Yukawa coupling and the highest powers of the strong gauge coupling. The \(M_S\)-suppressed effects are in turn included fully up to one loop and in the gaugeless limit at two loops. As the calculation of the three-loop corrections to the Higgs mass in Refs. [67, 68, 70] relied on an expansion to the first order in \(v^2\), no \(M_S\)-suppressed effects are actually included at three loops.
A crucial aspect of the FlexibleEFTHiggs approach, discussed in Refs. [143, 295], is that each of the terms on the right-hand side of Eq. (17) involves potentially large logarithms of the ratio between the SUSY scale and the EW scale, but these logarithms must cancel out in the combination. If the parameters entering the various terms are defined differently – e.g., HET couplings for \((M_h^2)_{{\scriptscriptstyle \mathrm{HET}}}\) and SM couplings for \((\Delta M_h^2)_{{\scriptscriptstyle \mathrm{SM}}}\) – the cancellation of the large logarithms holds only up to the loop order covered by the FO calculation. However, the residues of the cancellation include spurious, higher-loop logarithmic terms of the same order as those that are being resummed by the RG evolution, thus spoiling the resummation. To circumvent this problem,Footnote 27 the FO calculation of FlexibleEFTHiggs is reorganized in such a way that \((\Delta M_h^2)_{{\scriptscriptstyle \mathrm{SM}}}\) and \(v^2(M_S)\) are expressed in terms of HET parameters. An external-momentum expansion of the self-energies up to the considered loop order is also necessary to ensure the full cancellation of the large logarithms.
Finally, it was shown in Ref. [295] that the choice of expressing all loop corrections in terms of HET parameters ensures that the two- and higher-loop “leading-QCD” contributions to \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}(M_S)\), i.e. those that are controlled by the highest powers of the strong gauge coupling, do not involve powers of the ratio \(X_t/M_S\) higher than the fourth. This should result in a better convergence of the perturbative expansion in scenarios where that ratio is greater than 1.
5.4 A third hybrid approach
In late 2019, Ref. [296] presented yet another hybrid approach to the calculation of the Higgs mass in the MSSM. A prediction for \(M_h\) that includes both the resummation of higher-order logarithmic corrections and the effects suppressed by powers of \(v^2/M_S^2\) is obtained from:
where \((M_h^2)_{\mathrm{EFT}}\) is the result of the pure EFT calculation of Ref. [236], see Sect. 4.3.1, which includes the full NLL resummation of large logarithmic effects, plus a NNLL resummation in the gaugeless limit and a N\(^3\)LL resummation of the effects that involve only the top Yukawa coupling and the highest powers of the strong gauge coupling. The remaining terms on the right-hand side of Eq. (18) account for the \(M_S\)-suppressed effects at different loop orders. In particular, the term \(\Delta _v^{0\ell +1\ell }\) accounts for the tree-level and one-loop effects, and is obtained by subtracting the result of the pure EFT calculation of \(M_h^2\) provided by HSSUSY from the result of the hybrid calculation of \(M_h^2\) provided by FlexibleEFTHiggs, including only the NLL resummation of logarithmic effects (i.e., one-loop threshold corrections and two-loop RGEs) in each of the calculations. The term \(\Delta _v^{2\ell }\) contains instead the two-loop, \(M_S\)-suppressed effects controlled by \(y_t^4 g_s^2\) or by \(y_t^6\), and is computed from the difference between the known analytic formulas for the two-loop corrections to the lighter Higgs mass in the gaugeless limit and the same formulas expanded to the first order in \(v^2\).
We remark that the proposal of Ref. [296] remains at the level of “proof of concept”, as the script that combines the various ingredients entering Eq. (18) has not been released to the public so far. However, this hybrid calculation accounts for both the logarithmic and the \(M_S\)-suppressed effects at the same order in the relevant couplings as the calculation implemented in the latest version of FlexibleEFTHiggs, see Ref. [295]. Indeed, despite being organized quite differently from each other, the two hybrid calculations lead to very similar predictions for the Higgs mass in the MSSM scenarios considered in Refs. [295, 296].
5.5 Comparing the FO, EFT and hybrid calculations
The hybrid calculations of the Higgs mass described in this section are meant to provide a combination of the results of pure FO calculations, which are expected to be more reliable when the SUSY masses are near the EW scale, with those of pure EFT calculations, which are expected to be more reliable in heavy-SUSY scenarios. To illustrate this point, we compare in Fig. 3 the predictions for the mass of the SM-like Higgs boson obtained with the three approaches, in a simplified MSSM scenario defined as follows: all of the SUSY-breaking masses for sfermions and gauginos, as well as the CP-odd Higgs-boson mass \(M_A\) and the higgsino mass \(\mu \), are set equal to a common scale \(M_S\), which is varied between 300 GeV and 100 TeV; the stop mixing parameter is taken as \(X_t = -\sqrt{6}\,M_S\), and \(\tan \beta =20\) (this fixes the value of the trilinear Higgs-stop coupling \(A_t\)); the trilinear Higgs couplings to all other sfermions are set to zero. The sfermion masses and \(X_t\) are interpreted as \(\overline{\text {DR}}\)-renormalized parameters at the scale \(Q=M_S\). The left plot in Fig. 3 is obtained with FeynHiggs, while the right plot is obtained with different modules of the FlexibleSUSY package – namely, FlexibleSUSY proper, HSSUSY and FlexibleEFTHiggs. In each plot the blue dotted line is the result of the pure FO calculation, the black dashed line is the result of the pure EFT calculation, and the red solid line is the result of the hybrid calculation. The yellow band corresponds to the value of the Higgs mass, as measured by ATLAS and CMS [3] within one standard deviation of the experimental accuracy.
Comparison between the pure FO, pure EFT and hybrid calculations of the mass of the SM-like Higgs boson in an MSSM scenario with degenerate SUSY masses. The sfermion mass and mixing parameters are defined in the \(\overline{\text {DR}}\) scheme at the scale \(Q=M_S\). The left plot is produced with FeynHiggs, the right one with different modules of FlexibleSUSY
The comparison between the different curves in Fig. 3 shows that, both in FeynHiggs and in FlexibleSUSY, the hybrid calculation does indeed agree with the FO calculation at small \(M_S\) and with the EFT calculation at large \(M_S\). The small residual deviation between the hybrid and EFT curves for FeynHiggs at large \(M_S\) is due to two-loop corrections involving the EW gauge couplings that are included in the pure EFT calculation but not in the EFT component of the hybrid calculation. The kinks visible in the FlexibleSUSY curves around \(M_S\approx 750\) GeV originate from a switch of the mass hierarchy used to approximate the three-loop corrections in the calculation of Refs. [67, 68, 70]. Moreover, for \(M_S\lesssim 600\) GeV none of the mass hierarchies implemented in Himalaya reproduces this scenario, and the three-loop corrections are switched off. At small \(M_S\), the comparison between the three curves of each plot also shows that, in this scenario, the \(M_S\)-suppressed effects that are not accounted for by the EFT calculation can be relevant only for values of \(M_S\) that result in a very low prediction for the Higgs mass, which would be incompatible with the measured value even if one assumed a theoretical uncertainty of several GeV.
It is also worth noting that, while the EFT and hybrid predictions for the Higgs mass show a good agreement between FeynHiggs and FlexibleSUSY at large \(M_S\), the predictions of the FO components of the two hybrid calculations differ strikingly in this scenario: the prediction of FeynHiggs decreases steeply when \(M_S\) reaches a few TeV, whereas the prediction of FlexibleSUSY has a much milder behavior at large \(M_S\), and starts differing significantly from the EFT result only for \(M_S\) above \(20\!-\!30\) TeV. The origin of this difference resides in the treatment of the running top mass and the strong gauge coupling entering the loop corrections, which in FeynHiggs are defined as the SM parameters at the EW scale, whereas in FlexibleSUSY they are defined as the MSSM parameters at the SUSY scale. These choices are compensated for by appropriate counterterm contributions, so that the two FO calculations are both correct at the considered perturbative order. However, it appears that the choice implemented in the FO calculation of FlexibleSUSY provides a better approximation of the higher-order logarithmic corrections in this scenario. As discussed in Ref. [290], the FO prediction of FeynHiggs would indeed show a much milder dependence on \(M_S\), similar to the one in FlexibleSUSY, if the top mass entering the loop corrections was defined in the same way. It was also shown in Ref. [290] that the FO prediction of FeynHiggs has a milder dependence on \(M_S\) in scenarios defined in terms of OS parameters for the stop sector (the latter is the recommended choice for FO predictions in FeynHiggs). In general, the fact that effects that are formally of higher order can induce such a strong variation in the results of the FO calculation highlights the importance of resumming the large logarithmic corrections in scenarios with a large hierarchy of scales (indeed, FeynHiggs returns by default the results of its hybrid calculation).
Finally we stress that, in all of the considered hybrid approaches, the FO component of the calculation retains the \(n\times n\) structure of the Higgs mass matrix. As a result, the hybrid calculation accounts for the mixing effects in the Higgs sector – in the MSSM, these are contributions to the Higgs mass suppressed by powers of \(v^2/M_A^2\) – up to the loop level covered by the FO calculation, independently of the EFT used for the resummation of the higher-order logarithmic effects. Indeed, it was found in Ref. [246] that, in an MSSM scenario with squark masses of 100 TeV and \(M_A\) as low as 200 GeV, the predictions for the Higgs mass of the hybrid calculation in which the EFT includes only one light Higgs doublet, see Eq. (15), differ from those of the proper hybrid calculation in which the EFT is a 2HDM by at most \(2-3\) GeV. In contrast, in a pure EFT calculation the use of a theory with only one light Higgs doublet to describe a scenario with heavy SUSY and low \(M_A\) can lead to much larger deviations from the correct predictions for the Higgs mass.
5.6 Prospects
It is natural to expect that any future improvement in the accuracy of the FO and EFT calculations of the Higgs masses in SUSY models will eventually trickle down to the hybrid calculations. When a full two-loop calculation is finally completed, including all corrections controlled by the EW gauge couplings, a hybrid version that also allows for a full NNLL resummation of the logarithmic corrections will certainly follow. A generalization of the three-loop calculation of Refs. [67, 68, 70] that avoids the expansion in \(X_t/M_S\) and possibly also the recourse to different mass hierarchies would in turn improve the hybrid results of FlexibleSUSY and FeynHiggs.
As discussed in Sect. 5.2, another outstanding issue in the hybrid calculation of the Higgs masses is the treatment of the terms proportional to \(\ln (M_S^2/M_t^2)\) that spoil the resummation of the large logarithms when the stop mixing parameter is renormalized in the OS scheme. If the stops are so heavy that the un-resummed logarithmic terms significantly degrade the accuracy of the calculation, it is probably not worth adopting an OS scheme for the stop parameters in the first place, and they can be fixed directly in the \(\overline{\text {DR}}\) (or, for heavy gluino, \(\overline{\text {MDR}}\)) scheme. In SUSY scenarios with stop masses of a few TeV, however, the use of an OS scheme might still be preferable in order to directly connect the Higgs-mass predictions to the hoped-for future measurements of the stop properties at the (HL-)LHC. In this case, a possible path forward would be to devise a definition for the stop mixing parameter that connects it to some measurable quantity but does not induce the unwanted corrections. As long as the standard OS definition for \(X_t\) is adopted, the effect of the non-resummed logarithmic terms needs to be accounted for in the theoretical uncertainty of the Higgs-mass prediction. How such uncertainties should be estimated in the FO, EFT and hybrid calculations of the Higgs masses has been the subject of intensive study in recent years, as will be reviewed in the next section.
6 Estimating the theory uncertainty of the Higgs-mass calculations
6.1 Generalities
As is virtually always the case in theoretical particle physics, the calculation of the Higgs masses in realistic SUSY models is too complex to allow for exact solutions. Instead, it involves the truncation of some perturbative expansion, where the expansion parameter can be a loop factor, a whole tower of logarithmic corrections, or the ratio between two mass scales. Therefore, the result of any calculation of the Higgs masses should be accompanied by an estimate of its “theory uncertainty”, obtained by simulating the effect of the terms in the expansion that are of higher order with respect to the level of the truncation.Footnote 28 If the calculation is organized properly, it should be sufficient to simulate the effect of the first uncomputed term, which should be the one that gives the largest contribution to the final result.
There is a wide range of methods available to simulate the uncomputed terms of an expansion: for example, one can figure out their dependence on the relevant parameters and multiply by arbitrary factors of order one, or one can vary the renormalization scheme and scale of the parameters that enter the known terms of the expansion. It is usually advisable to compare different estimates, to make sure that the chosen method is not an outlier. On the other hand, some methods might be more or less appropriate to the specific calculation under consideration: e.g., scale variation may provide a poor simulation of the higher-order effects if most of the parameters are renormalized in an OS scheme and are thus scale-independent; even in minimal-subtraction schemes, scale variation may not simulate classes of terms that do not include an UV divergence. Moreover, most of these methods have in common a degree of subjectiveness: the choices of the arbitrary \({{{\mathcal {O}}}}(1)\) factors, or of the range for the scale variation, depend to some extent on how aggressive (or conservative) one wants the uncertainty estimate to be.
It is also worth noting that a given calculation is usually affected by different sources of theory uncertainty at the same time. For example, a FO calculation of the Higgs mass involves by definition a truncation in the loop expansion, but it might also neglect the effect of a subset of couplings within the considered loop order (e.g., when the gaugeless limit is adopted) or rely on the approximation of vanishing external momentum. Some of these sources of uncertainty may be correlated, as in the case of the MSSM where the gaugeless limit and the vanishing-momentum approximation neglect terms that involve the same couplings. However, since the theory uncertainty does not lend itself to a statistical interpretation, there is no definite prescription to combine different sources, and again more-conservative or less-conservative choices are possible.
Finally, we stress that the theory uncertainty of the Higgs-mass calculation in a given SUSY model depends inevitably on the considered point of the parameter space. In general, the uncertainties from uncomputed higher-order effects tend to be larger in points where there is a larger radiative correction to the tree-level prediction. However, even in points where the correction is comparable in size, the estimated uncertainties might differ, depending on whether the correction is dominated by the effects of large couplings (e.g., in scenarios with large \(X_t\) or, in the NMSSM, large \(\lambda \)) or by the effects of large scales (e.g., in scenarios with large \(M_S\)). In EFT calculations, the accuracy with which a given EFT describes the mass spectrum of the underlying SUSY model also depends on the considered point of the parameter space, and this should be reflected in the estimated uncertainty. In summary, any “one size fits all” estimate of the theory uncertainty should be treated with care, and any code that computes the Higgs masses in SUSY models should also provide a point-by-point estimate of the uncertainty of its prediction.
After a summary of the state of the uncertainty estimates up to the mid 2010s, in this section we will describe the considerable progress achieved in this context in the years of the KUTS initiative.
6.2 Pre-KUTS uncertainty estimates
OS calculation The first systematic attempt to estimate the theory uncertainty of the Higgs-mass prediction in the MSSM dates to 2002, when Ref. [64] discussed the status of the FO calculation that was then implemented in FeynHiggs. This calculation included the full one-loop corrections, the dominant two-loop corrections in the gaugeless and vanishing-momentum limits, namely those of \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) and \({{{\mathcal {O}}}}(\alpha _t^2)\), and also the two-loop \({{{\mathcal {O}}}}(\alpha _b\alpha _s)\) corrections relevant at large \(\tan \beta \). An OS scheme was adopted for the renormalization of the parameters in the quark/squark sector, while \(\tan \beta \), \(\mu \) and the Higgs field-renormalization constants were defined as \(\overline{\text {DR}}\) parameters.
The missing two-loop effects that were taken into account in the uncertainty estimate of Ref. [64] were the corrections controlled by the EW gauge couplings and the external-momentum dependence of the gaugeless corrections. The impact of these corrections was guessed by assuming that their size relative to the dominant corrections (i.e., the gaugeless and momentum-less ones) was the same as in the case of the fully-known one-loop corrections. For the mass of the lighter Higgs scalar, this resulted in an estimate of \(1{-}2\) GeV for the corrections arising from diagrams with D-term-induced Higgs-squark interactions, 1 GeV for the purely EW corrections (e.g. those from Higgs, gauge boson and chargino or neutralino loops), and 1 GeV for the momentum effects. An alternative estimate of the two-loop EW corrections was obtained by varying the scale associated with the \(\overline{\text {DR}}\)-renormalized parameters by a factor of two above and below the central value, which was chosen as \(Q=M_t\). This yielded a shift in the Higgs mass of about \(\pm 1.5\) GeV. It was assumed in Ref. [64] that there would be at least some partial compensation between the different missing two-loop corrections, and that their combined effect would induce a shift of less than 3 GeV in the prediction for the Higgs mass.
The other source of uncertainty taken into account in Ref. [64] were the three-loop effects. Their impact on the prediction for the Higgs mass was estimated by changing the definition of the top mass entering the two-loop corrections, which was taken as either the pole mass or the \(\overline{\text {MS}}\)-renormalized running mass of the SM. An alternative estimate consisted in computing explicitly the coefficient of \(\ln ^3(M_S/M_t)\) – i.e., the leading-logarithmic term in the three-loop corrections – in the gaugeless limit. In an MSSM scenario with \(M_S=1\) TeV, both approaches yielded an estimate of \(1{-}2\) GeV for the effects of the missing three-loop corrections on the lighter Higgs mass. Again, the combination of this uncertainty with the ones arising from the missing two-loop effects required some amount of guesswork. In view of possible cancellations between different missing corrections, a “realistic” estimate of the theory uncertainty of the Higgs-mass prediction was considered to be \(\pm 3\) GeV. At the end of 2004, a point-by-point uncertainty estimate based on Ref. [64] was implemented in FeynHiggs [297].
\(\overline{\text {DR}}\) calculations The next systematic study of the theory uncertainty of the Higgs-mass prediction dates to 2004, when Ref. [38] discussed the FO calculations implemented in the public codes SOFTSUSY, SuSpect and SPheno. These calculations included the full one-loop corrections, plus all of the two-loop corrections that involve the third-family Yukawa couplings in the gaugeless and vanishing-momentum limits. The \(\overline{\text {DR}}\) renormalization scheme was employed for all of the parameters entering the corrections.
Since the three codes allowed for the RG evolution of the MSSM Lagrangian parameters between different scales, the renormalization scale at which the pole Higgs masses are computed could be varied at will, and the shift in the Higgs mass resulting from this scale variation was used to estimate the impact of the missing two-loop and higher-order corrections. To fully capture the potentially large logarithmic effects, the scale of the Higgs-mass computation was varied between a value comparable to the EW scale (either \(M_Z\) or 150 GeV, depending on the scenario) and twice the average of the stop masses. In a number of scenarios where the prediction for the lighter Higgs mass was below 119 GeV – an entirely realistic value back then – the resulting estimate of the theory uncertainty was of \(2{-}3\) GeV. However, in a scenario with large stop mixing and a Higgs-mass predictionFootnote 29 around 129 GeV the estimated uncertainty reached \(4{-}5\) GeV.
As an alternative estimate of the theory uncertainty, Ref. [38] compared the results of the \(\overline{\text {DR}}\) calculation of SuSpect with those of the OS calculation of FeynHiggs, with an appropriate conversion of the MSSM input parameters between the two schemes. As FeynHiggs had in the meantime been upgraded to include all of the two-loop corrections controlled by the bottom Yukawa coupling in the gaugeless and vanishing-momentum limits, the predictions of the two codes differed only by two-loop effects controlled by the tau Yukawa coupling, which are all but negligible unless \(\tan \beta \) is very high, and by two-loop-EW and three-loop effects resulting from the difference in the renormalization schemes, which could be considered representative of the uncomputed corrections. The estimate of the theory uncertainty obtained in this way was in agreement with the one obtained from the scale variation: \(2{-}3\) GeV in most scenarios, rising to \(4{-}5\) GeV in the scenario with large stop mixing.
Finally, Ref. [38] estimated the impact of the missing momentum dependence of the two-loop corrections, using the method introduced in Ref. [64] and finding shifts in the light Higgs mass of half a GeV or even less in the considered scenarios. Overall, Ref. [38] quoted a range of \(3{-}5\) GeV, depending on the considered point of the MSSM parameter space, for a “reasonably conservative” estimate of the global theory uncertainty of the Higgs-mass calculation.
Discussion Although Refs. [38, 64] had been quite explicit on the fact that the estimate of the theory uncertainty should be treated as a function of the considered point of the parameter space, in the following years it became customary for phenomenological analyses of the MSSM to associate a fixed uncertainty of \(\pm 3\) GeV to the Higgs-mass prediction. Explicit computations of some of the missing corrections – namely, the two-loop EW effects at vanishing momentum [50], the two-loop momentum-dependent effects in the gaugeless limit [52, 58, 59], and the dominant three-loop effects [67, 68] – appeared to confirm the estimates of Refs. [38, 64]. However, the discovery in 2012 of a SM-like Higgs boson with mass around 125 GeV singled out precisely the regions of the MSSM parameter space in which an estimate of \(\pm 3\) GeV for the theory uncertainty of the then-available FO calculations might have been considered too optimistic. Indeed, in order to obtain through radiative corrections a squared mass for the light Higgs that is at least twice the tree-level value, it is necessary to have multi-TeV stop masses, in which case the higher-order logarithmic effects can become problematic, or large stop mixing, which also entails larger uncertainties, or both.
The considerable effort devoted over the years of the KUTS initiative to the improvement of the Higgs-mass calculations in SUSY models, going beyond FO and including the resummation of large logarithmic effects, was described in the previous sections. For example, the predictions of FeynHiggs for the light Higgs mass in scenarios with SUSY masses around 1 TeV and large stop mixing have shifted by more than 4 GeV, and are now in better agreement with those of the \(\overline{\text {DR}}\) codes. A parallel effort was devoted to point-by-point estimates of the theory uncertainty of the improved calculations, as will be discussed in the rest of this section. The adoption in phenomenological analyses of these new uncertainty estimates has lagged behind, and as late as 2020 the benchmark scenarios proposed in Ref. [299] for MSSM Higgs searches at the HL-LHC and the ILC still assumed a fixed \(\pm 3\) GeV uncertainty in the prediction for the light Higgs mass. However, in view of the numerous improvements that the Higgs-mass calculations have undergone since the times of Refs. [38, 64], it should now be legitimate to consider \(\pm 3\) GeV a rather conservative estimate of the theory uncertainty.
6.3 Advances during KUTS
For the sake of clarity, in this section we discuss separately the recent developments in the uncertainty estimates of the EFT, FO and hybrid approaches to the calculation of the Higgs mass. However, some of the studies we refer to addressed more than one approach (e.g., this was obviously the case for all of the papers devoted to the hybrid calculations).
6.3.1 Uncertainty of the EFT calculations
Since the beginning of the KUTS initiative, the renewed focus on the EFT calculations of the Higgs masses in SUSY models brought along the need for an estimate of the associated theory uncertainty. In scenarios with a strong hierarchy between mass scales, this uncertainty is expected to be smaller than the one of the FO calculations. Indeed, in the EFT approach the loop corrections computed at the various matching scales tend to be smaller than those encountered in the FO approach, since they are free from the logarithmically enhanced terms that are accounted for to all perturbative orders by the RG evolution. In 2014, in the context of discussing the uncertainty estimate of the EFT calculation in the simplest scenario where all SUSY masses are clustered around the same high scale and the EFT valid below that scale is just the SM, Ref. [227] identified three distinct sources of uncertainty:
-
SM uncertainties: arising from uncomputed higher-order terms in the relations between physical observables and running parameters of the SM Lagrangian at the EW scale, and in the evolution of the running parameters up to the SUSY scale;
-
SUSY uncertainties: arising from uncomputed higher-order terms in the boundary condition for the quartic Higgs coupling at the SUSY scale;
-
EFT uncertainties: arising from the restriction to a renormalizable EFT in the unbroken phase of the EW symmetry, which amounts to neglecting effects suppressed by powers of \(v^2/M_S^2\), where v represents the EW scale and \(M_S\) represents the SUSY scale.
This distinction and nomenclatureFootnote 30 have been adopted in a number of studies over the years. In the following we describe how the individual sources of uncertainty are estimated in the NNLL calculations of the Higgs mass implemented in the codes SusyHD [234], HSSUSY [300] and FeynHiggs [290], as well as in the N\(^3\)LL calculation that combines HSSUSY and Himalaya [236, 296].
SM uncertainties The estimates of the theory uncertainty associated with the low-energy part of the EFT calculation and with the RG evolution of the parameters take into account two contributions, which are expected to be the dominant ones: the missing higher-order terms in the relation between the pole Higgs mass and the parameters of the SM Lagrangian at the EW scale, and the effect of higher-order terms in the extraction of the top Yukawa coupling from the pole top mass. For an NNLL resummation of the large logarithms both calculations need to be performed at two loops, thus the estimate of the associated uncertainty requires a simulation of the corresponding three-loop effects.Footnote 31
Concerning the determination of the pole Higgs mass, SusyHD assumes a fixed uncertainty of \(\pm 150\) MeV, as estimated in Ref. [191] for the full two-loop calculation in the SM; HSSUSY estimates the uncertainty as the largest of the shifts induced by a variation of the renormalization scale in the calculation of the Higgs mass by a factor 2 or 1/2 with respect to the central value \(Q=M_t\) ; FeynHiggs estimates it as the shift induced by changing the definition the top mass entering the Higgs-mass corrections from the \(\overline{\text {MS}}\) parameter evaluated at \(Q=M_t\) to the pole mass.
Concerning the extraction of the top Yukawa coupling from the top mass, all codes simulate the higher-order effects by including the known three-loop QCD corrections of \({{{\mathcal {O}}}}(\alpha _s^3)\) from Refs. [301,302,303]. In a FO calculation of the Higgs mass, the resulting shift in \(y_t\) would only correspond to a four-loop effect. However, in the EFT calculation a three-loop shift in \(y_t\) affects the RG evolution of the quartic Higgs coupling between the EW and SUSY scales at the N\(^3\)LL level, providing an estimate of the uncertainty associated with the NNLL resummation.
Finally, in the N\(^3\)LL calculation that combines HSSUSY and Himalaya, both the determination of the pole Higgs mass and the extraction of the top Yukawa couplings are performed at three loops, including only the three-loop corrections that involve the highest powers of the strong gauge coupling. The associated uncertainties are estimated as in the NNLL calculation of HSSUSY, but the additional corrections included in the extraction of the top Yukawa coupling are the four-loop \({{{\mathcal {O}}}}(\alpha _s^4)\) ones from Ref. [304], allowing for an estimate of the missing N\(^4\)LL effects. It is, however, worth noting that the impact of the still-uncomputed N\(^3\)LL effects, i.e. those that do not involve the highest powers of \(\alpha _s\), is not estimated by this procedure.
SUSY uncertainties In the simplest heavy-SUSY scenario where the EFT is just the SM, as well as in split MSSM scenarios with only one light Higgs doublet, the missing higher-order terms in the boundary condition for the quartic Higgs coupling at the SUSY scale are the two-loop contributions that involve the EW gauge couplings (with the exception of the mixed QCD-EW corrections from Ref. [237], which, however, are not yet implemented in public codes), and all contributions from three loops on, with the exception of the three-loop \({{{\mathcal {O}}}}(y_t^4g_s^4)\) ones implemented in Himalaya.
To estimate the impact of these missing terms, SusyHD, HSSUSY and FeynHiggs consider the dependence of the Higgs-mass prediction on the matching scale where the boundary condition for \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) is computed (indeed, in a full calculation this dependence would be compensated for by the explicit scale dependence of the higher-order terms). We remark that this procedure requires that the running MSSM parameters entering the known part of the boundary conditions, which are usually given as input directly at the matching scale, be in turn evolved to the new matching scale. The uncertainty is identified with the largest of the shifts induced in the Higgs-mass prediction by a variation of the matching scale by a factor 2 or 1/2 with respect to the central value \(M_S\).
An alternative estimate of the SUSY uncertainty, implemented only in HSSUSY and FeynHiggs, consists in changing the definition of the top Yukawa coupling entering \(\Delta \lambda \), adapting accordingly the formulas for the two-loop contributions. In this case, the uncertainty is identified with the shift induced in the Higgs-mass prediction when the top Yukawa coupling entering the known contributions to \(\Delta \lambda \) is defined as the \(\overline{\text {DR}}\)-renormalized parameter of the MSSM instead of the \(\overline{\text {MS}}\)-renormalized parameter of the SM. Since this scheme variation induces also higher-order shifts that do not depend explicitly on the renormalization scale, it is treated as an independent source of uncertainty with respect to the scale variation, and the absolute values of the two estimates are added linearly.
In the N\(^3\)LL calculation that combines HSSUSY and Himalaya, additional sources of uncertainty are the combined expansions in ratios of particle masses and in the ratio \(x_t = X_t/M_S\) that are used to approximate the three-loop integrals in the \({{{\mathcal {O}}}}(y_t^4g_s^4)\) contributions to \(\Delta \lambda \). As detailed in Ref. [236], the uncertainty associated with the terms that are omitted in the expansion in mass ratios can be estimated by comparing the approximate result for the logarithmic part of the \({{{\mathcal {O}}}}(y_t^4g_s^4)\) contributions with the exact result that can be extracted from the three-loop RGE for \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\). The uncertainty associated with the terms that are omitted in the second expansion, i.e. those containing the highest powers of \(x_t\), can be estimated from the effect of the analogous terms entering a part of the calculation where the expansion is not needed. It was later pointed out in Ref. [295] that the variation of the matching scale provides an estimate of both of these sources of uncertainty. Reference [236] and, later, Ref. [239] also showed how for large \(x_t\) – e.g., for the often-considered value \(|x_t| = \sqrt{6}\), which maximizes the one-loop stop contribution to \(\Delta \lambda \) – the uncertainty associated with missing powers of \(x_t\) can become larger than the effect of the whole \({{{\mathcal {O}}}}(y_t^4g_s^4)\) contributions to \(\Delta \lambda \), in which case the inclusion of the three-loop terms does not actually improve the accuracy of the Higgs-mass calculation.
In phenomenological analyses of SUSY models, it sometimes happens that – either for the sake of simplicity or for lack of a better option – an EFT is used that does not fully reflect the considered hierarchy between mass scales. For example, the SM might be used as EFT below the SUSY scale even in scenarios where higgsinos and gauginos are much lighter than the sfermions. This would induce large logarithms in the boundary conditions for the couplings of the EFT at the SUSY scale, contrary to the spirit of the EFT approach. However, the presence of large terms in the threshold corrections would also be reflected in an enlarged estimate of the SUSY uncertainty.
EFT uncertainties As already discussed in Sects. 2 and 4, the standard approach of matching the high-energy SUSY theory to a renormalizable EFT in the unbroken phase of the EW symmetry leads to neglecting terms suppressed by powers of \(v^2/M_S^2\), which can be mapped to the effect of non-renormalizable operators with dimension six and higher.
To estimate the impact of the neglected terms, SusyHD, HSSUSY and FeynHiggs consider the shift induced in the Higgs-mass prediction when the boundary condition for the quartic Higgs coupling is shifted by an arbitrary term that scales like \(v^2/M_S^2\) times a loop factor. More specifically, SusyHD estimates an upper and a lower uncertainty by rescaling the one-loop contribution of each particle to \(\Delta \lambda \) by a factor \((1\pm 2\, v^2/M_i^2)\), where \(M_i\) is the mass of the particle; FeynHiggs does the same with a common rescaling factor \((1\pm 2\, v^2/M_S^2)\); HSSUSY estimates symmetric upper and lower uncertainties from the single rescaling factor \((1+2\, v^2/M_S^2)\). Incidentally, we remark that the presence of a 2 in the rescaling factors stems from the fact that in Ref. [234], where this procedure was first introduced, the Higgs vev was normalized as \(v\approx 246\) GeV. Had the authors of Ref. [234] adopted the same normalization for the Higgs vev as in this report, where \(v\approx 174\) GeV, their estimate of the uncertainty associated with the missing \({{{\mathcal {O}}}}(v^2/M_S^2)\) terms might well have been smaller by a factor of 2. This should be taken as a reminder of the degree of subjectiveness that inevitably affects any estimate of the effect of uncomputed corrections.
In 2017, Ref. [235] compared the estimate of the EFT uncertainty implemented in SusyHD with a direct calculation of the one- and two-loop effects proportional to \(y_t^2\,M_t^4/M_S^2\) and \(y_t^2\,g_s^2\,M_t^4/M_S^2\), respectively, which arise from the introduction in the EFT Lagrangian of the dimension-six operators \(|H|^6\) and \(|H|^2\,\overline{t_\mathrm{{\scriptscriptstyle R}}}\, H^\mathrm{{\scriptscriptstyle T}} \epsilon \,q_\mathrm{{\scriptscriptstyle L}}\). It was found in Ref. [235] that the uncertainty estimate of SusyHD is at its most conservative – namely, larger than the directly-computed effects by about a factor of three in the considered scenarios – when \(|X_t|/M_S\approx \sqrt{6}\), i.e. near the value for which a Higgs-mass prediction in the vicinity of 125 GeV can be obtained with a stop-mass parameter of about 2 TeV. In contrast, for \(X_t \ll M_S\) the estimate falls short of the computed effects. However, in that case stop masses of more than 10 TeV are necessary to obtain a phenomenologically acceptable prediction for the Higgs mass, rendering the \({{{\mathcal {O}}}}(v^2/M_S^2)\) effects essentially irrelevant.
Numerical example To illustrate the relative importance of the different sources of uncertainty described so far, we show in Fig. 4 the corresponding estimates as a function of a common SUSY scale \(M_S\), in the same MSSM scenario as considered in Fig. 3. The left plot is produced with FeynHiggs, the right one with HSSUSY.Footnote 32 We recall that, for the value of the stop mixing parameter adopted in this scenario, the expansion in \(X_t/M_S\) employed in the three-loop contribution to the threshold correction \(\Delta \lambda \) is unreliable, hence in the case of HSSUSY we restrict our discussion to the uncertainty of the NNLL calculation.
In each plot, the dotted red line represents the uncertainty of the Higgs-mass determination at the EW scale, which FeynHiggs estimates by scheme variation of the top mass and HSSUSY estimates by scale variation; the dashed red line represents the uncertainty associated with the extraction of the top Yukawa coupling from the top mass; the dotted blue line represents the uncertainty associated with the variation of the matching scale around the central value \(M_S\); the dashed blue line represents the uncertainty associated with the scheme change in the top Yukawa coupling entering the boundary condition for \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\); the dot-dashed green line represents the estimate of the uncertainty associated with the missing \({{{\mathcal {O}}}}(v^2/M_S^2)\) terms; finally, the solid black line corresponds to the total estimate of the theory uncertainty, obtained by summing linearly the absolute values of the individual estimates.
The comparison between the dotted and the dashed red lines in each of the plots of Fig. 4 shows that the largest contribution to the “SM uncertainty” comes from the determination of the top Yukawa coupling. The estimated uncertainty grows with \(M_S\), reflecting the effect of the top Yukawa coupling on the RG evolution of the quartic Higgs coupling. The comparison between the dotted red lines in the left and right plots shows that, in this scenario, the scale variation implemented in HSSUSY yields a significantly larger estimate for the uncertainty of the Higgs-mass determination at the EW scale than the scheme variation implemented in FeynHiggs.
The comparison between the dotted and the dashed blue lines in the plots of Fig. 4 shows that the estimate of the “SUSY uncertainty” arising from a variation of the matching scale is somewhat larger than the one arising from a change of scheme in the top Yukawa coupling. In addition, both of the estimates of the SUSY uncertainty tend to decrease with increasing \(M_S\). The latter is a consequence of the renormalization-scale dependence of \(y_t\) and \(g_s\), which in the SM become both smaller at higher scales. As a result, the overall impact of the threshold correction \(\Delta \lambda \) on the Higgs-mass prediction is suppressed, and the associated uncertainty follows suit.
The dot-dashed green lines in the plots of Fig. 4 show that the estimate of the “EFT uncertainty” associated with the missing \({{{\mathcal {O}}}}(v^2/M_S^2)\) terms can reach about 4.5 GeV at the lowest considered values of \(M_S\), but it gets quickly suppressed as \(M_S\) increases. In particular, in the range \(M_S\approx 2\!-\!4\) TeV, which corresponds to a Higgs-mass prediction in the vicinity of 125 GeV (see Fig. 3), the EFT uncertainty is already sub-dominant with respect to the other sources.
Finally, the solid black lines in the plots of Fig. 4 show that at small \(M_S\) the total uncertainty estimate of the EFT calculation is dominated by the missing \({{{\mathcal {O}}}}(v^2/M_S^2)\) effects, whereas for \(M_S\gtrsim 1\!-\!2\) TeV the largest source of uncertainty is the extraction of the top Yukawa coupling from the top mass. At large \(M_S\) the total uncertainty is estimated to be less than \(\pm 1\) GeV in this scenario, with a rather mild dependence on \(M_S\) which results from a partial cancellation between the opposite scale dependences of the “SM” and “SUSY” components. We also mention that the choice of adding up the absolute values of the different sources of uncertainty can be considered conservative, as it seems unlikely that the missing higher-order terms would all enter the Higgs-mass prediction with the same sign.
6.3.2 Uncertainty of the FO calculations
The intense activity aimed at improving the calculation of the Higgs masses in scenarios with heavy SUSY particles also highlighted the need for a reassessment of the existing uncertainty estimates for the FO calculations. In 2014, Ref. [227] stressed that a lingering spread of about 5 GeV between the predictions for \(M_h\) of the OS calculation of FeynHiggs and those of the \(\overline{\text {DR}}\) calculations of SOFTSUSY, SuSpect and SPheno in scenarios with stop masses around 1 TeV and large stop mixing pointed to a large theory uncertainty, possibly exceeding the \(\pm 3\) GeV that were commonly assumed since the early 2000s. In 2016, while discussing the two-loop \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) corrections to the Higgs masses in a SUSY model with Dirac gluinos, Ref. [173] noted that changes in the definition and/or scale of the strong gauge coupling \(\alpha _s\) – which had not been considered in the original uncertainty estimate of Ref. [64] – can induce a shift of up to 7 GeV in the prediction for \(M_h\). This is significantly larger than the shift induced by a change in the renormalization scheme of the parameters in the top/stop sector, despite the fact that both changes amount to three-loop \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\) effects in the Higgs mass. Later in 2016, the importance of the definition and scale choice for \(\alpha _s\) was also stressed in the context of the NMSSM in Ref. [164], which found that differences of up to 6 GeV in the Higgs-mass predictions of NMSSMCALC and FeynHiggs could be greatly reduced once the strong gauge coupling was computed at the same scale in the two codes. Again, the discrepancies induced by the scale choice for \(\alpha _s\) in the “out-of-the-box” predictions of the two codes amount to three-loop \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\) effects in the Higgs mass, and could in principle have been considered as part of the uncertainty estimate.
We now summarize how, over the years of the KUTS initiative, new estimates of the theory uncertainty were discussed for the FO calculations of the Higgs masses. Since the inadequacy of such calculations in scenarios with even moderately heavy SUSY particles had by then become apparent, the main practical purpose of these estimates was the comparison with the corresponding estimates for the EFT and hybrid calculations. Starting from the case of the MSSM, we discuss separately the uncertainties of the two-loop, fully \(\overline{\text {DR}}\) calculation implemented in codes such as FlexibleSUSY and SOFTSUSY (with the possible addition of the dominant three-loop effects from Himalaya), and those of the two-loop, mixed OS–\(\overline{\text {DR}}\) calculation of FeynHiggs.
FlexibleSUSY/SOFTSUSY/Himalaya: In 2016, Ref. [277] proposed a method to estimate the uncertainty of the two-loop calculation of the MSSM Higgs masses implemented in FlexibleSUSY, with the purpose of a comparison with the hybrid calculation of FlexibleEFTHiggs. A first estimate of the uncertainty relied on the extraction of the running top Yukawa coupling \(y_t\) from the pole top mass. The uncertainty was defined as the maximum difference between the predictions for the Higgs masses obtained with four definitions of \(y_t\) that are all equivalent at one loop, but differ by higher-order terms. Since two of these definitions differ from the others by two-loop \({{{\mathcal {O}}}}(\alpha _s^2)\) terms enhanced by \(\ln ^2(M_S/M_t)\), the variation of \(y_t\) in the one-loop part of the Higgs-mass calculation allows for a simulation of the three-loop LL terms – i.e., those of \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\) enhanced by \(\ln ^3(M_S/M_t)\) – that are expected to be dominant among the missing higher-order effects (at least until \(M_S\) becomes so large that the loop expansion breaks down). An alternative estimate of the uncertainty, added in quadrature to the first one, relied on a variation of the renormalization scale at which the calculation of the pole Higgs mass is performed. In particular, the uncertainty was defined as the maximal variation in the Higgs mass when the scale is varied by a factor 2 above and below its default value, which is taken as the average of the stop masses. It was pointed out in Ref. [277] that, as the considered scale variation does not cover the full range between the EW scale and the SUSY scale, this second method cannot simulate the missing LL effects but only the NLL ones, and it leads to a smaller uncertainty estimate than the first method.
In 2018, Ref. [300] estimated the theory uncertainty of the three-loop calculation of the MSSM Higgs masses obtained from the combination of SOFTSUSY and Himalaya, with the purpose of a comparison with the EFT calculation of HSSUSY. The uncertainty of the FO calculation was defined as the linear sum of five estimates, namely: the two already proposed in Ref. [277], i.e., a variation in the extraction of \(y_t\) and a variation in the scale at which the Higgs masses are computed; a variation – again, by a factor 2 above and below the default value – of the scale at which the running gauge and Yukawa couplings are extracted from physical observables; two additional estimates of higher-order effects in the determination of the strong and electromagnetic gauge couplings, respectively. In contrast to Ref. [277], the \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\) corrections were included in the calculation of the Higgs masses through Himalaya. Thus, the first of the estimates mentioned above compared two definitions of \(y_t\) that differ by two-loop LL terms of \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\), allowing for a simulation of the uncomputed three-loop LL terms of \({{{\mathcal {O}}}}(\alpha _t^2\alpha _s)\) in the Higgs-mass prediction. In simplified scenarios with a common SUSY scale \(M_S\), Ref. [300] found that the total uncertainty estimate of the FO calculation, which is more precise for a low SUSY scale, and the one of the EFT calculation, more precise for a high SUSY scale, coincide for values of \(M_S\) between 1 and 1.3 TeV, depending on the considered scenario.
In 2019, Ref. [296] estimated the theory uncertainty of the three-loop calculation of the MSSM Higgs masses obtained from the combination of FlexibleSUSY and Himalaya, again with the purpose of a comparison with the EFT calculation of HSSUSY. In contrast to Ref. [300], the uncomputed three- and four-loop LL terms were simulated by varying the renormalization scale at which the Higgs masses are computed in the whole range between \(M_t\) and \(M_S\). An additional estimate of the uncomputed four-loop LL terms, added linearly to the first estimate, consisted in including the two-loop SUSY-QCD corrections from Refs. [305,306,307] in the determination of the strong gauge coupling. The procedure proposed in Ref. [296] leads to a larger estimate for the theory uncertainty of the FO calculation compared to the one proposed in Ref. [300], and the value of \(M_S\) for which the FO and EFT calculations have a similar estimated uncertainty is lowered below 1 TeV.
FeynHiggs: In 2019, Ref. [290] presented a new estimate for the theory uncertainty of the FO (namely, full one-loop and gaugeless two-loop) calculation of the Higgs masses implemented in FeynHiggs, updating the estimate based on Ref. [64] that had been available in the code since 2004. Even in this case, the main purpose was the comparison with the uncertainties of the EFT and hybrid calculations of the Higgs masses implemented in the same code.
The first method proposed in Ref. [290] for estimating the uncertainty of the Higgs-mass calculation consists in changing the definition of the top mass entering the one- and two-loop corrections, switching between the \(\overline{\text {MS}}\)-renormalized mass parameter of the SM evaluated at the scale \(Q=M_t\), which is used by default in the code, and the pole mass. This method simulates the uncomputed two- and three-loop corrections that involve the top Yukawa coupling. However, since the considered definitions of the top mass do not differ by large logarithmic terms, the higher-order corrections are simulated only at the NLL level. A second estimate is therefore introduced to capture the three-loop LL terms that are expected to give the largest contribution to the uncertainty at large \(M_S\), i.e. those involving the highest powers of the strong gauge coupling. In this case, the uncertainty is defined as the shift induced in the Higgs mass when the \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) part of the two-loop corrections is multiplied by a factor \(1\pm \alpha _s/(4\pi )\ln (M_S^2/M_t^2)\), thus simulating the effect of \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\) corrections enhanced by \(\ln ^3(M_S^2/M_t^2)\). Once again, we note how the choice of the numerical coefficient for the factor that simulates the higher-order terms introduces an element of subjectiveness in this kind of estimates. Finally, a third uncertainty estimate targets the corrections controlled by the bottom Yukawa coupling, which can be numerically relevant only at large values of \(\tan \beta \). In particular, the uncertainty is defined as the shift induced in the Higgs mass when the so-called \(\Delta _b\) terms, i.e. a class of \(\tan \beta \)-enhanced terms that are by default absorbed in the one-loop corrections via a redefinition of the Higgs-sbottom coupling, see Refs. [35, 37, 39], are made to appear explicitly in the two-loop part of the corrections. We remark that this uncertainty estimate should be considered conservative, because the higher-order \(\tan \beta \)-enhanced effects that it simulates – e.g., three-loop terms enhanced by \(\tan ^2\beta \) – are in fact already accounted for (“resummed”) in the default determination of the Higgs mass. The absolute values of the three uncertainty estimates are added linearly.
In MSSM scenarios with \(M_S=1\) TeV and large stop mixing, the total uncertainty of the FO calculation of the lighter Higgs mass in FeynHiggs was estimated in Ref. [290] to be about \(2{-}3\) GeV, depending on the renormalization scheme employed for the stop parameters. As a result of the logarithmic enhancement of the uncomputed higher-order corrections, the uncertainty estimate of the FO calculation grows quickly for increasing \(M_S\), reaching as much as \(10{-}15\) GeV for \(M_S=10\) TeV. Once again, this highlights the need for a resummation of the large logarithmic corrections in scenarios where the stops have masses of even a few TeV.
Beyond the MSSM Over the years of the KUTS initiative, estimates of the theory uncertainty of the FO calculation of the Higgs masses have also been developed for a number of non-minimal SUSY models, see e.g. the studies in Ref. [173], already mentioned at the beginning of this Sect. 6.3.2, concerning SUSY models with Dirac gluinos.
For the NMSSM, Refs. [136, 137] (pre-KUTS) estimated the theory uncertainty of the one-loop calculation of the Higgs masses by varying between OS and \(\overline{\text {DR}}\) the renormalization scheme of the parameters entering the tree-level Higgs mass matrix, as well as the scheme of the quark masses entering the one-loop corrections. In addition, the scale at which the Higgs masses are computed in the \(\overline{\text {DR}}\) calculation was varied by a factor 2 above and below the default value, which was taken as the average stop mass. This yielded estimates of about \(10\%\) for the uncertainty of the one-loop prediction for the Higgs masses in scenarios with stop masses around 500 GeV or less. In 2014, Ref. [156] discussed the improvement in the theory uncertainty of the NMSSM Higgs-mass prediction that comes from the inclusion of the two-loop \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) corrections in the limit of vanishing external momentum. The uncertainty was estimated only by varying the renormalization scheme of the parameters in the top/stop sector between OS and \(\overline{\text {DR}}\). In scenarios with stop masses around 1 TeV, it was found that the inclusion of the \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) corrections drastically reduces the estimated uncertainty from \(15\%\!-\!25\%\) (depending on the stop mixing) to about \(1.5\%\). In 2016, Ref. [164] compared the Higgs-mass predictions obtained by NMSSMCALC adopting either the OS or the \(\overline{\text {DR}}\) scheme for the top/stop sector, and found discrepancies of less than 2 GeV in four representative NMSSM scenarios. It should, however, be recalled that, in the FO calculation of the Higgs masses, the uncertainty associated with the definition of \(\alpha _s\) – see the discussions in Refs. [164, 173] mentioned at the beginning of this section – significantly exceeds the uncertainty that can be estimated from a change of scheme in the top/stop sector. Reference [164] also investigated the effect of switching between the different prescriptions of FeynHiggs and NMSSMCALC for the OS renormalization of the EW parameters \((g, g^\prime , v)\) in the one-loop part of the calculation. This implied an estimate of at most \(\pm 1\) GeV for the uncertainty of the Higgs-mass prediction associated with the uncomputed two-loop corrections that involve the EW gauge couplings. The findings of Refs. [156, 164] were also reassessed in 2019, when Ref. [157] discussed the inclusion of the two-loop \({{{\mathcal {O}}}}(\alpha _t^2)\) corrections in the so-called “MSSM limit” (i.e., \(v_s\rightarrow \infty \) with \(\lambda \,v_s\) and \(\kappa \,v_s\) held fixed). The uncertainty of the calculation was estimated by varying the renormalization scheme of the top/stop parameters between OS and \(\overline{\text {DR}}\), and also by varying the scale in the \(\overline{\text {DR}}\) calculation by a factor of 2 above and below the default value. It was found in Ref. [157] that the inclusion of the \({{{\mathcal {O}}}}(\alpha _t^2)\) corrections actually worsens the estimated uncertainty of the Higgs-mass calculation, raising it to \(5\!-\!6\%\) in the considered scenarios. To explain this seemingly counter-intuitive finding, it was argued in Ref. [157] that the small scheme- and scale-dependence of the calculation that includes only the two-loop \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) corrections is due to accidental cancellations, and that the additional inclusion of the \({{{\mathcal {O}}}}(\alpha _t^2)\) corrections makes the uncertainty estimate sensitive to different classes of higher-order terms, for which these cancellations do not occur.
The uncertainty estimate introduced in Ref. [277] for the FO calculation of the Higgs masses implemented in FlexibleSUSY was in turn applied also to models beyond the MSSM. In NMSSM scenarios with vanishing stop mixing and \(\tan \beta = 5\), Ref. [277] estimated a theory uncertainty of about \(\pm 6\) GeV for \(M_S\approx 30\) TeV, where the prediction for the light Higgs mass can be in the vicinity of 125 GeV. In an E\(_6\)SSM scenario, also with vanishing stop mixing and \(\tan \beta = 5\), a suitable prediction for the Higgs mass can be obtained for \(M_S\approx 10\) TeV, but the estimated uncertainty of the FO calculation is as large as \(\pm 10\) GeV in that point. Similar results were found for the MRSSM, where the uncertainty estimate of Ref. [277] was applied to the FO calculation implemented in SARAH. In all these cases, the comparison with the hybrid calculation implemented in FlexibleEFTHiggs highlighted the importance of resumming the large logarithmic corrections in scenarios with heavy SUSY particles.
6.3.3 Uncertainty of the hybrid calculations
Just as the hybrid calculation of the Higgs mass combines an EFT component and a FO component, its uncertainty estimate stems from the combination of the uncertainties of the two components. A number of techniques employed in public codes to estimate the latter have been described in Sects. 6.3.1 and 6.3.2. We stress that the EFT and FO components of the hybrid calculation implemented in a given code do not necessarily coincide with the stand-alone EFT and FO calculations that may also be provided by the same code (e.g., due to the presence of subtraction terms), thus a dedicated estimate of the uncertainty of the hybrid calculation remains in order. This said, it is legitimate to expect that such estimate will be comparable to or lower than the individual estimates of the stand-alone calculations. In particular, the uncertainty of the hybrid calculation should agree with the one of the pure EFT calculation in scenarios with very heavy SUSY particles, and with the one of the pure FO calculation in (now experimentally challenged) scenarios where all SUSY particles are at the EW scale.
In the following we describe the uncertainty estimates that have been developed for the three hybrid approaches described in Sects. 5.2–5.4.
Hybrid approach of FeynHiggsThe uncertainty estimate of the hybrid calculation implemented in FeynHiggs was described in Ref. [290]. In its latest implementation, the hybrid prediction of FeynHiggs for the mass of the SM-like Higgs boson can be viewed as a complete EFT calculation, at full NLL and “gaugeless” NNLL order, supplemented with a FO calculation of the effects suppressed by powers of \(v^2/M_S^2\), at full one-loop and “gaugeless” two-loop order. Accordingly, FeynHiggs obtains the uncertainty of the hybrid result by combining the uncertainty of the EFT component, estimated as described in Sect. 6.3.1minus the contribution stemming from the \({{{\mathcal {O}}}}( v^2/M_S^2)\) terms, with the uncertainty of the FO calculation of the \({{{\mathcal {O}}}}( v^2/M_S^2)\) terms, estimated as described in Sect. 6.3.2. In particular, the “SM uncertainty” of the EFT component is estimated by changing the definition of the top mass entering the determination of the pole Higgs mass and by switching on the three-loop QCD corrections in the extraction of the top Yukawa coupling from the top mass; the “SUSY uncertainty” is estimated by varying the matching scale by a factor of 2 above and below the central value \(M_S\), and by changing the definition of the top Yukawa coupling entering the threshold corrections to the quartic Higgs coupling; the “EFT uncertainty” is, however, omitted, because the \({{{\mathcal {O}}}}( v^2/M_S^2)\) terms are accounted for by the FO component of the hybrid calculation. The uncertainty of the FO calculation of the \({{{\mathcal {O}}}}( v^2/M_S^2)\) terms is in turn estimated by changing the definition of the top mass, by multiplying the \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) part by a factor \(1\pm \alpha _s/(4\pi )\ln (M_S^2/M_t^2)\), and by switching off the resummation of the \(\Delta _b\) terms. All of the above-listed sources of uncertainty are summed linearly in absolute value.
As discussed in Sect. 5.2, the hybrid calculation of FeynHiggs involves additional sources of uncertainty when the input parameters that determine the stop masses and mixing are defined in the OS scheme. In that case, the stop mixing parameter \(X_t\) is converted to the \(\overline{\text {DR}}\) scheme, see Eq. (16), before being passed to the EFT component of the calculation. Moreover, the FO component contains two-loop counterterm contributions that do not vanish when \( v^2/M_S^2 \rightarrow 0\), but are not canceled out by the subtraction term introduced to avoid double counting, see Eq. (15). Indeed, these contributions do not have an equivalent in the EFT component, where all parameters are defined as \(\overline{\text {DR}}\). Both the uncertainty associated with the OS–\(\overline{\text {DR}}\) conversion of \(X_t\) and the uncertainty associated with the counterterm contributions in the FO component are estimated by switching between different definitions of the top mass, and by multiplying the strong gauge coupling \(\alpha _s\) by a factor \(1\pm \alpha _s/(4\pi )\ln (M_S^2/M_t^2)\). We remark that the latter procedure introduces \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\) terms enhanced by \(\ln (M_S^2/M_t^2)\) – i.e., terms that are formally of “gaugeless” NNLL order – in the uncertainty estimate. This reflects the fact that, when the stop masses and mixing are defined in the OS scheme, the hybrid procedure implemented in FeynHiggs provides only an incomplete resummation of the “gaugeless” NNLL corrections. As a result, the estimated uncertainty turns out to be somewhat larger than in the case in which the input parameters in the stop sector are defined directly in the \(\overline{\text {DR}}\) scheme. It is, however, important to note that additional sources of uncertainty must be considered if the \(\overline{\text {DR}}\) input parameters are extracted from (so-far hypothetical) measured quantities, such as, e.g., the stop pole masses and decay widths.
The study of theory uncertainties presented in Ref. [290] focused on the hybrid setup in which, in the EFT part of the calculation, the heavier Higgs doublet is decoupled together with the heavy SUSY particles at the scale \(M_S\). In scenarios where both Higgs doublets are light, this neglects the resummation of the corrections enhanced by \(\ln (M_S^2/M_A^2)\). It was shown in Ref. [290] that the use of an inappropriate EFT in the hybrid calculation is indeed reflected in an increase of the estimated uncertainty at low \(M_A\), compatible with the differences found in Ref. [246] between the calculation using the SM as EFT and the calculation using the 2HDM as EFT.
Hybrid approach of FlexibleEFTHiggsAs described in Sect. 5.3, the hybrid calculation of the SM-like Higgs mass implemented in FlexibleEFTHiggs is organized in a way similar to a pure EFT calculation. The only difference with respect to the pure EFT case is that the corrections to the Higgs mass suppressed by powers of \(v^2/M_S^2\) are absorbed in the boundary condition for the quartic Higgs coupling, via the requirement that a FO computation of the pole Higgs mass give the same result above and below the matching scale, see Eq. (17). Accordingly, the estimate of the theory uncertainty of the hybrid result is organized in a way similar to the one described in Sect. 6.3.1 for the EFT calculation, omitting, however, the contribution that stems from missing \({{{\mathcal {O}}}}( v^2/M_S^2)\) terms. In the latest implementation of the FlexibleEFTHiggs approach, described in Ref. [295], the “SUSY uncertainty” is taken as the largest of two estimates: the first considers the effect of varying the matching scale by a factor of 2 above and below the central value \(M_S\), while the second considers the effects of several non-logarithmic higher-order terms generated by changing the definition of the parameters that enter the known part of the boundary condition. We stress that, in this approach, the estimate of the “SUSY uncertainty” probes both the higher-order terms that do not vanish when \( v^2/M_S^2 \rightarrow 0\) and those suppressed by powers of \(v^2/M_S^2\). The “SM uncertainty” is in turn taken as the largest of two estimates, namely the effect of varying the scale at which the pole Higgs mass is computed by a factor of 2 above and below the central value \(Q=M_t\), and the effect of including higher-order terms in the extraction of the top Yukawa coupling from the top mass. The resulting estimates of the “SUSY” and “SM” uncertainties are then added linearly in the total uncertainty.
Third hybrid approach As detailed in Sect. 5.3, the hybrid approach proposed in Ref. [296] combines a pure EFT calculation of the SM-like Higgs mass with a separate calculation of the corrections suppressed by powers of \(v^2/M_S^2\). In Ref. [296] the hybrid result for the Higgs mass was compared with the pure EFT result provided by HSSUSY and with the FO (namely, three-loop) result obtained from the combination of FlexibleSUSY and Himalaya, showing the expected agreement with one or the other in the appropriate limits. The proposal of Ref. [296] for the uncertainty estimate of the hybrid result thus consisted in simply taking, in each point of the parameter space, the lowest uncertainty estimate between the one of the FO result and the one of the pure EFT result. These estimates are described in Sects. 6.3.1 and 6.3.2, respectively.
Comparison between the pure FO, pure EFT and hybrid calculations of the Higgs mass, with the corresponding estimates of the theory uncertainty, in an MSSM scenario with degenerate SUSY masses. The sfermion mass and mixing parameters are defined in the \(\overline{\text {DR}}\) scheme at the scale \(Q=M_S\). The left plot is produced with FeynHiggs, the right one with different modules of FlexibleSUSY
6.3.4 Comparing the uncertainties
To illustrate the estimates described in Sects. 6.3.1–6.3.3, we compare in Fig. 5 the uncertainties of the hybrid calculations implemented in FeynHiggs and in FlexibleEFTHiggs with those of their FO and EFT counterparts, in the same MSSM scenario as the one considered in Sect. 5.5. We recall that the parameters that determine the stop masses and mixing are here defined in the \(\overline{\text {DR}}\) scheme at the scale \(Q=M_S\). In view of the large stop mixing that characterizes this scenario, the predictions of FlexibleSUSY, HSSUSY and FlexibleEFTHiggs omit the three-loop corrections, as they rely on an expansion in the ratio \(X_t/M_S\,\). Consequently, in both the left and right plots of Fig. 5 the FO calculations include full one-loop and gaugeless two-loop corrections, and the EFT calculations provide a full NLL and gaugeless NNLL resummation of the logarithmic corrections. In each plot, the dotted-blue, dashed-black and full-red lines represent the predictions for the SM-like Higgs mass of the FO, EFT and hybrid calculation, respectively, and the shaded bands around each line represent the uncertainty estimates.
The shapes of the blue-shaded bands in the left and right plots of Fig. 5 show that, in this scenario, the FO calculations of FeynHiggs and FlexibleSUSY start losing accuracy as soon as \(M_S\gtrsim 1\) TeV. As mentioned in the description of Fig. 3, there is a rather dramatic difference between the FO predictions of the two codes at large \(M_S\), due to the different definitions of the top mass and the strong gauge coupling entering the radiative corrections.Footnote 33\(^,\)Footnote 34 However, the respective uncertainty bands are so large that they comfortably overlap. This highlights once again the inadequacy of the FO calculation in scenarios with multi-TeV SUSY masses.
The shape of the grey-shaded bands in Fig. 5 shows that the EFT calculation is expected to be less accurate at low \(M_S\), where the missing \({{{\mathcal {O}}}}( v^2/M_S^2)\) effects are most relevant. However, for values of \(M_S\) large enough that the EFT prediction for the SM-like Higgs mass is compatible with the LHC measurement, the grey-shaded bands have already shrunk to an almost-constant width, meaning that the \({{{\mathcal {O}}}}( v^2/M_S^2)\) effects are essentially negligible.
Finally, the comparison between the three shaded bands in each plot of Fig. 5 shows that, for both codes, the uncertainty estimate of the hybrid calculation in this scenario essentially coincides with the one of the EFT calculation as soon as \(M_S\gtrsim 2\) TeV. For low values of \(M_S\), the uncertainty estimate of the hybrid calculation of FeynHiggs essentially coincides with the one of the FO calculation in the same code as soon as \(M_S\lesssim 500\) GeV, whereas the uncertainty estimate of the hybrid calculation of FlexibleEFTHiggs remains smaller than the one of the FO calculation of FlexibleSUSY (the latter is obtained following Ref. [296], but taking into account the omission of the three-loop corrections). In the intermediate range of \(M_S\), the uncertainty of the hybrid calculation is, for both codes, smaller than the uncertainties of both the EFT and FO calculations, underscoring the fact that the hybrid calculation combines the advantages of the two approaches, while avoiding their drawbacks. For \(M_S\approx 2\!-\!4\) TeV, where the uncertainty band of the theoretical prediction intersects the one of the experimental measurement, the theory uncertainty of the hybrid calculation in both codes is about \(\pm 1\) GeV for this scenario.
6.4 The role of the parametric uncertainties
In addition to the theory uncertainty stemming from uncomputed higher-order terms, the prediction for the Higgs masses in SUSY models is subject to a “parametric” uncertainty, associated with the experimental uncertainty with which the input parameters – e.g., masses and couplings of the particles in the loops – are known. This uncertainty can be straightforwardly determined as the maximal shift in the prediction for the Higgs masses obtained by varying the input parameters within their experimental ranges. In phenomenological analyses of SUSY models, it is customary to discuss the two kinds of uncertainty without combining them, as they come from completely different and independent sources.
Due to the relatively large size of the top Yukawa coupling, and to the fact that it enters the top/stop contribution to the one-loop corrections at the fourth power, the uncertainty of the top-mass measurement is the one to which the parametric uncertainty of the Higgs-mass prediction is most sensitive. A well-known “rule of thumb” [308] (see also Refs. [38, 64]), which holds for MSSM scenarios with moderate to large \(\tan \beta \) and TeV-scale stops, states that each GeV of variation in \(M_t\) results in roughly one GeV of variation in the prediction for the SM-like Higgs mass. For example, in 2015 Ref. [234] showed that, in such scenarios, a variation in the pole top mass of 1.5 GeV – i.e., \(2\sigma \) according to the first combination of Tevatron and Run-1 LHC measurements in Ref. [309] – does indeed induce a shift of about 1.3 GeV in the prediction for \(M_h\). For low values of \(\tan \beta \), where a larger contribution from the top/stop loops is needed to obtain a prediction for the Higgs mass around 125 GeV, the induced shift can reach 2.5 GeV. This parametric uncertainty would have been comparable to, or even larger than, the estimated theory uncertainty of the EFT and hybrid calculations, at least in simplified MSSM scenarios with a realistic Higgs-mass prediction (see e.g. Fig. 5). However, the inclusion of Run-2 LHC data already brings the \(2\sigma \) uncertainty of the top-mass measurement down to 0.6 GeV [6]. It should be noted, on the other hand, that the question of how to relate the mass parameter that is measured at hadron colliders to a theoretically well-defined top-quark mass, suitable as input parameter for higher-order calculations, is still the subject of debate – see e.g. Refs. [310,311,312]. The related uncertainty should be taken into account as an additional source of parametric uncertainty in the Higgs-mass predictions. Future measurements at \(e^+ e^-\) colliders running at the \(t \bar{t}\) threshold would benefit from the fact that the relation between the measured mass parameter and a theoretically well-defined short-distance mass is well understood, and are expected to further reduce the \(2\sigma \) uncertainty to about 0.1 GeV [313].
Until superparticles are discovered, it is of course pointless to associate a parametric uncertainty to the input values of their masses and couplings. Even in the felicitous event of a discovery, it is unlikely that all of the SUSY parameters relevant to the Higgs-mass prediction will be independently measured in the medium term. Instead, as we illustrated in Sect. 2.1, the mass and couplings of the SM-like Higgs boson will serve as precision observables to constrain the SUSY parameters that are not directly accessible by experiment.
6.5 Prospects
As long as the dominant classes of higher-order terms are properly identified and simulated, the margin of improvement for a given estimate of the theory uncertainty of the Higgs-mass calculation is not large, because of the unavoidable subjectiveness involved in the choice of numerical coefficients, in the range of scale variation and so on. Only the explicit computation of the dominant missing terms can tell whether their estimate was too optimistic or too pessimistic. When the accuracy of the Higgs-mass calculation is thus improved, the existing uncertainty estimate must be adapted so that it simulates the dominant terms among those that remained uncomputed.
Rather than the development of new, more-refined techniques to estimate the theory uncertainty of the Higgs-mass calculation, the most natural direction of development in this domain is likely to be the application of the existing techniques to models or scenarios for which an uncertainty estimate is not currently available. For example, the uncertainty estimates discussed in Sects. 6.3.1 and 6.3.3 for the EFT and hybrid calculations all refer to scenarios in which there is only one Higgs doublet below the SUSY scale. It is fair to expect that they will soon be extended to scenarios with two light Higgs doublets and, beyond the MSSM, to scenarios in which the EFT features an even more complicated Higgs sector. In keeping with the trend towards an “automation” of the Higgs-mass calculations, it can also be expected that, in the medium term, estimates of the theory uncertainty similar to those described in this section will also be developed for the case of a general renormalizable theory, to be implemented in packages like SARAH.
Finally, it is worth noting that, in phenomenological analyses of SUSY models, the spectrum of superparticle masses is generally more complicated than in the simplified scenarios considered for illustration in this report (e.g., it might arise as the output of a spectrum generator). In realistic SUSY scenarios, the questions of which among the available EFTs (or EFT towers) better describes a given mass spectrum and of what is the optimal choice for the matching scale (or scales) might not be clear-cut. In this case, a comparison between the theory uncertainties associated with different EFT calculations can be used to investigate which one is most appropriate for the considered point of the parameter space.
7 Outlook
Resolving the underlying dynamics of electroweak symmetry breaking is one of the main goals of particle physics, and the predictions for the Higgs masses that characterize the SUSY extensions of the SM play a crucial role in this context. Indeed, the mass of the Higgs boson discovered at the LHC can now be considered an electroweak precision observable: much like, before the LHC era, the W mass and the Z-pole observables provided constraints on the Higgs mass within the SM, comparing the precisely-measured mass of the observed Higgs boson with the corresponding theoretical prediction places very sensitive constraints on the parameter space of the considered SUSY model.
The accuracy of the theoretical predictions for the Higgs masses in SUSY models has improved very significantly over the years that followed the Higgs discovery at the LHC. The progress in the calculations has been discussed in a series of (so far) eleven KUTS meetings, and is summarized in this report. The major lines of development included:
-
The improvement of the FO predictions for the Higgs masses in the simplest SUSY extension of the SM, the MSSM, with new calculations of two-loop corrections beyond the “gaugeless” and vanishing-momentum approximations, as well as of the dominant three-loop effects;
-
The precise calculation of the Higgs-mass spectrum in a number of non-minimal SUSY extensions of the SM, including among others the NMSSM, models with Dirac gauginos, and models with right-handed neutrinos;
-
A renewed focus on the all-order resummation of large logarithmic corrections even in scenarios with moderately heavy superparticles, through the development of EFT calculations of the Higgs masses and their combination with the existing FO calculations in several “hybrid” approaches. This led to the important result that somewhat larger stop masses than previously thought are needed in the MSSM to reproduce the observed value of the Higgs mass;
-
A new effort to assess, for each considered choice of SUSY parameters, the theory uncertainty of the Higgs-mass prediction that stems from uncomputed higher-order corrections. This showed that widely used “one size fits all” estimates of the uncertainty could be viewed as too optimistic or too pessimistic, depending on the considered regions of the parameter space.
Despite all of these developments, the quest for high-precision predictions for the Higgs masses in SUSY models is not by any means concluded. As described at the end of Sects. 3–6 of this report, efforts aimed at improving and extending the calculations, and KUTS meetings to discuss them, are bound to continue. An obvious question in this context is what should be the target for the precision of the theoretical predictions. Ideally, to fully exploit the potential of the Higgs-mass measurement in constraining the parameter space of SUSY models, one would need to bring the theory uncertainty of the prediction for the mass of the SM-like Higgs boson below the level of the current (and future) experimental precision. This would however require a reduction of the theory uncertainty by more than a factor of 10 compared to the current level, which is probably too ambitious a target in the medium term. A more realistic goal is that, in the coming years, the theory uncertainty of the Higgs-mass prediction be reduced by a factor of about \(2{-}3\), down to the level of the current “parametric” uncertainty that stems from the experimental uncertainty with which the SM input parameters are known. As discussed in Sect. 6.4, the dominant contribution to this parametric uncertainty comes from the value of the top mass measured at hadron colliders, whose relation with the theoretically well-defined top-mass parameter that is needed as input for the Higgs-mass calculation is an additional source of uncertainty. It is therefore unlikely that further reductions of the theory uncertainty would bring substantial benefits, at least until an improved measurement of the top mass, e.g. at future \(e^+ e^-\) colliders, reduces the associated parametric uncertainty down to the level of the experimental precision of the Higgs-mass measurement.
The urgency of further improvements in the accuracy of the Higgs-mass predictions in SUSY models will also depend on the experimental developments concerning the properties of the observed Higgs boson, the electroweak precision observables and the direct searches for BSM particles. In the MSSM, the minimal values of the stop masses that lead to a prediction for the Higgs mass compatible with the measured value lie typically above the current bounds from direct stop searches at the LHC. Therefore, the scenario of a SM-like Higgs boson with mass around 125 GeV and no hints for additional particles from direct BSM searches can still be considered a fully consistent realization of the MSSM. If no deviation from the SM is detected in the coming years, a SUSY model with superparticle masses beyond the kinematic reach of the LHC - or even of future hadron colliders such as the FCC-hh - will continue to be a viable possibility (one could invoke fine-tuning arguments to favor or disfavor certain classes of models). In this case, the requirement that the prediction for the mass of the SM-like Higgs boson agree – within the uncertainties – with the measured value will place constraints on the multi-dimensional space of experimentally inaccessible parameters of the considered model. For example, as can be inferred from Fig. 1 in Sect. 2.1, a lower bound on the stop masses of \(\mathcal{O}(10~\mathrm{TeV})\) from future searches at the FCC-hh would constrain the region of the MSSM parameter space with large \(\tan \beta \), which is consistent with a possible SUSY explanation of the \((g-2)_{\mu }\) anomaly. We also remark that, in the absence of new discoveries, the benefits of any possible improvement in the calculation of the Higgs masses will have to be assessed on a case-by-case basis. For example, in the simplified MSSM scenario with a common SUSY scale and a fixed value of \(\tan \beta \), the correlation between \(M_S\) and \(X_t\) discussed in Sect. 2.1 (see Fig. 2 there) illustrates the ultimate sensitivity on the unknown SUSY parameters that could be reached in the idealized situation where experimental and theory uncertainties are negligible. Even in that idealized situation, however, all correlations get blurred when more SUSY parameters are allowed to vary or non-minimal models are considered.
If, on the other hand, any significant deviations from the predictions of the SM are detected (e.g., with definitive confirmations of the lepton-flavor anomalies recently observed by LHCb, or of the long-standing \((g-2)_{\mu }\) anomaly) and/or any BSM particles are discovered, future investigations on the theory side will obviously focus on the classes of models that can accommodate the observed phenomenology. If SUSY models belong to this class, the techniques and results discussed in this report will be crucial to obtain accurate predictions for the Higgs masses, and the case for improving the calculations until the theory uncertainty matches the experimental accuracy of the Higgs-mass measurement will be even stronger. It is also worth stressing that, while these techniques were developed in the context of SUSY, they can be applied more generally to any BSM model that involves some kind of prediction for the quartic scalar couplings. In combination with direct experimental evidence for BSM physics, the Higgs-mass predictions will be a powerful tool for unraveling the nature of the new phenomena.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a review of theoretical studies and it does not rely on a dataset.]
Notes
The acronym KUTS originates as an inside joke, which the authors will explain on request.
The programs of the KUTS meetings are available at the web page https://sites.google.com/site/kutsmh/.
Due to the general nature of many of the concepts discussed in Sect. 2, we shall omit all citations there; see Ref. [5] for a pedagogical review of Higgs-mass calculations in SUSY models and an accompanying list of references. However, we aim to provide a comprehensive bibliography in the sections that follow.
With a slight abuse of notation, it has been common in the MSSM literature to denote the dominant one-loop corrections as \({{{\mathcal {O}}}}(\alpha _t)\) and the dominant two-loop corrections as \({{{\mathcal {O}}}}(\alpha _t^2)\) and \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\), where \(\alpha _t\equiv y_t^2/(4\pi )\) and \(\alpha _s \equiv g_s^2/(4\pi )\). We will follow this notation, although it leads to ambiguities when more couplings are involved in the corrections.
A common approximation in Higgs-mass calculations in SUSY models consists in neglecting the corrections that involve the Yukawa couplings of the first two generations, as they are usually negligible with respect to those that involve the third-generation couplings.
Descriptions of all of the public codes mentioned here and thereafter, including extended citation guides, are collected in the Appendix.
These mixed EW–QCD corrections are often called \({{{\mathcal {O}}}}(\alpha \alpha _s)\), which highlights the ambiguity of such notation: for example, they include both terms proportional to \(g^4\,g_s^2\) and terms proportional to \(g^2\,{y_t^2}\,g_s^2\).
Here and thereafter, a superfield is denoted by a “hat” over the symbol used for its scalar component. We adopt the conventions of Ref. [115] for the signs of the parameters in the superpotential and in the soft SUSY-breaking Lagrangian.
In the equations that illustrate the NMSSM Higgs sector we assume for simplicity that all parameters are real.
We recall that by \({{{\mathcal {O}}}}(\alpha _t \alpha _s, \alpha _b\alpha _s)\) we denote the two-loop corrections to the Higgs masses that involve the strong gauge coupling and the third-family Yukawa couplings in the gaugeless limit. In the NMSSM, these corrections include terms that depend also on various powers of the singlet-doublet coupling \(\lambda \).
We resort to this notation to distinguish the quartic Higgs coupling of the SM from the singlet-doublet superpotential coupling of the NMSSM, see Eq. (6). In our conventions the SM potential contains the quartic interaction term \(\frac{1}{2} \lambda _{{\scriptscriptstyle \mathrm{SM}}}|H|^4\).
At variance with the notation adopted for the mass corrections, we denote the various contributions to \(\Delta \lambda \) via the full combinations of couplings involved. For example, the dominant contributions involving the top Yukawa coupling are those of \({{{\mathcal {O}}}}(y_t^4)\) at one loop, and those of \({{{\mathcal {O}}}}(y_t^4 g_s^2)\) and \({{{\mathcal {O}}}}(y_t^6)\) at two loops.
See, however, Ref. [215] for the effect of dimension-six operators in a scenario with only one light stop.
The joke was apparently lost on the dozens of authors who cited that paper as if it had been a serious one.
With an impossibly cumbersome notation, these contributions could be collectively denoted as \({{{\mathcal {O}}}}\left( \,(y_t^2+y_b^2+y_\tau ^2)^3\,\right) \).
Namely, the two-loop corrections of \({{{\mathcal {O}}}}(y_t^2\, g^2 g_s^2)\), \({{{\mathcal {O}}}}(y_t^2 \,g^{\prime \,2} g_s^2)\), \({{{\mathcal {O}}}}(y_b^2\, g^2 g_s^2)\), \({{{\mathcal {O}}}}(y_b^2 \,g^{\prime \,2} g_s^2)\), \({{{\mathcal {O}}}}(g^4 g_s^2)\) and \({{{\mathcal {O}}}}(g^{\prime \,4} g_s^2)\).
Note that in this model there is no \({{{\mathcal {O}}}}(g^2)\) contribution to the quartic Higgs coupling at tree level, therefore all of the relevant two-loop diagrams can be obtained from the effective potential.
Since the gaugino masses feed into each other via two-loop corrections, this scenario involves additional fine tuning if the gap between the masses of gluino and EW gauginos is larger than a two-loop factor.
Reference [282] also showed how this technique can be used to obtain the one-loop contributions to the coefficients of the renormalizable operators of the EFT.
This issue had first surfaced during the preparation of the benchmark scenarios of Ref. [292].
For the time being the problem has not been addressed in SARAH, hence the accuracy of the resummation in that code’s hybrid mode is only LL.
An independent source of uncertainty for the Higgs-mass predictions in SUSY models are the experimental uncertainties in the measurements of the SM input parameters. This will be briefly discussed in Sect. 6.4.
For the two-loop calculations that are performed in the gaugeless limit the uncertainty estimate should also simulate the missing two-loop effects controlled by the EW gauge couplings.
Results qualitatively similar to the ones discussed in this section can be obtained also with SusyHD, see Ref. [234].
We recall that the FO prediction of FeynHiggs has a milder dependence on \(M_S\) in scenarios defined in terms of OS parameters for the stop sector (the latter is the recommended choice for FO predictions in FeynHiggs).
Within each group, the codes are listed in alphabetic order.
This is a preliminary reference, a dedicated publication is in preparation.
References
ATLAS Collaboration, G. Aad et al., Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1–29 (2012). https://doi.org/10.1016/j.physletb.2012.08.020. arXiv:1207.7214 [hep-ex]
CMS Collaboration, S. Chatrchyan et al., Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716, 30–61 (2012). https://doi.org/10.1016/j.physletb.2012.08.021. arXiv:1207.7235 [hep-ex]
ATLAS, CMS Collaboration, G. Aad et al., Combined measurement of the Higgs boson mass in \(pp\) collisions at \(\sqrt{s}=7\) and 8 TeV with the ATLAS and CMS experiments. Phys. Rev. Lett. 114, 191803 (2015). https://doi.org/10.1103/PhysRevLett.114.191803. arXiv:1503.07589 [hep-ex]
ATLAS, CMS Collaboration, G. Aad et al., Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at \( \sqrt{s}=7 \) and 8 TeV. JHEP 08, 045 (2016). https://doi.org/10.1007/JHEP08(2016)045. arXiv:1606.02266 [hep-ex]
P. Draper, H. Rzehak, A review of Higgs mass calculations in supersymmetric models. Phys. Rep. 619, 1–24 (2016). https://doi.org/10.1016/j.physrep.2016.01.001. arXiv:1601.01890 [hep-ph]
Particle Data Group Collaboration, P. Zyla et al., Review of particle physics. PTEP 2020(8), 083C01 (2020). https://doi.org/10.1093/ptep/ptaa104
H.P. Nilles, Supersymmetry, supergravity and particle physics. Phys. Rep. 110, 1–162 (1984). https://doi.org/10.1016/0370-1573(84)90008-5
H.E. Haber, G.L. Kane, The search for supersymmetry: probing physics beyond the standard model. Phys. Rep. 117, 75–263 (1985). https://doi.org/10.1016/0370-1573(85)90051-1
K. Inoue, A. Kakuto, H. Komatsu, S. Takeshita, Low-energy parameters and particle masses in a supersymmetric grand unified model. Prog. Theor. Phys. 67, 1889 (1982). https://doi.org/10.1143/PTP.67.1889
S. Li, M. Sher, Upper limit to the lightest Higgs mass in supersymmetric models. Phys. Lett. B 140, 339–343 (1984). https://doi.org/10.1016/0370-2693(84)90767-6
J. Gunion, A. Turski, Corrections to Higgs boson mass sum rules from the sfermion sector of a supersymmetric model. Phys. Rev. D 40, 2333 (1989). https://doi.org/10.1103/PhysRevD.40.2333
M.S. Berger, Radiative corrections to Higgs boson mass sum rules in the minimal supersymmetric extension to the standard model. Phys. Rev. D 41, 225 (1990). https://doi.org/10.1103/PhysRevD.41.225
Y. Okada, M. Yamaguchi, T. Yanagida, Upper bound of the lightest Higgs boson mass in the minimal supersymmetric standard model. Prog. Theor. Phys. 85, 1–6 (1991). https://doi.org/10.1143/ptp/85.1.1
J.R. Ellis, G. Ridolfi, F. Zwirner, Radiative corrections to the masses of supersymmetric Higgs bosons. Phys. Lett. B 257, 83–91 (1991). https://doi.org/10.1016/0370-2693(91)90863-L
H.E. Haber, R. Hempfling, Can the mass of the lightest Higgs boson of the minimal supersymmetric model be larger than m(Z)? Phys. Rev. Lett. 66, 1815–1818 (1991). https://doi.org/10.1103/PhysRevLett.66.1815
R. Barbieri, M. Frigeni, The supersymmetric Higgs searches at LEP after radiative corrections. Phys. Lett. B 258, 395–398 (1991). https://doi.org/10.1016/0370-2693(91)91106-6
J.R. Ellis, G. Ridolfi, F. Zwirner, On radiative corrections to supersymmetric Higgs boson masses and their implications for LEP searches. Phys. Lett. B 262, 477–484 (1991). https://doi.org/10.1016/0370-2693(91)90626-2
A. Brignole, J.R. Ellis, G. Ridolfi, F. Zwirner, The supersymmetric charged Higgs boson mass and LEP phenomenology. Phys. Lett. B 271, 123–132 (1991). https://doi.org/10.1016/0370-2693(91)91287-6
P.H. Chankowski, S. Pokorski, J. Rosiek, Charged and neutral supersymmetric Higgs boson masses: complete one loop analysis. Phys. Lett. B 274, 191–198 (1992). https://doi.org/10.1016/0370-2693(92)90522-6
A. Brignole, Radiative corrections to the supersymmetric charged Higgs boson mass. Phys. Lett. B 277, 313–323 (1992). https://doi.org/10.1016/0370-2693(92)90752-P
A. Brignole, Radiative corrections to the supersymmetric neutral Higgs boson masses. Phys. Lett. B 281, 284–294 (1992). https://doi.org/10.1016/0370-2693(92)91142-V
P.H. Chankowski, S. Pokorski, J. Rosiek, Complete on-shell renormalization scheme for the minimal supersymmetric Higgs sector. Nucl. Phys. B 423, 437–496 (1994). https://doi.org/10.1016/0550-3213(94)90141-4. arXiv:hep-ph/9303309
A. Dabelstein, The one loop renormalization of the MSSM Higgs sector and its application to the neutral scalar Higgs masses. Z. Phys. C 67, 495–512 (1995). https://doi.org/10.1007/BF01624592. arXiv:hep-ph/9409375
D.M. Pierce, J.A. Bagger, K.T. Matchev, R.-J. Zhang, Precision corrections in the minimal supersymmetric standard model. Nucl. Phys. B 491, 3–67 (1997). https://doi.org/10.1016/S0550-3213(96)00683-9. arXiv:hep-ph/9606211
R. Hempfling, A.H. Hoang, Two loop radiative corrections to the upper limit of the lightest Higgs boson mass in the minimal supersymmetric model. Phys. Lett. B 331, 99–106 (1994). https://doi.org/10.1016/0370-2693(94)90948-2. arXiv:hep-ph/9401219
S. Heinemeyer, W. Hollik, G. Weiglein, QCD corrections to the masses of the neutral CP - even Higgs bosons in the MSSM. Phys. Rev. D 58, 091701 (1998). https://doi.org/10.1103/PhysRevD.58.091701. arXiv:hep-ph/9803277
S. Heinemeyer, W. Hollik, G. Weiglein, Precise prediction for the mass of the lightest Higgs boson in the MSSM. Phys. Lett. B 440, 296–304 (1998). https://doi.org/10.1016/S0370-2693(98)01116-2. arXiv:hep-ph/9807423
R.-J. Zhang, Two loop effective potential calculation of the lightest CP even Higgs boson mass in the MSSM. Phys. Lett. B 447, 89–97 (1999). https://doi.org/10.1016/S0370-2693(98)01575-5. arXiv:hep-ph/9808299
S. Heinemeyer, W. Hollik, G. Weiglein, The masses of the neutral CP-even Higgs bosons in the MSSM: accurate analysis at the two loop level. Eur. Phys. J. C 9, 343–366 (1999). https://doi.org/10.1007/s100529900006. arXiv:hep-ph/9812472
J.R. Espinosa, R.-J. Zhang, MSSM lightest CP even Higgs boson mass to O(alpha(s) alpha(t)): the effective potential approach. JHEP 03, 026 (2000). https://doi.org/10.1088/1126-6708/2000/03/026. arXiv:hep-ph/9912236
M. Carena, H. Haber, S. Heinemeyer, W. Hollik, C. Wagner, G. Weiglein, Reconciling the two loop diagrammatic and effective field theory computations of the mass of the lightest CP-even Higgs boson in the MSSM. Nucl. Phys. B 580, 29–57 (2000). https://doi.org/10.1016/S0550-3213(00)00212-1. arXiv:hep-ph/0001002
J.R. Espinosa, R.-J. Zhang, Complete two loop dominant corrections to the mass of the lightest CP even Higgs boson in the minimal supersymmetric standard model. Nucl. Phys. B 586, 3–38 (2000). https://doi.org/10.1016/S0550-3213(00)00421-1. arXiv:hep-ph/0003246
G. Degrassi, P. Slavich, F. Zwirner, On the neutral Higgs boson masses in the MSSM for arbitrary stop mixing. Nucl. Phys. B 611, 403–422 (2001). https://doi.org/10.1016/S0550-3213(01)00343-1. arXiv:hep-ph/0105096
A. Brignole, G. Degrassi, P. Slavich, F. Zwirner, On the O(\(\alpha _t^2\)) two loop corrections to the neutral Higgs boson masses in the MSSM. Nucl. Phys. B 631, 195–218 (2002). https://doi.org/10.1016/S0550-3213(02)00184-0. arXiv:hep-ph/0112177
A. Brignole, G. Degrassi, P. Slavich, F. Zwirner, On the two loop sbottom corrections to the neutral Higgs boson masses in the MSSM. Nucl. Phys. B 643, 79–92 (2002). https://doi.org/10.1016/S0550-3213(02)00748-4. arXiv:hep-ph/0206101
A. Dedes, P. Slavich, Two loop corrections to radiative electroweak symmetry breaking in the MSSM. Nucl. Phys. B 657, 333–354 (2003). https://doi.org/10.1016/S0550-3213(03)00173-1. arXiv:hep-ph/0212132
A. Dedes, G. Degrassi, P. Slavich, On the two loop Yukawa corrections to the MSSM Higgs boson masses at large tan beta. Nucl. Phys. B 672, 144–162 (2003). https://doi.org/10.1016/j.nuclphysb.2003.08.033. arXiv:hep-ph/0305127
B. Allanach, A. Djouadi, J. Kneur, W. Porod, P. Slavich, Precise determination of the neutral Higgs boson masses in the MSSM. JHEP 09, 044 (2004). https://doi.org/10.1088/1126-6708/2004/09/044. arXiv:hep-ph/0406166
S. Heinemeyer, W. Hollik, H. Rzehak, G. Weiglein, High-precision predictions for the MSSM Higgs sector at \({\cal{O}}(\alpha _b\alpha _s)\). Eur. Phys. J. C 39, 465–481 (2005). https://doi.org/10.1140/epjc/s2005-02112-6. arXiv:hep-ph/0411114
M. Frank, L. Galeta, T. Hahn, S. Heinemeyer, W. Hollik, H. Rzehak, G. Weiglein, Charged Higgs boson mass of the MSSM in the Feynman diagrammatic approach. Phys. Rev. D 88(5), 055013 (2013). https://doi.org/10.1103/PhysRevD.88.055013. arXiv:1306.1156 [hep-ph]
W. Hollik, S. Paßehr, Two-loop top-Yukawa-coupling corrections to the charged Higgs-boson mass in the MSSM. Eur. Phys. J. C 75(7), 336 (2015). https://doi.org/10.1140/epjc/s10052-015-3558-7. arXiv:1502.02394 [hep-ph]
S. Heinemeyer, W. Hollik, G. Weiglein, FeynHiggs: a program for the calculation of the masses of the neutral CP even Higgs bosons in the MSSM. Comput. Phys. Commun. 124, 76–89 (2000). https://doi.org/10.1016/S0010-4655(99)00364-1. arXiv:hep-ph/9812320
T. Hahn, S. Heinemeyer, W. Hollik, H. Rzehak, G. Weiglein, FeynHiggs: a program for the calculation of MSSM Higgs-boson observables—version 2.6.5. Comput. Phys. Commun. 180, 1426–1427 (2009). https://doi.org/10.1016/j.cpc.2009.02.014
H. Bahl, T. Hahn, S. Heinemeyer, W. Hollik, S. Paßehr, H. Rzehak, G. Weiglein, Precision calculations in the MSSM Higgs-boson sector with FeynHiggs 2.14. Comput. Phys. Commun. 249, 107099 (2020). https://doi.org/10.1016/j.cpc.2019.107099. arXiv:1811.09073 [hep-ph]
B. Allanach, SOFTSUSY: a program for calculating supersymmetric spectra. Comput. Phys. Commun. 143, 305–331 (2002). https://doi.org/10.1016/S0010-4655(01)00460-X. arXiv:hep-ph/0104145
B. Allanach, A. Bednyakov, R. Ruiz de Austri, Higher order corrections and unification in the minimal supersymmetric standard model: SOFTSUSY3.5. Comput. Phys. Commun. 189, 192–206 (2015). https://doi.org/10.1016/j.cpc.2014.12.006. arXiv:1407.6130 [hep-ph]
A. Djouadi, J.-L. Kneur, G. Moultaka, SuSpect: a Fortran code for the supersymmetric and Higgs particle spectrum in the MSSM. Comput. Phys. Commun. 176, 426–455 (2007). https://doi.org/10.1016/j.cpc.2006.11.009. arXiv:hep-ph/0211331
W. Porod, SPheno, a program for calculating supersymmetric spectra, SUSY particle decays and SUSY particle production at e+ e\(-\) colliders. Comput. Phys. Commun. 153, 275–315 (2003). https://doi.org/10.1016/S0010-4655(03)00222-4. arXiv:hep-ph/0301101
W. Porod, F. Staub, SPheno 3.1: extensions including flavour, CP-phases and models beyond the MSSM. Comput. Phys. Commun. 183, 2458–2469 (2012). https://doi.org/10.1016/j.cpc.2012.05.021. arXiv:1104.1573 [hep-ph]
S.P. Martin, Complete two loop effective potential approximation to the lightest Higgs scalar boson mass in supersymmetry. Phys. Rev. D 67, 095012 (2003). https://doi.org/10.1103/PhysRevD.67.095012. arXiv:hep-ph/0211366
S.P. Martin, Two loop effective potential for the minimal supersymmetric standard model. Phys. Rev. D 66, 096001 (2002). https://doi.org/10.1103/PhysRevD.66.096001. arXiv:hep-ph/0206136
S.P. Martin, Strong and Yukawa two-loop contributions to Higgs scalar boson self-energies and pole masses in supersymmetry. Phys. Rev. D 71, 016012 (2005). https://doi.org/10.1103/PhysRevD.71.016012. arXiv:hep-ph/0405022
S.P. Martin, Evaluation of two loop self-energy basis integrals using differential equations. Phys. Rev. D 68, 075002 (2003). https://doi.org/10.1103/PhysRevD.68.075002. arXiv:hep-ph/0307101
S.P. Martin, D.G. Robertson, TSIL: a program for the calculation of two-loop self-energy integrals. Comput. Phys. Commun. 174, 133–151 (2006). https://doi.org/10.1016/j.cpc.2005.08.005. arXiv:hep-ph/0501132
S. Heinemeyer, H. Rzehak, C. Schappacher, Proposals for bottom quark/squark renormalization in the complex MSSM. Phys. Rev. D 82, 075010 (2010). https://doi.org/10.1103/PhysRevD.82.075010. arXiv:1007.0689 [hep-ph]
T. Fritzsche, S. Heinemeyer, H. Rzehak, C. Schappacher, Heavy scalar top quark decays in the complex MSSM: a full one-loop analysis. Phys. Rev. D 86, 035014 (2012). https://doi.org/10.1103/PhysRevD.86.035014. arXiv:1111.7289 [hep-ph]
T. Fritzsche, T. Hahn, S. Heinemeyer, F. von der Pahlen, H. Rzehak, C. Schappacher, The implementation of the renormalized complex MSSM in FeynArts and FormCalc. Comput. Phys. Commun. 185, 1529–1545 (2014). https://doi.org/10.1016/j.cpc.2014.02.005. arXiv:1309.1692 [hep-ph]
S. Borowka, T. Hahn, S. Heinemeyer, G. Heinrich, W. Hollik, Momentum-dependent two-loop QCD corrections to the neutral Higgs-boson masses in the MSSM. Eur. Phys. J. C 74(8), 2994 (2014). https://doi.org/10.1140/epjc/s10052-014-2994-0. arXiv:1404.7074 [hep-ph]
G. Degrassi, S. Di Vita, P. Slavich, Two-loop QCD corrections to the MSSM Higgs masses beyond the effective-potential approximation. Eur. Phys. J. C 75(2), 61 (2015). https://doi.org/10.1140/epjc/s10052-015-3280-5. arXiv:1410.3432 [hep-ph]
J. Carter, G. Heinrich, SecDec: a general program for sector decomposition. Comput. Phys. Commun. 182, 1566–1581 (2011). https://doi.org/10.1016/j.cpc.2011.03.026. arXiv:1011.5493 [hep-ph]
S. Borowka, J. Carter, G. Heinrich, Numerical evaluation of multi-loop integrals for arbitrary kinematics with SecDec 2.0. Comput. Phys. Commun. 184, 396–408 (2013). https://doi.org/10.1016/j.cpc.2012.09.020. arXiv:1204.4152 [hep-ph]
S. Borowka, T. Hahn, S. Heinemeyer, G. Heinrich, W. Hollik, Renormalization scheme dependence of the two-loop QCD corrections to the neutral Higgs-boson masses in the MSSM. Eur. Phys. J. C 75(9), 424 (2015). https://doi.org/10.1140/epjc/s10052-015-3648-6. arXiv:1505.03133 [hep-ph]
S. Borowka, S. Paßehr, G. Weiglein, Complete two-loop QCD contributions to the lightest Higgs-boson mass in the MSSM with complex parameters. Eur. Phys. J. C 78(7), 576 (2018). https://doi.org/10.1140/epjc/s10052-018-6055-y. arXiv:1802.09886 [hep-ph]
G. Degrassi, S. Heinemeyer, W. Hollik, P. Slavich, G. Weiglein, Towards high precision predictions for the MSSM Higgs sector. Eur. Phys. J. C 28, 133–143 (2003). https://doi.org/10.1140/epjc/s2003-01152-2. arXiv:hep-ph/0212020
S.P. Martin, Three-loop corrections to the lightest Higgs scalar boson mass in supersymmetry. Phys. Rev. D 75, 055005 (2007). https://doi.org/10.1103/PhysRevD.75.055005. arXiv:hep-ph/0701051
P. Draper, G. Lee, C.E.M. Wagner, Precise estimates of the Higgs mass in heavy supersymmetry. Phys. Rev. D 89(5), 055023 (2014). https://doi.org/10.1103/PhysRevD.89.055023
R.V. Harlander, P. Kant, L. Mihaila, M. Steinhauser, Higgs boson mass in supersymmetry to three loops. Phys. Rev. Lett. 100, 191602 (2008). https://doi.org/10.1103/PhysRevLett.100.191602. arXiv:0803.0672 [hep-ph]. [Erratum: Phys. Rev. Lett. 101, 039901 (2008). https://doi.org/10.1103/PhysRevLett.101.039901]
P. Kant, R. Harlander, L. Mihaila, M. Steinhauser, Light MSSM Higgs boson mass to three-loop accuracy. JHEP 08, 104 (2010). https://doi.org/10.1007/JHEP08(2010)104. arXiv:1005.5709 [hep-ph]
D. Kunz, L. Mihaila, N. Zerf, \(\cal{O}(\alpha _S^2)\) corrections to the running top-Yukawa coupling and the mass of the lightest Higgs boson in the MSSM. JHEP 12, 136 (2014). https://doi.org/10.1007/JHEP12(2014)136. arXiv:1409.2297 [hep-ph]
R.V. Harlander, J. Klappert, A. Voigt, Higgs mass prediction in the MSSM at three-loop level in a pure \(\overline{{\text{DR}}}\) context. Eur. Phys. J. C 77(12), 814 (2017). https://doi.org/10.1140/epjc/s10052-017-5368-6. arXiv:1708.05720 [hep-ph]
D. Stöckinger, J. Unger, Three-loop MSSM Higgs-boson mass predictions and regularization by dimensional reduction. Nucl. Phys. B 935, 1–16 (2018). https://doi.org/10.1016/j.nuclphysb.2018.08.005. arXiv:1804.05619 [hep-ph]
W. Hollik, D. Stockinger, MSSM Higgs-boson mass predictions and two-loop non-supersymmetric counterterms. Phys. Lett. B 634, 63–68 (2006). https://doi.org/10.1016/j.physletb.2006.01.030. arXiv:hep-ph/0509298
R. Harlander, D. Jones, P. Kant, L. Mihaila, M. Steinhauser, Four-loop beta function and mass anomalous dimension in dimensional reduction. JHEP 12, 024 (2006). https://doi.org/10.1088/1126-6708/2006/12/024. arXiv:hep-ph/0610206
R.V. Harlander, L. Mihaila, M. Steinhauser, The SUSY-QCD beta function to three loops. Eur. Phys. J. C 63, 383–390 (2009). https://doi.org/10.1140/epjc/s10052-009-1109-9. arXiv:0905.4807 [hep-ph]
A. Fazio, R.E. Reyes, The lightest Higgs boson mass of the MSSM at three-loop accuracy. Nucl. Phys. B 942, 164–183 (2019). https://doi.org/10.1016/j.nuclphysb.2019.03.008. arXiv:1901.03651 [hep-ph]
R.E. Reyes, A. Fazio, Comparison of the EFT hybrid and three-loop fixed-order calculations of the lightest MSSM Higgs boson mass. Phys. Rev. D 100(11), 115017 (2019). https://doi.org/10.1103/PhysRevD.100.115017. arXiv:1908.00693 [hep-ph]
S. Bauberger, A. Freitas, TVID: three-loop vacuum integrals from dispersion relations. arXiv:1702.02996 [hep-ph]
A. Pilaftsis, Higgs scalar-pseudoscalar mixing in the minimal supersymmetric standard model. Phys. Lett. B 435, 88–100 (1998). https://doi.org/10.1016/S0370-2693(98)00771-0. arXiv:hep-ph/9805373
D.A. Demir, Effects of the supersymmetric phases on the neutral Higgs sector. Phys. Rev. D 60, 055006 (1999). https://doi.org/10.1103/PhysRevD.60.055006. arXiv:hep-ph/9901389
A. Pilaftsis, C.E. Wagner, Higgs bosons in the minimal supersymmetric standard model with explicit CP violation. Nucl. Phys. B 553, 3–42 (1999). https://doi.org/10.1016/S0550-3213(99)00261-8. arXiv:hep-ph/9902371
S. Choi, M. Drees, J.S. Lee, Loop corrections to the neutral Higgs boson sector of the MSSM with explicit CP violation. Phys. Lett. B 481, 57–66 (2000). https://doi.org/10.1016/S0370-2693(00)00421-4. arXiv:hep-ph/0002287
M. Carena, J.R. Ellis, A. Pilaftsis, C. Wagner, Renormalization group improved effective potential for the MSSM Higgs sector with explicit CP violation. Nucl. Phys. B 586, 92–140 (2000). https://doi.org/10.1016/S0550-3213(00)00358-8. arXiv:hep-ph/0003180
T. Ibrahim, P. Nath, Corrections to the Higgs boson masses and mixings from chargino, W and charged Higgs exchange loops and large CP phases. Phys. Rev. D 63, 035009 (2001). https://doi.org/10.1103/PhysRevD.63.035009. arXiv:hep-ph/0008237
S. Heinemeyer, The Higgs boson sector of the complex MSSM in the Feynman diagrammatic approach. Eur. Phys. J. C 22, 521–534 (2001). https://doi.org/10.1007/s100520100819. arXiv:hep-ph/0108059
M. Carena, J.R. Ellis, A. Pilaftsis, C. Wagner, Higgs boson pole masses in the MSSM with explicit CP violation. Nucl. Phys. B 625, 345–371 (2002). https://doi.org/10.1016/S0550-3213(02)00014-7. arXiv:hep-ph/0111245
T. Ibrahim, P. Nath, Neutralino exchange corrections to the Higgs boson mixings with explicit CP violation. Phys. Rev. D 66, 015005 (2002). https://doi.org/10.1103/PhysRevD.66.015005. arXiv:hep-ph/0204092
J.R. Ellis, J.S. Lee, A. Pilaftsis, CERN LHC signatures of resonant CP violation in a minimal supersymmetric Higgs sector. Phys. Rev. D 70, 075010 (2004). https://doi.org/10.1103/PhysRevD.70.075010. arXiv:hep-ph/0404167
M. Frank, T. Hahn, S. Heinemeyer, W. Hollik, H. Rzehak, G. Weiglein, The Higgs boson masses and mixings of the complex MSSM in the Feynman-diagrammatic approach. JHEP 02, 047 (2007). https://doi.org/10.1088/1126-6708/2007/02/047. arXiv:hep-ph/0611326
S. Heinemeyer, W. Hollik, H. Rzehak, G. Weiglein, The Higgs sector of the complex MSSM at two-loop order: QCD contributions. Phys. Lett. B 652, 300–309 (2007). https://doi.org/10.1016/j.physletb.2007.07.030. arXiv:0705.0746 [hep-ph]
J. Lee, A. Pilaftsis, M. Carena, S. Choi, M. Drees, J.R. Ellis, C. Wagner, CPsuperH: a computational tool for Higgs phenomenology in the minimal supersymmetric standard model with explicit CP violation. Comput. Phys. Commun. 156, 283–317 (2004). https://doi.org/10.1016/S0010-4655(03)00463-6. arXiv:hep-ph/0307377
J. Lee, M. Carena, J. Ellis, A. Pilaftsis, C. Wagner, CPsuperH2.0: an improved computational tool for Higgs phenomenology in the MSSM with explicit CP violation. Comput. Phys. Commun. 180, 312–331 (2009). https://doi.org/10.1016/j.cpc.2008.09.003. arXiv:0712.2360 [hep-ph]
J. Lee, M. Carena, J. Ellis, A. Pilaftsis, C. Wagner, CPsuperH2.3: an updated tool for phenomenology in the MSSM with explicit CP violation. Comput. Phys. Commun. 184, 1220–1233 (2013). https://doi.org/10.1016/j.cpc.2012.11.006. arXiv:1208.2212 [hep-ph]
S. Heinemeyer, W. Hollik, F. Merz, S. Penaranda, Electroweak precision observables in the MSSM with nonminimal flavor violation. Eur. Phys. J. C 37, 481–493 (2004). https://doi.org/10.1140/epjc/s2004-02006-1. arXiv:hep-ph/0403228
J. Cao, G. Eilam, K.-I. Hikasa, J.M. Yang, Experimental constraints on stop-scharm flavor mixing and implications in top-quark FCNC processes. Phys. Rev. D 74, 031701 (2006). https://doi.org/10.1103/PhysRevD.74.031701. arXiv:hep-ph/0604163
A. Brignole, The supersymmetric Higgs boson with flavoured A-terms. Nucl. Phys. B 898, 644–658 (2015). https://doi.org/10.1016/j.nuclphysb.2015.07.025. arXiv:1504.03273 [hep-ph]
M. Arana-Catania, S. Heinemeyer, M. Herrero, S. Penaranda, Higgs boson masses and B-physics constraints in non-minimal flavor violating SUSY scenarios. JHEP 05, 015 (2012). https://doi.org/10.1007/JHEP05(2012)015. arXiv:1109.6232 [hep-ph]
M. Gómez, T. Hahn, S. Heinemeyer, M. Rehman, Higgs masses and electroweak precision observables in the lepton-flavor-violating MSSM. Phys. Rev. D 90(7), 074016 (2014). https://doi.org/10.1103/PhysRevD.90.074016. arXiv:1408.0663 [hep-ph]
W. Hollik, S. Paßehr, Two-loop top-Yukawa-coupling corrections to the Higgs boson masses in the complex MSSM. Phys. Lett. B 733, 144–150 (2014). https://doi.org/10.1016/j.physletb.2014.04.026. arXiv:1401.8275 [hep-ph]
W. Hollik, S. Paßehr, Higgs boson masses and mixings in the complex MSSM with two-loop top-Yukawa-coupling corrections. JHEP 10, 171 (2014). https://doi.org/10.1007/JHEP10(2014)171. arXiv:1409.1687 [hep-ph]
T. Hahn, S. Paßehr, Implementation of the \({\cal{O}}{(\alpha _t^2)}\) MSSM Higgs-mass corrections in FeynHiggs. Comput. Phys. Commun. 214, 91–97 (2017). https://doi.org/10.1016/j.cpc.2017.01.026. arXiv:1508.00562 [hep-ph]
S. Paßehr, G. Weiglein, Two-loop top and bottom Yukawa corrections to the Higgs-boson masses in the complex MSSM. Eur. Phys. J. C 78(3), 222 (2018). https://doi.org/10.1140/epjc/s10052-018-5665-8. arXiv:1705.07909 [hep-ph]
F. Staub, SARAH. arXiv:0806.0538 [hep-ph]
F. Staub, From superpotential to model files for FeynArts and CalcHep/CompHep. Comput. Phys. Commun. 181, 1077–1086 (2010). https://doi.org/10.1016/j.cpc.2010.01.011. arXiv:0909.2863 [hep-ph]
F. Staub, Automatic calculation of supersymmetric renormalization group equations and self energies. Comput. Phys. Commun. 182, 808–833 (2011). https://doi.org/10.1016/j.cpc.2010.11.030. arXiv:1002.0840 [hep-ph]
F. Staub, SARAH 3.2: Dirac gauginos, UFO output, and more. Comput. Phys. Commun. 184, 1792–1809 (2013). https://doi.org/10.1016/j.cpc.2013.02.019. arXiv:1207.0906 [hep-ph]
F. Staub, SARAH 4: a tool for (not only SUSY) model builders. Comput. Phys. Commun. 185, 1773–1790 (2014). https://doi.org/10.1016/j.cpc.2014.02.018. arXiv:1309.7223 [hep-ph]
F. Staub, Exploring new models in all detail with SARAH. Adv. High Energy Phys. 2015, 840780 (2015). https://doi.org/10.1155/2015/840780. arXiv:1503.04200 [hep-ph]
S.P. Martin, Two loop effective potential for a general renormalizable theory and softly broken supersymmetry. Phys. Rev. D 65, 116003 (2002). https://doi.org/10.1103/PhysRevD.65.116003. arXiv:hep-ph/0111209
M.D. Goodsell, K. Nickel, F. Staub, Two-loop Higgs mass calculations in supersymmetric models beyond the MSSM with SARAH and SPheno. Eur. Phys. J. C 75(1), 32 (2015). https://doi.org/10.1140/epjc/s10052-014-3247-y. arXiv:1411.0675 [hep-ph]
M. Goodsell, K. Nickel, F. Staub, Generic two-loop Higgs mass calculation from a diagrammatic approach. Eur. Phys. J. C 75(6), 290 (2015). https://doi.org/10.1140/epjc/s10052-015-3494-6. arXiv:1503.03098 [hep-ph]
H.K. Dreiner, K. Nickel, F. Staub, On the two-loop corrections to the Higgs mass in trilinear R-parity violation. Phys. Lett. B 742, 261–265 (2015). https://doi.org/10.1016/j.physletb.2015.01.047. arXiv:1411.3731 [hep-ph]
M.D. Goodsell, K. Nickel, F. Staub, The Higgs mass in the MSSM at two-loop order beyond minimal flavour violation. Phys. Lett. B 758, 18–25 (2016). https://doi.org/10.1016/j.physletb.2016.04.034. arXiv:1511.01904 [hep-ph]
M.D. Goodsell, F. Staub, The Higgs mass in the CP violating MSSM, NMSSM, and beyond. Eur. Phys. J. C 77(1), 46 (2017). https://doi.org/10.1140/epjc/s10052-016-4495-9. arXiv:1604.05335 [hep-ph]
M. Maniatis, The next-to-minimal supersymmetric extension of the standard model reviewed. Int. J. Mod. Phys. A 25, 3505–3602 (2010). https://doi.org/10.1142/S0217751X10049827. arXiv:0906.0777 [hep-ph]
U. Ellwanger, C. Hugonie, A.M. Teixeira, The next-to-minimal supersymmetric standard model. Phys. Rep. 496, 1–77 (2010). https://doi.org/10.1016/j.physrep.2010.07.001. arXiv:0910.1785 [hep-ph]
P. Fayet, Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino. Nucl. Phys. B 90, 104–124 (1975). https://doi.org/10.1016/0550-3213(75)90636-7
R.K. Kaul, P. Majumdar, Cancellation of quadratically divergent mass corrections in globally supersymmetric spontaneously broken gauge theories. Nucl. Phys. B 199, 36 (1982). https://doi.org/10.1016/0550-3213(82)90565-X
R. Barbieri, S. Ferrara, C.A. Savoy, Gauge models with spontaneously broken local supersymmetry. Phys. Lett. B 119, 343 (1982). https://doi.org/10.1016/0370-2693(82)90685-2
H.P. Nilles, M. Srednicki, D. Wyler, Weak interaction breakdown induced by supergravity. Phys. Lett. B 120, 346 (1983). https://doi.org/10.1016/0370-2693(83)90460-4
J. Frere, D. Jones, S. Raby, Fermion masses and induction of the weak scale by supergravity. Nucl. Phys. B 222, 11–19 (1983). https://doi.org/10.1016/0550-3213(83)90606-5
J. Derendinger, C.A. Savoy, Quantum effects and SU(2) \(\times \) U(1) breaking in supergravity gauge theories. Nucl. Phys. B 237, 307–328 (1984). https://doi.org/10.1016/0550-3213(84)90162-7
J.R. Ellis, J. Gunion, H.E. Haber, L. Roszkowski, F. Zwirner, Higgs bosons in a nonminimal supersymmetric model. Phys. Rev. D 39, 844 (1989). https://doi.org/10.1103/PhysRevD.39.844
M. Drees, Supersymmetric models with extended Higgs sector. Int. J. Mod. Phys. A 4, 3635 (1989). https://doi.org/10.1142/S0217751X89001448
U. Ellwanger, Radiative corrections to the neutral Higgs spectrum in supersymmetry with a gauge singlet. Phys. Lett. B 303, 271–276 (1993). https://doi.org/10.1016/0370-2693(93)91431-L. arXiv:hep-ph/9302224
P. Pandita, One loop radiative corrections to the lightest Higgs scalar mass in nonminimal supersymmetric Standard Model. Phys. Lett. B 318, 338–346 (1993). https://doi.org/10.1016/0370-2693(93)90137-7
P. Pandita, Radiative corrections to the scalar Higgs masses in a nonminimal supersymmetric Standard Model. Z. Phys. C 59, 575–584 (1993). https://doi.org/10.1007/BF01562550
T. Elliott, S. King, P. White, Squark contributions to Higgs boson masses in the next-to-minimal supersymmetric standard model. Phys. Lett. B 314, 56–63 (1993). https://doi.org/10.1016/0370-2693(93)91321-D. arXiv:hep-ph/9305282
T. Elliott, S. King, P. White, Radiative corrections to Higgs boson masses in the next-to-minimal supersymmetric Standard Model. Phys. Rev. D 49, 2435–2456 (1994). https://doi.org/10.1103/PhysRevD.49.2435. arXiv:hep-ph/9308309
S. King, P. White, Resolving the constrained minimal and next-to-minimal supersymmetric standard models. Phys. Rev. D 52, 4183–4216 (1995). https://doi.org/10.1103/PhysRevD.52.4183. arXiv:hep-ph/9505326
U. Ellwanger, C. Hugonie, Yukawa induced radiative corrections to the lightest Higgs boson mass in the NMSSM. Phys. Lett. B 623, 93–103 (2005). https://doi.org/10.1016/j.physletb.2005.07.039. arXiv:hep-ph/0504269
S. Ham, J. Kim, S. Oh, D. Son, The charged Higgs boson in the next-to-minimal supersymmetric standard model with explicit CP violation. Phys. Rev. D 64, 035007 (2001). https://doi.org/10.1103/PhysRevD.64.035007. arXiv:hep-ph/0104144
S. Ham, S. Oh, D. Son, Neutral Higgs sector of the next-to-minimal supersymmetric standard model with explicit CP violation. Phys. Rev. D 65, 075004 (2002). https://doi.org/10.1103/PhysRevD.65.075004. arXiv:hep-ph/0110052
S. Ham, Y. Jeong, S. Oh, Radiative CP violation in the Higgs sector of the next-to-minimal supersymmetric model. arXiv:hep-ph/0308264
G. Degrassi, P. Slavich, On the radiative corrections to the neutral Higgs boson masses in the NMSSM. Nucl. Phys. B 825, 119–150 (2010). https://doi.org/10.1016/j.nuclphysb.2009.09.018. arXiv:0907.4682 [hep-ph]
F. Staub, W. Porod, B. Herrmann, The electroweak sector of the NMSSM at the one-loop level. JHEP 10, 040 (2010). https://doi.org/10.1007/JHEP10(2010)040. arXiv:1007.4049 [hep-ph]
K. Ender, T. Graf, M. Muhlleitner, H. Rzehak, Analysis of the NMSSM Higgs boson masses at one-loop level. Phys. Rev. D 85, 075024 (2012). https://doi.org/10.1103/PhysRevD.85.075024. arXiv:1111.4952 [hep-ph]
T. Graf, R. Grober, M. Muhlleitner, H. Rzehak, K. Walz, Higgs boson masses in the complex NMSSM at one-loop level. JHEP 10, 122 (2012). https://doi.org/10.1007/JHEP10(2012)122. arXiv:1206.6806 [hep-ph]
G.G. Ross, K. Schmidt-Hoberg, F. Staub, The generalised NMSSM at one loop: fine tuning and phenomenology. JHEP 08, 074 (2012). https://doi.org/10.1007/JHEP08(2012)074. arXiv:1205.1509 [hep-ph]
U. Ellwanger, J.F. Gunion, C. Hugonie, NMHDECAY: a Fortran code for the Higgs masses, couplings and decay widths in the NMSSM. JHEP 02, 066 (2005). https://doi.org/10.1088/1126-6708/2005/02/066. arXiv:hep-ph/0406215
U. Ellwanger, C. Hugonie, NMHDECAY 2.0: an updated program for sparticle masses, Higgs masses, couplings and decay widths in the NMSSM. Comput. Phys. Commun. 175, 290–303 (2006). https://doi.org/10.1016/j.cpc.2006.04.004. arXiv:hep-ph/0508022
B. Allanach, P. Athron, L.C. Tunstall, A. Voigt, A. Williams, Next-to-minimal SOFTSUSY. Comput. Phys. Commun. 185, 2322–2339 (2014). https://doi.org/10.1016/j.cpc.2014.04.015. arXiv:1311.7659 [hep-ph]. [Erratum: Comput. Phys. Commun. 250, 107044 (2020)]
P. Athron, J.-H. Park, D. Stöckinger, A. Voigt, FlexibleSUSY—a spectrum generator generator for supersymmetric models. Comput. Phys. Commun. 190, 139–172 (2015). https://doi.org/10.1016/j.cpc.2014.12.020. arXiv:1406.2319 [hep-ph]
P. Athron, M. Bach, D. Harries, T. Kwasnitza, J.-H. Park, D. Stöckinger, A. Voigt, J . Ziebell, FlexibleSUSY 2.0: extensions to investigate the phenomenology of SUSY and non-SUSY models. Comput. Phys. Commun. 230, 145–217 (2018). https://doi.org/10.1016/j.cpc.2018.04.016. arXiv:1710.03760 [hep-ph]
J. Baglio, R. Gröber, M. Mühlleitner, D. Nhung, H. Rzehak, M. Spira, J. Streicher, K. Walz, NMSSMCALC: a program package for the calculation of loop-corrected Higgs boson masses and decay widths in the (complex) NMSSM. Comput. Phys. Commun. 185(12), 3372–3391 (2014). https://doi.org/10.1016/j.cpc.2014.08.005. arXiv:1312.4788 [hep-ph]
P.Z. Skands et al., SUSY Les Houches accord: interfacing SUSY spectrum calculators, decay packages, and event generators. JHEP 07, 036 (2004). https://doi.org/10.1088/1126-6708/2004/07/036. arXiv:hep-ph/0311123
B. Allanach et al., SUSY Les Houches accord 2. Comput. Phys. Commun. 180, 8–25 (2009). https://doi.org/10.1016/j.cpc.2008.08.004. arXiv:0801.0045 [hep-ph]
M.D. Goodsell, K. Nickel, F. Staub, Two-loop corrections to the Higgs masses in the NMSSM. Phys. Rev. D 91, 035021 (2015). https://doi.org/10.1103/PhysRevD.91.035021. arXiv:1411.4665 [hep-ph]
S.P. Martin, Taming the Goldstone contributions to the effective potential. Phys. Rev. D 90(1), 016013 (2014). https://doi.org/10.1103/PhysRevD.90.016013. arXiv:1406.2355 [hep-ph]
J. Elias-Miro, J. Espinosa, T. Konstandin, Taming infrared divergences in the effective potential. JHEP 08, 034 (2014). https://doi.org/10.1007/JHEP08(2014)034. arXiv:1406.2652 [hep-ph]
A. Pilaftsis, D. Teresi, Symmetry improved 2PI effective action and the infrared divergences of the standard model. J. Phys. Conf. Ser. 631(1), 012008 (2015). https://doi.org/10.1088/1742-6596/631/1/012008. arXiv:1502.07986 [hep-ph]
A. Pilaftsis, D. Teresi, Symmetry-improved 2PI approach to the Goldstone-boson IR problem of the SM effective potential. Nucl. Phys. B 906, 381–407 (2016). https://doi.org/10.1016/j.nuclphysb.2016.03.018. arXiv:1511.05347 [hep-ph]
N. Kumar, S.P. Martin, Resummation of Goldstone boson contributions to the MSSM effective potential. Phys. Rev. D 94(1), 014013 (2016). https://doi.org/10.1103/PhysRevD.94.014013. arXiv:1605.02059 [hep-ph]
J. Braathen, M.D. Goodsell, Avoiding the Goldstone Boson Catastrophe in general renormalisable field theories at two loops. JHEP 12, 056 (2016). https://doi.org/10.1007/JHEP12(2016)056. arXiv:1609.06977 [hep-ph]
S.P. Martin, Two loop scalar self energies in a general renormalizable theory at leading order in gauge couplings. Phys. Rev. D 70, 016005 (2004). https://doi.org/10.1103/PhysRevD.70.016005. arXiv:hep-ph/0312092
J. Braathen, M.D. Goodsell, F. Staub, Supersymmetric and non-supersymmetric models without catastrophic Goldstone bosons. Eur. Phys. J. C 77(11), 757 (2017). https://doi.org/10.1140/epjc/s10052-017-5303-x. arXiv:1706.05372 [hep-ph]
M. Mühlleitner, D.T. Nhung, H. Rzehak, K. Walz, Two-loop contributions of the order \( {\cal{O}}({\alpha }_t{\alpha }_s) \) to the masses of the Higgs bosons in the CP-violating NMSSM. JHEP 05, 128 (2015). https://doi.org/10.1007/JHEP05(2015)128. arXiv:1412.0918 [hep-ph]
T. Dao, R. Gröber, M. Krause, M. Mühlleitner, H. Rzehak, Two-loop \( {\cal{O}} \) ( \( {\alpha }_t^2 \) ) corrections to the neutral Higgs boson masses in the CP-violating NMSSM. JHEP 08, 114 (2019). https://doi.org/10.1007/JHEP08(2019)114. arXiv:1903.11358 [hep-ph]
T.N. Dao, L. Fritz, M. Krause, M. Mühlleitner, S. Patel, Gauge dependences of higher-order corrections to NMSSM Higgs boson masses and the charged Higgs decay \({H^{\pm } \rightarrow W^\pm h_{i}}\). Eur. Phys. J. C 80(3), 292 (2020). https://doi.org/10.1140/epjc/s10052-020-7837-6. arXiv:1911.07197 [hep-ph]
F. Domingo, S. Paßehr, Towards Higgs masses and decay widths satisfying the symmetries in the (N)MSSM. Eur. Phys. J. C80(12), 1124 (2020). https://doi.org/10.1140/epjc/s10052-020-08655-8. arXiv:2007.11010 [hep-ph]
P. Drechsel, L. Galeta, S. Heinemeyer, G. Weiglein, Precise predictions for the Higgs-boson masses in the NMSSM. Eur. Phys. J. C 77(1), 42 (2017). https://doi.org/10.1140/epjc/s10052-017-4595-1. arXiv:1601.08100 [hep-ph]
F. Domingo, P. Drechsel, S. Paßehr, On-shell neutral Higgs bosons in the NMSSM with complex parameters. Eur. Phys. J. C 77(8), 562 (2017). https://doi.org/10.1140/epjc/s10052-017-5104-2. arXiv:1706.00437 [hep-ph]
W.G. Hollik, S. Liebler, G. Moortgat-Pick, S. Paßehr, G. Weiglein, Phenomenology of the inflation-inspired NMSSM at the electroweak scale. Eur. Phys. J. C 79(1), 75 (2019). https://doi.org/10.1140/epjc/s10052-019-6561-6. arXiv:1809.07371 [hep-ph]
F. Staub, P. Athron, U. Ellwanger, R. Gröber, M. Mühlleitner, P. Slavich, A. Voigt, Higgs mass predictions of public NMSSM spectrum generators. Comput. Phys. Commun. 202, 113–130 (2016). https://doi.org/10.1016/j.cpc.2016.01.005. arXiv:1507.05093 [hep-ph]
P. Drechsel, R. Gröber, S. Heinemeyer, M.M. Muhlleitner, H. Rzehak, G. Weiglein, Higgs-boson masses and mixing matrices in the NMSSM: analysis of on-shell calculations. Eur. Phys. J. C 77(6), 366 (2017). https://doi.org/10.1140/epjc/s10052-017-4932-4. arXiv:1612.07681 [hep-ph]
P. Fayet, Massive gluinos. Phys. Lett. 78B, 417–420 (1978). https://doi.org/10.1016/0370-2693(78)90474-4
G. Belanger, K. Benakli, M. Goodsell, C. Moura, A. Pukhov, Dark matter with Dirac and Majorana gaugino masses. JCAP 08, 027 (2009). https://doi.org/10.1088/1475-7516/2009/08/027. arXiv:0905.1043 [hep-ph]
G.D. Kribs, E. Poppitz, N. Weiner, Flavor in supersymmetry with an extended R-symmetry. Phys. Rev. D 78, 055010 (2008). https://doi.org/10.1103/PhysRevD.78.055010. arXiv:0712.2039 [hep-ph]
K. Benakli, M.D. Goodsell, F. Staub, Dirac gauginos and the 125 GeV Higgs. JHEP 06, 073 (2013). https://doi.org/10.1007/JHEP06(2013)073. arXiv:1211.0552 [hep-ph]
K. Benakli, M. Goodsell, F. Staub, W. Porod, Constrained minimal Dirac gaugino supersymmetric standard model. Phys. Rev. D 90(4), 045017 (2014). https://doi.org/10.1103/PhysRevD.90.045017. arXiv:1403.5122 [hep-ph]
P. Dießner, J. Kalinowski, W. Kotlarski, D. Stöckinger, Higgs boson mass and electroweak observables in the MRSSM. JHEP 12, 124 (2014). https://doi.org/10.1007/JHEP12(2014)124. arXiv:1410.4791 [hep-ph]
M.D. Goodsell, M.E. Krauss, T. Müller, W. Porod, F. Staub, Dark matter scenarios in a constrained model with Dirac gauginos. JHEP 10, 132 (2015). https://doi.org/10.1007/JHEP10(2015)132. arXiv:1507.01010 [hep-ph]
P. Diessner, J. Kalinowski, W. Kotlarski, D. Stöckinger, Two-loop correction to the Higgs boson mass in the MRSSM. Adv. High Energy Phys. 2015, 760729 (2015). https://doi.org/10.1155/2015/760729. arXiv:1504.05386 [hep-ph]
J. Braathen, M.D. Goodsell, P. Slavich, Leading two-loop corrections to the Higgs boson masses in SUSY models with Dirac gauginos. JHEP 09, 045 (2016). https://doi.org/10.1007/JHEP09(2016)045. arXiv:1606.09213 [hep-ph]
K. Nickel, F. Staub, Precise determination of the Higgs mass in supersymmetric models with vectorlike tops and the impact on naturalness in minimal GMSB. JHEP 07, 139 (2015). https://doi.org/10.1007/JHEP07(2015)139. arXiv:1505.06077 [hep-ph]
M. Hirsch, M.E. Krauss, T. Opferkuch, W. Porod, F. Staub, A constrained supersymmetric left-right model. JHEP 03, 009 (2016). https://doi.org/10.1007/JHEP03(2016)009. arXiv:1512.00472 [hep-ph]
F. Borzumati, A. Masiero, Large muon and electron number violations in supergravity theories. Phys. Rev. Lett. 57, 961 (1986). https://doi.org/10.1103/PhysRevLett.57.961
S. Heinemeyer, M. Herrero, S. Penaranda, A. Rodriguez-Sanchez, Higgs boson masses in the MSSM with heavy Majorana neutrinos. JHEP 05, 063 (2011). https://doi.org/10.1007/JHEP05(2011)063. arXiv:1007.5512 [hep-ph]
P. Draper, H.E. Haber, Decoupling of the right-handed neutrino contribution to the Higgs mass in supersymmetric models. Eur. Phys. J. C 73, 2522 (2013). https://doi.org/10.1140/epjc/s10052-013-2522-7. arXiv:1304.6103 [hep-ph]
S. Heinemeyer, J. Hernandez-Garcia, M. Herrero, X. Marcano, A. Rodriguez-Sanchez, Radiative corrections to \(M_h\) from three generations of Majorana neutrinos and sneutrinos. Adv. High Energy Phys. 2015, 152394 (2015). https://doi.org/10.1155/2015/152394. arXiv:1407.1083 [hep-ph]
D. Lopez-Fogliani, C. Munoz, Proposal for a supersymmetric standard model. Phys. Rev. Lett. 97, 041801 (2006). https://doi.org/10.1103/PhysRevLett.97.041801. arXiv:hep-ph/0508297
T. Biekötter, S. Heinemeyer, C. Muñoz, Precise prediction for the Higgs-boson masses in the \(\mu \nu \) SSM. Eur. Phys. J. C 78(6), 504 (2018). https://doi.org/10.1140/epjc/s10052-018-5978-7. arXiv:1712.07475 [hep-ph]
T. Biekötter, S. Heinemeyer, C. Muñoz, Precise prediction for the Higgs-Boson masses in the \(\mu \nu \) SSM with three right-handed neutrino superfields. Eur. Phys. J. C 79(8), 667 (2019). https://doi.org/10.1140/epjc/s10052-019-7175-8. arXiv:1906.06173 [hep-ph]
T. Biekötter, munuSSM: a python package for the \(\mu \)-from-\(\nu \) supersymmetric standard model. Comput. Phys. Commun. 264, 107935 (2021). https://doi.org/10.1016/j.cpc.2021.107935. arXiv:2009.12887 [hep-ph]
T. Alanne, H. Gertov, F. Sannino, K. Tuominen, Elementary Goldstone Higgs boson and dark matter. Phys. Rev. D 91(9), 095021 (2015). https://doi.org/10.1103/PhysRevD.91.095021. arXiv:1411.6132 [hep-ph]
H. Gertov, A. Meroni, E. Molinaro, F. Sannino, Theory and phenomenology of the elementary Goldstone Higgs boson. Phys. Rev. D 92(9), 095003 (2015). https://doi.org/10.1103/PhysRevD.92.095003. arXiv:1507.06666 [hep-ph]
T. Alanne, H. Rzehak, F. Sannino, A.E. Thomsen, Raising the SUSY-breaking scale in a Goldstone–Higgs model. Mod. Phys. Lett. A 32(27), 1750143 (2017). https://doi.org/10.1142/S0217732317501437. arXiv:1606.03411 [hep-ph]
S.P. Martin, Two-loop scalar self-energies and pole masses in a general renormalizable theory with massless gauge bosons. Phys. Rev. D 71, 116004 (2005). https://doi.org/10.1103/PhysRevD.71.116004. arXiv:hep-ph/0502168
M.D. Goodsell, S. Paßehr, All two-loop scalar self-energies and tadpoles in general renormalisable field theories. Eur. Phys. J. C 80(5), 417 (2020). https://doi.org/10.1140/epjc/s10052-020-7657-8. arXiv:1910.02094 [hep-ph]
T. Hahn, S. Heinemeyer, W. Hollik, H. Rzehak, G. Weiglein, High-precision predictions for the light CP-even Higgs boson mass of the minimal supersymmetric standard model. Phys. Rev. Lett. 112(14), 141801 (2014). https://doi.org/10.1103/PhysRevLett.112.141801. arXiv:1312.4937 [hep-ph]
S. Bauberger, A. Freitas, D. Wiegand, TVID 2: evaluation of planar-type three-loop self-energy integrals with arbitrary masses. JHEP 01, 024 (2020). https://doi.org/10.1007/JHEP01(2020)024. arXiv:1908.09887 [hep-ph]
D. Buttazzo, G. Degrassi, P.P. Giardino, G.F. Giudice, F. Sala, A. Salvio, A. Strumia, Investigating the near-criticality of the Higgs boson. JHEP 12, 089 (2013). https://doi.org/10.1007/JHEP12(2013)089. arXiv:1307.3536 [hep-ph]
B.A. Kniehl, A.F. Pikelner, O.L. Veretin, Two-loop electroweak threshold corrections in the Standard Model. Nucl. Phys. B 896, 19–51 (2015). https://doi.org/10.1016/j.nuclphysb.2015.04.010. arXiv:1503.02138 [hep-ph]
S.P. Martin, D.G. Robertson, Standard model parameters in the tadpole-free pure \(\overline{{\rm MS}}\) scheme. Phys. Rev. D 100(7), 073004 (2019). https://doi.org/10.1103/PhysRevD.100.073004. arXiv:1907.02500 [hep-ph]
L.N. Mihaila, J. Salomon, M. Steinhauser, Gauge coupling beta functions in the standard model to three loops. Phys. Rev. Lett. 108, 151602 (2012). https://doi.org/10.1103/PhysRevLett.108.151602. arXiv:1201.5868 [hep-ph]
K. Chetyrkin, M. Zoller, Three-loop \(\beta \)-functions for top-Yukawa and the Higgs self-interaction in the Standard Model. JHEP 06, 033 (2012). https://doi.org/10.1007/JHEP06(2012)033. arXiv:1205.2892 [hep-ph]
L.N. Mihaila, J. Salomon, M. Steinhauser, Renormalization constants and beta functions for the gauge couplings of the Standard Model to three-loop order. Phys. Rev. D 86, 096008 (2012). https://doi.org/10.1103/PhysRevD.86.096008. arXiv:1208.3357 [hep-ph]
A. Bednyakov, A. Pikelner, V. Velizhanin, Anomalous dimensions of gauge fields and gauge coupling beta-functions in the Standard Model at three loops. JHEP 01, 017 (2013). https://doi.org/10.1007/JHEP01(2013)017. arXiv:1210.6873 [hep-ph]
A. Bednyakov, A. Pikelner, V. Velizhanin, Yukawa coupling beta-functions in the Standard Model at three loops. Phys. Lett. B 722, 336–340 (2013). https://doi.org/10.1016/j.physletb.2013.04.038. arXiv:1212.6829 [hep-ph]
K. Chetyrkin, M. Zoller, \(\beta \)-function for the Higgs self-interaction in the Standard Model at three-loop level. JHEP 04, 091 (2013). https://doi.org/10.1007/JHEP04(2013)091. arXiv:1303.2890 [hep-ph]. [Erratum: JHEP 09, 155 (2013)]
A. Bednyakov, A. Pikelner, V. Velizhanin, Higgs self-coupling beta-function in the Standard Model at three loops. Nucl. Phys. B 875, 552–565 (2013). https://doi.org/10.1016/j.nuclphysb.2013.07.015. arXiv:1303.4364 [hep-ph]
S.P. Martin, Three-loop standard model effective potential at leading order in strong and top Yukawa couplings. Phys. Rev. D 89(1), 013003 (2014). https://doi.org/10.1103/PhysRevD.89.013003. arXiv:1310.7553 [hep-ph]
S.P. Martin, D.G. Robertson, Higgs boson mass in the Standard Model at two-loop order and beyond. Phys. Rev. D 90(7), 073010 (2014). https://doi.org/10.1103/PhysRevD.90.073010. arXiv:1407.4336 [hep-ph]
S.P. Martin, D.G. Robertson, Evaluation of the general 3-loop vacuum Feynman integral. Phys. Rev. D95(1), 016008 (2017). https://doi.org/10.1103/PhysRevD.95.016008. arXiv:1610.07720 [hep-ph]
S.P. Martin, Effective potential at three loops. Phys. Rev. D96(9), 096005 (2017). https://doi.org/10.1103/PhysRevD.96.096005. arXiv:1709.02397 [hep-ph]
S.P. Martin, Four-loop standard model effective potential at leading order in QCD. Phys. Rev. D 92(5), 054029 (2015). https://doi.org/10.1103/PhysRevD.92.054029. arXiv:1508.00912 [hep-ph]
K. Chetyrkin, M. Zoller, Leading QCD-induced four-loop contributions to the \(\beta \)-function of the Higgs self-coupling in the SM and vacuum stability. JHEP 06, 175 (2016). https://doi.org/10.1007/JHEP06(2016)175. arXiv:1604.00853 [hep-ph]
L.J. Hall, M.B. Wise, Flavor changing Higgs-boson couplings. Nucl. Phys. B 187, 397–408 (1981). https://doi.org/10.1016/0550-3213(81)90469-7
R. Barbieri, M. Frigeni, F. Caravaglios, The supersymmetric Higgs for heavy superpartners. Phys. Lett. B 258, 167–170 (1991). https://doi.org/10.1016/0370-2693(91)91226-L
J. Espinosa, M. Quiros, Two loop radiative corrections to the mass of the lightest Higgs boson in supersymmetric standard models. Phys. Lett. B 266, 389–396 (1991). https://doi.org/10.1016/0370-2693(91)91056-2
J. Casas, J. Espinosa, M. Quiros, A. Riotto, The lightest Higgs boson mass in the minimal supersymmetric standard model. Nucl. Phys. B 436, 3–29, (1995). https://doi.org/10.1016/0550-3213(94)00508-C. arXiv:hep-ph/9407389. [Erratum: Nucl. Phys. B 439, 466–468 (1995)]
H.E. Haber, R. Hempfling, The renormalization group improved Higgs sector of the minimal supersymmetric model. Phys. Rev. D 48, 4280–4309 (1993). https://doi.org/10.1103/PhysRevD.48.4280. arXiv:hep-ph/9307201
M. Carena, J. Espinosa, M. Quiros, C. Wagner, Analytical expressions for radiatively corrected Higgs masses and couplings in the MSSM. Phys. Lett. B 355, 209–221 (1995). https://doi.org/10.1016/0370-2693(95)00694-G. arXiv:hep-ph/9504316
M. Carena, M. Quiros, C. Wagner, Effective potential methods and the Higgs mass spectrum in the MSSM. Nucl. Phys. B 461, 407–436 (1996). https://doi.org/10.1016/0550-3213(95)00665-6. arXiv:hep-ph/9508343
H.E. Haber, R. Hempfling, A.H. Hoang, Approximating the radiatively corrected Higgs mass in the minimal supersymmetric model. Z. Phys. C 75, 539–554 (1997). https://doi.org/10.1007/s002880050498. arXiv:hep-ph/9609331
J. Espinosa, I. Navarro, Radiative corrections to the Higgs boson mass for a hierarchical stop spectrum. Nucl. Phys. B 615, 82–116 (2001). https://doi.org/10.1016/S0550-3213(01)00429-1. arXiv:hep-ph/0104047
N. Arkani-Hamed, S. Dimopoulos, Supersymmetric unification without low energy supersymmetry and signatures for fine-tuning at the LHC. JHEP 06, 073 (2005). https://doi.org/10.1088/1126-6708/2005/06/073. arXiv:hep-th/0405159
G. Giudice, A. Romanino, Split supersymmetry. Nucl. Phys. B 699, 65–89, (2004). https://doi.org/10.1016/j.nuclphysb.2004.08.001. arXiv:hep-ph/0406088. [Erratum: Nucl. Phys. B 706, 487–487 (2005)]
M. Carena, G. Nardini, M. Quiros, C.E. Wagner, The effective theory of the light stop scenario. JHEP 10, 062 (2008). https://doi.org/10.1088/1126-6708/2008/10/062. arXiv:0806.4297 [hep-ph]
M. Binger, Higgs boson mass in split supersymmetry at two-loops. Phys. Rev. D 73, 095001 (2006). https://doi.org/10.1103/PhysRevD.73.095001. arXiv:hep-ph/0408240
N. Bernal, A. Djouadi, P. Slavich, The MSSM with heavy scalars. JHEP 07, 016 (2007). https://doi.org/10.1088/1126-6708/2007/07/016. arXiv:0705.1496 [hep-ph]
M.E. Machacek, M.T. Vaughn, Two loop renormalization group equations in a general quantum field theory. 1. Wave function renormalization. Nucl. Phys. B 222, 83–103 (1983). https://doi.org/10.1016/0550-3213(83)90610-7
M.E. Machacek, M.T. Vaughn, Two loop renormalization group equations in a general quantum field theory. 2. Yukawa couplings. Nucl. Phys. B 236, 221–232 (1984). https://doi.org/10.1016/0550-3213(84)90533-9
M.E. Machacek, M.T. Vaughn, Two loop renormalization group equations in a general quantum field theory. 3. Scalar quartic couplings. Nucl. Phys. B 249, 70–92 (1985). https://doi.org/10.1016/0550-3213(85)90040-9
M.-X. Luo, H.-W. Wang, Y. Xiao, Two loop renormalization group equations in general gauge field theories. Phys. Rev. D 67, 065019 (2003). https://doi.org/10.1103/PhysRevD.67.065019. arXiv:hep-ph/0211440
P.P. Giardino, P. Lodone, Threshold corrections to hard supersymmetric relations. Mod. Phys. Lett. A 29(19), 1450101 (2014). https://doi.org/10.1142/S0217732314501016. arXiv:1112.2635 [hep-ph]
G.F. Giudice, A. Strumia, Probing high-scale and split supersymmetry with higgs mass measurements. Nucl. Phys. B 858, 63–83 (2012). https://doi.org/10.1016/j.nuclphysb.2012.01.001. arXiv:1108.6077 [hep-ph]
E. Bagnaschi, G.F. Giudice, P. Slavich, A. Strumia, Higgs mass and unnatural supersymmetry. JHEP 09, 092 (2014). https://doi.org/10.1007/JHEP09(2014)092. arXiv:1407.4081 [hep-ph]
C. Tamarit, Decoupling heavy sparticles in hierarchical SUSY scenarios: two-loop renormalization group equations. arXiv:1204.2292 [hep-ph]
K. Benakli, L. Darmé, M.D. Goodsell, P. Slavich, A fake split supersymmetry model for the 126 GeV Higgs. JHEP 05, 113 (2014). https://doi.org/10.1007/JHEP05(2014)113. arXiv:1312.5220 [hep-ph]
P.J. Fox, D.E. Kaplan, E. Katz, E. Poppitz, V. Sanz, M. Schmaltz, M.D. Schwartz, N. Weiner, Supersplit supersymmetry. arXiv:hep-th/0503249
L.J. Hall, Y. Nomura, A finely-predicted Higgs boson mass from a finely-tuned weak scale. JHEP 03, 076 (2010). https://doi.org/10.1007/JHEP03(2010)076. arXiv:0910.2235 [hep-ph]
M. Cabrera, J. Casas, A. Delgado, Upper bounds on superpartner masses from upper bounds on the Higgs boson mass. Phys. Rev. Lett. 108, 021802 (2012). https://doi.org/10.1103/PhysRevLett.108.021802. arXiv:1108.3867 [hep-ph]
G. Degrassi, S. Di Vita, J. Elias-Miro, J.R. Espinosa, G.F. Giudice, G. Isidori, A. Strumia, Higgs mass and vacuum stability in the Standard Model at NNLO. JHEP 08, 098 (2012). https://doi.org/10.1007/JHEP08(2012)098. arXiv:1205.6497 [hep-ph]
J. Pardo Vega, G. Villadoro, SusyHD: Higgs mass determination in supersymmetry. JHEP 07(159) (2015). https://doi.org/10.1007/JHEP07(2015)159. arXiv:1504.05200 [hep-ph]
E. Bagnaschi, J. Pardo Vega, P. Slavich, Improved determination of the Higgs mass in the MSSM with heavy superpartners. Eur. Phys. J. C 77(5), 334 (2017). https://doi.org/10.1140/epjc/s10052-017-4885-7. arXiv:1703.08166 [hep-ph]
R. Harlander, J. Klappert, A. Ochoa Franco, A. Voigt, The light CP-even MSSM Higgs mass resummed to fourth logarithmic order. Eur. Phys. J. C 78(10), 874 (2018). https://doi.org/10.1140/epjc/s10052-018-6351-6. arXiv:1807.03509 [hep-ph]
E. Bagnaschi, G. Degrassi, S. Paßehr, P. Slavich, Full two-loop QCD corrections to the Higgs mass in the MSSM with heavy superpartners. Eur. Phys. J. C 79(11), 910 (2019). https://doi.org/10.1140/epjc/s10052-019-7417-9. arXiv:1908.01670 [hep-ph]
H. Bahl, I. Sobolev, G. Weiglein, Precise prediction for the mass of the light MSSM Higgs boson for the case of a heavy gluino. Phys. Lett. B 808, 135644 (2020). https://doi.org/10.1016/j.physletb.2020.135644. arXiv:1912.10002 [hep-ph]
H. Bahl, I. Sobolev, G. Weiglein, The light MSSM Higgs boson mass for large \(\tan \beta \) and complex input parameters. Eur. Phys. J. C80(11), 1063 (2020). https://doi.org/10.1140/epjc/s10052-020-08637-w. arXiv:2009.07572 [hep-ph]
D. Noth, M. Spira, Higgs boson couplings to bottom quarks: two-loop supersymmetry-QCD corrections. Phys. Rev. Lett. 101, 181801 (2008). https://doi.org/10.1103/PhysRevLett.101.181801. arXiv:0808.0087 [hep-ph]
D. Noth, M. Spira, Supersymmetric Higgs Yukawa couplings to bottom quarks at next-to-next-to-leading order. JHEP 06, 084 (2011). https://doi.org/10.1007/JHEP06(2011)084. arXiv:1001.1935 [hep-ph]
L. Mihaila, C. Reisser, \({\cal{O}}(\alpha _s^2)\) corrections to fermionic Higgs decays in the MSSM. JHEP 08, 021 (2010). https://doi.org/10.1007/JHEP08(2010)021. arXiv:1007.0693 [hep-ph]
M. Carena, J. Ellis, J. Lee, A. Pilaftsis, C. Wagner, CP violation in heavy MSSM Higgs scenarios. JHEP 02, 123 (2016). https://doi.org/10.1007/JHEP02(2016)123. arXiv:1512.00437 [hep-ph]
N. Murphy, H. Rzehak, Higgs-boson masses and mixings in the MSSM with CP violation and heavy SUSY particles. arXiv:1909.00726 [hep-ph]
M. Gorbahn, S. Jager, U. Nierste, S. Trine, The supersymmetric Higgs sector and \(B-\bar{B}\) mixing for large tan \(\beta \). Phys. Rev. D 84, 034030 (2011). https://doi.org/10.1103/PhysRevD.84.034030. arXiv:0901.2065 [hep-ph]
H. Bahl, W. Hollik, Precise prediction of the MSSM Higgs boson masses for low M\(_{A}\). JHEP 07, 182 (2018). https://doi.org/10.1007/JHEP07(2018)182. arXiv:1805.00867 [hep-ph]
G. Lee, C.E. Wagner, Higgs bosons in heavy supersymmetry with an intermediate m\(_A\). Phys. Rev. D 92(7), 075032 (2015). https://doi.org/10.1103/PhysRevD.92.075032. arXiv:1508.00576 [hep-ph]
H. Bahl, I. Sobolev, Two-loop matching of renormalizable operators: general considerations and applications. JHEP 03, 286 (2021). https://doi.org/10.1007/JHEP03(2021)286. arXiv:2010.01989 [hep-ph]
F. Lyonnet, I. Schienbein, F. Staub, A. Wingerter, PyR@TE: renormalization group equations for general gauge theories. Comput. Phys. Commun. 185, 1130–1152 (2014). https://doi.org/10.1016/j.cpc.2013.12.002. arXiv:1309.7030 [hep-ph]
F. Lyonnet, I. Schienbein, PyR@TE 2: a Python tool for computing RGEs at two-loop. Comput. Phys. Commun. 213, 181–196 (2017). https://doi.org/10.1016/j.cpc.2016.12.003. arXiv:1608.07274 [hep-ph]
L. Sartore, General RGEs for dimensionful couplings in the \(\overline{{\rm MS}}\) scheme. Phys. Rev. D 102(7), 076002 (2020). https://doi.org/10.1103/PhysRevD.102.076002. arXiv:2006.12307 [hep-ph]
L. Sartore, I. Schienbein, PyR@TE 3. Comput. Phys. Commun. 261, 107819 (2021). https://doi.org/10.1016/j.cpc.2020.107819. arXiv:2007.12700 [hep-ph]
P. Bhupal Dev, A. Pilaftsis, Maximally symmetric two Higgs doublet model with natural standard model alignment. JHEP 12, 024 (2014). https://doi.org/10.1007/JHEP12(2014)024. arXiv:1408.3405 [hep-ph]. [Erratum: JHEP 11, 147 (2015)]
A. Bednyakov, On three-loop RGE for the Higgs sector of 2HDM. JHEP 11, 154 (2018). https://doi.org/10.1007/JHEP11(2018)154. arXiv:1809.04527 [hep-ph]
I. Schienbein, F. Staub, T. Steudtner, K. Svirina, Revisiting RGEs for general gauge theories. Nucl. Phys. B 939, 1–48 (2019). https://doi.org/10.1016/j.nuclphysb.2018.12.001. arXiv:1809.06797 [hep-ph]
J. Oredsson, J. Rathsman, \(\mathbb{Z}_2\) breaking effects in 2-loop RG evolution of 2HDM. JHEP 02, 152 (2019). https://doi.org/10.1007/JHEP02(2019)152. arXiv:1810.02588 [hep-ph]
J. Oredsson, 2HDME: two-Higgs-doublet model evolver. Comput. Phys. Commun. 244, 409–426 (2019). https://doi.org/10.1016/j.cpc.2019.05.021. arXiv:1811.08215 [hep-ph]
F. Herren, L. Mihaila, M. Steinhauser, Gauge and Yukawa coupling beta functions of two-Higgs-doublet models to three-loop order. Phys. Rev. D 97(1), 015016 (2018). https://doi.org/10.1103/PhysRevD.97.015016. arXiv:1712.06614 [hep-ph]. [Erratum: Phys. Rev. D 101, 079903 (2020)]
S. Kanemura, Y. Okada, E. Senaha, C.-P. Yuan, Higgs coupling constants as a probe of new physics. Phys. Rev. D 70, 115002 (2004). https://doi.org/10.1103/PhysRevD.70.115002. arXiv:hep-ph/0408364
M. Krause, R. Lorenz, M. Muhlleitner, R. Santos, H. Ziesche, Gauge-independent Renormalization of the 2-Higgs-doublet model. JHEP 09, 143 (2016). https://doi.org/10.1007/JHEP09(2016)143. arXiv:1605.04853 [hep-ph]
L. Altenkamp, S. Dittmaier, H. Rzehak, Renormalization schemes for the two-Higgs-doublet model and applications to h \(\rightarrow \) WW/ZZ \(\rightarrow \) 4 fermions. JHEP 09, 134 (2017). https://doi.org/10.1007/JHEP09(2017)134. arXiv:1704.02645 [hep-ph]
S. Kanemura, M. Kikuchi, K. Sakurai, K. Yagyu, Gauge invariant one-loop corrections to Higgs boson couplings in non-minimal Higgs models. Phys. Rev. D 96(3), 035014 (2017). https://doi.org/10.1103/PhysRevD.96.035014. arXiv:1705.05399 [hep-ph]
E. Bagnaschi, F. Brümmer, W. Buchmüller, A. Voigt, G. Weiglein, Vacuum stability and supersymmetry at high scales with two Higgs doublets. JHEP 03, 158 (2016). https://doi.org/10.1007/JHEP03(2016)158. arXiv:1512.07761 [hep-ph]
E. Bagnaschi et al., Benchmark scenarios for low \(\tan \beta \) in the MSSM. LHCHXSWG-2015-002 (2015)
H. Bahl, S. Liebler, T. Stefaniak, MSSM Higgs benchmark scenarios for Run 2 and beyond: the low \(\tan \beta \) region. Eur. Phys. J. C 79(3), 279 (2019). https://doi.org/10.1140/epjc/s10052-019-6770-z. arXiv:1901.05933 [hep-ph]
A. Djouadi, J. Quevillon, The MSSM Higgs sector at a high \(M_{SUSY}\): reopening the low tan\(\beta \) regime and heavy Higgs searches. JHEP 10, 028 (2013). https://doi.org/10.1007/JHEP10(2013)028. arXiv:1304.1787 [hep-ph]
L. Maiani, A. Polosa, V. Riquer, Bounds to the Higgs sector masses in minimal supersymmetry from LHC data. Phys. Lett. B 724, 274–277 (2013). https://doi.org/10.1016/j.physletb.2013.06.026. arXiv:1305.2172 [hep-ph]
A. Djouadi, L. Maiani, G. Moreau, A. Polosa, J. Quevillon, V. Riquer, The post-Higgs MSSM scenario: habemus MSSM? Eur. Phys. J. C 73, 2650 (2013). https://doi.org/10.1140/epjc/s10052-013-2650-0. arXiv:1307.5205 [hep-ph]
A. Djouadi, L. Maiani, A. Polosa, J. Quevillon, V. Riquer, Fully covering the MSSM Higgs sector at the LHC. JHEP 06, 168 (2015). https://doi.org/10.1007/JHEP06(2015)168. arXiv:1502.05653 [hep-ph]
K. Cheung, R. Huo, J.S. Lee, Y.-L. Sming Tsai, Dark matter in split SUSY with intermediate Higgses. JHEP 04, 151 (2015). https://doi.org/10.1007/JHEP04(2015)151. arXiv:1411.7329 [hep-ph]
J. Braathen, M.D. Goodsell, P. Slavich, Matching renormalisable couplings: simple schemes and a plot. Eur. Phys. J. C 79(8), 669 (2019). https://doi.org/10.1140/epjc/s10052-019-7093-9. arXiv:1810.09388 [hep-ph]
M. Gabelmann, M. Mühlleitner, F. Staub, Automatised matching between two scalar sectors at the one-loop level. Eur. Phys. J. C 79(2), 163 (2019). https://doi.org/10.1140/epjc/s10052-019-6570-5. arXiv:1810.12326 [hep-ph]
M. Gabelmann, M.M. Mühlleitner, F. Staub, The singlet extended standard model in the context of split supersymmetry. Phys. Rev. D 100, 075026 (2019). https://doi.org/10.1103/PhysRevD.100.075026. arXiv:1907.04338 [hep-ph]
K. Benakli, M.D. Goodsell, S.L. Williamson, Higgs alignment from extended supersymmetry. Eur. Phys. J. C 78(8), 658 (2018). https://doi.org/10.1140/epjc/s10052-018-6125-1. arXiv:1801.08849 [hep-ph]
D. Liu, Leading Two-loop corrections to the mass of Higgs boson in the High scale Dirac gaugino supersymmetry. arXiv:1912.06168 [hep-ph]
P.J. Fox, G.D. Kribs, A. Martin, Split Dirac supersymmetry: an ultraviolet completion of Higgsino dark matter. Phys. Rev. D 90(7), 075006 (2014). https://doi.org/10.1103/PhysRevD.90.075006. arXiv:1405.3692 [hep-ph]
P. Athron, J.-H. Park, T. Steudtner, D. Stöckinger, A. Voigt, Precise Higgs mass calculations in (non-)minimal supersymmetry at both high and low scales. JHEP 01, 079 (2017). https://doi.org/10.1007/JHEP01(2017)079. arXiv:1609.00371 [hep-ph]
H. Bahl, S. Heinemeyer, W. Hollik, G. Weiglein, Reconciling EFT and hybrid calculations of the light MSSM Higgs-boson mass. Eur. Phys. J. C 78(1), 57 (2018). https://doi.org/10.1140/epjc/s10052-018-5544-3. arXiv:1706.00346 [hep-ph]
B. Henning, X. Lu, H. Murayama, What do precision Higgs measurements buy us? arXiv:1404.1058 [hep-ph]
R. Huo, Effective field theory of integrating out sfermions in the MSSM: complete one-loop analysis. Phys. Rev. D 97(7), 075013 (2018). https://doi.org/10.1103/PhysRevD.97.075013. arXiv:1509.05942 [hep-ph]
A. Drozd, J. Ellis, J. Quevillon, T. You, The universal one-loop effective action. JHEP 03, 180 (2016). https://doi.org/10.1007/JHEP03(2016)180. arXiv:1512.03003 [hep-ph]
J.D. Wells, Z. Zhang, Effective field theory approach to trans-TeV supersymmetry: covariant matching, Yukawa unification and Higgs couplings. JHEP 05, 182 (2018). https://doi.org/10.1007/JHEP05(2018)182. arXiv:1711.04774 [hep-ph]
M. Krämer, B. Summ, A. Voigt, Completing the scalar and fermionic universal one-loop effective action. JHEP 01, 079 (2020). https://doi.org/10.1007/JHEP01(2020)079. arXiv:1908.04798 [hep-ph]
M. Gaillard, The effective one loop Lagrangian with derivative couplings. Nucl. Phys. B 268, 669–692 (1986). https://doi.org/10.1016/0550-3213(86)90264-6
L.-H. Chan, Derivative expansion for the one loop effective actions with internal symmetry. Phys. Rev. Lett. 57, 1199 (1986). https://doi.org/10.1103/PhysRevLett.57.1199
O. Cheyette, Effective action for the standard model with large Higgs mass. Nucl. Phys. B 297, 183–204 (1988). https://doi.org/10.1016/0550-3213(88)90205-2
B. Henning, X. Lu, H. Murayama, How to use the Standard Model effective field theory. JHEP 01, 023 (2016). https://doi.org/10.1007/JHEP01(2016)023. arXiv:1412.1837 [hep-ph]
H. Bahl, W. Hollik, Precise prediction for the light MSSM Higgs boson mass combining effective field theory and fixed-order calculations. Eur. Phys. J. C 76(9), 499 (2016). https://doi.org/10.1140/epjc/s10052-016-4354-8. arXiv:1608.01880 [hep-ph]
H. Bahl, Pole mass determination in presence of heavy particles. JHEP 02, 121 (2019). https://doi.org/10.1007/JHEP02(2019)121. arXiv:1812.06452 [hep-ph]
H. Bahl, S. Heinemeyer, W. Hollik, G. Weiglein, Theoretical uncertainties in the MSSM Higgs boson mass calculation. Eur. Phys. J. C 80(6), 497 (2020). https://doi.org/10.1140/epjc/s10052-020-8079-3. arXiv:1912.04199 [hep-ph]
H. Bahl, N. Murphy, H. Rzehak, Hybrid calculation of the MSSM Higgs boson masses using the complex THDM as EFT (2020). https://old.inspirehep.net/record/1822166/export/hx. arXiv:2010.04711 [hep-ph]
E. Bagnaschi et al., MSSM Higgs boson searches at the LHC: benchmark scenarios for Run 2 and beyond. Eur. Phys. J. C 79(7), 617 (2019). https://doi.org/10.1140/epjc/s10052-019-7114-8. arXiv:1808.07542 [hep-ph]
I. Sobolev, Precise predictions for Higgs physics in supersymmetric models. Dissertation, Hamburg U. (2020). https://doi.org/10.3204/PUBDB-2020-02962
F. Staub, W. Porod, Improved predictions for intermediate and heavy supersymmetry in the MSSM and beyond. Eur. Phys. J. C 77(5), 338 (2017). https://doi.org/10.1140/epjc/s10052-017-4893-7. arXiv:1703.03267 [hep-ph]
T. Kwasnitza, D. Stöckinger, A. Voigt, Improved MSSM Higgs mass calculation using the 3-loop FlexibleEFTHiggs approach including \(x_{t}\)-resummation. JHEP 07(07), 197 (2020). https://doi.org/10.1007/JHEP07(2020)197. arXiv:2003.04639 [hep-ph]
R. Harlander, J. Klappert, A. Voigt, The light CP-even MSSM Higgs mass including N\(^{{\bf 3}} \)LO+N\(^{{\bf 3}}\)LL QCD corrections. Eur. Phys. J. C 80(3), 186 (2020). https://doi.org/10.1140/epjc/s10052-020-7747-7. arXiv:1910.03595 [hep-ph]
T. Hahn, W. Hollik, S. Heinemeyer, G. Weiglein, Precision Higgs masses with FeynHiggs 2.2. eConf C050318, 0106 (2005). arXiv:hep-ph/0507009
CDF, D0, Tevatron Electroweak Working Group Collaboration, P. Azzi, E. Barberis, L. Demortier, M. Grunewald, A. Juste, B. Klima, J. Konigsberg, A. Quadt, M. Strovink, E.J. Thomson, Combination of CDF and D0 results on the top-quark mass. arXiv:hep-ex/0404010
H. Bahl, P. Bechtle, S. Heinemeyer, S. Liebler, T. Stefaniak, G. Weiglein, HL-LHC and ILC sensitivities in the hunt for heavy Higgs bosons. Eur. Phys. J. C 80(10), 916 (2020). https://doi.org/10.1140/epjc/s10052-020-08472-z. arXiv:2005.14536 [hep-ph]
B. Allanach, A. Voigt, Uncertainties in the lightest \(CP\) even Higgs boson mass prediction in the minimal supersymmetric standard model: fixed order versus effective field theory prediction. Eur. Phys. J. C 78(7), 573 (2018). https://doi.org/10.1140/epjc/s10052-018-6046-z. arXiv:1804.09410 [hep-ph]
K. Chetyrkin, M. Steinhauser, Short distance mass of a heavy quark at order \(\alpha _s^3\). Phys. Rev. Lett. 83, 4001–4004 (1999). https://doi.org/10.1103/PhysRevLett.83.4001. arXiv:hep-ph/9907509
K. Chetyrkin, M. Steinhauser, The relation between the MS-bar and the on-shell quark mass at order \(\alpha _s^3\). Nucl. Phys. B 573, 617–651 (2000). https://doi.org/10.1016/S0550-3213(99)00784-1. arXiv:hep-ph/9911434
K. Melnikov, T.V. Ritbergen, The three loop relation between the MS-bar and the pole quark masses. Phys. Lett. B 482, 99–108 (2000). https://doi.org/10.1016/S0370-2693(00)00507-4. arXiv:hep-ph/9912391
P. Marquard, A.V. Smirnov, V.A. Smirnov, M. Steinhauser, Quark mass relations to four-loop order in perturbative QCD. Phys. Rev. Lett. 114(14), 142002 (2015). https://doi.org/10.1103/PhysRevLett.114.142002. arXiv:1502.01030 [hep-ph]
R. Harlander, L. Mihaila, M. Steinhauser, Two-loop matching coefficients for the strong coupling in the MSSM. Phys. Rev. D 72, 095009 (2005). https://doi.org/10.1103/PhysRevD.72.095009. arXiv:hep-ph/0509048
A. Bauer, L. Mihaila, J. Salomon, Matching coefficients for alpha(s) and m(b) to O(\(\alpha _s^2\)) in the MSSM. JHEP 02, 037 (2009). https://doi.org/10.1088/1126-6708/2009/02/037. arXiv:0810.5101 [hep-ph]
A. Bednyakov, Some two-loop threshold corrections and three-loop renormalization group analysis of the MSSM, in 16th International Seminar on High Energy Physics, (2010). arXiv:1009.5455 [hep-ph]
S. Heinemeyer, W. Hollik, G. Weiglein, Constraints on tan Beta in the MSSM from the upper bound on the mass of the lightest Higgs boson. JHEP 06, 009 (2000). https://doi.org/10.1088/1126-6708/2000/06/009. arXiv:hep-ph/9909540
ATLAS, CDF, CMS, D0 Collaboration, First combination of Tevatron and LHC measurements of the top-quark mass. arXiv:1403.4427 [hep-ex]
A.H. Hoang, I.W. Stewart, Top mass measurements from jets and the Tevatron top-quark mass. Nucl. Phys. Proc. Suppl. 185, 220–226 (2008). https://doi.org/10.1016/j.nuclphysbps.2008.10.028. arXiv:0808.0222 [hep-ph]
M. Butenschoen, B. Dehnadi, A.H. Hoang, V. Mateu, M. Preisser, I.W. Stewart, Top quark mass calibration for Monte Carlo event generators. Phys. Rev. Lett. 117(23), 232001 (2016). https://doi.org/10.1103/PhysRevLett.117.232001. arXiv:1608.01318 [hep-ph]
P. Nason, The top mass in hadronic collisions, in From My Vast Repertoire ...: Guido Altarelli’s Legacy, ed. by A. Levy, S. Forte, G. Ridolfi (2019), pp. 123–151. https://doi.org/10.1142/9789813238053_0008. arXiv:1712.02796 [hep-ph]
LCC Physics Working Group Collaboration, K. Fujii et al., Tests of the standard model at the international linear collider. arXiv:1908.11299 [hep-ex]
P. Bechtle, O. Brein, S. Heinemeyer, G. Weiglein, K.E. Williams, HiggsBounds: confronting arbitrary Higgs sectors with exclusion bounds from LEP and the Tevatron. Comput. Phys. Commun. 181, 138–167 (2010). https://doi.org/10.1016/j.cpc.2009.09.003. arXiv:0811.4169 [hep-ph]
P. Bechtle, O. Brein, S. Heinemeyer, G. Weiglein, K.E. Williams, HiggsBounds 2.0.0: confronting neutral and charged higgs sector predictions with exclusion bounds from LEP and the Tevatron. Comput. Phys. Commun. 182, 2605–2631 (2011). https://doi.org/10.1016/j.cpc.2011.07.015. arXiv:1102.1898 [hep-ph]
P. Bechtle, O. Brein, S. Heinemeyer, O. Stål, T. Stefaniak, G. Weiglein, K.E. Williams, \(HiggsBounds-4\): improved tests of extended Higgs sectors against exclusion bounds from LEP, the Tevatron and the LHC. Eur. Phys. J. C 74(3), 2693 (2014). https://doi.org/10.1140/epjc/s10052-013-2693-2. arXiv:1311.0055 [hep-ph]
P. Bechtle, D. Dercks, S. Heinemeyer, T. Klingl, T. Stefaniak, G. Weiglein, J. Wittbrodt, HiggsBounds-5: testing Higgs sectors in the LHC 13 TeV era (2020). https://old.inspirehep.net/record/1800733/export/hx. arXiv:2006.06007 [hep-ph]
P. Bechtle, S. Heinemeyer, O. Stål, T. Stefaniak, G. Weiglein, \(HiggsSignals\): confronting arbitrary Higgs sectors with measurements at the Tevatron and the LHC. Eur. Phys. J. C74(2), 2711 (2014). https://doi.org/10.1140/epjc/s10052-013-2711-4. arXiv:1305.1933 [hep-ph]
P. Bechtle, S. Heinemeyer, T. Klingl, T. Stefaniak, G. Weiglein, J. Wittbrodt, HiggsSignals-2: probing new physics with precision Higgs measurements in the LHC 13 TeV era (2020). https://old.inspirehep.net/record/1837082/export/hx. arXiv:2012.09197 [hep-ph]
F.E. Paige, S.D. Protopopescu, H. Baer, X. Tata, ISAJET 7.69: a Monte Carlo event generator for pp, anti-p p, and e+e\(-\) reactions. arXiv:hep-ph/0312045
B. Allanach, S.P. Martin, D.G. Robertson, R. Ruiz de Austri, The inclusion of two-loop SUSYQCD corrections to gluino and squark pole masses in the minimal and next-to-minimal supersymmetric standard model: SOFTSUSY3.7. Comput. Phys. Commun. 219, 339–345 (2017). https://doi.org/10.1016/j.cpc.2017.05.006. arXiv:1601.06657 [hep-ph]
B. Allanach, T. Cridge, The calculation of sparticle and Higgs decays in the minimal and next-to-minimal supersymmetric standard models: SOFTSUSY4.0. Comput. Phys. Commun. 220, 417–502 (2017). https://doi.org/10.1016/j.cpc.2017.07.021. arXiv:1703.09717 [hep-ph]
B. Allanach, M. Bernhardt, Including R-parity violation in the numerical computation of the spectrum of the minimal supersymmetric standard model: SOFTSUSY. Comput. Phys. Commun. 181, 232–245 (2010). https://doi.org/10.1016/j.cpc.2009.09.015. arXiv:0903.1805 [hep-ph]
B. Allanach, C. Kom, M. Hanussek, Computation of neutrino masses in R-parity violating supersymmetry: SOFTSUSY3.2. Comput. Phys. Commun. 183, 785–793 (2012). https://doi.org/10.1016/j.cpc.2011.11.024. arXiv:1109.3735 [hep-ph]
D. Chowdhury, R. Garani, S.K. Vempati, SUSEFLAV: program for supersymmetric mass spectra with seesaw mechanism and rare lepton flavor violating decays. Comput. Phys. Commun. 184, 899–918 (2013). https://doi.org/10.1016/j.cpc.2012.10.031. arXiv:1109.3551 [hep-ph]
A. Djouadi et al., SuSpect3, in Les Houches 2011: Physics at TeV colliders, New Physics Working Group Report (2012), pp. 92–95. arXiv:1203.1488 [hep-ph]
A. Djouadi, J. Kalinowski, M. Spira, HDECAY: a program for Higgs boson decays in the standard model and its supersymmetric extension. Comput. Phys. Commun. 108, 56–74 (1998). https://doi.org/10.1016/S0010-4655(97)00123-9. arXiv:hep-ph/9704448
A. Djouadi, J. Kalinowski, M. Muehlleitner, M. Spira, HDECAY: twenty\(_{++}\) years after. Comput. Phys. Commun. 238, 214–231 (2019). https://doi.org/10.1016/j.cpc.2018.12.010. arXiv:1801.09506 [hep-ph]
J. Baglio, T.N. Dao, M. Mühlleitner, One-loop corrections to the two-body decays of the neutral Higgs bosons in the complex NMSSM. Eur. Phys. J. C80(10), 960 (2020). https://doi.org/10.1140/epjc/s10052-020-08520-8. arXiv:1907.12060 [hep-ph]
T.N. Dao, M. Muhlleitner, S. Patel, K. Sakurai, One-loop corrections to the two-body decays of the charged Higgs bosons in the real and complex NMSSM (2020). https://old.inspirehep.net/record/1838985/export/hx. arXiv:2012.14889 [hep-ph]
S. King, M. Muhlleitner, R. Nevzorov, K. Walz, Exploring the CP-violating NMSSM: EDM constraints and phenomenology. Nucl. Phys. B 901, 526–555 (2015). https://doi.org/10.1016/j.nuclphysb.2015.11.003. arXiv:1508.03255 [hep-ph]
G. Belanger, F. Boudjema, A. Pukhov, A. Semenov, MicrOMEGAs: a program for calculating the relic density in the MSSM. Comput. Phys. Commun. 149, 103–120 (2002). https://doi.org/10.1016/S0010-4655(02)00596-9. arXiv:hep-ph/0112278
G. Belanger, F. Boudjema, A. Pukhov, A. Semenov, MicrOMEGAs 2.0: a program to calculate the relic density of dark matter in a generic model. Comput. Phys. Commun. 176, 367–382 (2007). https://doi.org/10.1016/j.cpc.2006.11.008. arXiv:hep-ph/0607059
G. Bélanger, F. Boudjema, A. Goudelis, A. Pukhov, B. Zaldivar, micrOMEGAs5.0: freeze-in. Comput. Phys. Commun. 231, 173–186 (2018). https://doi.org/10.1016/j.cpc.2018.04.027. arXiv:1801.03509 [hep-ph]
G. Belanger, F. Boudjema, C. Hugonie, A. Pukhov, A. Semenov, Relic density of dark matter in the NMSSM. JCAP 09, 001 (2005). https://doi.org/10.1088/1475-7516/2005/09/001. arXiv:hep-ph/0505142
F. Domingo, A new tool for the study of the CP-violating NMSSM. JHEP 06, 052 (2015). https://doi.org/10.1007/JHEP06(2015)052. arXiv:1503.07087 [hep-ph]
U. Ellwanger, C. Hugonie, NMSPEC: a Fortran code for the sparticle and Higgs masses in the NMSSM with GUT scale boundary conditions. Comput. Phys. Commun. 177, 399–407 (2007). https://doi.org/10.1016/j.cpc.2007.05.001. arXiv:hep-ph/0612134
D. Das, U. Ellwanger, A.M. Teixeira, NMSDECAY: a Fortran code for supersymmetric particle decays in the next-to-minimal supersymmetric standard model. Comput. Phys. Commun. 183, 774–779 (2012). https://doi.org/10.1016/j.cpc.2011.11.021. arXiv:1106.5633 [hep-ph]
M. Muhlleitner, A. Djouadi, Y. Mambrini, SDECAY: a Fortran code for the decays of the supersymmetric particles in the MSSM. Comput. Phys. Commun. 168, 46–70 (2005). https://doi.org/10.1016/j.cpc.2005.01.012. arXiv:hep-ph/0311167
I. Jack, D. Jones, A. Kord, Three loop soft running, benchmark points and semiperturbative unification. Phys. Lett. B 579, 180–188 (2004). https://doi.org/10.1016/j.physletb.2003.10.083. arXiv:hep-ph/0308231
I. Jack, D. Jones, A. Kord, Snowmass benchmark points and three-loop running. Ann. Phys. 316, 213–233 (2005). https://doi.org/10.1016/j.aop.2004.08.007. arXiv:hep-ph/0408128
P. Athron, S. King, D. Miller, S. Moretti, R. Nevzorov, The constrained exceptional supersymmetric standard model. Phys. Rev. D 80, 035009 (2009). https://doi.org/10.1103/PhysRevD.80.035009. arXiv:0904.2169 [hep-ph]
C. Degrande, C. Duhr, B. Fuks, D. Grellscheid, O. Mattelaer, T. Reiter, UFO—the universal FeynRules output. Comput. Phys. Commun. 183, 1201–1214 (2012). https://doi.org/10.1016/j.cpc.2012.01.022. arXiv:1108.2040 [hep-ph]
W. Kilian, T. Ohl, J. Reuter, WHIZARD: simulating multi-particle processes at LHC and ILC. Eur. Phys. J. C 71, 1742 (2011). https://doi.org/10.1140/epjc/s10052-011-1742-y. arXiv:0708.4233 [hep-ph]
A. Pukhov, CalcHEP 2.3: MSSM, structure functions, event generation, batchs, and generation of matrix elements for other packages. arXiv:hep-ph/0412191
A. Belyaev, N.D. Christensen, A. Pukhov, CalcHEP 3.4 for collider physics within and beyond the Standard Model. Comput. Phys. Commun. 184, 1729–1769 (2013). https://doi.org/10.1016/j.cpc.2013.01.014. arXiv:1207.6082 [hep-ph]
J .E. Camargo-Molina, B. O’Leary, W. Porod, F. Staub, Vevacious: A Tool For Finding The Global Minima Of One-Loop Effective Potentials With Many Scalars. Eur. Phys. J. C73(10), 2588 (2013). https://doi.org/10.1140/epjc/s10052-013-2588-2. arXiv:1307.1477 [hep-ph]
T. Hahn, Generating Feynman diagrams and amplitudes with FeynArts 3. Comput. Phys. Commun. 140, 418–431 (2001). https://doi.org/10.1016/S0010-4655(01)00290-9. arXiv:hep-ph/0012260
A. Vicente, FlavorKit: a brief overview. Nucl. Part. Phys. Proc. 273–275, 1423–1428 (2016). https://doi.org/10.1016/j.nuclphysbps.2015.09.230. arXiv:1410.2099 [hep-ph]
M.D. Goodsell, S. Liebler, F. Staub, Generic calculation of two-body partial decay widths at the full one-loop level. Eur. Phys. J. C 77(11), 758 (2017). https://doi.org/10.1140/epjc/s10052-017-5259-x. arXiv:1703.09237 [hep-ph]
M.D. Goodsell, F. Staub, Unitarity constraints on general scalar couplings with SARAH. Eur. Phys. J. C 78(8), 649 (2018). https://doi.org/10.1140/epjc/s10052-018-6127-z. arXiv:1805.07306 [hep-ph]
M.D. Goodsell, R. Moutafis, How heavy can dark matter be? Constraining colourful unitarity with SARAH. arXiv:2012.09022 [hep-ph]
Acknowledgements
The authors of this report wish to thank all of the colleagues who, directly or indirectly, contributed over the past seven years to the progress of the Higgs-mass calculations in SUSY models and to the success of the KUTS initiative. The work of P.S. and M.Go. has been supported in part by the French “Agence Nationale de la Recherche” (ANR), in the context of the LABEX ILP (ANR-11-IDEX-0004-02, ANR-10-LABX-63) and of the grant “HiggsAutomator” (ANR-15-CE31-0002). The work of S.H. has been supported in part by the MEINCOP (Spain) under contract FPA2016-78022-P and under contract PID2019-110058GB-C21, in part by the Spanish Agencia Estatal de Investigación (AEI), in part by the EU Fondo Europeo de Desarrollo Regional (FEDER) through the project FPA2016-78645-P, in part by the “Spanish Red Consolider MultiDark” FPA2017-90566-REDC, and in part by the AEI through the grant IFT Centro de Excelencia Severo Ochoa SEV-2016-0597. H.B., T.B., J.B., P.D., D.M., I.S. and G.W. acknowledge support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC 2121 “Quantum Universe” – 390833306. The work of H.E.H. has been partially supported by the U.S. Department of Energy Grant DE-SC0010107. The work of R.H., M.M., A.V., J.K. and M.Ga. has been supported by the DFG Grant 396021762 – TRR 257 “Particle Physics Phenomenology after the Higgs Discovery”. The work of R.H. and S.P. has also been supported by the BMBF Grant 05H18PACC2. G.L. acknowledges support by the Samsung Science and Technology Foundation under Project Number SSTF-BA1601-07, a Korea University Grant, and the support of the U.S. National Science Foundation through grant PHY-1719877. G.L. is grateful to the Technion–Israel Institute of Technology and the University of Toronto for partial support during completion of this work. The work of H.R. and N.M. was partially funded by the Danish National Research Foundation, grant number DNRF90. H.R. is also supported by the German Federal Ministry for Education and Research (BMBF) under contract number 05H18VFCA1. Part of this work was supported by a STSM Grant from COST Action CA16201 PARTICLEFACE. D.S. and T.K. acknowledge support by the DFG grant STO 876/2-2. C.E.M.W. is supported in part by the U.S. Department of Energy under contracts DEAC02-06CH11357 at Argonne and by the DOE grant DE-SC0013642 at the University of Chicago. The work of B.C.A has been partially supported by STFC Consolidated HEP theory grants ST/P000681/1 and ST/T000694/1. The work of S.B. has been supported in part by the Research Executive Agency (REA) of the European Union through the ERC Advanced Grants MC@NNLO (340983) and MathAm (395568). The work of T.N.D. is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under Grant number 103.01-2020.17. F.D. acknowledges support of the DFG grant SFB CRC-110 “Symmetries and the Emergence of Structure in QCD”.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editors: P. Slavich and S. Heinemeyer.
S. Borowka, P. Drechsel, L. Mihaila, N. Murphy, K. Nickel, F. Staub: Former academic affiliation.
Appendix A: Survey of public codes for the Higgs-mass calculation
Appendix A: Survey of public codes for the Higgs-mass calculation
In the body of the report we mentioned several public codes that provide a precise calculation of the Higgs masses in SUSY models. Most of these codes compute in addition the full spectrum of SUSY particle masses, as well as a number of other observables such as, e.g., the decays widths of the Higgs bosons. They are often denoted as “spectrum generators”. Moreover, there exist “spectrum-generator generators” that can compute the mass spectrum of a general renormalizable theory, and produce stand-alone codes dedicated to specific models.
In this appendix we provide a survey of public codes for the Higgs-mass calculation, grouping themFootnote 35 according to whether their results apply to the MSSM, to some non-minimal SUSY extension of the SM, or to a general renormalizable theory. For each code, we structure the description in the following fields:
- URL::
-
The address of the code’s web page.
- Model(s)::
-
The model (or models) for which the code computes the mass spectrum.
- Inputs::
-
General description of the input parameters required for the calculation. We specify whether the code accepts input parameters at some “high scale” (e.g., the GUT scale) from which they are evolved down with appropriate RGEs, or instead it accepts only “low-scale” inputs. The latter typically consist of OS parameters or running parameters at a scale comparable to the SUSY masses. Note that the codes also require a set of SM input parameters, which we refrain from listing here.
- Outputs::
-
General description of the results of the Higgs-mass calculation.
- CPV/FLV/RPV::
-
Common approximations in the Higgs-mass calculation consist in neglecting CP violation (CPV), flavor mixing in the sfermion mass matrices (FLV) and \(R\)-parity violation (RPV). We specify whether, and to what extent, these effects can be included in the calculation.
- SLHA format::
-
We specify whether the code accepts the SLHA format for the input and/or output parameters. In particular, the SLHA1 format [145] is restricted to the “vanilla” MSSM, whereas the SLHA2 format [146] covers also a number of extensions.
- Strategy::
-
The strategy adopted in the calculation of the Higgs masses. In particular, we specify whether the calculation follows a FO, EFT or hybrid approach.
- Corrections::
-
Details on the radiative corrections included in the Higgs-mass calculation. We recall that the “gaugeless limit” consists in neglecting all corrections that involve the EW gauge couplings. The “MSSM limit” of the NMSSM corresponds to taking \(v_s\rightarrow \infty \), with both \(\lambda v_s\) and \(\kappa v_s\) held fixed.
- Other features::
-
Information on additional outputs of the code beyond the Higgs-mass calculation.
- Extendability::
-
When relevant, we mention how the code can be extended to cover different models, include additional corrections and so on.
- Language::
-
Programming language, user interfaces and other technical information on the code.
- What to cite::
-
A list of references to cite when the results of the code are included in a publication (sometimes as a series of options depending on which features are employed).
1.1 A.1 MSSM codes
The MSSM is the simplest and certainly the most-studied SUSY extension of the SM. Indeed, some of the codes collected in this section include corrections to the Higgs masses that are currently not available for any other BSM model, namely two-loop momentum-dependent corrections and three-loop corrections. We include in this section also codes that deal with high-energy extensions of the MSSM (namely, seesaw models for the generation of the neutrino masses) since the particle content at the low scale – and thus the calculation of the Higgs masses – is the same as in the MSSM. Finally, we remark that both of the “spectrum-generator generators” listed in Sect. 1 can be used to produce codes that compute the Higgs mass spectrum of the MSSM.
1.1.1 A.1.1 CPSuperH
CPSuperH performs a FO calculation of the masses and mixing matrices of the Higgs bosons in the MSSM with complex parameters. It also computes a number of CPV and flavor observables.
- URL::
- Model(s)::
-
MSSM.
- Inputs::
-
Soft SUSY-breaking parameters, \(\mu \), \(\tan \beta \) and \(M_{H^\pm }\). The SUSY-breaking parameters in the stop sector are defined in the \(\overline{\text {MS}}\) scheme, at a scale of the order of the SUSY masses. High-scale boundary conditions are not supported.
- Outputs::
-
Pole Higgs masses and mixing matrix in the Higgs sector.
- CPV/FLV/RPV::
-
Complex parameters are supported. FLV and RPV are not supported.
- SLHA format::
-
Not supported.
- Strategy::
-
FO calculation of the Higgs masses and mixing.
- Corrections::
-
Full one-loop corrections, leading-logarithmic two-loop effects in the gaugeless limit.
- Other features::
-
Higgs couplings and branching ratios. Muon, electron, thallium, neutron, mercury, radium, and deuteron electric dipole moments (EDMs). Flavor observables such as \(B\rightarrow X_s \gamma \), \(B_s\rightarrow \mu \mu \), \(B_u\rightarrow \tau \nu \), \(B_d\rightarrow \tau \tau \), CP asymmetry in \(B\rightarrow X_s\gamma \), and the SUSY contributions to the \(B_d\) and \(B_s\) mixings. The anomalous magnetic dipole moment \((g-2)\) of the muon.
- Extendability::
-
A beta version with EFT resummation of the large logarithmic corrections, allowing to push the SUSY masses to arbitrary values, is available upon request.
- Language::
-
CPSuperH is written in Fortran.
- What to cite::
1.1.2 A.1.2 FeynHiggs
FeynHiggs performs a hybrid calculation of the pole masses and mixing matrices of the Higgs bosons in the MSSM with complex parameters, accounting for the possibility of flavor mixing in the sfermion mass matrices. It also computes a number of additional Higgs-related observables, as well as EW observables and EDMs.
- URL::
- Model(s)::
-
MSSM.
- Inputs::
-
Soft SUSY-breaking parameters, \(\mu \), \(\tan \beta \) and either \(M_A\) or \(M_{H^\pm }\). The SUSY-breaking parameters in the stop sector can be either OS or \(\overline{\text {DR}}\), at a scale of the order of the SUSY masses. High-scale boundary conditions are not supported.
- Outputs::
-
Pole Higgs masses, effective mixing matrix and “Z-factors” in the Higgs sector. Uncertainty estimate of the Higgs-mass predictions.
- CPV/FLV/RPV::
-
Complex parameters and flavor-mixing effects are supported. RPV is not supported.
- SLHA format::
-
SLHA conventions (SLHA1 and SLHA2) for input and output.
- Strategy::
-
FO calculation combined with an EFT calculation (“hybrid” code, see Sect. 5.2). The EFT calculation allows for either one or two light Higgs doublets, with several intermediate steps for the heavier Higgs, gaugino/higgsino and gluino mass scales.
- Corrections::
-
FO calculation: full one-loop corrections, including the effects of flavor mixing in the sfermion sector. Two-loop corrections in the vanishing-momentum and gaugeless limits, neglecting flavor mixing as well as the tau Yukawa coupling. Optionally, two-loop \({{{\mathcal {O}}}}(\alpha _t\alpha _s)\) momentum-dependent effects. EFT calculation: full NLL resummation of the large logarithmic corrections, NNLL resummation in the gaugeless limit, and three-loop \({{{\mathcal {O}}}}(y_t^4\,g_s^4)\) threshold corrections to \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) (the latter from Himalaya).
- Other features::
-
Calculation of Higgs widths and branching ratios (SM and MSSM), approximation for the LHC production cross sections, flavor observables, muon \((g-2)\), \(\Delta \rho \), \(M_W\), \(\sin ^2 {\theta _{\text {w}}}\), and EDMs. FeynHiggs can be directly linked to HiggsBounds [314,315,316,317] and HiggsSignals [318, 319] to check for collider constraints on the MSSM Higgs sector via a FeynHiggs-specific compiler option in those codes.
- Extendability::
-
An extension of FeynHiggs to the NMSSM, based on Ref. [160], is currently under construction.
- Language::
-
FeynHiggs is written in Fortran. It has four modes of operation: as a command-line tool, as a library for use with Fortran or C/C++, as a Mathematica program, and as a web page at http://feynhiggs.de/fhucc.
- What to cite::
-
Standard: Refs. [29, 42, 44, 64, 88, 189, 278, 288]. Additional references depending on usage: for the momentum-dependent two-loop corrections, Refs. [58, 62]; in case of complex parameters, Refs. [89, 98, 99, 239]; in case of the 2HDM as low-energy model, Refs. [246, 248, 291]; in the case of several Higgs bosons close in mass, Ref. [289]; for the estimate of the theory uncertainty, Ref. [290].
1.1.3 A.1.3 H3m
H3m computes the mass of the lighter CP-even Higgs boson in the MSSM, including the three-loop \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\) corrections from Refs. [67, 68].
- URL::
- Model(s)::
-
MSSM.
- Inputs::
-
Soft SUSY-breaking parameters, \(\mu \), \(\tan \beta \) and \(M_A\). The SUSY-breaking parameters are defined in the \(\overline{\text {DR}}\) scheme, at a scale \(M_S\) of the order of the SUSY masses. High-scale boundary conditions are not supported.
- Outputs::
-
Pole mass of the lighter CP-even Higgs boson.
- CPV/FLV/RPV::
-
Not supported.
- SLHA format::
-
Input file in the SLHA1 format.
- Strategy::
-
FO calculation of the lighter Higgs mass. The three-loop corrections are available in the form of asymptotic expansions for a number of mass hierarchies. The code determines the hierarchy that best fits the considered point of the MSSM parameter space. The one-and two-loop corrections are obtained via a call to FeynHiggs, and those involving top/stop loops are adapted to the \(\overline{\text {DR}}\) scheme.
- Corrections::
-
Full one-loop corrections, two-loop corrections in the vanishing-momentum and gaugeless limits (neglecting also the tau Yukawa coupling), three-loop \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\) corrections from Refs. [67, 68].
- Language::
-
H3m is a Mathematica program.
- What to cite::
1.1.4 A.1.4 Himalaya
Himalaya is a library of functions allowing for the inclusion of the three-loop corrections of Refs. [67, 68] in existing FO or EFT calculations of the lighter CP-even Higgs mass that adopt the \(\overline{\text {DR}}\) renormalization scheme for the SUSY parameters.
- URL::
- Model(s)::
-
MSSM.
- Inputs::
-
Soft SUSY-breaking parameters, \(\mu \), \(\tan \beta \) and \(M_A\). The SUSY-breaking parameters are defined in the \(\overline{\text {DR}}\) scheme, at a scale \(M_S\) of the order of the SUSY masses. High-scale boundary conditions are not supported. The code also requires the gauge and Yukawa couplings of the MSSM, as well as the parameter v, all defined in the \(\overline{\text {DR}}\) scheme at the scale \(M_S\).
- Outputs::
-
One-, two- and three-loop corrections to \(M_h\) for the FO calculation in the \(\overline{\text {DR}}\) scheme. One-, two- and three-loop contributions to \(\Delta \lambda \) for the EFT calculation. Estimates of the uncertainty associated with the expansion in mass ratios of the three-loop corrections.
- CPV/FLV/RPV::
-
Not supported.
- SLHA format::
-
Not supported.
- Strategy::
-
FO calculation: the three-loop corrections to \(M_h\) from Refs. [67, 68] are available in the form of asymptotic expansions for a number of mass hierarchies. The code determines the hierarchy that best fits the considered point of the MSSM parameter space. EFT calculation: the three-loop \({{{\mathcal {O}}}}(y_t^4 g_s^4)\) contribution to \(\Delta \lambda \) is extracted from the \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\) correction to \(M_h\) as described in Ref. [236].
- Corrections::
-
FO calculation: full one-loop, gaugeless and vanishing-momentum two-loop, and \({{{\mathcal {O}}}}(\alpha _t\alpha _s^2)\) three-loop contributions to \(\Delta M_h^2\). EFT calculation: full one-loop, gaugeless two-loop and \({{{\mathcal {O}}}}(y_t^4 g_s^4)\) three-loop contributions to \(\Delta \lambda \).
- Language::
-
Himalaya is a library of C++ functions. A Mathematica interface is provided.
- What to cite::
-
Refs. [70, 236] for the code and Refs. [67, 68] for the original three-loop calculation.
1.1.5 A.1.5 ISAJET
ISAJET is a package that generates \(e^+e^-\), pp, and \(p\bar{p}\) collider events for a variety of processes, both in the SM and in a number of BSM models which include the MSSM. The SUSY mass spectrum and the Higgs masses are calculated by the modules ISASUSY and ISASUGRA. Also provided is the module IsaTools, which computes several SUSY-related observables.
- URL::
- Model(s)::
-
MSSM.
- Inputs::
-
The module ISASUSY computes the mass spectrum of the MSSM starting from Lagrangian parameters at the weak scale. It requires as input the soft SUSY-breaking parameters, plus \(\mu \), \(\tan \beta \) and \(M_A\). The module ISASUGRA obtains the soft SUSY-breaking parameters via RG evolution starting from a set of high-scale boundary conditions. In this case \(\mu ^2\) and \(B_\mu \) are fixed by the minimum conditions of the Higgs potential. Thirteen variants of high-scale conditions are available, inspired by the gravity-mediated (SUGRA), gauge-mediated (GMSB), anomaly-mediated (AMSB) and generalized mirage-mediated mechanisms for SUSY breaking.
- Outputs::
-
Loop-corrected masses and effective couplings of the Higgs bosons.
- CPV/FLV/RPV::
-
Flavor-mixing effects in the RG evolution (but not in the Higgs-mass calculation) are optionally accounted for by the module RGEFLAV. CPV and RPV are not supported.
- SLHA format::
-
The SLHA1 format is supported for the output.
- Strategy::
-
FO calculation of the Higgs masses and mixing in the effective potential approach, expressing the corrections in terms of the running couplings of the MSSM.
- Corrections::
-
Two-loop RGEs for the MSSM. One-loop top/stop and bottom/sbottom contributions to the neutral and charged Higgs masses in the vanishing-momentum limit.
- Other features::
-
ISAJET generates hadron and \(e^+e^-\) collider events. ISASUSY and ISASUGRA compute the full spectrum of SUSY masses and decay rates. ISASUGRA also estimates, for a given choice of high-scale boundary conditions, the degree of fine-tuning required to maintain the weak scale around 100 GeV. IsaTools computes various SUSY-related observables, namely: the relic density of neutralino Dark Matter (DM); the cross sections for direct DM detection; several B-decay rates; the muon \((g - 2)\).
- Language::
-
ISAJET and its various SUSY modules are written in Fortran.
- What to cite::
-
Ref. [320].
1.1.6 A.1.6 MhEFT
MhEFT performs an EFT calculation of the CP-even Higgs masses in the MSSM with heavy SUSY, covering also scenarios in which the mass of the heavier Higgs doublet lies below the SUSY scale. The code also computes the decay widths of the lighter CP-even Higgs boson.
- URL::
- Model(s)::
-
MSSM.
- Inputs::
-
Soft SUSY-breaking parameters, \(\mu \), \(\tan \beta \) and \(M_A\). A common mass parameter \(M_S\) is assumed for all of the sfermions and for the gluino. All parameters are renormalized in the \(\overline{\text {MS}}\) scheme. The SUSY parameters are defined at the scale \(Q=M_S\), while \(\tan \beta \) and \(M_A\) are defined at the scale \(Q=M_A\).
- Outputs::
-
CP-even Higgs masses \(M_h\) and \(M_H\). Effective mixing angles \(\alpha \) and \(\sin (\beta -\alpha )\). The latter are also used to obtain the couplings of the lighter CP-even Higgs boson to third-generation fermions (normalized to their SM values) and the Hhh coupling.
- CPV/FLV/RPV::
-
Not supported.
- SLHA format::
-
Not supported.
- Strategy::
-
EFT calculation of the Higgs masses: SUSY particles decoupled at \(Q=M_S\), leaving the type-II 2HDM as low-energy model, possibly augmented with light higgsinos and EW gauginos. Intermediate threshold for the heavy Higgs doublet at \(Q=M_A\). Pole mass of the lighter CP-even Higgs boson computed at \(Q=M_t\).
- Corrections::
-
Two-loop RGEs of the type-II 2HDM, plus approximate one-loop effects of higgsinos and gauginos, for the evolution of the couplings between \(Q=M_S\) and \(Q=M_A\); three-loop RGEs of the SM below \(Q=M_A\). Threshold corrections \(\Delta \lambda _i\) at the scale \(Q=M_S\): one-loop stop, sbottom and stau contributions; two-loop \({{{\mathcal {O}}}}(y_t^4 g_s^2)\) contributions; approximate inclusion of the two-loop \({{{\mathcal {O}}}}(y_t^6)\) contributions in the limit \(M_A=M_S\). One-loop threshold corrections to the Yukawa couplings at \(Q=M_S\). One-loop correction to \(M_h\) computed in the SM at \(Q=M_t\).
- Other features::
-
Total width of the lighter CP-even Higgs boson. Partial widths, branching ratios, and ratios to the SM values for the decays of the lighter CP-even Higgs boson to third-generation fermions.
- Language::
-
MhEFT is a Mathematica program.
- What to cite::
1.1.7 A.1.7 SOFTSUSY
SOFTSUSY computes the mass spectrum of Higgs bosons and SUSY particles in the MSSM and in the NMSSM, accounting for the possibility of \(R\)-parity violation and of flavor mixing in the sfermion mass matrices. It accepts the SUSY parameters at an arbitrary (high or low) input scale. It also computes the widths and branching ratios for the decays of Higgs bosons and SUSY particles.
- URL::
- Model(s)::
-
MSSM and NMSSM. For the latter, see Sect. 1.
- Inputs::
-
Soft SUSY-breaking parameters in the \(\overline{\text {DR}}\) scheme at a user-defined scale \(Q_{{\scriptscriptstyle \mathrm{in}}}\), spanning from the EW scale to the GUT scale (templates for SUGRA, GMSB and AMSB boundary conditions are available). The parameter \(\tan \beta \) is given either at \(Q_{{\scriptscriptstyle \mathrm{in}}}\) or at \(Q=M_Z\). The parameters \(\mu ^2\) and \(B_\mu \) are fixed by the minimum conditions of the Higgs potential. Alternatively, \(\mu \) and either \(B_\mu \) or the pole mass \(M_A\) are given as input, and the soft SUSY-breaking parameters \(m_{H_1}^2\) and \(m_{H_2}^2\) are fixed by the minimum conditions.
- Outputs::
-
Pole Higgs masses, effective mixing angle \(\alpha \) in the neutral CP-even sector. Estimate of the theory uncertainty of the prediction for \(M_h\).
- CPV/FLV/RPV::
-
Flavor mixing in the sfermion mass matrices and \(R\)-parity-violating couplings are accounted for in the RG evolution of the parameters and in the determination of the SUSY mass spectrum, but their effects are not included in the radiative corrections to the Higgs masses. CPV is not supported.
- SLHA format::
-
SLHA conventions (SLHA1 and SLHA2) for input and output. Command-line input is also possible.
- Strategy::
-
FO calculation of the Higgs masses. The gauge and Yukawa couplings of the MSSM are extracted from the SM input parameters at the scale \(Q=M_Z\), while the soft SUSY-breaking parameters are given as input at \(Q_{{\scriptscriptstyle \mathrm{in}}}\). All parameters are evolved with the RGEs of the MSSM to the scale \(Q_{{\scriptscriptstyle \mathrm{EWSB}}}\) where the minimum conditions of the potential are imposed and the whole mass spectrum of the model is computed, including the radiative corrections. This scale is set by default to the geometric mean of the stop masses, but can be modified by the user.
- Corrections::
-
Two-loop RGEs for the MSSM, with optional inclusion of three-loop effects. The gauge and Yukawa couplings of the MSSM are extracted from the SM inputs at one loop, with optional inclusion of two-loop effects. Full one-loop corrections to the Higgs masses. Two-loop corrections to the neutral Higgs masses in the vanishing-momentum and gaugeless limits. Optional inclusion of the three-loop \({\mathcal {O}}(\alpha _t\alpha _s^2)\) corrections to \(M_h\) from Himalaya.
- Other features::
-
Full mass spectrum for the SUSY particles at one loop, with optional inclusion of two-loop SUSY-QCD corrections. In the presence of \(R\)-parity violation, the neutrino masses and mixing are also computed. Decay widths and branching ratios for SUSY particles and Higgs bosons are computed in the R-parity-conserving case. SOFTSUSY also estimates, for a given choice of high-scale boundary conditions, the degree of fine-tuning required to maintain the weak scale around 100 GeV.
- Language::
-
SOFTSUSY is written in C++.
- What to cite::
-
Standard: Ref. [45], which is the SOFTSUSY manual for the \(R\)-parity conserving MSSM. Additional references depending on usage: for the effects of three-loop RGEs and two-loop threshold corrections to gauge and Yukawa couplings, Ref. [46]; for the two-loop SUSY-QCD corrections to squark and gluino masses, Ref. [321]; for the decay calculations, Ref. [322]; for the R-parity-violating aspects, Ref. [323]; for the neutrino masses and mixing, Refs. [323, 324].
1.1.8 A.1.8 SPheno
SPheno computes the mass spectrum of Higgs bosons and SUSY particles in the MSSM, accounting for the possibility of \(R\)-parity- and lepton-flavor-violating terms and of flavor mixing in the sfermion mass matrices. It accepts the input SUSY parameters at an arbitrary (high or low) scale. It also computes the widths and branching ratios for the decays of Higgs bosons and SUSY particles, and a number of flavor-related observables.
- URL::
- Model(s)::
-
The MSSM, plus several seesaw extensions with additional states at the high scale. The Higgs-mass calculation in the seesaw extensions is the same as in the MSSM.
- Inputs::
-
Soft SUSY-breaking parameters in the \(\overline{\text {DR}}\) scheme at a user-defined scale \(Q_{{\scriptscriptstyle \mathrm{in}}}\), spanning from the EW scale to the GUT scale (templates for SUGRA, GMSB and AMSB boundary conditions are available). The parameter \(\tan \beta \) is given either at \(Q_{{\scriptscriptstyle \mathrm{in}}}\) or at \(Q=M_Z\). The parameters \(\mu ^2\) and \(B_\mu \) are fixed by the minimum conditions of the Higgs potential. Alternatively, \(\mu \) and either \(B_\mu \) or the pole mass \(M_A\) are given as input, and the soft SUSY-breaking parameters \(m_{H_1}^2\) and \(m_{H_2}^2\) are fixed by the minimum conditions.
- Outputs::
-
Pole Higgs masses, effective mixing angle \(\alpha \) in the neutral CP-even sector.
- CPV/FLV/RPV::
-
Flavor mixing in the sfermion mass matrices and the subset of \(R\)-parity-violating couplings that also violate lepton flavor are accounted for in the RG evolution of the parameters and in the determination of the SUSY mass spectrum, but their effects are not fully included in the radiative corrections to the Higgs masses. Complex parameters are supported, but the mixing between neutral CP-even and CP-odd Higgs bosons is not implemented.
- SLHA format::
-
SLHA conventions (SLHA1 and SLHA2) for input and output.
- Strategy::
-
FO calculation of the Higgs masses. The gauge and Yukawa couplings of the SM are extracted from the SM input parameters at the scale \(Q=M_Z\), evolved with the RGEs of the SM to a higher scale \(Q_{{\scriptscriptstyle \mathrm{EWSB}}}\) and there converted into their MSSM counterparts. Alternatively, they are converted directly at \(Q=M_Z\) and then evolved up to \(Q_{{\scriptscriptstyle \mathrm{EWSB}}}\) with the RGEs of the MSSM. The soft SUSY-breaking parameters are given as input at \(Q_{{\scriptscriptstyle \mathrm{in}}}\) and evolved with the RGEs of the MSSM to \(Q_{{\scriptscriptstyle \mathrm{EWSB}}}\). At this scale, which is set by default to the geometric mean of the stop masses but can be modified by the user, the minimum conditions of the potential are imposed and the whole mass spectrum of the model is computed, including the radiative corrections. In scenarios with heavy SUSY, a hybrid calculation of \(M_h\) is also available, providing a LL resummation of the large logarithmic corrections (see Sect. 5.3).
- Corrections::
-
Two-loop RGEs for the MSSM, three-loop RGEs for the SM. The gauge and Yukawa couplings of the SM are extracted from the SM inputs at one loop, but the extraction of the top Yukawa coupling includes also two-loop QCD effects. Full one-loop corrections to the Higgs masses, including the effects of flavor mixing in the sfermion sector. Two-loop corrections to the neutral Higgs masses in the vanishing-momentum and gaugeless limits, including only the third-generation Yukawa couplings. In the RPV case the Higgs-mass calculation includes only the one-loop top/stop and bottom/sbottom corrections in the effective potential approach.
- Other features::
-
Full mass spectrum for the SUSY particles at one loop. In the RPV and seesaw extensions, masses and mixing matrix of the neutrinos are also provided. Decay widths and branching ratios for SUSY particles and Higgs bosons. A large set of flavor observables (quark- and lepton-flavor-violating processes), muon \((g-2)\), \(\Delta \rho \) and EDMs.
- Extendability::
-
Versions of SPheno for SUSY models beyond the MSSM can be produced with SARAH, see Sect. 1.
- Language::
-
SPheno is written in Fortran 90.
- What to cite::
-
Standard: Refs. [48, 49]. For the hybrid calculation of \(M_h\), Ref. [294].
1.1.9 A.1.9 SuSeFLAV
SuSeFLAV computes the mass spectrum of Higgs bosons and SUSY particles in the MSSM and in its seesaw extension, starting from high-scale SUSY parameters. The code also computes a number of low-energy observables and, in the seesaw extension, lepton-flavor violating decays.
- URL::
- Model(s)::
-
The MSSM and its seesaw extension with three heavy right-handed neutrino superfields. The Higgs-mass calculation in the latter is the same as in the MSSM.
- Inputs::
-
The soft SUSY-breaking parameters are given as input in the \(\overline{\text {DR}}\) scheme at a high scale, namely the GUT scale for SUGRA boundary conditions and the messenger scale for GMSB boundary conditions. The parameter \(\tan \beta \) is given at \(Q=M_Z\). The parameters \(\mu ^2\) and \(B_\mu \) are fixed by the minimum conditions of the Higgs potential.
- Outputs::
-
Pole Higgs masses, effective mixing angle \(\alpha \) in the neutral CP-even sector.
- CPV/FLV/RPV::
-
Flavor mixing in the sfermion mass matrices is accounted for in the RG evolution of the parameters and in the determination of the SUSY mass spectrum at tree level, but its effects are not included in the radiative corrections. RPV and CPV are not supported.
- SLHA format::
-
SLHA2 conventions for input and output.
- Strategy::
-
FO calculation of the Higgs masses. The gauge and Yukawa couplings of the MSSM are extracted from the SM input parameters at the scale \(Q=M_Z\), while the soft SUSY-breaking parameters are given as input at the high scale. In the seesaw extension, the three right-handed neutrino superfields are decoupled from the RGEs at their respective mass scales. All parameters are evolved to the scale \(Q_{{\scriptscriptstyle \mathrm{EWSB}}}\), which is fixed as the geometric mean of the stop masses. At this scale the minimum conditions of the potential are imposed and the whole mass spectrum of the model is computed, including the radiative corrections.
- Corrections::
-
Two-loop RGEs for the MSSM and for the seesaw extension. The gauge and Yukawa couplings of the MSSM are extracted from the SM inputs at one loop, but the extraction of the top Yukawa coupling includes also the SM part of the two-loop QCD effects. Full one-loop corrections to the Higgs masses. Two-loop corrections to the neutral Higgs masses in the vanishing-momentum and gaugeless limits.
- Other features::
-
Full mass spectrum for the SUSY particles at one loop. SuSeFLAV also computes several low-energy observables, namely \(\Delta \rho \), the muon \((g-2)\) and \(B\rightarrow X_s\gamma \), and it estimates the degree of fine-tuning required to maintain the weak scale around 100 GeV. In the seesaw extension, the code computes also a number of lepton-flavor violating decays of the muon and the tau.
- Extendability::
-
A new version is under development, covering scenarios where the sfermions of the first two generations are heavy and also computing the decay rate of the proton.
- Language::
-
SuSeFLAV is written in Fortran 95.
- What to cite::
-
Ref. [325].
1.1.10 A.1.10 SuSpect
SuSpect computes the mass spectrum of Higgs bosons and SUSY particles in the MSSM. It accepts the SUSY parameters at an arbitrary (high or low) input scale.
- URL::
- Model(s)::
-
MSSM.
- Inputs::
-
Soft SUSY-breaking parameters in the \(\overline{\text {DR}}\) scheme at a user-defined scale \(Q_{{\scriptscriptstyle \mathrm{in}}}\), spanning from the EW scale to the GUT scale (templates for SUGRA, GMSB and AMSB boundary conditions are available). The parameter \(\tan \beta \) is given as input at \(Q=M_Z\). The parameters \(\mu ^2\) and \(B_\mu \) are fixed by the minimum conditions of the Higgs potential. Alternatively, \(M_A\) (either pole or running) and \(\mu \) are given as input, and the soft SUSY-breaking parameters \(m_{H_1}^2\) and \(m_{H_2}^2\) are fixed by the minimum conditions.
- Outputs::
-
Pole Higgs masses, effective mixing angle \(\alpha \) in the neutral CP-even sector.
- CPV/FLV/RPV::
-
Not supported.
- SLHA format::
-
SLHA1 conventions for input and output.
- Strategy::
-
FO calculation of the Higgs masses. The gauge and Yukawa couplings of the MSSM are extracted from the SM input parameters at the scale \(Q=M_Z\), while the soft SUSY-breaking parameters are given as input at \(Q_{{\scriptscriptstyle \mathrm{in}}}\). All parameters are evolved with the RGEs of the MSSM to the scale \(Q_{{\scriptscriptstyle \mathrm{EWSB}}}\), where the minimum conditions of the potential are imposed and the whole mass spectrum of the model is computed, including the radiative corrections. This scale is set by default to the geometric mean of the stop masses, but can be modified by the user.
- Corrections::
-
Two-loop RGEs for the MSSM. The gauge and Yukawa couplings of the MSSM are extracted from the SM inputs at one loop, but the extraction of the top Yukawa coupling includes also the SM part of the two-loop QCD effects. Full one-loop corrections to the Higgs masses. Two-loop corrections to the neutral Higgs masses in the vanishing-momentum and gaugeless limits.
- Other features::
-
Full mass spectrum for the SUSY particles at one loop. Check of precision observables such as the muon \((g-2)\) and \(B\rightarrow X_s\gamma \). Estimate of the degree of fine-tuning required to maintain the weak scale around 100 GeV.
- Language::
-
Version 2 of SuSpect is written in Fortran, while version 3, available since 2014, is written in C++. The two versions are developed in parallel.
- What to cite::
-
Standard: Ref. [47]. For version 3, cite also Ref. [326].Footnote 36
1.1.11 A.1.11 SUSYHD
SusyHD performs an EFT computation of the lighter CP-even Higgs mass of the MSSM in heavy-SUSY scenarios where the SUSY particles and the heavier Higgs doublet are decoupled at a common scale. The code also covers Split-SUSY scenarios where higgsinos and gauginos are decoupled at a lower scale than the heavy scalars.
- URL::
- Model(s)::
-
MSSM.
- Inputs::
-
Soft SUSY-breaking parameters, \(\mu \), \(\tan \beta \) and \(M_A\) in the \(\overline{\text {DR}}\) scheme at a user-defined input scale of the order of the SUSY masses. An OS definition for the parameters in the stop sector is also envisaged, but it leads to a large logarithmic term in the two-loop part of \(\Delta \lambda \).
- Outputs::
-
Pole mass of the lighter CP-even Higgs boson, plus uncertainty estimate.
- CPV/FLV/RPV::
-
Not supported.
- SLHA format::
-
Not supported.
- Strategy::
-
Pure EFT calculation of \(M_h\) with full NLL resummation of the large logarithmic corrections. The EFTs valid below the SUSY scale can be either directly the SM, or Split SUSY followed by the SM. In the former case, a partial NNLL resummation of the large logarithmic corrections is also provided.
- Corrections::
-
Three-loop RGEs for the SM and two-loop RGEs for Split SUSY, neglecting the effects of the Yukawa couplings of the first two generations. The threshold correction to the quartic Higgs coupling includes full one-loop contributions, two-loop \({{{\mathcal {O}}}}(y_t^4 g_s^2)\) contributions and two-loop \({{{\mathcal {O}}}}(y_t^6)\) contributions, the latter in the limit of degenerate masses for the stops and the heavy Higgs doublet. At the EW scale, the running gauge and Yukawa couplings of the SM and the relation between \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}\) and \(M_h\) are determined at two loops from the interpolation formulas of Ref. [191].
- Language::
-
SusyHD is a Mathematica program.
- What to cite::
-
Ref. [234].
1.2 A.2 Beyond-MSSM codes
In this section we collect codes for the computation of the Higgs-mass spectrum in SUSY models that feature an extended particle spectrum with respect to the MSSM. In particular, three of the listed codes are devoted to the NMSSM, and one to the \(\mu \nu \)SSM. We remark that both of the “spectrum-generator generators” listed in Sect. 1 can be used to produce codes that compute the Higgs mass spectrum of the NMSSM, and that SARAH can also produce a code for the \(\mu \nu \)SSM.
1.2.1 A.2.1 munuSSM
munuSSM computes the mass spectrum of the neutral scalars of the \(\mu \nu \)SSM (namely, Higgs bosons and sneutrinos) with full one-loop corrections. It relies on FeynHiggs to include also corrections beyond one loop in the MSSM limit. The code also computes the decays of all non-colored (neutral and charged) scalars.
- URL::
- Model(s)::
-
The \(\mu \nu \)SSM.
- Inputs::
-
The superpotential and soft-SUSY-breaking parameters, the sneutrino vevs and \(\tan \beta \). The non-SM input parameters that determine the tree-level masses of the neutral scalars are defined in the \(\overline{\text {DR}}\) scheme at a scale of the order of the SUSY masses. The soft SUSY-breaking parameters in the stop and sbottom sectors can optionally be defined in the OS scheme. High-scale boundary conditions are not supported.
- Outputs::
-
Pole masses of the eight CP-even and seven CP-odd neutral scalars of the model. Effective couplings of all neutral scalars to SM particles.
- CPV/FLV/RPV::
-
The Higgs and neutrino couplings of the \(\mu \nu \)SSM violate by construction lepton flavor and \(R\)-parity. CPV and flavor violation in the squark sector are not supported.
- SLHA format::
-
Not supported.
- Strategy::
-
FO calculation of the neutral scalar masses in the \(\mu \nu \)SSM, supplemented with higher-order corrections in the MSSM limit through an interface with FeynHiggs.
- Corrections::
-
Full one-loop corrections to the neutral scalar masses in the \(\mu \nu \)SSM. Higher-order corrections included in the MSSM limit: two-loop corrections in the gaugeless and vanishing-momentum limits, and the resummation (full NLL, gaugeless NNLL) of the large logarithmic corrections.
- Other features::
-
The package computes also the decay widths and branching ratios of all non-colored (neutral and charged) scalars. An automated interface to HiggsBounds [314,315,316,317] and HiggsSignals [318, 319] tests the considered scenario against the bounds from Higgs searches at colliders.
- Language::
-
munuSSM is a Python package, but some routines for numerically involved calculations are written in Fortran to allow for quadruple floating-point precision.
- What to cite::
-
Ref. [183] is the manual of munuSSM, and Refs. [181, 182] describe the one-loop calculation of the scalar masses in the \(\mu \nu \)SSM.
1.2.2 A.2.2 NMSSMCALC
NMSSMCALC performs a FO calculation of the Higgs masses in the \(Z_3\)-symmetric NMSSM, allowing for the possibility of CP violation. The code also computes the decay widths and branching ratios of the Higgs bosons, and, in the CPV case, a number of EDMs.
- URL::
- Model(s)::
-
The \(Z_3\)-conserving NMSSM.
- Inputs::
-
The input parameters for the Higgs sector are \(\tan \beta \), \(\lambda \), \(A_\lambda \), \(\mu _{\mathrm {eff}}=\lambda v_s\), \(\kappa \) and \(A_\kappa \), all defined in the \(\overline{\text {DR}}\) scheme at a user-defined scale \(Q_{{\scriptscriptstyle \mathrm{in}}}\). Optionally, \(A_\lambda \) can be replaced by the pole mass \(M_{H^\pm }\). In the CPV case the input parameters can be complex, but the imaginary parts of \(A_\lambda \) and \(A_\kappa \) are fixed by the minimum conditions of the potential; the phase of the vev \(v_2\) must also be supplied. The remaining input parameters are the soft SUSY-breaking masses for gauginos and sfermions, and the trilinear Higgs-sfermion couplings. The parameters in the stop sector can be defined either in the \(\overline{\text {DR}}\) scheme at the scale \(Q_{{\scriptscriptstyle \mathrm{in}}}\) or in the OS scheme. High-scale boundary conditions are not supported.
- Outputs::
-
Pole masses of the Higgs bosons; mixing matrices and “Z-factors” for the CP-even and CP-odd sectors in the CP-conserving case, or \(5\times 5\) mixing matrix and “Z-factors” in the CPV case.
- CPV/FLV/RPV::
-
Complex parameters are supported. FLV and RPV are not supported.
- SLHA format::
-
SLHA2 conventions for input and output.
- Strategy::
-
FO calculation of the Higgs masses and mixing.
- Corrections::
-
Full one-loop corrections to the Higgs masses. Two-loop \({\mathcal {O}}(\alpha _t\alpha _s)\) corrections to the Higgs masses in the vanishing-momentum limit, plus two-loop \({\mathcal {O}}(\alpha _t^2)\) corrections in the vanishing-momentum and MSSM limits.
- Other features::
-
Tree-level mass spectrum for the SUSY particles. Decay widths and branching ratios of the Higgs bosons into all possible two-fermion final states, off-shell decays into heavy quarks and gauge bosons. The two-body decays include all of the available QCD corrections, and those to down-type fermions include also SUSY effects through effective couplings. Decay width and branching ratios of the top quark (relevant in scenarios with light Higgs bosons). In the CPV case, EDMs of electron, neutron, mercury and thallium. The code produces also a table of Higgs couplings that can be passed to HiggsBounds [314,315,316,317] and HiggsSignals [318, 319] to test the considered scenario against the bounds from Higgs searches at colliders.
- Extendability::
-
An extension of the code featuring the full one-loop calculation of the two-body decays is available at the URLhttp://www.itp.kit.edu/~maggie/NMSSMCALCEW.
- Language::
-
NMSSMCALC is written in Fortran.
- What to cite::
-
Standard: the code manual, Ref. [144], plus Refs. [136, 137] for the one-loop corrections to the Higgs masses and Refs. [156, 157] for the two-loop corrections. Additional references depending on usage: for the decay calculation in NMSSMCALC, Refs. [327, 328]; for the decay calculation in NMSSMCALCEW, also Refs. [329, 330]; for the EDMs, Ref. [331].
1.2.3 A.2.3 NMSSMTools
NMSSMTools is a suite of codes for calculating the mass spectrum and the decays of Higgs bosons and SUSY particles in the general NMSSM, with input parameters given either at the SUSY scale or at a high (namely, GUT or messenger) scale.
- URL::
- Model(s)::
-
General NMSSM, with or without \(Z_3\) symmetry.
- Inputs::
-
SUSY-scale mode: the (possibly complex) superpotential and soft SUSY-breaking parameters, as well as \(\tan \beta \) and \(v_s\), are given as input in the \(\overline{\text {DR}}\) scheme at a user-defined scale \(Q_{{\scriptscriptstyle \mathrm{in}}}\) of the order of the SUSY masses. Exceptions are the soft SUSY-breaking masses of the Higgs doublets and of the singlet, which are determined by the minimum condition of the Higgs potential. High-scale mode: the parameters are given as input at the GUT scale or (for GMSB) at the messenger scale. In this case the three parameters that are chosen to be fixed by the minimum conditions of the potential depend on the considered SUSY-breaking mechanism at the high scale.
- Outputs::
-
Pole masses of the Higgs bosons; mixing matrices for the CP-even and CP-odd sectors in the CP-conserving case, or a single \(5\times 5\) mixing matrix in the CPV case.
- CPV/FLV/RPV::
-
Complex parameters are supported. FLV and RPV are not supported.
- SLHA format::
-
SLHA2 conventions for input and output.
- Strategy::
-
FO calculation of the Higgs masses and mixing. The EW gauge couplings and v are extracted from the SM inputs directly at the SUSY scale, whereas the Yukawa and strong-gauge couplings are evolved up from the EW scale.
- Corrections::
-
The two-loop RGEs of the NMSSM are used in the case of high-scale inputs. The extraction of the \(\overline{\text {DR}}\) parameters \((g, g^\prime , v)\) is performed at one loop. The extraction of the top and bottom Yukawa couplings includes also two-loop QCD corrections. Full one-loop corrections to the Higgs masses, including the effect of \(Z_3\)-violating couplings. In the CP-conserving case, two-loop \({{{\mathcal {O}}}}(\alpha _t\alpha _s + \alpha _b\alpha _s)\) corrections to the neutral Higgs masses in the vanishing-momentum limit. The two-loop corrections that involve only the third-family Yukawa couplings are included in the vanishing-momentum and MSSM limits. In the CPV case the two-loop corrections are included only at the leading-logarithmic order.
- Other features::
-
Tree-level mass spectrum for the SUSY particles. Decay widths and branching ratios for the Higgs bosons as well as the SUSY particles. The package includes modules to perform automatic scans of the parameter space, and to check whether a given point is constrained by measured Higgs couplings, collider searches for Higgs bosons and for SUSY particles, K- and B-physics observables, muon \((g-2)\), and EDMs (in the CPV case). It can also be linked to micrOMEGAs [332,333,334], which was adapted to the NMSSM in Ref. [335], to compute the relic density and the direct-detection cross sections of Dark Matter.
- Language::
-
NMSSMTools is written in Fortran.
- What to cite::
-
Standard: Refs. [139, 140]. Additional references depending on usage: in the CPV case, Ref. [336]; for scenarios with GUT-scale inputs, Ref. [337]; for SUSY particle decays, Ref. [338], which was based on Ref. [339]; for Dark Matter, Ref. [335].
1.2.4 A.2.4 SOFTSUSY
SOFTSUSY, whose general features are described in Sect. 1, also allows for the computation of the mass spectrum in the general NMSSM. We describe here the features that are specific to the NMSSM calculation.
- URL::
- Model(s)::
-
General NMSSM, with or without \(Z_3\) symmetry.
- Inputs::
-
In addition to the parameters that are in common with the MSSM, SOFTSUSY requires as input at the scale \(Q_{{\scriptscriptstyle \mathrm{in}}}\) the superpotential and soft SUSY-breaking parameters that involve the singlet. However, three among the Lagrangian parameters are fixed by the minimum conditions of the Higgs potential at the scale \(Q_{{\scriptscriptstyle \mathrm{EWSB}}}\) (e.g., in the \(Z_3\)-conserving NMSSM these are chosen as \(v_s\), \(\kappa \) and \(m_S^2\)).
- Outputs::
-
Pole Higgs masses, effective \(3\times 3\) mixing matrix in the CP-even sector and effective mixing angle in the CP-odd sector.
- CPV/FLV/RPV::
-
Not supported.
- SLHA format::
-
SLHA2 conventions for input and output. Command-line input is also possible.
- Strategy::
-
Same as for the MSSM calculation, see Sect. 1.
- Corrections::
-
Two-loop RGEs for the NMSSM. The gauge and Yukawa couplings are extracted from the SM inputs at one loop, with optional inclusion of two-loop effects in the MSSM limit. The EW parameter v is extracted at one loop. Full one-loop corrections to the Higgs masses, including the effect of \(Z_3\)-violating couplings. Two-loop \({{{\mathcal {O}}}}(\alpha _t\alpha _s + \alpha _b\alpha _s)\) corrections to the neutral Higgs masses in the vanishing-momentum limit. The two-loop corrections that involve only the third-family Yukawa couplings are included in the vanishing-momentum and MSSM limits.
- Other features::
-
Full mass spectrum for the SUSY particles at one loop, with optional inclusion of two-loop SUSY-QCD corrections. Decay widths and branching ratios for SUSY particles and Higgs bosons are also computed.
- What to cite::
1.3 A.3 Generic codes
In this section we describe codes that aim to work for any model, implementing general quantum field theory calculations and adapting them to the model under consideration. These are known as “metacodes” or “spectrum-generator generators”, because they produce as output a stand-alone code for the computation of the mass spectrum of the model that was defined as input by the user. For each metacode, we describe here the Higgs-mass calculation implemented in the generated codes.
1.3.1 A.3.1 FlexibleSUSY
FlexibleSUSY is a package that uses the analytic results for RGEs, tadpoles and self-energies provided by SARAH, as well as numerical routines from SOFTSUSY, to generate stand-alone spectrum generators for any SUSY (or non-SUSY) model defined by the user. When available, higher-order corrections beyond those provided by SARAH are included for specific models. In heavy-SUSY scenarios where the EFT valid below the SUSY scale is the SM, the package also provides a hybrid calculation of the SM-like Higgs mass following the FlexibleEFTHiggs approach (see Sect. 5.3). The module FlexibleBSM generates stand-alone codes for the pure EFT calculation of the Higgs masses, with user-supplied boundary conditions. Finally, the package contains pre-generated spectrum generators for several SUSY models, namely MSSM, NMSSM, E\(_6\)SSM and MRSSM. Below we list the general features of the spectrum generators produced by FlexibleSUSY, focusing on the case of SUSY models.
- URL::
- Model(s)::
-
Any renormalizable extension of the SM whose Lagrangian does not contain 3- or 4-tensor interactions.
- Inputs::
-
Superpotential parameters and soft SUSY-breaking parameters in the \(\overline{\text {DR}}\) scheme at a user-defined scale \(Q_{{\scriptscriptstyle \mathrm{in}}}\), spanning from the EW scale to the GUT scale. The parameter \(\tan \beta \) and all scalar vevs other than v are also required as input at the scale \(Q_{{\scriptscriptstyle \mathrm{in}}}\). For each of the scalars that acquire a vev, one of the parameters that contribute to the mass is fixed through the minimum conditions of the scalar potential.
- Outputs::
-
Pole Higgs masses, effective mixing matrices in the Higgs sector. Estimate of the theory uncertainty of the prediction for \(M_h\).
- CPV/FLV/RPV::
-
CPV and FLV are supported. RPV is not supported.
- SLHA format::
-
SLHA conventions (SLHA1 and SLHA2) for input and output.
- Strategy::
-
FO calculation: The gauge and Yukawa couplings of the SUSY model are extracted from the SM input parameters at a user-defined low-energy scale \(Q_{\scriptscriptstyle \mathrm{SM}}\), while the soft SUSY-breaking parameters are given as input at \(Q_{{\scriptscriptstyle \mathrm{in}}}\). All parameters are evolved with the RGEs of the SUSY model to the scale \(Q_{{\scriptscriptstyle \mathrm{EWSB}}}\), where the minimum conditions of the potential are imposed and the whole mass spectrum of the model is computed, including the radiative corrections. This scale is set by default to the geometric mean of the stop masses, but can be modified by the user.
Hybrid calculation: Only for scenarios where the EFT valid below the SUSY scale is the SM. The FO calculation of the Higgs masses is performed at a scale \(Q=M_S\) of the order of the SUSY masses, starting from an ansatz for the gauge and Yukawa couplings and the parameter v of the SUSY model, which we collectively denote as \(P^i(M_S)\). A matching condition for \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}(M_S)\) is thus extracted from the results of the FO calculation as described in Sect. 5.3, and \(P^i(M_S)\) are converted into their SM counterparts \(P^i_{\scriptscriptstyle \mathrm{SM}}(M_S)\). All parameters are then evolved down to a user-defined scale \(Q_{\scriptscriptstyle \mathrm{SM}}\), where the pole Higgs mass is computed within the SM. The ansatz for \(P^i(M_S)\) is adjusted until the values of \(P^i_{\scriptscriptstyle \mathrm{SM}}(Q_{\scriptscriptstyle \mathrm{SM}})\) obtained via RG evolution coincide with those extracted from a set of experimental observables.
EFT calculation: Standard multi-scale approach. The matching conditions for the couplings of the EFTs at each of the scales where some heavy particles are integrated out must be supplied by the user.
- Corrections::
-
FO calculation: Two-loop RGEs from SARAH for any model. For the MSSM, optional inclusion of the three-loop RGEs from Refs. [340, 341]. The gauge and Yukawa couplings and the parameter v of the SUSY model are extracted from the SM inputs at one loop, but the extraction of the top-Yukawa and strong-gauge couplings includes also the SM part of the two- and three-loop QCD effects (for the MSSM, the two-loop SUSY-QCD effects can also be included). Full one-loop corrections to the Higgs masses from SARAH for any model. For the MSSM, two-loop corrections to the neutral Higgs masses in the gaugeless and vanishing-momentum limits, and optional inclusion of the three-loop \({\mathcal {O}}(\alpha _t\alpha _s^2)\) corrections to \(M_h\) from Himalaya. For the NMSSM, two-loop \({{{\mathcal {O}}}}(\alpha _t\alpha _s + \alpha _b\alpha _s)\) corrections to the neutral Higgs masses in the vanishing-momentum limit, remaining gaugeless two-loop corrections in the vanishing-momentum and MSSM limits.
Hybrid calculation: For any model, the one-loop corrections to all of the Higgs masses are included as in the FO calculation, and the large logarithmic corrections to \(M_h\) are resummed at the NLL order. For the MSSM, where the FO calculation includes also two- and three-loop corrections, the resummation is extended to the NNLL order in the gaugeless limit, and it optionally includes also the N\(^3\)LL terms that involve the highest powers of the strong gauge coupling.
EFT calculation: For any model, FlexibleSUSY requires as input the one-loop matching conditions, and generates a stand-alone code for the EFT calculation of the Higgs masses at the NLL order. Pre-generated codes for various MSSM scenarios with hierarchical mass spectra are included in the package (see Sect. 4.3.5). In the simplest MSSM scenario where the EFT valid below the SUSY scale is the SM, the resummation of the large logarithmic corrections to \(M_h\) is performed at the same order as in the hybrid calculation described above. For the other MSSM scenarios the resummation is performed at the NLL order, but the known two-loop contributions to the matching conditions for the quartic Higgs coupling(s) are included.
- Other features::
-
Mass spectrum and mixing matrices at one loop for all BSM scalars and fermions. Effective Higgs couplings to photons and to gluons. Predictions for \(M_W\) and the running weak mixing angle, the muon \((g-2)\) and the EDMs of quarks and leptons. For the models with high-scale boundary conditions, the package includes a semi-analytic solver of the boundary-value problem (BVP). This allows for the study of models that are highly constrained (such as the CNMSSM or the CE\(_6\)SSM) or in which the BVP has multiple solutions.
- Language::
-
FlexibleSUSY is a Mathematica package. The spectrum generators produced by FlexibleSUSY are written in C++. A Mathematica interface for the spectrum generators is also provided.
- What to cite::
-
Standard: Refs. [142, 143], mentioning that the package includes numerical routines from SOFTSUSY [45, 141] and analytic results from SARAH [102,103,104,105,106]. Additional references depending on usage: for the hybrid calculation of FlexibleEFTHiggs, Ref. [277], as well as Ref. [295] in the case of the MSSM; for the three-loop corrections to the MSSM Higgs mass from Himalaya, Refs. [67, 68, 70, 236]; for the semi-analytic solver of the BVP, Ref. [342].
1.3.2 A.3.2 SARAH
SARAH is a multipurpose tool for any renormalizable model. To define a model, the user specifies the superfield content, the superpotential (or, for non-SUSY models, directly the field content and the Lagrangian), and the way gauge symmetries are broken and fields mix. SARAH then determines all mass matrices and interaction vertices, and uses them to adapt to the model under consideration the general formulas for the two-loop RGEs, for the one- and two-loop tadpoles and self-energies of the scalars, and for the one-loop self-energies of fermions and vector bosons. All of these results are given as output in analytical form and can be used by other codes such as, e.g., FlexibleSUSY (see Sect. 1). Most relevant here is the ability to produce stand-alone spectrum generators, similar to SPheno (see Sect. 1) and relying on that code’s library of routines. The Higgs-mass calculation can alternatively adopt the FO, EFT and hybrid approaches. Below we list the features of these spectrum generators, focusing on the case of SUSY models.
- URL::
- Model(s)::
-
Any renormalizable extension of the SM, modulo some restrictions for certain features. A library of pre-defined models, both SUSY and non-SUSY, is provided in the package.
- Inputs::
-
Superpotential parameters and soft SUSY-breaking parameters in the \(\overline{\text {DR}}\) scheme at a user-defined scale \(Q_{{\scriptscriptstyle \mathrm{in}}}\), spanning from the EW scale to the GUT scale. The parameter \(\tan \beta \) and all scalar vevs other than v are also required as input at the scale \(Q_{{\scriptscriptstyle \mathrm{in}}}\). For each of the scalars that acquire a vev, one of the parameters that contribute to the mass is fixed through the minimum conditions of the scalar potential.
- Outputs::
-
Pole Higgs masses, effective mixing matrices in the Higgs sector.
- CPV/FLV/RPV::
-
All supported.
- SLHA format::
-
SLHA conventions (SLHA1 and SLHA2) for input and output.
- Strategy::
-
FO calculation: The gauge and Yukawa couplings and the parameter v of the SM are determined at the scale \(Q=M_Z\), then evolved to a user-defined scale \(Q_{{\scriptscriptstyle \mathrm{EWSB}}}\) where they are converted into their SUSY counterparts. Alternatively, the gauge and Yukawa couplings and the parameter v of the SUSY model are extracted from the SM inputs directly at the scale \(Q_{{\scriptscriptstyle \mathrm{EWSB}}}\). The remaining parameters of the SUSY model are in turn evolved from \(Q_{{\scriptscriptstyle \mathrm{in}}}\) to \(Q_{{\scriptscriptstyle \mathrm{EWSB}}}\). At this scale, which is set by default to the geometric mean of the stop masses but can be modified by the user, the minimum conditions of the scalar potential are imposed and the whole mass spectrum is computed, including the radiative corrections.
Hybrid calculation: Only for scenarios where the EFT valid below the SUSY scale is the SM. The gauge and Yukawa couplings and the parameter v of the SM are extracted from a set of experimental observables at the scale \(Q=M_Z\), then evolved to a scale \(Q=M_S\) of the order of the SUSY masses, where they are converted into their SUSY counterparts and used for the FO calculation of the Higgs masses. A matching condition for \(\lambda _{{\scriptscriptstyle \mathrm{SM}}}(M_S)\) is thus extracted from the results of the FO calculation as described in Sect. 5.3, and it is used for an EFT calculation of \(M_h\).
Finally, the code allows for pure EFT calculations of the Higgs masses in which the matching conditions at each of the scales where some heavy particles are integrated out are obtained from the general analytic results of Refs. [271, 272].
- Corrections::
-
FO calculation: Two-loop RGEs for any model. The gauge and Yukawa couplings and the parameter v of the SUSY model are extracted from the SM inputs at one loop. Full one-loop corrections to the Higgs masses. Two-loop corrections to the neutral Higgs masses in the gaugeless and vanishing-momentum limits. For models beyond the MSSM, possible singularities in the two-loop corrections associated with the “Goldstone Boson Catastrophe” – see Sect. 3.2 – are addressed as described in Refs. [153, 155], requiring the partial inclusion of momentum-dependent effects.
Hybrid calculation: The one- and two-loop corrections to all of the Higgs masses are included as in the FO calculation, and the large logarithmic corrections to \(M_h\) are resummed at the LL order.
EFT calculation: The general formulas for two-loop RGEs and one-loop matching conditions allow for the NLL resummation of the large logarithmic corrections to the Higgs masses in any SUSY model with a hierarchical mass spectrum. The package contains pre-defined model files for several hierarchical scenarios in the MSSM and in the NMSSM (see Sect. 4.3.5).
- Other features::
-
Mass spectrum and decay widths at one loop for all BSM scalars and fermions. Unitarity constraints on the scalar couplings. Model files for Monte Carlo tools (UFO [343], WHIZARD [344], CalcHEP [345, 346]). Model files for other tools: Vevacious [347], FeynArts [348]. Flavor observables through FlavorKit [349]. LaTeX output.
- Language::
-
SARAH is a Mathematica package. The SPheno-like spectrum generators produced by SARAH are written in Fortran 90.
- What to cite::
-
Refs. [102,103,104,105,106] for the core functions, Refs. [109, 110, 155] for the two-loop corrections to the scalar masses. Additional references depending on usage: for the hybrid calculation, Ref. [294]; for the automated EFT calculation, Ref. [272]; for the decay widths, Ref. [350]; for the unitarity constraints, Refs. [351, 352] .

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Slavich, P., Heinemeyer, S., Bagnaschi, E. et al. Higgs-mass predictions in the MSSM and beyond. Eur. Phys. J. C 81, 450 (2021). https://doi.org/10.1140/epjc/s10052-021-09198-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-021-09198-2