Minimally deformed wormholes

Abstract

This work is devoted to the study of wormhole solutions in the framework of gravitational decoupling by means of the minimal geometric deformation scheme. As an example, to analyze how this methodology works in this scenario, we have minimally deformed the well-known Morris–Thorne model. The decoupler function f(r) and the $\theta$-sector are determined considering the following approaches: (i) the most general linear equation of state relating the $\theta _{\mu \nu }$ components is imposed and (ii) the generalized pseudo-isothermal dark matter density profile is mimicked by the temporal component of the $\theta$-sector. It is found that the first approach leads to a non-asymptotically flat space-time with an unbounded mass function. To address this issue we have matched both the wormhole and the Schwarzschild vacuum solutions, via a thin-shell at the junction surface. Using the second approach, it can be seen that, on one hand, the solution for $\gamma =1$ does not give place to a bounded mass and it presents a topological defect at large distances; on the other hand, the wormhole manifold is asymptotically flat in the $\gamma =2$ case. In order to satisfy the flare-out condition, we have found restrictions on the value of the $\alpha$ parameter, which is related with the amount of exotic matter distribution. Finally, the averaged weak energy condition has been analyzed by using the volume integral quantifier.

1 Introduction

Within the wide range of solutions that Einstein’s field equations possess, for example those representing stellar interiors [1], black holes [2] and cosmological scenarios [3], there are very particular ones that describe the connection between two very distant regions or between parallel Universes. At the beginning these objects were known as the Einstein–Rosen bridge and were developed in order to explain the particle problem in GR, more precisely to try to explain fundamental particles such as electrons in terms of space-time tunnels threaded by electric lines of force [4]. However, the major problem was the instability of these geometric structures. This means that the bridge is not able to remain open long enough for an object to pass through it (not even a photon). After that, the pioneering works by Morris and Thorne [5, 6] presented the minimum conditions to obtain a traversable wormhole space-time (Although the wormhole name was coined by Wheeler [7]). These objects have opened the intriguing and exciting possibility of time travel (theoretically speaking) in relatively short time periods. However, the existence of wormhole space-times requires to meet certain conditions such as [8]: (i) connect two infinite or asymptotically flat regions, (ii) the gravitational field inside the throat should be weak enough to allow a safe traversability (and to preclude the formation of event horizons), (iii) the matter distribution supporting the throat must be exotic. In particular, it must violate the null energy condition which basically states that a repulsive gravitational force holds the wormhole throat open.

The appearance of exotic matter seems to be a necessary condition to build up a well posed wormhole solution in the arena of General Relativity (GR from now on), regardless of whether it is a static or a dynamic solution [9, 10]. In this concern, some authors have investigated the possibility of using dark matter/fluid such as phantom energy or Chaplygin gas to construct wormholes structures [11,12,13,14,15,16,17,18,19]. However, sometimes it is desirable to avoid the so-called exotic matter. In this sense, the thin-shell formalism [20, 21] has been posed as an attractive approach to build wormhole space-times, since the exotic matter is confined into a finite region [22,23,24,25,26,27,28,29,30]. In a broader context, the thin-shell procedure has been used to build wormholes with cylindrical symmetry [31, 32], spherically symmetric wormholes in the light of linear [33] as well as non-linear electrodynamics [34,35,36]. Moreover, wormhole solutions with other type of symmetries have been investigated in [37,38,39] and also the possibility to obtain a traversable Schwarzschild-like wormhole has been considered [40]. Furthermore, recently [41] was studied and analyzed the behavior of wormhole structures in the realm of dark matter profiles, dark matter Bose–Einstein condensates [42] and non-linear equation of state [43], respectively.

The study of wormholes not only is carried out within the framework of GR. Recently there has been a growing interest in studying such solutions in the arena of Brans–Dicke theory [44, 45], f(R)-gravity [46,47,48,49,50,51,52,53], f(R, T)-gravity [54,55,56,57,58], Einstein–Cartan theory [59] and extra dimensions [60, 61]. The advantage of these modified or extended gravity theories is that the energy conditions can be satisfied for the usual matter sector due to the corrections introduced by the additional fields into the theory. Furthermore, in the context of a gravitational theory including torsion and a non-minimally coupled scalar field (scalar–tensor teleparallel theory), the existence of Lorentzian wormhole solutions were explored in Ref. [62]. In a broader scenario, traversable and asymptotically flat wormholes supported by GUP corrected Casimir energy along with two different equations of state were obtained in [63].

In recent years, the gravitational decoupling by means of minimal geometric deformation (MGD hereafter), was developed to study the inclusion of local anisotropies within the brane-world scenario and extended to the framework of stellar interiors in GR [64,65,66,67,68,69,70,71,72,73,74]. However, this versatile tool goes beyond the study of these seminal proposals. In this regard, black hole, modified gravity theories, cosmology, Dirac stars and thermodynamic scenarios, among others, have been developed within the MGD approach [75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104] (and references therein).

Taking into account these successful applications, in the present article we investigate the incidence of gravitational decoupling through MGD on wormhole space-times. Specifically, we have deformed the well-known Morris–Thorne (M–T hereinafter) solution [5, 6] to see how MGD works in this context. Interestingly, as the interpretation of the new ingredients (the so-called $\theta$-sector) introduced by the MGD approach is still open [84], in the present study we have solved the field equations by interpreting this sector as dark fluids (dark energy and dark matter), although the normal matter regime is included, too. To do this, we have firstly related the components of the $\theta$-sector by means of a general linear equation of state (EoS) and, secondly, we have imposed the temporal component of the $\theta _{\mu \nu }$ source to mimic a generalized pseudo-isothermal dark matter density profile (see the seminal work [105] for further details in considering this density profile). This information allows us to close the $\theta$-system determining the full $\theta _{\mu \nu }$ tensor (and, consequently, the full energy–momentum tensor of the solution) and the decoupler function, f(r), therefore closing the problem at least from a mathematical point of view. This approach motivates and also allows to support the idea that these type of solutions can be constituted by the dark sector, which dominates our Universe [11,12,13,14,15,16,17,18,19, 41,42,43]. Even more, it provides a possible interpretation of the contribution introduced by MGD.

The article is organized as follows: in Sect. 2 traversable wormholes generalities are presented; Sect. 3 describes the field equations and gravitational decoupling, explaining how MGD is applied in this context. Sect. 4 depicts the resulting wormhole models. Sects. 5 and 6 analyze the geometry and the matter distribution of the solutions. Finally Sect. 7 concludes the work.

The mostly positive signature $\{-,+,+,+\}$ is employed throughout the article and units where the coupling constant $\kappa \equiv \frac{8\,\pi \,G}{c^{4}}$ is equal to 1 are assumed.

2 Wormhole anatomy

In this section, the conditions to build a traversable and asymptotically flat wormhole space-time are revisited. To have a more complete vision about it then see the following Refs. [5, 6, 8]. In Schwarzschild-like coordinates $x^{\mu }\equiv \left( t,r,\theta ,\varphi \right)$ the most general line element describing a wormhole geometry is given by

$$\begin{aligned} ds^{2}=-e^{2\varPhi (r)}dt^{2}+\frac{dr^{2}}{1-\frac{b(r)}{r}}+r^{2}d\varOmega ^{2}, \end{aligned}$$

(1)

where $\varPhi$ is the so-called red-shift function and b the shape function. As we are considering a spherically symmetric and static solutions both $\varPhi$ and b are purely radial functions. Then, the minimal requirement to be satisfied for the wormhole geometry given by (1) are:

• 1. The throat size connecting the regions is defined by a global minimum radius $r=r_{0}$. In this respect, the radial coordinate is defined in the interval $r\in [r_{0},+\infty )$.

• 2. There are two coordinates patches covering the range $r\in [r_{0},+\infty )$. Each patch covers an asymptotically flat region of the wormhole throat, and both match at $r_{0}$.

• 3. The red-shift function $\varPhi$ must be finite everywhere, for $r\ge r_{0}$, in order to avoid an event horizon, so $e^{\varPhi (r)}>0$ for all $r>r_{0}$. Moreover,

  $$\begin{aligned} \lim _{r\rightarrow +\infty } \varPhi (r)=\varPhi _{0}, \end{aligned}$$

  where $\varPhi _{0}$ is finite and real.

• 4. The flare-out condition must hold

  $$\begin{aligned} \frac{b(r)-b^{\prime }(r)r}{b^{2}(r)}>0, \end{aligned}$$

  at or near the throat $r=r_{0}$.

• 5. The above condition implies that for all $r\ge r_{0}$: $b(r_{0})=r_{0}$ and $b^{\prime }(r_{0})\le 1$, where the equality holds only at the throat (weak equality). Furthermore, for all $r>r_{0}$ $\Rightarrow$ $b(r)<r$.

• 6. To ensure the asymptotic behavior, the shape function b(r) must fulfill

  $$\begin{aligned} \lim _{r\rightarrow +\infty } b(r)=\text {finite}. \end{aligned}$$

• 7. The previous requirement implies that the mass of the wormhole over long distances matches with the Schwarzs- child mass ı.e, $b=2M$.

3 Field equations

The starting point are the Einstein field equations, which are given by

$$\begin{aligned} G_{\mu \nu }\equiv R_{\mu \nu }-\frac{R}{2}g_{\mu \nu }=T_{\mu \nu }, \end{aligned}$$

(2)

As said before we are interested in including new components into the energy–momentum tensor which provide new insights about the material content threading the throat of the wormhole. So, following [74] a simple way to do that is by writing

$$\begin{aligned} T_{\mu \nu }={\tilde{T}}_{\mu \nu }+\alpha \theta _{\mu \nu }, \end{aligned}$$

(3)

where ${\tilde{T}}_{\mu \nu }$ is representing the so-called seed energy–momentum tensor, $\alpha$ is a dimensionless coupling constant and $\theta _{\mu \nu }$ is the new material sector which in principle could be a scalar, vector or tensor field. With the above prescription (3) at hand and considering the spherically symmetric and static line element (1), the set of Eq. (2) reads

$$\begin{aligned} {\tilde{\rho }}+\alpha \theta ^{0}_{\ 0}= & {} \frac{b^{\prime }}{ r^{2}}, \end{aligned}$$

(4)

$$\begin{aligned} {\tilde{p}}_{r}-\alpha \theta ^{1}_{\ 1}= & {} -\frac{b}{ r^{3}}, \end{aligned}$$

(5)

$$\begin{aligned} {\tilde{p}}_{t}-\alpha \theta ^{2}_{\ 2}= & {} \frac{b-rb^{\prime }}{2 r^{3}}. \end{aligned}$$

(6)

At this point some comments are pertinent. First, the system of Eqs.  (4)–(6) does not depend on the red-shift function $\varPhi$. This is because we are looking for traversable wormhole solutions (small or vanishing tidal forces), then to ensure this condition we have taken $\varPhi =0$. In addition this condition also guarantees that the solution does not have event horizons. Second, the seed energy–momentum tensor is describing an imperfect fluid distribution. It explicitly reads

$$\begin{aligned} {\tilde{T}}_{\mu \nu }=\left( {\tilde{\rho }} +{\tilde{p}}_{t}\right) U_{\mu }U_{\nu }+g_{\mu \nu }{\tilde{p}}_{t}+\left( {\tilde{p}}_{r}-{\tilde{p}}_{t}\right) \chi _{\mu }\chi _{\nu }, \end{aligned}$$

(7)

with ${\tilde{\rho }}$ is the energy–density, ${\tilde{p}}_{r}$ and ${\tilde{p}}_{t}$ being the pressures in the principal directions ı.e, the radial and tangential ones, respectively. The four-velocity of the above fluid distribution is characterized by the time-like vector $U^{\nu }$. Moreover $\chi ^{\nu }$ is a unit space-like vector in the radial direction (orthogonal to $U^{\nu }$), ı. e., $\chi ^{\nu }=\sqrt{1-b/r}\delta ^{\nu }_{r}$. The quantities at the left hand side of the Eqs. (4)–(6) can be denoted as the total or effective thermodynamic variables

$$\begin{aligned} {\rho }\equiv & {} {\tilde{\rho }}+\alpha \theta ^{0}_{\ 0}, \end{aligned}$$

(8)

$$\begin{aligned} {p}_{r}\equiv & {} {\tilde{p}}_{r}-\alpha \theta ^{1}_{\ 1}, \end{aligned}$$

(9)

$$\begin{aligned} {p}_{t}\equiv & {} {\tilde{p}}_{t}-\alpha \theta ^{2}_{\ 2}. \end{aligned}$$

(10)

However, the main point to be analyzed here are the effects introduced by the $\theta$-sector into the structure.

3.1 Gravitational decoupling by MGD

To split the complex set of Eqs. (4)–(6), we implement the gravitational decoupling by means of MGD (see [74] for further details). In this case the minimally deformed shape function b(r) is given by

$$\begin{aligned} b(r)\mapsto {\hat{b}}(r)+\alpha f(r), \end{aligned}$$

(11)

being ${\hat{b}}$ the original shape function and f(r) the decoupler function. Putting Eq. (11) into the set (4)–(6), we obtain the following system of equations

$$\begin{aligned} {\tilde{\rho }}= & {} \frac{{\hat{b}}^{\prime }}{ r^{2}}, \end{aligned}$$

(12)

$$\begin{aligned} {\tilde{p}}_{r}= & {} -\frac{{\hat{b}}}{ r^{3}}, \end{aligned}$$

(13)

$$\begin{aligned} {\tilde{p}}_{t}= & {} \frac{{\hat{b}}-r{\hat{b}}^{\prime }}{2 r^{3}}, \end{aligned}$$

(14)

subject to the following conservation equation

$$\begin{aligned} \nabla _{\mu }{\tilde{T}}^{\mu }_{\ \nu }=0 \rightarrow -{\tilde{p}}^{\prime }_{r}+\frac{2}{r}\left( {\tilde{p}}_{t}-{\tilde{p}}_{r}\right) =0. \end{aligned}$$

(15)

The second set of equations is given by

$$\begin{aligned} \theta ^{0}_{\ 0}= & {} \frac{f^{\prime }}{ r^{2}}, \end{aligned}$$

(16)

$$\begin{aligned} \theta ^{1}_{\ 1}= & {} \frac{f}{ r^{3}}, \end{aligned}$$

(17)

$$\begin{aligned} \theta ^{2}_{\ 2}= & {} \frac{rf^{\prime }-f}{2 r^{3}}. \end{aligned}$$

(18)

Along with the following conservation law

$$\begin{aligned} \nabla _{\mu }\theta ^{\mu }_{\ \nu }=0 \rightarrow \left( \theta ^{1}_{\ 1}\right) ^{\prime }-\frac{2}{r}\left( \theta ^{2}_{\ 2}-\theta ^{1}_{\ 1}\right) =0. \end{aligned}$$

(19)

The fact of both parts, namely ${\tilde{T}}_{\mu \nu }$ and $\theta _{\mu \nu }$ are independently conserved means that they are related gravitationally. Moreover, it should be noted that the conservation of the $\theta$-sector is a consequence of the conservation of $G_{\mu \nu }$ and ${\tilde{T}}_{\mu \nu }$. As it is well-known Bianchi’s identities invoke

$$\begin{aligned} \nabla _{\mu }G^{\mu }_{\ \nu }=0, \end{aligned}$$

(20)

then from Eqs. (2) and (3) one has

$$\begin{aligned} \nabla _{\mu }{\tilde{T}}^{\mu }_{\ \nu }+\alpha \nabla _{\mu }\theta ^{\mu }_{\ \nu }=0. \end{aligned}$$

(21)

Nevertheless, the first term in the left member of the above equation, is equal to zero. Since ${\tilde{T}}_{\mu \nu }$ corresponds to the usual matter sector its conservation comes from the underlying symmetries of the theory. In this case the symmetries of the theory correspond to the 4-dimensional space-time diffeomorphism ı.e, general coordinate transformations. Then taking into account the previous considerations finally one obtains $\nabla _{\mu }\theta ^{\mu }_{\ \nu }=0$. Of course, if one considers the effective $T_{\mu \nu }$, it is evident that $\nabla _{\mu }T^{\mu }_{\ \nu }=0$. It is worth mentioning that Eqs. (15) and (19) are the hydrostatic equation describing the balance of the configuration. As can be seen there is a missing term in both expressions. Specifically, the term proportional to $\varPhi ^{\prime }$ is absent. Indeed as we have considered $\varPhi =0$ this term is not present. However, when the red-shift function is not taken to be constant then the missing term is restored introducing into the system a gravitational gradient (related with tidal forces).

To close the discussion of this section, we remark that in order to preserve part of the wormhole structure described in Sect. 2 the decoupler function introduced in Eq. (11) must satisfy $f(r_{0})=0$. This is so because the non-deformed shape function ${\hat{b}}$ already meets the condition ${\hat{b}}(r_{0})=r_{0}$. In the next section we provide some examples of wormhole structures by extending the M–T model with the aforementioned methodology.

4 Specific solutions

As said before we considered as a seed space-time the well-known M–T wormhole solution [5, 6]. This wormhole space-time is described by the following metric

$$\begin{aligned} ds^{2}=-dt^{2}+\frac{dr^{2}}{1-\frac{r^{2}_{0}}{r^{2}}}+r^{2}d\varOmega ^{2}. \end{aligned}$$

(22)

It is clear from (22) that $\varPhi =0$ and $b(r)=r^{2}_{0}/r$. Geometrically speaking this solution reproduces an asymptotically flat space-time when $r\rightarrow +\infty$ and satisfies the flare-out condition. Besides, the matter distribution threading the throat violates the NEC as expected in the framework of GR [9, 10]. Nevertheless, it would be desirable that the minimally deformed solution can be supported by a minimal amount of exotic matter distribution, in contrast with usually occurs in the GR scenario, where large amounts of exotic matter are necessary to hold the wormhole structure. Of course, it will not be completely possible to avoid the use of exotic matter but, as said before, the MGD could act as an exotic matter regulator. To check these facts, in the next sections we explore in details about the geometric and matter distribution behavior.

4.1 Model # 1: linear equation of state

To solve the system (16)–(18) we impose the following equation of state (EoS from now here) relating the components of the $\theta$-sector

$$\begin{aligned} \theta ^{ 1}_{\ 1}=\omega \theta ^{0}_{\ 0}+\beta , \end{aligned}$$

(23)

where $\omega$ and $\beta$ are constant parameters, dimensionless and with units of $\text {length}^{-2}$, respectively. So, from Eqs. (16)–(17) one arrives at the following first order differential for f(r),

$$\begin{aligned} f^{\prime }-{\omega \ r}f-\frac{\beta }{\omega }r^{2}=0. \end{aligned}$$

(24)

The solution of (24) is given by

$$\begin{aligned} f(r)=\frac{\beta }{1-3\omega }r^{3}+r^{1/\omega }C_{1}, \end{aligned}$$

(25)

being $C_{1}$ an integration constant with units of $\text {length}^{(\omega -1)/\omega }$. Hence, the extended shape function (11) is

$$\begin{aligned} b(r)=\frac{r^{2}_{0}}{r}+\alpha \left( \frac{\beta }{1-3\omega }r^{3}+r^{1/\omega }C_{1}\right) . \end{aligned}$$

(26)

Therefore the complete deformed space-time is given by

$$\begin{aligned} ds^{2}= & {} -dt^{2}+\frac{dr^{2}}{1-\frac{r^{2}_{0}}{r^{2}}-\frac{\alpha }{r}\left( \frac{\beta }{1-3\omega }r^{3}+r^{1/\omega }C_{1}\right) }\nonumber \\&+r^{2}d\varOmega ^{2}. \end{aligned}$$

(27)

4.2 Model # 2: dark matter density profile

Here to close the system (16)–(18) we consider a generalized form of the pseudo-isothermal (PI) density profile of dark matter. Explicitly it reads

$$\begin{aligned} \theta ^{0}_{\ 0}(r)=a\left[ 1+\left( \frac{r}{b}\right) ^{2}\right] ^{-\gamma }, \end{aligned}$$

(28)

where a $(\text {km}^{-2})$, b (km) and $\gamma$ are non-zero positive constants. The limit case $\gamma =1$ corresponds to the original PI profile proposed for the first time by Kent [105]. Now, by equating Eqs. (16) and (28) one obtains the following first order ordinary differential equation in f(r)

$$\begin{aligned} f^{\prime }-a\left[ 1+\left( \frac{r}{b}\right) ^{2}\right] ^{-\gamma }r^{2}=0, \end{aligned}$$

(29)

whose solution is given by

$$\begin{aligned} f(r)=\frac{a}{3} \ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}}{b^{2}}\right] r^{3}+C_{2}, \end{aligned}$$

(30)

where ${}_2F_{1}$ is the usual Gaussian or ordinary hypergeometric function and $C_{2}$ is an integration constant. Hence from (11) one has

$$\begin{aligned} b(r)=\frac{r^{2}_{0}}{r}+\alpha \left( \frac{a}{3} \ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}}{b^{2}}\right] r^{3}+C_{2}\right) , \end{aligned}$$

(31)

then the full space-time is described by

$$\begin{aligned} ds^{2}= & {} -dt^{2}+\frac{dr^{2}}{1-\frac{r^{2}_{0}}{r^{2}}-\alpha \left( \frac{a}{3} \ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}}{b^{2}}\right] r^{2}+\frac{C_{2}}{r}\right) }\nonumber \\&+r^{2}d\varOmega ^{2}. \end{aligned}$$

(32)

5 Geometric analysis

Once the decoupler function f(r) is known the full $\theta$-sector can be obtained from Eqs. (16)–(18) and then the problem is solved. In this section we analyze the implications on the M–T wormhole solution introduced by the new components $\{f,\theta _{\mu \nu }\}$. We start this analysis by studying the geometric structure of the resulting solutions reported in the previous section.

5.1 Model #1

As mentioned previously, all the decoupler functions f(r) must be zero at the throat ı.e, $f(r_{0})=0$. This is so because the seed model already meets the condition $b(r_{0})=r_{0}$. So, from Eq. (25) we have

$$\begin{aligned} f(r_{0})=\frac{\beta }{1-3\omega }r^{3}_{0}+r^{1/\omega }_{0}C_{1}=0, \end{aligned}$$

(33)

from which we get

$$\begin{aligned} C_{1}=-\frac{\beta }{1-3\omega }r^{3-1/\omega }_{0}. \end{aligned}$$

(34)

Then we have

$$\begin{aligned} b(r)=\frac{r^{2}_{0}}{r}+\frac{\alpha \beta }{1-3\omega }\left( r^{3}-r^{1/\omega }r^{3-1/\omega }_{0}\right) . \end{aligned}$$

(35)

It is clear that $b/r\ne 0$ when $r\rightarrow +\infty$. This means that at large distances the Minkowski space-time is not recovered or equivalently the model is not asymptotically flat. Furthermore, the observed mass M of this model is not finite in such limit. In fact, from Eq. (4) the mass function m(r) of the wormhole can be easily obtained by a standard procedure [8] as follows

$$\begin{aligned} 4\pi \int ^{r}_{r_{0}}\left( {\bar{\rho }}+\alpha \theta ^{0}_{\ 0}\right) r^{2}dr=4\pi \int ^{r}_{r_{0}}b'(r)dr \end{aligned}$$

(36)

therefore,

$$\begin{aligned} {\tilde{m}}(r)\equiv 4\pi \int ^{r}_{r_{0}}\left( {\bar{\rho }}+\alpha \theta ^{0}_{\ 0}\right) r^{2}dr, \end{aligned}$$

(37)

is the usual mass, whereas the integral on the right hand side in the Eq. (36) gives place to

$$\begin{aligned} 4\pi \int ^{r}_{r_{0}}b'(r)dr=4\pi \left( b(r)-r_{0}\right) , \end{aligned}$$

(38)

where the condition at the wormhole throat, $b(r_{0})=r_{0}$, was employed.¹ In this way, one can define the total wormhole mass as an effective one as follows

$$\begin{aligned} {m}(r)\equiv 4\pi \left[ \int ^{r}_{r_{0}}\left( {\bar{\rho }}+\alpha \theta ^{0}_{\ 0}\right) r^{2}dr+r_{0}\right] =4\pi b(r). \end{aligned}$$

(39)

In the limit $r\rightarrow +\infty$ the above expression should be finite, that is,

$$\begin{aligned} \lim _{r\rightarrow +\infty }m(r)\!=\!4\pi \left[ r_{0}\!+\!\int ^{\infty }_{r_{0}} \left( {\bar{\rho }}+\alpha \theta ^{0}_{\ 0}\right) r^{2}dr\right] \!=\!M. \end{aligned}$$

(40)

So, by virtue of Eq. (39) the mass function associated in this case reads

$$\begin{aligned} m(r)=\frac{4\pi r^{2}_{0}}{r}+\frac{4\pi \alpha \beta }{1-3\omega }\left( r^{3}-r^{1/\omega }r^{3-1/\omega }_{0}\right) , \end{aligned}$$

(41)

which is unbounded as $r\rightarrow +\infty$. To cure the problem at large distances and make the solution asymptotically flat with a bounded mass one needs to join at some $r_{*}>r_{0}$ the wormhole geometry with the vacuum space-time given by the Schwarzschild solution

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2M_{\text {Sch}}}{r}\right) dt^{2}+\left( 1-\frac{2M_{\text {Sch}}}{r}\right) ^{-1}dr^{2}\nonumber \\&+r^{2}d\varOmega ^{2}, \end{aligned}$$

(42)

where $M_{\text {Sch}}$ represents the Schwarzschild mass. Then at the junction interface $\varSigma \equiv r=r_{*}$ one has

$$\begin{aligned} \left( 1-\frac{b(r)}{r}\right) \bigg |_{r=r_{*}}=\left( 1-\frac{2M}{r}\right) \bigg |_{r=r_{*}} \Rightarrow b(r_{*})=2M,\nonumber \\ \end{aligned}$$

(43)

where at the surface $\varSigma$ the total mass M of the wormhole coincides with the Schwarzschild mass $M_{\text {Sch}}$ and $r_{*}>r_{0}$. So, the space-time is defined by

$$\begin{aligned} \begin{aligned} ds^{2}&=-dt^{2}+\frac{dr^{2}}{1-\frac{r^{2}_{0}}{r^{2}}-\frac{\alpha \beta }{r\left( 1-3\omega \right) }\left( r^{3}-r^{1/\omega }r^{3-1/\omega }_{0}\right) } \\&\quad +r^{2}d\varOmega ^{2} \\&\quad \text{ for } \quad r_{0}\le r\le r_{*}, \end{aligned} \end{aligned}$$

(44)

and

$$\begin{aligned} \begin{aligned} ds^{2}=-dt^{2}+\frac{dr^{2}}{1-\frac{b(r_{*})}{r}} +r^{2}d\varOmega ^{2} \quad \text{ for }\quad r> r_{*}, \end{aligned} \end{aligned}$$

(45)

being $b(r_{*})=2M$. As we will see later, the above technique not only ensures the asymptotically flat behavior of the solution, but also confines the exotic matter within a finite region.

Despite having an unbounded mass, we must ensure that it is at least positive defined. Then, from expression (41) it is clear that the first member in the right hand side is positive everywhere, however the sign of the second one depends on the sign of the parameters $\{\alpha ,\beta ,\omega \}$, since the term inside the round parenthesis is always positive. As we shall see later, the EoS parameter $\omega$ will be constrained to represent some cosmic-like matter distribution. Therefore, $\omega$ will take both positive and negative values. So, to guarantee a positive defined wormhole mass M, we have the following possibilities

$$\begin{aligned}&\alpha>0 \quad \text{ and } \quad \beta >0 \ \Rightarrow \omega <{3}, \end{aligned}$$

(46)

$$\begin{aligned}&\alpha<0 \ (\alpha>0) \quad \text{ and } \quad \ \beta>0 \ (\beta <0) \ \Rightarrow \omega >{3}. \end{aligned}$$

(47)

As can be seen the value $\omega =1/3$ is not allowed. Now, to be a traversable wormhole solution, the flare-out condition must hold at the throat of the structure. Hence,

$$\begin{aligned} \begin{aligned} \left( \frac{b(r)-rb^{\prime }(r)}{b^{2}(r)}\right) \bigg |_{r=r_{0}}>0 \Rightarrow \frac{\alpha \beta r^{2}_{0}+2\omega }{\omega }>0. \end{aligned} \end{aligned}$$

(48)

From the above inequality and taking into account Eqs. (46)–(47), we can bound the dimensionless constant parameter $\alpha$. Thus, we are left only with two free parameters $\{\beta ,\omega \}$. Of course, the magnitude and sign of $\alpha$ strongly depends on the magnitude and sign of $\{\beta ,\omega \}$.

5.2 Model # 2

Following the same steps as before, from Eq. (30) one has

$$\begin{aligned} \begin{aligned} f(r_{0})=0 \Rightarrow C_{2}=-\frac{a}{3} \ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}_{0}}{b^{2}}\right] r^{3}_{0} \end{aligned}. \end{aligned}$$

(49)

Then, the deformed space-time is given by

$$\begin{aligned} \begin{aligned}&ds^{2}=-dt^{2}+r^{2}d\varOmega ^{2} \\&\quad +\frac{dr^{2}}{1-\frac{r^{2}_{0}}{r^{2}}-\alpha \frac{a}{3r}\left( {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}}{b^{2}}\right] r^{3}-{}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}_{0}}{b^{2}}\right] r^{3}_{0}\right) }. \end{aligned}\nonumber \\ \end{aligned}$$

(50)

In this case the flare-out condition reads

$$\begin{aligned} \begin{aligned}&\bigg (1+\frac{r^{2}}{b^{2}}\bigg )^{-\gamma }\bigg (-9ar^{5}\alpha +3r\bigg (1+\frac{r^{2}}{b^{2}}\bigg )^{\gamma }\\&\quad \bigg (6r^{2}_{0}-a \ r^{3}_{0}r\ \alpha \ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}_{0}}{b^{2}}\right] \\&\qquad + a \ r^{4}\ \alpha \ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}}{b^{2}}\right] \bigg )\bigg )\\&\quad \bigg (3r^{2}_{0}-a \ r^{3}_{0}r\ \alpha \ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}_{0}}{b^{2}}\right] \\&\qquad + a \ r^{4}\ \alpha \ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}}{b^{2}}\right] \bigg )^{-2}>0. \end{aligned} \end{aligned}$$

(51)

Next, evaluating Eq. (51) at $r=r_{0}$ one gets

$$\begin{aligned} \alpha < \frac{2}{ar^{2}_{0}}\left( 1+\frac{r^{2}_{0}}{b^{2}}\right) ^{\gamma }. \end{aligned}$$

(52)

For this model the mass function is given by

$$\begin{aligned} m(r)= & {} \frac{4\pi r^{2}_{0}}{r}+\alpha \frac{2a\pi }{3}\left( \ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}}{b^{2}}\right] r^{3}\right. \nonumber \\&\left. -\ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}_{0}}{b^{2}}\right] r^{3}_{0}\right) . \end{aligned}$$

(53)

As we are considering the space parameter $\{a,b,\gamma \}$ to be positive, it is clear from (53) that the mass function m(r) is positive defined everywhere if and only if $\alpha >0$. Then, combining this fact with the Eq. (52) one has the

$$\begin{aligned} 0<\alpha < \frac{2}{ar^{2}_{0}}\left( 1+\frac{r^{2}_{0}}{b^{2}}\right) ^{\gamma }, \end{aligned}$$

(54)

which assures $m(r)>0$. Although, the Eq. (52) is positive, since a should be positive in order to ensure a positive defined $\theta$-sector density $\theta ^{0}_{\ 0}$ given by Eq. (28). Moreover, as was mentioned in Sect. 2 (points 4 and 5), the flare-out condition implies at the wormhole throat $b'(r)|_{r=r_{0}}\le 1$.

As this point, it is instructive to analyze the behavior of the form function (31) at very large distances. To do this, we shall fix $\gamma =1$ and $\gamma =2$ (see below for further details). So, for $\gamma =1$ the form function (31) becomes

$$\begin{aligned} b(r)=\frac{r^{2}_{0}}{r}+\alpha \left[ r-\text {arctan}\left( \frac{r}{b}\right) -r_{0}+\text {arctan}\left( \frac{r_{0}}{b}\right) \right] ab^{2},\nonumber \\ \end{aligned}$$

(55)

and for $\gamma =2$,

$$\begin{aligned} \begin{aligned} b(r)&=\frac{r^{2}_{0}}{r}+\alpha \bigg [\frac{\text {arctan}\left( \frac{r}{b}\right) }{2b}-\frac{r}{2\left( b^{2}+r^{2}\right) }+\frac{r_{0}}{2\left( b^{2}+r^{2}_{0}\right) }\\&\quad -\frac{\text {arctan}\left( \frac{r_{0}}{b}\right) }{2b}\bigg ]ab^{4}, \end{aligned}\nonumber \\ \end{aligned}$$

(56)

where we have used the following relation between the hypergeometric function and the elementary arctan fucntion

$$\begin{aligned} \frac{\text {arctan}(x)}{x}={}_{2}F_{1}\left[ \frac{1}{2},1;\frac{3}{2};-x^{2}\right] . \end{aligned}$$

(57)

Evidently, when $r\rightarrow +\infty$ then $\text {arctan}(r)\rightarrow \pi /2$. Thus from (55), it is clear that b(r) is not finite at large distances, consequently the mass function is not bounded, although positive defined ($M\rightarrow +\infty$). Therefore, as done with the model $\#$1, it is necessary to perform a surgery with the outer vacuum space-time to cure this problem. Moreover, in this case the resulting space-time does not reproduce the Minkowski space-time in the mentioned limit. Concretely for Eq. (55) one obtains

$$\begin{aligned} \lim _{r \rightarrow +\infty }\frac{b(r)}{r} = \alpha , \end{aligned}$$

(58)

thus

$$\begin{aligned} ds^{2}=-dt^{2}+\frac{dr^{2}}{\left( 1-\alpha \right) }+r^{2}d\varOmega ^{2}, \end{aligned}$$

(59)

which is not the usual flat space, unless $\alpha =0$. However, the space-time given by (59) describes a space-time with a solid angle deficit (or excess) [40]. This can be seen directly by making the rescaling $R^{2}=\frac{r^{2}}{1-\alpha }$. Then the metric (59) becomes

$$\begin{aligned} ds^{2}=-dt^{2}+dR^{2}+\alpha R^{2}d\varOmega ^{2}. \end{aligned}$$

(60)

In this fashion the asymptotic metric (60) exhibits explicitly the presence of a solid angle deficit for $0<\alpha <1$, and a solid angle excess for $\alpha <0$ (this case is discarded due to Eq. (54)). It is remarkable to note that the solid angle of a sphere of unity radius is now $4\,\pi \,\left( 1-\alpha \right) < 4\, \pi$ for $0<\alpha <1$, and $4\,\pi \,\left( 1-\alpha \right) > 4\, \pi$ for $\alpha <0$. It is clear that the topological defect at large distances is introduced by the MGD grasp. Conversely, the Eq. (56) yields to a bounded mass and asymptotically flat space-time.

5.3 Asymptotic flatness analysis

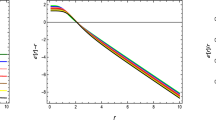
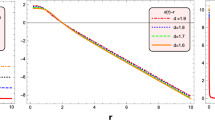
As has already been discussed, both models #1 and #2 give place to non-asymptotically flat wormholes. As depicted in Figs. 1 and 2 , the dimensionless shape function (solid line) tends to infinity when the radial coordinate, r, increases. In contrast, the GR limit $\alpha \rightarrow 0$ (solid black line), which corresponds to the non-deformed M–T solution (22), exhibits an asymptotically flat behavior with increasing r. Therefore, the following question arises: are all minimally deformed solutions non-asymptotically flat? In principle it is not possible to provided an answer to this claim. However, the analysis of the properties of any asymptotically flat space-time makes possible to obtain valuable information about this issue. As it is well-known, the metric tensor, $g_{\mu \nu }$, of any asymptotically flat space-time goes as

$$\begin{aligned} g_{\mu \nu }=\eta _{\mu \nu }+{\mathscr {O}}(1/r), \end{aligned}$$

(61)

when $r\rightarrow +\infty$, being $\eta _{\mu \nu }$ the Minkowski metric [106]. As the Ricci scalar involves second derivatives of the metric tensor, the Ricci scalar behaves as

$$\begin{aligned} R={\mathscr {O}}(1/r^{3}) \end{aligned}$$

(62)

when $r\rightarrow +\infty$. By taking advantage of this information, Eqs. (1) and (11) imply that the Ricci scalar reads

$$\begin{aligned} R(r)=\frac{2}{r}\left( b'(r)+\alpha f'(r)\right) , \end{aligned}$$

(63)

where we have considered that the red-shift function, $\varPhi (r)$, is zero. Therefore, to assure an asymptotically flat wormhole space-time, $f'(r)$ should be at least of order of ${\mathscr {O}}(1/r^{2})$. Of course, from the very beginning and knowing the metric tensor behavior (61) one can choose $f(r)={\mathscr {O}}(1/r)$ (assuming that the seed shape function b(r) already satisfies this condition, as it is done in this case by the choice $b(r)=r^{2}_{0}/r$). Nevertheless, this procedure implies that one is fixing the decoupler function, f(r), by hand in order to close the $\theta$-sector (16)–(18). On the contrary, if f(r) is obtained by assuming a specific behaviour for the $\theta$-sector (or by imposing some relation between its components), it is not possible to predict the behavior of the minimally deformed shape function at large distances. This information can be only revealed after the system of Eqs.  (16)–(18) has been solved. Therefore, the (non-) asymptotically flat behaviour depends on how the $\theta$-sector is closed. Interestingly, it is possible to satisfy at least the flare-out condition at the wormhole throat regardless of the non-asymptotically flat behavior of the solutions. As it is shown in Figs. 1 and 2 , the flare-out condition at the throat ı.e., $b'(r_{0})<1$ (dashed lines) is satisfied in all cases for both models. The M–T flare-out condition is also illustrated (dashed black curve). It should be noted that the flare-out condition at the wormhole throat is satisfied because the constant parameter $\alpha$ satisfies certain constraints imposed by (48) and (52) for the models $\#1$ and $\#2$, respectively. This signals that MDG is quite involved on this fundamental feature of wormhole structures.

Fig. 1

The trend of the dimensionless shape function $b(r)/r_{0}$ and the dimensionless flare-out condition $b'(r)r_{0}$ evaluated at the wormhole throat against the radial coordinate r (km), for the model $\#1$. The black curves represent the pure GR counterpart of the model ı.e., the Morris–Thorne (M–T) wormhole space-time. These curves were obtained by using the numerical values provided in Table 3

Fig. 2

The trend of the dimensionless shape function $b(r)/r_{0}$ and the dimensionless flare-out condition $b'(r)r_{0}$ evaluated at the wormhole throat against the radial coordinate r (km), for the model $\#2$. The black curves represent the pure GR counterpart of the model ı.e., the Morris–Thorne (M–T) wormhole space-time. These curves were obtained by using the numerical values provided in Table 5

5.4 The embedding diagram

Since we are dealing with spherically symmetric and static wormhole solutions, from the general line element (1) one can get relevant information about the form of the wormhole structure [8]. Focusing on an equatorial plane, $\varphi =\pi /2$, the solid angle element $d\varOmega ^{2}$ reduces to

Fig. 3

The figure shows the 2-dimensional wormhole embedding diagram for the model $\#1$. The vertical axis has been re-scaled by a factor $10^{33}$

Fig. 4

The figure shows 2-dimensional wormhole embedding diagram for the model $\#2$. The vertical axis has been re-scaled by a factor $10^{9}$

$$\begin{aligned} d\varOmega ^{2}=d\phi ^{2}. \end{aligned}$$

(64)

Besides, by fixing $t=\text {constant}$, the line element (1) becomes

$$\begin{aligned} ds^{2}=\frac{dr^{2}}{1-\frac{b(r)}{r}}+r^{2}d\phi ^{2}. \end{aligned}$$

(65)

To visualize this equatorial plane as a surface embedded in an Euclidean space, it is convenient to introduce cylindrical coordinates as

$$\begin{aligned} ds^{2}=dz^{2}+dr^{2}+r^{2}d\phi ^{2}, \end{aligned}$$

(66)

Fig. 5

The figure shows the three dimensional wormhole embedding diagram for the model $\# 1$ case $\omega _{b}=4/5$ (left diagram) and $\gamma =1$ (middle diagram) and $\gamma =2$ (right diagram) for model $\#2$

or, equivalently,

$$\begin{aligned} ds^{2}=\left[ 1+\left( \frac{dz}{dr}\right) ^{2}\right] dr^{2}+r^{2}d\phi ^{2}. \end{aligned}$$

(67)

Now, comparing (65) and (67), one obtains

$$\begin{aligned} \frac{dz}{dr}=\pm \left( \frac{r}{b(r)}-1\right) ^{-1/2}, \end{aligned}$$

(68)

where the function $z=z(r)$ defines the embedded surface [5, 6, 8]. Interestingly, when $r\rightarrow +\infty$ the expression (68) leads to

$$\begin{aligned} \frac{dz}{dr}\bigg |_{r\rightarrow +\infty }=0, \end{aligned}$$

(69)

which tells us that the embedding diagram provides two asymptotically flat patches. Of course, this is not the case as was pointed out before. In addition, note that the integration of Eq. (68) can not be done analytically. Therefore, a numerical treatment has been done in order to illustrate the wormhole shape given in Figs. 3 and  4, the 2-dimensional embedding diagram (the z(r) function) versus the radial coordinate r for both models. Furthermore, the 3-dimensional hyper-surfaces are shown in Fig. 5. The left one corresponds to the model $\#1$ for $\omega _{b}=4/5$ and the middle and right ones for the model $\#2$. The 2-dimensional and 3-dimensional diagrams corroborate the non-asymptotically flat nature of the solutions.

6 Matter distribution analysis

In this section we analyze the effective matter distribution and its behavior. In this concern, the so-called energy conditions (ECs) are thoroughly studied in order to impose some constraints on the space parameter $\{\alpha ,\beta ,\omega \}$, to obtain a wormhole solution threading by a minimum amount of exotic matter distribution in the present scenario ı.e., gravitational decoupling by means of MGD. Moreover, as the above models are not asymptotically flats, we investigate the presence of surface stresses at the junction interface, where if there are surface stresses on the hyper-surface $\varSigma$, one has a thin shell, otherwise the junction interface denotes a boundary surface.

6.1 Energy conditions

As was pointed out before, in working out wormhole structures in the GR scenario the so-called ECs are violated. This fact seems to be a necessary condition to build up a well posed wormhole structure in the framework of GR [9, 10]. This unusual situation occurs since the radial pressure $p_{r}$ is negative and greater in magnitude than the energy–density $\rho$. Then

$$\begin{aligned} \rho +p_{i}\ge 0, \quad i\in \{r,t\}, \end{aligned}$$

(70)

is not satisfied neither at the wormhole throat nor beyond it. The situation get worse when the energy–density is negative too. Hence, the WEC, expressed as

$$\begin{aligned} \rho +p_{i}\ge 0, \quad i\in \{r,t\} \quad \text{ and } \quad \rho \ge 0, \end{aligned}$$

(71)

is also violated. This kind of matter is known as exotic. From the physical point of view, a negative radial pressure can be interpreted as an anti-gravitational force which holds the wormhole throat open. In this regard, negative pressures are widely accepted at either a classical or quantum level. Conversely, a negative energy–density is not plausible (at least classically [107]). However, the main aim here is not only to analyze the NEC and WEC but also the strong (SEC) and dominant energy conditions (DEC), which read

$$\begin{aligned}&\rho +\sum _{r,t} p_i \ge 0, \end{aligned}$$

(72)

$$\begin{aligned}&\rho \ge |p_i|, \end{aligned}$$

(73)

respectively.

Now using the full geometry of the wormhole solutions and with the help of Eqs. (16)–(18), (23) and (28) we can determine the full components of the effective energy–momentum tensor (3) for each model.

Table 1 The general constraints on $\alpha$, obtained from the energy conditions for the model $\#$1, by considering both positive and negative EoS parameter $\omega$

Table 2 The numerical constraints imposed on $\alpha$ by the energy conditions and the flare-out condition, for different values of the EoS parameter $\omega$

For the model $\#$1 we have imposed the most general linear EoS (23) to close the $\theta$-sector, obtaining the decoupler function f(r) given by Eq. (25). Next, to check the feasibility of satisfying all the energy conditions (at least at the wormhole throat), we will consider several values for the parameter $\omega$. Specifically, we will take values corresponding to cosmic fluids, for example baryonic matter, phantom and quintessence fields, cosmological constant, and so on. Of course, the EoS of any cosmic fluid does not has the form given by (23) (actually this corresponds to the case $\beta =0$), for this reason we will call each of these cases phantom-like field and use the $\omega _{p}$ symbol to make the corresponding reference, for example. At this point, it is worth mentioning that in the realm of wormhole solutions within the framework of GR, it is not possible to satisfy at the same footing both, the flare-out condition and the ECs. However, the introduction of the pair $\{\theta _{\mu \nu },f\}$ could in principle reduce the usage of exotic matter to a minimal amount, leading to a partial violation of the energy conditions. Furthermore, a negative definite energy density could be avoided. In order to test the possibility of simultaneously satisfying both the flare-out condition and the ECs, we consider the following options for the EoS parameter $\omega$ known for some types of matter, fluid and field cosmic distributions [108, 109],

• baryonic-like matter: $0<\omega _{b}<1$,

• cosmological constant-like fluid: $\omega _{c}=-1$,

• quintessence-like field: $-1<\omega _{q}<-\frac{1}{3}$,

• phantom-like field: $\omega _{p}<-1$.

In this case the radiation-like matter corresponding to $\omega _{r}=1/3$ is not allowed, since as was previously noticed, the mass function (41) becomes singular. Before in going into the analysis, it is instructive to present the explicit form of the effective thermodynamic quantities describing the energy–momentum tensor of the matter distribution threading the wormhole solution. So, one has

Model $\#1$:

$$\begin{aligned} \rho= & {} -\underbrace{\frac{r^{2}_{0}}{r^{4}}}_{{\tilde{\rho }}}+\alpha \underbrace{\frac{\left( r^{3-{\omega }}r^{-3+{\omega }}-3\omega \right) }{\omega \left( 3\omega -1\right) }\beta }_{\theta ^{0}_{\ 0}}, \end{aligned}$$

(74)

$$\begin{aligned} p_{r}= & {} \underbrace{-\frac{r^{2}_{0}}{ r^{4}}}_{{\tilde{p}}_{r}}-\alpha \left[ \underbrace{\frac{\left( r^{3-{\omega }}r^{-3+{\omega }}-3\omega \right) }{\left( 3\omega -1\right) } \beta +\beta }_{\theta ^{1}_{\ 1}}\right] , \end{aligned}$$

(75)

$$\begin{aligned} p_{t}= & {} \underbrace{\frac{r^{2}_{0}}{r^{4}}}_{{\tilde{p}}_{t}}-\alpha \underbrace{\frac{\beta }{2\left( 1-3\omega \right) }\frac{\left( 2\omega +\left( \omega -1\right) r^{3-{\omega }}_{0}r^{-3+{\omega }}\right) }{\omega }}_{\theta ^{2}_{\ 2}}.\nonumber \\ \end{aligned}$$

(76)

In Table 1 we have placed the constraints on the constant $\alpha$, in order to satisfy the ECs. In this analysis we have considered as an example the case when $\beta >0$ and both positive and negative $\omega$. The case $\beta <0$, will not be considered here. However, if one wants to do it, the procedure runs in the same way like in the considered case. Next, taking into account the above assumptions from the flare-out condition we get

$$\begin{aligned} \omega>0 \Rightarrow \alpha > -\frac{2\omega }{\beta r^{2}_{0}}, \quad \omega<0 \Rightarrow \alpha < -\frac{2\omega }{\beta r^{2}_{0}}. \end{aligned}$$

(77)

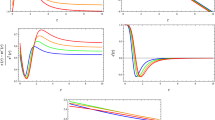
In Table 2 are summarized the numerical values for the coupling $\alpha$ in order to meet the flare-out and ECs. In obtaining these numerical values at the throat of the wormhole structure, we have considered in all cases $\beta =0.45\, (\text {km}^{-2})$ and the size of the wormhole throat $r_{0}=1\, (\text {km})$, for different values of the EoS parameter $\omega$ mentioned in Table 2. As was anticipated, it is not possible to satisfy at the same time the mentioned conditions. This fact can be observed from the second and sixth columns of Table 2, where $\alpha$ is subject to fulfill the ECs or the flare-out condition at the throat of the wormhole. In this regard, as we are interested on traversable wormholes, it is obvious that the flare-out condition must be satisfied. So, to fulfill it, we have taken for each $\omega$ appropriate values for $\alpha$. These values were considered by taking into account the constraints placed in Table 2. Specifically, these values are shown in Table 3 for each EoS parameter $\omega$. It is worth mentioning that the chosen numerical values for $\alpha$, do not deviate too much from the values that satisfy the NEC, WEC and DEC in the radial direction. This in order to control the violation of the ECs at the throat of the wormhole. As can be seen in Figs. 6 and 7 , for each case under consideration, the violation of the NEC, WEC and DEC in the radial direction occurs only at the throat, and beyond it they are satisfied. Furthermore, in the inside panels it is observed that the magnitude of such violation is minimal in relation to the GR picture. On the other hand, interestingly the remaining ECs are satisfied for all $r \in [r_ {0}, + \infty )$. Regarding, the individual behavior of the thermodynamic parameters $\{\rho , p_ {r}, p_ {t}\}$, a positive definite density $\rho$ is exhibited everywhere, although it is not bounded, which contrast the fact of not having a bounded mass. Instead, the radial pressure $p_{r}$ is negative throughout its domain, acting as a repulsive gravitational force, helping to keep the object’s throat open. Concerning the tangential pressure $p_{t}$, it is positive at the throat, but then it becomes negative. It should be noted that the amount of exotic matter is greatly reduced when $\omega$ moves from $\frac{4}{5}$ to $-\frac{4}{3}$. This indicates that a phantom-like field combined with the MGD scheme as an exotic matter regulator, is the best option to build up wormhole solutions supported by a small amount of exotic matter. This point will be clear soon, when the exotic matter quantifier will be calculated.

Table 3 The numerical values for $\alpha$, taking into account different choices for the EoS parameter $\omega$ and for $\beta =0.45\, (\text {km}^{-2})$ and $r_{0}=1\, (\text {km})$

Fig. 6

The density $\rho$, radial pressure $p_{r}$, tangential pressure $p_{t}$, NEC, WEC and SEC for the model $\#$1, using different values for the EoS parameter $\omega$ and $\alpha$ showed in Table 3. Besides, in building these curves against the dimensionless coordinate $r/r_{0}$ we have fixed $\beta =0.45\,(\text {km}^{-2})$ and the wormhole throat size $r_{0}=1$

Fig. 7

The dominant energy condition along the radial and tangential directions for the model $\#$1 against the dimensionless coordinate $r/r_{0}$ and different values mentioned in the Table 3, considering $\beta =0.45\,(\text {km}^{-2})$ and the wormhole throat size $r_{0}=1$

Model $\#2$:

In this case the energy–momentum tensor is being characterized by the following thermodynamic variables

$$\begin{aligned} \rho= & {} -\underbrace{\frac{r^{2}_{0}}{r^{4}}}_{{\tilde{\rho }}}+\alpha \underbrace{\left[ 1+\left( \frac{r}{b}\right) ^{2}\right] ^{-\gamma }a}_{\theta ^{0}_{\ 0}}, \end{aligned}$$

(78)

$$\begin{aligned} p_{r}= & {} \underbrace{-\frac{r^{2}_{0}}{ r^{4}}}_{{\tilde{p}}_{r}}-\alpha \underbrace{\left[ \frac{a}{3}\left( {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}}{b^{2}}\right] -{}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}_{0}}{b^{2}}\right] \frac{r^{3}_{0}}{r^{3}}\right) \right] }_{\theta ^{1}_{\ 1}}, \end{aligned}$$

(79)

$$\begin{aligned} p_{t}= & {} \underbrace{\frac{r^{2}_{0}}{r^{4}}}_{{\tilde{p}}_{t}}-\alpha \underbrace{\bigg [\frac{a}{6}\bigg (3\bigg (1+\frac{r^{2}}{b^{2}}\bigg )^{-\gamma }+ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}_{0}}{b^{2}}\right] \frac{r^{3}_{0}}{r^{3}}-{}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}}{b^{2}}\right] \bigg )\bigg ]}_{\theta ^{2}_{\ 2}}. \end{aligned}$$

(80)

The analysis of the matter content in this case, was carried out by considering positive integer values for $\gamma$. Specifically, we have considered the genuine PI dark matter profile corresponding to $\gamma =1$ and a generalized case by imposing $\gamma =2$. In Table 4, we have depicted the general constraints on $\alpha$ at the wormhole throat imposed by the ECs, while by using the numerical data presented in Table 5 for different values of the space parameter $\{a,b,\gamma \}$ and setting again the wormhole throat value $r_{0}=1$, in Table 6 are displayed the concrete numerical bounds Again, the NEC, WEC and DEC in the radial direction are violated at the wormhole throat, although are satisfying beyond it, what is more all are saturated as illustrates Fig. 8. In comparing both cases, namely $\gamma =1$ and $\gamma =2$ it is clear from the upper and lower left panels in Fig. 8 that for $\gamma =1$ the violation of the NEC and WEC is greater than the $\gamma =2$ case. The same scenario is observed in the upper and lower right panels regarding the DEC. Nevertheless, in such situation for $\gamma =1$ the DEC in the radial direction is saturated away the throat, while for $\gamma =2$ there is a small fluctuation (the red curve takes negative values) before reaching the saturation. It is important to stress that the Eq.  (28) assures the monotonically decreasing behavior of $\rho$ yielding to a bounded density and consequently to a finite bounded mass at very large distances. Moreover, the same trend is exhibited by the radial $p_{r}$ and tangential $p_{t}$ pressures as well as by the ECs. This is complete agreement with the asymptotically flat behavior, where at large radial coordinate, at least $\rho$ and $p_{r}$ should tend to zero [108]. It is evident that the modified PI dark matter profile offers a best scenario than the original PI ($\gamma =1$).

As it is observed on Tables 1 and 4 for the models $\#1$ and $\#2$ respectively, the $\alpha$ parameter can be taken to be 0 in order to satisfy the energy conditions. However, as it was mentioned above, the case $\alpha =0$ reduces to the GR case. In this situation the pure GR case (the seed solution given by (22)) is described by the original Morris–Thorne solution [5, 6]. As it is well-known, this space-time is supported by an exotic matter distribution in the GR scenario [5, 6]. Even more, if the energy conditions are satisfied then the flare-out condition will not and vice-versa [9]. So, in both cases, namely pure GR and GR + MGD, it is not possible for both the energy conditions and the flare-out one to be satisfied at the same footing [9]. Then, in order to explore new features of this space-time under the minimally deformation process, we have taken $\alpha \ne 0$ for both models (see Tables 3, 5).

6.2 The exoticity parameter, $\chi$

It is clear from previous discussions that the minimally deformed M–T wormhole solution is driven by an exotic matter distribution. Interestingly, the $\theta$-sector, interpreted as dark matter/energy distribution, greatly reduces the magnitude of the violation of the energy conditions, in contrast with the pure GR case [5, 6]. To check the feasibility of the MGD ingredients as exotic matter contributors which support the wormhole structure, one can use the so-called “exoticity” parameter, $\chi$ [5, 6], which is defined as

$$\begin{aligned} \chi =\frac{p_{r}-\rho }{|\rho |}, \end{aligned}$$

(81)

or, in terms of the shape function b(r),

$$\begin{aligned} \chi =\frac{b-rb'}{r|b'|}. \end{aligned}$$

(82)

This dimensionless parameter signals the presence of exotic matter if $\chi >0$. Of course, it can be seen from Eq. (81) that this requirement is satisfied if

$$\begin{aligned} |p_{r}|>|\rho |. \end{aligned}$$

(83)

Equivalently, from Eq. (82) one gets

$$\begin{aligned} |b|>|rb'|. \end{aligned}$$

(84)

In Figs. 9 and 10 we have plotted the exoticity parameter, $\chi$, for both models. As it can be shown, $\chi$ is positive at the wormhole throat in both cases. Therefore, the minimally M–T wormhole is driven by an exotic matter distribution, as previously established. This implies that the $\theta$-sector, representing the dark sector of the Universe, can be used to build up wormhole structures in the framework of GR+MGD supported by a small amount of exotic matter.

Table 4 The general constraints on $\alpha$, obtained from the energy conditions for the model $\#$2, taking into account that the space parameter $\{\gamma ,a,b\}$ is positive defined

Table 5 The selected numerical values for the coupling $\alpha$ for some values of $\gamma$, a and b, and considering the wormhole throat $r_{0}=1\,(\text {km})$

Table 6 The numerical data on the constraints for $\alpha$ corresponding to model $\#$2 obtained by fixing the numerical values depicted in Table 5

As was discussed before, a key element in studying traver- sable wormhole solutions is the flare-out condition. Following [5, 6], this condition can be rewritten at the wormhole throat, $r_{0}$, in terms of $\chi _{0}=\chi (r_{0})$ as follows

$$\begin{aligned} \chi _{0}=\frac{p_{r0}-\rho _{0}}{|\rho _{0}|}, \end{aligned}$$

(85)

where $\rho _{0}$ and $p_{r0}$ stand for $\rho _{0}=\rho (r_{0})$ and $p_{r0}=p_{r}(r_{0})$, respectively. Therefore, the flare-out condition written in terms of the exoticity parameter demands that $\chi _{0}$ should be strictly positive at the throat. This condition, coming from Eq. (83) evaluated at $r=r_{0}$, is satisfied as shown in Figs. 9 and 10. Interestingly, if one uses Eq. (82) instead of (81), the requirement for the flare-out condition is also meet. Of course, as we know that $b(r_{0})=r_{0}$ and $b'(r_{0})<1$, $b(r_{0})-r_{0}b'(r_{0})$ is always positive.

6.3 Volume integral quantifier

An important point to be considered at this stage, is the so-called volume integral quantifier given by

$$\begin{aligned} {\mathfrak {I}}_{V}\equiv \int \left[ \rho (r)+p_{r}(r)\right] dV. \end{aligned}$$

(86)

The above integral provides valuable information on the total amount of averaged null energy condition (ANEC) violating matter distribution in the space-time [110,111,112] (also see [113] for further analysis on this subject). Imposing a cut-off of the energy–momentum tensor at $r_{*}>r$, in spherical coordinates the integral ${\mathfrak {I}}_{V}$ becomes [110, 111],

Fig. 8

The thermodynamic variables and energy conditions against the dimensionless variable $r/r_{0}$, for the model $\#$2, taking the numerical data presented in Table 5

$$\begin{aligned} {\mathfrak {I}}_{V}&=\left[ r\left( 1+\frac{b(r)}{r}\right) \text {Ln}\left( \frac{e^{2\varPhi }}{1-b(r)/r}\right) \right] ^{r_{*}}_{r_{0}} \nonumber \\&\quad -\int ^{r_{*}}_{r_{0}}\left[ r-b^{\prime }(r)\right] \text {Ln}\left( \frac{e^{2\varPhi }}{1-b(r)/r}\right) dr \nonumber \\&= \int ^{r_{*}}_{r_{0}}\left[ r-b(r)\right] \left[ \text {Ln}\left( \frac{e^{2\varPhi }}{1-b(r)/r}\right) \right] ^{\prime }dr. \end{aligned}$$

(87)

For the model $\#$1 described by the form function (35), the Eq. (87) can be evaluated without specifying the numerical values for any parameter, yielding to

$$\begin{aligned} \begin{aligned} {\mathfrak {I}}_{V}&=\frac{r^{-\frac{1}{\omega }}_{0}}{\left( 1-3\omega \right) \omega }\bigg [\frac{2\,}{3}\,\beta \,\alpha \,\omega \,r_{*}\,r^{\frac{1}{\omega }}_{0}+\beta \,\alpha \,r^{\frac{1}{\omega }}_{*}r^{3}_{0}\left( \omega -1\right) \omega \\&\quad +\frac{2\omega }{r_{*}}r^{2+\frac{1}{\omega }}_{0}\left( 1-3\omega \right) -\frac{2\,}{3}\,\beta \,\alpha \,\omega \,r^{1+\frac{1}{\omega }}_{0}-\beta \,\alpha \,r^{3+\frac{1}{\omega }}_{0}\left( \omega -1\right) \omega \\&\quad -2\omega \,r^{1+\frac{1}{\omega }}_{0}\left( 1-3\omega \right) \bigg ]. \end{aligned}\nonumber \\ \end{aligned}$$

(88)

Taking the limit $r_{*}\rightarrow r_{0}$ in (88), one verifies that ${\mathfrak {I}}_{V}\rightarrow 0$, which reflects arbitrary small quantities of energy condition violating matter. Next, the evaluation of (87) for the model $\#$2 with $\gamma =1$ leads to

$$\begin{aligned} \begin{aligned} {\mathfrak {I}}_{V}&=2\frac{r^{2}_{0}}{r_{*}} +a\, b^{3}\, \alpha \, \text {arctan} \left[ \frac{b}{r_{*}}\right] -a\,b^{2}\,\alpha \bigg (b\,\text {arctan} \left[ \frac{r_{0}}{b}\right] \\&\quad -r_{0}\bigg )\text {Ln}r_{*}+\frac{i}{2}\,a\, b^{2}\, \alpha \left( \text {Li}_{2}\left[ -\frac{ir_{*}}{b}\right] -\text {Li}_{2}\left[ \frac{ir_{*}}{b}\right] \right) \\&\quad -2r_{0}-a\, b^{3}\, \alpha \, \text {arctan}\left[ \frac{b}{r_{0}}\right] +a\,b^{2}\,\alpha \bigg (b\,\text {arctan}\left[ \frac{r_{0}}{b}\right] \\&\quad -r_{0}\bigg )\text {Ln}r_{0}-\frac{i}{2}\,a\, b^{2}\, \alpha \left( \text {Li}_{2}\left[ -\frac{ir_{0}}{b}\right] -\text {Li}_{2}\left[ \frac{ir_{0}}{b}\right] \right) , \end{aligned}\nonumber \\ \end{aligned}$$

(89)

where $\text {Li}_{s}(z)$ is the polylogarithmic function, which for real or complex s and complex z subject to $|z|<1$ is defined by

$$\begin{aligned} \text {Li}_{s}(z)=\sum ^{\infty }_{n=1}\frac{z^{n}}{n^{s}}. \end{aligned}$$

(90)

So, the terms in (89) involving this object becomes

$$\begin{aligned} i\left( \text {Li}_{2}\left[ -\frac{ir_{*}}{b}\right] -\text {Li}_{2}\left[ \frac{ir_{*}}{b}\right] \right) =2\frac{r_{*}}{b}, \end{aligned}$$

(91)

and

$$\begin{aligned} i\left( \text {Li}_{2}\left[ -\frac{ir_{0}}{b}\right] -\text {Li}_{2}\left[ \frac{ir_{0}}{b}\right] \right) =2\frac{r_{0}}{b}. \end{aligned}$$

(92)

Again, in the limit $r_{*}\rightarrow r_{0}$ one gets ${\mathfrak {I}}_{V} \rightarrow 0$, confirming that to support this wormhole structure it is necessary only a small amount of ANEC violating matter distribution. Similarly, for $\gamma =2$ we have

$$\begin{aligned} \begin{aligned} {\mathfrak {I}}_{V}&=2\frac{r^{2}_{0}}{r_{*}}-\frac{a\,b^{4}\,\alpha \,r_{*}}{2\left( b^{2}+r^{2}_{*}\right) }\\&\quad -a\,b^{3}\,\alpha \,\text {arctan} \left[ \frac{b}{r_{*}}\right] +\frac{a\,b^{3}\,\alpha }{2\left( b^{2}+r^{2}_{0}\right) } \\&\quad \times \left[ \left( b^{2}+r^{2}_{0}\right) \,\text {arctan} \left[ \frac{r_{0}}{b}\right] -b\,r_{0}\right] \text {Ln}\,r_{*}\\&\quad -\frac{i}{4}\,a\, b^{3}\, \alpha \bigg (\text {Li}_{2}\left[ -\frac{ir_{*}}{b}\right] -\text {Li}_{2}\left[ \frac{ir_{*}}{b}\right] \bigg )\\&\quad -2r_{0}+\frac{a\,b^{4}\,\alpha \, r_{0}}{2\left( b^{2}+r^{2}_{0}\right) }\\&\qquad +a\,b^{3}\,\alpha \,\text {arctan} \left[ \frac{b}{r_{0}}\right] \\&\quad -\frac{a\,b^{3}\,\alpha }{2\left( b^{2}+r^{2}_{0}\right) }\left[ \left( b^{2}+r^{2}_{0}\right) \,\text {arctan}\left[ \frac{r_{0}}{b}\right] -b\,r_{0}\right] \text {Ln}\,r_{0}\\&\quad +\frac{i}{4}\,a\, b^{3}\, \alpha \bigg (\text {Li}_{2}\left[ -\frac{ir_{0}}{b}\right] -\text {Li}_{2}\left[ \frac{ir_{0}}{b}\right] \bigg ), \end{aligned} \end{aligned}$$

(93)

which tends to zero when $r_{*}\rightarrow r_{0}$.

6.4 Surface stresses

Given that the models $\#1$ and $\#2$ (the case $\gamma =1$) have not a bounded mass and taking into account that $\#$1 does not reproduce the Minkowski space-time when $r\rightarrow +\infty$, it is necessary to do a surgery at some point $r_{*}>r_{0}$ with the vacuum Schwarzschild space-time to cure this pathology. Thus the manifolds given by models $\#$1 and $\#$2 are describing the inner ${\mathscr {M}}^{-}$ space-time valid from $r\ge r_{0}$ up to $r\le r_{*}$ and the Schwarzschild solution describes the outer manifold ${\mathscr {M}}^{+}$ valid for all $r> r_{*}$. In this regard, on the junction interface $\varSigma : r=r_{*}$ in principle these manifolds could induce surface stresses ı.e, a surface energy–density $\sigma$ and a surface pressure ${\mathscr {P}}$. If the junction contains surface stresses, we have a thin shell, and if no surface stresses are present, the junction interface is denoted a boundary surface. To analyze the presence of surface stresses on the junction surface we shall employ the Israel–Darmois formalism [20, 21].

The extrinsic curvature across the surface $\varSigma$ is characterized by the symmetric extrinsic curvature tensor $K_{ij}$ (also known as the second fundamental form) given by

$$\begin{aligned} K_{i j}^{\pm }=-n_{\mu }\left( \frac{\partial ^{2} x^{\mu }}{\partial \xi ^{i} \partial \xi ^{j}}+\varGamma _{\alpha \beta }^{\nu \pm } \frac{\partial x^{\alpha }}{\partial \xi ^{i}} \frac{\partial x^{\beta }}{\partial \xi ^{j}}\right) , \end{aligned}$$

(94)

where the (±) superscripts correspond to the exterior and interior space-times, respectively. Besides, $\xi ^{i}=\{\tau ,\theta ,\varphi \}$ are the intrinsic coordinates on $\varSigma$ and $\tau$ is the proper time on the hyper-surface. It should be noted that due to spherical symmetry the computation is considerable reduced, namely $K^{i}_{\ j}=\left( K^{\tau }_{\ \tau },K^{\theta }_{\ \theta },K^{\theta }_{\ \theta }\right)$. Then the energy–momentum tensor $S^{i}_{\ j}$ induced on $\varSigma$ is given by the Lanczos equations, as follows

$$\begin{aligned} S^{i}_{\ j}=-\frac{1}{8\pi }\left( [K^{i}_{\ j}]-\delta ^{i}_{\ j}[K]\right) , \end{aligned}$$

(95)

where $[X]=X^{+}-X^{-}$ expresses the discontinuity in the second fundamental form and $K\equiv K^{i}_{\ i}$ denotes the trace of the extrinsic curvature tensor. In terms of the surface energy–density $\sigma$ and pressure ${\mathscr {P}}$ the energy–momentum tensor $S^{i}_{\ j}$ reads

$$\begin{aligned} S^{i}_{\ j}=\text {diag}\left( -\sigma ,{\mathscr {P}},{\mathscr {P}}\right) . \end{aligned}$$

(96)

So the Lanczos equations (95) can be expressed as²

$$\begin{aligned} \sigma= & {} -\frac{1}{4\pi }[K^{\theta }_{\ \theta }], \end{aligned}$$

(97)

$$\begin{aligned} {\mathscr {P}}= & {} \frac{1}{8\pi }\left( [K^{\tau }_{\ \tau }]+[K^{\theta }_{\ \theta }]\right) . \end{aligned}$$

(98)

Now, using (94), the non trivial components of the extrinsic curvature tensor for the line elements (1) and (42) are given by [13]

$$\begin{aligned} K^{\tau +}_{\ \tau }= & {} \frac{M}{r^{2}_{*}\sqrt{1-\frac{2M}{r_{*}}}}, \end{aligned}$$

(99)

$$\begin{aligned} K^{\theta +}_{\ \theta }= & {} {r_{*}}\sqrt{1-\frac{2M}{r_{*}}}, \end{aligned}$$

(100)

$$\begin{aligned} K^{\theta -}_{\ \theta }= & {} {r_{*}}\sqrt{1-\frac{b(r_{*})}{r_{*}}}. \end{aligned}$$

(101)

Next from Eqs. (97)–(98) and with the extrinsic curvature expressions (99)–(101), we obtain

$$\begin{aligned} \sigma= & {} -\frac{1}{4\pi r_{*}}\left( \sqrt{1-\frac{2M}{r_{*}}}-\sqrt{1-\frac{b(r_{*})}{r_{*}}}\right) , \end{aligned}$$

(102)

$$\begin{aligned} {\mathscr {P}}= & {} \frac{1}{8\pi r_{*}}\left( \frac{1-\frac{M}{r_{*}}}{\sqrt{1-\frac{2M}{r_{*}}}}-\sqrt{1-\frac{b(r_{*})}{r_{*}}}\right) . \end{aligned}$$

(103)

The surface mass of the thin shell can be computed as

$$\begin{aligned} M_{\text {shell}}=4\,\pi \,r^{2}_{*}\,\sigma =r_{*}\left( \sqrt{1-\frac{b(r_{*})}{r_{*}}}-\sqrt{1-\frac{2M}{r_{*}}}\right) , \end{aligned}$$

(104)

where M can be interpreted as the total mass of the system, in this case being the total mass of the wormhole in one asymptotic region [23]. From Eq. (104) one can solve for M, leading to

$$\begin{aligned} M=\frac{b(r_{*})}{2}+M_{\text{ shell } }\left( \sqrt{1-\frac{b(r_{*})}{r_{*}}}-\frac{M_{\text{ shell } }}{2 r_{*}}\right) . \end{aligned}$$

(105)

Following the same approach as given in [22,23,24,25,26] we study the surface stresses by introducing dimensionless parameters $\zeta =2M/r_{*}$, ${\bar{b}}(\zeta )=b(r_{*})/2\,M$, $\eta =8\,\pi \, M\,\sigma$ and $\varPi =16\,\pi \,M\,{\mathscr {P}}$. Therefore, Eqs. (102)–(103) become

$$\begin{aligned} \eta= & {} \zeta \,\left( \sqrt{1-\zeta \, {\bar{b}}(\zeta )}-\sqrt{1-\zeta }\right) , \end{aligned}$$

(106)

$$\begin{aligned} \varPi= & {} \zeta \left( \frac{1-\frac{\zeta }{2}}{\sqrt{1-\zeta }}-\sqrt{1-\zeta \,{\bar{b}}(\zeta )}\right) . \end{aligned}$$

(107)

To avoid a non-physical behavior one has the following constraint: $0<\zeta <1$. As at the junction interface the mass of the wormhole coincides with the Schwarzschild mass ı.e., $M=M_{\text {Sch}}$ this implies $b(r_{*})=2M$. So, replacing this result in the Eq. (102) (or Eq. (106)), it is not hard to show that the surface density $\sigma$ vanishes. Then, the thin shell is driven only by pressure ${\mathscr {P}}$. As it is appreciated, from Eq. (103) (or Eq. (107)), this quantity is always positive, thus the thin shell is threading by a normal matter distribution, that is, a matter satisfying the ECs. This is corroborated in Fig. 11, where we have displayed $\varPi$ for model $\#$1 and $\#$2 for the case $\omega =4/5$ and $\gamma =1$ (as an example), respectively. In doing that, we have selected two different values for M, namely 0.5 and 2. As said before, in both cases the dimensionless pressure $\varPi$ on the hyper-surface $\varSigma$ is positive defined. Therefore, all ECs are satisfied.

The surgery process should also ensure that $b(r_{*})/r_{*}<<1$ if the wormhole is to be used for traveling. This means that $r_{*}$ is large enough but finite, hence the mass function for every solution is also finite at large distances. Indeed

$$\begin{aligned} m(r_{*})=\frac{4\pi r^{2}_{0}}{r_{*}}+\frac{4\pi \alpha \beta }{1-3\omega }\left( r^{3}_{*}-r^{1/\omega }_{*}r^{3-1/\omega }_{0}\right) \end{aligned}$$

(108)

and

$$\begin{aligned} m(r_{*})= & {} \frac{4\pi r^{2}_{0}}{r_{*}}+\alpha \frac{2a\pi }{3}\left( \ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}_{*}}{b^{2}}\right] r^{3}_{*}\right. \nonumber \\&\left. -\ {}_2F_{1}\left[ \frac{3}{2},\gamma ;\frac{5}{2};-\frac{r^{2}_{0}}{b^{2}}\right] r^{3}_{0}\right) , \end{aligned}$$

(109)

are bounded after surgery.

Fig. 9

The exoticity parameter $\chi$ against the dimensionless radial coordinate $r/r_{0}$. These curves were obtained by considering the values mentioned in Table 3, for the model $\#$1

Fig. 10

The exoticity parameter $\chi$ versus the dimensionless radial coordinate $r/r_{0}$. These curves were obtained by considering the values mentioned in Table 5, for the model $\#$2

Fig. 11

The dimensionless pressure $\varPi$ on the surface interface $\varSigma$ against the dimensionless parameter $\zeta$. These curves were obtained by considering $\{\omega ;\alpha ;r_{0};r_{*}=\{\frac{4}{5};-3.450;1\,(\text {km});1.05\,(\text {km})\}$, for the the model $\#$1 and $\{\gamma ;\alpha ;r_{0};r_{*}=\{1;1.265;1\,(\text {km});2\,(\text {km})\}$ for the model $\#$2

7 Concluding remarks

In this work we have studied the impact of gravitational decoupling by means of minimal geometric deformation scheme on wormhole space-times, specifically on the well known Morris–Thorne wormhole model. We have faced the problem using two approaches in order to determine the $\theta$-sector and the decoupler function f(r). Those are: (i) the most general linear equation of state (23) depending on two constant parameters $\{\omega ,\beta \}$ was imposed and (ii) the temporal component of the $\theta _{\mu \nu }$ field ı.e, $\theta ^{0}_{\ 0}$ is was introduced in order to mimic a generalized pseudo-isothermal dark matter density profile (28), depending on three parameters $\{\gamma ,a,b\}$. These choices lead to solve an ordinary first order differential equation in f(r) (see Eqs. (24) and (29)). With the deformation function expression at hand the system of equations (16)–(18) for each model, is completely determined. Consequently, the effective thermodynamic quantities (8)–(10) and the minimally extended form function b(r) (11) are also obtained with the help of the seed wormhole space-time, given by (22). As the seed solution already meets all the requirements listed in Sect. 2, the new sector described by the pair $\{\theta _{\mu \nu },f(r)\}$ should satisfy some constraints to maintain the wormhole anatomy. In this concern, the decoupler function f(r) must be vanish at the throat $r_{0}$ of the wormhole ı.e, $f(r_{0})=0$. This is so because, the seed shape function ${\hat{b}}(r)$, evaluated at the wormhole throat leads to $r_{0}$. Besides, one of the conditions to be a traversable wormhole structure connecting two regions is the fulfillment of the so-called flare-out condition at the wormhole throat. Then, to meet the flare-out condition, in each case the dimensionless coupling constant $\alpha$ introduced by MGD has been restricted. As it is well-known, by construction a wormhole in the realm of GR can not satisfy at the same time the energy conditions everywhere and the flare-out condition [9, 10], and this case is not the exception. Nevertheless, the MGD approach could be understood in this context as an exotic matter regulator. Of course, the presence of the so-called exotic matter, is a necessary ingredient to support the wormhole structure, but sometimes it is desirable to control the amount of this exotic matter distribution, in order to have a small violation of the energy conditions at the wormhole throat and its neighborhood.

Regarding the wormhole geometry, we note that they are non-asymptotically flat. Specifically, the ratio b(r)/r and the mass function m(r) tends to infinity when $r\rightarrow +\infty$ for the model $\#1$. For model $\#2$, the geometry tends at large distances to a finite space-time with a topological defect with an unbounded mass function. To cure this issue, both models have been pasted with the Schwarzschild vacuum solution through a surgery process using the well-known Israel–Darmois junction conditions [20, 21] and the methodology presented in [22,23,24,25,26]. The resulting solutions are described by Eqs. (27) and (32) for $r_{0}\le r \le r_{*}$ and by the Schwarzschild space-time for $r>r_{*}$. After performing this procedure, both solutions become finite, their masses being bounded quantities. Furthermore, at the junction interface we have a thin shell confining the exotic matter inside the wormhole throat in a finite region. It is worth mentioning that the thin shell is supported by normal matter satisfying the energy conditions since the surface density, $\sigma$, vanishes. Therefore, the energy conditions are being only described by the lateral pressure ${\mathscr {P}}$ which is always positive. The non-asymptotically flat behavior of the models is based on how the $\theta$-sector is solved. In this sense, different forms of obtaining the pair $\{\theta _{\mu \nu },f\}$ lead to different wormhole geometries. One simple way to get an asymptotically flat wormhole is to impose from the very beginning the decoupler function f(r), assuring that f(r) falls at least as ${\mathscr {O}}(1/r)$.

Interestingly, in light of the results here reported, we can conclude that within the framework of GR with the application of gravitational decoupling by MGD scheme, it is possible to build up well-posed wormhole solutions threading by a small amount of exotic matter distribution. Furthermore, one can restrict the dimensionless coupling constant $\alpha$ to control the violation of the energy conditions at the wormhole throat, what is more a careful choice on $\alpha$ allows to satisfy the energy conditions away the wormhole throat and also helps to have a positive defined density everywhere. An important to point to be highlighted, is the introduction of deformation on the temporal component, in order to introduce a non vanishing red-shift function and also the study concerning the stability of the solutions against radial perturbations when large quantities of mass are injected through the structure. These issues will be addressed in future works.