Energy condition in unimodular f(R, T) gravity

Abstract

We study an interesting alternative of modified gravity theory, namely, the unimodular f(R, T) gravity in which R is the Ricci scalar and T is the trace of the stress–energy tensor. We study the viability of the model by using the energy conditions. We discuss the strong, weak, null and dominant energy conditions in terms of deceleration, jerk and snap parameters. We investigate energy conditions for reconstructed unimodular f(R, T) models and give some constraints on the parametric space of the model. We observe that by setting appropriately free parameters, energy conditions can be satisfied. Furthermore, we study the stability of the solutions in perturbations framework. In this case, we investigate stability conditions for de Sitter and power law solutions and we examine viability of cosmological evolution of these perturbations. The results show that for some values of the input parameters, for which energy conditions are satisfied, de Sitter and power-law solutions may be stable.

1 Introduction

Observations of type Ia Supernova(SN Ia) indicate that the universe currently is in a phase of positively accelerated expansion [1,2,3,4,5]. General Relativity (GR) based on the Einstein–Hilbert action can not explain the universe expansion in the early and late time. From a Quantum Field Theory (QFT) viewpoint, general relativity does not work as a fundamental theory. Therefore, it is reasonable to modify GR at the large and short distance. The simplest model which can explain the accelerated expansion of universe is $\Lambda CDM$ model that was originally introduced into general relativity by Einstein [6]. However, there are several problems in this model including fine tuning problem, coincidence problem and lack of dynamics for $\Lambda$. In principle, quantum field theoretical models predict that the cosmological constant, originating from the vacuum expectation value of certain quantum fields, is 60–120 orders higher in magnitude, comparison to the observed cosmological constant. In general relativity the cosmological constant is added by hand in the Einstein–Hilbert action, so essentially there is no intrinsic mechanism in the theory that can dynamically induce the cosmological constant. Consequently, for solving these problems many theories have been suggested such as scalar field models, modified gravity theories and extra dimension models which provide the late time cosmic acceleration. One of the popular models to describe the cosmic acceleration is the f(R) modified gravity model where f is an arbitrary function of Ricci scalar R. This theory extensively studied and has the interesting feature [7,8,9,10,11,12,13,14,15]. This model can explain the early inflation as well as the late time acceleration without necessity to introduce exotic matter. A generalization of f(R) is included an arbitrary coupling between matter and geometry. The non-minimal coupling of Ricci scalar and matter Lagrangian density was studied in [16,17,18,19,20,21,22]. In [23] a modification of general gravity was proposed by including coupling of an arbitrary function of the Ricci scalar with the trace of stress–energy tensor T, f(R, T) gravity. The cosmological aspects of this model were studied in [24,25,26]. The gravitational baryogenesis mechanism for this model have been studied in [27]. In [24], the author show the transition from matter dominated phase to the late time accelerated era of the universe in this scenario by using the cosmological reconstruction. reconstruction of f(R, T) describing is performed.The dependence on T can be act as a source of exotic fluid. In this scenario, the equations of motion show the presence of an extra-force acting on the test particles, and the motion are generally non-geodesic. This theory also relates the cosmic acceleration, not only due to the contribution of geometrical terms, but also to the matter contents [28].

Unimodular gravity is an alternative theory of the gravitational theories which solve the cosmological constant problem [29]. This theory first introduced by Einstein in 1919 [30]. In this case the cosmological constant is not only added by hand, but also derived from the trace-free part of the Einstein field equations. So, the cosmological constant appears as an integration constant in this theory. An interesting feature of this model is that it can be explained the current expansion of the universe by considering only single component such as the cosmological constant, or by the nonrelativistic matter [31, 32]. The technique of the theory is that the determinant of the metric $\sqrt{-g}$ to be a fixed number, or some function of the space-time coordinates. The extension of this model to the modified gravity is discussed in Refs. [33,34,35,36,37,38,39,40]. An interesting result is that unimodular gravity is classically equivalent to general relativity, however there is a discussion about this equivalence at the quantum level. Some more aspects of this model have been studied in [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. During the last years a new idea, called the generalized unimodular gravity was developed in papers [60,61,62,63].

In this papar, we consider a generalization of unimodular gravity by coupling between Ricci scalar R and trace of the stress–energy tensor T via a general function as unimodular f(R, T) gravity. We present the unimodular constrain by inserting the Lagrange multiplier in the action. The cosmological reconstruction of the unimodular f(R, T) gravity have been studied in [40]. At that literature, the authors investigated inflationary cosmology in this model and showed for some models of unimodular f(R, T) gravity were in good agreement with observational data from Planck probe. In this paper We investigate the viability of some particular models of unimodular f(R, T) graviy according to the energy conditions. Then we compare our results with observational data. This analysis gives some constraints on the parameters of model. The energy conditions are fundamental to the singularity theorems like black hole thermodynamics [64]. The energy condition have many important theoretical applications which is used in different contexts to derive general results that would hold for a variety of situations(for more detail see [65,66,67,68]). This scenario is firstly formulated in the context of general relativity. Recently the extention of these energy conditions to the modified gravity like f(R), f(G) and f(T) have been studied in several literature [69,70,71,72,73,74,75,76,77,78,79,80].

At end, we investigate stability of the cosmological solutions in the framework of perturbations. In this sense, we study the homogeneous and isotropic perturbations around the background solutions and obtain a stability condition for the power-law and de Sitter solutions. Then, we consider some specific models of unimodular f(R, T) gravity and show that for some values of input parameters, the stability of solutions are realized. Through this way and analyzing the energy conditions we can check the viability of cosmological solutions in this kind of extended theory of gravity.

The outline of this paper is as follows. In next section we introduce unimodular f(R, T) gravity and drive the basic equations of the model in FRW background. In Sect. 3 we define the energy conditions in GR as well as in a general modified gravitational framework. In Sect. 4 we analyze the energy conditions in unimodular f(R, T) gravity. In Sect. 5 we obtain the constraints imposed on the model in the framework of energy condition. In Sect. 5 we investigate the linear perturbations around the background solutions and derive the evolution equations of perturbations. We study the stability of de Sitter and power law solutions for some specific models of unimodular f(R, T). Finally we compare the results with the obtained constraints from the energy conditions. Section 6 is devoted to conclusion.

2 The unimodular f(R, T) gravity

The main motivation of unimodular gravity is to remove the cosmological constant from the gravitational equations of motion. Actually, the unimodular gravity solve the cosmological constant problem. The cosmology that obtain in unimodular gravity is classically equivalent to cosmology in general relativity in presence of a cosmological constant. The unimodular gravity theory is based on the assumption that the determinant of metrics is fixed, $g_{\mu \nu }\delta g^{\mu \nu }=0$. Whereas all of the components of metric are dynamical. This means that

$$\begin{aligned} \sqrt{-g}=\epsilon _0, \end{aligned}$$

(1)

where $\epsilon _0$ is constant. This constraint can obtain by inserting a Lagrange multiplier in the action. We extend the unimodular Einstein–Hilbert gravity formalism to the f(R, T) modified theory of gravity which the action is

$$\begin{aligned} S=\frac{1}{2\kappa ^2}{\int }{d^4x\Big [\sqrt{-g}f(R,T)-2\lambda (\sqrt{-g}-\epsilon _{0})\Big ]} +{\int }d^4x\sqrt{-g}\mathcal{{L}}_{m}, \end{aligned}$$

(2)

where f(R, T) is an arbitrary function of the Ricci scalar, R, and of the trace of the stress–energy tensor of the matter, $T_{\mu \nu }$. $\mathcal{{L}}_{m}$ is the matter Lagrangian density which depends only on the metric tensor components $g_{\mu \nu }$. The stress–energy tensor of matter is

$$\begin{aligned} T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}\mathcal{{L}}_{m})}{\delta g^{\mu \nu }}=g_{\mu \nu }\mathcal{{L}}_{m}-2\frac{\partial \mathcal{{L}}_{m}}{\partial g^{\mu \nu }}. \end{aligned}$$

(3)

We obtain the modified Einstein field equations by variation of action (2) with respect to the metric as follows

$$\begin{aligned}&f_{,R}(R,T)R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }f(R,T)+(g_{\mu \nu }\Box -\nabla _{\mu }\nabla _{\nu })f_{,R}(R,T)+\lambda g_{\mu \nu }\nonumber \\&\quad = \kappa ^2 T_{\mu \nu } -f_{,T}(R,T)(T_{\mu \nu }+\Theta _{\mu \nu }). \end{aligned}$$

(4)

where comma denotes partial derivative of f(R, T) with respect to R and T. We introduce $\Theta _{\mu \nu }$ as

$$\begin{aligned} \Theta _{\mu \nu }\equiv g^{\alpha \beta } \frac{\delta T_{\alpha \beta }}{\delta g^{\mu \nu }}=-2T_{\mu \nu }+g_{\mu \nu }\mathcal{{L}}_{m} -2g^{\alpha \beta }\frac{{\partial ^2}\mathcal{{L}}_{m}}{\partial g^{\mu \nu }\partial g^{\alpha \beta }}. \end{aligned}$$

(5)

The variation of the action with respect to Lagrange multiplier, $\lambda$ satisfy the unimodular constraint, $\sqrt{-g}=\epsilon _{0}$. Taking the trace of field equations (4) lead to

$$\begin{aligned} f_{,R}(R,T)R+3\Box f_{R}(R,T)-2f(R,T)+4\lambda =\kappa ^2 T-f_{,T}(R,T)(T+\Theta ), \end{aligned}$$

(6)

By using the above equation, the field equation (4) can be written as

$$\begin{aligned}&f_{,R}(R,T)\Big [R_{\mu \nu }-\frac{1}{3}g_{\mu \nu }R\Big ] \nonumber \\&\qquad -\nabla _{\mu }\nabla _{\nu }f_{,R}(R,T)+\frac{1}{6} f(R,T)g_{\mu \nu }-\frac{1}{3}\lambda g_{\mu \nu }\nonumber \\&\quad =\kappa ^2\Big [T_{\mu \nu }-\frac{1}{3}g_{\mu \nu }T\Big ] -f_{,T}(R,T)\Big [T_{\mu \nu }-\frac{1}{3}g_{\mu \nu }T\Big ]\nonumber \\&\qquad -f_{,T}(R,T)\Big [\Theta _{\mu \nu }-\frac{1}{3}g_{\mu \nu }\Theta \Big ]. \end{aligned}$$

(7)

So, we yield the usual f(R, T) equations with an additional cosmological constant. Now, we assume matter to be described by a perfect fluid with the stress–energy tensor

$$\begin{aligned} T_{\mu \nu }=(\rho _m+p_m)u_{\mu }u_{\nu }+p_m g_{\mu \nu }, \end{aligned}$$

(8)

where $u_{\mu }$ is the four-velocity, $u_{\mu }u^{\mu }=-1$. $\rho _m$ and $p_m$ are the energy density and pressure of matter with equation of state $p_m={\omega _m}\rho _m$. With comparison Eqs. (3) and (8) the matter Lagrangian can be taken as $\mathcal{{L}}_{m}=p_m$ [23]. So, for $\Theta _{\mu \nu }$ we find

$$\begin{aligned} \Theta _{\mu \nu }=-2T_{\mu \nu }+p_m g_{\mu \nu }. \end{aligned}$$

(9)

Then, we can rewritten the field equation (4) as

$$\begin{aligned}&f_{,R}(R,T)R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }f(R,T)+(g_{\mu \nu }\Box - \nabla _{\mu }\nabla _{\nu })f_{,R}(R,T)\nonumber \\&\quad +\lambda g_{\mu \nu }=\kappa ^2 T_{\mu \nu }+f_{,T}(R,T) T_{\mu \nu } \nonumber \\&\quad -p_m g_{\mu \nu }f_{,T}(R,T), \end{aligned}$$

(10)

By taking the covariant divergence of the field equation (4) we get the following relation for the stress–energy tensor

$$\begin{aligned} \nabla ^{\mu }T_{\mu \nu }= & {} \frac{1}{\kappa ^2+f_{,T}(R,T)}\Big [(p_m g_{\mu \nu }-T_{\mu \nu } )\nabla ^{\mu }f_{,T}\nonumber \\&-\frac{1}{2}g_{\mu \nu }f_{,T}\nabla ^{\mu }T+f_{,T}g_{\mu \nu }\nabla ^{\mu }p_m +g_{\mu \nu }\nabla ^{\mu }\lambda \Big ].\nonumber \\ \end{aligned}$$

(11)

where we have used $(\nabla _{\mu }\Box -\Box \nabla _{\mu })f_{,R}=R_{\mu \nu }\nabla ^{\nu }f_{,R}$. This equation shows that the stress–energy tensor of matter is not conserved. This is due to interaction between matter and curvature.

3 Energy conditions

The energy conditions are used in different contexts to derive general results that can constraint parameters of model. The energy conditions arise originally from the Raychaudhuri equations that describe the behavior of space-time congruence which is used to study the singularities of space-time. The Raychaudhuri equation firstly come from the strong and null energy conditions. For a congruence of timelike and nulllike geodesics with tangant vector field $u_{\mu }$ and $\kappa _{\mu }$, Raychaudhuri equations as the temporal variation of expansion $\theta$ [81, 82] are defined as

$$\begin{aligned} \frac{d\theta }{d\tau }= & {} -\frac{1}{3}\theta ^2-\sigma _{\mu \nu } \sigma ^{\mu \nu }+\omega _{\mu \nu } \omega ^{\mu \nu }-R_{\mu \nu }u^{\mu }u^{\nu } \end{aligned}$$

(12)

$$\begin{aligned} \frac{d\theta }{d\tau }= & {} -\frac{1}{2}\theta ^2-\sigma _{\mu \nu } \sigma ^{\mu \nu }+\omega _{\mu \nu } \omega ^{\mu \nu }-R_{\mu \nu }\kappa ^{\mu }\kappa ^{\nu } \end{aligned}$$

(13)

where $\theta$ and $R_{\mu \nu }$ are expansion scalar and Ricci tensor respectively. $\sigma _{\mu \nu }$ present the shear tensor to measure the distortion of the volume. $\omega _{\mu \nu }$ is the velocity tensor to measure the rotation of the curves. Since the shear is a spatial tensor, it implies $\sigma ^2=\sigma _\mu \sigma ^\mu \ge 0$. For any hypersurface of orthogonal congruence($\omega _{\mu \nu }=0$), the conditions for attractive gravity is $\theta <0$ which the Raychaudhuri equations impose

$$\begin{aligned}&SEC: R_{\mu \nu }u^{\mu }u^{\nu }\ge 0, \nonumber \\&NEC: R_{\mu \nu }\kappa ^{\mu }\kappa ^{\nu }\ge 0. \end{aligned}$$

(14)

For equivalence to GR, we can write the Eq. (10) in the following effective gravitational field equation

$$\begin{aligned} G_{\mu \nu }\equiv R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R=T_{\mu \nu }^{eff}, \end{aligned}$$

(15)

where

$$\begin{aligned} T_{\mu \nu }^{eff}= & {} \frac{1}{f_{,R}}\Big [\kappa ^2 T_{\mu \nu }+f_{,T} T_{\mu \nu }+\frac{1}{2}g_{\mu \nu } (f-Rf_{,R}-2p_m f_{,T}-2\lambda )\nonumber \\&-(g_{\mu \nu }\Box -\nabla _{\mu }\nabla _{\nu })f_{,R}\Big ]. \end{aligned}$$

(16)

$T_{\mu \nu }^{eff}$ is an effective stress–energy tensor which is depended on geometry and matter contributions. This relation shows that corrections of this modified gravity are applied to the right hand side of the Einstein’s field equations. This means that accelerated expansion of the universe comes from a geometrical contribution to the total cosmic energy density and the matter content of the universe. By taking the trace of the field equation we get $R=-T^{eff}$, so the Eq. (15) is equivalent to

$$\begin{aligned} R_{\mu \nu }=T_{\mu \nu }^{eff}-\frac{1}{2}T^{eff}g_{\mu \nu }. \end{aligned}$$

(17)

The combination of relation (17) and energy conditions (14) yeild

$$\begin{aligned} R_{\mu \nu }{u^\mu } {u^\nu }= & {} \left( T_{\mu \nu }^{eff}-\frac{1}{2}T^{eff}g_{\mu \nu }\right) {u^\mu } {u^\nu }\ge 0, \nonumber \\ R_{\mu \nu }{\kappa ^\mu } {\kappa ^\nu }= & {} \left( T_{\mu \nu }^{eff}-\frac{1}{2}T^{eff}g_{\mu \nu }\right) {\kappa ^\mu } {\kappa ^\nu }\ge 0. \end{aligned}$$

(18)

where $\kappa ^\mu$ and $u^\mu$ are lightlike and timelike vectors. So we have $\kappa ^{\mu }\kappa _{\mu }=0$. If we consider the perfect fluid as a total content of the universe the null and strong energy condition (18) reduce to

$$\begin{aligned} \rho _{eff}+p_{eff}\ge 0, \quad \,\rho _{eff}+3p_{eff}\ge 0. \end{aligned}$$

(19)

Note that from the strong energy condition $R_{\mu \nu }{u^\mu } {u^\nu }=(T_{\mu \nu }^{eff} -\frac{1}{2}T^{eff}g_{\mu \nu }){u^\mu } {u^\nu }\ge 0$ where equivalent to $T_{\mu \nu }^{eff}{u^\mu } {u^\nu }\ge \frac{1}{2}T^{eff}g_{\mu \nu }{u^\mu } {u^\nu }$ the weak enegy condition impose that

$$\begin{aligned} T_{\mu \nu }^{eff}{u^\mu } {u^\nu }\ge 0\, \quad \longrightarrow \,\quad \rho _{eff}\ge 0. \end{aligned}$$

(20)

The dominant energy condition state that matter must be move in the null or time-like world line. This means that no signal can propagate faster than light. It imply that $p_{eff}\le \rho _{eff}$. Now, we summerize the enegy conditions as follows

$\bullet$ Null energy condition(NEC):$\quad \rho _{eff}+p_{eff}\ge 0$

$\bullet$ Weak energy condition(WEC):$\quad \rho _{eff}\ge 0,\quad \rho _{eff}+p_{eff}\ge 0$

$\bullet$ Strong energy condition(SEC):$\quad \rho +3p_{eff}\ge 0, \quad \rho _{eff}+p_{eff}\ge 0$

$\bullet$ Dominant energy condition(DEC):$\quad \rho _{eff}\ge 0,\quad \rho _{eff}\pm p_{eff}\ge 0.$

We result from these conditions that the violation of NEC leads to violation of other conditions. We can express the energy conditions in modified theory of gravity are similar to those in general relativity with the difference that ordinary energy density $\rho _m$ and pressure $p_m$ is replaced by the effective one, $\rho _{eff}$ and $p_{eff}$.

4 Energy condition in unimodular f(R, T) gravity

In this section, we investigate the energy conditions in the modified gravity of unimodular f(R, T) gravity. For this purpose, at first we need to derive the effective energy density and pressure corresponding to the model. In present study for simplicity and also because the universe is nearly flat we consider the spatially flat Friedmann- Robertson-Walker (FRW) metric as

$$\begin{aligned} ds^{2}= -dt^{2} + a^{2}(t)dx_{i}dx^{i},\quad i=1,2,3 \end{aligned}$$

(21)

where a(t) is the scale factor. For this metric to satisfy the unimodular constraint we introduce a new time variable as

$$\begin{aligned} d\tau =a^3(t)dt, \end{aligned}$$

(22)

Note that this introduction is nothing but the change and the fixation of the lapse function in a certain way, which guarantees the unimodularity. So, the FRW metric (21) can be rewritten as the following form

$$\begin{aligned} ds^{2}= -a^{-6}(\tau )d\tau ^{2} +a^2(\tau )dx_{i}dx^{i},\quad i=1,2,3 \end{aligned}$$

(23)

where $g_{\mu \nu }=diag(-a^{-6}(\tau ),a^2(\tau ),a^2(\tau ),a^2(\tau ))$. It can be easily checked the unimodular constraint is satisfied. The Ricci scalar and non-vanishing component of Ricci tensor for FRW metric are as follows

$$\begin{aligned} R_{\tau \tau }=-3{\mathcal{{\dot{H}}}}-12\mathcal{{H}}^2,\quad R_{ij}=a^8({\mathcal{{\dot{H}}}}+6\mathcal{{H}}^2),\quad R=a^6(6{\mathcal{{\dot{H}}}}+30\mathcal{{H}}^2).\nonumber \\ \end{aligned}$$

(24)

where $\mathcal{{H}}=\frac{1}{a}\frac{da}{d\tau }$ is the generalized Hubble parameter. Thus, we derive the $\tau \tau$ and ii components of the field equations as

$$\begin{aligned}&-(3\mathcal{{\dot{H}}}+12\mathcal{{H}}^2)f_{,R}+\frac{1}{2}(f-2\lambda )a^{-6}+3\mathcal{{H}}{\dot{f}}_{,R}\nonumber \\&\quad = [\kappa ^2\rho _m+f_{,T}(\rho _m+p_m)]a^{-6} \end{aligned}$$

(25)

$$\begin{aligned}&(\mathcal{{\dot{H}}}+6\mathcal{{H}}^2)f_{,R}-\frac{1}{2}(f-2\lambda )a^{-6}-5\mathcal{{H}}{\dot{f}}_{,R} -\ddot{f}_{,R}=\kappa ^2p_ma^{-6} \end{aligned}$$

(26)

where a ”dot” marks derivative with respect to $\tau$. By using the metric (23), the Eq. (11) reach

$$\begin{aligned} {\dot{\rho }}_m+3\mathcal{{H}}(\rho _m+p_m)=-\frac{1}{\kappa ^2+f_{,T}}\big [(\rho _m+p_m) {\dot{f}}_{,T}+{\dot{p}}_{m}f_{,T}+{\dot{\lambda }}\big ].\nonumber \\ \end{aligned}$$

(27)

This equation shows that the general f(R, T) model not satisfy the normal conservation law. So, the massive test particles does not follow a geodesic line due to presence of extra force. In other word, the interaction of matter with geometry imposes an extra acceleration acting on the particle. To satisfy the standard conservation equation ${\dot{\rho }}_m+3H(\rho _m+p_m)=0$ the righ hand side of the above equation must be zero

$$\begin{aligned} -\frac{1}{2}{\dot{T}}f_{,T}+(\rho _m+p_m) {\dot{f}}_{,T}+{\dot{p}}_{m}f_{,T}+{\dot{\lambda }}=0 \end{aligned}$$

(28)

this equation induces an additional constraint on the theory. If we assume $T_{\mu \nu }^{eff}$ behave as the perfect fluid, then the Eq. (16) get

$$\begin{aligned} \rho _{eff}= & {} \frac{1}{f_{,R}}\Bigg [\rho _m(1{+}f_{,T}){-}\frac{1}{2}(f{-}Rf_{,R}{-}2p_mf_{,T}{-}2\lambda )-3a^6\mathcal{{H}}{\dot{f}}_{,R}\Bigg ],\nonumber \\ \end{aligned}$$

(29)

$$\begin{aligned} p_{eff}= & {} \frac{1}{f_{,R}}\Bigg [\frac{1}{2}(f-Rf_{,R}-2p_m f_{,T}-2\lambda )+a^6(\ddot{f}_{,R}+5\mathcal{{H}}{\dot{f}}_{,R})\Bigg ],\nonumber \\ \end{aligned}$$

(30)

where $\rho _{eff}$ and $p_{eff}$ are the effective energy density and pressure. By using these relations we obtain the energy conditions as

$$\begin{aligned}&NEC: \quad \rho _{eff}+p_{eff}=\frac{1}{f_{,R}}\Big [(\rho _m+p_m)(1+f_{,T}) \nonumber \\&\quad +a^6(\ddot{f}_{,R}+2\mathcal{{H}}{\dot{f}}_{,R})\Big ]\ge 0, \end{aligned}$$

(31)

$$\begin{aligned}&WEC: \quad \rho _{eff}=\frac{1}{f_{,R}}\Big [\rho _m(1+f_{,T})\nonumber \\&\quad -\frac{1}{2}(f-Rf_{,R}-2p_mf_{,T} -2\lambda )-3a^6\mathcal{{H}}{\dot{f}}_{,R}\Big ]\ge 0,\nonumber \\&\quad \rho _{eff}+p_{eff}\ge 0 \end{aligned}$$

(32)

$$\begin{aligned}&SEC: \quad \rho _{eff}+3p_{eff}=\frac{1}{f_{,R}}\Big [(\rho _m+3p_m)(1+f_{,T})\nonumber \\&\quad +(f-Rf_{,R}-2p_mf_{,T} -2\lambda )\nonumber \\&\quad +3a^6(\ddot{f}_{,R}+4\mathcal{{H}}{\dot{f}}_{,R})\Big ]\ge 0,\qquad \rho _{eff}+p_{eff}\ge 0, \end{aligned}$$

(33)

$$\begin{aligned}&DEC: \quad \rho _{eff}-p_{eff}=\frac{1}{f_{,R}}\Big [(\rho _m-p_m)(1+f_{,T})\nonumber \\&\quad -(f-Rf_{,R}-2p_mf_{,T} -2\lambda ) \nonumber \\&\quad -a^6(\ddot{f}_{,R}+8\mathcal{{H}}{\dot{f}}_{,R})\Big ]\ge 0,\qquad \nonumber \\&\quad \rho _{eff} +p_{eff}\ge 0,\quad \rho _{eff}\ge 0, \end{aligned}$$

(34)

For simplicity we assume $\kappa ^2=1$. In the following, we consider some special models of unimodular f(R, T) gravity and apply energy conditions to restrict the parameters of model. To study this bounds, we express the Hubble parameter, Ricci scalar and their derivatives in terms of cosmic of the parameters as

$$\begin{aligned} \mathcal{{\dot{H}}}= & {} -\mathcal{{H}}^2(4+q), \end{aligned}$$

(35)

$$\begin{aligned} \mathcal {\ddot{H}}= & {} \mathcal{{H}}^3(j+15q+32), \end{aligned}$$

(36)

$$\begin{aligned} \mathcal{{\dddot{H}}}= & {} \mathcal{{H}}^4(s-25j-249q-366), \end{aligned}$$

(37)

$$\begin{aligned} R= & {} -6a^6\mathcal{{H}}^2(1-q), \end{aligned}$$

(38)

$$\begin{aligned} {\dot{R}}= & {} -6a^6\mathcal{{H}}^3(j-q-2), \end{aligned}$$

(39)

$$\begin{aligned} {\ddot{R}}= & {} -6a^6\mathcal{{H}}^4(s+q^2-11q+3j-12). \end{aligned}$$

(40)

where q, j and s are the deceleration, jerk and snap parameters respectively and are defined as

$$\begin{aligned} q=-\frac{1}{H^2}\frac{\frac{d^2a}{dt}}{a(t)},\qquad j=-\frac{1}{H^3}\frac{\frac{d^3a}{dt}}{a(t)},\qquad s=-\frac{1}{H^4}\frac{\frac{d^4a}{dt}}{a(t)}. \end{aligned}$$

(41)

In our discussion the present day values of the Hubble parameter, deceleration parameter,the jerk and the snap parameters are $H_0=73.8$ [83], $q_0=-0.81\pm 0.14$, $j_0=2.16^{+0.81}_{-0.75}$ and $s_0=-0.22^{+0.21}_{-0.19}$ [84]. In this work we assume the ordinary matter of the universe is pressureless. By using these parameters we can rewrite energy conditions (31)–(34) in the explicit forms, as follows

$$\begin{aligned}&NEC: \nonumber \\&\quad \rho _m(1+f_{,T})-6\mathcal{{H}}^4a^{12}(s+q^2-13q+5j-16)\nonumber \\&\quad f_{,RR}+36\mathcal{{H}}^6a^{18}(j-q-2)^2f_{,RRR}\ge 0, \end{aligned}$$

(42)

$$\begin{aligned}&WEC: \nonumber \\&\quad \rho _m(1+f_{,T})-\frac{1}{2}f+\lambda -3a^6\mathcal{{H}}^2(1-q)\nonumber \\&\quad f_{,R}+18a^{12} \mathcal{{H}}^4(j-q-2)f_{,RR}\ge 0,\nonumber \\&\quad \rho _{eff}+p_{eff}\ge 0, \end{aligned}$$

(43)

$$\begin{aligned}&SEC:\nonumber \\&\quad \rho _m(1+f_{,T})+f-2\lambda +6a^6\mathcal{{H}}^2(1-q)\nonumber \\&\quad f_{,R}-18a^{12}\mathcal{{H}}^4(s+q^2-15q+7j-20)f_{,RR} \nonumber \\&\quad +108a^{18}\mathcal{{H}}^6(j{-}q{-}2)^2f_{,RRR}\ge 0,\qquad \rho _{eff}{+}p_{eff}\ge 0,\nonumber \\ \end{aligned}$$

(44)

$$\begin{aligned}&DEC:\nonumber \\&\quad \rho _m(1+f_{,T})-f+2\lambda -6a^6\mathcal{{H}}^2(1-q)\nonumber \\&\quad f_{,R}-6a^{12}\mathcal{{H}}^4(s+q^2-19q+11j-28)f_{,RR} \nonumber \\&\quad -36a^{18}\mathcal{{H}}^6(j-q-2)^2f_{,RRR}\ge 0,\nonumber \\&\quad \rho _{eff}+p_{eff}\ge 0, \qquad rho_{eff}\ge 0. \end{aligned}$$

(45)

5 Constraining F(R, T) models using energy conditions

To get some intersting feature of energy conditions, we consider some specific models of unimodular f(R, T) gravity. We can find the exact form of model trough reconstruction method and constraint the free parameters of model by using the energy conditions.

$\bullet$ $f(R,T)=f(R)+\beta T$

As a first case of a unimodular f(R, T) gravity model we assume that f(R, T) is given by

$$\begin{aligned} f(R,T)=f(R)+\beta T. \end{aligned}$$

(46)

where $\beta$ is an arbitrary constant. For this case, the field equations get the following form

$$\begin{aligned}&-(3\mathcal{{\dot{H}}}+12\mathcal{{H}}^2)f_{,R}\nonumber \\&\quad +\frac{1}{2}\big (f(R)+\beta T-2\lambda \big )a^{-6}+3\mathcal{{H}}{\dot{f}}_{,R}= (1+\beta )\rho _ma^{-6},\nonumber \\ \end{aligned}$$

(47)

and

$$\begin{aligned}&(\mathcal{{\dot{H}}}+6\mathcal{{H}}^2)f_{,R}\nonumber \\&\quad -\frac{1}{2}\big (f(R)+\beta T-2\lambda \big )a^{-6}-5\mathcal{{H}}{\dot{f}}_{,R} -\ddot{f}_{,R}=0, \end{aligned}$$

(48)

Now, we obtain the exact form of the model through the reconstruction method. To this end, we consider the scale factor in the form of

$$\begin{aligned} a(\tau )=\left( \frac{\tau }{\tau _0}\right) ^m\quad \Rightarrow \qquad \mathcal{{H}}=\frac{m}{\tau }, \end{aligned}$$

(49)

which is corresponding to power law and de sitter solutions. $\tau _0$ and m are arbitrary constant. If we consider $m=\frac{\alpha }{3\alpha +1}$ and $\tau _0=\frac{t_0}{3\alpha +1}$, the scale factor (49) is corresponding to power law solutions, $a(t)=(\frac{t}{t_0})^\alpha$. Also, a de Sitter cosmological evolution occurs when $m=\frac{1}{3}$ and $\tau _0=\frac{1}{3H_0}$ which can describe the initial inflation and late-time cosmic acceleration [36, 40]. So, the unimodular FRW metric (23) takes the following form

$$\begin{aligned} ds^2=-\Bigg (\frac{\tau }{\tau _0}\Bigg )^{-6m}d\tau ^2+\Bigg (\frac{\tau }{\tau _0}\Bigg )^{2m}dx_{i}dx^{i},\qquad i=1,2,3 \end{aligned}$$

(50)

in this case, if $\frac{1}{4}<m<\frac{1}{3}$ which implies $\alpha >1$, shows an an acceleration expansion of the universe. The radiation and dust dominated erea is described by $m=\frac{2}{9}$ and $m = \frac{1}{5}$.

For pressureless fluid, the conservation equation get

$$\begin{aligned} {\dot{\rho }}_m=-3\mathcal{{H}}\rho _m \quad \longrightarrow \quad {\rho }_m=\Bigg (\frac{\tau }{\tau 0}\Bigg )^{-3m} , \end{aligned}$$

(51)

For the scale factor (49), the trace of stress–energy tensor and the Ricci scalar get

$$\begin{aligned} T=-\Bigg (\frac{\tau }{\tau 0}\Bigg )^{-3m}, \quad R=\frac{6m(5m-1)}{\tau _0^2}\Bigg (\frac{\tau }{\tau _0}\Bigg )^{6m-2} . \end{aligned}$$

(52)

By contracting field equations (47) and (48) and by using Eqs. (49)–(52), we obtain partial differential equation as

$$\begin{aligned} \frac{2m(3m-1)}{\tau ^2}f_{,R}+2\frac{m}{\tau }{\dot{f}}_{,R}+\ddot{f}_{,R}+ (1+\beta )\Bigg (\frac{\tau }{\tau _0}\Bigg )^{-9m}=0, \end{aligned}$$

(53)

Note that we consider the pressurless fluid. The general solution of this differential equation is

$$\begin{aligned} f_{,R}(\tau )=C_1\tau ^{\mu _1}+C_2 \tau ^{\mu _2}+C\tau ^{-9m+2}, \end{aligned}$$

(54)

where $C_{1,2}$ are integration constants and

$$\begin{aligned} \mu _{1,2}= & {} -m+\frac{1}{2}\pm \frac{1}{2}{\sqrt{-20m^2+4m+1}},\nonumber \\ C= & {} \frac{(1+\beta )}{69m^2-25m+2}{\tau _0^{9m-2}}. \end{aligned}$$

(55)

By inserting the scalar Ricci and integrating of this equation, we obtain

$$\begin{aligned} f(R)=D_{1}R^\frac{\mu _{1}+6m-2}{6m-2}+D_{2}R^\frac{\mu _{2} +6m-2}{6m-2}+DR^\frac{-3m}{6m-2}, \end{aligned}$$

(56)

where

$$\begin{aligned} D_{1,2}= & {} C_{1,2}{\tau _0}^{\mu _{1,2}}\Bigg (\frac{6m-2}{\mu _{1,2}+6m-2}\Bigg )\Bigg (\frac{\tau _0^2}{30m^2-6m}\Bigg )^{\frac{\mu _{1,2}}{6m-2}},\nonumber \\ \end{aligned}$$

(57)

$$\begin{aligned} D= & {} -C{\tau _0}^{-9m+2}\Bigg (\frac{6m-2}{3m}\Bigg )\Bigg (\frac{\tau _0^2}{30m^2-6m}\Bigg )^{\frac{-9m+2}{6m-2}}. \end{aligned}$$

(58)

Then, we find the unimodular Lagrange multiplier from the Eq. (47)

$$\begin{aligned} \lambda (\tau )=N_{1}\tau ^{\mu _{1}+6m-2}+N_{2}\tau ^{\mu _{2}+6m-2}+N\tau ^{-3m}. \end{aligned}$$

(59)

where

Fig. 1

The allowed range of parameter m for energy conditions

Fig. 2

The allowed range of parameter m for energy conditions

$$\begin{aligned} N_{1,2}= & {} \Bigg [6m(5m-1)\Bigg (\frac{3m-1}{\mu _{1,2}+6m-2}+3m(1-4m)\Bigg )\Bigg ]\tau _0^{-6m}C_{1,2},\nonumber \\ \end{aligned}$$

(60)

$$\begin{aligned} N= & {} -\frac{1}{2}(3\beta -2){\tau _0^{3m}}\nonumber \\&+\frac{6m(1-4m)(1+\beta )}{69m^2-25m+2}{\tau _0^{3m-2}}\nonumber \\&-\frac{2(1+\beta )(5m-1)}{69m^2-25m+2}{\tau _0^{6m}}. \end{aligned}$$

(61)

Now, we investigate the energy conditions for the f(R, T) given in Eq. (46). Using this model, the energy conditions in terms of present day values of q, j and s become

$$\begin{aligned}&NEC: \nonumber \\&\quad \rho _{0m}(1+\beta )-6\mathcal{{H}}_0^4a_0^{12}(s_0+q_0^2-13q_0+5j_0-16)f_{,0RR}\nonumber \\&\quad +36\mathcal{{H}}_0^6a^{18}(j_0-q_0-2)^2f_{,0RRR}\ge 0, \end{aligned}$$

(62)

$$\begin{aligned}&WEC: \nonumber \\&\quad \rho _{0m}(1+\frac{1}{2}\beta )-\frac{1}{2}f(R)\nonumber \\&\quad +\lambda _0-3a_0^6\mathcal{{H}}_0^2 (1-q_0)f_{,0R}+18a_0^{12}\mathcal{{H}}_0^4(j_0-q_0-2)f_{,0RR}\ge 0, \nonumber \\&\quad \rho _{eff}+p_{eff}\ge 0, \end{aligned}$$

(63)

$$\begin{aligned}&SEC:\nonumber \\&\quad \rho _{0m}+f(R)-2\lambda _0+6a_0^6\mathcal{{H}}_0^2(1-q_0)f_{,0R}\nonumber \\&\quad -18a_0^{12}\mathcal{{H}}_0^4(s_0+q_0^2-15q_0+7j_0-20)f_{,0RR} \nonumber \\&\quad +108a_0^{18}\mathcal{{H}}_0^6(j_0-q_0-2)^2f_{,0RRR}\ge 0,\qquad \rho _{eff}+p_{eff}\ge 0, \end{aligned}$$

(64)

$$\begin{aligned}&DEC:\nonumber \\&\quad \rho _{0m}(1+2\beta )-f(R)+2\lambda _0-6a_0^6\mathcal{{H}}_0^2(1-q_0)f_{,-R}\nonumber \\&\quad -6a_0^{12}\mathcal{{H}}_0^4(s_0+q_0^2-19q_0+11j_0-28)f_{,0RR} \nonumber \\&\quad -36a_0^{18}\mathcal{{H}}_0^6(j_0-q_0-2)^2f_{,0RRR}\ge 0,\qquad \nonumber \\&\quad \rho _{eff}+p_{eff}\ge 0, \qquad \rho _{eff}\ge 0. \end{aligned}$$

(65)

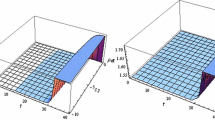
we take the f(R) which is given in Eq. (56). By considering the present day values of jerk, deceleration and snap parameters we find acceptable range of the parameters of the model for the energy conditions. Figures 1, 2 and 3 show the positively increasing behavior of energy conditions with respect to m and $C_2$ parameters which $C_2$ is the integral constant. In this case, all energy conditions are satisfied for all values of $C_1$. Figures 1 and 2a show the WEC is satisfied for $C_2>0$ and $0.243<m<0.257$. For $C_2<0$ the energy conditions are decrease and violate of WEC. Figure 2 shows the acceptable range of SEC. For $0.243<m<0.345$ and all vallues of $C_2$ the SEC is satisfied. Figures 1, 2a and 3 show the DEC is satisfied in $0.243<m<0.244$

Fig. 3

The allowed range of parameter m for energy conditions

$\bullet$ $f(R,T)=R+\xi R^n+2T$

Now, we take the special case of f(R, T) as

$$\begin{aligned} f(R,T)=R+\xi R^n+2T \end{aligned}$$

(66)

where $\xi$ and n are constant. For analysis the energy conditions we subsitute this f(R, T) in the energy conditions (42)–(45) and find viable range for the free parameters of the model. We constraint the model through this way. In following we address the evident conditions for which the energy conditions are satisfied

$*$ For $\xi >0$ the acceptable values of n are $n=\{\ldots ,-6,-4,-1,3,5,7,\ldots \}$ and $\xi <0$ with $n=\{\ldots ,-7,-5,-3,-2,2,4,6,\ldots \}$. Hence the NEC and WEC are satisfied. These results except values of $n=-1,-2$ are also valid for SEC.

$*$ $\xi >0$ with acceptable range of n as $n=\{\ldots ,-8,-6,-1,3,5,7,\ldots \}$ and $\{\ldots ,-7,-5,-2,4,6,8,\ldots \}$ for $\xi <0$ the DEC is satisfied. To analyze the energy conditions in this case one can state that for example if we consider $f(R,T)=R+\xi R^2+2T$ the weak energy condition is satisfied if and only if $\xi$ is negative. The function $f(R,T)=R-\frac{\mu ^4}{R}+2T$ violates the WEC because for $\xi =-\mu ^4$, $n=-1$ is not acceptable.

$\bullet$ $f(R,T)=R+2f(T)$

We consider a type of f(R, T) that includes a usual Einstein–Hilbert term plus terms of f(T) function which is depondent on the trace of stress–energy tensor

$$\begin{aligned} f(R,T)=R+2f(T). \end{aligned}$$

(67)

The field equations can be obtain

$$\begin{aligned} 3\mathcal{{H}}^2=[(1+2f_{,T})\rho _m-f(T)+\lambda ]a^{-6}, \end{aligned}$$

(68)

and

$$\begin{aligned} -2\mathcal{{\dot{H}}}-9\mathcal{{H}}^2=(f(T)-\lambda )a^{-6}, \end{aligned}$$

(69)

Contracting these two equation result the following equation

$$\begin{aligned} -2\mathcal{{\dot{H}}}-6\mathcal{{H}}^2=(1+2f_{,T})\rho _m, \end{aligned}$$

(70)

whose solution is given by

$$\begin{aligned} f(T)=-\frac{3m^2}{2\tau _0^2}(-T)^\frac{2(1-3m)}{3m}-\frac{1}{2}T, \end{aligned}$$

(71)

where $T=-\rho _m$. Then, by solving the constraint Eq. (28) we obtain the Lagrange multiplier as

$$\begin{aligned} \lambda =\frac{(15m-4)}{12(5m-1)}R -\frac{1}{2}T, \end{aligned}$$

(72)

We analyze the energy conditions in the form of f(R, T) that is given in Eq. (67). Hence, we rewrite the Eqs. (42)–(45) as follows

$$\begin{aligned}&NEC:\quad \rho _m(1+2f_{,T})\ge 0, \end{aligned}$$

(73)

$$\begin{aligned}&WEC:\quad \rho _m(1+2f_{,T})-f(T)+\lambda \ge 0,\qquad \rho _{eff}+p_{eff}\ge 0,\end{aligned}$$

(74)

$$\begin{aligned}&SEC:\quad \rho _m(1+2f_{,T})+2f(T)-2\lambda \ge 0,\qquad \rho _{eff}+p_{eff}\ge 0, \end{aligned}$$

(75)

$$\begin{aligned}&DEC:\quad \rho _m(1{+}2f_{,T}){-}2f(T){+}2\lambda {\ge }0,\qquad \rho _{eff}{+}p_{eff}{\ge }0, \qquad \rho _{eff}{\ge }0.\nonumber \\ \end{aligned}$$

(76)

In order to find the constraints on paremeters of the model, we assume that the standard matter satisfies all the energy conditions. Therefore, the NEC condition (73) reduces to $1+2f_{,T}\ge 0$. Then by substituting the f(T) from the Eq. (71) we obtain

$$\begin{aligned} 2m(1-3m)(0.42)^{\frac{2(1-3m)}{3m}}\ge 0. \end{aligned}$$

(77)

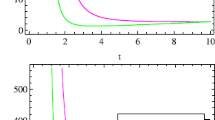
According to this relation the NEC is satisfied for $0<m<0.33$. Other choices of this parameter leads to violation of NEC. Figure 4 shows the behavior of energy conditions. In this figure the $\rho _{eff}$ and $\rho _{eff}-p_{eff}$ behave similarly but $\rho _{eff}+3p_{eff}$ behave oppositely. We express the viable range of m for energy conditions as fllows

(a) If $0<m<0.2$ or $0.26<m<0.33$ the WEC and DEC are satisfied.

(b) If $0.2<m<0.27$ or $0<m<0.18$ the SEC is satisfied.

Fig. 4

The allowed range of parameter m for energy conditions

6 Perturbations of flat FRW solutions in f(R, T) gravity

In this section, we study the homogenous and isotropic perturbations in our model and investigate the stability of de Sitter and power law solutions. At first, we assume a general solution in FRW cosmological background. For this purpose, we consider small deviations from the scale factor, energy density and Lagrange multiplier as

$$\begin{aligned}&a(\tau )=a_0(\tau )\Big (1+\delta (\tau )\Big ),\quad \rho _m(\tau )\nonumber \\&\quad =\rho _{m0}(\tau )\Big (1+\delta _m(\tau )\Big ),\quad \lambda (\tau )=\lambda _0(\tau )\Big (1+\delta _{\lambda }(\tau )\Big ).\nonumber \\ \end{aligned}$$

(78)

where $\delta (\tau )$, $\delta _m(\tau )$ and $\delta _{\lambda }(\tau )$ express the perturbations of background scale factor, matter density and Lagrange multiplier. To explore the behavior of linear perturbations, we expand the f(R, T) function in the power of R and T as

$$\begin{aligned} f(R,T)=f^0+f^0_{,R}(R-R_0)+f^0_{,T}(T-T_0)+\mathcal{{O}}(2), \end{aligned}$$

(79)

In what follows, to study the stability of solutions we consider two cosmological solutions including de Sitter and power law solutions.

6.1 Stability of de Sitter solutions

Let us consider the de Sitter solutions which enable to describe the inflation and late-time cosmic acceleration. Therefore, we set

$$\begin{aligned} H(t)=H_0, \quad a(t)=a_0 e^{H_0 t} \end{aligned}$$

(80)

where $H_0$ is constant. In unimodular gravity and by definition of time variable (22) we obtain

$$\begin{aligned} a(\tau )=(3H_0 \tau )^{\frac{1}{3}}, \end{aligned}$$

(81)

where $H_0$ is constant. By inserting the expression (78) into Eqs. (25) and (26) we obtain the perturbation equations up to the first order perturbations as follows

$$\begin{aligned}&{a_1}{\dddot{\delta }}(\tau ) +{a_2}{\ddot{\delta }}(\tau ) +{a_3}{{\dot{\delta }}}(\tau ) \nonumber \\&\quad +{a_4}\delta (\tau ) +{a_5}\delta _m(\tau ) +{a_6}\delta _ {\lambda } (\tau ) =0, \end{aligned}$$

(82)

$$\begin{aligned}&{b_1}{\ddddot{\delta }}(\tau ) +{b_2}\,{\dddot{\delta }}(\tau ) +{b_3}{\ddot{\delta }}(\tau ) \nonumber \\&\quad +{b_4}{{\dot{\delta }}}(\tau ) +{b_5}\,\delta (\tau ) +{b_6}\delta _m(\tau ) +{b_7}\,\delta _ {\lambda } (\tau )=0, \end{aligned}$$

(83)

and the conservation equation gives

$$\begin{aligned} {c_1}{\dot{\delta }}(\tau )+{c_2}{\dot{\delta }}_ m(\tau ) +{c_3}\, \delta (\tau ) +{c_4}\,\delta _ m(\tau )=0. \end{aligned}$$

(84)

where the coefficients $a_1\ldots a_6$, $b_1\ldots b_7$ and $c_1\ldots c_4$ are given in Appendix A. These coefficients depend on the values of the scale factor, f(R, T) and their derivatives evaluated in the background solution. Perturbations equations (82)–(84) get solutions in the forms $\delta _j=\Sigma {\eta _i e^{\nu _i \tau }}$ where $\eta _i$ are integral constants. The stability of the perturbations will depend on the sign of $\nu _i$. The negative sign of $\nu _i$ get the stable solutions, while the unstable solutions are obtained from the positive sign of $\nu _i$. the parameters $\nu _i$ depend on f(R, T) and other free parameters in the perturbation equations. So, we consider the unimodular f(R, T) models which was proposed in previous section and analyze the stability of solutions. Note that we assume the ordinary matter content of the universe is pressureless.

$\bullet$ $f(R,T)=f(R)+\beta T$

For this model and by using the f(R) is given in (56) and solving the perturbations equations we obtain the perturbations $\delta$, $\delta _m$ and $\delta _\lambda$. By increasing the time, the $\nu _i$ are negative and perturbations are decay for $-1<m<3$. Thus, the de Sitter solutions of perturbations are stable. For other values of m the perturbations will grow exponentially.

$\bullet$ $f(R,T)=R+\xi R^n+2T$

In this case, for $n>0$ the perturbations of scale factor, matter and Lagrange multiplier are unstable. If $n<0$ and $\xi <0$ as time evolves the amplitude of perturbations decrease and de Sitter solutions are stable while for $\xi >0$ the solutions become unstable.

We observed that some of conditions for stability are compatible with some constraints to satisfy the energy conditions. This present for some values of the input parameters, the acceptable models can be obtained.

$\bullet$ $f(R,T)=R+2f(T)$

Let us now investigate the behavior of perturbations in the linear regime for this unimodular f(R, T) model. We expand the f(T) function in power of T

$$\begin{aligned} f(T)=f^0+f^0_{,T}(T-T_0)+\mathcal{{O}}(2), \end{aligned}$$

(85)

By using the expression (78) and (85) the fields equations (68) and (69) get

$$\begin{aligned}&6{a_0^5}{{\dot{a}}_0}{{\dot{\delta }}}+18{a_0^4}{{\dot{a}}_0^2} {\delta }\nonumber \\&\quad +(2{\rho _{m0}^2}f^0_{,TT}-5\rho _{m0}f^0_{,T}-\rho _{m0})\delta _m-\lambda _0 \delta _{\lambda }-2f^0_{,T}\rho _{m0}=0\nonumber \\ \end{aligned}$$

(86)

$$\begin{aligned}&-2{a_0^6}{\ddot{\delta }}-18{a_0^5}{{\dot{a}}_0}{{\dot{\delta }}}-6{a_0^4} (2a_0{\ddot{a}_0}+7{{\dot{a}}^2}){\delta }\nonumber \\&\quad +\rho _{m0}f^0_{,T}\delta _m+\lambda _0 \delta _{\lambda }=0. \end{aligned}$$

(87)

We consider the f(T) function which is given in (71). By solving the perturbations equations (86) and (87) with the conservation Eq. (84) we find the general solution of perturbation equations in this case. In the range of $0<m<1$ we have $\nu _i<0$ and the perturbations of $\delta$, $\delta _m$ and $\delta _\lambda$ behave as damp oscillators with decreasing amplitude and tend to zero with cosmic time. Therefore, the de Sitter solutions are stable.

6.2 Stability of power law solutions

Now we consider the power law solutions which is corresponding to different phases of cosmic evolution such as radiation dominated, matter dominated or dark energy eras. For this case, the scale factor and Hubble parameter are expressed as

$$\begin{aligned} a(t)=\left( \frac{t}{t_0}\right) ^\alpha \quad , \quad H(t)=\frac{\alpha }{t}, \end{aligned}$$

(88)

where $t_0$ and $\alpha$ are constant. $\alpha =\frac{1}{2}$ and $\alpha =\frac{2}{3}$ correspond to solutions of radiation and matter dominated universe respectively. Also, $\alpha >1$ gives an accelerated expansion. Then, using the time variable (22) the scale factor get the following form

$$\begin{aligned} a(\tau )=\left( \frac{3\alpha +1}{t_0}\tau \right) ^{\frac{\alpha }{3\alpha +1}}, \end{aligned}$$

(89)

Now, we explore the stability of these solutions in the framework of perturbations in the f(R, T) models which present in previous subsection.

$\bullet$ $f(R,T)=f(R)+\beta T$

In this model, we solve the differential Eqs. (82)–(84). We find that for $\alpha =\frac{2}{3}$ the evolution of $\delta$, $\delta _m$ and $\delta _\lambda$ increase oscillatory with time. For $\alpha >1$ and $m<0$ the amplitude of perturbations decrease with time. So the power law solutions for this conditions are stable.

$\bullet$ $f(R,T)=R+\xi R^n+2T$

In this case, for $\alpha =\frac{2}{3}$, the perturbations behave as a damped oscillator by decreasing amplitude and the solutions are stable. If we consider $\alpha >1$ we find the stable solution for the conditions $\beta >0$ and $n>4$ and also the solutions become unstable for $n<4$. The evolution of perturbations grow exponentially with $\beta <0$ and all of the parameters n and the power law solutions are not stable for this case.

$\bullet$ $f(R,T)=R+2f(T)$

By solving the perturbation equations (86), (87) and (84) we obtain evolution of perturbation parameters. We can find the stability conditions by studying the perturbation equations. For $\alpha >1$ the perturbations increase with time. For the stable solutions we need to set the conditions $\alpha =\frac{2}{3}$ and $0<m<0.6$.

7 Conclusion

In this work we have studied a modified gravity theory namely unimodular f(R, T) gravity which is an alternative theory to explain the current cosmic acceleration without introducing the exotic component of dark energy or extra dimension. The main motivation to introduce the unimodular gravity is to solve the cosmological constant problem. The cosmological constant appears as a Lagrange multiplier in unimodular gravity. So, the huge discrepancy between the theoretical prediction and the observed value of the cosmological constant can be canceled in this theory. The unimodular f(R, T) gravity is equivalent to standard f(R, T) gravity with a cosmological constant. This theory was capable to explain the late time speed up and early time cosmological inflation. This modified gravity includes lots of models with some unknown parameters. The energy conditions is an approach to restrict these parameters. We constraint on the input parameters for each of the models by analysis the energy conditions in this theory and show which models of unimodular f(R, T) gravity can satisfy the energy conditions. To investigate the energy conditions we have introduced the effective energy density and pressure. In this respect, we have developed energy conditions for some specific models of unimodular f(R, T) gravity and expressed the null, weak, strong and dominant energy conditions for FRW universe with the pressureless ordinary matter in terms of present day values of deceleration (q), jerk (j) and snap (s) parameters. In order to get the application of energy conditions we have taken some special models of unimodular f(R, T) gravity. We can summarize the results as follows

$\bullet$ For $f(R,T)=f(R)+\beta T$ we found the function f(R) from reconstruction way and investigate the energy conditions for this kind of model. We showed that for a range of parameter $-0.144<m<-0.06$ and $0.243<m<0.25$ the WEC,NEC and DEC are satisfied.

$\bullet$ We applied the energy conditions to study the possible constraints on the $f(R,T)=R+\xi R^n+2T$. In this case, we observed that all conditions for which the NEC is satisfied, lead to achievement of WEC.

$\bullet$ It is shown that for the $f(R,T)=R+2f(T)$ the conditions for which the WEC is satisfied, also lead to the accomplishment of the DEC. The NEC is satisfied for $0<m<0.33$.

Furthermore, we have analyzed the stability of cosmological perturbations in this setup. For this purpose we perturbed the scale factor, matter density and Lagrange multiplier to check the viability of the model. In this respect, we have studied stability conditions for de Sitter and power law solutions for FRW metric in the framework of perturbations. We have obtained the differential equations under linear perturbations. We observed that the coefficient of these equations have been depended on functions of f(R, T) and their derivatives. So, to check the viability of the model we consider particular unimodular f(R, T) gravity and showed that this stability analysis can constraint the input parameters of model. Finally, we compared this result with the energy conditions. We showed that some of the stability conditions are compatible with the accomplishment of some of the energy conditions.

Appendix A

In this section we present the coefficients $a_1\ldots a_6$ and $b_1\ldots b_7$ of Eqs. (82) and (83):

$$\begin{aligned} a_1= & {} 54a_0^{11}{{\dot{a}}_0}f^0_{,RR}, \end{aligned}$$

(90)

$$\begin{aligned} a_2= & {} +3a_0^6f^0_{,1R}\nonumber \\&+108a_0^{14}{\dot{a}}_0f^0_{,RRR}(a_0^2\dddot{a}_0+13a_0{\dot{a}}_0\ddot{a}_0+16{\dot{a}}_0^3)\nonumber \\&+18f^0_{,RR}{a_0^9}(a_0^2\ddot{a}_0+72{{\dot{a}}_0^3}+51a_0{{\dot{a}}_0^2}), \end{aligned}$$

(91)

$$\begin{aligned} a_3= & {} +1080a_0^{13}{\dot{a}}_0^2f^0_{,RRR}(a_0^2\dddot{a}_0+13a_0{\dot{a}}_0\ddot{a}_0+16{\dot{a}}_0^3) \nonumber \\&+18f^0_{,RR}{a_0^9}{\dot{a}}_0(a_0^2\dddot{a}_0+228{{\dot{a}}_0^3}+97a_0{{\dot{a}}_0}{\ddot{a}_0})\nonumber \\&+18{\dot{a}}_0 a_0^{5}f^0_{,R}, \end{aligned}$$

(92)

$$\begin{aligned} a_4= & {} 36 a_0^{4}f^0_{,R}(2{{\dot{a}}_0^2}+a_0{\ddot{a}_0})\nonumber \\&+108{{\dot{a}}_0} a_0^{8}f^0_{,RR}(6a_0^2{\dddot{a}_0} a_0^{5}+85{{\dot{a}}_0{\ddot{a}_0}}a_0 +108{{\dot{a}}_0^3}+a_0^2{\ddot{a}_)^2})\nonumber \\&+648\,{{\dot{a}}_0} a_0^{15}f^0_{,RRR}({a_0^3}{\dddot{a}_0}{\ddot{a}_0}+64{{\dot{a}}_0^5} \nonumber \\&+4a_0^2{{\dot{a}}_0^2}{\dddot{a}_0}+13a_0^2{{\dot{a}}_0}{\ddot{a}_0^2}\nonumber \\&+48a_0{{\dot{a}}_0^3}{\ddot{a}_0}), \end{aligned}$$

(93)

$$\begin{aligned} a_5= & {} \frac{3}{2}\beta \rho _{0m}+\rho _{0m}, \end{aligned}$$

(94)

$$\begin{aligned} a_6= & {} \lambda _0, \end{aligned}$$

(95)

$$\begin{aligned} b_1= & {} 18{a_0^{12}}f^0_{,RR}, \end{aligned}$$

(96)

$$\begin{aligned} b_2= & {} 54{a_0^{10}}{{\dot{a}}_0}(9{a_0}+8{{\dot{a}}_0})f^0_{,RR}\nonumber \\&+288{a_0^{15}} ({a_0^2}{\dddot{a}_0}+13a_0{{\dot{a}}_0}{\ddot{a}_0}+16{{\dot{a}}_0^3})f^0_{,RRR}, \end{aligned}$$

(97)

$$\begin{aligned} b_3= & {} +36{{a}_0^{13}}({{a}_0^4}\,{\ddddot{a_0}}\, +13{a_0^3}{\ddot{a}_0^2})f^0_{,RRR}\nonumber \\&+2304a_0^{13}{{\dot{a}}_0^2}(3\dddot{a}_0\,a_0^2+48{{\dot{a}}_0^3}+34a_0{{\dot{a}}_0^2})f^0_{,RRR}\nonumber \\&+216{a_0^{18}}(32{a_0^2}{{\dot{a}}_0^3}{\dddot{a}_0}+169{a_0^2}{{\dot{a}}_0^2}{\ddot{a}_0^2}\nonumber \\&+416a_0{{\dot{a}}_0^4}{\ddot{a}_0}+{a_0^4}{\dddot{a}_0^2}+256{{\dot{a}}_0^6}\nonumber \\&+26{a_0^3}{{\dot{a}}_0}{\ddot{a}_0}{\dddot{a}_0})f^0_{,RRRR}\nonumber \\&+6{a_0^9}(648{{\dot{a}}_0^3}+97{a_0^2}{\ddot{a}_0}+635{a_0}{{\dot{a}}_0^2}\nonumber \\&+144a_0{{\dot{a}}_0}{\ddot{a}_0})f^0_{,RR}+89856{a_0^{14}}{{\dot{a}}_0^3}{\ddot{a}_0}f^0+5{a_0^6}f^0_{,R} \end{aligned}$$

(98)

$$\begin{aligned} b_4= & {} 2160{a_0^{17}}{{\dot{a}}_0}({a_0^{4}}{\dddot{a}_0^2}+32{a_0^{2}}{{\dot{a}}_0^3}{\dddot{a}_0}\nonumber \\&+416{a_0}{{\dot{a}}_0^4}{\ddot{a}_0}+256{{\dot{a}}_0^6}\nonumber \\&+26{a_0^{3}}{{\dot{a}}_0}{\ddot{a}_0}{\dddot{a}_0})f^0_{,RRRR}\nonumber \\&+365040{a_0^{19}}{{\dot{a}}_0^3}{\ddot{a}_0^2}f^0_{,RRRR}+72{a_0^{13}}(5{a_0^{3}}{{\dot{a}}_0} \,{\ddddot{a}_0}+64{a_0^{3}}{\dddot{a}_0}{\ddot{a}_0}\nonumber \\&+897{a_0^{2}}{\ddot{a}_0^2}{{\dot{a}}_0}+3840{{\dot{a}}_0^5})f^0_{,RRR}\nonumber \\&+6{a_0^{9}}(81{\dddot{a}_0}\,a_0^2+192{{\dot{a}}_0^3}+1219{a_0}{{\dot{a}}_0}{\ddot{a}_0})f^0_{,RR}\nonumber \\&+54{a_0^{5}}{{\dot{a}}_0}f^0_{,R}, \end{aligned}$$

(99)

$$\begin{aligned} b_5= & {} 1296a_0^{16}({a_0^5}{\ddot{a}_0}{\dddot{a}_0^2}+4{a_0^4}{{\dot{a}}_0^2}{\dddot{a}_0^2}\nonumber \\&+169{a_0^3}{{\dot{a}}_0^2}{\ddot{a}_0^3}+128{a_0^2}{{\dot{a}}_0^5}{\dddot{a}_0}\nonumber \\&+1092{a_0^2}{{\dot{a}}_0^4}{\ddot{a}_0^2}+1920{a_0}{{\dot{a}}_0^6}{\ddot{a}_0}+\nonumber \\&1024{{\dot{a}}_0^8}+26{a_0^4}{{\dot{a}}_0}{\ddot{a}_0^2}{\dddot{a}_0}\nonumber \\&+136{a_0^3}{{\dot{a}}_0^3}{\ddot{a}_0}{\dddot{a}_0})f^0_{,RRRR}\nonumber \\&+216{a_0^{12}}({a_0^4}{\ddot{a}_0}{\dddot{a}_0+4{a_0^3}{{\dot{a}}_0^2}{\dddot{a}_0}}+12{a_0^4}{\dddot{a}_0^2}+\nonumber \\&13{a_0^3}{\ddot{a}_0^3}+335{a_0^3}{{\dot{a}}_0}{\ddot{a}_0}{\dddot{a}_0}\nonumber \\&+476{a_0^2}{{\dot{a}}_0^3}{\dddot{a}_0}+2245{a_0^2}{{\dot{a}}_0^2}{\ddot{a}_0^2}\nonumber \\&+3584{{\dot{a}}_0^6}+5780{a_0}{{\dot{a}}_0^4}{\ddot{a}_0})f^0_{,RRR}+\nonumber \\&36{a_0^{8}}(6{a_0^3}{\ddddot{a}_0}+ 79{a_0^2}{\ddot{a}_0^2}+788{{\dot{a}}_0^4}+999{a_0}{{\dot{a}}_0^2}{\ddot{a}_0}\nonumber \\&+138{a_0^2}{{\dot{a}}_0}{\dddot{a}_0})f^0_{,RR}+6a_0^4(22{{\dot{a}}_0^2}+5a_0{\ddot{a}_0})f^0_{,R},\end{aligned}$$

(100)

$$\begin{aligned} b_6= & {} -\frac{1}{2}\beta \rho _{0m}, \end{aligned}$$

(101)

$$\begin{aligned} b_7= & {} -\lambda _0, \end{aligned}$$

(102)

Next we obtain the coefficients $c_1\ldots c_4$ related to conservation Eq. (84)

$$\begin{aligned} c_1= & {} 3a_0\rho _{0m}, \end{aligned}$$

(103)

$$\begin{aligned} c_2= & {} a_0{{\dot{\rho }}_{0m}}+3{{\dot{a}}_0}{{\rho }_{0m}}, \end{aligned}$$

(104)

$$\begin{aligned} c_3= & {} a_0\rho _{0m}, \end{aligned}$$

(105)

$$\begin{aligned} c_4= & {} a_0{{\dot{\rho }}_{0m}}+3{{\dot{a}}_0}{{\rho }_{0m}}, \end{aligned}$$

(106)

We see that these coefficients depend on the values of the scale factor, f(R, T) and their derivatives evaluated in the background solution.