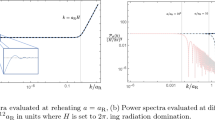
Abstract
We discuss the inflaton \(\phi \) in an environment of scalar fields \(\chi _{n}\) on flat and curved manifolds. We average over the environmental fields \(\chi _{n}\). We study a contribution of superhorizon \(k\ll aH\) as well as subhorizon \(k \gg aH\) modes \(\chi _{n}(\mathbf{k})\). As a result we obtain a stochastic wave equation with a friction and noise. We show that in the subhorizon regime in field theory a finite number of fields is sufficient to produce a friction and diffusion owing to the infinite number of degrees of freedom corresponding to different \(\mathbf{k}\) in \(\chi _{n}(\mathbf{k})\). We investigate the slow roll and the Markovian approximations to the stochastic wave equation. A determination of the metric from the stochastic Einstein–Klein–Gordon equations is briefly discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Inflation is generated by an interaction of gravity with a scalar field (inflaton) [1,2,3,4,5]. In a purely Hamiltonian system it is impossible to reach a thermodynamic equilibrium exhibited in the CMB radiation. The equilibration can be achieved by an interaction with an environment of other fields (heat bath). Then, the temperature of the inflaton subsystem is decreasing during inflation. In the standard (cold inflation) approach a mechanism of reheating [6, 7] is applied to raise the temperature. The presence of the environment limits the decrease of temperature [8,9,10]. Berera [11] described the effect of the environment by a stochastic modification of the inflaton equation. He derived a stochastic equation from a linear interaction with an infinite set of scalar fields in a heat bath. The model follows the well-known derivation of the Brownian motion from dynamical systems [12, 13]. We have obtained the same stochastic equation in the low momentum regime (\(k\simeq 0\)) by different mathematical methods in [14]. In [11, 14] the expansion of the environment has been neglected in the derivation (as we set \(a^{-2}k^{2}\simeq 0\)). What was essential for the result was an infinite set of fields with masses proportional to couplings. Such a relation allows to apply the Markov approximation. In Appendix B of Ref. [11] Berera derives the same diffusion equation if there is only one field in the environment but \(k \gg aH\).
In this paper we investigate models of an interaction with the environment in more detail starting from models in the Minkowski space. We consider some generalizations of the models of [11, 14]. The main new result concerns the calculation of the effect of the subhorizon modes \(k \gg aH\) on the wave equation of the inflaton. We show that if the momentum and scale-dependent term in the scalar-field equations is dominating (in the subhorizon regime \(k \gg aH\)) then we obtain a different diffusive inflaton equation than the one resulting from averaging over superhorizon modes (in disagreement with [11]). The appearance of the diffusive behaviour in this model is similar to the one discussed by Starobinsky and Vilenkin [15,16,17,18] when modes with large k of the quantum scalar field lead to a diffusive behaviour of the remaining superhorizon modes \(k\ll aH\) in an expanding universe. In such a case those authors were able to derive a stochastic wave equation describing quantum fluctuations in an arbitrary inflaton potential. Quantum as well as thermal fluctuations determine the CMB spectrum which can be compared with observations [19, 20].
The plan of this paper is the following. In Sect. 2 we review a minor generalization of the model of Refs. [11, 14]. In Sect. 3 we discuss in detail the model in Minkowski space-time. In Sect. 4 we study the environmental fields for subhorizon momenta in de Sitter space. In Sect. 5 we explore an expansion in a fixed homogeneous metric which is close to exponential. We eliminate the environmental fields, average over the initial values and obtain a stochastic wave equation for the inflaton with a friction and noise. We briefly discuss the slow roll conditions resulting from our modification of the stochastic equation for warm inflation. We show that in some approximations the resulting wave equation for the inflaton can be treated as a Markovian stochastic wave equation. In Sect. 6 we briefly discuss the Friedman equation which determines the homogeneous metric ( the Hubble variable as a function of the inflaton field). We believe that the averaging over the initial values simulates some quantum effects in cosmological models as the quantum field theory at finite temperature tends to the classical field theory with random initial conditions distributed according to the classical Gibbs law. The thermal noise in the inflaton equation can play a similar role as the scalar quantum fluctuations (discussed in [4]) which together with the quantum fluctuations of the gravitational field during de Sitter expansion (calculated earlier in [21]) lead to the correct evaluation of the power spectrum (this can be done by means of the methods developed in [22, 23]).
2 Scalar fields interacting linearly with an environment
We consider the Lagrangian which is an extension of the well-known oscillator model discussed in [12, 13]
where \(U(\phi )\) is a certain interaction. \(U(\phi )=\phi \) is a simple choice (considered in [11, 14]) but the results of averaging over \(\chi _{n}\) do not depend essentially on U. The number of particles in the classical mechanics of [12, 13] is infinite. Only in the limit of an infinite number of degrees of freedom the irreversible diffusive behaviour can appear. In field theory even with a finite number of fields we have an infinite number of degrees of freedom (the spatial Fourier modes). Averaging over those modes can lead to a diffusive dynamics. Equations of motion read
where \(g_{\mu \nu }\) is the metric tensor and \(g=\vert \det [g_{\mu \nu }]\vert \). We can consider classical as well as quantum systems (2)–(3). Eliminating the quantized fields \(\chi \) we obtain a quantum version of the environmental noise. The quantum noise can approximate the quantum fluctuations of scalar and gravitational fields as it does in the e-fold time [22, 23].
In the flat expanding metric
Equation (3) reads
where \(H=a^{-1}\partial _{t}a\). We can solve Eq. (3) for \(\chi _{n}\)
where we denote \(U(x)=U(\phi (x))\), \(G_{n}\) is the Green function of the operator \({{\mathcal {M}}}_{n}\), \({{\mathcal {A}}}_{n}\) is any operator commuting with \({{\mathcal {M}}}_{n}\) and \(\chi _{n}^{cl}\) are solutions of the homogeneous equation \({{\mathcal {M}}}_{n}\chi ^{cl}_{n}=0\). When we insert \(\chi _{n}\) of Eq. (6) in Eq. (2) then it takes the form
where
In the homogeneous metric (4) we can take the spatial Fourier transform of Eq. (3). Then, the operators \({{\mathcal {A}}}_{n}\) become just functions \(A_{n}(\mathbf{k})\). In classical field theory (with the energy-momentum tensor \(T^{\mu \nu }\)) in Minkowski space \(\int T^{00}(\chi )d\mathbf{x}\) is a constant of motion as long as there is no coupling to \(\phi \). Then, the Gibbs distribution at temperature \(\beta ^{-1}\) is \(d\chi \exp (-\beta \int T^{00}(\chi )d\mathbf{x})\). A natural covariant generalization to a manifold is the weight factor for classical configurations of the form
where the integral \(d^{4}x\) is over a volume \(\beta \) in space-time. There is an analog in quantum statistical mechanics to the formula (9) which is applied as a statistical operator in quantum non-equilibrium statistical mechanics. For a homogeneous metric (4) the volume \(\beta \) in Eq. (9) can be expressed as a time interval \([0,\beta ]\) times the space volume. After averaging over the solutions \(A_{n}\chi ^{cl}_{n}(t,\mathbf{k})\) the correlation function of the noise is
In this way we obtain a stochastic wave equation (7)with a friction \(\delta \phi \) and the noise \(\eta \). There is some arbitrariness in the choice of the potentials U and V, the number of fields \(\chi \), the masses and the couplings. In [11, 14] \(U(\phi )=\phi \), an infinite set of fields is chosen and the masses are proportional to the couplings. As shown in [14] if we ignore the k dependence of \({{\mathcal {M}}}_{n}\) (superhorizon domain) then we obtain a wave equation of warm inflation [8, 9] with the friction proportional to \(\partial _{t}\phi \) and the noise \(\eta \) as the white noise. In the Appendix B of Ref. [11] one field \(\chi \) with large momenta is discussed. It is claimed that its effect is the same as an infinite number of \(\chi \) fields leading to an alternative derivation of the same stochastic equation for inflaton. We disagree with this claim. For low momenta of the environmental fields another stochastic equation (studied in [30]) appears than for large momenta. We study these equations in detail in this paper beginning with the simple case of the Minkowski space in the next section.
3 Environment in the Minkowski background
In Minkowski space \(a=1\). We can solve Eq. (3) exactly for Fourier transforms
where \((\chi _{n0}(\mathbf{k}),\Pi _{n}(\mathbf{k}))\) are the initial values for the wave equation, \(U(s,\mathbf{k})\) means the Fourier transform of \(U(s,\mathbf{x})\) and
Inserting (11) in Eq. (2) we obtain an explicit formula
where
The friction term could also be expressed in a Lorentz covariant form (Eqs. (2)–(3) are Lorentz invariant in Minkowski space, hence solutions should preserve this invariance)
where \(sign(\tau )\) is an odd function with \(sign (\tau ) =1\) for \(\tau >0\) and \(x=(t,\mathbf{x})\).
The Hamiltonian for the wave fields \(\chi _{n}\) is (\(\Pi =\partial _{\tau }\chi \))
Then, the expectation value with respect to the Gibbs density (9) is
In quantum theory \(A^{*}_{n}(\mathbf{k})\) and \(A_{m}(\mathbf{k}^{\prime })\) become creation and annihilation operators. Then, the expectation value is
When we calculate the expectation value of \(\eta \) with respect to the measure \(dA\exp (-\beta {{\mathcal {H}}})\) then we obtain
In quantum theory we should consider an anticommutator on the lhs of Eq. (16). Then, \(\beta ^{-1}\omega _{n}^{-2}\rightarrow \omega _{n}^{-1}\frac{1}{2}\hbar \coth (\hbar \frac{1}{2}\beta \omega _{n})\) on the rhs. So that the quantum thermal expectation values tend to classical expectation values (in the Gibbs state) when \(\hbar \beta \rightarrow 0\).
Let us distinguish two regimes: small k and large k. In the first case we neglect \(\mathbf{k}\) in \(\omega _{n}\). Then
Let \((2\pi )^{\frac{3}{2}}\lambda _{n}={\tilde{\gamma }} m_{n}\) then
If \(m_{n}\) are uniformly distributed then (because of oscillations of the cosine) the sum (18) is concentrated at small \(t-t^{\prime }\). We could e.g. apply the Poisson summation formula (for \(m_{n}\simeq n\))
or approximate the sum in Eq. (18) by an integral over \(m_{n}\) leading to the \(\delta \) function. In both cases (for a large L or in the approximation \(\sum _{n}{\tilde{\gamma }}^{2} \cdots =\gamma ^{2}\int \ldots \)) we obtain
with a certain \(\gamma \simeq {\tilde{\gamma }}\).
Next let us consider the friction \(\delta \phi \) in Eqs. (7) and (13). Writing
and integrating by parts we get the term
which under the assumptions leading to Eq. (19)can be considered as modification of the potential \(V\rightarrow V+qU^{2}\) with \(q\simeq \delta (0)\) (this is the mass renormalization if \(U\simeq \phi \) as in the Leggett model [24]). The second term from the integration by parts
under the assumptions used at Eq. (19) is proportional to \(\delta (t)\) and to the initial values of the field. We will neglect this term for \(t> 0\). After the integration by parts the friction term takes the form
We have got the same kernel as the one in Eq. (16) which we approximated by \(\delta (t-s)\) in Eq. (19) for the correlation of the noise. In fact these kernels are related by a version of the fluctuation dissipation theorem [25]. With these approximations Eq. (2) in Minkowski space reads
with the noise (19). This is the equation which would have been derived in [11] and [14] when \(a=1\). Note that in the limit of a strong friction we obtain
Hence, \(U(\phi )\) behaves like a Brownian motion in classical field theory and in the high temperature limit of the quantum field theory. If \(V^{\prime }\) is of the same order as \(\gamma ^{2}U^{\prime }\partial _{t}U\) (this may be the case because of the \(U^{2}\) renormalization mentioned below Eq. (19)) then Eq. (20) after the neglect of the second order derivatives reads
U has a large time asymptotic distribution
where \(\int dU\frac{V^{\prime }}{U^{\prime }}(U)\) means that we first express \(V^{\prime }U^{\prime -1}\) as a function of U and subsequently calculate its indefinite integral. So, \(U^{\prime }\ne 0\) may change the form of the asymptotic behaviour of the inflaton modifying the discussion in [26].
We can derive the slow roll conditions leading to the approximation (21). They require \(\vert \partial _{t}^{2}\phi \vert \ll \gamma ^{2}\vert U^{\prime }\partial _{t}U\vert \) and \(\vert \partial _{t}^{2}\phi \vert \ll \vert V^{\prime }\vert \). These conditions are satisfied if
The slow roll approximation can be applied to quantum fields as well. We can see that with the friction term the quantum field behaves like a diffusion process. In a linear model when \(V=\frac{m^{2}}{2}\phi ^{2}\) and \(U^{\prime }=1\) then the slow roll requirement is \(m^{2} \ll \gamma ^{4}\) which does not depend on \(\phi \). The correlation functions in this model
are the same as the ones for the Ornstein–Uhlenbeck process [27]. The model (21) can be considered as a limit \(H \ll \gamma ^{2}\) of the model in de Sitter space discussed in the next section (in this sense \(\partial _{t}U\) brings the friction in the Minkowski space as the Hubble constant does in the de Sitter space, in both cases the strong friction approximation is applicable).
Next, assume that k is large in comparison to \(m_{n}\). Then, neglecting the masses in Eq. (16) we have
where
If \(\vert \mathbf{x}-\mathbf{x}^{\prime }\vert =0\) then
In general, from the integral ( [28], formula 3.721)
we have
Note that the covariance (25) is vanishing for the time-like separations
Let us still discuss various forms of the friction term \(\delta \phi \) in Eq. (7). If we do not integrate by parts then the friction in Eq. (7) has an explicitly Lorentz covariant form
where
is the commutator function for the massless quantum scalar field. The friction term in Eq. (13) can also be expressed in a Lorentz invariant way as
Now, Eq. (7) takes the form
The kernel in Eq. (13) with \( m_{n}=0\) after an integration by parts is
This kernel is the same as the covariance (25) of the noise and is vanishing for time-like separations.
The stochastic equation after an integration by parts reads
with the friction kernel K and the Gaussian noise (25). That the variance of the noise and the kernel of the friction are related follows from a version of the fluctuation dissipation theorem [25]. Let us note that the result (27)–(28) is exact if all \(m_{n}=0\) and if the initial values of the \(\chi _{n}\) fields are distributed according to the Gibbs weight factor \(\exp (-\beta {{\mathcal {H}}}_{n})\)(the number of fields is irrelevant). If
then we can approximate the kernel K by a \(\delta \)-function leading to the stochastic equation
where \(\eta \) in this approximation has the correlation (23). The condition (29) can be interpreted as a negligence of the spatial dependence of \(\phi \). If the spatial dependence of \(\phi \) is ignored then we could identify Eqs. (20) and (30) although we have derived them on a basis of different assumptions concerning the \(\chi \) fields (this could explain the “alternative” derivation of the stochastic equation in Appendix B of [11]). In the strong friction limit we obtain
In Eq. (30) we can take \(V^{\prime }\) into account and integrate both sides over \(\mathbf{x}\). Then, we could conclude that \(\int d\mathbf{y}U\) has an equilibrium distribution. In contradistinction to the strong friction limit of Eq. (20) only the space average tends to the Brownian motion in Eq. (30) (and eventually to an equilibrium). However, there is a distinction between the results (20) and (30). Equation (20) is derived under an assumption of an infinite number of \(\chi \) fields with properly chosen masses, whereas Eq. (30) follows from Eq. (27) which is exact if \(m_{n}=0\). In conclusion, in the strong friction limit the classical thermal field as well as the thermal quantum fields behave as a stochastic process. As an example, if in Eq. (30) we neglect second order time derivatives and assume \(V=U^{2}\) then
Hence, \(\int d\mathbf{y}U(t,\mathbf{y})\) is the Ornstein–Uhlenbeck stochastic process.
4 Exponentially expanding environment
In an expanding universe we write
Then, in the momentum space
where
First, let us consider low momenta \(a^{-1}k \ll H\) so that for a large time (as in [14]) we can neglect \(a^{-2}k^{2} \) term. Then, we assume that \(\omega _{n}^{2}>0\), H is slowly varying and \(\omega _{n} \) are approximately constant. The approximate solutions of Eq. (32) at \(\lambda =0\) are (the same as in Eq. (11))
They are normalized as
In de Sitter space \(H=const\). If we neglect \(a^{-2}k^{2}\) and assume \(m_{n}^{2}>\frac{9}{4}H^{2}\) then we can apply the same approximation as in Sect. 3. Now, Eq. (7) in de Sitter space reads (for \(a(t)=\exp (Ht)\))
where the last two terms on the lhs of Eq. (34) result from the integration by parts as in Eq. (20) with an extra term coming from the transformation (31).The noise has the covariance
At slow roll approximation with the neglect of second order derivatives we obtain
with \(a=\exp (Ht)\). The slow roll requirements are \(\vert \partial _{t}^{2}\phi \vert \ll \vert (3H+\gamma ^{2}(U^{\prime })^{2})\partial _{t}\phi \vert \) and \(\vert \partial _{t}^{2}\phi \vert \ll \vert V^{\prime } +\frac{3}{2}\gamma ^{2}HU^{\prime }U\vert \). These conditions are satisfied if
As an example, if \(H=const\), \(U^{\prime }=1\) and \(V^{\prime }=m^{2}\phi \) then the slow roll condition is \( m^{2}\ll (3H +\gamma ^{2})^{2}\). It does not depend on \(\phi \) and allows to solve the slow roll stochastic equation explicitly.If H is determined by Einstein equations then H depends on \(\phi \) (as will be discussed in Sect. 6). Then, the slow roll conditions still must involve some requirements allowing to determine H as a function of \(\phi \).
The solution of Eq. (36)in the limit of large \(\gamma \) is
The strong friction covariance \(\langle \delta U_{t}(\mathbf{x})\delta U_{t^{\prime }}(\mathbf{x}^{\prime })\rangle \) is \(\exp ( -3Ht-3Ht^{\prime })min(t,t^{\prime })\beta ^{-1}\gamma ^{-2}\delta (\mathbf{x}-\mathbf{x}^{\prime })\) . Hence, we get an extra damping factor in comparison to the case of the Minkowski space (discussed at the end of Sect. 3).
It is instructive to consider the soluble case of Eq. (36) with \(U^{\prime }=1\), \(V^{\prime }=m^{2}\phi \). Then, the solution (with zero initial condition) is the Ornstein–Uhlenbeck process
We have got the same result as the one for the de Sitter space with the Hubble constant \(H\rightarrow H+\frac{\gamma ^{2}}{3}\) or in Minkowski space with a friction (and \(H=0\)).
Another (complementary) regime is the one when the term \(a^{-2}k^{2}\) is dominating (\(a^{-1}k \gg H\) and \(a^{-1}k\gg m_{n}\)). In such a case \(\omega _{n}\simeq a^{-1}k\). Hence, in the solution (33) of the wave equation (32) (\(\lambda _{n}=0\))
where \(\tau \) is the conformal time. In the conformal time (for the exponential expansion \(a(t)=\exp (Ht)\))
Equation (5) reads
and Eq. (2)
The free Lagrangian of the \(\chi \) fields is
The statistical weight (9) with the Hamiltonian \({{\mathcal {H}}}=T^{00}\) (with the momentum \(\Pi =\tau ^{2}(\partial _{\tau }\chi \))) is
For a large k we may ignore the masses \(m_{n}\). Then, the solution of the free wave equation is
where \(H^{(1)}_{\frac{3}{2}}\) is the Hankel function [28].
We can write the general solution in the form
If we insert the solution (43) in the Hamiltonian (41) and neglect the terms (decaying fast for large \(\tau \);large \(\tau \) means small a, hence close to the Big Bang)
and \(\tau ^{-2}\int (\partial _{\tau }\chi )^{2}\) ,then
The \(\tau \)-dependence cancels for a large \(\tau \) in Eq. (45) as expressed in Eq. (41) because \(\tau ^{-2}\) in \(\sqrt{g}{{\mathcal {H}}}\) cancels with \(\tau ^{2}\) in \((\nabla \chi )^{2}\) resulting from the terms \(\tau \exp (ik\tau )\) in Eq. (43).
We can calculate the expectation value of the noise
with respect to the weight factor (41). We obtain
We can see that the last term of the sum in Eq. (47) is divergent at small k. This is a typical infrared divergence of a massless \(\chi \) field theory in de Sitter space. It means that instead of the random variable \(\eta \) we should consider \(\eta (x)-\eta (z)\) with a fixed \(z=(s,\mathbf{z})\). Then, the variance
is finite.
Using the formula (24) we calculate the Fourier transform in Eq. (47) (neglecting the terms decaying fast for a large time) with the result
When \( \vert \mathbf{x}-\mathbf{y}\vert \rightarrow 0\) then in Eq. (48) we obtain \(\delta (\tau -\tau ^{\prime })\) (this can be seen either from Eq. (47) or from Eq. (48) by a formal Taylor expansion in \( \vert \mathbf{x}-\mathbf{y}\vert \) ).
The solution of Eq. (38) with \(m_{n}=0\) (at large k we neglect the masses) can be expressed by the Green function \({{\mathcal {G}}}\) (discussed in detail in the next section, Eq. (73))
where \(\chi ^{cl}\) is the solution with \(\lambda _{n}=0\) and
Using the formulas 3.741 of [28]
and the integral (24) we can calculate the Fourier integrals in order to express the kernel \({{\mathcal {G}}}\) in configuration space
Note that
where \((x-x^{\prime })^{2}\) is the Minkowski distance. Hence, the leading term (for a large time) is Lorentz invariant.
After an insertion of the solution of Eq. (38) in Eq. (39) the stochastic equation (7) for \(\phi \) in the configuration space reads
For \(\vert \mathbf{x}-\mathbf{y}\vert \ll \vert \tau -\tau ^{\prime }\vert \) and large \(\tau \) and \(\tau ^{\prime }\) we get the stochastic equation
by an expansion of the kernel (51) in \(\vert \mathbf{x}-\mathbf{y}\vert \) and integration by parts over \(\tau ^{\prime }\) in Eq. (52) (as in an analogous derivation of Eq. (30)). The limit of small \(\vert \mathbf{x}-\mathbf{y}\vert \) of the noise follows from Eq. (48)
In the cosmic time Eq. (53) reads
With the neglect of \(\partial _{t}^{2}\phi \) (slow-roll) and \( \triangle \phi \) ( which disappears after a space average in Eq. (53)) we obtain
In the limit of the strong friction (only \(\kappa ^{2}\) terms on the lhs)
The solution is an Ornstein–Uhlenbeck process
such that
We can see that the classical field in a thermal environment tends to a diffusion process. We could prove the same behaviour for the quantum field in a thermal state. It seems that in both cases the appearance of fluctuations and friction is crucial for the diffusive behaviour. This phenomenon is similar to the diffusive behaviour of zero temperature quantum fields in de Sitter space which also results from “friction” \(H\partial _{t}\phi \) and from quantum fluctuations [15, 18, 29].
5 Environment in an almost exponential expansion
We consider a flat expanding metric which is close to de Sitter. For \(k\ll aH\) we may repeat the calculations of Sect. 4 and Ref. [14] leading to an analog of the stochastic equation (34) (in the cosmic time)
with the noise (19). It can be shown that without the friction terms Eq. (56) is invariant with respect to the general change of coordinates. With the friction terms even the Lorentz invariance is violated because in the derivation of Eq. (56) from Eqs. (2)–(3) we have neglected the spatial derivatives of \(\chi \) fields.
Next, we explore \(\chi \) fields with large \(k\gg aH\) in a conformal time (we follow to some extent our earlier paper [31])
where the conformal time \(\tau \) is
With a slowly varying H we have approximately
where
(t is the cosmic time).
If the expansion is close to exponential then with the relation (57) Eq. (3) is
where
Let
with
Then
We obtain another form of Eq. (3) if we write
with
Then
where
With \(\lambda _{n}=0\) the solution of Eq. (65) is the Hankel function [28] \({\tilde{\Psi }}_{n}=H_{\nu _{n}}^{(1)}(k\tau )\). For a general expanding metric the solution of a homogeneous Eq. (59) (\(\lambda _{n}=0\)) is
In general, we have a superposition of classical solutions with different k
The noise is
The solution of Eq. (62) with \(\lambda _{n}=0\) on the rhs is \(\psi _{\nu }=\tau ^{-\alpha +\mu }H_{\nu }\). Then, the solution of the wave equation (62) for \(\Psi _{n}\) with \(U(\phi )\) on the rhs is
where \({{\mathcal {G}}}\) is the Green function of the operator on the lhs of Eq. (62). The Green function can be constructed from the two independent solutions of the homogeneous equation (62)
The Bessel functions J and Y [28] are defined by the Hankel function \(H_{\nu }^{(1)}=J_{\nu }+iY_{\nu }\). The Green function for \(\tau <\tau ^{\prime }\) is
where w(k) is the wronskian. If a is close to exponential then \(w(k)=\frac{2k}{\pi }\). The Green function could also be expressed as
We insert the Green function (74) in Eq. (69) in order to calculate \(\delta \phi \) of Eq. (7) for a large time (we use the asymptotic expansion of \(H_{\nu }\) [28]). Then
where
From Eq. (75) there follows the stochastic equation (7)
In Eq. (77) we have a non-Markovian and non-local friction term. For a large time \({{\mathcal {G}}}\) can be approximated by the first term of Eq. (51). If we assume that only small \(\vert \mathbf{x}-\mathbf{y}\vert \) contribute and expand in this variable then
As a result for a small \(\vert \mathbf{x}-\mathbf{y}\vert \) we obtain a stochastic equation generalizing Eq. (53)
The covariance of the noise is equal to an expectation value with respect to the measure (9)
where (as \(m_{n}=0\))
The asymptotic behaviour of the product of Hankel functions in Eq. (80) (the leading term) does not depend on \(\nu \). Hence,the approximation (45) still holds true. As a consequence for a large time we obtain
In an expanding universe we cannot expect a stationary evolution of the inflaton if H is almost a constant. However, if in the stochastic equations derived in this paper we insert the formula for H in terms of the potentials which result from the slow-roll approximation then we can consider again the time evolution close to the slow-roll as discussed in [30] but now with the modified stochastic equation as briefly discussed in the next section.
6 Einstein–Klein–Gordon system
In this section we are going to determine the Hubble variable H and the expansion scale a as solutions of Einstein equations. We consider the Lagrangian (1) as a source of the energy momentum for Einstein equations
where \(G_{\mu \nu }\) is the Einstein tensor.
We consider first the superhorizon case (56) (we generalize the results of [26] from \(U=\phi \) to general U). We eliminate the environmental fields \(\chi _{n}\). Then, the energy-momentum
is not conserved. We have
The extra terms on the rhs of Eq. (85) come from the replacement of the \(\chi \) fields by noise. We can supplement the energy-momentum (84) by the dark energy-momentum. So that the total energy density \(\rho _{\phi }+\rho _{de}\) is conserved. The energy density compensating the non-conservation law (85) is defined by
Now, if we differentiate the Friedmann equation
then we obtain the same formula as if there were no \(\chi \) fields (and no noise)
Multiplying Eq. (56) by \(\partial _{t}\phi \) (neglecting the spatial derivatives) and using Eq. (88) we obtain the conservation law
If we neglect the rhs of Eq. (89) then this equation determines H as a function of fields. Equation (89) gives an alternative formula to the Friedmann equation (87) for expressing H as a function of \(\phi \) (we can include \(U(\phi )\) in the definition of H; the neglect of \((\partial _{t}\phi )^{2} \) in Eq. (89), which allows to determine \(H(\phi )\) can be formulated as an additional requirement for slow roll besides the one discussed below Eq. (36)). Assume that the slow roll conditions as formulated in Sect. 4 below Eq. (36) are satisfied and Eq. (89) defines \(H(\phi )\) then we can determine a as a function of \(\phi \)
With the explicit functions \(a(\phi )\) and \(H(\phi )\) we have now a complete probabilistic diffusion model (the noise is determined by Eq. (35)) which allows to determine the Fokker–Planck equation and calculate the probability distribution of \(\phi \) ( for \(U=\phi \) this problem has been investigated in [26, 30]).
Next we consider a modification of the Einstein–Klein–Gordon system in the subhorizon case. The formalism of Sect. 5 is not useful for an estimate of the dependence of the stochastic inflaton equation on the varying H because the approximation (57) is applicable only for a slowly varying H. For estimates of the subhorizon k we return to Eqs. (11)–(13). The solution of the wave equation for a time dependent \(\omega \) is \(\exp (i\int ^{t}\omega )\). Then an approximate Green function in Eqs. (11)–(13) is
which for a large k is approximated by
Inserting in Eqs. (2)–(3) the Green function (92) and the wave functions \(\exp (ik\int ^{t}a^{-1})\) we obtain in the limit \(\vert \tau -\tau ^{\prime }\vert \gg \vert \mathbf{x}-\mathbf{x}^{\prime }\vert \) the stochastic equation
where the noise \(\eta \) has the covariance
With Eq. (93) we can repeat the argument, which has been based on Eqs. (56), (83)–(89), in order to express H and a in terms of \(\phi \). The study of the Einstein–Klein–Gordon system without the assumption \(\vert \tau -\tau ^{\prime }\vert \gg \vert \mathbf{x}-\mathbf{x}^{\prime }\vert \) is more involved and requires a separate investigation because in this case H,a and the noise depend on \(\phi \) in a non-local way.
7 Summary and outlook
We considered a system of non-linear wave equations describing an interaction of the inflaton \(\phi \) with other scalar fields \(\chi _{n}\). In quantum mechanics if the fields \(\chi _{n}\) are not observable then we average over the states of \(\chi _{n}\). As a result the inflaton is described by a density matrix resulting from the averaging. The natural state for averaging is the Gibbs (thermal) state of maximal entropy for the \(\chi _{n}\) fields. Then, further evolution does not depend on the initial time when the interaction between the inflaton and the \(\chi _{n}\) fields is switched in. We discussed the model in the classical limit when the probability distribution is described by the canonical Hamiltonian of the \(\chi _{n}\) fields. In an expanding metric the canonical Hamiltonian depends on time. However, for large conformal time in models with an expansion close to the exponential the time-dependence disappears. The average over the environmental fields is reduced to an average over the initial values of the \(\chi _{n}\) fields in the Gibbs state. There is some arbitrariness in the choice of the environment; the number of fields \(\chi _{n}\), the couplings \(\lambda _{n}\), the masses \(m_{n}\) and the interaction \(\lambda _{n}\chi _{n} U(\phi )\) (we choose an interaction linear in the environmental fields). We discuss evolution of the inflaton field in an external expanding metric in two regimes. First, we choose the increasing masses proportional to couplings and assume negligible (superhorizon) momenta \(k\ll aH\) of an infinite set of the environmental fields. These assumptions after an averaging over \(\chi _{n}\) lead directly to a Markovian wave equation with a friction and white noise. In such a case the quantum evolution is described by a master equation of the Lindblad type. Another (subhorizon) limit discussed in this paper involves large momenta \(k\gg aH\) and \(k\gg m_{n}\). The number of fields \(\chi _{n}\) can be finite. After an averaging we obtain a wave equation for the inflaton which is non-local and non-Markovian in the friction and noise. If we restrict ourselves to correlations \(\langle \phi (\tau _{1},\mathbf{x}_{1}) \cdots \phi (\tau _{n},\mathbf{x}_{n})\rangle \) such that \(\vert \tau _{j}-\tau _{k}\vert \gg \vert \mathbf{x}_{j}-\mathbf{x}_{k}\vert \) then the stochastic wave equation has a Markovian limit as a diffusion wave equation with friction. This equation is different from the wave equation derived for low momenta of the environmental fields. Both equations may coincide in a linearized version after a spatial averaging. In the last section we discussed a determination of the expansion scale factor a from the Einstein–Klein–Gordon system of equations. In the superhorizon case it is possible to obtain a stochastic wave equation with \(a(\phi )\) and \(H(\phi )\) dependent on \(\phi \) and the noise independent of \(\phi \). In such a case we can calculate all expectation values on the basis of the Fokker–Planck equation. An interesting problem for further studies is the dependence of slow roll conditions and spectral indices on the interaction \(U(\phi )\). In the subhorizon case the noise and \(a(\phi )\) depend in a non-local way on \(\phi \). Only in the limit of small spatial distances (\(\vert \mathbf{x}_{j}-\mathbf{x}_{k}\vert \ll \vert \tau _{j}-\tau _{k}\vert \)) we are able to derive a Markovian stochastic wave equation with \(a(\phi )\) and \(H(\phi )\) determined by Einstein equations.
In this paper we concentrate our attention on the stochastic equations satisfied (in various regimes) by the inflaton interacting with an environment. The environment consists of superhorizon or subhorizon modes of the classical thermal environmental fields. In [15, 16] the subhorizon modes of the quantum field have been treated as the environment. The environmental modes are approximated by a noise. If the noise is approximately Markovian then the quantum states satisfy the irreversible Lindblad equation. It is well-known that Lindblad equation leads to decoherence (meaning a destruction of interference of quantum states). The interference is a substantial obstacle to the classical limit. In the standard model the large scale structure is formed from quantum fluctuations [4, 21] in the early universe. Hence, in the meantime quantum fluctuations should become classical. In [32, 33] it is shown that if initially the universe starts from the Gaussian state then with the time evolution determined by a linear perturbation theory the resulting squeezed state becomes classical. The measured CMB fluctuations are indistinguishable from classical fluctuations. At present, all observations [19, 20] show no departure from Gaussian correlations. However, it may be that prospective CMB measurements can reveal some non-Gaussian behavior. Such CMB results could show a destruction of interference of states in the early universe and the role of the environment in their decoherence as discussed in [34]. The noise in Einstein–Klein–Gordon system plays at least two roles:it leads to decoherence and it determines the power spectrum (as calculated in [23] with the quantum noise taking into account quantum gravitational fluctuations). The detailed analysis of the contribution of the noise from the environment to the power spectrum and to higher order correlation functions of the inflanton could give important information about the quantum state in an early universe and its classical limit.
Data Availability Statement
This manuscript has associated data in a data repository. [Authors’ comment: All data included in this manuscript are available upon request by contacting with the corresponding author (Zbigniew Haba).]
References
A.A. Starobinsky, Phys. Lett. B 91, 99 (1980)
A. Guth, Phys. Rev. D 23, 347 (1981)
A.A. Linde, Phys. Lett. B 108, 389 (1982)
V.F. Mukhanov, G.V. Chibisov, JETP Lett. 33, 532 (1981)
M. Sasaki, Prog. Theor. Phys. 76, 1036 (1986)
L. Kofman, A. Linde, A.A. Starobinsky, Phys. Rev. D 56, 3258 (1997)
B.A. Bassett, S. Tsujikawa, D. Wands, Rev. Mod. Phys. 78, 537 (2006)
A. Berera, Li-Zhi Fang, Phys. Rev. Lett. 74, 1912 (1995)
A. Berera, I.G. Moss, R.O. Ramos, Rep. Prog. Phys. 72, 026901 (2009)
A. Berera, Nucl. Phys. B 585, 666 (2000)
A. Berera, Phys. Rev. D 54, 2519 (1996)
G.W. Ford, J.T. Lewis, R.F. O’Connell, Phys. Rev. A 37, 4416 (1988)
G.W. Ford, M. Kac, J. Stat. Phys. 46, 803 (1987)
Z. Haba, Adv. High Energy Phys. 2018, 7204952 (2018). arXiv:1807.00639
A.A. Starobinsky, in Current Topics in Field Theory, Quantum Gravity and Strings, Lect. Notes Phys., vol. 246, ed. by H.J. Vega, N. Sanchez (Springer, Berlin, 1986), p. 107
A.A. Starobinsky, Phys. Lett. B 117, 175 (1982)
A. Vilenkin, L.H. Ford, Phys. Rev. D 26, 1231 (1982)
A. Vilenkin, Phys. Rev. D 27, 2848 (1983)
P.A.R. Ade et al., arXiv:1502.01589
K.T. Story et al., ApJ 779, 86 (2013)
A.A. Starobinsky, JETP Lett. 30, 682 (1979)
F. Finnelli, G. Marozzi, A.A. Starobinsky, G. Venturi, Phys. Rev. D 79, 044007 (2009)
V. Vennin, A.A. Starobinsky, Eur. Phys. J. C 75, 413 (2015)
A.O. Caldeira, A.J. Leggett, Phys. A 121, 587 (1983)
A. Sarracino, A. Vulpiani, arXiv:1909.03726
Z. Haba, Int. J. Mod. Phys. D 28, 1950085 (2019)
S. Chandrasekhar, Rev. Mod. Phys. 15, 1 (1943)
I.S. Gradstein, I.M. Ryhzik, Tables of Integrals, Series and Products (Nauka, Moscow, 1971) (in Russian)
A.A. Starobinsky, J. Yokoyama, Phys. Rev. D 50(6357), 99 (1994)
Z. Haba, Eur. Phys. J. C 79, 906 (2019)
Z. Haba, Phys. Lett. B 792, 320 (2019)
A. Albrecht, P. Ferreira, M. Joyce, T. Prokopec, Phys. Rev. D 50, 4807 (1994)
D. Polarski, A.A. Starobinsky, Class. Quantum Gravity 13, 377 (1996)
C. Kiefer, D. Polarski, Adv. Sci. Lett. 2, 164 (2009). arXiv:0810.0087
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Haba, Z. Stochastic inflaton wave equation from an expanding environment. Eur. Phys. J. C 80, 321 (2020). https://doi.org/10.1140/epjc/s10052-020-7877-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-7877-y