1 Introduction

In recent years, the field of cosmology has witnessed significant advancements driven by the quest to explain the observed accelerated expansion of the universe [1, 2]. The standard framework of General Relativity (GR), coupled with the presence of dark energy [3] or the introduction of a cosmological constant [4], provides a successful description of cosmic acceleration. However, the nature and origin of dark energy remain elusive, motivating researchers to explore alternative theories of gravity. One significant motivation behind modified gravity theories and scalar field theories is the necessity to elucidate the accelerated expansion of the universe and the presence of dark matter and dark energy [5,6,7,8]. GR faces challenges in comprehensively explaining these phenomena without resorting to ad hoc concepts like dark energy [9]. By modifying the gravitational equations [10, 11] or introducing additional scalar fields [12, 13], these alternative theories hold the potential to provide explanations for the observed cosmic acceleration and the behavior of dark matter.

Furthermore, cosmological inflation [14, 15] and the presence of singularities [16] pose significant challenges. GR struggles to explain the driving mechanisms behind inflation and the initial conditions that lead to its occurrence. Moreover, the existence of singularities, such as those within black holes and the Big Bang, raises questions about the applicability of GR in extreme conditions. Modified gravity theories and scalar field theories offer promising approaches to address these cosmological puzzles and overcome the singularities by introducing new gravitational degrees of freedom or incorporating quantum effects into the theory of gravity [6, 10, 11, 17].

However, there are challenges associated with these alternative theories. The mathematical complexity of the modified equations presents analytical and computational difficulties. Furthermore, experimental validation and observational constraints are necessary to distinguish between different theories and confirm their viability. Nevertheless, the pursuit of modified gravity theories and scalar field theories offers promising avenues for advancing our understanding of gravity, unifying gravitational and quantum physics, and providing comprehensive explanations for the observed universe. Ongoing research and future experimental advancements are crucial in shaping the development and refinement of these alternative frameworks beyond the realm of GR.

One alternative approach to address the observed accelerated expansion of the universe is through the modification of the gravitational Lagrangian. A notable example of such modifications is found in f(T) theories of gravity [18, 19]. In these theories, the gravitational Lagrangian is formulated in terms of the torsion scalar T alone, without the inclusion of additional scalar fields. This framework provides an avenue to investigate the accelerated expansion without resorting to exotic forms of energy or modifying the matter content of the universe. Numerous studies have focused on analyzing the cosmological implications of f(T) gravity [20,21,22]. These investigations involve examining the late-time cosmic acceleration, the evolution of perturbations, and the behavior of cosmological parameters. One notable result in the field is the derivation of cosmological solutions that can explain the accelerated expansion of the universe. These solutions often involve modifying the background evolution and introducing additional terms in the field equations. By comparing the predictions of f(T) gravity with observational data, such as the cosmic microwave background radiation and large-scale structure formation, researchers can constrain the parameter space of f(T) gravity and assess its compatibility with observations. A well-known article in the field of (f(T) gravity is written by Linder [23], which provides a comprehensive review of various aspects of f(T) gravity, including its theoretical foundations, cosmological implications, and observational constraints.

In order to encompass the combined effects of gravity and scalar fields in understanding the dynamics of the universe, the f(T) framework has been extended to the \(F(T,\phi )\) cosmological model [24], similar to the extension of the curvature-based f(R) theory to the \(F(T,X,\phi )\) model [25]. In this extended framework, the Lagrangian incorporates not only the torsion scalar T but also the scalar field \(\phi \), along with an arbitrary function F that describes the gravitational theory. This extension provides a more comprehensive approach to investigating the phenomenon of accelerated expansion, allowing for a deeper exploration of the underlying dynamics. The \(F(T,\phi )\) cosmological model has gained significant attention due to its capacity to incorporate both gravitational and scalar field effects. The torsion scalar T characterizes the torsion in spacetime and serves as a gravitational variable, while the scalar field \(\phi \) accounts for matter or dark energy contributions. The function \(F(T,\phi )\) generalizes the gravitational Lagrangian, enabling modifications and extensions beyond the standard Einstein–Hilbert action. The \(F(T,\phi )\) cosmological model has been the subject of numerous investigations in recent years. Researchers have explored various aspects of this model, including its cosmological solutions [24], the evolution of perturbations, and its compatibility with observational data. The study of this model provides valuable insights into the nature of gravity and its role in shaping the dynamics of the universe [24, 26, 27].

Furthermore, Noether symmetry has emerged as a popular and powerful tool in the study of modified gravity theories [28, 29]. Noether’s theorem, named after the mathematician Emmy Noether, establishes a connection between symmetries in physical systems and it’s conserved quantities. In the context of modified gravity, Noether symmetry provides a systematic approach to investigate the underlying symmetries of the theory and their associated conserved quantities.

The appeal of Noether symmetry in modified gravity lies in its ability to unveil deeper insights into the dynamics of gravitational theories. By identifying the symmetries of a modified gravity model, researchers can derive conserved quantities that shed light on the underlying structure of the theory and its physical implications. Noether symmetry also offers a powerful tool to constrain the parameter space of modified gravity theories, allowing for consistency checks and comparisons with observational data [30,31,32]. Furthermore, Noether symmetry provides a rigorous mathematical framework to explore the interplay between gravity and other fields, such as scalar fields or additional degrees of freedom. It allows for the construction of physically meaningful models with desirable properties by selecting the form of unknown functions in the gravitational theories.

In particular, this approach has been a frequently preferred method in obtaining exact cosmological solutions in various modified gravity theories. Some of the studies analyzed through this approach are f(R) theories [33,34,35,36], modified Gauss–Bonnet theories [37,38,39], f(T) teleparallel gravity models [40,41,42,43,44,45]. In addition to modified theories constructed by changing the geometric part, models containing scalar fields [46,47,48,49,50,51,52,53], fermionic fields within the framework of GR [54, 55] and within the framework of TG [56] and tachyonic fields [57, 58] in the context of TG were analyzed using this approach. Apart from the cosmological studies, analytical solutions have also been produced for spherically symmetric [59] and cylindrical symmetric spacetimes [60] using this approach. Recently, solutions have been presented for both isotropic and non-isotropic universe models through the Noether symmetry approach, considering curvature-based extended \(F(R, X,\phi )\) theories [61, 62]. As mentioned above, with the motivation offered by the Noether symmetry approach, the main purpose of this article is to conduct cosmological analyzes by investigating Noether symmetries in the context of \(F(T,X,\phi )\) gravity.

The paper is structured as follows: Sect. 2 provides a brief review of teleparallel gravity and \(f(T,\phi )\) theories, setting the foundation for the subsequent analysis. Section 3 delves into the framework of \(F(T,X,\phi )\) gravity, establishing the theoretical framework for the investigation. Section 4 conducts a comprehensive examination of the symmetry reduced Lagrangian and Noether equations within the context of \(F(T,X,\phi )\) gravity, specifically applied to the FRW universe model. Finally, the concluding section offers a concise summary of the obtained results, summarizing the key findings and implications of the study.

2 Teleparallel gravity

Teleparallel gravity (TG) is an alternative formulation of gravity that incorporates the concept of torsion. In GR, the gravitational field is defined by the curvature of spacetime. However, unlike GR, TG is constructed by utilizing torsion resulting from a teleparallel connection where the curvature is zero [18].

TG introduces the tetrad field \(e^{A}{}_{\mu }\) and the spin connection \(\mathcal {\omega }^{A}{}_{B\mu }\) as fundamental variables, providing a distinct framework for understanding gravity. Note that the presence of spin connection leads to local Lorentz invariance of the field equations [63]. In this framework, the tetrad field plays a crucial role in relating local Lorentz frames to spacetime coordinates. The tetrad field, represented by \(e^{A}{}_{\mu }\), connects the tangent space at each point in the manifold to the spacetime itself. The Greek indices, such as \(\mu \), represent the manifold, while the Latin indices, such as \(A\), denote coordinates on the tangent space.

One of the key applications of the tetrad field in TG is the construction of the metric tensor. The metric tensor, denoted by \(g_{\mu \nu }\), describes the geometry of the spacetime manifold. In teleparallel gravity, the metric tensor can be expressed in terms of the tetrad field as follows:

$$\begin{aligned} g_{\mu \nu } = \eta _{AB}e^{A}{}_{\mu }e^{B}{}_{\nu } \end{aligned}$$
(1)

where \(\eta _{AB}\) represents the components of the Minkowski metric. The Minkowski metric serves as a reference metric that characterizes flat spacetime. Furthermore, the tetrad field must satisfy an important condition known as the orthogonality condition. This condition ensures the proper relation between the local Lorentz frames and the spacetime manifold. Mathematically, the orthogonality condition is given by:

$$\begin{aligned} E_A{}^{\mu }e^B{}_{\mu } = \delta _A^B \end{aligned}$$
(2)

where \(E_A{}^{\mu }\) represents the inverse of the tetrad field, and \(\delta _A^B\) is the Kronecker delta symbol. This condition guarantees that the tetrad field properly connects the tangent space vectors to the spacetime coordinates.

By introducing the tetrad field and the spin connection as fundamental variables, TG offers a different perspective on gravity compared to the traditional metric-based approach of GR. The tetrad field allows for the exploration of the geometric properties of gravity, emphasizing the interplay between local Lorentz frames and the spacetime manifold. This alternative formulation provides insights into the geometrical nature of gravity and its connection to matter. The teleparallel connection, obtained by utilizing the tetrad field, serves as an alternative to the Levi-Civita connection in theories of gravity and incorporates torsion. It is represented by the symbol \(\varGamma ^\rho {}_{\mu \nu }\), which can be expressed in terms of the tetrad field \(e^{A}{}_{\mu }\) and the spin connection \(\omega ^A_{B \mu }\) as follow [64]

$$\begin{aligned} \varGamma ^\rho {}_{\mu \nu } = E_A{}^\rho \partial _\mu e^A{}_\nu + E_A{}^\rho \omega ^A_{B \mu } e^B{}_\nu \end{aligned}$$
(3)

where \(\partial _\mu \) represents the partial derivative with respect to the spacetime coordinate \(x_\mu \). It should be emphasized that a special choice of the so-called Weitzenböck frame is possible, in which the components of the spin connection vanishes. The torsion tensor \(T^\rho {}_{\mu \nu }\) captures the geometric properties of the intricate spacetime twisting in teleparallel gravity, playing a crucial role within this framework. It can be mathematically represented by the following equation [65]

$$\begin{aligned} T^\rho _{ \mu \nu } = \varGamma ^\rho {}_{\nu \mu } - \varGamma ^\rho {}_{\mu \nu }. \end{aligned}$$
(4)

The torsion scalar, which captures the overall torsion in TG, is defined as

$$\begin{aligned} T= S_{A}^{ \mu \nu } T^{A}_{ \mu \nu }, \end{aligned}$$
(5)

where \( S_{A}^{ \mu \nu } \) is the super-potential. The torsion tensor provides information about the properties of spacetime in TG while the gravitational Lagrangian is constructed by the torsion scalar.

Building upon teleparallel gravity, \(f(T)\) gravity extends the theory by introducing a general function \(f(T)\) of the torsion scalar \(T\). The action in \(f(T)\) gravity is given by the equation [19]

$$\begin{aligned} S_{f(T)} = \frac{1}{2\kappa }\int d^{4}x \left| e \right| f(T). \end{aligned}$$
(6)

This theory, whose various cosmological dynamics have been discussed in the literature, leads to second-order field equations.

These formulations and extensions in TG provide avenues for exploring the geometric properties of gravity, the behavior of scalar fields, and their interconnections. They offer exciting possibilities to deepen our understanding of the fundamental nature of gravity and its implications in the broader context of theoretical physics. Furthermore, the framework can be further extended to \(F(T,\phi ,X)\) gravity. This extension introduces additional degrees of freedom and allows for the exploration of gravitational theories that incorporate scalar fields and their interactions with the geometry of spacetime.

These formulations provide a rich and versatile framework for investigating deviations from GR and exploring alternative theories of gravity that incorporate torsion, scalar fields, and their interplay with the geometry of spacetime. They offer new perspectives and possibilities for understanding the fundamental nature of gravity and its connections with other fundamental forces in the universe.

3 \(F(T,X,\phi )\) gravity and cosmology

Let’s start with the following gravitation effect integral, which allows for non-minimal coupling between the torsion scalar, the scalar field, and its kinetic part [66]

$$\begin{aligned} S= & {} \int d^4xe\left[ F(T,X,\phi )+\mathcal {\ell }_m\right] , \end{aligned}$$
(7)

where e is the determinant of the tetrad field, F is a multivariate function that depends on the torsion scalar T, the scalar field \(\phi \), and the kinetic part of the scalar field X defined as \(X=-\frac{\epsilon }{2}\partial ^{\mu }\phi \partial _{\mu }\phi \) and \(\mathcal {\ell }_m\) is any matter Lagrangian. The modified field equations can be derived when one takes the variation of the integral of action with respect to the tetrad field such that [66, 67]

$$\begin{aligned}{} & {} {G}_{\mu \nu }F_{T}+\frac{1}{2}g_{\mu \nu }\left( F-F_{T}T\right) +S_{\nu \mu }{}^{\rho }{}\overset{\circ }{\nabla }_{\rho }F_{T}\nonumber \\{} & {} +\frac{\epsilon }{2}F_{X}\phi _{,\mu }\phi _{,\nu } = \varTheta _{\mu \nu }, \end{aligned}$$
(8)

and similarly with respect to the scalar field \(\phi \) one can read the modified Klein–Gordon equation as

$$\begin{aligned} g^{\mu \nu }\overset{\circ }{\nabla }_{\mu }\left( F_X \phi _{,\nu }\right) +\epsilon F_{\phi }=0 \,, \end{aligned}$$
(9)

where \(\overset{\circ }{\nabla }_{\mu }\) donates the Levi-Civita covariant derivative, we also use the notations \( F_{T}\equiv \partial F/\partial T\), \( F_{X}\equiv \partial F/\partial X\) and \( F_{\phi }\equiv \partial F/\partial \phi \). For our current analysis we will consider the spatially flat homogeneous and isotropic FRW metric to understand how the universe cosmologically evolves in \(F(T,X,\phi )\) theory

$$\begin{aligned} ds^2= & {} -dt^2+a(t)^2(dx^2+dy^2+dz^2), \end{aligned}$$
(10)

where a(t) is the scale factor and we consider the proper tetrad \(e^{a}_{\mu }=diag(1,a,a,a)\). For this frame one can compute the torsion scalar as \(T=-6\frac{\dot{a}^2}{a^2}\) [64] where the dot denotes the derivative with respect to cosmic time t. By substituting this tetrad field into the gravitational field equations (8) of the \(F(T,X,\phi )\) theory, we obtain

$$\begin{aligned} F-2TF_{T}-2XF_{X}= & {} \rho _{m}, \end{aligned}$$
(11)
$$\begin{aligned} F-2TF_{T}+4F_{T}\dot{H}+4\dot{F_{T}}H= & {} -P_{m}, \end{aligned}$$
(12)

where H is the Hubble parameter. Also \(\rho _{m}\) and \(P_{m}\) are functions of cosmic time and represent the energy density and pressure of the standard matter field. Additionally, the Klein–Gordon equation (9) is found as follows

$$\begin{aligned} F_{X}\ddot{\phi }+3F_{X}H\dot{\phi }+\dot{F_{X}}\dot{\phi }+\epsilon F_{\phi }= & {} 0. \end{aligned}$$
(13)

4 Noether symmetry analysis in \(F(T,X,\phi )\) gravity

First of all, this section is dedicated to rewriting the action integral of the theory of gravity \(F(T,X,\phi )\) given by (7) in the Lagrange formalism. A point-like Lagrangian derived from the theory of gravity is used for the Noether symmetry method, which provides analytical solutions to the field equations. For the construction of a point-like Lagrangian, we can set a canonical Lagrangian for the FRW metric as \(L=L(a,T,X,\phi ,\dot{a},\dot{T},\dot{X},\dot{\phi })\) defined on the configuration space \(Q=Q(a,T,X,\phi )\) and its tangent space by \(TQ=TQ(\dot{a},\dot{T},\dot{X},\dot{\phi })\). Now, by adopting the Lagrange multipliers procedure, which is frequently applied in cosmological analysis, we can rewrite the gravitational action (7) as follows

$$\begin{aligned} S = \int dt a^3\left[ F(T,X,\phi )-\lambda _{1}(T-\tilde{T}) -\lambda _{2}(X-\tilde{X})+\mathcal {\ell }_m\right] . \end{aligned}$$
(14)

Here, \(\lambda _{1}\) and \(\lambda _{2}\) represent Lagrange multipliers, and when the variation of equation (14) with respect to T and X is taken, they are found as \(\lambda _{1}=F_{T}\) and \(\lambda _{1}=F_{X}\), respectively. Also, in our case the dynamical system is subject to the constraints \(\tilde{T}=-6\frac{\dot{a}^2}{a^2}\) and \(\tilde{X}=\frac{\epsilon }{2}\dot{\phi }^2\). To proceed, one must choose the standard matter Lagrangian in Eq. (14). So we assume a space-time filled with a perfect fluid whose energy-momentum tensor satisfies the conservation law of energy, i.e.

$$\begin{aligned} \dot{\rho }_{m} 3H(w+1)\rho _{m}= & {} 0 \Rightarrow \rho _{m}=\rho _{m0}a^{-3(w+1)}, \end{aligned}$$
(15)

where \(w=\frac{p_{m}}{\rho _{m}}\) is the equation of state parameter for the perfect fluid and \(\rho _{m0}\) is the present value of the energy density. Therefore we have \(\mathcal {\ell }_m=\rho _{m0}a^{-3w}\). As a result, the point-like Lagrangian from Eq. (14) becomes

$$\begin{aligned} L= & {} a^3(F-TF_{T}-XF_{X})-6F_{T}a\dot{a}^2\nonumber \\ {}{} & {} +\frac{\epsilon }{2}F_{X}a^3\dot{\phi }^2-\rho _{m0}a^{-3w}, \end{aligned}$$
(16)

which has the generalized coordinates \(a, T, X, \phi \). Then, from the Euler-Lagrange equation we obtain the following field equations for a, T, X and \(\phi \), respectively

$$\begin{aligned}{} & {} 2F_{T}\left( 2\frac{\ddot{a}}{a}+\frac{\dot{a}^2}{a^2}\right) +4\dot{F_{T}}\frac{\dot{a}}{a}+\frac{\epsilon }{2}F_{X}\dot{\phi }^2 \nonumber \\ {}{} & {} \quad +F-TF_{T}-XF_{X} +w\rho _{m0}a^{-3(w+1)} = 0, \end{aligned}$$
(17)
$$\begin{aligned}{} & {} F_{TT}\left( T+6\frac{\dot{a}^2}{a^2}\right) +F_{TX}\left( X-\frac{\epsilon }{2}\dot{\phi }^2\right) = 0, \end{aligned}$$
(18)
$$\begin{aligned}{} & {} F_{XX}\left( X-\frac{\epsilon }{2}\dot{\phi }^2\right) + F_{TX}\left( T+6\frac{\dot{a}^2}{a^2}\right) = 0, \end{aligned}$$
(19)
$$\begin{aligned}{} & {} F_{X}\ddot{\phi }+3F_{X}H\dot{\phi }+\dot{F_{X}}\dot{\phi }+\epsilon F_{\phi } = 0. \end{aligned}$$
(20)

We note that when the expressions of the torsion scalar and X are taken into account, we see that Eqs. (18) and (19) are satisfied identically. Moreover, we also have the Hamilton constraint equation related to Lagrangian (16), which reads

$$\begin{aligned} E_{L}= & {} 6F_{T}\frac{\dot{a}^2}{a^2}-\frac{\epsilon }{2}F_{X}\dot{\phi }^2\nonumber \\ {}{} & {} +F-TF_{T}-XF_{X}-\rho _{m0}a^{-3(w+1)} = 0. \end{aligned}$$
(21)

These equations are identical to the field equations obtained above in tensorial form, and the unknown function \(F(T,X,\phi )\) they contain needs to be selected. Additionally, since the field equations have a nonlinear structure, one way to simplify them is to investigate Noether symmetries related to Lagrangian (16), which we will proceed from now.

Let us now consider the Noether symmetry operator and its first prolongation in accordance with Lagrangian (16), respectively, as follows

$$\begin{aligned} \textbf{X}= & {} \tau \frac{\partial }{\partial t}+\alpha \frac{\partial }{\partial a}+\beta \frac{\partial }{\partial T}+\gamma \frac{\partial }{\partial X}+\delta \frac{\partial }{\partial \phi }, \end{aligned}$$
(22)
$$\begin{aligned} \mathbf{X^{[1]}}= & {} \textbf{X}+(D_{t}\alpha -\dot{a}D_{t}\tau ) \frac{\partial }{\partial \dot{a}}+(D_{t}\beta -\dot{T}D_{t}\tau ) \frac{\partial }{\partial \dot{T}} \nonumber \\ {}{} & {} +(D_{t}\gamma -\dot{X}D_{t}\tau ) \frac{\partial }{\partial \dot{X}}+(D_{t}\delta -\dot{\phi }D_{t}\tau ) \frac{\partial }{\partial \dot{\phi }}, \end{aligned}$$
(23)

where \(D_{t}=\frac{\partial }{\partial t}+\dot{a}\frac{\partial }{\partial a}+\dot{T}\frac{\partial }{\partial X}+\dot{a}\frac{\partial }{\partial X}+\dot{\phi }\frac{\partial }{\partial \phi }\) is called the total derivative operator and are the coefficients of the Noether symmetry operator and depend on the dynamic variables \((a, T, X,\phi )\) and the cosmic time t. If one considers a function \(M(t,a,T,X,\phi )\) then the Noether symmetry condition associated with the Lagrangian is of the form (reffff)

$$\begin{aligned} \textbf{X}^{[1]}L + LD_{t}(\tau ) = D_{t}M. \end{aligned}$$
(24)

It should be noted that an important role of Noether symmetry is that it relates to conserved quantities for dynamical systems. Therefore, if X is the Noether symmetry vector, then in our case

$$\begin{aligned} I&= \tau L + \left( a-\tau \dot{a}\right) \frac{\partial L}{\partial \dot{a}}+ \left( T-\tau \dot{T}\right) \frac{\partial L}{\partial \dot{T}} \nonumber \\ {}&\quad + \left( X-\tau \dot{X}\right) \frac{\partial L}{\partial \dot{X}} + \left( \phi -\tau \dot{\phi }\right) \frac{\partial L}{\partial \dot{\phi }} - M. \end{aligned}$$
(25)

is the conserved quantity i.e I is a constant. The condition (24) for the point-like Lagrangian (16) gives the following system of partial differential equations

$$\begin{aligned}{} & {} F_{T}(\alpha +2a\alpha _{a}-a\tau _{t})+a(F_{TT}\beta +F_{T,X}\gamma +F_{T,\phi }\delta ) = 0, \end{aligned}$$
(26)
$$\begin{aligned}{} & {} F_{X}(3\alpha +2a\delta _{\phi }-a\tau _{t})+a(F_{TX}\beta +F_{XX}\gamma +F_{X\phi }\delta ) = 0, \end{aligned}$$
(27)
$$\begin{aligned}{} & {} 12F_{T}\alpha _{\phi }-\epsilon F_{X}a^2\delta _{a} = 0, \end{aligned}$$
(28)
$$\begin{aligned}{} & {} 12F_{T}\alpha _{t}-a^3(F-TF_{T}-XF_{X}-\rho _{m0}a^{-3w})\tau _{a}+M_{a} = 0, \end{aligned}$$
(29)
$$\begin{aligned}{} & {} a^3(F-TF_{T}-XF_{X}-\rho _{m0}a^{-3w})\tau _{T}-M_{T} = 0, \end{aligned}$$
(30)
$$\begin{aligned}{} & {} a^3(F-TF_{T}-XF_{X}-\rho _{m0}a^{-3w})\tau _{X}-M_{X} = 0, \end{aligned}$$
(31)
$$\begin{aligned}{} & {} F_{T}\alpha _{T} = 0, \quad F_{T}\alpha _{X} = 0, \quad F_{X}\delta _{T} = 0, \quad F_{X}\delta _{X} = 0, \end{aligned}$$
(32)
$$\begin{aligned}{} & {} F_{T}\tau _{a} = 0, \quad F_{T}\tau _{T} = 0, \quad F_{T}\tau _{x} = 0, \quad F_{T}\tau _{\phi } = 0, \end{aligned}$$
(33)
$$\begin{aligned}{} & {} F_{X}\tau _{a} = 0, \quad F_{X}\tau _{T} = 0, \quad F_{X}\tau _{x} = 0, \quad F_{X}\tau _{\phi } = 0, \end{aligned}$$
(34)
$$\begin{aligned}&a^3(F-TF_{T}-XF_{X}-\rho _{m0}a^{-3w})\tau _{t}\nonumber \\ {}&\quad +3[a^2(F-TF_{T}-XF_{X}) \nonumber \\ {}&\quad +w\rho _{m0}a^{-3w-1}]\alpha -a^3(TF_{TT}+XF_{TX})\beta \nonumber \\ {}&\quad -a^3(TF_{TX}+XF_{XX})\gamma \nonumber \\&\quad +a^3(F_{\phi }-TF_{T\phi }-XF_{X\phi })\delta -M_{t} = 0, \end{aligned}$$
(35)

where the subscripts represent the derivatives of the functions with respect to their arguments. These are Noether symmetry equations whose solutions give both the Noether symmetry coefficients and the form of \(F(T,X,\phi )\). However, trying to solve them directly is a very difficult task. Therefore, we will first choose some specific forms of \(F(T,X,\phi )\)) and then try to obtain the symmetry vector related to it.

4.1 Case 1: \(F(T,X,\phi )=T \phi ^m+h(\phi )X-\lambda \phi ^n\)

This case is related to the model in which the scalar field is non-minimally coupled to both the torsion scalar and the kinetic term. \(h(\phi )\) is any function of the scalar field coupled with the kinetic term X. \(\lambda \), n and m are the model parameters such that for \(m=2\) and \(h(\phi )=\frac{1}{2}\), Noether symmetry analysis was examined in reference [68,69,70], and also the case \(m=1\) and \(h(\phi )=\frac{const.}{\phi }\) was studied in [71]. However, this case we are dealing with is more general. After some manipulations, for the pressureless matter field, i.e. \(w=0\) we find the unknown functions in the Noether symmetry equations (26)–(35) as

$$\begin{aligned} \alpha= & {} \frac{c_{1}(m+n)a}{3(m-n)\rho _{m0}}-\frac{c_{3}(m+n)t-8c_4n}{8n}\nonumber \\ {}{} & {} a^{\frac{3m-n}{2n}}\phi ^{-\frac{(m-n)}{2}}, \end{aligned}$$
(36)
$$\begin{aligned} \delta= & {} -\frac{2c_{1}\phi }{(m-n)\rho _{m0}}+\frac{3c_{3}(m+n)t-24c_4n}{8n^2}\nonumber \\ {}{} & {} a^{\frac{3(m-n)}{2n}}\phi ^{\frac{(n-m+2)}{2}}, \end{aligned}$$
(37)
$$\begin{aligned} \tau= & {} -\frac{c_{1}}{\rho _{m0}}t+c_{5}, \quad \nonumber \\ M= & {} c_{1}t+c_{2}+c_{3}a^{\frac{3(m+n)}{2n}}\phi ^{\frac{(m+n)}{2}}, \end{aligned}$$
(38)
$$\begin{aligned} h(\phi )= & {} \frac{8n^{2}}{3\epsilon }\phi ^{m-2}. \end{aligned}$$
(39)

Thus, the Lagrangian (16) is reduced to the form

$$\begin{aligned} L= -6\phi ^m a \dot{a}^2+a^3 \left( \frac{2n^2}{3}\phi ^{m-2}\dot{\phi }^2-\lambda \phi ^n\right) -\rho _{m0}. \end{aligned}$$
(40)

Using the expressions (36)–(38), symmetry generators can be written as follows

$$\begin{aligned}{} & {} \begin{aligned} \mathbf{X_{1}}&= \frac{\partial }{\partial t}, \\ \mathbf{X_{2}}&= -\frac{t}{\rho _{m0}}\frac{\partial }{\partial t}+\frac{(m+n)a}{3(m-n)\rho _{m0}}\frac{\partial }{\partial a}-\frac{2\phi }{(m-n)\rho _{m0}}\frac{\partial }{\partial \phi }. \end{aligned} \end{aligned}$$
(41)
$$\begin{aligned}{} & {} \mathbf{X_{3}} = -\frac{(m+n)t}{8n}a^{\frac{3m-n}{2n}}\phi ^{-\frac{m-n}{2}}\frac{\partial }{\partial a}\nonumber \\{} & {} \quad \quad \quad +\frac{3(m+n)t}{8n^2}a^{\frac{3(m-n)}{2n}}\phi ^{\frac{n-m+2}{2}}\frac{\partial }{\partial \phi }, \end{aligned}$$
(42)
$$\begin{aligned}{} & {} \mathbf{X_{4}} =a^{\frac{3m-n}{2n}}\phi ^{-\frac{m-n}{2}}\frac{\partial }{\partial a}-\frac{3}{n}a^{\frac{3(m-n)}{2n}}\phi ^{\frac{n-m+2}{2}}\frac{\partial }{\partial \phi }. \end{aligned}$$
(43)

Using these symmetry generators in Eq (25), one can easily calculate the first integrals respectively as follows

$$\begin{aligned}{} & {} I_{1}=E_{L}=0, \end{aligned}$$
(44)
$$\begin{aligned}{} & {} I_{2}=-\frac{(m+n)I_{4}}{8n}t-a^{\frac{3(m-n)}{2n}}\phi ^{\frac{m+n}{2}}, \end{aligned}$$
(45)
$$\begin{aligned}{} & {} I_{3}=t+\frac{4a^{3}\phi ^{m}}{3(m-n)\rho _{m0}}\left( 3(m+n)\frac{\dot{a}}{a}+2n^2\frac{\dot{\phi }}{\phi }\right) , \end{aligned}$$
(46)
$$\begin{aligned}{} & {} I_{4}=-4a^{\frac{3(m+n)}{2n}}\phi ^{\frac{m+n}{2}}\left( \frac{3\dot{a}}{a}+\frac{n\dot{\phi }}{\phi }\right) . \end{aligned}$$
(47)

Also, these generators satisfy the following commutator relations.

$$\begin{aligned}{} & {} \left[ \mathbf{X_{1}},\mathbf{X_{2}}\right] =-\frac{\mathbf{X_{1}}}{\rho _{m0}}, \quad \left[ \mathbf{X_{1}},\mathbf{X_{3}}\right] =t\mathbf{X_{3}}, \nonumber \\{} & {} \left[ \mathbf{X_{2}},\mathbf{X_{3}}\right] =\frac{(m+n)}{2n\rho _{m0}}\mathbf{X_{3}}, \nonumber \\{} & {} \left[ \mathbf{X_{2}},\mathbf{X_{4}}\right] =\frac{(m+3n)}{2n\rho _{m0}}{} \mathbf{X_{4}}, \quad \left[ \mathbf{X_{1}},\mathbf{X_{4}}\right] =0, \quad \left[ \mathbf{X_{3}},\mathbf{X_{4}}\right] =0.\nonumber \\ \end{aligned}$$
(48)

To obtain analytical solutions to the equations of motion related to the Lagrangian given in Eq. (40), we focus only on the \(\mathbf{X_{4}}\) Noether symmetry which represents the scaling symmetry. Now, by adopting the procedure given in [28], we may both simplify the field equations and obtain a cyclic variable. In other words, the new Lagrangian written in terms of new variables gives field equations that can be solved much more easily than the old one. In this way, we can perform a transformation on the dynamic variables such that

$$\begin{aligned} \begin{aligned} a&= \left( \frac{3(n-m)}{n}z(t)\right) ^{\frac{n}{3(n-m)}}u(t)^{\frac{n}{6}}, \\ \phi&= \left( \frac{3(n-m)}{n}z(t)\right) ^{\frac{1}{m-n}}u(t)^{\frac{1}{2}}. \end{aligned} \end{aligned}$$
(49)

Here z(t), u(t)) are new variables and z(t) is a cyclic variable as seen below. Under these transformations, the Lagrangian (40) takes a simpler form as

$$\begin{aligned} L= 4nu^{\frac{m+n-2}{2}}\dot{u}\dot{z}+\lambda u^{n}-\rho _{m0}, \end{aligned}$$
(50)

which has the following field equations

$$\begin{aligned}{} & {} nu^{\frac{m+n-2}{2}}\dot{u}+I_{4}=0, \end{aligned}$$
(51)
$$\begin{aligned}{} & {} 4nu^{\frac{m+n-2}{2}}\ddot{z}-n\lambda u^{n-1}=0, \end{aligned}$$
(52)
$$\begin{aligned}{} & {} -4nu^{\frac{m+n-2}{2}}\dot{u}\dot{z}+\lambda u^{n}-\rho _{m0}=0, \end{aligned}$$
(53)

where \(I_{4}\) is a constant of motion related to the \(\mathbf{X_{4}}\) symmetry. The solution of Eq. (51) is

$$\begin{aligned} u=\left( -\frac{(m+n)I_{4}}{2n}t+u_{0}\right) ^{\frac{2}{m+n}}, \end{aligned}$$
(54)

where \(u_{0}\) is an integration constant and \(m\ne -n\). Substituting this expression into Eqs. (52) and (53), we have the solution

$$\begin{aligned} z=\frac{\lambda n\left( -\frac{(m+n)I_{4}}{2n}t+u_{0}\right) ^{\frac{m+3n}{m+n}}}{2I_{4}^2(m+3n)}+z_{0}t+z_{1}, \end{aligned}$$
(55)

where \(z_{0}\) and \(z_{1}\) are an integration constants and \(m\ne -3n\). Using these solutions in the last Eq. (53) one obtains the constraint \(z_{0}=\frac{\rho _{m0}}{4I_{4}}\). Going back to the transformation given by (49), the solutions for the scale factor and scalar field become as follows

$$\begin{aligned}{} & {} \begin{aligned} a&= \left[ \frac{3(n-m)}{n}\left( -\frac{(m+n)I_{4}}{2n}t+u_{0}\right) ^{-1}\right. \\ {}&\quad \times \left. \left( \frac{\lambda n\left( -\frac{(m+n)I_{4}}{2n}t+u_{0}\right) ^{\frac{m+3n}{m+n}}}{2I_{4}^2(m+3n)}+z_{0}t+z_{1}\right) \right] ^{-\frac{n}{3(m-n)}}, \end{aligned}\nonumber \\ \end{aligned}$$
(56)
$$\begin{aligned}{} & {} \begin{aligned} \phi&= \left[ \frac{3(n-m)}{n}\left( -\frac{(m+n)I_{4}}{2n}t+u_{0}\right) ^{\frac{m-n}{m+n}}\right. \\ {}&\quad \times \left. \left( \frac{\lambda n\left( -\frac{(m+n)I_{4}}{2n}t+u_{0}\right) ^{\frac{m+3n}{m+n}}}{2I_{4}^2(m+3n)}+z_{0}t+z_{1}\right) \right] ^{\frac{1}{m-n}}. \end{aligned}\nonumber \\ \end{aligned}$$
(57)

If we set the integral constants \(u_{0}\), \(z_{0}\) and \(z_{1}\) to be zero, the solution (56) reduces to power-law form. In the general case, some restrictions can be made on these constants by following the method in Ref. [72]. We first fix the beginning of time by subjecting ourselves to the condition \(a(0)=0\) which gives \(u_{0}=0\) from the scale factor (56). Then we may set the age of the universe as \(t_{0}=1\). Thus, we can use the \(a(t_{0})=1\) condition as a standard. This condition yields the following expression

$$\begin{aligned} z_{1}= & {} \frac{(m+n)\lambda 2^{\frac{-m}{m+n}}(-\frac{I_{4}(m+n)}{2n})^{\frac{2n}{m+n}}}{I_{4}(m+3n)}\nonumber \\{} & {} -\frac{n(-\frac{I_{4}(m+n)}{2n})^{\frac{m-n}{m+n}}}{3(m-n)}-z_{0}. \end{aligned}$$
(58)

The last condition we consider is related to the Hubble parameter. So that we assume a condition such that \(H(t_{0})=h_{0}\). We note that the parameter \(h_{0}\) is not the same as the value of the Hubble constant obtained from observations. From this condition we obtain

$$\begin{aligned} z_{0}= & {} \frac{3\lambda (-\frac{I_{4}(m+n)}{2n})^{\frac{2n}{m+n}}}{4}\nonumber \\{} & {} -\frac{(6h_{0}n(m+n)-2n^2)(-\frac{I_{4}(m+n)}{2n})^{\frac{2m}{m+n}}}{(m+n)^2}. \end{aligned}$$
(59)
Fig. 1
figure 1

The plot represents the scale factor versus the time t. Here, the values of the model parameters are taken as \(m=-3\), \(n= 3.1\), \(I_{4}= 0.1\), \(\lambda =0.2\) and \(h_{0}=0.75\). The present time \(t_{0}=1\) is indicated by a vertical line

Full size image
Fig. 2
figure 2

The plot represents the scalar field versus the time t. Here, the values of the model parameters are taken as \(m=-3\), \(n= 3.1\), \(I_{4}= 0.1\), \(\lambda =0.2\) and \(h_{0}=0.75\). The present time \(t_{0}=1\) is indicated by a vertical line

Full size image
Fig. 3
figure 3

The plot represents the Hubble versus the time t. Here, the values of the model parameters are taken as \(m=-3\), \(n= 3.1\), \(I_{4}= 0.1\), \(\lambda =0.2\) and \(h_{0}=0.75\). The present time \(t_{0}=1\) is indicated by a vertical line

Full size image
Fig. 4
figure 4

The plot represents the deceleration parameter versus the time t. Here, the values of the model parameters are taken as \(m=-3\), \(n= 3.1\), \(I_{4}= 0.1\), \(\lambda =0.2\) and \(h_{0}=0.75\). The present time \(t_{0}=1\) is indicated by a vertical line

Full size image
Fig. 5
figure 5

The plot represents the effective equation of state parameter versus the time t. Here, the values of the model parameters are taken as \(m=-3\), \(n= 3.1\), \(I_{4}= 0.1\), \(\lambda =0.2\) and \(h_{0}=0.75\). The present time \(t_{0}=1\) is indicated by a vertical line

Full size image

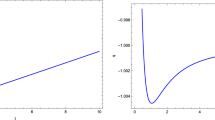
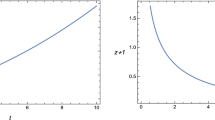
The graphical analysis of the time evolution of both the scale factor and the scalar field, as well as some cosmological parameters such as the Hubble parameter, the deceleration parameter and the effective equation of state parameter, is given in Figs. 1, 2, 3, 4 and 5. From Fig. 1 we clearly observe that our model represents an expanding model of the Universe in which the rate of expansion gradually decreases until it reaches zero in finite time (see Fig. 3). Figure 4 shows that a transition has occurred from the deceleration phase to the acceleration phase of the Universe. It can be seen from Fig. 2 that the scalar field gradually decreases from an infinite value to a minimum value and then increases with time.

4.2 Case 2: \(F(T,X,\phi )=T \phi ^m+P(X)\)

As a second model we consider \(F(T,X,\phi )=T \phi ^m+P(X)\) where m is a redefined arbitrary parameter and P(X) is a function dependent on the kinetic term. When this form of \(F(T,X,\phi )\) is used in Noether symmetry equations, their solutions are written as follows

$$\begin{aligned}{} & {} \alpha = \frac{b_{1}a}{3w}, \quad \delta = \frac{b_{1}(w-1)\phi }{wm} \end{aligned}$$
(60)
$$\begin{aligned}{} & {} \eta = -\frac{2 b_{1}(wm-w+1)X}{wm}, \quad \tau = b_{1}t+b_{2}, \quad M = b_{3},\nonumber \\ \end{aligned}$$
(61)
$$\begin{aligned}{} & {} P(X) = p_{0}X^{\frac{m(w+1)}{2(wm-w+1)}}, \end{aligned}$$
(62)

where \(b_{i}\) and \(p_{0}\) are an integration constants and \(w,m\ne 0\). Therefore, the Noether symmetry generators corresponding to these solutions are read as

$$\begin{aligned}{} & {} \mathbf{X_{1}} = \frac{\partial }{\partial t}, \end{aligned}$$
(63)
$$\begin{aligned}{} & {} \mathbf{X_{2}} = t\frac{\partial }{\partial t}+\frac{a}{3w}\frac{\partial }{\partial a}\nonumber \\{} & {} \quad \qquad +\frac{(w-1)\phi }{wm}\frac{\partial }{\partial \phi } -\frac{2(wm-w+1)X}{wm}\frac{\partial }{\partial X}. \end{aligned}$$
(64)

For this model, the first integral of the symmetry generator \(\mathbf{X_{1}}\) gives the Hamilton constraint equation in Eq. (21) and they give the commutator relation as \(\left[ \mathbf{X_{1}},\mathbf{X_{2}}\right] =\mathbf{X_{1}}\). To specify the invariant functions of the symmetry generator \(\mathbf{X_{2}}\) We need to solve the associated Lagrange system as [73]

$$\begin{aligned} \frac{dt}{t}=\frac{3w da}{a}=\frac{wm}{(w-1)}\frac{d\phi }{\phi }=-\frac{wm}{2(wm-w+1)}\frac{dX}{X}.\nonumber \\ \end{aligned}$$
(65)

The solutions of these equations are obtained as follows

$$\begin{aligned}{} & {} a=a_{0}t^{\frac{1}{3w}}, \end{aligned}$$
(66)
$$\begin{aligned}{} & {} \phi =\phi _{0}t^{\frac{w-1}{mw}}, \quad X=x_{0}t^{-2\frac{mw-w+1}{mw}}, \end{aligned}$$
(67)

where \(a_{0}\), \(\phi _{0}\) and x0 are an integration constants. By substituting these solutions into field equation (20), we find a relationship in the form \(w=\frac{m-6}{2(3m-2)}\). Thus, the scale factor and scalar field are expressed as follows

$$\begin{aligned}{} & {} a=a_{0}t^{\frac{2(3m-2)}{3(m-6)}}, \end{aligned}$$
(68)
$$\begin{aligned}{} & {} \phi =\phi _{0}t^{\frac{5m+2}{m(6-m)}}. \end{aligned}$$
(69)

On the other hand, for \(m=2\) and \(p_{0}=\frac{16}{3\epsilon }\) this model results in a de Sitter solution:

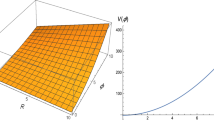
$$\begin{aligned} a=a_{0}e^{kt}, \quad \phi =\phi _{0}e^{-\frac{3k}{3}t}, \end{aligned}$$
(70)

with k being a real constant. The solution (68) is in power-law form. From this solution, the condition under which the universe can accelerate is given as \(\frac{2(3m-2)}{3(m-6)}>1\), that is: \(m<-14/3\) or \(m>6\). Moreover, one can calculate the effective equation of state parameter as \(w_{eff}=-1+\frac{m-6}{3m-2}\). The graphical behavior of this parameter as a function of m is plotted in Fig. 6.

Fig. 6
figure 6

Plot of the effective equation of state parameter against the parameter m

Full size image

Let us note that while dark energy is in the quintessence phase for \(m<-2\) and \(m>6\) values of the m parameter, it is in the phantom phase in the range of \(2/3<m<6\). Additionally, at the \(m\rightarrow 6\) limit, the equation of state parameter becomes close to \(-1\).

5 Summary and conclusion

In this study, we have explored an extended teleparallel \(F(T,X,\phi )\) gravity model using the Noether symmetry approach within a Friedmann–Lemaître–Robertson–Walker spacetime. By analyzing the model with specific forms of the function \(F(T,X,\phi )\), we have investigated its Noether symmetry properties and derived analytical solutions for the equations of motion.

In Case 1, the model \(F(T,X,\phi )=T \phi ^m+h(\phi )X-\lambda \phi ^n\) involves a non-minimal coupling between the scalar field, torsion scalar, and kinetic term. Through our analysis, we have observed an expanding Universe with a gradually decreasing rate of expansion, eventually reaching zero within a finite time interval. This behavior suggests a potential future endpoint or a scenario where the expansion of the Universe ceases. Additionally, we have noted a transition from a decelerating phase to an accelerating phase, driven by the evolution of the scalar field. Further investigations and comparisons with observational data are necessary to fully understand the implications of this model.

In Case 2, the model \(F(T,X,\phi )=T \phi ^m+P(X)\) incorporates a scalar field that is non-minimally coupled to the torsion scalar and a function dependent on the kinetic term. Through the analysis of Noether symmetry equations, power-law type solutions have been derived for both the scale factor and scalar field. The examination of the effective equation of state parameter has revealed various phases of dark energy, including quintessence-like and phantom-like behavior. Notably, when considering the special case of \(m=2\), a de Sitter solution representing exponential expansion has been obtained. However, to comprehensively evaluate the viability and implications of this model in cosmology, further research incorporating observational constraints is necessary.

It is worth emphasizing that the Noether symmetry technique has an important place in the literature as a geometric selection criterion in the comparison of various modified gravitational theories. In summary, our investigation of these two cases of the \(F(T,X,\phi )\) gravity model has provided valuable insights into the dynamics and behavior of the Universe within these frameworks. However, to comprehensively understand the viability and implications of these models in cosmology, additional research and consideration of observational constraints are required. This analysis is left to the next article as the subject of another study.