FCNC transitions of $\Lambda _b$ to neutron in Bethe–Salpeter equation approach

Abstract

In a covariant quark–diquark model, we investigate the rare decay of $\Lambda _b \rightarrow n l^+ l^-$ and $\Lambda _b \rightarrow n \gamma$ in the Bethe–Salpeter equation approach. In this model the baryons are treated as bound states of a constituent quark and a diquark interacting via a gluon exchange and the linear confinement. We find that the ratio of form factors R is varies from $-0.90$ to $-0.25$ and the branching ratios $Br(\Lambda _b \rightarrow n l^+ l^-)\times 10^{8}$ are $6.79(l=e),~4.08 ~ (l=\mu ),~2.9 ~(l=\tau )$ and the branching ratio $Br(\Lambda _b \rightarrow n \gamma )\times 10^{7} )=3.69$ in central values of parameters.

1 Introduction

The flavor changing neutral current (FCNC) decays of b-quark such as $b\rightarrow s \gamma ( l^+ l^-)$ can provide constrains on new physics, give essential information about the quark structure of heavy baryons and give more model-independent information such as CKM matrix elements. Significant experimental progresses about rare decays of the $\Lambda _b$ baryon have been achieved at LHCb [1,2,3,4,5]. The rare decay $\Lambda _b \rightarrow \Lambda \mu ^+ \mu ^-$ first observed by CDF collaboration in 2011 [6]. The radiative decay $\Lambda _b \rightarrow \Lambda \gamma$ was observed at LHCb in 2019 [2]. There have been also many theoretical works on the rare decays $\Lambda _b$ induced by $b \rightarrow s$ transition [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Ref. [32] gave the branching ratios $Br(\Lambda _b \rightarrow n l^+ l^-)\times 10^{8}= 3.19 \pm 0.46~(l=e),~3.76\pm 0.42~(l=\mu ),~1.65\pm 0.19~(l=\tau )$ in the context of light cone QCD sum rules (LCSR). The form form factors (FFs) of $\Lambda _b (\Lambda _b^*) \rightarrow N l^+ l^-$ were given in Ref. [34] in LCSR and taking into account the contribution of $\Lambda ^*_b$ the ranching ratios $Br(\Lambda _b \rightarrow Nl^+ l^-)\times 10^{8}= 8\pm 2~(l=e),~7\pm 2~(l=\mu ),~ 2\pm 0.4~(l=\tau )$ were obtained. Ref. [35] gave the branching ratios $Br(\Lambda _b \rightarrow n \mu ^+ \mu ^-)\times 10^{8}= 3.75\pm 0.38$ and $Br(\Lambda _b \rightarrow n \gamma )\times 10^{7}= 3.7$ in the relativistic quark–diquark picture in the QCD-motivated interquark potential model. Ref. [36] studied the $\Lambda _b \rightarrow N^* l^+ l^-$ decay in LCSR and gave the branching ratios $Br(\Lambda _b \rightarrow N^* l^+ l^-)\times 10^{8}= 4.62\pm 1.85~(l=e),~4.25\pm 1.5~(l=\mu ),$ and $0.25\pm 0.09(l=\tau )$. Ref. [33] gave analysed CP-violation in polarized $b \rightarrow d l^+ l^-$. With the experiment development, the transition $\Lambda _b \rightarrow n$ will be detected in the near future, so it is necessary to study $\Lambda _b \rightarrow n$ theoretically.

In this work, we will calculate the FFs of $\Lambda _b \rightarrow n$ in the Bethe–Salpeter equation approach in a covariant quark–diquark model. This model has been used to study nucleon electromagnetic form factors and N-$\Delta$ transition form factors [42,43,44]. In the previous works, heavy baryon properties have been studied extensively in this model [45,46,47,48,49,50, 52, 53]. The possible existence of diquark within baryons has been studied for a long time [37, 38, 41]. The negative neutron mean square charge radius can be explained by diquark model, which cannot be explained in pure SU(6) quark model [38].

In our model, $\Lambda _b$ can be regarded as a bound state of two particles: one is a heavy quark b and the other is a scalar diquark (ud). Using the SU(6) wave function of baryons, we can get the neutron wave function in the quark–diquark model [39, 40].

$$\begin{aligned} n^\uparrow= & {} \frac{1}{3\sqrt{3}} [3 d^\uparrow (du)_{00}+d^\uparrow (du)_{10}-\sqrt{2}d^\downarrow (du)_{11}\\&-\sqrt{2} u^\uparrow (dd)_{10}+2 u^\downarrow ( dd)_{11}], \end{aligned}$$

where the arrow $\uparrow ~(\downarrow )$ indicates the spin direction. Therefore, in our model only the $d^\uparrow (ud)_{00}/ \sqrt{3}$ component of the neutron contributes to $\Lambda _b \rightarrow n$ since $\Lambda _b$ has the structure $b(ud)_{00}$.

This paper is organized as follows. In Sect. 2, we will establish the BS equation for $q(ud)_{00}$ system ($q=b,~d$). In Sect. 3 we will derive the FFs for $\Lambda _b \rightarrow n$ in the BS equation approach. In Sect. 4 the numerical results for the decay FFs of $\Lambda _b \rightarrow n l^+ l^-$ will be given. Finally, the summary and discussion will be given in Sect. 5.

2 BS equation for $Q(ud)_{0 0}$ system

Following our previous work as is shown in Fig. 1, the BS equation of the $q(ud)_{0 0}$ system in momentum space satisfies the following homogeneous integral equation [45,46,47,48,49,50, 52]:

$$\begin{aligned} \chi _P(p)= & {} i S_F(p_1)\int \frac{d^4 p}{(2 \pi )^4} [ I\otimes I V_1(p,q)\nonumber \\&+ \gamma _\mu \otimes (p_2+q_2)^\mu V_2(p,q) ]\chi _P(q)S_D(p_2), \end{aligned}$$

(1)

where $S_F(p_1)$ and $S_D(p_2)$ are propagators of the q quark and the (ud) scalar diquark, respectively, $p_1=\lambda _1 P+p$ and $p_2=\lambda _2 P-p$ correspond to the momenta of the quark and the diquark, respectively. P is the momentum of the baryon. $V_1$ and $V_2$ are the scalar confinement and one-gluon-exchange terms in the kernel, respectively. Generally, the $q(ud)_{00}$ system needs two scalar functions to describe its BS wave function [45, 46, 49].

Fig. 1

The BS equation for the $q(ud)_{00}~(q=b,d)$ system in momentum space (K is the interaction kernel)

(2)

where $f_i~(i=1,2)$ are the Lorentz-scalar functions of $p_t^2$, u(P) is the spinor of the baryons, $p_t$ is the transverse projection of the relative momenta along the momentum P, $p_t^\mu = p^\mu -(v\cdot p) v^\mu$, and $p_l= \lambda _2 M- v \cdot p$ (where we defined $v^\mu =P^\mu /M$). We use $M,~m,\text {and}~m_D$ to represent the masses of the baryons, the q-quark and the (ud) diquark, respectively.

According to the potential model, $V_1$ and $V_2$ have the following forms in the covariant instantaneous approximation ($p_l=q_l$) [47, 48, 52, 53]:

$$\begin{aligned}&\tilde{V}_1(p_t-q_t) = \frac{8 \pi \kappa }{[(p_t-q_t)^2+\mu ^2]^2} \nonumber \\&\quad - (2\pi )^2\delta ^3(p_t-q_t)\int \frac{d^3k}{(2\pi )^3} \frac{8 \pi \kappa }{(k^2+\mu ^2)^2}, \end{aligned}$$

(3)

where $q_t$ is the transverse projection of the relative momenta along the momentum P and defined as $q_t^\mu = q^\mu -(v \cdot q) v^\mu$, $q_l=\lambda _2 M -v \cdot q$. The second term of $\tilde{V}_1$ is introduced to avoid infrared divergence at the point $p_t=q_t$, and $\mu$ is a small parameter to avoid the divergence in numerical calculations.

$$\begin{aligned} \tilde{V_2} (p_t-q_t) {=-} \frac{16 \pi }{3}\frac{\alpha ^2_{seff} Q^2_0}{[(p_t-q_t)^2{+}\mu ^2][(p_t{-}q_t)^2{+}Q_0^2]}, \end{aligned}$$

(4)

It was found that $Q_0^2=3.2$ GeV$^2$ can lead to consistent results with the experimental data by analyzing the electromagnetic FFs of the proton [7]. The parameters $\kappa$ and $\alpha _{seff}$ are related to the scalar confinement and the one-gluon-exchange diagram, respectively.

The quark and diquark propagators can be written as the follows:

(5)

$$\begin{aligned} S_D(p_2)= & {} \frac{i}{2 \omega _D} \bigg [\frac{1}{ p_l-\omega _D+i \epsilon } -\frac{1}{ p_l+ \omega _D-i\epsilon }\bigg ], \end{aligned}$$

(6)

where $\omega _q = \sqrt{m^2-p_t^2}~\text {and}~\omega _D = \sqrt{m_D^2-p_t^2}$. $\Lambda ^\pm$ are the projection operators which have the following relations:

(7)

$$\begin{aligned} \Lambda _q^\pm \Lambda _q^\pm= & {} \Lambda ^\pm _q, \end{aligned}$$

(8)

$$\begin{aligned} \Lambda ^\pm _q \Lambda ^\mp _q= & {} 0. \end{aligned}$$

(9)

Following our previous work, in order more precisely calculate the FFs of $\Lambda _b \rightarrow n$, we can take $E_0=-0.14$ GeV (where $E_0=M-m-m_D$ is the binding energy) and $\kappa$ to be about $0.05\pm 0.005$ GeV$^3$ for $\Lambda _b\rightarrow n$ [51]. Defining $\tilde{f}_{1(2)}=\int \frac{d p_l}{2 \pi }f_{1(2)}$, and using the covariant instantaneous approximation, $p_l=q_l$, the scalar BS wave functions satisfy the following coupled integral equation:

$$\begin{aligned} \tilde{f}_1(p_t)= & {} \int \frac{d^3q_t}{(2\pi )^3} M_{11}(p_t,q_t) \tilde{f}_1(q_t)\nonumber \\&+ M_{12}(p_t,q_t) \tilde{f}_2(q_t), \end{aligned}$$

(10)

$$\begin{aligned} \tilde{f}_2(p_t)= & {} \int \frac{d^3q_t}{(2\pi )^3} M_{21}(p_t,q_t) \tilde{f}_1(q_t)\nonumber \\&+ M_{22}(p_t,q_t) \tilde{f}_2(q_t), \end{aligned}$$

(11)

where

$$\begin{aligned}&M_{11}(p_t,q_t)=\frac{(\omega _q +m ) (\tilde{V}_1+ 2 \omega _D \tilde{V}_2)- p _t \cdot ( p _t+ q _t) \tilde{V}_2}{4 \omega _D \omega _q(-M + \omega _D+ \omega _q)} \nonumber \\&\quad -\frac{(\omega _q -m )(\tilde{V}_1- 2\omega _D \tilde{V}_2)+ p _t\cdot ( p _t+ q _t) \tilde{V}_2}{4 \omega _D \omega _c(M + \omega _D+ \omega _q)}, \end{aligned}$$

(12)

$$\begin{aligned}&M_{12}(p_t,q_t)\nonumber \\&\quad =\frac{- (\omega _q+m ) ( q _t + p _t)\cdot q_t\tilde{V}_2 + p _t\cdot q_t(\tilde{V}_1- 2 \omega _D \tilde{V}_2)}{4 \omega _D \omega _c(-M + \omega _D+ \omega _c)} \nonumber \\&\quad -\frac{(m - \omega _q ) ( q _t + p _t)\cdot q _t \tilde{V}_2 - p _t\cdot q _t (\tilde{V}_1+ 2\omega _D \tilde{V}_2)}{4 \omega _D \omega _q(M + \omega _D+ \omega _q)},\nonumber \\ \end{aligned}$$

(13)

$$\begin{aligned}&M_{21}(p_t,q_t)= \frac{(\tilde{V}_1+ 2 \omega _D \tilde{V}_2)-( -\omega _q+m ) \frac{( p _t+ q _t) \cdot p _t }{ p^2_t }\tilde{V}_2}{4 \omega _D \omega _q(-M + \omega _D+ \omega _q)} \nonumber \\&\quad -\frac{- (\tilde{V}_1- 2\omega _D \tilde{V}_2)+(\omega _q + m )\frac{( p _t+ q _t)\cdot p _t }{ p^2_t } \tilde{V}_2)}{4 \omega _D \omega _q(M + \omega _D+ \omega _q)}, \end{aligned}$$

(14)

$$\begin{aligned}&M_{22}(p_t,q_t)\nonumber \\&\quad = \frac{(m -\omega _q)( \tilde{V}_1+ 2 \omega _D \tilde{V}_2) \frac{ p_t \cdot q_t}{ p^2_t } - ( q^2_t+ p_t \cdot q_t) \tilde{V}_2}{4 \omega _D \omega _q(-M + \omega _D+ \omega _q)} \nonumber \\&\quad -\frac{ (m +\omega _q) (-\tilde{V}_1- 2 \omega _D \tilde{V}_2) \frac{p_t \cdot q_t}{p^2_t} + ( q^2_t+ p_t \cdot q_t)\tilde{V}_2)}{4 \omega _D \omega _q(M + \omega _D+ \omega _q)}.\nonumber \\ \end{aligned}$$

(15)

When $\frac{1}{m}\rightarrow 0$ [47], the quark propagator can be written as following,

(16)

considering the Dirac equation for $\Lambda _b$ we have

$$\begin{aligned} \phi (p)= & {} -\frac{i}{(E_0+m_D-p_l+i \epsilon )( p_l ^2-\omega ^2_D)}\nonumber \\&\times \int \frac{d^4 q }{(2\pi )^4}(\tilde{V}_1+2 p_l \tilde{V}_2)\phi (q), \end{aligned}$$

(17)

where the BS wave function of $\Lambda _b$ was given in the previous work [47] and has the form $\chi _P (v)=\phi (p)u_{\Lambda _b}(v,s)$ with $\phi (p)$ being the scalar BS wave function.

Generally, the BS wave function can be normalized under the condition of the covariant instantaneous approximation [53]:

$$\begin{aligned}&i \delta ^{i_1 i_2}_{j_1 j_2} \int \frac{d^4 q d^4 p}{(2\pi )^8}\bar{\chi }_P(p,s)\left[ \frac{\partial }{\partial P_0}I_p(p,q)^{i_1 i_2 j_2 j_1}\right] \chi _P(q,s^\prime )\nonumber \\&\quad =\delta _{s s^\prime }, \end{aligned}$$

(18)

where $i_{1(2)}$ and $j_{1(2)}$ represent the color indices of the quark and the diquark, respectively, $s^{(\prime )}$ is the spin index of the baryon, $I_p(p,q)^{i_1 i_2 j_2 j_1}$ is the inverse of the four-point propagator written as follows

$$\begin{aligned} I_p(p,q)^{i_1 i_2 j_2 j_1}= & {} \delta ^{i_1 j_1}\delta ^{i_2 j_2} (2 \pi )^4 \delta ^4(p-q)S^{ -1 }_F\nonumber \\&\times (p_1)S^{ -1 }_D(p_2). \end{aligned}$$

(19)

3 Matrix element of $\Lambda _b \rightarrow n l^+ l^-$ and $\Lambda _b \rightarrow n \gamma$ decays

In the standard model, the $\Lambda _b\rightarrow n l^+l^-$ transition is described by $b\rightarrow d l^+l^-$ at the quark level. The effective Hamiltonian describing the electroweak penguin and weak box diagrams related to this transition is given by

$$\begin{aligned}&\mathcal {H}( b\rightarrow d l^+l^-) = \frac{G_F\alpha }{2 \sqrt{2}\pi }V_{tb}V^*_{td}\bigg [ C^{eff}_9 \bar{d} \gamma _{\mu }(1-\gamma _5)b \bar{l}\gamma ^{\mu }l \nonumber \\&\quad - i C^{eff}_{7}\bar{d}\frac{2 m_b\sigma _{\mu \nu } q^{\mu }}{q^2}(1+\gamma _5) b \bar{l}\gamma ^{\mu }l \nonumber \\&\quad +C_{10} \bar{d}\gamma _{\mu }(1-\gamma _5) b \bar{l}\gamma ^{\mu }\gamma _5l \bigg ], \end{aligned}$$

(20)

where $G_F$ is the Fermi coupling constant, $\alpha$ is the fine structure constant at Z mass scale, $\epsilon ^\nu$ is the polarization vector of photon, respectively. q is the total momentum of the lepton pair and $C_i^{eff}~(i=7,~9,~10)$ are the Wilson coefficients, $C^{eff}_7=-0.313$, $C^{eff}_9=4.334$, $C_{10}=-4.669$ [56,57,58]. The amplitude is obtained by sandwiching the effective Hamiltonian between the initial and final states. The matrix element for $\Lambda _b \rightarrow n$ can be parameterized in terms of the FFs as the following:

$$\begin{aligned}&\langle n(P^\prime ) | \bar{d}\gamma _{\mu }b | \Lambda _b(P)\rangle = \bar{u}_{n}(P^\prime )\nonumber \\&\quad \times (g_1\gamma ^\mu + ig_2\sigma _{\mu \nu }p^{\nu }+g_3p_\mu )u_{\Lambda _b}(P),\nonumber \\&\langle n(P^\prime ) | \bar{d}\gamma _{\mu }\gamma _{5}b | \Lambda _b(P)\rangle = \bar{u}_{n}(P^\prime )\nonumber \\&\quad (t_1\gamma ^\mu +it_2\sigma _{\mu \nu }p^{\nu }+t_3p^\mu )\gamma _5u_{\Lambda _b}(P),\nonumber \\&\langle n (P^\prime ) | \bar{d}i\sigma ^{\mu \nu }q^{\nu }b | \Lambda _b(P)\rangle = \bar{u}_{n}(P^\prime )\nonumber \\&\quad (s_1\gamma ^\mu +is_2\sigma _{\mu \nu }q^{\nu }+s_3q^\mu )u_{\Lambda _b}(P),\nonumber \\&\langle n (P^\prime ) | \bar{d}i\sigma ^{\mu \nu }\gamma _5q^{\nu }b | \Lambda _b(P)\rangle = \bar{u}_{n}(P^\prime )\nonumber \\&\quad (d_1\gamma ^\mu +id_2\sigma _{\mu \nu }q^{\nu }+d_3q^\mu )\gamma _5u_{\Lambda _b}(P), \end{aligned}$$

(21)

where $P^\prime$ and P are the momenta of the neutron and $\Lambda _b$ respectively, $q=P-P^\prime$, $u_n$ and $u_{\Lambda _b}$ are the spinors of the initial and final baryons respectively, $g_i$, $t_i$, $s_i$, and $d_i$ ($i=1,2$ and 3) are the transition FFs which are Lorentz scalar functions of $q^2$. When working in the limit $m_b\rightarrow \infty$, the number of independent FFs is reduced to 2. The $\Lambda _b \rightarrow n$ matrix element with an arbitrary matrix $\Gamma$ is given by

(22)

where $\Gamma = \gamma _\mu ,~\gamma _\mu \gamma _5,~ q^\nu \sigma _{\nu \mu },q^\nu \sigma _{\nu \mu }\gamma _5$. $F_1$ and $F_2$ can be expressed as functions solely of $\omega =v\cdot P^\prime /m_{\Lambda }$, which is the energy of the neutron in the $\Lambda _b$ rest frame. The baryons states can be normalized as follows,

$$\begin{aligned} \langle n(P^\prime )|n(P)\rangle= & {} 2 E_n (2\pi )^3 \delta ^3(P-P^\prime ), \end{aligned}$$

(23)

$$\begin{aligned} \langle \Lambda _b(v^\prime ,P^\prime )|\Lambda _b(v,P)\rangle= & {} 2 v_0(2\pi )^3 \delta ^3(P-P^\prime ). \end{aligned}$$

(24)

Comparing Eqs. (21) with (22), we obtain the following relations:

$$\begin{aligned}&g_1~=~t_1~=~s_2~=~d_2~=~\bigg (F_1+\sqrt{r}F_2\bigg ),\nonumber \\&g_2~=~t_2~=g_3~=~t_3~=~\frac{1}{m_{\Lambda _{b}}}F_2, \nonumber \\&s_3~=~ F_2 (\sqrt{r}-1),~ d_3~=~ F_2(\sqrt{r}+1), \nonumber \\&s_1 ~=~ d_1~=~ F_2 m_{\Lambda _b} (1+r-2\sqrt{r}\omega ), \end{aligned}$$

(25)

where $r=m_n^2/m_{\Lambda _b}^2$. On the other hand, the transition matrix for $\Lambda _b\rightarrow n$ can be expressed in terms of the BS wave functions of $\Lambda _b$ and n,

$$\begin{aligned}&\langle n (P^\prime )|\bar{d}\Gamma b|\Lambda _b(P)\rangle \nonumber \\&\quad =\int \frac{d^4p}{(2\pi )^4} \bar{\chi }_{P^\prime }^{n}(p^\prime )\Gamma \chi _P^{\Lambda _b}(p)S^{-1}_D(p_2). \end{aligned}$$

(26)

where the $\chi _{P^\prime }^{n}$ and $\chi _{P^\prime }^{\Lambda _b}$ are the BS wave function of neutron and $\Lambda _b$ respectively.

Define

$$\begin{aligned}&\int \frac{d^4p}{(2 \pi )^4} f_1(p^\prime ) \phi (p) S^{-1}_D(p_2)=k_1(\omega ), \nonumber \\&\quad \int \frac{d^4p}{(2 \pi )^4} f_2(p^\prime )p_{t\mu }^\prime \phi (p) S^{-1}_D(p_2)\nonumber \\&\qquad =k_2(\omega ) v_{\mu } + k_3(\omega ) v^\prime _{\mu }, \end{aligned}$$

(27)

where $v^\prime = P^\prime /m_n$, then we find the following relations when $\omega \ne 1$:

$$\begin{aligned} k_3= & {} - \omega k_2, \nonumber \\ k_2= & {} \frac{1}{1-\omega ^2} \int \frac{d^4 p}{(2\pi )^4} f_2(p^\prime ) p^\prime _t \cdot v \phi (p) S^{-1}_D, \nonumber \\ F_1= & {} k_1- \omega k_2, \nonumber \\ F_2= & {} k_2. \end{aligned}$$

(28)

The differential decay rate of $\Lambda _b \rightarrow n l^+ l^-$ is obtained as:

$$\begin{aligned}&\mathcal {M}(\Lambda _b\rightarrow n l^{+} l^{-})=\frac{G_F \lambda _t}{2\sqrt{2}\pi } \nonumber \\&\quad \times \big [\bar{l}\gamma _{\mu }l\{\bar{u}_{n}[\gamma _{\mu }(A_1+B_1+ (A_1-B_1)\gamma _5 ) \nonumber \\&\quad + i\sigma ^{\mu \nu }p_{\nu }(A_2+B_2+ (A_2-B_2)\gamma _5 )]u_{\Lambda _b}\} \nonumber \\&\quad +\bar{l}\gamma _{\mu }\gamma _5l\{\bar{u}_{n}[\gamma ^{\mu }(D_1+E_1+ (D_1-E_1)\gamma _5 ) \nonumber \\&\quad + i\sigma ^{\mu \nu }p_{\nu }(D_2+E_2+ (D_2-E_2)\gamma _5 )\nonumber \\&\quad +p^{\mu }(D_3+E_3+ (D_3-E_3)\gamma _5 )]u_{\Lambda _b}\}\big ], \end{aligned}$$

(29)

where $\lambda _t=|V_{tb}*V_{td}^*|$, the parameters $A_i$, $B_i$ and $D_j$, $E_j$ ($i=1,2$ and $j=1,2,3$) are defined as

$$\begin{aligned}&A_i=\frac{1}{2}\bigg \{C^{eff}_{9}(g_i-t_i)-\frac{2C^{eff}_7 m_b}{p^2}(d_i +s_i )\bigg \},\nonumber \\&B_i = \frac{1}{2}\bigg \{C^{eff}_{9}(g_i+t_i) - \frac{2C^{eff}_7m_b}{p^2}(d_i -s_i )\bigg \}, \nonumber \\&D_j = \frac{1}{2}C_{10}(g_j-t_j), ~E_j=\frac{1}{2}C_{10}(g_j+t_j). \end{aligned}$$

(30)

In the physical region ($4m^2_l\le q^2\le (m_{\Lambda _b}-m_{n})^2$), the decay rate of $\Lambda _b\rightarrow n l^+l^-$ is obtained as

$$\begin{aligned}&\frac{d\Gamma (\Lambda _b\rightarrow n l^+l^-)}{dq^2}\nonumber \\&\quad =\frac{G^2_F\alpha ^2}{2^{13}\pi ^5m_{\Lambda _b}} |V_{tb}V^*_{td}|^2v_l\sqrt{\lambda (1,r,s)} \mathcal {M}(s), \end{aligned}$$

(31)

where $s= 1 +r - 2 \sqrt{r} \omega$, $\lambda (1,r,s)=1+r^2+s^2-2r-2s-2rs$, and $v_l=\sqrt{1-\frac{4m^2_l}{s * m^2_{\Lambda _b}}}$, and the decay amplitude is given as [26]

$$\begin{aligned} \mathcal {M}(s)= & {} \mathcal {M}_0(s) +\mathcal {M}_2(s), \end{aligned}$$

(32)

where

Fig. 2

The BS wave functions for the neutron

$$\begin{aligned}&\mathcal {M}_0(s)=32m^2_l m^4_{\Lambda _b}s(1+r-s)(|D_3|^2+|E_3|^2) \nonumber \\&\quad 64m^2_lm^3_{\Lambda _b}(1-r-s)Re(D^*_1E_3+D_3E^*_1)\nonumber \\&\quad +64m^2_{\Lambda _b}\sqrt{r}(6m^2_l-M^2_{\Lambda _b}s)Re(D_1^*E_1)\nonumber \\&\quad 64m^2_lm^3_{\Lambda }\sqrt{r}\big (2m_{\Lambda _b}s Re(D^*_3E_3)\nonumber \\&\quad +(1-r+s)Re(D^*_1D_3+E^*_1E_3)\big )\nonumber \\&\quad +32m^2_{\Lambda }(2m^2_l+m^2_{\Lambda }s)\nonumber \\&\quad \times \bigg \{(1-r+s)m_{\Lambda _b}\sqrt{r}Re(A^*_1A_2+B^*_1B_2)\nonumber \\&\quad -m_{\Lambda _b}(1-r-s)Re(A^*_1B_2+A^*_2B_1)\nonumber \\&\quad -2\sqrt{r}\big (Re(A^*_1B_1)+m^2_{\Lambda }s Re(A^*_2B_2)\big ) \bigg \}\nonumber \\&\quad + 8 m^2_{\Lambda _b}\bigg [4m^2_l(1+r-s)+m^2_{\Lambda _b}((1+r)^2- s^2)\bigg ]\nonumber \\&\quad \times (|A_1|^2+|B_1|^2)\nonumber \\&\quad +8m^4_{\Lambda _b}\bigg \{4m^2_l[\lambda +(1+r-s)s]\nonumber \\&\quad +m^2_{\Lambda _b}s[(1-r)^2-s^2]\bigg \}(|A_2|^2+|B_2|^2) \nonumber \\&\quad - 8m^2_{\Lambda _b}\bigg \{4m^2_l(1+r-s)-m_{\Lambda _b}[(1-r)^2-s^2]\bigg \}\nonumber \\&\quad \times (|D_1|^2+|E_1|^2) \nonumber \\&\quad + 8m^5_{\Lambda _b}sv^2\bigg \{-8m_{\Lambda _b}s\sqrt{r}Re(D^*_2E_2)\nonumber \\&\quad +4(1-r+s)\sqrt{r}Re(D^*_1D_2+E^*_1E_2)\nonumber \\&\quad -4(1-r-s) Re(D^*_1E_2+D^*_2E_1)\nonumber \\&\quad +m_{\Lambda _b}[(1-r)^2-s^2] (|D_2|^2+|E_2|^2)\bigg \}, \end{aligned}$$

(33)

$$\begin{aligned}&\mathcal {M}(s) = 8m^6_{\Lambda _b}s v_l^2\lambda (|A_2|^2+|B_2|^2+|C_2|^2+|D_2|^2) \nonumber \\&\quad - 8 m^4_{\Lambda _b}v_l^2\lambda (|A_1|^2+|B_1|^2+|C_1|^2+|D_1|^2). \end{aligned}$$

(34)

Table 1 The values of $\alpha _{seff}$ for the neutron and $\Lambda _b$

Similarly, the Hamiltonian for exclusive rare radiative decay $\Lambda _b \rightarrow n \gamma$ with $\gamma$ as a real photon is given by

$$\begin{aligned} \mathcal {H}( b\rightarrow d \gamma )= & {} - \frac{i G_F e}{ 4 \sqrt{2}\pi ^2}V_{tb}V^*_{td}C^{eff}_{7}\bigg [ m_b \bar{d} \sigma _{\mu \nu } q^{\mu } (1+\gamma _5) b\nonumber \\&+m_d \bar{d} \sigma _{\mu \nu } q^{\mu } (1-\gamma _5) b \bigg ]\epsilon ^\nu , \end{aligned}$$

(35)

where $\epsilon ^\nu$ is the polarization vector of the photon. Then, the decay width is given by

$$\begin{aligned} \Gamma (\Lambda _b \rightarrow n \gamma )= & {} \frac{\alpha G_F^2 m_b^2 m_{\Lambda _b}^3}{2^6 \pi ^4} |V_{tb} V^*_{td}|^2 |C_7^{eff}|^2\nonumber \\&\times [s_2^2(0) +d_2^2(0)] \bigg ( 1-\frac{m_n^2}{m^2_{\Lambda _b}} \bigg )^3. \end{aligned}$$

(36)

Fig. 3

The BS wave function for $\Lambda _b$

Fig. 4

The values of FFs (the lines become thicker with the increases of $\kappa$) and $R(\omega )$ with different values of $\kappa$

4 Numerical analysis and discussion

In this section we present a detailed numerical analysis of the rare decay $\Lambda _b \rightarrow n l^+ l^-$ and radiative decay $\Lambda _b \rightarrow n \gamma$. In our calculations, we take the masses of baryons as $m_{\Lambda _b}=5.62$ GeV, $m_n=0.94$ GeV [59], and the masses of quarks, $m_b=5.02$ GeV and $m_d=0.34$ GeV [46, 48, 49]. The variable $\omega$ varies from 1 to 3.073,  3.069,  1.89 for $e,~\mu ,~\tau$, respectively.

Solving Eqs. (10), (11) and (17) for the neutron and $\Lambda _b$ with the parameters we have taken, we get the numerical solutions of BS wave functions. In Table 1, we give the values of $\alpha _s$ with different values of $\kappa$ for the neutron and $\Lambda _b$ and in Figs. 2 and 3, we give the BS wave functions for the neutron and $\Lambda _b$.

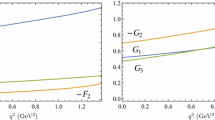
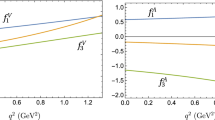
It can be seen from Table 1 that the dependence of $\alpha _{seff}$ for the neutron on $\kappa$ is obviously stronger than that for $\Lambda _b$. From the figures in Figs. 2 and 3, we find that BS wave functions of neutron is very similarly on different $\kappa$, the values of $f_1(p_t)$ is about from 0 to 0.14 $f_2(p_t)$ varies about from 0 to 0.06 and $\phi (p_t)$ varies from 0 to 0.17. In Fig. 4, we plot the FFs and $R(\omega )=F_2/F_1$ for different $\kappa$. From this figure, we find that $F_1(\omega )$ increases with the increase of $\kappa$, but the value of $R(\omega )$ is not sensitive to the change of the value of $\kappa$. The value of $R(\omega )$ varies from $-0.9$ to $-0.25$ when $\omega$ changes from 1 to 3.1.

Fig. 5

The decay widths of $\Lambda _b \rightarrow n l^+ l^-$ (the values of the decay width increase with the increase of $\kappa$ from 0.045 to 0.055) for the lines with the same color)

Table 2 The values of the branching ratios of $\Lambda _b\rightarrow n l^+ l^-$ and $\Lambda _b\rightarrow n \gamma$ and compare with other model

In the heavy quark limit, assuming the same shape for $F_1$ and $F_2$, the ratio $R=-0.35\pm 0.04$ (stat) $\pm 0.04$ (syst) was previously measured by the CLEO Collaboration using the experimental data for the semileptonic decay $\Lambda _c \rightarrow \Lambda e^+ \nu _e$ when $q^2$ changes from $m_\Lambda ^2$ to $m^2_{\Lambda _c}$ [55]. In the same region, we find that $R(\omega )$ varies from $-0.32$ to $-0.25$ in our model. In Ref. [13] $R(\omega )$ varies from $-0.42$ to $-0.83$ when $q^2$ change from 0 to $(M_{\Lambda _b}-M_{\Lambda })^2$, and in our model $R(\omega )$ change from $-0.25$ to $-0.75$ in the same region. However, in Ref. [14] gives the behaviour $R(q^2)\propto -1/q^2$, which agrees with the pQCD scaling law [54, 60, 61]. Therefore, using the CLEO Collaboration experimental data [55], we can estimate that the value of $R(\omega )$ should change from to $-0.91\pm 0.03$ to $-0.3 \pm 0.03$ approximately, which agrees with our result as shown in Fig. 4. From the data in Ref. [32], we find that $R(\omega _{max})=-2.75$ in LCSR and $R(\omega _{max})=-2.33$ by fit the data from LQCD [63, 64]. From the data with the contribution of $\Lambda ^*_b$ being considered Ref. [34], we find that $R(\omega _{max})=-3.47$ in LCSR. These results are much larger than experimental data $R(\omega _{max})=-0.35$ [55] and do not agree with our result.

In Fig. 5, we give the $q^2$-dependence of the decay widths of $\Lambda _b \rightarrow n l^- l^+(l= e, \mu , \tau )$ for different parameters. For the central values of parameters, we find that the branching ratio are $BR(\Lambda _b \rightarrow n l^- l^+)\times 10^8 = 6.79~(l=e),~4.08~(l=\mu ),~2.90~(l= \tau )$ and $BR(\Lambda _b \rightarrow n \gamma )\times 10^7 = 3.69$. Our result for the branching ratios of $BR(\Lambda _b \rightarrow n l^- l^+)$ and $BR(\Lambda _b \rightarrow n \gamma )$ are listed in Table 2 together those in other approaches.

Table 2, we can see that the rare semileptonic decay branching fractions are of order $10^{-8}$, and the rare radiative decay branching fraction is of order $10^{-7}$. In Ref. [32], the authors use the parameters from LCSR [62] and LQCD [63, 64] to fit the FFs of $\Lambda _b \rightarrow n$ and gave the branching ratio of $\Lambda _b \rightarrow n l^+ l^-$. In Ref. [34], the authors also calculated the FFs of $\Lambda _b \rightarrow n$ in the framework of LCSR, but their results were different. Our results for the branching ratios of $\Lambda _b \rightarrow n l^+ l^-~(l=e,~\tau )$ are very similar to those in Ref. [34], our result for $BR(\Lambda _b \rightarrow n \mu ^+ \mu ^-)$ agrees with that in Ref. [32]. Our radiative decay result $BR(\Lambda _b \rightarrow n \gamma )$ agrees with Ref. [35].

5 Summary

In our work, we calculated the FFs between baryons states induced by the rare $b \rightarrow d$ transition in the BS equation approach in a covariant quark–diquark model. In our model, $\Lambda _b$ is regarded as a bound state of the b-quark and the scalar ud diquark, thus only the $d^\uparrow (du)_{00}/ \sqrt{3}$ component of the neutron contributes to the FFs. We established the BS equations for the $q(ud)_{00} ~(q=b,d)$ system and derived the FFs for $\Lambda _b \rightarrow n$ in the BS equation approach. We solved the BS equation of $q(ud)_{00} ~(q=b,d)$ system and then we calculated the FFs and R numerically. Using these FFs, we obtained the branching ratios of $\Lambda _b \rightarrow n l^+ l^-$ and $\Lambda _b \rightarrow n \gamma$. Comparing with other works we found that our FFs are very different with other model [32, 35], but the branching fractions of the semileptonic decay are of the order $10^{-8}$ and the radiative branching ratio is of the order $10^{-7}$. On the other hand, we do not consider the long distance contributions in our present work because they have a small effect on width of this decay [65, 66]. In our future work we will consider such contributions while calculating the FFs in order to predict the branching ratios more precisely.

In the near future, our results can be tested at LHCb. Our model can be used to study the forward–backward asymmetries and CP violation in the rare decays of b baryons to check our FFs.