Semileptonic $\Xi _c$ baryon decays in the relativistic quark model

Abstract

The form factors of the weak $\Xi _c\rightarrow \Xi (\Lambda )$ transitions are calculated in the framework of the relativistic quark model based on the quasipotential approach. All relativistic effects including transformations of the baryon wave functions from the rest to moving reference frame and contributions of the intermediate negative energy states are systematically taken into account. The explicit analytic expressions which reliably approximate the momentum transfer $q^2$ dependence of the form factors in the whole accessible kinematical range are given. The calculated form factors are applied for the evaluation of the semileptonic $\Xi _c\rightarrow \Xi \ell \nu _\ell$ and $\Xi _c\rightarrow \Lambda \ell \nu _\ell$ ($\ell =e,\mu$) decay rates, different asymmetry and polarization parameters within helicity formalism. The obtained results are compared with available experimental data and previous calculations.

1 Introduction

This year significant experimental progress has been achieved in studying weak decays of the charmed $\Xi _c$ baryons. Until now the absolute branching fractions of both neutral $\Xi _c^0$ and charged $\Xi _c^+$ baryons were not measured. All decay modes were only measured relative to $\Xi _c^0\rightarrow \Xi ^-\pi ^+$ and $\Xi _c^+\rightarrow \Xi ^-\pi ^+\pi ^+$ modes [1]. This fact significantly complicated comparison of theoretical predictions with experimental data. However, recently the Belle Collaboration presented the first measurement of absolute branching fractions of the neutral $\Xi _c^0$ baryon in three decay modes including $\Xi _c^0\rightarrow \Xi ^-\pi ^+$ one [2]. Its branching fraction is $Br(\Xi _c^0\rightarrow \Xi ^-\pi ^+)=(1.80\pm 0.50\pm 0.14)\%$. Then the absolute branching fractions of its charged partner $\Xi _c$ were also reported [3] for three decay modes including $\Xi _c^+\rightarrow \Xi ^-\pi ^+\pi ^+$ with $Br(\Xi _c^+\rightarrow \Xi ^-\pi ^+\pi ^+)=(2.86\pm 1.21\pm 0.38)\%$. These results can be combined with $\Xi _c$ branching fractions measured relative to corresponding modes to get other absolute $\Xi _c$ branching fractions. Thus the experimental values of $\Xi _c$ semileptonic branching fractions can be determined.

In this paper we calculate the weak $\Xi _c\rightarrow \Xi (\Lambda )$ transition form factors in the framework of the relativistic quark model based on the quasipotential approach and use them to evaluate the semileptonic branching fractions of the $\Xi _c$ baryon. This model was successfully applied for studying semileptonic decays of bottom $\Lambda _b$ [4] and $\Xi _b$ [5] and charmed $\Lambda _c$ [6] baryons. The form factors are expressed as the overlap integrals of the baryon wave functions. The important advantage of the employed model is the comprehensive inclusion of the relativistic effects which allows us to explicitly determine the $q^2$ dependence of the form factors in the whole kinematical range, thus increasing reliability of the results. The calculated form factors can be then used for the determination of branching fractions and other important observables which can be measured experimentally. The results can be confronted with previous theoretical predictions and new experimental data.

2 Form factors of the weak $\Xi _c$ baryon decays

We consider the matrix element of the weak current $J_\mu ^W=V_\mu -A_\mu ={{\bar{q}}}\gamma _\mu (1-\gamma _5)c$ ($q=s,d$) between $\Xi _c$ and $\Xi$ or $\Lambda$ baryon states, respectively. In the quasipotential approach it is expressed through the overlap integral of the baryon wave functions $\Psi _{B\mathbf{p}_B}$ ($B=\Xi _c,\Xi ,\Lambda$) projected on the positive energy states ($\mathbf{p}_B$ is the baryon momentum) [4]

$$\begin{aligned}&\langle \Xi (\Lambda )(p_{{\Xi (\Lambda )}}) \vert J^W_\mu \vert \Xi _c(p_{\Xi _c})\rangle \nonumber \\&\quad =\int \frac{d^3p\, d^3q}{(2\pi )^6} \bar{\Psi }_{\Xi (\Lambda )\,\mathbf{p}_{{\Xi (\Lambda )}}}(\mathbf{p})\Gamma _\mu (\mathbf{p},\mathbf{q})\Psi _{\Xi _c\,\mathbf{p}_{\Xi _c}}(\mathbf{q}). \end{aligned}$$

(1)

Table 1 Form factors of the weak $\Xi _c\rightarrow \Xi$ transitions

Table 2 Form factors of the weak $\Xi _c\rightarrow \Lambda$ transitions

Here $\Gamma _\mu (\mathbf{p},\mathbf{q})$ is the two-particle vertex function which receives relativistic contributions both from the impulse approximation diagram and from the diagrams with the intermediate negative-energy states [4]. It is convenient to consider semileptonic decay in the rest frame of the initial $\Xi _c$ baryon. Then it is necessary to take the final $\Xi (\Lambda )$ in the moving frame [4].

The weak $\Xi _c\rightarrow \Xi (\Lambda )$ transition matrix elements are parametrized in terms of six invariant form factors [7]

$$\begin{aligned}&\langle \Xi (\Lambda )(p_{{\Xi (\Lambda )}},s') |V^\mu |\Xi _c(p_{\Xi _c},s)\rangle \nonumber \\&\quad = \bar{u}_{\Xi (\Lambda )}(p_{{\Xi (\Lambda )}},s') \Bigl [f_1^V(q^2)\gamma ^\mu \nonumber \\&\qquad -f_2^V(q^2)i \sigma ^{\mu \nu }\frac{q_\nu }{M_{\Xi _c}} +f_3^V(q^2)\frac{q^\mu }{M_{\Xi _c}}\Bigr ] u_{\Xi _c}(p_{\Xi _c},s),\nonumber \\&\langle \Xi (\Lambda )(p_{{\Xi (\Lambda )}},s')|A^\mu |\Xi _c(p,s)\rangle \nonumber \\&\quad = \bar{u}_{\Xi (\Lambda )}(p_{{\Xi (\Lambda )}},s')\Bigl [f_1^A(q^2)\gamma ^\mu \nonumber \\&\qquad -f_2^A(q^2)i\sigma ^{\mu \nu }\frac{q_\nu }{M_{\Xi _c}} +f_3^A(q^2)\frac{q^\mu }{M_{\Xi _c}}\Bigl ] \gamma _5 u_{\Xi _c}(p_{\Xi _c},s),\nonumber \\ \end{aligned}$$

(2)

where $M_{B}$ and $u_B(p,s)$ are masses and Dirac spinors of the initial and final baryons ($B=\Xi _c,\Xi ,\Lambda$), $q=p_{{\Xi (\Lambda )}}-p_{\Xi _c}$.

Comparing (1) with (2) we obtain these form factors in the framework of the relativistic quark model. They are expressed through the overlap integrals of the baryon wave functions [4] which are known from the calculations of the baryon mass spectra [8, 9]. The explicit expressions are given in Ref. [4]. They systematically take into account all relativistic effects including transformation of baryon wave functions from the rest to moving reference frame and contributions of the intermediate negative energy states.

Following Ref. [5] we fit the numerically calculated form factors by the following analytic expression

$$\begin{aligned} f(q^2)= \frac{1}{{1-q^2/{M_{\mathrm{pole}}^2}}} \{ a_0 + a_1 z(q^2) + a_2 [z(q^2)]^2 \}, \end{aligned}$$

(3)

where the variable

$$\begin{aligned} z(q^2) = \frac{\sqrt{t_+-q^2}-\sqrt{t_+-t_0}}{\sqrt{t_+-q^2}+\sqrt{t_+-t_0}}, \end{aligned}$$

(4)

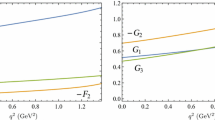
here $t_+=(M_{D_s(D)}+M_{K(\pi )})^2$ and $t_0 = q^2_{\mathrm{max}} = (M_{\Xi _c} - M_{\Xi (\Lambda )})^2$. The pole masses have the following values. For $\Xi _c\rightarrow \Xi$ transitions: $M_\mathrm{pole}\equiv M_{D_s^*}=2.112$ GeV for $f_{1,2}^V$; $M_\mathrm{pole}\equiv M_{D_{s1}}=2.535$ GeV for $f_{1,2}^A$ and $f_{3}^V$; $M_{\mathrm{pole}}\equiv M_{D_s}=1.969$ GeV for $f_{3}^A$. For $\Xi _c\rightarrow \Lambda$ transitions: $M_{\mathrm{pole}}\equiv M_{D^*}=2.010$ GeV for $f_{1,2}^V$; $M_{\mathrm{pole}}\equiv M_{D_{1}}=2.423$ GeV for $f_{1,2}^A$ and $f_{3}^V$; $M_{\mathrm{pole}}\equiv M_{D}=1.870$ GeV for $f_{3}^A$. The fitted values of the parameters $a_0$, $a_1$, $a_2$ as well as the values of form factors at maximum $q^2=0$ and zero recoil $q^2=q^2_{\mathrm{max}}$ of the final baryon are given in Tables 1 and 2. The difference of the fitted form factors from the calculated ones does not exceed 0.5%. The form factors are plotted in Figs. 1 and 2. We roughly estimate the total uncertainty of our form factor calculation to be about 5%.

Fig. 1

Form factors of the weak $\Xi _c\rightarrow \Xi$ transitions

Fig. 2

Form factors of the weak $\Xi _c\rightarrow \Lambda$ transitions

In Table 3 we compare our results for the values of form factors at $q^2=0$ with previous calculations. Results [10] are based on the light-front approach.¹ In this paper form factors $f_3^{V,A}(0)$ were not evaluated. We find good agreement for the form factors parametrizing both the $\Xi _c\rightarrow \Xi$ and $\Xi _c\rightarrow \Lambda$ weak transitions. In Ref. [11] the light cone QCD sum rules were employed for the calculation of the $\Xi _c\rightarrow \Xi$ transition form factors. Their form factors $f^V_{1,2,3}(0)$ parametrizing the vector current significantly differ from our results. The central values [11] of the form factor $f^V_{1}(0)$ is about 3 times smaller while those for $f^V_{2}(0)$ are a factor of about 2 larger than other predictions and form factors $f^V_{3}(0)$, $f^A_{2}(0)$ have even opposite signs.

Table 3 Comparison of the theoretical predictions for form factors of the $\Xi _c$ baryon weak transitions at $q^2=0$

3 Semileptonic $\Xi _c\rightarrow \Xi \ell \nu _\ell$ and $\Xi _c\rightarrow \Lambda \ell \nu _\ell$ decays

The differential and total semileptonic decay rates, branching fractions and different asymmetry and polarization parameters can be calculated using the decay form factors and the helicity formalism [7]. The relation between helicity amplitudes and decay form factors are the following.

$$\begin{aligned} H_{+\frac{1}{2} 0}^{V,A}= & {} \frac{\sqrt{(M_{\Xi _c}\mp M_{\Xi (\Lambda )})^2-q^2}}{\sqrt{q^2}}\nonumber \\&\times \bigg [(M_{\Xi _c}\pm M_{\Xi (\Lambda )}) f_1^{V,A}(q^2)\pm \frac{q^2}{M_{\Xi _c}} f_2^{V,A}(q^2)\bigg ],\nonumber \\ H_{+\frac{1}{2} +1}^{V,A}= & {} \sqrt{2[(M_{\Xi _c}\mp M_{\Xi (\Lambda )})^2-q^2]}\nonumber \\&\times \bigg [f_1^{V,A}(q^2)\pm \frac{M_{\Xi _c}\pm M_{\Xi (\Lambda )}}{M_{\Xi _c}}f_2^{V,A}(q^2)\bigg ],\nonumber \\ H_{+\frac{1}{2} t}^{V,A}= & {} \frac{\sqrt{(M_{\Xi _c}\pm M_{\Xi (\Lambda )})^2-q^2}}{\sqrt{q^2}}\nonumber \\&\times \bigg [ (M_{\Xi _c}\mp M_{\Xi (\Lambda )}) f_1^{V,A}(q^2)\pm \frac{q^2}{M_{\Xi _c}} f_3^{V,A}(q^2)\bigg ],\nonumber \\ \end{aligned}$$

(5)

and the amplitudes for negative values of the helicities are obtained from the relations

$$\begin{aligned} H^{V,A}_{-\lambda ',\,-\lambda _W}=\pm H^{V,A}_{\lambda ',\, \lambda _W}. \end{aligned}$$

The total helicity amplitude for the $V-A$ current is given by

$$\begin{aligned} H_{\lambda ',\, \lambda _W}=H^{V}_{\lambda ',\, \lambda _W} -H^{A}_{\lambda ',\, \lambda _W}. \end{aligned}$$

(6)

Fig. 3

Differential decay rates of the $\Xi _c\rightarrow \Xi \ell \nu _\ell$ (left) and $\Xi _c\rightarrow \Lambda \ell \nu _\ell$ (right) semileptonic decays

The differential decay rates and angular distributions are expressed in terms of the helicity structures which are the following combinations of the total helicity amplitudes (6)

$$\begin{aligned} \mathcal{H}_U(q^2)= & {} |H_{+1/2,+1}|^2+|H_{-1/2,-1}|^2,\nonumber \\ \mathcal{H}_L(q^2)= & {} |H_{+1/2,0}|^2+|H_{-1/2,0}|^2,\nonumber \\ \mathcal{H}_S(q^2)= & {} |H_{+1/2,t}|^2+|H_{-1/2,t}|^2,\nonumber \\ \mathcal{H}_{SL}(q^2)= & {} \mathrm{Re}(H_{+1/2,0}H_{+1/2,t}^\dag +H_{-1/2,0}H_{-1/2,t}^\dag ),\nonumber \\ \mathcal{H}_P(q^2)= & {} |H_{+1/2,+1}|^2-|H_{-1/2,-1}|^2,\nonumber \\ \mathcal{H}_{L_P}(q^2)= & {} |H_{+1/2,0}|^2-|H_{-1/2,0}|^2,\nonumber \\ \mathcal{H}_{S_P}(q^2)= & {} |H_{+1/2,t}|^2-|H_{-1/2,t}|^2. \end{aligned}$$

(7)

The expression for the differential decay rate is given by [7]

$$\begin{aligned}&\frac{d\Gamma (\Xi _c\rightarrow \Xi (\Lambda )\ell {{\bar{\nu }}}_\ell )}{dq^2}\nonumber \\&\quad =\frac{G_F^2}{(2\pi )^3} |V_{cq}|^2 \frac{\lambda ^{1/2}(q^2-m_\ell ^2)^2}{48M_{\Xi _c}^3q^2}\mathcal{H}_{tot}(q^2), \end{aligned}$$

(8)

Fig. 4

Forward–backward asymmetry $A_{FB}(q^2)$ in the $\Xi _c\rightarrow \Xi \ell ^+\nu _\ell$ (left) and $\Xi _c\rightarrow \Lambda \ell ^+\nu _\ell$ (right) semileptonic decays

Fig. 5

Convexity parameter $C_F(q^2)$ in the $\Xi _c\rightarrow \Xi \ell ^+\nu _\ell$ (left) and $\Xi \rightarrow \Lambda \ell ^+\nu _\ell$ (right) semileptonic decays

Fig. 6

Longitudinal polarization $P_L(q^2)$ of the final baryon in the $\Xi _c\rightarrow \Xi \ell ^+\nu _\ell$ (left) and $\Xi _c\rightarrow \Lambda \ell ^+\nu _\ell$ (right) semileptonic decays

Fig. 7

Longitudinal polarization $P_\ell (q^2)$ of the charged lepton in the $\Xi _c\rightarrow \Xi \ell ^+\nu _\ell$ (left) and $\Xi _c\rightarrow \Lambda \ell ^+\nu _\ell$ (right) semileptonic decays

where $G_F$ is the Fermi constant, $V_{cq}$ is the Cabibbo–Kobayashi–Maskawa (CKM) matrix element ($q=s,d$), $\lambda \equiv \lambda (M_{\Xi _c}^2,M_{\Xi (\Lambda )}^2,q^2) =M_{\Xi _c}^4+M_{\Xi (\Lambda )}^4+q^4-2(M_{\Xi _c}^2M_{\Xi (\Lambda )}^2 +M_{\Xi (\Lambda )}^2q^2+M_{\Xi _c}^2q^2)$, and $m_\ell$ is the lepton mass ($\ell =e,\mu$),

$$\begin{aligned}&\mathcal{H}_{tot}(q^2)\nonumber \\&\quad =[\mathcal{H}_U(q^2)+\mathcal{H}_L(q^2)] \left( 1+\frac{m_\ell ^2}{2q^2}\right) +\frac{3m_\ell ^2}{2q^2}\mathcal{H}_S(q^2) . \end{aligned}$$

(9)

Substituting in these expressions the $\Xi _c$ decay form factors calculated in the previous section we obtain the differential decay rates. We plot them for the $\Xi _c\rightarrow \Xi \ell \nu _\ell$ (left) and $\Xi _c\rightarrow \Lambda \ell \nu _\ell$ (right) semileptonic decays in Fig. 3.

Many important observables are expressed in terms of the helicity combinations (7) (see [7] for details):

• The forward–backward asymmetry of the charged lepton

  $$\begin{aligned} A_{FB}(q^2)= & {} \frac{\frac{d\Gamma }{dq^2}(\mathrm{forward})-\frac{d\Gamma }{dq^2}(\mathrm{backward})}{\frac{d\Gamma }{dq^2}}\nonumber \\= & {} \frac{3}{4}\frac{\mathcal{H}_P(q^2)-2\frac{m_\ell ^2}{q^2}\mathcal{H}_{SL}(q^2)}{\mathcal{H}_{tot}(q^2)};\qquad \end{aligned}$$

  (10)

• The convexity parameter

  $$\begin{aligned} C_F(q^2)=\frac{3}{4}\left( 1-\frac{m_\ell ^2}{q^2}\right) \frac{\mathcal{H}_U(q^2)-2\mathcal{H}_L(q^2)}{\mathcal{H}_{tot}(q^2)}; \end{aligned}$$

  (11)

• The longitudinal polarization of the final baryon $\Xi _c(\Lambda )$

  $$\begin{aligned}&P_L(q^2)\nonumber \\&\quad =\frac{[\mathcal{H}_P(q^2)+\mathcal{H}_{L_P}(q^2)]\left( 1+\frac{m_\ell ^2}{2q^2}\right) +3 \frac{m_\ell ^2}{2q^2}\mathcal{H}_{S_P}(q^2)}{\mathcal{H}_{tot}(q^2)};\nonumber \\ \end{aligned}$$

  (12)

• The longitudinal polarization of the charged lepton $\ell$

  $$\begin{aligned}&P_\ell (q^2)\nonumber \\&\quad =\frac{\mathcal{H}_U(q^2)+\mathcal{H}_L(q^2)-\frac{m_\ell ^2}{2q^2}[\mathcal{H}_U(q^2)+\mathcal{H}_L(q^2)+3\mathcal{H}_{S}(q^2)]}{\mathcal{H}_{tot}(q^2)}.\nonumber \\ \end{aligned}$$

  (13)

These observables are plotted for $\Xi _c\rightarrow \Xi \ell ^+\nu _\ell$ and $\Xi _c\rightarrow \Lambda \ell ^+\nu _\ell$ semileptonic decays in Figs. 4, 5, 6 and 7. The predictions for the decay branching fractions and asymmetry parameters are presented in Table 4. We calculated the decay rates using the CKM values $|V_{cs}|=0.995\pm 0.016$, $|V_{cd}|=0.220\pm 0.005$ [1]. The average values of the $\langle A_{FB}\rangle$, $\langle C_F\rangle$, $\langle P_L\rangle$ and $\langle P_\ell \rangle$ were obtained by separately integrating the numerators and denominators in Eqs. (10)–(13) over $q^2$. We roughly estimate uncertainties of our predictions for the branching fractions to be about 10%.

Table 4 $\Xi _c$ semileptonic branching fractions, asymmetry and polarization parameters

Table 5 Comparison of theoretical predictions for the $\Xi _c$ semileptonic decay branching fractions (in %) with available experimental data

Since possible violations of the charged lepton universality are now widely discussed in the literature [12] we present predictions for the corresponding ratios for the semileptonic $\Xi _c$ decays involving muons and electrons

$$\begin{aligned} R_{\Xi }= & {} \frac{Br(\Xi _c\rightarrow \Xi \mu \nu _\mu )}{Br(\Xi _c\rightarrow \Xi e\nu _e)}=0.969\pm 0.010,\nonumber \\ R_{\Lambda }= & {} \frac{Br(\Xi _c\rightarrow \Lambda \mu \nu _\mu )}{Br(\Xi _c\rightarrow \Lambda e\nu _e)}=0.980\pm 0.010. \end{aligned}$$

(14)

Most of the theoretical uncertainties cancels in these ratios, thus we roughly estimate them to be about 1%.

Theoretical predictions [10, 11, 13, 14] for the semileptonic $\Xi _c$ decay branching fractions are compared in Table 5. The light-front quark model is used for the weak decay form factor and branching fraction calculations in Ref. [10]. The predictions of Refs. [13, 14] are based on the application of the SU(3) flavor symmetry, while the light-cone QCD sum rules are employed in Ref. [11]. The experimental branching fractions are obtained by multiplying the CLEO II values [15] updated by PDG [1] for the ratios $\Gamma (\Xi _c^0\rightarrow \Xi ^-e^+\nu _e)/\Gamma (\Xi _c^0\rightarrow \Xi ^-\pi ^+)=3.1\pm 1.1$ and $\Gamma (\Xi _c^+\rightarrow \Xi ^0e^+\nu _e)/\Gamma (\Xi _c^+\rightarrow \Xi ^-\pi ^+\pi ^+)=2.3^{+0.7}_{-0.8}$ by the recently measured by the Belle Collaboration branching fractions $Br(\Xi _c^0\rightarrow \Xi ^-\pi ^+)=(1.80\pm 0.50\pm 01.14)\%$ [2] and $Br(\Xi _c^+\rightarrow \Xi ^-\pi ^+\pi ^+)=(2.86\pm 1.21\pm 0.38)\%$ [3]. We find reasonable agreement of our predictions for the CKM favored $\Xi _c\rightarrow \Xi \ell \nu _\ell$ decays with the results of Refs. [10, 13, 14] and experimental data, while the light-cone QCD sum rule values for branching fractions are substantially higher and disagree with data by more than a factor of 2 for the $\Xi _c^+\rightarrow \Xi ^0e^+\nu _e$ decay. Note that ARGUS Collaboration [16] measured the ratio $\Gamma (\Xi _c^0\rightarrow \Xi ^-e^+\mathrm{anything})/\Gamma (\Xi _c^0\rightarrow \Xi ^-\pi ^+)=1.0\pm 0.5$ (the value updated by PDG [1]) which combined with Belle data [2] leads to the semi-inclusive branching fraction $Br(\Xi _c^0\rightarrow \Xi ^-e^+\mathrm{anything})=(1.80\pm 1.07)\%$ in good agreement with our result. There is no data yet for the CKM suppressed $\Xi _c^+\rightarrow \Lambda \ell ^+\nu _\ell$ decays and theoretical evaluations give consistent predictions for the branching fractions about 0.1%.

We can combine our present predictions for the semileptonic $\Xi _c$ baryon decays with our previous analysis of the semileptonic $\Lambda _c$ decays [6] to test the flavor SU(3) symmetry. Under the exact SU(3) limit the following relations should hold [10, 13]

$$\begin{aligned} \frac{\Gamma (\Lambda _c\rightarrow n e\nu _e)}{|V_{cd}|^2}= & {} \frac{3\Gamma (\Lambda _c\rightarrow \Lambda e\nu _e)}{2|V_{cs}|^2}\nonumber \\= & {} \frac{6\Gamma (\Xi _c\rightarrow \Lambda e\nu _e)}{|V_{cd}|^2}\nonumber \\= & {} \frac{\Gamma (\Xi _c\rightarrow \Xi e\nu _e)}{|V_{cs}|^2}. \end{aligned}$$

(15)

In Table 6 we test these relations for the ratios $\Gamma /|V_{cq}|^2$, where the corresponding CKM matrix element is used. In first column we give the semileptonic decay process. In the second column we present predictions of our model. The third column contains the flavor SU(3) symmetry result using relations (15) and $\Gamma (\Lambda _c\rightarrow n e\nu _e)/|V_{cd}|^2$ as an input, while the last column gives the relative difference in %. From this table we see that the flavor SU(3) is broken for the charmed baryon semileptonic decays especially for $\Xi _c$ where its breaking is about 20–35%. This is the consequence of the larger mass of the s quark in comparison with the u, d quarks and the employed quark–diquark picture of baryons.

Table 6 Predictions for the ratios $\Gamma /|V_{cq}|^2$ in $\hbox {ps}^{-1}$ ($q=s,d$)

4 Conclusion

The relativistic quark model was used for the calculation of form factors of the semileptonic $\Xi _c$ transitions, both for the CKM favored $\Xi _c\rightarrow \Xi \ell ^+\nu _\ell$ and CKM suppressed $\Xi _c^+\rightarrow \Lambda \ell ^+\nu _\ell$ decays. All relativistic effects, including baryon wave function transformations from the rest to moving reference frame and contributions of the intermediate negative-energy states, were comprehensively taken into account. This allowed us to explicitly determine the momentum transfer $q^2$ dependence of the weak form factors in the whole kinematical range without additional model assumptions or extrapolations. We give the values of parameters in the analytic expression (3) which accurately approximates the numerically calculated form factors in Tables 1 and 2 and show the form factor $q^2$ dependence in Figs. 1 and 2.

Using the calculated form factors and helicity formalism we estimated important observables for the CKM favored and CKM suppressed $\Xi _c$ semileptonic decays: differential decay rates, branching fractions, different asymmetry and polarization parameters, which are given in Table 4 and plotted in Figs. 4, 5, 6 and 7. Our results for the branching fractions of the $\Xi _c\rightarrow \Xi \ell \nu _\ell$ decays are in reasonable agreement with previous calculations based on the light-front quark model [10] and application of the SU(3) flavor symmetry [13, 14], but significantly lower than the light-cone QCD sum rule predictions [11]. They agree with experimental values which can be obtained combining the corresponding decay ratios from PDG [1] and recent measurements of absolute branching fractions by the Belle Collaboration [2, 3]. Comparison of the present results for the semileptonic $\Xi _c$ decays with the previous ones for the $\Lambda _c$ decays [6] indicates a sizable SU(3) symmetry breaking which can reach 35%. This result is in accord with the conclusion of Ref. [10].

In this paper we limit our consideration to the $\Xi _c$ semileptonic decays. In principle it can be extended to $\Xi _c'$ baryons which differ by the spin of the diquark. However $\Xi _c'$ can decay radiatively to $\Xi _c$ with the evaluated width of a few keV (see e.g. [17] and references therein). A rough estimate of the $\Xi _c'$ semileptonic decay rates based on the heavy quark and flavor SU(3) symmetries indicate that they should be of the same order as the $\Xi _c$ semileptonic decay rates. Note that similar results were obtained in the light cone QCD sum rules [11]. Therefore the branching fractions of the $\Xi _c'$ semileptonic decays are expected to be of order of $10^{-8}-10^{-7}$. Taking into account that the total width of the $\Xi _c'$ baryon is not measured yet [1] due to the poor statistics it is very unlikely that decays with such small branching fractions will be observed experimentally.