Abstract
In this work, we calculate the amplitudes of the processes \(c{{\bar{c}}}({^3P_J}) \rightarrow DD,DD^*, D^*D^* \rightarrow c\bar{c}({^3P_J})\) in the leading order of the nonrelativistic expansion. The imaginary parts of the amplitudes are corresponding to the branch decay widths of the charmonium \(c{{\bar{c}}}({^3P_J}) \rightarrow DD,DD^*, D^*D^*\) and the real parts are corresponding to the mass shifts of the charmonium \(c{{\bar{c}}}({^3P_J})\) due to these decay channels. After absorbing the polynomial contributions which are pure real, the ratios between the branch decay widths and the corresponding mass shifts are only dependent on the center-of-mass energy. We find the decay widths and the mass shifts of the \(^3P_2\) states are exact zero in the leading order. The ratios between the branch decay widths and the mass shifts for the \(^3P_0, {^3P_1}\) states are larger than 5 when the center-of-mass energy is above the \(DD,DD^*, D^*D^*\) threshold. The dependence of the mass shifts on the center-of-mass energy is nontrivial especially when the center-of-mass energy is below the threshold. The analytic results can be extended to the b quark sector directly.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The energy spectrum of hadrons is a basic topic in the strong interaction. Up to now, it is still an unsolved problem due to the complex nonperturbative property of QCD. In literatures, many phenomenological models have been developed to study this problem in the quark level, such as the quark model [1,2,3], QCD sum rules [4,5,6,7,8], Bethe–Salpeter equation [9,10,11,12,13,14,15,16,17,18,19,20,21,22], and etc. In these methods, usually the annihilation effects are neglected since they are much smaller than the non-perturbative potential. Physically, if the annihilation effects can be taken as small comparing with the interaction which binds the quarks, then the imaginary part of the annihilation amplitude is corresponding to the branch decay width and the real part is corresponding to the perturbative mass shift. Theoretically such annihilation effects should be considered and estimated carefully when aiming to understand the energy spectrum precisely.
Experimentally, since 2003 many new charmonium-like states are reported by the collaborations of Belle [23,24,25,26,27,28,29], CDF [30, 31], D0 [32], BABAR [33, 34], Cleo-C [35], LHCb [36], BES [37], and CMS [38, 39]. These charmonium-like states cannot be well understood in the traditional quark model and their masses usually lie above the open charm threshold where some new decay modes are opened. In the previous study [40, 41], we studied the mass shifts of \(^1S_0\) and \(^3P_J\) heavy quarkonia due to the transition \(q{\bar{q}}\rightarrow 2g\rightarrow q{\bar{q}}\). Physically, when the masses of the states lie above the threshold of D or \(D^*\) pairs, the transitions \(c{{\bar{c}}}\) to these mesons’ pairs are opened. It is natural that these opened channels not only result in the visible branch decay widths but also give contributions to the mass shifts of the corresponding charmonium. When the masses of the charmonium lie about the threshold of the meson pairs, one can expect that the nonrelativistic expansion is applicable, which means that one can take the mesons \(D,D^*\) like the heavy quark in the nonrelativistic QCD to construct the effective nonrelativistic interactions order by order. In this work, we follow this spirit to calculate the amplitudes of \(c{{\bar{c}}} (^3P_J) \rightarrow DD, DD^*, D^*D^* \rightarrow c{{\bar{c}}} (^3P_J)\) in the leading order of non-relativistic expansion. The imaginary parts of the results are corresponding to the branch decay widths which can be used to determine the effective coupling constants. Furthermore, if these annihilation interactions are much smaller than the binding interaction, then the real parts can be used to estimate the corresponding mass shifts.
We organize the paper as follow. In Sect. 2 we describe the basic frame to calculate the amplitudes of \(c{{\bar{c}}} (^3P_J) \rightarrow DD, DD^*,D^*D^* \rightarrow {{\bar{c}}} (^3P_J)\) in the leading order of nonrelativistic expansion, in Sect. 3 we give the analytic results for the amplitudes in the leading order of nonrelativistic expansion, in Sect. 4, we present some numerical results to show some properties in detail.
2 Basic formula
When the mass of the charmonium is about \(2m_D\) or \(2m_{D^*}\) with \(m_{D,D^*}\) being the masses of the \(D,D^*\) mesons, the three-momenta of the c quarks and the mesons in the decay channels \(c{\bar{c}} (^3P_J)\rightarrow DD,DD^*,D^*D^*\) are much smaller than c quarks’ mass \(m_c\) or \(m_{D,D^*}\). In this case, one can take \(m_c\approx m_D \approx m_{D^*}\) as the large scale comparing with \(\Lambda _{\text {QCD}}\) and expand the interaction on the small variables \(|\overset{\rightharpoonup }{\mathbf {q}}|/m_c\) with \(\overset{\rightharpoonup }{\mathbf {q}}\) the three-momenta of the c quarks and the mesons. This nonrelativistic expansion is similar with the spirit of NRQCD where the contact four point interactions are introduced. Different from NRQCD, now there is no hard gluon in the decay channels \(c{\bar{c}} (^3P_J)\rightarrow DD,DD^*,D^*D^*\), but only nonrelativistic heavy quarks and heavy mesons. This means that there are only contact interactions between the c quarks and the \(D,D^*\) mesons.
To construct the interaction Lagrangian order by order on \(|\overset{\rightharpoonup }{\mathbf {q}}|/m_c\), one can use the same spirit with NRQCD [42] where only the three-dimension partial \(\overset{\rightharpoonup }{\mathbf {\nabla }}\) on the fields is used and naively one \(\overset{\rightharpoonup }{\mathbf {\nabla }}\) contributes one order. A little difference from NRQCD is that now the 0-component of the \(D^*\) field \(A^{\mu }\) is also a small variable since \(\partial _{\mu }A^{\mu }=\partial _{0}A^{0}-\overset{\rightharpoonup }{\mathbf {\nabla }}\cdot \overset{\rightharpoonup }{\mathbf {A}}=0\) for the on shell \(D^*\). This means that the inclusion of one \(A^{0}\) field also contributes one order like \(\overset{\rightharpoonup }{\mathbf {\nabla }}\). Then in the leading order there is no \(\overset{\rightharpoonup }{\mathbf {\nabla }}\) or \(A^{0}\) in the interaction Lagrangian. For convenience, one can also rewrite the Lagrangian in a covariant form and choose the leading order contribution finally. By this reason the most general interactions with C, P, T invariance in the leading order can be written as follows:
where \(\psi ,\phi ,A^{\mu }\) are the fields of the c quark, the D meson, and the \(D^*\) meson, respectively. Here we do not assume that there is spin asymmetry between the D and \(D^*\) mesons since the dynamics of the light quarks inside the D and \(D^*\) mesons may break the spin symmetry strongly. This means that the couplings \(g_{a,b,c}\) are independent.
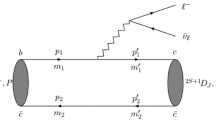
By these interactions, the Feynman diagrams for the amplitudes of \(c{{\bar{c}}} ({^3P_J})\rightarrow DD, DD^*,D^*D^* \rightarrow c\bar{c}({^3P_J})\) in the leading order are shown in Fig. 1a–c.
The diagrams for \(c{{\bar{c}}}(^3P_J)\rightarrow c{{\bar{c}}}(^3P_J)\) processes where a–d are corresponding to \(c{{\bar{c}}} \rightarrow DD \rightarrow c{{\bar{c}}}\), \(c{{\bar{c}}} \rightarrow DD^* \rightarrow c{{\bar{c}}}\), \(c{{\bar{c}}} \rightarrow D^*D^* \rightarrow c\bar{c}\), and \(c{{\bar{c}}}\rightarrow c{{\bar{c}}}\) via contact interactions
Similar with any effective theory, usually the contact interactions are needed to absorb the UV divergences in the loop diagrams. In the practical calculation, we find the following contact interactions are needed to absorb the UV divergences in Fig. 1a–c:
The physical reason of such contact interactions is related with the quantum number of \(^3P_{0,1}\): \({{\mathcal {L}}}^{c}_1\) is the contact interaction in the scalar channel and \({{\mathcal {L}}}^{c}_2\) is the contact interaction in the axial-vector channel. We want to point out that we just write down such contact interactions here to show the exact cancellations of the UV divergences and the polynomial contributions. In the practical calculation, one can get the same final results even without knowing the form of the contact interactions. The Feynman diagram for the contribution due to these contact interactions is shown in Fig. 1d.
In the center of mass frame, we choose the four external momenta as follows:
For simplicity we define \(P \overset{def}{=} (\sqrt{s},0,0,0)\) and use the instantaneous approximation for \(q_{i,f}\) which means that we assume \(q_i= (0,\mathbf{q} _i)\) and \( q_f= (0,\mathbf{q} _f)\), where we use the bold formatting to refer to the three momentum here and in the following.
To project the \(c{{\bar{c}}}\) pairs to the \(^3P_J\) states we use the project matrices in the on-shell case [43,44,45,46,47] which are defined as follows:
where the Clebsch–Gordan coefficients are the standard ones as in Refs. [44, 45], and the Dirac spinors are normalized as \(u^+u=\nu ^+\nu =1\), whose definitions are expressed as
with \(E_{1,2} =\sqrt{|\mathbf{p }_{1,2}|^2+m_c^2}\), \({\overline{p}}_{1,2}=(E_{1,2},\mathbf{p }_{1,2})\), \(\xi ^{1/2}=(1,0)^T\), \(\xi ^{-1/2}=(0,1)^T\), \(\eta ^{1/2}=(0,1)^T\), and \(\eta ^{-1/2}=(-1,0)^T\). Finally the project matrices can be written as
where \(E_{i,f}= \sqrt{|\mathbf{q} _{i,f}|^2+m_c^2}\), and
and \(N_{i,f}\) are the normalized global factors which can be expressed as follows in the nonrelativistic limit
In principle the form of the project matrix for a bounded \(c{\overline{c}}\) pair should be deduced from the Bethe–Salpeter wave function or similar Lorentz covariant matrix element, while in the ultra nonrelativistic limit the above expressions are expected to be correct.
In the leading order of nonrelativistic expansion, the structure of a meson \(H(^3P_J)\) can be expressed as follow:
where \(N_c=3\) and \(\phi (|\mathbf{p }|)\) is the wave function of \(H(^3P_J)\) in the momentum space which is defined as
with the normalization condition
Combining the structure of \(H(^3P_J)\) and the project matrices, the expression for the amplitudes in the leading order can be expressed as
where the index (X) refers to (a, b, c, d) which are corresponding to the contributions from the diagrams (a), (b), (c) and (d) shown in Fig. 1, respectively. \({\overline{G}}^{(X)}(^3P_J)\) are expressed as
with
where \(d=4-2\epsilon \) is the dimension, \(\mu \) is the introduced energy scale, \(c_f=\frac{\delta _{ij}}{\sqrt{N_c}}\delta _{ij}\frac{\delta _{i'j'}}{\sqrt{N_c}}\delta _{i'j'}=3\) is the color factor, and
and the propagators of the pseudoscalar S and the vector \(D_{\mu \nu }\) are defined as
In the practical calculation, the package FeynCalc [48, 49] is used to do the trace in the d dimension. The packages FIESTA [50, 51] and PackageX [52, 53] are independently used to do the loop integration for double check. After the loop integrations, \(G^{(X)}(s_i,s_f)\) can be expressed in the following form:
where \(C^{(X)}_i\) can be expressed as
with \({\hat{q}}_{i,f}\overset{def}{=}q_{i,f}/|\mathbf{q} _{i,f}|\), respectively.
To get the coefficients \({\overline{G}}^{(X)}(^3P_J)\), usually the sums of the spins and the integrations of the angles are calculated independently to simplify the expressions [54]. In our calculation, we directly calculate the sums of the spins and the integrations of the angles together after getting the expressions of \(C^{(X)}_{in}\). This method is more efficient and has been used in our previous work [40, 41]. The relevant expressions are listed in the Appendix.
3 The energy shift of \(^3P_J\) in the leading order
We expand \({\overline{G}}^{(X)}(^3P_J)\) on \(|\mathbf{q} _{i}|,|\mathbf{q} _{f}|\) to order 1 as following forms:
Here we want to emphasis that the contributions \({\overline{G}}^{(d)}(^3P_J)\) are used to absorb the UV divergences in \({\overline{G}}^{(a+b+c)}(^3P_J)\) and give no contributions to the decay widths of \(^3P_J\) states. The finite parts of the contributions \({\overline{G}}^{(d)}(^3P_J)\) are arbitrary. Actually, they not only absorb the UV divergences but also absorb the polynomial contributions in \({\overline{G}}^{(a+b+c)}(^3P_J)\). This situation is a little different from the results in the \(c\bar{c}(^3P_J)\rightarrow 2g \rightarrow c{{\bar{c}}}(^3P_J) \) cases where there are no any contact interactions in the original QCD interaction. The important point is that these absorptions are universal and independent on the processes, and we discuss the details in the following subsection.
3.1 The energy shift of \(^3P_0\) state
After the loop integration, the sum of the spins, the integration of the angles, and the Taylor expansion, we get the following results in the \(^3P_0\) channel.
where \(c^{(a,c,d)}_{0,poly}\) are some polynomial functions on s which include the UV divergences and are expressed as follows:
with\(\frac{1}{{\overline{\epsilon }}_{\text {UV}}}=\frac{1}{\epsilon _{\text {UV}}}-\gamma _E+\log (4\pi )\).
An important property of the two contributions \(c^{(a,c)}_{0,poly}\) is that they can be absorbed by the contact interactions \(\mathcal{L}_1^{c}\) independently. These contact interactions are independent and give no contributions to the decay widths of the charmonium. This means that their effects can be absorbed by the models which are used to calculate the energy spectrum and do not include the annihilation effects. Here we are only interested in the mass shifts due to the decay modes, then we only focus on the contributions including the imaginary parts due to the loop calculation and neglect the terms \(c^{(a,c)}_{0,poly}\). The choices of \(g_{10,11,12}\) which can cancel all the polynomial contributions in \(c_{0}^{(a,c)}\) can be got directly.
From Eq. (20), one can easily get the imaginary parts as follows:
Matching the amplitude with the corresponding amplitude in quantum mechanism with a perturbatively potential, one has
Finally the decay widths of \(^3P_0\) to DD, \(DD^*\) and \(D^*D^*\) in the leading order are expressed as follows:
where we have used the relation
The corresponding full mass shift labeled as \(\Delta m(^3P_0)\) is expressed as
where \({\overline{c}}_{0}^{(a,c)}=c_{0}^{(a,c)}-c_{0,poly}^{(a,c)}\).
3.2 The energy shift of \(^3P_1\) state
In the \(^3P_1\) channel, we have the following results
with
The polynomial terms are expressed as
with
At first glance, this property is very different from that in the \(^3P_0\) channel due to the nonzero values of \(c_{1,-2}\) and \(c_{1,-1}\). While actually when taking the nonrelativistic approximation \(m_D\approx m_{D^*}\), one has \(c_{1;-2},c_{1;-2} \approx 0\), this means that these contributions are very small in the nonrelativistic approximation and can be neglected. The numerical calculation also shows such property and we neglect these two terms in the following.
Similarly, the terms \(c^{(b,d)}_{1,poly}\) can be neglected when aiming to discuss the contributions from the annihilation effects. The corresponding imaginary parts can be expressed as
In the leading order, the decay width of \(^3P_1\) to DD, \(DD^*\) and \(D^*D^*\) are expressed as
and the corresponding full mass shift labeled as \(\Delta m(^3P_1)\) is expressed as
where \({\overline{c}}_{1}^{(b)}=c_{1}^{(b)}-c_{1,poly}^{(b)}\).
3.3 The energy shift of \(^3P_2\) state
For \(^3P_2\) state, we get
These results mean that the decay widths \(\Gamma (^3P_2\rightarrow DD,DD^*,D^*D^* )\) are exact zero and there are no mass shifts for the \(^3P_2\) states in the leading order. This is a strong property which can be tested by the experiments and be used to judge whether a state is a pure \(^3P_2\) heavy quarkonium or not.
3.4 Property of the analytic results
Comparing our results with those given by the \(^3P_0\) model in Ref. [55] and the Friedrichs model in Ref. [56], one can find that both the two methods give the zero results for \(c{\overline{c}}(^3P_0)\rightarrow DD^*\) and \(c{\overline{c}}(^3P_1)\rightarrow DD\). The contributions of \(c{\overline{c}}(^3P_1)\rightarrow D^*D^*\) and \(c{\overline{c}}(^3P_2)\rightarrow DD,DD^*,D^*D^*\) in Ref. [55] are nonzero, and even in the same order with the contribution in \(c{\overline{c}}(^3P_1)\rightarrow DD^*\). While in our results, \(c{\overline{c}}(^3P_1)\rightarrow D^*D^*\) and \(c{\overline{c}}(^3P_2)\rightarrow DD,DD^*, D^*D^*\) are exact zero.
To understand these exact zero results in our method, one can consider the decay widths in the hadronic level at first. The most general form for the amplitudes of \(c{\overline{c}}(^3P_J)\rightarrow DD,DD^*,D^*D^*\) with Lorentz invariance can be expressed as follows:
and
and
where \(P_i\) are the momenta of \(^3P_J\) meson, D meson and \(D^*\) meson, \(\epsilon _{\mu },X_{\mu }\) and \(X_{\mu \nu }\) are the polarization vectors of \(D^*\) meson,\(^3P_1\) and \(^3P_2\) meson, respectively, \(\{\ldots \}\) denotes to the linear combination of the terms in the braces. The properties that \(X^{\mu }_{\mu }=0\), \(X_{\mu \nu }=X_{\nu \mu }\), and \(\epsilon _{1\mu }^{*}\) and \(\epsilon _{2\nu }^{*}\) are symmetrical have been used.
Due to the P invariance, one can directly get that \(\mathcal{M}(^3P_0\rightarrow DD^*)=0\) and \({{\mathcal {M}}}(^3P_1\rightarrow DD)=0\) since the terms in the braces break the P invariance. In principle, other amplitudes are nonzero due to the symmetry.
When taking the nonrelativistic expansion on the three-momenta of the \(D,D^*\) mesons, in the leading order all \(P_i\) are parallel. This property means that \({{\mathcal {M}}}(^3P_1\rightarrow D^*D^*,~^3P_2\rightarrow DD,DD^*)=0\) in the leading order since \(P_i^{\mu }\epsilon ^*_{\mu },P_i^{\mu } X_{\mu }, P_i^{\mu }X_{\mu \nu }\) are zero when all \(P_i\) are parallel. Mathematically, all \(P_i^{\mu }\epsilon ^*_{\mu },P_i^{\mu } X_{\mu }, P_i^{\mu }X_{\mu \nu }\) are zero or small comparing with the mass \(m_D\).
For \({{\mathcal {M}}}(^3P_2\rightarrow D^*D^*)\), when only taking the nonrelativistic expansion on the three-momenta of the \(D,D^*\) mesons, there is a nonzero contribution like \(X_{\mu \nu }\epsilon _{1}^{*\mu }\epsilon _{2}^{*\nu }\) in the leading order. But when one considers the quark structure of the \(^3P_2\) meson and also takes the nonrelativistic expansion on the three-momenta of the quarks, then the interactions at the quark level in the leading order is \({{\mathcal {L}}}_3\) in Eq. (1). This interaction means that the final amplitude is like \(\{P_{i}^{\mu }P_j^{\nu }\}X_{\mu \nu }\epsilon _{1\rho }^*\epsilon _{2}^{*\rho }\) after considering both the nonrelativistic expansion on the \(D^*\) mesons and the c quarks. This is just zero in the leading order.
In summary, we get the following properties:
-
(1)
Due to the P invariance, \({{\mathcal {M}}}(^3P_0\rightarrow DD^*\), \(^3P_1\rightarrow DD)=0\).
-
(2)
Due to the nonrelativistic expansion on the three-momenta of the \(D,D^*\) mesons, \({{\mathcal {M}}}(^3P_1\rightarrow D^*D^*, ^3P_2\rightarrow DD,DD^*)=0\) in the leading order.
-
(3)
Due to the nonrelativistic expansion on the three-momenta of the \(D,D^*\) mesons and the quarks in \(^3P_2\) meson, \(\mathcal{M}(^3P_2\rightarrow D^*D^*)=0\) in the leading order.
In the practical calculation, we also take the following next leading order interaction as example
and we find nonzero result for \({{\mathcal {M}}}(^3P_2\rightarrow D^*D^*)\) in the next leading order.
From the above analysis, one can see that when go to beyond the leading order of nonrelativistic expansion, the amplitudes \(\mathcal{M}(^3P_1\rightarrow D^*D^*\), \(^3P_2\rightarrow DD,DD^*,D^*D^*)\) will not be zero. The calculation in Ref. [55] is based on the \(^3P_0\) model where a light quark pair is dynamically produced in the vacuum and the nonrelativistic wave functions of the mesons are used to estimate the contributions. This means that in Ref. [55] the three-momenta of the quarks and the \(D,D^*\) mesons are not expanded order by order and their momenta’ distributions are considered via some wave functions and the quark pair creation mechanism. This is very different from our method which is based on the general model independent interactions under the nonrelativistic expansion. In our calculation, all the dynamics of the light quark and \(D,D^*\) meason is absorbed by the coupling constants in the leading order of the nonrelativistic expansion. On another hand, we only consider the contributions due to the annihilation effects and neglect the polynomial contribution since the latter is uncertain.
4 Numerical results and discussion
To show the properties of the above analytic results more clearly, we present some numerical results in this section. Firstly we want to emphasize that the absolute values of \(\text {Re}[{\overline{c}}^{(a,b,c)}_{J}]\) and \(\text {Im}[c^{(a,b,c)}_{J}]\) can not determine the physical decay widths and the mass shifts directly, since there are some global unknown constant factors. But the ratios of the mass shifts and the decay widths \(-\text {Re}[{\overline{c}}^{(a,b,c)}_{J}]/2\text {Im}[c^{(a,b,c)}_{J}]\) are model independent. This means that if the decay widths are measured experimentally, the corresponding corrections to the masses of the heavy quarkonia can be got directly.
In Fig. 2 the dependence of \(\text {Im}[c^{(a,b,c)}_{J}]\), \(\text {Re}[{\overline{c}}^{(a,b,c)}_{J}]\) and their ratios on \(\sqrt{s}\) is presented, respectively, where we take \(m_D=1.87~\text {GeV}\) and \(m_{D^*}=2.01~\text {GeV}\) as inputs.
Numerical results for \(\text {Im}[c^{(a,b,c)}_{J}]\) vs. \(\sqrt{s}\), \(\text {Re}[{\overline{c}}^{(a,b,c)}_{J}]\) vs. \(\sqrt{s}\) and \(-2\text {Im}[c^{(a,b,c)}_{J}]/\text {Re}[{\overline{c}}^{(a,b,c)}_{J}]\) vs. \(\sqrt{s}\). The sub figures (a, b, c) are corresponding to \(\text {Im}[c^{(a,b,c)}_{J}]\) and \(\text {Re}[{\overline{c}}^{(a,b,c)}_{J}]\) vs. \(\sqrt{s}\), respectively. The sub figure (d) shows the results for \(-2\text {Im}[c^{(X)}_{J}]/\text {Re}[{\overline{c}}^{(X)}_{J}]\) vs. \(\sqrt{s}\)
The numerical results presented in Fig. 2 show four interesting properties:
-
(1)
The real parts \(\text {Re}[{\overline{c}}^{(a,c)}_{0}]\) and \(\text {Re}[{\overline{c}}^{(b)}_{1}]\) which are represented by the solid black curves are always negative. This means that after considering the annihilation effects, the masses of the \(^3P_{0,1}\) states move up and the masses of \(^3P_2\) states do not move.
-
(2)
When \(\sqrt{s}\) is on the threshold of \(DD,DD^*\) or \(D^*D^*\) the corresponding mass shifts are exact zero.
-
(3)
When \(\sqrt{s}\) is above the threshold, the mass shifts are much smaller than the corresponding decay widths, the largest mass shift is about 1/5 of the corresponding decay width when \(\sqrt{s}\approx 4.5\) GeV which is much larger than the threshold. This property gives a strong constrain on the mass shifts to all the \(^3P_{0,1}\) states.
-
(4)
When \(\sqrt{s}\) is below the mass-shell, although the decay widths are exact zero, but the mass-shifts are still nonzero and the dependence of \(\text {Re}[{\overline{c}}^{(a,b,c)}_{J}]\) vs. \(\sqrt{s}\) shows non-trivial property.
To show the non-trivial dependence of \(\text {Re}[{\overline{c}}^{(a,b,c)}_{J}]\) vs. \(\sqrt{s}\) more clearly, we present the dependence of \(\text {Re}[{\overline{c}}^{(a,b,c)}_{J}(s)]/\text {Re}[{\overline{c}}^{(a,b,c)}_{J}(s_0)]|\) vs. \(\sqrt{s}\) with \(s_0=3\) GeV in Fig. 3. The curves in Fig. 3 clearly show that when \(\sqrt{s}\) increases from 3 to 4.5 GeV the ratios of the mass shifts decrease from 1 to 0 at first and then increase from 0 to 0.5. For the states with the same quantum number, it means that the corresponding mass shifts are non-linear and can not be absorbed by some constants.
Experimentally, up to now there are still no definite results for the branch decay widths \(\Gamma (^3P_{0,1}\rightarrow DD,DD^*, D^*D^*)\) [57,58,59,60,61,62], this makes it difficult to determine the mass shifts certainly. The experiments reported that the decay widths \(\Gamma (X(3915),\chi _{c2}(3930)\rightarrow DD,DD^*, D^*D^*)\) are seen. By our calculation, we expect that the decay widths \(\Gamma (^3P_{2}\rightarrow DD,DD^*, D^*D^*)\) are zero in the leading order which suggests that the decay widths \(\Gamma (^3P_{2}\rightarrow DD,DD^*, D^*D^*)\) should be much smaller than \(\Gamma (^3P_{0}\rightarrow DD, D^*D^*)\) and \(\Gamma (^3P_{1}\rightarrow DD^*)\). A relative larger decay width of a resonance to \(DD,DD^*, D^*D^*\) suggests that it maybe is not a pure \(c{\bar{c}}(^3P_J)\) state. These properties are more reliable in the b quark part and can be tested by the further precise experiments. Furthermore, the similar discussion can be extended to the S wave states and compared with the similar studies in Ref. [63, 64].
In summary, the nonrelativistic asymptotic behaviors of the transitions \(c{\bar{c}}(^3P_J) \rightarrow DD,DD^*,D^*D^* \rightarrow c{\bar{c}}(^3P_J)\) with \(J=0, 1, 2\) are discussed. We find that the decay widths \(\Gamma (^3P_{0}\rightarrow DD^*),\Gamma (^3P_{1}\rightarrow DD,D^*D^*)\) and \(\Gamma (^3P_{2}\rightarrow DD,DD^*,D^*D^*)\) are exact zero in the leading order of nonrelativistic expansion. For other channels, the ratios between the branch decay widths and the mass shifts are larger than 5 when the center-of-mass energy is above the threshold. When below the threshold, the mass shifts are dependent on the center-of-mass energy nontrivially and can not be absorbed by a constant.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The results obtained and presented in the manuscript did not require any data.]
References
D.P. Stanley, D. Robson, Phys. Rev. D 21, 3180 (1980)
S. Ono, F. Schoberl, Phys. Lett. B 118, 419 (1982)
S. Godfrey, N. Isgur, Phys. Rev. D 32, 189 (1985)
M.A. Shifman, A.I. Vainshtein, V.I. Zakharov, Nucl. Phys. B 147, 385 (1979)
M.A. Shifman, A.I. Vainshtein, V.I. Zakharov, Nucl. Phys. B 147, 448 (1979)
Edward V. Shuryak, Phys. Rep. 115, 151 (1984)
L.J. Reinders, H. Rubinstein, S. Yazaki, Phys. Rep. 127, 1 (1985)
M. Nielsen, F.S. Navarra, S.H. Lee, Phys. Rep. 497, 41 (2010)
P. Jain, H.J. Munczek, Phys. Rev. D 44, 1873 (1991)
H.J. Munczek, P. Jain, Phys. Rev. D 46, 438 (1992)
P. Jain, H.J. Munczek, Phys. Rev. D 48, 5403 (1993)
Chao-Shang Huang Yuan-BenDai, Hong-Ying Jin, Z. Phys. C 60, 527 (1993)
K. Kusaka, A.G. Williams, Phys. Rev. D 51, 7026 (1995)
K.I. Aoki, T. Kugo, M.G. Mitchard, Phys. Lett. B 266, 467 (1991)
C.R. Munz, J. Resag, B.C. Metsch, H.R. Petry, Nucl. Phys. A 578, 418 (1994)
P. Maris, C.D. Roberts, Phys. Rev. C 56, 3369 (1997)
P. Maris, P.C. Tandy, Phys. Rev. C 60, 055214 (1999)
R. Alkofer, P. Watson, H. Weigel, Phys. Rev. D 65, 094026 (2002)
A. Krassnigg, Phys. Rev. D 80, 114010 (2009)
T. Hilger, M. Gmez-Rocha, A. Krassnigg, Phys. Rev. D 91, 114004 (2015)
C.S. Fischer, S. Stanislav, R. Williams, Eur. Phys. J. A 51, 10 (2015)
C. Popovici, T. Hilger, M. Gomez-Rocha, A. Krassnigg, Few Body Syst. 56, 481 (2015)
S.K. Choi et al. (Belle Collaboration), Phys. Rev. Lett. 91, 262001 (2003)
K. Abe et al. (Belle Collaboration), Phys. Rev. Lett. 94, 18200 (2005)
S.K. Choi et al. (Belle Collaboration), Phys. Rev. Lett. 100, 142001 (2008)
R. Mizuk et al. (Belle Collaboration), Phys. Rev. D 78, 072004 (2008)
K. Chilikin et al. (Belle Collaboration), Phys. Rev. D 90, 112009 (2014)
V. Bhardwaj et al. (Belle Collaboration), Phys. Rev. Lett. 111, 032001 (2013)
X.L. Wang et al. (Belle Collaboration), Phys. Rev. Lett. 99, 142002 (2007)
D. Acosta et al. (CDF Collaboration), Phys. Rev. Lett. 93, 072001 (2004)
T. Aaltonen et al. (CDF Collaboration), Phys. Rev. Lett. 102, 242002 (2009)
V.M. Abazov et al. (D0 Collaboration), Phys. Rev. Lett. 93, 162002 (2004)
B. Aubert et al. (BaBar Collaboration), Phys. Rev. Lett. 95, 142001 (2005)
B. Aubert et al. (BaBar Collaboration), Phys. Rev. Lett. 98, 212001 (2007)
Q. He et al. (CLEO Collaboration), Phys. Rev. D 74, 091104 (2006)
R. Aaij et al. (LHCb Collaboration), Phys. Rev. Lett. 110, 222001 (2013)
M. Ablikim et al. (BESIII Collaboration), Phys. Rev. Lett. 110, 252001 (2013)
S. Chatrchyan et al. (CMS Collaboration), JHEP 04, 154 (2013)
S. Chatrchyan et al. (CMS Collaboration), Phys. Lett. B 734, 261 (2014)
H.-Y. Cao, H.-Q. Zhou, Phys. Rev. D 99, 074007 (2019)
H.-Y. Cao, H.-Q. Zhou, Phys. Rev. D 100, 094004 (2019)
G.T. Bodwin, E. Braaten, G.P. Lepage, Phys. Rev. D 51, 1125 (1995) [Erratum: Phys. Rev. D 55, 5853 (1997)]
J.H. Kuhn, J. Kaplan, E.G.O. Safiani, Nucl. Phys. B 157, 125 (1979)
G.T. Bodwin, A. Petrelli, Phys. Rev. D 66, 094011 (2002)
G.T. Bodwin, A. Petrelli, Phys. Rev. D 87, 039902(E) (2013)
N. Brambilla, E. Mereghetti, A. Vairo, J. High Energy Phys. 08, 039 (2006)
N. Brambilla, E. Mereghetti, A. Vairo, J. High Energy Phys. 04, 058 (2011)
V. Shtabovenko, R. Mertig, F. Orellana, Comput. Phys. Commun. 207, 432 (2016)
R. Mertig, M. Bohm, A. Denner, Comput. Phys. Commun. 64, 345 (1991)
A.V. Smirnov, Comput. Phys. Commun. 204, 189 (2016)
A.V. Smirnov, Comput. Phys. Commun. 185, 2090 (2014)
H.H. Patel, Comput. Phys. Commun. 197, 276–290 (2015)
H.H. Patel, Comput. Phys. Commun. 218, 66–70 (2017)
J.H. Kuhn, J. Kaplan, E.G.O. Safiani, Nucl. Phys. B 157, 125 (1979)
T. Barnes, E.S. Swanson, Phys. Rev. C 77, 055206 (2008)
Z.-Y. Zhou, Z. Xiao, Phys. Rev. D 96, 099905 (2017)
K. Chilikin et al. (Belle Collaboration), Phys. Rev. D 95, 112003 (2017)
T. Aushev et al. (Belle Collaboration), Phys. Rev. D 81, 031103 (2010)
B. Aubert et al. (BaBar Collaboration), Phys. Rev. D 77, 011102 (2008)
T. Aushev et al. (Belle Collaboration), Phys. Rev. D 81, 031103 (2010)
B. Aubert et al. (BaBar Collaboration), Phys. Rev. D 81, 092003 (2010)
S. Uehara et al. (Belle Collaboration), Phys. Rev. Lett. 96, 082003 (2006)
Q.X. Yu, W.H. Liang, M. Bayar, E. Oset, Phys. Rev. D 99(7), 076002 (2019)
M. Bayar, N. Ikeno, E. Oset, Eur. Phys. J. C 80(3), 222 (2020)
Acknowledgements
The author Hai-Qing Zhou would like to thank Zhi-Yong Zhou and Dian-Yong Chen for their helpful discussion. This work was supported by the National Natural Science Foundation of China (Grand nos. 12075058 and 11975075). Hui-Yun Cao was supported by the Scientific Research Foundation of Graduate School of Southeast University (Grants no. YBPY1970).
Author information
Authors and Affiliations
Corresponding author
Appendix: The FIESTA integrations
Appendix: The FIESTA integrations
We define the following functions to refer to the results after summing the spins and integrating the angles:
where X are some functions dependent on \({{\hat{q}}}_{i}, {{\hat{q}}}_{f}, \epsilon _p(s_i)\), and \(\epsilon _p^*(s_f)\) with \({{\hat{q}}}_{i,f} \overset{def}{=} q_{i,f}/|\mathbf{q} _{i,f}|\), P(J, X, n) are not dependent on \(J_z\). When \(J=0,1,2\) and \( n=0,1\), we have
and others are zero.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Cao, HY., Zhou, HQ. Decay widths of \(^3 P_J\) charmonium to \(DD,DD^*,D^*D^*\) and corresponding mass shifts of \(^3 P_J\) charmonium. Eur. Phys. J. C 80, 975 (2020). https://doi.org/10.1140/epjc/s10052-020-08552-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-08552-0