1 Introduction

The radiating solution of Vaidya [1] has been paramount in the study of spherically symmetric spacetime exteriors in general relativity. Several well known solutions for radiating stars (by matching an interior solution to the radiating exterior) have been found [2,3,4,5,6,7]. The important result was that the pressure on the boundary of the radiating star, in general, should be nonvanishing and proportional to the heat flux. This provided a major avenue through which astrophysical applications could be studied in the context of general relativity. The generalised Vaidya spacetime was studied by Wang and Wu [8] and extensions of that work were given in [9] for various equations of state. These works include all the well known solutions of Einstein’s equations with the addition of the type II fluid. The generalised Vaidya solution has also proved pivotal in the study of spherically symmetric, dynamical gravitational collapse. Dawood and Ghosh [10] obtained a large family of solutions to the field equations for a type II fluid in general relativity, showing that some well known black hole solutions were a particular case of this family. The radiating Vaidya solution was also used to test the cosmic censorship conjecture (CCC) and the Papapetrou model [11, 12] is one of the earliest examples that counters the CCC. A physically reasonable field of matter was found, obeying the energy conditions, in a shell-focusing central singularity which was formed by shells of radiation imploding. Mkenyeleye et al. [13, 14] developed a general mathematical framework, in context of the CCC, to study the conditions on the mass function where the end state of future-directed nonspacelike geodesics is indeed the central singularity. This framework was utilised by Brassel et al. [15] with mass functions arising from various equations of state. It was found that collapse terminated with the formation of a naked singularity in all cases.

Such work has been extended to higher dimensions and modified theories of gravity. The need to modify general relativity arises from the fact that it is a global theory of gravity and thus has certain shortcomings. One of those is fundamental to cosmology; Einstein gravity cannot explain the late time expansion of the universe. The introduction of nonlinear forms of the Riemann and Ricci tensor, and the Ricci scalar is one such approach to modifying general relativity. It is indeed possible to propose a quadratic polynomial form of the Lagrangian which will still yield second order equations of motion [16, 17]. This form then generates the Einstein–Gauss–Bonnet (EGB) action, a modification of the usual Einstein–Hilbert action. Therefore, curvature terms which are quadratic in the spacetime will present as corrections to general relativity. Unless some surface term is involved or instigated, these higher order curvature terms will have no ramifications in four-dimensional gravity. A further point that should be highlighted is that EGB gravity can be considered a concomitant of low energy heterotic string theory [18, 19]. The higher dimensional EGB analogue of the vacuum Schwarzschild solution from general relativity was found by Boulware and Deser [20] and a radiating form of the mass function of that solution was studied by Kobayashi [21]. In the case of the latter solution, the energy momentum tensor was assumed, as in the case of general relativity, to be a superposition of a type I and type II fluid. Various solutions for the Boulware–Deser mass function were found by Brassel et al. [22] for various equations of state. These were the EGB analogues of those found in [8, 9]. New solutions to the EGB field equations for a static spherically symmetric interior of a fluid were found in [23,24,25], and the generalised Israel junction conditions on a membrane were derived in detail by Davis [26]. These results for type I or type II (or combinations of the two) fluids have proven fruitful in stellar modeling, both in general relativity and EGB gravity. A recent paper by Nikolaev and Maharaj [27] showed that the generalised Vaidya spacetime may be embedded in higher dimensional Euclidean spaces. This opens avenues for further astrophysical research in modified gravity theories.

An interesting question now arises with regards to the existence of different types of matter distributions including dust, radiation, a cosmological constant, negative pressures or any combination of these. Such an energy momentum tensor could provide significant insights into gravity under various different physical scenarios. An example of a matter field was introduced by Kiselev [28] and a static solution to the Einstein field equations was found, which was a generalisation of the Schwarzschild solution in an expanding background which was nonempty. The motivation for this generalisation was the fact that realistic black holes are not necessarily isolated nor embedded into vacuum backgrounds. The Kiselev solution, which is an example of a black hole solution coupled to one or more matter fields, is physically interesting due to its application to the study of distorted black holes [29,30,31]. With regards to matter fields in EGB gravity, Canfora et al. [32] considered a manifold which was a warped product of a four-dimensional expanding Friedmann–Robertson–Walker spacetime with a D-dimensional Euclidean constant curvature space with two independent scale factors. More recently, Pavluchenko [33] studied spatially flat expanding models in EGB gravity in five and six dimensions. Both dimensional cases produced different dynamical properties of the spacetime. Heydarzade and Darabi [34] extended the work of Kiselev [28] by considering a generalised Vaidya metric with the various matter fields. They studied the possibility of naked singularity formation in these differing surrounding fields. The work in this paper will be an extension of some of the work done in [34] extended to the regime of EGB gravity, as this has not been attempted before. We will assume a generalised Boulware–Deser spacetime with a generalised matter background. We should point out an interesting interpretation provided by Krasinski [35] in which the radiating Vaidya density is superposed with perfect fluids, anisotropic fluids and rotating fluids. This produces generalised inhomogeneous matter distributions in the manifold sourced by radiating matter. Such generalised radiating fields have been shown to reduce to expanding Friedmann–Robertson–Walker spacetimes at large distances. An example of a generalised, inhomogeneous matter source with a homogeneous limiting metric is given by Vaidya [36].

This paper is organised as follows: in the first section, we outline second order Lovelock gravity theory, EGB gravity. In Sect. 3, we assume the generalised form of the Boulware–Deser spacetime and allow the matter distribution to be a generalised field comprising of various different component distributions. The EGB field equations are then derived and solved for the mass function, which is expressed in terms of the equation of state parameter which takes into account the various distributions. This allows us to write expressions for the energy density and pressure of the spacetime. Section 4 entails the analysis of this mass function as well as the matter variables. Plots are generated for the mass of the matter distribution and its radial derivative, as well as for the energy density and pressure. We highlight the differences in the evolution of these quantities depending on the matter background. In Sect. 5 we study the effects of diffusion on the model and present two classes of solutions to the resulting diffusion equation, the more general class being expressed in terms of an exponential integral. The final section deals with the gravitational collapse of the Boulware–Deser spacetime and its effect on the solution found.

2 Einstein–Gauss–Bonnet gravity

The action in Lovelock gravity is given by

$$\begin{aligned} S=\int d^{N}x\sqrt{-g}\sum _{k=0}^{N/2}\alpha _{k}{\mathscr {R}}^k+S_{matter}, \end{aligned}$$
(1)

where we have

$$\begin{aligned} {\mathscr {R}}^k=\frac{1}{2^k}\delta _{a_{1}b_{1}...a_{k}b_{k}}^{c_{1}d_{1}...c_{k}d_{k}}\prod _{r=1}^{k}R^{a_{r}b_{r}}{}_{{}c_{r}d_{r}}, \end{aligned}$$

and \(\delta _{a_{1}b_{1}...a_{k}b_{k}}^{c_{1}d_{1}...c_{k}d_{k}}\) is the Kronecker delta. In this paper, we have considered Einstein–Gauss–Bonnet gravity, which is second order Lovelock gravity, so the above action reduces to

$$\begin{aligned} S=\int d^{N}x\sqrt{-g}(\alpha _{0}+\alpha _{1}{\mathscr {R}}+\alpha _{2}{\mathscr {R}}^2), \end{aligned}$$
(2)

where \(\alpha _{0}\) is the cosmological term, \(\alpha _{1}\) is the constant (set to unity) associated with the Einstein–Hilbert action \(({\mathscr {R}}=R)\) and \(\alpha _{2}=\alpha \) is the coupling constant associated with the second order (Gauss–Bonnet) action. Thus the modified form of the Einstein–Hilbert action (2) in five dimensions is

$$\begin{aligned} S=-\frac{1}{16\pi }\int \sqrt{-g}\left[ (R-2\varLambda +\alpha L_{GB})\right] d^5x. \end{aligned}$$
(3)

In the above, R is the five-dimensional Ricci scalar and \(\varLambda \) is the cosmological constant, which we have set to zero in this study. \({\mathscr {R}}^2=L_{GB}\) is the Lovelock term, given by

$$\begin{aligned} L_{GB}=R^2+R_{abcd}R^{abcd}-4R_{cd}R^{cd}, \end{aligned}$$
(4)

which is a linear combination of the quadratic terms in curvature. Upon varying (3) with respect to the action \(\delta S=0,\) we obtain the EGB field equations

$$\begin{aligned} {\mathscr {G}}_{ab}= T_{ab}, \end{aligned}$$
(5)

where

$$\begin{aligned} {\mathscr {G}}_{ab}=G_{ab}-\frac{\alpha }{2}H_{ab}. \end{aligned}$$
(6)

In the above, \(G_{ab}\) is the Einstein tensor, \(T_{ab}\) is the energy momentum tensor and \(H_{ab}\) is the Lovelock tensor which is defined as the following

$$\begin{aligned} H_{ab}= & {} g_{ab}L_{GB}-4RR_{ab}+8R_{ac}R^c{}_{{}b}\nonumber \\&+8R_{acbd}R^{cd}-4R_{acde}R_{b}{}^{{}cde}. \end{aligned}$$
(7)

The Lovelock tensor vanishes in the limit when \(\alpha \rightarrow 0\), and, as a result, Einstein gravity will be regained.

3 A generalised radiating solution

In this section we will demonstrate a viable radiating solution to the EGB field equations in the spacetime manifold which is our starting point. The static and spherically symmetric exterior vacuum solution to the Gauss–Bonnet action (2) was first obtained by Boulware and Deser [20]. A radiating analogue was first presented by Kobayashi [21] which acts as a Vaidya-like solution in EGB gravity. The radiating Boulware–Deser metric is given in the following form

$$\begin{aligned} ds^2= & {} -f(v,\textsf {r})dv^2+2dvd\textsf {r}\nonumber \\&+\, \textsf {r}^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2), \end{aligned}$$
(8)

where the function \(f(v,\textsf {r})\) is given by

$$\begin{aligned} f(v,\textsf {r})=1+\frac{\textsf {r}^2}{4\alpha }\left( 1-\sqrt{1+\frac{16M(v,\textsf {r})\alpha }{\textsf {r}^4}}\right) , \end{aligned}$$
(9)

where \(M(v,\textsf {r})\) represents the mass of the spherical radiating distribution. We are modeling a distribution which is not isolated and the matter field is not empty which was first studied by [28]. Following [34] we can consider a total energy momentum tensor of the form

$$\begin{aligned} T^a{}_{{}b}=\tau ^a{}_{{}b}+{\mathscr {T}}^a{}_{{}b}, \end{aligned}$$
(10)

where \(\tau ^a{}_{{}b}\) is the energy momentum tensor associated with null radiation

$$\begin{aligned} \tau ^a{}_{{}b}=\mu l^{a}l_{b}, \end{aligned}$$
(11)

with \(l_{a}=\delta _{a}^0\). In the above, \(\mu \) is the energy density of the outgoing radiation/ingoing accretion flow. The quantity \({\mathscr {T}}^a{}_{{}b}\) is the energy momentum tensor of the additional matter field defined by

$$\begin{aligned} {\mathscr {T}}^0{}_{{}0}= & {} -\rho _{s}(v,\textsf {r}), \end{aligned}$$
(12a)
$$\begin{aligned} {\mathscr {T}}^a{}_{{}b}= & {} -\rho _{s}(v,\textsf {r})\gamma \left[ -(1+3\beta )\left( \frac{\textsf {r}_{a}\textsf {r}^b}{\textsf {r}_{n}\textsf {r}^n}\right) +\beta \delta ^a{}_{{}b}\right] , \end{aligned}$$
(12b)

as was shown in [28]. The above equations (12) represent a generalised matter distribution where the subscript ‘s’ can represent a component matter field of the solution or any combination of these fields. The two arbitrary constant parameters \(\gamma \) and \(\beta \) depend on the internal structure of the additional matter field. This form of the energy momentum tensor for the generalised radiating field implies that the spatial profile of the Boulware–Deser solution is proportional to the time component describing the dynamical energy density \(\rho _{s}(v,\textsf {r})\) [34].

The field equations for the matter field (10) can be written as

$$\begin{aligned} {\mathscr {G}}^0{}_{{}0}= & {} T^0{}_{{}0} \quad \text {or} \quad {\mathscr {G}}^1{}_{{}1}=T^1{}_{{}1}, \end{aligned}$$
(13a)
$$\begin{aligned} {\mathscr {G}}^1{}_{{}0}= & {} T^1{}_{{}0}, \end{aligned}$$
(13b)
$$\begin{aligned} \mathscr {G}^2{}_{{}2}= & {} T^2{}_{{}2}\quad \text {or} \quad \mathscr {G}^3{}_{{}3}=T^3{}_{{}3}\quad \text {or} \quad \mathscr {G}^4{}_{{}4}=T^4{}_{{}4}, \end{aligned}$$
(13c)

for the spherically symmetric line element (8). In the above, the components of \(T^a{}_{{}b}\) contribute to the gravitational dynamics. In conventional matter distributions, the \({\mathscr {T}}^a{}_{{}b}\) are generally absent, for example see [9, 13, 23]. From [28], the isotropic averaging over the angles gives the following

$$\begin{aligned} \langle {\mathscr {T}}^a{}_{{}b}\rangle =\frac{\gamma }{3}\rho _{s}(v,\textsf {r})\delta ^a{}_{{}b}=p_{s}(v,\textsf {r})\delta ^a{}_{{}b}, \end{aligned}$$
(14)

where \(\langle \textsf {r}^a\textsf {r}_{b}\rangle =\frac{1}{3}\delta ^a{}_{{}b}\textsf {r}_{n}\textsf {r}^n\) was considered. We then have the barotropic equation of state for the additional field being given by

$$\begin{aligned} p_{s}(v,\textsf {r})=\omega _{s}\rho _{s}(v,\textsf {r}), \quad \omega _{s}=\frac{1}{3}\gamma , \end{aligned}$$
(15)

where \(p_{s}(v,\textsf {r})\) and \(\omega _{s}\) are the dynamical pressure and the constant equation of state parameter of the field, respectively. The Eqs. (10)–(12) and the EGB field equations (13) imply that \(\mathscr {T}^0{}_{{}0}= \mathscr {T}^1{}_{{}1}\) and \(\mathscr {T}^2{}_{{}2}= \mathscr {T}^3{}_{{}3} =\mathscr {T}^4{}_{{}4}\). This allows one to calculate the free parameter \(\beta \) as

$$\begin{aligned} \beta =-\frac{1+3\omega _{s}}{6\omega _{s}}, \end{aligned}$$
(16)

due to the principle of additivity [28, 34]. Substituting the parameters \(\gamma \) and \(\beta \) in (15) and (16) into (12), the nonvanising components of the energy momentum tensor for the additional field will be

$$\begin{aligned} {\mathscr {T}}^0{}_{{}0}= & {} {\mathscr {T}}^1{}_{{}1}=-\,\rho _{s}(v,\textsf {r}), \end{aligned}$$
(17a)
$$\begin{aligned} \mathscr {T}^2{}_{{}2}= & {} \mathscr {T}^3{}_{{}3} =\mathscr {T}^4{}_{{}4}=\frac{1}{2}(1+3\omega _{s})\rho _{s}(v,\textsf {r}). \end{aligned}$$
(17b)

The nonvanishing components of (6) are given by

$$\begin{aligned} {\mathscr {G}}^0{}_{{}0}= & {} {\mathscr {G}}^1{}_{{}1}=-\frac{3}{\textsf {r}^3}M_{\textsf {r}}, \end{aligned}$$
(18a)
$$\begin{aligned} {\mathscr {G}}^1{}_{{}0}= & {} \frac{3}{\textsf {r}^3}M_{v}, \end{aligned}$$
(18b)
$$\begin{aligned} \mathscr {G}^2{}_{{}2}= & {} \mathscr {G}^3{}_{{}3}=\mathscr {G}^4{}_{{}4} = -\frac{1}{\textsf {r}^2}M_{\textsf {rr}}, \end{aligned}$$
(18c)

after a lengthy calculation; see the Appendix for details. We can therefore finally write the EGB field equations. The \({\mathscr {G}}^0{}_{{}0}=T^0{}_{{}0}\) and \({\mathscr {G}}^1{}_{{}1}=T^1{}_{{}1}\) components give the following

$$\begin{aligned} \rho _{s}=\frac{3}{\textsf {r}^3}M_{\textsf {r}}. \end{aligned}$$
(19)

The \({\mathscr {G}}^1{}_{{}0}=T^1{}_{{}0}\) component gives

$$\begin{aligned} \frac{3}{\textsf {r}^3}M_{v}=\mu . \end{aligned}$$
(20)

Similarly, for the components \(\mathscr {G}^2{}_{{}2}=T^2{}_{{}2}\) and \(\mathscr {G}^3{}_{{}3}=T^3{}_{{}3}\) and \(\mathscr {G}^4{}_{{}4}=T^4{}_{{}4}\), we have

$$\begin{aligned} -\frac{1}{\textsf {r}^2}M_{\textsf {rr}}=\frac{1}{2}(1+3\omega _{s})\rho _{s}. \end{aligned}$$
(21)

Equations (18)–(21) give the EGB equations for the surrounding medium with the barotropic equation of state (15).

Fig. 1
figure 1

Plot indicating the temporal evolution of the mass function with respect to each of the matter field parameters

Full size image
Fig. 2
figure 2

Plot indicating the radial evolution of the mass function with respect to each of the matter field parameters

Full size image

Simultaneously solving the differential equations (19) and (21) will yield the solution for the mass function for the matter field as

$$\begin{aligned} M(v,\textsf {r})=\frac{-N_{s}(v)\textsf {r}^{1-\frac{3}{2}(1+3\omega _{s})}}{2-3(1+3\omega _{s})}+ c_{2}(v), \end{aligned}$$
(22)

where \(c_{2}(v)\) is the second integration function. We have annotated the first integration function as \(c_{1}(v)=-\,N_{s}(v)\) which could be considered a parameter for the additional dynamical field structure. Therefore by (15) and (19) we have

$$\begin{aligned} \rho _{s}= & {} -\frac{3}{2}N_{s}(v)\textsf {r}^{\frac{1}{2}(7+9\omega _{s})}, \end{aligned}$$
(23a)
$$\begin{aligned} p_{s}= & {} -\frac{3}{2}\omega _{s}N_{s}(v)\textsf {r}^{\frac{1}{2}(7+9\omega _{s})}. \end{aligned}$$
(23b)

The weak energy condition \(\rho _{s}\ge 0\) implies that we must have \(\omega _{s}N_{s}(v)\le 0\). This further implies the following regarding the surrounding field and the equation of state parameter:

  • If \(\omega _{s}>0\), then \(N_{s}(v)\le 0\).

  • If \(\omega _{s}<0\), then \(N_{s}(v)\ge 0\).

The equation of state parameter values \(\omega _{s}\) are as follows:

  • \(\omega _{s}=0\): dust

  • \(\omega _{s}=\frac{1}{3}\): radiation

  • \(\omega _{s}=-\,1\): cosmological-like

  • \(\omega _{s}=-\frac{2}{3}\): negative pressure

  • \(\omega _{s}=-\frac{4}{3}\): negative pressure

Therefore we regain the familiar equations of state for dust, radiation and the cosmological-like constant. Two other equations of state arise with negative pressures. The values \(\omega _{s}=-\frac{2}{3}\) and \(\omega _{s}=-\frac{4}{3}\) fall into the range allowed for quintessence and phantom fields respectively. However in our case we have obtained specific values using only curvature terms in EGB gravity whereas quintessence and phantom fields are generally evolving and require additional scalar fields.

Fig. 3
figure 3

Plot indicating the evolution of the radial derivative of the mass function with respect to \(\textsf {r}\), for each of the matter field parameters

Full size image

4 Physical analysis

In this section we will consider the analysis of the evolution of mass function surrounded by the various different matter fields mentioned previously. The behaviour of the energy density and pressure of the different matter fields will also be studied. We have assumed \(N_{s}(v)=v^2\) (for \(\omega _{s}=-\frac{4}{3},-\frac{2}{3},-1,0\)) and \(N_{s}(v)=-v^2\) (for \(\omega _{s}=\frac{1}{3}\)) so the above conditions are obeyed. Figure  1 depicts the evolutionary behaviour of the mass function with respect to the retarded time variable v. We have also set \(c_{s}(v)=v\) and \(\textsf {r}=2\). It can clearly be seen that the behaviour differs depending on the equation of state parameter \(\omega _{s}\). In the single case of the surrounding field being that of dust (\(\omega _{s}=0\)), the mass function increases over time. In all other cases, the mass function decreases, the sharpest of which is for the case of the surrounding field having negative pressure (\(\omega _{s}=-\frac{2}{3}\)), indicated by the dashed line in the plot.

Figure  2 shows the radial evolution of the mass function with respect to the equation of state parameters. The values we have assumed are the same as for the first plot, except we now have set \(v=2\). We have that the mass function increases with increasing radius, within the confines of a surrounding field of radiation (\(\omega =\frac{1}{3}\)). Initially, the increase is profound for a lower radius, before settling into a much slower increase as the radial coordinate becomes larger. With regards to all the other cases, the mass function decreases with increasing radius. In the case of the dust parameter (\(\omega _{s}=0\)) the decrease begins sharply before slowing with increasing \(\textsf {r}\), however, like the radiation case the mass function remains positive. This indicates that matter fields of dust or radiation are physically more realistic cases. For the remaining three cases, we have that the mass function is initially positive for small \(\textsf {r}\), however decreases with increasing \(\textsf {r}\), eventually becoming negative. It is also interesting to note that in the case of \(\omega _{s}=-\frac{4}{3}\), the mass function decreases at a slower rate than for the \(\omega _{s}=-\frac{2}{3}\) and cosmological constant-like (\(\omega _{s}=-1\)) cases, initially. However, it soon causes the mass function to decrease significantly faster than those two cases.

In Fig.  3, the radial derivative of the mass function is plotted against \(\textsf {r}\). It can clearly be seen that in the case of radiation (\(\omega _{s}=\frac{1}{3}\)), the rate of change of the mass function is positive and slows down as the radius of the fluid distribution increases. Conversely, for \(\omega _{s}=-\frac{2}{3}\), this rate of change is also positive but increases with increasing \(\textsf {r}\). The negative pressure and cosmological constant-like fields (\(\omega _{s}=-\frac{4}{3},-1\), respectively) show that, initially, the rate of change is seemingly unchanging. However, as \(\textsf {r}\) increases, these rates decrease more rapidly, becoming negative. The case \(\omega _{s}=-\frac{4}{3}\) also has a faster rate of decrease. Finally in the case of the matter field being dust (\(\omega _{s}=0\)), the rate of change is negative and increases initially severely, before slowing with larger \(\textsf {r}\), but never becoming positive.

Figures  4 and  5 depict the behavioural evolution of the energy density and pressure of the fluid distribution, respectively with respect to each of the equation of state parameters. It can clearly be seen that only when \(\omega _{s}=\frac{1}{3}\), do we have any realistic behaviour for the energy density in Fig.  4; as \(\textsf {r}\) increases, we have a positive decreasing energy density. The remaining cases all indicate negative densities implying that the radiation case is the more physically realistic case.

Fig. 4
figure 4

Plot indicating the evolution of the energy density of the matter field with respect to \(\textsf {r}\), for each of the constant parameters

Full size image

With regards to the pressure of the fluid distribution, every case is positive. For the cases \(\omega _{s}=\frac{1}{3}\) and \(\omega =-\frac{2}{3}\) we have that the pressure decreases as the radial coordinate increases which is, again, physically reasonable astrophysical behaviour. For the cases of cosmological constant-like (\(\omega _{s}=-1\)) and \(\omega _{s}=-\frac{4}{3}\), we have that the pressure is increasing with increasing \(\textsf {r}\). In fact, for the former case, the pressure increases linearly. For the final case of the dust background, the pressure vanishes by definition.

Fig. 5
figure 5

Plot indicating the evolution of the pressure of the fluid distribution with respect to \(\textsf {r}\), for each of the matter field parameters

Full size image

In summary, it can be seen from Figs. 1, 2, 3, 4 and 5 that the radiation case (\(\omega _{s}=\frac{1}{3}\)) produces the most realistic behaviour indicative of a physical model. Considering the fact that this mass function (22) is a Vaidya-like solution in EGB gravity, this is not surprising.

5 Diffusion

In order to understand several physical systems on a deeper level, the idea of diffusion is one that is of significant importance. Glass and Krisch [37] have shown that generalised Vaidya radiating distributions permit diffusive processes in globular clusters containing dark matter and atmospheres around black holes. Consequently effects of diffusive processes, in spacetimes with Vaidya-like geometries, have been studied in general relativity, including the treatment of Brassel et al. [9]. They obtained various diffusive solutions for the Vaidya mass function for different physical equations of state. We will be utilising their approach in this section.

It is interesting to determine the nature of diffusive processes in EGB gravity for the generalised matter field (10). The effects of the higher order curvature terms, indicative of the EGB theory, and the new matter distributions should lead to new solutions.

5.1 Derivation of the diffusion equation

Assuming that string diffusion is similar to point particle like diffusion, we have

$$\begin{aligned} \frac{\partial }{\partial v}n={\mathscr {D}}\nabla ^2n, \end{aligned}$$
(24)

where \(\nabla ^2=\textsf {r}^{-2}\left( \frac{\partial }{\partial \textsf {r}}\right) \textsf {r}^2(\frac{\partial }{\partial \textsf {r}})\) and \({\mathscr {D}}\) is the positive coefficient of self-diffusion, which is assigned as a constant. In the theory of classical transport, the diffusion equation is derived using Fick’s law as a commencement point. It is given by

$$\begin{aligned} \mathbf {J}_{(n)}=-{\mathscr {D}}\mathbf {\nabla }n, \end{aligned}$$
(25)

where the quantity \(\mathbf {\nabla }\) is a purely spatial gradient. The 4-current \(J^{a}_{(n);a}=0\), where we have

$$\begin{aligned} J^{a}_{(n);a}= & {} (n,\mathbf {J}_{(n)})\nonumber \\= & {} n\frac{\partial }{\partial u} - {\mathscr {D}}\left( \frac{\partial n}{\partial \textsf {r}}\right) \left( \frac{\partial }{\partial \textsf {r}}\right) , \end{aligned}$$
(26)

then gives the diffusion equation (24). Expressing the EGB field equations (19) and (20) as \(M_{\textsf {r}}=\frac{1}{3}\textsf {r}\rho _{s}\) and \(M_{v}=\frac{1}{3}\textsf {r}\mu \), we can write the integrability condition for the mass function M as

$$\begin{aligned} \frac{\partial \rho _{s}}{\partial v}=\frac{1}{\textsf {r}^3}\frac{\partial }{\partial \textsf {r}}(\textsf {r}^3\mu ). \end{aligned}$$
(27)

Comparing \(\frac{\partial \rho _{s}}{\partial v}\) in the above result (27) with the heat equation (24) (where n is replaced by \(\rho _{s}\)), we have, after some algebraic manipulation

$$\begin{aligned} \frac{\partial M}{\partial v}= {\mathscr {D}}\textsf {r}^3\frac{\partial \rho _{s}}{\partial \textsf {r}}. \end{aligned}$$
(28)

Solving the above equation for the mass function \(M(v,\textsf {r})\) will yield solutions to the field equations of EGB gravity. Using Eq. (19) and substituting it into (28) gives us the following

$$\begin{aligned} \frac{\partial M}{\partial v}={\mathscr {D}}\left( \frac{\partial ^2M}{\partial \textsf {r}^2}-\frac{3}{\textsf {r}}\frac{\partial M}{\partial \textsf {r}}\right) , \end{aligned}$$
(29)

which is of the functional form \(F_{1}({\dot{M}},M',M'')=0\). This is a generalisation of the result found in [9] for general relativity, and this can be further amplified. We require a functional form \(F_{2}({\dot{M}},M')=0\) in order to solve (29) entirely, and this necessitates isolating \(\frac{\partial ^2M}{\partial \textsf {r}^2}\) in our master equation (21) and substituting that result into (29). This finally yields

$$\begin{aligned} \frac{\partial M}{\partial v}+\frac{3{\mathscr {D}}}{2\textsf {r}}(3+3\omega _{s})\frac{\partial M}{\partial \textsf {r}}=0. \end{aligned}$$
(30)

The Eq. (30) is the diffusion equation in EGB gravity for the matter distribution (10) and the resulting equation of state (15). Note that (30) is a linear partial differential equation.

5.2 Solutions and consistency

The Eq. (30) can be solved trivially using the method of characteristics. Its solution is given by

$$\begin{aligned} M(v,\textsf {r})={\mathscr {F}}\left( \frac{1}{2}\textsf {r}-\frac{3{\mathscr {D}}}{2}(3+3\omega _{s})v\right) , \end{aligned}$$
(31)

which is an infinite family of solutions for M. To acquire the consistency condition on \({\mathscr {F}}\), we have to substitute the above Eq. (31) into (21). Doing this gives

$$\begin{aligned} \textsf {r}^2{\mathscr {F}}_{\textsf {rr}}+\frac{3}{2}(1+3\omega _{s}){\mathscr {F}}_{\textsf {r}}=0. \end{aligned}$$
(32)

With regards to solving (32), two cases arise.

5.2.1 Case I

A closed form solution to the consistency condition is possible if \(\omega _{s}=-\frac{1}{3}\). This reduces (32) to \(\textsf {r}^2{\mathscr {F}}_{\textsf {rr}}\) which has the solution

$$\begin{aligned} {\mathscr {F}}\left( \frac{1}{2}\textsf {r}-\frac{3{\mathscr {D}}}{2}(3+3\omega _{s})v\right)= & {} l_{1}\left( \frac{1}{2}\textsf {r}-\frac{3{\mathscr {D}}}{2}(3+3\omega _{s})v\right) \nonumber \\&+l_{2}, \end{aligned}$$
(33)

where \(l_{1}=l_{1}(v)\) and \(l_{2}=l_{2}(v)\) are functions of integration. It is important to note that the assumption placed on \(\omega _{s}\) above has no real significance since \(\omega _{s}=-\frac{1}{3}\), which doesn’t represent a realistic matter field.

5.2.2 Case II

In general, the differential equation (32) can be solved via a reduction of order, and has a solution in terms of an exponential integral, which is a special function in the complex plane. This solution is given in quadrature form by

$$\begin{aligned} {\mathscr {F}}=h_{1}\int e^{\frac{3+9\omega _{s}}{2\textsf {r}}}dr+h_{2}, \end{aligned}$$
(34)

where \(h_{1}=h_{1}(v)\) and \(h_{2}=h_{2}(v)\) are integration functions. The integral in the above solution is a special case of the general exponential integral. In full, the solution is given by

$$\begin{aligned} {\mathscr {F}}\left( \frac{1}{2}\textsf {r}-\frac{3{\mathscr {D}}}{2}(3+3\omega _{s})v\right) =h_{1}\left[ \textsf {r}e^{\frac{3+9\omega _{s}}{2\textsf {r}}}\right. \nonumber \\ \left. -\left( \frac{3+9\omega _{s}}{2}\right) \text {Ei}\left( \frac{3+9\omega _{s}}{2\textsf {r}}\right) \right] +h_{2}, \end{aligned}$$
(35)

where the notation Ei(...) represents an exponential integral. The solution (33) is contained in the above (35). Therefore, for the relevant values of the equation of state parameter \(\omega _{s}\), the expression (35) is a general family of new diffusive solutions to the EGB field equations for the mass function \(M(v,\textsf {r})\). Therefore, the diffusive processes for the generalised matter distribution (10) are different from general relativity.

Fig. 6
figure 6

Spacetime diagram depicting radiation shell collapse in five-dimensional EGB gravity

Full size image

6 Gravitational collapse

In general relativity, after the first analysis of vacuum collapse undertaken by Oppenheimer and Snyder [38], the generalised Vaidya metric has been used extensively to study gravitational collapse models as in [10, 39, 40]. Various models studied indicate that the collapse of the Vaidya spacetime can lead to the formation of locally naked singularities, see [11,12,13,14,15, 41, 42]. In modified theories of gravity, Dominguez and Gallo [43] later studied black hole solutions in Einstein–Gauss–Bonnet gravity. In the same theory, the gravitational contraction of the Boulware–Deser spacetime was studied in detail by [44,45,46]. It was shown that in five dimensions, the collapse of the Boulware–Deser spacetime terminated in the formation of an extended and weak curvature, initially naked conical singularity at the centre, which then subsequently becomes covered by an apparent horizon. This result was significantly different to the five-dimensional Vaidya collapse in general relativity. In dimensions higher than five, the collapse process was analogous to that of general relativistic collapse, as in the end point was a black hole with a strong curvature singularity. We consider the metric (8) from earlier

$$\begin{aligned} ds^2= & {} -f(v,\textsf {r})dv^2+2dvd\textsf {r}\nonumber \\&+\, \textsf {r}^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2), \end{aligned}$$
(36)

with

$$\begin{aligned} f(v,\textsf {r})=1+\frac{\textsf {r}^2}{4\alpha }\left( 1-\sqrt{1+\frac{16M(v,\textsf {r})\alpha }{\textsf {r}^4}}\right) . \end{aligned}$$
(37)

In the above, all of the metric functions are regular and well defined in the vicinity of \(\textsf {r}=0\), \(v\ge 0\), insinuating the absence of a strong curvature singularity. The Kretschmann invariant is calculated as

$$\begin{aligned} K= & {} -\frac{1}{2\alpha \textsf {r}^4}(\textsf {r}^2+16\alpha M)^{-3}\left[ \left( -\textsf {r}^2+\sqrt{\textsf {r}^4+16\alpha M}\right) ^2\right. \nonumber \\&\,\times \left( -7\textsf {r}^{12}-2\textsf {r}^{10}\sqrt{\textsf {r}^4+16\alpha M}-184\alpha \textsf {r}^8M\right. \nonumber \\&\,-2048\alpha ^2\textsf {r}^4M^2-6144\alpha ^3M^3\nonumber \\&\,+\left. \left. 32\alpha \textsf {r}^6M\sqrt{\textsf {r}^4+16\alpha M}\right) \right] , \end{aligned}$$
(38)

which diverges as \(K\approx \textsf {r}^{-4}\). This divergence proves that while the metric (37) is regular, the spacetime itself is singular. Therefore one could consider the spacetime metric as a whole as being quasi-regular. The spacetime singularity, in its very nature, is one that is conical and weak. This result is fundamentally different to radiating collapse in general relativity, where a sufficiently strong curvature singularity forms upon the cessation of collapse. There exists an open set of mass functions \(M(v,\textsf {r})\), including (22) and the diffusive mass function (33) for which the continual gravitational collapse of the Boulware–Deser spacetime will cease with the formation of a weak conical singularity at the centre of the black hole. Further to this notion, there will be no violation of any of the energy conditions for any stress energy tensor attached to the spacetime. In order to ascertain the dynamics of the trapping horizon, we let

$$\begin{aligned} f(v,\textsf {r})=0, \end{aligned}$$

which is

$$\begin{aligned} 1+\frac{\textsf {r}^2}{4\alpha }\left( 1-\sqrt{1+\frac{16\alpha M(v,\textsf {r})}{\textsf {r}^4}}\right) =0. \end{aligned}$$
(39)

Solving for the radial component \(\textsf {r}\) we have

$$\begin{aligned} \textsf {r}=\sqrt{2M(v,\textsf {r})-2\alpha }. \end{aligned}$$
(40)

Therefore for \(v\in [0, M^{-1}(\alpha )]\), the conical singularity at the centre (\(\textsf {r}=0\)) remains naked, before capitulating to the trapping horizon. If we consider our mass function from earlier

$$\begin{aligned} M(v,\textsf {r})=\frac{-N_{s}(v)\textsf {r}^{1-\frac{3}{2}(1+3\omega _{s})}}{2-3(1+3\omega _{s})}+v, \end{aligned}$$
(41)

where we have set the integration function \(c_{2}(v)=v\), then at \(\textsf {r}=0\) we have that \(v=\alpha \) in Eq. (40).

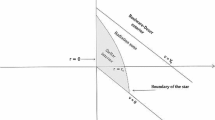
In Fig. 6 the radiating matter is falling into a five-dimensional quasi-regular black hole. Within the region \(0<v<\alpha \), there is no trapping horizon concealing the conical singularity, since the Gauss–Bonnet coupling constant \(\alpha \) is delaying its formation. The apparent horizon begins to form at \(v=\alpha \) and covers a region of null and trapped compact surfaces which descend into the black hole within \(\alpha<v<V_{0}\). At time \(v=V_{0}\) a single event horizon separates the exterior five-dimensional Boulware–Deser vacuum from the radiating trapped surfaces at

$$\begin{aligned} \textsf {r}=\sqrt{\frac{2}{1+9\omega _{s}}\left( N_{s}(v)\textsf {r}^{1-\frac{3}{2}(1+3\omega _{s})}\right) +2v-2\alpha }. \end{aligned}$$

Past this final trapping horizon is a quasi-regular black hole with a weak central conical singularity. An important note to make is the fact that the collapse process remains unchanged for all values of the equation of state parameter \(\omega _{s}\) and so for the generalised radiating field, collapse ceases in the same way.

7 Discussion

In this paper we considered a generalised radiating spacetime in EGB gravity with various types of matter fields. The Boulware–Deser spacetime, which is an analogous spacetime to the generalised Vaidya solution, was analysed with matter distributions sourced by a radiating metric which is Vaidya-like. The EGB field equations were derived and then solved for the mass function which was expressed in terms of the equation of state parameter which represented different equations of state. These fields included dust, radiation, cosmological constant-like and negative pressures. A physical analysis of the solution was then undertaken where the evolution of the behaviour of the mass function and matter variables was probed. We found that the behaviour differed greatly depending on the background matter distribution. The case of radiation proved to be the most consistently realistic background. This analysis is the first of its kind undertaken in EGB gravity and acts as an extension of the work done by [28, 34]. The effects of diffusion were also presented and two classes of solutions to the diffusion equation were found, with one class being a specific closed form family, and the other the most general family of solutions known. Finally, a discussion on gravitational collapse was given highlighting the work done in [44,45,46] with regards to the end state of Boulware–Deser collapse. Using our mass function, we showed that collapse terminates with a weak and conical singularity. The trapping horizon formation was initially delayed by the presence of the Gauss–Bonnet coupling constant, however eventually formed covering the singularity within the confines of a quasi-regular black hole. The generalised radiating field did not affect the gravitational collapse process in EGB gravity, as any of the values for the equation of state parameter \(\omega _{s}\) would result in the collapse terminating in the same way. This is fundamentally different to the general relativity case analysed in detail by [34].