Charged radiation collapse in Einstein–Gauss–Bonnet gravity

Abstract

We generalise the continual gravitational collapse of a spherically symmetric radiation shell of matter in five dimensional Einstein–Gauss–Bonnet gravity to include the electromagnetic field. The presence of charge has a significant effect in the collapse dynamics. We note that there exists a maximal charge contribution for which the metric functions in Einstein–Gauss–Bonnet gravity remain real, which is not the case in general relativity. Beyond this maximal charge the spacetime metric is complex. The final fate of collapse for the uncharged matter field, with positive mass, is an extended, weak and initially naked central conical singularity. With the presence of an electromagnetic field, collapse terminates with the emergence of a branch singularity separating the physical spacetime from the complex region. We show that this marked difference in singularity formation is only prevalent in five dimensions. We extend our analysis to higher dimensions and show that for all dimensions $N\ge 5$, charged collapse ceases with the above mentioned branch singularity. This is significantly different than the uncharged scenario where a strong curvature singularity forms post collapse for all $N\ge 6$ and a weak conical singularity forms when $N=5$. A comparison with charged radiation collapse in general relativity is also given.

1 Introduction

The allure of gravitational collapse is undeniable in gravitational physics, cosmology and astrophysics. This is due to it being a fundamental mechanism in the structural formation of the entire universe. Over a time period, initially smooth matter fields will contract to form small localised dense distributions which form the building blocks for galaxies, stellar groups, stars and planets. Galaxy formation is thought to be the result of monolithic collapse, i.e. every galaxy formed as the result of the contraction of a single, turbulent gas cloud [1]. Gravitational collapse is also prominent in the entire life cycle of a radiating star. Stars form as a result of the gravitational collapse of localised dense regions of molecular clouds in the interstellar medium [2], often referred to as star-forming regions or nurseries. Core contraction continues in a subtle fashion (called gravitational compression) throughout the star’s life as it burns off its matter content in the nuclear fusion process. At the end of the luminous phase of the star’s life cycle, when all the nuclear fuel has been exhausted and the matter content consists of the mostly very stable atomic nuclei ${}^{56}$Fe, ${}^{56}$Si or ${}^{60}$Zn, it will experience inwardly directed contraction due to gravity. Due to the enormous amount of energy being released in such a process, it remains a paramount case study in general relativity, modified gravity, high energy physics, astrophysics and even, due to the above mentioned stellar nucleosynthesis, nuclear physics. The end result of such a contraction is either a more compact object like a neutron star or, in the event of a more intense electromagnetic field, a pulsar or magnetar. Otherwise, in the case of truly massive stars, with masses above the Tolman–Oppenheimer–Volkoff limit, collapse proceeds in a continual manner without reaching an equilibrium end state. The singularity theorems of Penrose [3] then predict that the end state of gravitationally induced stellar collapse is a spacetime singularity.

The singularity theorems envisage that the end state of gravitational collapse is the formation of spacetime singularities [4]. Their incidence depends on certain circumstances such as gravity’s inherent attractive nature, the existence of trapped surfaces and the preservation of causality. These conditions hold within a variety of gravitational theories. There also exist a large family of solutions to Einstein’s field equations which are geodesically incomplete. In fact, one of the most important requirements for geodesic incompleteness is the existence of trapped surfaces [3]. These theorems do not take into account the nature of the spacetime singularities, only their formation. Whether or not it is possible for any future directed null geodesics to escape the confines of a black hole to infinity, leaving the singularity naked, is not regarded by the theorems of singularity formation. Penrose [5] proposed the cosmic censorship conjecture to avoid naked singularities. Should any matter distribution that is deemed physically realistic, collapse under its own gravity, the end state of this contraction must be a spacetime singularity which is covered by a trapping horizon for its entire existence. Therefore, the end state of collapse is a black hole with a central curvature singularity covered by the event horizon which acts as an aegis between it and the external universe. The event horizon is defined as the smooth boundary of the causal past of null infinity. As it stands there are no proofs for the conjecture and, in fact, the Vaidya–Papapetrou model [6, 7] is one of the earliest models proposed that counters cosmic censorship. Many other counterexamples exist in different contexts for certain matter distributions, for example [8,9,10,11,12,13,14,15,16]. It turns out that an increase in dimension may restore cosmic censorship in general relativity. Under certain physical conditions, it was demonstrated that collapse terminates with the formation of singularities which are no longer naked, in higher dimensions [12, 17, 18].

The generalisation of the Vaidya spacetime, which contains the additional Type II null string fluid, has been extensively studied in regards to the exteriors of radiating relativistic stars, dynamical black holes and even regular black holes. Various properties of the additional Type II null fluid were examined extensively in [19,20,21,22,23]. Contained within these models were the collapsing monopole, de-Sitter/Anti de-Sitter, the charged Vaidya models and the radiating dyon solution. With regard to regular black holes, several models were analysed in [24,25,26,27,28,29]. It must be mentioned that these models are in a sense contrived since the regularity of the solutions are artificial; coordinate transformations were used to design them. Some examples of similar regularity constructions can be found in [30,31,32].

In modified theories of gravity, Dominguez and Gallo [33] analysed black hole solutions in Einstein–Gauss–Bonnet gravity and Chowdhury et al. [34] found solutions in f(R) gravity using the idea of R-matching, an inescapable feature of f(R) collapse. The reason for modifying general relativity lies in the fact that it is a global theory of gravity and is therefore incomplete. General relativity itself extends Newtonian gravity and so considerations for its own extension are natural. It was shown by Lovelock [35, 36] that a polynomial form of the Lagrangian is possible leading to the Lovelock action. Therefore higher order curvature terms appearing in Lovelock gravity are corrections to general relativity. In fact, general relativity can be considered as first order Lovelock gravity, since it is the final limiting case. If the Lovelock polynomial is quadratic in order, we then have the Einstein–Gauss–Bonnet (EGB) action. This is then second order Lovelock gravity, or EGB gravity. Quadratic terms in curvature present as corrections to general relativity. The solution of Boulware and Deser [37] is indeed the higher dimensional EGB analogue of the Schwarzschild solution. As an ansatz to the radiating solution of Vaidya, the Boulware–Deser metric was studied as a radiating solution by Kobayashi [38] and Brassel et al. [39]. Several solutions with equations of state were found as EGB analogues of the Vaidya solutions found by Husain [19] and Wang and Wu [20]. The role of dimensions in any gravitational theory is an important one. It was demonstrated in [40] that naked singularities are inevitable upon the termination of radiation collapse in EGB gravity. For the five dimensional case, a massive timelike naked singularity formed post collapse while in dimensions of six and higher, a massless ingoing naked singularity resulted. The gravitational collapse of the radiating Boulware–Deser spacetime was analysed in detail by [41, 42] where it was shown that in five dimensions, the minimum dimension of the EGB theory, the collapse terminates with an extended weak and conical central singularity that is initially naked, before succumbing to a trapping horizon. This is a remarkable feature not present in general relativity. Conical singularities have been discussed in the literature by [43,44,45]. It should be noted that in all dimensions greater than six, collapse terminates with a strong curvature singularity for positive mass, mirroring general relativity, and thus highlighting the importance of the fifth dimension in EGB gravity. Weak and strong curvature singularities were discussed in [46]. Consider a volume element defined by linearly independent spacelike Jacobi fields¹ with zero vorticity propagating along null (timelike) geodesics or is orthogonal to its tangent vector. A gravitational curvature singularity is called strong if such a volume element vanishes at the spacetime singularity. Otherwise it is finite and called weak. The necessary and sufficient conditions for the formation of strong curvature singularities were given by Clarke and Królak [47].

An important feature of gravitational collapse, and one of the bases of this paper, is the notion of the electromagnetic field contribution. Charged collapse is well known in the literature since the discovery of the Reissner–Nordström [48,49,50,51] and Kerr–Newman [52, 53] metrics. In general relativity, charged collapse has been analysed in detail, for example see [54,55,56]. In modified theories of gravity, Ghosh [57] studied radiating black holes in five dimensional Einstein–Yang–Mills–Gauss–Bonnet (EYMGB) gravity, discussing the effect of the Yang-Mills gauge charge on the structure and locations of trapping horizons. Hansraj [58] obtained solutions in static Einstein–Gauss–Bonnet–Maxwell (EGBM) theory by utilising a coordinate redefinition which led to several new solutions. The charged Boulware–Deser metric, which is the basis of this treatment, was first studied in detail by Wiltshire [59] where a generalisation of the Birkhoff theorem was proved with the effect of the Gauss–Bonnet term. The conditions for horizon formation were also provided and compared to the general relativistic limit. Abbas and Ahmed [60] studied the contraction of a charged spherically symmetric fluid in f(R, T) gravity where the trapped surfaces, apparent horizon and singularity structure were addressed. More recently, the effects of the electromagnetic field on conformally flat collapsing stellar configurations with an anisotropic heat flow in f(R) gravity were studied in [61]. It was shown that the effect of the charge contribution and heat flux slowed down the rate of collapse. It should be noted however that in general relativity, the charge compression in collapsing a charged mass is significantly higher (around forty orders of magnitude) than the gravitational attraction. Therefore it is unlikely that a black hole forming in nature will have any significant charge contribution. Whether this is the case in modified theories of gravity is unknown in general.

1.1 This paper

We analyse the continual gravitational contraction of a charged spherically symmetric shell of radiation in five dimensional EGBM gravity. We will show that the final fate of such a collapse is a branch-like singularity which separates the physical collapsing spacetime from an unphysical region resulting from the charge contributing to the metric becoming complex. We compare this with the uncharged case where radiation collapse ceases with the formation of a necessarily weak and conical central singularity, under certain conditions for the mass function, which remains initially naked for a time before becoming shrouded by a trapping horizon within a black hole. This paper is organised in the following way: In Sect. 2 we give an overview of units and the role of dimension in gravity. In the following section we highlight some definitions indicative of the EGB theory. The gravitational collapse of a radiating spacetime within an electromagnetic field is considered in Sect. 5, where we highlight the differences in the collapse process with both the uncharged scenario and the general relativistic case. Finally, we briefly look at collapse in arbitrary dimensions, noting that the dimension critically alters the collapse dynamics of radiating matter in EGB gravity. A brief recap of charged radiation collapse in general relativity is given in Appendix B.

2 Higher dimensional preamble

The role of dimensions in all gravity theories is a germane one. In this research paper, we will utilise units where $G=c=1$. In arbitrary dimensions, Einstein’s coupling constant is expressed in terms of the factorial function and is given by

$$\begin{aligned} \kappa _{N}=\frac{2(N-2)\pi ^{\frac{N-1}{2}}}{(N-3)\left( \frac{N-1}{2}-1\right) !}. \end{aligned}$$

(1)

The surface area of the $(N-2)$-sphere is given by the following

$$\begin{aligned} {\mathscr {A}}_{N-2}=\frac{2\pi ^{\frac{N-1}{2}}}{\varGamma \left( \frac{N-1}{2}\right) }, \end{aligned}$$

(2)

where we note the presence of the Gamma function $\varGamma (\ldots )$. Since EGB gravity is only relevant in five dimensions or higher, these terms become important in the analysis, especially with regards to the electromagnetic field. The Lorentzian signature of the spacetime manifold is $(-,+,+,\ldots ,+)$. These expressions become especially critical when considering a charged radiating stellar mass, or black hole, which is the basis of this paper.

The surface gravity of a black hole is not well defined in general. However, it is possible to define it for a black hole whose event horizon is a Killing horizon.² Every stationary (non-rotating) black hole has a Killing horizon [62, 63]. The surface gravity ${\mathscr {K}}$ of a Killing horizon is the acceleration (as exerted at infinity) required to keep an object at the horizon of a black hole. It can be derived from the Raychauduri equation [64, 65] and is given by

$$\begin{aligned} {\mathscr {K}}k^{a}=k^{b}k^a{}_{;b}, \end{aligned}$$

(3)

where $k^{a}$ is a Killing vector. In the above, the semicolon represents covariant differentiation.

3 Second order Lovelock gravity

The Lovelock (or Lovelock–Zumino) action in arbitrary dimensions is given by

$$\begin{aligned} S=\int d^{N}x\sqrt{-g}\sum _{k=0}^{N/2}\alpha _{k}{\mathscr {R}}^k+S_{matter}, \end{aligned}$$

(4)

where we have

$$\begin{aligned} {\mathscr {R}}^k=\frac{1}{2^k}\delta _{a_{1}b_{1}\ldots a_{k}b_{k}}^{c_{1}d_{1}\ldots c_{k}d_{k}}\prod _{r=1}^{k}R^{a_{r}b_{r}}{}_{{}c_{r}d_{r}}, \end{aligned}$$

and $\delta _{a_{1}b_{1}\ldots a_{k}b_{k}}^{c_{1}d_{1}\ldots c_{k}d_{k}}$ is the Kronecker delta. In the context of Lovelock gravity in higher dimensions, some spherically symmetric exact solutions for cosmological backgrounds were found by Bajardi et al. [66]. They also obtained solutions in five dimensional, topological Chern–Simons gravity where it was shown that for particular Lovelock parameters, Anti-de Sitter invariant Chern–Simons gravity is contained in Lovelock gravity in five dimensions. If we consider second order Lovelock gravity, the action reduces to

$$\begin{aligned} S=\int d^{N}x\sqrt{-g}(\alpha _{0}+\alpha _{1}{\mathscr {R}}+\alpha _{2}{\mathscr {R}}^2), \end{aligned}$$

(5)

where $\alpha _{0}=\varLambda$ is the cosmological constant term, $\alpha _{1}$ is the constant (usually unity) associated with the Einstein–Hilbert action (${\mathscr {R}}=R$) and $\alpha _{2}=\alpha$ is the constant associated with the Gauss–Bonnet term. It is important to note that in order to avoid any pathologies, $\alpha >0$ [37]. In the above,

$$\begin{aligned} {\mathscr {R}}^2=L_{GB}=R^2+R_{abcd}R^{abcd}-4R_{cd}R^{cd}, \end{aligned}$$

(6)

is the second order Lovelock Lagrangian. Varying the second order action (5) with respect to the metric $g_{ab}$ gives the second order Lovelock or EGB field equations

$$\begin{aligned} G_{ab}-\frac{\alpha }{2}H_{ab}=\kappa _{N}T_{ab}. \end{aligned}$$

(7)

Here, $G_{ab}$ is the Einstein tensor, $T_{ab}$ is the energy momentum tensor and $H_{ab}$ is the Lovelock tensor which arises as a consequence of varying the action (5). It is given by

$$\begin{aligned} H_{ab}= & {} g_{ab}L_{GB}-4RR_{ab}+8R_{ac}R^c{}_{{}b}+8R_{acbd}R^{cd}\nonumber \\&-4R_{acde}R_{b}{}^{{}cde}. \end{aligned}$$

(8)

The nontrivial nature of this expression requires that the minimum dimension of the spacetime in EGB gravity has to satisfy $N\ge 5$. If we have that $N<5$, the Lovelock tensor (8) vanishes, and there is no contribution from the higher curvature of the theory.³ In the limit where $\alpha \rightarrow 0$, general relativity will be regained in five dimensions. For the case of a nonvanishing electromagnetic field, the Einstein–Gauss–Bonnet–Maxwell (EGBM) field equations are written as

$$\begin{aligned} G_{ab}-\frac{\alpha }{2}H_{ab}= & {} \kappa _{N}(T_{ab}+E_{ab}), \end{aligned}$$

(9a)

$$\begin{aligned} F_{ab;c}+F_{bc;a}+F_{ca;b}= & {} 0, \end{aligned}$$

(9b)

$$\begin{aligned} F^{ab}{}_{;b}= & {} {\mathscr {A}}_{N-2}J^a, \end{aligned}$$

(9c)

for a relevant energy momentum tensor $T_{ab}$ and the electromagnetic energy tensor $E_{ab}$. In the above, $J^a$ is the current and the fluid N-velocity is $\mathbf{u}$. The electromagnetic energy tensor can be written as

$$\begin{aligned} E_{ab}=\frac{1}{{\mathscr {A}}_{N-2}}\left( F_{a}{}^{c}F_{bc}-\frac{1}{4}F^{cd}F_{cd}g_{ab}\right) , \end{aligned}$$

(10)

and is expressed in terms of the Faraday tensor $F_{ab}=\varPhi _{b;a}-\varPhi _{a;b}$, the gauge potential $\varPhi$ and the surface area (2). We note that the tensor (10) is trace-free only in four dimensions.

4 The generalised radiating Boulware–Deser solution

The EGB analogue of the Schwarzschild solution was found by Boulware and Deser [37]. Similar to the Vaidya solution, this metric can be written in Eddington–Finkelstein coordinates and then can be made to radiate [38, 39, 41, 42]. The five dimensional radiating metric is given by

$$\begin{aligned} ds^2= & {} -f(v,r)dv^2+2dvdr\nonumber \\&+r^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2), \end{aligned}$$

(11)

where

$$\begin{aligned} f(v,r)=1+\frac{r^2}{4\alpha }\left( 1\pm \sqrt{1+\frac{8\alpha M(v,r)}{r^4}}\right) . \end{aligned}$$

(12)

We have that M(v, r) represents the gravitational mass of the five dimensional hypersurface. In the above expression (12), the negative branch solution has the general relativity limit as $\alpha \rightarrow 0$ [37]. The solution (12) comes about as a result of the generalised uncharged Type II matter with a string fluid. The negative branch solution (12) is essentially the EGB analogue of the Vaidya spacetime, to which it reduces in the general relativity limit when $\alpha \rightarrow 0$. This motivation is necessary to compare the EGB effects to those in the general relativistic limit. The energy momentum tensor is written as

$$\begin{aligned} T_{ab}={\tilde{\mu }} l_{a}l_{b}+({\tilde{\rho }}+{\tilde{P}})(l_{a}n_{b}+l_{b}n_{a})+{\tilde{P}}g_{ab}, \end{aligned}$$

(13)

where we have that

$$\begin{aligned} l_{a}= & {} \delta ^{0}{}_{a}, \end{aligned}$$

(14a)

$$\begin{aligned} n_{a}= & {} \frac{1}{2}f(v,r)\delta ^{0}{}_{a}+\delta ^{1}{}_{a}, \end{aligned}$$

(14b)

with the restrictions

$$\begin{aligned} l_{c}l^c=n_{c}n^c=0,l_{c}n^c=-1. \end{aligned}$$

(15)

The null vector $l^a$ is a double null eigenvector of the energy momentum tensor (13). The EGB field equations (7) take the simple form

$$\begin{aligned} {\tilde{\mu }}= & {} \frac{M_{v}}{2\pi ^2r^3}, \end{aligned}$$

(16a)

$$\begin{aligned} {\tilde{\rho }}= & {} \frac{M_{r}}{2\pi ^2r^3}, \end{aligned}$$

(16b)

$$\begin{aligned} {\tilde{P}}= & {} -\frac{M_{rr}}{6\pi ^2r^2}, \end{aligned}$$

(16c)

where

$$\begin{aligned} M_{v}=\frac{\partial M}{\partial v}, M_{r}=\frac{\partial M}{\partial r}. \end{aligned}$$

The Einstein tensor components and Lovelock tensor components will be presented in Appendix A. They are complicated in form but their union in (7) yields the simple expressions above.

The energy conditions for the Type II fluid (as shown in [21, 67, 69]) are

• The null energy condition:

  $$\begin{aligned} {\tilde{\mu }}\ge 0, {\tilde{\rho }}+{\tilde{P}}\ge 0. \end{aligned}$$

  (17)

• The weak energy condition:

  $$\begin{aligned} {\tilde{\mu }}\ge 0, {\tilde{\rho }}\ge 0, {\tilde{\rho }}+{\tilde{P}}\ge 0. \end{aligned}$$

  (18)

• The strong energy condition:

  $$\begin{aligned} {\tilde{\mu }}\ge 0, {\tilde{\rho }}+{\tilde{P}}\ge 0, {\tilde{\rho }}+3{\tilde{P}}\ge 0. \end{aligned}$$

  (19)

• The dominant energy condition:

  $$\begin{aligned} {\tilde{\mu }}\ge 0, {\tilde{\rho }}\ge |{\tilde{P}}|(\ge 0). \end{aligned}$$

  (20)

These are equivalent in the five-dimensional general relativity limit. Using (14) and (15), the surface gravity ${\mathscr {K}}$ can also be written as

$$\begin{aligned} {\mathscr {K}}=l^bn^an_{b;a}. \end{aligned}$$

(21)

5 Charged Boulware–Deser collapse

The charged analogue of the Boulware–Deser metric was first analysed in detail by Wiltshire [59]. If we consider the mass function in (12), we make the choice

$$\begin{aligned} M(v,r)=M(v)-\frac{\kappa _{5}Q(v)^2}{6{\mathscr {A}}_{3}r^{2}}, \end{aligned}$$

(22)

which gives⁴

$$\begin{aligned} M(v,r)=M(v)-\frac{Q(v)^2}{4r^2}, \end{aligned}$$

(23)

which is analogous to the choice made in the Appendix (B.7). This choice comes about by following the methodology used in Wang and Wu et al. [20]. We then have the metric for the charged Boulware–Deser spacetime

$$\begin{aligned} ds^2= & {} -f(v,r)dv^2+2dvdr\nonumber \\&+r^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2), \end{aligned}$$

(24)

where we now have

$$\begin{aligned} f(v,r)=1+\frac{r^2}{4\alpha }\left( 1-\sqrt{1+\frac{8\alpha M(v)}{r^4}-\frac{2\alpha Q(v)^2}{r^6}}\right) . \end{aligned}$$

(25)

The solution (25) was first found by Wiltshire [59]. In the limit when $\alpha \rightarrow 0$, the above reduces to the Vaidya metric (B.8) with nonzero charge q(v) (see Appendix B). The five dimensional gauge potential and five-current are given by

$$\begin{aligned} \varPhi _{a}=\frac{Q(v)}{2r^2}, \end{aligned}$$

and

$$\begin{aligned} J^a=\frac{Q_{v}}{4\pi ^2r^3}l^a. \end{aligned}$$

The electromagnetic field contribution (10) is built into the above definition (23) in five dimensions. In the above, $Q=Q(v)$ is the charge indicative of the Einstein–Gauss–Bonnet–Maxwell (EGBM) theory. Note that the five dimensional Einstein constant and surface area of the 3-sphere are incorporated into this definition analogously to (B.7).

Using (16), we can write the EGBM field equations (9) with the mass function (23) as

$$\begin{aligned} M(v,r)= & {} M(v)-\frac{Q(v)^2}{4r^2}, \end{aligned}$$

(26a)

$$\begin{aligned} {\tilde{\mu }}= & {} \frac{M_{v}}{2\pi ^2r^3}-\frac{QQ_{v}}{4\pi ^2r^5}, \end{aligned}$$

(26b)

$$\begin{aligned} {\tilde{\rho }}= & {} {\tilde{P}}=\frac{Q(v)^2}{4\pi ^2r^6}. \end{aligned}$$

(26c)

We note that in the absence of charge, $M(v,r)=M(v)$ in the above, and only one field equation (26b) will survive as expected.⁵ For the metric (25) the energy conditions (17)–(20) must be satisfied. From the field equations (26), this gives

$$\begin{aligned} M_{v}\ge & {} \frac{QQ_{v}}{2r^2}, \end{aligned}$$

(27)

$$\begin{aligned} Q(v)\ge & {} 0. \end{aligned}$$

(28)

Similarly to the general relativity case (shown in Appendix B), the condition (27) is violated near $r=0$ [70, 71]. For the case of the metric (25) the reason for this violation is different to the general relativity case, which we explain in the paragraphs below. The collapse dynamics of the charged Boulware–Deser spacetime differ significantly to its uncharged counterpart [41]. We observe from (25) that since the charge term $-\frac{2\alpha Q(v)^2}{r^6}$ has a negative sign, there must exist a maximal charge contribution before which this metric becomes complex. Therefore a branch singularity is generic for the charged collapse in EGB gravity [72, 73]. Considering the square root term in (25), this only remains real if

$$\begin{aligned} |Q(v)|\le \sqrt{\frac{r^2(r^4+8\alpha M(v))}{2\alpha }}, \end{aligned}$$

otherwise it becomes complex. There exists no real spacetime whenever the above inequality is violated. This inequality can be written as

$$\begin{aligned} r_{s}^6+8\alpha Mr_{s}^2-2\alpha Q^2\ge 0, \end{aligned}$$

(29)

which has six solutions for $r=r_{s}(v)$, two of which are real and one of which is positive. There exists a branch singularity at $r=r_{s}(v)$ for any value of the mass function M, if $Q\ne 0$, which separates the real spacetime from the complex metric. The positive real solution to the above inequality is given by

$$\begin{aligned} \small r_{s}\ge \frac{\sqrt{-3\left( 27\alpha Q+3\sqrt{E}\right) ^{\frac{1}{3}}\left( 24\alpha M-\left( 27\alpha Q+3\sqrt{E}\right) ^{\frac{2}{3}}\right) }}{3\left( 27\alpha Q+3\sqrt{E}\right) ^{\frac{1}{3}}}, \nonumber \\ \end{aligned}$$

(30)

where we have set $E=1536M^3\alpha ^3+81Q^2\alpha ^2$. This branch singularity forms at $r_{s}(0)=0=v$ and extends into the future. The value of the inequality determines the domain of r which is $0<r_{s}<r<\infty$; there is no spacetime at $r=0$, which is one reason the weak energy condition (27) is violated. The Kretschmann invariant $K=R_{abcd}R^{abcd}$ can be used to check whether any spacetime manifold has singularities. For the charged metric (25) it is given by

$$\begin{aligned} K= & {} \frac{1}{4\alpha ^2r^6(r^6+8\alpha Mr^2-2\alpha Q^2)^3}\left[ -20r^{24}\sqrt{F}\right. \nonumber \\&\times 88Q^8\alpha ^4+16Q^6\alpha ^3r^6\sqrt{F}-256Q^6\alpha ^3r^6\nonumber \\&+11264M^3\alpha ^3r^{12}-352MQ^4\alpha ^3r^8\sqrt{F}\nonumber \\&+2640MQ^4\alpha ^3r^8-2304M^2\alpha ^2r^{16}\nonumber \\&-122Q^2\alpha r^{18}-132Q^4\alpha ^2r^{12}+20r^{24}\nonumber \\&+12288M^4\alpha ^4r^8+1920M^2Q^2\alpha ^3r^{10}\sqrt{F}\nonumber \\&-400M\alpha r^{20}\sqrt{F}-8832M^2Q^2\alpha ^3r^{10}\nonumber \\&-2208MQ^2\alpha ^2r^{14}-3072M^3\alpha ^3r^{12}\nonumber \\&+351Q^4\alpha ^2r^{12}-12288M^3Q^2\alpha ^4r^6\nonumber \\&\left. +480M\alpha r^{20}+5568M^2Q^4\alpha ^4r^4 r^{18}\right. \nonumber \\&\left. +1120MQ^2\alpha ^2r^{14}\sqrt{F}+4032M^2\alpha ^2r^{16}\right. \nonumber \\&\left. +102Q^2\alpha r^{18}\sqrt{F}-1152MQ^6\alpha ^4r^2\right] , \end{aligned}$$

(31)

where we have set $F=1+\frac{8\alpha M}{r^4}-\frac{2\alpha Q^2}{r^6}$. We note the $r^6+8\alpha Mr^2-2\alpha Q^2$ term outside the bracket in (31), which is of the same form as (29). Therefore in the region $r_{s}^6+8\alpha Mr_{s}^2-2\alpha Q^2=0$, there is a curvature singularity; this branch singularity $r=r_{s}(v)$ is indeed the curvature singularity of the spacetime. It can be observed that in this case the Kretschmann invariant diverges at the branch $r=r_{s}(v)$ (see Figs. 1 and 2) as $K\approx r^{-24}$ which is significantly more than the uncharged case $(K\approx r^{-16})$, and even more so than the general relativistic charged Vaidya analogue $(K\approx r^{-8})$. This highlights the role of the curvature corrections of EGB gravity in tandem with the charge component Q of the electromagnetic field. There is no physical spacetime in the region $0<r_{s}$. In the limiting case of $Q=0$, the scalar (31) reduces to that of the uncharged metric studied in [40, 41].

Fig. 1

Plot indicating the behaviour of the Kretschmann scalars for the charged Vaidya and the charged Boulware–Deser (BD) spacetimes

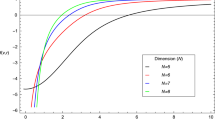
Figures 1 and 2 depict the behaviours of the Kretschmann scalars for the three spacetimes (B.8), (12) and (25). We have used the values $\alpha =2$, $m(v)=M(v)=15$ and $q(v)=Q(v)=2$. Figure 1 depicts the behaviour of the Kretschmann scalars for the charged Vaidya spacetime and the charged Boulware–Deser spacetime. The charged Vaidya metric diverges strongly near the singularity $r=0$ in a steadily decreasing manner with increasing r. However it is apparent that the divergence of the charged Boulware–Deser spacetime is negative nearer to the branch singularity $r=r_{s}\approx 0.258$, and then increases as one moves along the radial coordinate. This is an interesting feature since at some finite radial coordinate, the quantity (31) vanishes entirely before increasing steadily with increasing r. Figure 2 shows the behaviour of the Kretschmann invariants for the uncharged and charged Boulware–Deser metrics. We note that for the uncharged Boulware–Deser spacetime, the divergence pattern is similar to the charged Vaidya spacetime. Near the central singularity, the Kretschmann scalar diverges, before steadily decreasing with increasing r. We can clearly see in Figs. 1 and  2 that the charged Boulware–Deser spacetime diverges rapidly near the branch singularity located at $r=r_{s}\approx 0.258$.

Fig. 2

Plot indicating the behaviour of the Kretschmann scalars for the uncharged and charged Boulware–Deser (BD) spacetimes

The apparent horizon forms when

$$\begin{aligned} 1+\frac{r_{H}^2}{4\alpha }\left( 1-\sqrt{1+\frac{8\alpha M(v)}{r_{H}^4}-\frac{2\alpha Q(v)^2}{r_{H}^6}}\right) =0, \end{aligned}$$

(32)

which, after simplification, turns out to be a quartic polynomial in $r_{H}$. It yields four solutions, namely

$$\begin{aligned} r_{0}= & {} \pm \frac{1}{2}\sqrt{2M+2\sqrt{(M-2\alpha )^2-Q^2}-4\alpha }, \end{aligned}$$

(33a)

$$\begin{aligned} r_{1}= & {} \pm \frac{1}{2}\sqrt{2M-2\sqrt{(M-2\alpha )^2-Q^2}-4\alpha }, \end{aligned}$$

(33b)

Again, only the positive parts of (33a) and (33b) are applicable so we therefore have

$$\begin{aligned} r_{0}= & {} \frac{1}{2}\sqrt{2M+2\sqrt{(M-2\alpha )^2-Q^2}-4\alpha }, \end{aligned}$$

(34a)

$$\begin{aligned} r_{1}= & {} \frac{1}{2}\sqrt{2M-2\sqrt{(M-2\alpha )^2-Q^2}-4\alpha }. \end{aligned}$$

(34b)

Depending on the value of the discriminant

$$\begin{aligned} {\bar{\varDelta }}=(M-2\alpha )^2-Q^2, \end{aligned}$$

three cases arise.

• 1. If ${\bar{\varDelta }}<0$, no real solutions are possible, and there does not exist any physical horizon.

• 2. If we have that ${\bar{\varDelta }}=0$, then $M=2\alpha \pm Q$. Two scenarios are possible:

  • For the case, $M=2\alpha -Q$, no horizon formation takes place since the values under the square roots in system (34) will be negative, and so both $r_{0}$ and $r_{1}$ will be complex.

  • If $M=2\alpha +Q$ the above solutions coincide with the single extremal horizon in five dimensions, i.e. $r_{0}=r_{1}=r_{H}=\sqrt{M-2\alpha }$ from [41].

• 3. If ${\bar{\varDelta }}>0$, then there will exist two real physical apparent horizons for the charged radiating black hole. The solution (34a) will be the outer horizon and (34b) will represent the inner horizon. To an external observer, only the outer horizon will be visible. This is in line with the conclusions drawn in [59].

We now make the following observations:

• If the Gauss–Bonnet coupling constant vanishes $(\alpha =0)$ the solutions (34) reduce to charged Vaidya solutions in five dimensions

  $$\begin{aligned} r_{0,1}=\frac{1}{2}\sqrt{2m\pm 2\sqrt{m^2-q^2}}, \end{aligned}$$

  from (B.13).

• If the charge contribution is vanquished $(Q=0)$, the solutions (34) reduce to the single solution

  $$\begin{aligned} r_{H}=\sqrt{M-2\alpha }, \end{aligned}$$

  studied in [41].

Similarly, the mass function from setting (32) to zero can be written as

$$\begin{aligned} M=r_{H}^2+2\alpha +\frac{Q^2}{4r_{H}^2}:=M_{H}(r_{H}), \end{aligned}$$

(35)

where the horizon radius must satisfy $r_{H}>0$. When $Q=0$, (35) reduces to

$$\begin{aligned} M_{H}(r_{H})=r_{H}^2+2\alpha , \end{aligned}$$

which is monotonically increasing in the domain $0\le r<\infty$ and satisfies $M_{H}(0)=2\alpha$. In the case where $M(v)\le 2\alpha$ at a time v, there is no horizon formation. One horizon will form if $M(v)>2\alpha$; this apparent horizon formation is delayed by the EGB coupling constant $\alpha$ as shown in [41]. The effect of the charge Q is, thus, significant in EGB gravity. If we consider the square root in (32) and solve for the mass function M, this gives

$$\begin{aligned} M=-\frac{1}{8\alpha }r_{s}^4+\frac{Q^2}{4r_{s}^2}:=M_{s}(r_{s}), \end{aligned}$$

(36)

which further iterates that there is a branch singularity at $r=r_{s}$ for all M and nonzero Q.

Table 1 Singularity and horizon formation scenarios for different mass values with $\alpha =Q=2$. ($r_{s}$ - branch singularity, $r_{1}$ - inner horizon, $r_{0}$ - outer horizon)

In order to quantify this analysis, we assume $\alpha =2$, $M=15$ and $Q=2$ and calculate approximate values of the branch $r_{s}$, as well as the inner and outer horizons $r_{1}$ and $r_{0}$ respectively. This gives the three solutions

$$\begin{aligned} r_{s}= & {} \frac{\sqrt{2}\sqrt{(1+3\sqrt{899})^{\frac{2}{3}}-20}}{(1+3\sqrt{899})^{\frac{1}{6}}}\approx 0.258196,\\ r_{1}= & {} \frac{1}{2}\sqrt{22-3\sqrt{17}}\approx 0.302776,\\ r_{0}= & {} \frac{1}{2}\sqrt{22+3\sqrt{17}}\approx 3.302776, \end{aligned}$$

and it is clear that for these values, the branch singularity is covered by the two horizons within the domain for r which is $0<r_{s}<r_{1}\le r_{0}<\infty$. Table  1 depicts the different scenarios for the formation of singularities and horizons for differing mass values. We have used the values $\alpha =Q=2$ throughout; for these values the two critical solutions for the discriminant ${\bar{\varDelta }}=0=(M-2\alpha )^2-Q^2$ are $M=2$ and $M=6$. These are shown in the table. For $M=2$, no horizon will form since the values of the inner and outer horizons are imaginary numbers. From the table, we also note that for $0<M<2$ and $2<M<6$, no horizon will form since the discriminant ${\bar{\varDelta }}<0$. When $M=6$, we have $r_{0}=r_{1}=1$ and so there is one horizon which forms upon collapse. For all $M>6$, two horizons will always form covering the singularity $r_{s}$. It is interesting to note that as the values of the mass function increase, the value of the branch singularity $r_{s}$ appears to decrease, however this value will never terminate for $Q>0$.

Fig. 3

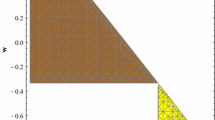
Spacetime diagram of possible charged radiation collapse scenario in five dimensional EGBM gravity. There is a branch singularity $r=r_{s}(v)$ which forms at $v=r_{s}(0)=0$ extending into the future separating the unphysical region from the rest of the collapsing spacetime. The apparent horizons form immediately at $v=r_{s}(0)=0$ covering the central singularity. Only the outer horizon $r=r_{0}$ is visible to an external observer at infinity. In the case of the discriminant ${\bar{\varDelta }}=0$, the inner and outer horizons coincide; there will be a single extremal horizon separating the singularity from the external universe, and so this diagram remains the same. It should be noted that this diagram also remains unchanged for all $N\ge 6$

Figure 3 depicts the possible collapse scenario, from an initially flat spacetime, for charged null matter. We have radiating charged null matter falling into a black hole. The two apparent horizons, of which only the outer is visible to an observer, form at $v=r_{s}(0)=0$ unlike in the uncharged scenario, and encompass trapped surfaces in a dense region $0<v<V_{0}$. The Gauss–Bonnet constant $\alpha$ does not delay the formation of the two apparent horizons, unlike the single horizon of the uncharged case. The presence of the charge contribution $\frac{2\alpha Q(v)^2}{r^6}$ in the metric (25) indicates that for a specific value of $r(=r_{s})$ (in tandem with Q), the metric becomes complex and there is no physical spacetime below this value. This contributes to the formation of a curvature singularity (a branch singularity) which separates the unphysical part of the metric from the rest of the collapsing spacetime. This singularity forms at $v=r_{s}(0)=0$ and extends into the future, however, covered by the two horizons. The electromagnetic field contribution is significant in the late stages of collapse in EGB gravity. This is unlike the general relativity case where the electromagnetic field contribution appears to be minimal. At a time $v=V_{0}$, the apparent horizons match smoothly to the two event horizons, of which the outer is visible to the external universe. The charged Boulware–Deser exterior is separated from the black hole by this outer horizon. Within the charged Boulware–Deser black hole resides a strong central curvature singularity separating the collapsing matter from the unphysical metric. Incidentally, the collapse scenario remains the same for all $N\ge 6$, so gravitational collapse in EGBM gravity is similar for all dimensions greater than five (see Sect. 6).

The collapse scenario differs when $Q=0$, as analysed by [40, 41]. The uncharged Boulware–Deser spacetime is, first of all, metric regular in five dimensions. The spacetime itself is singular due to the diverging diffeomorphism invariants [41]. Therefore collapse terminates with a sufficiently weak central conical singularity. This conical singularity exists for a period of time where it is naked, and this is due to the Gauss–Bonnet coupling constant $\alpha$ which delays the formation of the apparent horizon. There are also a separate class of curvature singularities in EGB gravity. In the case of uncharged null matter, (25) becomes

$$\begin{aligned} f(v,r)=1+\frac{r^2}{4\alpha }\left( 1-\sqrt{1+\frac{8\alpha M(v)}{r^4}}\right) . \end{aligned}$$

(37)

Upon inspection of the above metric, a zero within the square-root implies a curvature singularity. Two branches of solutions meet here and so the singularity is also a branch singularity⁶ at some finite radius $r=r_{s}$, however unlike in the charged situation, this can be resolved. Letting the square root $\sqrt{1+\frac{8\alpha M(v)}{r^4}}=0$ in (37) and solving for M yields

$$\begin{aligned} M(v)=-\frac{1}{8\alpha }r_{s}^4:=M_{s}(r_{s}), \end{aligned}$$

(38)

and should $r_{s}>0$ hold, the domain of r becomes $0<r_{s}<r<\infty$. We note that a branch singularity only forms for the case $M<0$ which is unphysical in itself. Therefore for any positive choice of the mass function M(v), collapse terminates with the above mentioned central conical singularity (see Fig. 4). The collapse situation differs in dimensions $N\ge 6$, in that collapse will terminate with a strong curvature singularity since the Boulware–Deser spacetime is metric singular for all dimensions greater than five. However, the branch singularity case mentioned above, i.e. $M<0$, holds for all dimensions greater than five.

These collapse scenarios in EGB gravity are fundamentally different to the higher dimensional Vaidya collapse in general relativity, highlighting the effect of the curvature corrections indicative of the Lovelock theory.

Fig. 4

Spacetime diagram of possible neutral radiation collapse in five dimensional EGB gravity for $M(v)>0$. There is a weak and conical naked singularity which forms within the region $0<v<V_{0}$, and there are families of trajectories which escape to infinity from the black hole. The apparent horizon forms in the region $V_{0}<v<V_{1}$ since the EGB coupling constant $\alpha$ initially delays its formation. We have radiating null matter focusing into the black hole and at $v=V_{0}$, null radiation falls through this distribution into the black hole

Fig. 5

Plot indicating the Hawking temperatures for the spacetime metrics (B.8), (37) and (25)

Table 2 Comparisons between spacetimes

In five dimensions, the temperature at the horizon is calculated as

$$\begin{aligned} {\mathscr {T}}(r_{H})=\frac{1}{{\mathscr {A}}_{3}}f'(r_{H}), \end{aligned}$$

(39)

where we have f(v, r) from (25) at the horizon. We note the presence of the surface area term ${\mathscr {A}}_{3}$, due to the horizon surrounding the 3-sphere in the five dimensional collapsing geometry. The surface gravity is equivalent to the definition [74]

$$\begin{aligned} {\mathscr {K}}=\frac{1}{2}f'(r_{H}). \end{aligned}$$

(40)

Note that the temperature at the horizon $r=r_{H}$ is equal to the Hawking temperature⁷ so one can write

$$\begin{aligned} {\mathscr {T}}(r_{H})=\frac{1}{{\mathscr {A}}_{3}}f'(r_{H})=\frac{2{\mathscr {K}}}{{\mathscr {A}}_{3}}, \end{aligned}$$

(41)

where we have used (40). The surface gravity of the charged metric (25) is given by

$$\begin{aligned} {\mathscr {K}}=\frac{r_{H}}{4\alpha }\left[ \frac{-1+\sqrt{\frac{8\alpha M}{r_{H}^4}-\frac{2\alpha Q^2}{r_{H}^6}}-\frac{\alpha Q^2}{r_{H}^6}}{\sqrt{\frac{8\alpha M}{r_{H}^4}-\frac{2\alpha Q^2}{r_{H}^6}}}\right] , \end{aligned}$$

(42)

where we note the charge contribution Q. When the charge vanishes, the above reduces to

$$\begin{aligned} {\mathscr {K}}=\frac{r_{H}}{4\alpha }\left[ \frac{-1+\sqrt{1+\frac{8\alpha M}{r_{H}^4}}}{\sqrt{1+\frac{8\alpha M}{r_{H}^4}}}\right] . \end{aligned}$$

(43)

The Hawking temperature at the horizon is given by

$$\begin{aligned} {\mathscr {T}}_{H}=\frac{r_{H}}{4\alpha \pi ^2}\left[ \frac{-1+\sqrt{\frac{8\alpha M}{r_{H}^4}-\frac{2\alpha Q^2}{r_{H}^6}}-\frac{\alpha Q^2}{r_{H}^6}}{\sqrt{\frac{8\alpha M}{r_{H}^4}-\frac{2\alpha Q^2}{r_{H}^6}}}\right] . \end{aligned}$$

(44)

The above quantity gives a measure of the black body radiation emanating from a black hole due to quantum effects near the horizon [75]. In Fig. 5 the Hawking temperatures for all three spacetimes are represented. We again have used the values $\alpha =2$, $m(v)=M(v)=15$ and $q(v)=Q(v)=2$. Now since the Hawking temperature is measured at the horizon, we consider each spacetime separately.

• 1. Charged Vaidya: Using the numerical values above, the outer horizon (B.13a) evaluates to

  $$\begin{aligned} r_{0}=\frac{1}{2}(\sqrt{13}+\sqrt{17})\approx 3.84328. \end{aligned}$$

  It can clearly be seen that the Hawking temperature is positive at this value and then steadily decreases with increasing r.

• 2. Uncharged Boulware–Deser: The value of the apparent horizon $r_{H}=\sqrt{M-2\alpha }$ evaluates to

  $$\begin{aligned} r_{H}=\sqrt{11}\approx 3.316625, \end{aligned}$$

  and it can be seen that the Hawking temperature corresponding to this value is also positive and slowly decreasing as expected with increasing r.

• 3. Charged Boulware–Deser: The value corresponding to the outer horizon (34a) is given by

  $$\begin{aligned} r_{0}=\frac{1}{2}\sqrt{22+3\sqrt{17}}\approx 3.302776. \end{aligned}$$

  Again, we observe that the Hawking temperature at this value is positive and expectedly decreasing as one moves away from the outer horizon to infinity.

We note that below the respective horizons, these temperatures diverge rapidly when nearing the central singularities.

In Table 2 we highlight the differences between the three spacetimes studied in this paper, with regards to the end state of gravitational collapse.

Another point to emphasise is the effect of the electromagnetic field on the gravitational collapse dynamics in EGB gravity compared to conventional Einstein gravity. In general relativity, the effect of the charge contribution appears to be minimal since the collapse dynamics of the Vaidya spacetime are not too different from its charged counterpart. Collapse for both spacetimes ceases with the formation of a strong curvature singularity which may or may not be naked [12, 13]. If it is not naked, it is covered within the confines of a black hole. Radiation collapse is markedly different in EGB gravity. Firstly, the gravitational collapse of the uncharged Boulware–Deser spacetime is critically affected by the presence of the Gauss–Bonnet constant $\alpha$. The metric is regular and well defined for all r, however the spacetime itself is singular due to its diverging diffeomorphism invariants. This implies that collapse terminates with the formation of an extended, weak conical singularity at the centre that is initially naked if $M(v)\ge 0$; the Gauss–Bonnet constant $\alpha$ delays its formation. Eventually the apparent horizon forms and matches smoothly with the event horizon forming a single trapping horizon that contains the trapped surfaces within a black hole with a centrally weak conical singularity. Secondly, the charged Boulware–Deser metric is dynamically very different to its uncharged counterpart. The metric is no longer regular or well defined. The presence of the charge contribution changes the type of singularity encountered upon the cessation of collapse; it ceases with the formation of a curvature singularity which is a branch singularity forming at $v=r_{s}(0)=0$ separating the spacetime from an unphysical region which is the result of a complex metric. The horizons can also form at $v=r_{s}(0)=0$ unlike with the uncharged case. The Gauss–Bonnet constant appears not to affect the collapse dynamics as profoundly as for the uncharged case. Only the outer horizon is visible to an external observer at infinity and covers all trapped surfaces within the confines of a black hole. A further point to highlight is the role of dimensions in this analysis. In EGB gravity, it is well known that $N=5$ and $N=6$ are the physically important dimensions. We note that the Boulware–Deser spacetime in $N\ge 6$ dimensions, whether charged or not, will collapse to a strong, central curvature singularity for all $M(v)\ge 0$ (or a branch-like singularity for the charged case). The uncharged case mirrors general relativistic collapse. It is only in five dimensions, where a marked difference can be seen in the collapse dynamics of the uncharged Boulware–Deser spacetime and its counterpart with the electromagnetic field contribution. This highlights that $N=5$ is the critical dimension in EGB gravity, and that the electromagnetic field effects are more profound in EGB gravity, than in general relativity.

6 Higher dimensions

Gravitational contraction in higher dimensions is vital with regards to modified or higher order theories of gravity. Higher dimensional collapse has been extensively studied, for example see [76,77,78] in general relativity and [42, 79, 80] in modified gravity. As iterated earlier, the collapse process of the Boulware–Deser spacetime in dimensions greater than five differs from the five dimensional case. For all $N>5$ the collapse ceases with the formation of a strong curvature singularity, whether the spacetime has a charge contribution or not. If the charge component is there, the result of collapse is a branch singularity separating the physical spacetime from the region where the metric function is complex. The N-dimensional generalised Boulware–Deser metric is given by

$$\begin{aligned} ds^2=-f(v,r)dv^2+2dvdr+r^2d\varOmega ^2_{N-2}, \end{aligned}$$

(45)

where we have the $(N-2)$-sphere

$$\begin{aligned} d\varOmega _{N-2}^2=\sum _{i=1}^{N-2}\left[ \prod _{j=1}^{i-1}\sin ^2(\theta _{j})\right] (d\theta _{i})^2. \end{aligned}$$

In the above

$$\begin{aligned} f(v,r)=1+\frac{r^2}{2{\hat{\alpha }}}\left( 1-\sqrt{1+\frac{4{\hat{\alpha }}}{N-3}\left( \frac{2M(v,r)}{r^{N-1}}\right) }\right) , \end{aligned}$$

(46)

where we have set ${\hat{\alpha }}=\alpha (N-3)(N-4)$ for neatness. In higher dimensions the choice of the mass function (23) becomes

$$\begin{aligned} M(v,r)=M(v)-\frac{\kappa _{N}Q(v)^2}{2(N-2){\mathscr {A}}_{N-2}r^{N-3}}, \end{aligned}$$

(47)

where we note the explicit appearance of Einstein’s gravitational constant and the surface area of the $(N-2)$-sphere. The electromagnetic stress energy tensor (10) is built into this definition (47) above. The metric (46) then becomes

$$\begin{aligned} f(v,r)= & {} 1+\frac{r^2}{2{\hat{\alpha }}}\left( 1-\sqrt{G(v,r)}\right) , \end{aligned}$$

(48)

with

$$\begin{aligned} G(v,r)= & {} 1+\frac{4{\hat{\alpha }}}{N-3}\left[ \frac{2M(v)}{r^{N-1}}-\frac{\kappa _{N}Q(v)^2}{(N-2){\mathscr {A}}_{N-2}r^{2N-4}}\right] . \end{aligned}$$

(49)

We note the following:

• When $N=5$, the above expression (48) reduces to (25) found by Wiltshire [59].

• When $N=5$ and $Q(v)=0$, the expression (48) reduces to the uncharged metric (37).

We also note that there exists a maximal charge contribution to the higher dimensional metric (48) for which it remains real. This contribution depends on the dimension N, surface area ${\mathscr {A}}_{N-2}$, Einstein’s gravitational constant $\kappa _{N}$ and the Gauss–Bonnet constant ${\hat{\alpha }}=\alpha (N-3)(N-4)$. It is given by

$$\begin{aligned} |Q(v)|\le \sqrt{\frac{(N-2)(N-3)}{4{\hat{\alpha }}\kappa _{N}}{\mathscr {A}}_{N-2}\left[ r^{2N-4}+\frac{8{\hat{\alpha }}M(v)}{N-3}r^{N-3}\right] }, \end{aligned}$$

for all dimensions $N\ge 5$ and $\alpha \ne 0$. This can also be written in the form

$$\begin{aligned} r_{s}^{2N-4}+\frac{8{\hat{\alpha }}M(v)}{(N-3)}r_{s}^{N-3}-\frac{4{\hat{\alpha }}\kappa _{N}Q(v)^2}{(N-2)(N-3){\mathscr {A}}_{N-2}}\ge & {} 0, \end{aligned}$$

(50)

where $r=r_{s}(v)>0$ denotes a branch singularity separating the physical spacetime from the complex metric, analogously to the five dimensional case. When $N=5$ this reduces to (29). Therefore, the collapse process of null radiating matter within an electromagnetic field is similar for all dimensions $N\ge 5$.

The dimension appears to focus the effects of the higher order curvature indicative of the theory. If we consider the general N-dimensional metric (46), the formation of the apparent horizon will occur when

$$\begin{aligned} 1+\frac{r_{H}^2}{2{\hat{\alpha }}}\left( 1-\sqrt{1+\frac{4{\hat{\alpha }}}{N-3}\left( \frac{2M(v,r)}{r_{H}^{N-1}}\right) }\right) =0. \end{aligned}$$

(51)

This simplifies to

$$\begin{aligned} {\hat{\alpha }}r_{H}^{N-5}+r_{H}^{N-3}-\frac{2M(v,r)}{N-3}=0. \end{aligned}$$

(52)

It is important to note that whenever the order of the polynomial is odd, there will always be at least one real root. When the order is even, this need not be the case; all roots could possibly be complex. It is indeed possible to incorporate the electromagnetic field into the generalised mass function M(v, r) in (52). This gives

$$\begin{aligned}&{\hat{\alpha }}r_{H}^{N-5}+r_{H}^{N-3}-\frac{2M(v)}{N-3}\nonumber \\&\quad +\frac{\kappa _{N}Q(v)^2}{(N-2)(N-3){\mathscr {A}}_{N-2}r_{H}^{N-3}}=0. \end{aligned}$$

(53)

Equivalently, we can solve the above for the mass function to get

$$\begin{aligned} M= & {} \frac{N-3}{2}r_{H}^{N-3}+\frac{(N-3){\hat{\alpha }}}{2r_{H}^{N-5}}\nonumber \\&+\frac{\kappa _{N}Q^2}{2(N-2){\mathscr {A}}_{N-2}r_{H}^{N-3}}:=M_{H}(r_{H}). \end{aligned}$$

(54)

When $N=5$ in (54), this reduces to (35), and so the form of $M_{H}(r_{H})$ is qualitatively the same for all dimensions $N\ge 5$. Therefore, as previously mentioned, the gravitational collapse of charged null matter in higher dimensions is not different to the five dimensional case in EGBM gravity. This is markedly different to the uncharged scenario where in five dimensions collapse ceases with a weak conical singularity (for positive mass) and for dimensions six and higher, collapse terminates with a strong curvature singularity.

We will present different cases for the polynomials in different dimensions in Table 3.

Table 3 Horizon formation polynomials

It is interesting to note that when the electromagnetic field is present, we see in Table 3 that the polynomial equations in r are always of even order. When $Q=0$, the order of the polynomial equations alters from even to odd, with odd dimensions corresponding to even ordered polynomials and even dimensions corresponding to odd ordered equations. We deduce from this that for vanishing charge, and for all even dimensions, it is guaranteed that the resulting polynomial equation for the horizon formation will yield at least one real root. If such a root is positive, this means that an apparent horizon will always form to cover the central singularity. We can state the following in a theorem:

Theorem 1

Consider an uncharged collapsing, inhomogeneous and radiating Boulware–Deser spacetime in $N>5$ dimensions, from a regular epoch with a generalised mass function M(v, r) that obeys all physically reasonable energy conditions and is at least $C^2$ in the entire spacetime manifold. Whenever the dimension of spacetime is even (i.e. $N=\{2k,k\ge 3,k\in {\mathbb {Z}}\})$, and the real solution to the horizon formation equation is positive, the final fate of collapse will be a strong curvature singularity that will eventually be covered by an event horizon.

7 Conclusion

In this paper we studied the continual gravitational contraction of a charged null radiation shell in five dimensional EGBM gravity. The final outcome of collapse was the formation of a curvature branch singularity covered by two trapping horizons, of which the outer is visible to the external universe. The charge contribution yielded a situation where the metric is complex in a certain region, separated by this branch singularity. This is very different to uncharged radiating collapse where, for a positive mass, the final end state was an extended weak conical singularity which remains initially naked before succumbing to an apparent horizon at a later time. The electromagnetic field contribution critically alters the dynamics of the collapse process of the radiating Boulware–Deser spacetime. In general relativity, the charge contribution to the collapse process appears to be minimal when compared to EGB gravity. The collapse of the Vaidya spacetime and its charged counterpart both cease with the formation of a strong curvature singularity which may or may not be naked.

In EGB gravity the electromagnetic field contribution alters the type of singularity formed, post collapse. When $Q=0$ and $M>0$, the Boulware–Deser spacetime collapses to a weak and conical singularity which is initially kept naked by the presence of the positive Gauss–Bonnet coupling constant $\alpha$; the curvature corrections directly affect the collapse and post collapse scenarios. While naked, families of trajectories can escape to infinity from the singularity. Eventually an apparent horizon forms which encloses all trapped surfaces and this horizon eventually matches smoothly to an event horizon when the collapse process is complete. The event horizon separates the trapped surfaces from the external five dimensional Boulware–Deser vacuum. When $Q\ne 0$, gravitational collapse abates with the formation of a branch curvature singularity covered by two trapping horizons, the outer of which is visible to any observer at infinity. The branch singularity $r=r_{s}(v)$ results from the fact that the metric is complex whenever the inequality

$$\begin{aligned} r_{s}^6+8\alpha Mr_{s}^2-2\alpha Q^2\ge 0, \end{aligned}$$

is violated. This marked difference only occurs when the dimension of the spacetimes is $N=5$. This is due to the fact that the five dimensional uncharged Boulware–Deser metric (12) is regular and everywhere well defined for all values of r. This is not the case for the charged analogue (25). This is fundamentally different to the general relativistic case of radiation contraction. We note also that for the charged Boulware–Deser metric in all dimensions $N\ge 5$, there exists a maximal contribution due to the electromagnetic field, for which the metric on the spacetime remains real. Otherwise it becomes complex. This is critically different to the charged Vaidya analogue in Einstein gravity. This highlights the effects of the higher order corrections as well as those corrections in tandem with the electromagnetic field.

For all dimensions $N\ge 6$ the collapse of the charged shells of radiation mirror five dimensional collapse. It is only in the uncharged scenario where the collapse dynamics differ from $N=5$ and $N\ge 6$. This reinforces the notion that the role of dimension in gravitational collapse cannot be underestimated, especially when the gravity theory has modified curvature components and an electromagnetic field affecting the dynamics of the model. What remains to be done is a singularity analysis of the five dimensional charged collapse model. Are naked singularities possible? The conditions for a locally naked singularity; the determining of the existence of outgoing nonspacelike geodesics, need to be analysed. This will allow one to ascertain whether cosmic censorship is violated or not. This will be the subject of future work.

It will also be an interesting endeavour to look for possible observational signatures for compactified higher dimensions, and whether the underlying theory of gravity is indeed EGB gravity. There are numerous qualitative differences between four and higher dimensional gravitational collapse of null or charged null dust in Einstein gravity and these differences escalate in the presence of Gauss–Bonnet term. For example, in five dimensional neutral null dust collapse in EGB gravity, there is a possibility of forming a weak curvature extended naked conical singularity at the centre, that may give rise to strong quantum gravity signatures, that are not shielded from the external observers by the horizon [41]. Furthermore, as we have already seen, after the black hole forms in the radiating EGB collapse, the surface gravity and hence the Hawking temperature of the black holes crucially depend on the EGB coupling constant $\alpha$. In four dimensional general relativity, we know that the Hawking temperature of solar mass black holes is significantly less than the cosmic microwave background radiation (CMBR) temperature, and hence these are not readily detectable. However in higher dimensional EGB scenarios, there exists a set of non-zero measures of parameter values, that can actually make a solar mass black hole “hotter" than the CMBR, and hence should be, in principle, detectable via a measure of their Hawking radiation.

Appendices

Appendix A: Nonvanishing Einstein and Lovelock tensor components

The nonvanishing Einstein tensor components for the generalised metric (12) are given by

$$\begin{aligned} G^0{}_{0}= & {} -\frac{3\left( r^4+4\alpha M-r^4\sqrt{{\mathscr {F}}(v,r)}+\alpha rM_{r}\right) }{2\alpha r^4\sqrt{{\mathscr {F}}(v,r)}}\nonumber \\&=G^1{}_{1}, \end{aligned}$$

(A.1a)

$$\begin{aligned} G^1{}_{0}= & {} \frac{3M_{v}}{2r^3\sqrt{{\mathscr {F}}(v,r)}}, \end{aligned}$$

(A.1b)

$$\begin{aligned} G^2{}_{2}= & {} \frac{1}{2\alpha r^4(r^4+8\alpha M)\sqrt{{\mathscr {F}}(v,r)}}\nonumber \\&\times \left[ 3r^8\sqrt{{\mathscr {F}}(v,r)}-\alpha r^6M_{rr}\right. \nonumber \\&-3r^8+4\alpha r^2M_{r}^2-36\alpha r^4M\nonumber \\&-32\alpha ^2rMM_{r}-32\alpha ^2r^2M^2\nonumber \\&\left. -8\alpha ^2r^2MM_{rr}+24\alpha r^4M\sqrt{{\mathscr {F}}(v,r)}\right] \nonumber \\&=G^3{}_{3}=G^4{}_{4}. \end{aligned}$$

(A.1c)

The Lovelock tensor components which are nonzero are

$$\begin{aligned} H^0{}_{0}= & {} -\frac{3}{\alpha ^2r^3(r^4+8\alpha M)}\left[ r^7\sqrt{{\mathscr {F}}(v,r)}\right. \nonumber \\&\left. +\alpha r^4M_{r}\sqrt{{\mathscr {F}}(v,r)}-r^7-8\alpha ^2MM_{r}\right. \nonumber \\&\left. -\alpha r^4M_{r}-8\alpha r^3M+4\alpha r^3\sqrt{{\mathscr {F}}(v,r)}\right] \nonumber \\= & {} H^1{}_{1}, \end{aligned}$$

(A.2a)

$$\begin{aligned} H^1{}_{0}= & {} \frac{3M_{v}\left( r^4\sqrt{{\mathscr {F}}(v,r)}-r^4-8\alpha M\right) }{\alpha r^3(r^4+8\alpha M)}, \end{aligned}$$

(A.2b)

$$\begin{aligned} H^2{}_{2}= & {} \frac{1}{\alpha ^2r^4(r^4+8\alpha M)\sqrt{{\mathscr {F}}(v,r)}}\left[ \alpha r^6M_{rr}\sqrt{{\mathscr {F}}(v,r)}\right. \nonumber \\&-\alpha r^6M_{rr}+4\alpha ^2r^2M_{r}^2-36\alpha r^4M\nonumber \\&\left. +8\alpha ^2r^2MM_{rr}\sqrt{{\mathscr {F}}(v,r)}-8\alpha ^2r^2MM_{rr}\right. \nonumber \\&\left. +24\alpha r^4M\sqrt{{\mathscr {F}}(v,r)}-32\alpha ^2rMM_{r}\right. \nonumber \\&\left. -3r^8+3r^8\sqrt{{\mathscr {F}}(v,r)}-32\alpha ^2M^2\right] \nonumber \\= & {} H^3{}_{3}=H^4{}_{4}. \end{aligned}$$

(A.2c)

Again, in the above,

$$\begin{aligned} M_{v}=\frac{\partial M}{\partial v}, M_{r}=\frac{\partial M}{\partial r}, \end{aligned}$$

and ${\mathscr {F}}(v,r)=\sqrt{1+\frac{8\alpha M}{r^4}}$. Using (A.1) together with (A.2) in (7) will yield the system (16). Despite the inherent complexity of the above expressions, it is remarkable, though not altogether surprising, that their combinations result in significant simplification.

Appendix B: Charged radiation collapse in general relativity: a recap

The generalised Vaidya spacetime in five dimensions is given by

$$\begin{aligned} ds^2= & {} -f(v,r)dv^2+2\epsilon dvdr\nonumber \\&+r^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2), \end{aligned}$$

(B.3)

where we have

$$\begin{aligned} f(v,r)=\left( 1-\frac{m(v,r)}{r^2}\right) , \end{aligned}$$

(B.4)

and m(v, r) is the gravitational mass of the body. We note that $\epsilon =\pm 1$, however since we are dealing with collapsing matter, we take $\epsilon =1$. The Einstein field equations $G_{ab}=\kappa _{5}T_{ab}$ then become

$$\begin{aligned} 3\pi ^2\mu= & {} \frac{3m_{v}}{2r^{3}}, \end{aligned}$$

(B.5a)

$$\begin{aligned} 3\pi ^2\rho= & {} \frac{3m_{r}}{2r^{3}}, \end{aligned}$$

(B.5b)

$$\begin{aligned} 3\pi ^2P= & {} -\frac{m_{rr}}{2r^{2}}, \end{aligned}$$

(B.5c)

where subscripts denote differentiation. In the above, $\mu$ is the energy density of the null dust, $\rho$ is the energy density of the null string, and P is the null string pressure. The system (B.5) comes about as a result of the generalised two-fluid energy momentum tensor

$$\begin{aligned} T_{ab}=\mu l_{a}l_{b}+(\rho +P)(l_{a}n_{b}+l_{b}n_{a})+Pg_{ab}, \end{aligned}$$

(B.6)

where the vectors $l_{a}=\delta ^{0}{}_{a}$ and $n_{a}=\frac{1}{2}f(v,r)\delta ^{0}{}_{a}+\delta ^{1}{}_{a}$ are null. For the case of the charged Vaidya (or Vaidya-Bonner) spacetime, the mass function is given by

$$\begin{aligned} m(v,r)=m(v)-\frac{q(v)^2}{4r^{2}}. \end{aligned}$$

(B.7)

Therefore the charged Vaidya spacetime in five dimensions is then

$$\begin{aligned} ds^2= & {} -\left( 1-\frac{m(v)}{r^2}+\frac{q(v)^2}{4r^4}\right) dv^2+2dvdr\nonumber \\&+r^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2). \end{aligned}$$

(B.8)

We note the presence of the charge contribution q in (B.8). When $q=0$, the above reduces to the Vaidya metric. We can also write (B.5) as the system

$$\begin{aligned} \mu= & {} \frac{m_{v}}{2\pi ^2r^{3}}-\frac{qq_{v}}{4\pi ^2r^5}, \end{aligned}$$

(B.9a)

$$\begin{aligned} \rho= & {} P=\frac{q(v)^2}{4\pi ^2r^6}, \end{aligned}$$

(B.9b)

where the role of the charge contribution $q^2$ is more clear. When $q=0$ we obtain the single field equation of the five dimensional Vaidya solution. This is consistent with [20]. The energy conditions (17)–(20) for (B.8) will be satisfied if we have that

$$\begin{aligned} m_{v}\ge \frac{qq_{v}}{2r^2},q(v)\ge 0, \end{aligned}$$

and there is a violation of the first condition near $r=0$. It was shown in [70] that the energy conditions can still be satisfied in such a scenario if the equation of motion includes a Lorentz force term.

1.1 Collapse

For the charged Vaidya metric (B.8) the diffeomorphism invariants are given by

$$\begin{aligned} R^{abcd}R_{abcd}= & {} \frac{9}{4r^8}\left( 7q^4r^{12}-8mq^2r^6+32m^2\right) , \end{aligned}$$

(B.10a)

$$\begin{aligned} R^{ab}R_{ab}= & {} \frac{99}{4}q^4r^4, \end{aligned}$$

(B.10b)

$$\begin{aligned} C^{abcd}C_{abcd}= & {} \frac{9}{8r^8}\left( \left( 8m-q^2r^6\right) ^2\right) , \end{aligned}$$

(B.10c)

where the Kretschmann scalar $K=R^{abcd}R_{abcd}$ clearly diverges as $K\approx r^{-8}$. This is indicative of a strong curvature singularity at $r=0$. The boundary of the apparent horizon is given by

$$\begin{aligned} 1-\frac{m(v)}{r_{H}^2}+\frac{q(v)^2}{4r_{H}^4}=0, \end{aligned}$$

(B.11)

where $r_{H}$ denotes the radius of the apparent horizon. This gives the four solutions

$$\begin{aligned} r_{0}= & {} \pm \frac{1}{2}\sqrt{2m+2\sqrt{m^2-q^2}}, \end{aligned}$$

(B.12a)

$$\begin{aligned} r_{1}= & {} \pm \frac{1}{2}\sqrt{2m-2\sqrt{m^2-q^2}}. \end{aligned}$$

(B.12b)

Only the positive parts of (B.12a) and (B.12b) are viable so we have

$$\begin{aligned} r_{0}= & {} \frac{1}{2}\sqrt{2m+2\sqrt{m^2-q^2}}, \end{aligned}$$

(B.13a)

$$\begin{aligned} r_{1}= & {} \frac{1}{2}\sqrt{2m-2\sqrt{m^2-q^2}}. \end{aligned}$$

(B.13b)

Three cases arise depending on the sign of the discriminant $\varDelta =m^2-q^2$.

• 1. If $\varDelta <0$, there exist no real solutions and so there is no physical apparent horizon.

• 2. If $\varDelta =0$, we have the $m=q$ and the solutions (B.13) coincide with the single extremal apparent horizon in five dimensions, i.e. $r_{0}=r_{1}=\sqrt{m}$.

• 3. If $\varDelta >0$, there exist two physical apparent horizons, an inner horizon $r_{1}$ (also called a Cauchy horizon [81]) and the outer horizon $r_{0}$ for the radiating black hole.

Alternatively, solving (B.11) for m gives

$$\begin{aligned} m=r_{H}^2+\frac{q^2}{4r_{H}^2}:=m_{H}(r_{H}), \end{aligned}$$

(B.14)

which is a condition at a time $v=v$. The mass function $m_{H}(r_{H})$ is defined in the domain $0\le r<\infty$ and clearly diverges as $r\rightarrow 0$ or $r\rightarrow \infty$. The minimum value of the mass is $m_{H}(r_{H})=q$ at $r_{H}=\sqrt{\frac{1}{2}q}$. Thus, at a time $v=v$,

• if $m(v)<q(v)$, there is no trapping horizon,

• if $m(v)>q(v)$, there are two trapping horizons,

• if $m(v)=q(v)$, there is one degenerate horizon.

Therefore, the end state of collapse for a charged Vaidya spacetime with $m(v)>q(v)$ is a black hole with a strong curvature singularity covered by two horizons,⁸ with the outer horizon being the only one visible to an external observer.

The surface gravity (3) in $(v,r,\theta ,\phi )$ coordinates [74] for the charged Vaidya spacetime (B.8), is calculated to be

$$\begin{aligned} {\mathscr {K}}=\frac{m}{r_{H}^3}-\frac{q^2}{2r_{H}^5}. \end{aligned}$$

(B.15)

In the absence of charge, the above reduces to the quantity ${\mathscr {K}}=m/r_{H}^3$ for the five dimensional Vaidya spacetime. Using (41), the Hawking temperature at the horizon in five dimensions is then given by

$$\begin{aligned} {\mathscr {T}}_{H}=\frac{2{\mathscr {K}}}{{\mathscr {A}}_{3}}=\frac{{\mathscr {K}}}{\pi ^2}, \end{aligned}$$

(B.16)

which gives

$$\begin{aligned} {\mathscr {T}}_{H}=\frac{1}{\pi ^2}\left[ \frac{m}{r_{H}^3}-\frac{q^2}{2r_{H}^5}\right] , \end{aligned}$$

(B.17)

from (B.15) for the charged Vaidya spacetime (B.8). Note that both the mass function m and charge contribution q depend on v.