Resonant $a_0(980)$ state in triangle rescattering $D_s^+\rightarrow \pi ^+\pi ^0\eta$ decays

Abstract

We study the $D_s^+\rightarrow \pi ^+(a_0(980)^0\rightarrow )\pi ^0\eta$, $\pi ^0(a_0(980)^+\rightarrow )\pi ^+\eta$ decays, which have been recently measured by the BESIII collaboration. We propose that $D_s^+\rightarrow \pi ^{+(0)}(a_0(980)^{0(+)}\rightarrow )\pi ^{0(+)}\eta$ receives the contributions from the triangle rescattering processes, where $M^0$ and $\rho ^+$ in $D_s^+\rightarrow M^0 \rho ^+$, by exchanging $\pi ^{0(+)}$, are formed as $a_0(980)^{0(+)}$ and $\pi ^{+(0)}$, respectively, with $M^0=(\eta ,\eta ')$. Accordingly, we calculate that $\mathcal{B}(D_s^+\rightarrow a_0(980)^{0(+)}\pi ^{+(0)})= (1.7\pm 0.2\pm 0.1)\times 10^{-2}$ and $\mathcal{B}(D_s^+\rightarrow \pi ^{+(0)}(a_0(980)^{0(+)}\rightarrow )\pi ^{0(+)}\eta ) =(1.4\pm 0.1\pm 0.1)\times 10^{-2}$, being consistent with the data.

1 Introduction

Recently, the BESIII collaboration has measured the branching fraction of the $D_s^+$ decay that involves one of the scalar mesons below 1 GeV, $a_0\equiv a_0(980)$, which still has a controversial identification [1,2,3,4,5,6]. Explicitly, the branching fractions are observed as [7]

$$\begin{aligned}&\mathcal{B}(D_s^+\rightarrow \pi ^{+(0)}(a_0^{0(+)}\rightarrow )\pi ^{0(+)}\eta )\nonumber \\&\quad =(1.46\pm 0.15\pm 0.23)\times 10^{-2}\,, \end{aligned}$$

(1)

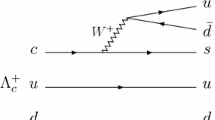
where the $D_s^+\rightarrow a_0^+\pi ^0$, $a_0^0\pi ^+$ decays are claimed as the W-annihilation (WA) dominant processes observed for the first time, as depicted in Fig. 1. Nonetheless, if $D_s^+\rightarrow a_0\pi$ proceeds through the WA $c\bar{s}\rightarrow W^+\rightarrow u\bar{d}$ decay, the G-parities of $u\bar{d}$ and $a_0\pi$ are odd and even, respectively [8, 9], such that $a_0\pi$ formed from $u\bar{d}$ violates G-parity conservation, indicating the suppressed WA process for $D_s^+\rightarrow a_0\pi$.

The same WA processes can also be applied to the $D^+$ section, being barely allowed by the current data. With $\mathcal{B}_{\text {WA}}(\eta ^{(\prime )}) \equiv \mathcal{B}(D^+\rightarrow \pi ^{+(0)}(a_0^{0(+)}\rightarrow )\pi ^{0(+)}\eta ^{(\prime )})$, we obtain that

$$\begin{aligned} \mathcal{B}_{\text {WA}}(\eta )\simeq & {} \bigg (\frac{f_D}{f_{D_s}}\bigg )^2 \bigg (\frac{|V_{cd}|}{|V_{cs}|}\bigg )^2\frac{\tau _{D}}{\tau _{D_s}} \bigg (\frac{m_{D_s}}{m_{D}}\bigg )^3\nonumber \\&\times \,\mathcal{B}(D^+_s\rightarrow \pi ^{+(0)}(a_0^{0(+)}\rightarrow )\pi ^{0(+)}\eta )\nonumber \\= & {} (1.2\pm 0.2)\times 10^{-3}, \end{aligned}$$

(2)

where $f_{D_{(s)}}$,$\tau _{D_{(s)}}$, $m_{D_{(s)}}$, and $V_{cq}$ ($q=d,s$) represent the decay constant, lifetime, mass for the $D^+_{(s)}$ meson, and the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements, respectively. It has been measured that $\mathcal{B}({\eta ,\eta '})\equiv \mathcal{B}(D^+\rightarrow \pi ^+\pi ^0\eta ,\pi ^+\pi ^0\eta ') =(1.4\pm 0.4,1.6\pm 0.5) \times 10^{-3}$ [10]. The fact of $\mathcal{B}(\eta )\simeq \mathcal{B}(\eta ')$ indicates that $D^+\rightarrow \pi ^+\pi ^0\eta ,\pi ^+\pi ^0\eta '$ have the same topologies except for the difference from the $\eta -\eta '$ mixing. With $\mathcal{B}_\rho (\eta ^{(\prime )}) \equiv \mathcal{B}(D^+\rightarrow \eta ^{(\prime )}(\rho ^+\rightarrow )\pi ^+\pi ^0)$ and $\mathcal{B}_{\text {WA}}(\eta ^{(\prime )})$ that mainly contribute to $\mathcal{B}(\eta ^{(\prime )})$, that is, $\mathcal{B}(\eta ^{(\prime )})=\mathcal{B}_\rho (\eta ^{(\prime )})+\mathcal{B}_{\text {WA}}(\eta ^{(\prime )})$, one should have $\mathcal{B}_{\rho ,\text {WA}}(\eta )\simeq \mathcal{B}_{\rho ,\text {WA}}(\eta ^{\prime })$. Nonetheless, due to $\mathcal{B}(a_0\rightarrow \pi \eta ')\simeq 0$, caused by $\mathcal{B}(a_0\rightarrow \pi \eta +K\bar{K})\simeq 100\%$ [10], it is estimated that $\mathcal{B}_{\text {WA}}(\eta ')= \mathcal{B}(D^+\rightarrow \pi ^{+(0)} a_0^{0(+)})\times \mathcal{B}(a_0^{0(+)}\rightarrow \pi ^{0(+)}\eta ^{\prime })\simeq 0$. This leads to $\mathcal{B}_{\text {WA}}(\eta )\gg \mathcal{B}_{\text {WA}}(\eta ')\simeq 0$, which strongly contradicts the relation of $\mathcal{B}_{\text {WA}}(\eta )\simeq \mathcal{B}_{\text {WA}}(\eta ^{\prime })$. According to the theoretical studies in Refs. [11, 12], it is obtained that $\mathcal{B}_\rho (\eta ,\eta ^{\prime })=(1.5\pm 0.5,1.2\pm 0.1)\times 10^{-3}$, which agree with $\mathcal{B}_{\rho }(\eta )\simeq \mathcal{B}_{\rho }(\eta ^{\prime })$; however, with $\mathcal{B}(\eta )=\mathcal{B}_\rho (\eta )+\mathcal{B}_{\text {WA}}(\eta )$, $\mathcal{B}_\rho (\eta )$ leaves tiny room for $\mathcal{B}(\eta )$ to accommodate $\mathcal{B}_{\text {WA}}(\eta )$. Therefore, it is reasonable to conclude that the W-annihilation topologies are unlikely to be the dominant contributions to $D_{(s)}^+\rightarrow \pi ^{+(0)}(a_0^{0(+)}\rightarrow )\pi ^{0(+)}\eta$.

Fig. 1

$D^+_{(s)}\rightarrow a_0^+\pi ^0$, $a_0^0\pi ^+$ via the W-annihilation diagrams

The nearly equal $\mathcal{B}(D_s^+\rightarrow \pi ^+ a_0^0,\pi ^0 a_0^+)\sim { O}(10^{-2})$ are much larger than the branching fractions of other measured pure W-annihilation decays [7], such as $\mathcal{B}(D_s^+\rightarrow \pi ^+\rho ^0)=(2.0\pm 1.2)\times 10^{-4}$. Besides, $\mathcal{B}(D_s^+\rightarrow \pi ^{+(0)} a_0^{0(+)})$ is close to $\mathcal{B}(D_s^+\rightarrow \pi ^+ \eta )=(1.70\pm 0.09)\times 10^{-2}$ and $\mathcal{B}(D_s^+\rightarrow \pi ^+ f_0(980))\sim { O}(10^{-2})$ [10], suggesting that $D_s^+\rightarrow \pi ^{+(0)}(a_0^{0(+)}\rightarrow )\pi ^{0(+)}\eta$ is more associated with the external W-boson emission processes. Particularly, the $D_s^+\rightarrow \eta \rho ^+,\eta '\rho ^+$ decays proceed through the external W-emission topology as depicted in Fig. 2, whose branching ratios are observed as large as $\mathcal{O}(10\%,5\%)$, respectively [10]. On the other hand, with $\mathcal{B}(D_s^+\rightarrow \eta \rho )\sim 10\%$, $D_s^+\rightarrow \eta (\rho ^+\rightarrow )\pi ^+\pi ^0$ could show up very prominently at the $\pi ^+\pi ^0$ invariant mass spectrum below 1 GeV, which might provide a possible $\pi ^+\pi ^0$ final state interaction for the $a_0^+$ formation. Nonetheless, $\pi ^+\pi ^0\rightarrow a_0^+$ $(a_0^+\rightarrow \pi ^+\pi ^0)$ is a disflavored strong interaction [10]. Moreover, without an extra particle emitting to change the helicity state, the vector to scalar transition through the strong interaction should be much suppressed due to the helicity conservation. We hence propose that, via the triangle rescattering diagrams in Fig. 3, $D_s^+\rightarrow \pi ^{+(0)}(a_0^{0(+)}\rightarrow )\pi ^{0(+)}\eta$ is able to receive the main contributions from $D_s^+\rightarrow \eta ^{(\prime )}\rho ^+$, where $\eta ^{(\prime )}$ and $\rho ^+$ exchange $\pi$ in the final state interaction, and transform as $a_0$ and $\pi$, respectively. In this report, we will calculate the $D_s^+\rightarrow \pi ^{+(0)}(a_0^{0(+)}\rightarrow )\pi ^{0(+)}\eta$ decays via the triangle rescattering diagrams, in order to explain the recent BESIII observation [7].

Fig. 2

The short-distance contribution to $D^+_s\rightarrow \eta ^{(\prime )}\rho ^+$ decay

Fig. 3

The triangle rescattering diagrams for a $D^+_s\rightarrow \pi ^+(a_0^0\rightarrow )\pi ^0\eta$ and b $D_s^+\pi ^0(a_0^+\rightarrow )\pi ^+\eta$

2 Formalism

The three-body $D^+_s\rightarrow \eta \pi ^+\pi ^0$ decay predominantly comes from $D^+_s\rightarrow \eta (\rho ^+\rightarrow )\pi ^+\pi ^0$. Besides, it receives the contributions from the $D^+_s\rightarrow \pi ^+(a_0^0\rightarrow )\pi ^0\eta$, $\pi ^0(a_0^+\rightarrow )\pi ^+\eta$ decays, which proceed through the triangle rescattering diagrams in Fig. 3a, b, respectively. These resonant $D_s^+$ decays involve $D^+_s\rightarrow \eta ^{(\prime )}\rho ^+$, $a_0\rightarrow \eta ^{(\prime )}\pi$ and $\rho ^+\rightarrow \pi ^+\pi ^0$. For $D^+_s\rightarrow \eta ^{(\prime )}\rho ^+$, the relevant effective Hamiltonian for the $c\rightarrow s u\bar{d}$ transition is given by [13]

$$\begin{aligned} \mathcal{H}_{eff}= & {} \frac{G_F}{\sqrt{2}} V_{cs}^*V_{ud} [c_1(\bar{u} d)(\bar{s} c)+c_2(\bar{s} d)(\bar{u} c)], \end{aligned}$$

(3)

where $G_F$ is the Fermi constant, $V_{ij}$ the CKM matrix elements, $c_{1,2}$ the Wilson coefficients, and $(\bar{q}_1 q_2)$ stand for $\bar{q}_1\gamma _\mu (1-\gamma _5)q_2$. The amplitude of the $D_s^+\rightarrow \eta ^{(\prime )}\rho ^+$ decay can be factorized as [14]

$$\begin{aligned}&\mathcal{A}(D_s^+\rightarrow \eta ^{(\prime )}\rho ^+)\nonumber \\&\quad =\frac{G_F}{\sqrt{2}}V_{cs}^*V_{ud} a_1 \langle \rho ^+|(\bar{u}d)|0\rangle \langle \eta ^{(\prime )}|(\bar{s} c)|D_s^+\rangle \,, \end{aligned}$$

(4)

where $a_1=c_1+c_2/N_c$, with $N_c$ the color number. The matrix elements in Eq. (4) are defined by [15]

$$\begin{aligned} \langle \rho ^+|(\bar{u}d)|0\rangle= & {} m_\rho f_\rho \epsilon _\mu ^*,\nonumber \\ \langle \eta ^{(\prime )}|(\bar{s} c)|D_s^+\rangle= & {} (p_{D_s}+p_{\eta ^{(\prime )}})_\mu F_+^{(\prime )}(q^2)+q_\mu F_-^{(\prime )}(q^2), \end{aligned}$$

(5)

with $q_\mu =(p_{D_s}-p_{\eta ^{(\prime )}})_\mu$, $\epsilon _\mu ^*$ the polarization vector and $f_\rho$ the decay constant. Besides, the form factor $F_{(\pm )}^{(\prime )}(q^2)$ is in the double-pole parameterization [15]:

$$\begin{aligned} F(q^2)=\frac{F(0)}{1-a(q^2/m_{D_s}^2)+b(q^4/m_{D_s}^4)}. \end{aligned}$$

(6)

Substituting the matrix elements in Eq. (4) with those in Eq. (5), we obtain $\mathcal{A}(D_s^+\rightarrow \eta ^{(\prime )}\rho ^+)$ $=G_{D_{s}\rho \eta ^{(\prime )}}\epsilon ^*\cdot (p_{D_s}+p_{\eta ^{(\prime )}})$ with $G_{D_s \rho \eta ^{(\prime )}}\equiv (G_F/\sqrt{2})V_{cs}^*V_{ud} a_1 m_\rho f_\rho F_+^{(\prime )}(m^2_\rho )$, while $F_-^{(\prime )}(t)$ gives the vanishing contribution due to $\epsilon \cdot q=0$. For the strong decays $a_0\rightarrow \alpha \beta$ and $\rho ^+\rightarrow \pi ^+\pi ^0$, one writes their amplitudes as

$$\begin{aligned}&\mathcal{A}(a_0\rightarrow \alpha \beta )=g_{a_0\alpha \beta },\;\;\nonumber \\&\mathcal{A}(\rho ^+\rightarrow \pi ^+\pi ^0)=g_{\rho \pi \pi }\epsilon \cdot (p_{\pi ^+}-p_{\pi ^0}), \end{aligned}$$

(7)

where $\alpha \beta$ could be $\eta ^{(\prime )}\pi$ or $K{\bar{K}}$, and $g_{a_0\eta ^{(\prime )}\pi }$ and $g_{\rho \pi \pi }$ are the strong coupling constants. We hence present the amplitudes of the resonant $D_s^+\rightarrow \pi ^+\pi ^0\eta$ decays as [16,17,18,19,20,21]

$$\begin{aligned} \mathcal{A}_\rho\equiv & {} \mathcal{A}(D_s^+\rightarrow \eta (\rho ^+\rightarrow )\pi ^+\pi ^0) =\frac{-i}{D_1}\hat{\mathcal{A}}_\rho (s-t), \nonumber \\ \mathcal{A}_{a(b)}^{(\prime )}\equiv & {} \mathcal{A}(D_s^+\rightarrow \pi ^{+(0)}(a_0^{0(+)}\rightarrow )\pi ^{0(+)}\eta ^{(\prime )})\nonumber \\= & {} \frac{1}{D_0}\hat{\mathcal{A}}^{(\prime )}\mathcal{T}_{a(b)}^{(\prime )},\nonumber \\ \mathcal{T}_{a(b)}^{(\prime )}= & {} -i\int \frac{d^4 q}{(2\pi )^4 } \frac{(2p_{D_s}-q)_{\mu }\left( -g^{\mu \nu }+\frac{q^{\mu }q^{\nu }}{q^2}\right) (q-2p_{\pi ^{+(0)}})_{\nu }}{D_1 D_2 D_3},\nonumber \\ \end{aligned}$$

(8)

with $s\equiv (p_{\pi ^0}+p_{\eta })^2$ and $t\equiv (p_{\pi ^+}+p_{\eta })^2$. Besides, we present that $\hat{\mathcal{A}}_\rho =G_{D_s\rho \eta }g_{\rho \pi \pi }$, $\hat{\mathcal{A}}=G_{D_s\rho \eta } g^2_{a_0\eta \pi }g_{\rho \pi \pi }$ and $\hat{\mathcal{A}}^{\prime }=G_{D_s\rho \eta ^{\prime }} g_{a_0\eta ^{\prime }\pi } g_{a_0\eta \pi } g_{\rho \pi \pi }$. For the propagators in Eq. (8), $D_i$ are given by

$$\begin{aligned}&D_0=x-m_{a_0}^{2}-\sum \limits _{\alpha \beta } {[\text {Re}\Pi ^{\alpha \beta }_{a_0}(m^2_{a_0})-\Pi ^{\alpha \beta }_{a_0}(x)]},\nonumber \\&D_1=q^2-m_{\rho }^2+im_\rho \Gamma _\rho \,,\nonumber \\&D_2=(p_{\pi ^{0(+)}}-q)^2-m_{\pi ^{0(+)}}^2+i\epsilon ^{+}, \nonumber \\&D_3=(q-p_{\eta ^{(\prime )}})^2-m_{\eta ^{(\prime )}}^2+i\epsilon ^{+}, \end{aligned}$$

(9)

where $x=(s,t)$ for $a_0^{(0,+)}$ in $\mathcal{A}_{(a,b)}^{(\prime )}$. The function of $\Pi ^{\alpha \beta }_{a_0}(x)$ in $1/D_0$ is adopted as [22],

Fig. 4

The partial distributions vs. $m_{\pi \eta }$, where the solid line is for $\mathcal{A}_\rho$ only, while the dashed line receive the contributions from $\mathcal{A}_\rho$ and $\mathcal{A}_{a,b}^{(\prime )}$, in comparison with the data points in [7]

Fig. 5

The partial distributions vs. $m_{\pi \eta }$ with the cut of $m_{\pi ^+\pi ^0}>1.0$ GeV, in comparison with the data points in [7]

$$\begin{aligned} \Pi ^{\alpha \beta }_{a_0}(x)= & {} \frac{g^{2}_{a_0 \alpha \beta }}{16\pi } \bigg \{\frac{m_{\alpha \beta }^+ m_{\alpha \beta }^-}{\pi x} \log \bigg [\frac{m_\beta }{m_\alpha }\bigg ]-\theta [x-(m_{\alpha \beta }^+)^2]\nonumber \\&\times \,\rho _{\alpha \beta }\biggl (i+\frac{1}{\pi } \log \biggl [\frac{\sqrt{x-(m_{\alpha \beta }^+)^{2}}+\sqrt{x-(m_{\alpha \beta }^-)^{2}}}{\sqrt{x-(m_{\alpha \beta }^-)^{2}}-\sqrt{x-(m_{\alpha \beta }^+)^{2}}}\biggr ]\biggr ) \nonumber \\&-\,\rho _{\alpha \beta }\biggl (1-\frac{2}{\pi } \arctan \biggl [\frac{\sqrt{-x+(m_{\alpha \beta }^+)^{2}}}{\sqrt{x-(m_{\alpha \beta }^-)^{2}}}\biggr ]\biggr ) (\theta [x-(m_{\alpha \beta }^-)^{2}]\nonumber \\&-\,\theta [x-(m_{\alpha \beta }^+)^{2}])\nonumber \\&+\,\rho _{\alpha \beta }\frac{1}{\pi } \log \bigg [\frac{\sqrt{(m_{\alpha \beta }^+)^{2}-x}+\sqrt{(m_{\alpha \beta }^-)^2-x}}{\sqrt{(m_{\alpha \beta }^-)^{2}-x}-\sqrt{(m_{\alpha \beta }^+)^2-x}}\bigg ] \theta [(m_{\alpha \beta }^-)^{2}-x]\bigg \},\nonumber \\ \end{aligned}$$

(10)

where $m_{\alpha \beta }^\pm =m_\alpha \pm m_\beta$ and $\rho _{\alpha \beta }\equiv \left| \sqrt{x-(m_{\alpha \beta }^+)^{2}}\sqrt{x-(m_{\alpha \beta }^-)^{2}}\right| /x$. Using $1/D_0$ that presents the propagator of $a_0$, instead of the Breit-Wigner function like $1/D_1$, we take into account the contributions from the virtual intermediate states of $\eta ^{(\prime )}\pi$ and $\bar{K}K$, such that the cusp effect at the threshold of $(m_K+m_{\bar{K}})$ can be given in the $\eta \pi$ invariant mass spectra [22, 23]. To proceed, we reduce $\mathcal{T}_{a,b}$ in Eq. (8) as $\mathcal{T}_a=\mathcal{T}(s)$ and $\mathcal{T}_b=-\mathcal{T}(t)$, with $\mathcal{T}(x)$ given by [21]

$$\begin{aligned} \mathcal{T}(x)= & {} -i(m_{D_s}^2-m_\rho ^2+im_\rho \Gamma _\rho +2m^{2}_{\pi }\nonumber \\&-\,2x+m_{\eta }^{2})\int \frac{d^4q}{(2\pi )^4}\frac{1}{D_1D_2D_3}\nonumber \\&-\,i\left( 1+\frac{m_{D_s}^2-m_{\eta }^{2}}{m_\rho ^2-im_\rho \Gamma _\rho }\right) \int \frac{d^4q}{(2\pi )^4}\frac{1}{D_1D_3}\nonumber \\&-\,i\int \frac{d^4q}{(2\pi )^4}\frac{1}{D_1D_2}\nonumber \\&+\,i\int \frac{d^4q}{(2\pi )^4}\frac{1}{q^2D_1}+i\frac{m_{D_s}^2-m_{\eta }^{2}}{m_\rho ^2-im_\rho \Gamma _\rho }\nonumber \\&\times \, \int \frac{d^4q}{(2\pi )^4}\frac{1}{q^2D_3} +i\int \frac{d^4q}{(2\pi )^4}\frac{1}{D_2D_3}\,, \end{aligned}$$

(11)

where $m_{\pi ^0(K^0)}^2\simeq m_{\pi ^+(K^+)}^2$ has been used. In the above, the integrations of the multi-point functions can be found in [24]. It is interesting to note that the ultraviolet divergences caused by the individual integrations cancel out [21, 25], such that a cut-off needs not to be introduced in our calculation. In the same way, we obtain $\mathcal{T}^{\prime }_{a(b)}$ by replacing $\eta$ in $\mathcal{T}_{a(b)}$ with $\eta '$. To integrate over the phase space in the three-body decay, we refer the general equation of the decay width in the PDG [10]

$$\begin{aligned} \Gamma =\int _{s}\int _{t} \frac{1}{(2\pi )^3}\frac{|\mathcal{A}|^2}{32m^3_{D_s}}ds dt. \end{aligned}$$

(12)

3 Numerical results and discussions

In the numerical analysis, we use $V_{cs}=V_{ud}=1-\lambda ^2/2$ with $\lambda =0.22453\pm 0.00044$ in the Wolfenstein parameterization and the decay constant $f_\rho =(210.6\pm 0.4)$ MeV [10]. For the strong coupling constants, it is given that $(g_{a_0\eta \pi },g_{a_0\eta '\pi },g_{a_0 K\bar{K}})= (2.87\pm 0.09,-2.52\pm 0.08,2.94\pm 0.13)$ GeV [21, 23], while $g_{\rho \pi \pi }=6.0$ is extracted from $\mathcal{B}(\rho ^+\rightarrow \pi ^+\pi ^0)\simeq 100\%$ [10]. We adopt $F_+^{(\prime )}(q^2)$ from Ref. [15] as $(F_+(0),\,a,\,b)=(0.78,\,0.69,\,0.002)$ and $(F'_+(0),\,a,\,b)=(0.73,\,0.88,\,0.018)$. By relating the calculated branching fraction of $D_s^+\rightarrow \eta \rho ^+$ to the measured value of $(7.4 \pm 0.6)\%$ [7], we determine $a_1=0.93\pm 0.04$, where $a_1$ of $\mathcal{O}(1.0)$ demonstrates the validity of the generalized factorization [14]. Consequently, we obtain the branching fractions for $D_s^+\rightarrow a_0^{+(0)}\pi ^{0(+)}$ and $\pi ^{+(0)}(a_0^{0(+)}\rightarrow )\pi ^{0(+)}\eta$ decays,

$$\begin{aligned}&\mathcal{B}(D_s^+\rightarrow a_0^{0(+)}\pi ^{+(0)})=(1.7\pm 0.2\pm 0.1)\times 10^{-2}\,,\nonumber \\&\mathcal{B}(D_s^+\rightarrow \pi ^{+(0)}(a_0^{0(+)}\rightarrow )\pi ^{0(+)}\eta )\nonumber \\&\quad =(1.4\pm 0.1\pm 0.1)\times 10^{-2}\,, \end{aligned}$$

(13)

where the uncertainties consider the main contributions from $a_1$ and $g_{a_0\alpha \beta }$, in order. We also draw the partial distributions in Figs. 4 and 5 to compare with the data.

Our results of the branching fractions, Eq. (13), agree with the data, Eq. (1). Besides, we predict $\mathcal{B}(D_s^+\rightarrow a_0^0\pi ^+)=\mathcal{B}(D_s^+\rightarrow a_0^+\pi ^0)$, which agrees with the observation that these two-body decays have equal sizes. The $D_s^+\rightarrow \rho \eta$ and $D_s^+\rightarrow \rho ^+\eta '$ decays both give triangle rescattering effects. Despite the fact that $\mathcal{B}(D_s^+\rightarrow \rho ^+\eta ')$ is a few times smaller than $\mathcal{B}(D_s^+\rightarrow \rho ^+\eta )$ [10], they give similar contributions to $\mathcal{B}(D_s^+\rightarrow a_0\pi )$ and $\mathcal{B}(D_s^+\rightarrow \pi (a_0\rightarrow )\eta \pi )$. Since $\Gamma _\rho \gg \Gamma _{\eta ^{(\prime )},\pi }$, the $\rho$ meson decay width is not negligible, which causes the width effect [21, 25, 26]. As a test, we also treat the $\rho$ meson as a stable particle. Without considering the $\rho$-meson decay width, it is found that the branching fractions of $D_s^+\rightarrow \pi a_0$ and $D_s^+\rightarrow \pi (a_0\rightarrow )\eta \pi$ are increased by 10%.

The contributions from $D_s^+\rightarrow \pi ^+(a_0^0\rightarrow )\pi ^0\eta$ and $D_s^+\rightarrow \pi ^0(a_0^+\rightarrow )\pi ^+\eta$ are concluded to interfere with a relative phase of $180^\circ$ in Ref. [7]. With $\rho ^+(q)\rightarrow \pi ^0(q-p_2)\pi ^+(p_2)$ and $\rho ^+(q)\rightarrow \pi ^+(q-p_2)\pi ^0(p_2)$ for $\mathcal{A}_{a,b}$, respectively, where $p_2$ is the energy flow for the out-going $\pi$ in the integration, it leads to $\mathcal{A}_{a}(\rho ^+\rightarrow \pi ^{+}\pi ^{0})=-\mathcal{A}_{b}(\rho ^+\rightarrow \pi ^{0}\pi ^{+})$ from Eq. (7). Clearly, the minus sign gives the theoretical explanation to the phase of $180^\circ$ in the data. The $\pi \eta$ invariant mass spectra in Figs. 4 and 5 are demonstrated to be consistent with the data [7].

4 Conclusions

In summary, we have proposed that $D_s^+\rightarrow \pi ^{+(0)}(a_0^{0(+)}\rightarrow )\pi ^{0(+)}\eta$ mainly proceeds through the triangle loops. By exchanging $\pi ^{+(0)}$, $M^0$ and $\rho ^+$ in $D_s^+\rightarrow M^0\rho ^+$ are formed as $a_0$ and $\pi ^{0(+)}$, respectively, where $M^0=(\eta ,\eta ')$. Particularly, we have presented that $\mathcal{B}(D_s^+\rightarrow a_0^{0(+)}\pi ^{+(0)})=(1.7\pm 0.2\pm 0.1)\times 10^{-2}$ and $\mathcal{B}(D_s^+\rightarrow \pi ^{+(0)}(a_0^{0(+)}\rightarrow )\pi ^{0(+)}\eta )=(1.4\pm 0.1\pm 0.1)\times 10^{-2}$, in good agreement with the data.