Study of the $D_s^+\rightarrow a_0(980) \rho$ and $a_0(980) \omega$ decays

Abstract

We study $D_{s}^{+}\rightarrow \rho ^{0(+)}a^{+(0)}_{0}$, $D_{s}^{+}\rightarrow \omega a^{+}_{0}$, and the resonant $D_{s}^{+}\rightarrow \rho a_0$, $a_{0}\rightarrow \eta \pi (KK)$ decays. In the final state interaction, where $D_s^+\rightarrow (\eta ^{(\prime )}\pi ^+,K^+{{\bar{K}}}^0)$ are followed by the $(\eta ^{(\prime )}\pi ^+,K^+{{\bar{K}}}^0)$ to $\rho ^{0(+)}a^{+(0)}_{0}$ rescatterings, we predict $\mathcal{B}(D_{s}^{+}\rightarrow \rho ^{0(+)}a^{+(0)}_{0})=(3.0\pm 0.3\pm 1.0)\times 10^{-3}$. Due to the cancellation of the rescattering effects and the suppressed short-distance W annihilation contribution, we expect that ${{\mathcal {B}}}(D_{s}^{+}\rightarrow \omega a^{+}_{0}) \simeq \mathcal{B}(D_s^+\rightarrow \pi ^+\pi ^0)<3.4\times 10^{-4}$. In our calculation, ${{\mathcal {B}}}(D_{s}^{+}\rightarrow \rho ^{0}(a^{+}_{0}\rightarrow )\eta \pi ^{+}) =(1.6^{+0.2}_{-0.3}\pm 0.6)\times 10^{-3}$ agrees with the data, whereas ${{\mathcal {B}}}(D_{s}^{+}\rightarrow \rho ^{+}(a^{0}_{0}\rightarrow )K^+K^-)$ is 10 times smaller than the observation, which requires a careful examination.

1 Introduction

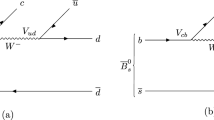
The two-body $D_s^+\rightarrow PP,PV$ decays with P(V) denoting the strangeless pesudoscalar (vector) meson have no configurations from the W-boson emission processes because ${{\bar{s}}}$ in $D_s^+$ cannot be eliminated, as drawn in Fig. 1 for the topological diagrams T and C. Interestingly, it leads to a specific exploration for the annihilation mechanism applied to $D_s^+\rightarrow \pi ^+\pi ^0,\pi ^{+}\rho ^{0},\pi ^+\omega$ [1,2,3,4,5,6].

In the short-distance W-boson annihilation (WA) $D_s^+(c{{\bar{s}}})\rightarrow W^+\rightarrow u{{\bar{d}}}$ process, $u{{\bar{d}}}$ can be seen to move in the opposite directions in the $D_s^+$ rest frame, such that there exists no orbital angular momentum between them. It indicates that $G(u{{\bar{d}}})=G(\pi ^+)=+1$ with G denoting the G-parity symmetry [3]. Since G-parity is a multiplicative quantum number, one obtains $G(\pi ^+\rho ^0,\pi ^+\pi ^0)=(+1,-1)$. Consequently, the WA $D_s^+\rightarrow \pi ^+\rho ^0(\pi ^+\pi ^0)$ decay due to $G(u{{\bar{d}}})=G(\pi ^+\rho ^0)[=-G(\pi ^+\pi ^0)]$ is a G-parity conserved (violated) process, which corresponds to the experimental result ${{\mathcal {B}}}(D_s^+\rightarrow \pi ^+\rho ^0)=(1.9\pm 1.2)\times 10^{-4}$ $[{{\mathcal {B}}}(D_s^+\rightarrow \pi ^+\pi ^0)<3.4\times 10^{-4}]$ [7]. By contrast, although the WA $D_s^+\rightarrow \pi ^+\omega$ decay violates the G-parity symmetry, ${{\mathcal {B}}}(D_s^+\rightarrow \pi ^+\omega )=(1.9\pm 0.3)\times 10^{-3}$ shows no suppression [7]. It is hence considered to receive the long-distance annihilation contribution [1, 3].

The $D_s^+\rightarrow SP,SV$ decays can help to investigate the short and long-distance annihilation mechanisms [8,9,10], where S stands for a non-strange scalar meson. For example, the WA process for $D_s^+\rightarrow a_0^{0(+)}\pi ^{+(0)}$ violates G-parity [9, 11], such that its branching fraction is expected as small as ${{\mathcal {B}}}(D_s^+\rightarrow \pi ^+\pi ^0)$. Nonetheless, one measures that ${{\mathcal {B}}}(D_s^+\rightarrow a_0^{0(+)}\pi ^{+(0)})\simeq 100 {{\mathcal {B}}}(D_s^+\rightarrow \pi ^+\rho ^0)$ [7, 12]. Clearly, it indicates the main contribution from the long-distance annihilation process [9]. Explicitly, the long-distance annihilation process for $D_s^+\rightarrow a_0^{0(+)}\pi ^{+(0)}$ starts with the $D_s^+\rightarrow \eta ^{(\prime )}\rho ^+$ weak decay, followed by the $\eta ^{(\prime )}$ and $\rho ^+$ rescattering. With the $\pi ^{+(0)}$ exchange, $\eta ^{(\prime )}$ and $\pi ^+$ are turned into $a_0^{+(0)}$ and $\pi ^{0(+)}$, respectively. Since BESIII has recently reported the first observation of the branching fractions of $D_s^+\rightarrow SV,S\rightarrow PP$ as [13, 14]

Fig. 1

Topological diagrams for the Cabibbo-allowed $D_s^+$ weak decays

$$\begin{aligned} {{\mathcal {B}}}_+(D_s^+\rightarrow a_0^+ \rho ^0,a_0^+\rightarrow \pi ^+\eta )&=(2.1\pm 0.8 \pm 0.5)\times 10^{-3} ,\nonumber \\ {{\mathcal {B}}}_0(D_s^+\rightarrow a_0^0 \rho ^+,a_0^0\rightarrow K^+ K^-)&=(0.7\pm 0.2\pm 0.1)\times 10^{-3} , \end{aligned}$$

(1)

we are wondering which of the short and long-distance annihilation processes can be the dominant contribution. Hence, we propose to study $D_s^+\rightarrow a_0^{+(0)} \rho ^{0(+)}$, $D_s^+\rightarrow a_0^+\omega$, and the resonant three-body $D_s^+\rightarrow a_0^{+(0)} \rho ^{0(+)}, a_0^{+(0)}\rightarrow [\eta \pi ^{+(0)},K^+{{\bar{K}}}^0(K^+ K^-)]$ decays, in order to analyze the data in Eq. (1). We will also test if ${{\mathcal {B}}}(D_s^+\rightarrow a_0^+ \rho ^0, a_0^+ \rho ^0)$ have nearly equal sizes as ${{\mathcal {B}}}(D_s^+\rightarrow a_0^+ \pi ^0)\simeq {{\mathcal {B}}}(D_s^+\rightarrow a_0^0 \pi ^+)$ that respects the isospin symmetry.

2 Formalism

Fig. 2

Triangle rescattering diagrams for $D^+_s\rightarrow \rho ^{0(+)}a_0^{+(0)}$ and $D^+_s\rightarrow \omega a_0^+$

Considering the short-distance WA processes, $D_s^+\rightarrow PP(PV)$ and $D_s^+\rightarrow SP(SV)$ both get an A term as the annihilation amplitude in Fig. 1. According to ${{\mathcal {B}}}(D_s^+\rightarrow \pi ^+\rho ^0)\simeq 10^{-4}$ that receives the short-distance WA contribution [7], one regards A to give ${{\mathcal {B}}}(D_s^+\rightarrow a_0^{+(0)} \rho ^{0(+)})$ not larger than $10^{-4}$. However, $\mathcal{B}_+$ in Eq. (1) suggests ${{\mathcal {B}}}(D_s^+\rightarrow a_0^+ \rho ^0)\simeq 10^{-3}$. This strongly suggests that the main contribution to $D_s^+\rightarrow a_0^{+(0)} \rho ^{0(+)}$ is from the long-distance annihilation process. For $D_s^+\rightarrow a_0^+\omega$, the WA contribution is suppressed with the G-parity violation, such that $A\simeq 0$. Therefore, we start with the triangle rescattering processes for $D_s^+\rightarrow a_0^{+(0)} \rho ^{0(+)}$ and $D_s^+\rightarrow a_0^+\omega$ as the most possible main contributions.

See Fig. 2, the rescattering processes for $D_s^+\rightarrow a_0^{+(0)} \rho ^{0(+)}$ include both the weak and strong decays. In our case, the weak decays come from $D^{+}_{s}\rightarrow \pi ^{+}\eta ^{(\prime )},K^{+}{\bar{K}}^0$, and the amplitudes are given by [2,3,4, 6]

$$\begin{aligned} {{\mathcal {M}}}_\eta (D^{+}_{s}\rightarrow \pi ^{+}\eta )= & {} \frac{G_F}{\sqrt{2}} V^*_{cs}V_{ud}(\sqrt{2}A\cos \phi -T\sin \phi ) ,\nonumber \\ {{\mathcal {M}}}_{\eta '}(D^{+}_{s}\rightarrow \pi ^{+}\eta ^{\prime })= & {} \frac{G_F}{\sqrt{2}}V^*_{cs}V_{ud}(\sqrt{2}A\sin \phi +T\cos \phi ) ,\nonumber \\ {{\mathcal {M}}}_K(D^{+}_{s}\rightarrow K^{+}{\bar{K}}^0)= & {} \frac{G_F}{\sqrt{2}}V^*_{cs}V_{ud}(C+A) , \end{aligned}$$

(2)

where $G_F$ is the Fermi constant, $V^*_{cs}V_{ud}$ the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements, and $V^*_{cs}V_{ud}\simeq 1$ presents the Cabibbo-allowed decay modes. In addition, (T, C, A) are the topological amplitudes, along with the mixing angle $\phi =43.5^\circ$ from the $\eta -\eta ^\prime$ mixing matrix [15, 16]:

$$\begin{aligned} \left( \begin{array}{c} \eta \\ \eta ^\prime \end{array}\right) = \left( \begin{array}{cc} \cos \phi &{} -\sin \phi \\ \sin \phi &{} \cos \phi \end{array}\right) \left( \begin{array}{c} \sqrt{1/2}(u{{\bar{u}}}+d\bar{d}) \\ s{{\bar{s}}} \end{array}\right) . \end{aligned}$$

(3)

For the strong decays $V,S\rightarrow PP$, the amplitudes are given by [9]

$$\begin{aligned}&{{\mathcal {M}}}_{\rho ^{0(+)}\rightarrow \pi ^{+(0)}\pi ^{-(+)}}=g_\rho \epsilon \cdot (q_1-q_2),\,\nonumber \\&{{\mathcal {M}}}_{a_0^+\rightarrow \eta ^{(\prime )}\pi ^+,K^+\bar{K}^0}=g_{\eta ^{(\prime )}},g_K , \end{aligned}$$

(4)

where $\epsilon _{\mu }$ is the polarization four vector of the $\rho$ meson, and $q_{1,2}^\mu$ are the four momenta of $\pi ^+\pi ^-(\pi ^0\pi ^+)$, respectively. The SU(3) flavor symmetry is able to relate different $V(S)\rightarrow PP$ decay channels [17, 18], such that we obtain $g_\rho /2$ for ${{\mathcal {M}}}_{\rho ^0\rightarrow K^+ K^-,{{\bar{K}}}^0 K^0}$, $g_\rho /\sqrt{2}$ for ${{\mathcal {M}}}_{\rho ^+\rightarrow K^+{{\bar{K}}}^0}$, and $(-)g_K/\sqrt{2}$ for ${{\mathcal {M}}}_{a^0_0\rightarrow K^+ K^-({{\bar{K}}}^0 K^0)}$, together with $(-)g_\rho /2$ for ${{\mathcal {M}}}_{\omega \rightarrow K^+ K^-(\bar{K}^0 K^0)}$.

By assembling the weak and strong couplings in the rescattering processes, we derive that

$$\begin{aligned}&{{\mathcal {M}}}(D_{s}^{+}\rightarrow \rho ^{0(+)}a^{+(0)}_{0}) ={{\mathcal {M}}}_a+\mathcal{M}_{a}^{\prime }+{{\mathcal {M}}}_{b}+{{\mathcal {M}}}_{c} , \nonumber \\&{{\mathcal {M}}}(D_{s}^{+}\rightarrow \omega a^{+}_{0}) = \hat{{\mathcal {M}}}_{b}+ \hat{{\mathcal {M}}}_{c} , \end{aligned}$$

(5)

with $M_a^{(\prime )}$ and $M_{b(c)}[{\hat{M}}_{b(c)}]$ for Fig. 2a, b(c), respectively. More explicitly, ${{\mathcal {M}}}_{a,b,c}$ are given by [9, 19, 20]

$$\begin{aligned}&{{\mathcal {M}}}_{a}=\int \frac{d^4{q}_{1}}{(2\pi )^{4}} \frac{\mathcal{M}_{\eta }{{\mathcal {M}}}_{\rho ^{0(+)}\rightarrow \pi ^+\pi ^{-(0)}} \mathcal{M}_{a^{+(0)}_{0}\rightarrow \eta \pi ^{+(0)}} F_{\pi }(q_{2}^2)}{(q_{1}^{2}-m_{\pi }^{2}+i\epsilon )[(q_1-p_2)^{2}-m_{\pi }^{2}+i\epsilon ][(q_1-p_1)^{2}-m_{\eta }^{2}+i\epsilon ]} ,\nonumber \\&{{\mathcal {M}}}_{b}=\int \frac{d^4{q}_{1}}{(2\pi )^{4}} \frac{{{\mathcal {M}}}_{K} {{\mathcal {M}}}_{\rho ^{0(+)}\rightarrow K^+K^-(K^+{{\bar{K}}}^0)} \mathcal{M}_{a_0^{+(0)}\rightarrow {\bar{K}}^0 K^{+(0)}} F_{K}(q_{2}^2)}{(q_{1}^{2}-m_{K}^{2}+i\epsilon )[(q_1-p_2)^{2}-m_{K}^{2}+i\epsilon ][(q_1-p_1)^{2}-m_{K}^{2}+i\epsilon ]} , \nonumber \\&{{\mathcal {M}}}_{c}=\int \frac{d^4{q}_{1}}{(2\pi )^{4}} \frac{{{\mathcal {M}}}_K {{\mathcal {M}}}_{\rho ^{0(+)}\rightarrow {\bar{K}}^0 K^{0(+)}} \mathcal{M}_{a_0^{+(0)}\rightarrow {{\bar{K}}}^0 K^{+(0)}} F_{K}(q_{2}^2)}{(q_{1}^{2}-m_{K}^{2}+i\epsilon )[(q_1-p_2)^{2}-m_{K}^{2}+i\epsilon ][(q_1-p_1)^{2}-m_{K}^{2}+i\epsilon ]} , \end{aligned}$$

(6)

with $q_2=q_1-p_2$ and $q_3=q_1-p_1$ following the momentum flows in Fig. 2. The form factor $F_M(q_{2}^2)\equiv (\Lambda _M^{2}-m^{2}_M)/(\Lambda _M^{2}-q^{2}_{2})$ with the cutoff parameter $\Lambda _M$ [$M=(\pi ,K)$] is to avoid the overestimation with $q_2$ to $\pm \infty$ [21]. Substituting $\eta ^\prime$ and $\omega$ for $\eta$ in ${{\mathcal {M}}}_a$ and $\rho ^0$ in ${{\mathcal {M}}}_{b(c)}$ leads to ${{\mathcal {M}}}_a^\prime$ and $\hat{{\mathcal {M}}}_{b(c)}$, respectively.

As a consequence, we find that

$$\begin{aligned} {{\mathcal {M}}}(D_{s}^{+}\rightarrow \rho ^{0}a^{+}_{0})= & {} {{\mathcal {M}}}(D_{s}^{+}\rightarrow \rho ^{+}a^{0}_{0}) ,\nonumber \\ {{\mathcal {M}}}(D_{s}^{+}\rightarrow \omega a^{+}_{0})= & {} 0 , \end{aligned}$$

(7)

where the first relation respects the isospin symmetry, whereas $\hat{{\mathcal {M}}}_{b}=- \hat{{\mathcal {M}}}_{c}$ due to ${{\mathcal {M}}}_{\omega \rightarrow K^+ K^-}=-{{\mathcal {M}}}_{\omega \rightarrow {{\bar{K}}}^0 K^0}$ cancels the rescattering contributions to $D_{s}^{+}\rightarrow \omega a^{+}_{0}$, which causes ${{\mathcal {M}}}(D_{s}^{+}\rightarrow \omega a^{+}_{0})=0$.

To deal with the triangle loops in Eq. (6), the equation in Refs. [22,23,24,25] can be useful, given by

$$\begin{aligned}&\int \frac{d^{4}q_1}{i \pi ^2}\frac{q_1^{\mu }}{(q_1^{2}-m_{1}^{2}+i\epsilon )[(q_1-p_2)^{2}-m_{2}^{2}+i\epsilon ][(q_1-p_1)^{2}-m_{3}^{2}+i\epsilon ]}\nonumber \\&\quad = -p_\rho ^\mu C_1(p_{a_0}^2,m_\rho ^2,m_{D_s}^2,m_1^2,m_2^2,m_3^2) -p_{D_s}^\mu C_2(p_{a_0}^2,m_\rho ^2,m_{D_s}^2,m_1^2,m_2^2,m_3^2) . \end{aligned}$$

(8)

By calculating the triangle rescattering processes, we obtain

$$\begin{aligned}&\Gamma (D_{s}^{+}\rightarrow \rho ^{0{+}}a^{+(0)}_{0})= \frac{|\mathbf {p}_{2}|^{3}}{8\pi m_{\rho }^2}|H|^2 ,\nonumber \\&\quad H=\frac{1}{8\pi ^2}\bigg (g_\rho g_\eta {{\mathcal {M}}}_\eta C_\eta +g_\rho g_{\eta '}{{\mathcal {M}}}_{\eta '} C_{\eta '} +g_\rho g_K {{\mathcal {M}}}_K C_K\bigg ) , \end{aligned}$$

(9)

with $C_{\eta ^{(\prime )}}=C_{2,\eta ^{(\prime )}}-C_{2,\eta ^{(\prime )}}^*$ and $C_K=C_{2,K}-C_{2,K}^*$ as the integrated results of the $C_2$ terms in Eq. (8), where $C_{2,M}^{(*)}$ are defined by

$$\begin{aligned} C_{2,\eta }^{(*)}= & {} C_2(m_\pi ,m_\pi (\Lambda _\pi ),m_\eta ) ,\nonumber \\ C_{2,\eta '}^{(*)}= & {} C_2(m_\pi ,m_\pi (\Lambda _\pi ),m_{\eta '}) ,\nonumber \\ C_{2,K}^{(*)}= & {} C_2(m_K,m_K(\Lambda _K),m_K) . \end{aligned}$$

(10)

However, the $C_1$ terms have been disappearing due to $p_\rho ^\mu \cdot \epsilon =0$ in the amplitudes.

For the three-body decays $D_{s}^{+}\rightarrow \rho ^{0(+)}(a^{+(0)}_{0}\rightarrow ) \eta \pi ^{+(0)}, K^+{{\bar{K}}}^0(K^+ K^-)$, we present [7]

$$\begin{aligned}&\Gamma (D_{s}^{+}\rightarrow \rho a_0,a_0\rightarrow \eta \pi (KK))\nonumber \\&\quad =\int \int \frac{1}{(2\pi )^3}\frac{|\mathbf {p}_{2}|^{2}}{32m_{D_{s}} m_{\rho }^2}|H|^2 \frac{g_{\eta (K)}^{2}}{\mid D_{a_{0}}(s)\mid ^{2}}ds dt , \end{aligned}$$

(11)

with $s=(p_{\eta (K)}+p_{\pi (K)})^{2}$ and $t=(p_{\rho }+p_{\pi (K)})^{2}$, such that the theoretical results can be compared to the data in Eq. (1). In the above equation, $1/D_{a_{0}}(s)$ presents the propagator for $a_0$, and we define [26]

$$\begin{aligned}&D_{a_{0}}(s)=s-m_{a_0}^{2}-\sum \limits _{\alpha \beta } { [\text {Re}\Pi ^{\alpha \beta }_{a_0}(m^2_{a_0})-\Pi ^{\alpha \beta }_{a_0}(s) ]} , \end{aligned}$$

(12)

where

$$\begin{aligned} \Pi ^{\alpha \beta }_{a_0}(x)= & {} \frac{G^{2}_{\alpha \beta }}{16\pi } \bigg \{\frac{m_{\alpha \beta }^+ m_{\alpha \beta }^-}{\pi x} \log \bigg [\frac{m_\beta }{m_\alpha }\bigg ]-\theta [x-(m_{\alpha \beta }^+)^2]\nonumber \\&\times \rho _{\alpha \beta }\bigg (i+\frac{1}{\pi } \log \bigg [\frac{\sqrt{x-(m_{\alpha \beta }^+)^{2}}+\sqrt{x-(m_{\alpha \beta }^-)^{2}}}{\sqrt{x-(m_{\alpha \beta }^-)^{2}}-\sqrt{x-(m_{\alpha \beta }^+)^{2}}}\bigg ]\bigg ) \nonumber \\&-\rho _{\alpha \beta }\bigg (1-\frac{2}{\pi } \arctan \bigg [\frac{\sqrt{-x+(m_{\alpha \beta }^+)^{2}}}{\sqrt{x-(m_{\alpha \beta }^-)^{2}}}\bigg ]\bigg )\nonumber \\&\quad \times (\theta [x-(m_{\alpha \beta }^-)^{2}]-\theta [x-(m_{\alpha \beta }^+)^{2}])\nonumber \\&+\rho _{\alpha \beta }\frac{1}{\pi } \log \bigg [\frac{\sqrt{(m_{\alpha \beta }^+)^{2}-x}+\sqrt{(m_{\alpha \beta }^-)^2-x}}{\sqrt{(m_{\alpha \beta }^-)^{2}-x}-\sqrt{(m_{\alpha \beta }^+)^2-x}}\bigg ]\nonumber \\&\quad \times \theta [(m_{\alpha \beta }^-)^{2}-x]\bigg \} ,\nonumber \\ \rho _{\alpha \beta }\equiv & {} \left| \sqrt{x-(m_{\alpha \beta }^+)^{2}}\sqrt{x-(m_{\alpha \beta }^-)^{2}}\right| /x , \end{aligned}$$

(13)

with $G_{\alpha \beta }=(g_{\eta ^{(\prime )}},g_K)$ for $\alpha \beta ={(\eta ^{(\prime )}\pi ,K {{\bar{K}}})}$ and $m_{\alpha \beta }^\pm =m_\alpha \pm m_\beta$.

3 Numerical results

In the numerical analysis, we adopt $V_{cs}=V_{ud}=1-\lambda ^2/2$ with $\lambda =0.22453\pm 0.00044$ in the Wolfenstein parameterization [7], along with $m_{a_0^0}=0.987$ GeV [27, 28]. The topological parameters (T, C, A) have been extracted as [6]

$$\begin{aligned} (|T|, |C|, |A|)= & {} (0.363\pm 0.001,0.323\pm 0.030,0.064\nonumber \\&\pm 0.004)~\text{ GeV}^{3}~ ,\nonumber \\ (\delta _C,\delta _A)= & {} (-151.3\pm 0.3,23.0^{+\;\;7.0}_{-10.0})^{\circ } , \end{aligned}$$

(14)

where $\delta _{C,A}$ are the relative strong phases. According to the extraction, we obtain ${{\mathcal {B}}}(D_s^+\rightarrow \pi ^{+}\eta ,\pi ^+\eta ^{\prime },K^{+}{\bar{K}}^0)= (1.8\pm 0.2,4.2\pm 0.5,3.1\pm 0.5)\times 10^{-2}$, consistent with the experimental values of $(1.68\pm 0.10,3.94\pm 0.25,2.95\pm 0.14)\times 10^{-2}$, respectively [7]. For $V,S\rightarrow PP$, the strong coupling constants read [7, 27, 28]

$$\begin{aligned} g_{\rho }= & {} 6.0 , (g_\eta ,g_{\eta '},g_K)=(2.87\pm 0.09,-2.52\nonumber \\&\quad \pm 0.08,2.94\pm 0.13)~\text {GeV} . \end{aligned}$$

(15)

Empirically, $\Lambda _M$ of ${{\mathcal {O}}}(1.0~\text {GeV})$ is commonly used to explain the data [29,30,31]; besides, it is obtained that $\Lambda _K-\Lambda _\pi =m_K-m_\pi$ [32]. Therefore, we are allowed to use $(\Lambda _\pi ,\Lambda _K)=(1.25\pm 0.25,1.60\pm 0.25)$ GeV, which result in

$$\begin{aligned} C_{\eta }= & {} [(0.57\pm 0.08)+i(0.17\pm 0.09)]~\text {GeV}^{-2} ,\nonumber \\ C_{\eta ^{\prime }}= & {} [(0.34\pm 0.03)-i(0.27\pm 0.07)]~\text {GeV}^{-2} ,\nonumber \\ C_{K}= & {} [(0.85\pm 0.03)-i(0.45\pm 0.08)]~\text {GeV}^{-2} , \end{aligned}$$

(16)

with $p_{a_0}^2=m_{a_0}^2$. Subsequently, we predict

$$\begin{aligned}&{{\mathcal {B}}}(D_{s}^{+}\rightarrow \rho ^{0(+)}a^{+(0)}_{0}) =(3.0\pm 0.3\pm 1.0)\times 10^{-3} ,\nonumber \\&{{\mathcal {B}}}(D_{s}^{+}\rightarrow \omega a^{+}_{0})=0 , \end{aligned}$$

(17)

where the first error in $\mathcal{B}(D_{s}^{+}\rightarrow \rho ^{0(+)}a^{+(0)}_{0})$ takes into account the uncertainties from $\Lambda _{\pi }$ and $\Lambda _{K}$, and the second one combines those from $V_{cs}^*$, $V_{ud}$, (T, C, A), and the strong coupling constants. For the resonant three-body decays, we obtain

$$\begin{aligned}&{{\mathcal {B}}}(D_{s}^{+}\rightarrow \rho ^{0(+)}(a^{+(0)}_{0}\rightarrow )\eta \pi ^{+(0)})\nonumber \\&\quad = (1.6^{+0.2}_{-0.3}\pm 0.6)\times 10^{-3} ,\nonumber \\&{{\mathcal {B}}}(D_{s}^{+}\rightarrow \rho ^{+}(a^{0}_{0}\rightarrow )K^+K^-,K^0{{\bar{K}}}^0)\nonumber \\&\quad = (0.9^{+0.1}_{-0.1}\pm 0.4,0.7^{+0.1}_{-0.1}\pm 0.3)\times 10^{-4} ,\nonumber \\&{{\mathcal {B}}}(D_{s}^{+}\rightarrow \rho ^{0}(a^{+}_{0}\rightarrow )K^+{\bar{K}}^0)\nonumber \\&\quad =(1.5^{+0.2}_{-0.3}\pm 0.6)\times 10^{-4} , \end{aligned}$$

(18)

where the sources of the two errors are the same as those in Eq. (17).

4 Discussions and conclusions

In the triangle loop, when the momentum flow approaches the mass shell for one of the three propagators, the integration with $i\epsilon \simeq im\Gamma$ gives rise to the imaginary parts in Eq. (16), where $\Gamma$ is a very tiny decay width for $\pi$, $\eta ^{(\prime )}$ or K. The off-shell integrations are responsible for the real parts in Eq. (16), for which we take ${{\mathcal {M}}}_a$ as our description. In principle, the integration allows a momentum flow from $-\infty$ to $+\infty$. However, when the exchange particle proceeds with $q_2^2$ around several GeV$^2$, instead of the infinity, the integration with $q_2^2\sim \pm \infty$ causes an overestimation [21]. We have accordingly introduced the form factor $F_\pi$ in Eq. (6) to cut off the contribution from $q_2^2\sim \pm \infty$. While $q_1^2$, $q_2^2$ and $q_3^2$ have been associated in the loop, $F_\pi$ also works to cut off the contributions from the propagators of the rescattering particles $\pi ^+$ and $\eta ^{(\prime )}$. Note that the single cutoff form factor has also been commonly used elsewhere [33,34,35].¹

The smallness of the WA $D_s^+\rightarrow MM$ decay can be traced back to its amplitude, given by [37,38,39]

$$\begin{aligned}&{{\mathcal {M}}}_{WA}(D_s^+\rightarrow MM) \propto f_{D_s} q^\mu \langle MM|{{\bar{u}}}\gamma _\mu (1-\gamma _5) d|0\rangle \nonumber \\&\quad \simeq (m_u+m_d)\langle MM|{{\bar{u}}}\gamma _5 d|0\rangle , \end{aligned}$$

(19)

where $q^\mu \langle MM|u\gamma _\mu d|0\rangle =0$ corresponds to the conservation of the vector current (CVC); most importantly, $m_{u(d)}\simeq 0$ causes the chiral suppression of the WA $D_s^+\rightarrow MM$ decay. According to the data, ${{\mathcal {B}}}(D_s^+\rightarrow \pi ^+\rho ^0)=(1.9\pm 1.2)\times 10^{-4}$ indicates that $\mathcal{B}_{WA}(D_s^+\rightarrow MM)$ should be around $10^{-4}$. In addition, ${{\mathcal {B}}}(D_s^+\rightarrow \pi ^+\pi ^0)<3.4\times 10^{-4}$ suggests that the G-parity violation suppresses the WA process even more. Therefore, since $D_s^+\rightarrow \rho a_0,\rho \pi$ are both the G-parity conserved processes, it is reasonable to present that ${{\mathcal {B}}}_{WA}(D_s^+\rightarrow \rho a_0) \simeq {{\mathcal {B}}}_{WA}(D_s^+\rightarrow \rho \pi )\sim 10^{-4}$. As a theoretical support, we present

$$\begin{aligned}&{{\mathcal {B}}}_{WA}(D_s^+(c{{\bar{s}}})\rightarrow \rho a_0)\nonumber \\&\quad =R_f\frac{(V_{cs}^* V_{ud}f_{D_s})^2\tau _{D_s}}{(V_{cb}V_{ud}^* f_{B_c})^2\tau _{B_c}} {{\mathcal {B}}}_{WA}(B_c^+(c{{\bar{b}}})\rightarrow \rho a_0) \sim 10^{-4} , \end{aligned}$$

(20)

in agreement with our estimation, where $R_f=3.1\times 10^{-2}$ is mostly from the phase space factors, and ${{\mathcal {B}}}_{WA}(B_c^+\rightarrow \rho a_0)\simeq 1.0\times 10^{-5}$ is adopted from Ref. [40].

Disregarding the WA contributions, we predict $\mathcal{B}(D_{s}^{+}\rightarrow \rho ^{0(+)}a^{+(0)}_{0})=3.0\times 10^{-3}$ in Eq. (17). It is found that the $\eta \pi ,\eta '\pi ,K^+\bar{K}^0$ rescatterings and their interferences give 6%, 7%, 30% and 59% of ${{\mathcal {B}}}(D_s^+\rightarrow a_0^{+(0)}\rho ^{0(+)})$, respectively. By contrast, the $\rho \eta ^{(\prime )}$ rescatterings from $D_s^+\rightarrow \rho \eta ^{(\prime )}$ dominantly contribute to $D_s^+\rightarrow a_0^{+(0)}\pi ^{0(+)}$, instead of $D_s^+\rightarrow K^* K$ [9]. Since $D_{s}^{+}\rightarrow \omega a^{+}_{0}$ has no rescattering effects; besides, the WA contribution is suppressed by the G-parity violation, we anticipate that $\mathcal{B}(D_{s}^{+}\rightarrow \omega a^{+}_{0}) \simeq \mathcal{B}(D_s^+\rightarrow \pi ^+\pi ^0)<3.4\times 10^{-4}$ [7].

In Eq. (18), $\mathcal{B}(D_{s}^{+}\rightarrow \rho ^{0}(a^{+}_{0}\rightarrow )\eta \pi ^{+}) =(1.6^{+0.2}_{-0.3}\pm 0.6)\times 10^{-3}$ is able to explain the data [see Eq. (1)], demonstrating the sufficient long-distance annihilation contribution. It is confusing that $\mathcal{B}(D_s^+\rightarrow a_0^0 \rho ^+,a_0^0\rightarrow K^+ K^-)$ is 10 times smaller than ${{\mathcal {B}}}_0$ in Eq. (1). For clarification, we take the approximate form of the resonant branching fraction: $\mathcal{B}(D_s^+\rightarrow SV,S\rightarrow PP)\simeq {{\mathcal {B}}}(D_s^+\rightarrow SV){{\mathcal {B}}}(S\rightarrow PP)$, together with the isospin relation: $\mathcal{B}(D_{s}^{+}\rightarrow \rho ^0 a^+_0)\simeq {{\mathcal {B}}}(D_{s}^{+}\rightarrow \rho ^+ a^0_{0})$, such that ${{\mathcal {B}}}_0/{{\mathcal {B}}}_+$ is reduced as $\mathcal{B}(a_0^0\rightarrow K^+ K^-)/{{\mathcal {B}}}(a_0^+\rightarrow \eta \pi ^+)\simeq 1/3$, disagreeing with ${{\mathcal {B}}}(a_0^0\rightarrow K^+ K^-)/{{\mathcal {B}}}(a_0^+\rightarrow \eta \pi ^+)=1/10$ from the experimental extraction [8]. Therefore, we conclude that there exists a possible contradiction between the observations in Eq. (1).

In our reasoning, the contradiction might be caused by $D_s^+\rightarrow \rho ^+ f_0,f_0\rightarrow K^+ K^-$ with $f_0\equiv f_0(980)$, which can be mistaken as $D_s^+\rightarrow \rho ^+ a_0^0,a_0^0\rightarrow K^+ K^-$ [41]. First, since $D_s^+\rightarrow \rho ^+ f_0$ is an external W-boson emission process, its branching fraction can be of order $10^{-3}$. Second, $a_0$ and $f_0$ are both scalar mesons, and have nearly the same masses and overlapped decay widths. As a result, it is possible that one cannot distinguish between the resonant signals of $D_s^+\rightarrow \rho ^+(f_0,a_0), (f_0,a_0)\rightarrow K^+ K^-$ in the $K^+ K^-$ invariant mass spectrum. For a careful examination, we suggest a measurement of ${{\mathcal {B}}}(D_{s}^{+}\rightarrow \rho ^{0}(a^{+}_{0}\rightarrow )K^+{\bar{K}}^0)/ \mathcal{B}(D_{s}^{+}\rightarrow \rho ^{+}(a^{0}_{0}\rightarrow )K^+ K^-)$, which will be observed around 2 if there exists no resonant $f_0\rightarrow K^+ K^-$ decay to be involved in ${{\mathcal {B}}}(D_{s}^{+}\rightarrow \rho ^+ K^+ K^-)$.

In summary, we have studied $D_{s}^{+}\rightarrow \rho ^{0(+)}a^{+(0)}_{0}$, $D_{s}^{+}\rightarrow \omega a_0^0$, and the resonant $D_{s}^{+}\rightarrow \rho a_0$, $a_{0}\rightarrow \eta \pi (KK)$ decays. In the final state interaction, where $D_s^+\rightarrow \eta ^{(\prime )}\pi ^+ (K^+{{\bar{K}}}^0)$ is followed by the $\eta ^{(\prime )}\pi ^+$ ($K^+{{\bar{K}}}^0$) to $\rho a_0$ rescattering, we have predicted $\mathcal{B}(D_{s}^{+}\rightarrow \rho ^{0(+)}a^{+(0)}_{0})=(3.0\pm 0.3\pm 1.0)\times 10^{-3}$. Because of the non-contribution of the rescattering effects and the suppressed short-distance W annihilation, it has been expected that ${{\mathcal {B}}}(D_{s}^{+}\rightarrow \omega a^{+}_{0}) \simeq {{\mathcal {B}}}(D_s^+\rightarrow \pi ^+\pi ^0)<3.4\times 10^{-4}$. For the resonant three-body decay, $\mathcal{B}(D_{s}^{+}\rightarrow \rho ^{0}(a^{+}_{0}\rightarrow )\eta \pi ^{+}) =(1.6^{+0.2}_{-0.3}\pm 0.6)\times 10^{-3}$ has been shown to agree with the data. We have presented $\mathcal{B}(D_{s}^{+}\rightarrow \rho ^{+}(a^{0}_{0}\rightarrow )K^+K^-)$ 10 times smaller than the observation, indicating that a more careful examination is needed.