1 Introduction

The establishment of a self-consistent quantum version of gravity is one of the most important problems of modern physics and is still unsolved despite many important attempts. However, the formulation of Quantum Field Theory (QFT) in curved spacetime provide us some important clues about a self-consistent quantum gravity. For instance, the particle creation and the thermal radiation of a black hole are the most spectacular of these clues. In this connection, Hawking, using the QFT in curved spacetime, proved that a black hole can emit particles formed by the quantum fluctuation near its event horizon [1,2,3]. Nowadays, various methods have been proposed to calculate the temperature of a black hole known as Hawking temperature. On the other hand, the Hamilton-Jacobi approach is an important version of the tunnelling method of the quantum mechanical point-like particles from a black hole [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Adopting this approach, Hawking temperature of various black holes were recovered by quantum tunnelling method of the particles across their event horizons. In all these studies, it is seen that the standard Hawking temperature is independent of the properties of a tunneling particle.

Besides the QFT in curved spacetime, there are some important candidate theories of quantum gravity such as the string theory and loop quantum gravity theory [21, 22]. In these theories, unlike QFT, the elementary particles are no longer point-like. Accordingly, it should be a minimal length in order of Planck scale. Due to this new interpretation of the elementary particles, the standard Heisenberg uncertainty principle is modified as generalized uncertainty principle (GUP) [23,24,25,26,27,28,29,30,31,32,33]. Moreover, the relativistic quantum mechanical wave equations such as Klein-Gordon, Dirac and vector boson equations are modified in the context of the GUP. Using these modified equations, Hawking temperature of many black holes was recalculated in the context of Hamilton-Jacobi approach. It was observed that the standard Hawking temperature is modified and it no longer depends only on the black hole but also on the properties of the tunnelling particle [34,35,36,37,38,39,40,41,42,43,44,45]. It is also stated that the tunnelling probability of the particles from a black hole is completely different from each other and thus leads to completely different Hawking temperatures [40,41,42,43,44]. Moreover, the stability of the (2+1)-dimensional charged rotating Banados-Teitelboim-Zanelli (CR-BTZ) black hole is investigated by using the modified Hawking temperature. And it points out that the black hole may undergo both first and second-type of phase transitions in the context of GUP whereas it undergoes only first phase transition in the absence of GUP [44]. With this motivation, we will investigate the GUP effect on the tunnelling probability of the scalar, Dirac and vector boson particles, respectively, and subsequently on the Hawking temperature of the 2+1-dimensional spinning dilaton black hole. Moreover, using the modified Hawking temperatures, we will analyze thermal stability condition of the black hole in the presence of quantum gravity effect for all of three type particles, respectively.

The paper is organized as follows: In Sect. 2, we introduce the 2+1 dimensional spinning dilaton black hole. In Sect. 3, we investigate the GUP effect on the tunnelling progress of the scalar particle from the black hole, and then, calculate the modified Hawking temperature. In Sects. 4 and 5, we repeat the same procedure for Dirac and vector boson particles, respectively, as we perform for the scalar particle in Sect. 3. In Sects. 6, the modified heat capacity of the black hole is calculated by using the modified Hawking temperatures, and subsequently, stability/instability and phase transition of the black hole are discussed. In the conclusion, the results are summarized.

2 2+1 dimensional spinning dilaton black hole

A dilaton field is a kind of scalar field arise in the low-energy string theories naturally [46, 47]. There are many studies investigate the effects of the dilaton field in both cosmological and black hole evolutions. Hence, in this study we focus on the 2+1 dimensional spinning dilaton black hole which is an exact solution of the field equation of the 2+1 dimensional low-energy string action. The black hole spacetime is given as follows;

$$\begin{aligned} ds^{2}=f(r)dt^{2}-\frac{1}{H(r)}dr^{2}+4rJdtd\varphi -R(r)^{2}d\varphi ^{2}, \end{aligned}$$
(1)

where the f(r), H(r) and R(r) are;

$$\begin{aligned} f(r)= & {} 8\varLambda r^{2}-r(M+\sqrt{M^{2}+32J^{2}\varLambda }),\\ R(r)^{2}= & {} r^2+r\frac{\sqrt{M^2+32\varLambda J^2}-M}{8\varLambda },\\ H(r)= & {} \frac{4r\varLambda -M}{2r}, \end{aligned}$$

with \(\varLambda \), M and J are the cosmological constant, the mass and angular momentum of the black hole, respectively [47]. The angular velocity of the horizon is determined as follows:

$$\begin{aligned} \varOmega _{h}= & {} \left( -\frac{g_{t\phi }}{g_{\varphi \varphi }}-\sqrt{\left( \frac{g_{t\varphi }}{g_{\varphi \varphi }}\right) ^2-\frac{g_{t t}}{g_{\varphi \varphi }}}\right) _{r=r_{h}}\nonumber \\= & {} \frac{16J\varLambda }{M+\sqrt{M^2+32J^2\varLambda }}. \end{aligned}$$
(2)

The event horizon of the black hole is located at

$$\begin{aligned} r_{h}=\frac{M}{4\varLambda }, \end{aligned}$$
(3)

which is obtained from \(H(r)=0\). As can be seen from Eq. (3), the black hole has only one event horizon that depends on the black hole mass and the cosmological constant. On the other hand, the event horizon does not depend on the angular momentum of the black hole. This indicates that the event horizons of the static and the 2+1 dimensional spinning dilaton black holes are the same. Hence, the Ricci scalar of the black hole is \(\frac{M+8r\varLambda }{2r^{3}}\) and the Ricci scalar diverges at \(r=0\).

Using the dragging coordinate transformation, we can avoid the dragging of the spacetime and matter near the event horizon of the black hole [7, 37, 44, 48,49,50,51,52,53,54,55]. In this context, the metric takes the following form

$$\begin{aligned} ds^{2}=F(r)dt^{2}-\frac{1}{H(r)}dr^{2}-R(r)^{2}d\phi ^{2}, \end{aligned}$$
(4)

with the following abbreviation,

$$\begin{aligned} F(r)=\frac{16r^2\varLambda (4r\varLambda -M)}{8r\varLambda -M+\sqrt{M^2+32\varLambda J^2}}, \end{aligned}$$

where the dragging coordinate transformation is carried out in terms of Killing vectors, \(\left( \partial _{t}\right) \) and \(\left( \partial _{\phi }\right) \), as \(d\phi \)=\(d\varphi -\frac{2rJ}{R(r)^2}dt\).

3 Tunneling of scalar particle from spinning dilaton black hole

We use Klein-Gordon equation that is modified in the context of GUP to investigate the quantum gravity effects on the tunneling process of the scalar particles from the black hole:

$$\begin{aligned}&\hbar ^{2}\partial _{t}\partial ^{t}\widetilde{\varPhi }+\hbar ^{2}\partial _{i}\partial ^{i}\widetilde{\varPhi }+ 2\alpha \hbar ^{4}\partial _{i}\partial ^{i}(\partial _{i}\partial ^{i}\widetilde{\varPhi })\nonumber \\&\quad +M_{0}^2 (1-2\alpha M_{0}^2)\widetilde{\varPhi }=0, \end{aligned}$$
(5)

where \(\widetilde{\varPhi }\) and \(M_{0}\) are the modified wave function and mass of the scalar particle, respectively [40, 42,43,44]. Also \(\alpha \)=\(\alpha _{0}/M_{p}^{2}\) with the \(M_{p}^{2}\) and \(\alpha _{0}\) are the Planck mass and dimensionless parameter, respectively. Then, the explicit form of the modified Klein-Gordon equation for the spinning black hole background is

$$\begin{aligned}&\frac{\hbar ^{2}}{F}\frac{\partial ^{2}\widetilde{\varPhi }}{\partial t^{2}}-\frac{\hbar ^{2}}{R^{2}} \frac{\partial ^{2}\widetilde{\varPhi }}{\partial \phi ^{2}}-\hbar ^{2}H\frac{\partial ^{2}\widetilde{\varPhi }}{\partial r^{2}} +\frac{2\alpha \hbar ^{4}}{R^{2}}\frac{\partial ^{2}}{\partial \phi ^{2}}\left( \frac{1}{R^2}\frac{\partial ^{2} \widetilde{\varPhi }}{\partial \phi ^{2}}\right) \nonumber \\&\quad +2\alpha \hbar ^{4}H\frac{\partial ^{2}}{\partial r^{2}}\left( H\frac{\partial ^{2}\widetilde{\varPhi }}{\partial r^{2}}\right) +M_{0}^{2}\left( 1-2\alpha M_{0}^{2}\right) \widetilde{\varPhi }=0. \end{aligned}$$
(6)

To reduce Eq. (6) to the Hamilton-Jacobi like equation, we use the following ansatz for the modified wave function of the scalar particle, \(\widetilde{\varPhi }\left( t,r,\phi \right) \);

$$\begin{aligned} \widetilde{\varPhi }\left( t,r,\phi \right) =A\exp \left( \frac{i}{\hbar }S\left( t,r,\phi \right) \right) , \end{aligned}$$
(7)

where \(A\left( t,r,\phi \right) \) is a function of space-time coordinates and \(S(t,r,\phi )\) is the classical action function. Setting it into the Eq. (6) and subsequently neglecting the higher order terms of \(\hbar \), we get the modified Hamilton-Jacobi equation as follows;

$$\begin{aligned}&\frac{1}{F}\left( \frac{\partial S}{\partial t}\right) ^{2}-H\left( \frac{\partial S}{\partial r}\right) ^{2}-\frac{1}{R^{2}}\left( \frac{\partial S}{\partial \phi }\right) ^{2}-M_{0}^{2}\nonumber \\&\qquad +2\alpha \left[ m_{0}^{2}-H^2\left( \frac{\partial S}{\partial r}\right) ^{2}-\frac{1}{R^4}\left( \frac{\partial S^4}{\partial \phi }\right) \right] =0. \end{aligned}$$
(8)

To solve this equation, the classical action function, \(S\left( t,r,\phi \right) \), can be separated as \(S\left( t,r,\phi \right) \)=\(-(E-j\varOmega _{h})t+j\phi +W(r)+C\) by using separation of variable method. Here, C is a complex constant, and E, j and W(r)=\(W_{0}(r)+\alpha W_{1}(r)\) are the particle’s energy, angular momentum, and radial trajectory, respectively. After some calculations, the radial trajectory of the tunneling scalar particle \(W_{\pm }(r)\) is written as

$$\begin{aligned} W_{\pm }(r)= & {} \pm \int \frac{\sqrt{(E-j\varOmega _{h})^2-F\left( M_{0}^{2}+j^{2}/R^{2}\right) }}{\sqrt{HF}}\nonumber \\&\quad \times \left[ 1+\alpha \varTheta \right] dr, \end{aligned}$$
(9)

where \(W_{+}(r)\) and \(W_{-}(r)\) correspond to the outgoing and incoming particle trajectories, respectively. Also, the abbreviation \(\varTheta \) is

$$\begin{aligned} \varTheta {=}\frac{F^{2}\left( M_{0}^{4}{-}j^{4}/R^{4}\right) {-}\left[ (E-j\varOmega _{h})^{2}{-}F\left( M_{0}^{2}{+}j^{2}/R^{2}\right) \right] ^{2}}{F\left[ (E-j\varOmega _{h})^{2}-F\left( M_{0}^{2}+j^{2}/R^{2}\right) \right] }. \end{aligned}$$

Then, the \(W_{\pm }(r_{h})\) are computed as

$$\begin{aligned} W_{\pm }(r_{h})= & {} \pm i\pi \frac{\left( E-j\varOmega _{h}\right) \sqrt{M+\sqrt{M^2+32J^2\varLambda }}}{4\varLambda \sqrt{2M}}\nonumber \\&\quad \times \left[ 1+\alpha \varSigma \right] , \end{aligned}$$
(10)

with the abbreviation \(\varSigma \) is

$$\begin{aligned} \varSigma =\frac{96\varLambda ^2j^2+3M_{0}^2M(M+\sqrt{M^2+32J^2\varLambda })}{2M(M+\sqrt{M^2+32J^2\varLambda }}. \end{aligned}$$

On the other hand, the tunneling probabilities of a particle crossing the outer horizon are given by

$$\begin{aligned} P_{out}= & {} \exp \left[ -\frac{2}{\hbar }ImW_{+}(r_{h}\right] , \nonumber \\ P_{in}= & {} \exp \left[ -\frac{2}{\hbar }ImW_{-}(r_{h}\right] . \end{aligned}$$
(11)

Hence, the tunneling probability of a particle is

$$\begin{aligned} \varGamma =e^{-\frac{2}{\hbar }ImS}=\frac{P_{out}}{P_{in}}=e^{-\frac{E}{T_{H}}}, \end{aligned}$$
(12)

where E is total energy of the tunnelling particle, and \(T_{H}\) is Hawking temperature. Then, the modified Hawking temperature of the scalar particle, \(T_{H}^{KG}\), is obtained as follows

$$\begin{aligned} T_{H}^{KG}=\frac{T_{H}}{\left[ 1+\alpha \varSigma \right] }, \end{aligned}$$
(13)

where \(T_{H}\) is the standard Hawking temperature of the black hole and its explicit expression is

$$\begin{aligned} T_{H}=\frac{\hbar \sqrt{2}}{\pi }\sqrt{\frac{M\varLambda ^2}{M+\sqrt{M^2+32J^2\varLambda }}}. \end{aligned}$$
(14)

Furthermore, neglecting the higher order \(\alpha \) terms (since \(\alpha \ll 1\)), we find the modified Hawking temperature of the black hole as follows;

$$\begin{aligned} T_{H}^{KG}\simeq T_{H}\left[ 1-\alpha \varSigma \right] . \end{aligned}$$
(15)

This result indicates that the modified Hawking temperature of the massive scalar particle is lower than the standard Hawking temperature. Moreover, it shows that the modified Hawking temperature depends on not only the cosmological constant, mass and angular momentum of the black hole but also the mass and angular momentum of the tunneling particle.

4 Tunneling of massive Dirac particle from spinning dilaton black hole

The modified Dirac equation is given as follows [40, 42,43,44];

$$\begin{aligned}&i\overline{\sigma }^{0}(x)\partial _{0}\widetilde{\varPsi }+i\overline{\sigma }^{i}(x)\left( 1-\alpha \mu _{0}^{2}\right) \partial _{i}\widetilde{\varPsi }\nonumber \\&\quad -\frac{\mu _{0}}{\hbar }\left( 1+\alpha \hbar ^{2}\partial _{j}\partial ^{j}-\alpha \mu _{0}^{2}\right) \widetilde{\varPsi }\nonumber \\&\quad +i\alpha \hbar ^{2}\overline{\sigma }^{i}(x)\partial _{i}\left( \partial _{j}\partial ^{j}\widetilde{\varPsi }\right) \nonumber \\&\quad -i\overline{\sigma }^{\mu }(x)\varGamma _{\mu }\left( 1+\alpha \hbar ^{2}\partial _{j}\partial ^{j}-\alpha \mu _{0}^{2}\right) \widetilde{\varPsi }=0, \end{aligned}$$
(16)

where \(\widetilde{\varPsi }\) is the modified Dirac spinor, \(\mu _{0}\) is mass of the Dirac particle, \(\overline{\sigma }^{\mu }(x)\) are the spacetime dependent Dirac matrices, and \(\varGamma _{\mu }(x)\) are spin affine connection for spin-1/2 particle given in the following definition in terms of metric tensor, \(g_{\mu \nu }(x)\), Christoffel symbols, \(\varGamma _{\nu \mu }^{\alpha }\), triads, \(e_{\nu }^{(j)}(x)\), and spacetime-dependent Dirac matrices \(\overline{\sigma }^{\mu }(x)\) [56]:

$$\begin{aligned} \varGamma _{\mu }(x)=\frac{1}{8}g_{\lambda \alpha }(e_{\nu ,\mu }^{i}e_{i}^{\alpha }-\varGamma _{\nu \mu }^{\alpha })[\overline{\sigma }^{\lambda }(x),\overline{ \sigma }^{\nu }(x)]. \end{aligned}$$

Using Eq. (4), the spinorial affine connections are derived in terms of Pauli matrices by the following way;

$$\begin{aligned} \varGamma _{0}= & {} -\frac{i}{4}\sqrt{\frac{H}{F}}F^{^{\prime }}{\sigma }^{3}{\sigma }^{1}\ ,\ \ \varGamma _{1}=0\ ,\nonumber \\ \varGamma _{2}= & {} \frac{1}{2}\sqrt{H(r)}R^{^{\prime }}{\sigma }^{1}{\sigma }^{2} \end{aligned}$$
(17)

where the prime denotes the derivative with respect to r. To proceed the tunneling probability of a massive Dirac particle from the black hole, we use the following ansatz for the modified wave function;

$$\begin{aligned} \widetilde{\varPsi }(x)=\exp \left( \frac{i}{\hbar }S\left( t,r,\phi \right) \right) \ \left( \begin{array}{c}A\left( t,r,\phi \right) \\ B\left( t,r,\phi \right) \\ \end{array}\right) \end{aligned}$$
(18)

where the \(A\left( t,r,\phi \right) \) and \(B\left( t,r,\phi \right) \) are the functions of spacetime coordinates. Setting the Eqs. (17) and (18) into the Eq. (16), we obtain the following coupled equations for the leading order in \(\hbar \) and \(\alpha \):

$$\begin{aligned}&A\left[ \frac{1}{\sqrt{F}}\left( \frac{\partial S}{\partial t}\right) +\mu _{0}\left( 1-\alpha \mu _{0}^{2}\right) +\frac{\alpha \mu _{0}}{R^{2}}\left( \frac{\partial S}{\partial \phi }\right) ^{2}\right. \nonumber \\&\quad \left. +\alpha \mu _{0}H\left( \frac{\partial S}{\partial r}\right) ^{2}\right] \nonumber \\&\quad +B\left[ i\sqrt{H}\left( 1-\alpha \mu _{0}^{2}\right) \left( \frac{\partial S}{\partial r}\right) +\frac{\left( 1-\alpha \mu _{0}^{2}\right) }{R}\left( \frac{\partial S}{\partial \phi }\right) \right. \nonumber \\&\quad \left. +i\alpha H^{3/2}\left( \frac{\partial S}{\partial r}\right) ^{3}\right] \nonumber \\&\quad +B\left[ i\frac{\alpha \sqrt{H}}{R^{2}}\left( \frac{\partial S}{\partial r}\right) \left( \frac{\partial S}{\partial \phi }\right) ^{2}+\frac{\alpha H}{R}\left( \frac{\partial S}{\partial \phi }\right) \left( \frac{\partial S}{\partial r}\right) ^{2}\right. \nonumber \\&\quad \left. + \frac{\alpha }{R^{3}}\left( \frac{\partial S}{\partial \phi }\right) ^{3}\right] =0,\nonumber \\&A\left[ -i\sqrt{H}\left( 1-\alpha \mu _{0}^{2}\right) \left( \frac{\partial S}{\partial r}\right) +\frac{\left( 1-\alpha \mu _{0}^{2}\right) }{R}\left( \frac{\partial S}{\partial \phi }\right) \right] \nonumber \\&\quad -A\left[ i\alpha H^{3/2}\left( \frac{\partial S}{\partial r}\right) ^{3}-i\frac{\alpha \sqrt{H}}{R^{2}}\left( \frac{\partial S}{\partial r}\right) \left( \frac{\partial S}{\partial \phi }\right) ^{2}\right] \nonumber \\&\quad +A\left[ \frac{\alpha H}{R}\left( \frac{\partial S}{\partial \phi }\right) \left( \frac{\partial S}{\partial r}\right) ^{2}+ \frac{\beta }{R^{3}}\left( \frac{\partial S}{\partial \phi }\right) ^{3}\right] \nonumber \\&\quad +B\left[ \frac{1}{\sqrt{F}}\left( \frac{\partial S}{\partial t}\right) -\mu _{0}\left( 1-\alpha \mu _{0}^{2}\right) \right] \nonumber \\&\quad -B\left[ \frac{\alpha \mu _{0}}{R^{2}}\left( \frac{\partial S}{\partial \phi }\right) ^{2}-\alpha \mu _{0}H\left( \frac{\partial S}{\partial r}\right) ^{2}\right] =0. \end{aligned}$$
(19)

The non-trivial solution of these equations can be obtained when the determinant of the coefficient matrix is zero. Subsequently, neglecting the terms including the higher order of the \(\alpha \) parameter leads to the modified Hamilton-Jacobi equation for the massive Dirac particle:

$$\begin{aligned}&2\alpha \left[ -\frac{2H}{R^{2}}\left( \frac{\partial S}{\partial r}\right) ^{2}\left( \frac{\partial S}{\partial \phi }\right) ^{2}-\frac{1}{R^{4}}\left( \frac{\partial S}{\partial \phi }\right) ^{4}-H^{2}\left( \frac{\partial S}{\partial r}\right) ^{4}\right] \nonumber \\&\quad +\frac{1}{F}\left( \frac{\partial S}{\partial t}\right) ^{2}{-}H\left( \frac{\partial S}{\partial r}\right) ^{2}{-}\frac{1}{R^2}\left( \frac{\partial S}{\partial \phi }\right) ^{2}{-}\mu _{0}^{2}{+}2\alpha \mu _{0}^{4}=0.\nonumber \\ \end{aligned}$$
(20)

Letting the explicit form of the classical action of the Dirac particle, \(S\left( t,r,\phi \right) \)=\(-(E-j\varOmega _{h})t+j\phi +K(r)+C\), in Eqs. (20), the radial trajectory of the particle, \(K_{\pm }(r)\), is obtained as follows:

$$\begin{aligned} K_{\pm }(r)= & {} \pm \int \frac{\sqrt{(E-j\varOmega _{+})^{2}-F\left( \mu _{0}^{2}+j^{2}/R^{2}\right) }}{\sqrt{HF}}\nonumber \\&\quad \times \left[ 1+\alpha \chi \right] dr,\nonumber \\ \end{aligned}$$
(21)

where \(K_{+}(r)\) and \(K_{-}(r)\) correspond to the outgoing and incoming particle trajectories, respectively, and the abbreviation \(\chi \) is

$$\begin{aligned} \chi =\frac{(E-j\varOmega _{+})^{2}\left[ 2\mu _{0}^{2}F-(E-j\varOmega _{+})^{2}\right] }{F\left[ (E-j\varOmega _{+})^{2}-F\left( \mu _{0}^{2}+j^{2}/R^{2}\right) \right] }. \end{aligned}$$

Then, it is computed as

$$\begin{aligned} K_{\pm }(r_{h})= & {} \pm i\pi \frac{\left( E-j\varOmega _{h}\right) \sqrt{M+\sqrt{M^2+32J^2\varLambda }}}{4\varLambda \sqrt{2M}}\nonumber \\&\quad \times \left[ 1+\alpha \varPi \right] , \end{aligned}$$
(22)

where the abbreviation \(\varPi \) is

$$\begin{aligned} \varPi =\frac{-32\varLambda ^2j^2+3\mu _{0}^2M(M+\sqrt{M^2+32J^2\varLambda })}{2M(M+\sqrt{M^2+32J^2\varLambda }}. \end{aligned}$$

Accordingly, inserting Eq. (22) in Eqs. (11) and (12), the modified Hawking temperature of the massive Dirac particle, \(T_{H}^{D}\), is obtained as

$$\begin{aligned} T_{H}^{D}=\frac{T_{H}}{\left[ 1+\alpha \varPi \right] }, \end{aligned}$$
(23)

or

$$\begin{aligned} T_{H}^{D}\simeq T_{H}\left[ 1-\alpha \varPi \right] . \end{aligned}$$
(24)

where \(T_{H}\) is the standard Hawking temperature of the black hole given in Eq. (14). This result shows that the modified Hawking temperature of the massive Dirac particle is lower than the standard Hawking temperature. Moreover, similarly that of scalar particle, it shows that the mass and angular momentum of the tunneling Dirac particle play important role in the thermodynamical evolution of the black hole. Another important result is the tunnelling probability and the modified Hawking temperature of the Dirac particle are completely different from that of scalar particle in the presence of the quantum gravity effect.

5 Tunneling of massive vector boson from spinning dilaton black hole

In this section, we performing the quantum gravity effect on the tunnelling process of the massive vector boson particle from the black hole. To do this, we are using the modified massive vector boson equation given as follows:

$$\begin{aligned}&i\beta ^{0}(x)\partial _{0}\widetilde{\varPsi }+i\beta ^{i}(x)\left( 1-\alpha m_{0}^{2}\right) \partial _{i}\widetilde{\varPsi }\nonumber \\&\quad +i\alpha \hbar ^{2}\beta ^{i}(x)\partial _{i}\left( \partial _{j}\partial ^{j}\widetilde{\varPsi }\right) \nonumber \\&\quad -\frac{m_{0}}{\hbar }\left( 1+\alpha \hbar ^{2}\partial _{j}\partial ^{j}-\alpha m_{0}^{2}\right) \widetilde{\varPsi }\nonumber \\&\quad -i\beta ^{\mu }(x)\varSigma _{\mu }\left( 1+\alpha \hbar ^{2}\partial _{j}\partial ^{j}-\alpha m_{0}^{2}\right) \widetilde{\varPsi }=0, \end{aligned}$$
(25)

where \(\mu _{0}\) is mass of the vector boson and \(\widetilde{\varPsi }\) is the modified wave function [41]. Also, \(\beta ^{\mu }(x)\) and \(\varSigma _{\mu }\) are the Kemmer matrices and spin connection coefficients for the vector boson with the following their expressions;

$$\begin{aligned} \beta ^{\mu }(x)= & {} \overline{\sigma }^{\mu }(x)\otimes I+I\otimes \overline{\sigma }^{\mu }(x),\nonumber \\ \varSigma _{\mu }\left( x\right)= & {} \varGamma _{\mu }(x)\otimes I+I\otimes \varGamma _{\mu }(x), \end{aligned}$$
(26)

respectively [57, 58]. To calculate the quantum gravity effect on the tunnelling probability of the massive vector boson from the black hole, we use the following ansatz for the modified wave function [41, 57, 58],

$$\begin{aligned} \widetilde{\varPsi }(x)=\exp \left( \frac{i}{\hbar }S\left( t,r,\phi \right) \right) \ \left( \begin{array}{c}A\left( t,r,\phi \right) \\ B\left( t,r,\phi \right) \\ B\left( t,r,\phi \right) \\ D\left( t,r,\phi \right) \\ \end{array}\right) . \end{aligned}$$
(27)

Accordingly, setting Eqs. (17) and (26) in Eq. (27), we obtain the following differential equations set:

$$\begin{aligned}&B\left[ \frac{1}{R}\left( \frac{\partial S}{\partial \phi }\right) {+}i\alpha \frac{\sqrt{H}}{R^{2}}\left( \frac{ \partial S}{\partial \phi }\right) ^{2}\left( \frac{\partial S}{\partial r}\right) {-}i\alpha m_{0}^{2}\sqrt{H}\left( \frac{\partial S}{\partial r}\right) \right] \nonumber \\&\quad +B\left[ i\sqrt{H}\left( \frac{\partial S}{\partial r}\right) +i\alpha H\sqrt{H}\left( \frac{\partial S}{\partial r}\right) ^{3}-\alpha \frac{m_{0}^{2}}{R}\left( \frac{\partial S}{\partial \phi }\right) \right] \nonumber \\&\quad +B\left[ +\alpha \frac{1}{R^{3}}\left( \frac{\partial S}{\partial \phi }\right) ^{3}+\alpha \frac{H}{R}\left( \frac{\partial S}{\partial \phi }\right) \left( \frac{\partial S}{\partial r}\right) ^{2}\right] \nonumber \\&\quad +A\left[ \frac{1}{\sqrt{F}}\left( \frac{\partial S}{\partial t}\right) +\frac{m_{0}\left( 1-\alpha m_{0}^{2}\right) }{2}\right] \nonumber \\&\quad +A\left[ \alpha \frac{m_{0}}{2R^{2}}\left( \frac{\partial S}{\partial \phi }\right) ^{2}+\alpha \frac{m_{0}H}{2}\left( \frac{\partial S}{\partial r}\right) ^{2}\right] =0\nonumber \\&A\left[ -i\sqrt{H}\left( \frac{\partial S}{\partial r}\right) +\alpha \frac{H}{R}\left( \frac{\partial S}{\partial \phi }\right) \left( \frac{\partial S}{\partial r}\right) ^{2}\right] \nonumber \\&\quad -A\left[ \alpha \frac{m_{0}^{2}}{R}\left( \frac{\partial S}{\partial \phi }\right) -i\alpha H\sqrt{H}\left( \frac{\partial S}{\partial r}\right) ^{3}\right] \nonumber \\&\quad +A\left[ \frac{\alpha }{R^{3}}\left( \frac{\partial S}{\partial \phi }\right) ^{3}+\frac{1}{R}\left( \frac{\partial S}{\partial \phi }\right) \right] \nonumber \\&\quad -A\left[ i\alpha \frac{\sqrt{H}}{R^{2}}\left( \frac{\partial S}{\partial \phi }\right) ^{2}\left( \frac{\partial S}{\partial r}\right) +i\alpha m_{0}^{2}\sqrt{H}\left( \frac{\partial S}{\partial r}\right) \right] \nonumber \\&\quad +B\left[ -m_{0}\left( 1-\alpha m_{0}\right) -\alpha m_{0}H\left( \frac{\partial S}{\partial r}\right) ^{2}-\alpha \frac{m_{0}}{R^{2}}\left( \frac{\partial S}{\partial \phi }\right) ^{2}\right] \nonumber \\&\quad +D\left[ -\frac{1}{R}\left( \frac{\partial S}{\partial \phi }\right) +\alpha \frac{m_{0}^{2}}{R}\left( \frac{\partial S}{\partial \phi }\right) \right] \nonumber \\&\quad -D\left[ \alpha \frac{H}{R}\left( \frac{\partial S}{\partial \phi }\right) \left( \frac{\partial S}{\partial r}\right) ^{2}-i\sqrt{H}\left( \frac{\partial S}{\partial r}\right) \right] \nonumber \\&\quad +D\left[ i\alpha m_{0}^{2}\sqrt{H}\left( \frac{\partial S}{\partial r}\right) -\frac{\alpha }{R^{3}}\left( \frac{\partial S}{\partial \phi }\right) ^{3}\right] \nonumber \\&\quad -D\left[ i\alpha \frac{\sqrt{H}}{R^{2}}\left( \frac{\partial S}{\partial \phi }\right) ^{2}\left( \frac{\partial S}{\partial r}\right) -i\alpha H\sqrt{H}\left( \frac{\partial S}{\partial r}\right) ^{3}\right] =0\nonumber \\&B\left[ -i\sqrt{H}\left( \frac{\partial S}{\partial r}\right) +\frac{1}{R}\left( \frac{\partial S}{\partial \phi }\right) -i\alpha \frac{\sqrt{H}}{R^{2}}\left( \frac{\partial S}{\partial \phi }\right) ^{2}\left( \frac{\partial S}{\partial r}\right) \right] \nonumber \\&\quad +B\left[ \frac{\alpha }{R^{3}}\left( \frac{\partial S}{\partial \phi }\right) ^{3}+\alpha \frac{H}{R}\left( \frac{\partial S}{\partial \phi }\right) \left( \frac{\partial S}{\partial r}\right) ^{2}-\alpha \frac{m_{0}^{2}}{R}\left( \frac{\partial S}{\partial \phi }\right) \right] \nonumber \\&\quad +B\left[ i\alpha m_{0}^{2}\sqrt{H}\left( \frac{\partial S}{\partial r}\right) -i\alpha H\sqrt{H}\left( \frac{\partial S}{\partial r}\right) ^{3}\right] \nonumber \\&\quad +D\left[ \frac{1}{\sqrt{F}}\left( \frac{\partial S}{\partial t}\right) -\frac{m_{0}\left( 1-\alpha m_{0}^{2}\right) }{2}\right] \nonumber \\&\quad -D\left[ \alpha \frac{m_{0}}{2R^{2}}\left( \frac{\partial S}{\partial \phi }\right) ^{2}-\alpha \frac{m_{0}H}{2}\left( \frac{\partial S}{\partial r}\right) ^{2}\right] =0, \end{aligned}$$
(28)

where the terms with \(\hbar \) are omited. Afterwards, the modified Hamilton-Jacobi equation for the massive vector boson particle is derived by setting the determinant of the coefficients matrix of \(A\left( t,r,\phi \right) \), \(B\left( t,r,\phi \right) \) and \(D\left( t,r,\phi \right) \) to zero;

$$\begin{aligned}&\frac{1}{F}\left( \frac{\partial S}{\partial t}\right) ^{2}-\frac{1}{R^{2}}\left( \frac{\partial S}{\partial \phi }\right) ^{2}-H\left( \frac{\partial S}{\partial r}\right) ^{2}-\frac{m_{0}^{2}}{4}\nonumber \\&\quad +\alpha \left[ \frac{9m_{0}^{2}H}{4}\left( \frac{\partial S}{\partial r}\right) ^{2}-\frac{3}{R^{4}}\left( \frac{\partial S}{\partial \phi }\right) ^{4}\right] \nonumber \\&\quad +\alpha \left[ -\frac{6H}{R^{2}} \left( \frac{\partial S}{\partial r}\right) ^{2}\left( \frac{\partial S}{\partial \phi }\right) ^{2}+\frac{9m_{0}^{2}}{4R^{2}}\left( \frac{\partial S}{\partial \phi }\right) ^{2}\right] \nonumber \\&\quad + \alpha \left[ \frac{1}{R^{2}F}\left( \frac{\partial S}{\partial t}\right) ^{2}\left( \frac{\partial S}{\partial \phi }\right) ^{2}-\frac{m_{0}^{2}}{F}\left( \frac{\partial S}{\partial t} \right) ^{2}\right] \nonumber \\&\quad + \alpha \left[ \frac{3m_{0}^{4}}{4}-3H^{2}\left( \frac{\partial S}{\partial r}\right) ^{4}+\frac{H}{F}\left( \frac{\partial S}{\partial t}\right) ^{2}\left( \frac{\partial S}{\partial r}\right) ^{2}\right] =0.\nonumber \\ \end{aligned}$$
(29)

The radial trajectory of the vector particle across the event horizon, \(K_{\pm }\left( r\right) \), is obtained by substituting the explicit form of \(S\left( t,r,\phi \right) \) in Eq. (29):

$$\begin{aligned} K_{\pm }(r)= & {} \pm \int \frac{\sqrt{(E-j\varOmega _{+})^{2}-F\left( m_{0}^{2}/4+j^{2}/R^{2}\right) }}{\sqrt{HF}}\nonumber \\&\quad \times \left[ 1+\alpha \varUpsilon \right] dr \end{aligned}$$
(30)

where \(\varUpsilon \) is is an abbreviation as

$$\begin{aligned} \varUpsilon =\frac{(E-j\varOmega _{+})^{2}\left[ 5m_{0}^{2}F-4(E-j\varOmega _{+})^{2}\right] }{4F\left[ (E-j\varOmega _{+})^{2}-F\left( m_{0}^{2}/4+j^{2}/R^{2}\right) \right] }. \end{aligned}$$

Finally, the integration in Eq. (30) are calculated as

$$\begin{aligned} K_{\pm }(r_{h})= & {} \pm i\pi \frac{\left( E-j\varOmega _{h}\right) \sqrt{M+\sqrt{M^2+32J^2\varLambda }}}{4\varLambda \sqrt{2M}}\nonumber \\&\times \left[ 1+\alpha \varDelta \right] . \end{aligned}$$
(31)

where the abbreviation \(\varDelta \) is

$$\begin{aligned} \varDelta =\frac{-128\varLambda ^2j^2+9m_{0}^2M(M+\sqrt{M^2+32J^2\varLambda })}{8M(M+\sqrt{M^2+32J^2\varLambda })}. \end{aligned}$$

Accordingly, the modified Hawking temperature of the massive vector boson particle becomes as follows:

$$\begin{aligned} T_{H}^{^{\prime }}=\frac{T_{H}}{\left[ 1+\alpha \varDelta \right] }, \end{aligned}$$
(32)

or

$$\begin{aligned} T_{H}^{^{\prime }}=T_{H}\left[ 1-\alpha \varDelta \right] \end{aligned}$$
(33)

with the standard Hawking temperature, \(T_{H}\), given in the Eq. (14). As can be seen from Eq. (33), the modified Hawking temperature of the vector boson particle is lower than the standard one. It is also different from both that of Dirac and scalar particles.

6 Quantum gravity correction to the Stability of the black hole

The heat capacity of a black hole provides important information about both the thermodynamic local stability and phase transitions of that black hole. Whether a black hole is thermally local stable is determined by whether its heat capacity is positive or negative. On the other hand, the phase transitions take place when the system is moving from an unstable state to a stable state. The phase transition points correspond to roots where the heat capacity vanishes or diverges. That the roots make the heat capacity vanish it corresponds to the first-type phase transition, whereas the roots where the heat capacity is divergent it corresponds to the second-type phase transition. The heat capacity expression at constant angular momentum, J, in term of mass, M, and modified Hawking temperature, \(T_{H}\), of the black hole is given as follows:

$$\begin{aligned} C_{J}=\left( \frac{\partial M}{\partial T_{H}}\right) _{J} \end{aligned}$$
(34)

In this context, to determine the thermal stability condition, and hence, the phase transition of the black hole under the quantum gravity effect, we will consider the modified Hawking temperatures of the scalar, Dirac, and vector boson particles calculated in the presence of GUP, separately. Therefore, using the modified Hawking temperatures of the scalar in Eq. (13), Dirac in Eq. (23), and vector boson in Eq. (32), particles with Eq. (3), respectively, the modified heat capacity of the black hole is obtained as follows:

$$\begin{aligned} C_{J}^{^{Scalar}}= & {} \frac{3\pi \varLambda ^{2}\xi \mathscr {X}}{4\hbar r_{h}\varLambda ^{3}\mathscr {Y}} , \end{aligned}$$
(35)
$$\begin{aligned} C_{J}^{^{Dirac}}= & {} \frac{9\pi \varLambda ^{2}\xi \mathscr {A}}{4\hbar r_{h}\varLambda ^{3}\mathscr {B}}, \end{aligned}$$
(36)
$$\begin{aligned} C_{J}^{^{Vector}}= & {} \frac{1521\pi \varLambda ^{2}\xi \mathscr {C}}{256\hbar r_{h}\varLambda ^{3}\mathscr {D}}, \end{aligned}$$
(37)

where \(\mathscr {X}\), \(\mathscr {Y}\), \(\mathscr {A}\), \(\mathscr {B}\), \(\mathscr {C}\) and \(\mathscr {D}\) are abbreviations (see Appendix) and \(\xi \) is

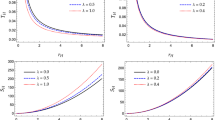
$$\begin{aligned} \xi =\sqrt{2r_{h}\left( \varLambda r_{h}^{2}+2J^{2}\right) \left( \varLambda r_{h}+\sqrt{\varLambda \left( \varLambda r_{h}^{2}+2J^{2}\right) }\right) }. \end{aligned}$$

To analyse the local stability properties of the black hole under quantum tunnelling process of the relativistic particles in the presence of GUP, we plot the heat capacities for special values of \(\varLambda \), \(\alpha \), j, \(\hbar \), J, and m. According to Eq. (35), the modified heat capacity of the spinning dilatonic black hole is always positive, hence, the black hole always stable according to the tunnelling process of a scalar particle in the context of GUP (red line in Fig. 1). In this case, there is no any phase transition. On the other hand, according to the tunnelling process of Dirac particle, the modified heat capacity given in Eq. (36) is negative for the region \(0<r_{h}<0.2\) while it is positive for the region \(0.2<r_{h}\). Therefore, the black hole is unstable in the region \(0<r_{h}<0.2\) while it is stable in the region \(0.2<r_{h}\). The modified heat capacity diverges at point \(r_{h}=0.2\), hence this point corresponds to the phase transition point known as second-type phase transition (red line in Fig. 2). Similarly, in view of the tunneling process of vector boson particle, the modified heat capacity given in Eq. (37) is negative for the region \(0<r_{h}<1.13\) while it is positive for the region \(1.13<r_{h}\) (red line in Fig. 3). Therefore, the stability/instability and phase transition situations of the black hole according to the tunnelling of vector boson particle are similar that of the Dirac particle.

In the absence of the quantum gravity effect, i.e. \(\alpha \)=0, the modified heat capacity reduced to the standard one given as follow:

$$\begin{aligned} C_{J}=\frac{4\pi \sqrt{2r_{h}\left( \varLambda r_{h}^{2}+2J^{2}\right) \left( \varLambda r_{h}+\sqrt{\varLambda \left( \varLambda r_{h}^{2}+2J^{2}\right) }\right) }}{\hbar \left( \sqrt{\varLambda (\varLambda r_{h}^{2}+2J^{2})}-\varLambda r_{h}\right) }\nonumber \\ , \end{aligned}$$
(38)

Due to the fact that \(\sqrt{\varLambda (\varLambda r_{h}^{2}+2J^{2})}>\varLambda r_{h}\), the standard heat capacity is always positive. Therefore, thermodynamically, the black hole is always stable in the absence of quantum gravity effect (blue lines in Figs. 1, 2, 3).

Fig. 1
figure 1

\(C_{Scalar}\)-\(r_{h}\) curve. The blue and red lines are correspond to the standard and the modified heat capacities of the spinning dilaton black hole, respectively. We set \(\varLambda =1, \alpha =10^{-2}, j=3, \hbar =J=m=1\)

Full size image
Fig. 2
figure 2

\(C_{Dirac}\)-\(r_{h}\) curve. The blue and red lines are correspond to the standard and the modified heat capacities of the spinning dilaton black hole, respectively. We set \(\varLambda =1, \alpha =10^{-2}, j=3, \hbar =J=m=1\)

Full size image
Fig. 3
figure 3

\(C_{Vector}\)-\(r_{h}\) curve. The blue and red lines are correspond to the standard and the modified heat capacities of the spinning dilaton black hole, respectively. We set \(\varLambda =1, \alpha =10^{-2}, j=3, \hbar =J=m=1\)

Full size image

7 Concluding remarks

Recent observational developments in black hole physics have demonstrated the importance of theoretical studies in this area. In this context, it is important to calculate the thermodynamics properties of a black hole by tunneling various relativistic quantum mechanical particles. Such studies can provide important clues about the evaporation process of a black hole. In this work, the impact of the GUP on the Hawking temperature of the 2+1 dimensional spinning dilaton black hole and its local stability/instabity and phase transition are investigated via quantum tunnelling process of the massive scalar, Dirac and vector boson particles, respectively, in the context of the Hamilton-Jacobi approach. For this purpose, the modified Klein-Gordon, Dirac and vector boson equations is used. Some important outcomes can be listed as follows:

  • In the absence of GUP effect, Hawking temperatures of the three different types of particles are the same and depend only on the properties of the black hole, i.e. they are not related to the particles properties.

  • In contrast to the standard results, our results demonstrate that the modified Hawking temperature depends not only on the black hole properties but also on GUP parameter, \(\alpha \), and hence on the properties of the tunneling particles. Furthermore, it is observed that the modified Hawking temperature is lower than that of the standard one.

  • In the presence of the GUP effect, tunnelling processes of the three different particles are completely different from each other, and hence their Hawking temperatures are completely different, as well.

  • According to Eq. (15), the modified Hawking temperature of the black hole is decreases via angular momentum of the scalar particle. However, according to Eq. (24), the total angular momentum (orbital+spin) of Dirac particle has an increasing effect on the Hawking temperature of the black hole. Moreover, the total angular momentum (orbital+spin) of the vector boson particle has a similar impact that of Dirac particle (see Eq. (33)). This case indicates that the total angular momentum (orbital+spin)-spacetime geometry interaction depends on the particle type in the presence of quantum gravity correction term. On the other hand, in the absence of this term, all types of particles interact with spacetime geometry in the same way.

  • In the case of the all three particles, the modified Hawking temperature decreases with mass of the tunneling particle (see Eqs. (15), (24) and (33)).

  • Thermodynamical local stability of the black hole is analyzed by using the modified Hawking temperatures of scalar, Dirac and vector boson particles for special values of \(\varLambda \), \(\alpha \), j, \(\hbar \), J, and m.

  • The black hole is always locally stable according to the scalar particle tunnelling in the presence of quantum gravity effect. Therefore, we can say that tunnelling of a scalar particle does not affect the local stability of the black hole (red line in Fig.  1).

  • On the other hand, according to the tunneling process of both Dirac and vector boson particles, the modified heat capacities given in Eqs. (36) and (37 diverge. Hence, the black hole may undergoes second-type of phase transitions in order to become stable in the presence of the quantum gravity effect (red lines in Figs. 2, 3). Also, for same values of \(\varLambda \), \(\alpha \), j, \(\hbar \), J, and m, the unstable region in the context of vector boson particle tunneling is wider than that of Dirac particle. This shows that, in the context of tunneling of the Dirac particle, the black hole may undergo stable earlier than that of the vector particle particle.

  • In the absence of GUP effect, all of the three modified heat capacities reduce to standard one (Eq. (38)), and in this situation, the black hole is always stable (blue lines in Figs. 1, 2, 3).

Finally, it is important to point out that the spin of the tunnelling particle may play an important role that can not be neglected during the evaporation of the spinning dilatonic black hole in the context of quantum gravity.