Probing double parton scattering via associated open charm and bottom production in ultraperipheral pA collisions

Abstract

In this article, we propose a novel channel for phenomenological studies of the double-parton scattering (DPS) based upon associated production of charm $c{\bar{c}}$ and bottom $b{\bar{b}}$ quark pairs in well-separated rapidity intervals in ultraperipheral high-energy proton–nucleus collisions. This process provides direct access to the double-gluon distribution in the proton at small-x and enables one to test the factorized DPS pocket formula. We have made the corresponding theoretical predictions for the DPS contribution to this process at typical LHC energies and beyond and we compute the energy-independent (but photon momentum fraction dependent) effective cross section.

1 Introduction

With an increase of collision energy, the probability for more than one parton–parton scattering to occur in the same proton–proton or proton–nucleus collision grows faster compared with that of the single-parton scattering (SPS) leading to the well-known phenomenon of multi-parton interactions (MPIs) known since a long time ago [1,2,3]. Due to measurements at the Large Hadron Collider (LHC), the physics of MPIs has attracted a lot of attention from both theoretical and experimental communities (for recent work on this topic, see e.g. Refs. [4,5,6,7,8,9,10,11,12] and the references therein). A first non-trivial example, the double-parton scattering (DPS), becomes particularly significant in production of specific multi-particle final states such as meson pairs [10], four identified jets [11] or leptons [12] etc. These processes are traditionally considered as an important source of information about a new class of non-perturbative QCD objects, the double-parton distribution functions (dPDFs) being now actively explored in the literature. They describe the number density and correlations of two colored partons in the proton, with given longitudinal momentum fractions $x_1$, $x_2$ and placed at a given transverse relative separation $\mathbf{b}$ of the two hard collisions [13] (for a detailed review on theoretical grounds, see e.g. Ref. [14] and the references therein).

Fig. 1

A schematic illustration of the $A+p \rightarrow A + (c{{\bar{c}}} b {{\bar{b}}}) + X$ cross section in pA UPCs

While complete theoretical predictions for dPDFs involving the unknown non-perturbative QCD parton correlation functions are not available, a few model calculations exist attempting to pick the most significant features of dPDFs [8, 9, 15,16,17]. In order to perform any comprehensive verification of such models, much more phenomenological information is needed as no direct measurement or extraction of dPDFs from the experimental data has yet been possible. Experimentally, a distinctive signature of DPS associated with the so-called effective cross section, $\sigma _{\mathrm{eff}}$, has already been identified and measured in different channels at central rapidities (see e.g. Refs. [11, 12, 18,19,20,21,22,23,24]), while many Monte-Carlo generators naturally incorporate MPIs as part of their framework [3].

The effective cross section is experimentally defined as ratio of double to product of two single inclusive production rates for final-state $A_1$ and $A_2$ systems in two independent hard scatterings and represents the effective transverse overlap area containing the interacting hard partons. With this definition, the DPS cross section is estimated as [5, 6, 25] (for a detailed review on this topic, see e.g. Refs. [26, 27]),

$$\begin{aligned} \sigma ^{A_1A_2}_{\mathrm{DPS}} = \frac{\kappa }{2} \frac{\sigma ^{A_1}_{\mathrm{SPS}}\sigma ^{A_2}_{\mathrm{SPS}}}{\sigma _{\mathrm{eff}}}, \end{aligned}$$

(1.1)

where $\sigma ^{A_{1,2}}_{\mathrm{SPS}}$ represents the corresponding SPS cross section for production of $A_{1,2}$ systems, and $\kappa$ is the symmetry factor depending on whether the final states are the same ($A_1 = A_2$, $\kappa = 1$) or different ($A_1 \not = A_2$, $\kappa = 2$). In general, $\sigma _\text {eff}$ depends on scales, momentum fractions, and parton flavors involved. In many theoretical studies it is, however, assumed that it is a constant geometrical factor; under this approximation (1.1) is known as the “pocket formula”.

Among the hadron final states, double open heavy flavor production is considered to be an important and promising tool for probing the DPS mechanism [28]. In particular, the LHCb Collaboration has recently reported an enhancement in the data on double charm production cross section in pp collisions [20, 29] that could not be described without a significant DPS contribution as was found in Ref. [30]. More possibilities have been recently discussed also in the case of $c{{\bar{c}}} b {{\bar{b}}}$ and $b{{\bar{b}}} b {{\bar{b}}}$ final states, as well as in associated production of open heavy flavor and jets, in Refs. [10, 31,32,33].

Within yet large experimental uncertainties, the c.m. collision energy dependence of the effective cross section is consistent with a constant $\sigma _{\mathrm{eff}}\sim 15$–20 mb for the channels probed by most of the existing measurements [11, 12, 18,19,20,21,22,23,24]. However, in associated production of heavy quarkonia such as double-$J/\psi$ and $J/\psi \Upsilon$, one discovers systematically lower values of $\sigma _{\mathrm{eff}}$ than in all the other channels studied so far [34,35,36,37]. Such a discrepancy may hint towards a non-universality of $\sigma _{\mathrm{eff}}$ due to e.g. spatial fluctuations of the parton densities [38]. Typically, measurements of the DPS contributions for different production processes need a dedicated experimental analysis and tools, and the precision is usually very limited and suffers due to large backgrounds coming from the standard SPS processes.

The use of ultraperipheral pA collisions (UPCs) for probing the DPS mechanism and further constraining the effective cross section has not yet been properly studied in the literature. In contrast, the SPS UPC case has been studied in, e.g., Refs. [39, 40]. In UPCs, the high-energy colliding systems pass each other at large transverse separations and thus do not undergo hadronic interactions. In this case, they interact electromagnetically via an exchange of quasi-real photons. The corresponding Weiszäcker–Williams (WW) photon flux [41, 42] is scaled with the square of electric charge of the emitter and is thus strongly enhanced for a heavy nucleus making the pA and AA UPCs more advantageous compared with that in pp collisions. It is worth noticing that the photon spectrum of a heavy nucleus is rather broad, where the peak-energy in the target rest frame scales linearly with the nuclear Lorentz factor which represents yet another advantage of UPCs. Finally, an additional reduction of the backgrounds is provided by tagging on the final-state nucleus identifying the momentum transfer taken by the exchanged photon, together with reconstructing the four-momenta of the produced final-state particles.

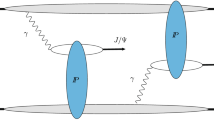
In this work, we explore possibilities for a new measurement of the gluon dPDF in the proton at small-x by means of $A+p \rightarrow A + (c{{\bar{c}}} b {{\bar{b}}}) + X$ reaction in high-energy pA UPCs schematically illustrated in Fig. 1. This process offers interesting possibilities and a cleaner environment for probing the DPS contribution compared with that in pp collisions.

In order to study the corresponding reaction in UPCs, we have to compute an effective cross section for the interaction of two partons (e.g. gluons) on one side with two photons on the other side, in contrast to the four parton case in regular pp or pA collisions. At small x and for hadronic final states, these partons are overwhelmingly likely to be gluons, so in the subsequent discussion we will simply refer to them as gluons. By exchanging the two-gluon initial state by two photons on the nucleus side, the effective cross section is expected to increase significantly. This is due to the fact that two photons from a single nucleus overlap much less than the two gluons, since the latter are well localized inside the nucleons, while photons are more spread out, specially in the case of UPCs, when they are required to be outside the nucleus. As far as we know, this effective cross section has not yet been calculated or measured earlier, but it is clearly important in order to better understand the impact-parameter dependence of parton distributions in general.

Regarding the order in coupling constants, the DPS process is of the order of $(\alpha \alpha _s)^2$, while the SPS process—$\alpha \alpha _s^3$, i.e. the SPS cross section is by default a factor of $\alpha _s/\alpha$ larger. However, the DPS reaction is expected to dominate the $c{{\bar{c}}} b {{\bar{b}}}$ production cross section over the SPS one at high energies, particularly, for a large separation between rapidities of $c{{\bar{c}}}$ and $b {{\bar{b}}}$ pairs. Indeed, in the case of a large invariant mass of the $c{{\bar{c}}} b {{\bar{b}}}$ system, the parton distributions are computed at larger x for the SPS case than that in DPS, since more energy in the initial state is needed, especially if there is a considerably large rapidity difference between the $c{{\bar{c}}}$ and $b{{\bar{b}}}$ pairs. As the PDFs decrease very fast with x in the case of gluons (and photons likewise), the SPS process is expected to be suppressed.

Thus, in order to extract the DPS contribution to this process, one should consider light $c{{\bar{c}}}$ and $b {{\bar{b}}}$ pairs produced at relatively large rapidity separation $\delta Y=Y_{c{{\bar{c}}}} - Y_{b{{\bar{b}}}} \gg 1$. This is required in order to maximize the invariant mass of the SPS $\gamma +g \rightarrow c{{\bar{c}}} b {{\bar{b}}}$ background process, and hence to sufficiently suppress the background compared with the DPS contribution whose dependence on $\delta Y$ is expected to be flatter. In the case of $c{{\bar{c}}} c {{\bar{c}}}$ and $b{{\bar{b}}} b {{\bar{b}}}$ production, however, such a separation would be much more difficult (if not impossible), since combining a quark Q and antiquark ${{\bar{Q}}}$ of the same flavor does not guarantee that they come from the same SPS process $\gamma +g\rightarrow Q {{\bar{Q}}}$. The relative $\delta P_\perp = P_\perp ^{c{{\bar{c}}}} - P_\perp ^{b{{\bar{b}}}}$ variable is of less importance for the SPS background suppression since both the SPS and the DPS components are peaked around a small $\delta P_\perp \approx 0$, while at large $\delta P_\perp$ the DPS term is nonzero only at the NLO level.

The relative SPS background suppression at large $\delta Y$ is only a qualitative expectation based upon simple kinematical arguments mentioned above. In this work, however, we focus only on the DPS contribution to the $c{{\bar{c}}}$ and $b {{\bar{b}}}$ pair production. The detailed analysis of the SPS $\gamma +g \rightarrow c{{\bar{c}}} b {{\bar{b}}}$ amplitude and the corresponding differential cross section falls beyond the scope of the current work and will be performed elsewhere.

The paper is organized as follows. In Sect. 2 we derive the formula for the UPC double heavy quark photoproduction, which is written with the help of an effective cross section that depends on the photon longitudinal momentum fraction. We also review the key components of such a calculation. In Sect. 3 we present our numerical results at LHC and larger energies. We conclude our paper in Sect. 4.

2 Double quark-pair production in UPC: DPS mechanism

In the high-energy limit, the cross section for $c{\bar{c}}b{\bar{b}}$ production via DPS can be represented as a convolution of the impact-parameter dependent differential probabilities to produce separate $c{\bar{c}}$ and $b{\bar{b}}$ pairs in pA collisions,

$$\begin{aligned}&\frac{d^4\sigma _{pA \rightarrow XA + c{\bar{c}} + b{\bar{b}}}}{dy_{c}dy_{{\bar{c}}}dy_{b}dy_{{\bar{b}}}} \nonumber \\&\quad = \int d^2 \vec {b} \, \Theta (b - R_A - R_p) \frac{d^2P_{pA \rightarrow XA + c{\bar{c}}}(b)}{dy_{c}dy_{{\bar{c}}}} \nonumber \\&\qquad \times \frac{d^2P_{pA \rightarrow XA +b{\bar{b}}}(b)}{dy_{b}dy_{{\bar{b}}}}. \end{aligned}$$

(2.1)

Here, $R_A$ and $R_p$ are the nuclei and the proton radii, respectively, $\vec b$ is the relative impact parameter ($b\equiv |{\vec b}|$). The $\Theta$-function represents an approximate absorption factor, which ensures that one considers only peripheral collisions when no nucleus break-up occurs [43]. Let us consider the ingredients of the DPS cross section (2.1) in detail.

2.1 SPS subprocess cross section

The differential probabilities P(b) in Eq. (2.1) can be deduced from the corresponding SPS cross sections. For instance, for SPS production of the $c{\bar{c}}$ pair we have

$$\begin{aligned}&\frac{d^3\sigma _{pA \rightarrow XA + c{\bar{c}}}}{dy_{c}dy_{{\bar{c}}}dp_\perp ^2} \nonumber \\&\quad = \int d^2 \vec {b}\, \Theta (b - R_A - R_p) \frac{d^3 P_{pA \rightarrow XA + c{\bar{c}}}(b)}{dy_{c}dy_{{\bar{c}}}dp_\perp ^2} \end{aligned}$$

(2.2)

where

$$\begin{aligned}&\frac{d^3 P_{pA \rightarrow XA + c{\bar{c}}}(b)}{dy_{c}dy_{{\bar{c}}}dp_\perp ^2} = \int d^2 \vec {b}_\gamma d^2 \vec {b}_g \, \delta ^{(2)} (\vec {b} + \vec {b}_g - \vec {b}_\gamma ) \nonumber \\&\quad \times \int d \xi d x \,N_\gamma (\xi ,\vec {b}_\gamma ) G_g(x, \vec {b}_g) {{{\mathcal {J}}}}\,\frac{d^3{\hat{\sigma }}_{\gamma g \rightarrow c{\bar{c}}}}{dy_{c}dy_{{\bar{c}}}d{\hat{t}}} \, \end{aligned}$$

(2.3)

in terms of the differential parton-level $\gamma +g \rightarrow c{\bar{c}}$ cross section,

$$\begin{aligned} \frac{d^3{\hat{\sigma }}_{\gamma g \rightarrow c{\bar{c}}}}{dy_{c}dy_{{\bar{c}}}d{\hat{t}}}&= \frac{d{\hat{\sigma }}_{\gamma g \rightarrow Q{\bar{Q}}}}{d{\hat{t}}} \, \delta \left( y_{c} - \frac{1}{2} \ln \left( \frac{\xi }{x} \frac{{\hat{u}}}{{\hat{t}}} \right) \right) \, \delta \nonumber \\&\quad \times \left( y_{{\bar{c}}} - \frac{1}{2} \ln \left( \frac{\xi }{x} \frac{{\hat{t}}}{{\hat{u}}} \right) \right) , \end{aligned}$$

(2.4)

written with the help of the modified Mandelstam variable

$$\begin{aligned} {\hat{t}}= (p_c - p_\gamma )^2 - m^2_Q = - \sqrt{{\hat{s}}}\bigg (\frac{\sqrt{{\hat{s}}}}{2}- \sqrt{\frac{{\hat{s}}}{4}-m^2_Q-p^2_\perp } \bigg ), \end{aligned}$$

(2.5)

and the Jacobian is

$$\begin{aligned} {{{\mathcal {J}}}}\equiv \Big |\frac{d{\hat{t}}}{dp^2_\perp }\Big |= \frac{\sqrt{{\hat{s}}}}{2\sqrt{\frac{{\hat{s}}}{4}-m^2_Q-p^2_\perp }}, \end{aligned}$$

(2.6)

as well as the photon $N_\gamma (\xi ,\vec {b}_\gamma )$ and gluon $G_g(x,\vec {b}_g)$ distributions for the longitudinal momentum fractions $\xi$, x and impact parameters $\vec {b}_\gamma$ and $\vec {b}_g$, respectively. The elementary cross section for the direct (fusion) subprocess reads in terms of the Mandelstam variables of the subprocess

$$\begin{aligned}&\frac{d^2{\hat{\sigma }}_{\gamma g \rightarrow Q{\bar{Q}}}}{d{\hat{t}}d{\hat{u}}} = \frac{\pi \alpha _s \alpha e^2_Q}{{\hat{s}}^2} \nonumber \\&\quad \times \bigg [ \frac{{\hat{t}}}{{\hat{u}}}+ \frac{{\hat{u}}}{{\hat{t}}}+\frac{4m^2_Q{\hat{s}}}{{\hat{t}}{\hat{u}}}\bigg (1-\frac{m^2_Q{\hat{s}}}{{\hat{t}}{\hat{u}}}\bigg ) \bigg ] \delta ({\hat{s}}+{\hat{t}}+{\hat{u}}). \end{aligned}$$

(2.7)

Provided that the quark mass regulates the infrared behavior of the integrals, there is no need to introduce additional low-$p_t$ cuts in order to unitarize the probabilities $P_{pA \rightarrow Q{\bar{Q}}}$ as for the heavy quarks they are below unity.

The standard WW photon flux is determined as

$$\begin{aligned} \frac{d^3N_\gamma (\omega ,{\vec b})}{d\omega d^2{\vec b}}= \frac{Z^2\alpha k^2}{\pi ^2\omega b^2} \Big [ K^2_1(k)+\frac{1}{\gamma ^2}K^2_0(k) \Big ], \quad k=\frac{b\, \omega }{\gamma },\nonumber \\ \end{aligned}$$

(2.8)

with the nucleus charge Z, the modified Bessel functions of the second kind $K_0$ and $K_1$, the fine structure constant $\alpha$, the photon energy $\omega$, the Lorentz factor $\gamma$ defined as, $\gamma = \sqrt{s} / 2 m_p$, where s is the center-of-mass (c.m.) energy per nucleon, and the proton mass $m_p=0.938$ GeV. For instance, at LHC pA 2016 run (with $\sqrt{s} = 8.16$ TeV) we have $\gamma _{\mathrm{Pb}} \approx 4350$, while for RHIC, $\gamma _{\mathrm{Au}} \approx 107$. For FCC collider (with $\sqrt{s} = 50$ TeV), we have $\gamma \approx 26652$. Since we would like to work with the photon momentum fraction instead of photon energy, we have

$$\begin{aligned} \frac{d^3 N_\gamma (\xi ,{\vec b})}{d\xi d^2{\vec b}}= \frac{\sqrt{s}}{2} \frac{d^3N_\gamma (\omega ,{\vec b})}{d\omega d^2{\vec b}} \qquad \text {with} \qquad \xi = \frac{2 \omega }{\sqrt{s}}. \end{aligned}$$

(2.9)

Another important ingredient is the impact-parameter dependent gluon distribution $G_g (x, \vec {b})$, which is often used in a factorized form,

$$\begin{aligned} G_g(x, {\vec b}) = g(x)\, f_g({\vec b}), \end{aligned}$$

(2.10)

where g(x) is the usual integrated gluon PDF, with an implicit factorization scale dependence, and $f_g (b)$ is the normalized spatial gluon distribution in the transverse plane

$$\begin{aligned} f_g ({\vec b}) = \frac{\Lambda ^2}{2 \pi } \frac{\Lambda b}{2} K_1(\Lambda b), \quad \int d^2 {\vec b} \, f_g ({\vec b}) = 1, \end{aligned}$$

(2.11)

as in Ref. [44]. Here, $\Lambda \approx 1.5$ GeV and the CT14nlo [45] collinear parton distributions are used with $\mu _F = {\hat{s}}$.

Consequently, the cross section for $c{{\bar{c}}}$ production in the SPS UPCs is related to the parton-level $\gamma +g \rightarrow c{\bar{c}}$ cross section as follows:

$$\begin{aligned} \frac{d^2\sigma _{pA \rightarrow XA + c{\bar{c}}}}{dy_{c}dy_{{\bar{c}}}}= & {} \int d^2 \vec {b} d^2 \vec {b}_\gamma d^2 \vec {b}_g d \xi d x\,\nonumber \\&\times \Theta (b - R_A - R_p) \delta ^{(2)} (\vec {b} + \vec {b}_g - \vec {b}_\gamma ) \nonumber \\&\times \,N_\gamma (\xi ,\vec {b}_\gamma ) G_g(x, \vec {b}_g) \frac{d^2{\hat{\sigma }}_{\gamma g \rightarrow c{\bar{c}}}}{dy_{c}dy_{{\bar{c}}}}.\nonumber \\ \end{aligned}$$

(2.12)

This expression can be rewritten in the following equivalent form:

$$\begin{aligned}&\frac{d^2\sigma _{pA \rightarrow XA + c{\bar{c}}}}{dy_{c}dy_{{\bar{c}}}} = \int d \xi \int d x \, {\overline{N}}_\gamma (\xi ) g(x) \frac{d^2{\hat{\sigma }}_{\gamma g \rightarrow c{\bar{c}}}}{dy_{c}dy_{{\bar{c}}}} \, \nonumber \\&\quad \times \int d^2 \vec {b}\, \Theta (b - R_A - R_p) T_{g\gamma } (\xi , \vec {b}), \end{aligned}$$

(2.13)

with the overlap function, which encapsulates all the impact-parameter dependence in the matrix element squared, defined as follows:

$$\begin{aligned}&T_{g\gamma } (\xi , \vec {b}) = \frac{1}{{\overline{N}}_\gamma (\xi )} \int d^2 \vec {b}_\gamma \, \Theta (b_\gamma - R_A)\nonumber \\&\quad \times N_\gamma (\xi ,\vec {b}_\gamma ) f_g(\vec {b} - \vec {b}_\gamma ), \end{aligned}$$

(2.14)

where

$$\begin{aligned} {\overline{N}}_\gamma (\xi ) = \int d^2 b \, \Theta (b - R_A) N_\gamma (\xi ,\vec b) \end{aligned}$$

(2.15)

is the number distribution of photons that can interact in the considering process (outside the nucleus) shown in Fig. 2. Here, it becomes apparent that the photon distribution is strongly peaked at low $\xi < 10^{-2}$. The distribution calculated with the WW flux is independent of energy if the Lorentz factor is very large, $\gamma \rightarrow \infty$.

Fig. 2

The number distribution of photons ${\overline{N}}_\gamma (\xi )$ (times $\xi$) outside the nucleus that can interact with gluons in the proton in the considering photoproduction process. For comparison, the gluon distributions at two factorization scales $2m_c$ and $2 m_b$

It is worth noticing that the last integral in Eq. (2.13) can be transformed as follows:

$$\begin{aligned}&\int d^2 \vec {b} \Theta (b - R_A - R_p) T_{g\gamma } (\xi , \vec {b}) \\&\quad = \int d^2 \vec {b} \frac{\Theta (b - R_A - R_p)}{{\overline{N}}_\gamma (\xi )} \int d^2 \vec {b}_\gamma \, \Theta (b_\gamma - R_A) \\&\qquad \times N_\gamma (\xi ,\vec {b}_\gamma ) f_g(\vec {b}_\gamma - \vec {b}) \\&\quad =1 - \int d^2 \vec {b} \int d^2 \vec {b}_\gamma \,\\&\qquad \times \frac{\Theta (b_\gamma \!- \!R_A) ( 1 \!-\! \Theta (b - R_A \!-\! R_p))}{{\overline{N}}_\gamma (\xi )}\\&\qquad \times N_\gamma (\xi ,\vec {b}_\gamma ) f_g(\vec {b}_\gamma - \vec {b}). \end{aligned}$$

This relation explicitly demonstrates that, if the gluon distribution is very localized, i.e. $R_p \rightarrow 0$ together with $b_\gamma \rightarrow b$, the second term vanishes, leaving no traces of the impact-parameter dependence in the SPS cross section (2.13).

For completeness, besides the direct production process whose formalism is discussed above, we have also included a sub-dominant resolved contribution following Ref. [39]. By including the resolved component with the gluon-initiated hard subprocess $gg\rightarrow Q{{\bar{Q}}}$ at leading order (LO), as an example, one is enabled to pick a gluon (with momentum fraction z) from the incident photon by means of a gluon PDF in the photon, $g^\gamma (z,\mu ^2)$, while the photon remnant hadronizes into an unobserved hadronic system. The corresponding contribution reads

$$\begin{aligned} \frac{d^2\sigma ^\text {Resolved, gluon}_{pA \rightarrow XA + c{\bar{c}}}}{dy_{c}dy_{{\bar{c}}}}= & {} \int d \xi d x {\overline{N}}_\gamma (\xi ) g(x) \\&\times \int d z g^{\gamma }(z) \, \frac{d^2{\hat{\sigma }}_{gg \rightarrow Q{\bar{Q}}}}{dy_{c}dy_{{\bar{c}}}}\\&\times \int d^2 \vec {b}\, \Theta (b - R_A - R_p) T_{g\gamma } (\xi , \vec {b}). \end{aligned}$$

In our numerical analysis, we also include the second relevant subprocess $q {{\bar{q}}}\rightarrow Q{{\bar{Q}}}$ at LO. The PDFs in the photon are taken from Ref. [46]. Such a resolved photon contribution increases the differential cross section only slightly and mostly at negative rapidities (for more details and the corresponding figures, see below).

2.2 Pocket formula for the DPS cross section in pA UPCs

Consider now the formalism for the DPS mechanism of direct $c{\bar{c}}b{\bar{b}}$ production in pA UPCs (while the resolved photon contributions to the DPS are also included into the numerical analysis).

In what follows, we define the nucleus with positive rapidity, and the proton with negative one, such that the longitudinal photon and gluon momentum fractions are given by

$$\begin{aligned} \xi _i= & {} \frac{m_{i,\perp }}{\sqrt{s}} ( e^{y_{Q_i}} + e^{y_{{{\bar{Q}}}_i} } ), \quad x_i = \frac{m_{i,\perp }}{\sqrt{s}} ( e^{-y_{Q_i}} + e^{-y_{{{\bar{Q}}}_i} } ),\nonumber \\&m^2_{i,\perp } = m_{Q_i}^2 + p_{i,\perp }^2, \end{aligned}$$

(2.16)

respectively, where the index $i=1,2$ denotes the elementary SPS processes or, equivalently, the heavy quark species the photon and gluon are coupled to, namely, $Q_{1,2}\equiv c,b$ in the process considered, $m_{i,\perp }$ is the transverse mass of the heavy quark, $y_{Q_i}$ ($y_{{{\bar{Q}}}_i}$) is the heavy quark (antiquark) rapidity. Then the invariant mass of each $Q_i{{\bar{Q}}}_i$ pair reads

$$\begin{aligned} M^2_{i,Q{\bar{Q}}}= 2x_i\xi _i s = 2m^2_{i,\perp }(1+\cosh (y_{Q_i}-y_{{{\bar{Q}}}_i})) \end{aligned}$$

(2.17)

such that

$$\begin{aligned} dx_id\xi _i=\frac{m^2_{i,\perp }}{s}\big |\sinh (y_{Q_i} -y_{{{\bar{Q}}}_i})\big |dy_{Q_i}dy_{{{\bar{Q}}}_i}. \end{aligned}$$

(2.18)

Consequently, the DPS cross section (2.1) can be rewritten in terms of parton-level elementary photon–gluon fusion cross sections as

$$\begin{aligned}&\frac{d^4\sigma _{pA \rightarrow XA + c{\bar{c}} + b{\bar{b}}}}{dy_{c}dy_{{\bar{c}}}dy_{b}dy_{{\bar{b}}}} = \int d^2 b \, \Theta (b - R_A - R_p) \nonumber \\&\quad \times \int d^2 \vec {b}_{\gamma ,1} \, \Theta (b_{\gamma ,1} - R_A)\nonumber \\&\quad \times \int d^2 \vec {b}_{\gamma ,2} \, \Theta (b_{\gamma ,2} - R_A) \nonumber \\&\quad \times \int d \xi _1 d \xi _2 d x_1 d x_2 N_{\gamma \gamma } (\xi _1, \vec {b}_{\gamma ,1}; \xi _2, \vec {b}_{\gamma ,2}) \nonumber \\&\quad \times G_{gg} (x_1, \vec {b}_{g,1}; x_2, \vec {b}_{g,2}) \frac{d^2{\hat{\sigma }}_{\gamma g \rightarrow c{\bar{c}}}}{dy_{c}dy_{{\bar{c}}}} \frac{d^2{\hat{\sigma }}_{\gamma g \rightarrow b{\bar{b}}}}{dy_{b}dy_{{\bar{b}}}} \end{aligned}$$

(2.19)

where $\vec {b}_{g,i} = \vec {b}_{\gamma ,i} - \vec {b}$ for $i = 1,2$, and $N_{\gamma \gamma }$ ($G_{gg}$) is the corresponding di-photon (di-gluon) distribution.

If we neglect any correlations between the individual photon and gluon exchanges, the di-photon and di-gluon distributions are conveniently represented in a factorized form, i.e.

$$\begin{aligned} N_{\gamma \gamma } (\xi _1, \vec {b}_{\gamma ,1}; \xi _2, \vec {b}_{\gamma ,2})= & {} N_\gamma (\xi _1, \vec {b}_{\gamma ,1}) N_\gamma (\xi _2, \vec {b}_{\gamma ,2}) \nonumber \\ G_{gg} (x_1, \vec {b}_{g,1}; x_2, \vec {b}_{g,2})= & {} G_g (x_1, \vec {b}_{g,1}) G_g (x_2, \vec {b}_{g,2}), \nonumber \\ \end{aligned}$$

(2.20)

in terms of the quasi-real single photon $N_\gamma (\xi , \vec {b})$ and gluon $G_g(x,\vec {b})$ distributions defined above. Note that the above factorization formulas are approximations valid for $\xi _{1,2},x_{1,2}\ll 1$ only [4, 9, 47,48,49].

Using Eqs. (2.20), (2.10), (2.11) and (2.14), it is straightforward to transform the resulting DPS cross section to the following simple form:

$$\begin{aligned}&\frac{d^4\sigma _{pA \rightarrow XA + c{\bar{c}} + b{\bar{b}}}}{dy_{c}dy_{{\bar{c}}}dy_{b}dy_{{\bar{b}}}} \nonumber \\&\quad = \int d \xi _1 d x_1 d \xi _2 d x_2 \,\, \frac{{\overline{N}}_\gamma (\xi _1) g(x_1) {\overline{N}}_\gamma (\xi _2) g(x_2)}{\sigma _\text {eff}(\xi _1, \xi _2)} \nonumber \\&\qquad \times \frac{d^2{\hat{\sigma }}_{\gamma g \rightarrow c{\bar{c}}}}{dy_{c}dy_{{\bar{c}}}} \, \frac{d^2{\hat{\sigma }}_{\gamma g \rightarrow b{\bar{b}}}}{dy_{b}dy_{{\bar{b}}}} \, \end{aligned}$$

(2.21)

where ${\overline{N}}_\gamma (\xi )$ is defined in Eq. (2.15), and the definition of the effective cross section,

$$\begin{aligned}&\sigma _\text {eff}(\xi _1, \xi _2) \nonumber \\&\quad \equiv \Bigg [\int d^2 b \, \Theta (b - R_A - R_p) T_{g\gamma }(\xi _1, b) T_{g\gamma }(\xi _2, b)\Bigg ]^{-1}, \end{aligned}$$

(2.22)

has been introduced. In this way we arrive at an analog of the pocket formula applicable for the DPS contribution to $c{\bar{c}}b{\bar{b}}$ production in pA UPCs. Equation (2.21) is valid also for the DPS contribution to the $c{{\bar{c}}} c{{\bar{c}}}$ and $b{{\bar{b}}} b{{\bar{b}}}$ production processes apart from the change in the symmetry factor.

Fig. 3

The DPS effective cross section as a function of $\sqrt{\xi _1 \xi _2}$

Fig. 4

The SPS $c{{\bar{c}}}$ quark production cross section in pA UPCs as a function of rapidity $y_c$. Energy of $\sqrt{s}=8.16$ TeV is shown in the left panel and $\sqrt{s}=50$ TeV is shown in the right panel. The heavy ion is coming from the left

In what follows, we wish to investigate the corresponding SPS and DPS differential (in rapidity) cross sections making predictions for future measurements.

3 Numerical results

In our numerical analysis of the SPS and DPS cross sections for heavy flavor production in pA UPCs, we consider lead nucleus, with radius $R_{\mathrm{Pb}}=5.5$ fm (the proton radius is fixed to $R_p=0.87$ fm), while the heavy quark masses are taken to be $m_c=1.4$ GeV and $m_b=4.75$ GeV.

In Fig. 3 the effective cross section for pA UPCs of Eq. (2.22) is plotted as a function of photon momentum fraction $\xi$. This plot carries essentially the information of where the photons are, but not of the number of photons outside the nucleus, as it is factored out in ${\overline{N}}_\gamma (\xi )$. The main contribution to this result arises when the two photons are inside the proton. With the model used here, the plot does not change with energy or factorization scale.

Take first the case when $\xi _1 =\xi _2$. For small $\xi$, the photons are spread too much and it is more rare that they overlap; then the effective cross section is larger. For large $\xi$, the photons are in a narrow shell just outside the nucleus, and if the width of this shell is smaller than the proton radius, it is clear that $\sigma _\text {eff}$ should also grow. That explains the minimum around $\xi \approx 0.07$, where half of the photons outside the nucleus have $b_\gamma - R_\text {Pb} < 1.0$ fm, i.e., approximately the proton radius.

In the case of $\xi _2 / \xi _1 > 1$, $\sigma _\text {eff}$ can have two minima, as shown in the plot. That happens because the two photon distributions have their maximum probability of finding the photons inside the proton at different $\xi$.

To better understand our double parton results, we recalculate the SPS cross section in Fig. 4. We show the differential cross section in c quark rapidity, for energies of 8.16 TeV and 50 TeV. The heavy ion comes from the left, while the proton comes from the right.

We detail the direct and the resolved contributions to the result. The resolved contribution is only relevant at small $z\xi$ and large x. Indeed, we see a harder decrease at positive rapidities than at negative rapidities, due to the nucleus photons having a sharper cutoff when $\xi \rightarrow 1$ than the proton gluons. The curves are almost flat at central rapidities; the resolved contribution makes it even flatter due to a small modification to the shape of the resulting differential cross section (mostly) in the negative rapidity domain. While the relative importance of the resolved contribution grows with energy, it remains minor compared with the direct one; see also Table 1.

Fig. 5

The DPS $c{{\bar{c}}} b{{\bar{b}}}$ production cross section in pA UPCs as a function of c-quark rapidity at fixed b rapidity (left panel) and as a function of b-quark rapidity at fixed c-quark rapidity (right panel)

For double parton scattering, we present, in Fig. 5, the $c{{\bar{c}}} b{{\bar{b}}}$ cross section with $y_{{{\bar{c}}}}, y_{{{\bar{b}}}}$ integrated out but differential in $y_c, y_b$ (at left and right panels, respectively). The production at central rapidities increases with rapidity; this is in contrast with the SPS case where it was flat. If the DPS was just the product of two SPS cross sections, we would not see such an increase. In effect, this is a result of the effective cross section in the denominator, which decreases as the photon energy fraction $\xi$ increases for $\xi < 0.07$. Therefore, this behavior corroborates our result that the pocket formula cannot have a constant effective cross section.

Fig. 6

The same as in Fig. 5 but for the ratios of the differential cross section at each fixed rapidity to a reference curve at fixed $y_c=0$ (left panel) and $y_b=0$ (right panel) and at each given energy

As a matter of fact, any differences (other than a multiplicative factor) between Figs. 5 and 4 are due to the dependence of the effective cross section on $\xi$. In addition, the different lines in Fig. 5 presenting different behaviors as the fixed rapidity is changed is a direct result of fact that the photon b distribution changes with $\xi$. In order to illustrate how the shape changes with rapidity, we have added an extra Fig. 6 showing the ratios of the differential cross section to a given reference curve at fixed $y_c=0$ (left panel) and $y_b=0$ (right panel) corresponding left and right panels of Fig. 5, respectively. As expected, the largest deviations in shapes emerge at forward rapidities corresponding to large $\xi$. It is much easier to see this effect in our UPC example than in standard four-gluon DPS, since the photon impact-parameter distributions have a clearer and stronger dependence on the longitudinal momentum fraction as opposed to gluons. Just to clarify, we remark again that no correlations between the two photons were taken into account, in the sense that picking the first photon does not change the distribution of the second photon. /

Table 1 Table with the integrated cross sections for DPS and SPS production processes

Fig. 7

DPS $c{{\bar{c}}} b {{\bar{b}}}$ production cross section in pA UPCs as a function of c rapidity with $y_b$ integrated (left panel) and as a function of b-quark rapidity with $y_c$ integrated (right panel)

In Fig. 7 we integrate over one more rapidity, leaving only $y_b$ or $y_c$ unintegrated. Together with Table 1, we see that we have a significant cross section, of the order of nanobarns, indicating that such an observable can be measured currently at the LHC and of course also at higher energy future colliders.

In the differential cross sections, e.g. shown in Figs. 4, 5, and 7, integrated over the antiquark rapidities, one can increase statistics by multiplying them by a factor of two (for SPS) or by the factor of four (for DPS) if a measurement detects open heavy flavored mesons containing both heavy quarks and antiquarks. In this case, charged $D^\pm$ and $B^\pm$ mesons should be detected in the DPS final state, simultaneously ensuring that $D^+D^-$ and $B^+B^-$ meson pairs are produced at well separated rapidity domains to suppress the SPS $\gamma +g \rightarrow c{{\bar{c}}} b {{\bar{b}}}$ background contribution. In principle, for this purpose it suffices to consider the individual (anti)quark rapidities $y_c$ (or $y_{{{\bar{c}}}}$) and $y_b$ (or $y_{{{\bar{b}}}}$) to be far apart from each other.

4 Conclusions

In this paper we investigated the double parton interaction between heavy ion and proton in ultraperipheral collisions. For the main contribution, where two photons from the heavy ion interact with two gluons from the proton, we developed a new pocket formula, with some peculiarities when compared with the usual one. In our case, as the distribution of photons is not as localized in impact parameter as the gluon distribution, the effective cross section is rather large, roughly dozens of barns. Another consequence is that the effective cross section is heavily dependent on the photon longitudinal momentum fraction, and this cannot be neglected. Therefore, we do not have a simple multiplication of SPS cross sections, but instead a convolution in the photon longitudinal momentum fraction.

We presented our results in terms of the cross section to produce c and b quarks as a function of rapidities. In this way, we can assert that each heavy quark gives us information about one of the gluons in the initial state. Therefore, this is an effective and direct probe of the double-gluon distribution that can be studied at the HL-LHC or at a future collider, e.g. at 50 TeV, for which the predictions are shown in Figs. 5 and 7.

We point out that the most efficient way of suppressing the SPS $\gamma +g \rightarrow c{{\bar{c}}} b {{\bar{b}}}$ background contribution is to measure the open charm and open bottom mesons at large relative rapidity separation of a few units. So, future measurements aiming at precision measurement of the DPS contribution in the considered process are encouraged to have the corresponding detectors covering different rapidity domains of the phase space (for example, the central and forward/backward cases).