Midrapidity inclusive densities in high energy pp collisions in additive quark model

Abstract

High energy (CERN SPS and LHC) inelastic pp ($p\bar{p}$) scattering is treated in the framework of the additive quark model together with Pomeron exchange theory. We extract the midrapidity inclusive density of the charged secondaries produced in a single quark–quark collision and investigate its energy dependence. Predictions for the $\pi p$ collisions are presented.

1 Introduction

Regge theory provides a useful tool for the phenomenological description of high energy hadron collisions [1–4]. The quantitative predictions of Regge calculus are essentially dependent on the assumed coupling of participating hadrons to the Pomeron. In our previous papers [5, 6] we described elastic pp ($p\bar{p}$) scattering and diffractive dissociation processes including the recent LHC data in terms of a simple Regge exchange approach in the framework of the additive quark model (AQM) [7, 9], or constituent quarks model as it is also referred to. It has been successfully applied to pp scattering processes at LHC energies [8]. In the present paper we consider the inclusive densities of produced secondaries in the midrapidity region in the same approach.

In AQM baryon is treated as a system of three spatially separated compact objects—the constituent quarks. Each constituent quark is colored and has an internal quark–gluon structure and a finite radius that is much less than the radius of the proton, $r_q^2 \ll r_p^2$. This picture is in good agreement both with SU(3) symmetry of the strong interaction and the quark–gluon structure of the proton [10–13]. The constituent quarks play the roles of incident particles in terms of which pp scattering is described in AQM.

In the case of inelastic pp collisions the secondary particles are produced in AQM in one or several qq collisions, so it opens the possibility to investigate inclusive densities of the secondaries produced in the single qq collision at the different initial energies. After that we can calculate the central inclusive densities in $\pi p$ collisions without any new parameters.

2 High energy pp interactions in AQM

Elastic amplitudes for large energy $s=(p_1+p_2)^2$ and small momentum transfer t are dominated by Pomeron exchange. We neglect the small difference in pp and $p\bar{p}$ scattering coming from the exchange of negative signature Reggeons, Odderon (see e.g. [14] and references therein), $\omega$-Reggeon etc., since their contributions are suppressed by s.

The single t-channel exchange results in the amplitude of constituent quarks scattering,

$$\begin{aligned} M_{qq}^{(1)}(s,t) = \gamma _{qq}(t) \cdot \left( \frac{s}{s_0}\right) ^{\alpha _P(t) - 1} \cdot \eta _P(t), \end{aligned}$$

(1)

where $\alpha _P(t) = \alpha _P(0) + \alpha ^\prime _P\cdot t$ is the Pomeron trajectory specified by the intercept and slope values $\alpha _P(0)$ and $\alpha ^\prime _P$, respectively. The Pomeron signature factor,

$$\begin{aligned} \eta _P(t) \,=\, i \,-\, \tan ^{-1} \left( \frac{\pi \alpha _P(t)}{2}\right) , \end{aligned}$$

determines the complex structure of the amplitude. The factor $\gamma _{qq}(t)=g_1(t)\cdot g_2(t)$ has the meaning of the Pomeron coupling to the beam and target particles, the functions $g_{1,2}(t)$ being the vertices of the constituent quark–Pomeron interaction (filled circles in Fig. 1). It is worth to emphasize that the qq interaction is described here by single effective Pomeron exchange between each qq pair. Generally it may include the contributions of several Gribov bare Pomerons [15] and the parameters of the effective Pomeron could be different from those of the bare Pomerons. At the same time the one quark interaction with the two different target quarks is mediated by the exchange of the two effective Pomerons. In this respect there is a close resemblance between the nucleon–nucleon scattering in AQM and the nucleus–nucleus scattering in Glauber theory. The qq interaction plays the same role in the first case as the NN interaction in the second.

The elastic pp scattering amplitude (or the $p\bar{p}$ scattering amplitude, here we do not distinguish between the two) is basically expressed as

$$\begin{aligned} M_{pp}(s,t)\,= & {} \,\int dK\,dK^\prime \psi ^*(k_i^\prime +Q_i^{\,\prime })\,\psi ^*(k_i+Q_i)\, \nonumber \\&\times V(Q,Q^{\,\prime })\,\psi (k_i^\prime )\,\psi (k_i). \end{aligned}$$

(2)

In this formula $\psi (k_i)\equiv \psi (k_1,k_2,k_3)$, is the initial proton wave function in terms of the quarks’ transverse momenta $k_i$, while $\psi (k_i+Q_i)\equiv \psi (k_1+Q_1,k_2+Q_2,k_3+Q_3)$ is the wavefunction of the scattered proton. The interaction vertex $V(Q,Q^{\,\prime })\equiv V(Q_1,Q_2,Q_3,Q_1^{\,\prime },Q_2^{\,\prime },Q_3^{\,\prime })$ stands for the multipomeron exchange, $Q_k$ and $Q_l^{\,\prime }$ are the momenta transferred to the target quark k or beam quark l by the Pomerons attached to them, Q is the total momentum transferred in the scattering, $Q^2=Q^{\prime \,2}=-t$.

The scattering amplitude is presented in AQM as a sum over the terms with a given number of Pomerons,

$$\begin{aligned} M_{pp}(s,t)\,=\,\sum _n M_{pp}^{(n)}(s,t), \end{aligned}$$

(3)

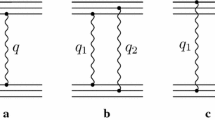
where the amplitudes $M_{pp}^{(n)}$ collect all diagrams comprising various connections of the beam and target quark lines with n Pomerons. Similar to Glauber theory [16, 17] one has to rule out the multiple interactions between the same quark pair. AQM permits the Pomeron to connect any two quark lines only once. It crucially decreases the combinatorics, leaving the diagrams with no more than $n=9$ effective Pomerons. Several AQM diagrams are shown in Fig. 1.

Fig. 1

The AQM diagrams for pp elastic scattering. The straight lines stand for quarks, the wavy lines denote Pomerons, Q is the momentum transferred, $t=-Q^2$. a The one of the single Pomeron diagrams, b and c represent double Pomeron exchange with two Pomeron coupled to the different quark b and to the same quarks c, $q_1+q_2=Q$

In the following we assume the Pomeron trajectory to have the simplest form,

$$\begin{aligned} \left( \frac{s}{s_0}\right) ^{\alpha _P(t) - 1}\,=\,e^{\Delta \cdot \xi } e^{-r_q^2\,q^2}, \quad \xi \equiv \ln \frac{s}{s_0},\quad r_q^2\equiv \alpha ^\prime \cdot \xi . \end{aligned}$$

The value $r_q^2$ defines the radius of the quark–quark interaction, while $S_0=(9~\mathrm{GeV})^2$ has the meaning of a typical energy scale in Regge theory.

In the first order there are nine equal quark–quark contributions due to one Pomeron exchange between qq pairs. The amplitude (2) reduces to a single term with $Q_1=Q_1^{\,\prime } = Q$, $Q_{2,3}=Q_{2,3}^{\,\prime } = 0$,

$$\begin{aligned} M_{pp}^{(1)}\,=\,9\biggl (\gamma _{qq}\eta _P(t) e^{\Delta \cdot \xi } \biggr )\,e^{-r_q^2\,Q^2}F_P(Q,0,0)^2, \end{aligned}$$

(4)

expressed through the overlap function

$$\begin{aligned} F_P(Q_1,Q_2,Q_3)\,= & {} \,\int dK\,\psi ^*(k_1,k_2,k_3)\, \nonumber \\&\times \psi (k_1+Q_1,k_2+Q_2,k_3+Q_3). \end{aligned}$$

(5)

The function $F_P(Q,0,0)$ plays the role of a proton form factor for the strong interaction in AQM.

The quarks’ wave function has been taken in the simple form of Gaussian packets,

$$\begin{aligned} \psi (k_1,k_2,k_3)= & {} N\left[ \,e^{-a_1(k_1^2+k_2^2+k_3^2)} +\,C_1\,e^{-a_2(k_1^2+k_2^2+k_3^2)}\right. \nonumber \\&\left. +\,C_2\,e^{-a_3(k_1^2+k_2^2+k_3^2)}\right] , \end{aligned}$$

(6)

normalized to unity. The parametrization by the single exponent is unable to reproduce the minimum in $\mathrm{d}\sigma /\mathrm{d}t$ distribution evidently seen in the experimental data for $\sqrt{s}=7$ TeV [18, 19]. The two exponential fit used in our previous papers [5, 6] reproduces this minimum but gives too low values of $\mathrm{d}\sigma /\mathrm{d}t$ at $|t| \sim 0.7 - 0.8$ Gev$^2$. In the present paper the wave function is parameterized by the sum of three Gaussian exponents, which allows for the better description of $\mathrm{d}\sigma /\mathrm{d}t$.

Now the parameters read

$$\begin{aligned} \Delta= & {} 0.14,\quad \alpha ^\prime =0.116\,\mathrm{GeV}^{-2},\quad \gamma _{qq}=0.45\,\mathrm{GeV}^{-2}.\\ a_1= & {} 9.0\,\mathrm{GeV}^{-2},\quad a_2=0.29\,\mathrm{GeV}^{-2},\nonumber \\ a_3= & {} 2.0\,\mathrm{GeV}^{-2},\quad C_1=0.024,\quad C_2=0.05. \end{aligned}$$

One has to remark here that we do not claim the real matter distribution inside the proton to be close to the Gaussian shape, this form is suitable only to perform all the integrals analytically. The value $a_1$ is quite compatible with the large proton size assumed above, whereas $a_{2,3}$ values manifest the presence of the small radius components in the proton wave function. However, their relative weights are small so the total wave function (6) matches the condition $r_p^2 \gg r_q^2$, which is effectively fulfilled for the mean radii that are important for the calculations validity.

Fig. 2

Left Differential cross section of the elastic pp scattering (solid line) and $\pi p$ scattering (dashed line), see Sect. 4, at $\sqrt{s} = 7$ TeV. The experimental points for pp scattering have been taken from [18, 19]. Right Pseudorapidity distribution of the secondaries $\mathrm{d}N^\mathrm{NSD}/\mathrm{d}\eta$ in pp scattering for the non-single diffractive events. The solid line shows the AQM estimates by Eq. (12). The experimental points have been taken from [20]

The higher orders elastic terms are expressed through the functions (5) integrated over Pomerons’ momenta,

(7)

The sum in this formula refers to all distinct ways to connect the beam and target quark lines with n Pomerons in the scattering diagram. The set of momenta $Q_i$ and $Q_l^{\,\prime }$ the quarks acquire from the attached Pomerons is particular for each connection pattern. A more detailed description can be found in [5].

With the amplitude (3) the differential cross section in the normalization adopted here is evaluated as

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}\,= & {} \,4\pi \,\bigl |M_{pp}(s,t)\bigr |^2\, \nonumber \\= & {} \,4\pi \,\left[ \bigl (\mathrm{Re}\, M_{pp}(s,t)\bigr )^2 + \bigl (\mathrm{Im}\, M_{pp}(s,t)\bigr )^2\right] . \end{aligned}$$

(8)

The optical theorem, which relates the total cross section and the imaginary part of the amplitude, in this normalization reads

$$\begin{aligned} \sigma _{pp}^{\mathrm{tot}}\,=\,8\pi \,\mathrm{Im}\, M_{pp}(s,t=0). \end{aligned}$$

(9)

The condition for the AQM applicability, $r_q^2/r_p^2 \ll 1$, holds rather well, since $r_p^2\simeq 12$ Gev$^{-2}$ whereas $r_q^2\simeq 1.5$ Gev$^{-2}$ at $\sqrt{s}\approx 7$ TeV.

The resulting differential cross sections for pp scattering at $\sqrt{s} = 7$ TeV are presented in Fig. 2 together with the predictions for $\pi p$ scattering at the same energy (see below).

3 AGK cuts and inclusive densities in pp and qq interactions

All amplitudes of the inelastic processes in high energy pp collisions can be treated as the sum of various absorptive parts of elastic pp amplitude; see the AGK cutting rules [21]. In the AQM the diagram with a single qq interaction, Fig. 3, has only one absorptive part.

Fig. 3

The first quark order diagram contributing to the inelastic particle production in pp collision

Fig. 4

The diagrams with a double interaction

The one-Pomeron cut in the left hand side of Fig. 3 corresponds to the multiperipheral ladder of the produced secondaries in the right hand side of Fig. 3. The resulting cross section is $\sigma ^{(1)}$.

In the case of double interaction in Fig. 1b the imaginary part is given by the sum of three different absorptive parts presented in Fig. 4. The first one, the cut between Pomerons, is shown in Fig. 4a. It describes the elastic and diffractive dissociation processes without production of secondaries in the central (midrapidity) region. The second absorptive part, Fig. 4b, corresponds to the cut of one Pomeron and gives the first rescattering correction to the processes in Fig. 3. The multipheripheral ladders in Figs. 3 and 4b are practically the same and have the same midrapidity inclusive densities $\mathrm{d}N_{qq}/\mathrm{d}y$. The absorptive part in Fig. 4b has the numerical factor −4 due to the combinatorics [21]. The third absorptive part is shown in Fig. 4c, where the cut slices both Pomerons. It means the simultaneous production of two multipheripheral ladders of the secondaries. These ladders are also practically identical to those in Figs. 3 and 4b and result in equal inclusive densities $\mathrm{d}N_{qq}/\mathrm{d}y$ (we neglect the very small numerical difference coming from the energy conservation). The combinatorial factor here is +2 [21]. The contribution to the inclusive density of the secondaries from Fig. 4c is $4\mathrm{d}N_{qq}/\mathrm{d}y$. It is compensated by the negative contribution $-4\mathrm{d}N_{qq}/\mathrm{d}y$ from the process in Fig. 4b. Finally, the sum of all absorptive parts collected in Fig. 4 yields a zero contribution to the inclusive densities of secondary particles in complete agreement with the AGK cutting rules [21].

Fig. 5

Left The pseudorapidity distributions of all charged secondaries produced in the inelastic pp and $p\bar{p}$ collisions at different energies together with their description in QGSM (solid curve). The dotted line shows the extracted $\mathrm{d}N_{qq}/\mathrm{d}\eta$ values. The dashed line presents the obtained pseudorapidity distribution of charged secondaries in the inelastic $\pi p$ collision. The experimental points are taken from Refs. [24, 25]. Right The total cross sections of pp (solid line) and $\pi p$ (dashed line) as the initial energy functions. The experimental pp points are taken from [26, 27]

Similarly, there is no contribution to the resulting inclusive density due to diagrams with a larger number of quark–quark interaction, therefore it is only the impulse approximation diagrams in Fig. 3 that provide the inclusive density of the secondaries produced in pp collisions in the midrapidity region,

$$\begin{aligned} \sigma _{pp}^{\mathrm{inel}}\cdot \frac{\mathrm{d}N_{pp}}{\mathrm{d}y} = 9\,\sigma _{qq}^{(1)}\cdot \frac{\mathrm{d}N_{qq}}{\mathrm{d}y}, \end{aligned}$$

(10)

where $\sigma _{qq}^{(1)}$ is the first order contribution to the total cross section. This equation is true as well for the pseudorapidity inclusive densities, which amounts to the replacement $\mathrm{d}y \rightarrow \mathrm{d}\eta$.

The cross section of pp interaction used in (10) depends on the way the value of the inclusive density is fixed. It is determined as the number of the secondaries divided by the number of events in the small interval $\mathrm{d}y$ in the midrapidity region. In the diffractive dissociation the secondaries are produced practically only in the fragmentation regions; therefore, the number of secondary particles in the midrapidity region does not change whether or not we include diffractive dissociation events in our sample. However, the number of events, i.e. the denominator in the definition of $\mathrm{d}N/\mathrm{d}y$, differs for these two cases, so the net value $\mathrm{d}N_{pp}/\mathrm{d}y$ in the left hand side of (10) has to be multiplied by $\sigma _{PP}^{\mathrm{inel}}$ if we take all inelastic events, or by $\sigma _{PP}^{\mathrm{nondiffr}}$ if we take the events without diffractive dissociation.

Let us try to estimate the energy dependence of $\mathrm{d}N_{qq}/\mathrm{d}y$ and $\mathrm{d}N_{qq}/\mathrm{d}\eta$ using the existing data. There are several available experimental points for $\mathrm{d}N_{pp}/\mathrm{d}\eta$ at the different energies measured in all inelastic events. They are shown in Fig. 5 together with the calculations of $\mathrm{d}N_{pp}/\mathrm{d}y$ and $\mathrm{d}N_{pp}/\mathrm{d}\eta$ in the quark–gluon string model (QGSM) [22, 23]. Actually QGSM output is employed here only to extrapolate the existing experimental data.

The inelastic cross section entering Eq. (10) can be obtained from the identity

$$\begin{aligned} \sigma _{pp}^{\mathrm{inel}}\,=\,\sigma _{pp}^{\mathrm{tot}} - \sigma _{pp}^{\mathrm{elastic}}, \end{aligned}$$

(11)

where the total cross section is evaluated through the optical theorem (9) by summing up all nine orders of AQM diagrams (7), while the elastic cross section, $\sigma _{pp}^{\mathrm{elastic}}$, is obtained by integrating differential cross section (8) over t. The cross section $\sigma _{qq}^{(1)}$ is given by the first order of the AQM amplitude (4).

Equations (10) and (11) allow one to find $\mathrm{d}N_{qq}/\mathrm{d}\eta$ values presented in Fig. 5. At the LHC energies $\sqrt{s} > 0.9$ TeV $\mathrm{d}N_{qq}/\mathrm{d}\eta$ becomes independent on the initial energy within our theoretical accuracy ${\sim }10~\%$.

Experimental papers often present the data for the energy dependence of the pseudorapidity distribution of the secondaries, $\mathrm{d}N^\mathrm{NSD}/\mathrm{d}\eta$, measured in the non-single diffractive events. It can be obtained by the formula

$$\begin{aligned} \frac{\mathrm{d}N^\mathrm{NSD}}{\mathrm{d}\eta }\,=\,\frac{\mathrm{d}N}{\mathrm{d}\eta }\, \frac{\sigma _{pp}^{\mathrm{inel}}}{\sigma _{pp}^{\mathrm{inel}}-2\sigma _{pp}^\mathrm{SD}}, \end{aligned}$$

(12)

where $\sigma _{pp}^\mathrm{SD}$ is the cross section of the single diffractive pp scattering (from one side). To make a quick estimate we have used $\sigma _{pp}^\mathrm{SD}$ values calculated in AQM in our previous paper [6]. The results are shown in Fig. 2 (right panel) together with the existing experimental points. We get a reasonable agreement, the ratio $\frac{\mathrm{d}N^\mathrm{NSD}}{\mathrm{d}\eta }/\frac{\mathrm{d}N}{\mathrm{d}\eta }\sim 1.1\div 1.15$ at the LHC energies.

4 Predictions for $\pi p$ collisions

To obtain the predictions of midrapidity inclusive densities in $\pi p$ collisions one needs to know the total $\pi p$ cross section. It has not been measured experimentally at the very high energies but can be calculated in AQM. In our approach the interaction of quarks and antiquarks constituting the pion are the same as those in the proton (so far as only Pomeron exchange is encountered). The amplitude of the elastic $\pi p$ collision is evaluated in AQM similarly to the elastic pp one, see (7),

(13)

Here $F_\pi$ and $F_P$ are the pion and proton form factors, while all other variables are the same as those for pp scattering.

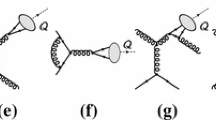
The quark combinatorics is more simple for $\pi p$ collisions compared to pp case. In particular, there are only six orders of the admissible diagrams. The sum for the first order contribution reduces to a single term, $6F_\pi (Q,0)\,F_P(Q,0,0)$, $Q^2=-t$. The second order sum includes three types of diagrams,

where the first two terms come from the diagram with both Pomerons coupled to the same quark line in the pion (first term, Fig. 6a) and in the proton (second term, Fig. 6b); in the third term they connect different quark lines (Fig. 6c). The numerical coefficients encounter the number of connections resulting in equal expressions after variables changing in the integrals (13).

Fig. 6

Second order AQM diagrams for $\pi p$ scattering

The rest orders have a similar structure derived from the combinatorics to redistribute $q_1,\ldots , q_n$ momenta among $Q_i$ and $Q_i^{\,\prime }$ groups. In the highest order, containing six effective Pomerons,

each quark from the proton interacts with both the quarks from the pion.

The differential and the total $\pi p$ cross sections are evaluated via Eq. (8) and the optical theorem (9) respectively. Our results for the elastic $\pi p$ scattering show a minimum at $\sqrt{s} = 7$ TeV placed at $-t\approx 0.65$ GeV$^2$ (Fig 2). The ratio of the total pp and $\pi p$ cross section in the optical approximation of AQM is well known to be 3/2 [7]. With the multiple rescattering included this value changes depending on the ratio of proton and pion radii. The experimental data [28] gives for the ratio $r_\pi ^2/r_p^2\approx 0.57$, so we take the pion wave function in the same form, Eq. (6), rescaling all radius parameters as $a_{1,2,3}^\pi = 0.57 a_{1,2,3}^p$. Actually the dependence $\sigma _{\pi p}^{\mathrm{tot}}$ on the parameters of $a_{1,2,3}$ and $C_{1,2}$ is rather weak. We get the ratio $\sigma _{pp}^{\mathrm{tot}}/\sigma _{\pi p}^{\mathrm{tot}} \approx 1.2 \div 1.3$. Unfortunately there are no experimental data on the $\pi p$ scattering at the LHC energies, the AQM results for them are presented in Fig. 5 together with the predictions for the pp case. Note here as well that AQM predictions for $\mathrm{d}\sigma _{pp}/\mathrm{d}t(t=0)$ are in good agreement with the data [5].

The obtained values $\sigma _{\pi p}^{\mathrm{tot}}$ allow one to find the midrapidity inclusive density in $\pi p$ collisions. The results for $\mathrm{d}N_{\pi p}/\mathrm{d}\eta (\eta =0)$ as a function of the initial energy are presented in Fig. 5. The obtained data can be used for the calculation of particle production at the very high energies; in particular, in cosmic ray physics.

5 Conclusion

In the framework of AQM we have extracted the inclusive density of the secondaries in qq interactions in the midrapidity region. We used these values to get a prediction for $\pi p$ collisions at high energies. These quantities can be useful to estimate the secondary production at the very high energies, say, in cosmic ray physics.

The applicability of AQM requires the contribution from the multipomeron qq interactions to be small compared to the interaction between different quarks responsible in this approach for the pp scattering. This is valid for the soft processes, whose amplitude is practically pure imaginary so that the qq cross section does not exceed the geometrical limit ${\sim }r_q^2$. On the other hand there are additional combinatorial factors increasing the pp cross section, so it can always be assumed to be larger than the qq one. A reasonable description of the elastic pp scattering has been reached without appealing to the enhanced diagrams with interacted Pomerons. It provides evidence that AQM is at work up to LHC energies. However, for the energies essentially above the LHC ones the multipomeron interactions would begin to play an important role, which could modify our results for asymptotically high energies.