Strong coupling constants and radiative decays of the heavy tensor mesons

Abstract

In this article, we analyze tensor-vector-pseudoscalar(TVP) type of vertices $D_{2}^{*+}D^{+}\rho$, $D_{2}^{*0}D^{0}\rho$, $D_{2}^{*+}D^{+}\omega$, $D_{2}^{*0}D^{0}\omega$, $B_{2}^{*+}B^{+}\rho$, $B_{2}^{*0}B^{0}\rho$, $B_{2}^{*+}B^{+}\omega$, $B_{2}^{*0}B^{0}\omega$, $B_{s2}^{*}B_{s}\phi$ and $D_{s2}^{*}D_{s}\phi$ in the frame work of three point QCD sum rules(QCDSR). According to these analysis, we calculate their strong form factors which are used to fit into analytical functions of $Q^{2}$. Then, we obtain the strong coupling constants by extrapolating these strong form factors into deep time-like regions. As an application of this work, the coupling constants for radiative decays of these heavy tensor mesons are also calculated at the point of $Q^{2}=0$. With these coupling constants, we finally obtain the radiative decay widths of these tensor mesons.

1 Introduction

With rapid developments of high-energy physics experiments, more and more new states of mesons have been confirmed by D0, CDF and LHCb collaborations [1,2,3,4,5,6,7]. The heavy-light mesons, which are composed of a heavy quark and a light quark, can be classified into the spin doublets in the heavy quark limit. For example, the $1S(0^{-},1^{-})$ doublets $(B,B^{*})$, $(D,D^{*})$, $(B_{s},B_{s}^{*})$, $(D_{s},D_{s}^{*})$ and the $1P(1^{+},2^{+})$ doublets $(B_{1},B_{2}^{*})$, $(B_{s1},B_{s2}^{*})$, $(D_{1},D_{2}^{*})$, $(D_{s1},D_{s2}^{*})$ have also been confirmed in experiments [5]. That is to say, the quantum numbers $I(J^{P})$ for heavy tensor mesons $D_{2}^{*}$, $B_{2}^{*}$, $D_{s2}^{*}$ and $B_{s2}^{*}$ are $\frac{1}{2}(2^{+})$, $\frac{1}{2}(2^{+})$, $0(2^{+})$ and $0(2^{+})$ respectively.

Compared with the $1S(0^{-},1^{-})$ and $1P(0^{+},1^{+})$ states of the heavy mesons, the $1P(1^{+},2^{+})$ doublets have been drawn little attention [8, 9]. The strong decay processes $D_{2}^{*}\rightarrow D^{*}\pi$, $D\pi$ [1, 10,11,12], $D_{s2}^{*}\rightarrow DK$ [1], $B_{2}^{*}\rightarrow B^{*}\pi$, $B\pi$ [1, 4], $B_{s2}^{*}\rightarrow BK, B^{*}K$ [2, 3, 6] have been observed in experiments. In reference [13], the strong decays of some excited charmed and beauty mesons into a light vector meson were analyzed by exploiting the effective field theory and a classification of the newly observed heavy-light mesons was proposed. In our previous work, we also studied some strong decay processes of these newly observed mesons and obtained their strong coupling constants and strong decay widths [14,15,16]. As a continuation of these work, we study the strong vertices $D_{2}^{*+}D^{+}\rho$, $D_{2}^{*0}D^{0}\rho$, $D_{2}^{*+}D^{+}\omega$, $D_{2}^{*0}D^{0}\omega$, $B_{2}^{*+}B^{+}\rho$, $B_{2}^{*0}B^{0}\rho$, $B_{2}^{*+}B^{+}\omega$, $B_{2}^{*0}B^{0}\omega$, $B_{s2}^{*}B_{s}\phi$ and $D_{s2}^{*}D_{s}\phi$ and obtain their strong coupling constants. These strong coupling constants not only play an essential role for understanding the inner structure of these mesons but also can help us to know about its decay behaviors. Besides, the strong coupling constants about the heavy-light mesons can also help us understanding the final-state interactions in the heavy quarkonium (or meson) decays [17,18,19]. With a fitted function about the strong form factors in Section 3, we can also obtain the coupling constants for the radiative decays with intermediate momentum $Q^2=0$, which will be used to calculate the radiative decay widths of these mesons.

To study the decay behaviors of mesons, we can adopt several theoretical models including perturbative and non-perturbative methods. The QCD sum rules, proposed by Shifman, Vainshtein, and Zakharov [20], connects hadron properties and QCD parameters [22]. It has been widely used to study the properties of the hadrons [22, 23, 25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. In this work, we analyze the tensor-vector-pseudoscalar(TVP) type of vertices and the radiative decays using the three-point QCD sum rules. It is noticed that we ignore the isospin breaking effects of u and d quark in our analysis. This is because that the masses of u and d quark are too small comparing with the heavy quark. Thus, the error coming from the isospin breaking effects can be ignored in the calculations about the properties of hadrons containing heavy quark(s). This paper is organized as follows. After the Introduction, we study the tensor-vector-pseudoscalar(TVP) type of strong vertices using the three point QCD sum rules with vector mesons being off-shell. In Sect. 3, we present the numerical results and discussions. Finally, the paper ends with the conclusions.

2 QCD sum rules for hadronic coupling constants

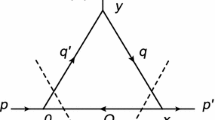
For tensor-vector-pseudoscalar(TVP) type of vertices, its three-point correlation function is written as,

$$\begin{aligned}&\Pi _{\mu \nu \tau }(p,p')\nonumber \\&\quad =i^{2}\int d^{4}x\int d^{4}ye^{i(p-p').x+ip'.y}\Big \langle 0|\mathcal {T}\Big (J_{\tau }(x)J_{{\mathbb {P}}}(y)J^{\dagger }_{\mu \nu }(0)\Big ) |0\Big \rangle ,\nonumber \\ \end{aligned}$$

(1)

where $J_{\mu \nu }$, $J_{\tau }$, and $J_{{\mathbb {P}}}$ denote interpolating currents of heavy tensor mesons, vector mesons and pseudoscalar mesons. These interpolating currents have the same quantum numbers with studied mesons [23, 61],

where

$$\begin{aligned} \overleftrightarrow {D}_{\mu }= & {} (\overrightarrow{\partial }_{\mu }-ig_{s}G_{\mu })-( \overleftarrow{\partial }_{\mu }+ig_{s}G_{\mu })\\ {\widetilde{g}}_{\mu \nu }= & {} g_{\mu \nu }-\frac{p_{\mu }p_{\nu }}{p^{2}} \end{aligned}$$

2.1 The hadronic side

To obtain hadronic representation, we insert a complete set of intermediate hadronic states into the correlation $\Pi _{\mu \nu \tau }(p,p')$. These intermediate states have the same quantum numbers with the current operators $J_{\mu \nu }$, $J_{\tau }$, and $J_{{\mathbb {P}}}$. After isolating ground-state contributions of these mesons [20, 22], the correlation function is expressed as,

$$\begin{aligned}&\Pi ^{hadr}_{\mu \nu \tau }(p,p',q) =\frac{\Big \langle 0| J_{{\mathbb {P}}}(0)|{\mathbb {P}}(p')\Big \rangle \Big \langle 0| J_{\tau }(0)|{\mathbb {V}}(q)\Big \rangle \Big \langle {\mathbb {T}}(p)|J_{\mu \nu }^{\dag }(0)|0\Big \rangle \Big \langle {\mathbb {P}}(p'){\mathbb {V}}(q)|L_{\mathbb {VPT}}|{\mathbb {T}}(p)\Big \rangle }{(M_{{\mathbb {P}}}^{2}-p'^{2})(M_{{\mathbb {V}}}^{2}-q^{2})(M_{ {\mathbb {T}}}^{2}-p^{2})} +\cdots \end{aligned}$$

(2)

The matrix elements appearing in this equation are substituted with the following parameterized equations,

$$\begin{aligned} \langle {\mathbb {T}}(p)| J^{\dagger }_{\mu \nu }(0)| 0\rangle= & {} f_{{\mathbb {T}}}M_{ {\mathbb {T}}}^{2}\xi ^{*}_{\mu \nu }(p),\\ \langle 0|J_{\tau }(0)|{\mathbb {V}}(q) \rangle= & {} f_{\tau }M_{\tau }\zeta _{\tau }(q),\\ \langle 0|J_{{\mathbb {P}}}(0)|{\mathbb {P}}(p') \rangle= & {} \frac{f_{{\mathbb {P}}}M_{{\mathbb {P}}}^{2}}{m_{Q}+m_{q}},\\ \langle {\mathbb {P}}(p'){\mathbb {V}}(q)|L_{\mathbb {VPT}}|{\mathbb {T}}(p) \rangle= & {} g\varepsilon ^{\alpha \beta \lambda \rho }p_{\alpha }\xi _{\beta \eta }p'^{\eta }q_{ \lambda }\zeta _{\rho }^{*}. \end{aligned}$$

with $q=p-p'$. Here, $f_{{\mathbb {T}}}$, $f_{{\mathbb {P}}}$ and $f_{\tau }$ are decay constants of the tensor mesons, pseudoscalar mesons and vector mesons, and g is the strong form factor of tensor-vector-pseudoscalar(TVP) type of vertices. Besides, $\xi _{\mu \nu }$, $\zeta _{\rho }$ are polarization vectors of the tensor mesons and vector mesons with the following properties,

$$\begin{aligned} \xi ^{*}_{\mu \nu }\xi _{\beta \eta }= & {} \frac{1}{2}\big [{\widetilde{g}}_{\mu \beta } {\widetilde{g}}_{\nu \eta }+{\widetilde{g}}_{\mu \eta }{\widetilde{g}}_{\nu \beta }\big ]-\frac{1}{3}{\widetilde{g}}_{\mu \nu }{\widetilde{g}}_{\beta \eta }\\ \zeta _{\rho }^{*}\zeta _{\tau }= & {} g_{\rho \tau }-\frac{p_{\rho }p_{\tau }}{p^{2}} \end{aligned}$$

With these above equations, the correlation function $\Pi _{\mu \nu \tau }(p,p',q)$ can be expressed as follows,

$$\begin{aligned}&\Pi ^{hadr}_{\mu \nu \tau }(p,p',q)\nonumber \\&\quad =\frac{gf_{{\mathbb {P}}}M^{2}_{{\mathbb {P}}}f_{ \tau }M_{\tau }f_{{\mathbb {T}}}M_{{\mathbb {T}}}^{2}}{(m_{Q}+m_{q})(M_{\tau }^{2}-q^{2})(M_{ {\mathbb {P}}}^{2}-p'^{2})(M_{{\mathbb {T}}}^{2}-p^{2})}\nonumber \\&\qquad \times \Big (\frac{1}{2}p'^{\mu }\varepsilon ^{\nu \tau pp'}+\frac{1}{2}p'^{\nu }\varepsilon ^{\mu \tau pp'}\nonumber \\&\qquad -\frac{p^{2}+p'^{2}-q^{2}}{4p^{2}}p^{\mu }\varepsilon ^{\nu \tau pp'}-\frac{p^{2}+p'^{2}+q^{2}}{4p^{2}}p^{\nu }\varepsilon ^{\mu \tau pp'}\Big )\nonumber \\&\qquad +\cdots \end{aligned}$$

(3)

2.2 The OPE side

In this part, we will briefly outline the operator product expansion(OPE) for the correlation function $\Pi _{\mu \nu \tau }(p,p',q)$ in perturbative QCD. Firstly, we contract all of the quark fields with Wick’s theorem, and rewrite the correlation function as follows,

$$\begin{aligned}&\Pi _{\mu \nu \tau }^{OPE}(p,p',q)\nonumber \\&\quad =-i^{4}\int d^{4}x\int d^{4}ye^{i(p-p').x+ip'.y}tr[S_{nm}^{q}(y-x)\gamma _{\tau }S_{mk}^{q}\nonumber \\&\qquad \times (x-z) \Gamma _{\mu \nu }S_{kn}^{Q}(z-y)\gamma _{5}|_{z=0}] \end{aligned}$$

(4)

where

(5)

and $S^{q}$($S^{Q}$) denote light(heavy) quark propagators which can be expressed as [22, 38].

(6)

(7)

where $t^{a}=\frac{\lambda ^{a}}{2}$, the $\lambda ^{a}$ is a Gell-Mann matrix, and n, m, k are color indices [22]. In the covariant derivative, the gluon $G_{\mu }(z)$ in Eq. (4) has no contributions as $G_{\mu }(z)=\frac{1}{2}z^{\lambda }G_{\lambda \mu }(0)+\cdots =0$. Using Eqs. (4), (5), (6) and (7), the perturbative contribution of the correlation function is written as

(8)

where

(9)

Putting all the quark lines on mass-shell by the Cutkoskys rules, we compute the integrals both in coordinate and momentum spaces. Then, we can obtain the spectral density by taking the imaginary parts of the correlation function,

$$\begin{aligned} \rho _{\mu \nu \tau }^{pert}(s,u,q^{2})= & {} \frac{3}{4\pi ^{2}\sqrt{\lambda }}\Big [[2A+1][A(m_{Q}-m_{q})\nonumber \\&-B(m_{q}-m_{Q})+m_{q}]\varepsilon ^{\mu \tau pp'}p_{\nu }\\&+[2B-2][A(m_{Q}-m_{q})-B(m_{q}-m_{Q})\nonumber \\&+m_{q}]\varepsilon ^{\mu \tau pp'}p'_{\nu }+[2A+1] \\&[A(m_{Q}-m_{q})-B(m_{q}-m_{Q})\nonumber \\&+m_{q}]\varepsilon ^{\nu \tau pp'}p_{\mu }+[2B-2]\\&\left. \Big [A(m_{Q}-m_{q})-B(m_{q}-m_{Q})\right. \nonumber \\&\left. +m_{q}\right] \Big ]\varepsilon ^{\nu \tau pp'}p'_{\mu }+\cdots \end{aligned}$$

where

$$\begin{aligned} A= & {} \frac{(u+m_{q}^{2}-m_{Q}^{2})(s+u-q^{2})-2u(u-q^{2}+m_{q}^{2}-m_{Q}^{2})}{\lambda (s,u,q^{2})} \\ B= & {} \frac{(u-q^{2}+m_{q}^{2}-m_{Q}^{2})(s+u-q^{2})-2s(u+m_{q}^{2}-m_{Q}^{2})}{\lambda (s,u,q^{2})} \\&\times \lambda (s,u,q^{2})=(s+u-q^{2})^{2}-4su \end{aligned}$$

During these derivations, we set $s=p^2$, $u=p'^2$ and $q=p-p'$ in the spectral densities. As a result, we can see that there are several different structures on hadronic side and OPE side. In general, we can choose either structure to study the hadronic coupling constant. In our calculations, we observe that the structure $\varepsilon ^{\nu \tau pp'}p_{\mu }$ can lead to pertinent result. Using dispersion relation, the perturbative term can be written as,

$$\begin{aligned} \Pi _{\mu \nu \tau }^{pert}(p,p^{\prime })= & {} \int _{s_{1}}^{s_{0}} \int _{u_{1}}^{u_{0}}\frac{\rho _{\mu \nu \tau }^{pert}(s,u,q^{2})}{(s-p^{2} )(u-p^{\prime 2})}\nonumber \\&\quad \times dsdu|_{-1\le \frac{2s(m_{q}^{2}-m_{Q}^{2}+u)+(m_{Q}^{2}-m_{q}^{2}-u+q^{2})(s+u-q^{2})}{\sqrt{(m_{Q}^{2}-m_{q}^{2}-u+q^{2})^{2}-4sm_{q}^{2}}\sqrt{\lambda (s,u,q^{2})}}\le 1}\nonumber \\ \end{aligned}$$

(10)

For non-perturbative terms, we take into account the contributions of $\langle q{\overline{q}}\rangle$, $\langle {\overline{q}}g\sigma .Gq\rangle$, $\langle g^{2}G^{2}\rangle$ and $\langle f^{3}G^{3}\rangle$. After performing double Borel transformation, we find that contributions of non-perturbative terms come only from condensate terms $\langle g^{2}G^{2}\rangle$, $\langle f^{3}G^{3}\rangle$. The expressions of these condensate terms are written as,

$$\begin{aligned} \Pi ^{\langle GG\rangle }_{\mu \nu \tau }= & {} \frac{\frac{\langle \alpha _{s}GG\rangle }{\pi }}{4\pi ^{2}}\Big \{\left[ iI_{\alpha 01}^{311}3m_{Q}+iI_{\alpha 10}^{311}m_{Q} \right. \\&+iI_{\alpha 01}^{411}m_{Q}^{2}(3m_{Q}-m_{q})\\&+iI_{\alpha 10}^{411}m_{Q}^{2}(m_{Q}-m_{q})+iI_{0}^{311}m_{Q}\\&\left. +iI_{0}^{411}m_{Q}^{3}\right] +\left[ iI_{\alpha 10}^{141}m_{q}^{2}(m_{Q}-m_{q})\right. \\&-iI_{\alpha 01}^{131}m_{q}-iI_{\alpha 01}^{141}m_{q}(m_{q}^{2}+m_{q}m_{Q})\\&\left. +iI_{0}^{141}m_{q}^{2}m_{Q}\right] \\&\left[ iI_{\alpha 10}^{114}m_{q}^{2}(m_{Q}-m_{q})+iI_{\alpha 01}^{114}m_{q}^{2}(3m_{Q}-m_{q})\right. \\&\left. +iI_{0}^{114}m_{q}^{2}m_{Q}-iI_{\alpha 10}^{113}m_{q}\right] \\&+\frac{1}{6}\left[ iI_{\alpha 01}^{122}(m_{q}-3m_{Q})+iI_{\alpha 10}^{122}(m_{q}-m_{Q})\right. \\&\left. -iI_{0}^{122}m_{Q}\right] +\frac{1}{6}\left[ iI_{\alpha 01}^{221}(m_{q}-3m_{Q})\right. \\&\left. -iI_{\alpha 10}^{221}(m_{Q}-m_{q})-iI_{0}^{221}m_{Q}\right] \\&+\frac{1}{6}\left[ iI_{\alpha 01}^{212}(9m_{Q}-m_{q})\right. \\&\left. -iI_{\alpha 10}^{212}(m_{q}-m_{Q})+iI_{0}^{212}3m_{Q}\right] \Big \}\\ \Pi ^{\langle GGG\rangle }_{\mu \nu \tau }= & {} \frac{\langle g_{s}^{3}G^{a}G^{b}G^{c}f^{abc}\rangle }{12\times (2\pi )^{4}} \Big \{\left[ iI_{\alpha 01}^{321}m_{Q}\right. \\&-iI_{\alpha 10}^{321}(m_{q}-3m_{Q})-iI_{0}^{321}m_{Q}\\&-iI_{\alpha 10}^{421}2m_{Q}^{2}(m_{q}-m_{Q})\\&-iI_{\alpha 01}^{421}2m_{Q}^{2}(m_{Q}+m_{q})\\&\left. -iI_{0}^{421}2m_{Q}^{3}\right] +\left[ iI_{\alpha 01}^{132}3(m_{Q}-m_{q})\right. \end{aligned}$$

$$\begin{aligned}&\qquad +iI_{\alpha 10}^{132}m_{Q}+iI_{0}^{142}2m_{Q}m_{q}^{2}\\&\qquad +iI_{\alpha 01}^{142}2m_{q}^{2}(3m_{Q}-m_{q})\\&\qquad \left. +iI_{\alpha 10}^{142}2m_{q}^{2}(m_{Q}-m_{q})+iI_{0}^{132}m_{Q}\right] \\&\qquad +[iI_{\alpha 01}^{231}(4m_{Q}-3m_{q})\\&\qquad -iI_{\alpha 10}^{231}(m_{q}-2m_{Q})+iI_{0}^{231}m_{Q}-iI_{0}^{141}12m_{q}\\&\qquad -iI_{\alpha 01}^{141}8m_{q}-iI_{\alpha 10}^{241}2m_{q}^{2}(m_{q}-m_{Q})\\&\qquad +iI_{0}^{241}m_{Q}m_{q}(m_{q}-12m_{Q})\\&\qquad +iI_{\alpha 01}^{241}2m_{q}(4m_{q}m_{Q}\\&\qquad -2m_{q}^{2}-4m_{Q}^{2})+[iI_{\alpha 01}^{123}(3m_{Q}-2m_{q})\\&\qquad +iI_{\alpha 10}^{123}(m_{Q}-3m_{q})+iI_{0}^{123}m_{Q}-iN_{0}^{124}4m_{q}\\&\qquad +iI_{\alpha 01}^{124}2m_{q}(3m_{q}m_{Q}-m_{q}^{2}-4m_{Q}^{2})\\&\qquad +iI_{\alpha 10}^{124}2m_{q}^{2}(m_{Q}-m_{q})\\&\qquad +iI_{0}^{124}2m_{q}m_{Q}(m_{q}-2m_{Q})\\&\qquad +6m_{q}^{2}\left[ iI_{\alpha 10}^{115}(4m_{q}-m_{Q})\right. \\&\qquad +iI_{\alpha 10}^{116}6m_{q}^{2}(m_{q}-m_{Q})+iI_{\alpha 01}^{115}(m_{q}+m_{Q})\\&\qquad +iI_{\alpha 01}^{116}6m_{q}^{2}(m_{q}+m_{Q})+iI_{0}^{115}m_{Q}\\&\qquad \left. +iI_{0}^{116}6m_{Q}m_{q}^{2}\right] -3\left[ iI_{\alpha 10}^{114}(4m_{q}-m_{Q})\right. \\&\qquad +iI_{\alpha 10}^{115}6m_{q}^{2}(m_{q}-m_{Q})+iI_{\alpha 01}^{114}(m_{q}+m_{Q})\\&\qquad +iI_{\alpha 01}^{115}6m_{q}^{2}(m_{q}+m_{Q})+iI_{0}^{114}m_{Q}\\&\qquad \left. +iI_{0}^{115}6m_{Q}m_{q}^{2}\right] -\frac{3}{8}m_{q}^{2}\left[ iI_{\alpha 01}^{151}(m_{q}-4m_{Q})\right. \\&\qquad +iI_{\alpha 01}^{161}m_{q}^{2}(m_{Q}-m_{q})-iI_{\alpha 10}^{151}(m_{q}-3m_{Q})\\&\qquad -iI_{\alpha 10}^{161}6m_{q}^{2}(m_{q}-3m_{Q})+iI_{0}^{151}m_{Q}\\&\qquad \left. +iI_{0}^{161}6m_{q}^{2}m_{Q}\right] +\frac{3}{16}\left[ iI_{\alpha 01}^{141}(m_{q}-4m_{Q})\right. \\&\qquad +iI_{\alpha 01}^{151}m_{q}^{2}(m_{Q}-m_{q})-iI_{\alpha 10}^{141}(m_{q}-3m_{Q})\\&\qquad -iI_{\alpha 10}^{151}6m_{q}^{2}(m_{q}-3m_{Q})+iI_{0}^{141}m_{Q}\\&\qquad \left. +iI_{0}^{151}6m_{q}^{2}m_{Q}\right] +\frac{3}{16}\left[ iI_{\alpha 01}^{511}6m_{Q}^{2}(3m_{Q}-m_{q})\right. \\&\qquad -iI_{\alpha 01}^{411}(m_{q}-12m_{Q})-iI_{\alpha 10}^{511}6m_{Q}^{2}(m_{q}\\&\qquad -m_{Q})-iI_{\alpha 10}^{411}(m_{q}-4m_{Q})+iI_{0}^{411}4m_{Q}\\&\qquad \left. +iI_{0}^{511}6m_{Q}^{3}\right] -\frac{3}{8}m_{Q}^{2}\left[ iI_{\alpha 01}^{611}6m_{Q}^{2}(3m_{Q}\right. \\&\qquad -m_{q})-iI_{\alpha 01}^{511}(m_{q}-12m_{Q})+iI_{0}^{511}4m_{Q}\\&\qquad -iI_{\alpha 10}^{611}6m_{Q}^{2}(m_{q}-m_{Q})-iI_{\alpha 10}^{511}(m_{q}-4m_{Q})\\&\qquad \left. +iI_{0}^{611}6m_{Q}^{3}\right] +\left[ iI_{\alpha 01}^{222}(3m_{Q}-m_{q})\right. \\&\qquad \left. -iI_{\alpha 10}^{222}(m_{q}-3m_{Q})+iI_{0}^{222}m_{Q}\right] \Big \} \end{aligned}$$

where

$$\begin{aligned} I_{0}^{abc}= & {} \frac{(-1)^{a+b+c}\pi ^{2}i}{\Gamma (a)\Gamma (b)\Gamma (c)(M_{1}^{2})^{b}(M_{2}^{2})^{c}(M^{2})^{a-2}}\nonumber \\&\times \int _{0}^{\infty }d\tau (\tau +1)^{a+b+c-4}\tau ^{1-b-c}\nonumber \\&\exp \left\{ -\frac{1}{\tau }\frac{Q^{2}}{M_{1}^{2}+M_{2}^{2}}-\frac{(\tau +1)m_{Q}^{2}}{M^{2}}\right. \nonumber \\&\left. \phantom {\left\{ -\frac{1}{\tau }\frac{Q^{2}}{M_{1}^{2}+M_{2}^{2}}-\frac{(\tau +1)m_{Q}^{2}}{M^{2}}\right. } -\frac{(\tau +1)m_{q}^{2}}{\tau M_{1}^{2}}-\frac{(\tau +1)m_{q}^{2}}{\tau M_{2}^{2}}\right\} \end{aligned}$$

(11)

$$\begin{aligned} I_{\alpha 01}^{abc}= & {} \frac{(-1)^{a+b+c}\pi ^{2}i}{\Gamma (a)\Gamma (b)\Gamma (c)(M_{1}^{2})^{b}(M_{2}^{2})^{c+1}(M^{2})^{a-3}}\nonumber \\&\times \int _{0}^{\infty }d\tau (\tau +1)^{a+b+c-5}\tau ^{1-b-c}\nonumber \\&\exp \left\{ -\frac{1}{\tau }\frac{Q^{2}}{M_{1}^{2}+M_{2}^{2}}-\frac{(\tau +1)m_{Q}^{2}}{M^{2}}\right. \nonumber \\&\left. -\frac{(\tau +1)m_{q}^{2}}{\tau M_{1}^{2}}-\frac{(\tau +1)m_{q}^{2}}{\tau M_{2}^{2}}\right\} \end{aligned}$$

(12)

$$\begin{aligned} I_{\alpha 10}^{abc}= & {} \frac{(-1)^{a+b+c}\pi ^{2}i}{\Gamma (a)\Gamma (b)\Gamma (c)(M_{1}^{2})^{b+1}(M_{2}^{2})^{c}(M^{2})^{a-3}}\nonumber \\&\times \int _{0}^{\infty }d\tau (\tau +1)^{a+b+c-5}\tau ^{1-b-c}\nonumber \\&\exp \left\{ -\frac{1}{\tau }\frac{Q^{2}}{M_{1}^{2}+M_{2}^{2}}-\frac{(\tau +1)m_{Q}^{2}}{M^{2}}\right. \nonumber \\&\left. -\frac{(\tau +1)m_{q}^{2}}{\tau M_{1}^{2}}-\frac{(\tau +1)m_{q}^{2}}{\tau M_{2}^{2}}\right\} \end{aligned}$$

(13)

Table 1 Input parameters used in this analysis

3 The results and discussions

Estimating the parameters of the lowest-lying hadronic state are in general plagued by the presence of unknown subtraction terms, the spectral function of excited and continuum states. This situation can be substantially improved by applying to both OPE side and phenomenological side the Borel transformation [61]. Thus, we perform the double Borel transform with respect to the variables $P^2=-p^2$, $P'^2=-p'^2$ and match OPE side with the hadronic representation Eq. (3), invoking the quark-hadron duality. Finally, we obtain the QCDSR as follows,

$$\begin{aligned}&\frac{gf_{{\mathbb {P}}}M^{2}_{{\mathbb {P}}}f_{\tau }M_{\tau }f_{{\mathbb {T}}}M_{{\mathbb {T}}}^{2}}{(m_{q}+m_{Q})(M_{\tau }^{2}+Q^{2})} \Big (-\frac{M_{{\mathbb {T}}}^{2}+M_{{\mathbb {P}}}^{2}-Q^{2}}{4M_{{\mathbb {T}}}^{2}}\Big ) \frac{1}{M_{1}^{2}M_{2}^{2}}\nonumber \\&\exp \left[ -\frac{M_{{\mathbb {T}}}^{2}}{M_{1}^{2}}\right] exp\left[ -\frac{M_{ {\mathbb {P}}}^{2}}{M_{2}^{2}}\right] \nonumber \\&\quad = \frac{1}{M_{1}^{2}M_{2}^{2}}\int _{s_{1}}^{s_{0}} \int _{u_{1}}^{u_{0}} \nonumber \\&\exp \left[ -\frac{s}{M_{1}^{2}}\right] exp\left[ -\frac{u}{M_{2}^{2}}\right] \rho ^{pert}(s,u,Q^{2})dsdu \nonumber \\&\qquad +\Pi ^{\langle GG\rangle }_{\mu \nu \tau }(M_{1}^{2},M_{2}^{2},Q^{2})+\Pi ^{\langle GGG\rangle }_{\mu \nu \tau }(M_{1}^{2},M_{2}^{2},Q^{2})\nonumber \\ \end{aligned}$$

(14)

Here, $Q^2=-q^2$, parameters $s_{0}$ and $u_{0}$ are used to further reduce the contributions from excited and continuum states. Its values are employed as $s_{0}=(m_{i}+\Delta _{i})^2$ and $u_{0}=(m_{o}+\Delta _{o})^2$, where $m_{i}$ and $m_{o}$ are ground state masses of the in-coming and out-coming hadron. In general, $\Delta _{i}$ and $\Delta _{o}$ are expected to be $0.3GeV\sim 0.5GeV$, which can guarantee the values of $s_{0}$ and $u_{0}$ be close to the mass squared of the first excited state of these in-coming and out-coming hadrons [14]. Parameters $M_1^2$ and $M_2^2$ in Eq. (14) are Borel parameters. In order to choose optimal values about these above parameters, two criteria should be considered. Firstly, pole contribution should be as large as possible comparing with contributions of higher and continuum states. Secondly, we should also ensure OPE convergence and the stability of our results. That is to say, the results which are extracted from sum rules, should be independent of the Borel parameters. One can consult Refs. [15, 16] for more technical details of these processes. As for the other parameters in Eq. (14), their values are all listed in Table 1.

The strong form factor g from Eq. (14) are obtained in deep space-like region $q^2 \rightarrow -\infty$, where the intermediate mesons are off-shell. In order to obtain strong coupling constants, we must extrapolate these results into deep time-like region. This extrapolation is model-dependent, thus there are no specific expressions for the dependence of the strong form factors on $Q^{2}$. In other works, different kinds of functions have been employed as their fitting functions such as exponential function [46, 69, 70], power-law function [45] or their combinations [40, 68]. In this work, our analysis indicates that this dependence can be appropriately fitted into the following exponential function,

$$\begin{aligned} g(Q^{2})=A\exp [{BQ^2}] \end{aligned}$$

(15)

Fig. 1

The strong form factor $g_{D_{2}^{*+}D^{+}\rho }$, and its fitted results as a function of $Q^2$

Fig. 2

The strong form factor $g_{D_{2}^{*0}D^{0}\rho }$, and its fitted results as a function of $Q^2$

Fig. 3

The strong form factor $g_{B_{2}^{*+}B^{+}\rho }$, and its fitted results as a function of $Q^2$

Fig. 4

The strong form factor $g_{B_{2}^{*0}B^{0}\rho }$, and its fitted results as a function of $Q^2$

Fig. 5

The strong form factor $g_{D_{2}^{*0}D^{0}\omega }$, and its fitted results as a function of $Q^2$

Fig. 6

The strong form factor $g_{D_{2}^{*+}D^{+}\omega }$, and its fitted results as a function of $Q^2$

Fig. 7

The strong form factor $g_{B_{2}^{*+}B^{+}\omega }$, and its fitted results as a function of $Q^2$

Fig. 8

The strong form factor $g_{B_{2}^{*0}B^{0}\omega }$, and its fitted results as a function of $Q^2$

Fig. 9

The strong form factor $g_{B_{s2}^{*}B_{s}\phi }$, and its fitted results as a function of $Q^2$

Fig. 10

The strong form factor $g_{D_{s2}^{*}D_{s}\phi }$, and its fitted results as a function of $Q^2$

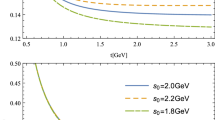
In Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10, we show the values of the strong form factors on $Q^2$ that are obtained from Eq. (14) and its fitting curve, where they are marked as Central value and Fitted curve of Central value separately. Thus, we can obtain the strong coupling constants by taking $Q^{2}=-m_{on-shell}^2$ for intermediate mesons in the fitting function Eq. (15). The values of fitted parameters A and B in Eq. (15) and the strong coupling constants are all listed in Table 2.

The uncertainties of strong form factors in Eq. (14) mainly come from input parameters $m_{D_{2}^{*+}}$,$m_{D_{2}^{0*}}$,$m_{u}$,$m_{b}$,$f_{\rho }$, $f_{\phi }$, $\langle {\overline{q}}q\rangle$, $\cdots$ Theoretically, we can calculate its values with uncertainty transfer formula $\delta =\sqrt{\Sigma _{i}(\frac{\partial f}{\partial x_{i}})^{2}(x_{i}-{\overline{x}}_{i})^{2}}$, where f denotes the strong form factor in Eq. (14), and $x_{i}$ denotes input parameters. For simplicity, the upper and lower limits of the results are estimated by taking $f^{upper(lower)}=f({\overline{x}}_{i}\pm \Delta x_{i})$, which are marked as Upper bound and Lower bound in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. After these approximations, they are also fitted into exponential functions and are also extrapolated into the physical regions in order to get the uncertainties of the strong coupling constants. These results are all listed in Table 2.

Finally, we give an analysis of the radiative decays of the heavy tensor mesons ${\mathbb {T}}\rightarrow {\mathbb {P}}\gamma$. The coupling constants of these radiative decays $g_{{\mathbb {T}}{\mathbb {P}}\gamma }$ can be easily obtained by setting $Q^2=0$ in Eq. (15). The radiative decay width can be expressed as the following representation,

$$\begin{aligned} \Gamma= & {} \frac{1}{2J+1}\sum \frac{|p|}{8\pi M_{i}^{2}}|T|^{2} \nonumber \\ p= & {} \frac{\sqrt{[M_{i}^{2}-(M_{f}+m)^{2}][M_{i}^{2}-(M_{f}-m)^{2}]}}{2M_{i}} \end{aligned}$$

(16)

where i and f denote the initial and final state mesons, J is the total angular momentum of the initial meson, $\sum$ denotes the summation of all the polarization vectors, and T denotes the scattering amplitudes. The radiative decays ${\mathbb {T}}\rightarrow {\mathbb {P}}\gamma$ can be described by the following electromagnetic lagrangian

$$\begin{aligned} \pounds =-eQ_{q}{\overline{q}}\gamma _{\mu }qA^{\mu } \end{aligned}$$

(17)

From this lagrangian, the decay amplitude can be written as,

$$\begin{aligned} T= & {} \left\langle {\mathbb {P}}(p')\gamma (q,\varepsilon )|{\mathbb {T}}(p,\xi _{\beta \eta }^{\omega })\right\rangle \nonumber \\= & {} \left\langle \gamma (q,\varepsilon )|{\mathbb {V}}(q,\zeta _{\rho })\right\rangle \frac{i}{ q^{2}-m_{{\mathbb {V}}}^{2}}\left\langle {\mathbb {P}}(p'){\mathbb {V}} (q,\zeta _{\rho } )|{\mathbb {T}}(p,\xi _{\beta \eta }^{\omega } )\right\rangle \nonumber \\= & {} \left\langle {\mathbb {P}}(p'){\mathbb {V}} (q,\zeta _{\rho } )|{\mathbb {T}}(p,\xi _{\beta \eta }^{\omega } )\right\rangle \frac{i}{q^{2}-m_{{\mathbb {V}} }^{2}}f_{{\mathbb {V}} }m_{{\mathbb {V}} }eQ_{q}(-i)\varepsilon _{\kappa }^{*}\zeta ^{\kappa }\nonumber \\= & {} g_{{\mathbb {T}}{\mathbb {P}}\gamma }\epsilon ^{\alpha \beta \lambda \rho }p_{\alpha }\xi _{\beta \eta }p'^{\eta }q_{\lambda }\zeta _{\rho }^{*}\frac{i}{q^{2}}f_{{\mathbb {V}} }m_{{\mathbb {V}} }eQ_{q}(-i)\varepsilon _{\kappa }^{*}\zeta ^{\kappa } \end{aligned}$$

(18)

Table 2 Strong coupling constants and fitted parameters about the central value, upper bound and lower bound

Here, $p_{\alpha }$, $p'^{\eta }$ and $q_{\lambda }$ are the four momenta of the tensor meson, pseudoscalar meson and $\gamma$. Besides, $\xi$, $\zeta$ and $\varepsilon$ are their polarization vectors, respectively. With Eqs. (16) and (17), we can obtain the radiative decay width of ${\mathbb {T}}\rightarrow {\mathbb {P}}\gamma$,

$$\begin{aligned} \Gamma= & {} \frac{1}{10}\alpha Q_{[u,d,s]}^{2}g_{{\mathbb {T}}{\mathbb {P}}\gamma }^{2}|\frac{f_{ {\mathbb {V}}}}{m_{{\mathbb {V}}}}|^{2}\left[ \frac{M_{T}^{2}-M_{P}^{2}}{2M_{T}}\right] ^{3} \nonumber \\&\times \left\{ \frac{1}{6}\left[ \frac{5M_{T}^{2}-2M_{P}^{2}}{2M_{T}}\right] ^{2}-\frac{2}{3}M_{T}^{2}\right\} \end{aligned}$$

(19)

where $\alpha =\frac{1}{137}$,$Q_{u}=\frac{2}{3}$,$Q_{d}=Q_{s}=-\frac{1}{3}$. Considering different decay channels, we obtain the widths of different radiative decays, which are listed in Table 3. From reference [62], we can see the decay widths of the tensor mesons, $\Gamma (D_{2}^{*0})=47.5\pm 1.1MeV$, $\Gamma (D_{2}^{*\pm })=46.7\pm 1.2MeV$, $\Gamma (D_{s2}^{*})=16.9\pm 0.8MeV$, $\Gamma (B_{2}^{*0})=24.2\pm 1.7MeV$, $\Gamma (B_{2}^{*+})=20\pm 5MeV$, $\Gamma (B_{s2}^{*})=1.47\pm 0.33MeV$. From these experimental data, we observe that the branching ratios of the calculated radiative decays are of the order of $10^{-2}\sim 10^{-5}$, which are measurable in the future by LHCb. In reference [71], the radiative decays of the heavy tensor mesons were also analyzed in the framework of the light cone QCD sum rules(LCSR) method. We observe that our results for mesons $D_{2}^{*}$ and $D_{s2}^{*}$ are comparable with its results. For mesons $B_{2}^{*}$ and $B_{s2}^{*}$, the results from QCD sum rules and light cone QCD sum rules vary widely, which need to be further studied by other theoretical methods or in experiments.

Table 3 The decay widths for different radiative decays

4 Conclusion

In this paper, we analyze the tensor-vector-pseudoscalar(TVP) type of vertices in the cases of light vector mesons $\rho$, $\omega$ and $\phi$ being off-shell. We firstly calculate its strong form factors in space-like regions($q^{2}<0$). Then, we fit the form factors into exponential functions which are used to extrapolate into time-like regions($q^{2}>0$) to obtain strong coupling constants. These strong coupling constants are important parameters in studying the strong decay behaviors of tensor mesons in the future. Setting intermediate momentum $Q^2=0$ in the fitted analytical functions about strong form factors, we also obtain the coupling constants of the radiative decays of the tensor mesons. With these coupling constants, we calculate the radiative decay widths of these tensor mesons and compare our results with experimental data and those of other research groups.