$B_{(s)}$ to light $2^{--}$ tensor meson form factors via LCSR in HQEFT and relevant semileptonic decays

Abstract

In this study, the form factors of $B_{(s)}$ to light D-wave tensor mesons with $J^{PC} = 2^{--}$ ($\rho _2$, $\omega _2$, $K_2$ and $\phi _2$) are calculated via the light cone sum rules (LCSR) in the framework of heavy quark effective eld theory (HQEFT). Firstly, the expressions of form factors in terms of the light cone distribution amplitudes (LCDAs) of tensor mesons are derived via the LCSR at the leading order of heavy quark expansion. Similar to the case of $2^{++}$ tensor mesons, the penguin type form factors can be obtained directly from the corresponding semileptonic ones. Considering the light tensor meson LCDAs to twist-3 and quark mass corrections, we give the numerical results of form factors systematically. Based on the form factors given here, we investigate the branching ratios, longitudinal polarization fractions and forward-backward asymmetries of relevant charged current induced semileptonic decays. Our results may be tested by more precise experiments in the future.

1 Introduction

Analysis of hadron spectrum provides a crucial test of QCD and has experienced a great advancement over the last ten years [1]. On one hand, there are several states predicted by the quark model but not yet observed experimentally; on the other, different experiments have discovered new states that do not exhibit the expected properties of conventional hadrons. The underlying structures of these new states are still unclear. For the light hadron spectrum sector, light meson families attract great physical interest. Investigating and exploring new light meson states is an interesting physical aim of currently running or forthcoming experiments like BESIII, GlueX, AMBER and PANDA. Theoretically, a lot of work has been devoted to better understand the new observed light hadron states and establish corresponding light meson spectrum [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17].

Checking the experimental status of light mesons, we can notice that the ground states of light meson families with $J^{PC}=2^{--}$, except $K_2(1820)$, have not been observed. The unflavored light mesons $\rho _2$ and $\omega _2$ are only collected into the ‘Further States’ section in Particle Date Group (PDG) [1]. In the conventional quark model, these states are viewed as a constituent quark-antiquark pair with total orbital angular momentum $L=2$ and spin $S=1$, i.e. the $1 ^3D_2$ states. It is of great importance to explore the full set of these states. The masses of light $2^{--}$ tensor mesons were extracted in Refs. [3, 15] with the QCD sum rules and Coulomb gauge Hamiltonian approach, respectively. Their mass spectrum and two-body strong decays were investigated phenomenologically [13]. The masses and decay constants of $\rho _2$, $\omega _2$ and $\phi _2$ at $T \ne 0$ were analyzed via the Thermal QCD sum rules [16]. A study of masses, strong and radiative decays of $2^{++}$ and $2^{--}$ tensor mesons on the same footing was performed in a chiral model that links them [17]. In addition, the light cone distribution amplitudes (LCDAs) of light $2^{--}$ meson states were studied via the QCD sum rules [18], which are relevant to the search of these particles in $B_{(s)}$ decays in experiments such as Belle II and LHCb.

In the past decades, many $B_{(s)}$ decays involving a light $2^{++}$ tensor meson have been observed [1], and several phenomena have attracted theoretical interests. For example, a large isospin violation was detected in the $B \rightarrow \omega K^*_2(1430)$ mode [19]. The $B \rightarrow \phi K^*_2(1430)$ decay is mainly dominated by the longitudinal polarization, in contrast with $B \rightarrow \phi K^*$ where the transverse polarization is comparable with the longitudinal one [20, 21]. Additionally, the predicted rates of relevant hadronic decays in the naive factorization scheme are in general too small by 1 to 2 orders of magnitude [22]. From the theoretical point of view, it will be interesting to observe the light $2^{--}$ tensor meson states in the $B_{(s)}$ decays, because this can not only further validate the quark model, but also help clarify the phenomena mentioned above.

Theoretical calculations of exclusive decays require the knowledge of nonperturbative QCD, which are generally parameterized in terms of decay constants, form factors and some nonfactorizable contributions. For heavy hadrons containing one heavy quark, it is useful to adopt the heavy quark effective field theory (HQEFT), in which a heavy quark expansion is performed and the calculation of nonperturbative QCD effects can be greatly simplified [23,24,25]. The $B_{(s)}$ to light $2^{++}$ tensor meson form factors were calculated via the LCSR in HQEFT and used to investigate the corresponding semileptonic decays [26]. In this study, we intend to calculate the form factors of $B_{(s)}$ to light $2^{--}$ tensor mesons systematically by using the LCSR in HQEFT and explore the relevant semileptonic decays, predicting the branching ratios, longitudinal polarization fractions and forward-backward asymmetries. Given that most of the light $2^{--}$ tensor mesons have not been well established in experiments, for simplicity, we neglect the possible mixtures between $K_2(1820)$ and its $2^{-+}$ partner $K_2(1770)$, and between $\omega _2$ and $\phi _2$ (as done in Refs. [3, 18]), and only consider the charged current induced semileptonic decays here.

The remaining part of this paper is organized as follows. In Sect. 2, we give the definitions of form factors and derive their expressions in terms of the LCDAs of light $2^{--}$ tensor mesons by using the LCSR in HQEFT. Numerical results and discussions of the form factors are presented in Sect. 3. Then, based on these form factors, we investigate the branching ratios, longitudinal polarization fractions and forward-backward asymmetries of relevant semileptonic decays in Sect. 4. Section 5 is our summary.

2 Definitions of form factors and LCSR in HQEFT

2.1 Definitions of form factors

Similar to the case of $2^{++}$ tensor mesons [26], the $B_{(s)}$ to light $2^{--}$ tensor meson form factors can be defined via the corresponding hadronic matrix elements as following:

$$\begin{aligned}{} & {} \langle T(P,\lambda ) | \bar{q} \gamma ^\mu \gamma ^5 b| H (p_H) \rangle \nonumber \\{} & {} \quad = \frac{2}{m_H + m_T} \varepsilon ^{\mu \nu \alpha \beta } e^{(\lambda ) *}_\nu p_{H \alpha } P_\beta A (q^2), \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \langle T(P,\lambda ) | \bar{q} \gamma ^\mu b| H (p_H) \rangle \nonumber \\{} & {} \quad = i (m_H + m_T) \left( e^{(\lambda ) * \mu } - \frac{e^{(\lambda )*} \cdot p_H}{ q^2 }q^\mu \right) V_1 (q^2) \nonumber \\{} & {} \qquad -i \frac{e^{(\lambda ) *} \cdot p_H}{m_H + m_T} \left( (p_H + P)^\mu - \frac{m^2_H - m^2_T}{q^2} q^\mu \right) V_2(q^2) \nonumber \\{} & {} \quad + 2 i m_T \frac{e^{(\lambda )*} \cdot p_H}{ q^2} q^\mu V_0(q^2), \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \langle T(P,\lambda ) | \bar{q} \sigma ^{\mu \nu } \gamma ^5 q_\nu b| H (p_H) \rangle \nonumber \\{} & {} \quad = -2 i T_1 (q^2) \varepsilon ^{\mu \nu \alpha \beta } p_{H \nu } P_\alpha e^{(\lambda ) *}_\beta , \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \langle T(P,\lambda ) | \bar{q} \sigma ^{\mu \nu } q_\nu b| H (p_H) \rangle \nonumber \\{} & {} \quad = -T_2(q^2) \left[ (m^2_H - m^2_T) e^{(\lambda )* \mu } - e^{(\lambda )*} \cdot p_H ( p_H + P)^\mu \right] \nonumber \\{} & {} \qquad - T_3(q^2) e^{(\lambda )*} \cdot p_H \left[ q^\mu - \frac{q^2}{m^2_H -m^2_T} (p_H + P)^\mu \right] ,\nonumber \\ \end{aligned}$$

(4)

where $e^{(\lambda ) * \mu } = \epsilon ^{(\lambda )* \mu \nu } q_\nu /m_H$, with $\epsilon ^{(\lambda ) \mu \nu }$ the polarization tensors of light tensor meson in the final state. $q^\mu = (p_H - P)^\mu$ and H denotes $B_{(s)}$. The polarization tensors $\epsilon ^{(\lambda ) \mu \nu }$ are symmetric and traceless, satisfying the divergence free condition $\epsilon ^{(\lambda ) \mu \nu } P_\nu =0$ and orthogonal condition $\epsilon ^{(\lambda ) \mu \nu } \epsilon ^{(\lambda ^\prime )*}_{\mu \nu } =\delta ^{\lambda \lambda ^\prime }$. $\varepsilon ^{\mu \nu \alpha \beta }$ is the total antisymmetric Levi-Civita symbol, with $\varepsilon ^{0123}=-1$. $V_1$, $V_2$, $V_0$, A and $T_1$, $T_2$, $T_3$ are the semileptonic and penguin type form factors, respectively. The latter are only relevant for rare decays induced by flavor changing neutral currents (FCNC).

To the leading order of heavy quark expansion in HQEFT, the hadronic matrix elements can be written as [23,24,25]

$$\begin{aligned}{} & {} \langle T ( P, \lambda ) | \bar{q} \varGamma b | H ( p_H) \rangle \nonumber \\{} & {} \quad = \sqrt{\frac{m_H}{\bar{\varLambda }_H}} \left[ \langle T(P, \lambda ) | \bar{q} \varGamma Q^{(+)}_v | M_v \rangle + {{\mathscr {O}}} ( 1/m_b) \right] , \end{aligned}$$

(5)

where the binding energy $\bar{\varLambda }_H = m_H - m_b$. $Q^{(+)}_v$ and $|M_v \rangle$ are the effective heavy quark field and heavy meson state in HQEFT, respectively. From heavy quark spin-flavor symmetry, the leading order hadronic matrix elements

$$\begin{aligned} \langle T(P, \lambda ) | \bar{q} \varGamma Q^{(+)}_v | M_v \rangle = - \textrm{Tr} \left[ \varOmega (v, P) \varGamma {{\mathscr {M}}}_v \right] , \end{aligned}$$

(6)

with

$$\begin{aligned}{} & {} \varOmega (v, P) = \left\{ L_1 (v \cdot P) e^{(\lambda )*} {\hspace{-0.57cm} /} \hspace{0.45cm} + L_2( v \cdot P) ( v \cdot e^{(\lambda ) *} ) \right. \nonumber \\{} & {} \quad \left. \hspace{1.5cm} + \left[ L_3 ( v \cdot P) e^{(\lambda )*} \hspace{-0.57cm} /\hspace{0.45cm} + L_4 ( v \cdot P) ( v \cdot e^{(\lambda ) *} ) \right] {\hat{P}} \hspace{-0.25cm} /\hspace{0.1cm} \right\} \gamma ^5, \nonumber \\ \end{aligned}$$

(7)

$$\begin{aligned}{} & {} {{\mathscr {M}}}_v = - \sqrt{\bar{\varLambda }} \frac{1+ v \hspace{-0.2cm} /}{2} \gamma ^5, \hspace{0.5cm} {\hat{P}}^\mu = \frac{P^\mu }{v \cdot P}. \end{aligned}$$

(8)

Here, $\bar{\varLambda }= \lim _{m_b \rightarrow \infty } \bar{\varLambda }_H$. $L_i (i=1, 2, 3, 4)$ are the leading order wave functions describing the heavy to light meson transition matrix elements in HQEFT. ${{\mathscr {M}}}_v$ is the heavy pseudoscalar meson wave function.

Combining Eqs. (1)–(8), we obtain

$$\begin{aligned} V_1(q^2)= & {} \frac{2i}{m_H + m_T} \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \left[ L_1 (v \cdot P) + L_3 (v \cdot P) \right] , \end{aligned}$$

(9)

$$\begin{aligned} V_2( q^2)= & {} i (m_H + m_T) \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \left[ \frac{L_2(v \cdot P)}{ m^2_H} \right. \nonumber \\{} & {} \left. + \frac{L_3 ( v \cdot P) - L_4 (v \cdot P) }{ m_H ( v \cdot P)} \right] , \end{aligned}$$

(10)

$$\begin{aligned} V_0 ( q^2)= & {} \frac{i}{m_T}\sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \Biggl [ L_1( v \cdot P) - L_2 ( v \cdot P) \Biggr . \nonumber \\{} & {} + \frac{m^2_T}{m_H v \cdot P} \left( L_3( v \cdot P) - L_4 ( v \cdot P) \right) \nonumber \\{} & {} \left. + \frac{v \cdot P}{ m_H} L_2 ( v \cdot P)+ L_4 ( v \cdot P) \right] , \end{aligned}$$

(11)

$$\begin{aligned} A (q^2)= & {} i \frac{m_H + m_T}{m_H ( v \cdot P)} \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} L_3 ( v \cdot P), \end{aligned}$$

(12)

$$\begin{aligned} T_1(q^2)= & {} i \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \left[ \frac{L^\prime _1 ( v \cdot P)}{m_H} + \frac{L^\prime _3 ( v \cdot P ) }{v \cdot P} \right] , \end{aligned}$$

(13)

$$\begin{aligned} T_2 (q^2)= & {} \frac{2i }{ m^2_H - m^2_T} \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \Biggl [ ( m_H - v \cdot P) L^\prime _1 ( v \cdot P) \nonumber \\{} & {} + \frac{m_H v \cdot P - m^2_T}{ v \cdot P} L^\prime _3 ( v \cdot P ) \Biggr ], \end{aligned}$$

(14)

$$\begin{aligned} T_3(q^2)= & {} i \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \Biggl [ - \frac{L^\prime _1 ( v \cdot P )}{m_H} + \frac{L^\prime _3 ( v \cdot P)}{v \cdot P} \nonumber \\{} & {} - \frac{m^2_H - m^2_T}{ m^2_H v \cdot P} L^\prime _4 ( v \cdot P) \Biggr ], \end{aligned}$$

(15)

with $v \cdot P = \frac{m^2_H + m^2_T -q^2}{2 m_H}$. $L^\prime _i (i=1, 3, 4)$ are generally different from corresponding $L_i$ as they arise from different matrix elements.

2.2 LCSR in HQEFT

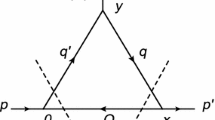
In this subsection, we shall calculate the leading order wave functions describing the heavy to light meson transition matrix elements in HQEFT, i.e. $L_i (i=1, 2, 3, 4)$ and $L^\prime _j (j=1, 3, 4)$ by using the LCSR. The procedure is similar to the case of $B_{(s)}$ decays into light $2^{++}$ tensor mesons [26]. Firstly, we define the following vacuum-tensor meson correlation functions:

$$\begin{aligned}{} & {} C^\mu _V ( P, q) = i \int d^4x e^{i q \cdot x} \nonumber \\{} & {} \quad \times \langle T ( P, \lambda ) | {{\mathscr {T}}} \{ \bar{q}_1(x) \gamma ^\mu b(x), \bar{b}(0) i \gamma ^5 q_2(0) \} | 0 \rangle , \end{aligned}$$

(16)

$$\begin{aligned}{} & {} C^\mu _A ( P, q) = i \int d^4x e^{i q \cdot x} \nonumber \\{} & {} \quad \times \langle T ( P, \lambda ) | {{\mathscr {T}}} \{ \bar{q}_1(x) \gamma ^\mu \gamma ^5 b(x), \bar{b}(0) i \gamma ^5 q_2(0) \} | 0 \rangle , \end{aligned}$$

(17)

$$\begin{aligned}{} & {} C^\mu _T ( P, q) = i \int d^4x e^{i q \cdot x} \nonumber \\{} & {} \quad \times \langle T ( P, \lambda ) | {{\mathscr {T}}} \{ \bar{q}_1(x) \sigma ^{\mu \nu } q_\nu b(x), \bar{b}(0) i \gamma ^5 q_2(0) \} | 0 \rangle , \end{aligned}$$

(18)

$$\begin{aligned}{} & {} C^{\prime \mu }_T ( P, q) = i \int d^4x e^{i q \cdot x} \nonumber \\{} & {} \quad \times \langle T ( P, \lambda ) | {{\mathscr {T}}} \{ \bar{q}_1(x) \sigma ^{\mu \nu } \gamma ^5 q_\nu b(x), \bar{b}(0) i \gamma ^5 q_2(0) \} | 0 \rangle , \nonumber \\ \end{aligned}$$

(19)

where ${{\mathscr {T}}}$ denotes the time ordered product of operators.

On one hand, inserting a complete set of states with $B_{(s)}$ meson quantum numbers between the currents in Eqs. (16)–(19) phenomenologically, we get

$$\begin{aligned}{} & {} C^\mu _V ( P, q) = \frac{\langle T( P, \lambda )| \bar{q}_1 \gamma ^\mu b | H \rangle \langle H| \bar{b} i \gamma ^5 q_2 | 0 \rangle }{ m^2_H - ( P+q)^2 }\nonumber \\{} & {} \quad + \sum _{H^\prime }\frac{\langle T( P, \lambda )| \bar{q}_1 \gamma ^\mu b | H^\prime \rangle \langle H^\prime | \bar{b} i \gamma ^5 q_2 | 0 \rangle }{ m^2_{H^\prime } - ( P+q)^2 }, \end{aligned}$$

(20)

$$\begin{aligned}{} & {} C^\mu _A ( P, q) = \frac{\langle T( P, \lambda )| \bar{q}_1 \gamma ^\mu \gamma ^5 b | H \rangle \langle H| \bar{b} i \gamma ^5 q_2 | 0 \rangle }{ m^2_H - ( P+q)^2 } \nonumber \\{} & {} \quad + \sum _{H^\prime }\frac{\langle T( P, \lambda )| \bar{q}_1 \gamma ^\mu \gamma ^5 b | H^\prime \rangle \langle H^\prime | \bar{b} i \gamma ^5 q_2 | 0 \rangle }{ m^2_{H^\prime } - ( P+q)^2 }, \end{aligned}$$

(21)

$$\begin{aligned}{} & {} C^\mu _T ( P, q) = \frac{\langle T( P, \lambda )| \bar{q}_1 \sigma ^{\mu \nu } q_\nu b | H \rangle \langle H| \bar{b} i \gamma ^5 q_2 | 0 \rangle }{ m^2_H - ( P+q)^2 } \nonumber \\{} & {} \quad + \sum _{H^\prime }\frac{\langle T( P, \lambda )| \bar{q}_1 \sigma ^{\mu \nu } q_\nu b | H^\prime \rangle \langle H^\prime | \bar{b} i \gamma ^5 q_2 | 0 \rangle }{ m^2_{H^\prime } - ( P+q)^2 }, \end{aligned}$$

(22)

$$\begin{aligned}{} & {} C^{\prime \mu }_T ( P, q) = \frac{\langle T( P, \lambda )| \bar{q}_1 \sigma ^{\mu \nu } \gamma ^5 q_\nu b | H \rangle \langle H| \bar{b} i \gamma ^5 q_2 | 0 \rangle }{ m^2_H - ( P+q)^2 } \nonumber \\{} & {} \quad + \sum _{H^\prime }\frac{\langle T( P, \lambda )| \bar{q}_1 \sigma ^{\mu \nu } \gamma ^5 q_\nu b | H^\prime \rangle \langle H^\prime | \bar{b} i \gamma ^5 q_2 | 0 \rangle }{ m^2_{H^\prime } - ( P+q)^2 }. \end{aligned}$$

(23)

Substituting Eqs. (5)–(8) into (20)–(23), we then have

$$\begin{aligned} C^\mu _V ( P, q)= & {} - \frac{2 i F}{2 \bar{\varLambda }_H - 2 v \cdot k} \left[ ( L_1( v \cdot P) + L_3 ( v \cdot P) )e^{(\lambda )* \mu } \right. \nonumber \\{} & {} - L_2 ( v \cdot P) ( e^{(\lambda )*} \cdot v ) v^\mu \nonumber \\{} & {} \left. - ( L_3 ( v \cdot P) - L_4 ( v \cdot P) ) \frac{e^{(\lambda ) *} \cdot v}{ v \cdot P} P^\mu \right] \nonumber \\{} & {} + \int ^\infty _{s_0} d s \frac{\rho _{TV} ( v \cdot P, s)}{ s - 2 v \cdot k } + \mathrm{subtr.}, \end{aligned}$$

(24)

$$\begin{aligned} C^\mu _A ( P, q)= & {} \frac{2 F}{2 \bar{\varLambda }_H - 2 v \cdot k} \frac{1}{v \cdot P} L_3 (v \cdot P) \varepsilon ^{\mu \nu \alpha \beta } e^{(\lambda ) *}_\nu P_\alpha v_\beta \nonumber \\{} & {} + \int ^\infty _{s_0} d s \frac{\rho _{TA} ( v \cdot P, s)}{ s - 2 v \cdot k } + \mathrm{subtr.}, \end{aligned}$$

(25)

$$\begin{aligned} C^\mu _T ( P, q)= & {} \frac{2 F}{2 \bar{\varLambda }_H - 2 v \cdot k} \left[ \Bigg ( ( m_H - v \cdot P) L^\prime _1 ( v \cdot P) \right. \nonumber \\{} & {} + \frac{m_H v \cdot P - m^2_T}{ v \cdot P} L^\prime _3 ( v \cdot P) \Bigg ) e^{(\lambda ) * \mu } + e^{(\lambda )*} \cdot v \nonumber \\{} & {} \times \left( - m_H L^\prime _1 (v \cdot P) \right. \nonumber \\{} & {} \left. + \frac{m^2_T - m_H v \cdot P}{v \cdot P} L^\prime _4 ( v \cdot P) \right) v^\mu \nonumber \\{} & {} + e^{(\lambda )*} \cdot v \left( - \frac{m_H}{v \cdot P} L^\prime _3 ( v \cdot P) \right. \nonumber \\{} & {} \left. \left. + \frac{m_H - v \cdot P}{v \cdot P} L^\prime _4 ( v \cdot P) \right) P^\mu \right] \nonumber \\{} & {} + \int ^\infty _{s_0} d s \frac{\rho _{TT} ( v \cdot P, s)}{ s - 2 v \cdot k } + \mathrm{subtr.}, \end{aligned}$$

(26)

$$\begin{aligned} C^{\prime \mu }_T ( P, q)= & {} - \frac{2i F}{2 \bar{\varLambda }_H - 2 v \cdot k} \left[ L^\prime _1 ( v \cdot P) + \frac{m_H}{v \cdot P} L^\prime _3 ( v \cdot P) \right] \nonumber \\{} & {} \times \varepsilon ^{\mu \nu \alpha \beta } e^{(\lambda )*}_\nu P_\alpha v_\beta \nonumber \\{} & {} + \int ^\infty _{s_0} d s \frac{\rho ^\prime _{TT} ( v \cdot P, s)}{ s - 2 v \cdot k } + \mathrm{subtr.}, \end{aligned}$$

(27)

where $k^\mu = ( P+q)^\mu - m_b v^\mu$ is the residual momentum in $B_{(s)}$ meson. F is the effective decay constant of heavy meson in HQEFT, defined as

$$\begin{aligned} \langle 0 | \bar{q} \varGamma Q^{(+)}_v | M_v \rangle = \frac{F}{2} \textrm{Tr} [ \varGamma {{\mathscr {M}}}_v ]. \end{aligned}$$

(28)

The integral terms represent contributions originating from the higher resonances. The subtractions ‘subtr.’ are introduced to ensure the convergence of integral terms, which vanish automatically after Borel transformation and therefore do not affect the physical results.

On the other hand, the vacuum-tensor meson correlation functions can be calculated theoretically and expressed as

$$\begin{aligned} C^\mu _V ( P, q)= & {} \int ^\infty _0 d s \frac{\rho ^{\textrm{th}}_{TV} ( v \cdot P, s)}{s - 2 v \cdot k} + \mathrm{subtr.}, \end{aligned}$$

(29)

$$\begin{aligned} C^\mu _A ( P, q)= & {} \int ^\infty _0 d s \frac{\rho ^{\textrm{th}}_{TA} ( v \cdot P, s)}{s - 2 v \cdot k} + \mathrm{subtr.}, \end{aligned}$$

(30)

$$\begin{aligned} C^\mu _T ( P, q)= & {} \int ^\infty _0 d s \frac{\rho ^{\textrm{th}}_{TT} ( v \cdot P, s)}{s - 2 v \cdot k} + \mathrm{subtr.}, \end{aligned}$$

(31)

$$\begin{aligned} C^{\prime \mu }_T ( P, q)= & {} \int ^\infty _0 d s \frac{\rho ^{\prime \mathrm th}_{TT} ( v \cdot P, s)}{s - 2 v \cdot k} + \mathrm{subtr.}. \end{aligned}$$

(32)

According to the assumption of quark hadron duality, starting from some effective threshold $s_0$, the theoretical spectral densities $\rho ^{\textrm{th}}_{TV}( v \cdot P, s)$, $\rho ^{\textrm{th}}_{TA}( v \cdot P, s)$, $\rho ^{\textrm{th}}_{TT}( v \cdot P, s)$, $\rho ^{\prime \mathrm th}_{TT}(v \cdot P, s)$ are equal to their physical counterparts $\rho _{TV}( v \cdot P, s)$, $\rho _{TA}( v \cdot P, s)$, $\rho _{TT}( v \cdot P, s)$, $\rho ^\prime _{TT}(v \cdot P, s)$, respectively. So, we obtain

$$\begin{aligned}{} & {} - \frac{2i F}{2 \bar{\varLambda }_H - 2 v \cdot k} \left[ ( L_1( v \cdot P) + L_3 ( v \cdot P) )e^{(\lambda )* \mu } \right. \nonumber \\{} & {} \qquad - L_2 ( v \cdot P) ( e^{(\lambda )*} \cdot v ) v^\mu - ( L_3 ( v \cdot P) - L_4 ( v \cdot P) ) \nonumber \\{} & {} \qquad \left. \times \frac{e^{(\lambda ) *} \cdot v}{ v \cdot P} P^\mu \right] = \int ^{s_0}_0 d s \frac{\rho _{TV} ( v \cdot P, s)}{ s - 2 v \cdot k } + \mathrm{subtr.}, \end{aligned}$$

(33)

$$\begin{aligned}{} & {} \frac{2 F}{2 \bar{\varLambda }_H - 2 v \cdot k} \frac{1}{v \cdot P} L_3 (v \cdot P) \varepsilon ^{\mu \nu \alpha \beta } e^{(\lambda ) *}_\nu P_\alpha v_\beta \nonumber \\{} & {} \quad = \int ^{s_0}_0 d s \frac{\rho _{TA} ( v \cdot P, s)}{ s - 2 v \cdot k } + \mathrm{subtr.}, \end{aligned}$$

(34)

$$\begin{aligned}{} & {} \frac{2 F}{2 \bar{\varLambda }_H - 2 v \cdot k} \left[ \left( ( m_H - v \cdot P) L^\prime _1 ( v \cdot P) + \frac{m_H v \cdot P - m^2_T}{ v \cdot P}\right. \right. \nonumber \\{} & {} \qquad \left. \times L^\prime _3 ( v \cdot P) \right) e^{(\lambda ) * \mu } + (e^{(\lambda )*} \cdot v) v^\mu \left( - m_H L^\prime _1 (v \cdot P) \right. \nonumber \\{} & {} \qquad \left. + \frac{m^2_T - m_H v \cdot P}{v \cdot P} L^\prime _4 ( v \cdot P) \right) + \frac{e^{(\lambda )*} \cdot v}{v \cdot P} P^\mu \nonumber \\{} & {} \qquad \left. \times \left( -m_H L^\prime _3 ( v \cdot P) + (m_H - v \cdot P) L^\prime _4 ( v \cdot P) \right) \right] \nonumber \\{} & {} \quad = \int ^{s_0}_0 d s \frac{\rho _{TT} ( v \cdot P, s)}{ s - 2 v \cdot k } + \mathrm{subtr.}, \end{aligned}$$

(35)

$$\begin{aligned}{} & {} \qquad - \frac{2i F}{2 \bar{\varLambda }_H - 2 v \cdot k} \left[ L^\prime _1 ( v \cdot P) + \frac{m_H}{v \cdot P} L^\prime _3 ( v \cdot P) \right] \nonumber \\{} & {} \qquad \times \varepsilon ^{\mu \nu \alpha \beta } e^{(\lambda )*}_\nu P_\alpha v_\beta = \int ^{s_0}_0 d s \frac{\rho ^\prime _{TT} ( v \cdot P, s)}{ s - 2 v \cdot k } + \mathrm{subtr.}. \end{aligned}$$

(36)

Defining $y = v \cdot P$, $\omega = 2 v \cdot k$ and performing two sequential Borel transformations on Eqs. (29)–(32), as detailed in Appendix A, we get

$$\begin{aligned} \rho ^{\textrm{th}}_{TV}= & {} {\hat{B}}^{-1/T}_{1/s} {\hat{B}}^\omega _T C^\mu _V ( y, \omega ), \end{aligned}$$

(37)

$$\begin{aligned} \rho ^{\textrm{th}}_{TA}= & {} {\hat{B}}^{-1/T}_{1/s} {\hat{B}}^\omega _T C^\mu _A ( y, \omega ), \end{aligned}$$

(38)

$$\begin{aligned} \rho ^{\textrm{th}}_{TT}= & {} {\hat{B}}^{-1/T}_{1/s} {\hat{B}}^\omega _T C^\mu _T ( y, \omega ), \end{aligned}$$

(39)

$$\begin{aligned} \rho ^{\prime \mathrm th}_{TT}= & {} {\hat{B}}^{-1/T}_{1/s} {\hat{B}}^\omega _T C^{\prime \mu }_T ( y, \omega ). \end{aligned}$$

(40)

Calculating the vacuum-tensor meson correlation functions at the leading order of heavy quark expansion in HQEFT and substituting into Eqs. (37)–(40), we have

$$\begin{aligned}{} & {} \rho ^{\textrm{th}}_{TV} ( y, s)= - \frac{1}{2y} \left\{ e^{(\lambda )* \mu } \left[ \frac{ f_T m^3_T}{y} g_a (u) - f^\perp _T m^2_T \phi _\perp (u) \right. \right. \nonumber \\{} & {} \quad \left. - \frac{f^\perp _T m^4_T}{2y^2} ( h_3(u) - \phi _\perp (u) ) \right] - e^{(\lambda )*} \cdot v v^\mu \left[ \frac{f_T m^5_T}{2 y^3} \right. \nonumber \\{} & {} \quad \times ( g_3 (u) + \phi _\parallel (u) - 2 g_a (u)) - \frac{f^\perp _T m^4_T}{2 y^2} \frac{\partial }{\partial u} h_p (u) \nonumber \\{} & {} \quad \left. - \frac{f^\perp _T m^4_T}{y^2} ( h_t (u) - \phi _\perp (u)) \right] + \frac{e^{(\lambda )*} \cdot v}{ y} P^\mu \nonumber \\{} & {} \quad \times \left[ \frac{f_T m^3_T}{y} ( \phi _\parallel (u) - g_a (u) ) + f^\perp _T m^2_T \phi _\perp (u) \right. \nonumber \\{} & {} \quad \left. \left. - \frac{f^\perp _T m^4_T}{y^2} ( h_t (u) - \frac{1}{2} \phi _\perp (u) - \frac{1}{2} h_3 (u) ) \right] \right\} _{u=1- \frac{s}{2y}}, \end{aligned}$$

(41)

$$\begin{aligned}{} & {} \rho ^{\textrm{th}}_{TA} ( y, s) = - \frac{i}{2y} \left[ \frac{f_T m^3_T}{2y^2} \frac{\partial }{\partial u} g_v (u) \right. \nonumber \\{} & {} \quad \left. + \frac{f^\perp _T m^2_T}{y} \phi _\perp (u) \right] _{u= 1- \frac{s}{2y}} \varepsilon ^{\mu \nu \alpha \beta } v_\nu P_\alpha e^{(\lambda )*}_\beta , \end{aligned}$$

(42)

$$\begin{aligned}{} & {} \rho ^{\textrm{th}}_{TT} ( y, s) = \frac{i}{2y} \left\{ e^{(\lambda )*\mu } \left[ \frac{f^\perp _T m^2_T ( m_H y - m^2_T) }{y} \phi _\perp (u) \right. \right. \nonumber \\{} & {} \quad + \frac{f^\perp _T m^4_T ( m_H -y)}{2 y^2} ( h_3(u) - \phi _\perp (u) ) \nonumber \\{} & {} \quad \left. - \frac{f_T m^3_T ( m_H-y)}{y} g_a (u) - \frac{f_T m^3_T ( m^2_T-y^2)}{2y^2} \frac{\partial }{\partial u} g_v (u) \right] \nonumber \\{} & {} \quad - e^{(\lambda )*} \cdot v v^\mu \left[ \frac{f^\perp _T m^4_T ( m_H y - m^2_T)}{y^3} ( h_t (u) - \frac{1}{2} \phi _\perp (u) \right. \nonumber \\{} & {} \quad - \frac{1}{2} h_3 (u) ) + \frac{f^\perp _T m^5_T }{2 y^2} ( h_3 (u) - \phi _\perp (u) ) \nonumber \\{} & {} \quad + \frac{f_T m^3_T ( m_H y - m^2_T ) }{y^2} ( - \phi _\parallel (u) + g_a (u) ) - \frac{f_T m^4_T }{y} g_a (u) \nonumber \\{} & {} \quad \left. - \frac{f_T m^5_T}{2 y^2} \frac{\partial }{ \partial u} g_v (u) \right] + \frac{e^{(\lambda )*} \cdot v }{y} P^\mu \left[ - f^\perp _T m^2_T m_H \phi _\perp (u) \right. \nonumber \\{} & {} \quad + \frac{f^\perp _T m^4_T ( m_H -y) }{ y^2} ( h_t (u) - \frac{1}{2} \phi _\perp (u) - \frac{1}{2} h_3 (u) ) \nonumber \\{} & {} \quad + \frac{f_T m^3_T ( m_H -y)}{y} ( - \phi _\parallel (u) + g_a (u) ) \nonumber \\{} & {} \quad \left. \left. - \frac{f_T m^3_T}{2} \frac{\partial }{\partial u} g_v (u) \right] \right\} _{u = 1- \frac{s}{2y}}, \end{aligned}$$

(43)

$$\begin{aligned}{} & {} \rho ^{\prime \textrm{th}}_{TT} ( y, s) = - \frac{1}{2y^2} \left[ f^\perp _T m^2_T m_H \phi _\perp (u) \right. \nonumber \\{} & {} \quad + \frac{f^\perp _T m^4_T}{2y} ( h_3 (u) - \phi _\perp (u))+ \frac{f_T m^3_T ( m_H -y) }{2y} \frac{\partial }{\partial u} g_v (u) \nonumber \\{} & {} \quad \left. - f_T m^3_T g_a (u) \right] _{u= 1- \frac{s}{2y}} \varepsilon ^{\mu \nu \alpha \beta } v_\nu P_\alpha e^{(\lambda ) *}_\beta . \end{aligned}$$

(44)

Here $\phi _\parallel (u)$, $\phi _\perp (u)$, $g_v(u)$, $g_a(u)$, $h_t(u)$, $h_p(u)$, $g_3(u)$, $h_3(u)$ are the LCDAs of $2^{--}$ tensor mesons, defined as [18]

$$\begin{aligned}{} & {} \langle T (P, \lambda ) | \bar{q}_1 (x) \gamma ^\mu \gamma ^5 q_2(0) | 0 \rangle = i f_T m^3_T \int ^1_0 d u e^{i u P \cdot x } \nonumber \\{} & {} \hspace{0.5cm} \times \left\{ P^\mu \frac{\epsilon ^{(\lambda )*}_{\alpha \beta } x^\alpha x^\beta }{ ( P \cdot x)^2} \phi _\parallel (u) + \left( \frac{\epsilon ^{(\lambda )*}_{\mu \alpha } x^\alpha }{ P \cdot x} \right. \right. \nonumber \\{} & {} \hspace{0.5cm} \left. - P^\mu \frac{\epsilon ^{(\lambda )*}_{\alpha \beta } x^\alpha x^\beta }{ ( P \cdot x)^2} \right) g_a (u) - \frac{1}{2} x^\mu \frac{\epsilon ^{(\lambda )*}_{\alpha \beta } x^\alpha x^\beta }{ ( P \cdot x)^3} m^2_T \nonumber \\{} & {} \hspace{0.5cm} \left. \times ( g_3(u) + \phi _\parallel (u) - 2 g_a (u) ) \right\} , \end{aligned}$$

(45)

$$\begin{aligned}{} & {} \langle T (P, \lambda ) | \bar{q}_1 (x) \gamma ^\mu q_2(0) | 0 \rangle = \frac{i}{2} f_T m^3_T \int ^1_0 d u e^{i u P \cdot x} \nonumber \\{} & {} \hspace{0.5cm} \times \varepsilon ^{\mu \nu \alpha \beta } \frac{x_\nu P_\alpha }{ P \cdot x} \epsilon ^{(\lambda )*}_{\beta \delta } x^\delta g_v (u), \end{aligned}$$

(46)

$$\begin{aligned}{} & {} \langle T (P, \lambda ) | \bar{q}_1 (x) \sigma ^{\mu \nu } \gamma ^5 q_2(0) | 0 \rangle = f^\perp _T m^2_T \int ^1_0 d u e^{iu P \cdot x}\nonumber \\{} & {} \hspace{0.5cm} \times \left\{ \frac{( \epsilon ^{(\lambda )* \mu \alpha } x_\alpha P^\nu - \epsilon ^{(\lambda )* \nu \alpha } x_\alpha P^\mu )}{ P \cdot x} \phi _\perp (u) \right. \nonumber \\{} & {} \hspace{0.5cm} + (P^\mu x^\nu - P^\nu x^\mu ) \frac{m^2_T \epsilon ^{(\lambda )*}_{\alpha \beta } x^\alpha x^\beta }{(P \cdot x)^3} ( h_t (u) - \frac{1}{2} \phi _\perp (u) \nonumber \\{} & {} \hspace{0.5cm} - \frac{1}{2} h_3 (u)) + \frac{1}{2} ( \epsilon ^{(\lambda )* \mu \alpha } x_\alpha x^\nu - \epsilon ^{(\lambda )* \nu \alpha } x_\alpha x^\mu ) \nonumber \\{} & {} \hspace{0.5cm} \left. \times \frac{m^2_T}{ ( P \cdot x )^2} ( h_3(u) - \phi _\perp (u) ) \right\} , \end{aligned}$$

(47)

$$\begin{aligned}{} & {} \langle T (P, \lambda ) | \bar{q}_1 (x) \gamma ^5 q_2(0) | 0 \rangle = \frac{1}{2} f^\perp _T m^4_T \int ^1_0 d u e^{ i u P \cdot x} \nonumber \\{} & {} \hspace{0.5cm} \times \frac{\epsilon ^{(\lambda )*}_{\alpha \beta } x^\alpha x^\beta }{P \cdot x} h_p (u), \end{aligned}$$

(48)

among which $\{\phi _\parallel (u), \phi _\perp (u) \}$, $\{g_v(u), g_a(u), h_t (u), h_p(u)\}$ and $\{g_3(u), h_3(u)\}$ are of twist-2, twist-3 and twist-4, respectively.

Table 1 Decay constants of light $2^{--}$ tensor mesons and Gegenbauer moments of their LCDAs [18], where $\bar{K}_2$ denotes the $K_2$ meson containing an antistrange quark

Substituting Eqs. (41)–(44) into (33)–(36) and performing Borel transformation ${\hat{B}}^\omega _T$ on both sides, we obtain the expressions of $L_i(i=1,2,3,4)$ and $L^\prime _j(j=1,3,4)$ as following:

$$\begin{aligned} L_1 (y)= & {} L^\prime _1 (y)\nonumber \\= & {} - \frac{i}{4 F} e^{2 \bar{\varLambda }_H/T} \int ^{s_0}_0 d s e^{-s/T} \frac{1}{y^2} \Bigg [ f_T m^3_T g_a (u) \nonumber \\{} & {} - \frac{f^\perp _T m^4_T}{2y} ( h_3 (u) - \phi _\perp (u))\nonumber \\{} & {} + \frac{f_T m^3_T}{2} \frac{\partial }{ \partial u} g_v (u) \Bigg ]_{u = 1- \frac{s}{2y}}, \end{aligned}$$

(49)

$$\begin{aligned} L_2 (y)= & {} - \frac{i}{4 F} e^{2 \bar{\varLambda }_H/T} \int ^{s_0}_0 d s e^{-s/T} \frac{1}{y^3} \left[ \frac{f_T m^5_T}{ 2 y} ( g_3 (u) \right. \nonumber \\{} & {} + \phi _\parallel (u) - 2 g_a (u) ) - f^\perp _T m^4_T ( h_t (u) - \phi _\perp (u) ) \nonumber \\{} & {} \left. - \frac{f^\perp _T m^4_T}{2} \frac{\partial }{\partial u} h_p (u) \right] _{u = 1 - \frac{s}{2y}}, \end{aligned}$$

(50)

$$\begin{aligned} L_3 (y)= & {} L^\prime _3(y)\nonumber \\= & {} \frac{i}{4 F} e^{2 \bar{\varLambda }_H/T} \int ^{s_0}_0 d s e^{-s/T} \frac{1}{y} \Bigg [ f^\perp _T m^2_T \phi _\perp (u) \nonumber \\{} & {} + \frac{f_T m^3_T}{2y} \frac{\partial }{\partial u} g_v (u) \Bigg ]_{u = 1 - \frac{s}{2y}}, \end{aligned}$$

(51)

$$\begin{aligned} L_4 (y)= & {} L^\prime _4(y)\nonumber \\= & {} - \frac{i}{4 F} e^{2 \bar{\varLambda }_H/T} \int ^{s_0}_0 d s e^{-s/T} \frac{1}{y^2} \Bigg [ f_T m^3_T ( \phi _\parallel (u) \nonumber \\{} & {} - g_a (u)) - \frac{f_T m^3_T}{2} \frac{\partial }{\partial u} g_v (u) - \frac{f^\perp _T m^4_T}{y} ( h_t(u) \nonumber \\{} & {} - \frac{1}{2} \phi _\perp (u) -\frac{1}{2} h_3(u) ) \Bigg ]_{u=1-\frac{s}{2y}}. \end{aligned}$$

(52)

Considering that $L^\prime _j = L_j(j=1,3,4)$, from Eqs. (9)–(15), it is straightforward to get the following relations between the semileptonic and penguin type form factors:

$$\begin{aligned} T_1 (q^2)= & {} \frac{m^2_H - m^2_T + q^2}{2 m_H} \frac{A(q^2)}{ m_H + m_T} + \frac{m_H + m_T}{2 m_H} V_1(q^2),\nonumber \\ \end{aligned}$$

(53)

$$\begin{aligned} T_2 (q^2)= & {} \frac{2}{ m^2_H - m^2_T} \Bigg [ \frac{(m_H-y)(m_H + m_T)}{2} V_1 (q^2) \nonumber \\{} & {} + \frac{m_H ( y^2- m^2_T)}{m_H + m_T} A (q^2) \Bigg ], \end{aligned}$$

(54)

$$\begin{aligned} T_3 (q^2)= & {} - \frac{m_H + m_T}{2 m_H} V_1(q^2) + \frac{m_H - m_T}{2 m_H} [ V_2(q^2) \nonumber \\{} & {} - V_3 (q^2) ] + \frac{m^2_H + 3 m^2_T -q^2}{2 m_H ( m_H + m_T)} A (q^2), \end{aligned}$$

(55)

with

$$\begin{aligned} V_3(q^2)= & {} \frac{2 m_T ( m_H + m_T)}{q^2} \left[ \frac{m_H + m_T}{2 m_T} V_1(q^2) \right. \nonumber \\{} & {} \left. - \frac{m_H - m_T}{2 m_T} V_2(q^2) - V_0(q^2) \right] . \end{aligned}$$

(56)

According to these relations, the penguin type form factors can be obtained directly from the corresponding semileptonic ones, which is similar to the case of $2^{++}$ tensor mesons.

3 Numerical results and discussions of form factors

With Eqs. (9)–(12) and (49)–(56) given above, we are now in a position to calculate the form factors of $B_{(s)}$ to light $2^{--}$ tensor mesons (including $\rho _2$, $\omega _2$, $K_2$ and $\phi _2$). For this purpose, it is required to know the LCDAs of $2^{--}$ tensor mesons, which have been studied via QCD sum rules in Ref. [18]. In this study, we consider the LCDAs to twist-3, i.e. neglect the contributions of $g_3(u)$ and $h_3(u)$.

The twist-2 LCDAs $\phi _\parallel (u)$ and $\phi _\perp (u)$ have the following forms [18]:

$$\begin{aligned} \phi _\parallel (u)= & {} 18 u (1-u) (2u-1) a^\parallel _1, \end{aligned}$$

(57)

$$\begin{aligned} \phi _\perp (u)= & {} 6u (1-u) + 18 u (1-u) (2u-1) a^\perp _1. \end{aligned}$$

(58)

Neglecting the three-particle LCDAs containing gluons, the twist-3 LCDAs $g_v(u)$, $g_a(u)$, $h_t (u)$ and $h_p(u)$ are related to the twist-2 ones through

$$\begin{aligned} g_v (u)= & {} 2 \bar{u} \int ^u_0 d v \frac{\tilde{\phi }_\parallel (v)}{\bar{v}} + 2 u \int ^1_u d v \frac{\tilde{\phi }_\parallel (v)}{v}, \end{aligned}$$

(59)

$$\begin{aligned} g_a (u)= & {} \int ^u_0 d v \frac{\tilde{\phi }_\parallel (v)}{\bar{v}} + \int ^1_u d v \frac{\tilde{\phi }_\parallel (v)}{v} + \tilde{\delta }_- \phi _\perp (u), \end{aligned}$$

(60)

$$\begin{aligned} h_t (u)= & {} \frac{3}{2} ( 2u -1) \left( \int ^u_0 d v \frac{\tilde{\phi }_\perp (v)}{ \bar{v}} - \int ^1_u d v \frac{\tilde{\phi }_\perp (v)}{ v} \right) \nonumber \\{} & {} + \delta _- \phi _\parallel (u), \end{aligned}$$

(61)

$$\begin{aligned} h_p (u)= & {} 3 \bar{u} \int ^u_0 d v \frac{\tilde{\phi }_\perp (v)}{\bar{v} } + 3 u \int ^1_u d v \frac{\tilde{\phi }_\perp (v ) }{ v }, \end{aligned}$$

(62)

where

$$\begin{aligned} \tilde{\phi }_\parallel ( v)= & {} \phi _\parallel (v) + \frac{1}{4} \tilde{\delta }_- (2v-1) \phi ^\prime _\perp (v ) - \frac{1}{4} \tilde{\delta }_+ \phi ^\prime _\perp (v), \end{aligned}$$

(63)

$$\begin{aligned} \tilde{\phi }_\perp (v)= & {} \phi _\perp (v) - \frac{1}{3} \delta _- \left( \phi _\parallel (v) - \frac{1}{2} (2v-1) \phi ^\prime _\perp (v) \right) \nonumber \\{} & {} - \frac{1}{2} \delta _+ \phi ^\prime _\parallel (v), \end{aligned}$$

(64)

with

$$\begin{aligned} \tilde{\delta }_\pm = \frac{f^\perp _T}{f_T} \frac{m_{q_1} \pm m_{q_2}}{m_T}, \hspace{0.5cm} \delta _\pm = \frac{f_T}{f^\perp _T} \frac{m_{q_1} \pm m_{q_2}}{m_T}. \end{aligned}$$

(65)

For the decay constants of light $2^{--}$ tensor mesons and Gegenbauer moments of their LCDAs, we use the values calculated via QCD sum rules [18], as shown in Table 1. For the masses of $B_{(s)}$, $K_2$ and light quarks, which have been well established in experiments, we take the latest values given by PDG [1]:

$$\begin{aligned} m_B= & {} 5.28\textrm{GeV}, \hspace{0.5cm} m_{B_s} = 5.37\textrm{GeV}, \hspace{0.5cm} m_{K_2} = 1.82\textrm{GeV}, \nonumber \\ m_{u(d)}= & {} 0.0035^{+0.0003}_{-0.0002}\textrm{GeV}, \hspace{0.5cm} m_s = 0.093^{+0.009}_{-0.003}\textrm{GeV}.\nonumber \\ \end{aligned}$$

(66)

For the light $2^{--}$ tensor mesons not yet observed, i.e. $\rho _2$, $\omega _2$ and $\phi _2$, we adopt the masses estimated using QCD sum rules [3]:

$$\begin{aligned} m_{\rho _2(\omega _2)}= 1.78 \pm 0.12\textrm{GeV}, \hspace{0.5cm} m_{\phi _2} =2.00\pm 0.16\textrm{GeV}. \nonumber \\ \end{aligned}$$

(67)

The binding energies of heavy mesons and effective decay constant in HQEFT have the typical values [24, 25]:

$$\begin{aligned} \bar{\varLambda }_B= & {} 0.53\textrm{GeV}, \hspace{0.5cm} \bar{\varLambda }_{B_s} = 0.62\textrm{GeV}, \nonumber \\ \bar{\varLambda }= & {} 0.53\textrm{GeV}, \hspace{0.5cm} F=0.30\textrm{GeV}^{3/2}. \end{aligned}$$

(68)

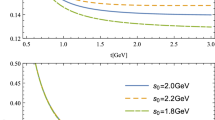
As shown in Eqs. (49)–(52), two free parameters, i.e. $s_0$ and T are involved in our calculations. $s_0$ is related to the threshold energy of $B_{(s)}$ and T is the Borel parameter. According to the requirements of LCSR, we choose the regions of these two parameters in which the curves of form factors are most stable. In the evaluation, we adjust $s_0$ and T for all the relevant $B \rightarrow T$ decays consistently and the same procedure is performed for the $B_s \rightarrow T$ decays. The variations of $B \rightarrow \rho _2, \omega _2, K_2, \bar{K}_2$ form factors as functions of T for different $s_0$ at the maximally recoiling point ($q^2=0$) are presented in Figs. 1, 2, 3 and 4, respectively.

Fig. 1

$B \rightarrow \rho _2$ form factors as functions of T for different $s_0$ at $q^2=0$

Fig. 2

$B \rightarrow \omega _2$ form factors as functions of T for different $s_0$ at $q^2=0$

Fig. 3

$B \rightarrow K_2$ form factors as functions of T for different $s_0$ at $q^2=0$

Fig. 4

$B \rightarrow \bar{K}_2$ form factors as functions of T for different $s_0$ at $q^2=0$

Note that we have only shown here the curves of semileptonic type form factors in that the penguin type form factors can be obtained directly from corresponding semileptonic ones as mentioned above. Based on these curves, we can see that it is reasonable to choose

$$\begin{aligned} s_0= 1.8 \pm 0.2 \textrm{GeV}, \hspace{0.5cm} T= 2.0 \pm 0.5 \textrm{GeV}, \end{aligned}$$

(69)

for the $B \rightarrow T$ decays. Similarly, we can determine the regions of $s_0$ and T for the $B_s \rightarrow T$ decays, which are found to be

$$\begin{aligned} s_0= 2.0 \pm 0.2 \textrm{GeV}, \hspace{0.5cm} T= 2.0 \pm 0.5 \textrm{GeV}. \end{aligned}$$

(70)

As well known, the LCSR is no longer reliable at large momentum transfer, i.e. $q^2 \sim m^2_b - 2 m_b \bar{\varLambda }$. Therefore, it is needed to extrapolate our LCSR results to the entire physical region via certain parametrization. Here, we shall adopt the Bourrely–Caprini–Lellouch (BCL) version of the z-series expansion [29,30,31,32]

$$\begin{aligned} F(q^2)= & {} \frac{F(0)}{1- q^2/m^2_{F,pole}} \nonumber \\{} & {} \times \left\{ 1+ \sum _{k=1}^N b_k \left[ z(q^2, t_0)^k - z(0, t_0)^k \right] \right\} , \end{aligned}$$

(71)

where $F \in \{V_1, V_2, V_0, A\}$, and

$$\begin{aligned} z(q^2, t_0) = \frac{\sqrt{t_+ - q^2}- \sqrt{t_+ - t_0}}{\sqrt{t_+ - q^2}+ \sqrt{t_+ - t_0}}, \end{aligned}$$

(72)

with $t_+ = (m_H + m_T)^2$, $t_0= (m_H + m_T) ( \sqrt{m_H}- \sqrt{m_T})^2$. For the resonance masses $m_{F, pole}$, we take the values from PDG [1] and heavy meson chiral perturbation theory [33], as listed in Table 2. In practice, we truncate the expansion at $N=2$.

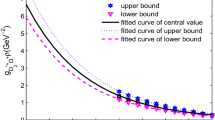
Using the LCSR predictions in low $q^2$ region (specifically, we choose $0 \le q^2 \le 6 \textrm{GeV}^2$) to fit the parameters $b_1$, $b_2$ in Eq. (71), we obtain the behaviors of form factors in the entire physical region, as shown in Fig. 5, 6, 7, 8, 9, 10 and 11. We can see that the form factor $V_2$ decreases monotonically with $q^2$, which is apparently different from the behaviors of other form factors. Additionally, the form factor A has obvious deviation with different $s_0$ and T at large $q^2$ region, which can be understood via its corresponding expressions, i.e. Eqs. (12), (51), as detailed in Appendix B. The numerical results of form factors for the $B_{(s)} \rightarrow T$ decays are presented in Table 3. The $B \rightarrow \rho _2$ form factors given here correspond to $\rho ^\pm _2$, and those for the case of $\rho ^0_2$ can be obtained by multiplying $1/\sqrt{2}$ according to its flavor content. The uncertainties originate from the free parameters $\{s_0, T\}$, the decay constants $\{f_T, f^\perp _T\}$, the Gegenbauer moment $a^\perp _1$, the light quark masses $m_q(q=u,d,s)$ and the ‘not observed’ light tensor meson masses $m_T(T=\rho _2, \omega _2, \phi _2)$, which are added in quadrature. For the form factors $V_1, V_0$, the uncertainties are about $(10-25)\%$ at $q^2=0$. The uncertainties of $V_2$ at $q^2=0$ are very different for the decays with unflavored light mesons $\rho _2, \omega _2, \phi _2$ in the final states and those with the flavored $K_2$, which are around (400–500)% and (30–40)%, respectively. The extremely large uncertainties of $V_2$ for the former case are due to the tininess of its central values at $q^2=0$. As indicated in Fig. 5, 6, 7, 8, 9, 10 and 11, the uncertainties of $V_2$ shall reduce significantly at large $q^2$ region. For the form factor A, the uncertainties vary in a relatively large range, approximately $(15-35)\%$ at $q^2=0$. Note that the uncertainties quoted here merely indicate variations in our results within the chosen ranges of relevant parameters mentioned above. For comparison, we also give the corresponding results of form factors without quark mass corrections in Table 4. It is found that the effects of quark mass corrections are most significant for the decays with $K_2$ in the final states, largely owing to the nonzero Gegenbauer moment $a^\perp _1$ of its LCDAs originating from the quark mass difference.

Table 2 The resonance masses entering the z-series expansion of form factors [1, 33], in units of GeV

Fig. 5

$B \rightarrow \rho _2$ form factors as functions of $q^2$

Fig. 6

$B \rightarrow \omega _2$ form factors as functions of $q^2$

Fig. 7

$B \rightarrow K_2$ form factors as functions of $q^2$

Fig. 8

$B \rightarrow \bar{K}_2$ form factors as functions of $q^2$

Fig. 9

$B_s \rightarrow K_2$ form factors as functions of $q^2$

Fig. 10

$B_s \rightarrow \bar{K}_2$ form factors as functions of $q^2$

Fig. 11

$B_s \rightarrow \phi _2$ form factors as functions of $q^2$

4 $B_{(s)}$ to light $2^{--}$ tensor meson semileptonic decays

In this section, we apply the form factors obtained above to investigate the relevant charged current induced semileptonic decays $B_{(s)} \rightarrow T l \nu _l$. Similar to the case of $2^{++}$ tensor mesons [26], the differential decay width w.r.t. $q^2$ can be written as

$$\begin{aligned} \frac{d \varGamma }{d q^2}= \frac{d \varGamma _L}{d q^2} + \frac{d \varGamma _T}{d q^2}, \end{aligned}$$

(73)

where $\frac{d \varGamma _L}{d q^2}$ and $\frac{d \varGamma _T}{d q^2}$ represent the longitudinal and transverse differential decay width, respectively. Their expressions take the following forms,

$$\begin{aligned} \frac{d \varGamma _L}{d q^2}= & {} \frac{G_F |V_{ub}|^2}{256 \pi ^3 m^3_H } \frac{\sqrt{\lambda _T}}{q^2} \left( 1 - \frac{m^2_l}{q^2} \right) X_L, \end{aligned}$$

(74)

$$\begin{aligned} \frac{d \varGamma _T}{d q^2}= & {} \frac{G_F |V_{ub}|^2}{256 \pi ^3 m^3_H } \frac{\sqrt{\lambda _T}}{q^2} \left( 1 - \frac{m^2_l}{q^2} \right) (X_+ + X_-), \end{aligned}$$

(75)

with

$$\begin{aligned} X_L= & {} \frac{\lambda _T}{9 m^2_H m^2_T } \left[ (2 q^2 \!\!+\! m^2_l) h_0(q^2)^2\!+\! 3 \lambda _T m^2_l V_0 (q^2)^2 \right] , \nonumber \\\end{aligned}$$

(76)

$$\begin{aligned} X_\pm= & {} \frac{\lambda _T}{12 m^2_H m^2_T } q^2 ( 2 q^2 + m^2_l) \Bigg [ ( m_H + m_T) V_1 (q^2) \nonumber \\{} & {} \mp \frac{\sqrt{\lambda _T}}{m_H + m_T} A(q^2) \Bigg ]^2, \end{aligned}$$

(77)

$$\begin{aligned} h_0 (q^2)= & {} \frac{1}{2 m_T} \Bigg [ ( m^2_H - m^2_T - q^2) ( m_H + m_T) V_1 (q^2) \nonumber \\{} & {} - \frac{\lambda _T}{m_H + m_T} V_2 (q^2) \Bigg ], \end{aligned}$$

(78)

$$\begin{aligned} \lambda _T= & {} (m^2_H - m^2_T -q^2)^2 - 4 m^2_T q^2. \end{aligned}$$

(79)

Here $m_l$ is the mass of charged lepton and $q^2$ corresponds to the momentum square of lepton pair.

Integrating Eq. (73) over $q^2$ in the entire physical region and using the lifetimes of $B_{(s)}$ (denoted as $\tau _H$ in the following) as inputs, we can obtain the branching ratio

$$\begin{aligned} Br = \frac{\tau _H}{\hbar } \int ^{(m_H - m_T)^2}_{m^2_l} d q^2 \frac{d \varGamma }{d q^2}. \end{aligned}$$

(80)

Furthermore, we can also study the longitudinal polarization fraction

$$\begin{aligned} f_L= \frac{\varGamma _L}{\varGamma } = \frac{\int ^{(m_H - m_T)^2}_{m^2_l} d q^2 \frac{d \varGamma _L}{d q^2}}{\int ^{(m_H - m_T)^2}_{m^2_l} d q^2 \frac{d \varGamma }{d q^2}}, \end{aligned}$$

(81)

the differential forward–backward asymmetry (FBA) of lepton

$$\begin{aligned} \frac{d A_{FB}}{d q^2}= & {} \frac{\left( \int ^1_0 - \int ^0_{-1} \right) d \cos \theta \frac{d^2 \varGamma }{d q^2 d \cos \theta }}{\frac{d \varGamma }{d q^2}} \nonumber \\= & {} \frac{\lambda ^{3/2}_T}{ X_L + X_+ + X_-} \left( \frac{m^2_l }{3 m^2_H m^2_T } h_0 (q^2) V_0 (q^2) \right. \nonumber \\{} & {} \left. - \frac{q^4 }{ 2 m^2_H m^2_T } V_1 (q^2) A(q^2) \right) , \end{aligned}$$

(82)

and corresponding total FBA

Table 3 The form factors of $B_{(s)} \rightarrow T$ decays, where the first, second and third results of $b_1, b_2$ correspond to the central, maximum and minimum values of form factors, respectively

$$\begin{aligned} A_{FB}= & {} \frac{1}{\varGamma } \int ^{(m^2_H- m^2_T)^2}_{m^2_l} d q^2 \left( \int ^1_0 - \int ^0_{-1} \right) d \cos \theta \frac{d^2 \varGamma }{d q^2 d \cos \theta } \nonumber \\= & {} \frac{1}{\varGamma } \frac{G_F |V_{ub}|^2}{256 \pi ^3 m^3_H } \frac{\lambda ^2_T}{q^2} \left( 1 - \frac{m^2_l}{q^2} \right) \left( \frac{m^2_l }{3 m^2_H m^2_T } h_0 (q^2) V_0 (q^2) \right. \nonumber \\{} & {} \left. - \frac{q^4 }{ 2 m^2_H m^2_T } V_1 (q^2) A(q^2) \right) . \end{aligned}$$

(83)

For the lifetimes of $B_{(s)}$, masses of charged leptons, CKM matrix element $|V_{ub}|$, Fermi coupling constant $G_F$ and reduced Plank constant $\hbar$, we use the latest values given by PDG [1]:

$$\begin{aligned} \tau _{\bar{B}^0}= & {} 1.519 \times 10^{-12} \textrm{s}, \hspace{0.5cm} \tau _{B^-} = 1.638 \times 10^{-12}\textrm{s}, \nonumber \\ \tau _{B_s}= & {} 1.521 \times 10^{-12} \textrm{s}, \hspace{0.5cm} m_e= 0.511\times 10^{-3} \textrm{GeV}, \nonumber \\ m_\mu= & {} 0.106 \textrm{GeV}, \hspace{0.5cm} m_\tau = 1.777 \textrm{GeV}, \nonumber \\ |V_{ub}|= & {} (3.82 \pm 0.20) \times 10^{-3}, \nonumber \\ G_F= & {} 1.166 \times 10^{-5} \textrm{GeV}^{-2}, \nonumber \\ \hbar= & {} 6.582 \times 10^{-25} \textrm{GeV} \cdot \textrm{s}. \end{aligned}$$

(84)

Table 4 The form factors of $B_{(s)} \rightarrow T$ decays without quark mass corrections, where the first, second and third results of $b_1, b_2$ correspond to the central, maximum and minimum values of form factors, respectively

The differential FBAs of lepton as functions of $q^2$ for the decays $\bar{B}^0_s \rightarrow K^+_2 l^- \bar{\nu }_l (l=e, \mu , \tau )$ are shown in Fig. 12. It is easily seen that the zero-crossing points increase significantly with the mass of charged lepton. For other charged current induced semileptonic decay modes, except for $B^0_s \rightarrow K^-_2 \tau ^+ \nu _\tau$, the behaviors of differential FBAs are similar. For the $B^0_s \rightarrow K^-_2 \tau ^+ \nu _\tau$ mode, the differential FBA is positive in the entire physical region and no zero-crossing point exists. The numerical results of branching ratios (Br), longitudinal polarization fractions ($f_L$), total FBAs ($A_{FB}$) and zero-crossing points of differential FBAs ($c_0$) for all the $B_{(s)} \rightarrow T l \nu _l$ decays are presented in Table 5. The first and second uncertainties of Br originate from the form factors and CKM matrix element $|V_{ub}|$, respectively, and the uncertainties of $f_L$, $A_{FB}$, $c_0$ only come from the form factors. We can find that the Br are at the order of ${{\mathscr {O}}}(10^{-5})$ and almost identical for $l=e, \mu$, while those for $l=\tau$ are significantly smaller, approximately one sixth of the former. The values of $f_L$ are also quite similar for $l=e, \mu$, and visibly smaller for $l=\tau$. The $A_{FB}$ are negative for $l=e, \mu$, and become positive for $l=\tau$. Since we adopt the same input parameters for $\rho _2$ and $\omega _2$ (cf. Table 1 and Eq. (67)), the results for the $B^- \rightarrow \rho ^0_2 l^- \bar{\nu }_l$ decays are almost the same as the corresponding values for the $B^- \rightarrow \omega _2 l^- \bar{\nu }_l$ modes. There are significant differences between the results for the $B^0_s \rightarrow K^-_2 l^+ \nu _l$ decays and those for the corresponding charge conjugate processes, i.e. the $\bar{B}^0_s \rightarrow K^+_2 l^- \bar{\nu }_l$ modes, which imply visible CP violations.

Fig. 12

The differential FBAs of lepton as functions of $q^2$ for the decays $\bar{B}^0_s \rightarrow K^+_2 l^- \bar{\nu }_l (l=e, \mu , \tau )$

Table 5 The numerical results of Br, $f_L$, $A_{FB}$ and $c_0$ for all the $B_{(s)} \rightarrow T l \nu _l$ decays

5 Summary

In this study, we calculate the form factors of $B_{(s)}$ decays into light $J^{PC}= 2^{--}$ tensor mesons $\rho _2$, $\omega _2$, $K_2$ and $\phi _2$ systematically by using the LCSR in HQEFT. We derive the expressions of form factors in terms of the LCDAs of tensor mesons, and find that the penguin type form factors can be obtained directly from the corresponding semileptonic ones at the leading order of heavy quark expansion, which is similar to the case of $2^{++}$ tensor mesons. Considering the light tensor meson LCDAs to twist-3 and quark mass corrections, we give the numerical results of form factors systematically. The uncertainties of form factors are considerably different for $V_{1(0)}$, $V_2$ and A. In particular, due to the tininess of corresponding central values, the uncertainties of $V_2$ at $q^2=0$ are extremely large for the decays with unflavored light mesons $\rho _2$, $\omega _2$, $\phi _2$ in the final states. Additionally, the effects of quark mass corrections are most significant for the decays with $K_2$ in the final states, largely because of the nonzero Gegenbauer moment $a^\perp _1$ of its LCDAs originating from the quark mass difference.

Based on the form factors given here, we investigate the relevant tree level charged current induced semileptonic decays $B_{(s)} \rightarrow T l \nu _l$. It is found that the zero-crossing points of differential FBAs increase significantly with the mass of charged lepton. The branching ratios are at the order of ${{\mathscr {O}}}(10^{-5})$ and almost identical for $l=e, \mu$, while those for $l=\tau$ are much smaller, approximately one sixth of the former. The longitudinal polarization fractions are also quite similar for $l=e, \mu$, and visibly smaller for $l=\tau$. The total FBAs are negative for $l=e, \mu$, and become positive for $l=\tau$. In addition, there are significant differences between the results for $B^0_s \rightarrow K^-_2 l^+ \nu _l$ decays and those for the corresponding charge conjugate processes, which imply visible CP violations. Our results may be tested by more precise experiments in the future.

Appendices

Appendix A: Derivation of the expressions for theoretical spectral densities in terms of corresponding correlation functions

In this appendix, we shall derive the expressions for theoretical spectral densities in terms of corresponding correlation functions. For convenience, we take $\rho ^{\textrm{th}}_{TV}$ as an example here, and the expressions for other theoretical spectral densities can be derived similarly.

As shown in Eq. (29), the vacuum-tensor meson correlation function can be expressed as the form of an integration over the theoretical spectral density, i.e.

$$\begin{aligned} C^\mu _V ( P, q) = \int ^\infty _0 d s \frac{\rho ^{\textrm{th}}_{TV} ( v \cdot P, s)}{s - 2 v \cdot k} + \mathrm{subtr.} \end{aligned}$$

(A.1)

Firstly, noting that $y= v \cdot P$, $\omega = 2 v \cdot k$ and performing the Borel transformation ${\hat{B}}^\omega _T$ on Eq. (A.1), we get

$$\begin{aligned} {\hat{B}}^\omega _T C^\mu _V (y, \omega )= & {} \int ^\infty _0 d s \rho ^{\textrm{th}}_{TV} (y, s) {\hat{B}}^\omega _T \left( \frac{1}{s - \omega } \right) \nonumber \\= & {} \int ^\infty _0 d s \rho ^{\textrm{th}}_{TV} (y, s) e^{-s/T}. \end{aligned}$$

(A.2)

Then, changing the integration variable of Eq.(A.2) from s to $s^\prime$ and performing the Borel transformation ${\hat{B}}^{-1/T}_{1/s}$ on this equation, we have

$$\begin{aligned} {\hat{B}}^{-1/T}_{1/s}{\hat{B}}^\omega _T C^\mu _V (y, \omega )= & {} \int ^\infty _0 d s^\prime \rho ^{\textrm{th}}_{TV} (y, s^\prime ) {\hat{B}}^{-1/T}_{1/s} \left( e^{-s^\prime /T} \right) \nonumber \\= & {} \int ^\infty _0 d s^\prime \rho ^{\textrm{th}}_{TV} (y, s^\prime ) \delta (s^\prime -s) \nonumber \\= & {} \rho ^{\textrm{th}}_{TV} (y, s), \end{aligned}$$

(A.3)

i.e.

$$\begin{aligned} \rho ^{\textrm{th}}_{TV} (y, s)={\hat{B}}^{-1/T}_{1/s}{\hat{B}}^\omega _T C^\mu _V (y, \omega ). \end{aligned}$$

(A.4)

Here, we have used the formulae for Borel transformation [27, 28]

$$\begin{aligned} {\hat{B}}^\omega _T \left( \frac{1}{s - \omega } \right) = e^{-s/T}, \hspace{0.5cm} {\hat{B}}^\omega _T e^{\lambda \omega } = \delta \left( \lambda - \frac{1}{T} \right) . \end{aligned}$$

(A.5)

Appendix B: Explanation of obvious deviation of the form factor A with different $s_0$ and T at large $q^2$ region

In this appendix, we shall explain the obvious deviation of the form factor A with different $s_0$ and T at large $q^2$ region. For simplicity and clarity, we compare the variation rates of A w.r.t. $s_0$, T with those of $V_1$ here.

According to Eqs. (9), (12), (49) and (51), the form factors $V_1$, A depend on $s_0$, T through the wave functions $L_1$, $L_3$. Firstly, taking the derivatives of $L_1$, $L_3$ w.r.t. $s_0$, we have

$$\begin{aligned} L_1 Ps_0= & {} - \frac{i}{4 F} e^{2 \bar{\varLambda }_H/T} e^{-s_0/T} \frac{1}{y^2} \left[ f_T m^3_T g_a (u) \right. \nonumber \\{} & {} - \frac{f^\perp _T m^4_T}{2y} ( h_3 (u) - \phi _\perp (u)) \nonumber \\{} & {} \left. + \frac{f_T m^3_T}{2} \frac{\partial }{ \partial u} g_v (u) \right] _{u = 1- \frac{s_0}{2y}}, \end{aligned}$$

(B.6)

$$\begin{aligned} L_3 Ps_0= & {} \frac{i}{4 F} e^{2 \bar{\varLambda }_H/T} e^{-s_0/T} \frac{1}{y} \left[ f^\perp _T m^2_T \phi _\perp (u) \right. \nonumber \\{} & {} \left. + \frac{f_T m^3_T}{2y} \frac{\partial }{\partial u} g_v (u) \right] _{u = 1 - \frac{s_0}{2y}}. \end{aligned}$$

(B.7)

Secondly, taking the derivatives of $L_1$, $L_3$ w.r.t. T, we get

$$\begin{aligned} L_1 PT= & {} \frac{i}{4 F T^2} e^{2 \bar{\varLambda }_H/T} \int _0^{s_0} d s (2 \bar{\varLambda }_H -s) e^{-s/T} \frac{1}{y^2} \nonumber \\{} & {} \times \left[ f_T m^3_T g_a (u) - \frac{f^\perp _T m^4_T}{2y} ( h_3 (u) - \phi _\perp (u)) \right. \nonumber \\{} & {} \left. + \frac{f_T m^3_T}{2} \frac{\partial }{ \partial u} g_v (u) \right] _{u = 1- \frac{s}{2y}}, \end{aligned}$$

(B.8)

$$\begin{aligned} L_3 PT= & {} -\frac{i}{4 F T^2} e^{2 \bar{\varLambda }_H/T} \int _0^{s_0} ds (2 \bar{\varLambda }_H -s) e^{-s/T} \frac{1}{y} \nonumber \\{} & {} \times \left[ f^\perp _T m^2_T \phi _\perp (u) + \frac{f_T m^3_T}{2y} \frac{\partial }{\partial u} g_v (u) \right] _{u = 1 - \frac{s}{2y}}. \end{aligned}$$

(B.9)

According to Eqs. (9), (12), the corresponding derivatives of form factors $V_1$, A w.r.t. $s_0$, T can be obtained via

$$\begin{aligned} V_1Ps_0= & {} \frac{2i}{m_H + m_T} \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \left[ L_1Ps_0\right. \nonumber \\{} & {} \left. + L_3Ps_0 \right] , \end{aligned}$$

(B.10)

$$\begin{aligned} APs_0= & {} i \frac{m_H + m_T}{m_H ( v \cdot P)} \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} L_3Ps_0, \end{aligned}$$

(B.11)

$$\begin{aligned} V_1PT= & {} \frac{2i}{m_H + m_T} \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \left[ L_1PT \right. \nonumber \\{} & {} \left. + L_3PT (v \cdot P) \right] , \end{aligned}$$

(B.12)

$$\begin{aligned} APT= & {} i \frac{m_H + m_T}{m_H ( v \cdot P)} \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} L_3PT, \end{aligned}$$

(B.13)

which are just the variation rates of $V_1$, A w.r.t. $s_0$, T. Adopting the central values for all input parameters, the variation rates of $V_1$, A w.r.t. $s_0$ and T as functions of $q^2$ for the $B \rightarrow \rho _2$ decays are shown in Figs. 13 and 14, respectively.

Fig. 13

The variation rates of $V_1$, A w.r.t. $s_0$ as functions of $q^2$ for the $B \rightarrow \rho _2$ decays, where the maximum value of $q^2$ has been chosen to be $6 \textrm{GeV}^2$ considering the reliability of LCSR

Fig. 14

The variation rates of $V_1$, A w.r.t. T as functions of $q^2$ for the $B \rightarrow \rho _2$ decays, where the maximum value of $q^2$ has been chosen to be $6 \textrm{GeV}^2$ considering the reliability of LCSR

It is easily seen that the magnitudes of variation rates of A w.r.t. $s_0$ and T at large $q^2$ region are significantly larger than the corresponding values of $V_1$. Therefore, the form factor A has obvious deviation with different $s_0$ and T at this region.