Strong decay of the heavy tensor mesons with QCD sum rules

Abstract

In the article, we calculate the hadronic coupling constants $G_{D_2^*D\pi }$, $G_{D_{s2}^*DK}$, $G_{B_2^*B\pi }$, $G_{B_{s2}^*BK}$ with the three-point QCD sum rules, then study the two-body strong decays $D_2^*(2460)\rightarrow D\pi$, $D_{s2}^*(2573)\rightarrow DK$, $B_2^*(5747)\rightarrow B\pi$, $B_{s2}^*(5840)\rightarrow BK$, and make predictions to be confronted with the experimental data in the future.

1 Introduction

The heavy-light mesons listed in the Review of Particle Physics can be classified into the spin doublets in the heavy quark limit, now the $\mathrm {1S}$ $(0^-,1^-)$ doublets $(B,B^*)$, $(D,D^*)$, $(B_s,B_s^*)$, $(D_s,D_s^*)$ and the $\mathrm {1P}$ $(1^+,2^+)$ doublets $(B_1(5721)$, $B^*_2(5747))$, $(D_1(2420)$, $D^*_2(2460))$, $(B_{s1}(5830)$, $B^*_{s2}(5840))$, $(D_{s1}(2536)$, $D^*_{s2}(2573))$ are complete [1]. The doublet components $(D_1(2420)$, $D^*_2(2460))$ are well established experimentally, while the quantum numbers of $D^*_{s2}(2573)$ are not as well established; the width and decay modes are consistent with the $J^P=2^+$ assignment [1]. In 2007, the D0 collaboration firstly observed the $B_1(5721)^0$ and $B_2(5747)^0$ [2], later the CDF collaboration confirmed them, and obtained the width $\Gamma (B_2^*)=\left( 22.7^{+3.8}_{-3.2} {}^{+3.2}_{-10.2}\right) \,\mathrm {MeV}$ [3]. Also in 2007, the CDF collaboration observed the $B_{s1}(5830)$ and $B_{s2}^*(5840)$ [4]. The D0 collaboration confirmed the $B_{s2}^*(5840)$ [5]. In 2012, the LHCb collaboration updated the masses $M_{B_{s1}}=(5828.40\pm 0.04\pm 0.04\pm 0.41)\,\mathrm { MeV}$ and $M_{B_{s2}^*}=(5839.99\pm 0.05\pm 0.11\pm 0.17)\,\mathrm {MeV}$, and one measured the width $\Gamma (B_{s2}^*)=(1.56\pm 0.13\pm 0.47)\,\mathrm {MeV}$ [6]. Recently, the CDF collaboration measured the masses and widths of the $B_1(5721)$, $B^*_2(5747)$, $B_{s1}(5830)$, and $B^*_{s2}(5840)$, and one observed a new excited state $B(5970)$ [7].

The $\mathrm {1P}$ $(1^+,2^+)$ doublets have drawn little attention compared to the $\mathrm {1S}$ $(0^-,1^-)$ and $\mathrm {1P}$ $(0^+,1^+)$ heavy-light mesons [8, 9]. We can study the masses, decay constants, and strong decays of the $\mathrm {1P}$ $(1^+,2^+)$ doublets based on the QCD sum rules to obtain fruitful information about their internal structures and examine the heavy quark symmetry. The P-wave, D-wave, and radial excited heavy-light mesons will be studied in detail in the future at the LHCb and KEK-B. Experimentally, the strong decays of the $\mathrm {1P}$ $(1^+,2^+)$ doublets take place through relative D-wave, the corresponding widths are proportional to $|\mathbf{p}|^{2L+1}$, with the angular momentum $L=2$ transferred in the decays. In these decays, the momentum $|\mathbf{p}|$ is small, the decays are kinematically suppressed. The strong decays $B_1(5721)^0\rightarrow B^{*+}\pi ^-$, $B_2(5747)^0 \rightarrow B^{*+}\pi ^-,\,B^{+}\pi ^-$ [2, 3], $B_{s1}(5830)^0 \rightarrow B^{*+}K^-$ [4–6], $B_{s2}^*(5840)^0 \rightarrow B^{+}K^-$ [4–6], $B_{s2}^*(5840)^0 \rightarrow B^{*+}K^-$ [6], $D_2^*(2460)^0\rightarrow D^{*+}\pi ^-,\, D^+\pi ^-$, $D_2^*(2460)^+\rightarrow D^0\pi ^+$, $D_1(2420)^0\rightarrow D^{*+}\pi ^-$, $D_1(2420)^+\rightarrow D^{*0}\pi ^+$ [1, 10–12], and $D_{s1}(2536)^+\rightarrow D^{*+}K^0,\,D^{*0}K^+$, $D_{s2}(2573)^+\rightarrow D^{0}K^+$ [1] have been observed.

The QCD sum rule (QCDSR) method is a powerful nonperturbative theoretical tool in studying the ground state hadrons, and it has given many successful descriptions of the masses, decay constants, hadronic form factors, hadronic coupling constants, etc. [13–17]. The hadronic coupling constants in the $D^*D \pi$, $D^* D_s K$, $D_s^* D K$, $B^*B \pi$, $B^{*}_{s}BK$, $DD\rho$, $D_{s}DK^*$, $B_{s}BK^*$, $D^{*}D \rho$, $D^{*}_{s}D K^{*}$, $B^{*}_{s}B K^{*}$, $D^* D^* \rho$, $B^{*}B^{*}\rho$, $B_{s0} B K$, $B_{s1}B^{*}K$, $D^{*}_{s}D K_1$, $B^{*}_{s}BK_1$, $J/\psi D D$, $J/\psi DD^*$, $J/\psi D^*D^*$, $B_c^*B_c\Upsilon$, $B_c^*B_c J/\psi$, $B_cB_c\Upsilon$, and $B_cB_c J/\psi$ vertices have been studied with the three-point QCDSR [18–34], while the hadronic coupling constants in the $D^* D \pi$, $D^*D_sK$, $D^*_sDK$, $B^* B \pi$, $DD\rho$, $DD_sK^*$, $D_sD_s\phi$, $BB\rho$, $D^{*}D\rho$, $D^*D_s K^*$, $D_s^*D_s \phi$, $B^*B\rho$, $D^*D^*\pi$, $D^*D_s^*K$, $B^*B^*\pi$, $D^* D^* \rho$, $D_0D\pi$, $B_0B\pi$, $D_0D_sK$, $D_{s0}DK$, $B_{s0}BK$, $D_1D^* \pi$, $B_1B^*\pi$, $D_{s1} D^* K$, $B_{s1} B^* K$, $B_1 B_0 \pi$, $B_2B_1\pi$, $B_2B^*\pi$, $B_1B^*\rho$, $B_1B\rho$, $B_2B^*\rho$, and $B_2B_1\rho$ vertices have been studied with the light-cone QCDSR [35–51]. The detailed knowledge of the hadronic coupling constants is of great importance in understanding the effects of heavy quarkonium absorptions in hadronic matter. Furthermore, the hadronic coupling constants play an important role in understanding final-state interactions in the heavy quarkonium (or meson) decays and in other phenomenological analyses. Some hadronic coupling constants, such as $G_{D_2^*D\pi }$, $G_{D_{s2}^*DK}$, $G_{B_2^*B\pi }$, and $G_{B_{s2}^*BK}$, can be directly extracted from the experimental data as the corresponding strong decays are kinematically allowed, we can confront the theoretical predications to the experimental data in the futures.

In Ref. [52, 53], Azizi et al. study the masses and decay constants of the tensor mesons $D_2^*(2460)$ and $D_{s2}^*(2573)$ with the QCDSR by only taking into account the perturbative terms and the mixed condensates in the operator product expansion. In Ref. [54], we calculate the contributions of the vacuum condensates up to dimension-6 in the operator product expansion and study the masses and decay constants of the heavy tensor mesons $D_2^*(2460)$, $D_{s2}^*(2573)$, $B_2^*(5747)$, and $B_{s2}^*(5840)$ with the QCDSR. The predicted masses of $D_2^*(2460)$, $D_{s2}^*(2573)$, $B_2^*(5747)$, and $B_{s2}^*(5840)$ are in excellent agreement with the experimental data, while the ratios of the decay constants obey $\frac{f_{D_{s2}^*}}{f_{D_{2}^*}}\approx \frac{f_{B_{s2}^*}}{f_{B_{2}^*}}\approx \frac{f_{D_{s}}}{f_{D}}\mid _\mathrm{exp}$, where exp denotes the experimental value [1]. In Ref. [55], Azizi et al. calculate the hadronic coupling constants $g_{D_2^*D\pi }$ and $g_{D_{s2}^*DK}$ with the three-point QCDSR by choosing the tensor structure $p_{\mu }p_{\nu }$, then study the strong decays $D_{2}^{*}(2460)^{0}\rightarrow D^+ \pi ^-$, and $D_{s2}^{*}(2573)^{+}\rightarrow D^{+} K^{0}$; the decay widths are too small to account for the experimental data, if the widths of the tensor mesons are saturated approximately by the two-body strong decays. In the article, we take the decay constants of the heavy tensor mesons as input parameters [54], analyze all the tensor structures to study the vertices $D_2^*D\pi$, $D_{s2}^*DK$, $B_2^*B\pi$, and $B_{s2}^*BK$ with the three-point QCDSR so as to choose the pertinent tensor structures (in this article, we choose the tensor structures $g_{\mu \nu }$ and $p^{\prime }_{\mu }p^{\prime }_{\nu }$, which differ from the tensor structure $p_{\mu }p_{\nu }$ chosen in Ref. [55]), then we obtain the corresponding hadronic coupling constants and study the two-body strong decays $D_2^*(2460)\rightarrow D\pi$, $D_{s2}^*(2573)\rightarrow DK$, $B_2^*(5747)\rightarrow B\pi$, $B_{s2}^*(5840)\rightarrow BK$. Finally we try to smear the large discrepancy between the theoretical calculations and the experimental data [55].

The article is arranged as follows: we derive the QCDSR for the hadronic coupling constants in the vertices $D_2^*D\pi$, $D_{s2}^*DK$, $B_2^*B\pi$, $B_{s2}^*BK$ in Sect. 2; in Sect. 3, we present the numerical results and calculate the two-body strong decays; and Sect. 4 is reserved for our conclusions.

2 QCD sum rules for the hadronic coupling constants

In the following, we write down the three-point correlation functions $\Pi _{\mu \nu }(p,p^\prime )$ in the QCDSR,

$$\begin{aligned} \Pi _{\mu \nu }(p,p^\prime )&= i^2\int d^4xd^4y e^{ip^\prime \cdot x}e^{i(p-p^\prime ) \cdot (y-z)} \nonumber \\&\quad \langle 0|T\left\{ J_{\mathbb {D}}(x)J_{\mathbb {P}}(y)J_{\mu \nu }^{\dagger }(z)\right\} |0\rangle \mid _{z=0}, \end{aligned}$$

(1)

(2)

where $Q=c,b$ and $q,q^\prime =u,d,s$, and the pseudoscalar currents $J_{ \mathbb {D}}(x)$ ($J_{ \mathbb {P}}(y)$) interpolate the heavy (light) pseudoscalar mesons $D$ and $B$ ($\pi$ and $K$), respectively. The tensor currents $J_{\mu \nu }(z)$ interpolate the heavy tensor mesons $D_2^*(2460)$, $D_{s2}^*(2573)$, $B_2^*(5747)$, and $B_{s2}^*(5840)$, respectively.

We can insert a complete set of intermediate hadronic states with the same quantum numbers as the current operators $J_{\mu \nu }(0)$, $J_{ \mathbb {D}}(x)$ and $J_{ \mathbb {P}}(y)$ into the correlation functions $\Pi _{\mu \nu }(p,p^\prime )$ to obtain the hadronic representation [13–15]. After isolating the ground state contributions from the heavy tensor mesons $\mathbb {T}$, heavy pseudoscalar mesons $\mathbb {D}$, and light pseudoscalar mesons $\mathbb {P}$, we get the following result:

$$\begin{aligned}&\Pi _{\mu \nu }(p,p^\prime )\nonumber \\&\quad =\frac{f_{\mathbb {T}}M_{\mathbb {T}}^2f_{\mathbb {D}}M_{\mathbb {D}}^2f_{\mathbb {P}}M_{\mathbb {P}}^2 \,\,G_{\mathbb {TDP}}(q^2)}{(m_Q+m_q)(m_{q}+m_{q^\prime })\left( M_{\mathbb {T}}^2-p^2\right) \left( M_{\mathbb {D}}^2-p^{\prime 2}\right) \left( M_{\mathbb {P}}^2-q^{2}\right) }\nonumber \\&\qquad \times \left\{ \frac{\lambda \left( M_\mathbb {T}^2,M_{\mathbb {D}}^2,q^2\right) }{12M_\mathbb {T}^2}g_{\mu \nu }\right. \nonumber \\&\qquad \left. +p^{\prime }_{\mu }p^{\prime }_{\nu }-\frac{M_\mathbb {T}^2+M_{\mathbb {D}}^2-q^2}{2M_\mathbb {T}^2}\left( p_{\mu }p^{\prime }_{\nu }+p^{\prime }_{\mu }p_{\nu } \right) \right. \nonumber \\&\qquad \left. +\left[ \frac{M_{\mathbb {D}}^2}{M_\mathbb {T}^2}+\frac{\lambda \left( M_\mathbb {T}^2,M_{\mathbb {D}}^2,q^2\right) }{6M_\mathbb {T}^4}\right] p_{\mu }p_{\nu }\right\} +\cdots , \nonumber \\&\quad =\Pi _1(p^2,p^{\prime 2})g_{\mu \nu }+\Pi _2(p^2,p^{\prime 2})p^{\prime }_{\mu }p^{\prime }_{\nu }\nonumber \\&\qquad +\Pi _3(p^2,p^{\prime 2})\left( p_{\mu }p^{\prime }_{\nu }+p^{\prime }_{\mu }p_{\nu } \right) +\Pi _4(p^2,p^{\prime 2})p_{\mu }p_{\nu }+\cdots , \nonumber \\ \end{aligned}$$

(3)

where $\lambda (a,b,c)=a^2+b^2+c^2-2ab-2bc-2ca$, the decay constants $f_{\mathbb {T}}$, $f_{\mathbb {D}}$, $f_{\mathbb {P}}$ and the hadronic coupling constants $G_{\mathbb {TDP}}$ are defined by

$$\begin{aligned}&\langle 0|J_{\mu \nu }(0)|\mathbb {T}(p)\rangle =f_{\mathbb {T}}M^2_{\mathbb {T}}\,\varepsilon _{\mu \nu }, \nonumber \\&\langle 0|J_{\mathbb {D}}(0)|\mathbb {D}(p^\prime )\rangle =\frac{f_{\mathbb {D}}M^2_{\mathbb {D}}}{m_Q+m_q} , \nonumber \\&\langle 0|J_{\mathbb {P}}(0)|\mathbb {P}(q)\rangle =\frac{f_{\mathbb {P}}M^2_{\mathbb {P}}}{m_q+m_{q^\prime }}, \end{aligned}$$

(4)

$$\begin{aligned}&\langle {\mathbb {D}}(p^\prime ){\mathbb {P}}(q)\mid \mathbb {T}(p)\rangle =G_{\mathbb {TDP}} \,\varepsilon _{\alpha \beta }(s,p)p^{\prime \alpha }q^\beta , \end{aligned}$$

(5)

the $\varepsilon _{\alpha \beta }$ are the polarization vectors of the tensor mesons with the following properties:

$$\begin{aligned} \sum _{s} \varepsilon ^*_{\mu \nu }(s,p)\varepsilon _{\alpha \beta }(s,p)&= \frac{\widetilde{g}_{\mu \alpha }\widetilde{g}_{\nu \beta }+\widetilde{g}_{\mu \beta }\widetilde{g}_{\nu \alpha }}{2} -\frac{\widetilde{g}_{\mu \nu }\widetilde{g}_{\alpha \beta }}{3}.\nonumber \\ \end{aligned}$$

(6)

In general, we expect that we can choose either component $\Pi _{i}(p^2,p^{\prime 2})$ (with $i=1,2,3,4$) of the correlations $\Pi _{\mu \nu }(p,p^\prime )$ to study the hadronic coupling constants $G_{\mathbb {TDP}}$. In calculations, we observe that the tensor structures $g_{\mu \nu }$ and $p_\mu ^{\prime }p_\nu ^{\prime }$ are the pertinent tensor structures. In Ref. [55], Azizi et al. take the tensor currents $\hat{J}_{\mu \nu }(z)=i\overline{Q}(z)\left( \gamma _\mu \mathop {D}\limits ^{\leftrightarrow }_\nu +\gamma _\nu \mathop {D}\limits ^{\leftrightarrow }_\mu \right) q(z)$, which couple both to the heavy tensor mesons and heavy scalar mesons; some contaminations are introduced.

Now, we briefly outline the operator product expansion for the correlation functions $\Pi _{\mu \nu }(p,p^\prime )$ in perturbative QCD. We contract the quark fields in the correlation functions $\Pi _{\mu \nu }(p,p^\prime )$ with the Wick theorem firstly,

$$\begin{aligned}&\Pi _{\mu \nu }(p,p^\prime )=\int d^4xd^4y e^{ip^\prime \cdot x}e^{i(p-p^\prime ) \cdot (y-z)} \mathrm{Tr}\nonumber \\&\quad \times \left\{ i\gamma _{5}S^q_{ij}(x-y)i\gamma _{5}S^{q^\prime }_{jk}(y-z)\Gamma _{\mu \nu } S^Q_{ki}(z-x) \right\} \mid _{z=0}, \nonumber \\ \end{aligned}$$

(7)

where

$$\begin{aligned} \Gamma _{\mu \nu }&= i\left( \gamma _\mu \mathop {\frac{\partial }{\partial z^\nu }}\limits ^{\leftrightarrow } +\gamma _\nu \mathop {\frac{\partial }{\partial z^\mu }}\limits ^{\leftrightarrow }-\frac{2}{3}\widetilde{g}_{\mu \nu } \gamma ^\tau \mathop {\frac{\partial }{\partial z^\tau }}\limits ^{\leftrightarrow }\right) , \end{aligned}$$

(8)

(9)

where $t^n=\frac{\lambda ^n}{2}$; the $\lambda ^n$ are the Gell-Mann matrices, and $i$, $j$, and $k$ are color indices [15]. We usually choose the full light quark propagators in the coordinate space. In the present case, the quark condensates and mixed condensates have no contributions, so we take a simple replacement $Q\rightarrow q/q^\prime$ to obtain the full $q/q^\prime$ quark propagators. In the leading-order approximation, the gluon field $G_\mu (z)$ in the covariant derivative has no contributions as $G_\mu (z)=\frac{1}{2}z^\lambda G_{\lambda \mu }(0)+\cdots =0$. Then we compute the integrals to obtain the QCD spectral density through a dispersion relation.

The leading-order contributions $\Pi _{\mu \nu }^{0}(p,p^{\prime })$ can be written as

(10)

where

(11)

We put all the quark lines on mass-shell using the Cutkosky rules, see Fig. 1, and obtain the leading-order spectral densities $\rho _{\mu \nu }$,

(12)

$$\begin{aligned}&= \frac{g_{\mu \nu }}{4\pi ^2\sqrt{\lambda (s,u,q^2)}}\left\{ m_Q^3(m_{q^\prime }-m_q)\right. \nonumber \\&\left. -q^2m_Q(m_Q+m_{q^\prime })+m_Q(sm_q-um_{q^\prime })\right. \nonumber \\&\left. + 6\left( u-s+q^2+2m_qm_Q-2m_{q^\prime }m_Q\right) d_2(0,0,m_Q)\right\} \nonumber \\&+\frac{3p^\prime _{\mu }p^\prime _{\nu }}{2\pi ^2\sqrt{\lambda (s,u,q^2)}}\left\{ u+q^2-m_Q^2+2m_Qm_q\right. \nonumber \\&+(s-2u-2q^2+m_Q^2-4m_qm_Q+2m_{q^\prime }m_Q)b_1(0,0,m_Q) \nonumber \\&\left. + \left( u-s+q^2+2m_qm_Q-2m_{q^\prime }m_Q\right) b_2(0,0,m_Q)\right\} +\cdots \nonumber \\ \end{aligned}$$

(13)

where we have used the following formulas:

$$\begin{aligned}&\int d^4k\, \delta ^3=\frac{\pi }{2\sqrt{\lambda (s,u,q^2)}}, \nonumber \\&\int d^4k\, \delta ^3 \,k_\mu =\frac{\pi }{2\sqrt{\lambda (s,u,q^2)}}\left[ a_1(m_A,m_B,m_Q)p_\mu \right. \nonumber \\&\qquad \left. +\,b_1(m_A,m_B,m_Q)p^\prime _\mu \right] , \nonumber \\&\int d^4k\, \delta ^3 \, k_{\mu } k_\nu =\frac{\pi }{2\sqrt{\lambda (s,u,q^2)}}\left[ a_2(m_A,m_B,m_Q)p_{\mu }p_\nu \right. \nonumber \\&\qquad \left. +b_2(m_A,m_B,m_Q)p^\prime _{\mu }p^\prime _{\nu } \right. \nonumber \\&\qquad \left. +c_2(m_A,m_B,m_Q)\left( p_{\mu }p^\prime _\nu +p^\prime _{\mu }p_\nu \right) \right. \nonumber \\&\qquad \left. +d_2(m_A,m_B,m_Q)g_{\mu \nu } \right] , \end{aligned}$$

(14)

$$\begin{aligned} \delta ^3&= \delta \left[ k^2-m_A^2 \right] \delta \left[ (k+p-p^\prime )^2-m_B^2 \right] \nonumber \\&\times \,\delta \left[ (k-p^\prime )^2-m_Q^2 \right] ,\nonumber \end{aligned}$$

$$\begin{aligned} b_1(m_A,m_B,m_Q)&= \frac{1}{\lambda (s,u,q^2)}\left[ m_Q^2(s-u+q^2)\right. \nonumber \\&\left. +\,u(u-s-2q^2)+q^2(q^2-s)\right. \nonumber \\&\left. -\,2sm_A^2+m_B^2(u+s-q^2)\right] , \nonumber \end{aligned}$$

$$\begin{aligned}&b_2(m_A,m_B,m_Q)=\frac{1}{\lambda (s,u,q^2)}\left[ (u-q^2-m_Q^2)^2\right. \nonumber \\&\quad \left. +\,2m_B^2(u-q^2-m_Q^2)-4sm_A^2\right] \nonumber \\&\quad +\,\frac{6s}{ \lambda ^2(s,u,q^2)} \left\{ q^2\left[ m_Q^4-(u+s-q^2)m_Q^2+su \right] \right. \nonumber \\&\quad \left. +\,m_A^2m_B^2(q^2-u-s)\right. \nonumber \\&\quad +\,m_A^2\left[ s(s-u-q^2)+m_Q^2(u-s-q^2)\right] \nonumber \\&\quad \left. +\,m_B^2\left[ u(u-s-q^2)+m_Q^2(s-u-q^2)\right] \right\} , \nonumber \\&d_2(m_A,m_B,m_Q)= \frac{1}{ 2\lambda (s,u,q^2) }\nonumber \\&\quad \times \, \left\{ q^2\left[ m_Q^4-(u+s-q^2)m_Q^2+su \right] \right. \nonumber \\&\quad \left. +\,m_A^2m_B^2(q^2-u-s)\right. \nonumber \\&\quad +\,m_A^2\left[ s(s-u-q^2)+m_Q^2(u-s-q^2)\right] \nonumber \\&\quad \left. +\,m_B^2\left[ u(u-s-q^2)+m_Q^2(s-u-q^2)\right] \right\} , \end{aligned}$$

(15)

here we have neglected the terms $m_A^4$ and $m_B^4$ as they are irrelevant in the present calculations. The gluon condensate contributions shown by the Feynman diagrams in Fig. 2 are calculated accordingly.

Fig. 1

The leading-order contributions, the dashed lines denote the Cutkosky cuts

Fig. 2

The gluon condensate contributions

We take quark–hadron duality below the continuum thresholds $s_0$ and $u_0$, respectively, and perform the double Borel transform with respect to the variables $P^2=-p^2$ and $P^{\prime 2}=-p^{\prime 2}$ to obtain the QCDSR,

$$\begin{aligned}&\Pi _1(M_1^2,M_2^2)=\frac{f_{\mathbb {T}}M_{\mathbb {T}}^2f_{\mathbb {D}}M_{\mathbb {D}}^2f_{\mathbb {P}}M_{\mathbb {P}}^2 \,\,G_{\mathbb {TDP}}(q^2)}{(m_Q+m_q)(m_{q}+m_{q^\prime })\left( M_{\mathbb {P}}^2-q^{2}\right) }\nonumber \\&\qquad \times \frac{\lambda \left( M_\mathbb {T}^2,M_{\mathbb {D}}^2,q^2\right) }{12M_\mathbb {T}^2}\exp \left( -\frac{M_\mathbb {T}^2}{M_1^2}-\frac{M_{\mathbb {D}}^2}{M_2^2}\right) \nonumber \\&\quad =\int ds du \exp \left( -\frac{s}{M_1^2}-\frac{u}{M_2^2}\right) \nonumber \\&\qquad \times \left\{ \frac{1}{4\pi ^2\sqrt{\lambda (s,u,q^2)}}\right. \nonumber \\&\qquad \times \left[ m_Q^3(m_{q^\prime }-m_q)-q^2m_Q(m_Q+m_{q^\prime })\right. \nonumber \\&\qquad \left. +m_Q(sm_q-um_{q^\prime })+ 6 \right. \nonumber \\&\qquad \times \left. \left( u-s+q^2+2m_qm_Q-2m_{q^\prime }m_Q\right) d_2(0,0,m_Q)\right] \nonumber \\&\qquad +\frac{1}{\sqrt{\lambda (s,u,q^2)}}\langle \frac{\alpha _sGG}{\pi }\rangle \nonumber \\&\qquad \times \left[ \frac{1}{9s}-\frac{s-u-3q^2}{12}\frac{\partial ^2}{\partial m_A^2\partial m_B^2}d_2(m_A,m_B,m_Q)\right. \nonumber \\&\qquad -\frac{s-3u-q^2}{12}\frac{\partial ^2}{\partial m_A^2\partial m_Q^2}d_2(m_A,0,m_Q)\nonumber \\&\qquad +\frac{s+u+q^2}{12}\frac{\partial ^2}{\partial m_B^2\partial m_Q^2}d_2(0,m_B,m_Q)\nonumber \\&\qquad \left. -\frac{1}{3}\frac{\partial }{\partial m_A^2}d_2(m_A,0,m_Q)-\frac{1}{2}\frac{\partial }{\partial m_B^2}d_2\right. \nonumber \\&\qquad \times \left. \left. (0,m_B,m_Q)-\frac{1}{2}\frac{\partial }{\partial m_Q^2}d_2(0,0,m_Q)\right] \right\} , \end{aligned}$$

(16)

$$\begin{aligned}&\Pi _2(M_1^2,M_2^2)=\frac{f_{\mathbb {T}}M_{\mathbb {T}}^2f_{\mathbb {D}}M_{\mathbb {D}}^2f_{\mathbb {P}}M_{\mathbb {P}}^2 \,\,G_{\mathbb {TDP}}(q^2)}{(m_Q+m_q)(m_{q}+m_{q^\prime })\left( M_{\mathbb {P}}^2-q^{2}\right) }\nonumber \\&\qquad \qquad \qquad \qquad \times \exp \left( -\frac{M_\mathbb {T}^2}{M_1^2}-\frac{M_{\mathbb {D}}^2}{M_2^2}\right) \nonumber \\&\quad =\int ds du \exp \left( -\frac{s}{M_1^2}-\frac{u}{M_2^2}\right) \nonumber \\&\qquad \times \left\{ \frac{3}{2\pi ^2\sqrt{\lambda (s,u,q^2)}}\left[ u+q^2-m_Q^2+2m_Qm_q\right. \right. \nonumber \\&\qquad +\left( s-2u-2q^2+m_Q^2-4m_qm_Q\right. \nonumber \\&\qquad \left. +2m_{q^\prime }m_Q\right) b_1(0,0,m_Q)\nonumber \\&\qquad \left. + \left( u-s+q^2+2m_qm_Q-2m_{q^\prime }m_Q\right) b_2(0,0,m_Q)\right] \nonumber \\&\qquad +\frac{1}{\sqrt{\lambda (s,u,q^2)}}\langle \frac{\alpha _sGG}{\pi }\rangle \nonumber \\&\qquad \times \left[ -\frac{s-u-3q^2}{12}\frac{\partial ^2}{\partial m_A^2\partial m_B^2}b_2(m_A,m_B,m_Q)\right. \nonumber \\&\qquad -\frac{s-3u-q^2}{12}\frac{\partial ^2}{\partial m_A^2\partial m_Q^2}b_2(m_A,0,m_Q)\nonumber \\&\qquad +\frac{s+u+q^2}{12}\frac{\partial ^2}{\partial m_B^2\partial m_Q^2}b_2(0,m_B,m_Q)\nonumber \\&\qquad -\frac{1}{3}\frac{\partial }{\partial m_A^2}b_2(m_A,0,m_Q)-\frac{1}{2}\frac{\partial }{\partial m_B^2}\nonumber \\&\qquad b_2(0,m_B,m_Q)-\frac{1}{2}\frac{\partial }{\partial m_Q^2}b_2(0,0,m_Q) \nonumber \\&\qquad +\frac{5}{6}\frac{\partial }{\partial m_A^2}b_1(m_A,0,m_Q)+\frac{11}{12}\frac{\partial }{\partial m_B^2}\nonumber \\&\qquad \times \left. \left. b_1(0,m_B,m_Q)+\frac{11}{12}\frac{\partial }{\partial m_Q^2}b_1(0,0,m_Q)\right] \right\} , \end{aligned}$$

(17)

where

$$\begin{aligned} \int dsdu\!=\!\int _{m_Q^2}^{s_0} ds \int _{m_Q^2}^{u_0}du \mid _{-1\le \frac{\left( u-q^2-m_Q^2\right) \left( s+u-q^2\right) -2s\left( u-m_Q^2\right) }{|u-q^2-m_Q^2|\sqrt{\lambda (u,s,q^2)}}\le 1},\nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned}&\frac{\partial ^2}{\partial m_i^2 \partial m_j^2 } f(m_A,m_B,m_Q)\doteq \frac{\partial ^2}{\partial m_i^2 \partial m_j^2 } \nonumber \\&\qquad \times f(m_A,m_B,m_Q)\mid _{m_A=0;m_B=0}, \frac{\partial }{\partial m_i^2} f(m_A,m_B,m_Q)\nonumber \\&\quad \doteq \frac{\partial }{\partial m_i^2} f(m_A,m_B,m_Q)\mid _{m_A=0;m_B=0}, \end{aligned}$$

(19)

and $f(m_A,m_B,m_Q)\!=\!b_1(m_A,m_B,m_Q)$, $b_2(m_A,m_B,m_Q)$, $d_2(m_A,m_B,m_Q)$, $\ldots$, $m_i^2,m_j^2=m_A^2$, $m_B^2$, $m_Q^2$.

3 Numerical results and discussions

The hadronic input parameters are taken as $M_{D^{*}_2(2460)^\pm }=(2464.3\pm 1.6)\,\mathrm {MeV}$, $M_{D^{*}_2(2460)^0}=(2461.8\pm 0.7)\,\mathrm {MeV}$, $M_{D^{*}_{s2}(2573)}=(2571.9\pm 0.8)\,\mathrm {MeV}$, $M_{B^{*}_2(5747)^0}=(5743\pm 5)\,\mathrm {MeV}$, $M_{B^{*}_{s2}(5840)^0}=(5839.96\pm 0.20)\,\mathrm {MeV}$, $M_{D^\pm }=(1869.5 \,\pm \, 0.4)\,\mathrm {MeV}$, $M_{D^0}=(1864.91 \,\pm \, 0.17)\,\mathrm {MeV}$, $M_{B^\pm }=(5279.25\pm 0.26)\,\mathrm {MeV}$, $M_{B^0}=(5279.55\pm 0.26)\,\mathrm {MeV}$, $M_{K^\pm }=(493.677\pm 0.013)\,\mathrm {MeV}$, $M_{K^0}=(497.614\pm 0.022)\,\mathrm {MeV}$, $M_{\pi ^\pm }\!=\!(139.57018\pm 0.00035)\,\mathrm {MeV}$, $M_{\pi ^0}=(134.9766\,\pm \, 0.0006)\,\mathrm {MeV}$, $f_\pi =130\,\mathrm {MeV}$, $f_K=156\,\mathrm {MeV}$ from the Particle Data Group [1]. The threshold parameters are taken as $s^0_{D^*_2}=(8.5\pm 0.5)\,\mathrm {GeV}^2$, $s^0_{D^*_{s2}}=(9.5\pm 0.5)\,\mathrm {GeV}^2$, $s^0_{B^*_2}=(39\pm 1)\,\mathrm {GeV}^2$, $s^0_{B^*_{s2}}=(41\pm 1)\,\mathrm {GeV}^2$, $u^0_{D}=(6.2\pm 0.5)\,\mathrm {GeV}^2$, $u^0_{B}=(33.5\pm 1.0)\,\mathrm {GeV}^2$ from the QCDSR [54, 56]. Then the energy gaps obey $\sqrt{s_0/u_0}-M_\mathrm{ground \, state}=$(0.4–0.6) GeV, and the contributions of the ground states are fully included.

The value of the gluon condensate $\langle \frac{\alpha _s GG}{\pi }\rangle$ is taken as the standard value $\langle \frac{\alpha _s GG}{\pi }\rangle =0.012 \,\mathrm {GeV}^4$ [17]. The masses of the $u$ and $d$ quarks are obtained through the Gell-Mann–Oakes–Renner relation, $f_{\pi }^2m_{\pi }^2=2(m_u+m_d)\langle \bar{q}q\rangle$, i.e. $m_u=m_d=6\,\mathrm {MeV}$ at the energy scale $\mu =1\,\mathrm {GeV}$.

In the article, we take the $\overline{MS}$ masses $m_{c}(m_c)=(1.275\pm 0.025)\,\mathrm {GeV}$, $m_{b}(m_b)=(4.18\pm 0.03)\,\mathrm {GeV}$ and $m_s(\mu =2\,\mathrm {GeV})=(0.095\pm 0.005)\,\mathrm {GeV}$ from the Particle Data Group [1], and we take into account the energy-scale dependence of the $\overline{MS}$ masses from the renormalization group equation,

$$\begin{aligned}&m_s(\mu )=m_s(\mathrm{2GeV} )\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(\mathrm{2GeV})}\right] ^{\frac{4}{9}},\nonumber \\&m_c(\mu )=m_c(m_c)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_c)}\right] ^{\frac{12}{25}},\nonumber \\&m_b(\mu )=m_b(m_b)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_b)}\right] ^{\frac{12}{23}},\nonumber \\&\alpha _s(\mu )=\frac{1}{b_0t}\nonumber \\&\quad \times \left[ 1-\frac{b_1}{b_0^2}\frac{\log t}{t} +\frac{b_1^2(\log ^2{t}-\log {t}-1)+b_0b_2}{b_0^4t^2}\right] , \end{aligned}$$

(20)

where $t=\log \frac{\mu ^2}{\Lambda ^2}$, $b_0=\frac{33-2n_f}{12\pi }$, $b_1=\frac{153-19n_f}{24\pi ^2}$, $b_2=\frac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi ^3}$, $\Lambda =213\,\mathrm {MeV}$, $296\,\mathrm {MeV}$ and $339\,\mathrm {MeV}$ for the flavors $n_f=5$, $4$, and $3$, respectively [1]. In Ref. [54], we study the masses and decay constants of the heavy tensor mesons using the QCDSR, and we obtain the values $M_{D_2^*}=(2.46\pm 0.09)\,\mathrm {GeV}$, $M_{D_{s2}^*}=(2.58\pm 0.09)\,\mathrm {GeV}$, $M_{B_2^*}=(5.73\pm 0.06)\,\mathrm {GeV}$, $M_{B_{s2}^*}=(5.84\pm 0.06)\,\mathrm {GeV}$, $f_{D_2^*}=(0.182\pm 0.020)\,\mathrm {GeV}$, $f_{D_{s2}^*}=(0.222\pm 0.021)\,\mathrm {GeV}$, $f_{B_2^*}=(0.110\pm 0.011)\,\mathrm {GeV}$, $f_{B_{s2}^*}=(0.134\pm 0.011)\,\mathrm {GeV}$. The predicted masses $M_{D_2^*}$, $M_{D_{s2}^*}$, $M_{B_2^*}$, and $M_{B_{s2}^*}$ are in excellent agreement with the experimental data.

In calculations, we take $n_f=4$ and $\mu =1(3)\,\mathrm {GeV}$ for the charmed (bottom) tensor mesons [54], and we evolve all the scale dependent quantities to the energy scales $\mu =1 \,\mathrm {GeV}$ and $\mu =3\,\mathrm {GeV}$, respectively, through the renormalization group equation. The same energy scales and truncations in the operator product expansion lead to the values $M_D=1.87\,\mathrm {GeV}$, $M_B=5.28\,\mathrm {GeV}$, $f_D=156\,\mathrm {MeV}$, and $f_{B}=168\,\mathrm {MeV}$. If we take into account the perturbative corrections, the experimental values $f_{D}=205\,\mathrm {MeV}$ and $f_{B}=190\,\mathrm {MeV}$ can be reproduced [1, 56, 57]. In this article, we take the values of the decay constants of the heavy-light mesons as $f_{D_2^*}=0.182\,\mathrm {GeV}$, $f_{D_{s2}^*}=0.222\,\mathrm {GeV}$, $f_{B_2^*}=0.110\,\mathrm {GeV}$, $f_{B_{s2}^*}=0.134\,\mathrm {GeV}$, $f_D=0.156\,\mathrm {GeV}$, and $f_{B}=0.168\,\mathrm {GeV}$, and we neglect the uncertainties so as to avoid doubling counting as the uncertainties originate mainly from the threshold parameters and heavy quark masses.

From the QCDSR in Eqs. (16) and (17), we can see that there are no contributions come from the quark condensates and mixed condensates, and no terms of the orders ${\mathcal {O}}\left( \frac{1}{M_1^2}\right)$, ${\mathcal {O}}\left( \frac{1}{M_2^2}\right)$, ${\mathcal {O}}\left( \frac{1}{M_1^4}\right)$, ${\mathcal {O}}\left( \frac{1}{M_2^4}\right)$, $\ldots$, which are needed to stabilize the QCDSR so as to warrant a platform. In this article, we take the local limit $M_1^2=M_2^2\rightarrow \infty$, and obtain the local QCDSR. The ground states, higher resonances, and continuum states have the same weight $\exp \left( -M_{\mathbb {T}}^2/M_1^2 -M_{\mathbb {D}}^2/M_2^2\right) =1$, we use the threshold parameters (or the cut-off) $s_0$ and $u_0$ to avoid the contaminations of the higher resonances and continuum states, while the threshold parameters $s_0$ and $u_0$ are determined by the conventional QCDSR [54]. At the QCD side, there are not terms of the orders ${{\mathcal {O}}\left( \frac{1}{M_1^2}\right) }$, ${\mathcal {O}}\left( \frac{1}{M_2^2}\right)$, ${\mathcal {O}}\left( \frac{1}{M_1^4}\right)$, ${\mathcal {O}}\left( \frac{1}{M_2^4}\right)$, which vanish in the limit $M_1^2=M_2^2\rightarrow \infty$, so the threshold parameters $s_0$ and $u_0$ survive in the local QCDSR.

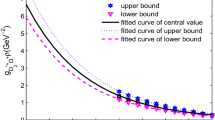
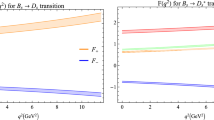
Now we obtain the hadronic coupling constants $G_{\mathbb {TDP}}(q^2=-Q^2)$ at the large space-like regions, for example, $Q^2\ge 3\,\mathrm {GeV}^2$, then fit the hadronic coupling constants $G_{\mathbb {TDP}}(Q^2)$ into the functions $A_i+B_{i}Q^2$, where $i=\mathrm {C,\,U,\,L}$, the C, U, and L denote the central values, upper bound and lower bound, respectively, the numerical values are shown in Table 1. If the heavy quark symmetry and chiral symmetry work well, the physical values of the hadronic coupling constants should have the relations

$$\begin{aligned} \frac{G_{D_{s2}^*DK}(Q^2=-M_{K}^2)}{G_{D_2^*D\pi }(Q^2=-M_{\pi }^2)}\approx \frac{G_{B_{s2}^*BK}(Q^2=-M_{K}^2)}{G_{B_2^*B\pi }(Q^2=-M_{\pi }^2)}&\approx 1.\nonumber \\ \end{aligned}$$

(21)

Table 1 The parameters of the hadronic coupling constants $G_{\mathbb {TDP}}(Q^2)$, where the $g_{\mu \nu }$ and $p^\prime _{\mu }p^\prime _{\nu }$ denote the tensor structures of the QCDSR, the units of the $G_{\mathbb {TDP}}(Q^2)$, $A_i$, $B_i$ and $Q^2$ are $\mathrm {GeV}^{-1}$, $\mathrm {GeV}^{-1}$, $\mathrm {GeV}^{-2}$ and $\mathrm {GeV}^{2}$, respectively

From Table 1, we can see that the ratios

$$\begin{aligned} \frac{G_{D_{s2}^*DK}(Q^2=-M_{K}^2)}{G_{D_2^*D\pi }(Q^2=-M_{\pi }^2)}\approx \frac{G_{B_{s2}^*BK}(Q^2=-M_{K}^2)}{G_{B_2^*B\pi }(Q^2=-M_{\pi }^2)}&\approx \frac{3}{4},\nonumber \\ \end{aligned}$$

(22)

which is smaller than the expectation 1. In calculations, we have used the $s$-quark mass $m_s=95\,\mathrm {MeV}$ at the energy scale $\mu =2\,\mathrm {GeV}$; if we take a larger value (the value of the $m_s$ varies in a rather large range [17]), say $m_s=130\,\mathrm {MeV}$, the relations in Eq. 21 can be satisfied. So in this article, we prefer the values $G_{D_2^*D\pi }(Q^2=-M_{\pi }^2)$ and $G_{B_2^*B\pi }(Q^2=-M_{\pi }^2)$ from the QCDSR as they suffer from much smaller uncertainties induced by the light quark masses, and we take the approximations $G_{D_{s2}^*DK}(Q^2=-M_{K}^2)=G_{D_2^*D\pi }(Q^2=-M_{\pi }^2)$ and $G_{B_{s2}^*BK}(Q^2=-M_{K}^2)=G_{B_2^*B\pi }(Q^2=-M_{\pi }^2)$ according to the heavy quark symmetry and chiral symmetry.

The perturbative QCD spectral densities associated with the tensor structure $g_{\mu \nu }$ have dimension (of mass) 2, while the perturbative QCD spectral densities associated with the tensor structure $p^\prime _{\mu }p^\prime _{\nu }$ have dimension 0, it is more reliable to take the perturbative QCD spectral densities associated with the tensor structure $g_{\mu \nu }$ as they can embody the energy dependence efficiently. The values of the hadronic coupling constants, which come from the QCDSR associated with the tensor $g_{\mu \nu }$, are much larger than that of the tensor $p^\prime _{\mu }p^\prime _{\nu }$. In this article, we prefer the values $G_{D_2^*D\pi }(Q^2=-M_{\pi }^2)=16.5^{+3.3}_{-3.5}\,\mathrm {GeV}^{-1}$, $G_{B_2^*B\pi }(Q^2=-M_{\pi }^2)=39.3^{+4.9}_{-5.2}\,\mathrm {GeV}^{-1}$ associated with the tensor $g_{\mu \nu }$, as they can also lead to much larger decay widths and are favorable in accounting for the experimental data.

We can take the hadronic coupling constants $G_{\mathbb {TDP}}(Q^2=-M^2_{\mathbb {P}})$ as basic input parameters and study the following strong decays:

$$\begin{aligned}&D_2^*(2460) \rightarrow D^+\pi ^-, \,D^0\pi ^0, \nonumber \\&D_{s2}^*(2573) \rightarrow D^0K^+, \,D^+K^0, \nonumber \\&B_2^*(5747) \rightarrow B^+\pi ^-, \, B^0\pi ^0, \nonumber \\&B_{s2}^*(5840) \rightarrow B^+K^-,\,B^0\bar{K}^0, \end{aligned}$$

(23)

which take place through a relative D-wave. The decay widths can be written as

$$\begin{aligned} \Gamma&= C_p\frac{G^2_{\mathbb {TDP}}|\mathbf{p}|^5}{60\pi M_{\mathbb {T}}^2}, \end{aligned}$$

(24)

where

$$\begin{aligned} |\mathbf{p}|&= \frac{\sqrt{\lambda \left( M_{\mathbb {T}}^2,M_{\mathbb {D}}^2, M_{\mathbb {P}}^2 \right) }}{2M_{\mathbb {T}}}, \end{aligned}$$

$C_p=1$ (or $\frac{1}{2}$) for the final states $\pi ^\pm$, $K$ (or $\pi ^0$). The numerical results are

$$\begin{aligned}&\Gamma (D_2^*(2460) \rightarrow D^+\pi ^-)=7.91^{+3.49}_{-3.00}\,\mathrm {MeV}, \nonumber \\&\Gamma (D_2^*(2460) \rightarrow D^0\pi ^0)=4.14^{+1.82}_{-1.57}\,\mathrm {MeV}, \nonumber \\&\Gamma (D_{s2}^*(2573) \rightarrow D^0K^+)=3.35^{+1.48}_{-1.27}\,\mathrm {MeV}, \nonumber \\&\Gamma (D_{s2}^*(2573) \rightarrow D^+K^0)=3.04^{+1.34}_{-1.15}\,\mathrm {MeV}, \nonumber \\&\Gamma (B_2^*(5747) \rightarrow B^+\pi ^-)=3.42^{+0.90}_{-0.85}\,\mathrm {MeV}, \nonumber \\&\Gamma (B_2^*(5747) \rightarrow B^0\pi ^0)=1.73^{+0.46}_{-0.43}\,\mathrm {MeV}, \nonumber \\&\Gamma (B_{s2}^*(5840) \rightarrow B^+K^-)=0.25^{+0.06}_{-0.06}\,\mathrm {MeV},\nonumber \\&\Gamma (B_{s2}^*(5840) \rightarrow B^0\bar{K}^0)=0.21^{+0.06}_{-0.05}\,\mathrm {MeV}. \end{aligned}$$

(25)

From the experimental data of the BaBar collaboration,

$$\begin{aligned}&\frac{\Gamma (D_2^*(2460) \rightarrow D^+\pi ^-)}{\Gamma (D_2^*(2460) \rightarrow D^+\pi ^-)+\Gamma (D_2^*(2460) \rightarrow D^{*+}\pi ^-)}\\&\quad =0.62\pm 0.03\pm 0.02\,[9]\, \end{aligned}$$

$$\begin{aligned} \frac{\Gamma (D_2^*(2460) \rightarrow D^+\pi ^-)}{\Gamma (D_2^*(2460) \rightarrow D^{*+}\pi ^-)}&= 1.47 \pm 0.03 \pm 0.16\,[10],\nonumber \\ \end{aligned}$$

(26)

we obtain the average,

$$\begin{aligned} \frac{\Gamma (D_2^*(2460) \rightarrow D^+\pi ^-)}{\Gamma (D_2^*(2460) \rightarrow D^{*+}\pi ^-)}&= 1.55, \end{aligned}$$

(27)

which is consistent with the PDG average $1.54\pm 0.15$ [1]. We assume

$$\begin{aligned}&\frac{\Gamma (D_2^*(2460) \rightarrow D^0\pi ^0)}{\Gamma (D_2^*(2460) \rightarrow D^{*0}\pi ^0)}\nonumber \\&\quad =\frac{\Gamma (D_2^*(2460) \rightarrow D^+\pi ^-)}{\Gamma (D_2^*(2460) \rightarrow D^{*+}\pi ^-)}=1.55, \end{aligned}$$

(28)

and we saturate the total decay width $\Gamma (D_2^*(2460))$ with the two-body strong decays $D_2^*(2460) \rightarrow D^+\pi ^-$, $D^{*+}\pi ^-$, $D^0\pi ^0$, $D^{*0}\pi ^0$, to obtain the theoretical value,

$$\begin{aligned} \Gamma (D_2^*(2460)^0 )&= (12{-}29)\,\mathrm {MeV}, \end{aligned}$$

(29)

which is much smaller than the experimental value,

$$\begin{aligned} \Gamma (D_2^*(2460)^0 )&= (49.0\pm 1.3)\,\mathrm {MeV} \quad \quad \mathrm{PDG's}\,\mathrm{average}\,[1]\,\nonumber \\&= (43.2 \pm 1.2 \pm 3.0)\, \mathrm{MeV}\quad \mathrm{from} \,\mathrm{the}\,\mathrm{final}\,\mathrm{state}\,\nonumber \\ D^{*+}\pi ^-\,[11],&= (45.6 \pm 0.4 \pm 1.1)\, \mathrm{MeV}\quad \mathrm{from} \,\mathrm{the} \,\mathrm{final} \, \mathrm{state}\nonumber \\&\quad D^{+}\pi ^-\,[11]. \end{aligned}$$

(30)

The strong decays $D_{s2}^*(2573) \rightarrow D^{*0}K^+, \,D^{*+}K^0$ are greatly suppressed in the phase space, while the strong decays $D_{s2}^*(2573) \rightarrow D_s^+\pi ^0,\,D_s^{*+}\pi ^0$ violate the isospin conservation and are also greatly suppressed. We saturate the total decay width $\Gamma (D_{s2}^*(2573) )$ with the two-body strong decays $D_{s2}^*(2573) \rightarrow D^0K^+$, $D^+K^0$, and we obtain the theoretical value,

$$\begin{aligned} \Gamma (D_{s2}^*(2573) )&= (4{-}9)\,\mathrm {MeV}, \end{aligned}$$

(31)

which is smaller than the experimental value,

$$\begin{aligned} \Gamma (D_{s2}^*(2573) )&= (17 \pm 4)\,\mathrm {MeV}\, [1]. \end{aligned}$$

(32)

At the bottom sector, we assume $\Gamma (B_2^*(5747)\rightarrow B^*\pi ) = \Gamma (B_2^*(5747)\rightarrow B\pi )$ according to the experimental value [1]

$$\begin{aligned} \frac{\Gamma (B_2^*(5747)\rightarrow B^*\pi )}{\Gamma (B_2^*(5747)\rightarrow B \pi )}&= 1.10\pm 0.42\pm 0.31, \end{aligned}$$

(33)

and neglect the kinematically suppressed decays $B_{s2}^*(5840)\rightarrow B^{*+}K^-,\,B^{*0}\bar{K}^0$ and the isospin violating decays $B_{s2}^* (5840)\rightarrow B_s^0\pi ^0,\,B_s^{*0}\pi ^0$, and we saturate the total decay widths $\Gamma (B_2^*(5747))$ and $\Gamma (B_{s2}^*(5840))$ with the two-body strong decays $B_2^*(5747)\rightarrow B^+\pi ^-, \, B^{*+}\pi ^-, \,B^0\pi ^0, \,B^{*0}\pi ^0$ and $B_{s2}^*(5840)\rightarrow B^+K^-,\,B^0\bar{K}^0$, respectively. Then we obtain the theoretical values,

$$\begin{aligned} \Gamma (B_2^*(5747)^0)&= (8{-}13)\,\mathrm {MeV},\nonumber \\ \Gamma (B_{s2}^*(5840))&= (0.4{-}0.6)\,\mathrm {MeV}, \end{aligned}$$

(34)

which are smaller than the experimental values,

$$\begin{aligned} \Gamma (B_2^*(5747)^0)&= (26 \pm 3 \pm 3)\,\mathrm {MeV} \, [7],\nonumber \\ \Gamma (B_{s2}^*(5840))&= (2.0 \pm 0.4 \pm 0.2)\, \mathrm {MeV}\, [7]. \end{aligned}$$

(35)

The perturbative $\mathcal {O}({\alpha _s})$ corrections increase the correlation function (or the product $f_Bf_{B^*}G_{B^*B\pi }$) by about $50\,\%$ in the light-cone QCD sum rules for the hadronic coupling constant $G_{B^*B\pi }$ [58]. In the present case, we can assume the perturbative $\mathcal {O}({\alpha _s})$ corrections also to increase the correlation functions (or the products $f_{\mathbb {T}}f_{\mathbb {D}}G_{\mathbb {TDP}}$) by about $50\,\%$. The perturbative $\mathcal {O}({\alpha _s})$ corrections to the decay constants $f_{\mathbb {T}}$ are negative [54], the net perturbative $\mathcal {O}({\alpha _s})$ corrections to the $f_{\mathbb {D}}G_{\mathbb {TDP}}$ are larger than $50\,\%$. If half of those perturbative $\mathcal {O}({\alpha _s})$ corrections are compensated by the perturbative $\mathcal {O}({\alpha _s})$ corrections to the decay constants $f_{\mathbb {D}}$, the hadronic coupling constants $G_{\mathbb {TDP}}$ are increased by about $30\,\%$; then taking into account the perturbative $\mathcal {O}({\alpha _s})$ corrections leads to the following replacements:

$$\begin{aligned}&G_{\mathbb {TDP}} \rightarrow 1.3G_{\mathbb {TDP}}, \nonumber \\&\Gamma (D_2^*(2460)^0 ) \rightarrow (20{-}49)\,\mathrm {MeV}, \nonumber \\&\Gamma (D_{s2}^*(2573) )\rightarrow (7{-}15)\,\mathrm {MeV},\nonumber \\&\Gamma (B_2^*(5747)^0)\rightarrow (14{-}22)\,\mathrm {MeV},\nonumber \\&Gamma(B_{s2}^*(5840)) \rightarrow (0.7{-}1.0)\,\mathrm {MeV}. \end{aligned}$$

(36)

Then the theoretical values $\Gamma (D_2^*(2460)^0 )$, $\Gamma (D_{s2}^*(2573))$, and $\Gamma (B_2^*(5747)^0)$ are compatible with the experimental data, while the theoretical value $\Gamma (B_{s2}^*(5840))$ is still smaller than the experimental value.

4 Conclusion

In the article, we choose the pertinent tensor structures to calculate the hadronic coupling constants $G_{D_2^*D\pi }$, $G_{D_{s2}^*DK}$, and $G_{B_2^*B\pi }$, $G_{B_{s2}^*BK}$ with the three-point QCDSR, then study the two-body strong decays $D_2^*(2460)\rightarrow D\pi$, $D_{s2}^*(2573)\rightarrow DK$, $B_2^*(5747)\rightarrow B\pi$, and $B_{s2}^*(5840)\rightarrow BK$. The predicted total widths are compatible with the experimental data, while the predicted partial widths can be confronted with the experimental data from the BESIII, LHCb, CDF, D0, and KEK-B collaborations in the future. We can also take the hadronic coupling constants as basic input parameters in many phenomenological analyses.