Core-envelope model of super dense star with distinct equation of states

Abstract

The aim of the present paper is to study an anisotropic spherically symmetric core-envelope model of a super dense star in which core is equipped with linear equation of state, consistent with the quark matter while the envelope is considered to be of quadratic equation of state by adopting the philosophy of Takisa et al. (Pramana J Phys 92:40, 2019). We demonstrate that all the physical parameters are realistic within the core as well as envelope of the stellar object and continuous at the junction. Our model is shown to be physically viable and substantiate with the strange stars SAX J1808.4-3658 and 4U1608-52. Further, We infer that if the mass of the star increases then central density results to higher values and core shrinks, which justifies the dominating effect of gravity for higher mass celestial objects.

1 Introduction

The composition of a super dense stellar material determines various macroscopic features including moment of inertia, degree of compactness, approximate values of mass and radius of a star. In order to construct a stellar model, an equation of state (EOS); a relation between pressure and energy-density of the stellar material is usually considered. However, it is believed that the interior configuration of a star has a deconfined quark core environed by an envelope consisting of baryonic matter [1]. Therefore, to use a single EOS may not be a suitable choice for realistic modelling of the whole star. The demand of more input parameters, viz, central density and density at the boundary suggests employing of two different EOS to construct a realistic stellar model.

A tentative insight of a quark phase in the interior of a compact star has been suggested by Witten [2] and Farhi and Jaffe [3] in independent works. Their works opened a new dimension of an entirely new class of compact stars known as strange stars. The matter compositions of these strange stars are in the form of a quark-gluon-plasma (QGP) state with a typical mass about $1-2M_{\odot }$ and radius about 10 km.

The precise form of stellar matter distribution is unknown if the matter density of a spherical stellar object is greater than the nuclear density [4,5,6]. The dubiety in the selection of a suitable type of EOS for stellar objects outside of the nuclear regime, core-envelope model or hybrid model may be a good choice in the modelling of these high dense stellar objects [7,8,9,10,11].

Empirically, in order to design the core envelope model, the Darmois-Isreali conditions should be satisfied at the junction of the core and the envelope. With this empirical aspect, many authors [1, 12,13,14,15,16,17,18,19,20,21,22] have developed stellar models, with an assumption of a core and an envelope, for highly dense relativistic objects. Eventually in most of the core-envelope solutions so far obtained have the continuity of only metric potentials and pressure at the junction of the core and the envelope. Negi et al. [23, 24] developed models considering the choices of core and envelope as Tolman IV and Tolman V solutions respectively for perfect fluid. In their solution, apart from the continuity of metric potentials, pressure, one more physical parameter, i.e., energy density was continuous at the junction. In recent past, many attempts have been made by various authors to find exact analytic solutions of the Einstein field system using linear EOS with MIT bag model [25,26,27,28,29,30,31] as well as quadratic EOS [32,33,34,35,36,37,38,39]. On the other hand, various authors [40,41,42,43,44,45] have also explored new solutions of the Einstein field equations for anisotropic fluid under the Karmarkar condition [46].

More recently, Takisa et al. [47] considered anisotropic fluid for core-envelope stellar model of PSR J1614-2230 with core layer having a quark matter distribution with linear EOS and envelope layer consisting of matter distribution with quadratic EOS. They successfully verified the continuity of some of the physical parameters, viz., energy density, pressures, anisotropy, radial sound speed and adiabatic index.

By motivation of the pioneer work of [47], we explore an anisotropic spherically symmetric core-envelope model of a super dense star in which core is equipped with linear EOS consistent with the quark matter while the envelope is considered to be of quadratic EOS with Tolman VII type metric potential $(g_{rr})$ such that $e^{\lambda }$ is 1 at origin thus geometrically non-singular. By virtue of this all physical parameters (density, pressures, red-shift, compactfication factor, anisotropic constants, causality condition, adiabatic index, energy conditions) are realistic within the core as well as the envelope of the stellar object and regular at the junction (interface). Our model is shown to be physically viable and substantiate with the strange stars SAX J1808.4-3658 and 4U1608-52 [48].

2 A system of the Einstein field equations

The inside of an anisotropic fluid sphere is described by the following spherically symmetric line element in Schwarzschild coordinates $(x^{i})= (t, r, \theta , \phi )$:

$$\begin{aligned} ds^2 = e^{\nu (r)}dt^2 - e^{\lambda (r)}dr^2 - r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2), \end{aligned}$$

(1)

where $\nu (r)$ and $\lambda (r)$ are known as the metric potentials.

Assuming the matter inside of the fluid sphere anisotropic, the Einstein field equations (for the units $G=c=1$ ) are given as

$$\begin{aligned} -8\pi T_{j}^{i} = {\mathcal {R}}^{i}_{j}-\frac{1}{2}{\mathcal {R}}g^{i}_{j}, \end{aligned}$$

(2)

where

$$\begin{aligned} T_{j}^{i} = [(p_t+\rho )v^{i}v_j-p_t g^{i}_{j}+(p_r-p_t)\chi ^i\chi _j], \end{aligned}$$

(3)

is the energy-momentum tensor, ${\mathcal {R}}^{i}_{j}$ is the Ricci tensor, ${\mathcal {R}}$ denotes the scalar curvature, $\rho$, $p_r$ and $p_t$ are the energy density, radial pressure appraised in the direction of the spacelike vector and transverse pressure in the orthogonal direction to $p_r$ respectively. In comoving coordinates $v^{i}=\sqrt{\frac{1}{g_{tt}}}\delta _{t}^{i}$ is the 4-velocity normalized in such a way that $g^i_{j}v^{i}v_j = 1$ and $\chi ^j= \sqrt{-\frac{1}{g_{rr}}}\delta _{r}^{i}$ is the unit spacelike vector in the radial direction, i.e., $g^{i}_{j}\chi ^i\chi _j=-1$.

For the geometry and matter accounted by the line element (1) and energy momentum tensor (3), the EFEs generate the following system of equations

$$\begin{aligned} 8\pi \rho= & {} \frac{(1 - e^{-\lambda })}{r^2} + \frac{{{\dot{\lambda }}}e^{-\lambda }}{r}, \end{aligned}$$

(4)

$$\begin{aligned} 8\pi p_r= & {} \frac{{{\dot{\nu }}} e^{-\lambda }}{r} - \frac{(1 - e^{-\lambda })}{r^2}, \end{aligned}$$

(5)

$$\begin{aligned} 8\pi p_t= & {} \frac{e^{-\lambda }}{4}\left( 2{\ddot{\nu }} + {{\dot{\nu }}}^2 - {{\dot{\nu }}}{{\dot{\lambda }}} + \frac{2{\dot{\nu }}}{r}-\frac{2{{\dot{\lambda }}}}{r}\right) , \end{aligned}$$

(6)

where $^{.}$ denotes the derivative with respect to the radial coordinate r.

Using Eqs. (5) and (6) we get the measure of anisotropy $(\varDelta )$ as

$$\begin{aligned} \varDelta= & {} 8\pi (p_t-p_r) \nonumber \\= & {} e^{-\lambda }\left[ {{\ddot{\nu }} \over 2}-{{{\dot{\lambda }}} {{\dot{\nu }}} \over 4}+{{{\dot{\nu }}}^2 \over 4}-{{{\dot{\nu }}}+{{\dot{\lambda }}} \over 2r}+{e^\lambda -1 \over r^2}\right] . \end{aligned}$$

(7)

The force due to the pressure anisotropy is repulsive if $p_t > p_r$, and attractive if $p_t < p_r$ [49]. The existence of outward force $p_t > p_r$, allows the building of more compact distribution when using anisotropic fluid than when using isotropic perfect fluid, $p_t=p_r$ [50].

In view of the following transformations $x=r^2$, $z(x)=e^{-\lambda (r)}$ and $y(x)=e^{\nu (r)}$, the system of equations (4-7) becomes

$$\begin{aligned} 8\pi \rho= & {} \frac{1-z}{x}-2{z'}, \end{aligned}$$

(8)

$$\begin{aligned} 8\pi p_r= & {} 2z\frac{y'}{y}-\frac{1-z}{x},\end{aligned}$$

(9)

$$\begin{aligned} 8\pi p_t= & {} z\Big [\Big (\frac{2{y''}}{y}-\frac{{y'}^2}{y^2}\Big )x+\frac{2 y'}{y}\Big ]+ {z'}\Big (1+x\frac{{y'}}{y}\Big ),\end{aligned}$$

(10)

$$\begin{aligned} 8\pi \varDelta= & {} z\left( \frac{2{y''}}{y}-\frac{{y'}^2}{y^2}\right) x+ {z'}\left( 1+x\frac{{y'}}{y}\right) +\frac{1-z}{x} . \end{aligned}$$

(11)

where $(')$ and $('')$ represent first and second derivatives with respect to x.

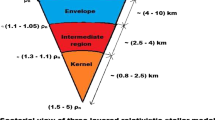
In relativistic stellar objects, the inside matter distribution may be compiled of two regions: an inner layer called as core and an outer layer named as envelope with distinct pressures. In order to make a core-envelope model for a given star, it is mandatory to classify space-time into a number of discrete regions. These regions comprise of the core ($0\le r \le R_C$, Region C), the envelope ($R_c\le r\le R_E$, Region E) and the exterior ($R_E > r$, Region B). The corresponding line elements for the three regions can be taken as

$$\begin{aligned} ds^2|_C= & {} e^{\nu _C(r)}dt^2 - e^{\lambda _C(r)}dr^2 - r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2), \nonumber \\\end{aligned}$$

(12)

$$\begin{aligned} ds^2|_{E}= & {} e^{\nu _E(r)}dt^2 - e^{\lambda _E(r)}dr^2 - r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2), \nonumber \\\end{aligned}$$

(13)

$$\begin{aligned} ds^2|_{B}= & {} \left( 1-\frac{2M}{r}\right) dt^2 - \left( 1-\frac{2M}{r}\right) ^{-1}dr^2 \nonumber \\&- r^2 (d\theta ^2 + \sin ^2{\theta }d\phi ^2). \end{aligned}$$

(14)

The exterior of a star for the Region B is the Schwarzschild exterior solution which is given in Eq. (14).

3 Conditions for a physically realistic core-envelope model

In order to make the model physically viable, one needs to verify the following conditions in core, envelope and exterior regions (conditions developed by [47] are further augmented):

• (i) Geometrical regularity: The metric potentials and matter variables should be defined at the center and should be well behaved throughout within the star [47].

• (ii) Density and pressures trends: The matter density $\rho$, radial pressure $p_r$ and transverse pressure $p_t$ the core and envelope of the star should be continuous at the junction, positive and monotonically decreasing outward. Further, the pressure-density ratios should be positive and less than 1 throughout within the star (Zeldovich’s condition [51]) and continuous at the junction.

• (iii) Mass-radius relation, Red-shift and Compactification factor: The mass function m(r), compactification parameter u(r) and gravitational red shift z(r) for the core and the envelope of the star should be continuous at the interface and increasing and decreasing respectively with the radial coordinate r.

• (iv) Anisotropic constant: The radial pressure should coincides with the tangential pressure at the core of the star and should be continuous at the interface besides being asymptotic and increasing outward.

• (v) Causal nature of radial sound speed: The radial sound speed of a compact star model should satisfy the causality condition at the center and should be monotonically decreasing outward besides being continuous at the interface.

• (vi) Adiabatic index: The adiabatic index should be continuous at the interface and should satisfy the Bondi condition.

• (vii) Energy conditions: The core and the envelope for the star should satisfy the energy conditions besides being continuous at the interface.

• (viii) TOV equation: The TOV condition should be satisfied within the star and all the three forces should be continuous at the interface resulting the system to be in static equilibrium.

• (ix) At the stellar boundary $p_r(R_{E}) = 0$ [47].

• (x) The metric potentials of the core region should match smoothly with the gravitational potentials of the envelope region [47].

• (xi) The gravitational potentials of the envelope layer should connected smoothly over the boundary with the Schwarzschild exterior metric [47].

Fig. 1

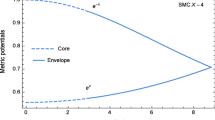
Variation of metric potentials with radial coordinate r for (i) SAX J1808.4-3658 (above) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393$ km; (ii) 4U1608-52 (below) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

Fig. 2

Variation of density with radial coordinate r for (i) SAX J1808.4-3658 (above) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U1608-52 (below) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

4 The core-envelope model

For core region ($0\le r\le R_C$), we choose Tolman VII type of $g_{11}$ for the gravitational potential $e^{\lambda }$ satisfying a linear EOS

$$\begin{aligned} z= & {} e^{-\lambda _C}=1-ax+bx^2, \end{aligned}$$

(15)

$$\begin{aligned} p_{r_C}= & {} \alpha \rho -\beta , \end{aligned}$$

(16)

where $a,~ b,~ \alpha$, and $\beta$ are constants. Substituting z value from Eq. (15) in Eq. (11) and using Eqs. 8, 9, 15 and 16 , we obtain the following differential equation:

$$\begin{aligned} \frac{y'(x)}{y(x)}=\frac{P_1+P_2 x}{2 \left( -a x+b x^2+1\right) }. \end{aligned}$$

(17)

On integrating Eq. (17), we get

$$\begin{aligned} y= & {} e^{\nu _{C}}\nonumber \\= & {} P_3 e^{\left( \frac{\frac{2 \left( a P_2+2 b P_1\right) \tan ^{-1}\left( \frac{2 b x-a}{\sqrt{4 b-a^2}}\right) }{\sqrt{4 b-a^2}}+P_2 \log \left( -a x+b x^2+1\right) }{4 b}\right) }, \end{aligned}$$

(18)

where $P_1=1(1+3\alpha )$, $P_2=-b(1+5\alpha )$ and $P_3$ is an integration constant. In view of Eqs. (15) and (18) and using $x=r^2$, the system of Eqs. (8)–(11) becomes

$$\begin{aligned} \rho _C= & {} \frac{3 a-5 b r^2}{8 \pi }, \end{aligned}$$

(19)

$$\begin{aligned} p_{r_C}= & {} \frac{-a+b r^2+P_2 r^2+P_1}{8 \pi },\end{aligned}$$

(20)

$$\begin{aligned} p_{t_C}= & {} -\frac{d_1+d_2}{d_3},\end{aligned}$$

(21)

$$\begin{aligned} \varDelta _C= & {} -\frac{ (d_4+d_5) r^2}{d_3}, \end{aligned}$$

(22)

where

$$\begin{aligned} d_1= & {} 4 (a-2 b r^2) (a r^2-b r^4-1)+P_1^2 r^2,\\ d_2= & {} P_2 r^2 (-6 a r^2+4 b r^4+P_2 r^4+8)\\&+P_1 (-2 a r^2+2 P_2 r^4+4),\\ d_3= & {} 32 \pi (a r^2-b r^4-1),\\ d_4= & {} 4 b (-a r^2+b r^4+1)+P_1^2 ,\\ d_5= & {} 2 P_1 (a-2 b r^2+P_2 r^2)+P_2 (-2 a r^2+P_2 r^4+4). \end{aligned}$$

The metric potentials $e^{-{\lambda _{C}}}, e^{\nu _E}$ and matter variables are continuous and well behaved in the core region.

Fig. 3

Variation of radial pressure with radial coordinate r for (i) SAX J1808.4-3658 (above) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U1608-52 (below) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

For envelope region ($R_C\le r\le R_E$), we choose the same Tolman VII type of $g_{11}$ satisfying a quadratic EOS

$$\begin{aligned} z= & {} e^{-\lambda _E}=1-ax+bx^2, \end{aligned}$$

(23)

$$\begin{aligned} p_{r_E}= & {} A \rho ^2+B \rho -C, \end{aligned}$$

(24)

Fig. 4

Variation of tangential pressure with radial coordinate r for (i) SAX J1808.4-3658 (above) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U1608-52 (below) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

Fig. 5

Variation of pressure and density ratios with radial coordinate r for (i) SAX J1808.4-3658 (above) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U1608-52 (below) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

where a,  b,  A,  B,  and C are constants. Putting z value from Eq. (23) in Eq. (11) and using Eqs. 8, 9, 23 and 24, we obtain the following differential equation:

$$\begin{aligned} \frac{y'(x)}{y(x)}=\frac{P_4+P_5 x+P_6x^2}{2 \left( -a x+b x^2+1\right) }, \end{aligned}$$

(25)

where $P_4=\frac{9 a^2 A}{8 \pi }+3 a B+a-8 \pi C$, $P_5=-\frac{15 (a A b)}{4 \pi }-5 b B-b$ and $P_6=\frac{25 A b^2}{8 \pi }$.

On integrating Eq. (25), we get

$$\begin{aligned} y= & {} e^{\nu _E}\nonumber \\= & {} P_7 \left( -a r^2+b r^4+1\right) ^{a P_6+b P_5} e^{\frac{2 b P_6 r^2-d_6}{4 b^2}}, \end{aligned}$$

(26)

where $P_7$ is an integration constant. In view of Eqs. (23) and (26) and taking $x=r^2$, the system of Eqs. (8)–(11) becomes,

$$\begin{aligned} \rho _E= & {} \frac{3 a-5 b r^2}{8 \pi }, \end{aligned}$$

(27)

$$\begin{aligned} p_{r_E}= & {} \frac{-a+b r^2+P_6 r^4+P_5 r^2+P_4}{8 \pi },\end{aligned}$$

(28)

$$\begin{aligned} p_{t_E}= & {} -\frac{d_7+d_8+d_9}{d_{3}}, \end{aligned}$$

(29)

$$\begin{aligned} \varDelta _E= & {} p_{t_E}-p_{r_E}, \end{aligned}$$

(30)

where

$$\begin{aligned} d_6= & {} \frac{2 (P_6 \left( a^2-2 b)+a b P_5+2 b^2 P_4\right) \tan ^{-1}\left( \frac{a-2 b r^2}{\sqrt{4 b-a^2}}\right) }{\sqrt{4 b-a^2}},\\ d_7= & {} 4 (a-2 b r^2) (a r^2-b r^4-1)+P_4^2 r^2,\\ d_8= & {} 2 P_6 r^4 (-5 a r^2+4 b r^4+P_5 r^4+6)\\&+P_5 r^2 (-6 a r^2+4 b r^4+P_5 r^4+8),\\ d_9= & {} 2 P_4 (-a r^2+P_6 r^6+P_5 r^4+2)+P_6^2 r^{10}. \end{aligned}$$

5 Matching conditions (interface at the core-envelope and boundary)

Gravitational potential and radial pressure must be continuous at the interface and at the boundary (Darmois-Isreali conditions). Therefore, we arrive with the following two set of conditions:

Fig. 6

Variation of mass with radial coordinate r for (i) SAX J1808.4-3658 (above) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U1608-52 (below) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

Fig. 7

Variation of red-shift with radial coordinate r for (i) SAX J1808.4-3658 (above) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U1608-52 (below) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

Fig. 8

Variation of compactification factor with radial coordinate r for (i) SAX J1808.4-3658 (above) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U1608-52 (below) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

5.1 Continuity of interface metrics

$$\begin{aligned} e^{\lambda _C}(R_C)= & {} e^{\lambda _{E}}(R_C), \end{aligned}$$

(31)

$$\begin{aligned} e^{\nu _C}(R_C)= & {} e^{\nu _{E}}(R_C),\end{aligned}$$

(32)

$$\begin{aligned} p_{r_C}(R_C)= & {} p_{r_{E}}(R_{C}). \end{aligned}$$

(33)

5.2 Continuity at the boundary

The envelope metric (13) must be connected smoothly over the boundary with the Schwarzschild exterior solution (14) at $r=R_{E}$ i.e.,

$$\begin{aligned} e^{\lambda _{E}}(R_{E})= & {} \Big (1-{2M\over R_{E}}\Big )^{-1}, \end{aligned}$$

(34)

$$\begin{aligned} e^{\nu _{E}}(R_{E})= & {} \Big (1-{2M\over R_{E}}\Big ), \end{aligned}$$

(35)

$$\begin{aligned} p_{r_{E}}(R_{E})= & {} 0, \end{aligned}$$

(36)

where $R_E$ is the radius of the star.

The six matching conditions (31)–(36) along with the twelve constants, namely $a, ~b,~ P_7,~ P_3,~ A,~ B,~ C,~ R_C,~ R_E, M, ~\alpha , ~\beta$ form an undetermined system of equations. Solving the above system of equations, the mass M and radius $R_E$ of the star are obtained as

$$\begin{aligned} M= & {} \frac{1}{2} R_E^2 (a-b R_E^2), \end{aligned}$$

(37)

$$\begin{aligned} R_E= & {} \frac{\sqrt{\frac{3 a A b+4 \pi \left( \sqrt{b^2 \left( 4 A C+B^2\right) }+b B\right) }{A b^2}}}{\sqrt{5}}, \end{aligned}$$

(38)

and the remaining constants $P_7,~ P_3,~ C,~ \beta$ are of the form

$$\begin{aligned} P_7= & {} \frac{\sigma _2 e^{\frac{\sigma _1-b P_6 R_E^2}{2 b^2}}}{R_E}, \end{aligned}$$

(39)

$$\begin{aligned} P_3= & {} \frac{\sigma _5 e^{\frac{\sigma _1-\sigma _3+\sigma _4}{2 b^2}} (-a R_E^2+b R_E^4+1){}^{-\frac{a P_6+b P_5}{4 b^2}}}{R_E},\end{aligned}$$

(40)

$$\begin{aligned} C= & {} \frac{(3 a-5 b R_E^2) (3 a A-5 A b R_E^2+8 \pi B)}{64 \pi ^2},\end{aligned}$$

(41)

$$\begin{aligned} \beta= & {} \frac{(3 a-5 b R_C^2) (8 \pi \alpha +5 A b (R_C^2-R_E^2))}{64 \pi ^2}+\sigma _6, \end{aligned}$$

(42)

where

$$\begin{aligned} \sigma _1= & {} \frac{(P_6 (a^2-2 b)+a b P_5+2 b^2 P_4) \tan ^{-1}\left( \frac{a-2 b R_E^2}{\sqrt{4 b-a^2}}\right) }{\sqrt{4 b-a^2}},\\ \sigma _2= & {} (R_E-2 M) (-a R_E^2+b R_E^4+1){}^{-\frac{a P_6+b P_5}{4 b^2}},\\ \sigma _3= & {} \frac{ (P_6 (a^2-2 b)+a b P_5+2 b^2 P_4) \tan ^{-1}\left( \frac{a-2 b R_C^2}{\sqrt{4 b-a^2}}\right) }{\sqrt{4 b-a^2}},\\ \sigma _4= & {} \frac{b (a P_2+2 b P_1) \tan ^{-1}\left( \frac{a-2 b R_C^2}{\sqrt{4 b-a^2}}\right) }{\sqrt{4 b-a^2}}+ b P_6 R_C^2-b P_6 R_E^2,\\ \sigma _5= & {} (R_E-2 M) (-a R_C^2+b R_C^4+1){}^{\frac{a P_6+b P_5-b P_2}{4 b^2}},\\ \sigma _6= & {} \frac{5 b C (R_C^2-R_E^2)}{3 a-5 b R_E^2}. \end{aligned}$$

The remaining seven constants $a,~b, ~c, ~\alpha ,~ A, ~B$ and $R_I$ are free parameters. These constants are selected in such a way that all the physical properties of the considered stellar objects are well-behaved.

6 Discussion and conclusion of physical features for core-envelope model

6.1 Geometrical regularity

The values of metric potentials for the stars SAX J1808.4-3658 and 4U1608-52 at the center (r=0) are specified as $e^{\nu }$=positive constant and $e^{\lambda }=1$. This shows that the metric potentials are regular and free from geometric singularities at the center of the star. Further, both metric potentials $e^{\nu }$ and $e^{-\lambda }$ are continuous at the interface and monotonically increasing and decreasing respectively with the radial coordinate r as well (Fig. 1).

6.2 Viable trends of physical parameters

6.2.1 Density and pressures trends

The matter density $\rho$, radial pressure $p_r$ and transverse pressure $p_t$ for the core and envelope of stars are continuous at the interface, positive and monotonically decreasing outward [53] (Figs. 2, 3 and 4). Further, the stars satisfy Zeldovich’s condition [51] i.e. the pressure-density ratios are positive and less than 1 throughout within the stars and continuous at the junction (Fig. 5).

Fig. 9

Variation of anisotropy with radial coordinate r for (i) SAX J1808.4-3658 (above) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U1608-52 (below) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

Fig. 10

Variation of radial velocity with radial coordinate r for (i) SAX J1808.4-3658 (left) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U160852 (right) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

Fig. 11

Variation of adiabatic index with radial coordinate r for (i) SAX J1808.4-3658 (above) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U160852 (below) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

Fig. 12

Variation of energy conditions with radial coordinate r for (i) SAX J1808.4-3658 (above) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U1608-52 (below) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

Fig. 13

Variation of balancing forces with radial coordinate r for (i) SAX J1808.4-3658 (above) with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U1608-52 (below) with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km

6.2.2 Mass-radius relation, red-shift and compactification factor

The mass function m(r) and gravitational red-shift z(r) for the core and envelope of stars SAX J1808.4-3658 and 4U1608-52 are continuous at the interface and increasing and decreasing respectively with radial coordinate r (Figs. 6, 7). Also, compactification parameter u(r) for the above stars is continuous at the interface and increasing in nature with r (Fig. 8) and lies within the Buchdahl limit [52].

6.2.3 Anisotropic constant

In Fig. 9, the radial pressure coincides with the tangential pressure at the core of stars and continuous at the interface and increasing outward [53].

6.2.4 Causal nature of radial sound speed

The radial sound speed of a compact star model satisfies the causality condition at the center and monotonically decreasing outward with the continuity at the interface. The profile of $v^2_r$ of both core and envelope of the stars are given in Fig. 10.

6.2.5 Adiabatic index

For a relativistic anisotropic sphere the stability counts on the adiabatic index $\varGamma _r$, the ratio of two specific heats, defined by [54],

$$\begin{aligned} \varGamma _r = \frac{\rho + p_r}{p_r} \frac{\partial p_r}{\partial \rho }. \end{aligned}$$

Bondi [55] suggested that for a stable Newtonian sphere, the $\varGamma$ value should be greater than $\frac{4}{3}$. The profiles of adiabatic indexes of the core and envelope of both stars are plotted in Fig. 11, which shows the adiabatic indexes are continuous at the interface and satisfy the Bondi condition [55].

6.2.6 Energy conditions

For a physically stable configuration, the core and envelope of the stars should satisfy the following inequalities simultaneously (which are known as energy conditions [29]): (i) null energy condition $\rho + p_r \ge 0$ (NEC) (ii) weak energy conditions $\rho + p_r \ge 0$, $\rho \ge 0$ ($\hbox {WEC}_r$) and $\rho + p_t \ge 0$, $\rho \ge 0$ ($\hbox {WEC}_t$) and (iii) strong energy condition $\rho +p_r+2p_t \ge 0$ (SEC). From Fig. 12, it is clearly visible that the variation of energy conditions with r of the core and the envelope of both the stars are continuous at the interface and satisfying realistic conditions.

6.3 TOV equation of core-envelope model

Equilibrium state under three forces, i.e., the resulting forces; gravitational ($F_g$), hydrostatic ($F_h$) and anisotropic ($F_a$) should be zero throughout within the star and continuous at the interface. The TOV equation [56] is given as

$$\begin{aligned} -{M_g(r)(\rho +p_r) \over r^2}~e^{(\lambda -\nu )/2}-{dp_r \over dr}+{2\varDelta (r) \over r}=0, \end{aligned}$$

(43)

where $M_g(r)$ is the gravitational mass within radius r and can be calculated as

$$\begin{aligned} M_g(r)= & {} {1\over 2}~r^2 \nu ' e^{(\nu -\lambda )/2}, \end{aligned}$$

(44)

from the Tolman–Whittaker formula and EFEs.

Equation (43) is equivalent to the following balanced force equation

$$\begin{aligned} F_g+F_h+F_a=0, \end{aligned}$$

(45)

where $F_g$, $F_h$ and $F_a$ respectively are components of Eq. (43) above.

From Fig. 13, we can visualize that the TOV condition is satisfied within the stars and all the three forces are continuous at the interface, thereby, concluding that the system is in static equilibrium.

Table 1 Values of constants that generate masses, core and envelope radii ($R_C$, $R_E$) for two strange stars

Table 2 The variation of physical parameters, i.e., adiabatic index, density, red-shift for (i) Model I with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) model II with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km; and $G=6.67 \times 10^{-11} \mathrm{m}^3\,\mathrm{kg}^{-1}\,\mathrm{s}^{-2}$, $M_{\odot }= 2\times 10^{30} \mathrm{kg}$ and $C=3\times 10^8\,\mathrm{ms}^{-1}$

7 Conclusion

In this paper, we have explored an anisotropic spherically symmetric core-envelope model of stars SAX J1808.4-3658 and 4U1608-52 in which core and envelope are considered with the linear and quadratic equation of states respectively. Our core-envelope model is physically viable and substantiate with the substantially strange stars (i) SAX J1808.4-3658 with mass $M=0.7 M_{\odot }$ and radius $R_E=6.2$ km for the values of $b = 0.000035/\mathrm{km}^2$, $B=0.00025/\mathrm{km}^2$, $A=90/\mathrm{km}^2$, $\alpha =0.1409/\mathrm{km}^2$, $R_C=3.393\,\mathrm{km}$; (ii) 4U160852 with mass $M=1.85 M_{\odot }$ and radius $R_E=8.2$ km for the values of $b = 0.00003/\mathrm{km}^2$, $B=0.00005/\mathrm{km}^2$, $A=155/\mathrm{km}^2$, $\alpha =0.312/\mathrm{km}^2$, $R_C=2.459$ km.

In [47], some of the physical properties like anisotropy is not increasing throughout the region of stars and the radial pressure and anisotropy both are not differentiable at the interface due to a sharp jerk at the junction region. However, in this paper we have verified that all the physical and geometrical parameters, including anisotropic, radial pressure, compactfication factor, energy conditions,and stability conditions using TOV equation balancing forces are with the viable trend and continuous with the smooth variations throughout inside the stars. Further, from Tables 1 and 2, we infer that if the mass of the star increases then central density results to higher values and core shrinks, which justifies the dominating effect of gravity for higher mass celestial objects.