Relativistic core-envelope anisotropic fluid model of super dense stars

Abstract

The objective of the present paper is to explore and study an anisotropic spherically symmetric core-envelope model of a super dense star in which core is outfitted with linear equation of state whereas the envelope is considered to be of quadratic equation of state. There is smooth matching between the three regions: the core, envelope and the Schwarzschild exterior metric. We investigate that all the physical and geometrical variables are realistic within the core as well as the envelope of the stellar object and continuous at the junction. Our model is shown to be physically plausible and validate with the intrinsic properties of the neutron star in Vela X-1, SMC X-4 and Her X-1. Further, We infer that with the increase of mass of star the core shrinks, which vindicates the dominating effect of gravity for higher mass astronomical objects.

1 Introduction

Neutron stars or strange stars are relativistic compact entities that are remnants of massive stars at the end of their death when the parent star has the mass of range of $8M_{{\odot }}-20M_{\odot }$. The complex composition of their core is unknown, however, it is supposed that they may comprise of a neutron super fluid or quark state of matter. The properties and characteristics of these giant gravity objects are yet to be solved completely . However, the Einstein field equations (EFEs) of General Relativity provide a powerful tool to infer these extremely dense objects . Therefore, since the inception of the EFEs, the relativists have been venturing to develop the stellar models which are close to the realistic in nature. Due to the strong nonlinearity of EFEs and the lack of appropriate algorithm to generate all solutions, it becomes difficult to obtain new exact solutions. A well number of exact solutions of field equations are known to date but not all of them are physically relevant in the description of relativistic structure of compact stellar objects. Two conventional approaches are followed to obtain for perfect fluid stellar model.

• (i) Oppenheimer–Volkoff method: In this approach one can start with an explicit equation of state and the integration starts at the center of the star with a prescribed central pressure. The integrations are processed until the pressure decreases to zero, justifying that boundary has reached. Such input equations of state do not normally allow for closed form solutions [1].

• (ii) Tolman’s method: In this approach one has to solve Einstein’s gravitational field equations. It is almost impossible to obtain an exact solution of such an under-determined system of nonlinear ordinary differential equations of second order. In order to explore exact solutions, one can solve the field equations by making an adhoc assumption for one of the metric functions or for the energy density. Hence the equation of state and other physical parameters can be computed from the resulting metric [2,3,4,5].

Although, the perfect fluid models are toy models of star, nevertheless, these models act as a seed models for the realistic stellar modeling by inclusion of anisotropy , charge or both. For a realistic model of stellar object, the perfect fluid is replaced by anisotropic fluid. An anisotropy is caused due to various reasons e.g. the existence of solid core, in presence of type P super-fluid, phase transition, rotation, magnetic field, mixture of two fluid and ultra high density of the order of ${10^{15} \hbox {gcm}^{-3}}$ which are the essential inherent physical properties of super-dense stars [6,7,8,9]. Various conventional approaches are followed to obtain for anisotropic fluid stellar model:

• (i) In order to solve the EFEs, one can assume suitable function of one of the metric potential and appropriate function of anisotropy so that the resulting solution may get realistic trend of physical and geometrical parameters [10,11,12,13].

• (ii) We can assume the one of the equations of state (linear, quadratic, polytropic or Vander Waals equation of state) with one of the metric potential and solve the EFEs and subsequently study the trends of physical and geometrical parameters [14,15,16,17,18,19,20,21,22,23,24,25,26,27].

• (iii) One can use class 1 condition for solving the field equations which basically tells us that 4-dimensional space-time can be embedded in 5-dimensional pseudo-Euclidean space. By following the Karmarker condition for using the class 1 metric and the relationship between metric potentials can be achieved [28,29,30,31,32].

• (iv) To develop a core-envelope model: The core is of Linear equation of state because it is of quark matter therefore, governed by MIT beg model i.e. linear equation of state. Further, the envelope is of quadratic equation of state because of the presence of baryonic matter. In the recent past several core envelope models for massive relativistic stars in general relativity have been studied [33,34,35,36,37,38].

In this paper, we assume a new function of metric potential $g_{rr}$ and explore a new exact solution of the EFEs and subsequently, develop a core-envelope model for super-dense stars by smoothly matching two interior regions and each satisfying a distinct equation of state. The exterior region is defined by the well known Schwarzschild exterior metric. We discuss the Einstein field equations in Sect. 2 for anisotropic fluid. In Sect. 3, we discuss the conditions for physically realistic core-envelope model. In Sect. 4, we explore the exact solutions of the core and envelop. In Sect. 5, we present junction conditions between two regions. A detailed physical analysis is carried out in Sect. 6. We also investigate some of the physical features of the model in connection with the neutron star in Vela X-1, SMC X-4 and Her X-1 in Sect. 7.

2 A system of the Einstein field equations

The interior of an anisotropic fluid sphere is described by the following spherically symmetric line element in Schwarzschild coordinates $(x^{i})= (t, r, \theta , \phi )$:

$$\begin{aligned} ds^2 = e^{\nu (r)}dt^2 - e^{\lambda (r)}dr^2 - r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2), \end{aligned}$$

(1)

where $\nu (r)$ and $\lambda (r)$ are known as the metric potentials.

Assuming the matter inside the fluid sphere is anisotropic, the EFEs (for the units $G=c=1$ ) are given as

$$\begin{aligned} -8\pi T_{j}^{i} = {\mathcal {R}}^{i}_{j}-\frac{1}{2}{\mathcal {R}}g^{i}_{j}, \end{aligned}$$

(2)

where

$$\begin{aligned} T_{j}^{i} = [(p_t+\rho )v^{i}v_j-p_t g^{i}_{j}+(p_r-p_t)\chi ^i\chi _j], \end{aligned}$$

(3)

is the energy-momentum tensor, ${\mathcal {R}}^{i}_{j}$ is the Ricci tensor, ${\mathcal {R}}$ denotes the scalar curvature, $\rho$, $p_r$ and $p_t$ are the energy density, radial pressure appraised in the direction of the spacelike vector and transverse pressure in the orthogonal direction to $p_r$ respectively. In comoving coordinates $v^{i}=\sqrt{\frac{1}{g_{tt}}}\delta _{t}^{i}$ is the 4-velocity normalized in such a way that $g^i_{j}v^{i}v_j = 1$ and $\chi ^j= \sqrt{-\frac{1}{g_{rr}}}\delta _{r}^{i}$ is the unit spacelike vector in the radial direction, i.e., $g^{i}_{j}\chi ^i\chi _j=-1$.

For the geometry and matter accounted by the line element (1) and energy momentum tensor (3), the EFEs generate the following system of equations

$$\begin{aligned} 8\pi \rho= & {} \frac{\left( 1 - e^{-\lambda }\right) }{r^2} + \frac{{{\dot{\lambda }}}e^{-\lambda }}{r}, \end{aligned}$$

(4)

$$\begin{aligned} 8\pi p_r= & {} \frac{{{\dot{\nu }}} e^{-\lambda }}{r} - \frac{\left( 1 - e^{-\lambda }\right) }{r^2}, \end{aligned}$$

(5)

$$\begin{aligned} 8\pi p_t= & {} \frac{e^{-\lambda }}{4}\left( 2{\ddot{\nu }} + {\dot{\nu }}^2 - {{\dot{\nu }}}{{\dot{\lambda }}} + \frac{2\dot{\nu }}{r}-\frac{2{{\dot{\lambda }}}}{r}\right) , \end{aligned}$$

(6)

where $^{.}$ denotes the derivative with respect to the radial coordinate r.

Using Eqs. (5) and (6) we get the measure of anisotropy $(\varDelta )$ as

$$\begin{aligned} \varDelta= & {} 8\pi (p_t-p_r) \nonumber \\= & {} e^{-\lambda }\left[ {{\ddot{\nu }} \over 2}-{{{\dot{\lambda }}} {\dot{\nu }} \over 4}+{{{\dot{\nu }}}^2 \over 4}-{{{\dot{\nu }}}+{{\dot{\lambda }}} \over 2r}+{e^\lambda -1 \over r^2}\right] . \end{aligned}$$

(7)

The force due to the pressure anisotropy is repulsive if $\varDelta >0$, and attractive if $\varDelta < 0$ [39]. The existence of outward force ($\varDelta >0$), allows the building of more compact distribution when using anisotropic fluid than isotropic perfect fluid ($\varDelta =0$) [8].

In view of the following transformations $x=r^2$, $z(x)=e^{-\lambda (r)}$ and $y(x)=e^{\nu (r)}$, the system of Eqs. (4–7) becomes

$$\begin{aligned} 8\pi \rho= & {} \frac{1-z}{x}-2{z'}, \end{aligned}$$

(8)

$$\begin{aligned} 8\pi p_r= & {} 2z\frac{y'}{y}-\frac{1-z}{x}, \end{aligned}$$

(9)

$$\begin{aligned} 8\pi p_t= & {} z\left[ \left( \frac{2{y''}}{y}-\frac{{y'}^2}{y^2}\right) x+\frac{2 y'}{y}\right] + {z'}\left( 1+x\frac{{y'}}{y}\right) ,\nonumber \\ \end{aligned}$$

(10)

$$\begin{aligned} 8\pi \varDelta= & {} z\left( \frac{2{y''}}{y}-\frac{{y'}^2}{y^2}\right) x+ {z'}\left( 1+x\frac{{y'}}{y}\right) +\frac{1-z}{x} . \end{aligned}$$

(11)

where $(')$ and $('')$ represent first and second derivatives with respect to x .

In relativistic stellar objects, the inside matter distribution may be compiled of two regions: an inner layer called as core and an outer layer named as envelope with distinct pressures. In order to make a core-envelope model for a given star, it is mandatory to classify space-time into a number of discrete regions. These regions comprise of the core ($0\le r \le R_C$, Region C), the envelope ($R_c\le r\le R_E$, Region E) and the exterior ($R_E > r$, Region B). The corresponding line elements for the three regions can be taken as

$$\begin{aligned} ds^2|_C= & {} e^{\nu _C(r)}dt^2 - e^{\lambda _C(r)}dr^2 - r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2), \nonumber \\ \end{aligned}$$

(12)

$$\begin{aligned} ds^2|_{E}= & {} e^{\nu _E(r)}dt^2 - e^{\lambda _E(r)}dr^2 - r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2), \nonumber \\ \end{aligned}$$

(13)

$$\begin{aligned} ds^2|_{B}= & {} \left( 1-\frac{2M}{r}\right) dt^2 - \left( 1-\frac{2M}{r}\right) ^{-1}dr^2 \nonumber \\&- r^2\left( d\theta ^2 + \sin ^2{\theta }d\phi ^2\right) . \end{aligned}$$

(14)

The exterior of a star for the Region B is the Schwarz-schild exterior solution which is given in Eq. (14).

3 Conditions for a physically realistic core-envelope model

In order to make the model physically doable, one needs to verify the following conditions in core (Region C), envelope (Region E) and exterior regions (Region B) (conditions developed by [38] are further augmented):

• (i) Geometrical non-singularity: The metric potentials and matter variables should be defined at the center and should be well behaved throughout the inside of the star [38].

• (ii) Density and pressures trends: The matter density $\rho$, radial pressure $p_r$ and transverse pressure $p_t$ the core and envelope of the star should be continuous at the junction, positive and monotonically decreasing outward. Further, the pressure-density ratios should be positive and less than 1 throughout within the star (Zeldovich’s condition [40]) and continuous at the junction.

• (iii) Mass-radius relation, Red-shift and Compactification factor: The mass function m(r), compactification parameter u(r) and gravitational red shift z(r) for the core and the envelope of the star should be continuous at the junction and increasing and decreasing respectively with the radial coordinate r.

• (iv) Anisotropic constant $\varDelta$: The radial pressure should coincides with the tangential pressure at the center of the star i.e. $\varDelta =0$ and should be monotonically increasing outward and asymptotic at the boundary. Further, for core-envelope model $\varDelta$ should be continuous at the junction.

• (v) Causality condition: The radial sound speed of a compact star model should satisfy the causality condition at the center and should be monotonically decreasing outward besides being continuous at the junction.

• (vi) Adiabatic index: The adiabatic index should be continuous at the junction and should satisfy the Bondi condition.

• (vii) Energy conditions: The core and the envelope for the star should satisfy the energy conditions besides being continuous at the junction.

• (viii) TOV condition: The TOV condition should be satisfied within the star and all the three forces should be continuous at the junction resulting the system to be in static equilibrium.

• (ix) At the stellar boundary $p_r(R_{E}) = 0$ [38].

• (x) The metric potentials of the core region should match smoothly with the gravitational potentials of the envelope region [38].

• (xi) The gravitational potentials of the envelope layer should connected smoothly over the boundary with the Schwarzschild exterior metric [38].

4 Relativistic core-envelope model

For core region ($0\le r\le R_C$), we choose a new function for metric potential $g_{rr}$ ($=e^{\lambda }$) also satisfying linear EOS

$$\begin{aligned} z=e^{-\lambda _C}= & {} \frac{a x}{(b x+1)^2}+1, \end{aligned}$$

(15)

$$\begin{aligned} p_{r_C}= & {} \alpha \rho -\beta , \end{aligned}$$

(16)

where $a,~ b,~ \alpha$, and $\beta$ are constants. Substituting z value from Eq. (15) in Eq. (11) and using Eqs. (8, 9, 15) and Eq. (16), we obtain the following differential equation:

$$\begin{aligned} \frac{y'(x)}{y(x)}+\frac{a (3 \alpha +(1-\alpha ) b x+1)+8 \pi \beta (b x+1)^3}{2(b x+1) \left( a x+(b x+1)^2\right) }=0.\nonumber \\ \end{aligned}$$

(17)

On integrating Eq. (17), we obtain

$$\begin{aligned} y= & {} e^{\nu _{C}}\nonumber \\= & {} c_1 (b x+1)^{2 \alpha } e^{p_2-4 \pi \beta x} p_1^{\frac{2 \pi a \beta }{b^2}-\alpha }, \end{aligned}$$

(18)

where

$$\begin{aligned} p_1= & {} a x+(b x+1)^2, \\ p_2= & {} \frac{\sqrt{a} \left( 4 \pi \beta (a+2 b)+(\alpha +1) b^2\right) \tanh ^{-1}\left( \frac{a+2 b (b x+1)}{\sqrt{a} \sqrt{a+4 b}}\right) }{b^2 \sqrt{a+4 b}}, \end{aligned}$$

and $c_1$ is an integration constant. In view of Eqs. (15) and (18) the system of Eqs. (8)–(11) becomes

$$\begin{aligned} \rho _C= & {} \frac{a (b x-3)}{8 \pi (b x+1)^3}, \end{aligned}$$

(19)

$$\begin{aligned} p_{r_C}= & {} \frac{a \alpha (b x-3)}{8 \pi (b x+1)^3}-\beta , \end{aligned}$$

(20)

$$\begin{aligned} p_{t_C}= & {} \frac{d_1+d_2+d_3}{d_4}, \end{aligned}$$

(21)

$$\begin{aligned} \varDelta _C= & {} p_{t_C}-p_{t_C} , \end{aligned}$$

(22)

where

$$\begin{aligned} d_1= & {} a^2 x \left( \alpha ^2 (b x{-}3)^2-4 \alpha b x (b x{-}7)+b x (2-b x){+}3\right) ,\\ d_2= & {} 32 \pi \beta (b x+1)^6 (2 \pi \beta x-1),\\ d_3= & {} 4 a (b x+1)^2 (\alpha (-(b x (b x-8)+3))\\&-4 \pi \beta x (b x+1) ((\alpha +2) b x-3 \alpha )),\\ d_4= & {} 32 \pi (b x+1)^4 \left( a x+(b x+1)^2\right) .\\ \end{aligned}$$

The metric potentials $e^{-{\lambda _{C}}}, e^{\nu _E}$ and matter variables are continuous and well behaved in the core region.

For envelope region ($R_C\le r\le R_E$), we choose the same type of metric potential $g_{rr}$ but satisfying quadratic EOS

$$\begin{aligned} z= & {} e^{-\lambda _E}=\frac{a x}{(b x+1)^2}+1, \end{aligned}$$

(23)

$$\begin{aligned} p_{r_E}= & {} P \rho ^2 -Q, \end{aligned}$$

(24)

where a,  b,  P and Q are constants. Putting z value from Eq. (23) in Eq. (11) and using Eqs. (8, 9, 23) and Eq. (24), we obtain the following differential equation:

$$\begin{aligned}&\frac{4 \pi Q}{\frac{a x}{(b x+1)^2}+1}+\frac{a}{2 (b x+1)^2 \left( \frac{a x}{(b x+1)^2}+1\right) }+\frac{y'(x)}{y(x)}\nonumber \\&\quad =\frac{\left( \frac{a x}{(b x+1)^2}+1\right) \left( a^2 P (b x-3)^2\right) }{4 \pi (b x+1)^6}. \end{aligned}$$

(25)

On integrating Eq. (25), we get

$$\begin{aligned} y= & {} e^{\nu _E}=C_2 d_9e^{\frac{d_5+d_6}{48 \pi }} \end{aligned}$$

(26)

where $C_2$ is an integration constant. In view of Eqs. (23) and (26) the system of Eqs. (8)–(11) becomes,

$$\begin{aligned} \rho _{E}= & {} \frac{a (b x-3)}{8 \pi (b x+1)^3}, \end{aligned}$$

(27)

$$\begin{aligned} p_{r_E}= & {} \frac{a^2 P \left( b r^2-3\right) ^2}{64 \pi ^2 \left( b r^2+1\right) ^6}-Q, \end{aligned}$$

(28)

$$\begin{aligned} p_{t_E}= & {} \frac{d_{11}+d_{12}+d_{13}-d_{14} d_{15}}{d_{10}}, \end{aligned}$$

(29)

$$\begin{aligned} \varDelta _E= & {} p_{t_E}-p_{r_E}, \end{aligned}$$

(30)

where

$$\begin{aligned} d_5= & {} \frac{P \left( a (3 b x (9 b x+22)+55)+48 b (b x+1)^2\right) }{(b x+1)^3}\\&-192 \pi ^2 Q x,\\ d_6= & {} \frac{3 \left( d_7-d_8\right) \tanh ^{-1}\left( \frac{a+2 b (b x+1)}{\sqrt{a} \sqrt{a+4 b}}\right) }{\sqrt{a} b^2 \sqrt{a+4 b}},\\ d_7= & {} 64 \pi ^2 a Q (a+2 b)\\ d_8= & {} b^2 \left( 9 a^2 P+42 a b P-16 \pi a+32 b^2 P\right) \\ d_9= & {} (b x+1)^{-\frac{3 P (3 a+8 b)}{16 \pi }} \left( a x+(b x+1)^2\right) ^{\frac{2 \pi a Q}{b^2}+\frac{3 P (3 a+8 b)}{32 \pi }}, \\ d_{10}= & {} 2048 \pi ^3 (b x+1)^{10} \left( a x+(b x+1)^2\right) ,\\ d_{11}= & {} a^4 P^2 x (b x-3)^4-2048 \pi ^3 a b Q x^2 (b x+1)^9,\\ d_{12}= & {} -32 \pi b P x^2 (b x-3) (3 b x-17) (a b x+a)^3\\ d_{13}= & {} 2048 \pi ^3 Q (b x+1)^{12} (2 \pi Q x-1),\\ d_{14}= & {} 32 \pi a^2 (b x-3) (b x+1)^5 \\ d_{15}= & {} P (x (b (x (4 \pi b Q x+3 b-8 \pi Q)-18)-12 \pi Q)+3)\\&+2 \pi x (b x+1)^2. \end{aligned}$$

Fig. 1

Variation of metric potentials with radial coordinate r for (i) the neutron star in Vela X-1(upper) (ii) SMC X-4 (middle) (iii) Her X-1 (lower)

Fig. 2

Variation of density with radial coordinate r for (i) the neutron star in Vela X-1(upper) (ii) SMC X-4 (middle) (iii) Her X-1 (lower)

Fig. 3

Variation of pressures with radial coordinate r for ((i) the neutron star in Vela X-1(upper) (ii) SMC X-4 (middle) (iii) Her X-1 (lower)

Fig. 4

Variation of pressures and density ratios with radial coordinate r for (i) the neutron star in Vela X-1(upper) (ii) SMC X-4 (middle) (iii) Her X-1 (lower)

5 Junction conditions

Junction conditions implies that the continuity of gravitational potentials and radial pressure at the junction and at the boundary. Hence, we get the following two set of conditions:

5.1 Junction conditions at the interface of core-envelope regions

$$\begin{aligned} e^{\lambda _C}(R_C)= & {} e^{\lambda _{E}}(R_C), \end{aligned}$$

(31)

$$\begin{aligned} e^{\nu _C}(R_C)= & {} e^{\nu _{E}}(R_C), \end{aligned}$$

(32)

$$\begin{aligned} p_{r_C}(R_C)= & {} p_{r_{E}}(R_{C}). \end{aligned}$$

(33)

5.2 Junction conditions at the envelope and the boundary

The envelope metric potentials in the Eq. (13) must be connected smoothly over the boundary (i.e. at $r=R_{E}$) with the Schwarzschild exterior solution which is given in Eq. (14). It implies that

$$\begin{aligned} e^{\lambda _{E}}(R_{E})= & {} \left( 1-{2M\over R_{E}}\right) ^{-1}, \end{aligned}$$

(34)

$$\begin{aligned} e^{\nu _{E}}(R_{E})= & {} \left( 1-{2M\over R_{E}}\right) , \end{aligned}$$

(35)

and

$$\begin{aligned} p_{r_{E}}(R_{E}) = 0, \end{aligned}$$

(36)

where $R_E$ is the radius of the star.

The six matching conditions (31–36)along with the eleven constants, namely $a, ~b,~ P,~ Q,~ C_1, ~C_2, ~ R_C,~ R_E,~ M, ~\alpha , ~\beta$ form an undetermined system of equations. Solving the above system of equations, the mass M of the star is obtained as

$$\begin{aligned} M= -\frac{a R_E^3}{2 \left( b R_E^2+1\right) {}^2}, \end{aligned}$$

(37)

and radius $R_E$ is obtained from the following expression

$$\begin{aligned} Q= & {} \frac{a^2 P \left( b R_E^2-3\right) {}^2}{64 \pi ^2 \left( b R_E^2+1\right) {}^6} , \end{aligned}$$

(38)

and the constants $C_1, ~C_2,~ \beta$ are of the form

$$\begin{aligned} C_1= & {} C_2 \sigma _6 \sigma _7\exp \left( \frac{-\frac{3 \left( \sigma _1+\sigma _2\right) \sigma _3}{\sqrt{a} b^2 \sqrt{a+4 b}}+\sigma _4+\sigma _5}{48 \pi }\right) , \end{aligned}$$

(39)

$$\begin{aligned} C_2= & {} \sigma _{12} \sigma _{13} e^{-\frac{\frac{3 \sigma _8 \sigma _9}{\sqrt{a} b^2 \sqrt{a+4 b}}-\sigma _{10}+\sigma _{11}}{48 \pi }} , \end{aligned}$$

(40)

$$\begin{aligned} \beta= & {} \frac{a \left( -\frac{a P \left( b R_C^2-3\right) {}^2}{\left( b R_C^2+1\right) {}^6}+\frac{a P \left( b R_E^2-3\right) {}^2}{\left( b R_E^2+1\right) {}^6}+\frac{8 \pi \alpha \left( b R_C^2-3\right) }{\left( b R_C^2+1\right) {}^3}\right) }{64 \pi ^2},\nonumber \\ \end{aligned}$$

(41)

where

Fig. 5

Variation of mass with radial coordinate r for (i) the neutron star in Vela X-1(upper) (ii) SMC X-4 (middle) (iii) Her X-1 (lower)

Fig. 6

Variation of red-shift with radial coordinate r for (i) the neutron star in Vela X-1(upper) (ii) SMC X-4 (middle) (iii) Her X-1 (lower)

Fig. 7

Variation of compactification factor with radial coordinate r for (i) the neutron star in Vela X-1(upper) (ii) SMC X-4 (middle) (iii) Her X-1 (lower)

$$\begin{aligned} \sigma _1= & {} a^2 \left( 9 b^2 P+64 \pi ^2 (\beta -Q)\right) +32 b^4 P,\\ \sigma _2= & {} 2 a b \left( 21 b^2 P+8 \pi \alpha b+64 \pi ^2 (\beta -Q)\right) ,\\ \sigma _3= & {} \tanh ^{-1}\left( \frac{a+2 b \left( b R_C^2+1\right) }{\sqrt{a} \sqrt{a+4 b}}\right) ,\\ \sigma _4= & {} 192 \pi ^2 R_C^2 (\beta -Q),\\ \sigma _5= & {} \frac{P \left( 3 b R_C^2 \left( b R_C^2 (9 a+16 b)+22 a+32 b\right) +55 a+48 b\right) }{\left( b R_C^2+1\right) {}^3},\\ \sigma _6= & {} \left( b R_C^2+1\right) {}^{-\frac{3 P (3 a+8 b)}{16 \pi }-2 \alpha },\\ \sigma _7= & {} \left( a R_C^2+\left( b R_C^2+1\right) {}^2\right) {}^{a \left( \frac{2 \pi (Q-\beta )}{b^2}+\frac{9 P}{32 \pi }\right) +\alpha +\frac{3 b P}{4 \pi }}\\ \sigma _8= & {} 64 \pi ^2 a Q (a+2 b)-b^2 \left( 9 a^2 P+42 a b P-16 \pi a+32 b^2 P\right) \\ \sigma _{9}= & {} \tanh ^{-1}\left( \frac{a+2 b \left( b R_E^2+1\right) }{\sqrt{a} \sqrt{a+4 b}}\right) \\ \sigma _{10}= & {} 192 \pi ^2 Q R_E^2\\ \sigma _{11}= & {} \frac{P \left( a \left( 3 b R_E^2 \left( 9 b R_E^2+22\right) +55\right) +48 b \left( b R_E^2+1\right) {}^2\right) }{\left( b R_E^2+1\right) {}^3} \\ \sigma _{12}= & {} \left( 1-\frac{2 M}{R_E}\right) \left( b R_E^2+1\right) {}^{\frac{3 P (3 a+8 b)}{16 \pi }}\\ \sigma _{13}= & {} \left( a R_E^2+\left( b R_E^2+1\right) {}^2\right) {}^{-\frac{2 \pi a Q}{b^2}-\frac{3 P (3 a+8 b)}{32 \pi }} \end{aligned}$$

The remaining six constants $a,~b, ~\alpha ,~ P, ~Q$ and $R_C$ are free parameters. These constants are selected in such a way that all the physical properties of the considered stellar objects are well-behaved.

Fig. 8

Variation of anisotropy with radial coordinate r for (i) the neutron star in Vela X-1(upper) (ii) SMC X-4 (middle) (iii) Her X-1 (lower)

Fig. 9

Variation of radial velocity with radial coordinate r for (i) the neutron star in Vela X-1(upper) (ii) SMC X-4 (middle) (iii) Her X-1 (lower)

Fig. 10

Variation of adiabatic index with radial coordinate r for (i) the neutron star in Vela X-1(upper) (ii) SMC X-4 (middle) (iii) Her X-1 (lower)

6 Discussion and conclusion for the core-envelope model

6.1 Geometrical non-singularity

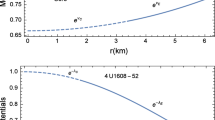
The metric potentials for the core of the neutron star in Vela X-1, SMC X-4 and Her X-1 at the center ($r = 0$), the values of $e^{\nu }$ are positive constant and $e^{\lambda }=1$. This shows that the metric potentials are regular and free from geometric singularities at the center of the star. Further, both the metric potentials $e^{\nu }$ and $e^{-\lambda }$ are continuous at the junction and monotonically increasing and decreasing respectively with the radial coordinate r as well (Fig. 1).

Fig. 11

Variation of energy conditions with radial coordinate r for (i) the neutron star in Vela X-1(upper) (ii) SMC X-4 (middle) (iii) Her X-1 (lower)

Fig. 12

Variation of balancing forces with radial coordinate r for (i) the neutron star in Vela X-1(upper) (ii) SMC X-4 (middle) (iii) Her X-1 (lower)

6.2 Doable tendency of physical parameters

6.2.1 Density and pressures trends

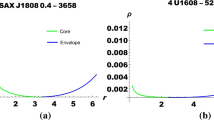
The matter density $\rho$, radial pressure $p_r$ and transverse pressure $p_t$ for the core and envelope of the the neutron star in Vela X-1, SMC X-4 and Her X-1 are continuous at the junction, positive and monotonically decreasing outward (Figs. 2, 3) [41]. Further, the stars satisfy Zeldovich’s condition [40] i.e. the pressure-density ratios are positive and less than 1 throughout within the stars and continuous at the junction (Fig. 4).

6.2.2 Mass-radius relation, red-shift and compactification factor

The mass function m(r) and gravitational red shift z(r) for the core and the envelope of the neutron star in Vela X-1, SMC X-4, Her X-1 are continuous at the junction and increasing and decreasing respectively with the radial coordinate r (Figs. 37, 6). Also, the compactification parameter u(r) for the above stars is continuous at the junction and increasing in nature with r (Fig. 7) and lies within the Buchdahl limit [42].

6.2.3 Anisotropic constant

In Fig. 8, the radial pressure coincides with the tangential pressure at the center of the stars and continuous at the junction and increasing outward [41].

6.2.4 causality condition

The radial sound speed of the neutron star in Vela X-1, SMC X-4 and Her X-1 satisfie the causality condition at the center and monotonically decreasing outward with the continuity at the junction. The profile of $v^2_r$ of both core and envelope of the stars are given in Fig. 9.

6.2.5 Adiabatic index

For a relativistic anisotropic sphere the stability counts on the adiabatic index $\Gamma _r$, the ratio of two specific heats, defined by [43],

$$\begin{aligned} \Gamma _r = \frac{\rho + p_r}{p_r} \frac{\partial p_r}{\partial \rho }. \end{aligned}$$

Bondi [44] suggested that for a stable Newtonian sphere, $\Gamma$ value should be greater than $\frac{4}{3}$. The profiles of adiabatic indexes of the core and the envelope of both the stars are plotted in Fig. 10. From the Fig. 10, it is clear that the adiabatic indexes are continuous at the junction and satisfies the Bondi condition [44].

Table 1 Values of constants that generate masses, core and envelope radii ($R_C$, $R_E$) for the three well-known compact stars

Table 2 The variation of physical parameters, i.e., adiabatic index, density, radial pressure and red-shift for three well-known neutron stars i.e. (i) Vela X-1 (ii) SMC X-4 and (iii) Her X-1 for the values of $G=6.67 \times {10^{-11} \hbox {m}^3 \hbox {kg}^{-1} \hbox {s}^{-2}}$, $M_{\odot }= 2\times {10^{30} \hbox {kg}}$ and $C=3\times {10^8 \hbox {ms}^{-1}}$

6.2.6 Energy conditions

For a physically stable configuration, the core and the envelope for the star should satisfy the following inequalities simultaneously (which are known as energy conditions [18]): (i) null energy condition $\rho + p_r \ge 0$ (NEC) (ii) weak energy conditions $\rho + p_r \ge 0$, $\rho \ge 0$ ($\hbox {WEC}_r$) and $\rho + p_t \ge 0$, $\rho \ge 0$ ($\hbox {WEC}_t$) and (iii) strong energy condition $\rho +p_r+2p_t \ge 0$ (SEC). From the Fig. 11 it is clearly visible that the variation of energy conditions with r of the core and envelope of the neutron star in Vela X-1, SMC X-4 and Her X-1 are continuous at the junction and satisfying realistic conditions.

6.3 TOV equation of core-envelope model

Equilibrium state under three forces, i.e., the resultant of the forces; gravitational ($F_g$), hydrostatic ($F_h$) and anisotropic ($F_a$) must be zero throughout within the stars and continuous at the junction. The TOV equation is given as [45]

$$\begin{aligned} -{M_g(r)(\rho +p_r) \over r^2}~e^{(\lambda -\nu )/2}-{dp_r \over dr}+{2\varDelta (r) \over r}=0, \end{aligned}$$

(42)

where $M_g(r)$ is the gravitational mass within the radius r and can be calculated as

$$\begin{aligned} M_g(r)= & {} {1\over 2}~r^2 \nu ' e^{(\nu -\lambda )/2}. \end{aligned}$$

(43)

from the Tolman-Whittaker formula and EFEs.

Equation (42) is equivalent to the following balanced force equation

$$\begin{aligned} F_g+F_h+F_a=0, \end{aligned}$$

(44)

where $F_g$, $F_h$ and $F_a$ respectively are components of Eqn. (42) above.

From Fig. 12, we can visualize that the TOV condition is satisfied within the stars and all the three forces are continuous at the junction, thereby, concluding that the system is in static equilibrium.

7 Conclusion

In this paper we have described an anisotropic spherically symmetric core-envelope model of compact stars Vela X-1, SMC X-4 and Her X-1 in which we equip core with linear equation of state while the envelope as quadratic equation of state so that the matter in the core becomes quark. From the Figs. 1, 3, we can visualize that the core, envelope layers and the Schwarzschild exterior connect smoothly at the junction. The values of constants, parameters that generate masses, core and envelope radii ($R_C$, $R_E$) for the neutron star Vela X-1, SMC X-4 and Her X-1 are given in Table 1. From the Table 2, we can observe that the pressure in the core layer has higher than in the envelope layer. Further, it justifies that if the mass of the star increases then the value of central density higher and core shrinks due to the dominating effect of gravity of astronomic objects of higher masses. The continuity of metric potentials and physical quantities i.e pressures, radial velocity, mass function, compactification factor, red-shift, adiabatic indexes, balancing forces, pressure density ratios and energy conditions are shown in figures for the compact stellar objects Vela X-1, SMC X-4 and Her X-1.

Hence we conclude that our core-envelope model is physically doable and substantiate with the following stars:

• (i) the neutron star in vela X-1 with mass $M = 1.77M_{\odot }$ and radius $R_E =9.56\,\hbox {km}$ for the values of $a =-0.007354/\hbox {km}^{2}$, $b = 0.0038/\hbox {km}^{2}$, $P = 108/\hbox {km}^{2}$, $\alpha = 0.170708 \,\hbox {km}^{2}$ and $R_C = 2.9\,\hbox {km}$;

• (ii) the compact star SMC X-4 of mass $M = 1.29M_{\odot }$ and radius $R_E =8.831\,\text{ km }$ for the values of $a =-0.00607/\hbox {km}^{2}$, $b = 0.0035/\hbox {km}^{2}$, $P = 115/\hbox {km}^{2}$, $\alpha = 0.1502/\hbox {km}^{2}$ and $R_C = 3.00547\,\text{ km }$;

• (iii) the strange star Her X-1 of mass $M = 0.85M_{\odot }$ and radius $R_E =8.1\text{ km }$ for the values of $a =-0.00005098/\hbox {km}^{2}$, $b = 0.004/\hbox {km}^{2}$, $P = 90/\hbox {km}^{2}$, $\alpha = 0.0.093761/\hbox {km}^{2}$ and $R_C = 3.45\,\text{ km }$;