1 Introduction

The entanglement entropy serves as a key quantity to measure how the subsystem and its complement are correlated [1]. In strongly coupled system, the entanglement entropy is expected to be a useful tool to keep track of the degree of freedom while other traditional methods might not be available. However, the calculation of entanglement entropy is usually a not easy task except for the case in \(1+1\) dimensions. In the spirit of the anti-de Sitter/conformal field theory (AdS/CFT) correspondence [2,3,4], Ryu and Takayanagi have provided a holographic proposal to compute the entanglement entropy in [5, 6]. It states that the entanglement entropy of a d+1 dimensional CFT at strong coupling can be investigated from a weakly coupled gravity dual characterized by an asymptotically \(\hbox {AdS}_d+2\) spacetime. With this elegant approach, the holographic entanglement entropy is widely used to study properties of phase transitions in holographic superconductor models [7,8,9,10,11,12]. The behavior of the entanglement entropy in metal/superconductor phase transition was studied in [13] and observed that the entanglement entropy is lower in the superconductor phase than in the normal phase. In the insulator/superconductor model, the non-monotonic behavior of the entanglement entropy was found in Ref. [14]. Then, the study of entanglement entropy was also extended to other various holographic superconductors applications [15,16,17,18,19,20,21,22,23,24,25,26].

The purpose of this paper is to study further the behaviors of the holographic entanglement entropy for metal/superconductor model with BI electrodynamics in higher dimensional AdS spacetime. On the one hand, the motivations for studying the entanglement entropy in higher dimensional black hole spacetime comes from the string theory which contains gravity and requires more than four dimensions [27, 28]. Furthermore, as mathematical objects, black hole spacetimes are among the most important Lorentzian Ricci-flat manifolds in any dimension [29]. On the other hand, the BI electrodynamics [30] introduced in 1930s by Born and Infeld to obtain a classical theory of charged particles with finite self-energy, is the only possible non-linear version of electrodynamics which is invariant under electromagnetic duality transformations and has been a focus for these years since most physical systems are inherently nonlinear to some extent [31,32,33,34,35,36,37,38]. The Lagrangian of the BI gauge field and its expression is given by

$$\begin{aligned} L_{BI}=\frac{1}{b^2}\left( 1-\sqrt{1+\frac{b^2 F^{\mu \nu }F_{\mu \nu }}{2}}\right) , \end{aligned}$$
(1)

where \(F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu \) is the strength of the BI electrodynamic field. b is the BI coupling parameter. In the limit \(b\rightarrow 0\), the BI field will reduce to the Maxwell field. It is also to be noted that the higher order terms in the factor b essentially correspond to the higher derivative corrections of the gauge fields [39, 40]. In the present work, we will study the properties of phase transitions of the holographic superconductor model by calculating the behaviors of the scalar operator and the entanglement entropy and see how the phase transition is affected by the BI electrodynamics and the width of the subsystem in higher dimensional AdS black hole spacetime.

The framework of this paper is as follows. In Sect. 2, we introduce the basic field equations of holographic superconductor model with BI electrodynamics in n-dimensional spacetime and study the properties of the phase transition by calculating the scalar operator. In Sect. 3, the behavior of the entanglement entropy in the holographic superconductor model are investigated in derail. In Sect. 4, we conclude our main results of this paper.

2 Holographic superconducting model with BI electrodynamics

2.1 Basic field equations

In this section, we will consider the n-dimensional action in a background of AdS spacetime which includes Einstein gravity, a massive charged complex scalar field and BI nonlinear gauge field.

$$\begin{aligned} S= & {} \int d^{d}x\sqrt{-g}\Bigg [\frac{1}{16\pi G}(R-2\Lambda )-|\nabla \psi \nonumber \\&- \ i q A\psi |^2-m^2|\psi |^2+L_{BI}\Bigg ], \end{aligned}$$
(2)

where R and g are, respectively, the Ricci scalar curvature and the determinant of the metric, \(\Lambda =-(d-1)(d-2)/2L^2\) is the cosmological constant, L is the AdS radius, \(\psi \) represents a scalar field with charge q and mass m, and \(L_{BI}\) is the Lagrangian of the BI gauge field.

Fig. 1
figure 1

The operators \(\langle \mathcal {O}_{+}\rangle \) (left plot) and \(\langle \mathcal {O}_{-}\rangle \) (right plot) with respect to the temperature T after condensation for different BI parameter. The four lines from top to bottom correspond to \(b=0\) (black), \(b=0.2\) (blue), \(b=0.4\) (red), and \(b=0.6\) (green) respectively

Full size image

In order to study the holographic entanglement entropy in BI electrodynamics, we will take the full backreaction. The metric ansatz for the d-dimensional planar black hole can be taken as

$$\begin{aligned} ds^2=-f(r)e^{-\chi (r)}dt^{2}+\frac{dr^2}{f(r)}+r^{2}h_{ij}dx^{i}dx^{j}, \end{aligned}$$
(3)

where \(h_{ij}dx^{i}dx^{j}\) is the line element of (d-2)-dimensional hypersurface with the curvature \(\kappa =0\). The Hawking temperature of this black hole, which will be interpreted as the temperature of the CFT, reads

$$\begin{aligned} T_{H}=\frac{f^{\prime }(r_{+})e^{-\chi (r_{+})/2}}{4\pi }, \end{aligned}$$
(4)

where \(r_{+}\) is the black hole horizon. Assuming the matter fields in the forms

$$\begin{aligned} A=\phi (r)dt,\quad \psi =\psi (r), \end{aligned}$$
(5)

where \(\psi (r)\) can be taken to be real without loss of generality. By varying action Eq. (2) with respect to the gravitational field \(g_{\mu \nu }\) ,the scalar field \(\psi \) and the gauge field \(A_\mu \), the field equations can be obtained as

$$\begin{aligned}&\chi ^{\prime }+\frac{2r}{d-2}\left( \psi ^{\prime 2}+\frac{q^{2}e^{\chi }\phi ^{2}\psi ^{2}}{f^{2}}\right) =0, \end{aligned}$$
(6)
$$\begin{aligned}&f^{\prime }-\left( \frac{(d-1)r}{L}-\frac{(d-3)f}{r}\right) \nonumber \\&\quad +\frac{r}{d-2} \left[ m^{2}\psi ^{2} +f\Bigg (\psi ^{\prime 2}+\frac{q^{2}e^{\chi }\phi ^{2}\psi ^{2}}{f^{2}}\right) \nonumber \\&\quad +\frac{1-\sqrt{1-b^2 e^{\chi }\phi '^2}}{b^2\sqrt{1-b^2 e^{\chi }\phi '^2}}\Bigg ]=0, \end{aligned}$$
(7)
$$\begin{aligned}&\psi ^{\prime \prime }+\left( \frac{d-2}{r}-\frac{\chi ^{\prime }}{2} +\frac{f^\prime }{f}\right) \psi ^\prime \nonumber \\&\quad +\frac{1}{f}\left( \frac{q^{2} e^{\chi }\phi ^2}{f}-m^2\right) \psi =0, \ \end{aligned}$$
(8)
$$\begin{aligned}&\phi ^{\prime \prime }+\left( \frac{d-2}{r}+\frac{\chi ^{\prime }}{2}\right) \phi ^\prime -\frac{(d-2)b^2e^{\chi }}{r}\phi '^3\nonumber \\&\quad -\frac{2q^{2}\psi ^{2}(1-b^2 e^{\chi }\phi '^2)^\frac{3}{2}}{f}\phi =0, \end{aligned}$$
(9)

where a prime denotes the derivative with respect to r, and \(16\pi G=1\) was used. For purpose of getting the solutions in superconducting phase where \(\psi (r)\ne 0\), we need to impose the boundary conditions. At the horizon \(r_+\), the regularity condition gives the boundary conditions [41]

$$\begin{aligned}&\phi (r)=\phi _1(r-r_+)+\phi _2(r-r_+)^2+\cdots , \end{aligned}$$
(10)
$$\begin{aligned}&\psi (r)=\psi _0+\psi _1(r-r_+)+\psi _2(r-r_+)^2+\cdots , \end{aligned}$$
(11)
$$\begin{aligned}&\chi (r)=\chi _0+\chi _1(r-r_+)+\chi _2(r-r_+)^2+\cdots , \end{aligned}$$
(12)
$$\begin{aligned}&f(r)=f_1(r-r_+)+f_2(r-r_+)^2+\cdots . \end{aligned}$$
(13)

And at the asymptotic AdS boundary (\(r\rightarrow \infty \)), the asymptotic behaviors of the solutions are

$$\begin{aligned} \chi \rightarrow 0,\quad f\sim \frac{r^2}{L^2}\quad \phi \sim \mu -\frac{\rho }{r^{d-3}}\quad \psi \sim \frac{\psi _{-}}{r^{\Delta _{-}}}+\frac{\psi _{+}}{r^{\Delta _{+}}}\, \end{aligned}$$
(14)

with

$$\begin{aligned} \Delta _\pm =\frac{1}{2}\big [(d-1)\pm \sqrt{(d-1)^2+4m^{2}}\big ], \end{aligned}$$
(15)

and \(\mu \) and \(\rho \) are interpreted as the chemical potential and charge density in the dual field theory. Considering Breitenlohner-Freedman bound [42, 43], the mass of the scalar field must be restricted as \(m^2>-(d-1)^2/4\). It should be noted that provided \(\Delta _{-}\) is larger than the unitarity bound, both \(\psi _{-}\) and \(\psi _{+}\) can be normalizable [44]. This means \(\psi _{-}\) or \(\psi _{+}\) can either be identified as a source or an expectation value. According to the AdS/CFT correspondence, they correspond to the vacuum expectation values \(\psi _{-}=\langle \mathcal {O}_{-}\rangle \), \(\psi _{+}=\langle \mathcal {O}_{+}\rangle \) of an operator \(\mathcal {O}\) dual to the scalar field [45, 46]. Without loss of generality, we will impose boundary condition that either \(\psi _{-}\) or \(\psi _{+}\) vanishes in the following calculation.

From the equations of motion for the system, we can get the useful scaling symmetries in the forms

$$\begin{aligned}&r\rightarrow \alpha r,\quad (x,y,z,t)\rightarrow (x,y,z,t)/\alpha ,\nonumber \\&\phi \rightarrow \alpha \phi ,\quad f\rightarrow \alpha ^2f, \end{aligned}$$
(16)
$$\begin{aligned}&L\rightarrow \alpha L,\quad r\rightarrow \alpha r,\quad t\rightarrow \alpha t,\quad q\rightarrow \alpha ^{-1} q, \end{aligned}$$
(17)
$$\begin{aligned}&e^{\chi }\rightarrow \alpha ^2e^{\chi },\quad \phi \rightarrow \alpha ^{-1}\phi ,\quad t\rightarrow t\alpha . \end{aligned}$$
(18)

Using the scaling symmetries Eq. (16), we can take \(r_+=1\) and the symmetries Eq. (17) allow us to set the \(L=1\). By applying the scaling symmetries Eq. (16), the useful quantities can be rescaled as

$$\begin{aligned} T\rightarrow & {} \alpha T,\quad \rho \rightarrow \alpha ^{d-2}\rho , \quad \langle \mathcal {O}_{-}\rangle \rightarrow \alpha ^{\Delta _-} \langle \mathcal {O}_{-}\rangle ,\nonumber \\ \langle \mathcal {O}_{+}\rangle\rightarrow & {} \alpha ^{\Delta _+} \langle \mathcal {O}_{+}\rangle . \end{aligned}$$
(19)

Therefore, we will use the following dimensionless quantities in next section

$$\begin{aligned} \langle \mathcal {O}_{+}\rangle ^{\frac{1}{\Delta _{+}}}/\rho ^{\frac{1}{d-2}},\quad \langle \mathcal {O}_{-}\rangle ^{\frac{1}{\Delta _{-}}}/\rho ^{\frac{1}{d-2}},\quad T/\rho ^{\frac{1}{d-2}}. \end{aligned}$$
(20)

2.2 Metal/superconductor phase transition

After the discussion in the above section, we here would like to study the properties of phase transition of this physic model through the condensation of the scalar operators \(\langle \mathcal {O}_{+}\rangle \) and \(\langle \mathcal {O}_{-}\rangle \). For concreteness, we investigate the behaviors of the scalar condensation for the system in five-dimensional AdS black hole space-time. Considering Breitenlohner-Freedman bound [42, 43], we here set \(q=2\) and \(m^2 =\sqrt{- \ 15/4}\). The behavior of the scalar condensation versus the temperature T for different BI parameter b is shown in Fig. 1. For a given b, the left panel shows that as the temperature T exceeds a critical value \(T_c\), the scalar field is vanishing and this can be identified as the metal phase. However, the condensation of the operators emerges as \(T<T_c\), which can be thought of as a superconductor phase. Near the phase transition point \(T_c\), the critical behavior is found to be \(\langle \mathcal {O}_{+}\rangle \varpropto (T_{c}-T)^{1/2}\), which means the phase transition is second order [45,46,47,48]. And it is noted that the curves for the scalar operators has similar behaviors to the BCS theory for different BI factor, where the condensation goes to a constant at zero temperature. In the right panel, it can be seen that the condensation of the operator \(\langle \mathcal {O}_{-}\rangle \) with respect of the temperature T is similar to the case of the operator \(\langle \mathcal {O}_{+}\rangle \). As the temperature is fixed, we observe that with the increase of the BI parameter the condensation gaps increases for both scalar operators \(\langle \mathcal {O}_{+}\rangle \) and \(\langle \mathcal {O}_{-}\rangle \), which implies that the scalar hair can be formed harder when the nonlinearity in the BI electromagnetic field becomes stronger. Interestingly, the condensation gap of the operator \(\langle \mathcal {O}_{+}\rangle \) is larger than the one of the operator \(\langle \mathcal {O}_{-}\rangle \) as the BI factor changes in same value. That is to say, the effect of the BI factor on the condensation of operator \(\langle \mathcal {O}_{+}\rangle \) is more powerful than the one of operator \(\langle \mathcal {O}_{-}\rangle \). From Table 1, we find that the critical temperature \(T_c\) for the operators \(\langle \mathcal {O}_{+}\rangle \) and \(\langle \mathcal {O}_{-}\rangle \) decreases as the BI factor increases, which agrees well with the results obtained in Fig. 1.

Table 1 The critical temperature \(T_c\) for the operators \(\langle \mathcal {O}_{+}\rangle \) and \(\langle \mathcal {O}_{-}\rangle \) for different BI parameter
Full size table
Fig. 2
figure 2

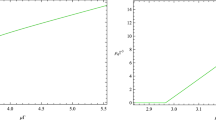
The entanglement entropy of the operator \(\langle O_{+}\rangle \) with respect to the temperature T and BI factor b for \(\ell \rho ^{\frac{1}{3}}=1\). The four lines in left plot from top to bottom correspond to \(b=0\) (black), \(b=0.2\) (blue), \(b=0.4\) (red), and \(b=0.6\) (green) respectively

Full size image

3 Entanglement entropy in holographic phase transition

In this section, we will study the phase transition in the holographic superconductor model with BI electrodynamics by the entanglement entropy. The entanglement entropy in conformal field theories can be calculated from the area of minimal surface in AdS spaces, and its formula is given by the “area law” [5, 6]

$$\begin{aligned} S_\mathcal {A}=\frac{Area(\gamma _{A})}{4G_{A}}, \end{aligned}$$
(21)

where \(\gamma _A\) is the minimal area surface in the bulk which ends on the boundary A, \(G_N \) is the Newton constant in the Einstein gravity on the AdS space, and \(S_A \) is the entanglement entropy for the subsystem A which can be chosen arbitrarily. Hereafter, we focus on the entanglement entropy for a straight geometry with a finite width \(\ell \) along the \(\textit{x}\) direction and infinitely extending in \(\textit{y}\) and \(\textit{z}\) directions. The holographic dual surface \(\gamma _{A}\) is defined as a three-dimensional surface

$$\begin{aligned}&t=0, \quad x=x(r),\quad -\frac{R}{2}<y< \frac{R}{2}(R\rightarrow \infty ),\nonumber \\&-\frac{W}{2}<z< \frac{W}{2}(W\rightarrow \infty ), \end{aligned}$$
(22)

and the holographic surface \(\gamma _{A}\) in direction stats from \(\textit{x}=\frac{\ell }{2}\) at \( r=\frac{1}{\epsilon }\), extends into the bulk until it reaches \(r=r_*\), then returns back to the AdS boundary \( r=\frac{1}{\epsilon }\) at \(\textit{x}=-\frac{\ell }{2}\) . The induced metric on the hypersurface A is

$$\begin{aligned} ds^2= & {} h_{ij}dx^i dx^j \nonumber \\= & {} \left( \frac{1}{f(r)} +r^2 \left( \frac{dx}{dr}\right) ^2\right) dr^2+r^2 dy^2+r^2dz^2. \end{aligned}$$
(23)

According to the Eq. (21), the entanglement entropy in the strip geometry is

$$\begin{aligned} S_\mathcal {A}[x]=\frac{RW}{2G_5}\int _{r_*}^{\frac{1}{\epsilon }} r^2\sqrt{\frac{1}{f(r)}+r^2(dx/dr)^2}dr, \end{aligned}$$
(24)
Fig. 3
figure 3

The entanglement entropy of the operator \(\langle O_{+}\rangle \) with respect to the temperature T for various widths \(\ell \) as \(b=0.4\). The red line is for \(\ell \sqrt{\rho }=1.1\), the blue line is for \(\ell \sqrt{\rho }=1.0\), and black one is for \(\ell \sqrt{\rho }=0.9\)

Full size image
Fig. 4
figure 4

The entanglement entropy of the operator \(\langle O_{-}\rangle \) with respect to the temperature T and BI factor b for \(\ell \rho ^{\frac{1}{3}}=1\). The four lines in left plot from top to bottom correspond to \(b=0\) (black), \(b=0.2\) (blue), \(b=0.4\) (red), and \(b=0.6\) (green) respectively

Full size image

where \(r=\frac{1}{\epsilon }\) is the UV cutoff. Noting that the above expression can be treated as the Lagrangian with x direction thought of as time. Therefore, the equation of motion for the minimal surface from Eq. (24) is given by

$$\begin{aligned} \frac{r^4(dx/dr)\sqrt{f(r)}}{\sqrt{1+r^2f(r)(dx/dr)^2}}=r_*^3 . \end{aligned}$$
(25)

We are interested in the case that the surface is smooth at \(r=r_*\) i.e. \(dx/dr|_{r=r_*}=0\). By using the variable \(z_s=1/r\) , the width \(\ell \) in terms of \(z_s\) is

$$\begin{aligned} \frac{l}{2}=\int ^{z_{*}}_{\varepsilon }dz_s\frac{z_s^{3}}{\sqrt{(z^{6}_{*} -z_s^{6})z_s^{2}f(z_s)}}, \end{aligned}$$
(26)

and the holographic entanglement entropy in the \(z_s\)-coordinate can be rewritten as

$$\begin{aligned} S_\mathcal {A}= & {} \frac{R W}{2G_5} \int ^{z_{*}}_{\varepsilon }dz_s\frac{z_{*}^{3}}{z_s^{2}} \frac{1}{\sqrt{(z^{6}_{*}-z_s^{6})z_s^{2}f(z_s)}}\nonumber \\= & {} \frac{R W}{4G_5}\left( \frac{1}{\varepsilon ^2}+s\right) , \end{aligned}$$
(27)

the first term \(1/\varepsilon \) is divergent as \(\varepsilon \rightarrow 0\). However, the second term dose not depend on the cutoff and is finite, so it is physical important. In the following we will study the entanglement entropy in the holographic superconductor model and explore its dependence on the factors of the temperature T, the BI factor b and the belt width \(\ell \).

3.1 Entanglement entropy for operator \(\langle \mathcal {O}_{+}\rangle \)

We show the behavior of the entanglement entropy of operator \(\langle \mathcal {O}_{+}\rangle \) with respects to the temperature T and BI factor b in Fig. 2 with the dimensionless quantities \(s/ \rho ^{\frac{1}{3}},\ \ell \rho ^{\frac{1}{3}}, T/\rho ^{\frac{1}{3}}\). The left panel shows the cases of \(\ell \rho ^{\frac{1}{3}}=1\) with various T and the right panel is the cases of \(T/\rho ^{\frac{1}{3}}=0.1\), \(\ell \rho ^{\frac{1}{3}}=1\) with various b. It can be seen from the left-hand diagram that the slop of the entanglement entropy at the phase transition points indicated by the vertical dotted lines is discontinuous but the value of the entanglement entropy is continuous. Which indicates some kind of new degrees of freedom like Cooper pair would emerge after the condensation and this phase transition can be regarded as the signature of the second order phase transition. With the increase of the BI factor b the critical temperature \(T_c\) of the phase transition decreases which means that the stronger BI electrodynamics correction makes the scalar hair harder to condense. Moreover, the entanglement entropy in the superconductor phases for different b denoted by the solid lines are lower than the ones in the normal phases represented by the dot-dashed lines and decreases monotonously as temperature decreases. That is to say, the scalar hair turns on at the critical temperature and the formation of Cooper pairs make the degrees of freedom decrease in the superconductor phase. As the factor b becomes lager entanglement entropy in the mental phase decreases. In the condensation phase, it can be seen from the right diagram that the entanglement entropy increases monotonically for bigger b and this behavior of entanglement entropy is quite different from the results discussed in four-dimensional spacetime [49], where the entanglement entropy first increases and forms a peak at the threshold then decreases monotonically with increase of the BI parameter.

To get further understanding of the influence of the width \(\ell \) on the entanglement entropy in the superconductor phase, we plot the corresponding results in Fig. 3. For a given b, we find that the entanglement entropy becomes smaller as the temperature T gets lower. With the growth of the belt width \(\ell \) the value of the entanglement entropy s increases.

3.2 Entanglement entropy for operator \(\langle \mathcal {O}_{-}\rangle \)

The dependence of the entanglement entropy for operator \(\langle \mathcal {O}_{-}\rangle \) on the temperature and the BI factor is exhibited in Fig. 4. The vertical dotted lines represent the critical temperature of the phase transition for the different value of the BI factor. The dashed line is from the metal phase and the solid one is from the superconductor phase. In the left panel, the critical temperature of phase transition decreases as the BI parameter becomes bigger. Which indicates the scalar hair becomes harder to be formed as the nonlinearity in the electromagnetic field increases. We also find that there exists a jump of the slop of the entanglement entropy at the phase transition point . In the right panel, the behavior of the entanglement entropy of operator \(\langle \mathcal {O}_{-}\rangle \) as a function of the BI factor is similar to the case of the operator \(\langle O_{+}\rangle \). However , the effect of the BI factor on the entanglement entropy of operator \(\langle \mathcal {O}_{-}\rangle \) is weaker than the one of operator \(\langle \mathcal {O}_{+}\rangle \) . In Fig. 5, it is shown that the influence of the width \(\ell \) on the entanglement entropy is analogous to that of Fig. 3 where the entanglement entropy increases as the width \(\ell \) increases.

Fig. 5
figure 5

The entanglement entropy of the operator \(\langle O_{-}\rangle \) with respect to the temperature T for various widths \(\ell \) as \(b=0.4\). The red line is for \(\ell \sqrt{\rho }=1.1\), the blue line is for \(\ell \sqrt{\rho }=1.0\), and black one is for \(\ell \sqrt{\rho }=0.9\)

Full size image

4 Conclusion

In this paper, we calculated the holographic metal/ superconductor phase transition with BI electrodynamics in higher dimensional AdS spacetime. We first explored the properties of the phase transition of this system by analyzing the behaviors of the scalar operator and found that the value of the critical temperature \(T_c\) of the phase transition becomes smaller as the BI factor b increases. This means that the BI correction to the usual Maxwell field hinders the formation of the scalar hair. By comparing the effects of the BI parameter on the condensation, we observer that the effect of the BI factor on the condensation of operator \(\langle \mathcal {O}_{+}\rangle \) is more powerful than the one of operator \(\langle \mathcal {O}_{-}\rangle \). Instead of the probe limit, when taking the full-backreaction into consideration, we observed that the curves for two scalar operators has similar behaviors to the BCS theory for different BI factor. In addition, to further study the properties of the phase transition, we used holographic methods to explored the behavior of the entanglement entropy in the holographic model. For both operators \(\langle \mathcal {O}_{+}\rangle \) and \(\langle \mathcal {O}_{-}\rangle \) , the critical temperature \(T_c\) of the phase transition obtained from the behaviors of entanglement entropy is the same as the threshold temperature obtained from the behaviors of the scalar operator. And the discontinuous slop of the entanglement entropy at the critical temperature \(T_c\) corresponds to second order phase transition in this physical system. Consequently, the entanglement entropy is indeed a good probe to study the properties of the phase transition, and that its behavior can indicate not only the appearance, but also the order of the phase transition. Furthermore, the entanglement entropy of operator \(<\mathcal {O}_{+}>\) in the condensation phase increases monotonically for bigger b and this behavior of entanglement entropy is quite different from the results discussed in four-dimensional spacetime [49], in which the result of the entanglement entropy first increases and forms a peak at the threshold then decreases monotonically with increase of the BI parameter.