1 Introduction

The anti-de Sitter/conformal field theory (AdS/CFT) correspondence [1,2,3] has been widely used to study strongly coupled dynamics of material systems in recent years. One of the novel results of this correspondence is the holographic description of the phenomenon of superconductivity [4,5,6,7,8]. It has been shown that the holographic model constructed by the Einstein–Maxwell-charged scalar field theory with negative cosmological constant undergoes a phase transition from the gravity background with no hair to the state with scalar hair as one tunes the temperature for black hole or the chemical potential for AdS soliton. Another remarkable achievements of this correspondence is the establishment of the holographic entanglement entropy (HEE) whereby one can investigate the HEE of CFTs from the minimal area of the Ryu–Takayanagi (RT) surface [9, 10]. More specifically, consider a strongly couple field theory with gravity dual, the entanglement entropy of subsystem \(\mathcal {A}\) with its complement in the d-dimensional boundary is given by searching for the RT surface \(\gamma _{\mathcal {RT}}\) that extended into the (d+1)-dimensional bulk with the same boundary boundary \(\partial {\mathcal {A}}\) of a region \(\mathcal {A}\). Then the HEE of \(\mathcal {A}\) with its complement is given by

$$\begin{aligned} S_\mathcal {A}=\frac{Area(\gamma _{RT})}{4G_{d+1}}, \end{aligned}$$
(1)

where \(Area(\gamma _{RT})\) and \(G_{d+1}\) are the minimal area of the RT surface and the Newton constant in the Einstein gravity on the AdS space, respectively. A proof of this formula (1) from the basic principle of holographic duality is shown in [11] and further analysis of the HEE are discussed in [12,13,14,15,16,17,18,19,20,21,22].

After the realization of entanglement entropy from holography, the properties of the phase transition probed by the HEE has been extensively studied in various holographic models and some interesting behaviors have been observed [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. In particular, the authors of [23] presented the investigation of the HEE for a strip geometry in AdS black hole background. It was observed that the HEE in the superconductor phase is always less than the one in the metal case and there is a discontinuity in the slope of the HEE at a second order of phase transition. For the the AdS soliton background, the behavior of the HEE with respect to chemical potential is non-monotonic in the superconducting phase and the rich phase structure is obtained [25, 26]. Extending the exploration of the HEE to the higher derivative correction to the gauge field, in our previous work [42], we investigated the behaviors of the HEE with Born–Infeld electrodynamics in insulator/superconductor transition and observed that the HEE gets lager as the strength of the Born–Infeld electrodynamics increases in the condensed phase. In the metal/superconductor transition, the HEE in the metal phase decreases monotonously but its value in the superconducting phase first increases and forms a peak, then decreases continuously [43]. We also studied the effect of the exponential nonlinear electrodynamics on the HEE in [44, 45]. It was found that the HEE is a good probe to study the properties of the holographic superconductor phase transition. As a matter of fact, the logarithmic nonlinear electrodynamics (LNE), which appears in the description of vacuum polarization effects, indicates exact 1-loop corrections for electrons in a uniform electromagnetic field background [46] and has been an interesting subject for many years [47,48,49,50,51,52,53,54,55,56,57]. The Lagrangian of the LEN is in the form [58]

$$\begin{aligned} \mathcal {L}_{LNE}=-\frac{2}{b^2}\ln {\left( 1+\frac{1}{8}b^2F^2\right) }, \end{aligned}$$
(2)

where \(F=F_{\mu \nu }F^{\mu \nu }\) and \(F^{\mu \nu }\) is the electromagnetic field tensor. The coupling parameter b indicates the strength of the nonlinearity. When the parameter \(b\rightarrow 0\),the Lagrangian of the LEN \(\mathcal {L}_{LNE}\) obviously reduce to the standard Maxwell form \(\mathcal {L}=-\frac{1}{4}F^2\). Considering the holographic superconductor models with LNE, the authors of [59,60,61] found that the critical temperature of the phase transition and the the scalar operator depend on the nonlinear parameter b.

In this paper, we further explore the properties of the phase transition with LNE by analyzing the behavior of HEE both in the backgrounds of the AdS soliton and AdS black hole. We find that the LNE does not effect the critical chemical potential and HEE at the critical point \(\mu _c\) in the insulator/superconductor system. In the superconductor phase, however, the HEE becomes bigger as the strength of LNE increases and the non-monotonic behavior of the HEE with respect to chemical potential is universal for different LNE parameter b. Moreover, there exists the “confinement/deconfinement ”phase transition in this physical model. With the increase of the factor b, the critical width of the phase transition and the corresponding HEE get bigger. In the metal/superconductor system, we find that the critical temperature and the HHE at the phase transition point become smaller with the increase of LNE factor. Which means the LNE correction to the usual Maxwell field makes phase transition harder to happen in the full-backreaction model. Interestingly enough, the HEE decreases in the metal phase with the increase of the LNE factor while an inverse behaviour is obtained in the superconductor phase. Compare with the effects of the other types of nonlinear electromagnetic fields, i.e., the Born–Infeld nonlinear electrodynamics(BINE) [42, 43] and the exponential nonlinear electrodynamics(ENE) [44, 45] on the HEE, we observe that the HEE with LNE at the “confinement/deconfinement” phase transition point is the smallest among the three kinds of electromagnetic fields. In other words, for a given b the “confinement/deconfinement” phase transition is more difficult to happen in a model with LNE than that with the BINE and the ENE. In the AdS black hole background, the HEE of the LNE at the phase transition point is larger than that of the BINE and the ENE for fixed b. Which implies that the metal/superconductor phase transition is easier to occur in holographic dual model with LNE.

The framework of this paper is as follows. In Sect. 2, we study the effect of the LNE on the HEE in AdS soliton background. In Sect. 3, we extend our investigation to the HEE of the the phase transition with LNE in AdS black hole background. Finally, the conclusion and discussion are included in Sect. 4.

2 HEE in AdS soliton background with LNE

2.1 Basic field equations

The Lagrange density describing a charged complex scalar field and a gauge field coupled in the gravitational background reads [61]

$$\begin{aligned} \mathcal {L}=R+\frac{12}{L^2}-|\nabla _{\mu }\psi -iqA_{\mu }\psi |^2-m^2|\psi |^2+\mathcal {L}_{LNE}, \end{aligned}$$
(3)

where R and d are,respectively, the Ricci scalar and the dimensionality of the spacetime. L is the AdS radius which will be scaled unity in the following calculation. \(\psi \) and \(A_{\mu }\) are the gauge and scalar fields. q is the coupling factor between the gauge field and the complex scalar field and m is the mass of the scalar field. The term \(\mathcal {L}_{LNE}\) stands for the Lagrange density of the LNE theory.

Since we are interested in the fully backreacted holographic superconductor, we choose the meteic of the AdS soliton as follows [62]

$$\begin{aligned} ds^2 =\frac{dr^2}{r^2B(r)}+r^2\left[ -e^{C(r)}dt^2+dx^2+dy^2+e^{A(r)}B(r)d\chi ^2\right] ,\nonumber \\ \end{aligned}$$
(4)

in order to obtain a smooth geometry at the tip \(r_0\) satisfying \(B(r_0)=0\), there should be a period \(\Gamma \) on the coordinate \(\chi \)

$$\begin{aligned} \Gamma =\frac{4\pi e^{-A(r_0)/2}}{r_0^2B'(r_0)}, \end{aligned}$$
(5)

For simplicity, we consider the electromagnetic field and the scalar field in the form [5]

$$\begin{aligned} A_t=\phi (r),\ \ \psi =\psi (r). \end{aligned}$$
(6)

Employing the above ansatz, we can obtain the equations of motion as follows

$$\begin{aligned}&\psi ''+\left( \frac{5}{r}+\frac{A'}{2}+\frac{B'}{B}+\frac{C'}{2}\right) \psi '\nonumber \\&\quad +\frac{1}{r^2B} \left( \frac{e^{-C}q^2\phi ^2}{r^2}-m^2\right) \psi =0, \end{aligned}$$
(7)
$$\begin{aligned}&\left( 1+\frac{1}{4}b^2e^{-C}B\phi '^2\right) \phi ''+\left( \frac{3}{r}+\frac{A'}{2}\right. \nonumber \\&\quad \left. +\frac{B'}{B} -\frac{C'}{2}\right) \phi '-\frac{1}{4}b^2e^{-C}B\left( \frac{3}{r}\right. \nonumber \\&\quad \left. +\frac{A'}{2}+\frac{C'}{2} \right) \phi '^3\nonumber \\&\quad - \frac{2q^2\psi ^2}{r^2B}\left( 1-\frac{1}{4}b^2e^{-C}B\phi '^2\right) ^2\phi =0\;, \end{aligned}$$
(8)
$$\begin{aligned}&A'-\frac{1}{r(6+rC')}\left( 2r^2C''+r^2C'^2+4rC'\right. \nonumber \\&\quad \left. -\frac{4\left( \frac{1}{2}e^{-C}\phi '^2-r^2\psi '^2+\frac{1}{4}b^2e^{-C}B\phi '^2r^2\psi '^2\right) }{1-\frac{1}{4}b^2e^{-C}B\phi '^2} \right) =0, \end{aligned}$$
(9)
$$\begin{aligned}&\left( \frac{3}{r}-\frac{C'}{2}\right) B'+\left( \frac{12}{r^2}\right. \nonumber \\&\quad \left. -\frac{1}{2}A'C'+\frac{e^{-C}\phi '^2}{r^2(1-\frac{1}{4}b^2e^{-C}B\phi '^2)}+ \psi '^2\right) B \nonumber \\&\quad +\frac{1}{r^2}\left( \frac{e^{-C}q^2\phi ^2\psi ^2}{r^2}+m^2\psi ^2-12\right. \nonumber \\&\quad \left. +\frac{2\ln {\left( 1-\frac{1}{4}b^2e^{-C}B\phi '^2\right) }}{b^2}\right) =0, \end{aligned}$$
(10)
$$\begin{aligned}&\left. C''+\frac{1}{2}C'^2+\left( \frac{5}{r}+\frac{A'}{2}+\frac{B'}{B}\right) C'\right. \nonumber \\&\quad \left. -\left( \frac{\phi '^2}{1-\frac{1}{4}b^2e^{-C}B\phi '^2}\right. \right. \nonumber \\&\quad \left. +\frac{2q^2 \phi ^2\psi ^2}{r^2B}\right) \frac{e^{-C}}{r^2} =0, \end{aligned}$$
(11)

where prime denotes derivative with respect to r. In order to solve the coupled and nonlinear equations (7)–(11) by using the numerical approach, we should specify the boundary conditions for the system [8].

At the tip \((r=r_0)\), the above equations can be expand in the form

$$\begin{aligned}&\psi (r)=\psi _0+\psi _1(r-r_0)+\cdots ,\nonumber \\&\phi (r)=\phi _0+\phi _1(r-r_0)+\cdots ,\nonumber \\&A(r)=A_0+A_1(r-r_0)+\cdots ,\nonumber \\&B(r)=B_0(r-r_0)+B_1(r-r_0)^2+\cdots ,\nonumber \\&C(r)=C_0+C_1(r-r_0)+\cdots , \end{aligned}$$
(12)

there are only four independent parameters \(r_0\), \(\psi (r_0)\), \(\phi (r_0)\) and \(C(r_0)\). Taking the following useful scaling scaling symmetries into the consideration

$$\begin{aligned}&r\rightarrow \alpha r,\quad (\chi ,x,y,t)\rightarrow (\chi ,x,y,t)/\alpha ,\quad \phi \rightarrow \alpha \phi , \end{aligned}$$
(13)
$$\begin{aligned}&C\rightarrow C-2\ln {\beta },\quad t \rightarrow \beta t,\quad \phi \rightarrow \phi /\beta , \end{aligned}$$
(14)

we can adjust the solutions to satisfy \(r_0=1\) and \(C(r_0)=0\). At the spatial infinity \((r\rightarrow \infty )\), the boundary conditions are

$$\begin{aligned}&\psi \sim \frac{\psi _{-}}{r^{\Delta _{-}}}+\frac{\psi _{+}}{r^{\Delta _{+}}},\ \phi \sim \mu -\frac{\rho _q}{r^{2}},\nonumber \\&A\sim \frac{A_4}{r^4}+\cdots ,\ \ \ \ B\sim 1 +\frac{B_4}{r^4}+\cdots ,\ \ \ \ C\sim \frac{C_4}{r^4}+\cdots \nonumber \\ \end{aligned}$$
(15)

Where \(\mu \) and \(\rho _q\) are interpreted as the chemical potential and charge density in the dual theory respectively. \(\Delta _{\pm }=2\pm \sqrt{4+m^{2}}\) are the conformal dimensions of the operators. Considering the BF bound \(m^2_{BF}=-4\) [63, 64] ,we focus on the case of \(m^2=-\frac{15}{4}\) and \(q=2\) in this paper. According to the AdS/CFT correspondence, the coefficients \(\psi _{-}\) and \(\psi _{+}\) correspond to the vacuum expectation values \(\psi _{-}=<O_{-}>\) and \(\psi _{+}=<O_{+}>\) of an operator \(\hat{O}\) dual to the scalar field. To obtain a stable theory, we fix \(\psi _-\) = 0 and consider \(\psi _+\) acting as the vacuum expectation value of the operator \(\hat{O}_+\) in our following calculation.

2.2 Insulator/superconductor phase transition

In this section, we want to study the properties of the phase transition in AdS soliton background with LNE through the behaviors of the scalar operator. In Fig. 1, we present behaviors of condensate of the scalar operator \(\langle \hat{O}_+\rangle \) and the charge density \(\rho _q\) with LNE versus chemical potential \(\mu \) in cases of \(m^2=-\frac{15}{4}\) , \(q=2\) and \(\Gamma =\pi \). It can be seen in the left panel that the condensation of the operator \(\langle \hat{O}_+\rangle \) emerges as the chemical potential \(\mu >\mu _c\), which implies the superconductor phase appears. However, when \(\mu <\mu _c\), the system is described by the AdS soliton solution itself and the operator \(\langle \hat{O}_+\rangle \) vanishes. This can be identified as the insulator phase [8]. At the phase transition point where \(\mu =\mu _c\), it is clear from the right panel that the insulator/superconductor phase transition here is typically second order. Figure 2 shows the phase structure of scalar operator with LNE in the holographic insulator/superconductor model. It is interesting to observe that the critical chemical potential \(\mu _c\) dose not change as the nonlinearity parameter b increases. This means that the LNE has no effect on the critical chemical potential \(\mu _c\) of the holographic insulator/superconductor phase transition with the full backreaction.

Fig. 1
figure 1

The condensate of operator \(\langle \hat{O}_+\rangle \) (left plot) and the charge density \(\rho _q\) versus chemical potential \(\mu \) for different LNE parameter b. The four curves in the left panel from button to top correspond to increasing |b|, i.e., |b| = 0.0 (black), 0.4 (blue), 0.6 (red) and 0.8 (green) respectively

Full size image

2.3 Holographic entanglement entropy in insulator/ superconductor transition

In this section, we would like to study the effect of the LNE on the HEE in AdS soliton background. Since the choice of the subsystem \(\mathcal {A}\) is arbitrary, we can define infinite entanglement entropies accordingly. Concretely, we focus on a strip shape which corresponds to the subsystem \(\mathcal {A}\) described by \( -\frac{\ell }{2}\le x \le \frac{\ell }{2},~-\frac{R}{2}<y<\frac{R}{2}\,(R\rightarrow \infty ),\ \ 0\le \chi \le \Gamma \). For the purpose of dealing with the UV divergence, we assume that the subsystem \(\mathcal {A}\) sites on the slice where \(r=1/\epsilon \). Specifically, the holographic surface \(\gamma _\mathcal {A}\) starts from \(x=\frac{\ell }{2}\) at \(r=\frac{1}{\epsilon }\), extends into the bulk until it reaches \(r=r_*\), then returns back to the AdS boundary \(r=\frac{1}{\epsilon }\) at \(x=-\frac{\ell }{2}\), where \(\epsilon \rightarrow 0\) stands for the UV cutoff and \(\ell \) is defined as the size of region \(\mathcal {A}\).

Fig. 2
figure 2

The phase structure of scalar operator with LNE in AdS soliton background. The critical chemical potential of the insulator/superconductor phase transition is \(\mu _c\Gamma =2.9662\)

Full size image

According to the proposal (1), the HEE of the subsystem \(\mathcal {A}\) with its complement is proportional to the minimal area surface \(\gamma _\mathcal {A}\) in the bulk with the same boundary, i.e., \(\partial \gamma _\mathcal {A}=\partial \mathcal {A}\). Then the area of the holographic surface \(\gamma _\mathcal {A}\) can be described by

$$\begin{aligned} Area(\gamma _\mathcal {A})[x]=2R\Gamma \int _{r_*}^{\frac{1}{\epsilon }}re^{\frac{A(r)}{2}}\sqrt{1+r^4B(r)(dx/dr)^2}dr. \end{aligned}$$
(16)
Fig. 3
figure 3

The HEE s with respect to the chemical potential \(\mu \) for various factors. The left-hand figure is the case of \(\ell \Gamma ^{-1}=0.165\) with different LEN parameter b. The four curves in the figure from button to top correspond to increasing |b|, i.e., |b| = 0.0 (black), 0.4 (blue), 0.6 (red) and 0.8 (green) respectively. The right-hand figure is the case of \(|b|=0.4\) with various width \(\ell \). The three curves in the figure from button to top correspond to increasing \(\ell \), i.e., \(\ell \Gamma ^{-1}=0.165\) (green), 0.181 (red) and \(\infty \)(blue) respectively

Full size image

By employing the Euler–Lagrange variation method, the minimality condition is given by

$$\begin{aligned} \frac{dx}{dr}=\pm \frac{1}{r^2\sqrt{B(r)[\frac{r^6e^A(r)B(r)}{r_*^6e^A(r_*)B(r_*)}-1]}}, \end{aligned}$$
(17)

in which the turning point \(r_*\) satisfies the stationary condition \(\frac{dx}{dr}|_{r=r_*}\rightarrow \infty \). Integrating the Eq. (17) with respect to the variable r, we have

$$\begin{aligned} \int _{r_*}^{\frac{1}{\epsilon }}\frac{dx}{dr}dr =\pm \int _{r_*}^{\frac{1}{\epsilon }} \frac{1}{r^2\sqrt{B(r)[\frac{r^6e^A(r)B(r)}{r_*^6e^A(r_*)B(r_*)}-1]}}dr, \end{aligned}$$
(18)

notice that the left-hand side of the equation is equal to \(\ell /2\). Therefore, \(+\) is a physical symbols in our calculation. Substituting Eq. (17) into Eq. (16), the HEE can be deduced from Eq. (1) in z-coordinate as

$$\begin{aligned}&S_\mathcal {A}=-\frac{R\Gamma }{2G_N}\int _{z_{*}}^{r_0\epsilon }\nonumber \\&\quad \frac{r_0^2}{z^3}e^\frac{A(z)}{2} \sqrt{1-\frac{z^6B(z_*)e^{A(z_*)}}{z_*^6B(z)e^{A(z)}}}dz\nonumber \\&\qquad +\frac{R\Gamma \ell }{4G_N}\sqrt{\frac{1}{z^6}B(z)e^{A(z)})}r_0^3\nonumber \\&\quad =\frac{R\pi }{4G_N}\left( \frac{1}{\epsilon ^2}+s\right) , \end{aligned}$$
(19)

and the belt width is

$$\begin{aligned} \frac{\ell }{2}=-\int _{z_{*}}^{r_0\epsilon } \frac{1}{r_0 \sqrt{B(z)\left( \frac{z_*^6B(z)e^{A(z)}}{z^6B(z_*)e^{A(z_*)})}-1\right) }}dz, \end{aligned}$$
(20)

where \(z=\frac{r_0}{r}\) is a dimensionless coordinate. It should be noted that s is independent of the cutoff \(\frac{1}{\epsilon }\) and is physical important. According to the discussion in section A, the physical quantities under the scaling symmetry Eq. (13) scale as

$$\begin{aligned}&\Gamma \rightarrow \frac{1}{\alpha }\Gamma , \qquad \mu \rightarrow \alpha \mu , \nonumber \\&\quad s\rightarrow \alpha ^2s,\qquad \ell \rightarrow \frac{1}{\alpha }\ell , \end{aligned}$$
(21)

Therefore, to study the physics, we will introduce the useful dimensionless quantities

$$\begin{aligned} \mu \Gamma ,\qquad s\Gamma ^2,\qquad \ell \Gamma ^{-1}. \end{aligned}$$
(22)

Now we are in position to study the behavior of HEE s in the insulator/ superconductor transition. In Fig. 3, we plot the HEE versus the chemical potential \(\mu \) for various factors. The left panel is the case of \(\ell \Gamma ^{-1}=0.165\) with different LEN parameter b and the right panel presents the case of \(b=0.4\) with various width \(\ell \). From the picture, we see that the threshold chemical potential \(\mu _t\Gamma =2.9662\) shown by the vertical dotted purple line is equal to the critical phase transition point \(\mu _c\Gamma =2.9662\) obtained from the behavior of the scalar operator in Fig. 2. This implies that the HEE can be used to probe the critical point of phase transition. The discontinuity in the slope of the HEE at \(\mu _c\) signals the some kind of new degrees of freedom like the Cooper pair would emerge and the phase transition is second order. Before the phase transition, the HEE presented by the horizontal dotted lines stay the same as the chemical potential changes. This is due to the fact that the system is described by the AdS soliton solution itself as the scalar field disappears, which can be interpreted as the insulator phase [8]. When \(\mu >\mu _c \), we observe that the behavior of HEE indicated by the solid curves with respect to the chemical potential is nontrivial. Explicitly, the HEE first rises and arrives its maximum at a certain value of chemical potential denoted as \(\mu _{max}\) with the increase of the factor \(\mu \), then decreases monotonously. That means the number of degree of freedom in the system first increases then reduces due to the condensation formed in the phase transition [27].

Considering the effect of the factor b on the HEE, it can be seen from the left panel of Fig. 3 that the HEE in insulator phase is independent of the LEN. Interestingly, the HEE in the superconductor phase becomes larger as the nonlinear parameter b increases, which corresponds to more degree of freedom in this system. Moreover, the value of \(\mu _{max}\) also increases as the factor b increases. For the critical chemical potential \(\mu _c\), note that, its value is a constant as the parameters b changes and this finding is consistent with the result in the picture of Fig. 2. That is, the LNE does not have any effect on the critical point of the phase transition in the system. As fixed b, in the right diagram of Fig. 3, we find that the HEE in the insulator and superconductor phases increases as the belt width increases.

Particularly, as can be seen from the right panel of Fig. 3 that the HEE approaches a certain value as the strip width increases to infinity for a given chemical potential. This indicates that there exists a critical width \(\ell _c\), at which the value of the HEE begins to be a constant. For clarity, we plot the behavior of the HEE versus the strip width by fixing the chemical potential for different strengths of the LNE in Fig. 4. The vertical dashed lines denote the value of the critical width \(\ell _c\) for various LEN parameter, the solid curves show the results of the connected geometry and the horizontal dotted curves denote the disconnected ones. Since the physical entropy is determined by the choice of the lowers one, it can be seen from the diagram that the physical favored result comes from the disconnected configuration as \(\ell >\ell _c\) for fixed b and the HEE is independent of the factor \(\ell \). When \(\ell <\ell _c\), the disconnect solution is not favored because its value is bigger than the one for the connect surface and in this case with the decrease of the belt strip the HEE decreases. The jump of the slope of the HEE at \(\ell =\ell _c\) indicates a phase transition occurs which is just the so-called “confinement/deconfinement” phase transition [65,66,67]. Furthermore, the critical width has nontrivial dependence on the strength of the nonlinearity in the LNE. That is, with the increase of the nonlinearity in the LNE the value of the critical width increases.

From above discussion, it can be concluded that there are totally four phases probed by the HEE for this holographic system, that is, the insulator phase, the superconductor phase, and their corresponding confinement/deconfinement phases. For the sake of clarity, we plot the picture to display the phase diagram of the holographic superconductor model in Fig. 5. Obviously, the insulator phase and the superconductor phase are separated by the purple vertical dashed line and the phase boundary between the confinement phase and the deconfinement phase is separated by the horizontal dashed line and the solid curve. In the insulator phase, we see that no matter what the value of b is, the critical belt width \(\ell _c\) of the confinement/deconfinement phase transition will not change. However, as the nonlinear parameter b increases, the critical width \(\ell _c\) in the superconductor phase becomes lager. Furthermore, we note that the width \(\ell _c\) has a non-monotonic change as the chemical potential increases. which is due to the fact that the HEE is not monotonic function of the chemical potential in the holographic superconductor model.

Fig. 4
figure 4

The HEE with respect to the strip width \(\ell \) for different parameter b with \(\mu \Gamma =6.9165\). The four curves from button to top correspond to increasing |b|, i.e., |b| = 0.0 (black), 0.4 (blue), 0.6 (red) and 0.8 (green) respectively. The corresponding critical widths are \(\ell _c\Gamma ^{-1}=0.2109\), \(\ell _c\Gamma ^{-1}=0.2122\), \(\ell _c\Gamma ^{-1}=0.2139\), \(\ell _c\Gamma ^{-1}=0.2164\), respectively

Full size image
Fig. 5
figure 5

The phase diagram of the HEE in the AdS soliton background with LNE field. The four curves from button to top correspond to increasing |b|, i.e., |b| = 0.0 (black), 0.4 (blue), 0.6 (red) and 0.8 (green) respectively

Full size image

3 HEE in AdS black hole background with LNE

3.1 Basic field equations

Since the HEE is a powerful tool to probe the properties of the insulator/ superconductor phase transition with LNE, in this section, we will extend our study of the HEE with LNE to the AdS black hole background. Tacking the full backreaction of the spacetime into account, the ansatz of the metric of the AdS black hole is

$$\begin{aligned}&ds^2=-f(r)e^{-\chi (r)}dt^{2}+\frac{dr^2}{f(r)}+r^{2}(dx^2+dy^2+d\rho ^2), \end{aligned}$$
(23)
Table 1 The results of the critical electric charge \(Q_c\) with different values of the LNE parameters b. Here, we set \(m^2=-\frac{15}{4}\),\(q=2\) and \(r_{+}=1\)
Full size table

The Hawking temperature of this black hole which will be interpreted as the temperature of the CFT reads

$$\begin{aligned} T_{H}=\frac{f^{\prime }(r_{+})e^{-\chi (r_{+})/2}}{4\pi }. \end{aligned}$$
(24)

where \(r_+\) is the horizon of the black hole. For simplicity, we consider the matter fields in the forms

$$\begin{aligned}&A=\phi (r)dt,~~\psi =\psi (r). \end{aligned}$$
(25)

We can obtain the following equations of motion

$$\begin{aligned}&\psi ^{\prime \prime }+\left( \frac{d-2}{r}-\frac{\chi ^{\prime }}{2}\right. \nonumber \\&\quad +\left. \frac{f^\prime }{f}\right) \psi ^\prime +\frac{1}{f}\left( \frac{q^{2}e^{\chi }\phi ^2}{f}-m^2\right) \psi =0, \end{aligned}$$
(26)
$$\begin{aligned}&\left( 1+\frac{1}{4}b^2e^{\chi }\phi '^2\right) \phi ^{\prime \prime }\nonumber \\&\quad +\left( \frac{d-2}{r}+\frac{\chi ^{\prime }}{2}\right) \phi ^\prime \nonumber \\&\quad + \frac{b^2e^{\chi ^{\prime }}(4-2d+r\chi ')}{8r} \phi '^3\nonumber \\&\quad - \frac{2q^{2}\psi ^{2}\left( 1-\frac{1}{4}b^2e^{\chi }\phi '^2\right) ^2}{f}\phi =0, \end{aligned}$$
(27)
$$\begin{aligned}&\chi ^{\prime }+\frac{2r}{d-2}\left( \psi ^{\prime 2}+\frac{q^{2}e^{\chi }\phi ^{2}\psi ^{2}}{f^{2}}\right) =0, \end{aligned}$$
(28)
$$\begin{aligned}&f^{\prime }+\frac{r}{d-2} \left( \left( m^{2}+\frac{q^{2}e^{\chi }\phi ^{2}}{f}\right) \psi ^2\right. \nonumber \\&\quad +f\psi ^{\prime 2}+\frac{b^2e^{\chi }\phi '^2+2\left( 1-\frac{1}{4}b^2e^{\chi }\phi '^2\right) \ln {\left( 1-\frac{1}{4}b^2e^{\chi }\phi '^2\right) }}{b^2\left( 1-\frac{1}{4}b^2e^{\chi }\phi '^2\right) } \nonumber \\&\quad -\left( \frac{(d-1)r}{L^2}-\frac{(d-3)f}{r}\right) =0 \end{aligned}$$
(29)

where the prime denotes the derivative with respect to r.

Applying the shooting method, we can obtain the numerical solutions to the equations of motion by integrating them from the horizon out to the infinity. At the event horizon \(r_+\) of the black hole, the boundary conditions are

$$\begin{aligned} \phi (r_+)=0,\quad f(r_+)=0, \end{aligned}$$
(30)

and at the asymptotic AdS boundary (\(r\rightarrow \infty \)), the solutions behave like

$$\begin{aligned}&\chi \rightarrow 0\,, f\sim r^2, \phi \sim \mu -\frac{Q}{r^{2}}\,,\nonumber \\&\quad \psi \sim \frac{\psi _{-}}{r^{\Delta _{-}}} +\frac{\psi _{+}}{r^{\Delta _{+}}}\,. \end{aligned}$$
(31)

where \(\Delta _{\pm }=2\pm \sqrt{4+m^{2}}\). \(\mu \) is interpreted as the chemical potential and Q plays the role of electric charge of the black hole [68]. Just as in the model of AdS solition, we also set \(\psi _{-}=0\) and use the operator \(\psi _{+}=\langle \psi _{+} \rangle \) to describe the scalar condensation in the dual CFT. From the equations of motion for the system, we can obtain the useful scaling transformations

$$\begin{aligned}&r\rightarrow \alpha r,\qquad (x,y,t)\rightarrow (x,y,t)/\alpha ,\nonumber \\&\quad \phi \rightarrow \alpha \phi ,\qquad f\rightarrow \alpha ^2f, \end{aligned}$$
(32)

where \(\alpha \) is a positive number. By using the transformations Eq. (32), we can set \(r_+=1\). And in the following calculation, we will present our results in terms of dimensionless quantities.

Note that, the background reduces to the Reissner–Nordstrom (RN)AdS black hole when the LNE factor tends to be zero. For the RN AdS black hole, there is an upper bound of electric charge \(Q_c\) contained inside the black hole, which implies the phase point of the black hole. As \(Q>Q_c\), the background will become unstable [69]. By using the numerical calculation, the \(Q_c=0.0123\) for the factors \(q=1,m^2=0,\kappa =1\) and \(r_{+}=0.1\), which is consistent with the result in [68]. When we take the LNE into the consideration, it can be seen from the Table 1 that the critical electric charge becomes bigger as the LNE factor increases, which indicates that the the stability of the background is kept well with stronger nonlinearity in the LNE field.

3.2 Metal/superconductor phase transition

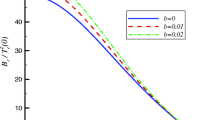
The behaviors of the metal/superconductor phase transition with LNE is shown in Fig. 6. From the left plot, we note that the operator \(\langle \mathcal {O}_{+}\rangle \) emerges at critical temperature \(T_c\), which implies the phase transition appears. The critical behavior near \(T_c\) is found to be \(\langle \mathcal {O}_{+}\rangle \varpropto (1-T/T_c)^{\frac{1}{2}}\). This shows that the transition is second order. Moreover, the curves for the scalar operators has similar behaviors to the BCS theory for different LNE factor, where the condensation goes to a constant at zero temperature. In the right plot, we find that the value of the critical temperature \(T_c\) decreases as the LNE factor b becomes bigger, which means that the LNE correction to the usual Maxwell field makes the scalar hair harder to form in the full-backreaction model. As the factor b approaches to zero, our result is consistent with the result in Ref. [6].

Fig. 6
figure 6

The operator \(\langle \hat{O}_+\rangle \) with respect to the temperature T for different LNE parameter b (right plot). The black line is for \(|b|=0.0\), the blue line is for \(|b|=0.4\) , the red line is for\(|b|=0.6\), and green line is for \(|b|=0.8\). The right plot presents the phase structure of scalar operator with LNE in AdS black hole background

Full size image
Fig. 7
figure 7

The HEE with respect to the temperature T for different parameters b and \(\ell \). In left panel,the black line is for \(|b|=0.0\), the blue line is for \(|b|=0.4\) , the red line is for\(|b|=0.6\), and green line is for \(|b|=0.8\). The three curves in the right figure from button to top correspond to increasing \(\ell \), i.e., \(\ell Q^{1/3}=0.9 \) (black), 1.0 (blue) and 1.1 (red) respectively

Full size image

3.3 Holographic entanglement entropy in metal/superconductor transition

In this section, we focus on the discussion by exploring the influence of the LNE on the HEE in AdS black hole. The HEE for a strip shape corresponding to a subsystem \(\mathcal {A}\) is described by a finite width \(\ell \) along the x direction and infinitely extending in y and \(\rho \) directions. According to the Eq. (1), we need to minimize the following function

$$\begin{aligned} S_\mathcal {A}[x]=\frac{V}{2G_5}\int _{\epsilon }^{z_*} \frac{1}{z^4}\sqrt{\frac{1}{f(z)}+z^2(dx/dz)^2}dz, \end{aligned}$$
(33)

where \(V=\int dyd\rho \). The parameter \(\epsilon \) is the UV cutoff and \(z_{*}\) satisfies the condition \(dr/dx|_{r=r_*}=0\) with \(z_{*}=1/r_*\). Noting that the above expression can be treated as the Lagrangian with x direction thought of as time. Therefore, we can deduce the equation of motion for the minimal surface from Eq. (33)

$$\begin{aligned} \frac{dx}{dz}=\int ^{z_{*}}_{\varepsilon }dz\frac{z^{3}}{\sqrt{(z^{6}_{*}-z^{6})z^{2}f(z)}} \end{aligned}$$
(34)

Substituting the Eq. (34) into the Eq. (33), we finally obtain the HEE \(S_\mathcal {A}\) as

$$\begin{aligned} S_\mathcal {A}= & {} \frac{V}{2G_5}\int ^{z_{*}}_{\varepsilon }dz\frac{z_{*}^{3}}{z^{2}} \frac{1}{\sqrt{(z^{6}_{*}-z^{6})z^{2}f(z)}}\nonumber \\= & {} \frac{V}{4G_5}\left( \frac{1}{\varepsilon ^2}+s\right) \end{aligned}$$
(35)

and the width \(\ell \) is

$$\begin{aligned} \ell= & {} \int _{-\frac{\ell }{2}}^{\frac{\ell }{2}}dx = 2\int _{\epsilon }^{z_*}\frac{dx}{dz}dz\nonumber \\= & {} 2\int ^{z_{*}}_{\varepsilon }dz\frac{z^{3}}{\sqrt{(z^{6}_{*}-z^{6})z^{2}f(z)}}. \end{aligned}$$
(36)

Note that the first term \(1/\varepsilon \) is divergent as \(\varepsilon \rightarrow 0\). However, the second term s dose not depend on the cutoff and is finite, so it is physical important.

The HEE with respect to the temperature T for various factors b and \(\ell \) is presented in Fig. 7. From the picture, we find that there is a jump in the slope of HEE at the critical point \(T_c\) denoted by the vertical dotted curves, which is similar to the case we discussed in the above section II where the the HEE for the insulator/superconductor phase transition has been studied in detail. Considering the in influence of the LNE, it is interesting to note that the HEE at \(T_c\) becomes lower as the LNE factor b increases. Moreover, a lager b corresponds to a smaller \(T_c\) which is consistent with the results obtained from the scalar operator in the right-hand graph of Fig. 6. And the value of the critical temperature \(T_c\) for different b obtained from the behaviors of HEE is equal to the phase transition point obtained from the behaviors of the scalar operator. That is to say, the HEE can probe not only the the order of phase transition but also the point of the phase transition. After the condensate, the HEE denoted by the solid curves are lower than the ones in the metal phases represented by the dot-dashed lines and decreases monotonously as temperature decreases. Which indicates the number of degree of freedom in the system reduces due to the condensation formed after the phase transition. For a given temperature T, the HEE in the superconductor phase becomes bigger with the increase of the factor b. This means the stronger the LNE correction is, the more the degrees of freedom will emerge. In the metal phase, however, the HEE decreases as the LEN parameter increases.

In the right panel, as the LNE parameter is fixed, we observe that the phase transition temperature is independent of the belt width \(\ell \). This indicates that the width of the belt geometry configuration has no effect on the critical point of the metal/superconductor phase transition. Interestingly, the value of the HEE at the phase transition point increase as the width increases which is quite different from the effect of the LNE factor presented in the left panel. We also note that the discontinuity in the slope of the HEE at the critical point still holds for different \(\ell \). Both in normal phase and superconductor phase, it can be seen from the picture that the HEE become lower as the width gets smaller.

4 Conclusion

We have investigated the behaviors of the HEE in holographic superconductor model with LNE both in the backgrounds of the AdS soliton and AdS black hole. We observed that the HEE is a good tool to probe the properties of the phase transition and its behavior can indicate not only the appearance but also the order of the phase transition.

In the AdS soliton background, by calculating the HEE for a belt geometry in the insulator/superconductor transition, we noted that the HEE has a discontinuous change in its slope at the phase transition point. Which means some kind of new degrees of freedom like the Cooper pair would emerge and the phase transition is second order. Above the critical point, the HEE in the superconductor phase first rises and then decreases monotonously as the chemical potential becomes lager. When taking the strength of the LEN into consideration, we found that the nonlinear parameter has no effect on the critical chemical potential and the HEE in the insulator phase. In the hair phase, with the increase of the LEN the HEE increases. Furthermore, the confinement/deconfinement phase transition occurs at the critical width in both the insulator phase and superconductor phase. And the critical width of the confinement/deconfinement phase transition gets bigger as the LEN factor increases. In the superconductor phase, the non-monotonic behavior of the critical width with respect to the chemical potential is similar to the case of the HEE.

Extending our study into the AdS black hole background, we observed that the HEE is sensitive to the LEN. Specifically, at the phase transition point, the bigger strength of the LNE corresponds to the smaller HEE. In the metal phase, the HEE decreases as we choose a larger LNE factor. However, the behavior of the HEE in the superconductor phase is quite different from the case in the normal phase. With the increase of the strength of the LEN the value of the HEE becomes bigger, which means the stronger the LNE correction is, the more the degrees of freedom will emerge. In addition, it is worth noting that the slope of the the HEE is discontinuous at transition point. Which means that, similar to the case in insulator/superconductor phase transition, the HEE can be used to probe the order of the phase transition in our general superconductor models with LEN. In other words, the discontinuity in the slope of the HEE at the phase transition point may be a general feature for the second order phase transition.